不同板宽的孔边的应力集中问题

合集下载

中心开小孔的平板孔边应力情况

中心开小孔的平板孔边应力情况说起平板上打小孔，很多人可能第一反应是：这事儿不就是在板子上戳个洞嘛，有啥难的。

嗯，确实，这个动作看起来简单，但是一旦我们把目光放到“应力”上，那就有点复杂了，嘿嘿，不是你想象的那种简单事儿。

在平板上打个小孔，尤其是孔的边缘，它的“应力情况”可不容小觑，稍微不注意，整个板子的稳定性可能就会大打折扣，得不偿失呀。

我们得知道，孔边的应力分布就像是“张扬的孩子”，它总是容易“跑偏”。

尤其是中心开小孔这种情况，孔周围的材料就像是被“压得喘不过气来”一样，四周的应力是特别集中的。

这种集中应力的情况，一旦板子承受不住，就可能会发生裂纹扩展，最后直接导致整个板子的断裂。

想象一下，如果一个平板就像一块饼干，给它中间戳个洞，那么剩下的部分不就特别容易碎吗？可不是嘛，整个结构的“抗压能力”就大大减弱了。

你说得了，怎么能这么脆弱呢？咱们做过力学课的朋友应该知道，材料的力学性能可不是一成不变的，尤其是边缘区域，它最容易“脆弱”。

因为，孔边缘就是应力集中的地方，力都在这儿堆积，哪怕孔的大小只有个头盖那么小，压力可一点也不小。

想象一下，当你给一块铁板打个小孔时，它周围的分子简直就像是在争先恐后地进行“最后一搏”，承受的压力往往是比其他地方要大得多。

就像你试图把气球吹得越来越大，气球表面会有一种“微妙”的膨胀感，到了极限，不就是爆炸嘛，和孔边的应力有异曲同工之妙。

更有意思的是，这个“集中应力”可不是每次都乖乖地呆在一个地方，它们是会随着板材的形状、材料的不同而变化的。

有的板子可能因为本身材质的强度比较高，导致孔边的应力集中比较少；而有的板子可能会因为某些微小的瑕疵，导致应力集中更严重。

这就像是你有时站在地铁里，一会儿被挤到这个方向，一会儿又被推到那个方向，搞得你晕头转向，根本没法放松。

那么问题来了，既然孔边的应力这么麻烦，咱们该如何应对呢？科学家和工程师早就给出了不少办法。

一个常见的技巧就是：孔的边缘不要太尖锐，最好是做个圆弧形的过渡。

带孔无限大板的应力集中问题浅析

带孔无限大板的应力集中问题浅析1 问题的提出带孔板件是工程中常用结构件,在航空工业中也广为应用。

带孔板件孔边存在小范围的高应力区。

根据板件宽度和孔径的相对比例,孔边最大应力水平可为板件远场(即远离孔边的区域)应力的几倍甚至十几倍;板件宽度和孔径之比越小,孔边最大应力越大。

这个现象被称为“应力集中”,通常定义孔边最大应力与板件远场应力之比为应力集中系数,以此来标示应力集中的程度。

由于孔边的高应力水平,带孔板件在承受较小载荷的情况下,孔边应力集中区域很可能已经产生塑性变形,带孔板件的破坏,包括静载下的破坏和疲劳破坏,通常是从带孔板件孔边应力集中区域萌生的。

因此,孔边的应力集中在很大程度上影响了构件的承载能力,进而损害了结构(件)的可靠性,是工程设计中需要重视的关键问题之一。

板件几何中心点为坐标原点,水平方向为坐标x方向,垂直方向为y方向。

孔心即为坐标原点。

根据弹性力学理论,带孔无限大板受y方向的均布应力,孔边的应力集中系数的基尔斯解答为:(1)(2)由上式可见,孔边最大应力集中系数Kx,max=3,特别应该强调指出的是,该应力集中系数不随孔径的变化而变化。

在弹性力学的理论框架内,这是学习弹性力学时应建立的基本概念。

但是,我们可以做这样的设想:对于无限大板,随着孔的缩小,孔边应力集中系数始终保持不变;当孔不断缩小,乃至于无限缩小,即孔径无限小,孔边应力集中系数还保持不变吗？很显然,当孔径无限小乃至等于零时,即没有孔的情况,板蜕变成完好的连续介质板,所谓的孔边应力集中现象也随之消失！是不是在孔缩小的过程中,孔边应力集中系数始终不变,无论孔径趋于多么小,而当孔径为零的时候,应力集中系数也突然变为零？毫无疑问,这样的物理过程——即孔不断缩小及孔边应力集中系数的相关变化的过程——并不符合逻辑。

2 有限元分析基于上面的讨论,作者利用有限元计算,对带孔无限大板孔边应力集中系数是否随孔径变化而变化这个问题,进行初步探讨。

孔边导角对开孔方形平板的应力集中理论解析

孔边导角对开孔方形平板的应力集中理论解析1. 理论背景开孔方形平板是一种常见的工程结构，在实际应用中常会遇到开孔边缘导角的情况。

研究开孔边缘导角对平板应力分布的影响，对于设计和优化结构具有重要意义。

2. 应力集中的原因开孔边缘导角会导致应力集中的现象。

在开孔边缘的导角处，弯曲变形和剪切变形将引起较大的应力集中。

3. 应力分析3.1 面内应力分析根据平面应力理论，考虑平板表面上的应力分量σx、σy和剪应力τxy，可以通过应力函数法等方法求解。

3.2 应力集中系数应力集中系数是描述应力集中程度的一个参数。

对于开孔边缘导角的方形平板，可以采用斯特拉斯解析法或有限元分析来计算应力集中系数Kt。

3.3 裂纹尖端应力分析对于已有裂纹的开孔边缘导角方形平板，可以采用线弹性力学理论进行裂纹尖端应力分析，计算应力强度因子K。

4. 影响因素4.1 开孔尺寸开孔尺寸对应力集中影响较大。

较小的开孔尺寸往往会引起更大的应力集中，进而降低结构的强度。

4.2 导角角度导角角度越小，应力集中越小。

大角度的导角将导致应力集中系数增加，进而削弱结构的强度。

5. 应力集中缓解方法为减小应力集中效应，可以采取以下方法：5.1 圆角缓和法在开孔边缘导角处增加合适的圆角，能够减小应力集中。

合理的圆角尺寸能够降低应力集中系数，从而提高结构的强度。

5.2 加固加强通过在开孔边缘导角处添加加固结构，如加强筋或加固片，可以显著减小应力集中。

5.3 材料选择在设计中选择具有良好韧性和抗拉强度的材料，能够有效减轻应力集中效应，提高结构的抗拉强度。

6. 实际案例以飞机结构为例，飞机机翼翼缘开孔处由于需满足动力特性和减重要求，常会出现开孔边缘导角，对于该种结构，深入分析应力集中情况，有效解决应力集中问题，对于保障飞行安全至关重要。

总结：开孔边缘导角对于开孔方形平板的应力集中有较大影响。

通过采用理论解析方法和有限元分析工具，可以对开孔边缘导角的平板进行应力集中分析，从而有效解决应力集中问题。

孔边导角对开孔方形平板应力集中问题的解析探究

孔边导角对开孔方形平板应力集中问题的解析探究引言：开孔方形平板在工程应用中非常常见，而孔边导角是一种常用的解决孔洞周边应力集中问题的方法。

本文旨在探究孔边导角对开孔方形平板应力集中问题的解析，并分析其优势和适用范围。

一、孔边导角的定义和作用孔边导角是指在开孔结构中，通过对孔洞边缘进行设计和处理，以减小或消除由孔洞引起的应力集中现象。

其主要作用在于改善结构的强度和耐久性，并提高结构的疲劳寿命。

二、孔边导角的原理与机制孔边导角通过改变孔边缘的几何形状和拉伸区域，使应力分布更加均匀，降低应力集中。

具体来说，孔边导角可以分为两个方面的效应：1. 几何效应：通过添加导角，增加孔洞周围的拱形区域，使应力场更加平缓，减少应力集中。

2. 拉伸效应：导角的形状可以改变孔洞周围材料的受力状态，使得应力场分布更加均匀，减小应力集中。

三、导角形状对应力集中的影响导角形状对应力集中的影响是一个重要的研究方向，常见的导角形状包括圆角、梯形、V型等。

以下是几种常见导角形状的特点和适用范围的分析：1. 圆角导角：圆角导角适用于一般应力集中问题，其拱形设计可以有效分散应力，减小应力集中的程度。

2. 梯形导角：梯形导角适用于孔边缘强度较低的情况，其逐渐变宽的设计可以缓解应力集中。

3. V型导角：V型导角适用于高应力集中问题，其尖锐的V型设计可以提供更大的拱形区域，明显降低应力集中。

四、孔边导角的优势和应用范围孔边导角的优势主要体现在以下几个方面：1. 改善结构强度和耐久性：孔边导角可以降低应力集中，使结构在受力时更加均匀，提高结构的强度和耐久性。

2. 延长结构的使用寿命：通过减小应力集中，孔边导角可以延长结构的使用寿命，减少结构的疲劳损伤和断裂风险。

3. 降低结构的重量和成本：采用合理的孔边导角可以减小结构的应力集中程度，降低结构的重量和成本。

孔边导角的应用范围广泛，适用于各类开孔结构，包括但不限于：航空航天器、汽车工程、机械结构等。

孔边应力集中的有限元分析

孔边应力集中的有限元分析
什么是孔边应力集中？孔边应力集中是指在多孔材料中，由于接触及材料性能不均匀，在接口连接处，特别是在毛细孔处，会出现本来不存在的高应力，有时它的值会超过孔内应力的数倍，也就是说会出现应力的集中。

孔边应力集中问题对许多领域有潜在的重要影响，其最明显的表现为孔边破坏，干涉，腐蚀破坏等破坏及形变。

有限元分析可以有效地准确评估单位孔边应力情况，并及时发现任何可能出现的不良情况。

有限元分析是利用计算机综合运算能力，运用有限元素方法建立数学模型，分析结构、材料或器件的状态和性能的一种技术。

有限元分析可以用来解决复杂的工程结构的力学性能的分析，尤其是在孔边应力集中问题上，有限元分析可以提供有效的方法来准确评估孔边应力。

首先，应当正确确定孔边结构及尺寸，并建立孔边应力集中分析所需的网格几何模型，分析过程将网格结构由混凝土体素切割成一系列有限元，然后计算出孔边应力。

计算结果取决于估算的应力边界条件，及在计算中所使用的材料及结构性能参数，例如混凝土的弹性模量，泊松比，孔的容积比等。

此外，当孔边应力集中发生时，有限元分析可以进一步验证材料应力是否达到应力破坏极限，以判断结构的安全及可靠性。

此外，如果使用了可满足特殊要求的新材料，在分析过程中，同时可以更换材料参数，虚拟试验其孔边应力集中性能。

最后，孔边应力集中分析中，有限元分析可以更精确，更准确地反映孔边结构，进而提供更准确及准确的孔边应力集中情况，从而更加有效地评估结构的安全及可靠性。

总之，有限元分析是解决孔边应力集中问题的一种有效方法。

它能够提供准确的孔边应力能够更加准确的评估结构的安全及可靠性，指导工程设计与实施。

应力集中产生的原因及后果

应力集中产生的原因及后果《应力集中产生的原因》你知道吗？在我们的生活中，很多东西都会出现应力集中的现象。

那到底为啥会这样呢？比如说一根细细的铁丝，要是上面有个小缺口，那这个缺口的地方就容易出现应力集中。

这是因为缺口改变了铁丝原本均匀的受力状态。

就好像一群小朋友整齐地排队往前走，突然有个小朋友跑开了，队伍就乱了，受力也就不均匀啦。

再比如一块木板，要是有个钉眼儿，那钉眼儿周围就可能应力集中。

这就好比一个完整的大家庭，突然少了一个人，整个家庭的结构和平衡就被打破了。

还有啊，零件的形状突变也会导致应力集中。

像那种有尖角或者突然变细的地方，力就容易在这儿扎堆。

就像我们走在路上，遇到一个急转弯，大家都容易往那个弯挤过去。

材料内部的缺陷也是原因之一。

如果材料里面有小气泡或者小裂缝，那在受力的时候，这些地方就会特别脆弱，应力也就集中在这儿了。

这就好像一个班级里，如果有几个同学总是捣乱，那老师的注意力就会集中在他们身上。

应力集中的产生往往是因为物体的结构、形状或者内部的不完美，导致了力的分布不均匀。

《应力集中产生的原因》咱们今天来聊聊应力集中是咋产生的。

再比如说，一张纸，你把一个角折起来，然后去拉这张纸，是不是折角的地方就很容易破？这也是应力集中。

那个折角就相当于受力的薄弱点。

还有那种有很多孔的铁板，孔的边缘就是应力容易集中的地方。

就好像一群人在排队，中间空了几个位置，这几个空位置周围的人就会感觉比较挤，力也就集中在这儿了。

另外，如果材料本身质量不好，有杂质或者不均匀，也会导致应力集中。

好比一群小伙伴一起跑步，有的人身体强壮，有的人身体虚弱，那虚弱的人就容易跟不上队伍，成为问题所在。

所以啊，应力集中的产生，要么是结构上有缺陷，要么是材料本身有问题。

《应力集中产生的原因》朋友，你知道应力集中是怎么来的不？还有啊，一块钢板，如果上面有个凹槽，当受到外力时，凹槽处就会承受更多的力，就像一个班级在拔河，突然有几个同学松手了，剩下的同学就会感到压力更大。

102024_圆孔的孔口应力集中公式详细推导

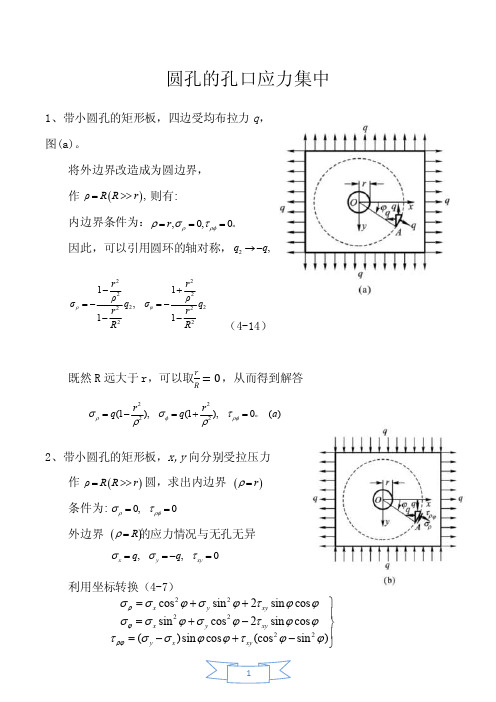
圆孔的孔口应力集中1、带小圆孔的矩形板，四边受均布拉力q ，图(a)。

将外边界改造成为圆边界，作则有: 内边界条件为：因此，可以引用圆环的轴对称，且 R ＞＞r ，得应力解答（4-14）既然R 远大于r ，可以取rR=0，从而得到解答2、带小圆孔的矩形板，x,y 向分别受拉压力作圆，求出内边界条件为:外边界的应力情况与无孔无异利用坐标转换（4-7）(),ρR R r =>>,,0R q ρρφρστ===。

,0,0r ρρφρστ===。

2,q q →-222222222211,11ρυr r ρρσq σq r r R R-+=-=---2222(1(1),0 ()r r q q a ρφρφσστρρ=-=+=。

()ρR R r =>>()r ρ=0,0ρρφστ==()R ρ=,,0x y xy q q σστ==-=222222cos sin 2sin cos sin cos 2sin cos ()sin cos (cos sin )x y xy x y xy y x xy ρϕρϕσσϕσϕτϕϕσσϕσϕτϕϕτσσϕϕτϕϕ⎫=++⎪=+-⎬⎪=-+-⎭（4-7）可得而这也是外界上的边界条件。

在孔边，边界条件是应用半逆解法求解（非轴对称问题）: 由边界条件，假设由Φσ～关系，假设， ∴设（c ）将（c ）代入相容方程（4-6），得（4-6）()()()22R =cos sin cos 2-2sin cos sin 2Rq q q a q q ρρρφρσϕϕϕτϕϕϕ==⎫-=⎪⎬==-⎪⎭()()=00 (b)rr ρρφρρστ===，。

cos2,sin 2;ρρυσυτυ∝∝cos 2Φυ∝()cos 2Φf ρυ=22222222222222242222211110110ρρρρϕρρρρϕρρρρϕ⎛⎫⎛⎫∂∂∂∂∂∂∇∇Φ=++++Φ= ⎪⎪∂∂∂∂∂∂⎝⎭⎝⎭⎛⎫∂∂∂→∇Φ=∇∇Φ=++Φ= ⎪∂∂∂⎝⎭22222222222211011()cos 20f ρυρρρρϕρρρρϕ⎛⎫∂∂∂++Φ=→ ⎪∂∂∂⎝⎭⎛⎫∂∂∂++= ⎪∂∂∂⎝⎭222222211()cos 2014()cos 2()cos 2()cos 2014()()()cos 20f ρυf υf f ρυf f f ρυρρρρϕρρϕρρρρρρ⎛⎫∂∂∂++=→ ⎪∂∂∂⎝⎭'''+-=→⎛⎫'''+-= ⎪⎝⎭删去因子cos 2φ以后，得23299()()()()0f f f f ρρρρρρρ''''''''''+-+=方程两边同乘以ρ4，得432()2()9()9()0f f f f ρρρρρρρρ''''''''''+-+=这是齐次欧拉方程。

有限元分析与应用(清华大学研究生精品建设课程教学大纲)

从教学思想和方法上对原课程进行改革，使学生从较高层次上理解有限元方法的
与要求
实质，掌握有限元分析的工具，并具备初步处理工程问题的能力;使该课程成为具有较
宽口径和较大覆盖面的、面向全校机械类专业的有限元分析及机械设计方面的研究生
专业基础课；并与本科的“有限元原理”课程进行统筹，注意课程体系的整体优化，
备注课堂讲授
课堂讲授
2
5~6 7~8 9~10 11~12 13 14
15
15 16 16
3. 杆梁结构的有限元分析原理 3.1 FEA 求解的完整过程 3.2 有限元分析的基本步骤及表达式 3.3 杆单元及坐标变换 3.4 梁单元及坐标变换
4. 连续体弹性问题的有限元分析原理 4.1 连续体的离散过程及有限元分析过程表达式 4.2 2D 单元(三节点,四节点)的构造 4.3 轴对称问题的单元的构造 4.4 3D 单元(四节点四面体,八节点六面体)的构造 4.5 等参单元的一般原理
清华大学研究生精品建设课程教学大纲
——有限元分析及应用（曾攀）
一、基本情况
课程编号中文课程名称英文课程名称任课教师 1
70120073
开课（院）系机械工程系
有限元分析及应用
Finite Element Analysis and Its Applications
曾攀
职称
教授
开课学期授课语言
践中进行教学的环节，使学生在实践中学到知识并增长才干，这需要精心组织和设计了上机内容，编写
出专门用于教学的适合引导学生上机的“上机操作指南”，以便学生能在较短的时间里基本掌握实际分
析工具，同时加深理论知识的理解。开展该 Project 的形式为：学生按照所编写的“上机操作指南”独立上机，助教博士生进行辅导并检查完成情况，记成绩。

孔边导角对开孔方形平板应力集中分析

孔边导角对开孔方形平板应力集中分析为了分析孔边导角对开孔方形平板的应力集中情况，首先需要明确开孔方形平板的几何形状和材料特性。

假设开孔方形平板的尺寸为L×L，材料为均匀弹性材料，并且假设孔边导角为α度。

分析过程可以分为以下几个步骤：1. 几何建模：为了进行有限元分析，首先需要根据开孔方形平板的尺寸和孔的位置进行几何建模。

利用计算机辅助设计（CAD）软件，可以绘制出准确的平板模型。

在模型中，需要标出孔的位置和孔边导角。

2. 网格划分和离散化：将平板模型进行离散化处理，将平板划分为有限的小单元，例如三角形或四边形单元。

划分网格的密度需要根据实际需求进行选择，较小的网格密度可以提高模拟结果的准确性。

利用有限元分析软件，如ANSYS或ABAQUS，可以自动生成网格。

3. 材料特性设定：将材料特性输入有限元分析软件中。

这些特性包括材料的弹性模量、泊松比等。

4. 加载和边界条件设置：根据实际情况，将适当的边界条件应用于开孔方形平板模型。

这些边界条件可以包括约束和加载。

约束条件可以是固定边界或自由边界。

加载条件可以是均布载荷、集中力、压力等。

5. 模拟计算：将设定好的材料特性、加载和边界条件输入有限元分析软件中，进行模拟计算。

软件将根据所设定的条件自动计算出开孔方形平板的应力状态。

6. 结果分析：根据有限元分析软件的计算结果，可以获得开孔方形平板在孔边导角处的应力分布情况。

可以通过色谱图、云图等方式来可视化表达应力分布。

同时，可以在特定位置上提取应力值进行分析。

在分析过程中，需要注意以下几点：1. 单元网格密度要足够细，以保证准确性。

在孔边附近，应增加网格密度，以更好地捕捉应力集中的情况。

2. 材料特性选取要准确。

根据实际材料的弹性模量和泊松比，输入准确的数值。

3. 边界条件要合理设定。

需要根据实际情况选择适当的约束和加载条件，以便获得准确的应力集中分析结果。

4. 结果分析时要进行合理的判断。

应根据开孔方形平板的应力分布情况，判断应力集中的位置和强度，并进行合理的优化设计。

有限宽中心圆孔板应力集中系数数值实验

有限宽中心圆孔板应力集中系数数值实验冯美生，张红珠辽宁工程技术大学力学与工程科学系，辽宁阜新（123000）摘要：在anays 平台上，采用有限元方法对拉伸有限宽中心圆孔板应力集中问题进行了数值实验，定义了应力集中的特征参数，定量分析特征尺度的变化规律，研究应力集中系数与孔径尺度的关系见图3，并与解析解比较，给出了解析解的适用范围。

关键词: 应力集中，应力集中系数，圆孔，特征尺度，数值实验1 引言受力的弹性平面板具有小孔，则孔边的应力将远大于无孔时的应力，也远大于距孔稍远处的应力，这种现象称为孔边应力集中。

应力集中现象是局部现象。

在几倍于孔径以外，应力几乎不受孔的影响，应力的分布情况以及数值都与无孔时相同。

一般来说，集中的程度越高，集中的现象越是局部性的，就是说应力随着与孔的距离增大而越快的趋进于无孔时的应力。

应力集中的程度，首先与孔的形状有关，一般来说，圆孔孔边的集中程度最低。

另外集中系数还与相对孔径尺度有关。

基于ansys 平台，通过数值试验的方法，研究不同板宽，不同孔径时的孔边应力集中问题，并与弹性力学的解析解进行比较，研究应力集中系数与孔径尺度的关系。

2 实例分析2.1力学模型及假设如图1所示，平面带孔平板，孔位于板正中，假设板为各向同性完全弹性，板左端固定，右端受均布荷载q 0=10N/mm 作用，长为200mm ，厚为10mm ，泊松比为0.3，E=2.1×1011Pa,板宽和孔径变化，数值实验其应力集中时的特征参数。

定义一个描述板宽与孔径的相对尺度的特征参数，0B R ε=，定义应力集中系数max 0k q σ=，其中B 为板宽，R 0为孔半径，max σ为孔边最大应力，q 0为均布荷载。

2.2数值实验在ansys 平台上变化各种ε值，计算相应的k 值，进行相应的数值研究。

整个过程采用APDL 语言[1]，基于命令流进行参数化处理。

正式试验前，已经用固定板宽和固定孔径的有限元模型在ansys 上进行了严格的精度计算和收敛性效验，网格划分的精度足够高，误差小于1％。

应力集中的实例

应力集中的实例1. 引言应力集中是指材料中的应力在某个局部区域内增加的现象。

在工程实践中，应力集中可能导致材料的破坏或失效，因此对应力集中的研究具有重要意义。

本文将介绍几个应力集中的实例，并分析其原因和对材料性能的影响。

2. 实例一：圆孔板的应力集中圆孔板是一种常见的结构，在受力时容易出现应力集中现象。

当在圆孔板上施加均匀的拉力时，应力集中会出现在孔边缘，导致孔边缘处的应力大于其他区域。

应力集中的原因主要是由于孔的存在导致了应力场的变化。

在没有孔的情况下，应力是均匀分布的，而在孔边缘附近，应力会急剧增加，形成应力集中现象。

应力集中会导致材料的破坏。

在拉伸过程中，孔边缘的应力会超过材料的屈服强度，从而导致材料的局部破坏。

因此，在设计圆孔板时，需要考虑应力集中现象，并采取相应的措施减轻应力集中。

3. 实例二：切口的应力集中切口是一种常见的材料缺陷，会导致应力集中现象。

当材料中存在切口时，切口附近的应力会明显增加，从而导致应力集中。

切口的存在会改变应力场的分布。

在切口附近，应力会急剧增加，形成应力集中。

切口的形状和尺寸对应力集中的程度有重要影响。

较小的切口可能只引起局部的应力集中，而较大的切口可能导致材料的破坏。

应力集中会对材料的性能产生重要影响。

在受力过程中，切口附近的应力会超过材料的屈服强度，从而导致材料的破坏。

因此，在设计和制造过程中，需要注意避免切口的存在，或者采取相应的措施减轻应力集中。

4. 实例三：焊接接头的应力集中焊接接头是一种常见的结构，在受力时容易出现应力集中现象。

焊接接头的应力集中主要是由于焊缝的存在导致的。

焊缝会改变材料的应力场分布。

在焊缝附近，应力会明显增加，形成应力集中。

焊接接头的几何形状和焊接工艺对应力集中的程度有重要影响。

焊缝的几何形状和尺寸，以及焊接的温度和应力都会对应力集中产生影响。

应力集中对焊接接头的性能有重要影响。

在受力过程中，焊接接头附近的应力会超过材料的屈服强度，从而导致焊接接头的破坏。

钢板开孔后应力集中现象

钢板开孔后应力集中现象引言：钢板是一种常用的结构材料，广泛应用于建筑、船舶、桥梁等领域。

然而，在钢板中开孔后，会出现应力集中现象，这是由于开孔破坏了钢板的完整性，导致应力分布不均匀。

本文将从应力集中的原因、影响以及解决方法等方面进行探讨。

一、应力集中的原因：1. 孔洞形状：孔洞形状对应力集中有很大影响。

通常情况下，边缘尖锐的孔洞会导致应力集中更为严重。

例如，圆形孔洞的应力集中程度较小，而方形或尖锐边缘的孔洞则容易导致应力集中。

2. 孔洞尺寸：孔洞尺寸对应力集中的大小有直接影响。

孔洞尺寸越大，应力集中越严重。

因此，在设计中需要合理控制孔洞的尺寸，避免过大的孔洞导致应力集中问题。

3. 材料性能：材料的硬度、韧性等性能也会影响应力集中。

一般来说，硬度较高的材料更容易出现应力集中现象。

二、应力集中对钢板的影响：1. 强度下降：应力集中会导致材料的应力集中系数增大，从而使钢板的强度下降。

当应力集中达到一定程度时，可能引发材料的破坏甚至断裂。

2. 疲劳寿命降低：应力集中会导致局部应力增大，从而降低钢板的疲劳寿命。

在受到循环载荷作用时，应力集中区域容易发生疲劳破坏。

3. 影响结构稳定性：应力集中会导致结构的稳定性下降。

当钢板受到应力集中作用时，可能引发结构的变形或失稳，影响整个结构的安全性。

三、应对应力集中的方法：1. 减小孔洞尺寸：合理控制孔洞的尺寸可以减小应力集中的程度。

在设计中，可以通过增加孔洞的数量或采用更小的孔径来达到减小应力集中的效果。

2. 改变孔洞形状：选择合适的孔洞形状也可以减小应力集中。

圆形孔洞的应力集中程度较小，可以考虑将方形孔洞改为圆形孔洞，从而降低应力集中问题。

3. 增加钢板厚度：增加钢板的厚度可以增加其抗弯刚度，减小应力集中的程度。

但需注意，在设计中需要综合考虑材料成本和结构重量等因素。

4. 引入应力分散结构：通过在孔洞周围引入应力分散结构，如加强筋、加强板等，可以减小应力集中的影响，提高钢板的抗应力集中能力。

求矩形板在拉伸状态下,中心孔断面及其孔内壁的应力分布

要分析矩形板在拉伸状态下中心孔的断面及其孔内壁的应力分布，我们首先需要理解拉伸应力在材料中的分布规律。

当矩形板受到拉伸时，其应力分布并不均匀。

在板的中部，由于两侧同时受力，应力值相对较低。

而在板的边缘，由于只有一侧受力，应力值较高。

这种应力分布通常会导致边缘部分首先达到其屈服点，也就是说，边缘部分会首先发生塑性变形。

对于中心孔的部分，孔的四周会受到来自矩形板的拉伸作用。

由于孔的存在，孔周围的应力分布会有所不同。

具体来说，孔的两侧（与拉伸方向垂直）受到的应力会高于孔的顶部和底部（与拉伸方向平行）。

进一步地，孔内壁的应力分布也会因为材料的流动和变形规律而有所不同。

在孔的边缘，由于应力集中，材料可能会优先在这里流动或变形。

综上所述，矩形板在拉伸状态下，中心孔断面及其孔内壁的应力分布具有以下特点：
1. 中心孔断面：应力在孔的四周较高，尤其是与拉伸方向垂直的两侧。

2. 孔内壁：应力分布不均，孔的边缘部分由于应力集中而更容易发生塑性变形。

为了得到更精确的应力分布，需要使用有限元分析或其他数值模拟方法来进一步研究。

含边端半圆孔有限宽平板的理论应力集中系数与孔径板宽的变化关系

有限元作业报告含边端半圆孔有限宽平板的理论应力集中系数与孔径/板宽的变化关系2013年11月目录目录 (I)第1章目的和意义 (1)1.1 应力集中 (1)1.2 理论应力集中系数 (1)1.3 平面问题的应力集中 (1)1.4 利用有限元分析 (1)第2章软件介绍 (2)2.1 MSC.PATRAN (2)2.2 MSC.NASTRAN (2)第3章基本模型和数据 (4)3.1 基本模型 (4)3.2 基本数据 (4)第4章计算分析 (5)学习体会和建议 (11)第1章目的和意义第1章目的和意义1.1 应力集中应力集中是应力在固体局部区域内显著增高的现象。

多出现于尖角、孔洞、缺口、沟槽以及有刚性约束处及其邻域。

应力集中会引起脆性材料断裂；使物体产生疲劳裂纹。

在应力集中区域，应力的最大值（峰值应力）与物体的几何形状和加载方式等因素有关。

局部增高的应力值随与峰值应力点的间距的增加而迅速衰减。

由于峰值应力往往超过屈服极限而造成应力的重新分配，所以，实际的峰值应力常低于按弹性力学计算出的理论峰值应力。

1.2 理论应力集中系数工程上，用应力集中系数来表示应力增高的程度。

它是峰值应力max σ与不考虑应力集中时适当选取的基准应力n σ的比值，恒大于1且与载荷大小无关。

峰值应力可根据弹性力学的理论或有限元计算得到，也可根据光弹性实验或其他实验应力分析方法测定。

其中基准应力是人为规定的，取值方式不唯一，在后面的分析中给出两种常用表达方式。

本文将用α来表示理论应力集中系数，其表达式为： nσσαmax =1.3 平面问题的应力集中由弹性理论可知，对于平面问题的应力集中问题，应力分布只取决于构建的形状以及边界上的载荷条件，而与材料的弹性常数无关，于是在实验应力分析中，利用力学性质不同的材料制作模型，以替代真实构件进行应力分析，对平面问题是精确的。

1.4 利用有限元分析早起理论应力集中系数通过复杂的计算，可以得到精确解。

钢板开孔后应力集中现象

钢板开孔后应力集中现象引言：钢板开孔是工程中常见的一种加工方式，通过在钢板上钻孔、切割或冲压等方法，来满足特定的设计要求。

然而，在钢板开孔后，我们需要注意到一个重要的问题，即应力集中现象。

本文将对钢板开孔后应力集中现象进行探讨，以及其对结构强度和稳定性的影响。

一、应力集中的原因钢板开孔后，周围的材料会发生应力重分布。

在开孔边缘附近，由于材料的完整性被破坏，导致应力集中。

应力集中的原因主要包括以下几个方面：1. 几何因素：开孔的形状和尺寸会对应力集中程度产生影响。

一般来说，孔径越大、孔边角越尖锐，应力集中效应越明显。

2. 材料性质：不同的材料具有不同的应力集中特性。

硬度大、韧性差的材料在开孔后应力集中现象更为明显。

3. 载荷作用：外界的载荷作用也会影响应力集中。

在开孔处施加不均匀的载荷，会导致应力集中的程度加剧。

二、应力集中的影响应力集中现象会对结构的强度和稳定性产生不利影响，具体体现在以下几个方面：1. 强度下降：应力集中会导致局部应力超过材料的屈服强度，造成局部形变甚至破裂。

这将降低结构的整体强度，影响其承载能力。

2. 疲劳寿命减少：应力集中还会加速材料的疲劳破坏过程。

在开孔处，应力集中会导致应力集中因子增大，从而加速疲劳裂纹的形成和扩展，降低结构的疲劳寿命。

3. 塑性变形：在应力集中区域，材料容易出现塑性变形。

这将导致结构的变形不均匀，进而影响其稳定性和工作性能。

三、应对应力集中的方法为了减轻钢板开孔后的应力集中现象，可以采取以下几种方法：1. 增加开孔的半径：通过增加开孔的半径，可以减小应力集中的程度。

这样可以提高结构的强度和稳定性。

2. 使用圆形孔：相对于其他形状的孔，圆形孔的应力集中效应较小。

因此，在设计中尽可能选择圆形孔，以减轻应力集中现象。

3. 使用合适的材料：选择合适的材料也可以减轻应力集中现象。

一般来说，具有良好韧性和高强度的材料对应力集中的抵抗能力更强。

4. 优化结构：通过优化结构设计，可以减少应力集中的发生。

应力集中分析

应力集中分析假设应力在整个横截面上均匀分布而且整个杆件是均匀的，则有公式A F=σ，F为该截面上的拉内力，A 为材料该截面的横截面积。

而实际上，构件并不是如此理想的，由于某种用途，在构件上经常需要有些孔洞、键槽、缺口、轴肩、螺纹或者是其他杆件在几何外形上的突变。

所以在实际工程中，这些看似细小的变形可能导致构件在这些部位产生巨大的应力，其应力峰值远大于由基本公式算得的应力值，这种现象称为应力集中，从而可能产生重大的安全隐患。

应力集中削弱了构件的强度，降低了构件的承载能力。

应力集中处往往是构件破坏的起始点，是引起构件破坏的主要因素。

同时，应力集中的存在降低了整个构件的材料利用率，因为可能为了一部分结构的稳定而采用较高的等级的材料，与此同时构件其他部分的强度并不需要如此高的性能。

因此，为了确保构件的安全使用，提高产品的质量和经济效益，必须科学地处理构件的应力集中问题。

一、应力集中的表现及解释（主要分析拉压应力）1、理论应力集中系数：工程上用应力集中系数来表示应力增高的程度。

应力集中处的最大应力max σ与基准应力n σ之比，定义为理论应力集中系数，简称应力集中系数，即n maxσσα= (4)在(4)式中，最大应力max σ可根据弹性力学理论、有限元法计算得到，也可由实验方法测得；而基准应力n σ是人为规定的应力比的基准，其取值方式不是唯一的，大致分为以下三种：(1) 假设构件的应力集中因素（如孔、缺口、沟槽等）不存在，以构件未减小时截面上的应力为基准应力。

(2) 以构件应力集中处的最小截面上的平均应力作为基准应力。

(3) 在远离应力集中的截面上，取相应点的应力作为基准应力。

理论应力集中系数反映了应力集中的程度，是一个大于1的系数。

而且实验结果还表明：洁面尺寸改变愈剧烈，应力集中系数就愈大。

2、几种常见表现[1]一块铝板，两端受拉，其中部横截面上的拉应力 (单位面积上的力) 均匀分布，记为，见图 1(a ) , 此时没有应力集中。

带孔无限大板的应力集中问题浅析

带孔无限大板的应力集中问题浅析摘要：通过有限元方法探讨单向受载带孔无限大板件孔边应力集中的问题：逐步增大模型垂直于载荷方向的尺寸模拟无限大板；在此基础上探讨孔边应力集中系数与孔的几何特征的关系，即变圆孔为椭圆，垂直于受载方向孔半轴不变，载荷方向孔半轴变化，孔边应力集中系数随曲率半径增大而减小；减小圆孔半径，最大应力集中系数随之减小，并减小到弹性力学理论值3以下。

上述结果说明连续介质力学理论有其自身的局限性，应力梯度在应力场变化很大的情况下对微元体平衡分析的影响不可忽视。

关键词：带孔板件应力集中系数几何特征应力梯度1、问题的提出带孔板件是工程中常用结构件，在航空工业中也广为应用。

带孔板件孔边存在小范围的高应力区。

根据板件宽度和孔径的相对比例，孔边最大应力水平可为板件远场（即远离孔边的区域）应力的几倍甚至十几倍；板件宽度和孔径之比越小，孔边最大应力越大。

这个现象被称为“应力集中”，通常定义孔边最大应力与板件远场应力之比为应力集中系数，以此来标示应力集中的程度。

由于孔边的高应力水平，带孔板件在承受较小载荷的情况下，孔边应力集中区域很可能已经产生塑性变形，带孔板件的破坏，包括静载下的破坏和疲劳破坏，通常是从带孔板件孔边应力集中区域萌生的。

因此，孔边的应力集中在很大程度上影响了构件的承载能力，进而损害了结构（件）的可靠性，是工程设计中需要重视的关键问题之一。

如图1所示，板件几何中心点为坐标原点，水平方向为坐标x方向，垂直方向为y方向。

孔心即为坐标原点。

根据弹性力学理论，带孔无限大板受y方向的均布应力，孔边的应力集中系数的基尔斯解答[1]为：由上式可见，孔边最大应力集中系数Kx,max = 3，特别应该强调指出的是，该应力集中系数不随孔径的变化而变化。

在弹性力学的理论框架内，这是学习弹性力学时应建立的基本概念。

但是，我们可以做这样的设想：对于无限大板，随着孔的缩小，孔边应力集中系数始终保持不变；当孔不断缩小，乃至于无限缩小，即孔径无限小，孔边应力集中系数还保持不变吗？很显然，当孔径无限小乃至等于零时，即没有孔的情况，板蜕变成完好的连续介质板，所谓的孔边应力集中现象也随之消失！是不是在孔缩小的过程中，孔边应力集中系数始终不变，无论孔径趋于多么小，而当孔径为零的时候，应力集中系数也突然变为零？毫无疑问，这样的物理过程——即孔不断缩小及孔边应力集中系数的相关变化的过程——并不符合逻辑。