最新王静龙《非参数统计分析》课后计算题参考答案
王静龙《非参数统计分析》教案

王静龙《非参数统计分析》(1-8章)教案(总77页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--.引言一般统计分析分为参数分析与非参数分析,参数分析是指,知道总体分布,但其中几个参数的值未知,用统计量来估计参数值,但大部分情况,总体是未知的,这时候就不能用参数分析,如果强行用可能会出现错误的结果。
例如:分析下面的供应商的产品是否合格?合格产品的标准长度为(±),随即抽取n=100件零件,数据如下:表经计算,平均长度为cm x 4958.8=,非常接近中心位置,样本标准差为()1047.0112=--=∑=ni i n x x s cm.一般产品的质量服从正态分布,),(~2δμN X 。
%66)1047.04958.84.8()1047.04958.86.8()4.8()6.8()6.84.8(≈-Φ--Φ=-Φ--Φ=≤≤σμσμX P这说明产品有接近三分之一不合格,三分之二合格,所以需要更换供应厂 商,而用非参数分析却是另外一个结果。
以下是100个零件长度的分布表:这说明有90%的零件长度在)2.05.8(±cm 之间,有9%的零件不合格,所以工厂不需要换供应商。
例2 哪一个企业职工的工资高? 表两个企业职工的工资显然,企业1职工的工资高,倘若假设企业1与企业2的职工工资分别服从正态分布),(),,(22σσb N a N ,则这两个企业职工的工资比较问题就可以转化为一个参数的假设检验问题,原假设为b a H =:0,备择假设为b a H >:0 则 ))11(,(~2σnmb a N y x +-- 若0H 为真,则)20()2(~11t n m t nm S y x t w =-++-=其中])()([2112122∑∑==-+--+=ni i m i i wy y x x n m S拒绝域为:}325.1{)}20({90.0≥=≥t t t 检测值为:282.1=t故不能拒绝原假设,认为两企业的工资水平无差异。
非参数统计答案范文

非参数统计答案范文1. 考察Mann-Whitney U检验:问题:对两组数据进行比较,数据不符合正态分布,要判断两组数据是否有显著差异。
如何选择合适的非参数检验方法?答案:Mann-Whitney U检验是一种适用于比较两组独立样本的非参数检验方法,适用于数据不符合正态分布的情况。
2. 考察Wilcoxon符号秩和检验:问题:对同一组数据进行配对比较,数据不符合正态分布,如何选择合适的非参数检验方法?答案:Wilcoxon符号秩和检验是一种适用于配对样本的非参数检验方法,适用于数据不符合正态分布的情况。
3. 考察Kruskal-Wallis检验:问题:有三组数据需要比较,但数据不符合正态分布,如何选择合适的非参数检验方法?答案:Kruskal-Wallis检验是一种适用于比较多组独立样本的非参数检验方法,适用于数据不符合正态分布的情况。
4. 考察Friedman检验:问题:有三组配对数据需要比较,但数据不符合正态分布,如何选择合适的非参数检验方法?答案:Friedman检验是一种适用于比较多组配对样本的非参数检验方法,适用于数据不符合正态分布的情况。
5. 考察Mood's中位数差异检验:问题:有两组独立样本数据需要比较,数据不符合正态分布,如何选择合适的非参数检验方法?答案:Mood's中位数差异检验是一种适用于比较两组独立样本的非参数检验方法,适用于数据不符合正态分布的情况。
6.考察符号检验:问题:对一组配对数据进行比较,但数据不符合正态分布,如何选择合适的非参数检验方法?答案:符号检验是一种适用于配对样本的非参数检验方法,适用于数据不符合正态分布的情况。
7.考察秩和检验:问题:有两组独立样本数据需要比较,如何选择合适的非参数检验方法?答案:秩和检验是一种适用于比较两组独立样本的非参数检验方法。
8. 考察Kolmogorov-Smirnov检验:问题:有一组数据需要验证其服从一些特定分布,如何进行检验?答案:Kolmogorov-Smirnov检验是一种非参数检验方法,可以用于验证数据是否符合一些特定分布。
王静龙《非参数统计分析》章教案

.引言一般统计分析分为参数分析与非参数分析,参数分析是指,知道总体分布,但其中几个参数的值未知,用统计量来估计参数值,但大部分情况,总体是未知的,这时候就不能用参数分析,如果强行用可能会出现错误的结果。
例如:分析下面的供应商的产品是否合格?合格产品的标准长度为(8.5±0.1),随即抽取n=100件零件,数据如下:表1.18.503 8.508 8.498 8.347 8.494 8.500 8.498 8.500 8.502 8.501 8.491 8.504 8.502 8.503 8.501 8.505 8.492 8.497 8.150 8.496 8.501 8.489 8.506 8.497 8.505 8.501 8.500 8.499 8.490 8.493 8.501 8.497 8.501 8.498 8.503 8.505 8.510 8.499 8.489 8.496 8.500 8.503 8.497 8.504 8.503 8.506 8.497 8.507 8.346 8.310 8.489 8.499 8.492 8.497 8.506 8.502 8.505 8.489 8.503 8.492 8.501 8.499 8.804 8.505 8.504 8.499 8.506 8.499 8.493 8.494 8.490 8.505 8.511 8.502 8.505 8.503 8.782 8.502 8.509 8.499 8.498 8.493 8.897 8.504 8.493 8.494 7.780 8.509 8.499 8.503 8.494 8.511 8.501 8.497 8.493 8.501 8.495 8.461 8.504 8.691经计算,平均长度为cm x 4958.8=,非常接近中心位置8.5cm ,样本标准差为()1047.0112=--=∑=ni in x x s cm.一般产品的质量服从正态分布,),(~2δμN X 。
王静龙《非参数统计分析》课后计算题参考答案汇编
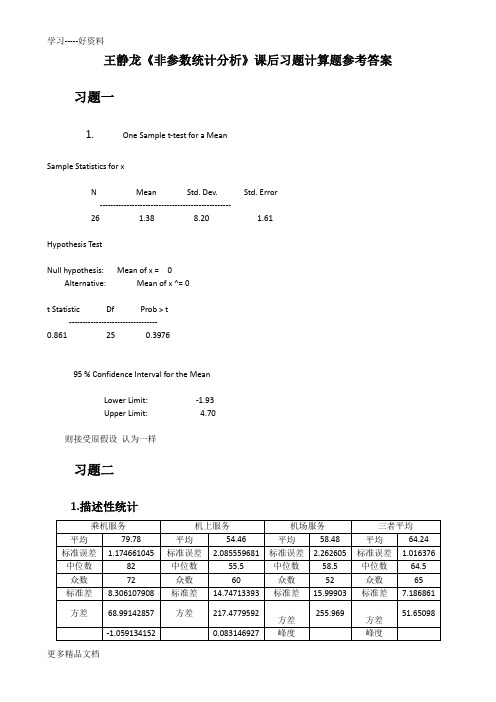
学习-----好资料更多精品文档王静龙《非参数统计分析》课后习题计算题参考答案习题一1.One Sample t-test for a MeanSample Statistics for xN Mean Std. Dev. Std. Error-------------------------------------------------26 1.38 8.20 1.61 Hypothesis TestNull hypothesis: Mean of x = 0Alternative: Mean of x ^= 0t Statistic Df Prob > t---------------------------------0.861 25 0.397695 % Confidence Interval for the MeanLower Limit: -1.93Upper Limit: 4.70则接受原假设认为一样习题二1.描述性统计更多精品文档习题三1.1{}+01=1339:6500:650013=BINOMDIST(13,39,0.5,1)=0.026625957S n H me H me P S +==<≤另外:在excel2010中有公式 BINOM.INV(n,p,a) 返回一个数值,它使得累计二项式分布的函数值大于或等于临界值a 的最小整数***0*0+1inf :2BINOM.INV(39,0.5,0.05)=141sup :1132S 1313n m i n d i n m m i n d d m i d αα==⎧⎫⎛⎫⎪⎪⎛⎫=≥⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭⎧⎫⎛⎫⎪⎪⎛⎫≤=-=⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭=≤=∑∑= 以上两种都拒绝原假设,即中位数低于65001.2学习-----好资料更多精品文档****01426201inf :221inf :122BINOM.INV(40,0.5,1-0.025)=26d=n-c=40-26=14580064006200nn i c n m i n c c i n m m i x x me x αα==⎧⎫⎛⎫⎪⎪⎛⎫=≤⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭⎧⎫⎛⎫⎪⎪⎛⎫=≥-⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭====∑∑2.{}+01=4070:6500:65002402*(1-BINOMDIST(39,70,0.5,1))=0.281978922S n H me H me P S +==≠≥=则接受原假设,即房价中位数是65003.1{}+01=15521552527207911::22n 1552=5.33E-112S n H p H p P S φ+=+==>≥≈比较大,则用正态分布近似**+**0:=1552155252720791inf :221inf :122m=BINOM.INV(2079,0.5,0.975)=1084nn i c n m i S n n c c i n m m i αα===+=⎧⎫⎛⎫⎪⎪⎛⎫=≤⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭⎧⎫⎛⎫⎪⎪⎛⎫=≥-⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭∑∑另外则拒绝原假设,即相信孩子会过得更好的人多3.2P 为认为生活更好的成年人的比例,则学习-----好资料更多精品文档1522=0.7465132079p 的比估计是:4.{}00.90610.90618154157860:65:6510.9060.094~(,)181541BINOMDIST(18153,157860,0.094,1)=0S n H P H P p S b n p P S +++===>=-=≥=-因为0〈0.05则拒绝原假设习题四1.()()++0.025+W =6+8+10+1+4+12+9+11+2+7=70p 2P W 70n=12c =65p 2P W 65=0.05≥≥符号秩和检验统计量:值为,当得所以值小于即拒绝原假设2.学习-----好资料更多精品文档()()++0.025+W =2.5+2.5+7+7+7+7+10.5+14+14+14+14+14+17.5+17.5+19+20+23+24=234.5p 2P W 234.5n=25 c =236p 2P W 236=0.05≥≥符号秩和检验统计量:值为,当得所以值小于即接受原假设{}011826:0:02182*(1-BINOMDIST(17,25,0.5,1))=0.043285251S n H me H me P S +===≠≥=+符号检验:则拒绝原假设学习-----好资料更多精品文档t t =0.861df=25 p=0.3976检验:统计量接受原假设3.(1)+0.0250.0250.025++=5+2+2=9833(1)322(3)0.052(9)0.05W n c n n d c P W P W ==+=-=≤=≤>查表可得:则 接受原假设Walsh 平均由小到大排列:50 55 60 65 65 70 70 70 75 75 75 80 80 80 80 80 80 80 85 85 85 8585 90 90 90 90 90 90 95 95 95 95 95 95 100 100 100 100 100 100 100 105 105学习-----好资料 更多精品文档105 105 105 110 110 110 110 110 115 115 120N=55 则对称中心为()()^281/290N W W θ+===()()1/1/1/40.527.50.5 1.967.771011461/40.527.50.5 1.9647.22898853d n n U c n n U αα--=+--=--==+++=++=因为c 不是整数,则^+1k d L k k w w θ()()介于与之间,其中表示比大的最小整数即为8 ^L θ为70与75之间,即为72.5 []-%72.5,105H L 则的点估计为90 95的区间估计为习题五1.171(,24,25,50)0.005060988i p P i p ===∑值很小,则拒绝原假设即认为女职工的收入比男职工的低。
非参数统计参考答案

内容:, ,上机实践:将MASS数据包用命令library(MASS)加载到R中,调用自带“老忠实”喷泉数据集geyer,它有两个变量:等待时间waiting和喷涌时间duration,其中…(1) 将等待时间70min以下的数据挑选出来;(2) 将等待时间70min以下,且等待时间不等于57min的数据挑选出来;(3) 将等待时间70min以下喷泉的喷涌时间挑选出来;(4) 将喷涌时间大于70min喷泉的等待时间挑选出来。
解:读取数据的R命令:library(MASS);#加载MASS包data(geyser);#加载数据集geyserattach(geyser);#将数据集geyser的变量置为内存变量(1) 依题意编定R程序如下:sub1geyser=geyser[which(waiting<70),1];#提取满足条件(waiting<70)的数据,which(),读取下标sub1geyser[1:5];#显示子数据集sub1geyser的前5行[1] 57 60 56 50 54(2) 依题意编定R程序如下:Sub2geyser=geyser[which((waiting<70)&(waiting!=57)),1];#提取满足条件(waiting<70& (waiting!=57)的数据.Sub2geyser[1:5];#显示子数据集sub1geyser的前5行[1] 60 56 50 54 60 ……原数据集的第1列为waiting喷涌时间,所以用[which(waiting<70),2](3)Sub3geyser=geyser[which(waiting<70),2];#提取满足条件(waiting<70)的数据,which(),读取下标Sub3geyser[1:5];#显示子数据集sub1geyser的前5行[1] ……原数据集的第2列为喷涌时间,所以用[which(waiting<70),2](4)Sub4geyser=geyser[which(waiting>70),1];#提取满足条件(waiting<70)的数据,which(),读取下标Sub4geyser[1:5];#显示子数据集sub1geyser的前5行[1] 80 71 80 75 77…….如光盘文件中的数据,一个班有30名学生,每名学生有5门课程的成绩,编写函数实现下述要求:(1) 以的格式保存上述数据;(2) 计算每个学生各科平均分,并将该数据加入(1)数据集的最后一列;(3) 找出各科平均分的最高分所对应的学生和他所修课程的成绩;(4) 找出至少两门课程不及格的学生,输出他们的全部成绩和平均成绩;(5) 比较具有(4)特点学生的各科平均分与其余学生平均分之间是否存在差异。
王静龙《非全全参数统计分析报告报告材料》课后计算题参考问题详解

王静龙《非参数统计分析》课后习题计算题参考答案习题一1. One Sample t-test for a MeanSample Statistics for xN Mea n Std. Dev. Std. Error 26 1.38 8.20 1.61Hypothesis TestNull hypothesis: Mea n of x = 0Alternative: Mea n of x A= 0t Statistic Df Prob > t0.861 25 0.397695 % Con fide nee In terval for the MeanLower Limit: -1.93Upper Limit: 4.70则接受原假设认为一样习题二1.描述性统计习题二 1.1S +=13 n =39 H o : me 二 6500: me :: 6500P 〈S 「3l=BINOMDIST(13,39,0.5,1) =0.026625957另外:在excel2010中有公式BINOM.INV(n,p,a) 返回一个数值,它使得累计二项式分布的函数值大于或等于临界值a 的最小整数BINO M 」N V(39,0.5,0.05)=14■v d * rZS +=13" = 13r 1 *广n m *'n""\ m :Eii=0J > CL》jd=sup d * :*2)以上两种都拒绝原假设, 即中位数低于 65001.2BINOM.INV(40,0.5,1 -0.025)=26 d=n-c=40-26=14x 14 二 5800 x 26 二 6400 me = x 20 = 62002.S +=40 n =70 H 0: me =6500: me= 65002P 「S — 40; -2*(1-BIN0MDIST(39,70,0.5,1)) =0.281978922则接受原假设,即房价中位数是 65003.1S +=1552 n =1552 527 二 2079 1 1H o : p 出:p —2 2n 比较大,则用正态分布近似另外:S +=1552 n =1552 527 = 2079I *(1 5 c =inf c : I [12 丿 iI *(1 : m = inf m : — 12丿 m=BINOM.INV(2079,0.5,0.975)=1084则拒绝原假设,即相信孩子会过得更好的人多3.2P 为认为生活更好的成年人的比例,则r 1 *5、 n m(n xa |m = i nf $ m :[S |[> 1 —— 1 I2 z U 丿 2j . * i -c nz P^S -1552」1039.5-1552+0.5「519.75=5.33E-112nm *zi =0-1 -21 J I n ) a ]实用文档p 的比估计是:1522=0.74651320794.S ” =18154 n =157860H 0 :F 0.906 =H1 : P0.906- 65p =1 -0.906 =0.094 S ~ b(n, p)P fS _18154: -1 -BIN0MDIST(18153,157860,0.094,1) =0因为0〈 0.05则拒绝原假设习题四 1.符号秩和检验统计量:+W =6+8+10+1+4+12+9+11+2+7=70p 值为2P(W +^70 ),当 n=12得5.025=65 所以p 值小于2P W + -65 =0.05 即拒绝原假设2.符号秩和检验统计量:W+=2.5+2.5+7+7+7+7+10.5+14+14+14+14+14+17.5+17.5+19+20+23+24=234.5p值为2P(W+^234.5,当n=25 得c°.°25=236所以p值小于2P W+-236 =0.05即接受原假设符号检验:+S =18 n =26H 0: me = 0 已:me = 02P〈S _18.;=2*(1-BIN0MDIST(17,25,0.5,1))=0.043285251则拒绝原假设t 检验:t 统计量=0.861 df=25 p=0.3976 接受原假设3.(1)W +=5+2+2=9 n =8 查表可得:00.025 =33 d -n(n 1)c_30.0250.025 '2 2P(W +乞3) =0.05 2P(W + 乞9) 0.05 则接受原假设7070 75 75 75 8080 80 80 80 80 80 85 85 85 8590 95 95 95 95 95 95 100 100 100 100 100 100 100 105 105 105 105 105 110 110 110 110 110 115 115 120AWalsh 平均由小到大排列: 50 55 60 65 65 70 85 9090 90 90 90d =n n 1 /4 -0.5 -U忙./2・.n n 1 2n 1 /24 =27.5-0.5 -1.96 .10 11 21/24 = 7.77101146c =n n 1 /4 0.5 5_一./2.. n n 1 2n 1 /24 =27.5 0.5 1.96、、10 11 21/24 =47.22898853因为c不是整数,则丸介于w(k)与w(k+1)之间,其中k表示比d大的最小整数即为8A九为70与75之间,即为72.5则H-L的点估计为9095%的区间估计为172.5,1051习题五1.122800 25200 26550 26550 26900 27350 28500 28950 29900 30150 30450 30450 30650 30800 31000 31300 31350 31350 31800 32050 32250 32350 32750 32900 33250 33550 33700 33950 34100 34800 35050 35200 3550035600 35700 35900 36100 36300 36700 37250 37400 37750 38050 38200 38200 38800 39200 39700 40400 41000-7p「yP(i,24,25,50) =0.005060988p值很小,则拒绝原假设即认为女职工的收入比男职工的低。
统计考试题目及答案解析

统计考试题目及答案解析一、单项选择题(每题2分,共20分)1. 以下哪个选项是统计学中的基本概念?A. 变量B. 常量C. 函数D. 集合答案:A2. 统计学中,数据的收集方法不包括以下哪一项?A. 观察法B. 实验法C. 调查法D. 假设法答案:D3. 在统计分析中,以下哪个指标用于衡量数据的离散程度?A. 平均数B. 中位数C. 众数D. 方差答案:D4. 以下哪个选项不是描述性统计的内容?A. 数据的整理和分类B. 数据的图形表示C. 数据的假设检验D. 数据的描述性指标计算答案:C5. 以下哪个选项是统计学中的参数估计方法?A. 点估计B. 区间估计C. 假设检验D. 以上都是答案:D6. 以下哪个选项是统计学中的非参数检验?A. t检验B. 方差分析C. 卡方检验D. 以上都不是答案:C7. 以下哪个选项是统计学中的相关分析方法?A. 回归分析B. 因子分析C. 聚类分析D. 判别分析答案:A8. 以下哪个选项是统计学中的抽样方法?A. 简单随机抽样B. 系统抽样C. 分层抽样D. 以上都是答案:D9. 以下哪个选项是统计学中的预测方法?A. 时间序列分析B. 因子分析C. 聚类分析D. 判别分析答案:A10. 以下哪个选项是统计学中的决策方法?A. 假设检验B. 方差分析C. 回归分析D. 以上都不是答案:A二、多项选择题(每题3分,共15分)1. 以下哪些选项是统计学中常用的数据类型?A. 定性数据B. 定量数据C. 计数数据D. 以上都是答案:D2. 以下哪些选项是统计学中常用的数据整理方法?A. 频数分布表B. 直方图C. 箱线图D. 以上都是答案:D3. 以下哪些选项是统计学中常用的数据描述性指标?A. 平均数B. 中位数C. 众数D. 以上都是答案:D4. 以下哪些选项是统计学中常用的数据图形表示方法?A. 条形图B. 折线图C. 散点图D. 以上都是答案:D5. 以下哪些选项是统计学中常用的数据检验方法?A. t检验B. 方差分析C. 卡方检验D. 以上都是答案:D三、简答题(每题5分,共10分)1. 请简述统计学中参数估计与假设检验的区别。
王静龙《非参数统计分析》(1-8章)教案汇编

.引言一般统计分析分为参数分析与非参数分析,参数分析是指,知道总体分布,但其中几个参数的值未知,用统计量来估计参数值,但大部分情况,总体是未知的,这时候就不能用参数分析,如果强行用可能会出现错误的结果。
例如:分析下面的供应商的产品是否合格?合格产品的标准长度为(8.5 _ 0.1),随即抽取n=100件零件,数据如下:表1.18.503 8.508 8.498 8.347 8.494 8.500 8.498 8.500 8.502 8.501 8.491 8.5048.502 8.503 8.501 8.505 8.492 8.497 8.150 8.496 8.501 8.489 8.506 8.4978.505 8.501 8.500 8.499 8.490 8.493 8.501 8.497 8.501 8.498 8.503 8.5058.510 8.499 8.489 8.496 8.500 8.503 8.497 8.504 8.503 8.506 8.497 8.5078.346 8.310 8.489 8.499 8.492 8.497 8.506 8.502 8.505 8.489 8.503 8.4928.501 8.499 8.804 8.505 8.504 8.499 8.506 8.499 8.493 8.494 8.490 8.5058.511 8.502 8.505 8.503 8.782 8.502 8.509 8.499 8.498 8.493 8.897 8.5048.493 8.494 7.780 8.509 8.499 8.503 8.494 8.511 8.501 8.497 8.493 8.5018.495 8.461 8.504 8.691经计算,平均长度为x - 8.4958cm,非常接近中心位置8.5cm,样本标准差为X j-X? n -1 = 0.1047 cm.—般产品的质量服从正态分布,X~N(・,2)。
最新非参数统计部分课后习题参考答案

课后习题参考答案第一章p23-252、(2)有两组学生,第一组八名学生的成绩分别为x 1:100,99,99,100,99,100,99,99;第二组三名学生的成绩分别为x 2:75,87,60。
我们对这两组数据作同样水平a=0.05的t检验(假设总体均值为u ):H 0:u=100 H 1:u<100。
第一组数据的检验结果为:df=7,t 值为3.4157,单边p 值为0.0056,结论为“拒绝H 0:u=100。
”(注意:该组均值为99.3750);第二组数据的检验结果为:df=2,t 值为3.3290,单边p值为0.0398;结论为“接受H 0:u=100。
”(注意:该组均值为74.000)。
你认为该问题的结论合理吗?说出你的理由,并提出该如何解决这一类问题。
答:这个结论不合理(6分)。
因为,第一组数据的结论是由于p-值太小拒绝零假设,这时可能犯第一类错误的概率较小,且我们容易把握;而第二组数据虽不能拒绝零假设,但要做出“在水平a时,接受零假设”的说法时,还必须涉及到犯第二类错误的概率。
(4分)然而,在实践中,犯第二类错误的概率多不易得到,这时说接受零假设就容易产生误导。
实际上不能拒绝零假设的原因很多,可能是证据不足(样本数据太少),也可能是检验效率低,换一个更有效的检验之后就可以拒绝了,当然也可能是零假设本身就是对的。
本题第二组数据明显是由于证据不足,所以解决的方法只有增大样本容量。
(4分)第三章p68-713、在某保险种类中,一次关于1998年的索赔数额(单位:元)的随机抽样为(按升幂排列): 4632,4728,5052,5064,5484,6972,7596,9480,14760,15012,18720,21240,22836,52788,67200。
已知1997年的索赔数额的中位数为5064元。
(1)是否1998年索赔的中位数比前一年有所变化?能否用单边检验来回答这个问题?(4分) (2)利用符号检验来回答(1)的问题(利用精确的和正态近似两种方法)。
王静龙《非参数统计分析》(1-8章)教案讲课讲稿

.引言一般统计分析分为参数分析与非参数分析,参数分析是指,知道总体分布,但其中几个参数的值未知,用统计量来估计参数值,但大部分情况,总体是未知的,这时候就不能用参数分析,如果强行用可能会出现错误的结果。
例如:分析下面的供应商的产品是否合格?合格产品的标准长度为(8.5±0.1),随即抽取n=100件零件,数据如下:表1.18.503 8.508 8.498 8.347 8.494 8.500 8.498 8.500 8.502 8.501 8.491 8.504 8.502 8.503 8.501 8.505 8.492 8.497 8.150 8.496 8.501 8.489 8.506 8.497 8.505 8.501 8.500 8.499 8.490 8.493 8.501 8.497 8.501 8.498 8.503 8.505 8.510 8.499 8.489 8.496 8.500 8.503 8.497 8.504 8.503 8.506 8.497 8.507 8.346 8.310 8.489 8.499 8.492 8.497 8.506 8.502 8.505 8.489 8.503 8.492 8.501 8.499 8.804 8.505 8.504 8.499 8.506 8.499 8.493 8.494 8.490 8.505 8.511 8.502 8.505 8.503 8.782 8.502 8.509 8.499 8.498 8.493 8.897 8.504 8.493 8.494 7.780 8.509 8.499 8.503 8.494 8.511 8.501 8.497 8.493 8.501 8.495 8.461 8.504 8.691经计算,平均长度为cm x 4958.8=,非常接近中心位置8.5cm ,样本标准差为()1047.0112=--=∑=ni in x x s cm.一般产品的质量服从正态分布,),(~2δμN X 。
统计学课后习题答案 第8章的习题答案

1. 解:根据题意建立原假设和备择假设:01:700;:700H H μμ≥<2x Z ===- 由于-2<-1.645,所以Z Z α<-,Z 值位于原假设0H 的拒绝域,所以拒绝0H ,即在显著性水平0.05下该批元件不合格。
2. 根据题意建立原假设和备择假设:01:250;:250H H μμ≤>20 3.336x t ====,0.05(24) 1.7109t =, 由于0.05(24),.t t t t α>>所以t 值位于原假设H 0,即在显著性水平0.05下该种化肥使得水稻明显增产。
3. 解:已知 0620.157,0.155,0.05, 1.96.400p p Z αα===== 根据题意建立原假设和备择假设:01:0.157;:0.157H P H P =≠0.10995P Z ===- -0.10995>-1.96,所以Z 值位于原假设H 0的接受域。
即在显著性水平0.05下随机调查的结果支持该市老年人口比重为15.7%。
4. 解:已知 09,100,99.98, 1.2122n x s μ====。
根据题意建立原假设和备择假设:01:100;:100H H μμ=≠0.020.04950.4041x t -====- -0.0495>-2.306,所以t 位于原假设H 0的接受域,即在显著性水平0.05下,打包机打包正常。
5. 解:已知00.05200,20,208.5,30,(19) 1.7291n x S t μ=====。
根据题意建立原假设和备择假设:01:200;:200H H μμ≤>8.5 1.2676.7083x t ==== t t α<,所以t 值位于原假设H 0的接受域,即在显著性水平0.05下,接受原假设,即在特定时间内每小时经过该地的汽车数量小于200辆。
6. 解:已知015,40,14.5, 2.3,0.05, 1.645n x S Z αμα======。
王静龙《非参数统计分析》课后计算题参考的答案解析
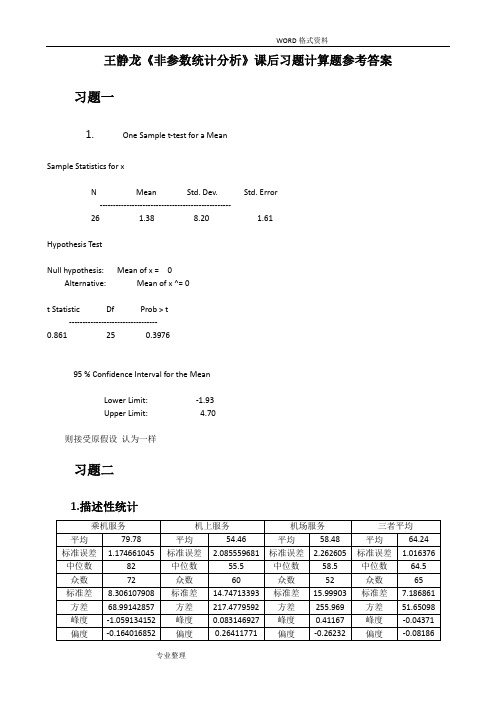
WORD格式资料王静龙《非参数统计分析》课后习题计算题参考答案习题一1.One Sample t-test for a MeanSample Statistics for xN Mean Std. Dev. Std. Error-------------------------------------------------26 1.38 8.20 1.61Hypothesis TestNull hypothesis: Mean of x = 0Alternative: Mean of x ^= 0t Statistic Df Prob > t---------------------------------0.861 25 0.397695 % Confidence Interval for the MeanLower Limit: -1.93Upper Limit: 4.70则接受原假设认为一样习题二1.描述性统计专业整理专业整理习题三1.1{}+01=1339:6500:650013=BINOMDIST(13,39,0.5,1)=0.026625957S n H me H me P S +==<≤另外:在excel2010中有公式 BINOM.INV(n,p,a) 返回一个数值,它使得累计二项式分布的函数值大于或等于临界值a 的最小整数***0*0+1inf :2BINOM.INV(39,0.5,0.05)=141sup :1132S 1313n m i n d i n m m i n d d m i d αα==⎧⎫⎛⎫⎪⎪⎛⎫=≥⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭⎧⎫⎛⎫⎪⎪⎛⎫≤=-=⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭=≤=∑∑= 以上两种都拒绝原假设,即中位数低于65001.2WORD 格式资料专业整理****01426201inf :221inf :122BINOM.INV(40,0.5,1-0.025)=26d=n-c=40-26=14580064006200n ni c n m i n c c i n m m i x x me x αα==⎧⎫⎛⎫⎪⎪⎛⎫=≤⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭⎧⎫⎛⎫⎪⎪⎛⎫=≥-⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭====∑∑2.{}+01=4070:6500:65002402*(1-BINOMDIST(39,70,0.5,1))=0.281978922S n H me H me P S +==≠≥=则接受原假设,即房价中位数是65003.1{}+01=15521552527207911::22n 1552=5.33E-112S n H p H p P S φ+=+==>≥≈比较大,则用正态分布近似**+**0:=1552155252720791inf :221inf :122m=BINOM.INV(2079,0.5,0.975)=1084nn i c n m i S n n c c i n m m i αα===+=⎧⎫⎛⎫⎪⎪⎛⎫=≤⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭⎧⎫⎛⎫⎪⎪⎛⎫=≥-⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭∑∑另外则拒绝原假设,即相信孩子会过得更好的人多3.2P 为认为生活更好的成年人的比例,则WORD 格式资料专业整理1522=0.7465132079p 的比估计是:4.{}00.90610.90618154157860:65:6510.9060.094~(,)181541BINOMDIST(18153,157860,0.094,1)=0S n H P H P p S b n p P S +++===>=-=≥=-因为0〈0.05则拒绝原假设习题四1.()()++0.025+W =6+8+10+1+4+12+9+11+2+7=70p 2P W 70n=12c =65p 2P W 65=0.05≥≥符号秩和检验统计量:值为,当得所以值小于即拒绝原假设2.专业整理()()++0.025+W =2.5+2.5+7+7+7+7+10.5+14+14+14+14+14+17.5+17.5+19+20+23+24=234.5p 2P W 234.5n=25 c =236p 2P W 236=0.05≥≥符号秩和检验统计量:值为,当得所以值小于即接受原假设{}011826:0:02182*(1-BINOMDIST(17,25,0.5,1))=0.043285251S n H me H me P S +===≠≥=+符号检验:则拒绝原假设WORD 格式资料专业整理t t =0.861df=25 p=0.3976检验:统计量接受原假设3.(1)+0.0250.0250.025++=5+2+2=9833(1)322(3)0.052(9)0.05W n c n n d c P W P W ==+=-=≤=≤>查表可得:则 接受原假设Walsh 平均由小到大排列:50 55 60 65 65 70 70 70 75 75 75 80 80 80 80 80 80 80 85 85 85 8585 90 90 90 90 90 90 95 95 95 95 95 95 100 100 100 100 100 100 100 105 105专业整理N=55 则对称中心为()()^281/290N W W θ+===()()1/1/1/40.527.50.5 1.967.771011461/40.527.50.5 1.9647.22898853d n n U c n n U αα--=+--=--==+++=++=因为c 不是整数,则^+1k d L k k w w θ()()介于与之间,其中表示比大的最小整数即为8 ^L θ为70与75之间,即为72.5 []-%72.5,105H L 则的点估计为90 95的区间估计为习题五1.171(,24,25,50)0.005060988i p P i p ===∑值很小,则拒绝原假设即认为女职工的收入比男职工的低。
非参数统计题目及答案

非参数统计题目及答案标准化管理处编码[BBX968T-XBB8968-NNJ668-MM9N]1.人们在研究肺病患者的生理性质时发现,患者的肺活量与他早在儿童时期是否接受过某种治疗有关,观察3组病人,第一组早在儿童时期接受过肺部辐射,第二组接受过胸外科手术,第三组没有治疗过,现观察到其肺活量占其正常值的百分比如下:以往的经验告诉我们,这三组病人的肺活量有如下关系:第二组≤第一组≤第三组,试判断这一经验是否可靠。
解:H 0:θ2≤θ1≤θ3 H 1:至少有一个不等式成立可得到 N=15由统计量H=)112+N N (∑=Ki i N R 1i 2-3(N+1)=)(1151512+(32×+29×+59×-3×(15+1)= 查表(5,5,5)在P(H ≥= P(H ≥= 即P (H ≥)﹥故取α=, P ﹥α ,故接受零假设即这一检验可靠。
2.关于生产计算机公司在一年中的生产力的改进(度量为从0到100)与它们在过去三年中在智力投资(度量为:低,中等,高)之间的关系的研究结果列在下表中:是否智力投资对改进生产力有帮助说明检验的步骤,包括零假设,备选假设,统计量,P值等等及你的结果。
(利用Jonkheere-Terpstra检验)解:H0:M低=M中=M高H1:M低﹤M中﹤M高U 12=0+9+2+8+10+9+10+2+10+10+8++3=U 13=10×8=80U 23=12+9+12+12+12+11+12+11=89J=∑≤jij U i =+80+89=大样本近似 Z=[]72)32()324121i 222∑∑==+-+--k i i i k i n n N N n N J ()(~N (0,1)求得 Z= Ф=取α= , P >α, 故接受原假设,认为智力投资对改进生产力有帮助。
非参数统计王星版第一章课后答案

850] 0.03421 0.07553 0.12521 0.16771 0.18180
#p=[0.00795
0.16538 0.12553 0.07418 0.03400 0.00850]
#1.5 uniroot(f=function(x) 2*x^3-4*x^2+3*x-6, interval=c(-10,10)) f=function(x){2*x^3-4*x^2+3*x-6} f(0) a=-10 b=10 root=function(a,b) { c=(a+b)/2; while(abs(f(c))>0.00001){ if(f(c)*f(a)<0){b=c; c=(a+b)/2;} else {a=c; c=(a+b)/2;}} c
# 当随机取 10000 次的一个结果 1684 1256 743 338 96]
a=[71 321 774 1255 1637 1825
# p=[0.0071 0.0321 0.0774 0.1255 0.1637 0.1825 0.1684 0.1256 0.0743 0.0338 0.0096] #当随机取十万次数据的一个结果 #a=[795 3400 3421 7553 12521 16771 18180 16538 12553 7418
Settings\\Administrator\\桌面\\非参数统计配套数据\\各章数据\\第 一章\\student.txt",header = T) student1=as.data.frame(student)
means=apply(student1[,2:6],1,mean) b1=data.frame(student1,means)
非参数统计(附答案)

《非参数统计》试卷注意事项:1.本试卷适用于经济统计专业学生使用。
2.本试卷共6 页,满分100分,答题时间120分钟。
题号 一 二 三 四 总分 得分一、 选择题(本大题共10小题,每小题1分,共10分)1、以下对非参数检验的描述,哪一项是错误的( )。
A.非参数检验方法不依赖于总体的分布类型 B.应用非参数检验时不考虑被研究对象的分布类型 C.非参数检验的假定条件比较宽松D.非参数检验比较简便2、秩和检验又叫做( )A 、参数检验B 、Wilcoxon 检验C 、非参数检验D 、近似正态检验 3、( )同分校正后,统计量会变小。
A. Kruskal-Wallis 检验B.弗里德曼(Friedman )检验C. Mann-Whitney 检验D. Spearman 等级相关检验 4、配对比较的秩和检验的基本意思是:如果检验假设成立,则对样本来说( )。
A.正秩和的绝对值小于负秩和的绝对值 B.正秩和的绝对值大于负秩和的绝对值C.正秩和的绝对值与负秩和的绝对值不会相差很大D.正秩和的绝对值与负秩和的绝对值相等5、成组设计多个样本比较的秩和检验,当组数大于3时,统计量H 近似( )分布A 、正态B 、2C 、FD 、二项 6、Wilcoxon 符号秩检验不适用于( )。
A 位置的检验 B 连续总体 C 随机性的检验 D 配对样本的检验7、成组设计两样本比较的秩和检验中,描述不正确的是( )。
A .遇有相同数据,若在同一组,取平均秩次 B .遇有相同数据,若在同一组,按顺序编秩2.本评卷人C .遇有相同数据,若不在同一组,按顺序编秩D .遇有相同数据,若不在同一组,取其秩次平均值8、m=4,n=7,Tx=14的双侧检验,则( ) A. Ty=41,在显著性水平0.05时接受原假设 B. Ty=41,在显著性水平0.05时拒绝原假设 C. Ty=42,在显著性水平0.05时拒绝原假设 D. Ty=42,在显著性水平0.05时接受原假设 9、序列3 5 2 7 9 8 6的一致对数目为( )。
非参数统计真题答案及解析

非参数统计真题答案及解析统计学作为一门重要的学科,对于量化研究各种现象和问题具有重要的作用。
在统计学中,参数统计和非参数统计是两个重要的分支。
参数统计是指根据总体的参数,通过样本数据对总体进行估计或假设检验。
而非参数统计则是在对总体参数没有明确假设的情况下,通过对样本数据的分析来进行统计推断。
本文将通过一些非参数统计的真题来深入讨论非参数统计的方法和应用。
一、Wilcoxon符号秩检验Wilcoxon符号秩检验是一种非参数的假设检验方法,用于比较两个相关配对样本的中位数是否存在差异。
该检验不依赖于数据的分布情况,适用于非正态分布的数据。
举例来说,某研究人员想要评估某种治疗方法对患者疼痛程度的影响。
该研究人员收集了30位患者的治疗前后的疼痛分数数据。
他们想知道,是否存在治疗前后的疼痛分数差异。
于是,他们可以使用Wilcoxon符号秩检验来判断。
在Wilcoxon符号秩检验中,我们的零假设(H0)是两组样本的中位数没有差异,而备择假设(H1)则是两组样本的中位数存在差异。
通过对样本数据进行计算,得到检验统计量的值,进而得到相应的p 值。
若p值小于给定的显著性水平(通常为0.05),则我们可以拒绝零假设,认为两组样本的中位数存在显著差异。
二、Mann-Whitney U检验Mann-Whitney U检验,又称为Wilcoxon秩和检验,是一种非参数的假设检验方法,用于比较两组独立样本的总体中位数是否存在差异。
该检验同样不依赖于数据的分布情况。
假设某研究人员想要比较两种不同的药物对患者血压的影响。
他们随机选择了一组患者,将他们分为两组,分别给予不同药物的治疗。
然后,他们测量了两组患者的血压数据,以了解是否存在差异。
在这种情况下,研究人员可以使用Mann-Whitney U检验进行分析。
在Mann-Whitney U检验中,我们的零假设(H0)是两组样本的中位数没有差异,而备择假设(H1)则是两组样本的中位数存在差异。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品文档精品文档王静龙《非参数统计分析》课后习题计算题参考答案习题一1.One Sample t-test for a MeanSample Statistics for xN Mean Std. Dev. Std. Error-------------------------------------------------26 1.38 8.20 1.61 Hypothesis TestNull hypothesis: Mean of x = 0Alternative: Mean of x ^= 0t Statistic Df Prob > t---------------------------------0.861 25 0.397695 % Confidence Interval for the MeanLower Limit: -1.93Upper Limit: 4.70则接受原假设认为一样习题二1.描述性统计精品文档习题三1.1{}+01=1339:6500:650013=BINOMDIST(13,39,0.5,1)=0.026625957S n H me H me P S +==<≤另外:在excel2010中有公式 BINOM.INV(n,p,a) 返回一个数值,它使得累计二项式分布的函数值大于或等于临界值a 的最小整数***0*0+1inf :2BINOM.INV(39,0.5,0.05)=141sup :1132S 1313n m i n d i n m m i n d d m i d αα==⎧⎫⎛⎫⎪⎪⎛⎫=≥⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭⎧⎫⎛⎫⎪⎪⎛⎫≤=-=⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭=≤=∑∑= 以上两种都拒绝原假设,即中位数低于65001.2精品文档精品文档****01426201inf :221inf :122BINOM.INV(40,0.5,1-0.025)=26d=n-c=40-26=14580064006200nn i c n m i n c c i n m m i x x me x αα==⎧⎫⎛⎫⎪⎪⎛⎫=≤⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭⎧⎫⎛⎫⎪⎪⎛⎫=≥-⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭====∑∑2.{}+01=4070:6500:65002402*(1-BINOMDIST(39,70,0.5,1))=0.281978922S n H me H me P S +==≠≥=则接受原假设,即房价中位数是65003.1{}+01=15521552527207911::22n 1552=5.33E-112S n H p H p P S φ+=+==>≥≈比较大,则用正态分布近似**+**0:=1552155252720791inf :221inf :122m=BINOM.INV(2079,0.5,0.975)=1084nn i c n m i S n n c c i n m m i αα===+=⎧⎫⎛⎫⎪⎪⎛⎫=≤⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭⎧⎫⎛⎫⎪⎪⎛⎫=≥-⎨⎬⎪ ⎪⎝⎭⎝⎭⎪⎪⎩⎭∑∑另外则拒绝原假设,即相信孩子会过得更好的人多3.2P 为认为生活更好的成年人的比例,则精品文档精品文档1522=0.7465132079p 的比估计是:4.{}00.90610.90618154157860:65:6510.9060.094~(,)181541BINOMDIST(18153,157860,0.094,1)=0S n H P H P p S b n p P S +++===>=-=≥=-因为0〈0.05则拒绝原假设习题四1.()()++0.025+W =6+8+10+1+4+12+9+11+2+7=70p 2P W 70n=12c =65p 2P W 65=0.05≥≥符号秩和检验统计量:值为,当得所以值小于即拒绝原假设2.精品文档精品文档()()++0.025+W =2.5+2.5+7+7+7+7+10.5+14+14+14+14+14+17.5+17.5+19+20+23+24=234.5p 2P W 234.5n=25 c =236p 2P W 236=0.05≥≥符号秩和检验统计量:值为,当得所以值小于即接受原假设{}011826:0:02182*(1-BINOMDIST(17,25,0.5,1))=0.043285251S n H me H me P S +===≠≥=+符号检验:则拒绝原假设精品文档精品文档t t =0.861df=25 p=0.3976检验:统计量接受原假设3.(1)+0.0250.0250.025++=5+2+2=9833(1)322(3)0.052(9)0.05W n c n n d c P W P W ==+=-=≤=≤>查表可得:则 接受原假设Walsh 平均由小到大排列:50 55 60 65 65 70 70 70 75 75 75 80 80 80 80 80 80 80 85 85 85 8585 90 90 90 90 90 90 95 95 95 95 95 95 100 100 100 100 100 100 100 105 105精品文档 精品文档105 105 105 110 110 110 110 110 115 115 120N=55 则对称中心为()()^281/290N W W θ+===()()1/1/1/40.527.50.5 1.967.771011461/40.527.50.5 1.9647.22898853d n n U c n n U αα--=+--=--==+++=++=因为c 不是整数,则^+1k d L k k w w θ()()介于与之间,其中表示比大的最小整数即为8 ^L θ为70与75之间,即为72.5 []-%72.5,105H L 则的点估计为90 95的区间估计为习题五1.171(,24,25,50)0.005060988i p P i p ===∑值很小,则拒绝原假设即认为女职工的收入比男职工的低。
1.2()+W =1+2+3.5+5+6+7+8+10+11.5+11.5+13+15+16+17.5+17.5+20+22+24+26+29+31+32+34+35+36+44.5=478n+m=50478(1)/2p=2P W 478=0.000327643Wilcoxon W W n N =⎛⎫-+≤Θ女女秩和因为N=,查不到表,则用其渐进正态分布求解n=26,m=24,N=50,=则拒绝原假设,认为女职工的收入低精品文档精品文档2.()B +W =1+2+3+4+5+6+8+10+12=51=n+m=1951p=2P W 51=2*0.001450862Wilcoxon W =⎛⎫≤ΘB 秩和因为N ,则用其渐进正态分布求解n=9,m=10,N=19,=则拒绝原假设,认为A 比B 的作用好7.()112+0.025W =1+5+7+8+10+11+16+18+19+20=115+n =20115p=2P W 115=158158>115.0Wilcoxon W c =≥月11111月秩和因为n=n ,n =10,n =10,n=20,所以,查表可得:因为,,所以p 值一定大于05则接受原假设,认为11月和12月的波动相同1/1//20.510*10/20.523.64/20.510*10/20.576.36d nm U c nm U αα--=--=--==++=++=位置参数检验:^^+1k d =-29L L k k w w θθ()()介于与之间,其中表示比大的最小整数即为24 [][][]^^176 =17U U w w θθ-c c 介于与之间,其中c 表示比c 小的最大整数即为所以,区间为:[-29,17] 即0在区间内则认为11月和12月的波动相同8精品文档精品文档()()()()()()()[]22112321241221()2269.251121247128822*4036.7659571212*471/21/144122*25796056.5-47*(47*47-1)/144202328.727347*46y i i i i i y y t t t M a R N E M n N nm D M d N N N N N τττ=====⎡⎤--⎢⎥=-⎢⎥⎣⎦⎡⎤-=-=⎢⎥⎣⎦⎡⎤=-+--⎣⎦-==∑∑∑尺度参数检验:所以渐进正态分布计p -p==4.25641E-05M E M ⎛⎫Θ算其值:则认为较小精品文档精品文档()()()()221123212412214()346.5+1-4N 1247+1288=22*=258.38297874*4712*47N+1116N 22*2548=24245-=6167.00503947*4616*47p A -p=y i i i i i y y t t tA a R N E A n N nm D M d N N E τττ=====⎡⎤-⎢⎥=⎢⎥⎣⎦⎡⎤-⎢⎥⎣⎦⎡⎤=-⎢⎥-⎣⎦⎡⎤⎢⎥⎣⎦Θ∑∑∑()()()所以渐进正态分布计算其值:=0.869085147A ⎛⎫则认为较大b b b<1y y M A ≠综合:因为比较小而比较大,可知 1 且应该有因为b<1,则认为机器一更有机会改进质量*答案是自己做的,但是有一次发现有个地方错了啊,还没改过来,仅作参考!。
