九年级数学四点共圆例题讲解

合集下载

四点共圆(知识讲解)

四点共圆（知识讲解）【学习目标】1. 理解四点共圆的定义；2. 掌握判断四点共圆的基本方法，并用于解决证明和计算问题。

【要点梳理】四点共圆常用的方法有：1、对角互补的四边形，四点共圆；2、外角等于内对角的四边形，四点共圆；3、同底同侧的顶角相等的两个三角形，四点共圆；4、到定点的距离等于定长的四个点，四点共圆。

【典型例题】类型一、四点共圆的判定1．如图，BD ，AH 分别是ABC 的高，求证：A 、B 、H 、D 四点共圆．【分析】取AB 的中点O ，连接DO 、HO ，根据BD ，AH 分别是△ABC 的高，可得△DAB和△HAB 都是直角三角形，斜边都是AB ，而点O 为斜边中点，则有DO ＝HO ＝12AB ＝AO ＝BO ，也就是说以O 为圆心、OA 为半径的圆，点D 、H 、B 也在这个圆上，即可证明A 、B 、H 、D 四点共圆．证明：如图，取AB 的中点O ，连接DO 、HO ，△BD ，AH 分别是ABC ∆的高，DAB ∴∆和HAB ∆都是直角三角形，且它们的斜边都是AB ，△点O 为斜边中点，12DO HO AB AO BO ∴====，也就是说，点D、H、B在以O为圆心、OA为半径的圆上，即点D、H、B、A都在以O为圆心、以OA为半径的圆上，故可得：A、B、H、D四点共圆．【点拨】本题考查了四点共圆，解答本题的关键是利用直角三角形斜边上的中线等于斜边的一半证得四点共圆．举一反三：【变式1】已知四边形ABCD为菱形，点E、F、G、H分别为各边中点，判断E、F、G、H四点是否在同一个圆上，如果在同一圆上，找到圆心，并证明四点共圆；如果不在，说明理由．【答案】点E、F、G、H四点是以AC，BD的交点O为圆心的同一个圆上，证明见分析.【分析】根据菱形的对角线互相垂直，以及直角三角形斜边中线等于斜边的一半，得出E、F、G、H到O点距离都等于定长即可.解：如图，连接AC，BD相交于点O，连接OE，OF，OG，OH，△四边形ABCD是菱形，△AB＝AD＝CD＝BC，AC△BD，△点E是AB的中点，△OE＝12AB，同理：OF＝12BC，OG＝12CD，OH＝12AD，△OE＝OF＝OG＝OH，△点E、F、G、H四点是以AC，BD的交点O为圆心的同一个圆上．【点拨】本题主要考查了四点共圆的条件，用到了菱形的性质及直角三角形斜边中线的性质，熟练掌握其性质是解题的关键.【变式2】如图，在Rt ABC中，△BAC＝90°，△ABC＝40°，将ABC绕A点顺时针旋转得到ADE，使D点落在BC边上．（1）求△BAD的度数；（2）求证：A、D、B、E四点共圆．【答案】（1）10°；（2）见分析【分析】（1）由三角形内角和定理和已知条件求得△C的度数，由旋转的性质得出AC＝AD，即可得出△ADC＝△C，最后由外角定理求得△BAD的度数；（2）由旋转的性质得到△ABC＝△AED，由四点共圆的判定得出结论．解：（1）△在Rt ABC中，△BAC＝90°，△ABC＝40°，△△C＝50°，△将ABC绕A点顺时针旋转得到ADE，使D点落在BC边上，△AC＝AD，△△ADC＝△C＝50°，△△ADC＝△ABC+△BAD＝50°，△△BAD＝50°－40°＝10°证明（2）△将ABC绕A点顺时针旋转得到ADE，△△ABC＝△AED，△A、D、B、E四点共圆．【点拨】本题考查了旋转的性质、等腰三角形的性质、外角定理以及四点共圆的判定，解题的关键是理解旋转后的图形与原图形对应边相等，对应角相等．【变式3】如图，在□ABCD中，△BAD为钝角，且AE△BC，A F△CD．(1) 求证：A、E、C、F四点共圆；(2) 设线段BD与(1)中的圆交于M、N．求证：BM = ND【分析】（1）只要证明A、E、C、F四点所构成的四边形的对角互补，则该四点共圆；（2）连接AC交BD于O，易得O是该圆的圆心，OM＝ON，所以可得BM＝ND．解：（1）△AE△BC，AF△CD，△△AEC=△AFC=90°，△△AEC+△AFC=180°，△A、E、C、F四点共圆；（2）由（1）可知，圆的直径是AC，连接AC交BD于O，△ABCD是平行四边形，△O为圆心，OB=OD，△OM=ON，△BM=ND.【点拨】本题主要考查了四点共圆的判定及平行四边形的性质，难度不大，能够灵活运用所学知识进行推理是解题关键.．类型二、利用四点共圆进行证明或求解2．如图，A 、B 、C 、D 四点共圆，且△ACB ＝△ACD ＝60°．求证：△ABD 是等边三角形．【分析】先根据同弧所对的圆周角相等得出△ADB ＝60°＝△ABD ，再用三角形的内角和定理求出△BAD ，即可得出结论．证明：△△ACB ＝60°，△△ADB ＝△ACB ＝60°，△△ACD ＝60°，△△ABD ＝△ACD ＝60°，在△ABD 中，△BAD ＝180°﹣△ADB ﹣△ABD ＝180°﹣60°﹣60°＝60°，△△ABD ＝△ADB ＝△BAD ＝60°，△△ABD 是等边三角形．【点拨】本题考查了等边三角形的性质与判定，圆周角定理，三角形的内角和定理，掌握圆周角定理是解答本题的关键；举一反三：【变式】如图所示中，60NAM ∠=︒，B ，C 分别在边AM 和AN 上，且2BC =，CP AN ⊥，BP AM ⊥垂足分别为C ，B ，求PA 的长.【答案】433PA =【分析】本题关键要建立未知线段PA 和已知线段BC 的关系，由A ，B ，P ，C 共圆，PA 和CE 为直径，于是在Rt CEB △中便可以建立CE 和BC 的关系，求出CE 的长即求出PA 的长.解：连结CD ，BD ，△,CP AN BP AM ⊥⊥，△90PCA PBA ∠=∠=︒△AD BD PD CD ===，△由圆的定义知点A ，B ，C ，P 在以D 为圆心，DA 为半径的圆上，作出辅助圆，延长CD 交圆D 于E ，连结BE ，△60BAC CEB ∠=∠=︒ 30ECB ∠=︒在Rt BCE 中，2BC =，△433EC =△433PA =【点拨】双直角三角形是典型的共圆图，解题中注意灵活应用.类型三、四点共圆综合应用3．定义：三角形一个内角的平分线和与另一个内角相邻的外角平分线相交所成的锐角称为该三角形第三个内角的遥望角．（1）如图1，△E 是△ABC 中△A 的遥望角．△若△A ＝40°，直接写出△E 的度数是；△求△E 与△A 的数量关系，并说明理由．（2）如图2，四边形ABCD 中，△ABC ＝△ADC ＝90°，点E 在BD 的延长线上，连CE ，若△BEC 是△ABC 中△BAC 的遥望角，求证：DA ＝DE ．【答案】（1）△20°；△12∠=∠E A ，理由见分析；（2）证明见分析【分析】（1）△根据题目定义推出△E ＝12△A ，从而得出结论；△直接根据求解△过程证明即可；（2）首先根据题意推出A 、B 、C 、D 四点共圆，然后作四边形ABCD 的外接圆交CE 于点F ，连接AF ，DF ，再根据圆的内接四边形的性质等推出△AFD ＝△DFE ，然后根据“遥望角”的定义推出△E＝△DAF，即可证△DAF△△DEF，从而得出结论．（1）解：△△△E是△ABC中△A的遥望角，△△EBC＝12△ABC，△ECD＝12△ACD，△△E＝△ECD﹣△EBD＝12（△ACD﹣△ABC）＝12△A，△△A＝40°，△△E＝20°．故答案为：20°；△12∠=∠E A，理由如下：△△E是△ABC中△A的遥望角，△△EBC＝12△ABC，△ECD＝12△ACD，△△E＝△ECD﹣△EBD＝12（△ACD﹣△ABC）＝12△A；（2）证明：△△ABC＝△ADC＝90°，△A、B、C、D四点共圆，作四边形ABCD的外接圆交CE于点F，连接AF，DF，△四边形FBCD内接于△O，△△DFC+△DBC＝180°，△△DFC+△DFE＝180°，△△DFE＝△DBC，△BD平分△ABC，△△ABD＝△DBC，△△ABD＝△AFD，△△AFD＝△DFE，△△BEC 是△ABC 中△BAC 的遥望角，由（1）得△E ＝12△BAC ，△△BAC ＝△BDC ，△△E ＝12△BDC ，△△E +△DCE ＝△BAC ，△△E ＝△DCE ，△△DCE ＝△DAF ，△△E ＝△DAF ，△DF ＝DF ，△AFD ＝△DFE ，△△DAF △△DEF （AAS ），△DA ＝DE ．【点拨】本题考查新定义问题，涉及三角形角平分线的拓展运用，圆的内接四边形的性质等，理解题目定义，灵活运用“四点共圆”的证明方法是解题关键．举一反三：【变式】在学习《圆》这一单元时，我们学习了圆周角定理的推论：圆内接四边形的对角互补；事实上，它的逆命题：对角互补的四边形的四个顶点共圆，也是一个真命题．在图形旋转的综合题中经常会出现对角互补的四边形，那么，我们就可以借助“对角互补的四边形的四个顶点共圆”，然后借助圆的相关知识来解决问题，例如：已知：ABC ∆是等边三角形，点D 是ABC ∆内一点，连接CD ，将线段CD 绕C 逆时针旋转60︒得到线段CE ，连接BE ，DE ，AD ，并延长AD 交BE 于点F ．当点D 在如图所示的位置时：（1）观察填空：△与ACD ∆全等的三角形是________；△AFB ∠的度数为（2）利用题干中的结论，证明：C ，D ，F ，E 四点共圆；（3）直接写出线段FD ，FE ，FC 之间的数量关系．____________________．【答案】（1）△BCE ∆：△60︒；（2）见分析；（3）FD FE FC +=．【分析】（1）△根据旋转的性质和等边三角形的性质可证△ACD△△BCE ；△根据已推导出的全等三角形和三角形内角和进行角度转化，可得△AFB 的大小；（2）根据△ACD△△BCE 得ADC BEC ∠∠=，推导得出四边形CDFE 中180BEC FDC ∠+∠=︒，从而证共圆；（3）先推导出△BDF 是等边三角形，可证△ABD△△CBP ，得出AD=FC ，从而得出数量关系．解：（1）△△△ABC 是等边三角形△AB=AC=BC ，△BAC=△ACB=△ABC=60°△将线段CD 绕C 逆时针旋转60︒得到线段CE△CE=CD ，△DCE=60°△△DCE 是等边三角形△△DCE=60°△△ACD+△DCB=60°，△BCE+△DCB=60°△△ACD=△BCE△△ACD△△BCE(SAS)△△△ACD△△BCE△△EBC=△DAC△△DAC+△BAD=△BAC=60°△△FBC+△BAD=60°△△AFB=180°－△ABC －△FBC －△BAF=180°－60°－60°=60°（2）△()ACD BCE SAS ∆∆≌．△ADC BEC ∠∠=，△180ADC FDC ∠+∠=︒，△180BEC FDC ∠+∠=︒．△C ，D ，F ，E 四点共圆；（证明不唯一）（3）结论：FD FE FC +=,如下图,连接BD△△ACD△△BCE△△CBE=△CAD ，AD=BE△△CAD+△BAD=60°，△BAD+△FBC=60° △△BAD+△ABD=△BDF=60° △△AFB=60°△△BDF 是等边三角形 △DF=BF,△FD+FE=BE△△ABD△△CBF(SAS)△AD=FC△FD+FE=FC【点拨】本题属于几何综合题，考查了旋转变换，全等三角形的判定与性质，等边三角形的判定与性质等知识，解题的关键是正确寻找全等三角形解决问题．。

专题3.8 四点共圆(隐圆压轴五)(解析版)

∴DG＝CG﹣CD＝＝，
在 Rt△ADG 中，由勾股定理得
＝
＝
，
∴
＝
＝
．
故答案为：6，
．
【变式 1-5】如图，AB⊥BC，AB＝5，点 E、F 分别是线段 AB、射线 BC 上的动点，以 EF 为斜边向上作等腰 Rt△DEF，∠D＝90°，连接 AD，则 AD 的最小值为．
【答案】．【解答】解：连接 BD 并延长，如图，
模型解读：
模型 1：对角互补型：若∠A+∠C=180º或∠B+∠D=180º, 则 A、B、C、D 四点共圆模型 2：同侧等角型（1）若∠A=∠C, 则 A、B、C、D 四点共圆
（2）手拉手(双子型)中的四点共圆条件：△OCD∽△OAB 结论：①△OAC∽△OBD ②AC 与 BD 交于点 E,必有∠AEB=∠AOB； ③点 E 在△OAB 的外接圆上,即 O、A、B、E 四点共圆.同理：ODCE 也四点共圆.
∴S△ABC＝
＝
＝300 km2．
则当△ADC 的面积最大时，四边形 ABCD 的面积最大．
当 AD＝CD 时，DF 最大，此时四边形 ABCD 的面积最大．
在 Rt△ACE 中，AC＝
＝10 km，AF＝ AC＝5
km，
∵∠ADF＝
＝30°，
∴DF＝ AF＝5 km，
∴S△ADC＝
Hale Waihona Puke ＝＝925 km2．
C．15
【答案】C
【解答】解：∵∠BAC＝60°，∠BDC＝120°，
∴A、E、D、F 四点共圆，
∵AD 平分∠BAC，
∴∠DAE＝∠DAF，
∴DE＝DF＝6，

九年级数学四点共圆例题讲解

九年级数学四点共圆例题讲解知识点、重点、难点四点共圆就是圆得基本内容，它广泛应用于解与圆有关得问题．与圆有关得问题变化多，解法灵活，综合性强，题型广泛，因而历来就是数学竞赛得热点内容。

在解题中，如果图形中蕴含着某四点在同一个圆上，或根据需要作出辅助圆使四点共圆，利用圆得有关性质定理，则会使复杂问题变得简单，从而使问题得到解决。

因此，掌握四点共圆得方法很重要。

判定四点共圆最基本得方法就是圆得定义：如果A、B、C、D四个点到定点O得距离相等，即OA＝OB＝OC ＝OD，那么A、B、C、D四点共圆．由此，我们立即可以得出1、如果两个直角三角形具有公共斜边，那么这两个直角三角形得四个顶点共圆。

将上述判定推广到一般情况，得：2、如果四边形得对角互补，那么这个四边形得四个顶点共圆。

3、如果四边形得外角等于它得内对角，那么这个四边形得四个顶点共圆。

4、如果两个三角形有公共底边，且在公共底边同侧又有相等得顶角，那么这两个三角形得四个顶点共圆。

运用这些判定四点共圆得方法，立即可以推出：正方形、矩形、等腰梯形得四个顶点共圆。

其实，在与圆有关得定理中，一些定理得逆定理也就是成立得，它们为我们提供了另一些证明四点共圆得方法．这就就是：1、相交弦定理得逆定理：若两线段AB与CD相交于E，且AE·EB=CE·ED，则A、B、C、D四点共圆。

2．割线定理得逆定理：若相交于点P得两线段PB、PD上各有一点A、C，且PA·PB =PC·PD，则A、B、C、D四点共圆。

3、托勒密定理得逆定理：若四边形ABCD中，AB·CD＋BC·DA=AC·BD，则ABCD就是圆内接四边形。

另外，证多点共圆往往就是以四点共圆为基础实现得一般可先证其中四点共圆，然后证其余各点均在这个圆上，或者证其中某些点个个共圆，然后判断这些圆实际就是同一个圆。

例题精讲例1：如图，P为△ABC内一点，D、E、F分别在BC、CA、AB上。

四点共圆例题及问题详解

例1 如图，E、F、G、H分别是菱形ABCD各边的中点．求证：E、F、G、H四点共圆．证明菱形ABCD的对角线AC和BD相交于点O，连接OE、OF、OG、OH．∵AC和BD 互相垂直，∴在Rt△AOB、Rt△BOC、Rt△COD、Rt△DOA中，E、F、G、H，分别是AB、BC、CD、DA的中点，即E、F、G、H四点共圆．(2)若四边形的两个对角互补(或一个外角等于它的内对角)，则四点共圆．例2 如图，在△ABC中，AD⊥BC，DE⊥AB，DF⊥AC．求证：B、E、F、C四点共圆．证明∵DE⊥AB，DF⊥AC，∴∠AED＋∠AFD=180°，即A、E、D、F四点共圆，∠AEF=∠ADF．又∵AD⊥BC，∠ADF＋∠CDF=90°，∠CDF＋∠FCD=90°，∠ADF=∠FCD．∴∠AEF=∠FCD，∠BEF＋∠FCB=180°，即B、E、F、C四点共圆．(3)若两个三角形有一条公共边，这条边所对的角相等，并且在公共边的同侧，那么这两个三角形有公共的外接圆．证明在△ABC中，BD、CE是AC、AB边上的高．∴∠BEC=∠BDC=90°，且E、D在BC的同侧，∴E、B、C、D四点共圆．∠AED=∠ACB，∠A=∠A，∴△AED∽△ACB．上述三种方法是证“四点共圆”的基本方法，至于证第四点在前三点(不在同一直线上)所确定的圆上就不叙述了．【例1】在圆内接四边形ABCD中，∠A-∠C=12°，且∠A∶∠B=2∶3．求∠A、∠B、∠C、∠D的度数．解∵四边形ABCD内接于圆，∴∠A+∠C=180°．∵∠A-∠C=12°，∴∠A=96°，∠C=84°．∵∠A∶∠B=2∶3，∠D=180°-144°=36°．利用圆内接四边形对角互补可以解决圆中有关角的计算问题．【例2】已知：如图1所示，四边形ABCD内接于圆，CE∥BD交AB的延长线于E．求证：AD·BE=BC·DC．证明：连结AC．∵CE∥BD，∴∠1=∠E．∵∠1和∠2都是所对的圆周角，∴∠1=∠2．∠1=∠E．∵四边形ABCD内接于圆，∴∠EBC=∠CDA．∴△ADC∽△CBE．AD∶BC=DC∶BE．AD·BE=BC· DC．本例利用圆内接四边形的一个外角等于内对角及平行线的同位角、圆中同弧所对的圆周角得到两个相似三角形的条件，进而得到结论．关于圆内接四边形的性质，还有一个重要定理．现在中学课本一般都不列入，现介绍如下：定理：圆内接四边形两条对角线的乘积等于两组对边乘积的和．已知：如图2所示，四边形ABCD内接于圆．求证：AC·BD=AB·CD＋AD·BC．证明：作∠BAE=∠CAD，AE交 BD于 E．∵∠ABD=∠ACD，即 AB·CD=AC·BE．①∵∠BAE+∠CAE=∠CAD+∠CAE，∴∠BAC=∠EAD．又∠ACB=∠ADE，AD·BC=AC·DE．②由①，②得AC·BE+AC·DE=AB·CE＋AD·BCAC·BD=AB·CD＋AD·BC这个定理叫托勒密(ptolemy)定理，是圆内接四边形的一个重要性质．这个证明的关键是构造△ABE∽△ACD，充分利用相似理论，这在几何中是具有代表性的．在数学竞赛中经常看到它的影子，希望能引起我们注意．命题“菱形都内接于圆”对吗？命题“菱形都内接于圆”是不正确的．所以是假命题．理由是：根据圆的内接四边形的判定方法之一，如果一个四边形的一组对角互补，那么这个四边形内接于圆．这个判定的前提是一组对角互补，而菱形的性质是一组对角相等．而一组相等的角，它们的内角和不一定是180°．如果内角和是180°，而且又相等，那么只可能是每个内角等于90°，既具有菱形的性质，且每个内角等于90°，那末这个四边形一定是正方形．而正方形显然是菱形中的特例，不能说明一般情形．判定四边形内接于圆的方法之二，是圆心到四边形四个顶点的距离相等．圆既是中心对称图形，又是轴对称图形，它的对称中心是圆心．菱形同样既是中心对称图形，又是轴对称图形，它的对称中心是两条对角线的交点．但菱形的对称中心到菱形各个顶点的距离不一定相等．所以，也无法确定菱形一定内接于圆；如果菱形的对称中心到菱形各边顶点的距离相等，再加上菱形的对角线互相垂直平分这些性质，那么这个四边形又必是正方形．综上所述，“菱形都内接于圆”这个命题是错误的．5圆的内接四边形例1 已知：如图7-90，ABCD是对角线互相垂直的圆内接四边形，通过对角线的交点E与AB垂直于点H的直线交CD于点M．求证：CM=MD．证明∠MEC与∠HEB互余，∠ABE与∠HEB互余，所以∠MEC=∠ABE．又∠ABE=∠ECM，所以∠MEC=∠ECM．从而CM=EM．同理MD=EM．所以CM=MD．点评本例的逆命题也成立（即图中若M平分CD，则MH⊥AB）．这两个命题在某些问题中有时有用．本例叫做婆罗摩笈多定理．例2 已知：如图7-91，ABCD是⊙O的内接四边形，AC⊥BD，分析一如图7-91（a），由于E是AB的中点，从A引⊙O的需证明GB=CD．但这在第七章ξ1.4圆周角中的例3已经证明了．证明读者自己完成．*分析二如图7-91（b），设AC，BD垂直于点F．取CD的有OE∥MF．从而四边形OEFM应该是平行四边形．证明了四边形OEFM是平行四边形，问题也就解决了．而证明四边形OEFM是平行四边形已经没有什么困难了．*分析三如图7-91（b），通过AC，BD的交点F作AB的垂线交CD于点M．连结线段EF，MO．由于OE⊥AB，FM⊥AB，所以OE∥FM．又由于EF⊥CD（见例1的点评），MO⊥CD，所以EF∥MO．所以四边形OEFM为平行四边形．从而OE=MF，而由例3 求证：圆内接四边形对边乘积的和等于对角线的乘积，即图中AB·CD+BC·AD=AC·BD．分析在AB·CD+BC·AD=AC·BD中，等号左端是两个乘积的和，要证明这种等式成立，常需把左端拆成两个单项式来证明，即先考虑AB·CD和BC·AD各等于什么，然后再考虑AB·CD+BC·AD是否等于AC·BD．而要考虑AB·CD和BC·AD各等于什么，要用到相似三角形．为此，如图7-92，作AE，令∠BAE=∠CAD，并且与对角线BD相交于点E，这就得到△ABE∽△ACD．由此求得AB·CD=AC·BE．在圆中又出现了△ABC∽△AED，由此又求得BC·AD=AC·ED．把以上两个等式左右各相加，问题就解决了．证明读者自己完成．点评本例叫做托勒玫定理．它在计算与证明中都很有用．意一点．求证：PA=PB+PC．分析一本例是线段和差问题，因此可用截取或延长的方法证明．如图7-93（a），在PA上取点M，使PM=PB，剩下的问题是证明MA=PC，这只要证明△ABM≌△CBP就可以了．证明读者自己完成．分析二如图7-93（a），在PA上取点M，使MA=PC，剩下的问题是证明PM=PB，这只要证明△BPM是等边三角形就可以了．证明读者自己完成．分析三如图7-93（b），延长CP到M，使PM=PB，剩下的问题是证明PA=MC，这只要证明△PAB≌△CMB就可以了．证明读者自己完成．读者可仿以上的方法拟出本例的其他证明．*本例最简单的证明是利用托勒玫定理（例3）．证明由托勒玫定理得PA·BC=PB·AC+PC·AB，由于BC=AC=AB，所以有PA=PB+PC．例2 如图7—116，⊙O1和⊙O2都经过A、B两点，经过点A的直线CD与⊙O1交于点C，与⊙O2交于点D．经过点B的直线EF与⊙O1交于点E，与⊙O2交于点F．求证：CE∥DF．分析：要证明CE∥DF．考虑证明同位角(或内错角)相等或同旁内角互补．由于CE、DF分别在两个圆中，不易找到角的关系，若连结AB，则可构成圆内接四边形，利用圆内接四边形的性质定理可沟通两圆中有关角的关系．证明：连结AB．∵ABEC是圆内接四边形，∵ADFB是圆内接四边形，∴∠BAD＋∠F=180°，∴∠E＋∠F=180°．∴CE∥CF．说明：(1)本题也可以利用同位角相等或内错角相等，两直线平行证明．如延长EF至G，因为∠DFG=∠BAD，而∠BAD=∠E，所以∠DFG=∠E．(2)应强调本题的辅助线是为了构成圆内接四边形，以利用它的性质，导出角之间的关系．(3)对于程度较好的学生，还可让他们进一步思考，若本题不变，但不给出图形，是否还有其他情况？问题提出后可让学生自己画图思考，通过讨论明确本题还应有如图7—117的情况并给予证明．例3 如图7—118，已知在△ABC中，AB=AC，BD平分∠B，△ABD的外接圆和BC 交于E．求证：AD=EC．分析：要证AD=EC，不能直接建立它们的联系，考虑已知条件可知∠ABD=∠DBE，容易看出．若连结DE，则有AD=DE．因此只要证DE=EC．由于DE和EC为△DEC的两边，所以只要证∠EDC=∠C．由已知条件可知∠C=∠ABC．因此只要证∠EDC=∠ABC．因为△EDC是圆内接四边形ABED的一个外角，所以可证∠EDC=∠ABC．问题可解决．证明：连结DE．∵BD平分∠ABC，∴，AD=DE．∵ABED是圆内接四边形，∵AB=AC，∴∠ABC=∠C，∴∠EDC＝∠C．于是有DE=EC．因此AD=EC．四、作业1．如图7—120，在圆内接四边形ABCD中，AC平分BD，并且AC⊥BD，∠BAD=70°18′，求四边形其余各角．2．圆内接四边形ABCD中，∠A、∠B、∠C的度数的比为2∶3∶6，求四边形各内角的度数．3．如图7—121，AD是△ABC外角∠EAC的平分线，AD与三角形的外接圆交于点D．求证：DB=DC．作业答案或提示：1．∠ABC=∠ADC=90°，∠BCD=109°42′．2．∠A=45°，∠B=67.5°，∠C=135°，∠D=112.5°．3．提示：因为∠DBC=∠DAC，∠EAD=∠DCB，∠EAD=∠DAC，所以∠DBC=∠DCB，因此DB=DC．判定四点共圆的方法引导学生归纳判定四点共圆的方法：(1)如果四个点与一定点距离相等，那么这四个点共圆．(2)如果一个四边形的一组对角互补，那么这个四边形的四个顶点共圆．(3)如果一个四边形的一个外角等于它的内对角，那么这个四边形的四个顶点共圆．(4)如果两个直角三角形有公共的斜边，那么这两个三角形的四个顶点共圆(因为四个顶点与斜边中点距离相等)．3．如图7—124，已知ABCD为平行四边形，过点A和B的圆与 AD、BC分别交于E、F．求证：C、D、E、F四点共圆．提示连结EF．由∠B+∠AEF=180°，∠B＋∠C=180°，可得∠AEF=∠C．四点共圆的应用山东宁阳教委教研室栗致根四点共圆在平面几何证明中应用广泛，熟悉这种应用对于开阔证题思路，提高解题能力都是十分有益的．一用于证明两角相等例1 如图1，已知P为⊙O外一点，PA切⊙O于A，PB切⊙O于B，OP交AB 于E．求证：∠APC＝∠BPD．证明连结OA，OC，OD．由射影定理，得AE2=PE·EO，又AE＝BE，则AE·BE ＝PE·EO……(1)；由相交弦定理，得AE·BE＝CE·DE……(2)；由(1)、(2)得CE·ED＝PE·EO，∴ P、C、O、D四点共圆，则∠1＝∠2，∠3＝∠4，又∠2=∠4．∴∠1＝∠3，易证∠APC＝∠BPD(∠4＝∠EDO)．二用于证明两条线段相筹例2 如图2，从⊙O外一点P引切线PA、PB和割线PDC，从A点作弦AE平行于DC，连结BE交DC于F，求证：FC＝FD．证明连结AD、AF、EC、AB．∵PA切⊙O于A，则∠1＝∠2．∵AE∥CD，则∠2＝∠4．∴∠1=∠4，∴P、A、F、B四点共圆．∴∠5＝∠6，而∠5＝∠2=∠3，∴∠3＝∠6．∵AE∥CD，∴EC=AD，且∠ECF=∠ADF，∴△EFC≌△AFD，∴FC＝FD．三用于证明两直线平行例3 如图3，在△ABC中，AB=AC，AD⊥BC，∠B的两条三等分线交AD于E、G，交AC于F、H．求证：EH∥GC．证明连结EC．在△ABE和△ACE中，∵AE＝AE，AB=AC，∠BAE＝∠CAE，∴△AEB≌AEC，∴∠5＝∠1＝∠2，∴B、C、H、E四点共圆，∴∠6＝∠3．在△GEB 和△GEC中，∵GE＝GE，∠BEG＝∠CEG，EB＝EC，∴△GEB≌△GEC，∴∠4=∠2＝∠3，∴∠4＝∠6．∴EH∥GC．四用于证明两直线垂直证明在△ABD和△BCE中，∵AB=BC，∠ABD＝∠BCE，BD＝CE，则△ABD≌△BCE，∴∠ADB=∠BEC，∴P、D、C、E四点共圆．设DC的中点为O连结OE、DE．易证∠OEC＝60°，∠DEO＝30°∴∠DEC＝90°，于是∠DPC=90°，∴ CP⊥AD．五用于判定切线例5 如图5，AB为半圆直径，P为半圆上一点，PC⊥AB于C，以AC为直径的圆交PA于D，以BC为直径的圆交PB于E，求证：DE是这两圆的公切线．证明连结DC、CE，易知∠PDC＝∠PEC＝90°，∴ P、D、C、E四点共圆，于是∠1=∠3，而∠3＋∠2＝90°，∠A＋∠2=90°，则∠1＝∠A，∴DE是圆ACD 的切线．同理，DE是圆BCE的切线．因而DE为两圆的公切线六用于证明比例式例6 AB、CD为⊙O中两条平行的弦，过B点的切线交CD的延长线于G，弦PA、PB分别交CD于E、F．证明如图6．连结BE、PG．∵BG切⊙O于B，则∠1=∠A．∵AB∥CD，则∠A＝∠2．于是∠1＝∠2，∴P、G、B、E四点共圆．由相交弦定理，得EF·FG=PF·FB．在⊙O中，由相交弦定理，得CF·FD=FP·FB．七用于证明平方式例7 ABCD为圆内接四边形，一组对边AB和DC延长交于P点，另一组对边AD和BC延长交于Q点，从P、Q引这圆的两条切线，切点分别是E、F，(如图 7)求证：PQ2＝QF2＋PE2．证明作△DCQ的外接圆，交PQ于M，连结MC，∵∠1=∠2＝∠3，则P、B、C、M四点共圆．由圆幂定理得PE2＝PC·PD＝PM·PQ，QF2=QC·QB＝QM·QP，两式相加得PE2＋QF2＝PM·PQ＋ QM·QP=PQ(PM＋QM)＝PQ·PQ=PQ2∴PQ2=PE2＋QF2．八用于解计算题例8如图8，△ABC的高AD的延长线交外接圆于H，以AD为直径作圆和AB、AC分别交于E、F点，EF交 AD于 G，若 AG=16cm，AH=25cm，求 AD的长．解连结DE、DF、BH．∵∠1=∠2＝∠C=∠H，∴B、E、G、H四点共圆．由圆幂定理，得AE·AB＝AG·AN．在△ABD中，∵∠ADB=90°，DE⊥AB，由射影定理，得AD2＝AE·AB，∴AD2＝AG·AH＝16×25＝400，∴AD=20cm．九用于证明三点共线例9如图9，D为△ABC外接圆上任意一点，E、F、G为D点到三边垂线的垂足，求证：E、F、G三点在一条直线上．证明连结EF、FG、BD、CD．∵∠BED=∠BFD=90°，则B、E、F、D四点共圆，∴∠1＝∠2，同理∠3＝∠4．在△DBE和△DCG中，∵∠DEB＝∠DGC，∠DBE＝∠DCG，故∠1=∠4，易得∠2＝∠3，∴ E、F、G三点在一条直线上．十用于证明多点共圆例10如图10，H为△ABC的垂心，H1、H2、H3为H点关于各边的对称点，求证：A、B、C、H1、H2、H3六点共圆．证明连结AH2，∵H与H2关于AF对称，则∠1=∠2．∵A、F、D、C四点共圆，则∠2＝∠3，于是∠1＝∠3，∴A、H2、B、c四点共圆，即H2在△ABC的外接圆上．同理可证，H1、H3也在△ABC的外接圆上．∴A、B、C、H1、H2、H3六点共圆．托勒密定理的数形转换功能山东临沂市四中姜开传临沂市第一技校刘久松圆内接四边形两组对边乘积的和等于其对角线的乘积，即在四边形 ABCD 中，有AB·CD＋AD·BC=AC·BD，这就是著名的托勒密定理．本刊1996年第2期给出了它的几种证法，作为续篇，本文就其数形转换功能举例说明如下：1 “形”转换为“数”对于某些几何问题，特别是圆内接多边形问题，如果能根据题设中隐含的数量关系，利用托勒密定理可将“形”转换为“数”，从而达到用代数运算来代替几何推理的目的．例1已知正七边形A1A2 (7)(第21届全俄数学奥林匹克竞赛题)对于这道竞赛题，原证较繁，但通过深挖隐含条件，利用托勒密定理可改变整个解题局面，使证题步骤简缩到最少．如图1，连 A1A5、A3A5，则A1A5=A1A4、A3A5=A1A3．在四边形A1A3A4A5中，由托勒密定理，得A3A4·A1A5＋A4A5·A1A3＝A1A4·A3A5，即A1A2·A1A4＋A1A2·A1A3＝A1A3·A1A4，两边同除以A1A2·A1A3·A1A4即得结论式．例2 如图2，A、B、C、D四点在同一圆周上，且BC＝CD＝4，AE=6，线段BE和DE的长都是整数，则BD的长等于多少？(1988年全国初中数学联赛题)此题若用其它方法解，往往使人一筹莫展．若运用托勒密定理，可使问题化难为易．由△CDE∽△BAE和△CBE∽△DAE，得由托勒密定理，得BD(AE＋CE)=4(AB＋AD)，亦即 CE(AE＋CE)＝16．设CE=x，整理上式，得x2＋6x－16＝0．解得x＝2(负值已舍)，故BE·DE＝CE·AE＝12．∵BD＜BC＋CD＝8，例3一个内接于圆的六边形，其五个边的边长都为81，AB是它的第六边，其长为31，求从B出发的三条对角线长的和．(第九届美国数学邀请赛试题)原解答过程冗长．若通过托勒密定理的桥梁作用，把“形”转换为“数”，可使问题化繁为简．如图3，设BD=a， BE=b，BF＝c，连AC、CE、AE，则CE＝AE＝BD＝a，AC=BF ＝c．在四边形BCDE中，由托勒密定理，得81b＋812＝a2①同理81b＋31·81=ac ②31a＋81a=bc ③解①、③、③组成的方程组，得a＝135，b＝144，c＝105故 a＋b＋c=384．2 “数”转换为“形”对于某些代数问题，若结构与托勒密定理相似，通过构造圆内接四边形，可把“数”转换为“形”，然后利用“形”的性质，使问题得到解决．这种解法构思巧妙，方法独特，富于创新，出奇制胜．例4 解方程若按常规方法解这个无理方程，过程繁冗．若由方程的结构特征联想到托勒密定理，则构造直径AC=x(x≥11)的圆及圆内接四边形ABCD，使BC=2，CD=11，如图 4，于是由托勒密定理，得在△BCD中，由余弦定理，得经检验x=14是原方程的根．求证： a2＋b2＝1．这道名题已有多种证法，而且被视为用三角换无法解代数问题的典范．下面再给出一各几何证法．易知0≤a、b≤1且a、b不全为零．当a、b之一为零时，结论显然成立．当a、b全不为零时，由已知等式联想到托勒密定理，作直径AC＝1的圆及圆内接四与已知等式比较，得BD＝1，即BD也为圆的直径，故a2＋b2=1例6设a＞c，b＞c，c＞0，此题若用常规方法证明也不轻松．下面利用托勒密定理给出它的一个巧证．由托勒密定理，得巧用托勒密定理证题河北晋州市数学论文研究协会张东海王素改在解证某些数学题时，如能巧用托勒密定理，可使解证过程简洁清新，兹举例说明．托勒密定理：圆内接四边形中，两条对角线的乘积等于两组对边乘积之和．一、构造“圆”，运用定理【例1】设a，b，x，y是实数，且a2＋b2=1，x2＋y2=1．求证：ax＋by≤1．证作直径AB=1的圆，在AB的两侧任作Rt△ACB和Rt△ADB，使AC=a，BC=b，BD=x， AD=y．(图1)由勾股定理知a，b，x，y满足条件．根据托勒密定理，有AC·BD＋BC·AD=AB·CD．∵ CD≤1，∴ax＋by≤1．二、利用无形圆，运用定理【例2】等腰梯形一条对角线的平方，等于一腰的平方加上两底之积．已知：梯形 ABCD中，AD=BC，AB∥CD．求证：BD2=BC2＋AB·CD．证∵等腰梯形内接于圆，由托勒密定理，有AC·BD=AD·BC＋AB·CD．∵AD=BC，AC=BD，∴BD2=BC2＋AB·CD．(图略)【例 3】已知：边长为 1的正七边形ABCDEFG中，对角线 AD=a，BG=b(a≠b)．求证：(a＋b)2(a－b)＝ab2．证连结BD，GE，BE，DG，则 BD=EG＝GB=b，DG=BE＝DA＝a， DE=AB=AG=1．(如图2)在四边形ABDG中，由托勒密定理，有AD·BG=AB·DG＋BD·AG，即ab=a＋b (1)同理在四边形BDEG中，得BE·DG=DE·BG＋BD·EG，即a2=b＋b2 (2)将(2)变形为b=a2－b2 (3)(1)×(3)，得ab2＝(a＋b)(a2－b2)．故ab2=(a＋b)2(a－b)．三、构造圆内接四边形，运用定理【例4】在△ABC中，∠A的内角平分线AD交外接圆于D．连结BD．求证：AD·BC=BD·(AB＋AC)．证(如图3) 连结DC．由托勒密定理．有AD·BC=AB·CD＋AC·BD．又∵∠1=∠2，∴BD=DC．∴AD·BC=AB·CD＋AC·BD=BD(AB＋AC)．即AD·BC=BD·(AB＋AC)．圆内接四边形的面积公式黑龙江绥化五中任天民设圆内接四边形ABCD中各边为a，b，c，d．连结 BD．由∠A＋∠C=180°，可以推出sinA=sinC，cosA=－cosC．并且S四边形ABCD=S△ABD＋S△BCD所以这样我们得出了圆内接四边形面积的计算公式．在上面的公式中，如果设某一边为零，(不仿设d=0)此时四边形变成三角形，该公式恰是计算三角形面积的海伦公式．圆内接四边形面积公式的得出是受三角形面积公式的启发，通过联想探索出来的，而且两者在形式上又是那么的相近．这种现象在数学中不胜枚举，如果同学们都能从特殊规律去探索一般规律，再从一般规律去认识特殊规律．那么对数学能力的培养将大有裨益．四条边定长四边形面积的最大值上海市育群中学李甲鼎四条边为定长的四边形不具稳定性，但在某种特定的位置下，它能内接于圆，成为圆内接四边形．并且此时达到变化过程中面积最大值．下文证明这个事实．已知：四边形ABCD中：AB＝a，BC＝b，CD=c，DA=d求证：四边形ABCD中有唯一四边形能内接于圆，且此时面积达到最大值．证明：(1)先证四边形四边定长，有唯一的四边形内接于圆，设∠ABC=α，∠ADC=β，AC=x．令α＋β=π，即cosα＋cosβ=0x的解唯一确定，代入(1)(2)后cosα、cosβ也随之唯一确，在α，β∈(0，π)的条件下α、β也同时唯一确定．∴四边形四边定长，对角互补，四边形是唯一的．即所得到的四边形为圆内接四边形．(2)当四边定长的四边形内接于圆时，此四边形面积最大．∵四边形ABCD的面积由余弦定理得a2＋b2－2abcosα=x2=c2＋d2－2cdcosβ显然当α＋β=π时(即为圆内接四边形时)S2达到最大值，即S最大．一个几何定理的应用江苏省徐州矿务局庞庄职校张怀林定理：如图1，在圆接四边形ABCD中弦AD平分∠BAC，则2ADcosα=AB＋AC．证明连接BD、DC、BC，设已知圆半径为R，则由正弦定理有：BD＝DC＝2Rsinα，BC＝2Rsin2α．由托勒密定理有AB·CD+AC·BD=AD·DC．∴(AB+AC)·2Rsinα=AD·2Rsin2α．则 2AD·cosα=AB＋AC．下面举例说明它的应用．例1如图2，已知锐角△ABC的∠A平分线交BC于L，交外接圆于N，过L 分别作LK⊥AB，LM⊥AC，垂足分别为K、M．求证：四边形AKNM的面积等于△ABC 的面积．(第28届IMO)证明由已知得∠BAN=∠CAN，由定理有 2ANcosα=AB＋AC，=AN·AL·cosα·sinα=AN·AK·sinα=AN·AM·sinα=2S△AKN＝2S△AMN．∴S△ABC=S四边形AKNM．(第21届全苏奥数)证明作正七边形外接圆，如图3所示．由定理有2c·cosα=b+c，又在等腰△A1A2A3中有2a·cosα=b．例3在△ABC中，∠C=3∠A，a＝27，c＝48，则b的值是____．(第36届AHSME试题) 解如图4．作△ABC的外接圆，在取三等分点D、E，连CD、CE．由已知得：∠ACD=∠DCE=∠ECB=∠A，CD=AB=48，由定理有 2CE·cosA=CB+CD ①2CD·cosA＝CE+AC ②又2CB·cosA=CE ③由②、③得：b=AC=CE·(CD-CB)/CB=35．托勒密定理及其应用河北省晋州市数学论文研究协会刘同林托勒密定理：圆内接四边形中，两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和)．已知：圆内接四边形ABCD，求证：AC·BD＝AB·CD＋AD·BC．证明：如图1，过C作CP交BD于P，使∠1=∠2，又∠3=∠4，∴△ACD∽△BCP．又∠ACB=∠DCP，∠5=∠6，∴△ACB∽△DCP．①＋②得 AC(BP＋DP)=AB·CD＋AD·BC．即AC·BD=AB·CD＋AD·BC．这就是著名的托勒密定理，在通用教材中习题的面目出现，不被重视．笔者认为，既然是定理就可作为推理论证的依据．有些问题若根据它来论证，显然格外简洁清新．兹分类说明如下，以供探究．一、直接应用托勒密定理例1如图2，P是正△ABC外接圆的劣弧上任一点(不与B、C重合)，求证：PA=PB＋PC．分析：此题证法甚多，一般是截长、补短，构造全等三角形，均为繁冗．若借助托勒密定理论证，则有PA·BC=PB·AC＋PC·AB，∵AB=BC=AC．∴PA=PB+PC．二、完善图形借助托勒密定理例2证明“勾股定理”：在Rt△ABC中，∠B=90°，求证：AC2=AB2＋BC2证明：如图3，作以Rt△ABC的斜边AC为一对角线的矩形ABCD，显然ABCD 是圆内接四边形．由托勒密定理，有AC·BD=AB·CD＋AD·BC．①又∵ABCD是矩形，∴AB=CD，AD=BC，AC=BD．②把②代人①，得AC2=AB2＋BC2．例3如图4，在△ABC中，∠A的平分线交外接∠圆于D，连结BD，求证：AD·BC=BD(AB＋AC)．证明：连结CD，依托勒密定理，有AD·BC＝AB·CD＋AC·BD．∵∠1=∠2，∴ BD=CD．故 AD·BC=AB·BD＋AC·BD=BD(AB＋AC)．三、利用“无形圆”借助托勒密定理例4等腰梯形一条对角线的平方等于一腰的平方加上两底之积．如图5，ABCD中，AB∥CD，AD=BC，求证：BD2=BC2＋AB·CD．证明：∵等腰梯形内接于圆，依托密定理，则有AC·BD=AD·BC＋AB·CD．又∵ AD=BC，AC=BD，∴BD2=BC2＋AB·CD．四、构造图形借助托勒密定理例5若a、b、x、y是实数，且a2＋b2=1，x2＋y2=1．求证：ax＋by≤1．证明：如图6，作直径AB=1的圆，在AB两边任作Rt△ACB和Rt△ADB，使AC＝a，BC=b，BD＝x，AD＝y．由勾股定理知a、b、x、y是满足题设条件的．据托勒密定理，有AC·BD＋BC·AD=AB·CD．∵CD≤AB＝1，∴ax＋by≤1．五、巧变原式妙构图形，借助托勒密定理例6已知a、b、c是△ABC的三边，且a2=b(b＋c)，求证：∠A=2∠B．分析：将a2=b(b＋c)变形为a·a=b·b＋bc，从而联想到托勒密定理，进而构造一个等腰梯形，使两腰为b，两对角线为a，一底边为c．证明：如图 7，作△ABC的外接圆，以 A为圆心，BC为半径作弧交圆于D，连结BD、DC、DA．∵AD=BC，∴∠ABD=∠BAC．又∵∠BDA=∠ACB(对同弧)，∴∠1=∠2．依托勒密定理，有BC·AD=AB·CD＋BD·AC．①而已知a2=b(b＋c)，即a·a=b·c＋b2．②∴∠BAC=2∠ABC．六、巧变形妙引线借肋托勒密定理例7在△ABC中，已知∠A∶∠B∶∠C=1∶2∶4，析证：将结论变形为AC·BC＋AB·BC=AB·AC，把三角形和圆联系起来，可联想到托勒密定理，进而构造圆内接四边形．如图8，作△ABC的外接圆，作弦BD=BC，边结AD、CD．在圆内接四边形ADBC中，由托勒密定理，有AC·BD＋BC·AD=AB·CD易证AB=AD，CD=AC，∴AC·BC＋BC·AB=AB·AC，关于圆内接四边形的若干共点性质浙江绍兴县鲁迅中学范培养设四边形ABCD内接于圆O，其边AB与DC的延长线交于P，AD与BC的延长线交于Q，由P作圆的两切线PM、PN，切点分别为M、N；由Q作圆的两切线QE、QF，切点分别为E、F(如图1)．则有以下一些共点性质：性质1 AC、BD、EF三直线共点．证明：如图1，设AC交EF于K1，则K1分EF所成的比为设BD交EF于K2，同理可得K2分EF所成的比为由(5)、(6)可得(1)=(2)，故K1、K2分EF所成的比相等．∴K1、K2重合，从而AC、BD、EF三直线共点．类似地 AC、BD、MN三直线共点，因此有以下推论 AC、BD、EF、MN四直线共点．性质2 AB、DC、EF三直线共点于P．(此性质等同于1997年中国数学奥林匹克第二试第四题)这里用上述证明性质1的方法证之．证明：如图2．设DC与EF的延长线交于P1，则P1分EF所成的比为设AB与EF的延长线交于P2，则P2分EF所成的比为由(5)、(6)可得(7)=(8)，故P1、P2分EF所成的比相等．∴P1、P2重合，从而AB、DC、EF三直线共点于P．推论 AD、BC、NM三直线共点于Q．性质 3 EM、NF、PQ三直线共点．证明：如图3，设EM的延长线交PQ于G1，妨上证法，G1分PQ所成的比为设NF的延长线交PQ于G2，则G2分PQ所成的比为(这里E、F、P三点共线及N、M、Q三点共线在性质2及推论中已证)．由△PME∽△PFM得由(11)、(12)及QE=QF、PN=PM可得(9)=(10)，故G1、G2分PQ所成的比相等．∴G1、G2重合，从而EM、NF、PQ三直线共点．性质4如果直线EN和MF相交，那么交点在直线PQ上，即 EN、MF、PQ三直线共点．证明从略，妨性质3的证法可得．性质5 EM、NF、AC三直线共点．证明：如图4，类似于性质1的证明，设EM与AC的延长线交于G3，则G3分AC所成的比为设NF与AC的延长线交于G4，则G4分AC所成的比为由(15)、(18)、(19)可得(13)=(14)，故G3、G4分AC所成的比相等．∴G3、G4重合，从而 EM、NF、AC 三直线共点．推论EM、NF、AC、PQ四直线共点．限于篇幅，仅列以上五条共点性质．有兴趣的读者不妨再探索其它共点性质例3在边长为a的正七边形ABCDEFG中，两条不相等的对角线长分别为t，m．证明如图4，连结AD、CE，令AE＝t，AC＝m，在圆内接四边形ACDE中，据托勒密定理，有AD·CE＝AE·CD＋AC·DE，即tm＝ta＋ma．托勒密定理及其应用河北省晋州市数学论文研究协会康美娈彭立欣托勒密定理圆内接四边形的两条对角线的乘积(两条对角线所包矩形的面积)，等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形面积之和)．证明如图1，过C作CP使∠1=∠2，又∠3＝∠4，∴△ACD∽△BCP．∴AC·BP=AD·BC ①又∠ACB=∠DCP，∠5=∠6，∴AC·DP=AB·CD．②①+②得AC(BP+PD)=AD·BC+AB·CD.故AC·BD=AD·BC+AB·CD.托勒密定理在教材中仅以习题的形式出现，若以此定理为根据，可使许多问题解证过程别具一格.例1已知P是正△ABC的外接圆劣弧上任意一点.求证:PA=BP+PC.证明如图2,ABPC是圆内接四边形,根据托勒密定理,有PA·BC=PB·AC+PC·AB.∵AB=BC=AC,∴PA=PB+PC.例2证明等腰梯形一条对角线的平方，等于一腰的平方加上两底之积．证明如图3，设在梯形ABCD中，AD=BC，AB∥CD．∵等腰梯形内接于圆，∴AC·BD=AD·BC+AB·CD．又AD＝BC，AC＝BD，∴BD2=BC2＋AB·CD．例3在边长为a的正七边形ABCDEFG中，两条不相等的对角线长分别为t，m．证明如图4，连结AD、CE，令AE＝t，AC＝m，在圆内接四边形ACDE中，据托勒密定理，有AD·CE＝AE·CD＋AC·DE，即tm＝ta＋ma．例4已知 a、b、x、y是实数，且a2＋b2=1，x2+y2=1．求证：ax＋by≤1．证明作直径AB=1的圆，在AB两侧作Rt△ACB和Rt△ADB，使AC=a，BC=b，BD=x，DA=y(如图5)．依勾股定理知a、b、x、y是满足题设条件的．依托勒密定理有AC·BD＋BC·AD＝AB·CD．又∵CD≤AB=1，∴ax+by≤1．例5△ABC的三个内角 A、 B、 C的对边分别为a、b、c，且a2=b(b＋c)．求证：A=2B．分析将a2＝b(b＋c)变形为a·a=b·b＋b·c，可联想到托勒密定理，进而构造一个圆内接等腰梯形，使两腰为b，两对角线为a，一底边为c．证明如图6，作△ABC的外接圆．以A为圆心，以BC为半径画弧交圆于D，连结BD、DA、DC．。

“四点共圆”模型(解析版)--初中数学专题训练

“四点共圆”模型1.识别几何模型。

2.利用“四点共圆”模型解决问题一．填空题(共3小题)1(2021秋•南京期中)如图，在⊙O的内接五边形ABCDE中，∠C=100°，BC=CD，则∠A+∠D =220°．【分析】连接BD，由∠C=100°，BC=CD得出∠CDB=40°，由四边形BAED内接于⊙O得出∠A +∠BDE=180°，即可求出答案．【解答】解：如图，连接BD，∵∠C=100°，BC=CD，∴∠CBD=∠CDB=40°，∵四边形BAED内接于⊙O，∴∠A+∠BDE=180°，∴∠A+∠CDE=∠A+∠BDE+∠CDB=180°+40°=220°，故答案为：220．【点评】本题考查了圆周角定理，掌握圆连接四边形的性质是解题的关键．2(2022•靖江市二模)如图，AB⊥BC，AB=5，点E、F分别是线段AB、射线BC上的动点，以EF 为斜边向上作等腰Rt△DEF，∠D=90°，连接AD，则AD的最小值为522．【分析】连接BD并延长，利用四点共圆的判定定理得到B，E，D，F四点共圆，再利用等腰直角三角形的性质和圆周角定理得到∠DBF=∠DEF=45°，得到点D的轨迹，最后利用垂线段最短和等腰直角三角形的性质解答即可得出结论．【解答】解：连接BD并延长，如图，∵AB⊥BC，∴∠ABC=90°，∠EDF=90°，∴∠ABC+∠EDF=180°，∴B，E，D，F四点共圆，∵△DEF为等腰直角三角形，∴∠DEF=∠DFE=45°，∴∠DBF=∠DEF=45°，∴∠DBF=∠DBE=45°，∴点D的轨迹为∠ABC的平分线上，∵垂线段最短，∴当AD⊥BD时，AD取最小值，∴AD的最小值为22AB=522，故答案为：522．【点评】本题主要考查了直角三角形的性质，等腰直角三角形的性质，四点共圆的判定圆周角定理，点的轨迹，垂线段的性质，利用已知条件求得点D 的轨迹是解题的关键．3(2022秋•大丰区期中)如图，△ABC 中，AD ⊥BC ，∠B =45°，∠C =30°．以AD 为弦的圆分别交AB 、AC 于E 、F 两点．点G 在AC 边上，且满足∠EDG =120°．若CD =4+22，则△DEG 的面积的最小值是　22+2　．【分析】连接EF ，利用四点共圆和同弧所对的圆周角相等证明EF ∥DG ，从而得到S △EDG =S △EDG ，当FG 最小时，△DFG 的面积就最小，作△DFG 的外接圆O ，过O 点作OH ⊥FG 交于点H ，连接OF 、OG ，DO +OH =(12+22)FG ，当DO +OH 最小时，FG 就最小，当D 、O 、H 三点共线时，DO +OH 最小，此时DH ⊥FG ，在Rt △FHO 中，(2FH )2=FH 2+(2+2-2FH )2，求出FH =2，可得FG 的最小值为22，再求S △DFG =22+2，即△DEG 的面积的最小值为22+2．【解答】解：连接EF ，AD ⊥BC ，∠B =45°，∠C =30°，∴∠B =45°，∠DAC =60°，∵∠BAC =105°，∵A 、E 、F 、D 四点共圆，∴∠EDF =75°，∵∠EDG =120°，∴∠FDG =45°，∵ED =ED，∴∠EFD =∠EAD =45°，∴∠EFD =∠FDG ，∴EF ∥DG ，∴S △EDG =S △EDG ，∵CD =4+22，∠C =30°，∴AC =833+463，AD =433+263，∴AC 边上的高=AD ⋅DC AC=2+2，∴当FG 最小时，△DFG 的面积就最小，作△DFG 的外接圆O ，过O 点作OH ⊥FG 交于点H ，连接OF 、OG ，∵∠FDG =45°，∴∠FOG =90°，∵OF =GO ，∴△FOG 是等腰直角三角形，∵∠FOH =12∠FOG =45°，∴△FOH 是等腰直角三角形，∴FH =OH =12FG ，FO =2FH ，∴DO +OH =22FG +12FG =(12+22)FG ，∴当DO +OH 最小时，FG 就最小，∵DO +OH ≥DH ，∴当D 、O 、H 三点共线时，DO +OH 最小，此时DH ⊥FG ，∴DH =2+2，在Rt △FHO 中，(2FH )2=FH 2+(2+2-2FH )2，解得FH =2或FH =4+32，∵OH =2+2=FH +FO ，∴FH =2，∴FG 的最小值为22，∴S △DFG =12×22×(2+2)=22+2，∴△DEG 的面积的最小值为22+2，故答案为：22+2．【点评】本题考查圆的综合应用，熟练掌握圆心角与圆周角的关系，四点共圆的性质，三角形外接圆的性质是解题的关键．二．解答题(共7小题)4(2022秋•宿城区期中)如图，BD ，CE 是△ABC 的高，BD ，CE 相交于点F ，M 是BC 的中点，⊙O 是△ABC 的外接圆．(1)点B ，C ，D ，E 是否在以点M 为圆心的同一个圆上？请说明理由．(2)若AB =8，CF =6，求△ABC 外接圆的半径长．【分析】(1)连接EM ，DM ，根据垂直定义可得∠BDC =∠BEC =90°，然后利用直角三角形斜边上的中线性质可得EM =BM =12BC ，DM =CM =12BC ，从而可得EM =BM =DM =CM ，即可解答；(2)连接AF 并延长交BC 于点G ，连接BO 并延长交⊙O 于点H ，连接AH ，CH ，根据三角形的高是交于一点的可得AG⊥BC，再根据直径所对的圆周角是直角可得∠BAH=∠BCH=90°，从而可得AG∥CH，AH∥CE，然后利用平行四边形的判定可得四边形AFCH是平行四边形，从而可得CF= AH=6，最后在Rt△BAH中，利用勾股定理进行计算即可解答．【解答】解：(1)点B，C，D，E在以点M为圆心的同一个圆上，理由：连接EM，DM，∵BD⊥AC，CE⊥AB，∴∠BDC=∠BEC=90°，∵M是BC的中点，∴EM=BM=12BC，DM=CM=12BC，∴EM=BM=DM=CM，∴点B，C，D，E在以点M为圆心的同一个圆上；(2)连接AF并延长交BC于点G，连接BO并延长交⊙O于点H，连接AH，CH，∵BD，CE是△ABC的高，BD，CE相交于点F，∴AG⊥BC，∵BH是⊙O的直径，∴∠BAH=∠BCH=90°，∴BA⊥AH，BC⊥CH，∴AG∥CH，∵CE⊥AB，∴AH∥CE，∴四边形AFCH是平行四边形，∴CF=AH=6，在Rt△BAH中，AB=8，∴BH=BA2+AH2=82+62=10，∴△ABC外接圆的半径长为5．【点评】本题考查了三角形的外接圆与外心，直角三角形斜边上的中线，点与圆的位置关系，确定圆的条件，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．5(兴化市校级期中)已知：如图，在正方形ABCD中，E、F分别是AD、CD的中点．(1)线段AF与BE有何关系．说明理由；(2)延长AF、BC交于点H，则B、D、G、H这四个点是否在同一个圆上．说明理由．【分析】(1)证明△ABE≌△DAF，证据全等三角形的对应边相等，以及直角三角形的两锐角互余即可证明AF相等且互相垂直；(2)证明△ADF≌△HCF，依据直角三角形斜边上的中线等于斜边的一半，即可证得B，C，D，H四点到C的距离相等，即可证得四点共圆．【解答】解：(1)AF=BE且AF⊥BE．证明：∵E、F分别是AD、CD的中点，∴AE=12AD，DF=12CD∴AE=DF又∵∠BAD=∠D=90°，AB=AD∴△ABE≌△DAF∴AF=BE，∠AEB=∠AFD∵在直角△ADF中，∠DAF+∠AFD=90°∴∠DAF+∠AEB=90°∴∠AGE=90°∴AF⊥BE(2)连接CG．∵DF=CF，∠D=∠FCH=90°，∠AFD=∠HFC∴△ADF≌△HCF∴BC=AD=CH=CD，在直角△BGH中，BC=CH，∴GC=12BH∴CB=CG=CD=CH，∴B，G，D，H在以C为圆心、BC长为半径的圆上．【点评】本题考查了全等三角形的判定与性质，以及直角三角形的性质，证明三角形全等是解题的关键．6(2022秋•建湖县期中)如图，在⊙O的内接四边形ABCD中，DB=DC，∠DAE是四边形ABCD 的一个外角．(1)若∠DAE=75°，则∠DAC=75°；(2)过点D作DE⊥AB于E，判断AB、AE、AC之间的数量关系并证明；(3)若AB=6、AE=2，求BD2-AD2的值．【分析】(1)根据四边形外接圆的性质，同弧所对的圆周角相等，可得∠DCB=∠DBC=∠DAC= 75°；(2)过点D作DF⊥AC于点F，可证明△BDE≌△CDF(AAS)，△ADE≌△ADF(AAS)，则AC= AF+FC=AE+BE=AE+AE+AB=2AE+AB；(3)在Rt△BDE中，BD2=64+DE2，，在Rt△AED中，AD2=4+ED2，再求解即可．【解答】解：(1)∵四边形ABCD是圆O的内接四边形，∴∠BCD+∠BAD=180°，∵∠DAE是四边形ABCD的一个外角，∴∠DAE=∠BCD，∵BD=CD，∴∠CBD=∠DCB，∵弧CD所对的圆周角分别为∠CAD、∠CBD，∴∠CBD=∠CAD，∵∠DAE=75°，∴∠DCB=∠DBC=∠DAC=75°，故答案为；75；(2)过点D作DF⊥AC于点F，∵DE⊥AB，∴∠DEA=90°，∵∠ABD=∠ACD，BD=CD，∠E=∠DFC=90°，∴△BDE≌△CDF(AAS)，∴DE=DF，AE=CF，∴∠ADE=∠ADF，又∵∠E=∠AFD，AD=AD，∴△ADE≌△ADF(AAS)，∴AE=AF，∴AC=AF+FC=AE+BE=AE+AE+AB=2AE+AB，即AC=2AE+AB；(3)在Rt△BDE中，BD2=BE2+DE2，在Rt△AED中，AD2=AE2+ED2，∵AB=6，AE=2，∴BE=8，∴BD2=64+DE2，AD2=4+ED2，∴BD2-AD2=60．【点评】本题考查圆的综合应用，熟练掌握同弧所对的圆周角相等，四点共圆的性质，直角三角形勾股定理，三角形全等的判定及性质是解题的关键．7(2023•淮安区一模)综合与实践“善思”小组开展“探究四点共圆的条件”活动，得出结论：对角互补的四边形四个顶点共圆．该小组继续利用上述结论进行探究．提出问题：如图1，在线段AC同侧有两点B，D，连接AD，AB，BC，CD，如果∠B=∠D，那么A，B，C，D四点在同一个圆上．探究展示：如图2，作经过点A，C，D的⊙O，在劣弧AC上取一点E(不与A，C重合)，连接AE，CE，则∠AEC+∠D=180°(依据1)∵∠B=∠D∴∠AEC+∠B=180°∴点A，B，C，E四点在同一个圆上(对角互补的四边形四个顶点共圆)∴点B，D在点A，C，E所确定的⊙O上(依据2)∴点A，B，C，D四点在同一个圆上反思归纳：(1)上述探究过程中的“依据1”、“依据2”分别是指什么？依据1：圆内接四边形对角互补；依据2：　过不在同一直线上的三个点有且只有一个圆　．(2)如图3，在四边形ABCD中，∠1=∠2，∠3=45°，则∠4的度数为45°．拓展探究：(3)如图4，已知△ABC是等腰三角形，AB=AC，点D在BC上(不与BC的中点重合)，连接AD．作点C关于AD的对称点E，连接EB并延长交AD的延长线于F，连接AE，DE．①求证：A，D，B，E四点共圆；②若AB=22，AD•AF的值是否会发生变化，若不变化，求出其值；若变化，请说明理由．【分析】(1)根据圆内接四边形的性质、过三点的圆解答即可；(2)根据四点共圆、圆周角定理解答；(3)①根据轴对称的性质得到AE=AC，DE=DC，∠AEC=∠ACE，∠DEC=∠DCE，进而得到∠AED=∠ABC，证明结论；②连接CF，证明△ABD∽△AFB，根据相似三角形的性质列出比例式，计算即可．【解答】(1)解：依据1：圆内接四边形对角互补；依据2：过不在同一直线上的三个点有且只有一个圆，故答案为：圆内接四边形对角互补；过不在同一直线上的三个点有且只有一个圆；(2)解：∵∠1=∠2，∴点A，B，C，D四点在同一个圆上，∴∠3=∠4，∵∠3=45°，∴∠4=45°，故答案为：45°；(3)①证明：∵AB=AC，∴∠ABC=∠ACB，∵点E与点C关于AD的对称，∴AE=AC，DE=DC，∴∠AEC=∠ACE，∠DEC=∠DCE，∴∠AED=∠ACB，∴∠AED=∠ABC，∴A，D，B，E四点共圆；②解：AD•AF的值不会发生变化，理由如下：如图4，连接CF，∵点E与点C关于AD的对称，∴FE=FC，∴∠FEC=∠FCE，∴∠FED=∠FCD，∵A，D，B，E四点共圆，∴∠FED=∠BAF，∴∠BAF=∠FCD，∴A，B，F，C四点共圆，∴∠AFB=∠ACB=∠ABC，∵∠BAD=∠FAB，∴△ABD∽△AFB，∴AD AB =AB AF，∴AD•AF=AB2=8．【点评】本题考查的是四点共圆、相似三角形的判定和性质、轴对称的性质，正确理解四点共圆的条件是解题的关键．8(2022秋•靖江市期末)小明在学习了《圆周角定理及其推论》后，有这样的学习体会：在Rt△ABC 中，∠C=90°，当AB长度不变时，则点C在以AB为直径的圆上运动(不与A、B重合)．[探索发现]小明继续探究，在Rt△ABC中，∠C=90°，AB长度不变．作∠A与∠B的角平分线交于点F，小明计算后发现∠AFB的度数为定值，小明猜想点F也在一个圆上运动．请你计算∠AFB的度数，并简要说明小明猜想的圆的特征．[拓展应用]在[探索发现]的条件下，若AB=23，求出△AFB面积的最大值．[灵活运用]在等边△ABC中，AB=23，点D、点E分别在BC和AC边上，且BD=CE，连接AD、BE交于点F，试求出△ABF周长的最大值．【分析】[探索发现]根据角平分线的定义，三角形内角和定理可求∠AFB=135°，再由已知结论可得F点在以AB为定弦，∠AFB为定角的圆上；[拓展应用]设F点在圆O上，连接OA、OB，则O与C点共圆；过点F作FH⊥AB交于点H，设AB的中点为D，当H点与D点重合时，FH的长度最大，此时△FBA的面积最大，△FAB是等腰三角形，求出FD的长再求三角形面积即可；[灵活运用]通过证明△ABD≌△BCE(SAS)，可得∠AFB=120°，再由题干已知可知F点在以AB 为定弦，∠AFB为定角的圆上，设△ABF的外接圆为O，当△ABF的高经过圆心O时，△ABF的周长有最大值，此时△ABF是等腰三角形．【解答】解：[探索发现]∵∠ACB=90°，∴∠CAB+∠CBA=90°，∵AF是∠CAB的平分线，BF是∠CBA的平分线，∴∠FAB+∠FBA=45°，∴∠AFB=135°，∴F点在以AB为定弦，∠AFB为定角的圆上；[拓展应用]设F点在圆O上，连接OA、OB，∵∠AOB=90°，∵∠ACB+∠AOB=180°，∴O与C点共圆，过点F作FH⊥AB交于点H，设AB的中点为D，当H点与D点重合时，FH的长度最大，此时△FBA的面积最大，∵FH⊥AB，D是AB的中点，∴FA=FB，∵∠AFB=135°，∴∠FAB=∠FBA=22.5°，∴∠CAB=∠CBA=45°，∴△ABC是等腰直角三角形，连接CF，则C、F、D三点共线，过点F作FP⊥AC交于点P，∴FP=FD，AP=AD，∵AB=23，∴AC=6，AD=AP=3，∴CP=6-3，∵∠FCP=45°，∴CF=2CP=23-6，∴FD=3-(23-6)=6-3，×23×(6-3)=32-3，∴△AFB的面积=12∴△AFB面积的最大值为32-3；[灵活运用]∵△ABC是等边三角形，∴AB=BC，∠ACB=∠ABC=60°，∵BD=CE，∴△ABD≌△BCE(SAS)，∴∠CBE=∠BAD，∴∠AFE=∠ABF+∠BAF=∠ABF+∠CBE=∠ABC=60°，∴∠AFB=120°，∵AB=23，∴F点在以AB为定弦，∠AFB为定角的圆上，设△ABF的外接圆为O，当△ABF的高经过圆心O时，△ABF的周长有最大值，连接AO、BO，∵∠AFB=120°，∴∠AOB=120°，∵OA=BO，∴∠OAB=30°，∵AB=23，∴AH=3，在Rt△AOH中，OH=AH•tan30°=1，OA=2OH=2，∴HF=OF-OH=1，∴AF=BF=2，∴△ABF周长的最大值为4+23．【点评】本题考查圆的综合应用，熟练掌握三角形全等的判定及性质，定角定弦的三角形与圆的关系是解题的关键．9(2022秋•鼓楼区期中)以下是“四点共圆”的几个结论，你能证明并运用它们吗？Ⅰ．若两个直角三角形有公共斜边，则这两个三角形的4个顶点共圆(图1、2)；Ⅱ．若四边形的一组对角互补，则这个四边形的4个顶点共圆(图3)；Ⅲ．若线段同侧两点与线段两端，点连线的夹角相等，则这两点和线段两端点共圆(图4)．(1)在图1、2中，取AC的中点O，根据直角三角形斜边上的中线等于斜边的一半得OA=OB=OC =OD，即A，B，C，D共圆；(2)在图3中，画⊙O经过点A，B，D(图5)．假设点C落在⊙O外，BC交⊙O于点E，连接DE，可得∠BED+∠A=180°，所以∠BED=180°-∠A，得出矛盾；同理点C也不会落在⊙O内，即A，B，C，D共圆．结论Ⅲ同理可证．(3)利用四点共圆证明锐角三角形的三条高交于一点．已知：如图6，锐角三角形ABC的高BD，CE相交于点H，射线AH交BC于点F．求证：AF是△ABC的高．(补全以下证明框图，并在图上作必要标注)(4)如图7，点P是△ABC外部一点，过P作直线AB，BC，CA的垂线，垂足分别为E，F，D，且点D，E，F在同一条直线上．求证：点P在△ABC的外接圆上．【分析】(1)根据直角三角形斜边中线的性质可得结论；(2)由圆周角的性质可得∠BED+∠A=180°，再结合题干条件，得出矛盾，由此可得出结论；(3)如图，连接DE，由点B、C、D、E四点共圆得∠BDE=∠ECB，由点A、D、H、E四点共圆得∠BDE=∠BAF，从而证明∠BAF+∠ABF=90°即可；(4)连接BP和CP，由点A，E，P，F四点共圆可得，∠BEF=∠BPF，由点C，P，D，F四点共圆可得∠CDF=∠CPF，再由外角的性质及角的和差可得∠BAC=∠BPC，由此可得点A，B，C，P四点共圆，即点P在△ABC的外接圆上．【解答】解：(1)在图1、2中，取AC的中点O，根据直角三角形斜边上的中线等于斜边的一半，得OA =OB=OC=OD，即A，B，C，D共圆；故答案为：直角三角形斜边上的中线等于斜边的一半；(2)在图3中，画⊙O经过点A，B，D(图5)．假设点C落在⊙O外，BC交⊙O于点E，连接DE，可得∠BED+∠A=180°，∴∠BED=180°-∠A，得出矛盾；同理点C也不会落在⊙O内，即A，B，C，D共圆．结论Ⅲ同理可证．故答案为：∠BED+∠A；180°-∠A；(3)如图6，连接DE，由点B、C、D、E四点共圆得∠BDE=∠ECB，由点A、D、H、E四点共圆得∠BDE=∠BAF，∴∠ECB=∠BAF，∵∠BEC=90°，∴∠ECB+∠ABF=90°，∴∠BAF+∠ABF=90°，∴∠BFA=90°，∴AF为△ABC的边BC上的高．(4)如图7，连接BP和CP，由点A，E，P，F四点共圆可得∠BEF=∠BPF，由点C，P，D，F四点共圆可得∠CDF=∠CPF，∵∠ADE=∠CDF，∴∠ADE=∠CPF，∵∠BAC=∠BEF+∠ADE，∠BPC=∠BPF+∠CPF，∴∠BAC=∠BPC，∴点A，B，C，P四点共圆，即点P在△ABC的外接圆上．【点评】本题考查了圆的定义，直角三角形斜边上的中线等于斜边一半，圆内接四边形对角互补，圆周角定理，内心的定义．第(3)(4)题解题关键是选取适当的四点证明共圆，再利用圆周角定理证明角相等．10(2022秋•仪征市期中)【问题提出】苏科版九年级(上册)教材在探究圆内接四边形对角的数量关系时提出了两个问题：1．如图(1)，在⊙O的内接四边形ABCD中，BD是⊙O的直径．∠A与∠C、∠ABC与∠ADC有怎样的数量关系？2．如图(2)，若圆心O不在⊙O的内接四边形ABCD的对角线上，问题(1)中发现的结论是否仍然成立？(1)小明发现问题1中的∠A与∠C、∠ABC与∠ADC都满足互补关系，请帮助他完善问题1的证明：∵BD 是⊙O 的直径，∴∠A =∠C =90°，∴∠A +∠C =180°，∵四边形内角和等于360°，∴∠ABC +∠ADC =180°．(2)请回答问题2，并说明理由；【深入探究】如图(3)，⊙O 的内接四边形ABCD 恰有一个内切圆⊙I ，切点分别是点E 、F 、G 、H ，连接GH ，EF ．(3)直接写出四边形ABCD 边满足的数量关系AD +BC =AB +CD ；(4)探究EF 、GH 满足的位置关系；(5)如图(4)，若∠C =90°，BC =3，CD =2，请直接写出图中阴影部分的面积．【分析】(1)根据直径所对的圆周角是直角，四边形的内角和定理进行求解即可；(2)连接AC 、BD ，根据同弧所对的圆周角相等，三角形的内角和定理进行求解即可；(3)连接AI 、BI 、CI 、DI ，根据切线长定理进行求解即可；(4)连接EH 、IH 、IG 、IF 、GF ，根据切线的性质，四点共圆的性质可得∠GIF =∠ADC ，再由同弧所对的圆周角相等，可得∠GFE =∠GHE ，根据三角形内角和定理，可得∠DEH =∠GFE ，则∠FEH +∠EHG =∠FEH +∠IEF +∠DEH =∠EID =90°，即可证明EF ⊥GH ；(5)连接BD ，可得BD 是圆O 的直径，连接IF 、IH ，先推导出∠BIF +∠DIH =90°，再证明四边形IHCF 是正方形，可得∠HIF =90°，即可知I 点在BD 上，根据已知求出S 四边形ABCD =3×2=6，通过证明△DHI ∽△IFB ，求出IH =65，可求S ⊙I =3625π，则阴影部分的面积=6-3625π．【解答】解：【问题提出】(1)∵BD 是⊙O 的直径，∴∠A =∠C =90°，∴∠A +∠C =180°，∵四边形内角和等于360°，∴∠ABC +∠ADC =180°；故答案为：∠A =∠C =90°，∠ABC +∠ADC =180°；(2)成立，理由如下：连接AC 、BD ，∵∠DAC =∠CBD ，∠ACD =∠ABD ，∴∠DAC +∠ACD =∠DBC +∠ABD =∠ABC ，∵∠DAC +∠ACD +∠ADC =180°，∴∠ABC +∠ADC =180°；同理，∠BAD +∠BCD =180°；【深入探究】(3)AD +BC =AB +CD ，理由如下：连接AI 、BI 、CI 、DI ，∵圆I 是四边形ABCD 的内切圆，∴AG =AE ，DE =DH ，CH =CF ，BF =BG ，∴AD +BC =AE +ED +BF +CF =AG +DH +BG +CH =AB +CD ，即AD +BC =AB +CD ，故答案为：AD +BC =AB +CD ；(4)EF ⊥GH ，理由如下：连接EH 、IH 、IG 、IF 、GF ，∵四边形ABCD 是圆O 的内接四边形，∴∠B +∠D =180°，∵BG ⊥IG ，IF ⊥BF ，∴∠BGI =∠IFB =90°，∴∠B +∠GIF =180°，∴∠GIF =∠D ，∵GI =IF ，∴∠GFI =90°-12∠GIF ，∵ED =DH ，∴∠DEH =90°-12∠D ，∴∠GFI =∠DEH ，∵GE =GE ，∴∠GFE =∠GHE ，∴∠GHE =∠GFI +∠IFE ，∵IF =IE ，∴∠IFE =∠IEF ，∴∠FEH +∠EHG =∠FEH +∠IEF +∠DEH =∠EID =90°，∴EF ⊥GH ；(5)连接BD ，∵∠C =90°，∴∠A =90°，∵ABCD 是圆O 的内接圆，∴BD 是圆O 的直径，连接IF、IH，∵I是四边形ABCD的内切圆圆心，∴∠ADI=∠IDH，∠ABI=∠FBI，∵IH⊥CD，IF⊥BC，∴∠BIF=90°-∠IBF，∠DIH=90°-∠IDH，∴∠BIF+∠DIH=180°-(∠IBF+∠IDH)=180°-12(∠ADC+∠ABC)，∵∠ABC+∠ADC=180°，∴∠BIF+∠DIH=90°，∵IF⊥FC，IH⊥CD，∠C=90°，IH=IF，∴四边形IHCF是正方形，∴∠HIF=90°，∴I点在BD上，∵BC=3，CD=2，∴S四边形ABCD=3×2=6，∵∠DIH+∠IDH=90°，∠IBF+∠IDH=90°，∴∠DIH=∠IBF，∵∠IHD=∠IFB=90°，∴△DHI∽△IFB，∴IH BF =DHIF，即IH3-IH=2-IHIH，解得IH=6 5，∴S⊙I=3625π，∴阴影部分的面积=6-3625π．【点评】本题考查圆的综合应用，熟练掌握四边形的内切圆性质，外接圆性质，三角形相似的判定及性质，切线的性质，四点共圆的性质是解题的关键．一．选择题(共3小题)11(2022•思明区二模)如图，四边形ABCD是⊙O的内接四边形，点E为边CD上任意一点(不与点C，点D重合)，连接BE，若∠A=60°，则∠BED的度数可以是()A.110°B.115°C.120°D.125°【分析】四边形ABCD 是⊙O 的内接四边形，则∠A 和∠C 互补，已知∠A =60°，则∠C 的度数为120°，而∠BED 大于∠C 的度数，从而得出答案．【解答】解：∵四边形ABCD 是⊙O 的内接四边形，∴∠A +∠C =180°，∵∠A =60°，∴∠C =120°，∵∠BED =∠C +∠CBE ，∴∠BED >120°，∴∠BED 可能为125°．故选：D ．【点评】本题主要考查了圆内接四边形以及三角形外角的性质，解题的关键是根据圆内接四边形的对角互补求出∠C 的度数，再根据外角的性质对∠BED 的度数做出正确的推断．12(2023•泾阳县模拟)刘徽是中国古代卓越的数学家之一，他在《九章算术》中提出了“割圆术”，即用内接或外切正多边形逐步逼近圆来近似计算圆的面积．如图，已知⊙O 的半径为2，则⊙O 的内接正六边形ABCDEF 的面积为()A.6B.63C.65D.43【分析】连接OA 、OB ，根据正多边形和圆的关系可判断出△OAB 为等边三角形，过点O 作OM ⊥AB 于点M ，再利用勾股定理即可求出OM 长，进而可求出△AOB 的面积，最后利用⊙O 的面积约为6S △AOB 即可计算出结果．【解答】解：如图，连接OA 、OB ，由题意可得：∠AOB =360÷6=60°，∵OA =OB =2，∴△OAB 为等边三角形，∴AB =2，过点O 作OM ⊥AB 于点M ，则AM =BM =1，在Rt △AOMR 中，OM =22-12=3，∴S △AOB =12×2×3=3，∴⊙O 的面积约为6S △AOB =63．故选：B ．【点评】本题主要考查正多边形与圆、勾股定理等，正确应用正六边形的性质是解题关键．13(2023•蜀山区校级模拟)如图，△ABC 中，∠BAC =60°，AD 平分∠BAC ，∠BDC =120°，连接BD ，CD 并延长分别交AC ，AB 于点E 和点F ，若DE =6，DF CD=35，则BD 的长为()A.10B.12C.15D.16【分析】由AEDF四点共圆，得到DE=DF，再证明△CDE∽△CAF，得到AF与AC的比，延长CF 到P，使DP=DB，得到△BDP为等边三角形，在证明出△AFC∽△PFB，证出PF与PB，利用DF 即可求出BD．【解答】解：∵∠BAC=60°，∠BDC=120°，∴A、E、D、F四点共圆，∵AD平分∠BAC，∴∠DAE=∠DAF，∴DE=DF=6，∵∠BDC=120°，∴∠CDE=60°=∠FAC，∵∠ACD=∠ACD，∴△CDE∽△CAF，∴AF：AC=DE：CD=6：10=3：5，如图，延长CF到P，使DP=DB，∵∠PBD=60°，∴△BDP为等边三角形，∴∠P=60°，∴△AFC∽△PFB，∴PF：PB=AF：AC=3：5，设每一份为k，∴PB=PD=5k，PF=3k，∴DF=2k=6，∴k=3，∴BD=5k=15．故选：C．【点评】本题考查了三角形相似的性质、等边三角形的性质等知识点的应用，四点共圆的应用及相似比的转化是解题关键．二．填空题(共2小题)14(2023•银川校级二模)如图，在直径为AB的⊙O中，点C，D在圆上，AC=CD，若∠CAD= 28°，则∠DAB的度数为34°．【分析】利用等腰三角形的性质可得∠CAD =∠CDA =28°，从而利用三角形内角和定理可得∠ACD =124°，然后根据圆内接四边形对角互补求出∠ABD =56°，再根据直径所对的圆周角是直角可得∠ADB =90°，从而求出∠DAB 的度数．【解答】解：∵AC =CD ，∠CAD =28°，∴∠CAD =∠CDA =28°，∴∠ACD =180°-∠CAD -∠CDA =124°，∵四边形ABCD 是⊙O 的内接四边形，∴∠ACD +∠ABD =180°，∴∠ABD =180°-∠ACD =56°，∵AB 是⊙O 的直径，∴∠ADB =90°，∴∠DAB =90°-∠ABD =34°．故答案为：34°．【点评】本题考查了等腰三角形的性质，圆周角定理，圆心角、弧、弦的关系，熟练掌握圆周角定理是解题的关键．15(2023•海曙区校级一模)如图，在等腰三角形纸片ABC 中，AB =AC ，将该纸片翻折，使得点C 落在边AB 的F 处，折痕为DE ，D ，E 分别在边BC ，AC 上，∠AFD =∠DEF ，若DE =4，BD =9，则DF =6，△ABC 的面积为　45154　．【分析】根据折叠的性质可得∠CED =∠DEF ，∠C =∠DFE ，以此可得∠CED =∠AFD ，因此可判断A 、F 、D 、E 四点共圆，由圆周角定理可得∠DAF =∠DEF ，∠CAD =∠DFE ，进而得到∠AFD =∠DAF ，∠CAD =∠C ，则DF =AD =CD ，由等腰三角形的性质可得∠B =∠C ，以此可证明△BAD∽△CED ，由相似三角形的性质可求得DF =AD =CD =6，则BC =15，BG =CG =152，DG =32，根据勾股定理求出AG ，再算出△ABC 的面积即可求解．【解答】解：连接AD ，过点A 作AG ⊥BC 于点G ，如图，根据折叠的性质可得，∠CED =∠DEF ，∠C =∠DFE ，∵∠AFD =∠DEF ，∴∠CED =∠AFD ，∴A 、F 、D 、E 四点共圆，∴∠DAF =∠DEF ，∠CAD =∠DFE ，∴∠AFD =∠DAF ，∠CAD =∠C ，∴DF =AD =CD ，∵AB =AC ，∴∠B =∠C ，∵∠CED =∠DEF =∠DAF ，∴△BAD ∽△CED ，∴AD DE =BD CD，∵DE =4，BD =9，DF =AD =CD ，∴DF 4=9DF，∴DF =AD =CD =6，∴BC =BD +CD =9+6=15，∵AG ⊥BC ，AB =AC ，∴BG =CG =12BC =152，∴DG =CG -CD =152-6=32，在Rt △ADG 中，由勾股定理得AG =AD 2-DG 2=62-32 2=3152，∴S △ABC =12BC ⋅AG =12×15×3152=45154．故答案为：6，45154．【点评】本题主要考查四点共圆的判定、相似三角形的判定与性质、等腰三角形的性质，圆周角定理、勾股定理，正确作出辅助线，通过所给条件推出A 、F 、D 、E 四点共圆，以此得到DF =AD =CD 是解题关键．三．解答题(共7小题)16(2022秋•南关区校级期末)【问题情境】如图①，在四边形ABCD 中，∠B =∠D =90°，求证：A 、B 、C 、D 四点共圆．小吉同学的作法如下：连结AC ，取AC 的中点O ，连结OB 、OD ，请你帮助小吉补全余下的证明过程；【问题解决】如图②，在正方形ABCD 中，AB =2，点E 是边CD 的中点，点F 是边BC 上的一个动点，连结AE ，AF ，作EP ⊥AF 于点P ．(1)如图②，当点P 恰好落在正方形ABCD 对角线BD 上时，线段AP 的长度为　102　；(2)如图③，过点P 分别作PM ⊥AB 于点M ，PN ⊥BC 于点N ，连结MN ，则MN 的最小值为　132-52　．【分析】【问题情境】连结AC，取AC的中点O，连结OB、OD，根据直角三角形斜边上的中线等于斜边的一半，可得OD=OA=OC=OB，以此即可证明；【问题解决】(1)根据题意可得AE=AD2+DE2=5，由【问题情境】结论可知A、D、E、P四点共圆，根据圆周角定理以及正方形的性质可得∠PDE=∠PAE=45°，则△PAE为等腰直角三角形，设AP长为a，则PE长为a，根据勾股定理列出方程，求解即可；(2)由【问题情境】结论可知A、D、E、P四点共圆，过点O作OG⊥AD于点G，作OH⊥AB于点H，连接OB交⊙O于点P′，连接PB，根据题意可得四边形MBNP为矩形，则要求MN的最小值，即求PB的最小值，根据平行线的性质和中点的定义可得OG为△ADE的中位线，得AG=1，OG=12，同理可证四边形AHOG为矩形，以此得到OH=AG=1，BH=32，根据勾股定理得OB=OH2+BH2=132，根据两点之间线段最短得PB+OP≥OB，以此即可求出PB的最小值，从而求得MN的最小值．【解答】【问题情境】证明：如图，连结AC，取AC的中点O，连结OB、OD，∵∠ADC=∠ABC=90°，O为AC的中点，∴OA=OB=OC=OD=12AC，∴A、B、C、D四点共圆；【问题解决】解：(1)∵四边形ABCD为正方形，点E是边CD的中点，AB=2，∴AD=2，DE=1，∴AE=AD2+DE2=5，由【问题情境】结论可知，A、D、E、P四点共圆，如图，∴∠PAE=∠PDE，∵BD为正方形ABCD的对角线，∴∠PDE=∠PAE=45°，∵EP⊥AF，∴△PAE为等腰直角三角形，设AP长为a，则PE长为a，∴AP2+PE2=AE2，即a2+a2=52，解得：a1=102，a2=-102(不合题意，舍去)，∴线段AP的长度为102；故答案为：10 2；(2)由【问题情境】结论可知，A、D、E、P四点共圆，如图，过点O作OG⊥AD于点G，作OH⊥AB于点H，连接OB交⊙O于点P′，连接PB，∵PM⊥AB，PN⊥BC，∴∠PMB=∠MBN=∠PNB=90°，∴四边形MBNP为矩形，∴MN=PB，要求MN的最小值，即求PB的最小值，由(1)知，AE=5，∴OA=52，∵OG⊥AD，且点O为AE的中点，∴OG∥DE，∴OG为△ADE的中位线，∴AG=1，OG=12，∵OG⊥AD，OH⊥AB，∴四边形AHOG为矩形，∴AH=OG=12，OH=AG=1，∴BH=32，在Rt△BHO中，OB=OH2+BH2=13 2，根据两点之间线段最短得，PB+OP≥OB，PB≥OB-OP=132-52，∴PB的最小值为132-52，∴MN的最小值为132-52．故答案为：132-52．【点评】本题主要考查四点共圆、正方形的性质，等腰直角三角形的性质、勾股定理、中位线的判定与性质、平行线的判定与性质，属于圆的综合题，熟练掌握相关知识是解题关键．17(2023•萍乡模拟)如图，点A，B，C在⊙O上，且∠ABC=120°，请仅用无刻度的直尺，按照下列要求作图．(保留作图痕迹，不写作法)(1)在图(1)中，AB>BC，作一个度数为30°的圆周角；(2)在图(2)中，AB=BC，作一个顶点均在⊙O上的等边三角形．【分析】(1)作直径AD，连接CD，AC，则∠ADC=60°，∠DAC=30°；(2)作直径BE，连接EC，AE，AC，△ACE即为所求．【解答】解：(1)如图1中，∠CAD即为所求；(2)如图2中，△ACE即为所求．【点评】本题考查作图-复杂作图，等边三角形的判定和性质，圆周角定理等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．18(2022•芜湖一模)如图，在正方形ABCD中，P是边BC上的一个动点(不与点B，C重合)，作点B关于直线AP的对称点E，连接AE，再连接DE并延长交射线AP于点F，连接BF和CF．(1)若∠BAP=α，则∠AED=45°+α(用含α的式子直接填空)；(2)求证：点F在正方形ABCD的外接圆上；(3)求证：AF-CF=2BF．【分析】(1)由轴对称的性质得∠EAP=∠BAP=a，AE=AB，由正方形的性质得∠BAD=90°，AB =AD，则∠DAE=90°-2a，AD=AE，由等腰三角形的性质即可得出结论；(2)由轴对称的性质得∠AEF=∠ABF，AE=AB，证出AE=AD，由等腰三角形的性质得∠ADE =∠AED，证∠ADE+∠ABF=180°，则∠BFD+∠BAD=180°，得∠BFD=90°即可；(3)过点B作BM⊥BF交AF于点M，则∠MBF=90°，证△BMF是等腰直角三角形，得BM=BF，FM=2BF，证△AMB≌△CFB(SAS)，得AM=CF，进而得出结论．【解答】解：(1)∵点B关于直线AP的对称点E，∠BAP=α，∴∠EAP=∠BAP=α，AE=AB，∵ABCD 是正方形，∴AD =AB ，∠BAD =90°，∴AE =AD ，∠DAE =90°-2α，∴∠ADE =∠AED =12(180°-∠DAE )=12(90°+2α)=45°+α，故答案为：45°+α；(2)证明：由(1)∠AED =45°+α，又∵∠BAE =2α，∴∠EFA =∠BFA =45°，∠BFD =90°，连接BD ，则∠BCD =90°，∴∠BCD =∠BAD =∠BFD =90°，∴B 、F 、C 、D 和A 、B 、C 、D 都在以BD 为直径的圆上，即点F 在正方形ABCD 的外接圆上；(3)过点B 作BM ⊥BF 交AF 于M 点，则∠MBF =90°，∵四边形ABCD 是正方形，∴AB =CB ，∠ABC =90°，∴∠MBF =∠ABC ，∴∠ABM =∠CBF ，∵点E 与点B 关于直线AP 对称，∴∠BFD =90°，∴∠MFB =∠MFE =45°，∴△BMF 是等腰直角三角形，∴BM =BF ，FM =2BF ，在△AMB 和△CFB 中，AB =BC ∠ABM =∠CBF BM =BF，∴△AMB ≌△CFB (SAS )，∴AM =CF ，∴AF =FM +AM =2BF +CF ，∴AF -CF =2BF ．【点评】本题考查了正方形的性质、轴对称的性质、等腰直角三角形的判定与性质、全等三角形的判定与性质、等腰三角形的判定与性质等知识，解题关键是熟练掌握矩形的性质和轴对称的性质，证明三角形全等．19(2021秋•鹿城区校级期中)如图，△ABC 内接于⊙O ，CD ⊥AB ，CB =10cm ，CD =8cm ，AB =14cm ．(1)∠A 度数45°．(直接写出答案)(2)求BC 的长度．(3)P 是⊙O 上一点(不与A ，B ，C 重合)，连结BP ．①若BP 垂直△ABC 的某一边，求BP 的长．②将点A 绕点P 逆时针旋转90°后得到A ′，若A ′恰好落在CD 上，则CA '的长度为4.(直接写出答案)【分析】(1)利用勾股定理，等腰三角形的判定和三角形的内角和定理解答即可；(2)连接OB ，OC ，利用圆周角定理求得圆心角的度数，再利用弧长公式解答即可；(3)①连接AP ，利用等腰直角三角形的性质求得BE ，利用全等三角形的判定与勾股定理求得PE ，则BP 可求；②连接AA ′，PD ，设PD 与AC 交于点E ，通过证明P ，A ，D ，A ′四点共圆，利用圆周角定理和垂径定理得到PD 经过圆心O ，过点O 作OF ⊥AB 于点F ，利用垂径定理和勾股定理求得OE ，连接OC ，利用勾股定理求得圆的半径，再利用等腰直角三角形的性质求得PA ，勾股定理求得DA ′，则CA ′=CD -DA ′．【解答】解：(1)在Rt △BCD 中，CB =10cm ，CD =8cm ，∴BD =BC 2-CD 2=102-82=6(cm )，∴AD =AB -BD =14-6=8cm =CD ，∴∠A =∠ACD ，∵CD ⊥AB ，∴∠ADC =90°，∴∠A =180o -∠ADC 2=180o -90°2=45°，故答案为：45°；(2)连接OB ，OC ，如图，∵∠BAC =45°，∴∠BOC =90°，在Rt △BOC 中，OB =OC ，CB =10cm ，∴OB =22BC =52(cm )，∴BC 的长度=90π×52180=52π2cm ；(3)①∵P 是⊙O 上一点(不与A ，B ，C 重合)，BP 垂直△ABC 的某一边，∴点P 只能在AC上，连接AP ，如图，由(1)知：∠CAB =45°，∵BP ⊥AC ，。

人教版九年级数学上册圆《探究四点共圆的条件》示范公开课教学课件

综上所述，点D既不在圆外，也不在圆内，
∴点D在过点A，B，C的圆上
即四边形ABCD的四个顶点共圆.
四点共圆的判定方法2:对角互补的四边形的四个顶点共圆.
归纳总结
四点共圆的条件：
方法1：到定点的距离等于定长的四个点共圆
方法2：对角互补的四边形的四个顶点共圆
半径
例题讲析
例题：如图在四边形ABCD中, 对角线BD平分∠ABC, ∠A+∠C=180°.
求证：四边形ABCD的四个顶点共圆.
推理论证
求证:对角互补的四边形的四个顶点共圆.
已知：如图，在四边形ABCD中，∠ABC+∠ADC=180°.
求证：四边形ABCD的四个顶点共圆.
证明：经过点A，B，C作一个⊙O，
若点D在圆外，
设AD交⊙O于点E，连接EC
则∠ABC+∠AEC=180°
而∠AEC是△CDE的外角,∠AEC＞∠D
C
A
B
（不能作圆）
①假设命题的结论不成立；
（不在同一直线上的三
个点可以确定一个圆）
反证法的基本思路：②经过推理得出矛盾；
③得出原命题成立.
提出问题
问题4：在平面内过A,B,C,D四点作圆.
①当四点在同一条直线上时；
（不能作圆）
②当四点中任意三点在同一条直线上时；
（不能作圆）
③当四点中任意三点不在同一直线上时；
140° .
∠ABC=40°,则∠ADC=
图1
图2
图3
拓展提升
4.如图4, 在正方形ABCD中，点E, F分别是BC,CD边的中点，连接AE,BF交于点P,
连接PD,求tan∠APD的值.
图4

中考数学满分之路(二)—四点共圆

中考数学满分之路（二） ——四点共圆一、使用定义解题圆的定义平面上到一个定点的距离等于定长的点的集合叫做圆. 在题目中出现共端点的等线段时，可尝试作出圆辅助求解.例（1）如图，四边形ABCD 中，DC ∥AB ，BC ＝1，AB ＝AC ＝AD ＝2，则BD 的长为______.（2）如图，在等腰△ABC中，AB AC =D 为BC 边上异于中点的点，点C 关于直线AD 的对称点为点E ，EB 的延长线与AD 的延长线交于点F ，则AD AF ⋅的值为______.E1. 如图，抛物线2y ax bx c =++经过点(2,5)A -，与x 轴相交于(1,0)B -，(3,0)C 两点. （1）求抛物线的函数表达式；（2）点D 在抛物线的对称轴上，且位于x 轴的上方，将△BCD 沿直线BD 翻折得到△'BC D ，若点'C 恰好落在抛物线的对称轴上，求点'C 和点D 的坐标；（3）设点P 是抛物线上位于对称轴右侧的一点，点Q 在抛物线的对称轴上，当△CPQ 为等边三角形时，求直线BP 的函数表达式.2. 问题背景如图1，等腰△ABC 中，AB =AC ，∠BAC =120°，作AD ⊥BC 于点D ，则D 为BC 的中点，∠BAD =12∠BAC =60°，于是2BC BDAB AB= 迁移应用（1）如图2，△ABC 和△ADE 都是等腰三角形，∠BAC =∠DAE =120°，D ，E ，C 三点在同一条直线上，连接BD ．ⅰ)求证：△ADB ≌△AEC ；ⅱ)请直接写出线段AD ，BD ，CD 之间的等量关系式. 拓展延伸（2）如图3，在菱形ABCD 中，∠ABC =120°，在∠ABC 内作射线BM ，作点C 关于BM 的对称点E ，连接AE 并延长交BM 于点F ，连接CE ，CF .ⅰ)求证：△CEF 是等边三角形； ⅱ)若AE =5，CE =2，求BF 的长.图1图2图33. 如图，AB 是半圆⊙O 的直径，点C 为半圆⊙O 上的点，连接AC ，BC ，点E 是AC 的中点，点F 是射线OE 上一点.（1）如图1，连接F A ，FC ，若2AFC BAC ∠=∠，求证：F A ⊥AB ；（2）如图2，过点C 作CD ⊥AB 于点D ，点G 是线段CD 上一点（不与点C 重合），连接F A ，FG ，FG 与AC 相交于点P ，且AF FG =.①试猜想∠AFG 和∠B 的数量关系，并证明；②连接OG ，若OE BD =，90GOE ∠=，⊙O 的半径为2，求EP 的长.图1 图2二、圆内接四边形的性质与判定定理性质定理1 圆的内接四边形的对角互补.定理2 圆内接四边形的外角等于它的内角的对角.圆周角定理的推论同弧所对的圆周角相等.判定圆内接四边形判定定理1 如果一个四边形的对角互补，那么这个四边形的四个顶点共圆.推论如果四边形的一个外角等于它的内角的对角，那么这个四边形的四个顶点共圆.圆内接四边形判定定理2 如果一个四边形一边与一对角线的夹角等于其对边与另一对角线的夹角，那么这个四边形的四个顶点共圆.上述定理在应用时的书写格式如下①∵A，B，C，D四点共圆，∴∠BAD＋∠BCD＝180°.②∵A，B，C，D四点共圆，∴∠DCE＝∠BAD.③∵A，B，C，D四点共圆，∴∠ACB＝∠ADB. ④∵∠BAD＋∠BCD＝180°，∴A，B，C，D四点共圆.⑤∵∠DCE＝∠BAD，∴A，B，C，D四点共圆.⑥∵∠ACB＝∠ADB，∴A，B，C，D四点共圆.EE4. 如图，矩形ABCD 的对角线AC ，BD 相交于点O ，过点O 作OE AC ⊥交AB 于点E ，若4BC =，△AOE 的面积为6，则sin BOE ∠的值为______.5. 如图，点B 在线段AC 上，点D ，E 在AC 同侧，90A C ∠=∠=，BD BE ⊥，AD BC =. （1）求证：AC AD CE =+；（2）若3AD =，5CE =，点P 为线段AB 上的动点，连接DP ，作PQ DP ⊥，交直线BE 与点Q ；ii ）当点P 从A 点运动到AC 的中点时，求线段DQ 的中点所经过的路径（线段）长.DBP6. 如图，已知△ABC 是等边三角形，点D ，E 分别在边AC ，AB 上，且CD AE =，BD 与CE 相交于点P . （1）求证：△ACE ≌△CBD ；（2）如图2，将△CPD 沿直线CP 翻折得到对应的△CPM ，过C 作CG ∥AB ，交射线PM 于点G ，PG 与BC 相交于点F ，连接BG .ⅰ）试判断四边形ABGC 的形状，并说明理由；ⅱ）若四边形ABGC的面积为，1PF =，求CE 的长.图1图2三、与圆有关的比例线段相交弦定理圆内的两条弦，被交点分成的两条线段长的积相等.割线定理从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等. 切割线定理从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段的比例中项.上述定理在应用时的书写格式如下由相交弦定理，得PA PB PC PD ⋅=⋅.由割线定理，得PA PB PC PD ⋅=⋅.由切割线定理，得2PA PB PC =⋅.7. 如图，已知AB 是⊙O 的直径，C 为⊙O 上一点，延长BC 至D ，使CD ＝BC ，CE ⊥AD 于E ，BE 交⊙O 于F ，AF 交CE 于P . 求证：PE ＝PC .P8. 如图1，线段AB 是⊙O 的直径，弦CD ⊥AB 于点H ，点M 是CBD 上任意一点，AH ＝4，CD ＝16.（1）求⊙O 的半径r 的长度；10r =；（2）求tan ∠CMD ；（3）如图2，直线BM 交直线CD 于点E ，直线MH 交⊙O 于点N ，连接BN 交CE 于点F ，求H E H F ⋅的值.图1图29. 已知BC 为⊙O 的直径，AC 为⊙O 的切线，C 为切点，AD ＝BD .（1）如图1，求证：∠A ＝45°；（2）如图2，E 为⊙O 上一点，连接DE 交BC 于点F ，过点F 作BC 的垂线交BE 于点G ，求证：FG ＝FC ；（3）如图3，在（2）的条件下，若EG BDF 的面积为15（BF ＞BD ），求⊙O 的面积.图1BC图2CB图3BC10. （蝴蝶定理）如图，过⊙O的弦PQ的中点M引任意两条弦AB，CD，连接AD，BC分别交PQ于X，Y两点. 求证：MX＝MY.证明：分别取AD ，CB 的中点E ，F ，连接OE ，OF ，OM ，OX ，OY ，ME ，MF ， ∵∠A ＝∠C ，∠D ＝∠B ，∴△ADM ∽△CBM ， ∴AM ADCM CB=，又AD ＝2AE ，CB ＝2CF ， ∴22AD AE AE CB CF CF ==，∴AM AECM CF=，又∠A ＝∠C ， ∴△AEM ∽△CFM ，∴∠AEM ＝∠CFM ，∵点M ，E ，F 分别是⊙O 的弦PQ ，AD ，CB 的中点， ∴OM ⊥PQ ，OE ⊥AD ，OF ⊥CB ，∴∠OEX ＋∠OMX ＝180°，∠OFY ＋∠OMY ＝180°， ∴O ，M ，X ，E 四点共圆，O ，M ，Y ，F 四点共圆， ∴∠MOX ＝∠AEM ，∠MOY ＝∠CFM ，又∠AEM ＝∠CFM ， ∴∠MOX ＝∠MOY ，又OM ＝OM ，∠OMX ＝∠OMY ＝90°， ∴△OMX ≌△OMY ，∴MX ＝MY . 证法二证明：过点D 作DE ∥PQ 交⊙O 于另一点E ，连接MO 并延长交DE 于E ， ①当PQ 为直径时，四边形ACBD 为矩形，易证MX ＝MY ； ②当PQ 不是直径时，由垂径定理推论，得OM ⊥PQ ，又DE ∥PQ ， ∴MN ⊥DE ，又MN 过圆心O ，∴MN 垂直平分DE ， ∴MD ＝ME ，∴∠MDE ＝∠MED ，又PQ ∥DE ，∴∠PMD ＝∠MDE ，∠QME ＝∠MED ， ∴∠PMD ＝∠QME ，∠QME ＝∠MDE ，∵C ，D ，B ，E 四点共圆，∴∠MDE ＋∠CBE ＝180°， ∴∠QME ＋∠CBE ＝180°， ∴M ，E ，B ，Y 四点共圆，∴∠MEY ＝∠MBC ，又∠MBC ＝∠ADC ，∴∠ADC ＝∠MEY ，又MD ＝ME ，∠PMD ＝∠QME ， ∴△MDX ≌△MEY ，∴MX ＝MY .证明：过X 作'XX AB ⊥于'X ，过X 作"XX CD ⊥于"X ，过Y 作'YY CD ⊥于'Y ，过Y 作"YY AB ⊥于"Y ，∵∠A ＝∠C ，∠D ＝∠B ，''90AX X CY Y ∠=∠=，""90CX X BY Y ∠=∠=， ∴△'AX X ∽△'CY Y ，△"DX X ∽△"BY Y ， ∴''AX XX CY YY =，……①，""DX XX BY YY =，……②， ①×②，得'"'"AX DX XX XX CY BY YY YY ⋅=⋅， ∴'""'AX DX XX XX CY BY YY YY ⋅=⋅⋅，又由相交弦定理及平行线分线段成比例定理，得PX QX MX MXQY PY MY MY ⋅=⋅⋅， ∴22()()()()MP MX MP MX MX MP MY MP MY MY -⋅+=-⋅+，即222222MP MX MX MP MY MY -=-，根据比例的基本性质，得22222222222222()1()MP MX MX MP MX MX MP MP MY MY MP MY MY MP --+====--+， ∴22MX MY =，∴MX ＝MY . 证法四证明：连接PA ，PD ，QC ，QB ，根据共圆定理，（共圆定理：同圆或等圆中的三角形面积比等于三边乘积之比）得PAD QCB S PA PD AD PA PD ADS QB QC BC QB QC BC∆∆⋅⋅==⋅⋅⋅⋅，又△PAM ∽△BQM ,△PDM ∽△CQM ，△ADM ∽△CBM ， ∴22PAD AMDQCB CMBS PA PD AD AM MP AM AM S S QB QC BC MQ MC MC MC S ∆∆∆∆=⋅⋅=⋅⋅==， ∴QCB PAD AMD CMB S S S S ∆∆∆∆=，即PX QYMX MY=， ∴1MY QY MY QY MQ MX PX MX PX MP +====+， ∴MX ＝MY .B证明：连接AO 并延长交⊙O 于另一点E ，连接CO 并延长交⊙O 于另一点F ，连接BF ，DE 交于点G ，六边形CFBAED 内接于⊙O ，CF 交AE 于点O ，FB 交ED 于点G ，BA 交DC 于点M ，根据帕斯卡定理，得M ，O ，G 三点共线，连接MG ，GX ，GY ，∵AE ，CF 为⊙O 的直径，∴∠ADE ＝90°，∠CBF ＝90°， ∵MP ＝MQ ，PQ 不是⊙O 的直径，（PQ 为直径时，易证） ∴OM ⊥PQ ，∴D ，G ，M ，X 四点共圆，B ，G ，M ，Y 四点共圆， ∴∠MGX ＝∠ADM ，∠MGY ＝∠CBM ，又∠ADM ＝∠CBM ， ∴∠MGX ＝∠MGY ，又MG ＝MG ，∠GMX ＝∠GMY ， ∴△GMX ≌△GMY ， ∴MX ＝MY .帕斯卡定理如果一个六边形内接于一条二次曲线(圆、椭圆、双曲线、抛物线)，那么它的三对对边的交点在同一条直线上.B中考不考系列（二）——2019IMO第2题在三角形ABC中，点A1在边BC上，点B1在边AC上. 点P和Q分别在线段AA1和BB1上，且满足PQ平行于AB. 在直线PB1上取点P1，使得点B1严格位于点P与点P1之间，并且∠PP1C＝∠BAC. 类似地，在直线QA1上取点Q1，使得点A1严格位于点Q与点Q1之间，并且∠CQ1Q＝∠CBA.证明：点P，Q，P1，Q1共圆.证明：延长1AA ，1BB 分别交△ABC 的外接圆于2A ，2B ，连接22A B ， ∵PQ ∥AB ，∴22ABB PQB ∠=∠，又222ABB AA B ∠=∠， ∴222PQB AA B ∠=∠，∴22,,,P Q A B 四点共圆，连接2B C ，∵1PPC BAC ∠=∠，2BB C BAC ∠=∠， ∴12PPC BB C ∠=∠，∴121,,,P B B C 四点共圆，连接12PB ，∵11212B PB B CB ∠=∠，222AA B ACB ∠=∠， ∴2122B PP B A P ∠=∠，∴122,,,P A P B 四点共圆，连接2A C ，∵1CQ Q CBA ∠=∠，2CA A CBA ∠=∠， ∴12CQ Q CA A ∠=∠，∴121,,,Q A A C 四点共圆，连接12Q A ，∵11212AQ A ACA ∠=∠，222BB A BCA ∠=∠， ∴2122A QQ A B Q ∠=∠，∴122,,,Q B Q A 四点共圆， ∴2112,,,,,P Q A Q P B 六点共圆， ∴点11,,,P Q P Q 共圆.上述答案是从官方答案翻译而来.【附】官方答案.。

2024年中考数学常见几何模型全归纳(全国通用)专题31 圆中的重要模型之四点共圆模型(解析版)

专题31圆中的重要模型之四点共圆模型四点共圆是初中数学的常考知识点，近年来，特别是四点共圆判定的题目出现频率较高。

相对四点共圆性质的应用，四点共圆的判定往往难度较大，往往是填空题或选择题的压轴题，而计算题或选择中四点共圆模型的应用（特别是最值问题），通常能简化运算或证明的步骤，使问题变得简单。

本文主要介绍四点共圆的四种重要模型。

四点共圆：若在同一平面内，有四个点在同一个圆上，则称这四个点共圆，一般简称为“四点共圆”。

模型1、定点定长共圆模型（圆的定义）【模型解读】若四个点到一定点的距离相等，则这四个点共圆。

这也是圆的基本定义，到定点的距离等于定长点的集合。

条件：如图，平面内有五个点O、A、B、C、D，使得OA=OB=OC=OD，结论：A、B、C、D四点共圆（其中圆心为O）。

【答案】2【分析】首先连接OE，由角器上对应的读数．【详解】解：连接OE，A ．13B ．52∵在ABC 中，90BAC【答案】30【分析】连接AC 与BD 又易知在Rt ACD △中，【详解】解：连接AC 与∵四边形形ABCD 是矩形，12OA OB OC OD AC又∵DE BF 于E ，即是直角三角形，∴12OE BD ，∴OA OC OD OE ，∴点A B 、、，由旋转的性质可知：AF AB ，【答案】122【分析】（1）根据条件，证明AOD COD△△△△，代入推断即可.（2）通过AOG ABC证明ODF CBF△△，代入推断即可.又∵∵CE CF∴CEF CFE模型2、定边对双直角共圆模型C同侧型异侧型1）定边对双直角模型（同侧型）条件：若平面上A、B、C、D四个点满足90ABD ACD，结论：A、B、C、D四点共圆，其中AD为直径。

2）定边对双直角模型（异侧型）条件：若平面上A、B、C、D四个点满足90ABC ADC，结论：A、B、C、D四点共圆，其中AC为直径。

【点睛】本题考查了圆的直径所对的圆周角为【点睛】此题主要考查圆内接四边形，直角三角形斜边上的中线等于斜边的一半和等腰三角形的性质等知识点，解答此题的关键是添加辅助线构造特殊三角形，求出线段．模型3、定边对定角共圆模型条件：如图1，平面上A 、B 、C 、D 四个点满足ADB ACB ，结论：A 、B 、C 、D 四点共圆．条件：如图2，AC 、BD 交于H ，AH CH BH DH ，结论：A B C D 、、、四点共圆.例1．（2023·江苏·九年级假期作业）如图，在Rt ABC 中，∠BAC ＝90°，∠ABC ＝40°，将 ABC 绕A 点顺时针旋转得到 ADE ，使D 点落在BC 边上．（1）求∠BAD 的度数；（2）求证：A 、D 、B 、E 四点共圆．【答案】（1）10°；（2）见解析【分析】（1）由三角形内角和定理和已知条件求得∠C 的度数，由旋转的性质得出AC ＝AD ，即可得出∠ADC ＝∠C ，最后由外角定理求得∠BAD 的度数；（2）由旋转的性质得到∠ABC ＝∠AED ，由四点共圆的判定得出结论．【详解】解：（1）∵在Rt ABC 中，∠BAC ＝90°，∠ABC ＝40°，∴∠C ＝50°，∵将 ABC 绕A 点顺时针旋转得到 ADE ，使D 点落在BC 边上，∴AC ＝AD ，∴∠ADC ＝∠C ＝50°，∴∠ADC ＝∠ABC +∠BAD ＝50°，∴∠BAD ＝50°－40°＝10°证明（2）∵将 ABC 绕A 点顺时针旋转得到 ADE ，∴∠ABC ＝∠AED ，∴A 、D 、B 、E 四点共圆．【点睛】本题考查了旋转的性质、等腰三角形的性质、外角定理以及四点共圆的判定，解题的关键是理解旋转后的图形与原图形对应边相等，对应角相等．例3．（2022·江苏无锡·中考真题）△ABC是边长为5的等边三角形，△DCE是边长为3的等边三角形，直线BD与直线AE交于点F．如图，若点D在△ABC内，∠DBC=20°，则∠BAF＝________°；现将△DCE 绕点C旋转1周，在这个旋转过程中，线段AF长度的最小值是________．【答案】804##4【分析】利用SAS 证明△BDC ≌△AEC ，得到∠DBC =∠EAC =20°，据此可求得∠BAF 的度数；利用全等三角形的性质可求得∠AFB =60°，推出A 、B 、C 、F 四个点在同一个圆上，当BF 是圆C 的切线时，即当CD ⊥BF 时，∠FBC 最大，则∠FBA 最小，此时线段AF 长度有最小值，据此求解即可．【详解】解：∵△ABC 和△DCE 都是等边三角形，∴AC =BC ，DC =EC ，∠BAC =∠ACB =∠DCE =60°，∴∠DCB +∠ACD =∠ECA +∠ACD =60°，即∠DCB =∠ECA ，在△BCD 和△ACE 中，CD CE BCD ACE BC AC，∴△ACE ≌△BCD （SAS ），∴∠EAC =∠DBC ，∵∠DBC =20°，∴∠EAC =20°，∴∠BAF =∠BAC +∠EAC =80°；设BF 与AC 相交于点H，如图：∵△ACE ≌△BCD ∴AE =BD ，∠EAC =∠DBC ，且∠AHF =∠BHC ，∴∠AFB =∠ACB =60°，∴A 、B 、C 、F 四个点在同一个圆上，∵点D 在以C 为圆心，3为半径的圆上，当BF 是圆C 的切线时，即当CD ⊥BF 时，∠FBC 最大，则∠FBA 最小，∴此时线段AF 长度有最小值，在Rt △BCD 中，BC =5，CD =3，∴BD 4，即AE =4，∴∠FDE =180°-90°-60°=30°，∵∠AFB =60°，∴∠FDE =∠FED =30°，∴FD =FE ，过点F 作FG ⊥DE 于点G ，∴DG =GE =32，∴FE =DF =cos 30DG∴AF =AE -FE 80；【点睛】本题考查了旋转的性质，等边三角形的性质，圆周角定理，切线的性质，解直角三角形，解答本题的关键是明确题意，找出所求问题需要的条件．例4．（2022·贵州遵义·统考中考真题）探究与实践：“善思”小组开展“探究四点共圆的条件”活动，得出结论：对角互补的四边形四个顶点共圆．该小组继续利用上述结论进行探究．提出问题：如图1，在线段AC 同侧有两点B ，D ，连接AD ，AB ，BC ，CD ，如果B D ，那么A ，B ，C ，D 四点在同一个圆上．探究展示：如图2，作经过点A ，C ，D 的O ，在劣弧AC 上取一点E （不与A ，C 重合），连接AE ，CE 则180AEC D （依据1）B D ∵180AEC B点A ，B ，C ，E 四点在同一个圆上（对角互补的四边形四个顶点共圆）点B ，D 在点A ，C ，E 所确定的O 上（依据2）点A ，B ，C ，E 四点在同一个圆上(1)反思归纳：上述探究过程中的“依据1”、“依据2”分别是指什么？依据1：__________；依据2：__________．(2)图3，在四边形ABCD 中，12 ，345 ，则4 的度数为__________．(3)拓展探究：如图4，已知ABC 是等腰三角形，AB AC ，点D 在BC 上（不与BC 的中点重合），连接AD ．作点C 关于AD 的对称点E ，连接EB 并延长交AD 的延长线于F ，连接AE ，DE ．①求证：A ，D ，B ，E与判定，掌握以上知识是解题的关键．模型4、对角互补共圆模型P条件：如图1，平面上A、B、C、D四个点满足ABC ADC，结论：A、B、C、D四点共圆．条件：如图2，BA、CD的延长线交于P，PA PB PD PC，结论：A、B、C、D四点共圆.A．2B．22【答案】A【分析】先根据等腰三角形的性质可得,,,A B E D四点共圆，在以BE为直径的圆上，连接【答案】43/113【分析】过点B作BH AM交F，点A,M,B,C四点共圆，得法求解，12AMBS AM DE△【详解】解析：过点B作BH 于点，如图所示：【答案】52 2【分析】连接BD并延长，利用四点共圆的判定定理得到的性质和圆周角定理得到DBF性质解答即可得出结论．(1)求证：A ，E ，B ，D 四点共圆；(2)如图2，当AD CD 时，O 是四边形AEBD O 的切线；(3)已知1206BC ，，点M 是边BC 的中点，此时P 是四边形出圆心P 与点M 距离的最小值．【答案】(1)证明见解析(2)证明见解析(3)32（3）解：如图所示，作线段AB 的垂直平分线，分别交∵120AB AC BAC ，，∴B课后专项训练1．（2023秋·河北张家口·九年级校考期末）如图①，若BC是Rt△ABC和Rt△DBC的公共斜边，则A、B、C、D在以BC为直径的圆上，则叫它们“四点共圆”．如图②，△ABC的三条高AD、BE、CF相交于点H，则图②中“四点共圆”的组数为（）A．2B．3C．4D．6【答案】D【分析】根据两个直角三角形公共斜边时，四个顶点共圆，结合图形求解可得．【详解】解：如图，以AH为斜边的两个直角三角形，四个顶点共圆（A、F、H、E），以BH为斜边的两个直角三角形，四个顶点共圆（B、F、H、D），以CH为斜边的两个直角三角形，四个顶点共圆（C、D、H、E），以AB为斜边的两个直角三角形，四个顶点共圆（A、E、D、B），以BC为斜边的两个直角三角形，四个顶点共圆（B、F、E、C），以AC为斜边的两个直角三角形，四个顶点共圆（A、F、D、C），共6组．故选D．【点睛】本题考查四点共圆的判断方法．解题的关键是明确有公共斜边的两个直角三角形的四个顶点共圆．，．下2．（2023·安徽合肥·校考一模）如图，O是AB的中点，点B，C，D到点O的距离相等，连接AC BD列结论不一定成立的是（）A ．12B ．3=4C ．180ABC ADCD ．AC 平分BAD【答案】D 【分析】以点O 为圆心，OA 长为半径作圆．再根据圆内接四边形的性质，圆周角定理逐项判断即可．【详解】如图，以点O 为圆心，OA 长为半径作圆．由题意可知：OA OB OC OD ．即点A 、B 、C 、D 都在圆O 上．A ．∵ AB AB ，∴12 ，故A 不符合题意；B ．∵ BCBC ，∴3=4 ，故B 不符合题意；C ．∵四边形ABCD 是O 的内接四边形，∴180ABC ADC ，故C 不符合题意；D ．∵ BC 和CD不一定相等，∴BAC 和DAC 不一定相等，∴AC 不一定平分BAD ，故D 符合题意．故选：D ．【点睛】本题考查圆周角定理及其推论，充分理解圆周角定理是解答本题的关键．3．（2023·江苏宿迁·九年级校考期末）如图，在Rt ABC △中，90ACB ，3BC ，4AC ，点P 为平面内一点，且CPB A ，过C 作CQ CP 交PB 的延长线于点Q ，则CQ 的最大值为（）【点睛】本题考查相似三角形的判定和性质以及四点共圆，掌握同圆或等圆中，同弧所对的圆周角相等确定四点共圆，利用相似三角形性质得到线段间等量关系是解题关键．4．（2023·北京海淀·九年级校考期中）如图，点接AC，BD．请写出图中任意一组互补的角为【答案】DAB【分析】首先判断出点【答案】130【分析】根据题意得到四边形【详解】解：由题意得到∴四边形ABCD为圆∵∠ABC＝50°，∴∠【点睛】此题考查了圆内接四边形的性质，熟练掌握圆内接四边形的性质是解本题的关键．6．（2023·浙江金华·A．3B．1∵PE AB 于点E ，PD AC 于点，∴90AEP ADP ，∴180AEP ADP ，∴A 、E 、D 四点共圆，PA 是直径，在Rt PDC 中，45C ，∴△是等腰直角三角形，45APD ∴APD △也是等腰直角三角形，45PAD ，∴PED PAD ∴45AED ，∴AED C ，∵EAD CAB ，∴AED ∽设2AD x ，则2PD DC x ，22x ，如图2，取AP 的中点O 则2AO OE OP x ，∵604515EAP BAC PAD ，过E 作EM AP 于M ，则EM x，cos30OM OE ，∴36222OM x x ，∴6226222AM x x x ，由勾股定理得： 222226222AE AM EM x x ＋【答案】3632 /323 【分析】数形结合，根据动点的运动情况判断点【详解】解：如图旋转，连接以BC 为直径作O ，以AE 为半径作在ABD △和ACE △中AB AC AD AE BAD CAEPBC PBA ACB PBC 90BAC BPC EAD ∵，122AB ∵，A 的半径为62∴又∵90BAC EAD ，CAD，∵33BC ，OP BC∵MQ，MC与圆O相切，1QOM COM COP 【答案】(1)见详解（2）证明：如下图所示由题意可知AC 逆时针旋转90得到边AE ，90E ACB ，则90ACB ∵，AE BF ∥，90 ∵，90EFC ，，F ，E 四点共圆．．∵四边形ABCD是菱形，AC，且 GOC GCO90＝＝∵，点90DHC DOC＝BDF OCH＝，且BF OM ∵，点＝＝90AED AOD尝试应用如图2，点D 为等腰Rt ABC △外一点，AB AC ，BD CD ，过点A 的直线分别交DB 的延长线和CD 的延长线于点N ，M ，求证：12ABN ACM S S AN AM △△．问题拓展如图3，ABC 中，AB AC ，点D ，E 分别在边AC ，BC 上，60BDA BEA ，AE ，BD ，直接写出BE 的长度（用含a ，b 的式子）∵ABC 为等腰直角三角形，∴AB AC ，又∵BD CD ，即：=90BDC ，∴A 、B 在ABN 与ACE △中，AB AC ABN ACE BN CE，∴∴BAN BAE CAE BAE BAC ∴1122AME AMC S AE AM AN AM S S △△∴60AFB BAF ABF ，AB AF AC ，∵60BDA BEA ，∴A 、D 、E 、B 、F 五点共圆，则：13 ，24 ，60BEF AEB ，【答案】问题情境：见解析；问题解决：（1）102；（2）13522【分析】[问题情境]连结AC ，取AC 的中点O ，连结OB 、OD ，根据直角三角形斜边上的中线等于斜边的一半，可得OD OA OC OB ，以此即可证明；[问题解决]（1）根据题意可得225AE AD DE ，由[问题情境]结论可知A 、D 、E 、据圆周角定理以及正方形的性质可得45PDE PAE ，则PAE △为等腰直角三角形，设AP 长为a ，根据勾股定理列出方程，求解即可；（2）由[问题情境]结论可知A 、D 、E 、P 四点共圆，过点O 作OG AD 于点G ，作OH 接OB 交O 于点P ，连接PB ，根据题意可得四边形MBNP 为矩形，则要求MN 的最小值，即求值，根据平行线的性质和中点的定义可得OG 为ADE V 的中位线，得1AG ，12OG ，同理可证四边形1【翻折】(1)如图1，将DEF 沿线段AB 翻折，连接CF ，下列对所得四边形ACBF 的说法正确的是平分CBF 、CAF ，②AB 、CF 互相平分，③12ACBF S AB CF 四边形，④A 、C 、B 、F 四点共圆．AB 垂直平分CF ，故②ABC ABF ACBF S S S 四边形1122AB AB FG 12AB CG 取AB 的中点O ，连接CO FO ，ABC ABF △、△均为直角三角形，∴OB OC OA OF ，∴A 、B 、F 四点共圆，故（）沿线段向左平移，∴AB CF ，CF BE 的中点，∴BE BD BF特殊情况分析：(1)如图1，正方形ABCD 中，点P 为对角线时针旋转ADC 的度数，交直线BC 于点Q ．小明的思考如下：连接DQ ，∵AD CQ ∥，90ADC DCQ ，∴ACQ DAC ∵90DPQ ，∴180DPQ DCQ ，∴点D P Q 、、PDQ PCQ DQP PCD∵在菱形ABCD 中BC AD ∥，180ADC DCQ ，DPQ ADC ，∵180DPQ DCQ ，∴点P C Q 、、、共圆，∴DQP ACD ，ACB PDQ ，∵AC 为菱形ABCD 的对角线，ACB ACD ，∴PDQ DQP ，∴ DP PQ ；（3）解：3PQ 或3．由于点P 为对角线AC 上一个动点，分两类情况讨论如下：所示：180302ADC ACD，。

苏教版九年级四点共圆知识点详解

知识点
四点共圆的判定一：
若四个点到一定点的距离相等，则这四个点在同一个圆上（即这四点共圆）
解析：点A,B,C,D四点到O点的距离相同，则A,B,C,D四点共圆
典例精讲
锐角△ABC的三条高AD、BE、CF交于H，在A、B、C、D、E、F、H七个点中．能
组成四点共圆的组数是（）
A、4组
B、5组
第一讲四点共圆的性质及判定
CONTENTS
1 技巧讲解 2 例题讲解 3 对应习题 4 课程总结
初中数学知识点精讲课程
P a r t 1 四点共圆的性质及判定
知识点
一.四点共圆的判定方法：
1、若四个点到一定点的距离相等，则这四个点在同一个圆上（即这四点共圆）。 2、若一个四边形的一组对角的和等于180度，则这个四边形的四个顶点共圆。 3、若一个四边形的一个外角等于它的内对角，则这个四边形的四个顶点共圆。 4、若两个点在一条线段的同旁，并且和这条线段的两端连线所夹的角相等，那么这两个点和这条线的两个端点共圆。 5、若、两线段相交于点，且，则、、、四点共圆。 6、若、两线段延长后相交于点，且，则、、、四点共圆。 7、若四边形两组对边乘积的和等于对角线的乘积，则四边形的四个顶点共圆。
证明在△ABC 中，BD、CE 是 AC、AB 边上的高． ∴∠BEC=∠BDC=90°，且 E、D 在 BC 的同侧， ∴E、B、C、D 四点共圆． ∠AED=∠ACB，∠A=∠A， ∴△AED∽△ACB．
变式练习
在半⊙O中，AB为直径，直线CD交半圆于C、D，交AB延长线于M（MB<MA， AC<MD），设 K是△AOC与△DOB的外接圆除点O外的另一个交点，求证：∠MKO=90°
P

人教版数学九年级上册四点共圆,解题妙不可言

人教版数学九年级上册四点共圆，解题妙不可言四点共圆是一种重要的解题方法，熟练判断四点共圆，并灵活运用圆的相关性质，能有效进行解题.1.对角互补的四边形四点共圆证线段线段例1如图1，在四边形ABCD 中，∠A=∠BCD=90°，BC=CD=210，CE AD 于点E ．求证：AE=CE ；（2）若tanD=3，求AB 的长．（2018年北京石景山区模拟题）分析：根据∠A=∠BCD=90°，利用对角互补的四边形共圆，作出这个圆，从而把问题转化为圆的知识，在圆的背景下求解，可以帮助同学们更容易找到求解思路.解：如图1，因为∠A+∠BCD=180°,所以四边形ABCD 四点共圆，延长CE 交圆于点F ，连接AF ，因为∠A=∠AEC=90°，所以AB ∥CF ，所以BC=AF,因为BC=CD ，所以AF=CD ，因为∠EAF=∠ECD ， ∠F=∠D ，所以△AEF ≌△CED ，所以AE=CE.（2）略点评：对角互补的四边形内接于圆，借助四点共圆，可以创造出更多解题所必需的条件，如夹在两平行弦之间的弦相等，为三角形的全等提供“S ”元素.2.对角互补的四边形四点共圆综合题例2 如图2，四边形ABCD 中，AC ，BD 是它的对角线，∠ADC=∠ABC=90°，∠BCD 是锐角.（1）若BD=BC ，求证：sin ∠BCD=ACBD ；（2）若AB=BC=4,AD+CD=6，求：AC BD 的值. （3）若BD=CD ，,AB=6，BC=8。

求：sin ∠BCD 的值.分析：根据∠ADC=∠ABC=90°，可以判定四边形ABCD 是满足四点共圆，且直径为AC ，作出直径为AC 的圆，就把普通的计算转化为圆的基本计算，充分利用圆的知识使得计算更加简便，提高计算的效率.解：（1）因为∠ADC=∠ABC=90°，所以四点A,B,C,D 都在直径为AC 的圆上，如图2，因为BD=BC ，所以∠BCD=∠BDC ，因为∠BAC=∠BDC ，所以∠BAC=∠BCD ，在直角三角形ABC 中， sin ∠BAC=AC BC ，所以sin ∠BCD=ACBD ；（2）如图3，因为AB=BC=4，所以AC=42，延长DC 到点E ，使得CE=AD ，连接BE ，根据四边形的外角等于内对角，所以∠BCE=∠BAD ，所以△BAD ≌△BCE ，所以BD=BE ， ∠ABD=∠CBE ，因为∠ABC=90°，AD+CD=6，所以∠DBE=90°，DE=6，所以BD=32，所以AC BD =432423=. （3）如图4，因为BD=CD ，作直径DF ，交BC 于点E ，连接BF ，则BE ⊥DF ，∠DBF=90°，BE=EC=4, 因为AB=6，BC=8，所以AC=DF=10，易证△DEB ∽△BEF ，所以2BE =DE ∙EF,所以16=（10-EF ）∙EF,整理，得2EF -10EF+16=0,解得EF=2或EF=8(（舍去），当EF=2时，BF=25,所以sin ∠BCD=sin ∠F=BF BE =524=552.点评：把一般几何问题转化为四点共圆问题，充分利用圆周角定理，垂径定理，把问题顺利求解，且思路顺畅，是值得熟练掌握的好方法.3.圆定义共圆和同底同侧等角的三角形，四顶点共圆，探究综合题例3 如图5，△ABC 和△ADE 都是等边三角形，将△ADE 绕点A 旋转（保持点D 在△ABC 的内部），连接BD ，CE.（1）求证：BD=CE ；（2）当AB=4,AD=2, ∠DEC=60°时，求BD 的长；（3）设射线BD 和射线CE 相交于点Q ，连接QA ，直接写出旋转过程中，QD,QE,QA 之间的数量关系.分析：第一问：这是常规性的旋转问题，只要牢牢抓住旋转的全等性，借助三角形的全等结论就顺利得出.第二问：解决起来就需要多方面的思考：一是平行线的判定问题，二是三点共线问题，三是三点共圆问题，四是三角形的相似问题，五是一元二次方程的根的问题，都需要缜密思考，规范解答，和谐思考才能顺利得解.第三问：看似简单，但是要真正找到三者的数量关系，还需要动一番脑筋，特别是利用同底同侧对等角的三角形，则四点共圆，把问题转化成圆的相关知识解决，使得解题流畅，简洁，这里的分类思想也发挥着重要的作用.解：（1）如图5，由△ABC 和△ADE 都是等边三角形，所以AB=AC,AD=AE ，∠BAD+∠DAC=60°, ∠CAE+∠DAC=60°,所以∠BAD=∠CAE ，所以△BAD ≌△CAE ，所以BD=CE ；（2）根据（1）知道：∠BDA=∠CEA ，因为∠DEC=60°，所以∠CEA=∠BDA=120°，所以∠ADE+∠BDA=180°，所以B,D,E 三点共线，设点G 是AB 的中点，则AG=AD=AE=DE=2,所以点G,D,E 在以A 为圆心，半径为2的圆上，延长GA 交圆于点F ，连接DG,EF ，如图6，易证△BGD ∽△BEF ，所以BFBD BE BG =,所以BG ∙BF =BD ∙BE,所以12=BD(BD+2), 整理，得2BD +2BD-12=0,解得BD=-1+13或BD=-1-13 (（舍去），所以BD 的长为13-1；（3）当点D 在三点B,D,E 共线时的左边时，如图7，QD,QE,QA 之间的数量关系是： QD=QA+QE.理由如下：根据（1）知道：∠ABD=∠ACE ，所以∠QBC+∠QCB=60°-∠ABD +60°+∠ACE=120°，所以∠BQC=60°，因为∠DAE=60°，所以∠BQC=∠DAE ，所以A,D,E,Q 四点共圆，延长AQ 到点F ，使得QF=QE,连接EF ，则∠FQE=∠ADE=60°，所以△QEF 是等边三角形，所以∠DQE=∠AFE=60°，∠FAE=∠QDE,EF=QE ，所以△FAE ≌△QDE ，所以AF=QD ，所以QD=QA+QF=QA+QE.当点D 在三点B,D,E 共线时的右边时，如图8，QD,QE,QA 之间的数量关系是：QA=QD+QE.请同学们仿照上述证明，结合图形自己给出证明.点评：四点共圆是一种非常有效的解题方法，希望同学们能尽量熟练掌握，不仅能开阔自己的视野，提高解题的效率，更重要的是丰富自己的知识储备，不受知识的局限，让自己的数学解题游刃有余，提高自己数学解题能力.4.同底同侧等角的三角形，四顶点共圆，判定四边形的形状例4 如图9，已知△ABC和△ADE都是等边三角形，点D在边BC上，点E在边AD的右侧，连接CE．（1）求证：∠ACE=60°；（2）在边AB上取一点F，使BF=BD，联结DF、EF．求证：四边形CDFE是等腰梯形．分析：第一问：充分利用三角形的全等，结论就顺利得到.第二问：证明抓住两个关键点，一是证明DF=CE,二是证明CD∥EF，利用好等边三角形的性质，四点共圆的判定方法，可以巧妙破解.解：（1）由△ABC和△ADE都是等边三角形，所以AB=AC,AD=AE，∠BAD+∠DAC=60°, ∠CAE+∠DAC=60°,所以∠BAD=∠CAE，所以△BAD≌△CAE，所以∠ABD=∠ACE=60°；（2）由BF=BD，∠ABD=60°，所以△BFD是等边三角形，所以BD=DF=CE.因为∠ADE=∠ACE=60°，所以A,D,C,E四点共圆，因为∠AFD+∠AED=180°，所以点A,F,D,E四点共圆，所以点A,F,D,C,E五点共圆，所以∠AFE=∠ADE=60°，所以∠AFE=∠B，所以CD∥EF，所以四边形CDFE是等腰梯形．点评：此题也可以用其他方法求解，感兴趣的同学可以自我尝试一下.例1 如图，E、F、G、H分别是菱形ABCD各边的中点．求证：E、F、G、H 四点共圆．证明菱形ABCD的对角线AC和BD相交于点O，连接OE、OF、OG、OH．∵AC和BD 互相垂直，∴在Rt△AOB、Rt△BOC、Rt△COD、Rt△DOA中，E、F、G、H，分别是AB、BC、CD、DA的中点，即E、F、G、H四点共圆．(2)若四边形的两个对角互补(或一个外角等于它的内对角)，则四点共圆．例2 如图，在△ABC中，AD⊥BC，DE⊥AB，DF⊥AC．求证：B、E、F、C四点共圆．证明∵DE⊥AB，DF⊥AC，∴∠AED＋∠AFD=180°，即A、E、D、F四点共圆，∠AEF=∠ADF．又∵AD⊥BC，∠ADF＋∠CDF=90°，∠CDF＋∠FCD=90°，∠ADF=∠FCD．∴∠AEF=∠FCD，∠BEF＋∠FCB=180°，即B、E、F、C四点共圆．(3)若两个三角形有一条公共边，这条边所对的角相等，并且在公共边的同侧，那么这两个三角形有公共的外接圆．证明在△ABC中，BD、CE是AC、AB边上的高．∴∠BEC=∠BDC=90°，且E、D在BC的同侧，∴E、B、C、D四点共圆．∠AED=∠ACB，∠A=∠A，∴△AED∽△ACB．上述三种方法是证“四点共圆”的基本方法，至于证第四点在前三点(不在同一直线上)所确定的圆上就不叙述了．【例1】在圆内接四边形ABCD中，∠A-∠C=12°，且∠A∶∠B=2∶3．求∠A、∠B、∠C、∠D的度数．解∵四边形ABCD内接于圆，∴∠A+∠C=180°．∵∠A-∠C=12°，∴∠A=96°，∠C=84°．∵∠A∶∠B=2∶3，∠D=180°-144°=36°．利用圆内接四边形对角互补可以解决圆中有关角的计算问题．【例2】已知：如图1所示，四边形ABCD内接于圆，CE∥BD交AB 的延长线于E．求证：AD·BE=BC·DC．证明：连结AC．∵CE∥BD，∴∠1=∠E．∵∠1和∠2都是所对的圆周角，∴∠1=∠2．∠1=∠E．∵四边形ABCD内接于圆，∴∠EBC=∠CDA．∴△ADC∽△CBE．AD∶BC=DC∶BE．AD·BE=BC· DC．本例利用圆内接四边形的一个外角等于内对角及平行线的同位角、圆中同弧所对的圆周角得到两个相似三角形的条件，进而得到结论．关于圆内接四边形的性质，还有一个重要定理．现在中学课本一般都不列入，现介绍如下：定理：圆内接四边形两条对角线的乘积等于两组对边乘积的和．已知：如图2所示，四边形ABCD内接于圆．求证：AC·BD=AB·CD ＋AD·BC．证明：作∠BAE=∠CAD，AE交 BD于 E．∵∠ABD=∠ACD，即 AB·CD=AC·BE．①∵∠BAE+∠CAE=∠CAD+∠CAE，∴∠BAC=∠EAD．又∠ACB=∠ADE，AD·BC=AC·DE．②由①，②得AC·BE+AC·DE=AB·CE＋AD·BCAC·BD=AB·CD＋AD·BC这个定理叫托勒密(ptolemy)定理，是圆内接四边形的一个重要性质．这个证明的关键是构造△ABE∽△ACD，充分利用相似理论，这在几何中是具有代表性的．在数学竞赛中经常看到它的影子，希望能引起我们注意．命题“菱形都内接于圆”对吗？命题“菱形都内接于圆”是不正确的．所以是假命题．理由是：根据圆的内接四边形的判定方法之一，如果一个四边形的一组对角互补，那么这个四边形内接于圆．这个判定的前提是一组对角互补，而菱形的性质是一组对角相等．而一组相等的角，它们的内角和不一定是180°．如果内角和是180°，而且又相等，那么只可能是每个内角等于90°，既具有菱形的性质，且每个内角等于90°，那末这个四边形一定是正方形．而正方形显然是菱形中的特例，不能说明一般情形．判定四边形内接于圆的方法之二，是圆心到四边形四个顶点的距离相等．圆既是中心对称图形，又是轴对称图形，它的对称中心是圆心．菱形同样既是中心对称图形，又是轴对称图形，它的对称中心是两条对角线的交点．但菱形的对称中心到菱形各个顶点的距离不一定相等．所以，也无法确定菱形一定内接于圆；如果菱形的对称中心到菱形各边顶点的距离相等，再加上菱形的对角线互相垂直平分这些性质，那么这个四边形又必是正方形．综上所述，“菱形都内接于圆”这个命题是错误的．5圆的内接四边形例1 已知：如图7-90，ABCD是对角线互相垂直的圆内接四边形，通过对角线的交点E与AB垂直于点H的直线交CD于点M．求证：CM=MD．证明∠MEC与∠HEB互余，∠ABE与∠HEB互余，所以∠MEC=∠ABE．又∠ABE=∠ECM，所以∠MEC=∠ECM．从而CM=EM．同理MD=EM．所以CM=MD．点评本例的逆命题也成立（即图中若M平分CD，则MH⊥AB）．这两个命题在某些问题中有时有用．本例叫做婆罗摩笈多定理．例2 已知：如图7-91，ABCD是⊙O的内接四边形，AC⊥BD，分析一如图7-91（a），由于E是AB的中点，从A引⊙O的需证明GB=CD．但这在第七章ξ 1.4圆周角中的例3已经证明了．证明读者自己完成．*分析二如图7-91（b），设AC，BD垂直于点F．取CD的有OE∥MF．从而四边形OEFM应该是平行四边形．证明了四边形OEFM是平行四边形，问题也就解决了．而证明四边形OEFM是平行四边形已经没有什么困难了．*分析三如图7-91（b），通过AC，BD的交点F作AB的垂线交CD于点M．连结线段EF，MO．由于OE⊥AB，FM⊥AB，所以OE∥FM．又由于EF⊥CD（见例1的点评），MO⊥CD，所以EF∥MO．所以四边形OEFM为平行四边形．从而OE=MF，而由例3 求证：圆内接四边形对边乘积的和等于对角线的乘积，即图中AB·CD+BC·AD=AC·BD．分析在AB·CD+BC·AD=AC·BD中，等号左端是两个乘积的和，要证明这种等式成立，常需把左端拆成两个单项式来证明，即先考虑AB·CD和BC·AD各等于什么，然后再考虑AB·CD+BC·AD是否等于AC·BD．而要考虑AB·CD和BC·AD各等于什么，要用到相似三角形．为此，如图7-92，作AE，令∠BAE=∠CAD，并且与对角线BD相交于点E，这就得到△ABE∽△ACD．由此求得AB·CD=AC·BE．在圆中又出现了△ABC∽△AED，由此又求得BC·AD=AC·ED．把以上两个等式左右各相加，问题就解决了．证明读者自己完成．点评本例叫做托勒玫定理．它在计算与证明中都很有用．意一点．求证：PA=PB+PC．分析一本例是线段和差问题，因此可用截取或延长的方法证明．如图7-93（a），在PA上取点M，使PM=PB，剩下的问题是证明MA=PC，这只要证明△ABM≌△CBP就可以了．证明读者自己完成．分析二如图7-93（a），在PA上取点M，使MA=PC，剩下的问题是证明PM=PB，这只要证明△BPM是等边三角形就可以了．证明读者自己完成．分析三如图7-93（b），延长CP到M，使PM=PB，剩下的问题是证明PA=MC，这只要证明△PAB≌△CMB就可以了．证明读者自己完成．读者可仿以上的方法拟出本例的其他证明．*本例最简单的证明是利用托勒玫定理（例3）．证明由托勒玫定理得PA·BC=PB·AC+PC·AB，由于BC=AC=AB，所以有PA=PB+PC．例2 如图7—116，⊙O1和⊙O2都经过A、B两点，经过点A的直线CD与⊙O1交于点C，与⊙O2交于点D．经过点B的直线EF与⊙O1交于点E，与⊙O2交于点F．求证：CE∥DF．分析：要证明CE∥DF．考虑证明同位角(或内错角)相等或同旁内角互补．由于CE、DF分别在两个圆中，不易找到角的关系，若连结AB，则可构成圆内接四边形，利用圆内接四边形的性质定理可沟通两圆中有关角的关系．证明：连结AB．∵ABEC是圆内接四边形，∴∠BAD=∠E．∵ADFB是圆内接四边形，∴∠BAD＋∠F=180°，∴∠E＋∠F=180°．∴CE∥CF．说明：(1)本题也可以利用同位角相等或内错角相等，两直线平行证明．如延长EF至G，因为∠DFG=∠BAD，而∠BAD=∠E，所以∠DFG=∠E．(2)应强调本题的辅助线是为了构成圆内接四边形，以利用它的性质，导出角之间的关系．(3)对于程度较好的学生，还可让他们进一步思考，若本题不变，但不给出图形，是否还有其他情况？问题提出后可让学生自己画图思考，通过讨论明确本题还应有如图7—117的情况并给予证明．例3 如图7—118，已知在△ABC中，AB=AC，BD平分∠B，△ABD的外接圆和BC交于E．求证：AD=EC．分析：要证AD=EC，不能直接建立它们的联系，考虑已知条件可知∠ABD=∠DBE，容易看出．若连结DE，则有AD=DE．因此只要证DE=EC．由于DE和EC为△DEC的两边，所以只要证∠EDC=∠C．由已知条件可知∠C=∠ABC．因此只要证∠EDC=∠ABC．因为△EDC是圆内接四边形ABED的一个外角，所以可证∠EDC=∠ABC．问题可解决．证明：连结DE．∵BD平分∠ABC，∴，AD=DE．∵ABED是圆内接四边形，∴∠EDC=∠ABC．∵AB=AC，∴∠ABC=∠C，∴∠EDC＝∠C．于是有DE=EC．因此AD=EC．四、作业1．如图7—120，在圆内接四边形ABCD中，AC平分BD，并且AC⊥BD，∠BAD=70°18′，求四边形其余各角．2．圆内接四边形ABCD中，∠A、∠B、∠C的度数的比为2∶3∶6，求四边形各内角的度数．3．如图7—121，AD是△ABC外角∠EAC的平分线，AD与三角形的外接圆交于点D．求证：DB=DC．作业答案或提示：1．∠ABC=∠ADC=90°，∠BCD=109°42′．2．∠A=45°，∠B=67.5°，∠C=135°，∠D=112.5°．3．提示：因为∠DBC=∠DAC，∠EAD=∠DCB，∠EAD=∠DAC，所以∠DBC=∠DCB，因此DB=DC．判定四点共圆的方法引导学生归纳判定四点共圆的方法：(1)如果四个点与一定点距离相等，那么这四个点共圆．(2)如果一个四边形的一组对角互补，那么这个四边形的四个顶点共圆．(3)如果一个四边形的一个外角等于它的内对角，那么这个四边形的四个顶点共圆．(4)如果两个直角三角形有公共的斜边，那么这两个三角形的四个顶点共圆(因为四个顶点与斜边中点距离相等)．3．如图7—124，已知ABCD为平行四边形，过点A和B的圆与 AD、BC分别交于 E、F．求证：C、D、E、F四点共圆．提示连结EF．由∠B+∠AEF=180°，∠B＋∠C=180°，可得∠AEF=∠C．四点共圆的应用山东宁阳教委教研室栗致根四点共圆在平面几何证明中应用广泛，熟悉这种应用对于开阔证题思路，提高解题能力都是十分有益的．一用于证明两角相等例1 如图1，已知P为⊙O外一点，PA切⊙O于A，PB切⊙O于B，OP交AB于E．求证：∠APC＝∠BPD．证明连结OA，OC，OD．由射影定理，得AE2=PE·EO，又AE＝BE，则AE·BE＝PE·EO……(1)；由相交弦定理，得AE·BE＝CE·DE……(2)；由(1)、(2)得CE·ED＝PE·EO，∴ P、C、O、D四点共圆，则∠1＝∠2，∠3＝∠4，又∠2=∠4．∴∠1＝∠3，易证∠APC＝∠BPD(∠4＝∠EDO)．二用于证明两条线段相筹例2 如图2，从⊙O外一点P引切线PA、PB和割线PDC，从A点作弦AE平行于DC，连结BE交DC于F，求证：FC＝FD．证明连结AD、AF、EC、AB．∵PA切⊙O于A，则∠1＝∠2．∵AE∥CD，则∠2＝∠4．∴∠1=∠4，∴P、A、F、B四点共圆．∴∠5＝∠6，而∠5＝∠2=∠3，∴∠3＝∠6．∵AE∥CD，∴EC=AD，且∠ECF=∠ADF，∴△EFC≌△AFD，∴FC＝FD．三用于证明两直线平行例3 如图3，在△ABC中，AB=AC，AD⊥BC，∠B的两条三等分线交AD于E、G，交AC于F、H．求证：EH∥GC．证明连结EC．在△ABE和△ACE中，∵AE＝AE，AB=AC，∠BAE＝∠CAE，∴△AEB≌AEC，∴∠5＝∠1＝∠2，∴B、C、H、E四点共圆，∴∠6＝∠3．在△GEB和△GEC中，∵GE＝GE，∠BEG＝∠CEG，EB＝EC，∴△GEB ≌△GEC，∴∠4=∠2＝∠3，∴∠4＝∠6．∴EH∥GC．四用于证明两直线垂直证明在△ABD和△BCE中，∵AB=BC，∠ABD＝∠BCE，BD＝CE，则△ABD≌△BCE，∴∠ADB=∠BEC，∴P、D、C、E四点共圆．设DC的中点为O 连结OE、DE．易证∠OEC＝60°，∠DEO＝30°∴∠DEC＝90°，于是∠DPC=90°，∴ CP⊥AD．五用于判定切线例5 如图5，AB为半圆直径，P为半圆上一点，PC⊥AB于C，以AC为直径的圆交PA于D，以BC为直径的圆交PB于E，求证：DE是这两圆的公切线．证明连结DC、CE，易知∠PDC＝∠PEC＝90°，∴ P、D、C、E四点共圆，于是∠1=∠3，而∠3＋∠2＝90°，∠A＋∠2=90°，则∠1＝∠A，∴DE是圆ACD的切线．同理，DE是圆BCE的切线．因而DE为两圆的公切线六用于证明比例式例6 AB、CD为⊙O中两条平行的弦，过B点的切线交CD的延长线于G，弦PA、PB分别交CD于E、F．证明如图6．连结BE、PG．∵BG切⊙O于B，则∠1=∠A．∵AB∥CD，则∠A＝∠2．于是∠1＝∠2，∴P、G、B、E四点共圆．由相交弦定理，得EF·FG=PF·FB．在⊙O中，由相交弦定理，得CF·FD=FP·FB．七用于证明平方式例7 ABCD为圆内接四边形，一组对边AB和DC延长交于P点，另一组对边AD和BC延长交于Q点，从P、Q引这圆的两条切线，切点分别是E、F，(如图 7)求证：PQ2＝QF2＋PE2．证明作△DCQ的外接圆，交PQ于M，连结MC，∵∠1=∠2＝∠3，则P、B、C、M四点共圆．由圆幂定理得PE2＝PC·PD＝PM·PQ，QF2=QC·QB ＝QM·QP，两式相加得PE2＋QF2＝PM·PQ＋ QM·QP=PQ(PM＋QM)＝PQ·PQ=PQ2∴PQ2=PE2＋QF2．八用于解计算题例8如图8，△ABC的高AD的延长线交外接圆于H，以AD为直径作圆和AB、AC分别交于E、F点，EF交 AD于 G，若 AG=16cm，AH=25cm，求 AD的长．解连结DE、DF、BH．∵∠1=∠2＝∠C=∠H，∴B、E、G、H四点共圆．由圆幂定理，得AE·AB＝AG·AN．在△ABD中，∵∠ADB=90°，DE⊥AB，由射影定理，得AD2＝AE·AB，∴AD2＝AG·AH＝16×25＝400，∴AD=20cm．九用于证明三点共线例9如图9，D为△ABC外接圆上任意一点，E、F、G为D点到三边垂线的垂足，求证：E、F、G三点在一条直线上．证明连结EF、FG、BD、CD．∵∠BED=∠BFD=90°，则B、E、F、D 四点共圆，∴∠1＝∠2，同理∠3＝∠4．在△DBE和△DCG中，∵∠DEB＝∠DGC，∠DBE＝∠DCG，故∠1=∠4，易得∠2＝∠3，∴ E、F、G三点在一条直线上．十用于证明多点共圆例10如图10，H为△ABC的垂心，H1、H2、H3为H点关于各边的对称点，求证：A、B、C、H1、H2、H3六点共圆．证明连结AH2，∵H与H2关于AF对称，则∠1=∠2．∵A、F、D、C 四点共圆，则∠2＝∠3，于是∠1＝∠3，∴A、H2、B、c四点共圆，即H2在△ABC的外接圆上．同理可证，H1、H3也在△ABC的外接圆上．∴A、B、C、H1、H2、H3六点共圆．相关资源托勒密定理的数形转换功能山东临沂市四中姜开传临沂市第一技校刘久松圆内接四边形两组对边乘积的和等于其对角线的乘积，即在四边形ABCD中，有AB·CD＋AD·BC=AC·BD，这就是著名的托勒密定理．本刊1996年第2期给出了它的几种证法，作为续篇，本文就其数形转换功能举例说明如下：1 “形”转换为“数”对于某些几何问题，特别是圆内接多边形问题，如果能根据题设中隐含的数量关系，利用托勒密定理可将“形”转换为“数”，从而达到用代数运算来代替几何推理的目的．例1已知正七边形A1A2 (7)(第21届全俄数学奥林匹克竞赛题)对于这道竞赛题，原证较繁，但通过深挖隐含条件，利用托勒密定理可改变整个解题局面，使证题步骤简缩到最少．如图1，连 A1A5、A3A5，则A1A5=A1A4、A3A5=A1A3．在四边形A1A3A4A5中，由托勒密定理，得A3A4·A1A5＋A4A5·A1A3＝A1A4·A3A5，即A1A2·A1A4＋A1A2·A1A3＝A1A3·A1A4，两边同除以A1A2·A1A3·A1A4即得结论式．例2 如图2，A、B、C、D四点在同一圆周上，且BC＝CD＝4，AE=6，线段BE和DE的长都是整数，则BD的长等于多少？(1988年全国初中数学联赛题)此题若用其它方法解，往往使人一筹莫展．若运用托勒密定理，可使问题化难为易．由△CDE∽△BAE和△CBE∽△DAE，得由托勒密定理，得BD(AE＋CE)=4(AB＋AD)，亦即 CE(AE＋CE)＝16．设CE=x，整理上式，得x2＋6x－16＝0．解得x＝2(负值已舍)，故BE·DE＝CE·AE＝12．∵BD＜BC＋CD＝8，例3一个内接于圆的六边形，其五个边的边长都为81，AB是它的第六边，其长为31，求从B出发的三条对角线长的和．(第九届美国数学邀请赛试题)原解答过程冗长．若通过托勒密定理的桥梁作用，把“形”转换为“数”，可使问题化繁为简．如图3，设BD=a， BE=b，BF＝c，连AC、CE、AE，则CE＝AE＝BD＝a，AC=BF＝c．在四边形BCDE中，由托勒密定理，得81b＋812＝a2①同理81b＋31·81=ac ②31a＋81a=bc ③解①、③、③组成的方程组，得a＝135，b＝144，c＝105故 a＋b＋c=384．2 “数”转换为“形”对于某些代数问题，若结构与托勒密定理相似，通过构造圆内接四边形，可把“数”转换为“形”，然后利用“形”的性质，使问题得到解决．这种解法构思巧妙，方法独特，富于创新，出奇制胜．例4 解方程若按常规方法解这个无理方程，过程繁冗．若由方程的结构特征联想到托勒密定理，则构造直径AC=x(x≥11)的圆及圆内接四边形ABCD，使BC=2，CD=11，如图 4，于是由托勒密定理，得在△BCD中，由余弦定理，得经检验x=14是原方程的根．求证： a2＋b2＝1．这道名题已有多种证法，而且被视为用三角换无法解代数问题的典范．下面再给出一各几何证法．易知0≤a、b≤1且a、b不全为零．当a、b之一为零时，结论显然成立．当a、b全不为零时，由已知等式联想到托勒密定理，作直径AC＝1的圆及圆内接四与已知等式比较，得BD＝1，即BD也为圆的直径，故a2＋b2=1例6设a＞c，b＞c，c＞0，此题若用常规方法证明也不轻松．下面利用托勒密定理给出它的一个巧证．由托勒密定理，得巧用托勒密定理证题河北晋州市数学论文研究协会张东海王素改在解证某些数学题时，如能巧用托勒密定理，可使解证过程简洁清新，兹举例说明．托勒密定理：圆内接四边形中，两条对角线的乘积等于两组对边乘积之和．一、构造“圆”，运用定理【例1】设a，b，x，y是实数，且a2＋b2=1，x2＋y2=1．求证：ax＋by≤1．证作直径AB=1的圆，在AB的两侧任作Rt△ACB和Rt△ADB，使AC=a，BC=b，BD=x， AD=y．(图1)由勾股定理知a，b，x，y满足条件．根据托勒密定理，有AC·BD＋BC·AD=AB·CD．∵ CD≤1，∴ax＋by≤1．二、利用无形圆，运用定理【例2】等腰梯形一条对角线的平方，等于一腰的平方加上两底之积．已知：梯形 ABCD中，AD=BC，AB∥CD．求证：BD2=BC2＋AB·CD．证∵等腰梯形内接于圆，由托勒密定理，有AC·BD=AD·BC＋AB·CD．∵AD=BC，AC=BD，∴BD2=BC2＋AB·CD．(图略)【例 3】已知：边长为 1的正七边形ABCDEFG中，对角线 AD=a，BG=b(a ≠b)．求证：(a＋b)2(a－b)＝ab2．证连结BD，GE，BE，DG，则 BD=EG＝GB=b，DG=BE＝DA＝a，DE=AB=AG=1．(如图2)在四边形ABDG中，由托勒密定理，有AD·BG=AB·DG＋BD·AG，即ab=a＋b (1)同理在四边形BDEG中，得BE·DG=DE·BG＋BD·EG，即a2=b＋b2 (2)将(2)变形为b=a2－b2 (3)(1)×(3)，得ab2＝(a＋b)(a2－b2)．故ab2=(a＋b)2(a－b)．三、构造圆内接四边形，运用定理【例4】在△ABC中，∠A的内角平分线AD交外接圆于D．连结BD．求证：AD·BC=BD·(AB＋AC)．证(如图3) 连结DC．由托勒密定理．有AD·BC=AB·CD＋AC·BD．又∵∠1=∠2，∴BD=DC．∴AD·BC=AB·CD＋AC·BD=BD(AB＋AC)．即AD·BC=BD·(AB＋AC)．圆内接四边形的面积公式黑龙江绥化五中任天民设圆内接四边形ABCD中各边为a，b，c，d．连结 BD．由∠A＋∠C=180°，可以推出sinA=sinC，cosA=－cosC．并且S四边形ABCD=S△ABD＋S△BCD所以这样我们得出了圆内接四边形面积的计算公式．在上面的公式中，如果设某一边为零，(不仿设d=0)此时四边形变成三角形，该公式恰是计算三角形面积的海伦公式．圆内接四边形面积公式的得出是受三角形面积公式的启发，通过联想探索出来的，而且两者在形式上又是那么的相近．这种现象在数学中不胜枚举，如果同学们都能从特殊规律去探索一般规律，再从一般规律去认识特殊规律．那么对数学能力的培养将大有裨益．四条边定长四边形面积的最大值上海市育群中学李甲鼎四条边为定长的四边形不具稳定性，但在某种特定的位置下，它能内接于圆，成为圆内接四边形．并且此时达到变化过程中面积最大值．下文证明这个事实．已知：四边形ABCD中：AB＝a，BC＝b，CD=c，DA=d求证：四边形ABCD中有唯一四边形能内接于圆，且此时面积达到最大值．证明：(1)先证四边形四边定长，有唯一的四边形内接于圆，设∠ABC=α，∠ADC=β，AC=x．令α＋β=π，即cosα＋cosβ=0x的解唯一确定，代入(1)(2)后cosα、cosβ也随之唯一确，在α，β∈(0，π)的条件下α、β也同时唯一确定．∴四边形四边定长，对角互补，四边形是唯一的．即所得到的四边形为圆内接四边形．(2)当四边定长的四边形内接于圆时，此四边形面积最大．∵四边形ABCD的面积由余弦定理得a2＋b2－2abcosα=x2=c2＋d2－2cdcosβ显然当α＋β=π时(即为圆内接四边形时)S2达到最大值，即S最大．一个几何定理的应用江苏省徐州矿务局庞庄职校张怀林定理：如图1，在圆接四边形ABCD中弦AD平分∠BAC，则2ADcos α=AB＋AC．证明连接BD、DC、BC，设已知圆半径为R，则由正弦定理有：BD＝DC＝2Rsinα，BC＝2Rsin2α．由托勒密定理有AB·CD+AC·BD=AD·DC．∴(AB+AC)·2Rsinα=AD·2Rsin2α．则2AD·cosα=AB＋AC．下面举例说明它的应用．例1如图2，已知锐角△ABC的∠A平分线交BC于L，交外接圆于N，过L分别作LK⊥AB，LM⊥AC，垂足分别为K、M．求证：四边形AKNM的面积等于△ABC的面积．(第28届IMO)证明由已知得∠BAN=∠CAN，由定理有2ANcosα=AB＋AC，=AN·AL·cosα·sinα=AN·AK·sinα=AN·AM·sinα=2S△AKN＝2S△AMN．∴S△ABC=S四边形AKNM．(第21届全苏奥数)证明作正七边形外接圆，如图3所示．由定理有2c·cosα=b+c，又在等腰△A1A2A3中有2a·cosα=b．例3在△ABC中，∠C=3∠A，a＝27，c＝48，则b的值是____．(第36届AHSME试题)解如图4．作△ABC的外接圆，在取三等分点D、E，连CD、CE．由已知得：∠ACD=∠DCE=∠ECB=∠A，CD=AB=48，由定理有2CE·cosA=CB+CD ①2CD·cosA＝CE+AC ②又2CB·cosA=CE ③由②、③得：b=AC=CE·(CD-CB)/CB=35．托勒密定理及其应用河北省晋州市数学论文研究协会刘同林托勒密定理：圆内接四边形中，两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和)．已知：圆内接四边形ABCD，求证：AC·BD＝AB·CD＋AD·BC．证明：如图1，过C作CP交BD于P，使∠1=∠2，又∠3=∠4，∴△ACD∽△BCP．又∠ACB=∠DCP，∠5=∠6，∴△ACB∽△DCP．①＋②得AC(BP＋DP)=AB·CD＋AD·BC．即AC·BD=AB·CD＋AD·BC．这就是著名的托勒密定理，在通用教材中习题的面目出现，不被重视．笔者认为，既然是定理就可作为推理论证的依据．有些问题若根据它来论证，显然格外简洁清新．兹分类说明如下，以供探究．一、直接应用托勒密定理例1如图2，P是正△ABC外接圆的劣弧上任一点(不与B、C重合)，求证：PA=PB＋PC．分析：此题证法甚多，一般是截长、补短，构造全等三角形，均为繁冗．若借助托勒密定理论证，则有PA·BC=PB·AC＋PC·AB，∵AB=BC=AC．∴PA=PB+PC．二、完善图形借助托勒密定理例2证明“勾股定理”：在Rt△ABC中，∠B=90°，求证：AC2=AB2＋BC2证明：如图3，作以Rt△ABC的斜边AC为一对角线的矩形ABCD，显然ABCD是圆内接四边形．由托勒密定理，有AC·BD=AB·CD＋AD·BC．①又∵ABCD是矩形，。

(完整版)初三上专题四点共圆

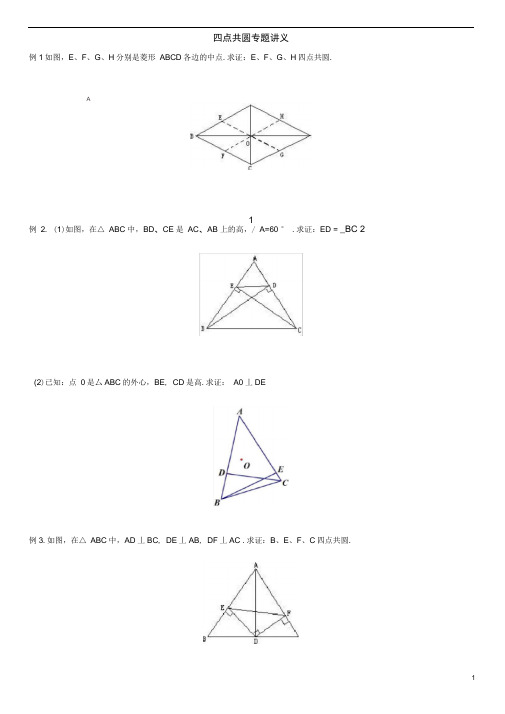
四点共圆专题讲义例1如图，E、F、G、H分别是菱形ABCD各边的中点.求证：E、F、G、H四点共圆.A1例2. (1)如图，在△ ABC 中，BD、CE 是AC、AB 上的高，/ A=60 ° .求证：ED = _BC 2(2)已知：点0是厶ABC的外心，BE, CD是高.求证：A0丄DE例3.如图，在△ ABC中，AD丄BC, DE丄AB, DF丄AC .求证：B、E、F、C四点共圆.〔、〈* ---- 空R；°7、 / f —*ff A OA=OB=OC/ ADC= / ABC=90°/ ACD= / ABD=90°/ B+ / D=180。

或/A+ / BCD=180。

或/A= / DCE/ A= / D 或/ B= /C1. ______________________________________________________2. _______________________________________________________3.________________________________________________________4.例4•求证：圆内接四边形对边乘积的和等于对角线的乘积，即图中练习1.在△ ABC中，BA BC , BAC , M是AC的中点，P是线段BM上的动点，将线段PA绕点P顺时针旋转2得到线段PQ .(1)若60且点P与点M重合(如图1),线段CQ的延长线交射线BM于点D，请补全图形，并写出/ CDB 的度数；(2)在图2中，点P不与点B, M重合，线段CQ的延长线与射线BM交于点D，猜想/ CDB的大小(用含的代数式表示)，并加以证明；(3)对于适当大小的，当点P在线段BM上运动到某一位置(不与点B, M重合)时，能使得线段CQ的延长线与射线BM交于点D，且PQ = QD，请直接写出的范围.AB • CD + BC • AD=AC • BD .练习2.在△ ABC中，/ A=30°, AB=2j3，将△ ABC绕点B顺时针旋转(0° < <90°),得到△ DBE，其中点A的对应点是点D，点C的对应点是点E，AC、DE相交于点F，连接BF.(1)如图1,若=60°，线段BA绕点B旋转得到线段BD.请补全△ DBE，并直接写出/ AFB的度数；(2)如图2,若=90°，求/ AFB的度数和BF的长；(3)如图3,若旋转(0 ° < <90 °),请直接写出/ AFB的度数及BF的长(用含的代数式表示)•练习3 .已知，点P是/ MON的平分线上的一动点，射线PA交射线OM于点A,将射线PA绕点P逆时针旋转交射线ON 于点B，且使/ APB+ / MON=180°.(1)利用图1，求证：PA=PB ;(2)如图2,若点C是AB与OP的交点，当S APOB=3S APCB时，求PB与PC的比值；图1(3)若/ MON=60°, OB=2，射线AP交ON于点D，且满足且/ PBD = Z ABO，请借助图3补全图形，并求OP长. 练习4 .已知，在△ABC中，AB=AC .过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角0, 直线a交BC边于点P (点P不与点B、点C重合)，A RMN的边MN始终在直线a上(点M在点N的上方)，且BM = BN，连接CN .(1)当/ BAC=Z MBN=90°时，①如图a，当0=45°时，/ ANC的度数为___________ ;②如图b，当0工45时，①中的结论是否发生变化？说明理由；(2)如图C,当/ BAC= / MBN丰90时，请直接写出/ ANC与/ BAC之间的数量关系，不必证明.练习5.已知：Rt A A'BC'和Rt A ABC 重合，A'C'B = / ACB=90° , BA'C' = / BAC=30° ,现将Rt A A'BC'绕点B按逆时针方向旋转角 a (60°w a 90°)，设旋转过程中射线C'C'和线段AA'相交于点D,连接BD .(1)当a=60时时，A'B过点C,如图1所示，判断BD和AA'之间的位置关系，不必证明；(2)当a=90 °时，在图2中依题意补全图形，并猜想(1)中的结论是否仍然成立，不必证明；(3)如图3,对旋转角a (60°v av90° )，猜想(1)中的结论是否仍然成立；若成立，请证明你的结论；若不成立，请说明理由.图1 图2 图3练习6 .在等边厶ABC 外侧作直线 AP ,点B 关于直线AP 的对称点为D ，连接AD , BD , CD ，其中CD 交直线AP 于点 E .设/ PAB = ，/ ACE = ，/ AEC =. (1)依题意补全图1 ;(2)若 =15°，直接写出和的度数；⑶ 如图2,若60° < <120。

第28讲四点共圆问题(解析版)

第28讲四点共圆问题一、解答题1．已知直线:l y x m +＝交抛物线2:4C y x =于,A B 两点．（1）设直线l 与x 轴的交点为T ．若=2AT TB ，求实数m 的值；（2）若点,M N 在抛物线C 上，且关于直线l 对称，求证：,,,A B M N 四点共圆．【答案】（1）8m ＝－；（2）证明见解析．【分析】（1）设()()1122,,,A x y B x y ，直线方程代入抛物线方程后由判别式得m 的范围，由韦达定理得1212,y y y y +，再由向量的数乘可得122y y +＝0，结合韦达定理可得12,,y y m 值；（2）设()()3344,,,M x y N x y ，由对称性得434y y =--，4342x m x =---．再由,M N 在抛物线上，代入变形得3y 与m 的关系，然后计算MA MB ⋅，得MA MB ⊥，同理NA NB ⊥，得证四点共圆．【详解】解：由24y x m y x=+⎧⎨=⎩得2440y y m -+=．设()()1122,,,A x y B x y ，则12124,4y y y y m +==．因为直线l 与C 相交，所以16160,m ∆->= 得1m <．（1）由2AT TB =，得1220y y +=，所以240y +=，解得24,y =- 从而18y =，因为124,y y m =所以432,m =-解得8m =-．（2）设()()3344,,,M x y N x y ，因为,M N 两点关于直线y x m =+对称，则4343223443434=144y y y y y y x x y y --==-+-解得434y y =--．又434322y y x x m ++=+ 于是3343422y y x x m --++=+ 解得4342x m x =---．又点N 在抛物线上，于是233()()4442y m x --=---．因为2334,y x =所以23341640y y m =+++，于是13231323()()()()MA M x x x x y y y y B ⋅=--+--222233121323()()(-)(-)4444y y y y y y y y =--()()()13231323()1616y y y y y y y y --=--+⎡⎤⎣⎦ ()()132********()1616y y y y y y y y y y --⎡⎤=++++⎣⎦ ()()2231333404()1616y y y y y m y --==+++ 因此MA MB ⊥，同理,NA NB ⊥于是点,M N 在以AB 为直径的圆上，即,,,A B M N 四点共圆．【点睛】方法点睛：本题考查直线与抛物线相交问题，解题方法是设而不求的思想方法，如设交点坐标为()()1122,,,A x y B x y ，直线方程代入抛物线方程后应用韦达定理可得1212,y y y y +，再利用向量的线性运算求得12,y y 关系，从而可求得12,,y y m 值．2．已知椭圆22:14x C y +=上三点A 、M 、B 与原点O 构成一个平行四边形AMBO ．（1）若点B 是椭圆C 的左顶点，求点M 的坐标；（2）若A 、M 、B 、O 四点共圆，求直线AB 的斜率．【答案】（1）1,2⎛-± ⎝⎭；（2）．【分析】（1）由已知可得()2,0B -，由//AM BO ，且AM BO =，设()00,M x y ， ()002,A x y +代入椭圆方程解方程即可得解；（2）因为A 、M 、B 、O 四点共圆，则平行四边形AMBO 是矩形且OA OB ⊥，设直线AB 的方程为y kx m =+，与椭圆方程联立，根据韦达定理代入 12120OA OB x x y y →→⋅=+=，化简计算求解即可.【详解】解析：（1）如图所示：因为()2,0B-，四边形AMBO 为平行四边形，所以//AM BO ，且2AM BO ==．设点()00,M x y ，则()002,A x y +因为点M 、A 在椭圆C 上，所以()2200202014214x y x y ⎧+=⎪⎪⎨+⎪+=⎪⎩，解得001x y =-⎧⎪⎨=⎪⎩，所以1,2M ⎛⎫-± ⎪ ⎪⎝⎭．（2）因为直线AB 的斜率存在，所以设直线AB 的方程为y kx m =+，()11,A x y ，()22,B x y ．由2214y kx m x y =+⎧⎪⎨+=⎪⎩消去y 得()222418440k x kmx m +++-=，则有122814km x x k -+=+，21224414m x x k-=+．因为平行四边形AMBO ，所以()1212,OM OA OB x x y y →→→=+=++．因为122814kmx x k -+=+，所以()12122282221414km my y k x x m k m k k -+=++=⋅+=++，所以2282,1414kmm M k k -⎛⎫ ⎪++⎝⎭．因为点M 在椭圆C 上，所以将点M 的坐标代入椭圆C 的方程化得22441m k =+．① 因为A 、M 、B 、O 四点共圆，所以平行四边形AMBO 是矩形，且OA OB ⊥，所以12120OA OB x x y y →→⋅=+=．因为2222121212122414m k y y kx m kx mk x x km x x mk，所以22212122244401414m m k x x y y k k--+=+=++，化得22544m k =+．②由①②解得2114k =，23m =，此时>0∆，因此2k =±．所以所求直线AB 的斜率为2±．【点睛】本题主要考查了联立直线与椭圆的方程利用韦达定理列式表达斜率以及垂直的方法进而代入求解的问题，考查计算能力和逻辑推理能力，属于难题. 3．已知抛物线P ：22y px =（0p >）上的点3,4a ⎛⎫⎪⎝⎭到其焦点的距离为1．（Ⅰ）求p 和a 的值；（Ⅰ）求直线l ：y x m =+交抛物线P 于两点A 、B ，线段AB 的垂直平分线交抛物线P 于两点C 、D ，求证：A 、B 、C 、D 四点共圆．【答案】（Ⅰ）12p =，2a =±；（Ⅰ）证明见解析. 【分析】（Ⅰ）根据抛物线的定义可得点3,4a ⎛⎫⎪⎝⎭到其焦点的距离等于该点到准线距离，即可求出p ，从而得到抛物线方程，再计算出参数a 的值；（Ⅰ）设()11,A x y ，()22,B x y ，联立直线与抛物线方程，消元、列出韦达定理，即可求出线段AB 的中点M 的坐标，因为直线CD 为线段AB 的垂直平分线，直线CD 的方程为1y x m =-+-，设()33,C x y ，()44,D x y ，求出线段CD 的中点坐标，再利用勾股定理计算可得；【详解】解：（Ⅰ）22y px =的准线为2px =-，因为点3,4a ⎛⎫⎪⎝⎭到其焦点的距离等于该点到准线距离，所以3124p +=，故12p =，即2y x =，又3,4a ⎛⎫⎪⎝⎭在2y x =上，所以a =；（Ⅰ）设()11,A x y ，()22,B x y ，联立2y x x x m⎧=⎨=+⎩，得20y y m -+=，则121y y +=，12y y m ⋅=，且140m ->，即14m <，则12A y B =-=，且线段AB 中点的纵坐标为12122y y +=，则12x m =-，所以线段AB 中点为11,22M m ⎛⎫-⎪⎝⎭，因为直线CD 为线段AB 的垂直平分线，直线CD 的方程为1y x m =-+-，联立21y xy x m⎧=⎨=-+-⎩，得210y y m ++-=，设()33,C x y ，()44,D x y ，则341y y +=-，341y y m ⋅=-故34y D y C =-= 线段CD 中点为31,22N m ⎛⎫--⎪⎝⎭，因为()21154108242m CD m -⎛⎫=-= ⎪⎝⎭，22225422AN AM m MN -==+=+，所以12AN CD =，所以点A 在以CD 为直径的圆上，同理点B 在以CD 为直径的圆上，所以A 、B 、C 、D 四点共圆．【点睛】(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系； (2)有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点，若过抛物线的焦点，可直接使用公式|AB |＝x 1＋x 2＋p ，若不过焦点，则必须用一般弦长公式．4．已知直线1:360l x y --=与x 轴，y 轴分别交于A ，B ，线段AB 的中垂线2l 与抛物线()2:20E y px p =>有两个不同的交点C 、D ．（1）求p 的取值范围；（2）是否存在p ，使得A ，B ，C ，D 四点共圆，若存在，请求出p 的值，若不存在，请说明理由．【答案】（1）16,9⎛⎫+∞ ⎪⎝⎭（2）存在，5p = 【分析】（1）求出,A B 两点坐标，得出其中垂线方程为380x y ++=，与抛物线方程联立根据0∆>即可得结果；（2）设()11,C x y ，()22,D x y ，线段CD 的中点为()00,M x y ，将（1）和韦达定理可得()98,3M p p --，CD =2214MA CD =，代入两点间距离公式可解得p 的值. 【详解】（1）因为直线1:360l x y --=与x 轴，y 轴分别交于A ，B . 所以()2,0A ，()0,6B -，所以线段AB 的中点为()1,3-，3AB k =，所以线段AB 的中垂线2l 的方程为()1313y x +=--，即380x y ++=. 将38x y =--代入()2:20E y px p =>，得26160y py p ++=，因为2l 与E 有两个不同的交点C ，D . 所以2364160p p ∆=-⨯>，又0p >，所以169p >，即p 的取值范围为16,9⎛⎫+∞ ⎪⎝⎭. （2）若A ，B ，C ，D 四点共圆，由对称性可知，圆心应为线段CD 的中点，设()11,C x y ，()22,D x y ，线段CD 的中点为()00,M x y ，则1212616y y p y y p +=-⎧⎨=⎩，所以12032y y y p +==-，003898x y p =--=-，CD ====若A ，B ，C ，D 四点共圆，则12MA CD =，即2214MA CD =，所以()()2220012409164x y p p -+=⨯-. 所以()222910990160p p p p -+=-，解得5p =，又5p =满足169p >，所以存在5p =，使得A ，B ，C ，D 四点共圆. 【点睛】本题主要考查了直线与抛物线的位置关系，圆内接四边形的特征，考查了学生的计算能力，属于中档题. 5．已知斜率为k 的直线交椭圆()2230x y λλ+=>于A ，B 两点，AB 的垂直平分线与椭圆交于C ，D两点，点()01,N y 是线段AB 的中点.（1）若03y =，求直线AB 的方程以及λ的取值范围；（2）不管λ怎么变化，都有A ，B ，C ，D 四点共圆，求0y 的取值范围. 【答案】（1）40x y +-=，12λ>；（2）{}3,3-. 【分析】（1）将直线AB 的方程()13y k x =-+代入椭圆方程223x y λ+=，再利用根与系数的关系可得()1223123k k x x k -+==+，从而可求出k 的值，进而可得到直线AB 的方程，由判别式大于零可求出λ的取值范围；（2）设直线AB 的方程为()01y k x y =-+，代入椭圆方程中，利用根与系数的关系，再利用弦长公式表示出AB ,由于DC 是AB 的垂直平分线，所以同理可表示DC 的长，求出CD 中点P 的横坐标，则可求出点P 到AB 的距离d ，由A ，B ，C ，D 四点共圆22222CD AB d ⎛⎫⎛⎫⇔=+ ⎪ ⎪⎝⎭⎝⎭，将AB ，DC ，d代入化简可得222211313k k k k++=++，从而可求出k 的值，进而可求得0y 【详解】设()11,A x y ，()22,B x y .（1）当03y =时，直线AB 的方程为()13y k x =-+，将AB 方程代入223x y λ+=得：()()()22232330kxk k x k λ++-+--=.①由()1223123k k x x k -+==+，解得1k =-，此时AB 的方程为40x y +-=. 将1k =-代入①，得248160x x λ-+-=. 由()6416160λ∆=-->，解得12λ>. （2）设直线AB 的方程为()01y k x y =-+，将方程代入223x y λ+=得：()()()22200320kxk y k x y k λ++-+--=.②由题意()0122123k k y x x k-+==+，即03ky -=.12AB x =-===同理得CD ==⎝⎭所以CD 中点P 的横坐标0032221112131313y ky k k x k k k⎛⎫--- ⎪+-⎝⎭===+++，点P 到AB 的距离d1=，由A ，B ，C ，D 四点共圆22222CD AB d ⎛⎫⎛⎫⇔=+ ⎪ ⎪⎝⎭⎝⎭，即()()2222222211912133313kk k k k k λλ⎛⎫++⎛⎫⎡⎤-++=--+ ⎪ ⎪⎣⎦+⎝⎭⎝⎭+，③ 不管λ怎么变化，都有A ，B ，C ，D 四点共圆，即上式恒成立，所以222211313k k k k++=++，解得21k =，此时③式成立.代入②，由0∆>得12λ>. 所以0y 的取值范围为{}3,3-. 【点睛】关键点点睛：此题考查直线与椭圆的位置关系，考查计算求解能力，解题的关键是由A ，B ，C ，D 四点共圆22222CD AB d ⎛⎫⎛⎫⇔=+ ⎪ ⎪⎝⎭⎝⎭，将AB ，DC ，d 代入化简可得222211313k k k k ++=++，从而可求出k 的值，进而可求得0y ，考查数学转化思想，属于较难题6．已知椭圆22221x y a b+=(0)a b >>的左，右焦点分别为1F ，2F ，且126F F ||=，直线y kx =与椭圆交于A ，B 两点．（Ⅰ）若△12AF F 的周长为16，求椭圆的标准方程；（Ⅰ，且A ，B ， 1F ，2F 四点共圆，求椭圆离心率e 的值；（Ⅰ）在（Ⅰ）的条件下，设00(,)P x y 为椭圆上一点，且直线PA 的斜率1(2,1)k ∈--，试求直线PB 的斜率2k 的取值范围．【答案】（Ⅰ（Ⅰ）23=e ．（Ⅰ【解析】试题解析：（Ⅰ）由题意得3c =，根据2216a c +=，得5a =．结合222a b c =+，解得2225,16a b ==（Ⅰ）设1122(,),(,)A x y B x y由AB 、EF 互相平分且共圆，易知，22AF BF ⊥，因为211(3,)F A x y =-，222(3,)F B x y =-，所以221(F A F B x ⋅=- 即 128x x =-，所以有结合229b a +=．解得212a =，所以离心率（若设1111(,),(,)A x y B x y --相应给分）（解法二）设）（11,y x A ，又AB 、EF 互相平分且共圆，所以AB 、EF 是圆的直径，所以92121=+y x ，又由椭圆及直线方程综合可得：⎪⎪⎪⎩⎪⎪⎪⎨⎧=+==+1429221221112121b y a x x y y x 前两个方程解出1,82121==y x ，将其带入第三个方程并结合92222-=-=a c a b ，解得：122=a ，23=e ．…8分（Ⅰ）由（Ⅰ由题可设1111(,),(,)A x y B x y --，又22012201222201013(1)3(1)112124x x y y x x x x ----==--- ，由121k -<<-考点：1．椭圆的标准方程及其几何性质；2．直线与椭圆的位置关系．7．如图，在平面直角坐标系xOy 中，已知椭圆22221(0)x y a b a b+=>>的右焦点为F ，P 为右准线上一点．点Q 在椭圆上，且FQ FP ⊥．（1）若椭圆的离心率为12，短轴长为（2）若在x 轴上方存在,P Q 两点，使,,,O F P Q 四点共圆，求椭圆离心率的取值范围．【答案】（1）22143x y +=；（21e <<. 【分析】（1）设椭圆的焦距为2c，由题意，可得222122c a b a b c ⎧=⎪⎪⎪=⎨⎪=+⎪⎪⎩，即可求得椭圆C 的标准方程；（2）设2(a P c，)t ，0(Q x ，0)y ，可得FPQ ∆的外接圆即为以PQ 为直径的圆200()()()()0a x x x y t y y c--+--=，可得20a x c c =-，根据点P ，Q 均在x 轴上方，可得 210e e +->，解得即可；【详解】解：（1）设椭圆的焦距为2c，由题意，可得222122c a b a b c ⎧=⎪⎪⎪=⎨⎪=+⎪⎪⎩，解得2a =，b =∴椭圆的方程为22143x y +=，（2）设2(a P c，)t ，0(Q x ，0)y ， FP FQ ⊥，则FPQ ∆的外接圆即为以PQ 为直径的圆200()()()()0a x x x y t y y c --+--=，由题意，焦点F ，原点O 均在该圆上， ∴200200()()00a c c x ty c a x ty c⎧--+=⎪⎪⎨⎪+=⎪⎩，消去0ty 可得2200()()0a a c c x x c c ---=， 20a x c c∴=-，点P ，Q 均在x 轴上方，2a a c c c∴-<-<，即220c ac a +->，210e e ∴+->，01e <<，∴1e <<，故e 的范围为1,12⎛⎫⎪ ⎪⎝⎭．【点睛】本题考查椭圆的标准方程及简单几何性质，直线的圆锥曲线的位置关系，考查圆的方程及点到直线的距离公式，直线的斜率公式，考查计算能力，解题时要认真审题，属于中档题．8．已知抛物线2:4E y x =的焦点为F ，准线为l O ，为坐标原点，过F 的直线m 与抛物线E 交于A B 、两点，过F 且与直线m 垂直的直线n 与准线l 交于点M ．（1）若直线m ||||AF BF 的值；（2）设AB 的中点为N ，若O M N F 、、、四点共圆，求直线m 的方程．【答案】（1）||3||AF BF =或||1||3AF BF =；（2）1)y x =-．【分析】（1）由抛物线的定义建立方程即可.（2）设直线m 的方程为1x ty =+，用t 表示,M N 坐标，再结合条件得到0OM ON ⋅=，建立关于t 的方程即可获解.【详解】（1）设||||AF BF λ=，当1λ>时，设||0BF k =>，则||AF k λ=，直线m ∴直线m 的倾斜角为60︒，由抛物线的定义，有()()1cos60cos602AB AF BF k k k k λλ⋅︒=+⋅︒=+⨯=-， 112λλ+∴=-，解得：3λ=，若01λ<<时，同理可得：13λ=，||3||AF BF ∴=或||1||3AF BF =．（2）设直线m 的方程为1x ty =+，代入24y x =，得2440y ty --=．设()()1122,,,A x y B x y ，则12124,4y y t y y +==-．由2211224,4y x y x ==，得()22221212212122(4)2(4)424444y y y y y y t x x t +--⨯-+=+===+，所以()221,2N t t +．因为直线m 的斜率为1t，所以直线n 的斜率为t -，则直线n 的方程为(1)t y x --=．由1(1)x y t x =-⎧⎨=--⎩，，解得(1,2)M t -．若O M N F 、、、四点共圆，再结合FN FM ⊥，得OM ON ⊥，则()2212122210OM ON t t t t ⋅=-⨯++⋅=-=，解得2t =±，所以直线m的方程为1)y x =-．【点睛】（1）有些题目可以利用抛物线的定义结合几何关系建立方程获解；（2）直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系.9．如图，已知椭圆C 的方程为22221(0)x y a b a b+=>>，c 为半焦距，椭圆C 的左、右焦点分别为12,F F ，椭圆C 的离心率为e ．（1）若椭圆过点(e ，两条准线之间的距离为4b ，求椭圆C 的标准方程；（2）设直线y kx =与椭圆C 相交于A ，B 两点，且12,,,A F B Fc ≤，试求2k 的最大值．【答案】（1）22142x y +=（2）13 【分析】(1)利用准线,以及222a b c =+求出离心率,又因为椭圆过点,2e ⎛ ⎝⎭,确定方程.(2)将直线方程代入椭圆方程, 根据中心对称性和12,,,F B F 四点共圆，所以22AF BF ⊥. 所以三角形2ABF 是直角三角形,()()22221 211e k e -=-+,根据2213e ≤<得出2k 取得最大值.【详解】（1）因为两条准线之间的距离为4b ，所以224a b c=，又222a b c =+，故22b c =，因为222b a c =-，所以222a c c -=，解得2e =，因为椭圆C过点e ⎛ ⎝⎭，所以2222212b b ⎛⎫ ⎪⎝⎭⎝⎭+=，故222b c ==，24a =，所以椭圆C 的标准方程为22142x y +=. （2）设()()1122,,,A x y B x y ，由22221,,x y a b y kx ⎧+=⎪⎨⎪=⎩得()2222220b a k x a b +-=，解得12x x ==.由椭圆的中心对称性得，12AF B AF B ∠=∠，因为12,,,A F B F 四点共圆，所以12AF B AF B π∠+∠=，所以22AF B π∠=，即22AF BF ⊥，所以三角形2ABF 是直角三角形，且22OF AB =，所以122|c x x =-，即22c =，故()()22222221c b a k k a b +=+，所以()()()2222222221c a c a k k a a c -+=+-，即()()()22222111e e k k e -+=+-，分离k ，e 得，()()22221211e k e -=-+，c ≤，所以()22222222213b c a cc e ≤⇔-≤⇔≤<，令21,t e =-则1,03t ⎡⎫∈-⎪⎢⎣⎭，所以2221t k t =+，令()21(0)213t k t t t =-≤<+，则()2211(0)21213t k t t t t t ==-≤<++，易得当103t -≤<，()k t 单调递减，所以13t =-时，()k t 取最大值，即2k 取得最大值为13．【点睛】本题考查椭圆方程,直线与椭圆的位置关系,含参分式的最值,属于难题.10．如图,在平面直角坐标系xOy 中,椭圆C ：22221x y a b +=(a ＞b ＞0)经过点(﹣2,0)和⎛ ⎝⎭,椭圆C 上三点A ,M ,B 与原点O 构成一个平行四边形AMBO .（1）求椭圆C 的方程；（2）若点B 是椭圆C 左顶点,求点M 的坐标；（3）若A ,M ,B ,O 四点共圆,求直线AB 的斜率.【答案】（1）24x ＋y 2＝1；（2）M (－；（3）【分析】(1)将点()2,0-和⎛ ⎝⎭代入椭圆22x a ＋22y b ＝1求解即可. (2)根据平行四边形AMBO 可知AM ∥BO ,且AM ＝BO ＝2.再设点M (x 0,y 0),则A (x 0＋2,y 0),代入椭圆C 求解即可.(3) 因为A ,M ,B ,O 四点共圆,所以平行四边形AMBO 是矩形,且OA ⊥OB ,再联立直线与椭圆的方程,结合韦达定理代入OA ·OB ＝x 1x 2＋y 1y 2＝0求解即可.【详解】（1）因为椭圆22x a ＋22y b ＝1(a ＞b ＞0)过点()2,0-和⎛ ⎝⎭, 所以a ＝2,21a ＋234b ＝1,解得b 2＝1,所以椭圆C 的方程为24x ＋y 2＝1. （2）因为B 为左顶点,所以B (－2,0).因为四边形AMBO 为平行四边形,所以AM ∥BO ,且AM ＝BO ＝2.设点M (x 0,y 0),则A (x 0＋2,y 0).因为点M ,A 在椭圆C 上,所以()2200202014214x y x y ⎧+=⎪⎪⎨+⎪+=⎪⎩解得001x y =-⎧⎪⎨=⎪⎩所以M (－（3）因为直线AB 的斜率存在,所以设直线AB 的方程为y ＝kx ＋m ,A (x 1,y 1),B (x 2,y 2).由2214y kx m x y =+⎧⎪⎨+=⎪⎩消去y ,得(4k 2＋1)x 2＋8kmx ＋4m 2－4＝0, 则有x 1＋x 2＝2814km k -+,x 1x 2＝224414m k-+. 因为平行四边形AMBO ,所以OM ＝OA ＋OB ＝(x 1＋x 2,y 1＋y 2).因为x 1＋x 2＝2814km k -+,所以y 1＋y 2＝k (x 1＋x 2)＋2m ＝k ·2814km k -+＋2m ＝2214m k +,所以M (2814km k -+,2214m k +). 因为点M 在椭圆C 上,所以将点M 的坐标代入椭圆C 的方程,化得4m 2＝4k 2＋1.①因为A ,M ,B ,O 四点共圆,所以平行四边形AMBO 是矩形,且OA ⊥OB ,所以OA ·OB ＝x 1x 2＋y 1y 2＝0.因为y 1y 2＝(kx 1＋m )(kx 1＋m )＝k 2x 1x 2＋km (x 1＋x 2)＋m 2＝222414m k k -+, 所以x 1x 2＋y 1y 2＝224414m k-+＋222414m k k -+＝0,化得5m 2＝4k 2＋4.② 由①②解得k 2＝114,m 2＝3,此时△＞0,因此k ＝±2. 所以所求直线AB 的斜率为±2. 【点睛】本题主要考查了椭圆方程的基本求法,同时也考查了联立直线与椭圆的方程,利用韦达定理列式表达斜率以及垂直的方法,进而代入求解的问题.属于难题.11．如图，在平面直角坐标系xOy 中，已知P 为椭圆2222:1(0)x y C a b a b+=>>上异于长轴端点的一点，过P 与x 轴平行的直线交椭圆C 的两条准线于点1T ，2T ，直线11T F ，22T F 交于点Q .（1）若12PF F ∆与12QF F ∆的面积相等，求椭圆C 的离心率；（2）若126F F =，12503TT =. ①求椭圆C 的标准方程；②试判断点P ，1F ，Q ，2F 是否四点共圆，并说明理由.【答案】（1）2；（2）①2212516x y +=； ②P ，1F ，Q ，2F 四点共圆，理由见解析. 【分析】（1）设()()000,0P x y y ≠，210,a T y c ⎛⎫- ⎪⎝⎭，可表示出直线11T F 的方程，从而求得Q 点坐标；根据三角形面积相等可构造关于,a c 的齐次方程，进而求得离心率；（2）①根据126F F =，12503TT =和椭圆,,a b c 的关系，可求得,,a b c 的值，进而得到椭圆方程； ②设过点Q ，1F ，2F 三点的圆的方程为()2229x y s s +-=+，代入Q 点坐标可求得方程为2200982932y x y y y ⎛⎫+--= ⎪⎝⎭；验证可知P 点坐标满足方程，由此得到四点共圆. 【详解】设()()000,0P x y y ≠，()1,0F c -，()2,0F c ，（1）由题意得：210,a T y c ⎛⎫- ⎪⎝⎭，220,a T y c ⎛⎫ ⎪⎝⎭. 直线11T F 的方程为：()02y y x c a c c=+-+，直线22T F 的方程为：()02y y x c a c c =--，将直线11T F 与22T F 联立可得：2020x c y y b =⎧⎪⎨=-⎪⎩，即点2020,c y Q b ⎛⎫- ⎪⎝⎭.12PF F ∆与12QF F ∆的面积相等， ()2000220c y y y c a∴=-≠-，2221c c a ∴=--，2c e a ∴==，即椭圆C的离心率为2. （2）①126F F =，12503TT =，26c ∴=，25023a c ⋅=，解得：3c =，225a =，22216b ac ∴=-=， ∴以椭圆C 的标准方程为2212516x y +=.②由①知：()13,0F -，()23,0F ，090,16y Q ⎛⎫-⎪⎝⎭. 设过点Q ，1F ，2F 三点的圆的方程为()2229x y s s +-=+，即2229x y sy +-=.将090,16y Q ⎛⎫- ⎪⎝⎭代入该方程得：009832y s y =-， ∴过Q ，1F ，2F 三点的圆的方程为：2200982932y x y y y ⎛⎫+--=⎪⎝⎭，将()00,P x y 代入该方程左边，则22000098232y x y y y ⎛⎫+-- ⎪⎝⎭22000009825121632y y y y y ⎛⎫⎛⎫=-+-- ⎪ ⎪⎝⎭⎝⎭9=， ∴点P 也在过点Q ，1F ，2F 三点的圆上，从而点P ，1F ，Q ，2F 四点共圆.【点睛】本题考查直线与椭圆的综合应用问题，涉及到椭圆离心率和标准方程的求解、四点共圆问题的证明；证明四点共圆问题的关键是能够通过三点坐标确定三点所在圆的方程，进而代入第四个点的坐标，验证其满足方程即可.12．（题文）（题文）已知点F (p2,0)，直线l: x =−p2，点Μ是l 上的动点，过点Μ垂直于y 轴的直线与线段ΜF 的垂直平分线相交于点Ν．（1）求点Ν的轨迹方程；（2）若p =2，直线y =x 与点Ν的轨迹交于A 、B 两点，试问Ν的轨迹上是否存在两点C 、D ，使得A 、B 、C 、D 四点共圆？若存在，求出圆的方程；若不存在，请说明理由．【答案】（1）y 2=2px ；（2）存在a >72且a ≠4，a ≠8的无数个圆(x −a)2+(y +a −4)2=a 2+(−a +4)2满足条件. 【解析】试题分析：（1）借助点在线段ΜF 的中垂线上建立等式并化简即可；（2）依据题设条件建立方程,通过方程有无解的分析析作出推理和判断即可.试题解析：解: （1）设Ν(x,y)，依题意，|ΝF |=|ΝΜ|，即√(x −p2)2+y 2=|x +p2|．化简整理得y 2=2px ．（2）把y =x 与y 2=4x 联立，解得Α(0,0)，Β(4,4)，则线段ΑΒ的垂直平分线方程y =−x +4 若存在C 、D 两点，使得Α、Β、C 、D 四点共圆，则圆心必在直线y =−x +4上，设圆心坐标(a,−a +4)，则半径r =√a 2+(−a +4)2， ∴圆的方程为(x −a)2+(y +a −4)2=a 2+(−a +4)2，将x =y 24代入并整理得y 4+(16−8a)y 2+32(a −4)y =0，则y(y −4)(y 2+4y +32−8a)=0，∴ y 1=0或y 2=4或y 2+4y +32−8a =0， ∴ y 2+4y +32−8a =0应有除y 1=0、y 2=4之外的两个根，∴ Δ>0，且32−8a ≠0，42+4×4+32−8a ≠0，解得a >72且a ≠4，a ≠8． ∴存在a >72且a ≠4，a ≠8的无数个圆(x −a)2+(y +a −4)2=a 2+(−a +4)2满足条件．考点：(1)轨迹方程与探求方法；(2)圆的方程及简单高次方程的求解等有关知识的运用. 13．从抛物线24y x =上各点向x 轴作垂线段，记垂线段中点的轨迹为曲线P ．（1）求曲线P 的方程，并说明曲线P 是什么曲线；（2）过点()2,0M 的直线l 交曲线P 于两点A 、B ，线段AB 的垂直平分线交曲线P 于两点C 、D ，探究是否存在直线l 使A 、B 、C 、D 四点共圆？若能，请求出圆的方程；若不能，请说明理由．【答案】（1）曲线P 的方程为2y x =，曲线P 是焦点为1,04⎛⎫⎪⎝⎭的抛物线；（2）存在；圆N 的方程为227113222x y ⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭或227113222x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭．【分析】（1）设抛物线2y x =上的任意点为()00,S x y ，垂线段的中点为(),x y ，根据中点坐标公式得出002x x y y =⎧⎪⎨=⎪⎩，代入等式2004y x =化简可得出曲线P 的方程，进而可得出曲线P 的形状；（2）设直线l 的方程为2x ty =+，将直线l 的方程与曲线P 的方程联立，列出韦达定理，求出AB ，求出线段AB 的中点的坐标，进一步求出线段AB 的中垂线CD 的方程，求出CD ，根据四点共圆结合垂径定理可得出关于t 的等式，求出t 的值，进一步可求得圆的方程，由此可得出结论. 【详解】（1）设抛物线2y x =上的任意点为()00,S x y ，垂线段的中点为(),x y ，故002x x y y =⎧⎪⎨=⎪⎩，则002x x y y =⎧⎨=⎩，代入2004y x =得()224y x =，得曲线P 的方程为2y x =，所以曲线P 是焦点为1,04⎛⎫⎪⎝⎭的抛物线；（2）若直线l 与x 轴重合，则直线l 与曲线P 只有一个交点，不合乎题意. 设直线l 的方程为2x ty =+，根据题意知0t ≠，设()11,A x y 、()22,B x y ，联立22y x x ty ⎧=⎨=+⎩，得220y ty --=，280t ∆=+>，则12y y t +=，122y y ⋅=-，则12A y y B =-==，且线段AB 中点的纵坐标为1222y y t +=，即2121222222x x y y t t ++=⋅+=+，所以线段AB 中点为22,22t t M ⎛⎫+ ⎪⎝⎭，因为直线CD 为线段AB 的垂直平分线，可设直线CD 的方程为1x y m t=-+，则21222t t m t ⎛⎫+=-⨯+ ⎪⎝⎭，故252t m +=，联立22152y x t x y t ⎧=⎪⎨+=-+⎪⎩，得()222250ty y t t +-+=，设()33,C x y 、()44,D x y ，则341y y t +=-，()234152y y t ⋅=-+，故34y CD =-==线段CD 中点为22151,222t N tt ⎛⎫++- ⎪⎝⎭，假设A 、B 、C 、D 四点共圆，则弦AB 的中垂线与弦CD 中垂线的交点必为圆心，因为CD 为线段AB 的中垂线，则可知弦CD 的中点N 必为圆心，则12AN CD =，在Rt AMN △中，222AN AM MN =+，所以22212CD AM MN ⎛⎫=+ ⎪⎝⎭，则()()222222221111111121018442222t t t t t t tt ⎛⎫⎛⎫⎛⎫⎛⎫+++=++++++ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，故4228810t t t +--=，即()()24264222198880t t t t t t t t -+++--==，解得21t =，即1t =±，所以存在直线l ，使A 、B 、C 、D 四点共圆，且圆心为弦CD 的中点N ，圆N 的方程为227113222x y ⎛⎫⎛⎫-++= ⎪ ⎪⎝⎭⎝⎭或227113222x y ⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭．【点睛】方法点睛：求动点的轨迹方程有如下几种方法：（1）直译法：直接将条件翻译成等式，整理化简后即得动点的轨迹方程；（2）定义法：如果能确定动点的轨迹满足某种已知曲线的定义，则可利用曲线的定义写出方程；（3）相关点法：用动点Q 的坐标x 、y 表示相关点P 的坐标0x 、0y ，然后代入点P 的坐标()00,x y 所满足的曲线方程，整理化简可得出动点Q 的轨迹方程；（4）参数法：当动点坐标x 、y 之间的直接关系难以找到时，往往先寻找x 、y 与某一参数t 得到方程，即为动点的轨迹方程；（5）交轨法：将两动曲线方程中的参数消去，得到不含参数的方程，即为两动曲线交点的轨迹方程. 14．在平面直角坐标系xOy 中，已知抛物线()2:20E y px p =>的焦点为F ，准线为l ，P 是抛物线上E 上一点，且点P 的横坐标为2，3PF =.（1）求抛物线E 的方程；（2）过点F 的直线m 与抛物线E 交于A 、B 两点，过点F 且与直线m 垂直的直线n 与准线l 交于点M ，设AB 的中点为N ，若O 、M N 、F 四点共圆，求直线m 的方程.【答案】（1）24y x =（2）)1y x =-【分析】（1）由抛物线的定义可得22pPF =+，即可求出p ，从而得到抛物线方程；（2）设直线m 的方程为1x ty =+，代入24y x =，得2440y ty --=.设()11,A x y ，()22,B x y ，列出韦达定理，表示出中点N 的坐标，若O 、M 、N 、F 四点共圆，再结合FN FM ⊥，得OM ON ⊥，则0OM ON ⋅=即可求出参数t ，从而得解；【详解】解：（1）由抛物线定义，得232pPF =+=，解得2p =，所以抛物线E 的方程为24y x =.（2）设直线m 的方程为1x ty =+，代入24y x =，得2440y ty --=.设()11,A x y ，()22,B x y ，则124y y t +=，124y y =-.由2114y x =，2224y x =，得()()()22222121212122424424444y y y y t y y x x t +--⨯-+=+===+，所以()221,2N t t +.因为直线m 的斜率为1t，所以直线n 的斜率为t -，则直线n 的方程为()1y t x =--.由()1,1,x y t x =-⎧⎨=--⎩解得()1,2M t -.若O 、M 、N 、F 四点共圆，再结合FN FM ⊥，得OM ON ⊥，则()2212122210OM ON t t t t ⋅=-⨯++⋅=-=，解得t =±所以直线m的方程为)1y x =-. 【点睛】本题考查抛物线的定义及性质的应用，直线与抛物线综合问题，属于中档题.15．已知椭圆C ：22221(0)x y a b a b +=>>的左､右顶点分别为A ，B，离心率为3，P 是C 上异于A ，B的动点.（1）证明：直线AP ，BP 的斜率之积为定值，并求出该定值.（2）设||AB =，直线AP ，BP 分别交直线l ：x =3于M ，N 两点，O 为坐标原点，试问：在x 轴上是否存在定点T ，使得O ，M ，N ，T 四点共圆？若存在，求出点T 的坐标；若不存在，请说明理由.【答案】（1）证明见解析，定值13-；（2）存在，定点11,03T ⎛⎫⎪⎝⎭.【分析】（1）由题意知(,0),(,0)A a B a -，设P (x 0，y 0)，y 0≠0，则2200221x y a b+=，然后利用斜率公式求200022000y y y x a x a x a ⋅=+--化简可得结果；（2）由题意先求出椭圆C 的方程为2213x y +=，设直线AP的方程为(y k x =+，则直线BP 的方程为1(3y x k =-，直线方程与椭圆方程联立可求出(3,3)M k，1N k ⎛⎫- ⎪⎝⎭，假设△MNO 的外接圆恒过定点T (t ，0)，t ≠0，然后求出线段MN 的垂直平分线所在直线的方程和线段OT 的垂直平分线所在直线的方程，从而可求出圆心2t E ⎛⎪⎪⎝⎭，再由|OE |=|ME |，可求出t 的值，进而得O ，M ，N ，T 四点共圆【详解】（1）由题意知(,0),(,0)A a B a -，设P (x 0，y 0)，y 0≠0，则2200221x y a b+=，所以直线AP 与BP 的斜率之积22022222200022222200001131x b a y y y b a c x a x a x a x a a a ⎛⎫- ⎪-⎝⎭⋅===-=-=-+--⎭=--⎝，即直线AP ，BP 的斜率之积为定值13-.（2）存在.理由如下：由题意知2a =，得a =因为c a =c =所以b 2=1，所以椭圆C 的方程为2213x y +=.设直线AP的方程为(y k x =+，则直线BP的方程为1(3y x k=-.联立(3,y k x x ⎧=+⎪⎨=⎪⎩可得(3,3)M k +，同理可得1N k ⎛⎫ ⎪⎝⎭. 假设△MNO 的外接圆恒过定点T (t ，0)，t ≠0，因为线段MN的垂直平分线所在直线的方程为y =，线段OT 的垂直平分线所在直线的方程为2t x =，所以圆心2t E ⎛⎪ ⎪⎝⎭. 又|OE |=|ME |解得t =113.所以存在定点11,03T ⎛⎫⎪⎝⎭，使得O ，M ，N ，T 四点共圆.【点睛】此题考查直线与椭圆的位置关系，考查椭圆中的定点问题，考查计算能力，属于中档题16．在平面直角坐标系xOy 中，已知抛物线()2:20E y px p =>的焦点为F ，准线为l ，P 是抛物线E 上一点，且点P 的横坐标为2，3PF =. （1）求抛物线E 的方程；（2）过点F 的直线m 与抛物线E 交于A 、B 两点，过点F 且与直线m 垂直的直线n 与准线l 交于点M ，设AB 的中点为N ，若O 、M 、N 、F 四点共圆，求直线m 的方程.【答案】（1）24y x =（2）)1y x =-【分析】（1）首先根据抛物线的定义和题中条件求出抛物线的焦准距，即可得到抛物线的方程；（2）首先设直线m 的方程，然后与抛物线联立，利用韦达定理求出点N 坐标，然后设直线n 的方程求出点M 的坐标，最后利用O 、M 、N 、F 四点共圆即可求出直线m 的方程. 【详解】（1）由抛物线定义，得232pPF =+=，解得2p =，所以抛物线F 的方程为24y x =；（2）设直线m 的方程为1x ty =+，代入24y x =，得2440y ty --=，设()11,A x y ，()22,B x y ，则124y y t +=，124y y =-，由2114y x =，2224y x =，得()()()22222121212122424424444y y y y t y y x x t +--⨯-+=+===+，所以()221,2N t t +，因为直线m 的斜率为1t，所以直线n 的斜率为t -，则直线n 的方程为()1y t x =--，由()11x y t x =-⎧⎨=--⎩解得()1,2M t -，若O 、M 、N 、F 四点共圆，再结合FN FM ⊥，得OM ON ⊥，则()2212122210OM ON t t t t ⋅=-⨯++⋅=-=，解得t =m 的方程为)1y x =-. 【点睛】本题主要考查了抛物线的定理，直线与抛物线的交点问题，属于一般题.。

第四讲四点共圆问题

第四讲四点共圆问题“四点共圆”问题在数学竞赛中经常出现，这类问题一般有两种形式：一是以“四点共圆”作为证题的目的，二是以“四点共圆”作为解题的手段，为解决其他问题铺平道路.判定“四点共圆”的方法，用得最多的是统编教材《几何》二册所介绍的两种（即P 89定理和P 93例3），由这两种基本方法推导出来的其他判别方法也可相机采用. 1 “四点共圆”作为证题目的例1．给出锐角△ABC ，以AB 为直径的圆与AB 边的高CC ′及其延长线交于M ，N .以AC 为直径的圆与AC 边的高BB ′及其延长线将于P ，Q .求证：M ，N ，P ，Q 四点共圆.(第19届美国数学奥林匹克)分析：设PQ ，MN 交于K 点，连接AP ，AM .欲证M ，N ，P ，Q 四点共圆，须证 MK ·KN ＝PK ·KQ ，即证(MC ′-KC ′)(MC ′+KC ′) ＝(PB ′-KB ′)·(PB ′+KB ′)或MC ′2-KC ′2=PB ′2-KB ′2 . ①不难证明 AP =AM ，从而有 AB ′2+PB ′2=AC ′2+MC ′2. 故 MC ′2-PB ′2=AB ′2-AC ′2ABCK M NPQ B ′C ′=(AK 2-KB ′2)-(AK 2-KC ′2)=KC ′2-KB ′2. ②由②即得①，命题得证.例2．A 、B 、C 三点共线，O 点在直线外，O 1，O 2，O 3分别为△OAB ，△OBC ， △OCA 的外心.求证：O ，O 1，O 2， O 3四点共圆.(第27届莫斯科数学奥林匹克)分析：作出图中各辅助线.易证O 1O 2垂直平分OB ，O 1O 3垂直平分OA .观察△OBC 及其外接圆，立得∠OO 2O 1=21∠OO 2B =∠OCB .观察△OCA 及其外接圆，立得∠OO 3O 1=21∠OO 3A =∠OCA .由∠OO 2O 1=∠OO 3O 1 O ，O 1，O 2，O 3共圆.利用对角互补，也可证明O ，O 1，O 2，O 3四点共圆，请同学自证.2 以“四点共圆”作为解题手段这种情况不仅题目多，而且结论变幻莫测，可大体上归纳为如下几个方面. (1)证角相等例3．在梯形ABCD 中，AB ∥DC ，AB ＞CD ，K ，M 分别在AD ，BC 上，∠DAM ＝∠CBK .A BCOO O O 123？？求证：∠DMA ＝∠CKB .（第二届袓冲之杯初中竞赛）分析：易知A ，B ，M ，K 四点共圆.连接KM ，有∠DAB ＝∠CMK .∵∠DAB +∠ADC ＝180°，∴∠CMK +∠KDC ＝180°.故C ，D ，K ，M 四点共圆 ∠CMD ＝∠DKC . 但已证∠AMB ＝∠BKA ， ∴∠DMA ＝∠CKB .(2)证线垂直例4．⊙O 过△ABC 顶点A ，C ，且与AB ， BC 交于K ，N (K 与N 不同).△ABC 外接圆和△BKN 外接圆相交于B 和 M .求证：∠BMO =90°. (第26届IMO 第五题)分析：这道国际数学竞赛题，曾使许多选手望而却步.其实，只要把握已知条件和图形特点，借助“四点共圆”，问题是不难解决的. 连接OC ，OK ，MC ，MK ，延长BM 到G .易得∠GMC =∠BAC =∠BNK =∠BMK .而∠COK =2·∠BAC =∠GMC +A BC D K M ··ABO K N CMG∠BMK =180°-∠CMK ，∴∠COK +∠CMK =180°⇒C ，O ，K ，M 四点共圆. 在这个圆中，由OC =OK ⇒ OC =OK ⇒∠OMC =∠OMK . 但∠GMC =∠BMK ，故∠BMO =90°. (3)判断图形形状例5．四边形ABCD 内接于圆，△BCD ，△ACD ，△ABD ，△ABC的内心依次记为I A ，I B ，I C ，I D .试证：I A I B I C I D 是矩形.(第一届数学奥林匹克国家集训选拔试题) 分析：连接AI C ，AI D ，BI C ，BI D 和DI B .易得∠AI C B =90°+21∠ADB =90°+21 ∠ACB =∠AI D B ⇒A ，B ，I D ，I C 四点共圆.同理，A ，D ，I B ，I C 四点共圆.此时 ∠AI C I D =180°-∠ABI D =180°-21∠ABC ， ∠AI C I B =180°-∠ADI B =180°-21∠ADC ， ABCDI C I DAI I B∴∠AI C I D +∠AI C I B =360°-21(∠ABC +∠ADC ) =360°-21×180°=270°. 故∠I B I C I D =90°.同样可证I A I B I C I D 其它三个内角皆为90°.该四边形必为矩形. (4)计算例6．正方形ABCD 的中心为O ，面积为1989㎝2.P 为正方形内一点，且∠OPB =45°，P A :PB =5:14.则PB =__________ (1989，全国初中联赛)分析：答案是PB =42㎝.怎样得到的呢？连接OA ，OB .易知O ，P ，A ，B四点共圆，有∠APB =∠AOB =90°. 故P A 2+PB 2=AB 2=1989. 由于P A :PB =5:14，可求PB . (5)其他例7．设有边长为1的正方形，试在这个正方形的内接正三角形中找出面积最大的和一个面积最小的，并求出这两个面积(须证明你的论断).··P OA BCD(1978，全国高中联赛)分析：设△EFG 为正方形ABCD 的一个内接正三角形，由于正三角形的三个顶点至少必落在正方形的三条边上，所以不妨令F ，G 两点在正方形的一组对边上. 作正△EFG 的高EK ，易知E ，K ，G ，D 四点共圆⇒∠KDE =∠KGE =60°.同理，∠KAE =60°.故△KAD 也是一个正三角形，K 必为一个定点.又正三角形面积取决于它的边长，当KF 丄AB 时，边长为1，这时边长最小，而面积S =43也最小.当KF 通过B 点时，边长为2·32-，这时边长最大，面积S =23-3也最大. 例8．NS 是⊙O 的直径，弦AB 丄NS 于M ，P 为ANB 上异于N 的任一点，PS 交AB 于R ，PM 的延长线交⊙O 于Q .求证：RS ＞MQ .(1991，江苏省初中竞赛)分析：连接NP ，NQ ，NR ，NR 的延长线交⊙O 于Q ′.连接MQ ′，SQ ′.易证N ，M ，R ，P 四点共圆，从而，∠SNQ ′=∠MNR =∠MPR =∠SPQ =∠SNQ .根据圆的轴对称性质可知Q 与Q ′关于NS 成轴对称⇒MQ ′=MQ .A BCDEF KG ······又易证M，S，Q′，R四点共圆，且RS是这个圆的直径(∠RMS=90°)，MQ′是一条弦(∠MSQ′＜90°)，故RS ＞MQ′.但MQ=MQ′，所以，RS＞MQ.练习题1.⊙O1交⊙O2于A，B两点，射线O1A交⊙O2于C点，射线O2A交⊙O1于D点.求证：点A是△BCD的内心.(提示：设法证明C，D，O1，B四点共圆，再证C，D，B，O2四点共圆，从而知C，D，O1，B，O2五点共圆.)2.△ABC为不等边三角形.∠A及其外角平分线分别交对边中垂线于A1，A2；同样得到B1，B2，C1，C2.求证：A1A2=B1B2=C1C2.(提示：设法证∠ABA1与∠ACA1互补造成A，B，A1，C四点共圆；再证A，A2，B，C四点共圆，从而知A1，A2都是△ABC的外接圆上，并注意∠A1AA2=90°.)3.设点M在正三角形三条高线上的射影分别是M1，M2，M3(互不重合).求证：△M1M2M3也是正三角形.4.在Rt△ABC中，AD为斜边BC上的高，P是AB上的点，过A 点作PC的垂线交过B所作AB的垂线于Q点.求证：PD丄QD.(提示：证B，Q，E，P和B，D，E，P分别共圆)5.AD，BE，CF是锐角△ABC的三条高.从A引EF的垂线l1，从B引FD的垂线l2，从C引DE的垂线l3.求证：l1，l2，l3三线共点.(提示：过B作AB的垂线交l1于K，证：A，B，K，C四点共圆)。

数学北师大版九年级下册四点共圆

第二讲：四点共圆一．有关定理或结论1．共斜边的两个直角三角形的四个顶点共圆，且直角三角形的斜边为圆的直径． 2．共底边的两个三角形顶角相等，且在底边的同侧，则四个顶点共圆． 3．若四边形的两个对角互补(或一个外角等于它的内对角)，则四点共圆．4．相交弦逆定理:凸四边形ABCD 其对角线AC 、BD 交于P,PD BP PC AP ⋅=⋅⇔四点共圆。

5．割线长定理:凸四边形ABCD 其边的延长线AB 、CD 交于P.PD PC PB PA ⋅=⋅⇔四点共圆。

图3 图4 图5二．证“四点共圆”的基本方法例1．如图1，⊙1o ，⊙2o ，⊙3o … 都经过点A 和B.点P 是线段AB 延长线上任意一点，且PC ，PD ，PE …分别与⊙1o ，⊙2o ，⊙3o …相切于点C,D,E,…。

求证：C,D,E …在同一个圆上。

例2. 如图，在△ABC 中，AD ⊥BC ，DE ⊥AB ，DF ⊥AC ．求证：B 、E 、F 、C 四点共圆．例3．如图3，在梯形ABCD 中，AB ∥DC ，AB ＞CD ，K ，M 分别在AD ，BC 上， ∠DAM ＝∠CBK.求证：C ，D ，K ，M 四点共圆例4. 如图，E 、F 、G 、H 分别是菱形ABCD 各边的中点．求证：E 、F 、G 、H 四点共圆． AB C D A B C D P A BCD PC图3MK BACD三．四点共圆的应用1. 用于证明两角相等例1.如图，梯形ABCD中AB//DC, 且∠CBN 求证：∠CNB = ∠2.用于证明两条线段相等例2. 已知: 圆O的弦CF、DE交于点B, PB//EF, 交CD的延长线于点P, PA与圆O切于点A.求证: PA=PB .3. 用于证明两直线平行例3 如图3，在△ABC中，AB=AC，AD⊥BC，∠B的两条三等分线交AD于E、G，交AC于F、H．求证：EH∥GC．4.用于证明两直线垂直5. 用于判定切线例5 如图5，AB为半圆直径，P为半圆上一点，PC⊥AB于C，以AC为直径的圆交PA于D，以BC为直径的圆交PB于E，求证：DE是这两圆的公切线．6. 用于证明比例式例6 AB、CD为⊙O中两条平行的弦，过B点的切线交CD的延长线于G，弦PA、PB分别交CD 于E、F．7. 用于证明平方式例7:已知: 点P是等边⊿ABC外接圆的劣弧BC上任意一点, AP交BC于点D.求证: PA2=AC2+PB•PC.8. 用于解计算题例8如图8，△ABC的高AD的延长线交外接圆于H，以AD为直径作圆和AB、AC分别交于E、F点，EF交 AD于 G，若 AG=16cm，AH=25cm，求 AD的长．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

九年级数学四点共圆例题讲解知识点、重点、难点四点共圆是圆的基本内容，它广泛应用于解与圆有关的问题．与圆有关的问题变化多，解法灵活，综合性强，题型广泛，因而历来是数学竞赛的热点内容。

因此，掌握四点共圆的方法很重要。

判定四点共圆最基本的方法是圆的定义：如果A、B、C、D四个点到定点O的距离相等，即OA＝OB＝OC＝OD，那么A、B、C、D四点共圆．由此，我们立即可以得出1.如果两个直角三角形具有公共斜边，那么这两个直角三角形的四个顶点共圆。

将上述判定推广到一般情况，得：2.如果四边形的对角互补，那么这个四边形的四个顶点共圆。

3.如果四边形的外角等于它的内对角，那么这个四边形的四个顶点共圆。

4.如果两个三角形有公共底边，且在公共底边同侧又有相等的顶角，那么这两个三角形的四个顶点共圆。

运用这些判定四点共圆的方法，立即可以推出：正方形、矩形、等腰梯形的四个顶点共圆。

其实，在与圆有关的定理中，一些定理的逆定理也是成立的，它们为我们提供了另一些证明四点共圆的方法．这就是：1.相交弦定理的逆定理：若两线段AB和CD相交于E，且AE·EB=CE·ED，则A、B、C、D四点共圆。

2．割线定理的逆定理：若相交于点P的两线段PB、PD上各有一点A、C，且PA·PB =PC·PD，则A、B、C、D四点共圆。

3.托勒密定理的逆定理：若四边形ABCD中，AB·CD＋BC·DA=AC·BD，则ABCD是圆内接四边形。

例题精讲例1：如图，P为△ABC内一点，D、E、F分别在BC、CA、AB上。

已知P、D、C、E四点共圆，P、E、A、F 四点共圆，求证：B、D、P、F四点共圆。

证明连PD、PE、PF．由于P、D、C、F四点共圆，所以∠BDP =∠PEC．又由于A、E、P、F四点共圆，所以∠PEC =∠AFP．于是∠BDP=∠AFP，故B、D、P、F四点共圆。

例2：设凸四边形ABCD的对角线AC、BD互相垂直，垂足为E，证明：点E关于AB、BC、CD、DA的对称点共圆。

证明以E 为相似中心作相似变换，相似比为12，此变换把E 关于AB 、BC 、CD 、DA 的对称点变为E 在AB 、BC 、CD 、DA 上的射影P 、Q 、R 、S （如图）.只需证明PQRS 是圆内接四边形。

由于四边形ESAP 、EPBQ 、EQCR 及ERDS 都是圆内接四边形（每个四边形都有一组对角为直角），由E 、P 、B 、Q 共圆有∠EPQ =∠EBQ.由E 、Q 、C 、R 共圆有∠ERQ=∠ECQ ，于是∠EPQ ＋∠ERQ = ∠EBQ ＋∠ECQ=90°.同理可得∠EPS ＋∠ERS =90°.从而有∠SPQ ＋∠QRS =180°，故PQRS 是圆内接四边形。

例3：梯形ABCD 的两条对角线相交于点K ，分别以梯形的两腰为直径各作一圆，点K 位于这两个圆之外，证明：由点K 向这两个圆所作的切线长度相等。

证明如图，设梯形ABCD 的两腰为AB 和CD ，并设AC 、BD 与相应二圆的第二个交点分别为M 、N.由于∠AMB 、∠CND 是半圆上的圆周角，所以∠AM B =∠CND = 90°．从而∠BMC =∠BNC=90°，故B 、M 、N 、C 四点共圆，因此∠MNK =∠ACB ．又∠ACB =∠KAD ，所以∠MNK =∠KAD.于是M 、N 、D 、A 四点共圆，因此KM ·KA = KN ·KD.由切割线定理得K 向两已知圆所引的切线相等。

例4：如图，A 、B 为半圆O 上的任意两点，AC 、BD 垂直于直径EF ，BH ⊥OA ，求证：DH =AC.证法一在BD 上取一点A'，使A'D = AC ，则ACDA'是矩形。

连结A'H 、AB 、OB.由于BD ⊥EF 、BH ⊥OA ，所以∠BDO =∠BHO =90°.于是D 、B ，H 、O 四点共圆，所以∠HOB =∠HDB .由于∠AHB =∠AA'B =90°，所以A 、H 、A'、B 四点共圆。

故∠DA'H =∠OAB ，因此∠DHA'=∠OBA.而OA = OB ，所以∠OBA=∠OAB ，于是∠DHA '=∠D A'H.所以DH =DA'，故DH = AC.证法二设圆O'为点D 、B 、H 、O 四点所共的圆，过H 作HG ⊥DH ，与圆O'交于G(如图)，则∠AOC =∠HBD =∠DGH ，GD = OB = OA.因此Rt △OAC ≌Rt △GDH ，故DH =AC.证法三因为D 、B 、H 、O 四点共圆，且直径为OB ．而Rt △AOC 的斜边为OA ，利用正弦定义及正弦定理，得,.sinsinAC DH OAOBAOCDBH由于OA =OB ，∠AOC =∠DB H ，所以DH = AC.例5：如图，已知锐角三角形ABC ，以AB 为直径的圆与AB 边的高线CC'及其延长线交于M 、N ，以AC 为直径的圆与AC 边的高线BB'及其延长线交于P 、Q ，求证：M 、N 、P 、Q 四点共圆。

证明设BC 上的高为AA'，△ABC 的垂心为H ，则A'在以AB 为直径的圆上，从而AH ×HA'=MH ×HN.同理AH ×HA'=PH ×HQ.于是MH ×HN = P H ×HQ ，故M 、N 、P 、Q 四点共圆。

说明另证：在Rt △ABM 和Rt △ACP 中，AM'=AC'·AB ，AP 2=AB'·AC.又△ABB'∽△ACC'，有AC'·AB =AB'·AC ．于是AM 2=AP 2，即AM =AP ．但M 、N 关于AB 对称，P 、Q 关于AC 对称，故AM =AN ，AP=AQ .因此M 、N 、P 、Q 在以A 为圆心的圆上。

也可由MH ×HN =BH ×HB'=CH ×HC'=PH ×HQ 推出M 、N 、P 、Q 四点共圆。

例6：如图，ABCD 是圆内接四边形，AD 、BC 的延长线交于P ，△PAB 与△PCD 的外心、垂心分别是1O 、2O 和1H 、2H ，求证：1O 、2O 、1H 、2H 四点共圆。

证明因为1H 是△PAB 的垂心，所以1H PB ＋∠ABP =90°.又因为2O 是△PCD 的外心，所以212O P CC D P 90°.而212CDPCO P ，所以2O PCCDP =90°.因为A 、B 、C 、D 四点共圆，所以∠CDP =∠ABP ，所以12H PBO PC ，所以2H 、1O 、P 三点共线．同理可证2H 、2O 、P 三点共线。

显然△PAB ≌△PCD ，因此1122PH PO PH PO ，即1221PH PO PH PO ，故1O 、2O 、1H 、2H 四点共圆。

例7：两个等圆彼此相交，从它们的对称中心引出两条射线交圆周于不在同一条直线上的四个点，试证：这四个点必在同一个圆周上。

证明如图，设过两圆的对称中心O 的二条射线为11A B 、22A B ，1A 、2A 位于第一个圆周上，而1B 、2B 位于第二个圆周上。

设点3A 、3B 和4B 分别是点2B 、1A 和2A 关于点O 的对称点，根据相交弦定理有3B O ·1OB =2B O ·4OB .因为3B O =1OA ，4OB =2OA ，从而1OA ·1OB =2OB ·2OA ，故1A 、1B 、2A 、2B 四点必在同一个圆周上。

例8：如图，AB 为定⊙O 中的定弦，作⊙O 的弦11C D 、22C D 、…、20002000C D ，对其中每一i （i ＝1，2，…，2000）i i C D 都被弦AB 平分于i M 点，过i i C D 、分别作⊙O 的切线，两切线交于i P ，求证：122000P P P 、、、必在同一个圆周上，并指出圆心是什么点。

证明连结i OC 、i OD ．对每一个i （i = 1，2，…，2000），因为i i C D 均被AB 平分于i M ，所以i i i i i i C M M D AM M B .又i i PC 、i i PD分别切⊙O 于i i C D 、，故知i i i O C P D 、、、四点共圆，且i OP 通过i i C D 的中点i M ，所以i i i i i i C M M D PM M O ，所以i i i i i AM M B PM M O .故A 、O 、B 、i P四点共圆，即122000P P P 、、、必在同一个圆周上。

因为O 、A 、B 为定点，所以圆心即为△OAB 的外心。

九年级数学四点共圆例题讲解

四点共圆(知识讲解)

专题3.8 四点共圆(隐圆压轴五)(解析版)

九年级数学四点共圆例题讲解

四点共圆例题及问题详解

最新九年级数学四点共圆例题讲解

“四点共圆”模型(解析版)--初中数学专题训练

人教版九年级数学上册圆《探究四点共圆的条件》示范公开课教学课件

中考数学满分之路(二)—四点共圆

2024年中考数学常见几何模型全归纳(全国通用)专题31 圆中的重要模型之四点共圆模型(解析版)

苏教版九年级四点共圆知识点详解

人教版数学九年级上册 四点共圆,解题妙不可言

(完整版)初三上专题四点共圆

第28讲 四点共圆问题(解析版)

第四讲 四点共圆问题

数学北师大版九年级下册四点共圆

人教版数学九年级上册四点共圆,解题妙不可言

第28讲四点共圆问题(解析版)

第四讲四点共圆问题