含孔复合材料层合板孔边应力集中的近似计算
含裂纹复合材料板的应力计算

6.0GPa;泊松比地一0.3。用本文介绍的方法可
以得到裂纹周围应力精确解析解。文中所有的计
算和应力分布图都在软件Mathematica中生成。 对裂纹周围应力在外荷载作用下沿裂纹边界进行
仿真分析,其结果如图3所示。从图3可以看出,
当外荷载逐渐增加时,沿裂纹周围应力也相应增
大。但是在裂纹尖端处应力为无穷大。
P(z1)+妒(z1)+’b(z2)+驴(z2)一一I F%ds+CI一,l —o
,ul妒(名1)+p1P(z1)+p2(z2)+P2妒(22)一
}
一只R。山+G一,z
J
(8)
式中,C,、C2为常数;9(互。)为P(z。)的共轭复数,其他类 似;S。、S为边界上的弧长元素。
对于本文所要采取的方法来说,接下来的问
i//
L———_一
蓁二::i
礤一O.5
—2. O
一1.O
O
1.0
极角0/(。)
图4
2.0 布
(a)
(b)
图2 椭圆孔转化为裂纹的示意图
考虑带有图2b所示裂纹的对中面对称的正
交各向异性板,板因承受两端均匀分布在边缘上
的拉力而变形,其作用点远离裂纹,纤维量 E。=135GPa,E。=9.5GPa;剪切模量G12—
Hanser Verlag,1971.
[3]杨丽敏,柳春图,曾晓辉.计算Reissner理论各向异 性板应力强度因子的半权函数法I-J].机械强度,
2006,28(1):113一117.
·1603·
中国机械工程第18卷第13期2007年7月上半月
混凝土锯切加工过程的基本特征
袁 慧1 王成勇1 胡珊珊1’2 胡映宁2 王智伟2 丁海宁2
含孔复合材料层合板的疲劳寿命研究

2010年第29卷5月第5期机械科学与技术M echanical Science and T echno l ogy for A erospace Eng ineer i ng M ay V o.l 292010N o .5收稿日期:2009-03-09基金项目: 十一五 民机专项科研项目资助作者简介:鲁国富(1980-),博士研究生,研究方向为直升机旋翼部件疲劳寿命研究,luguof uawu i @126.co m;张呈林(联系人),教授,博士生导师,z clntae @nu aa .edu .cn鲁国富含孔复合材料层合板的疲劳寿命研究鲁国富,刘 勇,张呈林(南京航空航天大学直升机旋翼动力学国家级重点实验室,南京 210016)摘 要:建立了三维有限元模型,分析了复合材料层合板的应力场。
使用修正H ash i n 失效准则判定复合材料的失效模式,并突降失效单元的材料性能。
疲劳载荷引起复合材料刚度降和强度降依靠缓降模型实现。
笔者将突降模型和缓降模型植入有限元模型中,模拟了复合材料层合板在拉伸和压缩疲劳载荷下的渐进损伤过程,并计算了层合板的纵向刚度损伤和疲劳寿命。
层合板的纵向刚度损伤具有三阶段特点,与试验观察是一致的。
层合板疲劳寿命预测值与试验值吻合地很好。
关 键 词:孔;复合材料;疲劳;损伤中图分类号:TB332 文献标识码:A 文章编号:1003 8728(2010)05 0684 06A Study of the Fatigue Life of La m i nated Co mposites w it h a HoleLu G uof u ,L i u Y ong ,Zhang Cheng li n(N ationa lK ey L abo ra t o ry o f R otorcraft A e romechan i cs ,N anji ng U n i versity o fA eronautic and A stronautic ,N an jing 210016)Abst ract :W e buil d 3D finite e le m ent m ode l to analyze the stress fi e l d of la m i n ated co m posites .The m od ified H ash i n fail u re cr iterion is used to judge t h e failure m ode o f co m posite m ateria,l and the m aterial property of fail u re ele m en ts is degraded in the instantaneous w ay .The stiffness and streng t h degradation of co m posite m ateri a l is caused by fati g ue loading based on the prog ressive degradation m ode.l The instantaneous degradati o n mode l and the progressive degradation m odel are i n corporated i n the finite ele m ent m ode l to si m ulate the progressi v e da m age process o f la m i n ated co mposites under tensi o n and co mpressi o n fatigue l o ad i n gs ,and to ca lculate l o ng itud i n al stiff ness da m age and fati g ue life of la m i n ated co m posites .The longitudina l stiffness da m age of l a m inated co m posites has t h e three stage characteristics ,wh ich agrees w ith the test resul.t The fatigue life pred icti o n o f la m inated co m posites is in good agree m ent w ith experi m ental values .K ey w ords :ho le ;co m posite m ateria;l fatigue ;da m age 复合材料由于其比强度和比刚度高、可设计性强等特点,已在航空航天领域得到广泛应用。
含孔洞复合材料结构的拉伸性能仿真

第1期纤维复合材料㊀No.1㊀1002024年3月FIBER ㊀COMPOSITES ㊀Mar.2024含孔洞复合材料结构的拉伸性能仿真陈英函,刘甲秋,于柏峰,刘㊀佳,郝晨伟(哈尔滨玻璃钢研究院有限公司,哈尔滨150028)摘㊀要㊀本文针对含中心孔洞和含多孔复合材料结构模型,利用Fibersim 进行铺层设计并检验铺层角度是否偏差,对于含中心孔洞复合材料结构采用分区域铺覆的设计方法进行探究,发现可以达到在制造中节省材料成本的作用㊂将两种结构进行仿真失效计算同时与不开孔状态的复合材料结构进行比较,得出失效比值㊂关键词㊀Fibersim;有限元仿真;复合材料;铺层设计Simulation of Tensile Properties of CompositeStructures Containing HolesCHEN Yinghan,LIU Jiaqiu,YU Baifeng,LIU Jia,HAO Chenwei(Harbin FRP Institute Co.,Ltd.,Harbin 150028)ABSTRACT ㊀In this paper,we use Fibersim to design the lay -up for center hole and porous composite structure model,check whether the layup angle is deviated or not,and explore the design method of lay -up by area for center pore compos-ite structures,and find that it can achieve the role of saving the material cost in manufacturing.The two structures were sub-jected to simulated failure calculations while comparing them with the composite structure in the unopened state to derive the failure ratio.KEYWORDS ㊀fibersim;finite element simulation;composite material;lay -up design通讯作者:陈英函,硕士,助理工程师㊂研究方向为复合材料结构设计与仿真㊂E -mail:1374057740@1㊀引言航空航天领域中许多构件由碳纤维复合材料制成[1],其中由碳纤维复合材料制成的开孔板在复杂的服役环境下会引起应力集中进而产生损伤,这类损伤会导致构件的服役寿命减退和降低承载能力[2-3]㊂因此,研究人员对含孔复合材料构件进行了进一步的研究[4]㊂碳纤维复合材料开孔对力学性能影响较大[5-6],因此对于复合材料开孔性能的研究极为重要,Khashaba [7]等通过实验研究发现随着碳纤维复合材料开孔尺寸的增加,复合材料的抗压强度和刚度都会减小㊂卿光辉[8]等基于增强应变理论建立了非协调广义混合模型计算含孔复合材料层合板的应力集中系数,所得模型计算结果好,精度高并具有适用性㊂王振兴[9]等基于复合材料S -N 曲线分析对比了在开孔情况和不开孔情况下的浆叶疲劳寿命,发现开孔情况会产生更大的应力集中,从而影响桨叶的疲劳寿命㊂Fibersim 是一款处理复合材料铺层复杂性问题的专业软件[10],能够模拟复合材料铺层真实角度㊀1期含孔洞复合材料结构的拉伸性能仿真偏差进行改进,本文利用Fibersim 对含中心孔复合材料结构以及含多孔复合材料结构进行铺层的设计及铺层角度的查看校验,分析了两种结构失效的最大载荷并与不开孔状态下的复合材料结构进行比较,得出失效比值㊂2㊀含孔洞复合材料结构基于Fibersim 与仿真软件可以进行数据交互的特点,选取典型的含中心孔以及多孔复合材料结构进行算例的仿真分析,材料属性选取如表1所示㊂表1㊀材料属性纵向弹性模量E 1/MPa 横向弹性模量E 2/MPa 泊松比v 剪切模量G 12/MPa 剪切模量G 23/MPa 密度ρ/g㊃cm 320900094500.27550039001.54㊀㊀失效准则选用Tssi -Wu 应力准则,根据该准则,材料不发生破坏的条件如公式(1)所示㊂F =F 1σ1+F 2σ2+F 11σ21+F 22σ22+F 66τ212+2F 12σ1σ2<1(1)其中,各种强度指标按照以下各式确定,如公式(2)所示㊂F 1=1X t -1X cF 2=1Y t -1Y cF 11=1X t X cF 22=1Y t Y c F 66=1S 2F 12=F ∗12X t X c Y t Y cìîíïïïïïïïïïïïïïïïï(2)其中,F ∗12的值在-1到1之间,一般选取-1/2㊂2.1㊀含中心孔复合材料结构针对含中心孔复合材料结构示意如图1所示,模型尺寸为300mm ˑ300mm,中心含有直径为150mm 的孔洞㊂采用Fibersim 对铺贴面,边界进行提取,并利用点位定义铺层原点和零度方向,其信息如图2所示㊂㊀㊀基于该构型进行复合材料铺层的设计,铺层角度设置为(0/45/-45/90)5s ,复合材料单层厚度为0.05mm,总共铺层数为40层,整体厚度2mm㊂对于每一层的铺层设计,采用纤维影响因子的值为0.3,通过对铺层角度仿真模拟真实铺贴时角度是否偏差,如图3(a)~3(d)所示分别显示为在0ʎ,45ʎ,-45ʎ,90ʎ铺层角度下的角度信息,信息显示图1㊀含中心孔复合材料结构示意图图2㊀含中心孔复合材料结构0ʎ坐标方向图3㊀各角度铺层仿真信息该模型的实际铺层角度与理论铺层角度无偏差㊂101纤维复合材料2024年㊀由于在生产制造中,按图3所示进行预浸料准备时会先利用下料机切出整体模型再去除中心圆形孔洞,这样造成不必要的浪费,基于此对于各个角度进行铺层设计的优化,给出如图4所示建立基于区域划分的铺层设置㊂㊀㊀查看基于分区铺覆下的铺层角度是否有偏差,优化后的各铺层角度信息如图5所示,各个铺层角度均无偏差㊂图4㊀各角度铺层分区信息图图5㊀优化后的各铺层角度信息㊀㊀对图1所示的含中心孔洞复合材料结构,按图5所示节省用料10%以上,并且随着中心开孔直径的增加,节省用料比率越高㊂同时针对此开孔结构利用表1属性进行有限元仿真,网格划分如图6所示㊂对模型采用下端固定约束,在上表面加载拉力作用,查看失效结果,发现当加载力的大小为22437N 时模型出现首层失效,失效时观察不同角度失效系数结果如图7所示,并且发现失效发生在90ʎ铺层的孔洞附近位置㊂图6㊀网格划分示意图图7㊀含中心孔复合材料结构失效结果图㊀㊀将开孔模型与未开孔的模型做失效结果对比,对比结果如表2所示,含中心孔复合材料结构的首201㊀1期含孔洞复合材料结构的拉伸性能仿真层失效载荷是未开孔结构的0.347㊂表2㊀比对结果模型失效载荷失效比值含中心孔复合材料结构22437N 0.347未开孔结构64525N1㊀㊀2.2㊀含多孔复合材料结构针对含多孔复合材料结构示意如图8所示,模型尺寸为200mm ˑ600mm,含有三个直径为100mm 的孔洞,孔间距为200mm㊂图8㊀含多孔复合材料示意图基于该构型按照如含中心复合材料结构铺层进行设计,铺层的零度坐标如图9所示㊂图9㊀含多孔复合材料结构0ʎ坐标方向㊀㊀基于该构型进行复合材料铺层的设计,铺层角度设置为(0/45/-45/90)5s ,复合材料单层厚度为0.05mm,总共铺层数为40层,整体厚度2mm㊂对于每一层的铺层设计,采用纤维影响因子的值为0.3,通过对铺层角度仿真模拟真实铺贴时角度是否偏差,如图10(a)~10(d)所示,分别显示为在0ʎ,45ʎ,-45ʎ,90ʎ铺层角度下的角度信息,信息显示该模型的实际铺层角度与理论铺层角度无偏差,同样可以采用如含中心孔洞复合材料结构相似的分区域铺层设计方法以达到在制造中节省材料的目的㊂图10㊀各角度铺层仿真信息㊀㊀对模型采用下端固定约束,在上表面加载拉力作用,查看失效结果,发现当加载力的大小为54221N 时模型出现首层失效,失效时观察不同角度失效系数结果如图11所示,并且发现失效发生在90ʎ铺层距边线较近的孔洞边缘位置㊂将含多孔复合材料模型与未开孔的模型做失效结果对比,对比结果如表3所示,含中心孔复合材料结构的首层失效载荷是未开孔结构的0.403㊂301纤维复合材料2024年㊀图11㊀含多孔复合材料结构失效结果图表3㊀比对结果模型失效载荷失效比值含多孔复合材料结构54221N0.403未开孔结构134576N13㊀结语(1)利用Fibersim针对含中心孔复合材料进行分区域的铺层设计,节省材料在10%以上㊂㊀㊀(2)将本文含中心孔洞复合材料和含多孔复合材料结构与未开孔结构进行对比,其失效比值分别为0.347和0.403㊂(3)本文采用首层失效进行结果的判断,只能作为单层失效的标准,不能反映结果的最终承载能力㊂参考文献[1]蔡菊生.先进复合材料在航空航天领域的应用[J].合成材料老化与应用,2018,47(6):94-97.[2]MOURE M M,HERRERO C J,GARCíA C S K,et al.Design tool to predict the open-hole failure strength of composite laminates sub-jected to inplane loads[J].Composite Structures,2020,238: 111970.[3]SAYAR H,AZADI M,GHASEMI A,et al.Clustering effect on damage mechanisms in open-hole laminated carbon/epoxy compos-ite under constant tensile loading rate,using acoustic emission[J]. Composite Structures,2018,204:1-11.[4]郭峰,王哲峰,王共冬,等.低温条件下含孔碳纤维复合材料层合板拉伸损伤特性研究[J].复合材料科学与工程,2022(04):56-61.[5]姚辽军,赵美英,周银华.不同孔径复合材料层合板应变集中及失效强度分析[J].机械科学与技术,2011,30(5):761-764.[6]韩小平,郭章新,朱西平,等.含孔复合材料层合板孔边的应力集中[J].复合材料学报,2009,26(1):168-173. [7]KHASHABA U A,KHDAIR A I.Open hole compressive elastic and strength analysis of CFRE composites for aerospace applications [J].Aerospace Science and Technology,2017,60:96-107.[8]卿光辉,王绍波.含孔复合材料层合板的应力集中分析[J].中国民航大学学报,2019,37(05):55-59.[9]汪振兴,陶宪斌,杨建灵,等.直升机复合材料开孔对桨叶疲劳寿命的影响[J].中国科技信息,2020(20):23-25. [10]洪清泉,吕长,王招.Fibersim复合材料设计与工艺技术应用[M].清华大学出版社,2019,1(4):39-42.401。
含中心圆孔复合材料层合板失效分析及强度预测研究

含中心圆孔复合材料层合板失效分析及强度预测研究拓宏亮;马晓平;卢智先【摘要】对复合材料结构进行开孔将会导致结构强度显著下降.以含中心圆孔的复合材料层合板为研究对象,根据ASTM D 5766标准对三种不同铺层比例的含中心圆孔复合材料层合板进行拉伸试验,研究不同铺层比例对复合材料开孔拉伸试验件的拉伸性能和失效模式的影响.基于连续介质损伤力学,分别采用最大应变失效准则和基于物理失效机制的三维非线性Puck失效准则预测纤维和基体损伤的起始,通过应变表征损伤演化,建立含中心圆孔复合材料层合板的三维有限元模型;并进行数值分析,通过与试验结果对比,表明该模型能有效预测含中心圆孔复合材料层合板的拉伸强度和损伤扩展过程.【期刊名称】《航空工程进展》【年(卷),期】2018(009)002【总页数】8页(P259-266)【关键词】复合材料层合板;中心圆孔;连续介质损伤力学;失效分析;有限元方法【作者】拓宏亮;马晓平;卢智先【作者单位】西北工业大学航空学院,西安 710072;西北工业大学航空学院,西安710072;中国科学院工程热物理研究所,北京100190;西北工业大学航空学院,西安710072【正文语种】中文【中图分类】TB330 引言先进复合材料由于其高比强度、高比刚度,可设计性以及良好的抗腐蚀性能等优点,已在航空航天工程领域被广泛应用,现已成为衡量飞行器先进性的重要指标之一。
由于结构功能和装配的需要,复合材料结构必须含有不同尺寸和形状的开孔。
开孔将会造成应力集中和纤维被切断,导致结构强度显著下降。
因此,需要对含孔复合材料层合板的拉伸性能和失效机理展开深入研究。
复合材料带孔平板在拉伸载荷作用下主要存在的损伤模式有纤维断裂、基体开裂以及其混合模式。
各损伤模式之间具有关联性,可能相互交叉并诱发其他混合形式的损伤。
F.K.Chang等[1]结合Yamada-Sun失效准则和Hashin失效准则[2]建立了二维渐进损伤模型来预测开孔层合板的强度和损伤累积过程;P.P.Camanho等[3]提出了新的退化方式,将其扩展到三维有限元模型;鲁国富等[4]在应力计算中采用了修正的Newton-Raphson迭代方法,建立了含缺口的三维有限元模型;姚辽军等[5-6]利用二维非线性Hashin准则模型研究了不同孔径、不同铺层比例对复合材料开孔层合板强度的影响规律;李明等[7]通过试验并结合场变量子程序研究了开孔的形状和大小对层合板强度的影响;黎增山等[8]引入层间界面单元来预测分层损伤,模型能够模拟含孔层合板拉伸过程中的损伤起始、扩展和最终破坏模式和失效强度;朱建辉等[9]基于修正的Hashin准则和Camanho材料性能退化模型,建立了层合板的损伤分析方法,研究了层合板在压缩载荷作用下的承载能力和失效模式;李沛城等[10]基于应变破坏准则建立了层合板三维连续损伤介质模型,能够有效模拟开孔层合板损伤起始、扩展和失效过程,并具有较高的计算精度和效率;urin等[11]提出了一种简化的强度分析方法,通过与大量试验数据进行对比,验证了方法的准确性;Z.C.Su等[12]利用连续壳单元和内聚力单元建立了复合材料层合板的渐进损伤模型,研究了开孔板的尺寸效应;B.Y.Chen等[13]结合弥散裂纹理论和内聚力单元研究了尺寸效应对开孔拉伸强度的影响,并和M.R.Wisnom等[14]的试验结果良好吻合;李秋漳等[15]基于连续介质损伤力学提出了复合材料层合板含中心圆孔的数值模型,分别采用Puck准则和Aymerich准则对层内和层间损伤进行判定,对不同孔径和铺层的层合板进行拉伸失效分析;吴义韬等[16]提出了预测复合材料层合板面内渐进损伤的分析模型,涵盖复合材料面内损伤起始、演化直至最终失效的全过程,并完成了对两种铺层层合板在拉伸和压缩载荷作用下的失效分析。
含孔复合材料层合板失效准则研究_徐明

ö2
÷
ø
≥
1
(7)
当 α = β = 1 时 ,纤 维 拉 伸 方 向 采 用 Hashin 准
则;当 α = β = 0 时,纤维拉伸方向采用最大应力准
则。 纤维断裂的破坏主要是由沿纤维方向的正应力
控制的,因此 Shahid Iqbal 等 对 [12] 失效准则做了改 进,采用最大应力判据即令 α = β = 0 ,取得了良好的 效果。法向分层破坏主要是由层合板厚度方向的正 应力控制的,考虑到在长度方向单向拉伸载荷作用 下层合板的失效形式为纤维断裂、基体断裂、基纤剪 切,从而用最大应力准则得到公式(6)-(7),进而得 到公式(1)-(7)所示的混合三维失效准则。
1446.51 1171.41 69.64 187.29
S/ MPa
95.935
3.1.1 模型的建立 该层合板的几何尺寸为 0.24m × 0.04m,中心孔
孔径为 0.008m,铺层角度为[45/-45/0/0/-45/90/ 0/90/45/0]S。有限元网格模型如图 2 所示,单元数
图 2 含中心孔层合板静强度分析有限元模型
2
ö
÷
ø
+
æ
ç
è
σ23 S23
ö2
÷
ø
≥
1
基纤剪切 (σ11 ≤ 0) :
æ
ç
è
σ11 XC
ö2
÷
ø
+
æ
ç
è
σ12 S12
2
ö
÷
ø
+
æ
ç
è
σ13 S13
ö2
÷
ø
≥
1
(2) (3) (4) (5)
什么是应力集中应力集中的计算方法

什么是应力集中应力集中的计算方法应力集中指物体中应力局部增高的现象,一般出现在物体形状急剧变化的地方,如缺口、孔洞、沟槽以及有刚性约束处。
那么你对应力集中了解多少呢?以下是由店铺整理关于什么是应力集中的内容,希望大家喜欢!应力集中的简介应力集中是指结构或构件的局部区域的最大应力值比平均应力值高的现象。
应力集中能使物体产生疲劳裂纹,也能使脆性材料制成的零件发生静载断裂。
在应力集中处,应力的最大值(峰值应力)与物体的几何形状和加载方式等因素有关。
局部增高的应力随与峰值应力点的间距的增加而迅速衰减。
由于峰值应力往往超过屈服极限(见材料的力学性能)而造成应力的重新分配,所以,实际的峰值应力常低于按弹性力学计算得到的理论峰值应力。
应力集中对构件强度的影响对于由脆性材料制成的构件,应力集中现象将一直保持到最大局部应力到达强度极限之前。
因此,在设计脆性材料构件时,应考虑应力集中的影响。
对于由塑性材料制成的构件,应力集中对其在静载荷作用下的强度则几乎无影响。
所以,在研究塑性材料构件的静强度问题时,通常不考虑应力集中的影响。
但是应力集中对构件的疲劳寿命影响很大,因此无论是脆性材料还是塑性材料的疲劳问题,都必须考虑应力集中的影响。
应力集中的计算方法在无限大平板的单向拉伸情况下,其中圆孔边缘的k=3;在弯曲情况下,对于不同的圆孔半径与板厚比值,k=1.8~3.0;在扭转情况下,k=1.6~4.0。
如下图所示的带圆孔的板条,使其承受轴向拉伸。
由试验结果可知 : 在圆孔附近的局部区域内,应力急剧增大,而在离开这一区域稍远处,应力迅速减小而趋于均匀。
这种由于截面尺寸突然改变而引起的应力局部增大的现象称为应力集中。
在I —I 截面上,孔边最大应力max与同一截面上的平均应力之比,用a表示称为理论应力集中系数,它反映了应力集中的程度,是一个大于1 的系数。
而且试验结果还表明 : 截面尺寸改变愈剧烈,应力集中系数就愈大。
因此,零件上应尽量避免带尖角的孔或槽,在阶梯杆截面的突变处要用圆弧过渡。
【2019年整理】复合材料层合板接头疲劳预测方法
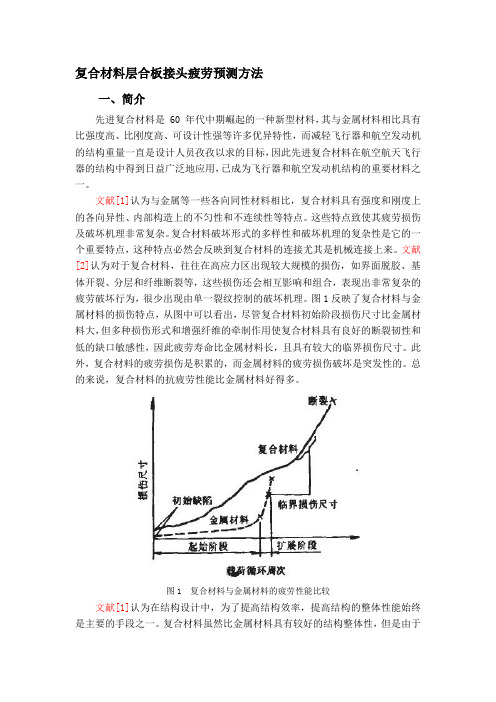
复合材料层合板接头疲劳预测方法一、简介先进复合材料是 60 年代中期崛起的一种新型材料,其与金属材料相比具有比强度高、比刚度高、可设计性强等许多优异特性,而减轻飞行器和航空发动机的结构重量一直是设计人员孜孜以求的目标,因此先进复合材料在航空航天飞行器的结构中得到日益广泛地应用,已成为飞行器和航空发动机结构的重要材料之一。
文献[1]认为与金属等一些各向同性材料相比,复合材料具有强度和刚度上的各向异性、内部构造上的不匀性和不连续性等特点。
这些特点致使其疲劳损伤及破坏机理非常复杂。
复合材料破坏形式的多样性和破坏机理的复杂性是它的一个重要特点,这种特点必然会反映到复合材料的连接尤其是机械连接上来。
文献[2]认为对于复合材料,往往在高应力区出现较大规模的损伤,如界面脱胶、基体开裂、分层和纤维断裂等,这些损伤还会相互影响和组合,表现出非常复杂的疲劳破坏行为,很少出现由单一裂纹控制的破坏机理。
图1反映了复合材料与金属材料的损伤特点,从图中可以看出,尽管复合材料初始阶段损伤尺寸比金属材料大,但多种损伤形式和增强纤维的牵制作用使复合材料具有良好的断裂韧性和低的缺口敏感性,因此疲劳寿命比金属材料长,且具有较大的临界损伤尺寸。
此外,复合材料的疲劳损伤是积累的,而金属材料的疲劳损伤破坏是突发性的。
总的来说,复合材料的抗疲劳性能比金属材料好得多。
图1 复合材料与金属材料的疲劳性能比较文献[1]认为在结构设计中,为了提高结构效率,提高结构的整体性能始终是主要的手段之一。
复合材料虽然比金属材料具有较好的结构整体性,但是由于设计、工艺和使用维护等方面的需要或限制,就需要存在一些设计和工艺分离面、维护口盖和多种外挂接口等等。
而这些部位的载荷传递必须有相应的连接方式来解决,所以连接设计在复合材料结构中是必不可少的关键环节。
文献[3]认为飞行器结构有70%以上的破坏都是发生在连接部位。
文献[4]认为结构系统的抗疲劳可靠性设计一直是工程界关注的焦点。
基于复合材料高阶理论的层合板面内应力分析

基于复合材料高阶理论的层合板面内应力分析【摘要】根据整体-局部1,2-3高阶理论求解受正弦载荷的不同跨厚比的四边简支板的面内应力和,并与有限元分析软件ABAQUS的计算结果以及精确解进行对比。
数值结果表明,当板的跨厚比小于20时,高阶理论的面内应力结果比ABAQUS的计算结果精确;当板的跨厚比大于20时,两者的结果比较接近。
【关键词】复合材料;层合板;ABAQUS;面内应力;跨厚比;高阶理论对于复合材料层合板结构,由于每层的材料为不同的各向异性材料以及铺层的角度和层数的不同,因此提出和建立一般的位移场模型是非常困难的。
起初,人们以克希霍夫假设[1]和折合刚度的方法建立了经典层合板理论。
这种经典层合板理论在分析跨厚比比较大,也就是比较薄的层合板的力学问题时,由于可以忽略剪切的影响,所以计算过程简单而且计算结果也比较精确。
但是,对于分析跨厚比比较小,也就是中厚度层合板的力学问题时,剪切变形比较大,经典层合板理论将不再适用。
Pagano从三维线性弹性理论[2-4]出发研究并导出了复合材料层合板在特殊载荷作用下的三维弹性解,数值结果表明这种三维弹性理论对分析中厚度的层合板是比较精确的。
但是由于复合材料层合板具有各向异性和呈层性等特点,采用三维弹性理论会比较复杂,并且在分析实际工程问题时会比较困难。
因此,既简单又精确的各种高阶层合板理论陆续被建立起来[5-6]。
本文主要介绍由Li和Liu提出的整体-局部1,2-3高阶理论[7],并利用此理论计算不同跨厚比下3层层合板的面内应力,同时利用ABAQUS计算相同跨厚比下层合板的面内应力。
通过两者的计算结果与精确解对比发现,ABAQUS 对分析跨厚比比较大,也就是比较薄的层合板时计算结果还是比较精确的,但是当分析中厚度层合板时,ABAQUS的计算结果误差就比较大了,整体-局部1,2-3高阶理论则会得出比较精确的结果。
1 复合材料层合板理论经过数十年的发展,至今已提出了多种复合材料层合板理论:经典层合板理论,一阶剪切变形理论,高阶剪切理论,分层理论,三维弹性理论。
带孔复合材料层板动态拉伸破坏的应变率效应

带孔复合材料层板动态拉伸破坏的应变率效应荆臻;田常录;吴健;王纬波;赵军华;孙琎【摘要】采用三维Hashin准则作为纤维束损伤判据,根据材料不同损伤模式制定相应的材料性能退化方案,并考虑应变率效应对材料的强度性能进行修正,建立含孔复合材料层合板的渐进损伤分析模型,模拟材料在不同应变率下的损伤破坏过程.通过动态拉伸试验,获得材料在不同应变率下的载荷-位移关系及孔边不同位置的时间-应变关系,讨论了应变率对材料拉伸性能的影响及试件孔边的应力集中情况.有限元分析结果与试验数据相一致,证明了本文所提出分析模型的正确性和有效性.【期刊名称】《南京航空航天大学学报》【年(卷),期】2019(051)001【总页数】8页(P55-62)【关键词】带孔层合板;应变率效应;冲击拉伸;应力集中【作者】荆臻;田常录;吴健;王纬波;赵军华;孙琎【作者单位】江南大学机械工程学院江苏省食品先进制造装备技术重点实验室,无锡,214122;江南大学机械工程学院江苏省食品先进制造装备技术重点实验室,无锡,214122;中国船舶科学研究中心,无锡,214082;中国船舶科学研究中心,无锡,214082;江南大学机械工程学院江苏省食品先进制造装备技术重点实验室,无锡,214122;江南大学机械工程学院江苏省食品先进制造装备技术重点实验室,无锡,214122【正文语种】中文【中图分类】O385纤维增强树脂基复合材料凭借高比强度、高比模量、耐高温以及可设计性强等出色的综合性能,已被大量运用于航空航天、国防军工以及交通运输、化工和建筑等领域[1-4]。
在实际应用中,出于结构连接的需要,不可避免地对层合板进行开孔等操作,这破坏了材料自身的连续性,降低了结构强度[5-7]。
研究显示,开孔使某船用层合板的强度下降了40%~60%[8]。
而运用在航空航天、国防军工以及交通领域的结构,往往在很短的时间内承受极大的应力,由于复合材料存在应变率效应的问题,其破坏形式与应变率密切相关[9-10]。
含孔复合材料层合板拉伸失效分析

含孔复合材料层合板拉伸失效分析许良;何懿;马少华;回丽【摘要】对国产T700/双马树脂基复合材料的含孔层合板进行了拉伸失效分析研究,分析了不同开孔直径和开孔形状对复合材料层合板拉伸性能的影响,利用有限元软件ABAQUS建立逐渐损伤失效模型,对复合材料层合板的拉伸强度进行数值模拟.研究结果表明:对于不同开孔直径的复合材料层合板,随着圆孔直径的增大,拉伸强度显著下降,对于不同开孔形状的复合材料层合板,含圆孔的层合板拉伸强度最大,然后依次是椭圆孔、方形孔、菱形孔,层合板的断裂模式都为过孔破坏.数值模拟得到的强度值与试验测量的强度值吻合较好,为含孔复合材料层合板的强度预测提供了一种有效的方法.【期刊名称】《科学技术与工程》【年(卷),期】2018(018)034【总页数】6页(P242-247)【关键词】复合材料层合板;开孔直径;开孔形状;拉伸强度;断裂模式;数值模拟【作者】许良;何懿;马少华;回丽【作者单位】沈阳航空航天大学机电工程学院,沈阳110136;沈阳航空航天大学机电工程学院,沈阳110136;沈阳航空航天大学机电工程学院,沈阳110136;沈阳航空航天大学航空制造工艺数字化国防重点实验室,沈阳110136【正文语种】中文【中图分类】V257复合材料具有优异的特性,例如高比强度比刚度、高抗冲击性、耐高温、耐腐蚀性好、可设计性强、良好的疲劳性能和工艺性,已经被广泛应用在航空航天等领域[1—3]。
在实际使用过程中,需要在复合材料结构中加工一些孔,如螺栓孔、检查用的通孔、装配孔等,当加工孔时,会切断复合材料结构中的部分碳纤维,在孔的边缘会引起严重的应力集中,并且孔的周围会发生纤维断裂、基体开裂、基体纤维剪切破坏、分层等损伤,这些将严重影响复合材料结构的强度。
因此,国内外大量学者对复合材料的开孔拉伸性能进行了重点研究[4—7]。
而复合材料的强度预测比较复杂,传统的设计、试验、再设计的方法将耗费大量的人力和财力。
含孔复合材料层合板孔口缝合补强的层间应力分析

料层 间应 力 的有 限 元 分 析 方 法 。金 春 花 _ 介 绍 了 5 缝合层 合 板 层 间应 力 的存 在 和产 生 的 原 因 。 同时 对 缝合 复合 材料 的层 间应 力进 行 了试 验 研 究 , 出 给 了一个 判断 复合 材料层 间破坏 的强度 准则 。 为 了分 析并 进一 步 解 决孔 边 分 层 问题 , 文 使 本 用AAU B Q S有 限元 软 件 中 的空 间分布情况 , 并将缝合后 的层 间应力值与缝合前的相关数值进 行 了比较 , 主要研 究 了不 同缝合 参数 对孔边层 间应力 的影响。通过有限元模 拟计算可得 , 层合板 缝合补 强后 , 孔边 的层间应力 比未 缝合前 显著减小 , 孔边 附近层 间应力 的分布与相邻铺层 的铺层角有关, 同铺层之 间的层 间应力沿孔边 区域存 在应力的转换 点, 不 并且存在 显著差别 。
组常微分方程 的特征值 问题 。对 不同铺层层压 计算所用的复合材料层板 以及孔 口缝合 的工
艺参 数 由 6 5研 究 所 提 供 _ 。层 板 材 料 为 : 3 0 2 6 ] T 0/
板 的层 间应 力进行 了计 算 和 比较 , 证 了方法 的有 验 效 性 。张培 新 _ 研 究 了任 意 多 向铺 层 层 压 复 合 材 4
@ 2 1 SiT c. nr 0 1 c. eh E gg ,
力 学
含孔复合材料层合板 孔 口缝合 补强 的层 问应 力分析
王 彬 郭章新 沈创石
( 西北工业大学力学与土木建筑学院, 西安 7 0 2 ) 1 19
摘
要
使用有 限元模拟计算 了含孔复合材料层合板开 口缝合补强结构。研 究 了含孔复合材料 层合 板在轴 向拉伸 载荷作用
复合材料层合板预紧螺栓连接应力分析

施加 。利用降温模拟螺栓预紧力的方法不受螺栓结
构形式 、分布情况等因素影响 ,适用于所有预紧螺栓
连接 。
4 计算结果分析 411 预紧力对孔边拉应力的影响
由于在层合板受力端只作用了 280 N 的拉力 , 所以模型是在弹性小变形范围内求解的 。只取上板 分析 ,因为模型中上板和下板的应力分布相同 。为 了消除边界的影响 ,文中将受拉端部分去除 ,只取上 板接触部分作应力分析 。图 2 ( a)和图 2 ( b)分别给 出了在 3 kN 预紧力下 45°和 0方向铺层的拉应力云 图 。 ( - 45°方向铺层的应力分布可参照 45°方向铺 层的应力分布 )
会有较大的误差 ,目前较为有效的途径是采用有限 元方法进行数值计算和分析 。
在总结以往螺栓连接模拟方法的前提下 ,笔者 研究了预紧力的施加方法和有限元非线性接触算 法 [ 2 ] ,应用 AN SYS软件 [ 3 ] 对复合材料层合板钛合 金受剪螺栓连接结构建立了全尺寸三维有限元接触 模型 ,并利用降温法模拟螺栓预紧力 ,得到了预紧力 对层合板孔边拉应力和层间应力 [ 6 ]的影响关系 ,为 复合材料层合板的螺栓连接计算提供了方法和参考 依据 。
收稿日期 : 2008 - 07 - 23 基金项目 :国家自然科学基金项目 ( 10477018)和西北工业大学科技
创新基金项目 (W016143)资助 作者简介 :张永杰 (1979 - ) ,博士 ,研究方向为飞行器结构设计与有
限元数值计算方法 , zyj19191 @ nwpu. edu. cn; 孙 秦 (联 系人 ) ,教授 ,博士生导师 , sunqin@ nwpu. edu. cn
+
{
R
e j
}
T
缓和开孔矩形薄板应力集中方法的弹性分析

问题 不受此 限制 , 忽略 上述三 个方程 , 只 考 虑 2 2 2 2 52ε + 5ε = 5γ x/ 5y y/ 5 x xy / 5 x 5 y 即可 , 因而平面 应力问题也称为近似的二维问题 , 只有当板很薄 ( z 向厚度可以忽略) 时 , 其解答才具有足够的精度 [ 4 ] . 2) 沿 y 轴 (φ = π/ 2) , 2 2 2 σ ρ φ = q + qa ( k - 1 ) ( v - 1 ) / 2 M + 3a (k 4 φ 很快趋于 q ( 无孔情 1) ( v + 1) /ρ N , 随着ρ 的增加 ,σ
( 8)
4
,C =
q
4
求得其他待定系数
) = c1 sin φ + c2 co s φ, 把 解微分方程得 : g (φ ) 代入 u′ g (φ ρ, u ′ φ 的表达式 : u′ ρ =
2 qa ( k - kv - 1 + v) , 2M 4 qa ( 1 + v - k - kv ) , 4N 2 qa ( k - 1 - v + kv ) , 2N
( 22)
2 2 2 后者在考虑应变协调时 , 除满足 52ε z/ 5y + 5ε y/ 5 x 2 = 5γ xy / 5 x 5 y 外 , 实 际 还 应 满 足 以 下 三 个 方 程 : 2 2 2 2 52ε = 0 ,5 ε = 0 ,5 ε z/ 5x z/ 5y z / 5 x 5 y = 0 . 即ε z 只 ε 能是 x , y 的一次函数 : z = ax + by + c. 为使研究的
ρ( 1 - v) - 2 H ρ( 1 + v) cos 2φ - 4 vI ρ co s 2φ] + [2 G E′
复合材料厚层合板力学性能等效方法研究

复合材料厚层合板力学性能等效方法研究江彬彬;王志瑾【摘要】基于复合材料三维等效弹性常数理论,分别建立了厚复合材料悬臂梁和三点弯曲厚复合材料层合板的等效模型进行数值分析,并和逐层细分模型结果对比,研究了子层对等效模型位移计算误差的影响,分析了等效模型层间应力的计算精度.研究表明,对于子层厚度比<0.2的厚复合材料层合板,采用等效模型进行数值分析,可以得到较高精度的位移-应力分析结果.以等效模型得到的层间应力作为设计约束时,厚复合材料层合板的设计是偏安全的.【期刊名称】《机械制造与自动化》【年(卷),期】2018(047)004【总页数】4页(P63-66)【关键词】复合材料;厚层合板;三维弹性常数;力学性能;等效模型;层间应力【作者】江彬彬;王志瑾【作者单位】南京航空航天大学飞行器先进设计技术国防重点实验室,江苏南京210016;南京航空航天大学飞行器先进设计技术国防重点实验室,江苏南京210016【正文语种】中文【中图分类】V214.80 引言随着结构设计水平的提高和材料工艺的完善,飞机结构上复合材料的应用不断扩大,逐步出现了厚复合材料层合结构[1-2]。
如某直升机主旋翼翼梁由60层石墨/环氧材料铺成[3],F-22机翼采用自动铺带技术,蒙皮最厚处达到14.2 mm,水平尾翼转轴最厚处铺层数达450层以上[4]。
为了减少有限元分析模型的规模,一般采用三维弹性常数等效理论分析厚复合材料层合结构[5]。
Chou等[6]假设材料面外应力和面内应变连续,用控制体积法推导出由不同铺设方向单层组成的层合板的等效性能。
Sun等[7]基于子层概念,针对均衡铺层的复合材料结构,提出了三维等效弹性常数理论。
张剑等[8]根据三维等效弹性常数理论,分析了复合材料大层数矩形厚截面层压杆的扭转问题,给出了剪应力在横截面内的分布规律。
目前,对于三维等效弹性常数理论中子层对计算精度的影响、层间应力的计算等还没有深入研究。
本文基于三维等效弹性常数理论[7],通过厚复合材料悬臂梁算例,研究了子层厚度比和位移计算精度及计算效率的关系,通过三点弯曲厚复合材料层合板算例,研究了等效模型计算层间应力。
含孔复合材料层合板拉伸强度研究_李明

纤维增强复合材料结构由于具有比强度大、比 刚度高、抗腐蚀性能好以及良好的可设计性,近年 来在航空和航天领域被广泛地应用,已成为飞机和 航空发动机结构的重要材料之一[1 -4]. 纤维增强复 合材料的引入很大程度地提高了飞机的整体性,但 由于检查、拆装、维护的需要以及工艺限制,在纤维 增强复合材料结构件中,经常会存在一些孔. 如用 于螺栓连接的螺栓孔,用于检查的通孔,以及装配 孔,等等. 例如在鹰狮 JAS 39 的翼梁上就存在着很 多各种形状的孔[5],如图 1 所示. 而这些孔对复合 材料结构的强度将会产生一定的影响.
纤维增强复合材料结构由于具有比强度大比刚度高抗腐蚀性能好以及良好的可设计性近年来在航空和航天领域被广泛地应用已成为飞机和航空发动机结构的重要材料之一纤维增强复合材料的引入很大程度地提高了飞机的整体性但由于检查拆装维护的需要以及工艺限制在纤维增强复合材料结构件中经常会存在一些孔
第 43 卷 增刊 1 2011 年 3 月
复合材料层合结构的强度预测及失效分析是
基金项目: 国家“973”基金( 2006CB601206) ; 国家自然科学基金 ( 90816024,10872059) 资助项目.
设计复合材料结构时所必需解决的关键问题,是 安全、经济地应用复合材料的前提. 因此,它在复 合材料研究领域中很早受到重视并得到了较为广 泛的研究. 由于影响其强度的因素很多,失效形式 具有多样性,如纤维断裂、基体开裂、基体纤维剪 切破坏、分层等,使得强度预测变得比较复杂. 另 外,传统的设计、试验错误、再设计的方法将耗费 大量的时间和费用. 因此,运用有限元软件模拟复 合材料层合结构的失效过程并预测最终失效强度 具有重要的应用价值,而对于含孔复合材料层合 板的强度预测更是当前国际上复合材料领域的研 究热点. Chang 等[6]首先提出用于分析含孔单向 层合板在拉伸载荷作用下极限强度的逐渐损伤模 型,并对不同铺层顺序层合板的损伤扩展和破坏 情况 进 行 了 研 究. 程 小 全 等[7] 采 用 有 限 元 软 件
带有六边形孔的复合材料板之孔边应力计算

第26卷第8期 V ol.26 No.8 工 程 力 学 2009年 8 月 Aug. 2009 ENGINEERING MECHANICS39———————————————收稿日期:2008-03-26;修改日期:2009-03-20作者简介:*李 成(1962―),男,新疆乌鲁木齐市人,教授,博士,主要从事固体力学、复合材料结构强度研究(E-mail: chengli@); 郑艳萍(1975―),女,河南平顶山市人,讲师,硕士,主要从事复合材料结构强度研究(E-mail: zhengyanping@); 铁 瑛(1978―),女,河南洛阳市人,讲师,博士,主要从事复合材料结构强度研究(E-mail: tieying@).文章编号:1000-4750(2009)08-0039-05带有六边形孔的复合材料板之孔边应力计算*李 成,郑艳萍,铁 瑛(郑州大学机械工程学院,河南,郑州 450001)摘 要:针对不同的六边形孔,采用复变函数理论中的保角变换原理,对某些算法进行一定的改进,建立一个准确的解析分析方法,从而得到含复杂孔形复合材料板孔边应力场的解析计算公式。
由于弯曲和剪切荷载对含孔复合材料构件危害较大,因此,从工程实际出发,该文以含六边形孔的复合材料板为例,采用所建立的计算模型,对其在剪切荷载、弯矩作用下的孔边应力分布,以及应力峰值进行较为全面的分析、计算。
针对相关几何参数的变化,例如长宽比的变化对孔边应力场的影响进行分析。
并对剪切荷载和弯矩对具有不同几何尺寸的六边形孔边应力场的影响进行比较。
同时对两种荷载对孔边应力场的影响也进行比较。
关键词:含孔复合材料板;六边形孔;应力峰值;保角变换;剪切荷载;弯矩 中图分类号:V214.8 文献标识码:ACALCULATION ON HOLE-EDGE STRESS OF COMPOSITE MATERIALPLATE WITH HEXAGON HOLES*LI Cheng , ZHENG Yan-ping , TIE Ying(School of Mechanical Engineering, Zhengzhou University, Zhengzhou, Henan 450001, China)Abstract: An accurate analytic method of a composite material plate with different hexagon holes is founded based on the conformal mapping of complex function theory. The analytic equations of a hole-edge stress field of a complex hole-shape are gained. Because the bending moment and shearing force can cause great harms to a composite material structure with holes, as an example of composite material plates with hexagon holes, the comprehensive analysis and calculation on the distributions and the peak values of the hole-edge stress are made by shearing load and bending moment according to the calculation model. The analysis is made for the influence of geometric parameters on the hole-edge stress field, such as the ratio of length to width. The comparison is made between the influence of shearing load and that of bending moment on the hole-edge stress field of a hexagon hole with various parameters. And so does the influence of two types of loads on the hole-edge stress field.Key words: composite material plate with hole; hexagon holes; peak value of stress; conformal mapping;shearing load; bending moment相对于含孔均质材料,含孔复合材料问题更为复杂。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
{ R } =
1 h
[Aij ]
{ E}
( 1)
A 11 A 12 A 16
[ A ij ] =
A 22 A 26
对称
A 66
h
n
Q E A ij =
Q 2
( k)
- h ij
dz
=
2
Qij ( k) ( hk - hk- 1 ),
k=1
i, j = 1, 2, 6
其中 A ij是层合板面内刚度系数; Q(ijk) 是第 k 个铺层
在国内, 王启智等 [ 6~ 8] 用近似解析方法和有限 元法推导出拉伸正交各向异性有限宽板偏心圆孔的 应力集中系数的显式表达式, 进一步采用渐近修正 方法, 得到有限域中高精度应力集中系数表达式。
收稿日期: 2008-01-19; 修订日期: 2008-05-24 作者简介: 朱 西平 ( 1957) ), 男, 教授, 主要从事复合材料 及其结构 的 力学 分 析方 面的 研 究, ( E-m ail) zxpzxp@ nwpu. edu. cn。
E1
图 1为由一层合板等效而成的单向板。对于图
1所示的简单载荷情况, U为单向板纤维方向 x c与
加载方向 x 之间的夹角, 即 ( 6) 式 中所表示的等效
单向板的偏转角。
图 1 等效偏轴单向板 F ig. 1 Equivalen t unidirectional com po site lam inate
W u和 M u[ 1] 将各向同性含孔板的应力集中因 子推广应用到正交各向异性含孔板和含孔圆柱壳, 并提出一个计算应力集中因子的经验公式。 T an[ 2] 建立了含椭圆孔正交各向异性复合材料板的近似应 力分析方法, 并推广应用到点应力破坏准则和平均 应力破坏准则, 预测含椭圆孔的纤维增强复合材料 板的强度。 R om eo[ 3] 依据 L ekhn itskii[ 4] 理论, 采用综 合变量法研究了同时承受双轴荷载和剪力的含矩形 开口的各向异性板开口附近的应变分布, 其结果与 相关实验、有 限元 数 值 模拟 相 当 吻合。 Cheng 和 M aa[ 5] 基于连续损伤力学理论, 提出一种损伤模型, 研究含孔层合板拉伸破坏强度。
纵观以前的研究工作, 对于含孔各向异性板的 应力集中问题已进行了充分的研究, 但针对含孔复 合材料层板的应力集中, 由于孔边应力计算很复杂, 目前尚未见到对此类问题的精确解析解的报道, 解 决这类问题, 大多采用数值模拟计算和实验方法, 理 论分析及计算只限于正交各向异性复合材料, 尚不 能推广到其它一般铺层情况。
的单向纤维 层板, 相当于 用材 料主 方向 弹性常 数
E 1, E 2, M12, G 12表示弹性常数 Ex, Ey, Mxy, Gxy。其偏转 角 U的计算公式如下:
1 = 1 cos4 U + 1 sin4 U+ ( 1 -
Ex E 1
E2
G 12
2M12 ) co s2 Us in2 U
( 6)
根据图 1, 孔边任意一点 B 从 x c轴算起的极角 为 H, 则 B点的应力为 [ 4] :
RH =
p
E E
H 1
{
[
-
cos2 U+
( k + n ) sin2 U] k cos2 H+
[ ( 1 + n ) cos2 U- k sin2 U] sin2 H- n( 1 +
k + n ) sinUcosUsinHco sH}
本文针对含圆孔有限大复合材料层板的应力集 中问题, 提出一种计算孔边应力分布及应力集中系 数的方法。根据所推导的计算公式, 分析讨论了板 宽 /孔径比、铺层比例、铺层方式、材料性能参数等因 素对孔边应力集中的影响。
1 含圆孔层合板应力集中系数计算公式
无限大各向异性板中圆孔周围应力问题的解已 由多位学者给出, 后来又有学者针对有限宽各向异 性板孔边应 力集中 问题, 得到 不同 的宽 度修正 公 式 [ 2, 8] 。
EH
E1
1G 12
2T12 E1
sin2 Ucos2 U+
sin4 U E2
上式为无限宽含孔层合板孔边 应力集中系数
K ] 的计算公式, 对于有限宽板, 需要加一个修正因
子。采用 T an [ 2] 给出的宽度修正公式, 即:
]
K K
=
2
3( 1- d /W ) + ( 1 - d /W
)
3
+
1 2
单向纤维层板承受偏轴载荷时, 其力学行为表 现为各向异性, 相当于各向异性板承受单轴拉伸载 荷情况。复合材料层合板厚度方向的尺寸与其它两 个方向相比要小得多。如果不考虑层合板的各个铺 层之间界面上物性有突变的局部性质, 忽略层板厚 度方向上的层间应力作用, 层合板从宏观上可看作 为均质的各向异性板, 其宏观弹性性质可以通过各 个铺层的弹性常数来确定。
第 29卷 第 2期 2009年 4月
航空材料学报
JOURNAL OF A ERONAUT ICAL MAT ER IA LS
V o l1 29, N o12 A pril 2009
含孔复合材料层合板孔边应力集中的近似计算
朱西平, 郭章新, 韩小平, 支希哲
(西北工业大学 工程力学系, 西安 710072)
( 7)
n=
2
E1 E2
T12
+
E1 G 12
k=
E1 E2
式中, EH是极角为 H且与孔边相切方向上的杨氏模
量, 且:
1 = sin4 H+
EH
E1
1G 12
2T12 E1
sin2 Hcos2 H+
cos4 H E2
( 8)
p 为单向板拉伸时远离孔边的横截面上的应力, 而
应力集中系数定义为 RH /p, 我们所关心的是最小截 面处孔边应力集中, 由图 1可知, 此时最小截面处 H
有限宽度复合材料层合 板应力集中系数的表达式, 分析讨论了板宽 /孔径比、铺 层比例、铺层方式、材料 性能参数等
因素对孔边应力集中的 影响。
关键词: 含孔复合材料层板; 各向 异性板; 孔边应力; 应力集中系数
中图分类号: TB332
文献标识码: A
文章编号: 1005-5053( 2009) 02-0071-05
根据上面给定的计算用基本参数, 采用本文方 法, 先将层合板划归为各向异性板, 再将各向异性板 等效为一偏轴拉伸的单向纤维板。经过计算, 得到 等效单 向板的偏转角 为 U= 4121b, 在最 小截面处 H= 90b+ U, 根据公式 ( 8) 计算出相关参数 n, k 以及 EH值, 即: n = 5187, k = 3171, EH = 67173G Pa。
摘要: 针对含圆孔 有限大复合材料层板的应力集中问题, 提出一种计算 孔边应力分布及应力集中系数的方法: 先利
用经典层板理论, 将复合材料层合板化归为各向异性板; 再将各向异性板等效转换为 一偏轴拉伸 的单向纤维 层板;
最后利用含圆孔偏轴单向板的孔 边应力计算公式来分析 一般铺 层层合 板孔边应 力集中 情况。根据 所推导 的含孔
A26 =
A 22 A 26
A66
对称
A 66
A22
=
A 11A 66
-
A
2 16
$
A66
=
A 11A 22
-
A
2 12
$
A16
=
A 12A 26
- A 22A 16 $
A26
=
A 12A 16
- A 11A 26 $
$=
A 11A 22A 66 +
2A 12A 16A 26
-
A
22A
2 16
-
A
11A
工程实际中, 复合材料的应用日益增多, 由于结 构装配或功能方面的需求, 常常需要在复合材料层 板上打孔或开口。对于开口结构来说, 特别突出的 一个问题是孔边区域的应力集中, 在载荷作用下, 孔 口附近会产生分层开裂损伤, 这些内部分层难以发 现, 对结构是一大潜在威胁, 它可能会对复合材料结 构的承载能力、使用寿命产生严重影响, 因此, 国内 外许多学者进行了研究。
Wd M
6
#
(K ] - 3) 1 - WdM 2
( 10)
M2 =
1-
Байду номын сангаас
8
[
2
3 +
(
1 - d /W ) ( 1 - d /W
)
3
-
1]
-
1
2( d /W ) 2
其中 M 是放大因子。
这样利用上述一系列公式, 就可得到有限宽含
孔层合板孔边应力集中系数 K。
2 算例分析和近似计算公式的考核
考虑一含圆孔复合材料层板, 铺层为 ( 45/ 02 / -
图 2 孔径 /板宽比 对孔边应力集中影响 F ig12 Effect of the ra tio of ho le d iam e ter to
p late w idth on SCF
可以看出本文公式解与有限元解很好吻合 ( 最 大偏差约 10% ) 。孔径 /板宽比对 孔边应力集中影 响很大, 随 着 d /w 的增大, 应力 集中系数增大。而 当 d /w = 0125时, 其结果与无限大板的精确值基本 一致, 因此, 当板宽 /孔径比值 w /d\ 4时, 就可以认 为是小孔洞情况, 近似按无限大板处理。
-
1 G 12
)
co
s3
Us inU-
(E22 +
