中考数学一轮复习 考点跟踪训练39 几何应用性问题 浙教版
浙教版中考数学第一轮复习图形的性质(二)好题精选

绝密★启用前浙教版2019中考数学第一轮复习图形的性质(二)四边形好题精选题号一二三总分得分注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上第Ⅰ卷(选择题)请点击修改第I卷的文字说明评卷人得分一.选择题(共15小题)1.如图,在平行四边形ABCD中,对角线AC、BD相交成的锐角α=30°,若AC=8,BD=6,则平行四边形ABCD的面积是()A.6 B.8 C.10 D.122.如图,小明从A点出发,沿直线前进12米后向左转36°,再沿直线前进12米,又向左转36°…照这样走下去,他第一次回到出发地A点时,一共走了()米.A.100 B.120 C.140 D.603.如图,在▱ABCD中,AB⊥AC,若AB=4,AC=6,则BD的长是()A.8 B.9 C.10 D.114.如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F 是CD的中点,则EF的最大值为()A.B.4 C.5 D.5.如图,▱ABCD,BE:AE=4:1.若△AEF的面积为2cm2,则△ADF的面积为()cm2A.8 B.10 C.18 D.326.正方形ABCD在直角坐标系中的位置如图表示,将正方形ABCD绕点A顺时针方向旋转180°后,B点的坐标是()A.(2,0)B.C.(2,﹣1)D.(2,1)7.如图,有两个正方形A,B,现将B放置在A的内部得到图甲.将A,B并列放置,以正方形A与正方形B的边长之和为新的边长构造正方形得到图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的面积之和为()A.13 B.14 C.15 D.168.将矩形OABC如图放置,O为原点,若点A的坐标是(﹣1,2),点B的坐标是(2,),则点C的坐标是()A.(4,2)B.(2,4)C.(,3)D.(3,)9.如图所示,将长方形ABCD分成15个大小相等的小正方形,E、F、G、H分别在AD、AB、BC、CD边上,且是某个小正方形的顶点.若四边形EFGH的面积为3,则长方形ABCD的面积为()A.5 B.6 C.7 D.810.顺次连接一个四边形四边中点得到的图形是菱形,则这个四边形满足()A.菱形B.矩形C.正方形D.对角线相等11.某小区有一块边长为a的正方形场地,规划修建两条宽为b的绿化带.方案一如图甲所示,绿化带面积为S甲;方案二如图乙所示,绿化带面积为S乙.设k=(a>b>0),下列选项中正确的是()A.B.C.D.12.如图,矩形ABCD中,AB=8,BC=6,对角线AC,BD交于点O,过点O作OG⊥AB于点G.延长AB至E,使BE=AB,连接OE交BC于点F,则BF的长为()A.B.1 C.D.213.如图,在菱形ABCD中,∠A=60°,AD=4,点P是AB边上的一个动点,点E、F分别是DP、BP的中点,则线段EF的长为()A.2 B.4 C.2D.214.如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都是1,正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积为()A.B.C.3 D.515.正方形ABCD中,点E、F分别在CD、BC边上,△AEF是等边三角形.以下结论:①EC=FC;②∠AED=75°;③AF=CE;④EF的垂直平分线是直线AC.正确结论个数有()个.A.1 B.2 C.3 D.4第Ⅱ卷(非选择题)请点击修改第Ⅱ卷的文字说明评卷人得分二.填空题(共10小题)16.在▱ABCD中,AE平分∠BAD交边BC于E,DF⊥AE,交边BC于F,若AD=10,EF=4,则AB=.17.将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=30°,那么∠1+∠2=°.18.如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去第n个正方形的边长为.19.边长为a的菱形是由边长为a的正方形“形变”得到的,若这个菱形一组对边之间的距离为h,则称为为这个菱形的“形变度”.(1)一个“形变度”为2的菱形与其“形变”前的正方形的面积之比为.(2)如图,A、B、C为菱形网格(每个小菱形的边长为1,“形变度”为)中的格点,则△ABC 的面积为.20.如图,已知正六边形ABCDEF,则∠ADF=度.21.如图,E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC、GA、GF,已知AG⊥GF,AC=2,则AB的长为.22.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G,连接DG.点E从点C运动到点D的过程中,DG的最小值为.23.如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AE,延长EF交边BC于点G,连结AG,CF,则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤S△FGC=;其中正确的结论有.24.如图,菱形ABCD和菱形BEFG的边长分别是5和2,∠A=60°,连结DF,则DF的长为.25.如图,边长为1的正△ABO的顶点O在原点,点B在x轴负半轴上,正方形OEDC边长为2,点C在y轴正半轴上,动点P从点A出发,以每秒1个单位的速度沿着△ABO的边按逆时针方向运动,动点Q从D点出发,以每秒1个单位的速度沿着正方形OEDC的边也按逆时针方向运动,点Q比点P迟1秒出发,则点P运动2016秒后,则PQ2的值是.评卷人得分三.解答题(共15小题)26.如图,矩形ABCD的对角线AC,BD交于点O,以OC,OD为邻边作平行四边形OCED,连接OE.(1)求证:四边形OBCE是平行四边形;(2)连接BE交AC于点F.若AB=2,∠AOB=60°,求BF的长.27.如图,在四边形ABCD中,E、F分别为对角线BD上的两点,且BE=DF.(1)若四边形AECF是平行四边形,求证:四边形ABCD是平行四边形;(2)若四边形AECF是菱形,则四边形ABCD是菱形吗?请说明理由?(3)若四边形AECF是矩形,则四边形ABCD是矩形吗?不必写出理由.28.如图1,△ABD和△BDC都是边长为1的等边三角形.(1)四边形ABCD是菱形吗?为什么?(2)如图2,将△BDC沿射线BD方向平移到△B1D1C1的位置,则四边形ABC1D1是平行四边形吗?为什么?(3)在△BDC移动过程中,四边形ABC1D1有可能是矩形吗?如果是,请求出点B移动的距离(写出过程);如果不是,请说明理由(图3供操作时使用).29.“三等分一个角”是数学史上一个著名问题.今天人们已经知道,仅用圆规和直尺是不可能作出的,在探索中,有人曾利用过如下的图形:其中,ABCD是长方形,F是DA延长线上一点,G是CF上一点,并且∠ACG=∠AGC,∠GAF=∠GF A,你能证明∠ECB=∠ACB吗?30.如图,在矩形ABCD中,AB=6,BC=8,动点P在边AD上以每秒2个单位的速度从A出发,沿AD向D运动,同时动点Q在边BD上以每秒5个单位的速度从D出发,沿DB向B运动,当其中有一个点到达终点时,另一个点也随之停止运动.设运动时间为t秒.(1)填空:当某一时刻t,使得t=1时,P、Q两点间的距离PQ=;(2)是否存在以P、D、Q中一点为圆心的圆恰好过另外两个点?若存在求出此时t的值;若不存在,请说明理由.31.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC,且DE=AC,连接CE、OE,连接AE交OD于点F.(1)求证:OE=CD;(2)若菱形ABCD的边长为8,∠ABC=60°,求AE的长.32.【问题】用n边形的对角线把n边形分割成(n﹣2)个三角形,共有多少种不同的分割方案(n ≥4)?【探究】为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进转化,最后猜想得出结论.不妨假设n边形的分割方案有P n种.探究一:用四边形的对角线把四边形分割成2个三角形,共有多少种不同的分割方案?如图①,图②,显然,只有2种不同的分割方案.所以,P4=2.探究二:用五边形的对角线把五边形分割成3个三角形,共有多少种不同的分割方案?不妨把分割方案分成三类:第1类:如图③,用A,E与B连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案,所以,此类共有P4种不同的分割方案.第2类:如图④,用A,E与C连接,把五边形分割成3个三角形,有1种不同的分割方案,可视为种分割方案.第3类:如图⑤,用A,E与D连接,先把五边形分割转化成1个三角形和1个四边形,再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案,所以,此类共有P4种不同的分割方案.所以,P5=P4++P4==5(种)探究三:用六边形的对角线把六边形分割成4个三角形,共有多少种不同的分割方案?不妨把分割方案分成四类:第1类:如图⑥,用A,F与B连接,先把六边形分割转化成1个三角形和1个五边形,再把五边形分割成3个三角形,由探究二知,有P5种不同的分割方案.所以,此类共有P5种不同的分割方案.第2类:如图⑦,用A,F与C连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案.所以,此类共有P4种分割方案第3类:如图⑧,用A,F与D连接,先把六边形分割转化成2个三角形和1个四边形.再把四边形分割成2个三角形,由探究一知,有P4种不同的分割方案.所以,此类共有P4种分割方案.第4类:如图⑨,用A,F与E连接,先把六边形分割转化成1个三角形和1个五边形.再把五边形分割成3个三角形,由探究二知,有P5种不同的分割方案.所以,此类共有P5种分割方案.所以,P6=P5+P4+P4+P5=P5+=14(种)探究四:用七边形的对角线把七边形分割成5个三角形,则P7与P6的关系为:P7=P6,共有种不同的分割方案.……【结论】用n边形的对角线把n边形分割成(n﹣2)个三角形,共有多少种不同的分割方案(n≥4)?(直接写出P n与P n﹣1的关系式,不写解答过程).【应用】用八边形的对角线把八边形分割成6个三角形,共有多少种不同的分割方案?(应用上述结论,写出解答过程)33.如图,A,B,C,D为矩形的四个顶点,AB=4cm,AD=2cm,动点P、Q分别从点A,C同时出发,都以1cm/s的速度运动,其中点P由A运动到B停止,点Q由点C运动到点D停止.(1)求四边形PBCQ的面积;(2)P、Q两点从出发开始到几秒时,点P、Q、D组成的三角形是等腰三角形?34.解决问题(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD.求证:EF=BE+FD.小明想到条件∠EAF=∠BAD应用需要转化,将△ADF绕顶点A旋转到△ABG处,此时△ABG≌△ADF,把线段BE、FD集中到一起,进一步可以再证明EF=EG=BE+FD.证明:(1)延长EB到G,使BG=DF,连接AG.∵∠ABG=∠ABC=∠D=90°,AB=AD∴△ABG≌△ADF.小明没有证明结束,请你补齐证明过程.基本运用:请你用第(1)题的解答问题的思想方法,解答下面的问题(2)已知如图2,△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点,且∠EAF=45°,求证:EF2=BE2+CF2;拓展延伸(3)已知如图3,等边△ABC内有一点P,AP=8,BP=15,AP=17,求∠APB的度数.35.如图,在平面直角坐标系中,点A的坐标为(5,0),点B的坐标为(8,4),点C的坐标为(3,4),连接AB、BC、OC(1)求证四边形OABC是菱形;(2)直线l过点C且与y轴平行,将直线l沿x轴正方向平移,平移后的直线交x轴于点P.①当OP:P A=3:2时,求点P的坐标;②点Q在直线1上,在直线l平移过程中,当△COQ是等腰直角三角形时,请直接写出点Q的坐标.36.如图,在△ABC中,∠C=90°,AC=BC,AB=8.点P从点A出发,以每秒2个单位长度的速度沿边AB向点B运动.过点P作PD⊥AB交折线AC﹣CB于点D,以PD为边在PD右侧做正方形PDEF.设正方形PDEF与△ABC重叠部分图形的面积为S,点P的运动时间为t秒(0<t<4).(1)当点D在边AC上时,正方形PDEF的边长为(用含t的代数式表示).(2)当点E落在边BC上时,求t的值.(3)当点D在边AC上时,求S与t之间的函数关系式.(4)作射线PE交边BC于点G,连结DF.当DF=4EG时,直接写出t的值.37.如图,以长方形OBCD的顶点O为坐标原点建立平面直角坐标系,B点坐标为(0,a),C点坐标为(c,b),且a、b、C满足+|2b+12|+(c﹣4)2=0.(1)求B、C两点的坐标;(2)动点P从点O出发,沿O→B→C的路线以每秒2个单位长度的速度匀速运动,设点P的运动时间为t秒,DC上有一点M(4,﹣3),用含t的式子表示三角形OPM的面积;(3)当t为何值时,三角形OPM的面积是长方形OBCD面积的?直接写出此时点P的坐标.38.在菱形ABCD中,∠ADC=60°,BD是一条对角线,点P在边CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,在BD上取一点H,使HQ=HD,连接HQ,AH,PH.(1)依题意补全图1;(2)判断AH与PH的数量关系及∠AHP的度数,并加以证明;(3)若∠AHQ=141°,菱形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)39.如图,在矩形ABCD中,AB=3,BC=4,将对角线AC绕对角线交点O旋转,分别交边AD、BC于点E、F,点P是边DC上的一个动点,且保持DP=AE,连接PE、PF,设AE=x(0<x<3).(1)填空:PC=,FC=;(用含x的代数式表示)(2)求△PEF面积的最小值;(3)在运动过程中,PE⊥PF是否成立?若成立,求出x的值;若不成立,请说明理由.40.如图(1),在Rt△ABC,∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG和正方形BCED,连接AD、CF,AD与CF交于点M.(1)求证:△ABD≌△FBC;(2)如图(2),已知AD=8,求四边形AFDC的面积;(3)在△ABC中,设BC=a,AC=b,AB=c,当∠ACB≠90°时,c2≠a2+b2.在任意△ABC中,c2=a2+b2+k.就a=5,b=4的情形,探究出k的取值范围.参考答案与试题解析一.选择题(共15小题)1.如图,在平行四边形ABCD中,对角线AC、BD相交成的锐角α=30°,若AC=8,BD=6,则平行四边形ABCD的面积是()A.6 B.8 C.10 D.12【分析】先过点D作DE⊥AC于点E,由在▱ABCD中,AC=8,BD=6,可求得OD的长,又由对角线AC、BD相交成的锐角α为30°,求得DE的长,△ACD的面积,则可求得答案.【解答】解:过点D作DE⊥AC于点E,∵在▱ABCD中,AC=8,BD=6,∴OD=BD=3,∵∠α=30°,∴DE=OD•sin∠α=3×=1.5,∴S△ACD=AC•DE=×8×1.5=6,∴S▱ABCD=2S△ACD=12.故选:D.【点评】此题考查了平行四边形的性质以及三角函数的知识.注意准确作出辅助线是解此题的关键.2.如图,小明从A点出发,沿直线前进12米后向左转36°,再沿直线前进12米,又向左转36°…照这样走下去,他第一次回到出发地A点时,一共走了()米.A.100 B.120 C.140 D.60【分析】根据多边形的外角和为360°,由题意得到小明运动的轨迹为正10边形的周长,求出即可.【解答】解:由题意得:360°÷36°=10,则他第一次回到出发地A点时,一共走了12×10=120(米).故选:B.【点评】此题考查了多边形的内角与外角,熟练掌握多边形的外角和定理是解本题的关键.3.如图,在▱ABCD中,AB⊥AC,若AB=4,AC=6,则BD的长是()A.8 B.9 C.10 D.11【分析】直接利用平行四边形的性质得出AO的长,再利用勾股定理得出BO的长,进而得出答案.【解答】解:∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,∵AB⊥AC,AB=4,AC=6,∴AO=3,则BO==5,∴BD=2BO=10.故选:C.【点评】此题主要考查了平行四边形的性质以及勾股定理,正确得出BO的长是解题关键.4.如图,在矩形ABCD中,AB=3,AD=4,以BC为斜边在矩形的外部作直角三角形BEC,点F 是CD的中点,则EF的最大值为()A.B.4 C.5 D.【分析】取BC中点O,连接OE,OF,根据矩形的性质可求OC,CF的长,根据勾股定理可求OF 的长,根据直角三角形的性质可求OE的长,根据三角形三边关系可求得当点O,点E,点F共线时,EF有最大值,即EF=OE+OF.【解答】解:如图,取BC中点O,连接OE,OF,∵四边形ABCD是矩形∴AB=CD=3,AD=BC=4,∠C=90°∵点F是CD中点,点O是BC的中点∴CF=,CO=2∴OF==∵点O是Rt△BCE的斜边BC的中点∴OE=OC=2∵根据三角形三边关系可得:OE+OF≥EF∴当点O,点E,点F共线时,EF最大值为OE+OF=2+=故选:D.【点评】本题考查了矩形的性质,三角形三边关系,勾股定理,直角三角形的性质,找到当点O,点E,点F共线时,EF有最大值是本题的关键.5.如图,▱ABCD,BE:AE=4:1.若△AEF的面积为2cm2,则△ADF的面积为()cm2A.8 B.10 C.18 D.32【分析】证明△DFC∽△EF A,得,根据已知得==,所以=5,由同高三角形面积的比等于对应底边的比,可得结论.【解答】解:∵四边形ABCD是平行四边形,∴CD∥AB,AB=CD,∴△DFC∽△EF A,∴,∵BE:AE=4:1,∴==,∴=5,∴=5,∵△AEF的面积为2cm2,∴△ADF的面积为10cm2,故选:B.【点评】此题主要考查了平行四边形的性质以及相似三角形的判定与性质,熟练掌握相似三角形的判定和性质是解题关键.6.正方形ABCD在直角坐标系中的位置如图表示,将正方形ABCD绕点A顺时针方向旋转180°后,B点的坐标是()A.(2,0)B.C.(2,﹣1)D.(2,1)【分析】依据题意画出图形,然后依据旋转的性质确定出点B′的坐标即可.【解答】解:如图所示:过点B′作B′E⊥x轴,垂足为E.由旋转的性质可知:OA=AE=1,OB=BE′=1,∴点B′的租表为(2,﹣1).∴旋转后B点的坐标是(2,﹣1).故选:C.【点评】本题主要考查的是旋转的性质,熟练掌握旋转的性质是解题的关键.7.如图,有两个正方形A,B,现将B放置在A的内部得到图甲.将A,B并列放置,以正方形A与正方形B的边长之和为新的边长构造正方形得到图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的面积之和为()A.13 B.14 C.15 D.16【分析】设正方形A的边长为a,正方形B的边长为b,由图形得出关系式求解即可.【解答】解:设正方形A的边长为a,正方形B的边长为b,由图甲得a2﹣b2﹣2(a﹣b)b=1即a2+b2﹣2ab=1,由图乙得(a+b)2﹣a2﹣b2=12,2ab=12,所以a2+b2=13,故选:A.【点评】本题主要考查了正方形的性质,完全平方公式的几何背景,解题的关键是根据图形得出数量关系.8.将矩形OABC如图放置,O为原点,若点A的坐标是(﹣1,2),点B的坐标是(2,),则点C的坐标是()A.(4,2)B.(2,4)C.(,3)D.(3,)【分析】首先构造直角三角形,利用相似三角形的判定与性质以及结合全等三角形的判定与性质得出CM=,MO=3,进而得出答案.【解答】解:如图:过点A作AE⊥x轴于点E,过点B作BF⊥⊥x轴于点F,过点A作AN⊥BF于点N,过点C作CM⊥x轴于点M,∵∠EAO+∠AOE=90°,∠AOE+∠MOC=90°,∴∠EAO=∠COM,又∵∠AEO=∠CMO,∴∠AEO∽△COM,∴==,∵∠BAN+∠OAN=90°,∠EAO+∠OAN=90°,∴∠BAN=∠EAO=∠COM,在△ABN和△OCM中,∴△ABN≌△OCM(AAS),∴BN=CM,∵点A(﹣1,2),点B的纵坐标是,∴BN=,∴CM=,∴MO=3,∴点C的坐标是:(3,).故选:D.【点评】本题主要考查了矩形的性质以及相似三角形的判定与性质以及结合全等三角形的判定与性质等知识,正确得出CM的长是解题关键.9.如图所示,将长方形ABCD分成15个大小相等的小正方形,E、F、G、H分别在AD、AB、BC、CD边上,且是某个小正方形的顶点.若四边形EFGH的面积为3,则长方形ABCD的面积为()A.5 B.6 C.7 D.8【分析】设小正方形的边长a,那么矩形的面积=(S△AEF+S△BFG)×2+S四边形EFGH.【解答】解:设小正方形的边长a,那么矩形的面积=(S△AEF+S△BFG)×2+S四边形EFGH,即:3a×5a=(2a×a÷2+a×4a÷2)×2+1,9a2=3,则a=(a>0),故矩形的面积=3a×5a=5.故选:A.【点评】此题主要考查了三角形面积求法,本题从矩形的面积表示方法入手进行计算是解题关键.10.顺次连接一个四边形四边中点得到的图形是菱形,则这个四边形满足()A.菱形B.矩形C.正方形D.对角线相等【分析】根据三角形的中位线定理和菱形的判定定理解答.【解答】解:当四边形对角线相等时,顺次连接这个四边形四边中点得到的图形是菱形,∵E,F,G,H分别为矩形各边的中点,∴EH=BD,EH∥BD,FG=BD,FG∥BD,EF=AC,∴EH=FG,EH∥FG,∴四边形EFGH是平行四边形,当AC=BD时,EF=EH,∴平行四边形EFGH是菱形,故选:D.【点评】本题考查的是菱形的判定、矩形的性质,掌握三角形的中位线定理和矩形的性质定理是解题关键.11.某小区有一块边长为a的正方形场地,规划修建两条宽为b的绿化带.方案一如图甲所示,绿化带面积为S甲;方案二如图乙所示,绿化带面积为S乙.设k=(a>b>0),下列选项中正确的是()A.B.C.D.【分析】由题意可求S甲=2ab﹣b2,S乙=2ab,代入可求k的取值范围.【解答】解:∵S甲=2ab﹣b2,S乙=2ab.∴k===1﹣∵a>b>0∴<k<1故选:B.【点评】本题考查了正方形的性质,能用代数式正确表示阴影部分面积是本题的关键.12.如图,矩形ABCD中,AB=8,BC=6,对角线AC,BD交于点O,过点O作OG⊥AB于点G.延长AB至E,使BE=AB,连接OE交BC于点F,则BF的长为()A.B.1 C.D.2【分析】由OG∥BC可知即可求解.【解答】解:∵OG∥BC,∴,其中:OG=BC=3,BE=AB=2,GE=BG+BE=6解得:BF=1,故选:B.【点评】本题考查的是矩形性质,涉及到平行线分线段成比例,是一道基本题.13.如图,在菱形ABCD中,∠A=60°,AD=4,点P是AB边上的一个动点,点E、F分别是DP、BP的中点,则线段EF的长为()A.2 B.4 C.2D.2【分析】如图连接BD.首先证明△ADB是等边三角形,可得BD=4,再根据三角形的中位线定理即可解决问题.【解答】解:如图连接BD.∵四边形ABCD是菱形,∴AD=AB=4,∵∠A=60°,∴△ABD是等边三角形,∴BA=AD=4,∵PE=ED,PF=FB,∴EF=BD=2.故选:A.【点评】本题考查菱形的性质、三角形的中位线定理、等边三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,本题的突破点是证明△ADB是等边三角形.14.如图,已知直线l1∥l2∥l3∥l4,相邻两条平行线间的距离都是1,正方形ABCD的四个顶点分别在四条直线上,则正方形ABCD的面积为()A.B.C.3 D.5【分析】过D点作直线EF与平行线垂直,与l1交于点E,与l4交于点F.易证△ADE≌△DFC,得CF=1,DF=2.根据勾股定理可求CD2得正方形的面积.【解答】解:作EF⊥l2,交l1于E点,交l4于F点.∵l1∥l2∥l3∥l4,EF⊥l2,∴EF⊥l1,EF⊥l4,即∠AED=∠DFC=90°.∵ABCD为正方形,∴∠ADC=90°.∴∠ADE+∠CDF=90°.又∵∠ADE+∠DAE=90°,∴∠CDF=∠DAE.在△ADE和△DCF中∴△ADE≌△DCF(AAS),∴CF=DE=1.∵DF=2,∴CD2=12+22=5,即正方形ABCD的面积为5.故选:D.【点评】此题主要考查了正方形的性质和面积计算,根据平行线之间的距离构造全等的直角三角形是关键.15.正方形ABCD中,点E、F分别在CD、BC边上,△AEF是等边三角形.以下结论:①EC=FC;②∠AED=75°;③AF=CE;④EF的垂直平分线是直线AC.正确结论个数有()个.A.1 B.2 C.3 D.4【分析】由题意可证△ABF≌△ADE,可得BF=DE,即可得EC=CF,由勾股定理可得EF=EC,由平角定义可求∠AED=75°,由AE=AF,EC=FC可证AC垂直平分EF,则可判断各命题是否正确.【解答】解:∵四边形ABCD是正方形,∴AB=AD=BC=CD,∠B=∠C=∠D=∠DAB=90°∵△AEF是等边三角形∴AE=AF=EF,∠EAF=∠AEF=60°∵AD=AB,AF=AE∴△ABF≌△ADE∴BF=DE∴BC﹣BF=CD﹣DE∴CE=CF故①正确∵CE=CF,∠C=90°∴EF=CE,∠CEF=45°∴AF=CE,∵∠AED=180°﹣∠CEF﹣∠AEF∴∠AED=75°故②③正确∵AE=AF,CE=CF∴AC垂直平分EF故④正确故选:D.【点评】本题考查了正方形的性质,全等三角形的性质和判定,等边三角形的性质,线段垂直平分线的判定,熟练运用这些性质和判定解决问题是本题的关键.二.填空题(共10小题)16.在▱ABCD中,AE平分∠BAD交边BC于E,DF⊥AE,交边BC于F,若AD=10,EF=4,则AB=7或3.【分析】根据平行线的性质得到∠ADF=∠DFC,根据角平分线的定义得到∠BAE=∠DAE,推出AB =BE,根据已知条件推出∠ADF=∠ADC,得到∠ADF=∠CDF,推出CF=CD,于是得到结论.【解答】解:①如图1,在▱ABCD中,∵BC=AD=10,BC∥AD,CD=AB,CD∥AB,∴∠DAE=∠AEB,∠ADF=∠DFC,∵AE平分∠BAD交BC于点E,∴∠BAE=∠DAE,∴∠BAE=∠AEB,∴AB=BE,∵DF⊥AE,∴∠DAE+∠ADF=90°,∵∠BAD+∠ADC=180°,∴∠ADF=∠ADC,∴∠ADF=∠CDF,∵∠ADF=∠DFC,∴∠DFC=∠CDF,∴CF=CD,∴AB=BE=CF=CD∵EF=4,∴BC=BE+CF﹣EF=2AB﹣EF=2AB﹣4=10,∴AB=7;②在▱ABCD中,∵BC=AD=10,BC∥AD,CD=AB,CD∥AB,∴∠DAE=∠AEB,∠ADF=∠DFC,∵AE平分∠BAD交BC于点E,∴∠BAE=∠DAE,∴∠BAE=∠AEB,∴AB=BE,∵DF⊥AE,∴∠DAE+∠ADF=90°,∵∠BAD+∠ADC=180°,∴∠ADF=∠ADC,∴∠ADF=∠CDF,∵∠ADF=∠DFC,∴∠DFC=∠CDF,∴CF=CD,∴AB=BE=CF=CD∵EF=5,∴BC=BE+CF=2AB+EF=2AB+4=10,∴AB=3;综上所述:AB的长为7或3.故答案为:7或3.【点评】本题考查了等腰三角形的判定和性质,平行线的性质,平行四边形的性质,解答本题的关键是判断出AB=BE=CF=CD.17.将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=30°,那么∠1+∠2=72°.【分析】分别根据正三角形、正四边形、正五边形各内角的度数及平角的定义进行解答即可.【解答】解:如图,∵∠3=30°,正三角形的内角是60°,正四边形的内角是90°,正五边形的内角是108°,∴∠4=180°﹣60°﹣30°=90°,∴∠5+∠6=180°﹣80°=90°,∴∠5=180°﹣∠2﹣108°①,∠6=180°﹣90°﹣∠1=90°﹣∠1 ②,∴①+②得,180°﹣∠2﹣108°+90°﹣∠1=90°,即∠1+∠2=72°.故答案为:72.【点评】本题考查的是三角形内角和定理,熟知正三角形、正四边形、正五边形各内角的度数是解答此题的关键.18.如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此下去第n个正方形的边长为()n﹣1..【分析】首先求出AC、AE、AG的长度,然后猜测命题中隐含的数学规律,即可解决问题;【解答】解:∵四边形ABCD为正方形,∴AB=BC=1,∠B=90°,∴AC2=12+12,AC=同理可得:AE=()2,AG=()3…,∴第n个正方形的边长a n=()n﹣1.故答案为()n﹣1.【点评】此题主要考查了正方形的性质、勾股定理及其应用问题;应牢固掌握正方形有关定理并能灵活运用.19.边长为a的菱形是由边长为a的正方形“形变”得到的,若这个菱形一组对边之间的距离为h,则称为为这个菱形的“形变度”.(1)一个“形变度”为2的菱形与其“形变”前的正方形的面积之比为1:2.(2)如图,A、B、C为菱形网格(每个小菱形的边长为1,“形变度”为)中的格点,则△ABC 的面积为.【分析】(1)分别表示出正方形的面积和菱形的面积,再根据“形变度”为2,即可得到菱形与其“形变”前的正方形的面积之比;(2)根据两面积之比=菱形的“形变度”,即可解答.【解答】解:(1)∵边长为a的正方形面积=a2,边长为a的菱形面积=ah,∴菱形面积:正方形面积=ah:a2=h:a,∵菱形的变形度为2,即=2,∴“形变度”为2的菱形与其“形变”前的正方形的面积之比=1:2,故答案为:1:2;(2)∵菱形的边长为1,“形变度”为,∴菱形形变前的面积与形变后的面积之比为,∴S△ABC=(36﹣)×=故答案为:.【点评】本题考查了正方形的性质,菱形的性质,根据题意得出菱形形变前的面积与形变后的面积之比是解题关键.20.如图,已知正六边形ABCDEF,则∠ADF=30度.【分析】连接OF,由多边形是正六边形可求出∠AOF的度数,再根据圆周角定理即可求出∠ADF的度数.【解答】解:由题意知:AD是正六边形的外接圆的半径,找到AD的中点O,连接OF,∵六边形ABCDEF是正六边形,∴∠AOF==60°,∴∠ADF=∠AOF=×60°=30°.故答案为:30°.【点评】本题考查的是正多边形和圆及圆周角定理,根据题意作出辅助线构造出圆心角是解答此题的关键.21.如图,E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,连接AC、HE、EC、GA、GF,已知AG⊥GF,AC=2,则AB的长为2.【分析】如图,连接BD.由△ADG∽△GCF,设CF=BF=a,CG=DG=b,可得=,推出=,可得b=a,在Rt△GCF中,利用勾股定理求出b,即可解决问题;【解答】解:如图,连接BD.∵四边形ABCD是矩形,∴∠ADC=∠DCB=90°,AC=BD=2,∵CG=DG,CF=FB,∴GF=BD=,∵AG⊥FG,∴∠AGF=90°,∴∠DAG+∠AGD=90°,∠AGD+∠CGF=90°,∴∠DAG=∠CGF,∴△ADG∽△GCF,设CF=BF=a,CG=DG=b,∴=,∴=,∴b2=2a2,∵a>0.b>0,∴b=a,在Rt△GCF中,3a2=3,∴a=1,∴AB=2b=2.故答案为2.【点评】本题考查三角形中位线定理、矩形的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.22.如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G,连接DG.点E从点C运动到点D的过程中,DG的最小值为.【分析】首先证明∠CGB=90°,推出点G的运动轨迹是以BC为直径的⊙O,当O,G,D共线时,DG的值最小;【解答】解:如图,∵四边形ABCD是正方形,∴BC=CD,∠BCE=∠CDF=90°,∵CE=DF,∴△BCE≌△CDF(SAS),∴∠EBC=∠FCD,∵∠FCD+∠BCG=90°,∴∠CBE+∠BCG=90°,∴∠CGB=90°,∴点G的运动轨迹是以BC为直径的⊙O,当O,G,D共线时,DG的值最小,最小值=﹣=,故答案为.【点评】本题考查正方形的性质、全等三角形的判定和性质、三角形的三边关系等知识,解题的关键是确定出DG最小时点G的位置,也是本题的难点.23.如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AE,延长EF交边BC于点G,连结AG,CF,则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤S△FGC=;其中正确的结论有①②③④⑤.。
浙江省中考数学一轮复习 专题练习3 图形的变换(1) 浙教版-浙教版初中九年级全册数学试题
图形的变换(1)班级某某学号一、选择题1.下列图形中可以作为一个三棱柱的展开图的是()A. B. C. D.2.下列四个立体图形中,左视图为矩形的是()A.①③ B.①④ C.②③ D.③④3.如图所示,该几何体的俯视图是( )开图,其中的六个正方形内分别标有数字“0”、“1”、“2”、“5”和汉字、“数”、“学”,将其围成一个正方体后,则与“5”相对的是()A. 0 B. 2 C.数 D.学ABCD中AB=16,如图所示裁出一扇形ABE,将扇形围成一个圆锥(AB和AE重合),则此圆锥的底面半径为()6.如图所示,将正方形纸片三次对折后,沿图中AB线剪掉一个等腰直角三角形,展开铺平得到的图形是()A.B.C.D.7.在下列图形中(每个小四边形皆为全等的正方形),可以是一个正方体表面展开的是()(A)(B)(C)(D)8.在下面的网格图中,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B,C两点的坐标分别为(﹣1,﹣1),(1,﹣2),将△ABC绕点C顺时针旋转90°,则点A的对应点的坐标为()A.(4,1) B.(4,﹣1) C.(5,1) D.(5,﹣1)9.如图,△ABC,△EFG均是边长为2的等边三角形,点D是边BC、EF的中点,直线AG、FC相交于点M.当△EFG绕点D旋转时,线段BM长的最小值是()10.在△ABC 中,已知AB =2a ,∠A =30°,CD 是AB 边的中线,若将△ABC 沿CD 对折起来,折叠后两个小△ACD 与△BCD 重叠部分的面积恰好等于折叠前△ABC 的面积的14,有如下结论: ①AC 边的长可以等于a ; ②折叠前的△ABC 的面积可以等于23a ; ③折叠后,以A 、B 为端点的线段AB 与中线CD 平行且相等。
其中,正确结论的个数是( )A. 0个B. 1个C. 2个D. 3个 二.填空题11.如图是一个长方体的三视图(单位:cm ),根据图中数据计算这个长方体的体积是cm 3.60cm 2,母线长10cm ,则圆锥的高是cm .13.如图,在平面直角坐标系中,点A 的坐标为(0,6),将△OAB 沿x 轴向左平移得到△O ′A ′B ′,点A 的对应点A ′落在直线y =﹣x 上,则点B 与其对应点B ′间的距离为.14.如图,在Rt △ABC 中,∠ACB =90°,点D 在AB 边上,将△CBD 沿CD 折叠,使点B 恰好落在AC 边上的点E 处.若∠A =26°,则∠CDE =.题第1815.如图,将一X 边长为6cm 的正方形纸片按虚线裁剪后,恰好围成底面是正六边形的棱柱,则这个六棱柱的侧面积为cm 2.16.在▱ABCD 中,AB <BC ,已知∠B =30°,AB =2,将△ABC 沿AC 翻折至△AB ′C ,使点B ′落在▱ABCD所在的平面内,连接B ′D.若△AB ′D 是直角三角形,则BC 的长为.17.如图,在等边△ABC 内有一点D ,AD =5,BD =6,CD =4,将△ABD 绕A 点逆时针旋转,使AB 与AC 重合,点D 旋转至点E ,则∠CDE 的正切值为.18.如图,四边形ABCD 是矩形纸片, 2=AB .对折矩形纸片ABCD ,使AD 与BC重合,折痕为EF ;展平后再过点B 折叠矩形纸片,使点A 落在EF 上的点N ,折痕BM 与EF 相交于点Q ;再次展平,连接BN ,,延长MN 交BC 于点G .有如下结论:①︒=∠60ABN ; ②1=AM ; ③33=QN ; ④△BMG 是等边三角形; ⑤P 为线段BM 上一动点,H 是BN 的中点,则PH PN +的最小值是3.其中正确结论的序号是. 三.解答题AB Cl19.如图,在边长为1个单位长度的小正方形格中,给出了△ABC (顶点是格线的交点).(1)请画出△ABC 关于直线l 对称的△A 1B 1C 1;(2)将线段AC 向左平移3个单位,再向下平移5个单位,画出平移得到的线段A 2C 2,并以它为一边作一个格点△A 2B 2C 2,使A 2B 2=C 3B 2.20.已知:在Rt △ABC 中,∠B =90°,BC =4cm ,AB =8cm ,D 、E 、F 分别为AB 、AC 、BC 边上的中点。
浙江省中考数学一轮复习 考点跟踪训练44 分类讨论型问

考点跟踪训练44 分类讨论型问题一、选择题(每小题6分,共30分)1.如图,点A 的坐标是(2,2),若点P 在x 轴上,且△APO 是等腰三角形,则点P 的坐标 不可能是( )A .(4,0)B .(1,0)C .(-2 2,0)D .(2,0)2.若函数y =⎩⎪⎨⎪⎧x 2+2(x≤2),2x (x >2),则当函数值y =8时,自变量x 的值是( ) A .± 6 B .4C .±6或4D .4或- 63.(2011·台湾)若钝角三角形ABC 中,∠A=27°,则下列何者不可能是∠B 的度数?( )A. 37°B. 57°C. 77°D. 97°4.矩形一个内角的平分线分矩形一边长为1 cm 和3 cm 两部分,则这个矩形的面积为多少cm 2?( )A .4B .12C .4或12D .6或85.P 是菱形ABCD 的对角线AC 上一动点,过点P 垂直于AC 的直线交菱形ABCD 的边于 M 、N 两点,设AC =2,BD =1,AP =x ,则△AMN 的面积为y ,则y 关于x 的函数图 象的大致形状是( )二、填空题(每小题6分,共30分)6.(2012·资阳)直角三角形的两边长分别为16和12,则此三角形的外接圆半径是________.7.已知正方形ABCD ,以CD 为边作等边△CDE,则∠AED 的度数是________.8.(2011·泰州)如图,平面内4条直线l 1、l 2、l 3、l 4是一组平行线,相邻2条平行线的距离都是1个单位长度,正方形ABCD 的4个顶点A 、B 、C 、D 都在这些平行线上,其中 点A 、C 分别在直线l 1、l 4上,该正方形的面积是________平方单位.9.(2012·衢州)如图,已知函数y =2x 和函数y =k x的图象交于A 、B 两点,过点A 作AE⊥x 轴于点E ,若△AOE 的面积为4,P 是坐标平面上的点,且以点B 、O 、E 、P 为顶点的 四边形是平行四边形,则满足条件的P 点坐标是________.10.(2011·德州)长为1,宽为a 的矩形纸片(12<a<1),如图1那样折一下,剪下一个边长等于矩形宽度的正方形(称为第一次操作);再把剩下的矩形如图2那样折一下,剪下一个边 长等于此时矩形宽度的正方形(称为第二次操作);如此反复操作下去.若在第n 此操作 后,剩下的矩形为正方形,则操作终止.当n =3时,a 的值为________.三、解答题(每小题20分,共40分)11.(2012·黔东南)我州某教育行政部门计划今年暑假组织部分教师到外地进行学习,预订宾馆住宿时,有住宿条件一样的甲、乙两家宾馆供选择,其收费标准均为每人每天120 元,并且各自推出不同的优惠方案.甲家是35人(含35人)以内的按标准收费,超过35人的,超出部分按九折收费;乙家是45人(含45人)以内的按标准收费,超过45人的, 超出部分按八折收费.如果你是这个部门的负责人,你应选哪家宾馆更实惠些?12.(2011·广安)某园艺公司对一块直角三角形的花圃进行改造,测得两直角边长为6m 、8m.现要将其扩建成等腰三角形,且扩充部分是以8m 为直角边的直角三角形...........求扩建后的 等腰三角形花圃的周长.四、附加题(共20分)13.(2012·河南)如图,在平面直角坐标系中,直线y =12x +1与抛物线y =ax 2+bx -3交于A 、B 两点,点A 在x 轴上,点B 的纵坐标为3.点P 是直线AB 下方的抛物线上一动点 (不与A 、B 重合),过点P 作x 轴的垂线交直线AB 于点C ,作PD⊥AB 于点D.(1)求a ,b 及sin ∠ACP 的值;(2)设点P 的横坐标为m.①用含m 的代数式表示线段PD 的长,并求出线段PD 长的最大值;②连接PB ,线段PC 把△PDB 分成两个三角形,是否存在适合的m 值,使这两个三角形的面积之比为9∶10?若存在,直接写出m 值;若不存在,说明理由.。
【大题精编】2023届浙江省中考数学复习 专题9 几何综合问题 解答题30题专项提分计划解析版

【大题精编】2023届浙江省中考数学复习专题9 几何综合问题解答题30题专项提分计划(浙江省通用)1.(2022·浙江衢州·模拟预测)(1)如图1,在矩形ABCD 中,ADC Ð的平分线交BC 于点.E 交AB 的延长线于点F ,求证:BE BF =;(2)如图2,若G 是EF 的中点,连接AG 、CG 、AC ,请判断AGC V 的形状,并说明理由.(3)如图3,作BED Ð的角平分线EH 交AB 于点H ,已知9AB =,2BH AH =,求BC 的长.(2)解:AGC V 为等腰直角三角形,理由如下:如图,连接BG,由(1)可知BEF △为等腰直角三角形,∴AF AD BC ==,∵G 为EF 中点,∴BG FG =,45EBG Ð=°,在△AGF 和△CGB 中,GF GB F CBG AF BC =ìïÐ=Ðíï=î,∴()SAS AGF CGB ≌△△,∴AG CG =,AGF BGC Ð=Ð,∴BGF AGB AGB AGC Ð+Ð=Ð+Ð,∴90AGC BGF Ð=Ð=°,∴AGC V 为等腰直角三角形;(3)解:如图,在BH 上截取BN BE =,连接NE ,∵92AB BH AH ==,,∴36AH BH ==,,∵45BEF Ð=°,∴135BED Ð=°,∵EH 平分BED Ð,∴67.5BEH Ð=°,2.(2022·浙江宁波·校考模拟预测)如图1,在ABC V 中,90C Ð=°,30B Ð=°,作CAB Ð平分线AF 交BC 于点F ,以AF 为边作等腰直角AFE △,且90AFE Ð=°,如图2将AFE △绕点F 每秒3°的速度顺时针旋转得到三角形DFE (当点D 落在射线FB 上时停止旋转),则旋转时间为t 秒.(1)当t = 秒,DE AB ∥;(2)在旋转过程中,DF 与AB 的交点记为M ,如图3,若AMF V 为等腰三角形,求t 的值;(3)当边DE 与边AB 、BC 分别交于点P 、Q 时,如图4,连接AE ,设BAE x Ð=°,AED y Ð=°,DFB z Ð=°,试探究x ,y ,z 之间的关系.【答案】(1)5(2)10或25或40(3)105x y z ++=【分析】(1)根据平行线的性质可得,45DEF BPE Ð=Ð=°,再利用三角形外角的性质得BFE Ð的度数,从而得出旋转的角度,可得答案;(2)分AFM FAM Ð=Ð或AFM AMF Ð=Ð或MAF AMF Ð=Ð,分别求出旋转的角度,从而解决问题;(3)利用三角形外角的性质知BPE BAE AED x y =Ð+Ð=°+°Ð,45BQP DFB D z Ð=Ð+Ð=°+°,再根据三角形内角和定理可得答案.【详解】(1)解:当DE AB ∥时,45DEF BPE Ð=Ð=°,∴453015BFE BPE B Ð=Ð-Ð=°-°=°,∵起始状态30BFE Ð=°,∴()301535t =-¸=,故答案为:5;(2)解:当30AFM FAM Ð=Ð=°,30310t =°¸°=,当75AFM AMF Ð=Ð=°时,75325t =°¸°=,当30MAF AMF Ð=Ð=°时,120AFM Ð=°,120340t =°¸°=,综上:t =10或25或40;(3)解:∵BPE Ð是APE V 的外角,∴BPE BAE AED x y =Ð+Ð=°+°Ð,∵BQP Ð是DFQ V 的外角,∴45BQP DFB D z Ð=Ð+Ð=°+°,在BQP V 中,3045180B BQP BPQ z x y Ð+Ð+Ð=°+°+°+°+°=°,∴105x y z ++=.【点睛】本题是三角形综合题,主要考查了旋转的性质,平行线的性质,三角形内角和定理,三角形外角的性质,等腰三角形的性质等知识,运用分类思想是解决问题(2)的关键.运用三角形外角的性质是解决问题(3)的关键.3.(2022·浙江杭州·翠苑中学校考二模)在图1,图2,图3中,AF BE ,是ABC V 的中线,AF BE ⊥,垂足为P .设BC a AC b AB c =,=,=.(1)①如图1,当=45ABE а,c ==a ,b = .②如图2,当30ABE Ð=°,8c =时,=a ,b = .(2)观察(1)中的计算结果,猜想222a b c ,,三者之间的关系,用等式表示出来,并利用图3证明.),连接EF ,则EF 是ABC V AE EF ^,,是等腰直角三角形,也是等腰直角三角形,21EP FP ==,,,②如图2,连接EF ,则EF 是ABC V 的中位线.30ABE AE BF AB Ð=°^,,Q 434AP BP AP \===,,12,32PF EF PE \====27,213AE BF \==,如图3,连接EF ,则EF 是∴1,2EF AB EF AB =∥,∴ABP FEP V V ∽,∴2AP BP FP EP ==,4.(2022·浙江丽水·一模)在菱形ABCD 中,6AB =,=60A а,点E 在AD 边上,4AE =,点P 是边AB 上一个动点,连结EP ,将AEP △沿EP 翻折得到FEP V .(1)当EF AB ∥时,求AEP Ð的度数;(2)若点F 落在对角线BD 上,求证:DEF BFP V :V ;(3)若点P 在射线BA 上运动,设直线PF 与直线BD 交于点H ,问当AP 为何值时,BHP V 为直角三角形.∵菱形ABCD 中,=60A а,∴AD =AB ,ADB V 是等边三角形,∴60ADB ABD Ð=Ð=°∵FEP V 是由AEP △翻折得到,∴60EFP A Ð=Ð=°,由翻折的性质可得:AP =FP ,EF 设AP =x ,则FP =x ,∵∠PHB =90°,∴150APF Ð=°,30BPH Ð=°30K Ð=°由折叠的性质可得:APE FPE Ð=Ð∵EQ ⊥AB ,60A Ð=°∴30AEQ Ð=°,PEQ EPQ Ð=Ð=∴122AQ AE ==,2242EQ =-∵EM ⊥AB ,60EAM Ð=°,∴60AEM Ð=°,12AM AE =由折叠的性质可得:APE Ð∵EM ⊥AB ,45APE Ð=°∴2EM PM a ==+,在Rt AEM V 中,EM AE =由翻折的性质可得:AP =FP ,EF =∵∠PHB =90°,∠PBH =60°,∴30BPH Ð=°,∵60EAB Ð=°∴120PAE PFE Ð=Ð=°5.(2022·浙江绍兴·一模)如图①,在正方形ABCD 中,点E 与点F 分别在线段,AC BC 上,且四边形DEFG 是正方形.(1)试探究线段AE与CG的关系,并说明理由.AB,(2)如图②若将条件中的四边形ABCD与四边形DEFG由正方形改为矩形,=3 BC.=4AE CG在(1)中的关系仍然成立吗?若成立,请证明,若不成立,请写出你认①线段,为正确的关系,并说明理由.△为等腰三角形时,求CG的长.②当CDE6.(2022·浙江嘉兴·一模)如图1,已知正方形ABCD 和正方形CEFG ,点B 、C 、E 在同一直线上,(1)BC m m =>,1CE =.连接AF BG 、.(1)求图1中AF 、BG 的长(用含m 的代数式表示).(2)如图2,正方形ABCD 固定不动,将图1中的正方形CEFG 绕点C 逆时针旋转a 度(090a °<£°),试探究AF 、BG 之间的数量关系,并说明理由.(3)如图3,在(2)条件下,当点A ,F ,E 在同一直线上时,连接CF 并延长交AD 于点H ,若FH =,求m 的值.∵正方形ABCD 和正方形CEFG ∴∠ABC =∠BCD =∠CGD =∠CGH 在Rt △BCG 中,由勾股定理,得∵正方形ABCD和正方形∴∠ACB=∠FCG=45°,∴∠ACB+∠ACG=∠FCG+∠∴∠BCG=∠ACF,∵正方形ABCD和正方形∴∠CAD=∠CFE=45°,CD∵∠CFE=∠CAF+∠ACF,∴∠FAH=∠ACF,∵∠AHF=∠CHA,7.(2022·浙江宁波·校考三模)【基础巩固】(1)如图①,在四边形ABCD 中,AD BC ∥,ACD B Ð=Ð,求证∶ABC DCA V V ∽;(2)【尝试应用】如图②,在平行四边形ABCD 中,点E 在BC 上,AED Ð与C Ð互补,24BE EC ==,,求AE 的长;(3)【拓展提高】如图③,在菱形ABCD 中,E 为其内部一点,AED Ð与C Ð互补,点F 在CD 上,EF AD ∥,且2AD EF =,31AE CF ==,,求DE 的长.∵四边形ABCD 是菱形,∴AB CD ∥,AB CD =∵EF AD ∥,∴四边形AGFD 是平行四边形,8.(2022·浙江温州·统考模拟预测)已知:如图,MAN Ð为锐角,AD 平分MAN Ð,点B ,点C 分别在射线AM 和AN 上,AB AC =.(1)若点E 在线段CA 上,线段EC 的垂直平分线交直线AD 于点F ,直线BE 交直线AD 于点G ,求证:EBF CAG Ð=Ð;(2)若(1)中的点E 运动到线段CA 的延长线上,(1)中的其它条件不变,猜想EBF Ð与CAG Ð的数量关系并证明你的结论.【答案】(1)见解析;(2)见解析.【分析】(1)如图1,连接EF 、CF ,由中垂线的性质就可以得出EF CF =,就有FEC FCE Ð=Ð,由AFB AFC V V ≌就可以得出ABF ACF Ð=Ð,由180FEC FEA Ð+Ð=°就可以得出180FEC FEA Ð+Ð=°,得出A 、B 、F 、E 四点共圆,再得出EBF CAG Ð=Ð;(2)如图2,连接EF 、CF ,由中垂线的性质就可以得出EF CF =,就有FEC FCE Ð=Ð,由AFB AFC V V ≌就可以得出ABF ACF Ð=Ð,就有AEF ABF Ð=Ð,近而得出A 、B 、F 、E 四点共圆,就有EBF FAC Ð=Ð,从而得出180EBF CAG Ð+Ð=°.【详解】(1)解:如图1,连接EF 、CF ,EC Q 的垂直平分线交直线AD ,EF CF \=,FEC FCE \Ð=Ð,AD Q 平分MAN Ð,BAF CAF\Ð=Ð.在AFB △和AFC △中AB AC BAF CAF AF AF =ìïÐ=Ðíï=îAFB AFC \V V ≌,ABF ACF \Ð=Ð,ABF ACF \Ð=Ð,ABF FCE \Ð=Ð.180FEC FEA Ð+Ð=°Q ,180ABF AEF \Ð+Ð=°,则A 、B 、F 、E 四点共圆,EBF CAG \Ð=Ð;(2)解:180EBF CAG Ð+Ð=°理由:如图2,连接EF 、CF ,EC Q 的垂直平分线交直线AD ,EF CF \=,FEC FCE \Ð=Ð,AD Q 平分MAN Ð,BAF CAF \Ð=Ð.在AFB △和AFC △中AB AC BAF CAFAF AF =ìïÐ=Ðíï=îAFB AFC \V V ≌,ABF ACF \Ð=Ð,ABF FCE \Ð=Ð.则A 、B 、F 、E 四点共圆,EBF FAC \Ð=Ð.180FAC CGA Ð+Ð=°Q ,180EBF CAG Ð+Ð=°Q .【点睛】本题考查角平分线的性质的运用,中垂线的性质的运用,全等三角形的判定及性质的运用,四点共圆的判定及性质的运用,解答时证明三角形全等是关键.9.(2022·浙江杭州·校考二模)如图,在正方形ABCD 中,对角线AC ,BD 相交于点O ,点E ,F 分别在AD ,DC 上(不与A ,D ,C 重合),连接BE ,AF ,BE 与AF 交于点G ,与AC 交于点H .已知AF BE =,AF 平分DAC Ð.(1)求证:AF BE ⊥.(2)若BHO △的面积为1S ,BDE △的面积为2S ,求12S S 的值.10.(2022·浙江丽水·统考一模)如图,在矩形ABCD 中,302DBC AB Ð=°=,,连接对角线BD ,点E 以1个单位每秒的速度从点D 出发,向点B 运动,运动时间为t ,过点E 作EM AE ^,交BC 于点M .(1)如图1,当2t =时,求ME 的长.(2)在点E 在运动过程中,AME Ð的大小是否发生变化?如果变化,请说明理由;如果不变,请求出AME Ð的大小.)90,,ABM AON AO OC \Ð=Ð=°=Q ∴NO 垂直平分AC ,CN AN \=,,AN MN =Q CN MN \=.【点睛】本题综合考查了等边三角形、全等三角形、相似三角形和三角函数等知识,灵活运用条件证明等边三角形求证所需条件,掌握各种全等三角形、相似三角形的判定方法是解题的关键.11.(2022·浙江金华·校联考模拟预测)如图1,在平行四边形ABCD 中,AD ∥BC ,E 是CD 的中点,AE ⊥AB ,AE ,BC 的延长线交于点F ,在线段BF 上取点M ,N (点M在B ,N 之间),使得BM =FN =18MN .当点P 从点M 匀速运动到点N 处时,点Q 恰好从点F 匀速运动到点A 处.连接AP .设MP =x ,AQ =y ,已知y =-x +8.(1)求BF ,AF 的长.(2)当PQ ⊥BC 时(如图2),求FPQ △的周长.(3)①当V APQ 是以AP 为腰的等腰三角形时,求x 的值.②将PQ 绕点Q 顺时针旋转90°得线段P ¢Q ,若点P ¢落在四边形ABCD 的内部,请直接写出x 的取值范围.12.(2022·浙江丽水·统考一模)如图,矩形ABCD ,点P 是对角线AC 上的动点(不与A 、C 重合),连接PB ,作PE PB ^交射线DC 于点E .已知6AD =,8AB =.设AP 的长为x .(1)如图1,PM AB ^于点M ,交CD 于点N .求证:BMP PNE △△∽;(2)试探究:PE PB是否是定值?若是,请求出这个值;若不是,请说明理由;(3)当PCE V 是等腰三角形时,请求出所有x 的值.图甲【点睛】本题主要考查了矩形的性质、相似三角形的判定和性质、勾股定理以及等腰三13.(2022·浙江宁波·统考二模)【证明体验】(1)如图1,△ABC 中,D 为BC 边上任意一点,作DE AC ^于E ,若12CDE A Ð=Ð,求证:△ABC 为等腰三角形;【尝试应用】(2)如图2,四边形ABCD 中,90D Ð=°,AD CD =,AE 平分BAD Ð,180BCD EAD Ð+Ð=°,若2DE =,6AB =,求AE 的长;【拓展延伸】(3)如图3,△ABC 中,点D 在AB 边上满足CD BD =,1902ACB B Ð=°+Ð,若AC =,20BC =,求AD 的长.14.(2022·浙江杭州·统考二模)如图1,在矩形ABCD 中,AC 与BD 交于点O ,E 为AD 上一点,CE 与BD 交于点F .(1)若AE CE =,BD CE ^,①求tan DEC Ð.②如图2,连接AF ,当3BC =时,求AF 的值.(2)设()01DE k k AD =<<,记CBF V 的面积为1S ,四边形ABFE 的面积为2S ,求21S S 的最大值.15.(2022·浙江金华·校联考三模)在四边形ABCD 中,5AB AD ==,10BC CD ==,90B Ð=°.(1)如图1,①求证:90D Ð=°;②求C Ð的正切值;(2)如图2,动点M 从点D 出发,以1个单位每秒速度,沿折线DA AB -运动,同时,动点N 从点B 出发,以2个单位每秒速度,沿射线BC 运动,当点M 到达点B 时,点M ,N 同时停止运动,设运动时间为t 秒,以MN 为斜边作Rt MNP △,使点P 落在线段AB 或AD 上,在整个运动过程中,当不再连接其他线段,且图中存在与MNP △相似的三角形时,求t 的值.DE CF =,设DE CF x ==,则10CE x =-,根据勾股定理列出关于x 的方程,解方程得出x 的值,即可得出结果;(2)按照点M 、N 、P 的位置,MNP NPB D D ∽或MNP PNB D D ∽,以及当三角形全等也是特殊的相似,进行分类讨论,求出t 的值即可.【详解】(1)证明:①连接AC ,如图所示:∵在△ABC 和△ADC 中,AB AD BC CD AC AC =ìï=íï=î,∴()SSS ABC ADC D D ≌,∴90D B Ð=Ð=°;②过点A 作AE BC ∥,交CD 于点E ,过点E 作EF ⊥BC 于点F ,如图所示:90EFC B Ð=Ð=°Q ,∴AB EF ∥,∴四边形ABFE 为平行四边形,∵∠EFC =90°,∴四边形ABFE 为矩形,∴5EF AB ==,∠AEF =90°,∴EF AD =,90DAE AED Ð+Ð=°Q ,90DEA CEF Ð+Ð=°,∴DAE CEF Ð=Ð,90D EFC Ð=Ð=°Q ,∴()ASA ADE EFC D D ≌,∴DE CF =,设DE CF x ==,则10CE x =-,∵222CE CF EF =+,()222105x x \-=+,(2)①当点M 在AD 上,BA ,交EM 于点G ,如图所示:∵MNP NPB D D ∽,∴NMP BNP Ð=Ð,PNM Ð∵90PMN PNM Ð+Ð=°,7②当点M 在AD 上,MNP PNB D D ∽时,过点交EM 于点G ,过点P 作PH ⊥MN 于点∵ME BC ∥,∴18090GEF EFB Ð=°-Ð=°,∴90GEF EFB B Ð=Ð=Ð=°,∴四边形GEFB 为矩形,③当M 与A 点重合,N 与C 点重合时,相似比为1,符合要求,此时1052t ==④当点M 在AB 上,N 在BC 的延长线上时,∵MN =MN ,∴此时MNP MNB D D ≌,∴NP =NB =2t ,PM =MB =10-t ,【点睛】本题主要考查了三角形全等的判定和性质,三角形相似的判定和性质,解直角三角形,矩形的判定和性质,平行四边形的判定和性质,熟练掌握相关的三角形判定的性质和判定,作出辅助线,进行分类讨论是解题的关键.16.(2022·浙江金华·校联考二模)如图,菱形ABCD 中,5AB =,8AC =,点E 是射线AC 上的一个动点,将线段BE 绕点E 顺时针旋转90°到EF ,连接DE 、DF .(1)求证:ED EF =;(2)如图2,连接BD ,CF ,当BED V 与EFC V 相似时,求CE 的长;(3)当点D 关于直线EF 的对称点落在菱形的边上时,求AE 的长.(3)①当点F 与点D 重合时,点E 在AO 上时,点目要求,如图所示:根据解析(1)可知,BE =DE ,∵EO ⊥BD ,∴90BED Ð=°,∵BO =DO ,∴132EO BD ==,∵AO =4,∴1AE AO EO =-=;。
浙江省中考数学总复习 考点跟踪训练36 几何作图(无答案)(2021年整理)

浙江省中考数学总复习考点跟踪训练36 几何作图(无答案)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(浙江省中考数学总复习考点跟踪训练36 几何作图(无答案))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为浙江省中考数学总复习考点跟踪训练36 几何作图(无答案)的全部内容。
考点跟踪训练36 几何作图A组基础过关练一、选择题1. (2013南通)如图,用尺规作出∠OBF=∠AOB,作图痕迹是( )A。
以点B为圆心,OD为半径的圆B。
以点B为圆心,DC为半径的圆C. 以点E为圆心,OD为半径的圆D。
以点E为圆心,DC为半径的圆2. (2013河北)已知:线段AB、BC,∠ABC=90°.求作:矩形ABCD.以下是甲、乙两同学的作业:甲:①以点C为圆心,AB长为半径画弧;②以点A为圆心,BC长为半径画弧;③两弧在BC 上方交于点D,连接AD、CD,四边形ABCD即为所求(如图1).乙:①连接AC,作线段AC的垂直平分线,交AC于点M;②连接BM并延长,在延长线上取一点D,使MD=MB,连接AD、CD,四边形ABCD即为所求(如图2).对于两人的作业,下列说法正确的是( )A. 两人都对 B。
两人都不对C. 甲对,乙不对D. 甲不对,乙对3。
(2014河北)如图,已知△ABC(AC<BC),用尺规在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是()A. B。
C。
D。
二、填空题4. (2014河南)在△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于12BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD。
浙教版中考实际应用性问题(含知识要点,例题及练习参考答案)

专题一 实际应用性问题实际应用性问题是指有实际背景或实际意义的数学问题.这些问题充分表达了贴近学生生活、关注社会热点、形式多样等特点,注重考查学生思维的灵活性和深刻性,要求解题者具有较丰富的生活常识和较强的阅读水平以及数学建模水平.实际应用性问题涉及的背景有商品买卖、存款和贷款,最优方案、行程问题、交通运输、图案设计、农业生产和生物繁殖等.实际应用性问题在各地的试卷中成为必考内容,表达了素质教育的要求和新课程标准的理念,由于它们来自生活和生产实践,所以参考条件较多,思维也有一定的深度,解答方法灵活多样.【典型例题】例1. 某饮料厂为了开发新的产品,用A 、B 两种果汁原料各19千克、17.2千克,试制甲、〔1〕假设甲种饮料需配制x 千克.请你写出满足题意的不等式组,并求出其解.〔2〕设甲种饮料每千克本钱为4元,乙种饮料每千克本钱为3元.这两种饮料的本钱总额为y 元,请写出y 与x 的函数表达式.并根据〔1〕的运算结果,确定当甲种饮料配制多少千克时,甲、乙两种的本钱总额最低.分析:根据表格的信息和其他条件知甲种原料用量不大于19千克,乙种原料用量不大于17.2千克,可得出〔1〕的不等式组.〔2〕由“本钱总额=甲种饮料本钱+乙种饮料本钱〞这个关系式,可列出函数表达式.再运用函数的性质,可确定最低总本钱.解:〔1〕由条件得05025019030450172..()..().x x x x +-≤+-≤⎧⎨⎩ 解得2830≤≤x 〔2〕依题意得y x x x x =+-=+≤≤43501502830()()由一次函数性质知:k =1>0,y 随x 的增大而增大.∴当x =28时,甲、乙两种饮料的本钱总额最少.即y =28+150=178〔元〕.例2. 高为12.6米的教学楼ED 前有一棵大树AB 〔如图甲〕.〔1〕某一时刻测得大树AB,教学楼ED在阳光下的投影长分别是BC=2.4米,DF=7.2米,求大树AB的高度.〔2〕用皮尺、高为h米的测角仪,请你设计另一种测量大树AB高度的方案.要求:a. 在图乙上画出你设计的测量方案示意图,并将应测数据标记在图上.〔长度用字母m、n…表示,角度用希腊字母α、β…表示〕b. 根据你所画的示意图和标注的数据,计算大树AB高度.〔用字母表示〕分析:〔1〕可用同一时刻物高与影长成正比获得大树高度.〔2〕中的设计方案,要求同学们能根据平时的学习体验及解直角三角形的有关知识获得测量大树的方案.注意的是不要无视了测角仪的高度.解:〔1〕连AC、EF∵太阳光线是平行线,∴AC∥EF∴∠ACB=∠EFD∵∠ABC=∠EDF=90°∴△ABC∽△EDF∴ABEDBCDF=∴AB1262472 ...=∴AB=4.2答:大树AB的高是4.2米.〔2〕如图测角仪高度为h米,用皮尺可测得测角仪离树距离为m米,用测角仪测得树顶仰角为α, 即BN=GM=m在Rt△AMG中,AG=m·tanα∴AB=〔m·tanα+h〕米例3. 甲、乙两同学开展“投球进筐〞比赛,双方约定:①比赛分6局进行,每局在指定区域内将球投向筐中,只要投进一次后该局便结束.②假设一次未进可再投第二次,以此类推,但每局最多只能投8次,假设8次投球都未进,该局也结束;③计分规那么如下:a. 得分为正数或0;b. 假设8次都未投进,该局得分为0;c. 投球:次数越多,得分越低;d. 6局比赛的总分高者获胜.〔1〕设某局比赛第n 〔n =1,2,3,4,5,6,7,8〕次将球投进,请你按上述约定,用公式、表格或语言表达等方式,为甲、乙两位同学制定一个把n 换算为得分M 的计分方案.〔2〕假设两人6局比赛的投球情况如下.〔其中的数字表示该局比赛进球时的投球次数,“×〞表示该局比赛8次投球都未进〕.第一局 第二局 第三局 第四局 第五局 第六局 甲 5 × 4 8 1 3 乙 8 2 4 2 6 × 根据上述计分规那么和你制定的计分方案,确定两人谁在这次比赛中获胜.分析:将实际问题中的计分与投球次数之间进行量化的设计方案,只要满足计分规那么的要求即可.因而可获得不同方案.解:〔1〕方案一,如下表:n 〔次〕 1 2 3 4 5 6 7 8 M 〔分〕 8 7 6 5 4 3 2 1 〔未进球计0分〕,显然上述方案符合计分规那么要求.方案二:将球投进筐的次数n 〔次〕与得分M 〔分〕之间用关系式表示为:次未进时计分为M n12080() 显然这一计分方案也符合计分规那么的要求.〔2〕由方案一:可算得甲的得分为:4+0+5+1+8+6=24〔分〕乙的得分为:1+7+5+7+3=23〔分〕由此可知,在这次比赛中甲获胜.由方案二:甲的每局得分分别为:24分、0分、30分、15分、120分、40分;乙的每局得分分别为:15分、60分、30分、60分、20分、0分.∴甲的总得分为229分;乙的总得分为185分.由此知:甲在这次比赛中获胜.例4. 光华农机租赁公司共有50台联合收割机,其中甲型20台,乙型30台,现将这50台联合收割机派往A 、B 两地区收割小麦;其中30台派往A 地区,20台派往B 地区. 两地区与该农机租赁公司商定的每天的租赁价格见下表:每台甲型收割机的租金 每台乙型收割机的租金 A 地区 1800元 1600元B 地区 1600元 1200元〔1〕设派往A 地区x 台乙型联合收割机,租赁公司这50台联合收割机一天获得的租金为y 〔元〕,求y 与x 间的函数关系式.并写出x 的取值范围.〔2〕假设使农机租赁公司这50台联合收割机一天获得的租金总额不低于79600元,说明有多少种分派方案,并将各种方案设计出来.〔3〕如果要使这50台联合收割机每天获得的租金最高,请你为光华农机租赁公司提出一条合理的建议.分析:在〔1〕中,由派往A 地乙型收割机为x 台.能够正确地用代数式表示往A 地的甲型收割机,派往B 地的甲、乙型收割机是问题的关键.根据条件可得相应的租赁费用和调运方案.解:〔1〕假设派往A地区的乙型收割机为x台.那么派往A地区的甲型收割机为〔30-x〕台派往B地区的乙型收割机为〔30-x〕台派往B地区的甲型收割机为[20-〔30-x〕]=〔x-10〕台∴y=1600x+1800(30-x)+1200(30-x)+1600(x-10) =200x+74000.由实际问题情境,必有xxx≥-≥-≥⎧⎨⎪⎩⎪0 300100∴1030≤≤x即x的取值范围是:10≤x≤30〔x是正整数〕〔2〕由题意得:200x+74000≥79600解得:x≥28由于10≤x≤30∴x取28、29、30这三个值.∴有3种不同分配方案.①当x=28时,即派往A地区甲型收割机2台,乙型收割机28台,派往B地区甲型收割机18台,乙型收割机2台.②当x=29时,即派往A地区甲型收割机1台,乙型收割机29台,派往B地区甲型收割机19台,乙型收割机1台.③当x=30时,即30台乙型收割机全部派往A地区;20台甲型收割机全部派往B地区.〔3〕由于一次函数y=200x+74000的性质知:y随着x的增大而增大.∴当x=30时,y取得最大值.如果要使农机租赁公司这50台联合收割机每天获得租金最高,只需x=30,此时y=6000+74000=80000.建议农机租赁公司将30台乙型收割机全部派往A地区,20台甲型收割机全部派往B地区,可使公司获得的租金最高.例5. 如图〔1〕,一个无盖的正方体盒子的棱长为10cm,顶点C1处有一只昆虫甲,在盒子的内部顶点A处有一只昆虫乙,〔盒壁厚度忽略不计〕〔1〕假设昆虫甲在顶点C1处静止不动,如图〔1〕,在盒子的内部我们先取棱BB1的中点E,再连结AE、EC1,昆虫乙如果沿路径A→E→C1爬行,那么可以在最短的时间内捕捉到昆虫甲,仔细体会其中的道理,并在图〔1〕中画出另一条路径,使昆虫乙从顶点A沿这条路径爬行,同样可以在最短的时间内捕捉到昆虫甲.〔请简要说明画法〕.〔2〕如图〔2〕假设昆虫甲从顶点C1以1cm/s的速度在盒子的内部沿棱C1C向下爬行.同时昆虫乙从顶点A以2cm/s的速度在盒壁上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?〔精确到1s〕.分析:此题难点是两个点是动点,且昆虫乙的路径不惟一,因而确定昆虫乙的几种可能路径是关键;这就必须了解正方体的平面展开图.在〔1〕中,类似地在DD 1、CD 、A 1B 1、A 1D 1或BC 的中点与A,C 1连结的线段上找到由A →C 1的最短路径;在〔2〕中可利用直角三角形的知识获得结论.解:〔1〕略.〔2〕由〔1〕知:当昆虫甲从顶点C 1沿棱C 1C 向顶点C 爬行的同时,昆虫乙可以沿以下四种路径中的任意一种爬行.可以看出,图〔3〕、〔4〕的路径相等,图〔5〕、〔6〕的路径相等.①设昆虫甲从顶点C 1沿棱C 1C 向顶点C 爬行的同时,昆虫乙从顶点A 按路径A →E →F 爬行捕捉到昆虫甲需x 秒钟.由图〔3〕在Rt △ACF 中()()21020222x x =-+解得x =10设昆虫甲从顶点C 1沿棱C 1C 向顶点C 爬行的同时,昆虫乙从顶点A 按路径A →E 3→F 爬行捕捉昆虫甲需y 秒钟.由图〔5〕,在Rt △ADF 中()()22010222y y =-+解得y ≈8∴昆虫乙从顶点A 爬行捕捉昆虫甲至少需8s.数学应用与实践包含实际问题中的方案设计问题以及依据数学特征进行的活动,操作和用数学知识解决实际问题等,解这类问题时应注重于对生活中的实际问题进行恰当的分析,从中能够找出与之相关的数学模型,并借助数学知识予以解决,其中所涉及的分类讨论思想、实际问题模型化的思想以及转化的思想方法十分重要,是解决这类问题的关键.【模拟试题】〔做题时间:45分钟〕一、填空.1. 一商店把某件商品按九折出售仍可获得20%的利润率,假设该商品的进价是每价30元,那么该件商品的标价是_____________.2. 小明家粉刷房间,雇了5个工人,干了10天完成,用去涂料费为4800元,粉刷的面积为150m2,最后结算工钱时,有以下三种方案:〔1〕按工算,每人每天工资30元;〔2〕按涂料费用算,涂料费用的30%作为工钱.〔3〕按粉面积算,每平方米付工钱12元.请你帮小明家出主意,选择方案_____________付钱最合算.3. 某公司今年5月份的纯利是a万元,如果每个月纯利润的增长率都是x,那么预计7月份的纯利润将到达_____________万元.4. 有一旅客携带了30kg行李从南京国际机场乘飞机去天津,按民航规定,旅客最多可免费携带20kg行李,超过局部每公斤按飞机票价的1.5%购置行李票,现该旅客购置了120元的行李票,那么他的飞机票价格应是_____________.5. 某兴趣小组决定去市场购置A、B、C三种仪器,其单价分别为3元,5元,7元,购置这批仪器需花费62元,后经过讨价还价,最后以每种各下降1元成交,结果只花了50元就买下了这批仪器,那么A种仪器最多可买_____________件.6. 某市近年来经济开展迅速,据统计,该市国内生产总值1990年为8.6亿元,1995年为10.4亿元,2000年为12.9亿元,经论证,上述数据适合一个二次函数关系,请你根据这个函数关系,预测2022年该市国内生产总值将到达_____________亿元.7. 如图1,某公园入口原有三级台阶,每级台阶高为20cm,宽为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起点为C,现在斜坡的坡度∠BCA设计为12°,求AC的长度为_____________.图18. 居民楼的采光是人们关心的一个重要问题,冬至是一年中太阳光与地面所成夹角最小的时期,此时只要太阳光在如图2,两楼之间不互相挡住阳光,那么一年四季均不为互相挡住阳光了,设此时太阳光与地面的夹角为30°,两楼高均为30米,问两楼之间的水平距离L至少为_____________米时两楼之间才能不互相挡住阳光照射.图2二、选择题.9. 某商品价格为a 元,降价10%后,又降价10%,销售猛增,商店决定再提价20%,提价后这种商品的价格为〔 〕A. a 元B. 1.08a 元C. 0.972a 元D. 0.96a 元10. 小李买了20本练习本,店主给他八折优惠,结果廉价了32元,那么每本练习本的标价是〔 〕A. 2元B. 4元C. 8元D. 6元11. 小王在一次野外活动中捡到一块矿石,回家后,他使用一把刻度尺,一只圆柱形的玻璃杯和足量的水,就测量出这块石头的体积,如果他量出玻璃杯的内直径d,把矿石完全浸在水中,测出杯中水面上升了的高度为h,那么小王的这块石头的体积是〔 〕A. π42d h B. π22d h C. πd h 2 D. 42πd h 12. 如图3,边长为12m 的正方形塘的周围是草地,池塘边A 、B 、C 、D 处各有一棵树,且AB =BC =CD =3m,现在用长为4m 的绳子将一头羊拴在其中的一棵树上,为了使羊在草地上活动区域的面积最大,应将绳子拴在〔 〕图3A. A 处B. B 处C. C 处D. D 处13. 如图4,在正方形铁片上剪下一个圆形和扇形,使之恰好围成一个圆锥模型,设圆的半径为r,扇形的半径为R,那么圆形的半径与扇形半径之间的关系是〔 〕图4A. R r =2B. R r =94C. R r =3D. R r =414. 如图5在一个房间内,有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA 为a m,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面的墙上,此时梯子顶端距离地面的距离NB 为b m,梯子的倾斜为45°,这间房间的宽AB 一定是〔 〕A. a b m +2B. a b m -2C. b mD. a m图5三、15. 某下岗工人在再就业中央的扶持下,创办了“润扬〞报刊零售点,对经营的某种晚报,该工人提供了如下信息:①买进每份0.2元,卖出每份0.3元;②一个月内〔以30天计〕,有20天每天可以卖出200份,其中10天每天只能卖出120份;③一个月内,每天从报社买进的报纸份数必须相同,当天卖不掉的报纸,以每份0.1元退回给报社.〔〔2〕设每天从报社买进该晚报x 份〔120200≤≤x 〕时,月利润为y 元,试求出y 与x 的函数关系式,并求月利润的最大值.16. 足球比赛的记分规那么为:胜一场得3分,平一场得1分,输一场得0分,一支球队在某个赛季中共需比赛14场中,现已比赛了8场,输了1场,得17分.请问:〔1〕前8场球比赛中,这支球队共胜了多少场?〔2〕这支球队打满14场赛,最高能得多少分?〔3〕通过比赛情况的分析,这支球队打满14场比赛得分不低于29分,就可以到达预期目标,请你分析一下,在后面的六场赛中这支球队至少要胜几场,才能到达预期目标.17. 某农场为防风沙在一山坡上种植一片树苗,并安装了自动喷灌设备,一瞬间,喷出的水流呈抛物线.如图6所示,建立直角坐标系,喷水头B 高出地面1.5米,喷水管与山坡所成的夹角∠BOA 约为63°,水流最高点C 的坐标为〔2,3.5〕.图6〔1〕求此水流抛物线的解析式;〔2〕求山坡所在的直线OA 的解析式〔解析式中的系数精确到0.1〕;〔3〕计算水喷出后落在山坡上的最远距离OA 〔精确到0.1米〕18. 某生活小区的居民筹集资金1600元,方案一块上、下两底分别为10m 、20m 的梯形空地上种植花木〔如图7〕.图7〔1〕他们在△AMD 和△BMC 地带上种植太阳花,单价为8元/m 2,当△AMD 地带种满花后,〔图7中阴影局部〕共花了160元,请计算种满△BMC 地带所需的费用.〔2〕假设其余地带要种的有玫瑰和茉莉花两种花木可供选择,单价分别为12元/m 2和10元/m 2,应选择种哪种花木,刚好用完所筹集的资金?19. 我市某中学要印制本校高中招生的录取通知书,有两个印刷厂前来联系制作业务,甲厂的优惠条件是:按每份定价1.5元的八折收费,另收900元制版费;乙厂的优惠条件是:每份定价1.5元的价格不变,而制版费900元那么六折优惠,且甲乙两厂都规定:一次印刷的数量至少是500份.〔1〕分别求两个印刷厂的收费y〔元〕与印刷数量x〔份〕的函数关系,并指出自变量x的取值范围.〔2〕如何根据印刷的数量选择比拟合算的方案?如果这个中学要印制2000份录取通知书,那么应中选择哪一个厂?需要多少费用?请做完之后,再看答案【试题答案】一、填空:1. 402. 应选方案〔2〕3. a x ()12+4. 8005. 56. 16.11亿元7. 约222cm8. 303米≈52米二、选择:9. C 10. C 11. A12. B 13. D 14. D三、解做题:15. 〔1〕300 390〔2〕y x x =+≤≤240120200() 当x =200时,y 最大值为440元16. 〔1〕答:前8场比赛中,这个球队共胜了5场〔2〕最高能得17+〔14-8〕×3=35分〔3〕由题意得:以后的6场比赛中,只要得分不低于12分即可,故胜不少于4场一定能到达目标,而胜3场平3场,正好到达预期目标,所以在以后的比赛中这个球队至少要胜3场17. 〔1〕设y a x n k =-+()2, 由题意得:y a x =-+().2352将B 〔0,1.5〕代入得a =-12∴抛物线的解析式为y x =--+122722() 或y x x =-++122322 〔2〕∠AOX =27°,设坡面所在直线上一点坐标为〔x,y 〕那么tan tan 2727°,°==y xy x 即坡面OA 所在直线方程为y x =12〔3〕由y x y x x ==-++⎧⎨⎪⎪⎩⎪⎪12122322 解得x y ==⎧⎨⎩3819..,∴OA =+381922..≈4.2米 答:略.18. 解:〔1〕∵四边形ABCD 是梯形,∴AD ∥BC,∴△AMD ∽△CMB∴S S AD BC AMDCMB △△==()214∵种植△AMD 地带花费160元,∴1608202=()m ∴S cm CMB △=802, △BMC 地带的花费为80×8=640〔元〕 〔2〕解设△AMD,△BMC 的高分别为h 1,h 2,梯形ABCD 的高为h, ∵S h AMD △==1210201,∴h 14=, 又h h h 122128==,∴ ∴S AD BC h ABCD 梯形××=+==12123012180() ∴S S AMB DMC △△°-+=-=180208080 ∴160+640+80×12=1760〔元〕 160+640+80×10=1600〔元〕∴应种植茉莉花刚好用完所筹资金.19. 解:〔1〕y x 甲×=+1580%900. =+≥12900500.()x x 且为自然数y x 乙×=+1590060%. =+15540.x〔2〕由〔1〕得:y y x 甲乙-=-36003. 当360030-=.x即x =1200时,费用相同当x >1200时,甲廉价,当x <1200时,乙廉价. 那么当x =2000时,应选甲要:1220009003300.×+=〔元〕。
浙江省中考数学总复习 考点跟踪训练42 相似三角形的应用(无答案)
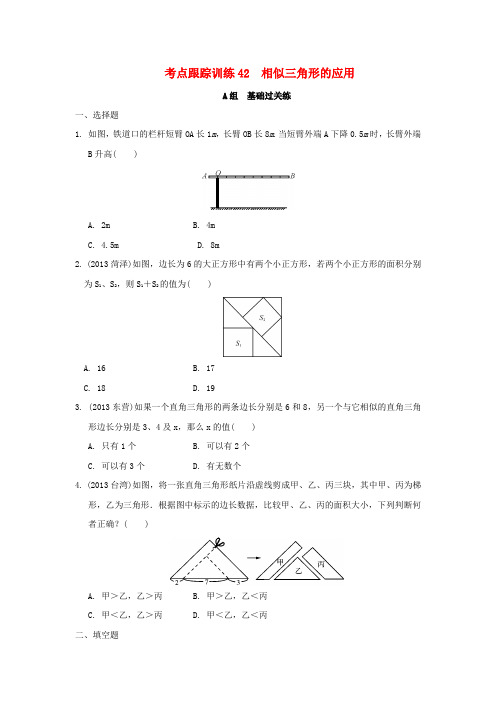
考点跟踪训练42 相似三角形的应用A组基础过关练一、选择题1. 如图,铁道口的栏杆短臂OA长1m,长臂OB长8m.当短臂外端A下降0.5m时,长臂外端B升高( )A. 2mB. 4mC. 4.5mD. 8m2. (2013菏泽)如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2的值为( )A. 16B. 17C. 18D. 193. (2013东营)如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3、4及x,那么x的值( )A. 只有1个B. 可以有2个C. 可以有3个D. 有无数个4. (2013台湾)如图,将一张直角三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断何者正确?( )A. 甲>乙,乙>丙B. 甲>乙,乙<丙C. 甲<乙,乙>丙D. 甲<乙,乙<丙二、填空题5. (2013济宁)如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为________cm.6. (2014娄底)如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的距离DB=12m,则旗杆AB的高为________m.7. (2014牡丹江)在同一时刻两根木竿在太阳光下的影子如图所示,其中木竿AB=2m,它的影子BC=1.6m,木竿PQ的影子有一部分落在了墙上,PM=1.2m,MN=0.8m,则木竿PQ 的长度为________m.8. 如图,△ABC是一块锐角三角形的材料,边BC=120mm,高AD=80mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是________mm.三、解答题9. (2014陕西)某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度,两人在确保无安全隐患的情况下,先在河岸边选择了一点B(点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸).①小明在B点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部点D处,如图所示,这时小亮测得小明眼睛距地面的距离AB=1.7米;②小明站在原地转动180°后蹲下,并保持原来的观察姿态(除身体重心下移外,其他姿态均不变),这时视线通过帽檐落在了DB 延长线上的点E 处,此时小亮测得BE =9.6米,小明的眼睛距地面的距离CB =1.2米.根据以上测量过程及测量数据,请你求出河宽BD 是多少米?10. 如图,△ABC 是一张锐角三角形的硬纸片.AD 是边BC 上的高,BC =40cm ,AD =30cm .从这张硬纸片剪下一个长HG 是宽HE 的2倍的矩形EFGH.使它的一边EF 在BC 上,顶点G 、H 分别在AC 、AB 上,AD 与HG 的交点为M. (1)求证:AM AD =HG BC;(2)求这个矩形EFGH 的周长.B 组 能力提升练1. (2013新疆)如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t 秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )A. 2B. 2.5或3.5C. 3.5或4.5D. 2或3.5或4.52. (2014绍兴)把标准纸一次又一次对开,可以得到均相似的“开纸”.现在我们在长为22、宽为1的矩形纸片中,画两个小矩形,使这两个小矩形的每条边都与原矩形纸的边平行,或小矩形的边在原矩形的边上,且每个小矩形均与原矩形纸相似,然后将它们剪下,则所剪得的两个小矩形纸片周长之和的最大值是________.3. (2014玉林)如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP、BP.(1)求证:四边形BMNP是平行四边形;(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.4. (2014珠海)如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF 与边CD 相交于点G ,连接BE 与对角线AC 相交于点H ,AE =CF ,BE =EG. (1)求证:EF∥AC; (2)求∠BEF 的大小; (3)求证:AH GF =11+tan 15°.。
2016年最新浙教版中考数学第一轮复习第39课 几何应用性问题(精品课件)

用代数方法解几何应用题
几何求值问题,当未知量不能直接求出时,一般需设出 未知数, 继而建立方程(组), 用解方程(组)的方法去求结果, 这是解题中常见的具有导向作用的一种思想.
识点,揭示实际问题的数学本质,把实际问题转化成数学问 助学微博 题.几何应用性问题的解题策略是:将实际问题几何化(从 实际问题中抽象出基本几何图形),解题时需要画出图形, 在图形中标出已知线段长和角的度数等, 注意几何与代数的 联系,及数学思想方法的综合运用.
Hale Waihona Puke ∴总费用=(6×4+2×1.5+18)×80 =3600(元).
探究提高
适当分割,将图形转化为便于求长度、面积的 几何图形.
知能迁移 1 已知△ABC 中,∠ACB=90°(如图),点 P 到 ∠ACB 两边的距离相等,且 PA=PB. (1)先用尺规作出符合要求的点 P(保留作图痕迹,不需要 写作法),然后判断△ABP 的形状,并说明理由; (2)设 PA=m,PC=n,试用 m、n 的代数式表示△ABC 的周 长和面积.
0.8 4.8 解析 根据相似比,得 = ,x=9.6, 1.6 x 故树的高度为 9.6 米.
基础自测
3.如图,农村常搭建横截面为半圆形的全封闭塑料薄膜蔬 菜大棚.如果不考虑塑料薄膜埋在土里的部分,那么搭 建一个这样的蔬菜大棚需用塑料薄膜的面积是 ( B ) 2 A.64π m 2 B.68π cm C.78π m2 D.80π m2
浙教版初中数学初三中考冲刺:几何综合问题--知识讲解(提高)

中考冲刺:几何综合问题—知识讲解(提高)【中考展望】几何综合题是中考试卷中常见的题型,大致可分为几何计算型综合题与几何论证型综合题,它主要考查学生综合运用几何知识的能力.这类题型在近几年全国各地中考试卷中占有相当的分量,不仅有选择题、填空题、几何推理计算题以及代数与几何的综合计算题,还有更注重考查学生分析问题和解决问题能力的探究性的问题、方案设计的问题等等.主要特点是图形较复杂,覆盖面广、涉及的知识点较多,题设和结论之间的关系较隐蔽,常常需要添加辅助线来解答.几何综合题的呈现形式多样,如折叠类型、探究型、开放型、运动型、情景型等,背景鲜活,具有实用性和创造性,考查方式偏重于考查考生分析问题、探究问题、综合应用数学知识解决实际问题的能力.以几何为主的综合题常常在一定的图形背景下研究以下几个方面的问题:1、证明线段、角的数量关系(包括相等、和、差、倍、分及比例关系等);2、证明图形的位置关系(如点与线、线与线、线与圆、圆与圆的位置关系等);3、几何计算问题;4、动态几何问题等.【方法点拨】一、几何计算型综合问题,常常涉及到以下各部分的知识:1、与三角形有关的知识;2、等腰三角形,等腰梯形的性质;3、直角三角形的性质与三角函数;4、平行四边形的性质;5、全等三角形,相似三角形的性质;6、垂径定理,切线的性质,与正多边形有关的计算;7、弧长公式与扇形面积公式.二、几何论证型综合题的解答过程,要注意以下几个方面:1、注意图形的直观提示,注意观察、分析图形,把复杂的图形分解成几个基本图形,通过添加辅助线补全或构造基本图形;2、注意分析挖掘题目的隐含条件、发展条件,为解题创造条件打好基础,要由已知联想经验,由未知联想需要,不断转化条件和结论来探求思路,找到解决问题的突破点;3、要运用转化的思想解决几何证明问题,运用方程的思想解决几何计算问题,还要灵活运用数学思想方法如数形结合、分类讨论、转化、方程等思想来解决问题.【典型例题】类型一、动态几何型问题1.(2016•太原校级自主招生)如图1,在正方形ABCD中,点E、F分别是边BC、AB上的点,且CE=BF,连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.(1)请判断:FG与CE的数量关系和位置关系;(不要求证明)(2)如图2,若点E、F分别是CB、BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请出判断判断予以证明;(3)如图3,若点E、F分别是BC、AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.【思路点拨】(1)结论:FG=CE,FG∥CE.如图1中,设DE与CF交于点M,首先证明△CBF≌△DCE,推出DE⊥CF,再证明四边形EGFC是平行四边形即可.(2)结论仍然成立.如图2中,设DE与CF交于点M,首先证明△CBF≌△DCE,推出DE⊥CF,再证明四边形EGFC是平行四边形即可.(3)结论仍然成立.如图3中,设DE与FC的延长线交于点M,证明方法类似.【答案与解析】解:(1)结论:FG=CE,FG∥CE.理由:如图1中,设DE与CF交于点M.∵四边形ABCD是正方形,∴BC=CD,∠ABC=∠DCE=90°,在△CBF和△DCE中,,∴△CBF≌△DCE,∴∠BCF=∠CDE,CF=DE,∵∠BCF+∠DCM=90°,∴∠CDE+∠DCM=90°,∴∠CMD=90°,∴CF⊥DE,∵GE⊥DE,∴EG∥CF,∵EG=DE,CF=DE,∴EG=CF,∴四边形EGFC是平行四边形.∴GF=EC,∴GF=EC,GF∥EC.(2)结论仍然成立.理由:如图2中,设DE与CF交于点M.∵四边形ABCD是正方形,∴BC=CD,∠ABC=∠DCE=90°,在△CBF和△DCE中,,∴△CBF≌△DCE,∴∠BCF=∠CDE ,CF=DE ,∵∠BCF+∠DCM=90°,∴∠CDE+∠DCM=90°,∴∠CMD=90°,∴CF ⊥DE ,∵GE ⊥DE ,∴EG ∥CF ,∵EG=DE ,CF=DE ,∴EG=CF ,∴四边形EGFC 是平行四边形.∴GF=EC ,∴GF=EC ,GF ∥EC .(3)结论仍然成立.理由:如图3中,设DE 与FC 的延长线交于点M .∵四边形ABCD 是正方形,∴BC=CD ,∠ABC=∠DCE=90°,∴∠CBF=∠DCE=90°在△CBF 和△DCE 中,,∴△CBF ≌△DCE ,∴∠BCF=∠CDE ,CF=DE∵∠BCF+∠DCM=90°,∴∠CDE+∠DCM=90°,∴∠CMD=90°,∴CF ⊥DE ,∵GE ⊥DE ,∴EG ∥CF ,∵EG=DE ,CF=DE ,∴EG=CF ,∴四边形EGFC 是平行四边形.∴GF=EC ,∴GF=EC ,GF ∥EC .【总结升华】本题考查四边形综合题、正方形的性质、平行四边形的判定和性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形,注意这类题目的解题规律,图形变了,条件不变,证明的方法思路完全一样,属于中考常考题型.举一反三:【变式】已知:如图(1),射线//AM 射线BN ,AB 是它们的公垂线,点D 、C 分别在AM 、BN 上运动(点D 与点A 不重合、点C 与点B 不重合),E 是AB 边上的动点(点E 与A 、B 不重合), 在运动过程中始终保持EC DE ⊥,且a AB DE AD ==+.(1)求证:ADE ∆∽BEC ∆;(2)如图(2),当点E 为AB 边的中点时,求证:CD BC AD =+;(3)设m AE =,请探究:BEC ∆的周长是否与m 值有关?若有关,请用含有m 的代数式表示BEC ∆的周长;若无关,请说明理由.【答案】(1)证明:∵EC DE ⊥,∴︒=∠90DEC .∴︒=∠+∠90BEC AED . 又∵︒=∠=∠90B A ,∴︒=∠+∠90EDA AED .∴EDA BEC ∠=∠.∴ADE ∆∽BEC ∆.(2)证明:如图,过点E 作EF BC //,交CD 于点F ,∵E 是AB 的中点,容易证明)(21BC AD EF +=. 在DEC Rt ∆中,∵ CF DF =,∴ CD EF 21=. ∴ )(21BC AD +CD 21=. ∴ CD BC AD =+.(3)解:AED ∆的周长DE AD AE ++=m a +=,m a BE -=.设x AD =,则x a DE -=.∵ ︒=∠90A ,∴ 222AD AE DE +=.即22222x m x ax a +=+-. ∴ am a x 222-=. 由(1)知ADE ∆∽BEC ∆,∴ 的周长的周长BEC ∆∆ADE BE AD =m a a m a --=222am a 2+=. ∴ BEC ∆的周长⋅+=ma a 2ADE ∆的周长a 2=. ∴ BEC ∆的周长与m 值无关.2.在△ABC 中,∠ACB=45º.点D (与点B 、C 不重合)为射线BC 上一动点,连接AD ,以AD 为一边且在AD 的右侧作正方形ADEF .(1)如果AB=AC .如图①,且点D 在线段BC 上运动.试判断线段CF 与BD 之间的位置关系,并证明你的结论.(2)如果AB ≠AC ,如图②,且点D 在线段BC 上运动.(1)中结论是否成立,为什么?(3)若正方形ADEF 的边DE 所在直线与线段CF 所在直线相交于点P ,设AC=3=BC ,CD=x ,求线段CP 的长.(用含x 的式子表示)【思路点拨】(1)由题干可以发现,正方形中四条边的垂直关系是不动的,于是利用角度的互余关系进行传递,就可以得解.(2)是典型的从特殊到一般的问法,那么思路很简单,就是从一般中构筑一个特殊的条件就行,和上题一样找AC 的垂线,就可以变成第一问的条件,然后一样求解.(3)D 在BC 之间运动和它在BC 延长线上运动时的位置是不一样的,所以已给的线段长度就需要分情况去考虑到底是4+X 还是4-X.分类讨论之后利用相似三角形的比例关系即可求出CP.【答案与解析】(1)结论:CF ⊥BD ;证明如下: AB=AC ,∠ACB =45º,∴∠ABC=45º.由正方形ADEF 得 AD=AF ,∵∠DAF=∠BAC =90º,∴∠DAB=∠FAC ,∴△DAB ≌△FAC , ∴∠ACF=∠ABD .∴∠BCF=∠ACB+∠ACF= 90º.即 CF ⊥BD .(2)CF ⊥BD .(1)中结论仍成立.理由是:过点A 作AG ⊥AC 交BC 于点G ,∴AC=AG可证:△GAD ≌△CAF ∴∠ACF=∠AGD=45º∠BCF=∠ACB+∠ACF= 90º. 即CF ⊥BD(3)过点A 作AQ ⊥BC 交CB 的延长线于点Q ,①点D 在线段BC 上运动时,∵∠BCA=45º,可求出AQ= CQ=4.∴DQ=4-x ,易证△AQD ∽△DCP ,∴CP CD DQ AQ= ,∴44CP x x =-, 24x CP x ∴=-+.②点D 在线段BC 延长线上运动时,∵∠BCA=45°,∴AQ=CQ=4,∴DQ=4+x .过A 作AQ ⊥BC ,24x CP x ∴=+. 【总结升华】此题综合性强,需要综合运用全等、相似、正方形等知识点,属能力拔高性的题目.3.(2015•河南模拟)如图,正方形ABCD 的边长为6,点E 是射线BC 上的一个动点,连接AE 并延长,交射线DC 于点F ,将△ABE 沿直线AE 翻折,点B 坐在点B ′处.自主探究:(1)当=1时,如图1,延长AB ′,交CD 于点M . ①CF 的长为 ;②判断AM 与FM 的数量关系,并证明你的结论.(2)当点B ′恰好落在对角线AC 上时,如图2,此时CF 的长为 ,= .拓展运用:(3)当=2时,求sin ∠DAB ′的值.【思路点拨】(1)①利用相似三角形的判定与性质得出FC=AB即可得出答案;②利用翻折变换的性质得出∠BAF=∠MAF,进而得出AM=FM;(2)根据翻折变换的性质得出∠BAE=∠MAF,进而得出AM=MF,利用△ABE∽FCE得出答案即可;(3)根据①如图1,当点E在线段BC上时,延长AB′交DC边于点M,②如图3,当点E在线段BC 的延长线上时,延长AD交B′E于点N,分别利用勾股定理求出即可.【答案与解析】解:(1)①当=1时,∵AB∥FC,∴△ABE∽FCE,∴==1,∴FC=AB=6,②AM=FM,理由如下:∵四边形ABCD是正方形,∴AB∥DC,∴∠BAF=∠AFC,∵△ABE沿直线AE翻折得到△AB′E,∴∠BAF=∠MAF,∴∠MAF=∠AFC,∴AM=FM;(2)如图2,∵当点B′恰好落在对角线AC上时,∴∠1=∠2,∵AB∥FC,∴∠1=∠F,∴∠2=∠F,∴AC=FC,∵AB=BC=6,∴AC=FC=6,∵AB∥FC,∴△ABE∽FCE,∴===,(3)①如图1,当点E在线段BC上时,延长AB′交DC边于点M,∵AB∥CF,∴△ABE∽△FCE,∴==2,∵AB=6,∴CF=3,∴DF=CD+CF=9,由(1)知:AM=FM,∴AM=FM=9﹣DM,在Rt△ADM中,由勾股定理得:DM′2=(9﹣DM)2﹣62,解得:DM=,则MA=,∴sin∠DAB′==,②如图3,当点E在线段BC的延长线上时,延长AD交B′E于点N,由(1)知:AN=EN,又BE=B′E=12,∴NA=NE=12﹣B ′N ,在Rt △AB ′N 中,由勾股定理得:B ′N 2=(12﹣B ′N )2﹣62,解得:B ′N=, AN=,∴sin ∠DAB ′==.故答案为:6;6,. 【总结升华】此题主要考查了翻折变换的性质以及相似三角形的判定与性质和勾股定理等知识,熟练利用相关性质和进行分类讨论得出是解题关键.类型二、几何计算型问题4.已知如图,在梯形ABCD 中,24AD BC AD BC ==∥,,,点M 是AD 的中点,MBC △是等边三角形.(1)求证:梯形ABCD 是等腰梯形;(2)动点P 、Q 分别在线段BC 和MC 上运动,且60MPQ =︒∠保持不变.设PC x MQ y ==,, 求y 与x 的函数关系式;(3)在(2)中,当y 取最小值时,判断PQC △的形状,并说明理由.【思路点拨】(1)属于纯静态问题,只要证两边的三角形全等就可以了.(2)是双动点问题,所以就需要研究在P,Q 运动过程中什么东西是不变的.题目给定∠MPQ=60°,其实就是将静态的那个等边三角形与动态条件联系了起来.因为最终求两条线段的关系,所以很自然想到要通过相似三角形找比例关系.(3)条件又回归了当动点静止时的问题,由第二问所得的二次函数,很轻易就可以求出当x 取对称轴的值时y 有最小值,接下来就变成了“给定PC=2,求△PQC 形状”的问题了,由已知的BC=4,自然看出P 是中点,于是问题轻松求解.【答案与解析】(1)证明:∵MBC △是等边三角形∴60MB MC MBC MCB ===︒,∠∠∵M 是AD 中点∴AM MD =∵AD BC ∥∴60AMB MBC ==︒∠∠,60DMC MCB ==︒∠∠∴AMB DMC △≌△∴AB DC =∴梯形ABCD 是等腰梯形.(2)解:在等边MBC △中,4MB MC BC ===,60MBC MCB ==︒∠∠,60MPQ =︒∠ ∴120BMP BPM BPM QPC +=+=︒∠∠∠∠ ∴BMP QPC =∠∠∴BMP CQP △∽△ ∴PC CQ BM BP= ∵PC x MQ y ==, ∴44BP x QC y =-=-, ∴444x y x -=- ∴2144y x x =-+(3)解:PQC △为直角三角形, ∵()21234y x =-+ ∴当y 取最小值时,2x PC ==∴P 是BC 的中点,MP BC ⊥,而60MPQ =︒∠,∴30CPQ =︒∠,∴90PQC =︒∠∴PQC △为直角三角形.【总结升华】以上题目是动点问题,这一类问题的关键就在于当动点移动中出现特殊条件,例如某边相等,某角固定时,将动态问题化为静态问题去求解.如果没有特殊条件,那么就需要研究在动点移动中哪些条件是保持不变的.举一反三:【:几何综合问题 例3】【变式】已知:如图,N 、M 是以O 为圆心,1为半径的圆上的两点,B 是MN 上一动点(B 不与点M 、N 重合),∠MON=90°,BA ⊥OM 于点A ,BC ⊥ON 于点C ,点D 、E 、F 、G 分别是线段OA 、AB 、BC 、CO 的中点,GF 与CE 相交于点P ,DE 与AG 相交于点Q .(1)四边形EPGQ (填“是”或者“不是”)平行四边形;(2)若四边形EPGQ 是矩形,求OA 的值.【答案】(1)是.证明:连接OB,如图①,∵BA⊥OM,BC⊥ON,∴∠BAO=∠BCO=90°,∵∠AOC=90°,∴四边形OABC是矩形.∴AB∥OC,AB=OC,∵E、G分别是AB、CO的中点,∴AE∥GC,AE=GC,∴四边形AECG为平行四边形.∴CE∥AG,∵点D、E、F、G分别是线段OA、AB、BC、CO的中点,∴GF∥OB,DE∥OB,∴PG∥EQ,∴四边形EPGQ是平行四边形;(2)解:如图②,5.在ABCD中,过点C作CE⊥CD交AD于点E,将线段EC绕点E逆时针旋转90得到线段EF (如图1)(1)在图1中画图探究:①当P为射线CD上任意一点(P1不与C重合)时,连结EP1绕点E逆时针旋转90得到线段EC1.判断直线FC1与直线CD的位置关系,并加以证明;②当P2为线段DC的延长线上任意一点时,连结EP2,将线段EP2绕点E 逆时针旋转90得到线段EC2.判断直线C1C2与直线CD的位置关系,画出图形并直接写出你的结论.(2)若AD=6,tanB=43,AE=1,在①的条件下,设CP1=x,S11P FC=y,求y与x之间的函数关系式,并写出自变量x的取值范围.图1 备用图【思路点拨】(1)本题在于如何把握这个旋转90°的条件.旋转90°自然就是垂直关系,于是出现了一系列直角三角形,于是证角、证线就手到擒来了.(2)是利用平行关系建立函数式,但是不要忘记分类讨论.【答案与解析】(1)①直线1FG与直线CD的位置关系为互相垂直.证明:如图1,设直线1FG 与直线CD 的交点为H .∵线段1EC EP 、分别绕点E 逆时针旋转90°依次得到线段1EF EG 、,∴111190PEG CEF EG EP EF EC ∠=∠===°,,.∵1190G EF PEF ∠=-∠°,1190PEC PEF ∠=-∠°, ∴11G EF PEC ∠=∠. ∴11G EF PEC △≌△. ∴11G FE PCE ∠=∠. ∵EC CD ⊥,∴190PCE ∠=°, ∴190G FE ∠=°.∴90EFH ∠=°.∴90FHC ∠=°.∴1FG CD ⊥.②按题目要求所画图形见图1,直线12G G 与直线CD 的位置关系为互相垂直.(2)∵四边形ABCD 是平行四边形,∴B ADC ∠=∠. ∵461tan 3AD AE B ===,,, ∴45tan tan 3DE EBC B =∠==,. 可得4CE =.由(1)可得四边形EFCH 为正方形.∴4CH CE ==. FDC BAE 图1 G 2 G 1P 1 H P 2①如图2,当1P 点在线段CH 的延长线上时,∵1114FG CP x PH x ===-,, ∴11111(4)22P FG x x S FG PH -=⨯⨯=△. ∴212(4)2y x x x =->. ②如图3,当1P 点在线段CH 上(不与C H 、两点重合)时,∵1114FG CP x PH x ===-,, ∴11111(4)22P FG x x S FG PH -=⨯=△. ∴212(04)2y x x x =-+<<. ③当1P 点与H 点重合时,即4x =时,11PFG △不存在.综上所述,y 与x 之间的函数关系式及自变量x 的取值范围是212(4)2y x x x =->或212(04)2y x x x =-+<<. 【总结升华】本题着重考查了二次函数的解析式、图形的旋转变换、三角形全等、探究垂直的构成情况等重要知识点,综合性强,能力要求较高.考查学生分类讨论,数形结合的数学思想方法. 举一反三: 【变式】已知,点P 是∠MON 的平分线上的一动点,射线PA 交射线OM 于点A ,将射线PA 绕点P 逆时针旋转交射线ON 于点B ,且使∠APB+∠MON=180°.(1)利用图1,求证:PA=PB ;(2)如图2,若点C是AB与OP的交点,当S△POB=3S△PCB时,求PB与PC的比值;(3)若∠MON=60°,OB=2,射线AP交ON于点D,且满足且∠PBD=∠ABO,请借助图3补全图形,并求OP的长.【答案】(1)作PE⊥OM,PF⊥ON,垂足为E、F∵四边形OEPF中,∠OEP=∠OFP=90°,∴∠EPF+∠MON=180°,已知∠APB+∠MON=180°,∴∠EPF=∠APB,即∠EPA+∠APF=∠APF+∠FPB,∴∠EPA=∠FPB,由角平分线的性质,得PE=PF,∴△EPA≌△FPB,即PA=PB;。
中考数学总复习《几何综合问题(一次函数的实际综合应用)》专项提升训练(带答案)

中考数学总复习《几何综合问题(一次函数的实际综合应用)》专项提升训练(带答案)学校:___________班级:___________姓名:___________考号:___________1.点P 是平面直角坐标系中的一点且不在坐标轴上,过点P 向x 轴,y 轴作垂线段,若垂线段的长度的和为2,则点P 叫做“好垂点”.例如:如图中的()11P ,是“好垂点”.(1)在点()1,2A ,()133522B C ⎛⎫-- ⎪⎝⎭,,,中,是“好垂点”的点为 ; (2)求函数21y x =-+的图象上的“好垂点”的坐标.(3)若二次函数223y x bx =+-的图象上存在4个“好垂点”,求b 的取值范围.(4)已知T 的圆心T 的坐标为()10-,,半径为r . 若T 上存在“好垂点”,则r 的取值范围是 .2.如图,在平面直角坐标系中,直线2y x =+与x 轴、y 轴分别交于A 、B 两点,点()2,C m 为直线2y x =+上一点,直线y x b =-+过点C .(1)求m 和b 的值;(2)直线y x b =-+与x 轴交于点D ,动点P 从点D 开始以每秒1个单位的速度向x 轴负方向运动(点P 不与点D ,点A 重合).若点P 在线段DA 上,设点P 的运动时间为t 秒. ①若ACP △的面积为10,求t 的值;②是否存在t 的值,使ACP △是以AP 为腰的等腰三角形?若存在,求出t 的值;若不存在,请说明理由.为顶点的三角形与BCO相似?若存在,求、C分别在>.AB BC为顶点的三角形与OAC相似?两点,点(2C,(1)求m 和b 的值;(2)直线12y x b =-+与x 轴交于点D ,动点P 从点D 开始以每秒1个单位的速度向x 轴负方向运动.设点P 的运动时间为t 秒.①若点P 在线段DA 上,且ACP △的面积为10,求t 的值;②是否存在t 的值,使ACP △为等腰三角形?若存在,直接写出t 的值;若不存在请说明理由. 6.如图,在平面直角坐标系中,正方形ABCD 的顶点A 为()2,0,顶点D 为()0,4.(1)直接写出直线BC 的解析式:____________;(2)点M 与点A 关于y 轴对称,点N 为正方形边上一点,且45DMN ∠=,直接写出点N 的坐标:____________;(3)将正方形沿y 轴向下平移(0)t t >个单位,直至点D 落在x 轴上.设正方形在x 轴下方的部分面积为S ,求S 关于t 的函数关系式,并写出相应自变量t 的取值范围.7.如图,在平面直角坐标系中,直线24y x =-+与x 轴交于点A ,与y 轴交于点B ,过点B 的直线交x 轴于C (点C 在A 左侧),且ABC 面积为10.(1)求点C的坐标及直线BC的解析式;(2)如图1,设点F为线段AB中点,点G为y轴上一动点,连接FG,以FG为边向FG左侧作等腰直角FGQ,其中90∠=︒,在G点的运动过程中,当顶点Q落在直线BC上时,求点G的坐FGQ标;(3)如图2,若M为线段BC上一点,且满足AMB AOB=S S△△,点E为直线AM上一动点,在x轴上是否存在点D,使以点D,E,B,C为顶点的四边形为平行四边形?若存在,请求出点D的坐标;若不存在,请说明理由.8.在同一平面直角坐标系中,我们规定点的两种移动方式:从点(,)x y移动到点(2,1)++称为x y一次甲方式移动;从点(,)x y移动到点(1,3)x y++称为一次乙方式移动.(1)若原点O经过两次甲方式移动,得到点M;原点O经过两次乙方式移动,得到点N.设过点M,N的直线为1l,求直线1l的解析式;(2)若原点O连续移动10次(每次按甲方式或乙方式移动),最终移动到点Q.试说明:无论每次按甲方式还是乙方式移动,最终点Q都落在一条确定的直线上;设这条直线为2l,请求出直线2l的解析式;(3)将(2)中的直线2l向下平移30个单位得到直线3l.分别在上述直线1l2l3l上取点AB C设点A B C的横坐标分别为a b c且a b试探究:当A B C三点共线时a b c之间有何数量关系?说明理由.9.【问题提出】△的面积为3 则ABC的面积(1)如图①点D为ABC的边AC的中点连接BD若ABD为_______;【问题探究】(2)如图②在平面直角坐标系中点A在第一象限连接OA作AB x⊥轴于点B若2AB OB = 25OA = 过点B 的直线l 将OAB 分成面积相等的两部分 求直线l 的函数表达式;【问题解决】(3)如图③ 在平面直角坐标系中 四边形OABC 是某市将要筹建的高新技术开发区用地示意图 其中O 为坐标原点 ()()()24,728,425,0A B C ,, 为了方便驻区单位 计划过点O 修一条笔直的道路1l (路宽不计) 并且使直线1l 将四边形OABC 分成面积相等的两部分 记直线1l 与AB 所在直线的交点为D 再过点A 修一条笔直的道路2l (路宽不计) 并且使直线2l 将OAD △分成面积相等的两部分 你认为直线1l 和2l 是否存在?若存在 请求出直线1l 和2l 的函数表达式;若不存在 请说明理由.10.如图 在矩形ABCD 中 4AD = 6AB = 动点P Q 均以每秒1个单位长度的速度分别从点D 点C 同时出发 其中点P 沿折线D A B →→方向运动 点Q 沿折线C B A →→方向运动 当两者相遇时停止运动.运动时间为t 秒 PQD 的面积为y .(1)请直接写出y 关于t 的函数表达式并注明自变量t 的取值范围;(2)在给定的直角坐标系中画出这个函数的图象 并写出该函数的一条性质; (3)结合函数图象 直接写出PQD 的面积大于4时t 的取值范围.11.如图 在平面直角坐标系中 直线AB 交x 轴 y 轴于(,0)A a 和(0,)B b 两点 其中a 和b 是方程212320x x -+=的两个实数根 且b a >.使PBC的面积最大?若存在PBC面积的最大值.若没有13.如图点()4,C t在第四象限段OB上.连接于点E交折线段(1)求点A B的坐标;(2)设点E F的纵坐标分别为1y2y当04≤≤时12m-为定值求t的值;y y(3)在(2)的条件下分别过点E F作EG FH垂直于y轴垂足分别为点G H当06≤≤时求长方形EGHF周长的最大值.m14.已知四边形OABC是边长为4的正方形分别以OA OC、所在的直线为x轴y轴建立如图所示的平面直角坐标系直线l经过A C、两点.(1)求直线l的函数表达式;(2)如下图若点D是OC的中点E是直线l上的一个动点求使OE DE+取得最小值时点E的坐标.(3)如下图过点O作AC的垂线垂足为点M点P是直线l上的一个点点Q是y轴上的一个点以,,O P Q为顶点的三角形与OMP全等请直接写出所有符合条件的点P的坐标.15.如图1 在平面直角坐标系xoy中等腰直角AOB的斜边OB在x轴上顶点A的坐标为()2,2与AOB重叠部分为轴对称图形时轴交于点(4,0)A-使得QAB为等腰直角三角形?若存在参考答案:5b<(4)2-或8423.(1)1 (2)4 (3)352+或352或32或3132+或3132-+4.(1)()4,8- (2)16y x=- (3)存在 ()()()()0,2,0,4,0,6,0,12---5.(1)4m = 5b = (2)①7 ②存在 4t =秒或()1242-秒或()1242+秒或8秒6.(1)214=-+y x (2):10877,⎛⎫ ⎪⎝⎭或401877⎛⎫⎪⎝⎭, (3)当02t <≤时 254S t =;当24t <≤时 55S t =-7.(1)443y x =+ ()3,0C -; (2)1230,7G ⎛⎫ ⎪⎝⎭或()20,1G -; (3)19,03⎛⎫- ⎪⎝⎭或1,03⎛⎫ ⎪⎝⎭或31,03⎛⎫ ⎪⎝⎭. 8.(1)210y x =-+ (2)250y x =-+ (3)43b c a =-9.(1)6;(2)24y x =-+;(3)存在 直线1l 的函数表达式为17y x = 直线2l 的函数表达式为152y x =- 10.(1)()()30442847t t y t t ⎧<≤⎪=⎨-+<<⎪⎩ (2)当04x <≤时 y 随x 的增大而增大 当47x <≤时 y 随x 的增大而减小 (3)463t <<解题过程:(1)解:依题意 44614AD BC AB ++=++=则相遇时间为14711=+; DP CQ t ==当04t <≤时 点P 在AD 上 Q 在BC 上 ∴1632y t t =⨯=当47t <≤时 142PQ t =-∴()11414222y PQ AD t =⨯=⨯⨯-428t =-+4∴4a = 8b =∴224845AB =+=;(2)设OBD ∠的度数为m ︒ 而90BOE ∠=︒ ∴90BEO m ∠=︒-︒∴90FED BEO m ∠=∠=︒-︒∵DE 的垂直平分线交x 轴负半轴于点F∴FE FD =∴90FED FDE m ∠=∠=︒-︒∴()1802902DFE m m ∠=︒-︒-︒=︒;(3)如图 过B 作BQ DF ⊥于Q 过D 作DT BO ⊥于T由(2)得90FDE FED m ∠=∠=︒-︒∵BF BD =∴90BFD BDF m ∠=∠=︒-︒∴()1802902FBD m m ∠=︒-︒-︒=︒∵BF BD = BQ DF ⊥∴FBQ DBQ DBT m ∠=∠=∠=︒而DT BO ⊥ DQ BQ ⊥∴FQ DQ DT == 设FQ DQ DT x === OT y =FOD BOD S S = DFE BOE S S =2OE xy = 解得4xy OE =FOD BOD S S =可得:24xy y x ⎛⎫+ ⎪28320y +-=解得:434y =-12.(1)223y x x =--+(2)存在()1,2Q -使得QAC △的周长最小(3)存在31524P ⎛⎫- ⎪⎝⎭,使得PBC 面积最大 最大为278 解题过程:(1)解:将1,0A ()3,0B -代入2y x bx c =-++中得10930b c b c -++=⎧⎨--+=⎩ ∴23b c =-⎧⎨=⎩. ∴抛物线解析式为:223y x x =--+;(2)解:∵抛物线解析式为()222314y x x x =--+=-++ ∴抛物线的对称轴为直线=1x -连接BQ由对称性可知BQ AQ =∴AQC 的周长CA AC AQ AC CQ BQ =++=++ ∵A C 为定点∴AC 为定值∴当CQ BQ +最小时 AQC 的周长最小∴当B C Q 三点共线时 CQ BQ +最小 即AQC 的周长最小在223y x x =--+中 当0x =时 2233y x x =--+=C ∴的坐标为()0,3设直线BC 解析式为y kx b '=+∴303k b b ''-+=⎧⎨=⎩∴13k b =⎧⎨='⎩3yx 3y x 中 当时 1y =-+()1,2-∴存在()1,2Q -使得QAC 的周长最小;)解:设()PBPC S S =△∴当S 四边形BPCO S ∴四边形12BE =⋅∴点P 坐标为31524⎛⎫- ⎪⎝⎭,∴存在31524P ⎛⎫- ⎪⎝⎭,使得PBC 面积最大 最大为278.13.(1)()0,9A ()6,0B(2)6-(3)26解题过程:(1)解:∵直线392y x =-+交y 轴于点A 交x 轴于点B∴当0y =时 得:3902x -+= 解得:6x =当0x =时 得:9y =∴()0,9A ()6,0B ;(2)设OC 的解析式为y kx = 过点()4,C t ∴4t k =∴4tk =∴OC 的解析式为()04ty x t =<∵点(),0P m 在线段OB 上 过点P 作x 轴的垂线 交边AB 于点E 交折线段OCB 于点F 且点EF 的纵坐标分别为1y 2y 04m ≤≤∴1392y m =-+ 24ty m =∴1233992424t t y y m m m ⎛⎫-=-+-=-+ ⎪⎝⎭∵12y y -为定值 即3924t m ⎛⎫-+ ⎪⎝⎭为定值∴3024t+=解得:6t =-;(3)①当04m ≤≤时129EF y y =-=(定长) 在点P 运动到图中点P ' 此时直线经过点C 即4m =∴044k b b=+⎧⎨=⎩ 解得14k b =-⎧⎨=⎩ 直线l 的函数表达式4y x =-+;(2)解:如图所示 连接BE BD ,由正方形的性质可得OA BA BC OC ===又∵AC AC =∴()SSS OAC BAC △≌△∴OAE BAE ∠=∠又∵AE AE =∴()SAS OAE BAE △≌△∴OE BE =∴DE OE DE BE +=+∴当B D E 、、三点共线时 DE BE +最小 即此时OE DE +取得最小值 设DB 所在直线为()1110y k x b k =+≠∵点D 是OC 的中点 ()04C ,∴()02D ,又∵()44B ,∴111442k b b =+⎧⎨=⎩∴11122k b ⎧=⎪⎨⎪=⎩ ∴直线DB 为122y x =+33⎝⎭∴()224x x +=∴422x =-在4y x =-+中 当422x =-时 22y =∴P 点坐标为()42222-,; 如图所示 当POM OPQ △≌△时同理可得PQ CQ OM CM === 24OC OM == ∴22PQ CQ OM CM ====∴422OQ =+∴P 点坐标为()22422-+,; 如图所示 当OMP PQO ≌△△时∴PM OQ OM PQ ==,同理可得2222OM CM OC === 设OQ PM x == 则4CQ PQ x ==- 242222CP CQ x CM MP x ==-=+=+ 解得422x =-直线AOB COP S S S ∆∆=-1122AM OB OP PC =⋅-⋅2111424222m m m =⨯⨯-⋅=-.当24m <<时 如图②.COB AOP S S S ∆∆=-1122PC OB OP AM =⋅-⋅114222m m m =⨯⨯-⨯=.当4m >时 如图③COP AOB S S ∆∆=-1122PC OP OB AM =-2111424222m m m =-⨯⨯=-.与AOB重叠部分为轴对称图形无重叠部分(3)Q 的坐标为(3,7)-或(7,4)-或7(2-7)2 解题过程:(1)在94y x =中 令2x =得92y =9(2,)2C ∴; 设直线1l 的解析式为y kx b =+ 把(4,0)A - 9(2,)2C 代入得: 40922k b k b -+=⎧⎪⎨+=⎪⎩解得343k b ⎧=⎪⎨⎪=⎩ ∴直线1l 的解析式为334y x =+; (2)如图:设(,0)M m 则3(,3)4D m m + 9(,)4E m m 2DE =39|3|244m m ∴+-= 3322m ∴-=或3322m -=- 解得23m =或103m = M ∴的坐标为2(3 0)或10(3 0); (3)在334y x =+中 令0x =得3y =(0,3)B ∴①当B 为直角顶点时 过B 作BH y ⊥轴于H 如图:QAB 为等腰直角三角形 AB QB ∴= 90QBA ∠=︒ 90ABO QBH BQH ∴∠=︒-∠=∠ 90AOB QHB ∠=︒=∠ (AAS)ABO BQH ∴≌ 4OA BH ∴== 3OB QH == 7OH OB BH ∴=+= Q ∴的坐标为(3,7)-; ②当A 为直角顶点时,过Q 作QT x ⊥轴于T , 如图:同理可得(AAS)AQT BAO ≌ 3AT OB ∴== 4QT OA == 7OT OA AT ∴=+= Q ∴的坐标为(7,4)-; ③当Q 为直角顶点时,过Q 作WG y ⊥轴于G 过A 作AW WG ⊥于W ,如图:同理可得(AAS)AQW QBG ≌ AW QG ∴= QW BG = 设(,)Q p q ∴(4)3q p p q =-⎧⎨--=-⎩ 解得7272p q ⎧=-⎪⎪⎨⎪=⎪⎩Q ∴的坐标为7(2-, 7)2; 综上所述 Q 的坐标为(3,7)-或(7,4)-或7722⎛⎫- ⎪⎝⎭,。
浙江省中考数学总复习 考点跟踪训练45 代数应用性问题(1)(无答案)(2021年整理)

浙江省中考数学总复习考点跟踪训练45 代数应用性问题(1)(无答案)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(浙江省中考数学总复习考点跟踪训练45 代数应用性问题(1)(无答案))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为浙江省中考数学总复习考点跟踪训练45 代数应用性问题(1)(无答案)的全部内容。
考点跟踪训练45 代数应用性问题(1)A组基础过关练一、选择题1。
(2014六盘水)青蛙是我们人类的朋友,为了了解某池塘里青蛙的数量,先从池塘里捕捞20只青蛙,作上标记后放回池塘,经过一段时间后,再从池塘中捕捞出40只青蛙,其中有标记的青蛙有4只,请你估计一下这个池塘里有多少只青蛙?( )A。
100只 B. 150只C。
180只 D. 200只2。
(2013山西)王先生到银行存了一笔三年期的定期存款,年利率是4。
25%,若到期后取出得到本息和(本金+利息)33852元.设王先生存入的本金为x元,则下面所列方程正确的是( )A。
x+3×4。
25%x=33825 B. x+4。
25%x=33825C。
3×4.25%x=33825 D。
3(x+4。
25%x)=338253. 如图所示的两台天平保持平衡,已知每块巧克力的重量相等,且每个果冻的重量也相等,则每块巧克力和每个果冻的重量分别为( )A。
10g,40g B. 15g,35gC。
20g,30g D. 30g,20g4。
(2013东营)要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排21场比赛,则参赛球队的个数是()A. 5个 B。
浙江省中考数学总复习 考点跟踪训练47 几何应用性问题(无答案)

考点跟踪训练47 几何应用性问题A 组 基础过关练一、选择题1. (2014黄石)如图,一个矩形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度数是( )A. 30°B. 60°C. 90°D. 120°2. (2014扬州)如图,已知正方形的边长为1,若圆与正方形的四条边都相切,则阴影部分的面积与下列各数最接近的是( )A. 0.1B. 0.2C. 0.3D. 0.43. (2014荆州)如图,已知圆柱底面的周长为4dm ,圆柱高为2dm ,在圆柱的侧面上,过点A 和点C 嵌有一圈金属丝,则这圈金属丝的周长最小为( )A. 42dmB. 22dmC. 25dmD. 45dm4. (2014南通)如图,一个半径为r 的圆形纸片在边长为a(a≥23r)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( )A. π3r 2B. (33-π)3r 2C. (33-π)r2D. πr2二、填空题5. (2013宿迁)如图,为测量位于一水塘旁的两点A、B间的距离,在地面上确定点O,分别取OA、OB的中点C、D,量得CD=20m,则A、B之间的距离是________m.6. (2013泰安)如图,某海监船向正西方向航行,在A处望见一艘正在作业渔船D在南偏西45°方向,海监船航行到B处时望见渔船D在南偏东45°方向,又航行了半小时到达C 处,望见渔船D在南偏东60°方向,若海监船的速度为50海里/小时,则A、B之间的距离为________海里(取3≈1.7 ,结果精确到0.1海里).7. (2014襄阳)如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为________m(结果保留根号)8. (2013福州)如图,由7个形状、大小完全相同的正六边形组成网格,正六边形的顶点称为格点.已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是________.三、解答题9. (2013绵阳)对正方形ABCD进行分割,如图1,其中E、F分别是BC、CD的中点,M、N、G分别是OB、OD、EF的中点,沿分化线可以剪出一副“七巧板”,用这些部件可以拼出很多图案,图2就是用其中6块拼出的“飞机”.若△GOM的面积为1,求“飞机”的面积.B组能力提升练1. (2014深圳)小明去爬山,在山脚看山顶角度为30°,小明在坡比为5∶12的山坡上走1300米,此时小明看山顶的角度为60°,求山高( )A. 600-250 5B. 6003-250C. 350+350 3D. 500 32. (2013漳州)如图,一个宽为2厘米的刻度尺(刻度单位:厘米),放在圆形玻璃杯的杯口上,刻度尺的一边与杯口外沿相切,另一边与杯口外沿两个交点处的读数恰好是3和9,那么玻璃杯的杯口外沿半径为________厘米.3. (2013邵阳)如图所示,某窗户由矩形和弓形组成,已知弓形的跨度AB=3cm,弓形的高EF=1cm,现计划安装玻璃,请帮工程师求出AB所在圆O的半径r.。
浙江省中考数学一轮复习 考点跟踪训练48 几何型综合问题(无答案)

一、选择题(每小题6分,共30分)1.(2011·潜江)如图,AB∥EF∥CD,∠ABC=46°,∠CEF =154°,则∠BCE 等于( )A .23°B .16°C .20°D .26°2.(2011·枣庄)如图,这是一个正面为黑、反面为白的未拼完的拼木盘,给出如下四块正 面为黑、反面为白的拼木,现欲拼满拼木盘使其颜色一致,那么应该选择的拼木是( )3.(2012·荆门)如图,△ABC 是等边三角形,P 是∠ABC 的平分线BD 上一点,PE⊥AB 于 点E ,线段BP 的垂直平分线交BC 于点F ,垂足为点Q.若BF =2,则PE 的长为( )A .2B .2 3C. 3 D .34.(2012·恩施)如图,菱形ABCD 和菱形ECGF 的边长分别为2和3,∠A=120°,则图中 阴影部分的面积是( )A. 3 B .2C .3 D. 25.(2012·宜宾)如图,在四边形ABCD 中,DC∥AB,CB⊥AB,AB =AD ,CD =12AB ,点E、F分别为AB、AD的中点,则△AEF与多边形BCDFE的面积之比为( )A.17B.16C.15D.14二、填空题(每小题6分,共30分)6.(2011·黄石)有甲、乙两张纸条,甲纸条的宽是乙纸条宽的2倍,如图.将这两张纸条交叉重叠地放在一起,重合部分为四边形ABCD,则AB与BC的数量关系为________.7.(2011·宁波)如图,在△ABC中,AB=AC,D、E是△ABC 内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6 cm,DE=2 cm,则BC=________cm.8.(2012·武汉)在平面直角坐标系中,点A的坐标为(3,0),点B为y轴正半轴上的一点,点C是第一象限内一点,且AC=2.设tan∠BOC=m,则m的取值范围是________.9.(2012·绍兴)如图,在矩形ABCD中,点E、F分别在BC、CD上,将△ABE沿AE折叠,使点B落在AC上的点B′处,又将△CEF沿EF折叠,使点C落在EB′与AD的交点C′处.则BC∶AB的值为________.10.(2012·陕西)如图,从点A(0,2)发出的一束光,经x轴反射,过点B(4,3),则这束光从点A到点B所经过路径的长为________.三、解答题(每小题20分,共40分)11.(2012·恩施)如图,用纸折出黄金分割点:裁一张正方的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落到线段EA上,折出点B的新位置为B′,因而EB′=EB.类似地,在AB上折出点B″,使AB″=AB′,这时点B″就是AB的黄金分割点.请你证明这个结论.12.(2012·盐城)如图所示,AC⊥AB,AB=2 3,AC=2,点D是以AB为直径的半圆O 上一动点,DE⊥CD交直线AB于点E,∠DAB=α(0°<α<90°).(1)当α=18°时,求BD的长;(2)当α=30°时,求线段BE的长;(3)若要使点E在线段BA的延长线上,则α的取值范围是________.(直接写出答案)四、附加题(共20分)13.(2012·连云港)已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3.(1)如图1,P为AB边上的一点,以PD、PC为边作PCQD,请问对角线PQ、DC的长能否相等,为什么?(2)如图2,若P为AB边上一点,以PD、PC为边作PCQD,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由;(3)若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE、PC为边作PCQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由;(4)如图3,若P为DC边上任意一点,延长PA到E,使AE=nPA(n为常数),以PE、PB为边作PBQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.。
2023年浙教版数学平面几何应用题及答案

2023年浙教版数学平面几何应用题及答案一、直线和点的方程1. 已知直线L过点A(-3, 4)且与x轴垂直,求直线L的方程。
解析:直线L与x轴垂直,说明直线L的斜率为0。
由点斜式的定义可知直线L的方程为:y - y1 = m(x - x1),其中x1为已知点的横坐标,y1为已知点的纵坐标,m为斜率。
代入已知条件可得:y - 4 = 0(x + 3)y - 4 = 0y = 4因此,直线L的方程为y = 4。
2. 已知直线L过点A(2, -5)且平行于y轴,求直线L的方程。
解析:直线L平行于y轴,说明直线L的斜率为不存在。
由点斜式的定义可知直线L的方程为:x - x1 = 0,其中x1为已知点的横坐标。
代入已知条件可得:x - 2 = 0因此,直线L的方程为x = 2。
二、直线的交点和距离3. 已知直线L1过点A(1, 3),直线L2过点B(-2, 5),求直线L1与直线L2的交点坐标。
解析:设直线L1的方程为y = k1x + b1,直线L2的方程为y = k2x + b2。
其中k1、k2为直线的斜率,b1、b2为直线的截距。
由已知条件可得到以下方程组:k1 * 1 + b1 = 3k2 * (-2) + b2 = 5解方程组可得到直线L1与直线L2的交点坐标为(2, 1)。
4. 已知直线L1过点A(1, 2),直线L2过点B(4, 6),求直线L1与直线L2的距离。
解析:直线L1的方程为y = k1x + b1,直线L2的方程为y = k2x + b2。
其中k1、k2为直线的斜率,b1、b2为直线的截距。
设直线L的斜率为k,则直线L的法线的斜率为-k1/k。
由已知条件可得到以下方程组:k1 * 1 + b1 = 2k2 * 4 + b2 = 6-1/k = (k2 - k1)/(4 - 1)解方程组可得到直线L1与直线L2的距离为sqrt((k2 - k1)^2 + (b2 -b1)^2)。
三、平行线和垂线5. 已知直线L1过点A(2, 3),直线L2过点B(1, 4),判断直线L1与直线L2的关系。
浙教版初中数学几何计算型综合问题(含答案)

几何计算型综合问题【考点透视】几何计算型综合问题,是以计算为主线的综合各种几何知识的问题.在近年全国各地中考试卷中占有相当的分量.这类问题的主要特点是包含知识点多、覆盖面广、逻辑关系复杂、解法灵活.考查方式偏重于考查考生分析问题、探究问题、综合应用数学知识解决实际问题的能力,要求学生熟练掌握三角形、四边形、三角函数、圆等几何知识,较熟练地应用转化思想、方程思想、分类讨论思想、数形结合思想等常见的数学思想. 解题时必须在充分利用几何图形的性质及题设的基础上挖掘几何图形中隐含的数量关系和位置关系,在复杂的“背景”下辨认、分解基本图形,或通过添加辅助线补全或构造基本图形,并善于联想所学知识,突破思维障碍,合理运用方程等各种数学思想才能解决.值得注意的是近年中考几何综合计算的呈现形式多样,如折叠类型、探究型、开放型、运动型、情境型等,背景鲜活,具有实用性和创造性,在考查考生计算能力的同时,考查考生的阅读理解能力、动手操作能力、抽象思维能力、建模能力……力求引导考生将数学知识运用到实际生活中去.【典型例题】例1 在生活中需要测量一些球(如足球、篮球…)的直径,某学校研究性学习小组,通过实验发现下面的测量方法:如图,将球放在水平的桌面上,在阳光的斜射下,得到球的影子AB,设光线AD、CB分别与球相切于点E、F,则E、F即为球的直径.若测得AB的长为41.5cm,∠ABC=37°.请你计算出球的直径(精确到1cm)分析:本题实际上是解直角梯形ABFE中的问题,作AG⊥CB于G,在Rt△ABG中,求出AG即可.解:作AG⊥CB于G,∵AD、CB分别与圆相切于E、F,∴EF⊥FG,EF⊥EA,∴四边形AGFE是矩形,∴AG=EF在Rt△ABG中,AB=41.5,∠ABG=37°,∴AG=AB·sin∠ABG=41.5×sin37°≈25.∴球的直径约为25cm.说明:将几何计算题与研究性学习问题和方案设计问题有机的结合起来,是近年中考题的又一热点.这类题一般难度不太大,关键是考查建模能力.例2.在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在DABCQ P直线翻折得△AB ’E ,那么△AB ’E 与四边形AECD 重叠部分的面积是 .分析:解答本题首先要根据题意,画出图形(如图11-2)然后根据对称性和相关几何知识进行求解.解:在Rt △ABE 中,∵∠B=45°,AB=2,∴AE=BE=2 ,∴S △ABE =1. 由翻折知:△AB ’E ≌△ABE ,∴EB ’=EB=2 ∴B ’C=BB ’-BC=22-2, ∵四边形ABCD 是菱形,∴CF ∥BA .∴∠ B ’FC=∠B ’AB=90°, ∠B ’CF=∠B=45° ∴CF=2222-=BC ∴S △B’FC =221CF =32-2∴S 阴=S △AB’E -S △CFB’=22-2.说明:图形折叠问题的本质是全等变换, 也是近年中考题中的一个亮点.这类问题的解决方法是要抓住因折叠而形成的等线段和等角,这些相等关系是解决问题的关键.常用代数方程求解.例3.如图,在矩形ABCD 中,AB=12cm ,BC=6cm ,点P 沿AB 边从点A 开始向点B 以2cm/s 的速度移动;点Q 沿DA 边从点D 开始向点A 以1cm/s 的速度移动.如果P 、Q 同时出发,用t(s)表示移动的时间(0≤t ≤6),那么: ⑴当t 为何值时,△QAP 为等腰直角三角形?⑵求四边形QAPC 的面积;提出一个与计算结果有关的结论; ⑶当t 为何值时,以点Q 、A 、P 为顶点的三角形与△ABC 相似?分析:⑴中应由△QAP 为等腰直角三角形这一结论,需补充条件AQ=AP,由AQ=6-t ,AP=2t ,可求出t 的值;⑵中四边形QAPC 是一个不规图形,其面积可由矩形面积减去△DQC 与△PBC 的面积求出;⑶中由于题目中未给出三角形的相似对应方式,因此须分类讨论.解:⑴AP=2t ,DQ=t ,QA=6-t ,当QA=AP ,即6-t=2t ,t=2(s )时,△QAP 为等腰直角三角形;⑵S △DQC =21·12·t=6t, S △PBC =21·6·(12-2t)=36-6t, ∴S 四边形QAPC =12·6-6t -(36-6t )=36(cm 2),由计算结果可见:在P 、Q 两点移动的过程中,四边形QAPC 的面积始终保持不变; ⑶∵∠QAP=∠ABC=90°,①当BC AP AB QA =时,△QAP ∽△ABC ,∴62126tt =-,解之得t=1.2(s ); ②当AB AP BC QA =时,△PAQ ∽△ABC ,∴12266tt =-,解之得t=3(s ). 故当t=1.2s 或3s 时,以点Q 、A 、P 为顶点的三角形与△ABC 相似.说明:本例是动态几何题,同时也是一道探究题.要求学生具有一定的发现、归纳和表达能力,这就要求我们通过计算分析,抓其本质,揭示出变中不变的规律.其结论也可提出:“P 、Q 两点到对角线AC 的距离之和保持不变”,四边形QAPC 的面积也可由△QAC 与△CAP 的面积求出,;⑶中考察了分类讨论的数学思想,结论具有一定的开放性.例4. 当你进入博物馆的展览厅时,你知道站何处观赏最理想?如图,设墙壁上的展品最高处点P 距离场面a 米,最低处点Q 距离场面b 米,观赏者的眼睛点E 距离地面m 米.当过点P 、Q 、E 三点的圆与过点E 的水平线相切于点E 时,视角∠PEQ 最大,站在此处观赏最理想.(1)设点E 到墙壁的距离为x ,求a 、b 、m 、x 的关系式; (2)当a=2.5,b=2,m=1.6时,求:○1和墙壁的距离为x 米;○2视角∠PEQ 的度数(精确到1度) 解:(1)∵水平直线HE 切⊙O 于点E. ∴HE 2=QH ·HP又HE=x ,QH=b -m ,PH=a -m , ∴x 2=(a -m )(b -m ).(2)○1当a=2.5,b=2,m=1.6时,由(1)中所得: x 2=(2.5-1.6)(2-1.6)∴x=0.6 ∴点E 与墙壁距离x 的值为0.6米.○2作OD ⊥PR 于D ,则∠POQ=2∠POD ,∵∠POQ=2∠PEQ , ∴∠PEQ=∠POD.在Rt △POD 中,tan ∠POD=125=OD PD ∴∠PEQ=23°说明:将几何计算题富于一个实际情境是中考中的一个新视点,符合新课程标准的精神,在今后的中考命题将会有很强的生命力,解这类题时,要能从实际中抽象出纯数学问题,然后利用相关知识解决问题.复习中应注意对常规题进行演变,有对针性训练.例5.如图,方形ABCD 的AB 边为直径,在正方形内部作半圆,圆心为O ,DF 切半圆于F点E ,交AB 的延长线于点F ,BF=4. 求:(1)cos ∠F 的值;(2)BE 的长.分析:(1)要求cos ∠F 的值,就要把∠F “放”到直角三角形中,由于DF 是半圆切线,只要连结OF 即可,然后利用相似三角形与切割线定理,求出OF 、EF ;(2)利用勾股定理和相似三角形即可求得.解:(1)连结OE.∵DF 切半圆于E , ∴∠OEF=90°,在正方形ABCD 中,AB=AD ,∠DAF=90°, ∴∠OEF=∠DAF.又∵∠F 为公共角,∴△OEF ∽△DAF. ∴21===AB OE DA OE AF EF .即AF=2EF. ∵DF 切半圆O 于E ,∴EF 2=FB ·FA=BF ·2EF , ∴EF=2BF=8,AF=2EF=16.∴AB=AF -BF=12,FO=21AB+BF=21×12+4=10. 在Rt △OEF 中,cos ∠F=54108==FO EF . (2)连结AE ,∵DF 切半圆于E ,∴∠EAF=∠BEF. ∵∠F=∠F ,∴△BEF ∽△EAF. ∴21168===AF EF EA BE .设BE=k(k >0),则AE=2k , ∵AB 为半圆O 的直径, ∴∠AEB=90°.在Rt △AEB 中,AE 2+BE 2=AB 2,(2k )2+k 2=122, ∴BE=k=5512. 说明:在相似形、圆等问题中渗透三角形函数知识、方程知识,围绕有关相似比、面积之比来命题是近年中考题命题又一新特点.解这类题要善于把三角函数的值与线段比相互转化,并能设参数来表示有关线段,运用勾股定理或相似三角形的有关比例式来解决.例6.已知:如图与⊙O 2相交于A 、B 两点,O 1在⊙O 2上,⊙O 2的弦BC 切⊙O 1与B ,延长BO 1、CA 交于点P ,PB 与⊙O 1交于点D .O 2O 1图①图②⑴求证:AC 是⊙O 1的切线;⑵如果PD=1,⊙O 1的半径为2,求BC 的长.分析:⑴由于AC 与⊙O 1有共公点A ,只要证AC ⊥AO 1即可. ⑵欲证AD ∥O 1C ,借公共弦这一“桥梁”.证∠ACO 1=∠PAD , ⑶根据图形借助切割线及其推论或三角形相似,通过线段比来解决.解:⑴连结AO 1,∵BC 是⊙O 1的切线,∴∠O 1BC=90°, ∵四边形AO 1BC 是⊙O 2的内接四边形,∴∠O 1BC+∠O 1AC=180°.∴∠O 1AC=90°,∴AC 是⊙O 1的切线 ⑵连结AB,∵PC 切⊙O 1于点A, ∴∠PAD=∠ABP, 又∠ACO 1=∠ABO 1 ,∴∠PAD=∠ACO 1 ∴AD ∥O 1C⑶∵PC 是⊙O 1的切线,PB 是⊙O 1的割线,∴PA 2=PD·PB ∵PD=1,PB=5,∴PA=5∵AC 、BC 分别切⊙O 1于A 、B ∴O 1B ⊥BC ,O 1A ⊥PC ∴∠PBC=∠PAO 1=90° 又∠P=∠P ∴△PBC ∽△PAO 1 ∴552,1==BC PA PB AO BC 即 ∴BC=52 说明:解几何计算综合题要善于把复杂的几何图形“分解”为若干个基本图形,并综合这些基本图形的性质及图形中元素的内在联系去思考,则能快速找到解题途径.如本题若把原图分解为下列①②两个图形,则⑶的解题思路一目了然.例7.有一长方形的餐厅,长10m ,宽7m ,现只摆放两套同样大小的圆桌和椅子,一套圆桌和椅子占据的地面部分可看成半径为1.5m 的圆形(如图1所示).在保证通道最狭窄处的宽度不小于0.5m 的前提下,问此餐厅内能否摆下三套或四套同样大小的圆桌和椅子呢?请在摆放三套或四套的两种方案中选取一种,在右下方14×20方格纸内画出设计示图1图2图3图4意图.(提示:①画出的圆应符合比例要求;②为了保证示意图的清晰,请你在有把握后才将设计方案正式画在方格纸上)分析:这是一道方案设计问题,图2中每一正方形小格宽度均表示0.5m ,餐厅内能否摆下三套或四套同样大小的圆桌和椅子,就看能否在图2中画出三个或四个半径为三格宽的圆,并使圆与圆之间、圆与方格纸外边框之间的间距不少于一格,我们可以按画三个圆、画四个圆分别计算.解:此餐厅内能摆下三套和四套同样大小的圆桌和椅子.摆放三套与四套的设计方案参考图3、图4,只要满足如下条件:① 每个圆的半径为1.5cm ;② 每个圆的圆心到方格纸外边框的距离不小于2cm ; ③ 任意两圆的圆心距不小于3.5cm.说明:对于一道运用几何计算进行探索的综合型问题,要注意相关的条件,可以先假设结论成立,然后通过计算求相应的值,再作存在性的判断.该试题是在考生容易想象的情境中考查学生用数学的能力,源于生活,打破常规,重视学生探究问题的能力的培养和动手操作意识的形成,这是今后中考试题的一个方向.ABCPQABC习题11⒈如图,在△ABC 中,已知BC=6,∠C=600,sinA=0.8,求AB 和AC 的长.(结果保留根号)⒉如图,挂着“庆祝凤凰广场竣工”条幅的氢气球升在广场上空,已知气球的直径为4m ,在地面A 点测得气球中心O 的仰角∠OAD=60°,测得气球的视角∠BAC=2°(AB 、AC 为⊙O 的切线,B 、C 为切点)则气球中心O 离地面的高度OD 为( )。
2012年中考复习考点跟踪训练《代数应用性问题(3)》

2012年中考复习考点跟踪训练(三十九)《代数应用性问题(3)》一、选择题1.如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4 m ,如果在坡度为0.75的山坡上种树,也要求株距为4 m ,那么相邻两树间的坡面距离为( )A .5 mB .6 mC .7 mD .8 m 答案 A解析 如图,在Rt △ABC 中,ACBC=0.75,BC =4,则AC =3,AB =5.2.如图,小红同学要用纸板制作一个高4 cm ,底面周长是6π cm 的圆锥形漏斗模型,若不计接缝和损耗,则她所需纸板的面积是( )A .12π cm 2B .15π cm 2C .18π cm 2D .24π cm 2答案 B解析 因为底面周长为6π,设底面半径为r ,所以2πr =6π,r =3,又h =4,所以l =5,S 圆锥侧=πrl =15π,应选B.3.某班在布置新年联欢会会场时,需要将直角三角形纸裁成长度不等的矩形彩条,如图,在Rt △ABC 中,∠C =90°,AC =30 cm ,AB =50 cm ,依次裁下宽为1 cm 的矩形纸条a 1、a 2、a 3……,若使裁得矩形纸条的长都不小于5 cm ,则每张直角三角形彩纸能裁成的矩形纸条的总数是( )A .24B .25C .26D .27 答案 C解析 如图,在△ABC 中,可求得BC =40,设B 1C 1∥BC ,得B 1C 1=5,由△AB 1C 1∽△ABC ,得B 1C 1BC =AC 1AC ,于是540=AC130,∴AC 1=3.75,∴CC 1=26.25≈26.4.如图,在正方形铁皮上(图①)剪下一个圆形和扇形,使之恰好围成(图②)所示的一个圆锥模型,该圆的半径为r ,扇形的半径为R ,则圆的半径与扇形的半径之间的关系为( )A .R =2rB .R =94r C .R =3r D .R =4r答案 D解析 由图①,可知圆锥侧面展开图圆心角为90°,则rR×360=90,R =4r .5.(2010·达州)如图,在一块形状为直角梯形的草坪中,修建了一条由A →M →N →C 的小路(M 、N 分别是AB 、CD 中点).极少数同学为了走“捷径”,沿线段AC 行走,破坏了草坪,实际上他们仅少走了( )A .7 mB .6 mC .5 mD .4 m 答案 B解析 在Rt △ABC 中,AC =122+162=20;过D 画DE ⊥BC 于E ,在Rt △CDE 中,CD =122+52=13,所以NC =6.5,又MN =12×(11+16)=13.5,所以AM +MN +NC =6+6.5+13.5=26,与AC 相差6米. 二、填空题6.如图,A 是硬币圆周上一点,硬币与数轴相切于原点O (A 与O 点重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点A 恰好与数轴上点A ′重合,则点A ′对应的实数是________.答案 π解析 由题意,可知线段AA ′长等于圆的周长π×1=π.7.(2010·江西)一大门的栏杆如图所示,BA 垂直于地面AE 于A ,CD 平行于地面AE ,则∠ABC+∠BCD=________度.答案270解析过B画BG∥CD,则∠BCD+∠CBG=180°,又CD∥AE,所以BG∥AE. ∠ABF +∠BAE=180°,可知∠BAE=90°,所以∠ABF=90°,∠ABC+∠BCD=180°+90°=270°.8.(2010·宁波)如图,某河道要建造一座公路桥,要求桥面离地面高度AC为3米,引桥的坡角∠ABC=15°,则引桥的水平距离BC的长是________米(精确到0.1米).答案11.2解析过A作∠BAD=∠B=15°,交BC于D,则BD=AD,∠ADC=30°.在Rt△ADC 中,由∠ADC=30°,得AD=2AC=2×3=6,所以DC=3AC=3 3,故BC=BD+DC=6+3 3≈11.2.9.如图,已知零件的外径为25 mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC =OD)量零件的内孔直径A B.若OC∶OA=1∶2,量得CD=10 mm,则零件的厚度x=________mm.答案 2.5解析由题意,易知△OAB∽△OCD,OC∶OA=CD∶AB.∵OC∶OA=1∶2,∴CD∶AB=1∶2,AB=2CD=20,∴x=(25-20)÷2=2.5.10.(2010·江西)如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕点A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC(假设AC>AB),影长的最大值为m,最小值为n,那么下列结论:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.其中,正确的结论的序号是__________.答案①③④解析如图所示,当木杆绕点A按逆时针方向旋转时,有m>AC,①成立,则②不成立;当旋转到达地面时,为最短影子,n=AB,③成立;由此可知,影子的长度先增大,后减小,④成立.三、解答题11.如图,路灯(P 点)距地面8米,身高1.6米的小明从距路灯的底部(O 点)20米的A 点,沿OA 所在的直线行走14米到B 点时,身影的长度是变长了还是变短了?变长或变短了多少米?解 由题意可知:△POM ∽△EAM ,△PON ∽△FBN , 又∵OA =20,AB =14,∴OB =6, ∴AM OM =AEPO,∴AM AM +20=1.68,解得AM =5(米).又BN ON =FB PO, ∴BN BN +6=1.68,解得BN =1.5(米),AM >BN , ∴身影变短了3.5米. 12.(2011·成都)某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABC D.已知木栏总长为120m ,设AB 边的长为x m ,长方形ABCD 的面积为S (m 2).(1)求S 与x 之间的函数关系式(不要求写出自变量x 的取值范围).当x 为何值时,S 取得最值(请指出是最大值还是最小值)?并求出这个最值;(2)学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆,其圆心分别为O 1和O 2,且O 1到AB 、BC 、AD 的距离与O 2到CD 、BC 、AD 的距离都相等,并要求在苗圃内药材种植区域外四周至少要留够0.5m 宽的平直路面,以方便同学们参观学习.当(1)中S 取得最大值时,请问这个设计是否可行?若可行,求出圆的半径;若不可行,请说明理由.解 (1)S =x (120-2x )=-2(x -30)2+1800,当x =30时,S 取最大值为1800.(2)如图所示,过O 1、O 2分别作到AB 、BC 、AD 和CD 、BC 、AD 的垂线,垂足如图,根据题意可知,O 1E =O 1F =O 1J =O 2G =O 2H =O 2I ;当S 取最大值时,AB =CD =30,BC =60,∴O 1F =O 1J =O 2G =O 2I =12AB =15,∴O 1E =O 2H =15,∴O 1O 2=EH -O 1E -O 2H =60-15-15=30, ∴两个等圆的半径为15,由于圆O 1、圆O 2相切,所以左右不能够留0.5米的平直路面. ∴设计不可行. 13.(2011·江西)图甲是一个水桶模型示意图,水桶提手结构的平面图是轴对称图形,当点O 到BC (或DE )的距离大于或等于⊙O 的半径时(⊙O 是桶口所在圆,半径为OA ),提手才能从图甲的位置转到图乙的位置,这样的提手才合格.现用金属材料做了一个水桶提手(如图丙A -B -C -D -E -F ,C -D 是圆弧,其余是线段),O 是AF 的中点,桶口直径AF =34 cm ,AB =FE =5 cm ,∠ABC =∠FED =149°.请通过计算判断这个水桶提手是否合格.(参考数据:314≈17.72,tan 73.6°≈3.40,sin 75.4°≈0.97.)解 解法一:如图,连接OB ,过点O 作OG ⊥BC 于点G . 在Rt △ABO 中,AB =5,AO =AF2=17,∴ tan ∠ABO =AO AB =175=3.4,∴∠ABO =73.6°,∴∠GBO =∠ABC -∠ABO =149°-73.6°=75.4°. 又 ∵OB =52+172=314≈17.72, ∴在Rt △OBG 中, .OG =OB ·sin ∠OBG =17.72×0.97≈17.19>17. ∴水桶提手合格.解法二:如图,连接OB ,过点O 作OG ⊥BC 于点G . 在Rt △ABO 中,AB =5,AO =17, ∴ tan ∠ABO =AO AB =175=3.4,∴∠ABO =73.6°.要使OG ≥OA ,只需∠OBC ≥∠ABO ,∵∠OBC =∠ABC -∠ABO =149°-73.6°=75.4°>73.6°, ∴水桶提手合格.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点跟踪训练39 几何应用性问题
一、选择题
1.如图,在平地上种植树木时,要求株距(相邻两树间的水平距离)为4 m ,如果在坡度为0.75的山坡上种树,也要求株距为4 m ,那么相邻两树间的坡面距离为( )
A .5 m
B .6 m
C .7 m
D .8 m 答案 A
解析 如图,在Rt△ABC 中,AC BC
=0.75,BC =4,则AC =3,AB =5.
2.如图,小红同学要用纸板制作一个高4 cm ,底面周长是6π cm 的圆锥形漏斗模型,若不计接缝和损耗,则她所需纸板的面积是( )
A .12π cm 2
B .15π cm 2
C .18π cm 2
D .24π cm 2
答案 B
解析 因为底面周长为6π,设底面半径为r ,所以2πr =6π,r =3,又h =4,所以l =5,S 圆锥侧=πrl =15π,应选B.
3.某班在布置新年联欢会会场时,需要将直角三角形纸裁成长度不等的矩形彩条,如图,在Rt△ABC 中,∠C =90°,AC =30 cm ,AB =50 cm ,依次裁下宽为1 cm 的矩形纸条a 1、a 2、a 3……,若使裁得矩形纸条的长都不小于5 cm ,则每张直角三角形彩纸能裁成的矩
形纸条的总数是( )
A .24
B .25
C .26
D .27 答案 C
解析 如图,在△ABC 中,可求得BC =40,设B 1C 1∥BC ,得B 1C 1=5,由△AB 1C 1∽△ABC ,得
B 1
C 1BC =AC 1AC ,于是540=AC 1
30
,∴AC 1=3.75,∴CC 1=26.25≈26.
4.如图,在正方形铁皮上(图①)剪下一个圆形和扇形,使之恰好围成(图②)所示的一个圆锥模型,该圆的半径为r ,扇形的半径为R ,则圆的半径与扇形的半径之间的关系为( )
A .R =2r
B .R =9
4r C .R =3r D .R =4r
答案 D
解析 由图①,可知圆锥侧面展开图圆心角为90°,则r R
×360=90,R =4r .
5.(2010·达州)如图,在一块形状为直角梯形的草坪中,修建了一条由A →M →N →C 的小路(M 、N 分别是AB 、CD 中点).极少数同学为了走“捷径”,沿线段AC 行走,破坏了草坪,实际上他们仅少走了( )
A .7 m
B .6 m
C .5 m
D .4 m 答案 B
解析 在Rt△ABC 中,AC =122
+162
=20;过D 画DE ⊥BC 于E ,在Rt△CDE 中,CD =
122+52
=13,所以NC =6.5,又MN =12×(11+16)=13.5,所以AM +MN +NC =6+6.5+13.5
=26,与AC 相差6米.
二、填空题
6.如图,A 是硬币圆周上一点,硬币与数轴相切于原点O (A 与O 点重合).假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点A 恰好与数轴上点A ′重合,则点A ′对应的实数是________.
答案 π
解析 由题意,可知线段AA ′长等于圆的周长π×1=π.
7.(2010·江西)一大门的栏杆如图所示,BA 垂直于地面AE 于A ,CD 平行于地面AE ,则
∠ABC+∠BCD=________度.
答案270
解析过B画BG∥CD,则∠BCD+∠CBG=180°,又CD∥AE,所以BG∥AE. ∠ABF+∠BAE =180°,可知∠BAE=90°,所以∠ABF=90°,∠ABC+∠BCD=180°+90°=270°.
8.(2010·宁波)如图,某河道要建造一座公路桥,要求桥面离地面高度AC为3米,引桥的坡角∠ABC=15°,则引桥的水平距离BC的长是________米(精确到0.1米).
答案11.2
解析过A作∠BAD=∠B=15°,交BC于D,则BD=AD,∠ADC=30°.在Rt△ADC中,由∠ADC=30°,得AD=2AC=2×3=6,所以DC=3AC=3 3,故BC=BD+DC=6+3 3≈11.2.
9.如图,已知零件的外径为25 mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径A B.若OC∶OA=1∶2,量得CD=10 mm,则零件的厚度x=________mm.
答案 2.5
解析由题意,易知△OAB∽△OCD,OC∶OA=CD∶AB.∵ OC∶OA=1∶2,∴CD∶AB=1∶2,AB=2CD=20,∴x=(25-20)÷2=2.5.
10.(2010·江西)如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕点A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC(假设AC>AB),影长的最大值为m,最小值为n,那么下列结论:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.其中,正确的结论的序号是__________.
答案①③④
解析如图所示,当木杆绕点A按逆时针方向旋转时,有m>AC,①成立,则②不成立;当旋转到达地面时,为最短影子,n=AB,③成立;由此可知,影子的长度先增大,后减小,
④成立.
三、解答题
11.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A 点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
解由题意可知:△POM∽△EAM,△PON∽△FBN,
又∵OA=20,AB=14,∴OB=6,
∴AM
OM
=
AE
PO
,
∴
AM
AM+20
=
1.6
8
,解得AM=5(米).
又BN
ON
=
FB
PO
,
∴
BN
BN+6
=
1.6
8
,解得BN=1.5(米),AM>BN,
∴身影变短了3.5米.
12.(2011·成都)某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABC D.已知木栏总长为120m,设AB边的长为x m,长方形ABCD的面积为S(m2).
(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围).当x为何值时,S取得最值(请指出是最大值还是最小值)?并求出这个最值;
(2)学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆,其圆心分别为O1和O2,且O1到AB、BC、AD的距离与O2到CD、BC、AD的距离都相等,并要求在苗圃内药材种植区域外四周至少要留够0.5m宽的平直路面,以方便同学们参观学习.当(1)中S取得最大值时,请问这个设计是否可行?若可行,求出圆的半径;若不可行,请说明理由.解(1)S=x(120-2x)=-2(x-30)2+1800,当x=30时,S取最大值为1800.
(2)如图所示,过O 1、O 2分别作到AB 、BC 、AD 和CD 、BC 、AD 的垂线,垂足如图,根据题意可知,O 1E =O 1F =O 1J =O 2G =O 2H =O 2I ;当S 取最大值时,AB =CD =30,BC =60,
∴O 1F =O 1J =O 2G =O 2I =1
2
AB =15,
∴O 1E =O 2H =15,
∴O 1O 2=EH -O 1E -O 2H =60-15-15=30,
∴两个等圆的半径为15,由于圆O 1、圆O 2相切,所以左右不能够留0.5米的平直路面. ∴设计不可行.
13.(2011·江西)图甲是一个水桶模型示意图,水桶提手结构的平面图是轴对称图形,当点O 到BC (或DE )的距离大于或等于⊙O 的半径时(⊙O 是桶口所在圆,半径为OA ),提手才能从图甲的位置转到图乙的位置,这样的提手才合格.现用金属材料做了一个水桶提手(如图丙A -B -C -D -E -F ,C -D 是圆弧,其余是线段),O 是AF 的中点,桶口直径AF =34 cm ,AB =FE =5 cm ,∠ABC =∠FED =149°.请通过计算判断这个水桶提手是否合格.
(参考数据:314≈17.72,tan 73.6°≈3.40,sin 75.4°≈0.97.)
解 解法一:
如图,连接OB ,过点O 作OG ⊥BC 于点G . 在Rt△ABO 中,AB =5,AO =
AF
2
=17,
∴ tan∠ABO =AO AB =17
5
=3.4,
∴∠ABO =73.6°,
∴∠GBO =∠ABC -∠ABO =149°-73.6°=75.4°. 又 ∵OB =52
+172
=314≈17.72, ∴在Rt△OBG 中,
.OG =OB ·sin∠OBG =17.72×0.97≈17.19>17. ∴水桶提手合格.
解法二:
如图,连接OB ,过点O 作OG ⊥BC 于点G . 在Rt△ABO 中,AB =5,AO =17,
∴ tan∠ABO =AO AB =17
5
=3.4,
∴∠ABO =73.6°.
要使OG ≥OA ,只需∠OBC ≥∠ABO ,
∵∠OBC =∠ABC -∠ABO =149°-73.6°=75.4°>73.6°, ∴水桶提手合格.。
