ch变化中的电场和磁场动生感生电动势的计算
大学物理动生电动势和感生电动势

dt
S不变
dB Ek dl dS L S dt
dB dS S dt
揭示了电场和磁场是相互联系的。
10 - 2 动生电动势和感生电动势
第十三章电磁感应
dB Ek dl dS L S dt
dl Rd
2
b
d
vB dl
R
v
B
vBR
2
cos d
方向:a
vB2 R
b
a
10 - 2 动生电动势和感生电动势
第十三章电磁感应
二
感生电动势(阅读)
1、感生电动势 由于磁场发生变化 而激发的电动势
G S N
是什么力使电荷运 动而在电路中产生 电流的呢???
R
10 - 2 动生电动势和感生电动势
第十三章电磁感应
例5. 匀强磁场B,导体棒OP绕OZ轴旋转,角 速度 , OP=b, 为已知 OZ轴∥ B 。求PO两端的电势差?
思路:d ( v B ) dl
vB cos dl
rB sin d l
R
B
解:方法一 作辅助线,形成闭合回路
i 0 半圆 ab 2 RBv
方向:a
a
b
10 - 2 动生电动势和感生电动势
第十三章电磁感应
有一半圆形金属导线在匀强磁场中作切割磁
力线运动。已知: v , B , R.
求:动生电动势。 解:方法二
d ( v B ) dl 0 vB sin 90 dl cos
(D) 两环中感应电动势相等。
大学物理知识点(磁学与电磁感应)

y
Idl B
B
dF
dF
I
Idl
x L 任意闭合平面载流导线在均匀磁场中所受的力为零 。 F3 P 注:载流线圈在均匀磁 F2 M 场中所受力矩不一定为 零 B I O F 1 M Npm B en N F4
在均匀磁场中
F BIL
o
P
**应用介质中安培环路定理解题方法**
I 0 Bo
2R
2 IR 0 pm B 0 3 3
2x
2πx
注意:在一定的x处,磁场强弱随载流环的半径变 化,故可用求极值的方法讨论轴线某一定点处磁 场随载流环半径变化的趋势。
无限长柱面电流的磁场
无限长柱体电流的磁场
L1
r
R
I
L2
r
B
0 I
2π R
o R
r
二、磁场的基本性质
1、 感生电动势
S定
B dS i s t
方向由楞次定律判断
o
B变
2、 感生电场
B Ei dl s t dS
感生电场是涡旋场,其电场线与磁感 应强度增大的方向成左手螺旋关系。
3、 感生电场与感生电动势的计算 感生电场 : 当变化的磁场的分布具有特殊对称性时: 1 dB Ei r (r R) 2 dt
五、磁场的能量
1、通电线圈的自感磁能 2、磁场的磁能
1 2 Wm LI 2
目前范畴内:
1 1 2 1 2 w m H B BH 2 2 2
W m V w m dV
电磁学基本物理图象
运动
电荷
激 发
电流
激 发
动生电动势感生电动势感生电场普遍环路定理

THANKS FOR WATCHING
感谢您的观看
感应加热
感应加热器利用动生电动势对金属进 行加热。当金属在变化的磁场中时, 会在金属内部产生动生电动势,从而 产生电流并加热金属。
02 感生电动势
定义与产生机制
定义
当磁场发生变化时,会在导体中产生电动势。这个电动势被 称为感生电动势。
产生机制
磁场的变化会在导体中激发出电场,这个电场驱动导体中的 自由电荷移动,从而产生感生电动势。
感生电场的应用实例
电磁感应
当线圈中的磁场发生变化时,会在线 圈中产生感生电动势,进而产生电流。
磁记录
利用感生电场可以记录磁场的变化, 从而实现信息的存储和读取。
04 普遍环路定理
定理的表述与证明
表述
在磁场中,如果闭合回路的磁通量发生变化,那么就会产生电动势。这个电动势的大小等于回路的磁通量变化率 与回路的长度成正比。
证明
根据法拉第电磁感应定律和安培环路定律,通过引入磁场线穿过闭合回路的磁通量概念,可以推导出普遍环路定 理。
普遍环路定理的应用场景
电机工程
普遍环路定理是电机设计中的重 要理论依据,用于计算和预测电 机在不同工作状态下的电动势和
电流。
电力系统
在电力系统中,普遍环路定理用于 分析和计算电力传输过程中的电压 和电流变化,以确保电力供应的稳 定性和可靠性。
感生电动势的计算公式
公式
E = -dΦB/dt,其中E是感生电动势,ΦB是磁通量。
解释
这个公式表示,当磁通量发生变化时,就会产生感生电动势。负号表示电动势的 方向与磁通量变化的方向相反。
感生电动势的应用实例
01
02
03
感应炉
电动势复习举例

导率为 的磁介质 B1 n1I1
l N 1
N2
线圈1产生的磁场通过线圈2的磁通链数
由互感定义
M 21
21 I1
21 N2
N1N2S
l
n1n2V
N1 l
I1S
同理可求出:
M 12
12 I2
N2 N1S
l
n2n1V
可知:
M 21 M12 M
例 6 一密绕的螺绕环,单位长度的匝数为 n 2000m 1,环的横截面积为 S 10cm 2,另一个 N 10匝的小线圈套绕在环上,
Ir
2
1O
R
但基于和上面同样的原因 ,以小线圈通有电流来计 算互感系数是困难的。由 于两线圈互感系数是相同 的,可通过假设线圈2通有 电流I2来计算互感。
假设线圈2通有电流I2,则线圈中心磁场为 B 0I2
2R
由于R>>r,小线圈面积内磁场可看作是均匀的,大
小即为线圈中心的磁感应强度大小。则穿过小线圈
AB
B
A (vBAB
sin
2
)dl cos 0
vBAB L
0IvL 2 (a vt)
AB
DC
C
D (vBDC
sin
)dl
2
cos 0
vBDC L
0IvL
DC
2 (a b vt)
B I
v C L
A
D
ab
方向:顺时针。
AB
DC
0IvL( 1 2 a vt
1) a b vt
v
B
C
I L
A
D
ab
解:(1)电流恒定,线框平移. 通量求导法:
大学物理电场磁场电磁感应公式总结

对未来学习或研究方向展望
深入学习电磁理论
在大学物理的基础上,可以进一步深入学习电磁场理论,了解电磁波的传播、辐射和散射等现象,为后续的 学术研究或工程应用打下基础。
拓展应用领域
电磁场理论在各个领域都有广泛的应用,如无线通信、电子技术、材料科学等。未来可以将所学的电磁场理 论知识应用到相关领域中,解决实际问题。
交流电的有效值是根据电流的热效应来规定的,对于正弦 交流电,有效值$I = frac{I_m}{sqrt{2}}$。
交流电路中电场、磁场关系分析
电场与磁场相互垂直
在交流电路中,电场和磁场是相 互垂直的,且都垂直于电流的传 播方向。
电磁感应定律
变化的磁场会产生电场,从而产 生感应电动势,感应电动势的大 小与磁通量变化的快慢成正比, 即$e = -n frac{dPhi}{dt}$。
电感和电容
在交流电路中,电感对电流的变 化有阻碍作用,电容对电压的变 化有阻碍作用。电感和电容都是 储能元件,它们在交流电路中的 特性与其在直流电路中的特性有 很大不同。
变压器原理和应用举例
变压器原理
变压器是利用电磁感应原理来改变交流电压的装置。它由两个或多个匝数不同的线圈绕在同一个铁芯上制 成。当原线圈中加上交流电压时,在铁芯中就会产生交变磁通,从而在副线圈中产生感应电动势。
电场
电场强度、电势、高斯定理、静 电场的环路定理等概念和公式, 以及它们在求解电场分布、电势 能和电场力等问题中的应用。
磁场
磁感应强度、磁场线、磁通量、 安培环路定律等概念和公式,以 及它们在求解磁场分布、磁力和 磁矩等问题中的应用。
电磁感应
法拉第电磁感应定律、楞次定律、 自感和互感等概念和公式,以及 它们在求解感应电动势、感应电 流和磁场能量等问题中的应用。
电磁感应——动生电动势总结

b a
b
εi
3、应用计算式计算在磁场中运动导线上的动生电动势
K K 速度也可以不同, v、 B
在一般情况下,磁场可以不均匀,导体在磁场中运动时各部分的
K 和 l 也可以不相互垂直,在这些情况下计算
运动导体内产生的总动生电动势应采取这样的步骤:
K K 先以一端为起点,在位置 l 处选取线元 dl ,计算线元上产生的动
生电动势;进而对整个处于磁场中的运动导体部分作积分,得到
总动生电动势。
K K K dε 动 = (v × B ) ⋅ d l
ε动 = ∫
L
L
K K K (v × B ) ⋅ d l
对于闭合回路
ε 动 为正时,表示电动势 为负。因此,由上式算出的电动势有正负之分, K K ε 动 为负时,则表示电动势的方向逆着dl 的方向。 方向顺着 dl 的方向;
a
K v
K B
b
K f
K K u fb 1
K K u +v
K K K K P = ( f1 + f2 ) ⋅ (v + u ) K K K K K = (−ev × B − eu × B) ⋅ (v + u ) = −evBu + euBv = 0
总洛仑兹力与总速 度垂直,不做功!
讨 论
(2)回路中的电能从何而来?
ε动的正负来判断电动势的方向。
实验演示
3、动生电动势产生过程中的能量转换
每个电子受的洛仑兹力
K B⊗
K f2
a
−eK uFra bibliotekK K K f l = f1 + f 2 K K K f1 = − ev × B
K f1 K f2
12.2 动生电动势和感生电动势
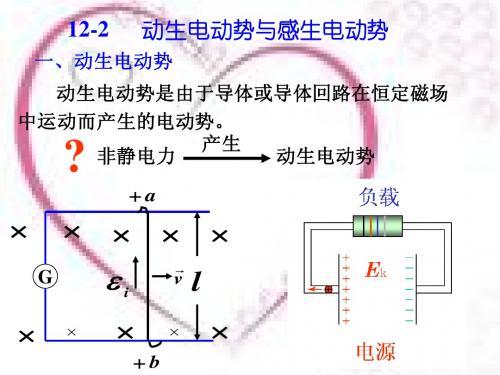
此时电荷积累停止, 两端形成稳定的电势差 两端形成稳定的电势差。 此时电荷积累停止,ab两端形成稳定的电势差。 洛仑兹力是产生动生电动势的根本原因 洛仑兹力是产生动生电动势的根本原因. 是产生动生电动势的根本原因
动生电动势的公式
非静电力
f = −e(v × B)
f 定义 Ek为非静电场强 Ek = = v ×B −e
S
A B ××× ×
ω ××v × ×
非均匀磁场
例 一直导线CD在一无限长直电流磁场中作 一直导线 在一无限长直电流磁场中作 切割磁力线运动。 切割磁力线运动。求:动生电动势。 动生电动势。 解:方法一
dε = ( v × B )⋅ dl I l dl µ0I 0 0 D sin90 dl cos180 =v C 2πl b a µ0vI dl =− 方向 D→C → 2πl µ0vI a+b dl µ0vI a + b ε =− ∫a l = − 2π ln a 2π
×××× ⊗ o ×××× B ×××× h
C
∂B ∂t
××
L
D
解:
ε i = ∫ E涡 • dl
L
r dB E涡 = 2 dt
dε = E涡 • dl r dB dl cosθ = 2 dt
h dB dl = 2 dt
⊗o
B
⊗
θ
∂B ∂t
E涡
r h
l dl
L
θ
C
D
h dB 1 dB εCD = ∫L dl = 2hL dt 2 dt
O
解:方法一 取微元
dε = ( v × B )⋅ dl
= Bvdl = Blωdl
εi = ∫ dεi = ∫0 Blωdl
动生电动势与感生电动势

【解】由于金属棒处在通电导线的非均匀磁场中,因此必
须将金属棒分成很多长度元dx,规定其方向由A指向B。这样 在每一dx处的磁场可以看作是均匀的,其磁感应强度的大小为
B 0I
2x
根据动生电动势的公式可知,dx小段上的动生电动势为
d动
(v
B)
dl
Bv
cos
dx
0I
2x
vdx
由于所有长度元上产生的动生电动势的方向都相同,所以金
d
dt
d dt
S
B
dS
又根据电动势的定义可得
L EK dl
式中,EK为感生电场的电场强度。感生电场的电场强度是 非静电性场强。
则有
L EK
dl
d dt
B dS B dS
s
s t
dB
s
S t
若闭合回路是静止的,即所包围面积S不随时间变化,即
S 0 ,则上式可写成
t
B L EK dl s t dS
性场强为
Ek
fL (e)
vB
根据电动势的定义可得,动生电动势为
a
动
L Ek
dl
(v B) dl
b
上式是动生电动势的一般表达式。由上式可知,动生电动势
的方向是非静电性场强 Ek v B 在运动导线上投影的指向。
【例9-2】如下图所示,长直导线 中通有电流I=10A,有一长l=0.1m的 金属棒AB,以v=4m·s-2的速度平行于 长直导线作匀速运动,棒离导线较近的 一端到导线的距离a=0.1m,求金属棒 中的动生电动势。
1861年,英国物理学家麦克斯韦提出感生电场的假设,认为 由于磁场变化而产生一种电场,是这个电场使导体中自由电子作 定向运动而形成电流。麦克斯韦还认为,即使没有导体,这种电 场同样存在。这种由变化磁场激发的电场称为感生电场。
(18)动生电动势、感生电动势new
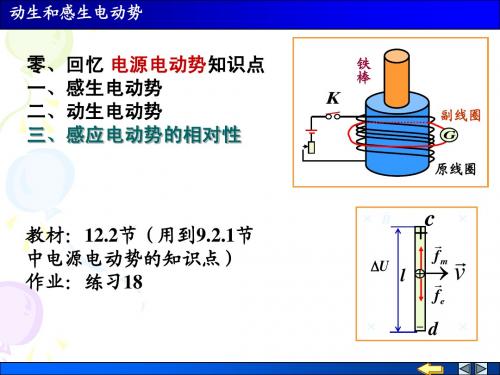
+ + + + + + + Fm - + + + O+ + + +
+ v
+
它驱使电子沿导线由P向O移动。 ②由于洛仑兹力的作用使 O 端出现过剩负电荷, P 端出现过剩正电荷 。在导线内部产生静电场,方向 P O ,电子同时受到电场力作用 平衡时
Fm Fe eEk
Fe eE Fm Ek v B e
变化、取向变化等 动生电动势 感生电动势
2)导体不动,磁场变化 回 忆 电动势
I
Ek
+
Ek : 非静电的电场强度.
闭合电路的总电动势
-
Ek dl
E k dl
l
动生和感生电动势
一、动生电动势(motional emf) 动生电动势是由于导体或导体回路在恒定磁场 中运动而产生的电动势。 动生电动势的物理机制到底是什么?
原 因
非静 电力 来源
由于 B的变化引起
回路中 m变化 感生电场力
动生和感生电动势
【习题】感生电场的计算 B L E涡 dl S t dS
对称性才有可能 计算出来
E感生具有某种
动生和感生电动势
例1 局限于半径 R 的圆柱形空间内分布有均匀磁场, 方向如图。磁场的变化率 B t 0 B 求: 圆柱内、外的 E 涡 分布。 t 解: r R B B l E涡 dl t dS
S
L
B 是曲面上的任一面元上磁感应强度的变化率 t
动生电动势-感生电动势

• ••• ••••••
• • • • • • • • • •
• ••• ••••••
• • •
• • •
• • •
• •o •
•••
• R• •
••
• b•
••
• • •
• • •
R • • • • • • • • • •
• ••• ••••••
a • • • • • • • • • • B • • • • • • • • • •
i
dm
dt
B
dS
S t
i oa ab bo ab
ab
(b) Ei
(a)
dl
S
B
dS
t
a
其中 S 为 oabo 围成的面积。
P. 26 / 34 .
0
dl
Blv sin
若棒右移 ,则 i 指向:a
b;
a B
若棒左移,则 i 指向: b a。
Chapter 8. 电磁感应 §8. 2 动生作电者动:势杨感茂生田电动势
P. 9 / 34 .
例 如图,∞载流 I 直导线与导体棒相互垂直,棒以 v 沿
垂直于棒方向运动,已知:a、b。求导体棒的电动势。
(a) l
b v B
v
(vB sin 90o ) dl cos(90o )
0
dl a B
若 i > 0,则 i 指向与 dl 同向;否则,反向。
或
vB
在导体上的分量方向即为
i
指向。
Chapter 8. 电磁感应 §8. 2 动生作电者动:势杨感茂生田电动势
• ••• ••• •••
1 2
第十三章第2次课 动生电动势和感生电动势

d dt
思考题: N
S
I
条形磁铁靠近线圈时, 线圈中那端电势高?
三角形线框靠近直导线时, 线框中电动势方向如何?
概念检测 如题图所示,一根长为l 的金属细杆ab绕竖直轴 O1O2以角速度在水平面内旋转,O1O2在离细杆a端l/3 处,若已知地球磁场在竖直方向的分量为B,则ab两 端间的电势差Uab O1 A. 大于零 B. 小于零 C. 因为没有电流, 所以Uab等于零
麦克斯韦提出了感生电场(涡旋电场)的概念
变化的磁场在其周围空间激发一 种电场,称为感生电场(涡旋电场)
——感生电场(涡旋电场)假设
麦克斯韦 (1831-1879)
变化的 激发 感生 作用 自由 引起 电荷 电场 磁场
感生电 动势
麦克斯韦假设(1861): 揭示了 电磁场的新效应。
感生电场:
Ei
R 2 dB Ei 2 r dt
r
(r R)
R dB 2 dt
Ei
变化的磁场只限于r≤R区域, 但它所激发的涡旋电场不限于 r≤R区域
o
R
r
(2) 如果将长度为l的导棒ab放在螺线管内,求导棒ab 两端的感生电动势
R
O
a
l
b
方法一: 在导棒上选一线元 dl
O
R
a
h
r
Ei
该线元上的感生电动势 d Ei dl
第十三章 电磁感应
一、电磁感应的基本现象
复习
二、楞次定律 闭合回路中感应电流的方向总是使得它所 激发的磁场来阻碍引起感应电流的磁通量的变 化。 三、法拉第电磁感应定律
四、动生电动势
dΦ dt
大学物理常用公式(电场磁场 热力学)

第四章 电 场一、常见带电体的场强、电势分布 1)点电荷:2014q E r πε=04q U rπε=2)均匀带电球面(球面半径R )的电场:200()()4r R E qr R r πε≤⎧⎪=⎨>⎪⎩00()4()4qr R r U q r R R πεπε⎧>⎪⎪=⎨⎪≤⎪⎩3)无限长均匀带电直线(电荷线密度为λ):02E rλπε=,方向:垂直于带电直线。
4)无限长均匀带电圆柱面(电荷线密度为λ): 00()()2r R E r R rλπε≤⎧⎪=⎨>⎪⎩5)无限大均匀带电平面(电荷面密度为σ)的电场:0/2E σε=,方向:垂直于平面。
二、静电场定理 1、高斯定理:0e Sq E dS φε=⋅=∑⎰静电场是有源场。
q ∑指高斯面内所包含电量的代数和;E指高斯面上各处的电场强度,由高斯面内外的全部电荷产生;SE dS ⋅⎰指通过高斯面的电通量,由高斯面内的电荷决定。
2、环路定理:0lE dl⋅=⎰ 静电场是保守场、电场力是保守力,可引入电势能三、求场强两种方法1、利用场强势叠加原理求场强 分离电荷系统:1ni i E E ==∑;连续电荷系统:E dE =⎰2、利用高斯定理求场强 四、求电势的两种方法1、利用电势叠加原理求电势 分离电荷系统:1nii U U==∑;连续电荷系统: U dU =⎰2、利用电势的定义求电势 rU E dl =⋅⎰电势零点五、应用点电荷受力:F qE = 电势差: bab a b aU U U E dr =-=⋅⎰a由a 到b六、导体周围的电场1、静电平衡的充要条件: 1)、导体内的合场强为0,导体是一个等势体。
2)、导体表面的场强处处垂直于导体表面。
E ⊥表表面。
导体表面是等势面。
2、静电平衡时导体上电荷分布: 1)实心导体: 净电荷都分布在导体外表面上。
2)导体腔内无电荷: 电荷都分布在导体外表面,空腔内表面无电荷。
3)导体腔内有电荷+q ,导体电量为Q :静电平衡时,腔内表面有感应电荷-q ,外表面有电荷Q +q 。
动生电动势和感生电动势

动生电动势和感生电动势
d d 感应电动势 N dt dt 引起磁通量变化的原因 ?
磁场恒定,导体运动
导体不动,磁场变化
P.1
1、电动势定义
I
Ek
+
-
Ek : 非静电电场强度.
Ek dl
P.2
2、感应电动势的分类: (1)动生电动势 稳恒磁场中的导体运动 , 或者回路面积 变化、取向变化等。 (2)感生电动势: 导体不动,磁场变化。
OP
P.5
动生
OP
(v B) dl
混合积:(a b ) c
× × P ×
(vB sin ) cosdl
OP
×
× × ×
×
(v × B) ×
× ×
×
特例 B均匀,杆 l水平运动:
l×
×
× v×
× B
× O ×
OP
l
l (vB sin 900 )cos00 dl (v B) dl 0
vBl
vBdl vBl
0
P.6
2、计算方法
d动生 (v B) dl
动生
×
×
× P× B × dl
× ×
OP
(v B) dl
1 2 d BL 2 dt 1 2 BL 2
×
×
× P × × × ×
× ×
B ×
×
×
×
o
×
×
×
×
×
×
×
6.4 感生电动势和感生电场

变化的磁场 B 适用。 (2)由法拉第电磁感应定律计算 d 闭合回路: 感
dt
E 感 d l 0 就最好。
非闭合回路: 做辅助线,如果对辅助线有
三
螺线管磁场变化引起的感生电场
P236
P236 例1:无限长螺线管的电流随时间作线性变
dB 化,其内部的 B 也随时间作线性变化,已知 的
C E感(径向)
C
B
D
C
A
D
管外无限远处:
E感 0
D A
D
C
E 感 dl 0
C B
E感径向 dl
E感径向 dl
ABCDA
E感 dl
B
A
C
B
D
A
B
A
E 感轴向 d l 0
故 E 感 的轴向分量为零。
数值,求无限长螺线管内外空间 E 感 分布。(默认 E 感 在趋于无限远时趋于零)
dt
解:无限长螺线管内外空间的磁场 管内磁场均匀,方向平行于轴线,大小为
B内 0 n I 管外: B 0
磁场的附近空间产生 E 感。
螺线管中的电流变化,磁场也随之变化,必在
当I作线性变化时,
E感
r dB 2 dt
2 dt E 感 方 向 : 与 B的 变 化 相 反
E感 大 小 :
r dB
dB 若 B , 0, E 感 0, 与 L同 向 ; dt
dB 若 B , 0, E 感 0, 与 L 反 向 。 dt n (B) 即计算结果 E 感 0 ε感 时, E 感 与 L 同向,
电磁感应复习提纲

电磁感应1. 电磁感应现象:2. 楞次定律:闭合回路中产生的感应电流具有确定的方向,它总是使感应电流所产生的通过回路的磁通量,去补偿或者反抗引起感应电流的磁通量的变化。
3. 法拉第电磁感应定律:通过回路所包围的磁通量发生变化时产生的感应电动势与磁通量对时间的变化率成正比。
εi =-d /d t(εi =-d Ψ/d t , Ψ=N ) ; 说明1:感生电荷量q :如果闭合回路的电阻R ,通过导线任一界面的感生电荷量为 q i =⎰21d i t t t I =(1/R )(1-2); 说明2:感应电流产生的条件 感应电流产生的条件:凡是谈及感应电流,一般都是对闭合的导体回路而言。
这里一定要抓住磁通量的变化,不管这种变化是外界引起的还是回路本身运动、形变、电流变化引起的,只有在磁通量变化的过程中才有感应电流。
说明3:感应电动势与回路是否闭合、导体是否存在无关。
例1:尺寸相同的铁环与铜环所包围的面积中,通以相同变化率的磁通量,则环中: (A) 感应电动势不同, 感应电流不同. (B) 感应电动势相同,感应电流相同. (C) 感应电动势不同, 感应电流相同. (D) 感应电动势相同,感应电流不同. 说明4:感应电动势的方向(具体见例) 电磁感应定律是电动势与磁通量变化率的关系,实验测得电动势的方向与磁通量变化率正值方向成左手关系,当转换成右手关系是发现:大拇指指向磁通量变化率正值方向,四指绕行方向所得到的电动势方向与实验测得相反,于是负号修正。
根据此思想,可衍生以下几种方式判断方向的方法:(1) 右手大拇指指向磁通量变化率负值方向,四指绕行方向即电动势(电流)方向。
(这就是楞次定律,感应电流就是要产生负磁通量变化率来试图抵消线圈中的正值磁通量变化率或者产生正磁通量变化率来试图补偿线圈中的负值磁通量变化率)(2) 右手大拇指指向自定义的面的法向方向,四指绕行方向即电动势(电流)标定方向(将环路方向与电动势方向绑定)。
动生电动势和感生电动势

m1
三、电子感应加速器
原理:在电磁铁的两磁极间放一个真空室,电磁铁是由
交流电来激磁的。
当磁场发生变化时,两极间任意闭合回路的磁通发生变化, 激起感生电场,电子在感生电场的作用下被加速,电子在 Lorentz力作用下将在环形室内沿圆周轨道运动。
轨道环内的磁场 等于它围绕面积 内磁场平均值的 一半。
解:法拉第电机可视为无数铜棒一 端在圆心,另一端在圆周上,即为 并联,因此其电动势类似于一根铜 棒绕其一端旋转产生的电动势。
w
B
o a
R
U0 Ua o Bwl dl
U0
Ua
1 2
BR2w
二、感生电动势
1、感生电动势
由于磁场的变化而在回路中产生的感应电 动势称为感生电动势.
2、感生电场
变化的磁场在其周围空间激发的一种能够产生感生电动势 的电场,这种电场叫做感生电场,或涡旋电场。
是以轴为圆心的一系列同心圆,同一同心圆
上任一点的感生电场的Ek大小相等,并且方
向必然与回路相切。于是沿L取Ek的线积分,
有:
L Ek dl Ek 2 r
EkΒιβλιοθήκη 2rr 2dB dt
若r<R,则 Br 2
L
Ek
dl
- d dt
r 2
dB dt
r dB Ek 2 dt
若r≥R,则
BR2
2、涡流的热效应
电阻小,电流大,能 够产生大量的热量。
3、应用
高频感应炉 真空无按触加热
加热
4、涡流的阻尼作用
当铝片摆动时,穿过运动铝片的磁通量 是变化的,铝片内将产生涡流。根据楞 次定律感应电流的效果总是反抗引起感 应电流的原因。因此铝片的摆动会受到 阻滞而停止,这就是电磁阻尼。
感应电场

1 3 ( ktg) x cos t dx ( ktg) x cos t 3
S
x 0 2
dx
x
d 1 2 dx 3 ktg( 3 x cos t sin tx ) dt 3 dt
感生 动生
1 3 3 3 2 ktgv t sin t ktgv t cos t 3
dl h sec2 d,
2 t
r h sec
B t
h sec B d h sec2 d cos 2 t
h 2 2 h2
2
B sec2 d t t tg 2 h L sec d 2h 2 B tg L
1 1
积 分 方 向
L
i E感 dl
b a
4、
E感
B 与 t 构成左旋关系。
B t
E感
E感
B t
?
如果变化的磁场空间中不存在任何导体, 那么此空间是否不存在感生电场?
动生电动势 特 点 原 因 非的 静来 电源 力 结 论 磁场不变,闭合电路的 整体或局部在磁场中运 动导致回路中磁通量的 变化 由于S的变化引起 回路中变化 非静电力就是洛仑兹 力,由洛仑兹力对运 动电荷作功而产生电 动势
E 是发散场 E 是涡旋场
四. 涡电流(涡流)
1. 涡电流的概念
大块的金属在磁场中运动,或处在变化的磁 场中,金属内部也要产生感应电流,这种电流在 金属内部自成闭合回路,称为涡电流或涡流。 涡流线 交 流 电 源 铁 芯 中 的 涡 电 流
铁芯
2.涡电流的热效应
利用涡电流进行加热的方法叫做感应加热。
× B × ×
感生电动势与动生电动势的叠加计算-诏安中学教研网

感生电动势与动生电动势的叠加计算 - 诏安中学教研网感生电动势与动生电动势的叠加计算诏安第一中学郭勇其,,,,法拉第电磁感应定律的一般形式为,其中为磁通量的变化量,E,,t,,的变化可归结为三种:一种是磁场不变,导体回路或导体回路中的部分在磁场中做切割磁感线运动运动;我们把这一种情况产生的感应电动势称为动生电动E,Blv势,其大小为;第二种就是导体不动,磁场发生变化;这种情况产生的,B感应电动势称为感生电动势,其大小为;第三种就是导体回路或导体E,S,t 回路中的部分在磁场中做切割磁感线运动,同时磁场发生变化;这种情况产生的,,,(B,S),S,B,S感应电动势大小为,其中即为动生E,,,B,SB,Blv,t,t,t,t,t,B电动势,即为感生电动势。
前两种情况在平时的考试和练习中比较常见,S,t第三种情况随着高考对能力考查要求的提高,也有渗透到考题中。
例1(2000年上海物理卷第23题第(,)问)(如图所示,固定水平桌面上的金属框架cdef,处在竖直向下的匀强磁场中,金属棒ab搁在框架上,可无摩擦滑动,此时adeb构成一个边长为的正方形,棒的电lBr阻为,其余部分电阻不计,开始时磁感强度为。
0(3)若从时刻起,磁感强度逐渐减小,当棒以恒定速度向右作匀速vt,0t运动时,可使棒中不产生感应电流,则磁感强度应怎样随时间变化(写出B与的关系式),解析:磁场发生变化,同时导体在磁场中做切割磁感线运动,这种情况产生,S,B的感应电动势为就是第三种情况,即E,B,S,棒中不产生感应电流,,t,t,S,B,S,(l,x),x则,即……?;本题中有(B,S,0B,B,Bl,BlvxE,0,t,t,t,t,t ,x为棒向右移动的位移,等于移动的速度),S,l(l,vt),则?式可写为v,t ,B……?;将?式写成微分形式并分离变量得:Blv,l(l,vt),0,tdBvdt……?;对?式积分得lnB,ln(l,vt),A(,为积分常数),也就,,0Bl,vt Bl0是有ln[B,(l,vt)],A,注意到t=0时B=B,解得:。
电磁学6章(2-5)

导线中的感应电动势。
解:1)设直导线中通有电流 I1 。建立坐标系
I1 在 x 处产生的B为:
B 0I1 2x
x
d
o
通过面元 l dx 的磁通为:dΨ 0I1 l d x
2x
I
l a
dx
x
Ψ da 0I1 l d x 0I1l ln d a
d 2x
2
d
M Ψ 0l ln d a
I1 2
二、感生电动势: 导体或导体回路不动,由于磁场随时间变化,
导体或导体回路内产生的感应电动势。
1、感生电动势: 由法拉第电磁感应定律:
E
dΦ
d
Bd S
dt
dt S
S 不 变 , 只 有B 随 时 间 变 化:
设 B BeB d
e
B是沿
B方向的单位矢量
B
E
dt
Bd S
S
S
t eB dS
B
r
R
O
r
E感 d l E感 2r
E感 d l E
L
B
d
S
S t
B d S B r 2
S t
t
L
2rE感
B t
r 2
B
∴
r B E感 2 t
“-”号表示场强的方向与 t 成左螺旋关系。 与选定正方向相反。沿逆时针方向。
2)在螺线管外( r > R )
取半径为r 的同心圆L 作为积分路径,选顺时针方向作为
变换统一起来。
同一问题在不同参考系中可以得到完全相反的结论。
如图:在 S 系中导体沿 x 轴运动,均匀
静止磁场沿 z 轴的负方向,a 端有正电荷
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
求:金属棒中的 ε感 =?
的金属棒 ,
r ×B
o
r E外
Rh
r
r
r E内
θ
a
r dl
θ
b
r dl
c
l
R
R
解一: 感应电场分布
E内=
r 2
dB dt
E外=
R2 2r
dB dt
×
r B
o
r E外
Rh
r
r
r E内
θ
a
r dl
θ
b
r dl
c
l
R
R
E内=
r 2
dB dt
E外=
R2 2r
静电场 起源 由静止电荷激发
电 电场线为非闭合曲线 场 线 形 状
感生电场 由变化的磁场激发
电场线为闭合曲线
r B
r dB > 0
dt
r E感
静电场
感生电场
有源
∫ ∑ r
sE静
⋅
d
r S
=
1
ε0
q内
∫无源r r
sE感 ⋅ dS = 0
性质
保守
∫r
r
L E静 ⋅dl = 0
非保守(涡旋)
∫L
rr E感 ⋅ dl =−
r ⊗B
↑ vr
Me N
vr × Bra a +b
l
穿过回路 φm 不变 .
ε
= − dφm
dt
= ε MeN
+ ε NM
=0
∫ εMeN= −εNM =εMN =
N
(vr
×
r B)
⋅
r dl
∫ =
a+b
v
⋅
µ0I
cos
M
π d l=
−
µ0Iv ln a + b
,
a − b 2π l
2π a − b
dt
如果回路不闭合,需加辅助线使其闭合。
ε 大小和方向可分别确定 .
例1:长 L
以ω
的逆铜时棒针转OA动,,绕铜其棒固与定Br端垂O 直在均,匀求磁ε 场动
r B
=
中
?
⋅ ⋅ r
B
vr
ω Al
r
vr
Lr ×B
dl
o⋅
⋅
解一 :取线元
r dl
v = ωl
( vr
×
r B
)与
r dl
同向
dε
=
(vr ×
d
(vr
×
r B)⋅
r dl
=
vBcd
=
vBr
c
+
×
r B
r
c
vr 30°
o 30°
d
a 设导线不动
∫ ε 感=
∂Br
⋅
r dS
=
k
⋅
πr
2
s ∂t
6
+
b
ε
=
ε动
+ε 感
=
vBr
−
k πr 2
6
+
自学: P 321 [例6]
例题:P 342 11 - 11
已知:I = I 0cos ω t , a , b , vr
dt
12
dt
练习:P 342 11 -10
r ×B
o
a
A aD
已知:半径 a , 磁场 dB > 0 dt
等腰梯形边长 a , 2a
求: 各边 ε感 , ε 总
2a
解: 连接 OA , OD
B
C
r E 感 ⊥ 半径
εOA = εOD = εAB = εCD = 0
取三角形回路 OAD
φm = B⋅ S∆OAD =
求:ε = ?
解: 同时存在 ε 动 , ε 感
I
b
直接由法拉第电磁感应定律求解:
a dS →vr
r B=?
dS = ?
o
x dφm = ? φm = ?
ε =?
I
b
B = µ 0I 2π x
a dS →vr
dS = adx
o
x
dφm
=
r B
⋅
d
r S
=
µ 0 Ia 2π
dx x
∫ ∫ φm =
dφm
R
or
E内
a
b
R
r E外
c
R
Q
r E感
⊥
半径
ε oa = ε oc = 0
εoac = εoa +εac +εoc = εac
通过 ∆oac 的磁通:
∫ φm =
r B
s
⋅
r dS
=
B( S∆oab
+
S扇)
=
B(
3
3 +π R2)
12
ε = − dφm =− 3 3 + π R 2 d B a : − ; c : +
= πa 2 dB − 3 a 2 dB = (π − 3 )a 2 dB
+
6 dt 4 dt 6 4 dt
练习:P 342 11 -9
已知: q = −e , r = 1.0m < R , ∆EK = 700eV
求: dφm
dt
r
, E感
解: (1)由动能定理
×R
o
r
×r
B
∆EK = A = qε = −eε
∫ εMeN= −εNM =εMN =
N
(vr
×
r B)
⋅
r dl
∫ =
a+b
v
⋅
µ0I
cos
M
πdl= −
µ0Iv ln a + b
,
a − b 2π l
2π a − b
I
⊗
r B
↑ vr
Me
o vr × Bra
N
a+b
l
UM >UN
UM
−UN
=
µ 0 Iv 2π
ln a + b a−b
,
三 .感生电动势
r Er感
L
E感
作如图环路 L
∫L
r E感
⋅
r dl
=
E感
⋅
2πr
× R
r
oBr
I
∫ ∫ = −
s
r ∂B ∂t
⋅
r dS
=
−
∫s
dB dt
dScosπ
=
dB dS
s dt
∫ r ≤ R : dBdS = dB πr 2
s dt
dt
E感
=
dB ⋅πr 2
dt
2πr
=
r 2
dB dt
∝
r
L
L
× R
r
3 a2B 4
ε AD
= ε∆OAD =
dφm
dt
=
3 a2 dB 4 dt
A→D
×
r B
取三角形回路 OBC
A B
o
a
aD
2a C
φm
=
B⋅
S扇OAD
=
πa 2
6
B
ε BC
= ε ∆OBC
=
dφm
dt
= πa2
6
dB dt
B→C
梯形回路 ABCD
ε = ε AB + ε BC + ε CD + ε DA
•产生 FεrK动的=非fr静m 电=力q:vr洛×仑B兹r 力的一个分力
r EK
=
vr
×
r B
•计算(两种方法)
(1)由电动势定义求
∫ ∫ ε 动 =
rr L EK ⋅ dl =
(vr
×
r B
)
⋅
r dl
L
∫ ε 动 =
+
(
vr
×
r B
)
⋅
r dl
−
(经内电路)
(2)由法拉第定律求 ε = − dψm
x+b
=
x
µ0 Ia dx 2π x
=
µ 0 Ia ln 2π
x+b x
=
µ 0a 2π
I 0cos ω t ⋅ ln
x+b x
I
b
φm
=
µ0a 2π
I0cosωt ⋅ ln
x
+ x
b
a
o
dS →vr x
ε = − dφm
dt
ε = µ0 I0a [ωsinωt ⋅ ln x + b + cosωt ⋅ b dx ]
求感生电场分布 .
dt
⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅L⋅ ⋅ ⋅ ⋅ ⋅ ⋅ ⋅
对称性分析(P 320 证明) 作同轴圆柱形高斯面
2R
z轴
r B
y径
x切
⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗
r E 感径 = 0
r E 感轴 = 0
r E感
只有以螺线管轴线为中心的圆周切向分量
感生电场线是在垂直于轴线平面内, 以轴线为中心的一系列同心圆。
= µ0 Iv ( b − b ) 2π x x + a
