弧齿锥齿轮几何参数计算

弧齿锥齿轮铣齿计算

弧齿锥齿轮铣齿计算弧齿锥齿轮是传动行业中常用的一种齿轮，其结构相对复杂，铣齿计算难度较大。

本文将围绕弧齿锥齿轮铣齿计算进行分步骤的阐述。

第一步：确定齿轮参数在进行弧齿锥齿轮铣齿计算之前，需要确定齿轮参数，包括轴距、锥距、锥度、压力角等参数。

这些参数需要在设计时给出，或者由实际应用中的传递比、轴功率等参数推算得出。

第二步：计算齿数弧齿锥齿轮铣齿计算的第一步是计算齿数。

通常情况下，弧齿锥齿轮的齿数较小，一般不超过20个。

计算齿数需要使用弧齿锥齿轮铣刀的几何参数，以及齿面曲线的基本方程。

每个齿面曲线可以看做一条螺旋线，其截面积呈三角形状。

根据这些参数计算得出的齿数，不一定是整数，需要舍入到最接近的整数。

第三步：计算铣刀参数在确定齿数之后，就可以开始计算铣刀参数了。

铣刀的参数包括齿宽、齿高、齿间隙等。

齿宽可以由齿数和啮合角度计算得出；齿高可以由矢高、压力角等参数计算得出；齿间隙可以采用经验数据或理论计算得出。

第四步：计算加工参数铣齿前需要确定加工参数，包括进给量、转速等。

这些参数需要根据加工机床和工件材质等具体情况进行选取，以获得最佳的加工效果。

进给量的选择要尽量保证加工效率和质量，而转速的选择则要考虑切削油，刀具材料等方面的因素。

第五步：检验加工精度最后一步是检验加工精度。

通过测量齿轮的齿高、齿宽、轴向距离、齿距等参数，可以判断齿轮加工的精度是否符合要求。

如果齿轮加工精度不足，则需要对铣刀的加工参数进行调整，并重新进行铣齿计算。

综上所述，弧齿锥齿轮铣齿计算需要经过齿轮参数计算、齿数计算、铣刀参数计算、加工参数选择和加工精度检验等多个步骤，这些步骤需要根据具体的工件、机床和材料等因素进行调整。

只有经过认真的计算和精细的加工，才能获得符合要求的弧齿锥齿轮。

全工序法弧齿锥齿轮加工参数计算方法

全工序法弧齿锥齿轮加工参数计算方法
全工序法是一种用于弧齿锥齿轮加工的常用方法，它通过一系列工序来逐步完成锥齿轮的加工。

以下是全工序法中常用的弧齿锥齿轮加工参数计算方法：
1.齿轮模数：齿轮模数是弧齿锥齿轮加工的基本参数，表示
齿轮齿数与有效齿轮直径的比值，用M表示。

根据具体
应用需求和设计要求，选择合适的齿轮模数。

2.压力角：压力角是指斜齿轮齿廓与法线之间的夹角，常用
标准值为20度。

选择合适的压力角，以确保齿轮的传动
效果和强度。

3.齿数：根据需要计算齿数。

在弧齿锥齿轮加工中，通常齿
数是通过参考传动比和齿轮齿数之间的关系来计算的。

4.锥度：锥度是指齿轮齿条与齿轮轴的夹角，常用度数表示。

计算锥度的方法包括参考标准值、设计要求和实际使用情
况。

5.齿轮齿宽：齿轮齿宽是指齿轮齿条的宽度，一般由设计要
求和传动功率等因素决定。

6.齿根圆直径：计算齿根圆直径以确定弧齿锥齿轮的基准尺
寸。

齿根圆直径是齿轮齿廓最低点的圆形位置。

7.齿顶圆直径：计算齿顶圆直径以确定弧齿锥齿轮的基准尺
寸。

齿顶圆直径是齿轮齿廓最高点的圆形位置。

8.齿廓修形参数：根据特定设计要求和加工方法，确定齿廓
修形参数，如修形系数和修形位移。

以上仅是全工序法中一些常用的弧齿锥齿轮加工参数计算方法的概述。

在实际应用中，还需结合具体工件的设计要求、加工设备和工艺流程等因素来确定适当的参数值。

弧齿锥齿轮几何参数设计

第14章弧齿锥齿轮的轮坯设计14.1 弧齿锥齿轮的基本概念14.1.1 锥齿轮的节锥对于相交轴之间的齿轮传动，一般采用锥齿轮。

锥齿轮有直齿锥齿轮和弧齿锥齿轮。

弧齿锥齿轮副的形式如图14-1所示，与直齿锥齿轮相比，轮齿倾斜呈弧线形。

但弧齿锥齿轮的节锥同直齿锥齿轮的节锥一样，相当于一对相切圆锥面作纯滚动，它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的（图14-2）。

两个相切圆锥的公切面成为齿轮副的节平面。

齿轮轴线与节平面的夹角，即节锥的半锥角称为锥齿轮的节锥角δ1或δ2。

两齿轮轴线之间的夹角称为锥齿轮副的轴交角∑。

节锥任意一点到节锥顶点O 的距离称为该点的锥距R i ，节点P 的锥距为R 。

因锥齿轮副两个节锥的顶点重合，则 21δδ+=∑大小轮的齿数之比称为锥齿轮的传动比1212z z i =(14-1) 小轮和大轮的节点半径r 1、r 2分别为11sin δR r = 22sin δR r = (14-2)它们与锥齿轮的齿数成正比，即121212sin sin z z r r ==δδ (14-3) 传动比与轴交角已知，则节锥可惟一的确定，大、小轮节锥角计算公式为∑+∑=cos 1sin 12122i i tg δ 21δδ-∑= (14-4)当090=∑时，即正交锥齿轮副，122i tg =δ 14.1.2弧齿锥齿轮的旋向与螺旋角1．旋向弧齿锥齿轮的轮齿对母线的倾斜方向称为旋向，有左旋和右旋两种（图14-3）。

面对轮齿观察，由小端到大端顺时针倾斜者为右旋齿轮（图14-3b ），逆时针倾斜者则为左旋齿（图14-3a ）。

大小轮的旋向相图14-2 锥齿轮的节锥与节面(a) 左旋 (b) 右旋图14-3 弧齿锥齿轮的旋向图14-1 弧齿锥齿轮副反时，才能啮合。

一般情况下，工作面为顺时针旋转的（从主动轮背后看，或正对被动轮观察），主动锥齿轮的螺旋方向为左旋，被动轮为右旋（图14-1）；工作面为逆时针旋转的，情况相反。

弧齿锥齿轮主要参数的测绘计算

弧齿锥齿轮主要参数的测绘计作者: 日期:弧齿锥齿轮主要参数的测绘计算零部件加工部麻俊方弧齿锥齿轮具有承载能力高、运转平稳、噪音低等特点，在汽车行业中得到了广泛的应用。

通常由一对弧齿锥齿轮组成汽车驱动桥主减速器的主要传动机构。

弧齿锥齿轮的设计与测绘计算均比较复杂，下面仅介绍几种主要参数的测绘计算方法。

1.轴交角一对弧齿锥齿轮副的住从动齿轮中心轴线交于一点。

轴线间的交角刀可成任意角度，但在绝大多数汽车驱动桥上，主减速齿轮副都采用90°相交的布置。

2.齿制渐开线锥齿轮的齿制很多，多达40多种，我国常用的齿制有Gleason（格利森）制、Oerlikon（奥利康）制、Kingelnberg（克林贝格）制三种。

其中应用最广泛也是最常见到的是Gleaso n（格利森）制弧齿锥齿轮。

不同的齿制，对应不同的参数计算方法与计算公式，在测量齿轮时一定要注意区分。

3•模数弧齿锥齿轮模数是一个变值，由大端向小端与锥距成比例缩小，通常以大端面模数叫来计算。

GB12368-9C规定了锥齿轮大端端面模数，其中以》1为例，有1、1.125、1.375、1.5、1.75、2等等。

但是所测量的齿轮模数不一定为整数，也不一定符合标准模数系列。

对于模数的测绘与计算，有以下方式：1. 由测量的锥距R,可初步估算锥齿轮的大端模数叫h(用深度尺来测量)加以复核。

对于等顶隙收缩齿(格里森制)，齿顶高系数ha = 0.85,顶隙系*数C *=0.188则齿高 h=(2 ha +C *)m 。

*由此得出模数m=h(2ha +C *),进而复核模数m s 。

tm s—2.测量出锥齿轮的周节t ，根据公式来进行计算，这种方法要求测量数据准确无误，且被测绘齿轮无磨损现象。

3. 由齿顶圆直径反求模数。

首先测绘出齿顶圆的直径尺寸，利用齿顶圆计算公式，然后反求模数。

所使用的反求公式为4. 由刀顶距的数值计算模数。

弧齿锥齿轮铣刀盘的刀顶距W 叫席2式中ms—大端模数的估算数值;1 0.5— L e ；R因为2 Z2 ^ 、、， ,于是便可确定锥齿轮大端模数m 2R人『云。

圆弧齿锥齿轮计算公式

圆弧齿锥齿轮计算公式(总3页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--圆弧齿锥齿轮计算公式圆弧齿锥齿轮计算公式：1大端分度圆dd1=Z1m,d2=Z2m2分锥角δδ1=arctan(Z1/Z2),δ2=90-δ13锥距RR=d1/2sinδ1=d2/2sinδ24齿距pp=πm5齿高hh=(2ha*+c*)m6齿顶高haha=(ha*+x)m7齿根高hfhf=(ha*+c*-x)m8顶隙cc=c*m9齿根角θfθf1=arctg(hf1/R),θf2=ar ctg(hf2/R)10齿顶角θaθa1=θf2,θa2=θf1(等顶隙收缩齿)11顶锥角δaδa1=δ1+θf2,δa2=δ2+θf112根锥角δfδf1=δ1-θf1,δf2=δ2-θf213顶圆直径dada1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2,14分锥顶点至轮冠距离AkAk1=d2/2-ha1sinδ1,=d1/2-ha2sinδ215齿宽中点分度圆直径dmdm1=d1-bsinδ1,dm2=d2-bsinδ216齿宽中点模数mmmm=dm1/z1=dm2/z217中点分度圆法向齿厚smnsmn=πcosβm+2xtanα+xt)mm18中点法向齿厚半角ψmnψmn=smnsinδcos2βm/dm19中点分圆法向弦齿厚smnsmn=smn(1-ψmn2/6)20中点分圆法向弦齿高hamham=ha-btanθa/2+smnψmn/421当量齿数ZvZv=Z/cosδcos3βm22端面重合度εαεα=[Z1(tanαvat1-tanαt)/cosδ1 +Z2(tanαvat2-tanαt)/cosδ2]/2π其中:tanαt=(tanα/cosβm)cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]εα=23齿线重合度εβεβ=btanβmπ/mm24总重合度ε=(εα2+εβ2)1/2关于弧半径：求扇形弧半径扇形弧即指整个圆圈中的一部分。

圆弧齿锥齿轮计算公式

圆弧齿锥齿轮计算公式(总3页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--圆弧齿锥齿轮计算公式圆弧齿锥齿轮计算公式：1大端分度圆dd1=Z1m,d2=Z2m2分锥角δδ1=arctan(Z1/Z2),δ2=90-δ13锥距RR=d1/2sinδ1=d2/2sinδ24齿距pp=πm5齿高hh=(2ha*+c*)m6齿顶高haha=(ha*+x)m7齿根高hfhf=(ha*+c*-x)m8顶隙cc=c*m9齿根角θfθf1=arctg(hf1/R),θf2=ar ctg(hf2/R)10齿顶角θaθa1=θf2,θa2=θf1(等顶隙收缩齿)11顶锥角δaδa1=δ1+θf2,δa2=δ2+θf112根锥角δfδf1=δ1-θf1,δf2=δ2-θf213顶圆直径dada1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2,14分锥顶点至轮冠距离AkAk1=d2/2-ha1sinδ1,=d1/2-ha2sinδ215齿宽中点分度圆直径dmdm1=d1-bsinδ1,dm2=d2-bsinδ216齿宽中点模数mmmm=dm1/z1=dm2/z217中点分度圆法向齿厚smnsmn=πcosβm+2xtanα+xt)mm18中点法向齿厚半角ψmnψmn=smnsinδcos2βm/dm19中点分圆法向弦齿厚smnsmn=smn(1-ψmn2/6)20中点分圆法向弦齿高hamham=ha-btanθa/2+smnψmn/421当量齿数ZvZv=Z/cosδcos3βm22端面重合度εαεα=[Z1(tanαvat1-tanαt)/cosδ1 +Z2(tanαvat2-tanαt)/cosδ2]/2π其中:tanαt=(tanα/cosβm)cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]εα=23齿线重合度εβεβ=btanβmπ/mm24总重合度ε=(εα2+εβ2)1/2关于弧半径：求扇形弧半径扇形弧即指整个圆圈中的一部分。

圆弧齿锥齿轮计算公式

圆弧齿锥齿轮计算公式(总3页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--圆弧齿锥齿轮计算公式圆弧齿锥齿轮计算公式：1大端分度圆dd1=Z1m,d2=Z2m2分锥角δδ1=arctan(Z1/Z2),δ2=90-δ13锥距RR=d1/2sinδ1=d2/2sinδ24齿距pp=πm5齿高hh=(2ha*+c*)m6齿顶高haha=(ha*+x)m7齿根高hfhf=(ha*+c*-x)m8顶隙cc=c*m9齿根角θfθf1=arctg(hf1/R),θf2=ar ctg(hf2/R)10齿顶角θaθa1=θf2,θa2=θf1(等顶隙收缩齿)11顶锥角δaδa1=δ1+θf2,δa2=δ2+θf112根锥角δfδf1=δ1-θf1,δf2=δ2-θf213顶圆直径dada1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2,14分锥顶点至轮冠距离AkAk1=d2/2-ha1sinδ1,=d1/2-ha2sinδ215齿宽中点分度圆直径dmdm1=d1-bsinδ1,dm2=d2-bsinδ216齿宽中点模数mmmm=dm1/z1=dm2/z217中点分度圆法向齿厚smnsmn=πcosβm+2xtanα+xt)mm18中点法向齿厚半角ψmnψmn=smnsinδcos2βm/dm19中点分圆法向弦齿厚smnsmn=smn(1-ψmn2/6)20中点分圆法向弦齿高hamham=ha-btanθa/2+smnψmn/421当量齿数ZvZv=Z/cosδcos3βm22端面重合度εαεα=[Z1(tanαvat1-tanαt)/cosδ1 +Z2(tanαvat2-tanαt)/cosδ2]/2π其中:tanαt=(tanα/cosβm)cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]εα=23齿线重合度εβεβ=btanβmπ/mm24总重合度ε=(εα2+εβ2)1/2关于弧半径：求扇形弧半径扇形弧即指整个圆圈中的一部分。

弧齿锥齿轮主要参数的测绘计算

弧齿锥齿轮主要参数的测绘计算零部件加工部麻俊方弧齿锥齿轮具有承载能力高、运转平稳、噪音低等特点，在汽车行业中得到了广泛的应用。

通常由一对弧齿锥齿轮组成汽车驱动桥主减速器的主要传动机构。

弧齿锥齿轮的设计与测绘计算均比较复杂，下面仅介绍几种主要参数的测绘计算方法。

1.轴交角一对弧齿锥齿轮副的住从动齿轮中心轴线交于一点。

轴线间的交角∑可成任意角度，但在绝大多数汽车驱动桥上，主减速齿轮副都采用90°相交的布置。

2.齿制渐开线锥齿轮的齿制很多,多达40多种,我国常用的齿制有Gleason(格利森）制、Oerlikon(奥利康)制、Kingelnberg(克林贝格）制三种。

其中应用最广泛也是最常见到的是Gleason(格利森）制弧齿锥齿轮。

不同的齿制，对应不同的参数计算方法与计算公式，在测量齿轮时一定要注意区分。

3.模数弧齿锥齿轮模数是一个变值，由大端向小端与锥距成比例缩小，通常以大端面模数s m 来计算。

GB12368-90规定了锥齿轮大端端面模数，其中以≥1为例，有1、1.125、1.375、1.5、1.75、2等等。

但是所测量的齿轮模数不一定为整数，也不一定符合标准模数系列。

对于模数的测绘与计算，有以下方式：⒈由测量的锥距R ，可初步估算锥齿轮的大端模数s m 。

因为2212mR z z z =+，于是便可确定锥齿轮大端模数22122/m R z z =+。

然后实测齿高h(用深度尺来测量)加以复核。

对于等顶隙收缩齿(格里森制)，齿顶高系数*a h ＝0.85，顶隙系数C *=0.188,则齿高h=(2*a h +C *)m 。

由此得出模数m=h(2*a h +C *)，进而复核模数m s。

⒉ 测量出锥齿轮的周节t ，根据公式s tm π=来进行计算，这种方法要求测量数据准确无误，且被测绘齿轮无磨损现象。

⒊ 由齿顶圆直径反求模数。

首先测绘出齿顶圆的直径尺寸，利用齿顶圆计算公式，然后反求模数。

弧齿锥齿轮的几何尺寸计算表

2
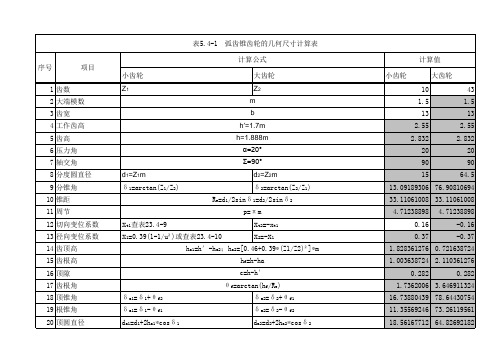
13.09189306 76.90810694 33.11061008 33.11061008 4.71238898 0.16 0.37 4.71238898 -0.16 -0.37
xt1查表23.4-9 x1=0.39(1-1/u²)或查表23.4-10
xt2=-xt1 x2=-x1
hf=h-ha c=h-h′ θ f=arctan(பைடு நூலகம்f/Re) δ δ
s2=p/2-(ha1-ha2)tanα /cosβ m-xt1m
Smn1=(0.5πcosβm+2x1tanα+xt1)mm ψmn=Smn*cosδ*cos²βm/(mmZ) Kψ mn=1-ψ mn²/6 S′mn=SmnKψmn h′am1=ha1-0.5b*tanθf2+0.25Smn1ψmn1 查表23.4-11 N0=（θ
f1+θf2）sinβm/20
Smn2=πmmcosβm-Smn1
h′am2=ha2-0.5b*tanθf1+0.25Smn2ψmn2
1.472078944 0.525395815 9.262878463 9.262878463
设定值传动比 4.3 齿顶高系数顶隙系数 0.85 0.188
da1=d1+2ha1*cosδ
da2=d2+2ha2*cosδ
21 锥点至轮冠距离 22 理论弧齿厚 23 侧隙 24 中点螺旋角 25 齿宽系数 26 中点模数 27 中点法向模数 28 中点法向齿厚 29 中点法向齿厚半角 30 中点齿厚角系数 31 中点分度圆弦齿厚 32 中点分度圆弦齿高 33 刀盘直径 34 刀号
表5.4-1 序号 1 齿数 2 大端模数 3 齿宽 4 工作齿高 5 齿高 6 压力角 7 轴交角 8 分度圆直径 9 分锥角 10 锥距 11 周节 12 切向变位系数 13 径向变位系数 14 齿顶高 15 齿根高 16 顶隙 17 齿根角 18 顶锥角 19 根锥角 20 顶圆直径 δ δ

弧齿锥齿轮设计计算

准双曲面齿轮设计计算
小轮齿数 16 小轮螺旋角 54 大轮齿数 41 工作齿高系数 4.000 输入齿轮基本参数大轮齿面宽偏置距 29.2 38.6 锥度系数压力角和 0.788532 38 大轮节径刀盘半径 190.5 95.25 大轮齿顶高系数齿侧间隙 0.325 0.20--0.30 计算刀盘半径 95.24998171 旋向小轮大轮左旋右旋偏置顶系下 0.1250
19 下38.6 107.52 2.7719 6.668 8.5281 9.440 -3.543 15.51547 -4.812 23.86825 -1.819 89.93 50.973 60.46 25.63205 62.3573 29.79222 64.44521 23.63867 58.02087 54.49766 30.86347 0 右旋 190.5 0.20--0.30 190.5 120.7404 193.0721
名
准双曲面齿轮计算结果称小轮 16
大轮 41 4.646
ห้องสมุดไป่ตู้
齿数模数压力角小轮偏置外锥距齿顶高齿根高工作齿高全齿高节锥定点到交错点的距离面锥顶点到交错点的距离根锥顶点到交错点的距离轮冠到交错点的距离前冠到交错点的距离节锥角面锥角根锥角中点螺旋角旋向节锥直径侧隙刀具直径外径

圆弧齿锥齿轮计算公式演示教学

圆弧齿锥齿轮计算公式圆弧齿锥齿轮计算公式：1大端分度圆dd1=Z1m,d2=Z2m2分锥角δδ1=arctan(Z1/Z2),δ2=90-δ13锥距RR=d1/2sinδ1=d2/2sinδ24齿距pp=πm5齿高hh=(2ha*+c*)m6齿顶高haha=(ha*+x)m7齿根高hfhf=(ha*+c*-x)m8顶隙cc=c*m9齿根角θfθf1=arctg(hf1/R),θf2=arctg(hf2/R) 10齿顶角θaθa1=θf2,θa2=θf1(等顶隙收缩齿)顶锥角δaδa1=δ1+θf2,δa2=δ2+θf112根锥角δfδf1=δ1-θf1,δf2=δ2-θf213顶圆直径dada1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2, 14分锥顶点至轮冠距离AkAk1=d2/2-ha1sinδ1,=d1/2-ha2sinδ215齿宽中点分度圆直径dmdm1=d1-bsinδ1,dm2=d2-bsinδ216齿宽中点模数mmmm=dm1/z1=dm2/z217中点分度圆法向齿厚smnsmn=(0.5πcosβm+2xtanα+xt)mm18中点法向齿厚半角ψmnψmn=smnsinδcos2βm/dm19中点分圆法向弦齿厚smnsmn=smn(1-ψmn2/6)20中点分圆法向弦齿高hamham=ha-btanθa/2+smnψmn/421当量齿数ZvZv=Z/cosδcos3βm端面重合度εαεα=[Z1(tanαvat1-tanαt)/cosδ1+Z2(tanαvat2-tanαt)/cosδ2]/2π其中:tanαt=(tanα/cosβm)cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]εα=1.29723齿线重合度εβεβ=btanβmπ/mm24总重合度ε=(εα2+εβ2)1/2关于弧半径：求扇形弧半径扇形弧即指整个圆圈中的一部分。

通常的已知条件是由水平线除２组成的大边和以垂直线组成的小边。

弧齿锥齿轮几何参数设计.doc

弧齿锥齿轮几何参数设计..第14章弧齿锥齿轮的轮坯设计图14-1 弧齿锥齿轮副14.1 弧齿锥齿轮的基本概念14.1.1 锥齿轮的节锥图14-2 锥齿轮的节锥与节面对于相交轴之间的齿轮传动，一般采用锥齿轮。

锥齿轮有直齿锥齿轮和弧齿锥齿轮。

弧齿锥齿轮副的形式如图14-1所示，与直齿锥齿轮相比，轮齿倾斜呈弧线形。

但弧齿锥齿轮的节锥同直齿锥齿轮的节锥一样，相当于一对相切圆锥面作纯滚动，它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的（图14-2）。

两个相切圆锥的公切面成为齿轮副的节平面。

齿轮轴线与节平面的夹角，即节锥的半锥角称为锥齿轮的节锥角d1或d2。

两齿轮轴线之间的夹角称为锥齿轮副的轴交角S。

节锥任意一点到节锥顶点O的距离称为该点的锥距Ri，节点P的锥距为R。

因锥齿轮副两个节锥的顶点重合，则大小轮的齿数之比称为锥齿轮的传动比(14-1)小轮和大轮的节点半径r1、r2分别为(14-2)它们与锥齿轮的齿数成正比，即(14-3)传动比与轴交角已知，则节锥可惟一的确定，大、小轮节锥角计算公式为(14-4)(a) 左旋(b) 右旋图14-3 弧齿锥齿轮的旋向当时，即正交锥齿轮副，14.1.2弧齿锥齿轮的旋向与螺旋角1．旋向弧齿锥齿轮的轮齿对母线的倾斜方向称为旋向，有左旋和右旋两种（图14-3）。

面对轮齿观察，由小端到大端顺时针倾斜者为右旋齿轮（图14-3b），逆时针倾斜者则为左旋齿（图14-3a）。

大小轮的旋向相反时，才能啮合。

一般情况下，工作面为顺时针旋转的（从主动轮背后看，或正对被动轮观察），主动锥齿轮的螺旋方向为左旋，被动轮为右旋（图14-1）；工作面为逆时针旋转的，情况相反。

这样可保证大小轮在传动时具有相互推开的轴向力，从而使主被动轮互相推开以避免齿轮承载过热而咬合。

2．螺旋角图14-4 弧齿锥齿轮的齿线与螺旋角弧齿锥齿轮轮齿的倾斜程度由螺旋角bi来衡量。

弧齿锥齿轮纵向齿形为节平面与轮齿面相交的弧线，该弧线称为节线，平面齿轮的节线称为齿线。

全工序法弧齿锥齿轮加工参数计算方法

全工序法弧齿锥齿轮加工参数计算方法在机械制造领域，齿轮是一种非常常见的零部件，广泛应用于各种机械传动系统中。

在齿轮中，弧齿锥齿轮因其结构特点和使用场合的不同而显得尤为重要。

全工序法弧齿锥齿轮是一种加工工艺较为复杂的齿轮类型，需要考虑多个参数才能获得最佳的加工效果。

我们来了解一下什么是全工序法弧齿锥齿轮。

全工序法是指在一台机床上完成齿轮的所有加工工序，包括铣齿、车齿、滚挤等。

相较于分工序法，全工序法能够保证齿轮的几何精度和表面粗糙度，并且能够提高生产效率，因此在实际应用中得到广泛的应用。

而弧齿锥齿轮是一种齿轮的结构形式，其齿廓呈弧形。

在加工过程中，需要考虑齿轮的模数、螺旋角、齿顶间隙等参数，以确保加工出理想的弧齿锥齿轮。

在进行全工序法弧齿锥齿轮加工参数计算时，首先要确定齿轮的模数。

模数是描述齿轮齿形和尺寸的重要参数，一般根据传动比、齿数和中心距来确定。

模数的选择直接影响到齿轮的传动性能和加工成本，因此需要根据具体的使用要求来确定模数值。

要考虑弧齿锥齿轮的螺旋角。

螺旋角是指齿轮轴线上齿顶锥面与轴线的夹角，是描述螺旋齿轮齿形的重要参数。

在全工序法弧齿锥齿轮的加工过程中，螺旋角的选择直接影响到齿轮的传动效果和噪音水平。

通常情况下，螺旋角的选择要根据齿轮的使用环境和传动要求来确定，以获得最佳的传动性能。

齿顶间隙也是全工序法弧齿锥齿轮加工过程中需要考虑的重要参数之一。

齿顶间隙是指齿轮齿顶与对齿轮啮合的齿条或齿轮齿顶之间的间隙，是保证齿轮啮合顺畅的重要因素。

在加工过程中，齿顶间隙的选择需要考虑到齿轮的使用要求和加工工艺，以确保齿轮在高速、大扭矩等工况下能够正常运行。

全工序法弧齿锥齿轮加工参数计算是一个复杂而又重要的过程，需要综合考虑多个因素才能获得理想的加工效果。

在实际应用中，需要根据具体的使用情况和加工设备的性能来确定最佳的加工参数，以确保获得高质量的弧齿锥齿轮。

在我的个人观点和理解中，全工序法弧齿锥齿轮加工参数计算是一个重要而又复杂的工艺过程，需要综合考虑多个因素来进行合理的选择。

4弧齿锥齿轮的加工调整计算

4弧齿锥齿轮的加工调整计算四弧齿锥齿轮是一种常见的齿轮类型，广泛应用于机械设备中。

在加工和调整四弧齿锥齿轮时，需要进行一系列的计算和调整，以保证齿轮的性能和运行精度。

本文将详细介绍四弧齿锥齿轮的加工调整计算。

首先，需要明确四弧齿锥齿轮的基本参数。

四弧齿锥齿轮由齿数、模数、部分齿宽系数、螺旋角等参数决定。

在加工和调整过程中，需要根据这些参数计算齿轮的各种尺寸和角度。

一、计算齿轮的齿数和模数：齿数是齿轮的重要参数之一，一般根据设计要求来确定。

模数是齿轮的副产物，是齿宽与齿数的比值。

根据齿数和模数可以计算出齿轮的模数。

齿轮的模数计算公式为：m=Z/b。

其中，m为模数，Z为齿数，b为齿宽。

二、计算齿轮的齿宽和齿高：齿宽是齿轮的另一个重要参数，一般由设计要求和工艺条件来确定。

根据齿宽和模数可以计算出齿轮的齿高。

齿轮的齿高计算公式为：h=1.25m。

其中，h为齿高、m为模数。

三、计算齿轮的分度圆半径和齿根半径：分度圆半径是齿轮最重要的参数之一，是齿轮齿槽几何形状的基准。

根据模数和齿数可以计算出齿轮的分度圆半径。

齿轮的分度圆半径计算公式为：Rm=Zm。

其中，Rm为分度圆半径，Z为齿数。

齿根半径是齿轮齿根处几何形状的基准。

根据模数可以计算出齿轮的齿根半径。

齿轮的齿根半径计算公式为：Rh=1.2m。

其中，Rh为齿根半径，m为模数。

四、计算齿轮的螺旋角和压力角：螺旋角和压力角是齿轮的重要几何参数，决定了齿轮的传动性能和运动特性。

根据设计要求和工艺条件来确定。

螺旋角的计算公式为：α=arctan(tanβ/cosγ)。

其中，α为螺旋角，β为压力角，γ为齿轮轴线与交点线之间的夹角。

压力角的计算公式为：β=10°-24°-45°(z1/z2)。

其中，β为压力角，z1为主齿轮的齿数，z2为从齿轮的齿数。

以上是四弧齿锥齿轮加工调整的一般计算方法。

在实际加工和调整过程中，还需要结合具体的工艺要求和设备精度进行一系列修正和调整。

弧齿锥齿轮主要参数的测绘计算

弧齿锥齿轮测绘计算
弧齿锥齿轮是传动装置中常用的机械零部件，其主要参数的测绘计算
对于产品的质量至关重要。

测绘计算通常包含三个步骤：测量齿距、
测量基本圆的参数、计算副圆和半螺距参数。

第一步，测量齿距。

齿距是指齿轮相邻齿节圆心距离，它是齿轮的核
心参数，影响到齿轮的齿廓特性及传动整体特性，因此必须准确测量，在测量之前，要仔细检查齿轮和齿轮毂的形状和尺寸，确保使用正确
的测量工具，避免测量误差。

第二步，测量基本圆参数。

齿轮的基本尺寸参数是圆的相应参数，要
准确地测量每一个参数，如节圆的半径、圆弧的中径、角等，以保证
基本尺寸的准确性，否则可能会产生传动特性的差异。

第三步，计算副圆和半螺距参数。

副圆和半螺距是齿轮传动中互动作
用重要因素，左右面齿轮必须正确配准，因此需要准确计算副圆和半
螺距参数，确保互动特性和传动效率达到设计要求。

综上，正确测绘计算弧齿锥齿轮的参数有助于保障齿轮产品质量，使
弧齿锥齿轮传动均能达到设计要求，以实现传动效果。

弧齿锥齿轮参数计算工具及强度校核

弧齿锥齿轮参数计算工具及强度校核
本文介绍了一种弧齿锥齿轮参数计算工具及强度校核方法。

首先介绍了弧齿锥齿轮的基本概念和几何参数，然后对弧齿锥齿轮的参数计算进行了详细的介绍。

接着，介绍了弧齿锥齿轮的强度校核方法，包括使用ANSI/AGMA标准的计算方法和基于有限元分析的校核方法。

最后，通过一个实例进行了弧齿锥齿轮的计算和校核。

这种工具和方法可以大大提高弧齿锥齿轮的设计效率和准确性，对于机械设计工程师和研究人员具有一定的参考价值。

- 1 -。

弧齿锥齿轮设计计算

齿侧间隙 0.20--0.30 95.24998171
旋向小轮大轮左旋右旋偏置顶系下 0.1250
准双曲面齿轮设计计算
输入齿轮基本参数
小轮齿数
大轮齿数
大轮齿面宽
偏置距
大轮节径
16
41
小轮螺旋角工作齿高系数
54
4.000
29.2 锥度系数 0.788532
38.6 压力角和
38
大轮1齿90顶.5高系数
0.325
计算刀盘半径
准双曲面齿轮计算结果
名
称
小轮大轮
齿数
16
41
模数
4.646
压力角
19
小轮偏置
23.86825 -1.819
89.93 50.973
60.46
25.63205 62.3573
29.79222 64.44521
23.63867 58.02087
54.49766 30.86340--0.30 190.5
外径
120.7404 193.0721
刀盘半径 95.25
下38.6
外锥距
107.52
齿顶高
2.7719
齿根高工作齿高
6.668 8.5281
全齿高
9.440
节锥定点到交错点的距离
-3.543
面锥顶点到交错点的距离 15.51547 -4.812
根锥顶点到交错点的距离轮冠到交错点的距离前冠到交错点的距离节锥角面锥角根锥角中点螺旋角旋向节锥直径

标准锥齿轮有关参数计算公式及示例

齿数
Z
大端模数
m
齿宽
b
齿顶高系数 ha*
顶隙系数
c*
压力角
α
轴交角
∑
高变位系数 X
切向变位系数 Xt
标准锥齿轮有关参数计算公式及
mm mm
° °
大端分度圆直径 d mm
分度锥角
δ°
大端锥距
R mm
大端齿距
p mm
大端齿顶高 ha mm
大端齿根高 hf mm
大端全齿高 h mm
大端齿顶圆直径 da mm
冠顶距
Aa mm
齿根高
θf °
无根切许用最大 θ
齿根角
fmax °
齿顶角顶锥角根锥角
θa ° δa ° δf °
大端分度圆弧齿
厚
S mm
大端分度圆弦齿
厚
S平均 mm
大端分度圆弦齿 ha平
高
均 mm
刨齿机用的齿角 λ °
标准锥齿轮有关参数计算公式及示例
X2=-X1 Xt2=-Xt1
19 3 28 1 0.2 20 90
59 3 28 1 0.2 20 90
-0.41 -0.015
177
72.149682 92.975803 9.424778
1.77 4.83 6.6 178.08512 26.815207 2.973785
12.876983
1.460182 73.609864 69.175896
3.772022
2.37
h=ha+hf
6.6
da=d+2hacosδ
65.05274
Aa=Rcosδ-hasinδ
87.203372