计算机数学基础期末复习
山东大学计算机基础复习题

二、单项选择题(本题共20个小题,每小题1分,共20分)1.关于信息技术(Information Technology,IT)下列说法正确的是([1])。
A、现代信息技术是指以微电子技术、计算机技术和通信技术为特征的技术。
B、信息技术就是计算机技术和计算机网络技术。
C、在信息处理的每一个环节,都必须使用信息技术。
D、信息技术无法对工业社会形成的传统设备进行技术改造,成为智能设备。
2.二进制是由下列哪位科学家首先提出来的([2])。
A、莱布尼兹B、布尔C、巴贝奇D、图灵3.关于思维,下列说法不正确的是([3])。
A、思维是人类的大脑对外部客观世界概括的和间接的反应。
B、思维是人类凭借知识、经验对客观事物进行的间接反应。
C、思维是在表象、概念的基础上进行分析、综合、判断、推理等认识活动的过程。
D、思维是人类与生俱来的,与后天的学习无关。
4.巴贝奇的“分析机”到他终生都没有制造出来,下列说法正确的是([4])。
A、设计原理有错误B、设计思想太过超前C、设计图纸不够完善D、机械加工的工艺水平达不到它要求的精度5.第三代计算机采用的逻辑运算器件([5])。
A、电子管B、晶体管C、集成电路D、大规模集成电路6.在计算机中,引入16进制,主要目的是([6])。
A、计算机中的数据存储采用16进制。
B、计算机中的数据运算采用16进制。
C、书写二进制串方便。
D、计算机的内存地址采用16进制编制7.设计算机字长为8位,采用补码表示,可表示的整数的取值范围是([7])。
A、0~128B、-127~128C、-128~127D、-128~1288.在数值数据的表示中,我们经常提到数的定点表示和浮点表示。
对于这两种表示方法,以下说法错误的是([8])。
A、定点表示经常用来表示整数,小数点的位置是确定的。
B、浮点数一般用来表示带小数位的数字,小数点的位置是浮动的,浮动的位数用阶码表示。
C、单精度浮点数占16位字长,双精度浮点数有32位字长。
大学计算机基础理论知识点复习

理论知识点一、基础部分1、进制转换1)最大数概念(各进制数的比较、各进制数的表示、鉴别方法、基数、位权等)2)进制转换(含小数)二进制、十进制、八进制与十六进制的表示与转换3)逻辑运算(与或非)逻辑与、或、非运算、二进制的加减运算2、数据在计算机中的表示:1)数字(基本概念、定点数、浮点数、字节与位关系、存储单位KB、MB、GB意义和转换)基数:2,位权:20,21,22,23浮点数:小数点的位置可浮动,由尾数与阶码构成。
围由阶码位数决定,精度由尾数的位数决定1byte =8bits1KB = 1024 = 2 10个字节1MB = 1,048,576 = 220字节1GB = 10亿字节=230字节1TB = 10000亿字节= 240字节1PB = 10000000亿字节= 250字节1GB = 1024*1024*1024 BYTE1Mbps =1000000bps1MHZ =1000000 HZ2)西文(基本概念、特定ASCII值和推算、比较ASCII大小、存放空间计算)ASCII码:美国国家标准信息交换码(用7位二进制表示)。
A-Z: 41H - 5AH 、65 - 90a-z: 61H - 7AH、97 -1220-9: 30H - 39H、48 - 57空格:20H、323)中文(基本概念、存放空间计算、机码、国标码。
类似DA 9A是1个汉字39 、4A是数字或字母等、输入码、字形码(点阵与矢量))汉字环境:输入码(不同的输入方式的编码,外码)机码(2Bytes)编码方式:1 XXXXXXX 1 XXXXXXX国标码(2Bytes)编码方式:0 XXXXXXX 0XXXXXXXGB2312-80:含6763个汉字GB18030:27484个汉字和6000多个藏、蒙和维吾尔等文字字形码:点阵:16*16,24*24,32*32,48*48矢量:以.ttf格式保存在控制面板的“字体”中3、计算机发展(现代计算机体系结构、计算机的分代依据、计算机分类、IT、计算机主要应用领域、MIS、OA、CAI等缩写)电子计算机发展的4个阶段——电子管、晶体管、中小集成电路、大超大集成电路微机发展的几个阶段——按照中央处理器CPU来划分4、计算机安全(病毒和木马、操作系统与软件的补丁和更新、防火墙)计算机病毒:一种人为设计危害计算机系统和网络的程序。
计算机数学基础(1)期末要点(03夏)

计算机数学基础(1)期末复习要点与模拟练习师范部冯泰一、关于期末考核1.本学期的结业考核由形成性考核和期末考核构成.形成性考核由平时作业成绩构成,占结业考核成绩的20%, 期末考核成绩占结业考核成绩的80%.2.期末考核实行全国统一考核,根据本课程考试说明,由中央电大统一命题,统一考核时间,制定统一评分标准.开办试点的地方电大组织考核.期末考核的考核内容和要求以考核说明为准;采用闭卷笔试,试卷满分100分;时限120分钟.试题类型及分数:单项选择题和填空题,分数约占25%.解答与计算题,分数约占56%;证明题,分数约占19%.3, 考核试卷分数分布:第1编数理逻辑约30分,第2编集合论约30分,第3编图论约25分,第4编代数系统约15.4. 易、中、较难题目在试卷中占的比例是4:4:2.二、各章基本问题与重点第1章命题逻辑基本问题:1. 命题符号化,是否命题判断或求真值.2. 命题公式赋值,及类型判别.3. 命题公式等值判别或证明.方法有真值表法、等值演算法和主范式法.4. 求范式和主范式.5. 蕴含式(推理理论)证明:方法有:真值表法、等值演算法、主析取范式法、构造证明法――直接法、附加前提证明法和反证法.重点:真值表,命题公式的赋值于命题公式类型以及公式之间等值的判别,求主范式和构造推理证明.第2章谓词逻辑基本问题:1. 命题符号化.2. 求辖域、约束变元、自由变元.3. 给定解释求谓词公式的真值(多为个体域有限的情形).4. 判断谓词公式是否重言式(用代换实例)、永假式或可满足式?5. 求前束范式.6. 谓词公式等值式的证明.重点:求辖域、变元,在有限个体域内求谓词公式的真值,求前束范式.第3章集合及其运算基本问题:1. 求集合表达式(列举法或描述法).2. 判断集合与元素、集合与集合的关系,用∈,∉,⊂,⊆,⊄?3. 求幂集.4. 包含或相等的化简或证明.5. 求笛卡儿积,或某些等式证明.重点:求幂集合,集合(包括笛卡儿积)的化简或等式证明.第4章二元关系与函数基本问题:1. 求关系的表达式,关系矩阵、关系图,Dom(R),Ran(R).2. 验证或证明关系的性质.3. 求复合关系、逆关系及其矩阵.4. 求关系闭包.5. 关系计算:求⋃,⋂,-,~,⊕6. 验证或证明关系R是等价关系或偏序关系.7. 求等价关系的等价类.8. 作偏序关系的哈斯图,求极大(小)元、最大(小)元.9. 验证是否是函数,是满射、单射、双射?求函数定义域、值域.10. 求复合函数、反函数.判别是否存在反函数?重点:求关系的表达式(矩阵或关系图),判别关系的性质,求复合关系和逆关系,证明是否等价关系或偏序关系,作哈斯图求极(最)大极(最)小元.第5章图的基本概念基本问题:1. 图G与G=<V,E>互求.2. 判断简单图、多重图、完全图.3. 求补图.子图或生成子图.4. 求结点度数或用握手定理求结点数,或判断是否度数序列.5. 判断是否同构,主要用必要条件判断不同构.6. 用握手定理或推理进行证明.7. 求图中通路、回路、长度或通路、回路的数目(主要用定理8)8.判断是否连通、强连通、单侧连通或弱连通.9. 求点割集、割点和边割集、割边.10. 求图的关联矩阵、邻接矩阵和可达矩阵.重点:作图,用握手定理求结点或推理证明,求通路、回路及其长度,判别强(单侧、弱)连通,求有向图的邻接矩阵并求结点之间的通路或回路条数.第6章几种特殊的图基本问题:1.判断或作欧拉图,求欧拉通路、回路.2. 判断或作哈密顿图,求哈密顿通路、回路,说明不是哈密顿图.3. 判断是否可平面图,将可平面图改画为平面图.4. 求连通平面图的面、边界和次数.5. 用第6,7,8作某些证明.6. 判断是否树.7. 求树枝的内点和求树叶数.8. 求最小生成树和权.9. 画根树,求层数和树高.10. 求简单的二元完全树的内点和树叶.重点:欧拉(哈密顿)通路、回路的判别,平面图的判别,平面图的面、边的关系,定理6,7,求树的结点或边,最小生成树.第7章群基本问题:1. 验证代数运算f在A上封闭,即<A,f>是代数系统.2. 验证代数运算有结合律,交换律等.3. 验证代数运算f,g有无分配律,吸收律等.4. 求运算的单位元,逆元..5. 判断是否半群、群、交换群、循环群,求生成元和循环群的子群..7. 在群中进行计算、化简等.8. 求复合置换、逆置换等.9. 证明群同态、同构,找同态(同构)映射.重点:验证是否二元运算以及结合律、交换律、求单位元和逆元,半群、群,交换群和循环群,置换.第8章其它代数系统基本问题:1. 验证是否为环?2. 给出偏序集,判断是否为格?3. 在格中进行计算、化简或证明等.4. 判断是否为布尔代数(简单的,告知验证H1,H2,H3,H4).5. 布尔代数式的化简、求值或证明.重点:环的定义,偏序格的判别,布尔式的化简或证明.三、模拟练习题模拟练习题(1)(一) 单项选择题1. 给定无向图如图1所示,下面给出的顶点集的子集中,不是点割集的为()(A) {b,d} (B) {d}(C) {a,c} (D) {e,g}f b图12. 无向完全图K 3的不同构的生成子图有( )个. (A) 6 (B) 5 (C) 4 (D) 33. 在自然数集合N 上,下列运算可结合的是( ) (A) ),max(y x y x =* (B)y x y x +=*2 (C)22y x y x +=* (D) y x y x -=*4. 设N 为自然数集合,<N , >在下面4种运算下不构成代数系统的是( ) (A) x y = x +y -2xy (B) x y = x +y(C) x y = x ∙y (D) x y = |x |+|y |(其中,+、—分别为普通加法和减法)5. 2所示,是格的为( )图2(二) 填空题6. 若命题变元P ,Q ,R 赋值为(1,0,1),则命题公式G =)())((Q P R Q P ∨⌝∨→∧的真值是 .7. 设N (x ):x 是自然数,Z (y );y 是整数,则命题“自然数都是整数,而有的整数不是自然数”符号化为 .8. 设A ,,B 为任意集合,命题A -B =∅⇔A=B 的真值为 .9. 设A ,B 为有限集,且|A|=m ,|B|=n ,那末A 与B 间存在双射,当且仅当 . 10. 在有向图的邻接矩阵中,第i 行元素之和,第j 列元素之和分别为 .(三) 化简解答题11. 做命题公式))(()(P Q P Q P ∨∧→→的真值表,并判断该公式的类型. 12.化简集合表达式:((A ⋃B ⋃C )⋂(A ⋃C ))-((C ⋃(C -B )-A ) 13. (1)将命题公式)(P R Q P →⌝∧∨⌝化为只含⌝和∧的尽可能简单的等值式. (2) 求谓词公式))(())((a f R x Q P x ∨→∀的真值.其中P :4>3,Q (x ):x >1,R (x ):x ≤2,f (0)=0,f (4)=4.a :4. 个体域D ={0,4}. (四) 计算解答题14. (1) 设R 和S 是集合A ={1,2,3}上的二元关系,R ={<1,2>,<3,1>} S ={<1,2>,<2,1>,<3,3>}求R ∙S ,写出它的矩阵M R ∙S .(2) 求布尔表达式c b c b a c b a E ++∙+=)(),,(的对偶式,并求当a ,b ,c 取值0,0,1时,E (a ,b ,c )以及其对偶式的真值.15. 指出谓词公式)(),())(),()((x S y x xH x P z x G x F x ∧∃∧∨→∀中∀x 和∃x 的辖域,并指出该公式的约束变元和自由变元以及约束出现次数和自由出现次数. 16. 已知带权图G ,如图3所示.试求图G 的最小生成树,并计算该生成树的权. 17. 设简单连通无向图G 有12条边,G 中有1度结点2个,2度结点2个,4度结点3个,其余结点度数不超过3.求G 中至少有多少个结点.试作一个满足该条件的简单无向图. 图3(五) 证明题18. 证明如果R 和S 是非空集合A 上的等价关系,则S R ⋂也是A 上的等价关系. 19. 设R *是非0实数集,在R *上定义集合S 为},00{*R b a b a S ∈⎥⎦⎤⎢⎣⎡= 证明 (S ,*)是代数系统,满足结合律,交换律,存在单位元,S 的每个元素有逆元.其中*是矩阵的乘法运算.模拟练习题(2)(一) 单项选择题1. 设命题公式G :)(R Q P ∧→⌝,则使公式G 取真值为1的P ,Q ,R 赋值分别是 ( )0,0,1)D (0,1,0)C (1,0,0)B (0,0,0)A (2. 谓词公式)(y yP ∀取真值为1的充分必要条件是( ) (A) 对任意y ,使P (y )都取真值1(B) 存在一个y 0,使P (y 0)取真值1 (C) 存在某些y ,使P (y )都取真值1 (D) 存在y 0,使P (y 0)取真值03. 设G ⇔∀x ∃yP (x ,y )→Q (z ,w ),下面三个命题为真的是( ) (A) G 是前束范式 (B) G 不是前束范式 (C) G 不是一阶公式 (D) G 是永真式4. 设集合A ={{1,2,3},{4,5},{6,7,8}},则下列各式为真的是( ) (A) 1∈A (B) {{4,5}}⊂A (C) {1,2,3}⊆A (D) ∅∈A5. 已知集合A ={a ,b ,c }上的二元关系R 的关系矩阵M R =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001011010,那么R =( ),(A) {<a ,b >,<b ,a >,<b ,b >,<a ,c >} (B) {<a ,b >,<b ,a >,<b ,b >,<c ,b >} (C) {<a ,b >,<a ,a >,<b ,b >,<c ,a >} (D) {<a ,b >,<b ,a >,<b ,b >,<c ,a >} (二) 填空题6.令P :天气晴朗,Q :我去爬山,R :我有时间,则命题“如果天气好,而且我又有时间,那么我就去爬山”符号化为7. 设R ,S 都是集合A 上的等价关系,则对称闭包s (R ⋂S )= ,自反闭r (R ⋂S )=,传递闭包t (R ⋂S )= .8. 设f :A →B 是双射函数,则f -1是函数,并且是从B 到A 的 .9.设有向图D =<V ,E >的邻接矩阵为A (D )=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1100100001000120,那么∣E ∣= . 10. 无向连通图G 含有欧拉通路的充分必要条件是 (三) 化简解答题11. (1) 求命题公式(P ∨⌝Q )→(P ∧Q )的成真赋值 (2)设集合A ={1,2},求P (∅)×P (A ).12. 设f 是一元运算,P 是一元谓词,Q 是二元谓词,给定解释如下 ,1)3(,0)2(,2)3(,3)2(},3,2{=====P P f f D I 1)3,3()3,2(,0)2,3()2,2(====Q Q Q Q 求在解释I 下)()))),(((x xP y x f Q y x ∃→∃∀的真值.13. 判断下列各式哪些是正确的?哪些是错误的? (1)A B B A =⋃-)( (2)A A B A =-⋃)((3)A A A =⊕ (4)∅=-⋂A B A )( (5) ∅=∅⋃∅}{ (6) ∅=∅⋂∅}{(7) }{}}{,{}{∅=∅∅⋂∅ (8) }}{,{}{}}{,{∅∅=∅-∅∅ (9) {∅,{∅}}-∅={{∅}} (10) }{}}{{}}{,{∅=∅-∅∅ (四) 计算解答题14. 已知集合A 及其A 上偏序关系R ,和偏序集<A ,R >的 哈斯图如图1.试写出二元关系R 的集合表达式,并求A 的子集B ={1,3,4}的极大元、极小元、最大元、最小元以及 最小上界和最大下界.15. 有向图D =<V ,E >如图2所示:7∙ 6∙∙5 4∙ 3∙ ∙21∙图1vv 图2(1)写出D的邻接矩阵A及其2,3次幂;(2)根据(1)中计算结果回答以下问题:①D中V3到V4长度小于等于3的通路有几条?②D中V3到V3长度小于等于3的回路有几条?③D中长度等于3的通路有几条?其中有几条是回路?16. 设S=Q⨯Q,其中Q是有理数集合.在S上定义二元运算*,,<><∀有a>∈b,,,Sxybya,,ax*,x+ay>=<><b><假设代数系统(S,*)的单位元是<1,0>,试求S中每个元素的逆元.17. 已知(L,∧,∨)是格,且二元运算∧和∨满足分配律,∀a,b,c∈L,化简表达式((a∧b)∨ (a∧c))∧ ((a∧b)∨ (b∧c))(五) 证明题18. 构造推理证明:(P→(⌝Q∨R))∧(S→P)∧Q⇒S→R19.证明给定的图G(如图3所示)不是哈密尔顿图.图3四、模拟练习题解答模拟练习题(1)解答(一) 单项选择题1. B2. C3. A4. A5. D(二) 填空题6. 17. ∀x(N(x)→Z(x))∧∃x(Z(x)∧⌝N(x))8. 09. m=n.10. 结点v i的出度和结点v j的入度(三) 化简解答题11. . 命题公式的真值表原式为可满足式.12. ((A⋃B⋃C)⋂(A⋃C))-((C⋃(C-B)⋂~A)=(A⋃C)-(C⋂~A)(两次用吸收律)=((A⋃C)⋂(~C⋃A)=(A ⋂~C )⋃(C ⋂~C)⋃A ⋃(A ⋂C ) =(A ⋂~C )⋃∅⋃A =A13. (1))(P R Q P →⌝∧∨⌝)()(P R Q P ∨∧⌝∧⌝⇔ )()(R P Q P ⌝∧⌝⌝∧⌝∧⌝⇔不惟一.(2) ))(())((a f R x Q P x ∨→∀=))4(()))4(())0(((f R Q P Q P ∨→∧→ =00)11()01(⇔∨→∧→(四) 计算解答题14. (1) R ∙S = {<1,2>,<3,1>}∙{<1,2>,<2,1>,<3,3>}=}2,3,1,1{><><⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=∙010000001SR M(2) 110)11(10)100()1,0,0(=++∙=++∙+=Ec b c b a c b a E ++∙+=)(),,(的对偶式为c b c b a ∙∙+∙)(,其真值是010110)100(=∙∙=∙∙+∙15. ∀x 的辖域为:F (x )→G (x ,z )∨P (x )∃x 的辖域为:H(x ,y ) x 既是约束变元,也是自由变元,约束出现4次,自由出现1次.y 是自由变元,自由出现1次.. z 是自由变元,自由出现1次.)()))),(((x xP y x f Q y x ∃→∃∀))3()2())),3((())),2(((P P y f yQ y f yQ ∨→∃∧∃⇔10))3,2()2,2(())3,3()2,3((∨→∨∧∨⇔Q Q Q Q 11)10()10(⇔→∨∧∨⇔16. 做法如下:①选边1; ②选边2; ③选边3; ④选边5;⑤选边7最小生成树为{1,2,3,5,7}.如解答图4 中粗线所示.权数为18. 解答图4 17. 设图G 有x 个结点,有握手定理2⨯1+2⨯2+3⨯4+3⨯(x -2-2-3)≥12⨯2271821243≥-+=xx ≥9图G 至少有9个结点. 解答图5 满足条件的图如解答图5所示. (五) 证明题 18. ① S R x x S x x R x x A x ⋂>∈⇒<>∈<>∈<∈∀,,,,,,所以S R ⋂有自反性;②,,A y x ∈∀因为R ,S 是对称的,S y x R y x S R y x >∈<∧>∈⇔<⋂><,,,S x y R x y S R >∈<∧>∈<⇔,,,对称的S R x y ⋂>∈⇔<,所以,R ⋂S 是对称的. ③ A z y x ∈∀,,,因为R ,S 是传递的, S R z y S R y x ⋂>∈<∧⋂>∈<,,S z y R z y S y x R y x >∈<∧>∈<∧>∈<∧>∈⇔<,,,, S z y S y x R z y R y x >∈<∧>∈<∧>∈<∧>∈⇔<,,,,S R z x S z x R z x S R ⋂>∈⇔<>∈<∧>∈<⇒,,,,传递所以,S R ⋂是传递的. 总之,R ⋂S 是等价关系.19. 首先证*在S 上封闭.任取S 中的元素⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡y x b a 00,00,其中a ,b ,x ,y ∈R *.S by ax y x b a ∈⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡*⎥⎦⎤⎢⎣⎡000000,因为ax ,by ∈R *.即*在S 上封闭.且有 ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡*⎥⎦⎤⎢⎣⎡by ax y x b a 000000=⎥⎦⎤⎢⎣⎡*⎥⎦⎤⎢⎣⎡b a y x 0000 即运算*满足交换律.任取S 中的元素⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡d c y x b a 00,00,00,其中a ,b ,x ,y ,c ,d ∈R *,有 ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡byd axc d c by ax d c y x b a 0000*0000*)00*00(⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡byd axc yd xc b a d c y x b a 0000*00)00*00(*00 可见,*满足结合律.设单位元为E =⎥⎦⎤⎢⎣⎡y o x 0,任取S 中的元素⎥⎦⎤⎢⎣⎡b a 00, 有 ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡yb xa b a y x b a by ax y x b a 0000*00000000*00 得到⎩⎨⎧==b by a ax ,由a ,b 的任意性,得x=1,y=1,有E =⎥⎦⎤⎢⎣⎡1001∈S,即E 是S 上关于运算*的单位元.任取S 中的元素⎥⎦⎤⎢⎣⎡b a 00如果其逆元为X =⎥⎦⎤⎢⎣⎡y x 00,应有 ⎥⎦⎤⎢⎣⎡b a 00*⎥⎦⎤⎢⎣⎡y x 00=⎥⎦⎤⎢⎣⎡b a 00*⎥⎦⎤⎢⎣⎡y x 00=⎥⎦⎤⎢⎣⎡1001 得到⎩⎨⎧==11by ax ,因为a ,b 不为0,得b y a x 1,1==.显然x ,y 不为0,即x ,y ∈R *,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡y x 1001∈S ,它是⎥⎦⎤⎢⎣⎡b a 00的逆元.S 的每个元素都有逆元,模拟练习题(2)解答(一) 单项选择题1. D2. A3. B4. B5. D(二) 填空题6. P ∧Q →R7. R ⋂S , R ⋂S , R ⋂S8. 双射9. 7 10. 至多有两个奇数度的结点(三) 化简解答题11. (1) (P ∨⌝Q )→(P ∧Q )⇔(⌝P ∧Q )∨(P ∧Q )⇔(⌝P ∨P ∧Q ⇔Q ,成真赋值:01,11. (2) P (A )={∅,{1},{2}{1,2}}P (∅)⨯P (A )={<∅,∅>,,<∅,{1}>,.<∅,{2}>,<∅,{1,2}>} 12. )()))),(((x xP y x f Q y x ∃→∃∀))3()2())),3((())),2(((P P y f yQ y f yQ ∨→∃∧∃⇔10))3,2()2,2(())3,3()2,3((∨→∨∧∨⇔Q Q Q Q 11)10()10(⇔→∨∧∨⇔13. (1) 不对.改正:B A B B A ⋃=⋃-)(; (2) 不对.改正:A B A B A -=-⋃)((3) 不对.改正:∅=⊕A A (4)正确. (5) 不对.改正:}{}{∅=∅⋃∅; (6) 正确.(7) 正确. (8) 不对.改正:}}{{}{}}{,{∅=∅-∅∅; (9) 不对.改正:{∅,{∅}}-∅={∅,{∅}};(10) 正确.(四) 计算题14. A ={1,2,3,4,5,6,7}, B ={1,3,4},R ={<1,2>,<1,3><1,4>,<1,5>,<1,6>,<1,7>,<5,7>,<3,6>,<4,6>}⋃I AB 的极大元:3,4;极小元:1.最大元:无;最小元:1.最小上界:6;最大下界:1.15. (1) D 的邻接矩阵及它的幂如下⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1111111110111001)(,101110111001010)(,1001100101000010)(32D A D A D A (2) ①3条 ② 1条 ③13条;4条. 16. 设,,S b a >∈<∀其逆元记作><y x ,,有*,><b a >>=<+>=<<0,1,,b ay ax y x , >>=<+>=<<><0,1,,*,y bx ax b a y x得到⎪⎩⎪⎨⎧=+=+=001y bx b ay ax解得aby a x -==,1(0≠a ) 对任意S b a >∈<,,只要0≠a ,那末><b a ,的逆元为>-<aba ,1. 17. ((a ∧b ) ∨ (a ∧c )) ∧((a ∧b ) ∨(b ∧c ))=(a ∧b ) ∨ ( (a ∧c ) ∧ (b ∧c ))(分配律) =(a ∧b ) ∧ ((a ∧b ) ∧c ) (幂等律) =a ∧b (吸收律)(五) 证明题18. 前提:P →(⌝Q ∨R ),S →P ,Q结论:S →R 证明①S 附加前提 ② S →P 前提引入 ③ P ①,②假言推理 ④P →(⌝Q ∨R ) 前提引入⑤ ⌝Q ∨R ④,⑤假言推理 ⑥ Q 前提引入⑦ ⌝⌝Q ⑥E 1双重否定⑧R ⑦,⑤析取三段论19. 在图G 中取两点a ,c 如解答图1所示.选V 1={a ,c }⊂V (G ), 有P (G -V 1)=3>⎪V 1⎪=2, 由第6章定理的逆否结论,可知该图不是哈密顿图. 解答图1 注意:证明方法和子集V 1的取法都不惟一.附:《计算机数学基础(1)》离散数学试题(2003年1月用试卷)一、单项选择题(每小题2分,共10分) 1.下列命题公式等值的是( )BB A A QP Q Q P Q B A A B A A Q P Q P ),()D (),()C ()(),()B (,)A (∧∨⌝∨∨⌝∨→→→⌝→→∨⌝∧⌝2. 谓词公式)(y yP ∀取真值为1的充分必要条件是( )(A) 对任意y ,使P (y )都取真值1 (B) 存在一个y 0,使P (y 0)取真值1 (C) 存在某些y ,使P (y )都取真值1 (D) 存在y 0,使P (y 0)取真值03. 设集合A ={0,b },B ={1,b ,3},则A ⋃B 上的恒等关系是 ( ).(A) {<0,0>,<1,1>,<3,3>} (B){<0,0>,<1,1>,<b ,b >,<3,3>} (C) {<1,1>,<b ,b >,<3,3>} (D) {<0,1>,<1,b ><b ,3>,<3,0>}4. 已知集合A ={a ,b ,c }上的二元关系R 的关系矩阵M R =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡001011010,那么R =( ), (A) {<a ,b >,<b ,a >,<b ,b >,<a ,c >} (B) {<a ,b >,<b ,a >,<b ,b >,<c ,b >}(C) {<a ,b >,<a ,a >,<b ,b >,<c ,a >} (D) {<a ,b >,<b ,a >,<b ,b >,<c ,a >} 5.设V ={a ,b ,c ,d },与V 能构成强连通图的边集E =( )(A) {<a ,b >,<a ,c >,<d ,a >,<b ,d >,<c ,d >}(B) {<a ,d >,<b ,a >,<b ,c >,<b ,d >,<d ,c >} (C){<a ,c >,<b ,a >,<b ,c >,<d ,a >,<d ,c >} (D) {<a ,d >,<b ,a >,<b ,d >,<c ,d >,<d ,c >} 二、填空题(每小题3分,共15分)6. 设命题公式G :P →⌝(Q →P ),则使公式G 为假的真值指派是 .7. 设P :我们划船,G :我们跑步,那么命题“我们不能既划船,又跑步”可符号化为8. 设个体域D ={1,2},那么谓词公式)()(y yB x xA ∀∨∃消去量词后的等值式为 .9.设有向图D =<V ,E >的邻接矩阵为A (D )=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡1100100001000120,那么∣E ∣= . 10. 无向连通图G 含有欧拉回路的充分必要条件是 .三、化简解答题(每小题8分,共32分)11. 回答问题:下列集合中哪些是相等的, 说明理由. A 1={a ,b } A 2={b ,a } A 3={a ,a ,b } A 4={a ,b ,c }A 5={0))()((=---c x b x a x x } A 6={0)(2=++-ab b a x x }(2) 设无向图G =<V ,E >, 那么图G 中∣V ∣与∣E ∣满足什么条件,图G 一定是树. 13.判别谓词公式),(),(y x xF y y x yF x ∃∀→∀∃的类型.四.计算题(每小题8分,共24分)14.求命题公式))()((Q P P Q P ∧⌝∧→→的主合取范式.15. 设全集E =(a ,b ,c ,d ,e ,f ), A ={a ,d },B ={a ,b ,e },C ={b ,d },求下列集合: (1) C B A ~)(⋃⋂; (2))()(A P A A ⋃⊕.第12题图 12. (1)设图G (如第12题图), 作图G 的嵌入图,说明图G 是 平面图.16. 已知图D (如第16题图)的邻接矩阵为A (D )=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡010110100101111043214321v v v v v v v v 求从v 2到v 4长度为2和从v 3到v 3长度为2的通路条数,并将它们具体写出.17. 设代数系统(Z ,*),其中Z 是整数集,二元运算定义为2*,,-+=∈∀b a b a Z b a , ∀Z a ∈,求a 的逆元.五、证明题(第18题10分,第19题9分)18. 设R 是集合A 上的对称关系和传递关系,试证明:若对∀a ∈A ,∃b ∈A ,使得(a ,b )∈R ,则R 是等价关系. 19. 设格(L ,∧,∨)满足分配律,证明,,,L c b a ∈∀有b ac b b a c a b a ∧=∧∨∧∧∧∨∧))()(())()((《计算机数学基础(1)》离散数学试题解答一、单项选择题(每小题2分,共15分) 1.C 2. A 3.B 4.D 5.A 二、填空题(每小题3分,共15分)6. 1,0;1,17. )(Q P ∧⌝或Q P ⌝∨⌝ 8. A (1)∨A (2)∨(B (1)∧B (2)) 9. 710. 不含有奇数度结点.三、化简解答题(每小题8分,共32分)11.集合中的元素是无序的,且不能重复,故A 1=A 2=A 3;因为(x -a )(x -b )(x -c )=0的解为x =a ,b ,c ,而x 2-(a +b )x +ab =0的解为x =a ,b. 故有A 1=A 2=A 3=A 6,A 4=A 5 12. (1)图G 的嵌入图,如第12题答案图. 故图G 为平面图(2) 图G 连通且∣E ∣=∣V ∣-1, 那么图G 一定是树.13. 设I 为任意一个解释,D 为I 的个体域. 若在解释I 下,该公式的前件为0,无论 ),(y x xF y ∃∀如何取值,第16题图第12题答案图),(),(y x xF y y x yF x ∃∀→∀∃为1;若在解释I 下,该公式的前件为1,则,0D x ∈∃使得),(y x yF ∀为1,它蕴含着),(,0y x F D y '∈'∀为1),(y x xF '∃⇒为1,由y '的任意性,必有),(y x xF y ∃∀为1,于是),(),(y x xF y y x yF x ∃∀→∀∃为1. 总之,对任意解释I ,),(),(y x xF y y x yF x ∃∀→∀∃为1. 该公式为永真式.四、计算题(每小题8分,共24分)14. ))()((Q P P Q P ∧⌝∧→→)()()()00()())())()((Q P Q P Q Q P P Q P P Q P Q P Q P P Q P ⌝∨⌝∧∨⌝⇔⌝∧∨⌝⇔∧∨⌝⇔∧⌝∧∨∧⌝∧⌝∨⌝⇔∧⌝∧∨⌝∨⌝⇔15. (1) },,,{},,,{}{~)(f e c a f e c a a C B A =⋃=⋃⋂; (2)∅=⋂-⋃=⊕)()()(A A A A A A . }},{},{},{,{)(d a d a A P ∅=.故)()(A P A A ⋃⊕=}},{},{},{,{d a d a ∅16. A 2(D )=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡2120020********* 从矩阵A 2(D )中a 24=2,a 33=2可知,从v 2到v 4长度为2的通路有2条. 它们是: v 2v 3v 4,和v 2v 1v 4, 从v 3到v 3长度为2的通路有2条. 它们是: v 3v 4v 3,和v 3v 2v 3, 17. 易知,二元运算满足交换律. ∵对∀a ∈Z , a *2=a +2-2=a =2*a ,即2∈Z 是单位元.∀a ∈Z , a 的逆元记作a -1, 有22*11=-+=--a a a a (单位元)∴ a -1=4-a五、证明题(第18题10分,第19题9分)18. 已知R 是对称关系和传递关系,只需证明R 是自反关系. ∀a ∈A ,∃b ∈A ,使得(a ,b )∈R ,因为R 是对称的,故(b ,a )∈R ; 又R 是传递的,(a ,b )∈R ,(b ,a )∈R ⇒(a ,a )∈R ,由元素a 的任意性,知R 是自反的. 所以,R 是等价关系. 19. ))()(())()((c b b a c a b a ∧∨∧∧∧∨∧=))()(()(c b c a b a ∧∧∧∨∧ (分配律) =))(()(c b a b a ∧∧∨∧ (幂等律)=b a ∧ (吸收律)。
大学计算机基础期末考试复习重点

1.电子管计算机没有系统软件,只能用机器语言和汇编语言编程。
晶体管计算机有了系统软件,基础操作系统概念。
2.计算机中的数据表示单位:位(b)字节(B)字(W)3.字节:以八位二进位制代码为一个单位存放在一起成为一个字节,一个中文字占用两个字节。
4.字:计算机能够同时处理一组二进位制字符串成为计算机的一个字;一个字有若干个字节组成,组成一个字的二进位制代码的位数叫做该字的字长,字长越长计算机的处理速度越快,字长也是衡量计算及性能的指标。
5.各进位制之间的转换。
6.计算机中的数据编码:原码:正0,负1;反码:正不变,反除符号位其余取反;补码:正不变,负同反低位多加1.7.ASCII码顺序;数字,大写字母,小写字母。
8.BCD码:从0000-1111中选择前十个0000-1001来表示0-9,有压缩型BCD码,和非压缩型BCD码,压缩型BCD码是用一个字节存放两位十进位制数,非压缩型BCD码,高四位总是0000,低四位表示一位十进位制数。
9.国标区位码,行为区,列为位。
10.国标码=区位码的十六进位制表示+2020H 机内码=国标码+8080H11.微机的基本结构—总线结构(运算器,控制器,存储器,输入设备,输出设备)12.微机系统分为硬件系统和软件系统,硬件系统包括主机和外部设备;软件系统包括系统软件和应用软件,CPU由运算器和控制器组成,又叫微处理器,内存储器由RAM(随机)和ROM(只读),一旦断电,RAM中的信息将会消失。
对于ROM,CPU对其只取不存。
13.存储器中以字节为基本单位。
14.操作系统是计算机中的一个系统软件,他是这样一些程序模块的集合,它能有效地组织和管理系统中的硬件和软件资源,合理的组织计算机的工作流程,控制程序执行,并向用户提供各种服务功能,使得用户能够灵活,方便和有效的使用计算机,是整个计算机系统能够高效的进行。
15.操作系统的作用?(1)管理系统中的各种资源(2)为用户提供良好的界面16.什么是多道程序?在内存中存放多道用户程序,当一程序在执行过程中需要等待外部设备的输入或输出时,让另一程序使用处理器,而CPU会一直处理程序,从而大大提高CPU 的使用效率。
计算机基础知识复习资料

计算机基础知识复习资料Ch1 计算机基础知识§1.1 现代信息技术1.1.1、特征:●以数字技术和电子技术为基础;●以计算机及其软件为核心;●采用电子技术(包括激光技术)进行信息的收集、传递、加工、存储、显示与控制。
1.1.2、数字技术一、二进位数字——比特(bit,binary digit)信息的基本单位组成数字信息的最小单位只有两种状态(数字0或1),没有颜色、大小和重量二、字节(byte)——B1B=8b三、比特的存储形式●计算机内:2的幂次方作为单位千字节(KB)1KB = 210 B = 1 024 B兆字节(MB)1MB = 220 B = 1 024 KB吉字节(GB)1GB = 230 B = 1 024 MB太字节(TB)1TB = 240 B = 1 024 GB●其他(例如U盘、光盘等外存储器):10的幂次方作为单位eg:1 MB = 1000 KB = 1 000 000 B1 GB = 1 000 000 KB四、比特的传输(单位:b/s 或bps)在数据通信和计算机网络中传输二进位信息时,单位是每秒多少比特,用10的幂次方进行计算。
千比特每秒(kb/s)1kb/s = 103 b/s兆比特每秒(Mb/S)1Mb/s = 106 b/s吉比特每秒(Gb/s)1Gb/s = 109 b/s太比特每秒(Tb/s)1Tb/s = 1012 b/s注意一般k表示1000,K表示1024五、比特与进制数(二、八、十六)二进制数(B):0 、1八进制数(Q):0 、1 、2 、3 、4 、5 、6 、7十六进制数(H):0 、1 、2 、3 、4 、5 、6 、7 、8 、9 、A、B、C、D、E、F注意在VB 中,“&O ”为八进制数的前缀,“&H ”为十六进制数的前缀 I 、进制数之间的转换:1、十进制→二进制整数部分:除以2逆序取余法Exa :将57转换为二进制数余数低位2 | 57 ...............1 2 | 28 ............0 2 | 14 ............0 2 | 7 .........1 2 | 3 .........1 2 | 1 (1)高位所以(57)10 = (111001)2 小数部分:乘以2正序取整法 Exa :将(0.875)10转换成二进制小数整数部分高位0.875×2 = 1.75 1 0.75×5 = 1.5 1 0.5×2=1 1所以(0.875)10 = (0.111)2 低位 2、二进制→十进制设二进制数为K n K n-1…K 1K 0 .K -1K -2……K-m,,则其对应的十进制数S 为S=K n ×2n + K n-1×2n-1 + …K 1×21 + K 0×20 + K -1×2-1 + … +K -m ×2-m3、八进制→二进制(P10)4、二进制→八进制(P10)5、十六进制→二进制(P10)6、二进制→十六进制(P10)7、八进制→十六进制:八进制→二进制→十六进制8、十六进制→八进制:十六进制→二进制→八进制 II 、比特的逻辑运算基本逻辑运算??+∨∧””、“—“—非””、“”、“—“—或””、“—“—与-NOT OR AND运算规则:Exa (2008 秋):二进制数10111000和11001010进行逻辑“与”运算,结果在与10100110进行逻辑“或”运算,最终结果的十六进制数形式为()A 、A2B 、DEC 、AED 、95 Ans :C III 、数值的表示● 无符号整数的表示(在计算机内部以原码形式表示)● 带符号整数的表示(在计算机内部以补码形式表示)带符号的整数必须使用一个二进制数作为其符号位,一般总是最高位。
计算机基础复习资料整理

计算机基础复习要点整理一、人物英国数学家巴贝奇研制的分析机因具备现代计算机的5大装置(输入、处理、存储、控制和输出)而被尊称为计算机之父;英国科学家图灵因提出图灵机模型和人工智能而被尊称为计算机科学之父;美籍匈牙利数学家冯诺依曼因提出现代计算机的思想体系(存储程序和控制程序)以及二进制而被尊称为电子计算机之父。
岛正利被称为微型计算机之父。
钱天白教授因登记注册了我国的顶级域名.cn并建立第一个CN域名服务器而被尊称为“中国上网第一人”。
北大教授王选因首创用矢量法描述汉字笔画轮廓,解决汉字排版问题而被尊称为当代毕升。
二、重大事件1946年世界上公认的第一台电子计算机ENIAC在美国宾夕法尼亚大学研制成功。
2001年我国推出首例具有自主知识产权的32位嵌入式CPU是“方舟1号”,2002年9月,我国具有自主知识产权的第一款商用化通用化高性能CPU“龙芯1号”,这标志我国结束“无芯”历史。
长城0520CH是我国自行研制的第一台能处理汉字的微型计算机三、基本知识和理论1、计算机怎样分代?答:按照计算机采用逻辑元件的不同,可以将计算机分代为:以电子管为逻辑元件的第一代计算机,以晶体管为逻辑元件的第二代计算机,以集成电路为逻辑元件的第三代计算机和以超大规模集成电路为逻辑原件的第四代计算机。
按计算机技术发展变化的历程,又可分为大型机、小型机、微型机、客户机/服务器和互联网5个发展阶段。
2、计算机怎样分类?答:1989年美国IEEE(电气和电子工程师学会)将计算机分为巨型机、大型机、小型机、微型机、工作站和个人计算机6大类。
按照日常所见又分为:服务器、台式机、笔记本、掌上计算机和嵌入式计算机5大类。
3、计算机发展趋势如何?答:计算机发展趋势是巨型化、微型化、网络化和智能化4、被看好的未来计算机是那几类?答:科学界看好的未来计算机目前有生物计算机、光子计算机和量子计算机。
5、什么是计算机?答、计算机也称为电脑,是用来处理数字、文字、图形图像、声音等各种形式信息的一种电子设备。
高职高专《计算机数学基础》 期末复习

机动 目录 上页 下页 返回 结束
第十章、矩阵、行列式
行列式的计算 矩阵的乘法运算 矩阵的秩 逆矩阵的求法 P250 、1(1)---(3) P260 、3、5、6 P265、1(1)、2 P270、1(1)
第十一章、线性方程组的解
非齐次线性方程组的解法 齐次线性方程组的解法
2 = lim (1 + − ) x →∞ x
x − ( −2 ) 2
2 = lim (1 + − ) x →∞ x
x − 2
−2
= e −2
第二章、求导
一般求导问题 隐函数的求导问题 参数方程所确定的函数求导问题 积分上限函数的求导问题
3、常系数齐次线性微分方程 、
y′′ + p y′ + q y = 0 ( p, q为 数) 常
特征方程: r 2 + pr + q = 0, 特征根 实根 通 解
r1 x
y = C1e
+ C2e
r2 x
y = (C1 + C2 x ) e
r1 x
y = eα x (C1 cos β x + C2 sin β x )
两个重要极限
(1)
sin x lim =1 x→0 x
2、( )( ) 、(1)( 、( )(2)
sin∆ 更一般地: 更一般地: lim =1 ∆→0 ∆
(2)
1 x lim(1 + ) = e x→∞ x
∆→∞
lim(1 + x) = e
x→0
1 x
更一般地: 更一般地: lim(1 + 1 )∆ = e或lim(1 + ∆) = e
计算机数学基础答案

一.课后习题参考答案1.(P30,第1题)求下列极限:(1)2223lim 321x x x x x →∞++++; (2)x x x x x x ++++∞→23221lim ; (3)()143lim 22++→x x x ; (4)11lim 21+++→x x x x ; (5)2x →; (6)39lim 23--→x x x ;((7)20x →; (8)201lim sin .x x x →解:(1)22221123232lim lim 32131132x x x x x x x x x x →∞→∞⎛⎫++ ⎪++⎝⎭==++⎛⎫++ ⎪⎝⎭; (2)x x x x x x ++++∞→23221lim .01011.21111lim 232==⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=∞→x x x x x x ; (3)().2112423143lim 222=+⨯+⨯=++→x x x ;(4).3211lim21=+++→x x x x ; (5)20x →==; (6)39lim 23--→x x x ()()333lim3-+-=→x x x x ().63lim 3=+=→x x ;(7)221x x x →→=((221lim lim 12x x x x→→+==-+=--;(8)因为20lim 0,x x →= 且1sin1x ≤ ,所以201lim sin 0.x x x→=2.(P30,第2题)求下列极限:(1)()0tan 3lim x x x →;(2)()lim 2sin 02nn n x x →∞≠;(3)()10lim 12x x x →+;(4)2lim 1.xx x →∞⎛⎫- ⎪⎝⎭解:(1)()()00tan 3sin 31lim3lim .31133cos3x x x x x x x→→==⨯⨯=;(2)sin2lim 2sin lim.22n n n n n nxx x x x→∞→∞==; (3)()()211220lim 12lim 12xx x x x x e →→⎡⎤+=+=⎢⎥⎣⎦; (4)22222lim 1lim 1.xxx x e x x ---→∞→∞⎡⎤⎛⎫⎛⎫⎢⎥-=-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦3.(P38,第1题)设()33522---=x x x x f ,求极限()x f x 3lim →,指出()x f 的间断点,能否补充定义使之连续.解:()3352lim lim 233---=→→x x x x f x x ()()3123lim3-+-=→x x x x ().712lim 3=+=→x x函数()x f 在3=x 处无定义,但在3=x 附近有定义,故3=x 就是()x f 的间断点. 若补充()73=f ,则能使()x f 在3=x 处连续.4.(P39,第2题)求下列函数的间断点,并指出间断点的类型. (1)()221+x ;(2)23122+--x x x ;(3)2sin x x;(4)⎩⎨⎧>-≤-=;1,3,1,1x x x x y ;(5)⎪⎩⎪⎨⎧>-=<+=.0,12,0,0,0,12x x x x x y解:(1)函数()221+x 在2-=x 处无定义,但在2-=x 的附近有定义,故2-=x 为()221+x 的间断点。
2023-2024期末计算机应用基础理论复习题

2023-2024(1)《计算机应用基础》理论复习题一、单选题1、计算机系统成为能存储、处理、传播文字、声音、图象等多种信息载体的实体,称为计算机的技术。
CA、智能化B、数码化C、多媒体D、多元化2、是指只表现自己而不进行破坏的计算机病毒。
CA、恶性病毒B、宏病毒C、良性病毒D、寄生性病毒3、以下不属于局域网拓扑结构类型的是oDA、总线型B、环型C、星型D、全互连型4、一般认为,信息(Information)是。
AA、反映事物属性的原始事实B、记录下来的可鉴别的符号C、人们关切的事情的消息D、数据5、下列对于声音的描述中,正确的是。
CA、声音是一种与时间有关的离散波形B、利用计算机录音时,首先要对模拟声波进行编码C、利用计算机录音时,首先要对模拟声波进行采样D、数字声音的存储空间大小只与采样时间长度和量化位数有关6、在OSl七层协议中,作为整个协议层次结构中实现点对点的牢靠传输的是一层。
BA、网络B、数据链路C、传输D、会话7、JPEG格式是一种。
CA、可缩放的动态图像压缩方式B、不行选择压缩比例的有损压缩方式C、不行逆压缩编码方式D、不支持24位真彩色色调压缩方式8、目前按USB2.0标准,USB的传输速率可以达到480。
BA^GbpsB、MbpsC、KbpsD、bps9、通常一条指令被分为“操作码”和“操作数”两部分。
“操作码”用于说明oCA、操作对象B、操作过程C、操作类型D、操作流程10、电子信箱地址的格式是。
AA、用户名@主机域名B、主机名@用户名C、用户名.主机域名D、主机域名.用户名11、下列对系统防火墙的描述错误的是。
DA、限制对系统的访问B、集中的平安管理C、增加的保密性D、防止内部和外部的威逼12、卫星线路是微波传输一种,不受和通信距离的限制。
AA、地理环境B、物理环境C、外界环境D、操作环境13、一幅辨别率为160X120的图象,在辨别率为640X480的VGA显示器上的大小为该屏幕的oAA、十六分之一B、八分之一C、四分之一D、以上都不对14、色调为数用8位二进制数来表示每个像素的颜色是,能表示中不同颜色。
《计算机数学基础》

《计算机数学基础》计算机数学基础随着计算机技术的迅速发展和广泛应用,计算机数学基础已成为各领域中不可或缺的技术支撑。
本文将介绍计算机数学基础知识,包括整数、字符串、有理数、实数和复数等,以及计算机算法和计算机在各领域中的应用。
一、计算机数学基础知识整数整数是一类基本的数学对象,通常用来表示一个有限的非负数。
在计算机中,整数可以进行加、减、乘、除等基本运算。
根据表示方法的不同,整数可分为有符号整数和无符号整数。
有符号整数可以表示正数、负数和零,而无符号整数只能表示正数和零。
字符串字符串是一系列字符的组合,是计算机中常用的数据类型之一。
字符串可以进行长度计算、子串查找、拼接等操作。
在计算机中,字符串通常以数组的形式进行存储,以便进行各种操作。
有理数有理数是两个整数之比,可以表示为分数形式,如2/3。
有理数可以进行加、减、乘、除等基本运算,但在计算机中,有理数的表示和计算比整数和实数要复杂得多。
实数实数是连续的、无限的、有理数和无理数的集合。
在计算机中,实数通常采用浮点数表示,可以表示分数和整数。
实数的运算包括加、减、乘、除、乘方和开方等。
复数复数是实数的扩展,可以表示为实部和虚部的形式,如2+3i。
复数在计算机中通常采用数组形式存储,可以进行加、减、乘、除等基本运算。
二、计算机算法计算机算法是解决特定问题或执行特定任务的一组有序的步骤。
算法是计算机科学的核心,它可以解决各种复杂的问题,如排序、搜索、插入、删除等。
在实际应用中,算法需要根据具体问题进行设计和优化。
三、计算机应用计算机在各领域中都有着广泛的应用,如科学计算、图像处理、机器人控制等。
在科学计算领域,计算机可以快速准确地处理大量数据,为科学研究提供强有力的支持;在图像处理领域,计算机可以对图像进行各种处理,如图像增强、图像变换等;在机器人控制领域,计算机可以实现对机器人的精确控制,完成各种复杂任务。
总之,计算机数学基础是计算机科学的重要基础之一,它为计算机技术的发展提供了强有力的支撑。
数学计算机重点知识点总结

数学计算机重点知识点总结一、数学基础知识1. 代数代数是数学中的一个重要分支,涉及到代数式、代数方程、函数、不等式等内容。
代数在数学计算机中有着重要的作用,例如在编程中使用变量和函数来进行计算和处理数据。
2. 函数函数是数学中的一个重要概念,它描述了输入和输出之间的关系。
在计算机中,函数可以用来实现特定的计算功能,例如数学函数、逻辑函数、程序函数等。
3. 微积分微积分是数学中的一门基础学科,包括微分和积分两个方面。
在计算机中,微积分常用于描述和处理连续变化的现象,例如在图像处理、物理模拟、优化算法等领域。
4. 离散数学离散数学是数学中的一个重要分支,研究离散对象和离散结构的性质和关系。
在计算机中,离散数学常用于描述和处理离散的数据和问题,例如在算法设计、图论、逻辑设计等领域。
5. 概率论与统计学概率论和统计学是数学中的两个重要分支,涉及到随机现象的描述和分析、数据的收集和分析等内容。
在计算机中,概率论和统计学常用于描述和分析随机事件、进行数据挖掘和机器学习等领域。
二、计算机基础知识1. 数据结构与算法数据结构和算法是计算机科学中的两个基础概念,涉及到数据的组织和存储方式以及针对数据的各种计算方法。
在数学计算机中,数据结构和算法常用于实现各种计算功能、优化算法等。
2. 计算机体系结构计算机体系结构包括计算机的硬件结构和软件结构,涉及到计算机组成原理、操作系统、编程语言等内容。
在数学计算机中,计算机体系结构是实现各种计算功能和优化算法的基础,并且对于理解计算机运行原理和性能优化有重要意义。
3. 编程语言编程语言是计算机中实现各种计算功能的工具,包括高级语言和低级语言等。
在数学计算机中,编程语言常用于实现数学模型和算法、进行数据分析和处理等。
4. 算法设计与分析算法设计与分析是计算机科学中的一个重要内容,涉及到设计高效的算法和分析算法的性能。
在数学计算机中,算法设计与分析常用于优化各种计算功能,如图算法、排序算法、搜索算法等。
大学计算机基础_北京航空航天大学中国大学mooc课后章节答案期末考试题库2023年

大学计算机基础_北京航空航天大学中国大学mooc课后章节答案期末考试题库2023年1.可以通过给print( )函数添加参数end以决定输出后附加字符串,实现是否换行的功能。
end参数默认为newline,即输出末尾附加换行。
参考答案:正确2.Button组件创建普通按钮,按钮上可以显示文本或图像,以表达按钮被按下后所执行的______。
参考答案:操作3.TCP/IP参考模型最多将网络结构划分为5层:从下至上依次为:物理层、数据链路层、传输层、网际层和应用层。
参考答案:错误4.逻辑代数只包括逻辑与、逻辑或、逻辑非这三种逻辑运算。
参考答案:错误5.最简单的按钮只需指定按钮的父窗口、显示在按钮上的内容(文本、位图、图像),以及当按钮被按下时的______,以便按钮被按下时调用该函数,执行相应的操作。
参考答案:回调函数6.图灵机从纸带上的某个起始点出发,读写头的动作只是由当前指令决定。
参考答案:错误7.英国数学家、逻辑学家、密码学家图灵,被后人誉为“计算机科学之父”和“人工智能之父”。
参考答案:正确8.图灵机蕴含了哪些计算思想?参考答案:通用图灵机模型是计算机的计算能力的极限_程序也是数据_所有规则构成指令集9.使用Matplotlib绘图时,如果希望在一张图纸中同时绘制多个具有独立坐标系的图,需要进行多轮次绘制,再手工拼在一起。
参考答案:错误10.一个算法的时间复杂度和空间复杂度往往是相互影响的,当追求一个较低的时间复杂度时,可能会导致占用较多的存储空间。
参考答案:正确11.科学抽象的过程依次是______、______和______。
参考答案:分离,提纯,简化12.雷达图适用于比较同类事物的不同属性,例如两种汽车,在油耗、空间、价格、保养等角度的异同。
在绘制雷达图时,“属性”的选择多多益善,没有限制,因为这样更能体现同类事物的区别。
参考答案:错误13.数据结构线性表(a1, a2, …ai…, an)中,数据元素ai的直接后继元素是________。
计算机数学基础试题及答案

计算机数学基础试题及答案尊敬的读者,本文将为您提供一份计算机数学基础试题及答案。
希望通过这些试题的讨论和答案的解析,能够帮助您更好地理解和应用计算机数学基础知识。
试题一:离散数学1. 什么是二进制数?2. 请举例说明二进制数的运算规则。
3. 什么是排列组合?4. 请计算C(5,2)的值。
5. 请计算5!的值。
答案一:1. 二进制数是由0和1组成的数字系统,是计算机中常用的表示方式。
2. 以两个二进制数的加法为例,对应的运算规则如下:0 + 0 = 00 + 1 = 11 + 0 = 11 + 1 = 10 (进位)3. 排列组合是离散数学中的一个重要概念,用于计算某个集合中元素的排列或组合方式的总数。
4. C(5,2)表示从5个元素中选出2个元素的组合数。
计算公式为C(5,2) = 5! / (2! * (5-2)!) = 10。
5. 5!表示5的阶乘,计算公式为5! = 5 * 4 * 3 * 2 * 1 = 120。
试题二:线性代数1. 什么是向量?2. 请说明向量的加法和数乘规则。
3. 什么是矩阵?4. 请计算矩阵相乘的规则。
5. 请计算以下矩阵相乘的结果:A = [[1, 2], [3, 4]]B = [[5, 6], [7, 8]]答案二:1. 向量是有方向和大小的量,由一组按照特定顺序排列的数值表示。
2. 向量的加法规则是对应位置上的数值相加,数乘规则是将向量的每一个分量与一个数相乘。
3. 矩阵是由一组按行和列排列的数值组成的矩形阵列。
4. 矩阵相乘的规则是:若矩阵A的列数等于矩阵B的行数,那么它们可以进行相乘运算。
结果矩阵的行数等于矩阵A的行数,列数等于矩阵B的列数。
5. 输入矩阵A和B的计算机执行矩阵相乘运算,结果为:AB = [[19, 22], [43, 50]]试题三:概率论与统计学1. 什么是概率?2. 请说明条件概率和贝叶斯公式。
3. 什么是均值和标准差?4. 请计算以下数据集的均值和标准差:[2, 4, 6, 8, 10]5. 请计算以下数据集的方差:[1, 3, 5, 7, 9]答案三:1. 概率是用来描述某个事件发生的可能性的数值。
大学计算机基础期末知识点整理

期末考试的<大学计算机基础>复习题1、第一台计算机ENIAC淡生于1946年,是电子管计算机;第二代是晶体管计算机;第三代是中小规模集成电路;第四代是大规模集成电路;2、计算机的应用领域主要有:科学计算;信息管理;实时控制;办公、生产自动化;人工智能,网络通信;电子商务;辅助设计(CAI);辅助设计(CAD);3、计算机的信息表示形式为二进制,它采用了冯。
诺依曼的思想原理,即以0 和1两个数字形式用于展现,“逢二进一”;它的基本信息单位为位,即一个二进制位。
常用的换算单位有:1 B ===8bit; 1KB====1024B ;1MB====1024KB; 1GB===1024MB;1TB===1024GB;1个汉字===2B;4、二进制换算法则:将十进制转化为二进制时除二取佘;二进制转化为八进制时以三位为一组,三位的权重等于八进进中的一位权重,二进制转化为十六进制时以四位为一组;5、对于字符的编码,普遍采用的是ASCII码,中文含义为美国标准信息交换码;被国际标准化组织ISO 采纳,作用通用信息交换标准。
6、计算机的系统的组成由软件系统和硬件系统两部分组成;7、硬件系统包括运算器,控制器,存储器,输入,输出设备,控制器和运算器合成为中央处理器即CPU ,存储器主要有内存和外内之分;内存又分为只读存储器(ROM)和随机存储器(RAM),断电内容丢失的是RAM,外存主要有硬盘(GB),软盘(3。
5寸,1。
44MB),光盘(650MB左右),移动存储器优盘(MB),MP3(MB)等;8、软件指在硬件设备上运行的各种程序及其有关的资料。
主要有系统软件(操作系统、语言处理程序、数据库管理系统)和应用程序软件即实用程序(如WPS,OFFICE,PHOTOSHOP等)。
9、计算机性能的衡量指标有:10、计算机语言的发展经历了机器语言,汇编语言,高级语言;计算机能识别的语言是计算机语言;11、显示器的分辩率是显示器一屏能显示的像素数目,是品价一台计算机好坏的主要指标。
计算机数学基础》课后习题解答(一)

习题1.1 单项选择题(1) 函数 ()29x x f -=的定义域是(D )A. {}3|±≤x xB. ()[)+∞-∞-,33, C 。
{}33|<<-x x D. {}33|≤≤-x x (2) 函数 ()43lg 2-+=x x y 的定义域是(A)A 。
{}{}1|4|>-<x x x xB 。
{}14|<<-x xC 。
{}{}4|1|>-<x x x x D. {}41|<<-x x (3).下列各组函数中表示同一个函数的是(A)。
A. x y =与2x y = B 。
x y =与2x y =C. x y =与xx y 2= D. x y =与x a a y log =(4).下列函数中值域为R 的是(D).A 。
132+-=x x y ; B 。
21x y =; C 。
x y -=5; D 。
x y 21log =。
(5)。
下列函数中在区间()1,0上是增函数的是(D ). A. 23-=xy ; B 。
x y 32log =;C. xy ⎪⎭⎫ ⎝⎛=32; D 。
xy ⎪⎭⎫⎝⎛=23。
(6)。
下列函数是偶函数的为(C).A 。
x y 2=;B 。
x y 2log =;C 。
1=y ;D 。
x x y sin cos +=.(7)。
函数⎪⎭⎫ ⎝⎛+=43sin πx y 的最小正周期是(C ).A 。
π2; B.3π; C 。
32π; D 。
23π.(8)。
下列函数在定义域中既是奇函数又是单调增函数的是(D )。
A 。
x y tan =; B. x y 3=; C 。
x y 3log =; D. 31x y =. (9).函数x y 8=的反函数是(C)。
A. )0(log 32>=x x y ;B. x y -=8;C 。
)0(log 312>=x x y ; D 。
计算机期末必考知识点总结

计算机期末必考知识点总结一、计算机基础知识1. 计算机的概念和发展历史- 计算机的定义和特点- 计算机的五大发展阶段:电子管计算机、晶体管计算机、集成电路计算机、大规模集成电路计算机和超大规模集成电路计算机- 计算机的性能指标:速度、存储容量、可靠性、功耗等2. 计算机的组成和工作原理- 计算机的五大基本组成部分:运算器、控制器、存储器、输入设备、输出设备- 冯・诺依曼结构和哈佛结构- 计算机的工作原理:指令的执行过程、数据的存储和传输方式等3. 数字逻辑电路- 与门、或门、非门、与非门、或非门、异或门的真值表和逻辑表达式- 组合逻辑电路和时序逻辑电路- 计算机中常用的数字逻辑电路:加法器、减法器、比较器、多路选择器、译码器、编码器等4. 计算机数制和编码- 常用的计算机数制:二进制、十进制、八进制、十六进制- 原码、反码、补码的定义和计算方法- ASCII码和Unicode编码的概念和应用5. 计算机存储器- 存储器的分类:主存储器(RAM和ROM)和辅助存储器(硬盘、光盘、U盘等)- 计算机存储器的层次结构:缓存、主存、辅存- 主存储器的组织方式:存储单元和单元编址、存储器的容量和带宽等概念6. 计算机硬件- CPU的组成和功能:运算器、控制器、寄存器等- 比特、字节和字的概念- 输入设备和输出设备的分类和特点- 硬盘、内存条、显示器等计算机硬件的原理和使用二、操作系统1. 操作系统的概念和功能- 操作系统的定义和特点- 操作系统的主要功能:进程管理、内存管理、文件系统、设备管理等2. 进程管理- 进程和线程的概念和特点- 进程的状态和转换:创建、就绪、运行、阻塞、终止- 进程调度算法:先来先服务、短作业优先、最高响应比优先、时间片轮转等 - 进程同步与互斥:临界区、互斥量、信号量等3. 内存管理- 内存的分段和分页管理- 虚拟内存的概念和实现原理- 页面置换算法:最佳算法、先进先出算法、最近最久未使用算法等- 页面置换的性能评价指标:缺页率、命中率等4. 文件系统- 文件的组织和结构:顺序文件、索引文件、哈希文件等- 文件的存储方式:连续分配、链式分配和索引分配- 文件访问和管理:文件打开、关闭、读写等操作- 文件保护和安全性:文件权限、登录验证、访问控制等5. 设备管理- 设备管理的基本概念和功能- 设备的分配和调度:独占设备和共享设备的分配算法- 中断和DMA的原理和应用- 磁盘调度算法:先来先服务、最短寻道时间优先、电梯算法等6. 操作系统的分类和应用- 手机操作系统(Android、iOS等)- 服务器操作系统(Windows Server、Linux等)- 嵌入式操作系统(RTOS等)- 实时操作系统(RTOS、Linux等)三、网络技术1. 计算机网络的概念和分类- 计算机网络的定义和特点- 按规模分类:局域网(LAN)、城域网(MAN)、广域网(WAN)等 - 按拓扑结构分类:总线型、环型、星型、网状型等2. 传输层协议- 传输层的主要功能和特点- TCP协议和UDP协议的概念和应用- TCP连接的建立和终止:三次握手、四次挥手等过程- TCP可靠传输的实现机制:滑动窗口、超时重传等3. 网络层协议- 网络层的主要功能和特点- IP协议和ICMP协议的概念和应用- IP地址的分类和分组- 路由选择算法:静态路由、动态路由等4. 数据链路层协议- 数据链路层的主要功能和特点- 帧的结构和格式- CSMA/CD协议和CSMA/CA协议的原理和应用- 以太网、令牌环网、ATM等局域网技术的概念和特点5. 物理层协议- 物理层的基本概念和功能- 常用的物理层传输介质:双绞线、同轴电缆、光纤等- 调制解调器的工作原理和应用- 数据的编码和解码:NRZ编码、曼彻斯特编码、差分曼彻斯特编码等四、数据库1. 数据库的概念和特点- 数据库的定义和基本特点- 数据库管理系统(DBMS)的功能和作用- 数据库的三级模式结构:外模式、概念模式、内模式2. 关系数据库- 关系模型的概念和特点- 实体、属性、关系的概念和表示方法- 数据库的设计和规范化:函数依赖、范式等- SQL语言的基本操作:查询、插入、删除、更新等3. 数据库索引和查询优化- 索引的概念和分类- B树和B+树的原理和应用- 查询优化的基本原理和方法- 数据库的并发控制和事务处理:锁、并发控制算法、事务的ACID特性等4. 数据库安全和备份- 数据库安全性的需求和威胁- 用户账户管理和权限控制- 数据库的备份和恢复策略- 数据库的容灾和故障恢复机制五、编程语言1. 编程语言的概念和分类- 编程语言的定义和特点- 编程语言的分类:高级语言、汇编语言、机器语言等- 常见的编程语言:C、C++、Java、Python等2. C语言- C语言的特点和优势- C语言的基本语法:变量、常量、运算符、控制语句等- 函数的定义和调用- 数组、指针、结构体和文件操作等基本概念和应用3. 面向对象编程- 面向对象编程的概念和特点- 类、对象、继承、封装、多态等面向对象编程的基本概念- C++和Java语言中的面向对象编程实现- 面向对象的设计原则和模式:单一职责原则、开闭原则、工厂模式、单例模式等4. 网络编程- Socket编程的基本概念和原理- TCP和UDP协议在网络编程中的应用- 客户端和服务器端的实现方法- HTTP协议和Web编程的基本概念和应用5. 数据结构和算法- 数据结构的概念和分类- 线性表、树、图等常见数据结构的定义和应用- 常用的算法和数据处理方法:排序、查找、递归、动态规划等- 算法的时间复杂度和空间复杂度的概念和计算方法以上就是计算机期末必考的知识点总结,希望可以帮助大家复习和提高考试成绩。
大学计算机基础期末复习提纲(2023年下学期)
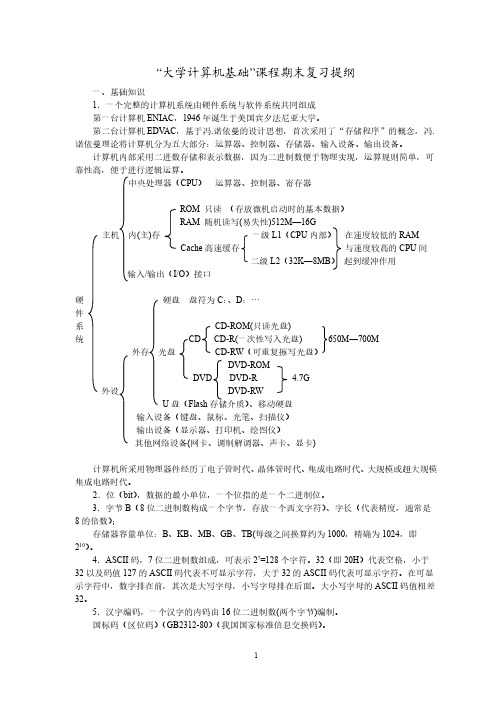
“大学计算机基础”课程期末复习提纲一、基础知识1.一个完整的计算机系统由硬件系统与软件系统共同组成第一台计算机ENIAC,1946年诞生于美国宾夕法尼亚大学。
第二台计算机EDV AC,基于冯.诺依曼的设计思想,首次采用了“存储程序”的概念,冯.诺依曼理论将计算机分为五大部分:运算器、控制器、存储器、输入设备、输出设备。
计算机内部采用二进数存储和表示数据,因为二进制数便于物理实现,运算规则简单,可靠性高,便于进行逻辑运算。
中央处理器(CPU)运算器、控制器、寄存器ROM 只读(存放微机启动时的基本数据)RAM 随机读写(易失性)512M—16G主机内(主)存一级L1(CPU内部)在速度较低的RAMCache高速缓存与速度较高的CPU间二级L2(32K—8MB)起到缓冲作用输入/输出(I/O)接口硬硬盘盘符为C:、D:…件系CD-ROM(只读光盘)统CD CD-R(一次性写入光盘) 650M—700M外存光盘CD-RW(可重复擦写光盘)DVD-ROMDVD DVD-R 4.7G外设DVD-RWU盘(Flash、移动硬盘输入设备(键盘、鼠标、光笔、扫描仪)输出设备(显示器、打印机、绘图仪)其他网络设备(网卡、调制解调器、声卡、显卡)计算机所采用物理器件经历了电子管时代、晶体管时代、集成电路时代、大规模或超大规模集成电路时代。
2.位(bit),数据的最小单位,一个位指的是一个二进制位。
3.字节B(8位二进制数构成一个字节,存放一个西文字符)、字长(代表精度,通常是8的倍数);存储器容量单位:B、KB、MB、GB、TB(每级之间换算约为1000,精确为1024,即210)。
4.ASCII码,7位二进制数组成,可表示27=128个字符。
32(即20H)代表空格,小于32以及码值127的ASCII码代表不可显示字符,大于32的ASCII码代表可显示字符。
在可显示字符中,数字排在前,其次是大写字母,小写字母排在后面。
计算机数学基础复习要点

计算机数学基础复习要点计算机数学基础是学习计算机的必备知识,因此学习者若要深入了解计算机的运行原理,则必须全面、系统地复习数学基础。
以下是计算机数学基础复习要点:
一、代数学
1、线性代数:研究“数量集合”中的“线性方程组”以及结构,包括基本术语、系数矩阵、行最简表示、求秩和投影空间等。
2、解析几何:研究空间直线、面和体的位置、运动关系及其符号表示,研究向量的运算、投影函数等。
3、实变函数:研究函数的概念及定义,函数求导、积分、极限等相关运算规律,概率论基础等。
二、数学逻辑
1、基本数学逻辑:合取范式、析取范式、命题函数、免费变量、逻辑证明步骤等。
2、数学归纳:研究归纳法的定义和特点,以及归纳证明、反证法
等原理。
3、递归:研究数学递推和归纳的联系,建立数学递推式,探索递
归解法的含义及其应用。
三、概率统计
1、基本概率理论:研究事件及其集合,概率的基本概念及其特性、随机变量及其概率分布,离散随机变量的基本分布及其近似分布,随
机样本的提取及其特点等。
2、极限定理:研究大数定理、中心极限定理、方差极限定理等定
理的原理及其应用,以及预测变量示性统计量的分布特点。
3、假设检验:通过正态分布、t分布、卡方分布及其他分布证明
随机变量或示性统计量的概率、置信度,进行假设检验,确定概率的
有效性。
计算机数学基础是学习计算机的关键性内容,必须要掌握起来。
因此,学习计算机的学生需要严格按照上述复习要点,逐一梳理、提
炼,以期大量积累,深入理解计算机运行原理,系统、总结概括数学基础知识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.考核对象
开放教育试点计算机科学与技术专业(试卷代号:4012)学生。
3.考核要求分三个层次,有关概念、性质和定理等理论方面的要求从高到低为理解。了解和知道:有关方法、公式和法则等的要求从高到低为熟练掌握,掌握和会。
Ⅱ、考核内容与考核要求
第9章数值分析中的误差
考核知识点
1.误差的来源与基本概念
2.数值计算中的若干准则
考核要求
1.了解误差分析的基本意义及其重要性。
2.知道产生误差的主要来源。
3.了解误差的基本概念:绝对误差和绝对误差限、相对误差和相对误差限、有效数学等。
4.了解数值计算中应注意的几条原则。
第10章线性方程组的数值解法
3.知谴陆6,拆求积公式和高斯点的概念。会用高斯—教,lLg蘸求跟妊蛀式。
4.知道插值型求导公式概念,掌握两点求导公式和三点求导公式。
第13章方程求根
考核知识点
1.二分法
2.迭代法
3.牛顿法
4.弦截法
考核要求
1.掌握方程求根的二分法,知道其收敛性;掌握迭代法,知道其收敛性。
2.熟练掌握牛顿法。
3.掌握弦截法。
(C)对称且严格对角占优矩阵(D)正定对称矩阵
6.解常微分方程初值问题的欧拉法的局部截断误差是( )
(A)O(h5)(B)O(h4)(C)O(h3)(D)O(h2)
7.已知函数y=f(x)在5个互异节点处的函数值,其一阶、二阶均差均不为0,三阶均差是1,那么用这5对数值作的插值多项式P(x)是( )
计算机数学基础(2)期末复习指导
Ⅰ、计算机数学基础(2)考核说明
数值分析部分
1.《计算机数学基础》是开放教育本科计算机科学与技术专业学生必修的一门专业基础课程,是学习专业理论必不可少的数学工具。通过本课程数值分析部分内容的学习,使学生掌握数值分析的基本概念和基本方法,进一步提高使用计算机进行科学和
工程计算的能力。课程的结业考核,考核合格水准应达到高等学校该专业本科教育的要求。
第14章常微分方程的数值解法
考核知识点
1.欧拉法
2.龙格一库塔法
考核要求
1.掌握求一阶常微分方程初值问题的欧拉法和改进的欧拉法,知道其局部截断误差。
2.知道求一阶常微分方程初值问题的龙格一一库塔法的基本思想。掌握龙格一库塔法。知道龙格一一库塔法的局部截断误差。
Ⅲ、计算机数学基础(2)综合练习题
一、单项选择题
4.本课程的结业考核实行形成性考核和期末结业性考试。形成性考核占结业考核成绩的20%,即形成性考核的成绩满分为20分;期末结业性考试成绩占结业考核成绩的80%,即期末考核成绩满分80分。结业考核成绩满分100分,60分为合格。
5.试题题型
一、单项选择题(15分左右)、二、填空题(15分左右)、三、计算题(每小题15分,共60分)、四、证明题(本题10分)。
X(k+1)=BX(k)+f,k=1,2,…
都收敛的充分必要条件是( )
4若误差限为0.5×10-5,那么近似数0.003400有( )位有效数字.
(A) 2 (B) 3 (C) 4 (D) 6
5.当线性方程组AX=b的系数矩阵A是( )时,用列主元消去法解AX=b,A的主对角线的元素一定是主元.
(A)上三角形矩阵(B)主对角线元素不为0的矩阵
考核知识点
1.高斯消去法
2.迭代法
考核要求
1.了解线性方程组高斯消去法的基本思想,熟练掌握高斯顺序消去法和列主元消去法。
2.掌握线性方程组雅可比迭代法和高斯——赛德尔迭代法。
3.知道线性方程组迭代解的收敛概念和上述两种迭代法的收敛性。
第11章函数插值与最小二乘拟合
考核知识点
1.函数插值概念
2.拉格朗日插值多项式
15.设n阶矩阵A=(aij)n,若满足( ),称A为严格对角占优矩阵.
1.数a*=0.69314718…的有四位有效数字的近似值是( )
(A) 0.69314 (B) 0.6930 (C) 0.6932 (D) 0.69315
2.等距二点的求导公式是().
(A) (B)
(C) (D)
3.设线性方程组X=BX+f,n阶矩阵B的特征根为 ,对任意初始向量X(0)及f,对应此方程组的迭代格式
9.有3个不同节点的高斯求积公式的代数精度是( )次的.
(A) 5(B) 6(C) 7(D) 3
10.解微分方程初值问题的方法,( )的局部截断误差为O(h3).
(A)欧拉法(B)改进欧拉法(C)三阶龙格-库塔法(D)四阶龙格-库塔法
11.以下误差限公式不正确的是( ).
(A) (B)
(C) (D)
6.了解曲线拟合最小二乘法的意义。掌握线性拟合和二次多项式拟合的方法。
第12章数值积分与微分
考核知识点
1.数值积分与代数精度
2.等距节点的求积公式
3.高斯求积公式
4.数值微分
考核要求
1.理解数值积分的基本思想和代数精度的概念。
2.了解牛顿一科茨求积公式和科茨系数的性质。熟练掌握复化梯形求积公式和复化抛物线求积公式。
3.牛顿插值多项式
4.分段插值(分段线性插值、三次样条插值)
5.最小二乘拟合
考核要求
1.理解插值概念。
2.熟练掌握拉格朗日插值公式,知道拉格朗日插值余项公式。
3.掌握牛顿插值公式.了解均差概念和性质,掌握均差表的计算,知道牛顿插值的余项。
4.掌握分段线性插值的方法。
5.知道三次样条插值函数的概念,会求三次样条插值函数。
(A)五次多项式(B)四次多项式(C)三次多项式(D)二次多项式
4.已知当x=1,2时的函数值f(1),f(2),则f(1)( )
8下列条件中,不是分段线性插值函数P(x)必须满足的条件为( )
(A)P(xk)=yk,(k=0,1,…,n) (B)P(x)在[a,b]上连续
(C)P(x)在各子区间上是线性函数(D)P(x)在各节点处可导
12.步长为h的等距节点的插值型求积公式,当n=2时的牛顿-科茨求积公式为().
(பைடு நூலகம்)
(B)
(C) 〕
(D)
13.已知等距节点的插值型求积公式 ,那么 =( ).
(A) 1 (B) 2 (C) 3 (D) 4
14.下列各数中,绝对误差限为0.000 05的有效近似数是( )
(A)-2.180. (B) 2.1200 (C)-123.000 (D) 2.120
