王健阵列天线讲义5
【成电】【阵列天线讲义】王建教授的概要

阵列天线分析与综合前言任何无线电设备都需要用到天线。
天线的基本功能是能量转换和电磁波的定向辐射或接收。
天线的性能直接影响到无线电设备的使用。
现代无线电设备,不管是通讯、雷达、导航、微波着陆、干扰和抗干扰等系统的应用中,越来越多地采用阵列天线。
阵列天线是根据电磁波在空间相互干涉的原理,把具有相同结构、相同尺寸的某种基本天线按一定规律排列在一起组成的。
如果按直线排列,就构成直线阵;如果排列在一个平面内,就为平面阵。
平面阵又分矩形平面阵、圆形平面阵等;还可以排列在飞行体表面以形成共形阵。
在无线电系统中为了提高工作性能,如提高增益,增强方向性,往往需要天线将能量集中于一个非常狭窄的空间辐射出去。
例如精密跟踪雷达天线,要求其主瓣宽度只有1/3度;接收天体辐射的射电天文望远镜的天线,其主瓣宽度只有1/30度。
天线辐射能量的集中程度如此之高,采用单个的振子天线、喇叭天线等,甚至反射面天线或卡塞格伦天线是不能胜任的,必须采用阵列天线。
对一些雷达设备、飞机着陆系统等,其天线要求辐射能量集中程度不是很高,其主瓣宽度也只有几度,虽然采用一副天线就能完成任务,但是为了提高天线增益和辐射效率,降低副瓣电平,形成赋形波束和多波束等,往往也需要采用阵列天线。
在雷达应用中,其天线即需要有尖锐的辐射波束又希望有较宽的覆盖范围,则需要波束扫描,若采用机械扫描则反应时间较慢,必须采用电扫描,如相控扫描,因此就需要采用相控阵天线。
在多功能雷达系统中,既需要在俯仰面进行波束扫描,又需要改变相位展宽波束,还需要仅改变相位进行波束赋形,实现这些功能的天线系统只有相控阵天线才能完成。
随着各项技术的发展,天线馈电网络与单元天线进行一体化设计成为可能,高集成度的T/R组件的成本越来越低,使得在阵列天线中的越来越广泛的采用,阵列天线实现低副瓣和极低副瓣越来越容易,功能越来越强。
等等。
综上所述,采用阵列天线的原因大致有如下几点:■容易实现极窄波束,以提高天线的方向性和增益;■易于实现赋形波束和多波束;■易于实现波束的相控扫描;■易于实现低副瓣电平的方向图。
阵列天线PPT课件

.
35
N元非等幅均匀阵列
• 阵因子比较 • 二项式分布阵列 • 多尔夫-切比雪夫多项式阵列 • 泰勒分布阵列
.
36
N元非等幅均匀阵列
• 阵因子比较 • 二项式分布阵列 • 多尔夫-切比雪夫多项式阵列 • 泰勒分布阵列
.
37
阵因子
• 均匀幅值阵列具有最小的半功率波束宽度 • 二项式分布幅值阵列能够实现最小的副瓣电平 • 二项式分布幅值阵列单元间距小于半波长时,副瓣
.
N元等幅均匀线阵
求解最大值点:
阵列存在唯一的一个最大值点,即m=0 求解阵因子的3dB波束点:
.
线阵实例 1: 侧射阵
• 波束最大指向θ0=90°(线阵沿Z轴),当单元 的波束最大指向和阵因子的最大波束指向均指向 θ0=90°时,便可达到最佳的侧射阵。 • 对于单元天线的波束指向要求,可以通过选择 合适的辐射单元来满足要求 • 对于阵因子的波束指向要求,可以通过合理的 调整阵列单元间的间距、每个单元的相位激励实 现。
.
N元非等幅均匀阵列
• 阵因子比较 • 二项式分布阵列 • 多尔夫-切比雪夫多项式泰勒线阵—线源激励计算
线源激励幅度的分布为
i1
Ii (p)12 Sn(m)com s()p m1
1
m0
Sn(m)=(i1[m (i )1!(i)!]21m)!ii1112A2m (2i12)2 0mi
➢在每个天线单元的馈端 以及电缆的公共馈端处各 接入一个开关 ➢控制联动开关可使波束 从边射移到45°方向
.
相控阵
➢ 每个阵列单元都有移相器和衰减器,所有馈电 电缆都布置成等长度的组合结构
.
相控阵
➢端馈相控阵也需要逐个单元配有移相器和衰减 器,由于在单元之间引入了递进的相位移,随着 频率的变化,在额定的相位移之外,还需要附加 相反的相位变化作为补偿
第十六讲_阵列天线

n=0
均匀直线阵
阵列方向函数的幅度:
Nϕ sin 2 fα (α ) = ϕ sin 2
fα (α ) max Nϕ sin 2 = =N ϕ sin 2 ϕ =0
Fα (α ) max
Nϕ N sin sin (ψ + kd cos α ) 1 2 = 1 2 = N N ϕ 1 sin sin ψ + kd cos α 2 2
2、
π
d=λ
fα (α ) = 2 cos ψ + kd cos α) 2 ( /
π 2π d = 2 cos ( + cos α)= 2 cos ( + π cos α) 4 λ2 4
π
均匀直线阵
1、定义:N个阵列单元以相同的间距排列在一条直线上构成 的阵列。若阵列单元的激励幅度相等相位依次等幅递增,称 为N元直线阵列。 N 2 1 2、阵列方向函数: ϕ = ψ + kd cos α E1 = E1m I1 jnψ E n = E1e jnψ e jknd cosα = E1e jnϕ I n = I1e
= E1m F(α ) fα (α ) E=E1 + E 2
= E1m f阵列
方向图乘积定理:f阵列 = F(α ) fα (α )
阵元相似性:天线形式一致,辐射场形式一致 阵列单元辐射场的坐标要和阵列一致 方向图乘积定理可以推广到多元阵列 阵列单元不同:幅度和相位以及排列位置 阵列因子
F(α ) =1 f阵列 fα (α ) →
总的辐射方向函数为:
F总 =F(θ )fα x (α ) fα z (θ ) 3 sin (ψ + kd cos α ) 2 = sinθ sin ( k2h cos θ ) sin ( kh cos θ ) )
王健阵列天线讲义3

2.1.2 切比雪夫多项式
切比雪夫多项式是如下二阶微分方程的解 d 2Tm dT (1 − x ) 2 − x m + m 2Tm = 0 dx dx
2
(2.1) (2.2) (2.3)
令 则上式可简化为: 其两个解分别是 和
x = cos u
d 2Tm + m 2Tm = 0 2 du
Tm ( x ) = cos( mu ) = cos( m cos −1 x ) , Tm ( x ) = sin( mu ) = sin( m cos −1 x )
■基本步骤:
(1) 根据单元数 N 的奇偶选择阵因子 Sodd (u ) 或 Seven (u ) ; (2) 展开阵因子中的每一项,使其只含 cos(u ) 的形式; (3) 由分贝表示的主副瓣比 R0 dB 换算成无量纲形式 R0 = 10 TN −1 ( x0 ) = R0
←右半单元 ←左半单元
= I1e
1 − j ( kd cosθ +α ) 2
+ I 2e
3 − j ( kd cosθ +α ) 2
+ IM e
= 2∑ I n cos[
n =1
M
2n − 1 ( kd cos θ + α )] 2
(2.13)
令u =
πd α (cosθ − cosθ 0 ) ,而 cosθ 0 = − ,去掉因子 2,得归一化阵因子 λ kd
…… …… ……
上面给出的切比雪夫多项式只适用于 | x |≤ 1 的范围。当 | x |> 1 时,要满足
x = cos u ,则 u 必须是一个纯虚数,即 u = jv (v 为实数)。此时
阵列天线分析与综合_7

b2
N
⎥ ⎥
""⎥
⎢⎣bN1
bN 2
"
bNN
⎥ ⎦
∫ ∫ blm
=
1 2
π 0
el
⋅ em*
sinθ dθ
=
1 2
π e jk ( zm − zl ) cosθ sinθ dθ
0
=
sin k(zm − zl ) k(zm − zl )
=
⎧1 ⎩⎨0
, ,
l=m l≠m
(4.11) (4.12)
blm 为实数,显然满足 blm = bm* l ,则矩阵[B]也为厄米(Hermite)矩阵。 矩阵[A]和矩阵[B]主要取决于单元间相对位置,因此称它们为结构矩阵。把
[e]
=
⎢⎢1⎥⎥ ⎢# ⎥
,
[ A]
=
[e][e]+
=
⎢⎢1 ⎢
1" "
1⎥⎥ ⎥
,
⎢⎣1⎥⎦
⎢⎣1 1 " 1⎥⎦
blm
=
sin k(zm − zl k(zm − zl )
)
=
sin[(m − l)π (m − l)π
]
=
⎧1 ⎨⎩ 0
, ,
l=m l≠m
得本征值方程 (1 − p) 1 1 (1 − p)
4.1.1 线阵方向图函数的矩阵表示
一个单元数为 N,间距和激励为任意的线阵辐射场方向图函数可写作
N
∑ E(θ ,ϕ ) = f (θ ,ϕ )
I e e jαn jkzn cosθ n
n=1
(4.5)
式中, f (θ ,ϕ ) 为单元方向图函数,为简化分析,设 f (θ ,ϕ ) =1,即单元为理想 点源,此时上式可写作
天线原理与设计(王建)3PDF版(优选.)

+
I1 I0
e− jβ r1 ]
r1
作远场近似:对幅度 1/ r1 ≃ 1/ r0
对相位 r1 = r0 − rˆ0izˆd = r0 − d cosθ
(1.89)
并设
I1 / I0 = me− jα
(1.90)
式中,m为两单元电流幅度比,α为两单元电流之间的相
位差,若α>0,则I1滞后于I0;若α<0,则I1超前于I0 ; 若α=0 ,则I1与I0同相位。式(1.89)可写作
(1.93)
合成相差
ψ = β d cosθ − α
(1.94)
由式(1.92)可见,二元阵总场方向图由两部分相乘而 得,第一部分f0(θ,φ)为单元天线的方向图函数;第二部 分fa(θ,φ)称为阵因子,它与单元间距d、电流幅度比值m、 相位差α和空间方向角θ有关,与单元天线无关。因此 得方向图相乘原理:
(1.106)
阵因子为
N −1
N −1
∑ ∑ = E0
e = E jn( β d cosθ −α ) 0
e jnψ = E0 fa (ψ )
n=0
n=0
+ 2 + e jβd sinθ sinϕ ]
=
j 60I r
e− jβ r
− jβ d sinθ sinϕ
f0 (θ ,ϕ )[e 2
+ e ] jβ d sinθ sinϕ 2
2
=
j 60I r
e− jβ r
f0
(θ
,ϕ
)4
cos2
(
βd 2
sinθsinຫໍສະໝຸດ )=j 60I r
e− jβ r
天线阵列 讲稿

当 θ m = π / 2 时,上式与侧射阵的主瓣宽度公式相同。 若在正侧向两边 ±φm 内扫描,取 θ m = 90o ± φm 得:
2ϕ 0.5 = 51
λ
L cos φm
(o )
(5.27)
由此式可见,与侧射阵相比,波束最大值发生偏移时半功率波瓣宽度将变宽。
5、副瓣位置和副瓣电平
(1)副瓣位置
y 轴上振子的场为: E1 = j
I1l η e − jβ r sin γ 2λ r Il x 轴上振子的场为: E2 = j 2 η e − jβ r sin ϕ 2λ r E1 和 E2 方向相反,则总场为 Il Il ET = E1 − E2 = j 1 η e − jβ r [cos ϕ ± jsin ϕ ] = j 1 η e − j(β r ∓ϕ ) 2λ r 2λ r
(5.6)
130
《天线原理与设计》讲稿
王建
思考:如何导出短振子旋转场天线的立体方向图函数? 广播、电视台的发射天线采用的一种蝙蝠翼天线也是一种旋转场天线,见书 上图 5-2。
5.2 均匀直线式天线阵
等间距为 d 的 N 单元直线阵如图 5-2 所示。 在前面第一章中对均匀直线式天 线阵作过简单介绍,得到了 N 元均匀直线阵的阵因子为
SLL = 20 lg | F (ψ s1 ) |= −13.5 (dB)
(5.31)
6、方向性系数 D
由方向性系数公式
D=
π
4π
∫
2π
0
dϕ ∫ F 2 (θ )sin θ dθ
0
π
=
2
∫
π
0
F 2 (θ )sin θ dθ
(5.1)
式中已代入关系 I 2 = I1e ± jπ / 2 。计入时间因子 e jω t ,则
天线原理与设计(王建)6PDF版

(1) 传输线模式
见图(b),由端口a-b或e-f向短路端看去的输入阻抗为
Zt = jZ0 tan(β l / 2)
(4.19)
式中,Z0是双线传输线的特性阻抗。b、e两点等电位, 则a-b两点的输入电流为
(2) 天线模式
U /2 It = Zt
(4.20)
见图(c),由于c、d两点同电位,g、h同
f0
f0
π
RA
(4.12)
由此式可见,对称振子的频带宽度与它的平均特性阻抗
Z'0有关。如果RA不变,那么Z'0愈小带宽就愈宽。由Z'0的
表示
Z0′
= 120[ln(
2l ρe
)
− 1]
(4.13)
可见,减小Z'0的有效途径是增大振子的截面半径。在中、 短波波段,广泛采用架设在地面上一定高度的水平对称
天线原理与设计
教师: 王建 电子工程学院二系
第四章 双极与单极天线
双极天线就是前面提到的对称振子天线,这种天线 从馈电输入端看去有两个臂。所谓单极天线,就是从输 入端看去只有一个臂的天线,如导电平板上的鞭天线, 垂直接地天线等。
4.1 近地水平与垂直半波天线
1、近地水平半波天线
近地水平半波振子天线广泛应用于短波(λ=10~100 米)通信中,其振子臂可由黄铜线、钢包线和多股软铜线 水平拉直构成,中间由高频绝缘子连接两臂,可由双线 传输线馈电,如下图所示。
链接
4.2 对称天线的频带宽度
天线的电气参量大多数都是频率的函数。当工作频 率偏离中心频率(设计频率)时,可能使方向图发生畸变, 增益下降,馈电传输线上驻波增大等。因此,工程上往 往要规定一个频率范围。在此频率范围内,天线的电特 性变化不影响工作,这个频率范围就是工作频带宽度。
王健阵列天线讲义2
§1.7 谢昆诺夫单位圆辅助分析阵列特性
39
阵列天线分析与综合讲义
王建
1.7.1 谢昆诺夫单位圆
一个 N 单元直线阵, 其馈电幅度为 I n , n = 0,1, 2," , N − 1 , 相邻单元相位差为
α ,等间距 d 排列,则其阵因子为
S = ∑ I n e jnu , u = kd cosθ + α
(1.139)
(1.140)
可画出正弦分布直线阵列的归一化方向图如图 1-21 所示。
(a) 直角坐标方向图 (b) 极坐标方向图 图 1-21 N=5,d=λ/2 时的正弦幅度分布直线阵列方向图
最大值为: Smax = Sodd (u ) |u =0 = 6 + 2 = 7.414 零点位置:由 | Sodd (u ) |= 0 确定,即
(1) 奇数阵列
36
阵列天线分析与综合讲义
王建
Sodd = ∑ I (nd )e jnu
n =0
N −1
← I (ζ ) = 1 + sin[
nπ )e jnu N −1
πζ
( N − 1)d
], ζ = nd
= ∑ e jnu + ∑ sin(
n =0 n =0
N −1
N −1
= S1 (u ) + S2 (u )
阵列天线分析与综合讲义
王建
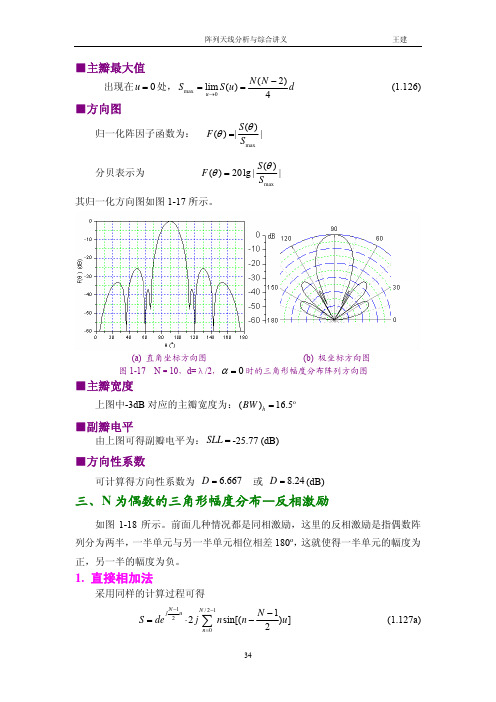
N ( N − 2) d 为同相激励的偶数单元三角形分布阵列最大值。结果如 4 图 1-19 所示。这种反相激励阵列形成的方向图称为差方向图。
式中, S max =
(a) 直角坐标方向图 (b) 极坐标方向图 图 1-19 N=10,d=λ/2 时的反相激励三角形分布阵列方向图
阵列天线分析与综合_6

sinθ cosϕ − sinθ0 cosϕ0
(sinθ cosϕ − sinθ0 cosϕ0 )2 + (sinθ sinϕ − sinθ0 sinϕ0 )2
(3.89)
只要给定 a, ϕn , In , N , (θ0, ϕ0 ) 或αn ,就可计算并绘出圆环阵的方向图。
【例 3.4】有一个均匀圆环阵,其激励幅度 In = I0 = 1,激励相位αn = 0 ;沿圆
3.8.1 圆口径泰勒空间因子
设在 xy 平面上有一个半径为 a 的圆形口径如下图 3-30 所示。若设口径上场
分布为连续分布 I (ρ,ϕ ′) ,口径外场分布为零,则远区场为
∫ ∫ E = j e− jkr (1 + cosθ ) 2π dϕ ′ a I (ρ,ϕ ′)e jkρ sinθ cos(ϕ −ϕ ′)ρd ρ
(3.85)
波束在最大指向方向(θ0,ϕ0 ),满足关系: ka sinθ0 cos(ϕ0 − ϕn ) + αn = 0 ,得
αn = −ka sinθ0 cos(ϕ0 − ϕn )
(3.86)
可得
N
∑ S (θ ,ϕ ) = Ine jka[sinθ cos(ϕ−ϕn )−sinθ0 cos(ϕ0 −ϕn )] n=1
(3.103)
(3.104)
通过对上式计算,当圆环半径 a ≈ 7λ / 8 时,其方向性系数在θ0 = 0 处达到最大; 当 a ≈ λ / 2 、7λ / 4 时,其方向性系数在θ0 = π / 2, ϕ0 = 0 处达到最大;当 a ≈ 3λ / 4 时,其方向性系数在θ0 = π / 2, ϕ0 = 30o 处达到最大。
阵列天线分析与综合讲义
王建
阵列天线分析与综合_1

第一章 直线阵列的分析
§1.1 引言
■导出直线阵列阵因子的方法
(1) 求解面电流源的辐射场,然后根据阵列为离散源组合 在一起的特点对面电流源进行抽样,就可得到直线阵列 的阵因子。
(2) 先确定阵列中某单元天线的远区辐射场表示,然后取 远区近似并考虑波程差,把阵列中所有单元天线的辐射 场叠加起来,求得阵列的总辐射场,从而求得阵因子。
e jkr j F ( , ) 4 r
k
(1.5)
式中, / 为传播媒质中的波阻抗,方向图函数为
F ( , ) k sin
s jk ( x sin cos z cos ) J z ( x , z )e dxdz
(1.17)
把式(1.17)代入 (1.16) ,并取阵因子的模值,得 sin( Nu / 2) sin[ N (kd cos x ) / 2] | S (u) | I 0 I0 sin(u / 2) sin[(kd cos x ) / 2]
(1.18)
对于并排振子均匀直线阵,由式(1.11)可得其 yz面 (φ=π/2)方向图函数为 sin( N / 2) (1.19) | F ( ) | kI 0 f 0 ( ) sin( / 2)
2 cos(kL cos ) cos( kL) dz k sin
N 1 n 0 j( kxn cos x n ) I e n
(1.11)
式中,f0(θ)为单元方向图,带入正弦分布g(z'),可得
f 0 ( ) sin g ( z)e
L jkz cos
(1.12)
阵因子方向图函数为
S ( , )
N 1 n 0 jkxn sin cos I e n
天线技术课件西电第二版第5章

即
E ? 2E0
(5-1-2)
由式(5-1-2)可以得出结论:在输入功率相同的条件下,
远区M点所得到的场强,二元阵比单个振子时增强了 n 倍。同
理可以证明: 若功率不变, 将能量分配到n个振子上,则场强
将增加为n倍,即 E ? nE0 。
第 5章 阵列天线(天线阵)
Ⅰ?
r1
N
d
M
r2
Ⅱ?
dcos ?
? f2(?
)
?e?
j? r2
因此,在远区M点的合成场强为: E=E 1+E2, 即
? ? E ?
j
60 I1m r1
?
f1(?
)
?e?
j? r1
1?
me j(?
? ?d cos?
)
? E1 ?(1 ? me j(? ) ? ?d cos? )
? E1(1 ? me j(? ) ? ?d cos? ) ? E1(1 ? me j? )
第 5章 阵列天线(天线阵) 2.方向性增强原理
N
?
M r0
Ⅰ 图5-2 天线单元
第 5章 阵列天线(天线阵)
振子Ⅰ的输入功率为PA、输入电阻为PA ,则输入电流为
IA ?
2 PA RA
(5-1-1)
在与振子轴垂直而相距r0的M点的场强E0,与输入电流成正 比例关系(参考式 (3-1-7))。我们把它写成 E0=AIA,其中,A是 一个与电流无关的比例系数。 将式(4 - 1-1)代入得
图5-3 两个天线单元构成的二元阵
第 5章 阵列天线(天线阵)
应当注意的是,电场增强为 倍只是对正前方M点而言, 在其他方向上就要具体分析了。如果讨论图5-3的N点方向, 当 两射线的行程差为d cosθ=λ/2 时,其引起的相位差将为π, 这表 示两振子到达该点的场强等值反相,合成场为零。所以说把能 量分配到各振子上去以后,方向性可以增强的根本原因是由于 各振子的场在空间相互干涉,结果使某些方向的辐射增强, 另 一些方向的辐射减弱,从而使主瓣变窄。
王健阵列天线讲义6

D=
| S (θ 0 ,ϕ 0 ) |2 W
(3.104)
通过对上式计算,当圆环半径 a ≈ 7λ / 8 时,其方向性系数在 θ 0 = 0 处达到最大; 当 a ≈ λ / 2 、7λ / 4 时, 其方向性系数在 θ 0 = π / 2, ϕ 0 = 0 处达到最大; 当 a ≈ 3λ / 4 时,其方向性系数在 θ 0 = π / 2, ϕ 0 = 30o 处达到最大。
3.8.1 圆口径泰勒空间因子
设在 xy 平面上有一个半径为 a 的圆形口径如下图 3-30 所示。 若设口径上场 分布为连续分布 I ( ρ , ϕ ′) ,口径外场分布为零,则远区场为
E= j
2π a e − jkr (1 + cosθ ) ∫ dϕ ′∫ I ( ρ , ϕ ′)e jk ρ sin θ cos(ϕ −ϕ ′) ρ d ρ 0 0 2λ r
N m =1 n =1
N
N
m −α n )
⋅∫
2π
0
dϕ ∫ e jk ρmn sin θ cos(ϕ −ϕ mn )] sin θ dθ
0
π
= 4π ∑ ∑ I m I n e j (αm −αn ) ⋅ ∫
π /2
0
J 0 (k ρmn sin θ )sin θ dθ
(3.101)
= 4π W
式中,
阵列天线分析与综合讲义
王建
§3.5 圆环阵意义的 阵列结构,可应用于无线电测向、导航、地下探测、声纳等系统中。
3.5.1 方向图函数
设有一个圆环阵,放置在 xy 平面内,圆环的半径为 a,有 N 个单元分布在 圆环上,如图 3-27 所示。第 n 个单元的角度为 ϕ n ,其位置坐标为( xn , yn ),该单 元的远区辐射场为
王健阵列天线讲义4

§2.6 伍德沃德—劳森抽样法简称伍德沃德法。
这种方法是用于天线波束赋形的一种常用的方向图综合方法,它是对所需方向图在不同离散角度处进行抽样来实现预期方向图的。
与各方向抽样和联系的是谐波电流,谐波电流对应的场叫做构成函数。
综合方法分为连续的线源和离散的线阵分别讨论。
对于连续线源。
其构成函数为形式,对于离散线阵,其构成函数为形式。
各谐波电流激励系数等于所要求的方向图在对应抽样点上的幅度。
谐波电流的有限项之和为源的总激励。
构成函数的有限项之和则为综合的方向图,其中每一项代表一个电流谐波产生的场。
sin()/m m a u u m m sin()/(sin )m m a nu n u m a 伍德沃德方法中有关公式的处理类似于信号理论中的香农(Shannon)抽样定理。
该定理指出:“一个有限频带的函数,如果最高频率为()g t h f ,则函数可以用等间隔的抽样唯一地表示。
抽样间隔必须不大于()g t 1/(2)/2h h t f T Δ==,为对应于最高频率的周期”。
用类似的方法综合天线方向图时,其抽样间隔应取h T /L λ弧度,L 为源的长度。
2.6.1连续线源(1) 连续线源上的电流分布对于长为L 的连续线源,伍德沃德方法是令连续线源的总电流I (z )在线上用若干谐波电流()n I z 的有限和来表示:()(),/2/2N n n N I z I z L z L =−=−≤∑≤ (2.119)式中谐波电流为cos (),/2/2n jkz n n a I z e L z L Lθ−=−≤≤ (2.120) n θ代表所需方向图的抽样角度。
(2N 个偶数抽样)1,2,,n =±±± N N (2N +1个奇数抽样)0,1,2,,n =±±± (2) 谐波电流产生的场方向图由各谐波电流()n I z 产生的场方向图函数(即构成函数)为/2/2(cos cos )cos /2/2()()n L L jkz jkz n n n L L a S I z e dz e L θθθθ−−−==∫∫dzsin[(cos cos )]2(cos cos )2n n n kL a θθθθ−=− (2.121) 其最大值发生在n θθ=处。
阵列天线分析与综合

W
=
NN
Im Ine j(αm −αn )
m=1 n=1
sin(k ρmn ) k ρmn
此式的导出用了关系
∫π 0
/2
J0(x sinθ
)sinθ dθ
=
π J1/ 2(x) = sin x
2x
x
把式(3.101)代入(3.97)得
D = | S(θ0,ϕ0 ) |2 W
(3.101) (3.102)
∑ 于是式(3.91)变为:
Sh (ϕ
)
=
NI
∞ m = −∞
e−
jmNϕ
/ 2J mN
(2ka
sin
ϕ 2
)
(3.93)
此为阵列平面内的阵因子,它与θ 角无关。这说明调整单元激励相位αn 为式(3.92) 式表示,则可使圆环阵的最大指向在阵列平面内。
2. 主瓣最大值指向 z 轴方向
此时θ0 = 0 ,可得,αn = 0 ,即阵列单元同相激励,最大值在阵面侧向。 ρ = a sinϕ
阵列天线分析与综合讲义
王建
§3.5 圆环阵列的分析
多个单元分布在一个圆环上的阵列称为圆环阵列。这是一种有实际意义的 阵列结构,可应用于无线电测向、导航、地下探测、声纳等系统中。
3.5.1 方向图函数
设有一个圆环阵,放置在 xy 平面内,圆环的半径为 a,有 N 个单元分布在 圆环上,如图 3-27 所示。第 n 个单元的角度为ϕn ,其位置坐标为( xn, yn ),该单 元的远区辐射场为
−ϕn 2
),
m ≠ n,
⎪⎩0 ,
m=n
(3.98) (3.99)
ϕ mn
=
tan−1( sinϕm cosϕm
阵列天线PPT课件

• 提出目的: 为了加强天线的方向性!
❖ 天线阵: 将若干辐射单元按某种方式排列,形成天线阵. (辐射单元:天线元/阵元)
❖ 天线阵的辐射场: 由天线元所产生的矢量场叠加,其上的电流振幅和相位分布 满足适当的关系得到. (相似元:各阵元的形状与尺寸相同,相同姿态排列)
第1页/共27页
1
例: 三个间距为 2 的同性元组成的三元阵,各元激励的相位相同,振 幅为:1:2:1,试讨论这三个阵的方向图.
振幅1:2:1的三元阵可以 等效为两个检举为 的二元阵 组成的二元阵,所以元2 因子和阵 因子都是一个二元阵.
元因子、阵因子的表达式 均可 表示成 :
第25页/共27页
第26页/共27页
r2 [(r1 sin cos d)2 r12 sin2 sin2 r12 cos2 ]2
1
二
[r以12
r1[1
二22r1ddss元iinn 阵ccooss 为 d(例2d])22
1
]2
r1(1 dr1sin cos ) r1
r1
r1 dsin cos
z
M
如图: 天线阵间距
d
第5页/共27页
天线方向图乘积定理:
在各天线元为相似元的条件下,天线 图的乘积函数是单元因子和天线阵因子 之积.
F(, ) cos 2
第6页/共27页
对于半波阵子来说:
已推得:
h 2 h 2h
2
z E
0 时,E面方向图(zox平面):
x
FE
cos cos 2
cos 1 ( kdsin )
;
r1
沿x轴排列;
2
半波振子:
r2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3.14)
(2.15)
式中
(3.16)
阵列天线分析与综合讲义
王建
为该单元在阵面上的位置坐标。不论行数 N x 和列数 N y 为何值,式(3.16)是相对 于阵列中心的位置坐标。坐标原点到远区场点的射线 r 的单位矢量为
ˆ=x ˆ cos ϕ sin θ + y ˆ sin ϕ sin θ + z ˆ cos θ r
, Nx −1 , Ny −1
ˆ m + yy ˆ n = xmd ˆ x + ynd ˆ y ρ mn = xx
144
阵列天线分析与综合讲义
王建
图 3-3 矩形栅格排列的矩形平面阵
3.2.1 阵因子方向图函数及波束指向
1. 阵因子方向图函数
设第 mn 个单元的激励电流为 I mn ,则其远区辐射场可表示为 Emn = CI mn e − jkRmn e − jkr − jk ( Rmn − r ) = CI mn e Rmn r
一、对称振子平面阵结构及坐标系
矩形网格、矩形边界的对称振子平面阵结构及建立的坐标系如图 3-6 所示。 平面阵共有 N x 列, N y 行,列间距为 d x ,行间距为 d y 。
148
阵列天线分析与综合讲义
王建
图 3-6 对称振子平面阵结构及建立的坐标系
为了使阵列天线仅向正前方辐射,阵列的后面可加反射板。为简化分析, 反射板可看作是一金属反射面,见图 3-7。反射面与阵列表面之间的距离为 d z , 约为中心频率对应波长 λ0 的四分之一,即 d z 像。
αx
kd x
)2 + (
αy
kd y
)2 < 1
(3.12)
当 kd x 和 kd y 给定时, α x 和 α y 将受上式限定。 由 cos ϕ 0 sin θ 0 =
S y (θ , ϕ ) =
N y −1 n =0
αx
kd x
, sin ϕ 0 sin θ 0 =
αy
kd y
和 S x (θ , ϕ ) =
(a) 二维极坐标图 (b) 三维方向图 图 3-4 矩形栅格矩形平面阵方向图
当 α x = α y = 0 时,则为侧射平面阵,其最大指向为 z 轴方向 θ 0 = 0 ; 当 α x = 0 , α y ≠ 0 且变化时,则平面阵波束将在 yz 平面内扫描; 当 α y = 0 , α x ≠ 0 且变化时,则平面阵波束将在 xz 平面内扫描; 当 α y ≠ 0 , α x ≠ 0 且两者均变化时,则平面阵波束将在空间任意方向变化。 在理想情况下,平面阵波束在某一平面(xz)内扫描的情况如下图 3-5 所示。 其中图(a)为侧射情况;图(b)和(c)为扫描情况;图(d)则为极端情况,此时平面阵 两个半空间的波束交叠在一起,形成端射方向图,这种情况在实际的相控阵中 是不可能实现的。一般相控阵能做到偏离侧向 ±60o 扫描已经很难得了,而图(d) 相当于 ±90o 扫描。 因为 sin 2 θ 0 ≤ 1 ,我们定义平面阵两个半空间的波束 S x 和 S y 重合的条件为 (
143
阵列天线分析与综合讲义
王建
图 3-1 几种典型平面阵形式
如果雷达采用单脉冲体制,且在俯仰和方位两个面内均要实现差方向图, 则要求平面阵列分为四个象限,如下图 3-2 所示。
图 3-2 划分为四个象限的矩形和圆形平面阵
对于矩形栅格排列的矩形平面阵,如果各单元的激励幅度按行和列是可分 离的(即对所有 m 和 n 均满足 I mn = I xm ⋅ I yn ),则平面阵的方向图就等于两个正交 的直线阵列方向图的乘积。因此,可把直线阵列的分析与综合的原理和方法直 接应用于这种平面阵。 对于圆形边界的圆形平面阵,不论采用哪种栅格排列,则可采用专用的圆 形口径综合方法来综合出口径分布。
式中,C 为与 mn 无关的单元因子,且用了关系 1/ Rmn ≈ 1/ r 。波程差为
ˆ ⋅ ρ mn = − ( xm cos ϕ + yn sin ϕ ) sin θ = − ( md x cos ϕ + nd y sin ϕ ) sin θ Rmn − r = − r
则第 mn 个单元的远区辐射场为
=C
e − jkr S (θ , ϕ ) r
式中阵因子为
S (θ , ϕ ) =
N x −1 N y −1 m =0 n =0
∑ ∑
I mn e
jk ( md x cos ϕ + nd y sin ϕ ) sin θ
(3.1)
− jnα y
如果平面阵按列的分布为 I xm = I xm e − jmα x ,按行的分布为 I yn = I yn e
阵列天线分析与综合讲义
王建
第三章
平面阵列的分析与综合 §3.1 引言
前面两章分别介绍了直线阵列的分析与综合问题,本章讨论平面阵列的分 析与综合问题。对于常用的矩形栅格排列的矩形平面阵列来说,可把直线阵列 的分析与综合方法直接应用于平面阵。但是对于某些情况,如圆形平面阵,三 角形栅格平面阵等,则要求采用专用于平面阵列的分析与综合方法。因此本章 既要介绍如何把直线阵列的基本原理和方法直接应用于平面阵列,也将介绍平 面阵列的专用分析与综合方法。 常见的平面阵有一些基本类型,我们以栅格形式和边界形式来讨论,见如 下图 3-1。 ■基本栅格形式:包括矩形栅格、三角形栅格、同心圆环和椭圆环栅格等。 ■基本边界形式:有矩形、六边形(矩形切角形成)、圆形、椭圆形等。 矩形栅格、三角形栅格构成的平面阵,其外观可以是矩形、六边形、圆形 等。 同心圆环栅格阵列一般是圆形平面阵列。 同心椭圆环栅格阵列一般是椭圆形平面阵列。
式中, cos θ x = cos ϕ sin θ , cos θ y = sin ϕ sin θ ,则式(3.4)和(3.5)可简写作 S x (u x ) =
N x −1 m =0
(3.6)
∑ I xme jmu
N y −1 n =0
x
(3.7)
S y (u y ) =
∑
I yn e
jnu y
(3.8) sin( N y u y / 2) sin( N x u x / 2) , S y (u y ) = sin(u x / 2) sin(u y / 2) (3.9)
(3.17)
,则 (3.2)
I mn = I xm ⋅ I yn = I xm I yn e
− j ( mα x + nα y )
式中, I xm 和 I yn 分别为沿 x 和 y 方向排列的直线阵列的幅度分布; α x 和 α y 分别 是沿 x 和 y 方向排列的直线阵列的均匀递变相位。对所有 m 和 n 满足式(3.2)的 单元电流分布我们称为可分离型分布。把它代入式(3.1)可得
S (θ , ϕ ) = S x (θ , ϕ ) ⋅ S y (θ , ϕ )
145
(3.3)
阵列天线分析与综合讲义
王建
式中,
S x (θ , ϕ ) =
S y (θ ,ϕ ) =
N x −1 m =0
பைடு நூலகம்
∑I
N y −1 n =0
xm
e jm ( kd x cosϕ sinθ −α x )
(3.4)
∑I
yn
e
jn ( kd y sin ϕ sin θ −α y )
(3.5)
式(3.3)说明,矩形栅格的矩形平面阵列,如果其馈电分布是可分离型的,则该平 面阵列的阵因子方向图就是沿 x 和 y 方向排列的直线阵列阵因子方向图的乘积。 这印证了方向图相乘原理。若取
⎧ux = kd x cos ϕ sin θ − α x = kd x cosθ x − α x ⎨ ⎩u y = kd y sin ϕ sin θ − α y = kd y cosθ y − α y
Nx = Ny = 4 dx = d y = λ / 2
N x = 8, N y = 4 d x = λ / 4, d y = λ / 2
αx = α y = 0
α x = π / 3, α y = 0
α x = π / 2, α y = 0
α x = kd x , α y = 0
图 3-5 平面阵波束在 xz 平面内扫描变化情况
146
(3.11)
阵列天线分析与综合讲义
王建
当给定间距 d x 和 d y ,给定均匀递变相位 α x 和 α y 和工作频率 f,则平面阵的 波束指向( θ 0 , ϕ 0 )就确定了。 对自由空间中的平面阵,其阵因子有两个波束,一个指向 z>0 的半空间;一 个指向 z<0 的半空间,如下图 3-4 所示。
Emn = CI mn e − jkr jk ( md x cos ϕ + nd y sin ϕ ) sin θ e r
N x −1 N y −1 m =0 n =0
整个平面阵列的远区辐射场为
ET = ∑∑ Emn
m n
e − jkr =C r
∑ ∑
I mn e
jk ( md x cos ϕ + nd y sin ϕ ) sin θ
S (θ , ϕ ) = S x (θ , ϕ ) ⋅ S y (θ , ϕ )
=
N x −1 m =0
∑ I xme
jmkd x (cos ϕ sin θ − cos ϕ 0 sin θ 0 )
⋅
N y −1 n =0
∑
I yn e
jnkd y (sin ϕ sin θ − sin ϕ 0 sin θ 0 )
N x −1 m =0
∑ I xme jm( kd cosϕ sinθ −α ) ,
x x
