实验三 香农编码
编码理论实验报告

一、实验目的1. 理解编码理论的基本概念和原理;2. 掌握哈夫曼编码和香农编码的方法;3. 熟悉编码效率的计算方法;4. 培养编程能力和实践操作能力。
二、实验原理1. 编码理论:编码理论是研究信息传输、存储和处理中信息压缩和编码的理论。
其目的是在保证信息传输质量的前提下,尽可能地减少传输或存储所需的数据量。
2. 哈夫曼编码:哈夫曼编码是一种根据字符出现频率进行编码的方法,字符出现频率高的用短码表示,频率低的用长码表示,从而达到压缩数据的目的。
3. 香农编码:香农编码是一种基于信息熵的编码方法,根据字符的概率分布进行编码,概率高的字符用短码表示,概率低的字符用长码表示。
4. 编码效率:编码效率是指编码后数据长度与原始数据长度的比值。
编码效率越高,表示压缩效果越好。
三、实验内容1. 使用MATLAB软件实现哈夫曼编码和香农编码;2. 对给定信源进行编码,并计算编码效率;3. 对比哈夫曼编码和香农编码的效率。
四、实验步骤1. 编写哈夫曼编码程序:首先,统计信源中各个字符的出现频率;然后,根据频率构造哈夫曼树;最后,根据哈夫曼树生成编码。
2. 编写香农编码程序:首先,计算信源熵;然后,根据熵值生成编码。
3. 编码实验:对给定的信源进行哈夫曼编码和香农编码,并计算编码效率。
4. 对比分析:对比哈夫曼编码和香农编码的效率,分析其优缺点。
五、实验结果与分析1. 哈夫曼编码实验结果:信源:'hello world'字符频率:'h' - 2, 'e' - 1, 'l' - 3, 'o' - 2, ' ' - 1, 'w' - 1, 'r' - 1, 'd' - 1哈夫曼编码结果:'h' - 0'e' - 10'l' - 110'o' - 1110' ' - 01'w' - 101'r' - 100'd' - 1001编码效率:1.52. 香农编码实验结果:信源:'hello world'字符频率:'h' - 2, 'e' - 1, 'l' - 3, 'o' - 2, ' ' - 1, 'w' - 1, 'r' - 1, 'd' - 1香农编码结果:'h' - 0'e' - 10'l' - 110'o' - 1110' ' - 01'w' - 101'r' - 100'd' - 1001编码效率:1.53. 对比分析:哈夫曼编码和香农编码的效率相同,均为1.5。
实验四_香农编码
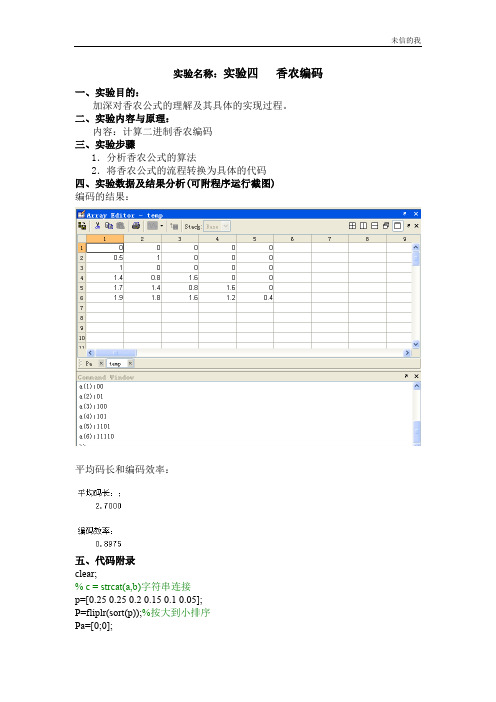
实验名称:实验四香农编码一、实验目的:加深对香农公式的理解及其具体的实现过程。
二、实验内容与原理:内容:计算二进制香农编码三、实验步骤1.分析香农公式的算法2.将香农公式的流程转换为具体的代码四、实验数据及结果分析(可附程序运行截图)编码的结果:平均码长和编码效率:五、代码附录clear;% c = strcat(a,b)字符串连接p=[0.25 0.25 0.2 0.15 0.1 0.05];P=fliplr(sort(p));%按大到小排序Pa=[0;0];%累加和的定义----第一行为累加和,第二行为Ki %求累加和for x=1for y=1:1:5%Pa(x,y)=1;Pa(x,y+1)=P(x,y)+ Pa(x,y);endend%ceil 是取向离它最近的大整数圆整for i=2for j=1:1:6Pa(i,j)=ceil( -log2(P(1,j)) );endend%信源熵H=0;L=0;for i=1:1:6H=H-P(i)*log2(P(i));L=L+P(i)*Pa(2,i);endu=H/L;disp('平均码长:;');disp(L);disp('编码效率:');disp(u);%求各符号的编码temp=[];%临时的编码值:1:6for m=1:1:6fprintf('a(%d):',m);for n=1:1:abs(Pa(2,m))temp(m,n)=Pa(1,m)*2;if temp(m,n)>=1O(m,n)=1;Pa(1,m)=temp(m,n)-1;elseO(m,n)=0;Pa(1,m)=temp(m,n);endfprintf('%d',O(m,n));endfprintf('\n');end六、其他:实验总结、心得体会及对本实验方法、手段及过程的改进建议等。
实验起初是想把累加和及Ki和编码放在一个二维矩阵中,但具体的实现较为复杂,所以最后改为逐行存放并成功完成了实验。
数字图像处理实验报告 (图像编码)

实验三图像编码一、实验内容:用Matlab语言、C语言或C++语言编制图像处理软件,对某幅图像进行时域和频域的编码压缩。
二、实验目的和意义:1. 掌握哈夫曼编码、香农-范诺编码、行程编码2.了解图像压缩国际标准三、实验原理与主要框架:3.1实验所用编程环境:Visual C++6.0(简称VC)3.2实验处理的对象:256色的BMP(BIT MAP )格式图像BMP(BIT MAP )位图的文件结构:(如图3.1)图3.1 位图的文件结构具体组成图:单色DIB 有2个表项16色DIB 有16个表项或更少 256色DIB 有256个表项或更少 真彩色DIB 没有调色板每个表项长度为4字节(32位) 像素按照每行每列的顺序排列每一行的字节数必须是4的整数倍biSize biWidth biHeight biPlanes biBitCount biCompression biSizeImagebiXPelsPerMeter biYPelsPerMeter biClrUsedbiClrImportantbfType=”BM ” bfSizebfReserved1 bfReserved2 bfOffBits BITMAPFILEHEADER位图文件头 (只用于BMP 文件)BITMAPINFOHEADER位图信息头Palette 调色板DIB Pixels DIB 图像数据3.3 数字图像基本概念数字图像是连续图像(,)f x y 的一种近似表示,通常用由采样点的值所组成的矩阵来表示:(0,0)(0,1)...(0,1)(1,0)(1,1)...(1,1).........(1,0)(1,1)...(1,1)f f f M f f f M f N f N f N M -⎡⎤⎢⎥-⎢⎥⎢⎥⎢⎥----⎣⎦每一个采样单元叫做一个像素(pixel ),上式(2.1)中,M 、N 分别为数字图像在横(行)、纵(列)方向上的像素总数。
信息论与编码实验2-实验报告

信息论与编码实验2-实验报告信息论与编码实验 2 实验报告一、实验目的本次信息论与编码实验 2 的主要目的是深入理解和应用信息论与编码的相关知识,通过实际操作和数据分析,进一步掌握信源编码和信道编码的原理及方法,提高对信息传输效率和可靠性的认识。
二、实验原理(一)信源编码信源编码的目的是减少信源输出符号序列中的冗余度,提高符号的平均信息量。
常见的信源编码方法有香农编码、哈夫曼编码等。
香农编码的基本思想是根据符号出现的概率来分配码字长度,概率越大,码字越短。
哈夫曼编码则通过构建一棵最优二叉树,为出现概率较高的符号分配较短的编码,从而实现平均码长的最小化。
(二)信道编码信道编码用于增加信息传输的可靠性,通过在发送的信息中添加冗余信息,使得在接收端能够检测和纠正传输过程中产生的错误。
常见的信道编码有线性分组码,如汉明码等。
三、实验内容与步骤(一)信源编码实验1、选取一组具有不同概率分布的信源符号,例如:A(02)、B (03)、C(01)、D(04)。
2、分别使用香农编码和哈夫曼编码对信源符号进行编码。
3、计算两种编码方法的平均码长,并与信源熵进行比较。
(二)信道编码实验1、选择一种线性分组码,如(7,4)汉明码。
2、生成一组随机的信息位。
3、对信息位进行编码,得到编码后的码字。
4、在码字中引入随机错误。
5、进行错误检测和纠正,并计算错误纠正的成功率。
四、实验结果与分析(一)信源编码结果1、香农编码的码字为:A(010)、B(001)、C(100)、D (000)。
平均码长为 22 比特,信源熵约为 184 比特,平均码长略大于信源熵。
2、哈夫曼编码的码字为:A(10)、B(01)、C(111)、D (00)。
平均码长为 19 比特,更接近信源熵,编码效率更高。
(二)信道编码结果在引入一定数量的错误后,(7,4)汉明码能够成功检测并纠正大部分错误,错误纠正成功率较高,表明其在提高信息传输可靠性方面具有较好的性能。
实验四-香农编码

海南大学信息科学技术学院信息安全专业《信息论与编码》实验报告一、 实验目的:了解掌握香农编码二、 实验环境:CodeBlocks三、 实验要求编程,对某一离散无记忆信源实现香农编码,输出消息符号及其对应的码字。
设离散无记忆信源⎭⎬⎫⎩⎨⎧=⎪⎪⎭⎫ ⎝⎛01.010.015.017.018.019.020.0)(7654321a a a a a a a X p X ,∑==ni ia p 11)(。
二进制香农编码过程如下: 1、将信源发出的N 个消息符号按其概率的递减次序依次排列。
2、按下式计算第i 个消息的二进制代码组的码长,并取整。
3、为了编成唯一可译码,首先计算第i 个消息的累加概率4、将累加概率Pi (为小数)变成二进制数5、除去小数点,并根据码长li ,取小数点后li 位数作为第i 个消息的码字。
四、 实验过程:代码:#include<stdio.h>#include<math.h>void main(){int i,n, j,k;float sum=0;float p[100]={0}; //无记忆信源X 的概率分布float m;float Pa[100]={0}; //累加概率的数组int l[100];char c[100][100];printf("请输入信源X的个数:");scanf("%d",&n);printf("请输入p[X]的概率分布\n");for(i=0;i<n;i++)scanf("%f",&p[i]);for(i=0;i<=n;i++) //判断概率和为1sum=sum+p[i];while(sum!=1){printf("错误输入,请重输\n");printf("请输入x的个数\n");scanf("%d",&n);printf("\n");printf("请输入p[i]的概率分布\n");for(i=0;i<n;i++)scanf("%f",&p[i]);for(i=0;i<n;i++)sum=sum+p[i];}for(j=0;j<n-1;j++) //将概率按从大到小排序 for(i=0;i<n-1-j;i++)if(p[i]<p[i+1]){m=p[i];p[i]=p[i+1];p[i+1]=m;}printf("p[i]由大到小的顺序为\n:");for(i=0;i<n;i++)printf("%5.2f",p[i]);printf("\n");Pa[0]=0;for(j=1;j<n+1;j++) //计算累加概率{Pa[j]=Pa[j-1]+p[j-1];}printf("累加和Pi为:");for(j=0;j<n;j++)printf("%5.2f",Pa[j]);printf("\n");printf("码长:");for(i=0;i<n;i++) //计算码长{m=log(1/p[i])/log(2);if(m==(int)m)l[i]=(int)m;elsel[i]=(int)(m+1);}for(i=0;i<n;i++)printf(" %d ",l[i]);printf("\n");for(i=0;i<n;i++) //将累加概率转换成二进制数{for(k=0;k<l[i];k++){Pa[i]=Pa[i]*2;if(Pa[i]>=1){Pa[i]=Pa[i]-1;c[i][k]='1';}else{c[i][k]='0';}}}for(i=0;i<n;i++){for(k=0;k<l[i];k++)printf("%c",c[i][k]);printf("\n");}}五、实验结果:。
《信息论与编码技术》实验教案

技术选型
根据实际需求选择合适的差错控制编码技术, 包括线性分组码、卷积码等。
实现与测试
通过编程实现所选差错控制编码技术的编码和解码过程,并进行测试和性能分 析。
04
现代编码技术实验
Turbo码编译码原理及性能评估
Turbo码基本原理
介绍Turbo码的结构、编码原理、迭代译码原理等基本概念。
编译码算法实现
《信息论与编码技术》实验教案
目录
• 课程介绍与实验目标 • 信息论基础实验 • 编码技术基础实验 • 现代编码技术实验 • 信息论与编码技术应用案例分析 • 课程总结与展望
01
课程介绍与实验目标
信息论与编码技术课程概述
课程背景
信息论与编码技术是通信工程、 电子工程等专业的核心课程,主 要研究信息的传输、存储和处理 过程中的基本理论和方法。
2. 根据概率分布生成模拟信源序列;
03
离散信源及其数学模型
3. 计算信源熵、平均符号长度等参数;
4. 分析实验结果,理解信源熵的物理 意义。
信道容量与编码定理验证
实验目的
理解信道容量的概念、计算方法和物理意义,验证香农编码定理的正确性。
实验内容
设计并实现一个信道模拟器,通过输入不同的信道参数和编码方案,计算并输出信道容量、误码率等关键参数。
数据存储系统中纠删码技术应用
纠删码基本原理
阐述纠删码的基本概念、原理及其在数据存储系统中的应用价值。
常用纠删码技术
介绍常用的纠删码技术,如Reed-Solomon码、LDPC码等,并分 析其性能特点。
纠删码技术应用实践
通过实验,将纠删码技术应用于数据存储系统中,评估其对系统可 靠性、数据恢复能力等方面的提升效果。
信息论实验报告香农编码

目录实验目的: (2)实验要求: (2)程序算法: (2)程序运行结果: (4)程序操作步骤: (5)试验中遇到的困难及解决方法: (5)实验心得及体会: (5)实验目的:1.进一步熟悉使用C++编程语言及软件。
2.进一步认识shannon编码过程,并能在学习中灵活运用。
实验要求:要求:(a) 允许使用的编程语言:C、C++、Basic、Pascal、Fortran、Java、Perl、Tk/Tcl(b) 输入:信源符号个数q、信源符号s0,...,sq−1,信源概率分布p0,...,pq−1。
(c) 输出:信源符号与码字的对应关系表(编码表)。
(d) 源程序格式整齐清晰,注释简单明了。
程序算法:(a) 将q 个信源符号按其概率的递减次序排列:p(s0) > p(s1) > ... > p(sq−1)(b) 计算出各个信源符号的累加概率:(c) 按下式计算第i 个消息的二元代码组的码长li:(d) 将累加概率F(si)(十进制小数)变换成二进制小数。
根据码长li 取小数点后li 个二进制符号作为第i 个消息的码字。
程序代码:#include <iostream>#include <math.h>using namespace std;void InsertSort(double r[],char m[] ,int n)//直接插入排序算法按照概率从大到小排列符号和相应概率{for(int i=1;i<n;i++){r[n]=r[i]; //设置哨兵m[n]=m[i]; //设置哨兵for(int j=i-1;(r[n]>r[j])&&(j>=0);j--)//寻找插入位置{r[j+1]=r[j];//记录后移m[j+1]=m[j];//记录后移}r[j+1]=r[n];m[j+1]=m[n];}}void Leijia(double p[], int s)//将当前概率及之前概率相加{for(int r=1;r<s;r++)p[r]=p[r-1]+p[r];}void main(){int geshu,erjinzhi[100][100];int z=0,g=0;double gailv[100],L[100];char fuhao[100];cout<<"请输入需要编码的字符个数(小于100)"<<endl; cin>>geshu;cout<<"请按照先后顺序输入符号"<<endl;for(int i=0;i<geshu;i++)cin>>fuhao[i];cout<<"请输入各相应符号的概率"<<endl;for(int j=0;j<geshu;j++)cin>>gailv[j];InsertSort( gailv,fuhao, geshu);for(z=0;z<geshu;z++){L[z]=-log(gailv[z])/log(2);L[z]=ceil(L[z]);//向上取整求所需要的位数}Leijia( gailv, geshu);for( z=0;z<geshu;z++)//求相应的二进制编码{gailv[z]=gailv[z]-floor(gailv[z]);for( g=0;g<L[z];g++){if((gailv[z]*2)>=1){erjinzhi[z][g]=1;gailv[z]=(gailv[z]*2)-1;}else{erjinzhi[z][g]=0;gailv[z]=gailv[z]*2;}}}cout<<"各信源符号及相应码字分别为"<<endl; for(z=0;z<geshu;z++){cout<<fuhao[z]<<'\t';for( g=0;g<L[z];g++)cout<< erjinzhi[z][g];cout<<endl;}}程序运行结果:程序操作步骤:1.按照提示输入所要编码的符号个数并回车2.按顺序输入要求个数的符号并回车3.按顺序输入各符号相应的概率并回车4.即可得到各符号相应的shannon编码试验中遇到的困难及解决方法:本次试验相对而言比较简单,但由于长时间没有联系C++语言有些生疏。
信源熵的计算

桂林电子科技大学数学与计算科学学院实验报告 实验室: 实验日期: 2010年 11月 11日院(系) 数学与计算科学学院 年级、专业、班 0800710310 姓名 何帅 成绩课程名称 信息与编码 实验项目名 称 信源熵的计算 指导教师一 实验目的1、掌握香农编码的原理2、掌握二进制小数的输出方法二 实验内容与步骤Shannon 码编码步骤为:1、将信源S 的所有符号按概率从大到小排列:12q P P P ≥≥≥ 2、对第i 个信源符号i s 取整数码长[]1log 1,i i l P ⎡⎤=+⎢⎥⎣⎦为取整运算 3、计算累加概率111,0,(2)i i i k k R R R P i -===≥∑ 4、将i R 变换成二进制数12j i j j R x ∞-==∑,并按步骤2中计算的长度i l 取i R 的二进制系数j x ,组合起来即为i s的香农码字i W 程序:#include<stdio.h>#include<iostream.h>#include<math.h>double P[6]={0.25,0.1,0.2,0.25,0.15,0.05},Pax[6],machang[6];void main(){double temp;for(int a=1;a<6;a++){for(int i=0;i<6-a;i++)if(P[i]<P[i+1]){temp=P[i];P[i]=P[i+1];P[i+1]=temp;}}for(int i=0;i<6;i++)cout<<P[i]<<" ";cout<<endl;for(i=0;i<6;i++){Pax[0]=0.0;Pax[i+1]=Pax[i]+P[i];}cout<<"概率累加和为:"<<endl;for(i=0;i<6;i++)cout<<Pax[i]<<" ";cout<<endl;for(i=0;i<6;i++){double m=log(1/P[i]/log(2));if(m-int(m)==0)machang[i]=log(1/P[i])/log(2);elsemachang[i]=int(m)+1;cout<<P[i]<<"的码长为:"<<machang[i]<<endl;}for(i=0;i<6;i++){for(int j=0;j<machang[i];j++){int n=int(Pax[i]*2);cout<<n;if((Pax[i]*2-1)>0){Pax[i]=Pax[i]*2-1;continue;}if((Pax[i]*2-1)==0)Pax[i]=Pax[i]*2-1;elsePax[i]=Pax[i]*2;}cout<<endl;}}运行结果:三实验体会心得通过本次实验学习了求香农编码的基本步骤,同时学习了如何在C++下实现,在编程中主要是注意求二进制数是通过乘2取整得到的。
实验二 Shannon编码

实验二Shannon编码一、实验目的及要求a)实验目的1.通过本实验实现信源编码——Shannon编码2.编写M文件实现,掌握Shannon编码方法b)实验要求1.了解Matlab中M文件的编辑、调试过程2.编写程序实现Shannon编码算法二、实验步骤及运行结果记录a)实验步骤1.输入Shannon编码程序2.运行程序,按照提示输入相应信息,并记录输入信息,及运行结果。
3.思考:在程序中加入排序子程序,使其在输入信源概率时,不要求输入顺序。
b)实验结果y =0.2000 0 2.3219 3.00000.1900 0.2000 2.3959 3.00000.1800 0.3900 2.4739 3.00000.1700 0.5700 2.5564 3.00000.1500 0.7400 2.7370 3.00000.1000 0.8900 3.3219 4.00000.0100 0.9900 6.6439 7.0000code =000;code = 001;code = 011;code =100;code = 101;code =1110;code =1111110三、实验流程图(附一)四、程序清单,并注释每条语句(附二)五、实验小结香农编码是码符号概率大的用短码表示,概率小的是用长码表示,程序中对概率排序,最后求得的码字就依次与排序后的符号概率对应。
此程序缺点是,第一个码字都是以0开始,因为对累加概率求二进制后,小数点后的数都是0,取几位由码长确定,而香农编码是不唯一的,如果手动编码就不存在这样的问题。
后面求得的编码没有下标就需要注意是与上面排序后的信源符号对应。
附一附二N=input('请输入信源符号个数:')%输入信源符号个数p=zeros(1,N);%生成1*4的零矩阵for i=1:Np(1,i)=input('请输入各信源符号出现的概率:')%输入各个信源符号的概率endp=fliplr(sort(p));%将概率从大到小进行排序if abs(sum(p)-1)>10e-10error('输入概率不符合概率分布')%检验所输入的概率是否正确endy=zeros(N,4);%生成N*4零矩阵for i=1:Ny(i,1)=p(1,i);%将各个符号出现的概率放入y矩阵的第一列中y(1,2)=0;if i>1y(i,2)=y(i-1,2)+y(i-1,1); %第二列其余的元素用此式求得,即为累加概率endy(i,3)=log2(1./p(i))%求各个信源符号的信息熵放入y矩阵的第三列中y(i,4)=ceil(y(i,3))%求码长endA=y(:,2);%取出y中的第二列元素B=y(:,4);%取出y中的第四列元素for i=1:Ncode=shannoncode(A(i),B(i))%生成码字endfunction [C]=shannoncode(A,B)%对累加概率求二进制的函数C=zeros(1,B);%生成零矩阵用于存储生成的二进制数,对二进制的每一位进行操作temp=A;%temp赋初值for i=1:B%累加概率转化为二进制,循环求二进制的每一位,A控制生成二进制的位数 temp=temp*2;if temp>1temp=temp-1;C(1,i)=1;elseC(1,i)=0;endendend。
信息论与编码实验报告

信息论与编码实验报告一、实验目的信息论与编码是一门涉及信息的度量、传输和处理的学科,通过实验,旨在深入理解信息论的基本概念和编码原理,掌握常见的编码方法及其性能评估,提高对信息处理和通信系统的分析与设计能力。
二、实验原理(一)信息论基础信息熵是信息论中用于度量信息量的重要概念。
对于一个离散随机变量 X,其概率分布为 P(X) ={p(x1), p(x2),, p(xn)},则信息熵H(X) 的定义为:H(X) =∑p(xi)log2(p(xi))。
(二)编码原理1、无失真信源编码:通过去除信源中的冗余信息,实现用尽可能少的比特数来表示信源符号,常见的方法有香农编码、哈夫曼编码等。
2、有噪信道编码:为了提高信息在有噪声信道中传输的可靠性,通过添加冗余信息进行纠错编码,如线性分组码、卷积码等。
三、实验内容及步骤(一)信息熵的计算1、生成一个离散信源,例如信源符号集为{A, B, C, D},对应的概率分布为{02, 03, 01, 04}。
2、根据信息熵的定义,使用编程语言计算该信源的信息熵。
(二)香农编码1、按照香农编码的步骤,首先计算信源符号的概率,并根据概率计算每个符号的编码长度。
2、确定编码值,生成香农编码表。
(三)哈夫曼编码1、构建哈夫曼树,根据信源符号的概率确定树的结构。
2、为每个信源符号分配编码,生成哈夫曼编码表。
(四)线性分组码1、选择一种线性分组码,如(7, 4)汉明码。
2、生成编码矩阵,对输入信息进行编码。
3、在接收端进行纠错译码。
四、实验结果与分析(一)信息熵计算结果对于上述生成的离散信源,计算得到的信息熵约为 184 比特/符号。
这表明该信源存在一定的不确定性,需要一定的信息量来准确描述。
(二)香农编码结果香农编码表如下:|信源符号|概率|编码长度|编码值|||||||A|02|232|00||B|03|174|10||C|01|332|110||D|04|132|111|香农编码的平均码长较长,编码效率相对较低。
信息论课程实验报告—Shannon编码

: 六、实验器材(设备、元器件) 实验器材(设备、元器件)
PC 机一台,装有 VC++6.0 或其它 C 语言集成开发环境。
七、实验步骤及操作: 实验步骤及操作:
1)排序; 2)计算码长; 3)递归调用香农算法得到相应的码字。
八、实验数据及结果分析: 实验数据及结果分析:
s 2 s3 s4 s5 s6 s 7 s8 S s1 题目:已知信源: = ,给出其一个 P 0.20, 0.18, 0.17, 0.15, 0.15, 0.05, 0.05, 0.05 香农码,并求其平均码长和编码效率。
else k[i]=temp+1; } } void code(int *k,double *pa,string *str,int n) { for(int i=0;i<n;i++) { double s=pa[i]; for(int j=0;j<k[i];j++) { s=2*s; if(s>=1) { str[i]+="1"; s=s-1; } else str[i]+="0"; } } } void main() { int n; cout<<"信源符号个数 n= "; cin>>n; double *p=new double[n]; cout<<"信源符号的概率依次为(以回车表示概率的结束): "; for(int i=0;i<n;i++) { cin>>p[i]; } bubble(p,n); double *pa=new double[n]; leijia(p,pa,n); int *k=new int[n]; length(p,k,n); string *str=new string[n]; code(k,pa,str,n); cout<<setw(10)<<"pa(i)"<<setw(10)<<"Pa(a,j)"<<setw(10)<<"Ki"<<setw(10)<<"码字"<<endl; for(i=0;i<n;i++) { cout<<setw(10)<<p[i]<<setw(10)<<pa[i]<<setw(10)<<k[i]<<setw(10)<<str[i]<<endl; } }
香农编码

cin>>p[i];
}
排序函数:void sort(double p[])
{
double t;
for (int i=0;i<f;i++)
{
for(int j=f-1;j>i;j--)
{
if (p[j]>p[j-1])
{t=p[j];p[j]=p[j-1];p[j-1]=t;}
{
x=pp[i];
for(int m=1;m<l[i]+1;m++)
{
x=x*2.0;
if(x>=1.0){c[j]=1;x=x-1.0;}
else{c[j]=0;}
j++;
}
}
}
输出函数:
void output(int l[],int c[],double p[],double pp[])
{
int m=0;
cout<<endl;
m=m+j;
}}
求解结果:
例5.1.2的求解结果
五、总结
一上机才发现,自己C和C++又该复习了,主要是很多语法怎么使用都记不太清楚了,但是以前通过复习的资料,自己还是很快很够把握一些基本的知识了,所以编写程序不是特别的难了,对于香农编码而言,主要是弄清楚各个步骤,像求码长、累加和、概率排序,每个模块建立一个函数,使得程序简单易读,自己的思路也更清晰明了。编码的原理我们都很清楚,主要就是在一些C和C++基本知识上的巩固才能做好这次的实验。
二进制香农编码的步骤如下:(1)、将信源符号按概率从大到小的顺序排列(2)、对第j个前的概率进行累加得到pa(aj)(3)、由-logp(ai) ki<1-logp(ai)求得码字长度ki (4)、将pa(aj)用二进制表示,并取小数点后ki位作为符号ai的编码。
信息论与编码实验指导书

没实验一 绘制二进熵函数曲线(2个学时)一、实验目的:1. 掌握Excel 的数据填充、公式运算和图表制作2. 掌握Matlab 绘图函数3. 掌握、理解熵函数表达式及其性质 二、实验要求:1. 提前预习实验,认真阅读实验原理以及相应的参考书。
2. 在实验报告中给出二进制熵函数曲线图 三、实验原理:1. Excel 的图表功能2. 信源熵的概念及性质()()[]()[]())(1)(1 .log )( .)( 1log 1log )(log )()(10 , 110)(21Q H P H Q P H b nX H a p H p p p p x p x p X H p p p x x X P X ii i λλλλ-+≥-+≤=--+-=-=≤≤⎩⎨⎧⎭⎬⎫-===⎥⎦⎤⎢⎣⎡∑四、实验内容:用Excel 或Matlab 软件制作二进熵函数曲线。
具体步骤如下:1、启动Excel 应用程序。
2、准备一组数据p 。
在Excel 的一个工作表的A 列(或其它列)输入一组p ,取步长为0.01,从0至100产生101个p (利用Excel 填充功能)。
3、取定对数底c ,在B 列计算H(x) ,注意对p=0与p=1两处,在B 列对应位置直接输入0。
Excel 中提供了三种对数函数LN(x),LOG10(x)和LOG(x,c),其中LN(x)是求自然对数,LOG10(x)是求以10为底的对数,LOG(x,c)表示求对数。
选用c=2,则应用函数LOG(x,2)。
在单元格B2中输入公式:=-A2*LOG(A2,2)-(1-A2)*LOG(1-A2,2) 双击B2的填充柄,即可完成H(p)的计算。
4、使用Excel 的图表向导,图表类型选“XY 散点图”,子图表类型选“无数据点平滑散点图”,数据区域用计算出的H(p)数据所在列范围,即$B$1:$B$101。
在“系列”中输入X值(即p值)范围,即$A$1:$A$101。
香农三大定理[宝典]
![香农三大定理[宝典]](https://img.taocdn.com/s3/m/71be0b29b80d6c85ec3a87c24028915f804d8499.png)
香农三大定理首先我们要知道香农三大定理,这样有助于我们理解香农极限。
香农第一定理(可变长无失真信源编码定理)设信源S的熵H(S),无噪离散信道的信道容量为C,于是,信源的输出可以进行这样的编码,使得信道上传输的平均速率为每秒(C/H(S)-a)个信源符号.其中a可以是任意小的正数, 要使传输的平均速率大于(C/H(S))是不可能的。
于是,C/H(S)便是可变长无失真信源编码的香农极限。
香农第二定理(有噪信道编码定理)设某信道有r个输入符号,s个输出符号,信道容量为C,当信道的信息传输率R码长N足够长,总可以在输入的集合中(含有r^N个长度为N 的码符号序列),找到M (M<=2^(N(C-a))),a为任意小的正数)个码字,分别代表M个等可能性的消息,组成一个码以及相应的译码规则,使信道输出端的最小平均错误译码概率Pmin达到任意小,此时的信道容量即为信道的香农极限。
香农第三定理(保失真度准则下的有失真信源编码定理)设R(D)为一离散无记忆信源的信息率失真函数,并且选定有限的失真函数,对于任意允许平均失真度D>=0,和任意小的a>0,以及任意足够长的码长N,则一定存在一种信源编码W,其码字个数为M<=EXP{N[R(D)+a]},而编码后码的平均失真度D'(W)<=D+a。
D'(W)即为平均失真度的香农极限。
总而言之,香农极限是在香农三大定理的极值,也就是其极限情况。
2001年2月24日,当代最伟大的数学家和贝尔实验室最杰出的科学家之一,84岁的香农(Claude Elwood Shannon)博士不幸去世。
香农1916年生于美国,1940年获得麻省理工学院数学博士学位和电子工程硕士学位。
1941年他加入了贝尔实验室数学部,在此工作了15年。
1948年6月和10月,由贝尔实验室出版的《贝尔系统技术》杂志连载了香农博士的文章《通讯的数学原理》,该文奠定了香农信息基本理论的基础。
信息论实验报告(实验三、香农编码)
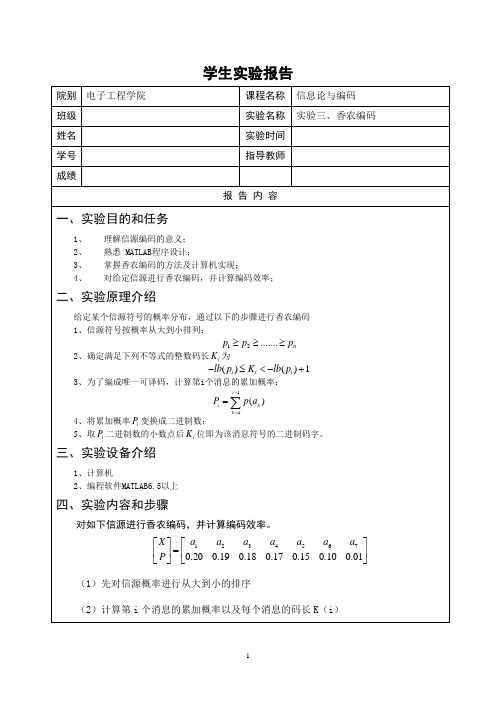
学生实验报告 院别 电子工程学院课程名称 信息论与编码 班级实验名称 实验三、香农编码 姓名实验时间 学号指导教师 成绩报 告 内 容 一、实验目的和任务1、理解信源编码的意义; 2、熟悉 MATLAB 程序设计; 3、掌握香农编码的方法及计算机实现; 4、 对给定信源进行香农编码,并计算编码效率;二、实验原理介绍给定某个信源符号的概率分布,通过以下的步骤进行香农编码1、信源符号按概率从大到小排列;12.......n p p p ≥≥≥2、确定满足下列不等式的整数码长i K 为()()1i i i lb p K lb p -≤<-+3、为了编成唯一可译码,计算第i 个消息的累加概率:4、将累加概率i P 变换成二进制数;5、取i P 二进制数的小数点后i K 位即为该消息符号的二进制码字。
三、实验设备介绍1、计算机2、编程软件MATLAB6.5以上四、实验内容和步骤对如下信源进行香农编码,并计算编码效率。
12345670.200.190.180.170.150.100.01X a a a a a a a P ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦(1)先对信源概率进行从大到小的排序(2)计算第i 个消息的累加概率以及每个消息的码长K (i )11()i i k k P p a -==∑(3)调用子函数将累加概率的十进制表示转换成二进制(4)取第i个累加概率二进制的小数点后的K(i)位,即为该消息符号的二进制码字。
五、实验数据记录六、实验结论与心得通过本次实验,加强了对matlab程序的学习,进一步提高了我的编程能力。
信源编码实验

实验2 信源编码实验一、实验目的● 掌握香农、霍夫曼编码的方法和手段。
● 通过信源编译码,理解香农第一定理。
二、实验原理 设离散无记忆信源12112,,,,,,()1(),(),,(),,()()=⎧⎫⎡⎤==⎨⎬⎢⎥⎣⎦⎩⎭∑ni n ii i n x x x x X p x p x p x p x p x P X二进制香农码的编码步骤如下:⏹ 将信源符号按概率从大到小的顺序排列,为方便起见,令 p (x 1)≥ p (x 2)≥…≥ p (x n )⏹ 令p (x 0)=0,用p a (x j ),j =i +1表示第i 个码字的累加概率,则:10()(),1,2,,-===∑j a j i i p x p x j n⏹ 确定满足下列不等式的整数k i ,并令k i 为第i 个码字的长度 -log 2 p (x n )≤k i <- log 2 p (x n )+1⏹ 将p a (x j ) 用二进制表示,并取小数点后k i 位作为符号x i 的编码。
霍夫曼编码步骤如下:⏹ 将信源符号按概率从大到小的顺序排列,令p (x 1)≥ p (x 2)≥…≥ p (x n )⏹ 给两个概率最小的信源符号p (x n -1)和p (x n )各分配一个码位“0”和“1”,将这两个信源符号合并成一个新符号,并用这两个最小的概率之和作为新符号的概率,结果得到一个只包含(n -1)个信源符号的新信源。
称为信源的第一次缩减信源,用S 1表示。
⏹ 将缩减信源S 1的符号仍按概率从大到小顺序排列,重复步骤2,得到只含(n -2)个符号的缩减信源S 2。
⏹ 重复上述步骤,直至缩减信源只剩两个符号为止,此时所剩两个符号的概率之和必为1。
然后从最后一级缩减信源开始,依编码路径向前返回,就得到各信源符号所对应的码字。
三、实验内容1、有一单符号离散无记忆信源123456,,,,,()0.250.250.200.150.100.05⎡⎤⎧⎫=⎨⎬⎢⎥⎣⎦⎩⎭X x x x x x x P X对该信源编二进制香农码。
香农编码实验报告

仙农编码实验报告一、实验目的实验仙农编码算法二、实验步骤1、输入信源个数n2、输入n个信源的概率3、由大到小重新排列信源4、实现信源概率的叠加5、计算码长l6、编码7、计算平均码长pl、信源熵Hx以及编码效率q三、源程序:#include<iostream>#include<math.h>#include<string>using namespace std;void input(int n,float *g){//输入信源概率for(int i=0;i<n;i++){cout<<"请输入第"<<i+1<<"个信源的概率: ";cin>>g[i];}}void rank(int n,float *g){//重新排列float templ;for(int i=0;i<n;i++){for(int j=i+1;j<n;j++){if(g[i]<g[j]){templ=g[i];g[i]=g[j];g[j]=templ;}}}}void output(int n,float *g){cout<<endl;cout<<"**********从大到小重新排列后的信源**********";cout<<endl;for(int i=0;i<n;i++){cout<<"第"<<i+1<<"个信源的概率是:"<<g[i]<<endl;}cout<<endl;}void add(int n,float *g,float *a){ //a[i]为累加概率的数组cout<<"**********累加概率***********"<<endl;a[0]=0.00; //令累加概率的第一个值为0for(int i=1;i<n;i++){a[i]=a[i-1]+g[i-1];}for(i=0;i<n;i++){cout<<"第"<<i+1<<"个累加概率为"<<a[i]<<endl;}}void length(int n,float *g,int *k){//求码字的长度k[i] cout<<endl;cout<<"**********计算码长**********"<<endl;for(int i=0;i<n;i++){for(int j=0;j<10;j++){if(j<1-log(g[i])/log(2) && j>=-log(g[i])/log(2) )k[i]=j;}float l=-log(g[i])/log(2);int temp=int(l);if(l-temp==0) k[i]=temp;else k[i]=temp+1;cout<<"第"<<i+1<<"个信源的码长为:"<<k[i]<<endl;}}void XN_Code(int n,float *a,int *k,string *Str){//编码cout<<endl;cout<<"**********编码**********"<<endl;for(int i=0;i<n;i++){float s=a[i];for(int j=0;j<k[i];j++){ //k[i]为码长s=s*2;if(s>=1){Str[i]+="1";s=s-1;}elseStr[i]+="0";}}for(i=0;i<n;i++){cout<<"第"<<i+1<<"个信源的码字为:"<<Str[i]<<endl;}}void main(){int n,k[10];float p[10],pa[10],pl=0,Hx=0,q;//pl为平均码长string Str[10];cout<<"请输入信源的个数:(小于等于10)"<<endl;cin>>n;input(n,p); //输入信源的概率rank(n,p); //从小到大重新排列输入的概率output(n,p); //输出重新排列的概率add(n,p,pa); //累加概率length(n,p,k);//求码长XN_Code(n,pa,k,Str);//编码for(int i=0;i<n;i++){ //求平均码长pl+=p[i]*k[i];Hx=Hx-p[i]*(log(p[i])/log(2));}q=Hx/pl*100;cout<<"平均码长为:"<<pl<<"比特/符号"<<endl;cout<<"该信源的信源熵为:"<<Hx<<"比特/符号"<<endl;cout<<"编码效率为:"<<q<<"%"<<endl;}四、运行结果:。
实验2-编码相关实验实验报告

信息论与编码实验二实验报告学生姓名周群创指导教师张祖平学号0909110814专业班级电子信息1101一、实验目的1.掌握香农码和Huffman 编码原理和过程。
2.熟悉 matlab 软件的基本操作,练习使用matlab 实现香农码和Huffman 编码。
3.熟悉 C/C++语言,练习使用C/C++实现香农码和Huffman 编码。
4.应用 Huffman 编码实现文件的压缩和解压缩。
二、 实验原理香农编码:香农第一定理指出了平均码长与信源之间的关系,同时也指出了可以通过编码使平均码长达到极限值,这是一个很重要的极限定理。
如何构造这种码?香农第一定理指出,选择每个码字的长度K i 满足下式I(x i )≤K ﹤I(x i )+1, i就可以得到这种码。
这种编码方法就是香农编码。
香农第一定理:设离散无记忆信源为[SP ]=[s1 s2 ....][.........sq p(s1) p(s2) .....p(sq) ]熵为H(S ),其N 次扩展信源为熵为H(SN)。
码符号集X=(x1,x2,…,xr )。
先对信源S N 进行编码,总可以 找到一种编码方法,构成惟一可以码,使S 中每个信源符号所需的平均码长满足:当N→∞时L 是平均码长λ是ai对应的码字长度哈夫曼编码:要完成哈夫曼的编码和解码需要首先建立哈夫曼树,之后对所有字符根据权重进行编码,最后再对文件内容进行编码和解码。
首先定义适合哈夫曼树的节点类型,需要定义的有当前节点的字符,当前节点的左子、右子和父亲指针。
在建立哈夫曼树之前还需要对出现的字符和权重进行统计和记录,并且定义一个可以筛选出最小权重的函数。
初始化树节点之后开始建立哈夫曼树。
先在所有可能出现的字符中筛选出当前权重最小的两个字符,将这两个字符分别作为新节点的左子和右子建立一个小的二叉树,并将两个字符的权重之和赋值给新节点,将新二叉树放入筛选字符中,再将筛选过的两个字符从筛选列表中淘汰掉。
信息论与编码-曹雪虹-课后习题答案 (2)

《信息论与编码》-曹雪虹-课后习题答案第二章2.1一个马尔可夫信源有3个符号{}1,23,u u u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
解:状态图如下状态转移矩阵为:1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩2.2 由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p =0.8,(0|11)p =0.2,(1|00)p =0.2,(1|11)p =0.8,(0|01)p =0.5,(0|10)p =0.5,(1|01)p =0.5,(1|10)p =0.5。
画出状态图,并计算各状态的稳态概率。
解:(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p ==(0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p ==(1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p ==于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭状态图为:设各状态00,01,10,11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.3 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求:(1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;(3) 两个点数的各种组合(无序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三 香农编码
一、[实验目的] 1、理解香农第一定理指出平均码长与信源之间的关系; 2、加深理解香农编码具有的重要的理论意义。
二、[实验环境] windows XP,MATLAB 7 三、[实验原理] 香农第一定理: 设离散无记忆信源为 ⎡ S ⎤ ⎡ s1 ⎢ P ⎥ = ⎢ p (s1) ⎣ ⎦ ⎣ 熵为 H(S),其 N 次扩展信源为
bin(i4,i5)='0'; else bin(i4,i5)='1'; end end end end shangnon=char(bin) %计算平均码长 for l=1:7 L=sum(L.*S); end L %计算编码效率 HS=sum(-S.*log2(S)); xiaolv=HS/L
H (S) 1 LN H (S) + > ≥ logr N N logr
当 N→ ∞时 lim
N →∞
LN = H r (S ) N
qN
LN 是平均码长
四、[实验内容]
LN = ∑ p(α i )λi
i =1
λi 是 αi 对应的码字长度
根据实验原理,设计 shannon 编码方法,在给定
S P
=
s1 0.2
s2 s3 s4 0.19 0.18 0.17
s5 s6 s7 0.15 0.10 0.01
条件下,实现香农编码并算出编码效率。
五、[实验过程]
每个实验项目包括: 1) 设计思路
1.将消息符号概率降序排列 2.计算累加概率 3.计算码长,取整 4.去除小数点,将累加概率变换成二进制数 5.取小数点后k位数作为代码组 6、实验代码:
s 2 ..... sq ⎤ p (s 2) .... p (sq )⎥ ⎦
⎡ S N ⎤ ⎡ α1 ⎢ ⎥=⎢ ⎣ P ⎦ ⎣ p(α1)
N
α 2 ..... α q ⎤ p(α 2) .... p (α q )⎥ ⎦
熵为 H(S )。码符号集 X=(,x2,…,xr) 。先对信源 S N 进行编码,总可以 找到一种编码方法, 构成惟一可以码, 使 S 中每个信源符号所需的平均码长满足:
实验结果:
S = 0.2000 L = 3 S1 = 0 r = 0 0 0 1 1 1 1 shangnon = 000 001 011 100 101 1110 1111110 L = 3.1400 xiaolv = 0.8308 0 0 1 0 0 1 1 0 1 1 0 1 1 1 0 1 0 1 1 0 1 0 0 0 0 1 0 1 0 0 0 0 1 0 1 0 1 1 0 0 1 0 0.2000 0.3900 0.5700 0.7400 0.8900 0.9900 3 3 3 3 4 7 0.1900 0.1800 0.1700 0.1500 0.1000 0.0100
2)实验中出现的问题及解决方法;
1、香农编码是码符号概率大的用短码表示,概率小的是用长码表示,程序中需 要对概率进行排序,对此我们调用matlab的库函数。 2、最后需要注意的是,求得的码字依次与排序后的符号概率对应。
六、[实验总结] 通过实验我进一步加深了对信源编码的理解, 尤其是香浓编码定理及其对信 源进行编码的具体过程。 香农编码, 是码符号概率大的信源符号用短码表示, 概率小的是用长码表示。 概率越大, 包含的信息量越少, 概率越小, 包含的不确定性越大, 即信息量越多, 要无失真的表示信源符号,所需要的二进制数位数就多。
