大学物理综合测试题(下册)及详解
大学物理考卷答案(下学期)

大学物理考卷(下学期)一、选择题(每题4分,共40分)A. 速度B. 力C. 位移D. 加速度2. 在国际单位制中,下列哪个单位属于电学基本单位?A. 安培B. 伏特C. 欧姆D. 瓦特A. 物体不受力时,运动状态不会改变B. 物体受平衡力时,运动状态会改变C. 物体受非平衡力时,运动状态不变D. 物体运动时,必定受到力的作用A. 功B. 动能C. 势能D. 路程A. 速度大小B. 速度方向C. 动能D. 动量6. 下列哪个现象属于光的衍射?A. 彩虹B. 海市蜃楼C. 水中倒影D. 光照射在单缝上产生的条纹A. 恢复力与位移成正比B. 恢复力与位移成反比C. 恢复力与位移的平方成正比D. 恢复力与位移的平方成反比8. 一个电路元件的电压u与电流i的关系为u=2i+3,该元件是:A. 电阻B. 电容C. 电感D. 非线性元件A. 电磁波在真空中传播速度小于光速B. 电磁波在介质中传播速度大于光速C. 电磁波在真空中传播速度等于光速D. 电磁波在介质中传播速度等于光速10. 一个理想变压器的初级线圈匝数为1000匝,次级线圈匝数为200匝,若初级线圈电压为220V,则次级线圈电压为:A. 110VB. 220VC. 440VD. 880V二、填空题(每题4分,共40分)1. 在自由落体运动中,物体的加速度为______。
2. 一个物体做匀速圆周运动,其线速度的大小不变,但方向______。
3. 惠更斯原理是研究______现象的重要原理。
4. 一个电阻的电压为10V,电流为2A,则该电阻的功率为______。
5. 根据电磁感应定律,当磁通量发生变化时,会在导体中产生______。
6. 在交流电路中,电阻、电感和电容元件的阻抗分别为______、______和______。
7. 一个单摆在位移为0时速度最大,此时摆球所受回复力为______。
8. 光的折射率与光的传播速度成______比。
9. 一个电子在电场中受到的电势能变化量为______。
《大学物理》下册试卷及答案(K12教育文档)

《大学物理》下册试卷及答案(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(《大学物理》下册试卷及答案(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为《大学物理》下册试卷及答案(word版可编辑修改)的全部内容。
2008—2009《大学物理》(下)考试试卷一、选择题(单选题,每小题3分,共30分):1、两根无限长平行直导线载有大小相等方向相反的电流I ,I 以dI/dt 的变化率增长,一矩形线圈位于导线平面内(如图所示),则 。
(A),矩形线圈中无感应电流;(B),矩形线圈中的感应电流为顺时针方向; (C),矩形线圈中的感应电流为逆时针方向; (D),矩形线圈中的感应电流的方向不确定;2,如图所示的系统作简谐运动,则其振动周期为 。
(A ),k m T π2=;(B), k m T θπsin 2=; (C ), km T θπcos 2=; (D), θθπcos sin 2k m T =;3,在示波器的水平和垂直输入端分别加上余弦交变电压,屏上出现如图所示的闭合曲线,已知水平方向振动的频率为600Hz ,则垂直方向的振动频率为 。
(A ),200Hz ;(B), 400Hz;(C ), 900Hz;(D), 1800Hz ;4,振幅、频率、传播速度都相同的两列相干波在同一直线上沿相反方向传播时叠加可形成驻波,对于一根长为100cm的两端固定的弦线,要形成驻波,下面哪种波长不能在其中形成驻波? .(A),λ=50cm;(B), λ=100cm;(C),λ=200cm;(D), λ=400cm;5,关于机械波在弹性媒质中传播时波的能量的说法,不对的是。
大学物理下考试题及答案

大学物理下考试题及答案一、选择题(每题2分,共20分)1. 根据麦克斯韦方程组,电磁波在真空中的传播速度是多少?A. 100m/sB. 300m/sC. 1000m/sD. 3×10^8 m/s答案:D2. 一个物体的动能是其势能的两倍,如果物体的总能量是E,那么它的势能U是多少?A. E/2B. E/3C. 2E/3D. E答案:B3. 在理想气体状态方程PV=nRT中,P代表的是:A. 温度B. 体积C. 压力D. 气体常数答案:C4. 下列哪个现象不是由量子力学效应引起的?A. 光电效应B. 原子光谱C. 超导现象D. 布朗运动答案:D5. 一个电子在电场中受到的电场力大小是1.6×10^-19 N,如果电子的电荷量是1.6×10^-19 C,那么电场强度E是多少?A. 1 N/CB. 10 N/CC. 100 N/CD. 1000 N/C答案:A6. 根据狭义相对论,一个物体的质量m与其静止质量m0之间的关系是:A. m = m0B. m = m0 / sqrt(1 - v^2/c^2)C. m = m0 * sqrt(1 - v^2/c^2)D. m = m0 * (1 - v^2/c^2)答案:C7. 一个物体从静止开始自由下落,其下落的高度h与时间t之间的关系是:A. h = 1/2 gt^2B. h = gt^2C. h = 2gtD. h = gt答案:A8. 在双缝干涉实验中,相邻的明亮条纹之间的距离是相等的,这种现象称为:A. 单缝衍射B. 多缝衍射C. 双缝干涉D. 薄膜干涉答案:C9. 一个电路中的电阻R1和R2并联,总电阻Rt可以用以下哪个公式计算?A. Rt = R1 + R2B. Rt = R1 * R2 / (R1 + R2)C. Rt = 1 / (1/R1 + 1/R2)D. Rt = (R1 * R2) / (R1 + R2)答案:C10. 根据热力学第一定律,一个系统吸收了100 J的热量,同时对外做了50 J的功,那么系统的内能增加了多少?A. 50 JB. 100 JC. 150 JD. 200 J答案:B二、填空题(每题2分,共20分)11. 光的粒子性质在________现象中得到了体现。
大学物理(下)练习题及答案

xyoa•••a-(0,)P y qq-大学物理(下)练习题第三编 电场和磁场 第八章 真空中的静电场1.如图所示,在点((,0)a 处放置一个点电荷q +,在点(,0)a -处放置另一点电荷q -。
P 点在y 轴上,其坐标为(0,)y ,当y a ?时,该点场强的大小为(A) 204q y πε; (B) 202q y πε;(C)302qa y πε; (D)304qa y πε.[ ]2.将一细玻璃棒弯成半径为R 的半圆形,其上半部均匀分布有电量Q +, 下半部均匀分布有电量Q -,如图所示。
求圆心o 处的电场强度。
3.带电圆环的半径为R ,电荷线密度0cos λλφ=,式中00λ>,且为常数。
求圆心O 处的电场强度。
4.一均匀带电圆环的半径为R ,带电量为Q ,其轴线上任一点P 到圆心的距离为a 。
求P 点的场强。
5.关于高斯定理有下面几种说法,正确的是(A) 如果高斯面上E r处处为零,那么则该面内必无电荷;(B) 如果高斯面内无电荷,那么高斯面上E r处处为零;(C) 如果高斯面上E r处处不为零,那么高斯面内必有电荷;(D) 如果高斯面内有净电荷,那么通过高斯面的电通量必不为零; (E) 高斯定理仅适用于具有高度对称性的电场。
[ ]6.点电荷Q 被闭合曲面S 所包围,从无穷远处引入另一点电荷q 至曲面S 外一点,如图所示,则引入前后(A) 通过曲面S 的电通量不变,曲面上各点场强不变;(B) 通过曲面S 的电通量变化,曲面上各点场强不变;(C) 通过曲面S 的电通量变化,曲面上各点场强变化;(D) 通过曲面S 的电通量不变,曲面上各点场强变化。
[ ]7.如果将带电量为q 的点电荷置于立方体的一个顶角上,则通过与它不相邻的每个侧面的电场强度通量为xq g S Q g(A)06q ε; (B) 012q ε; (C) 024q ε; (D) 048q ε. [ ]8.如图所示,A 、B 为真空中两个平行的“无限大”均匀带电平面,A 面上的电荷面密度721.7718A C m σ--=-⨯⋅,B 面上的电荷面密度723.5418B C m σ--=⨯⋅。
江西理工大学大学物理(下)习题册及答案详解

班级_____________ 学号___________姓名________________ 简谐振动1. 一质点作谐振动, 振动方程为X=6COS (8πt+π/5) cm, 则t=2秒时的周相为:π5116, 质点第一次回到平衡位置所需要的时间为:s 0375.0.2. 一弹簧振子振动周期为T 0, 若将弹簧剪去一半, 则此弹簧振子振动周期T 和原有周期T 0之间的关系是:022T T =.3. 如图为以余弦函数表示的谐振动的振动曲线, 则其初周相φ=3π-,P 时刻的周相为:0.4. 一个沿X 轴作谐振动的弹簧振子, 振幅为A , 周期为T , 其振动方程用余弦函数表示, 如果在t=0时, 质点的状态分别是:(A) X 0=-A; (B) 过平衡位置向正向运动;(C) 过X=A/2 处向负向运动; (D) 过A x 22-= 处向正向运动.2 1 0 P t(s) X(m)试求出相应的初周相之值, 并写出振动方程.)2cos()(ππ+=t TA x A ; )22cos()(ππ-=t T A x B)32cos()(ππ+=t T A x C ; )452cos()(ππ+=t T A x D5.一质量为0.2kg 的质点作谐振动,其运动议程为:X=0.60 COS(5t -π/2)(SI)。
求(1)质点的初速度;(2)质点在正向最大的位移一半处所受的力。
解(1))5sin(00.32π--==t dtdxv 10.00.3,0-==s m v t(2)x x dtdv a 2520-=-==ω 22.5.7,30.0--===s m a m x AN ma F 5.1-==班级_____________ 学号___________姓名________________简谐振动的合成1. 两个不同的轻质弹簧分别挂上质量相同的物体1和2, 若它们的振幅之比A 2 /A 1=2, 周期之比T 2 / T 1=2, 则它们的总振动能量之比E 2 / E 1 是( A )(A) 1 (B) 1/4 (C) 4/1 (D) 2/11)()(;)(2222221122112=⋅==A A T T E E T A m E π2.有两个同方向的谐振动分别为X 1=4COS(3t+π/4)cm ,X 2 =3COS(3t -3π/4)cm, 则合振动的振幅为:cm A 1=, 初周相为:4πφ=. 3. 一质点同时参与两个同方向, 同频率的谐振动, 已知其中一个分振动的方程为X 1=4COS3t cm, 其合振动的方程为分振动的振幅为A 2 =cm 44. 动方程分别为X 1=A COS(ωt+π/3), X 2 =A COS (ωt+5π/3), X 3 =A COS(ω程为:)6cos(3πω+=t A x5. 频率为v 1和v 2的两个音叉同时振动时,可以听到拍音,可以听到拍音,若v 1>v 2,则拍的频率是(B )(A)v 1+v 2 (B)v 1-v 2 (C)(v 1+v 2)/2 (D)(v 1-v 2)/26.有两个同方向,同频率的谐振动,其合成振动的振幅为0.20m ,周相与第一振动周相差为π/6。
吉林大学大学物理作业答案综合练习题(下)(二)
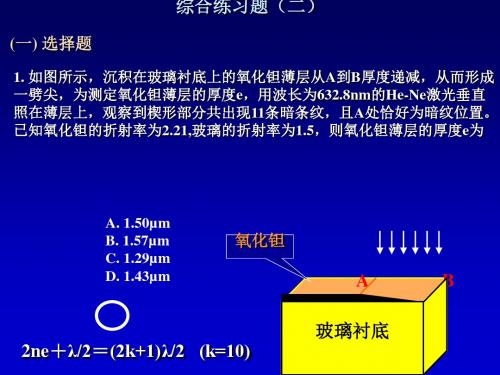
A. 1.50µm B. 1.57µm C. 1.29µm D. 1.43µm
氧化钽
A
B
玻璃衬底 玻璃衬底
2ne+λ/2=(2k+1)λ/2 (k=10)
2.物体在周期性外力作用下发生受迫振动,且周期性外力的频率与物体固 有频率相同。若忽略阻力,在稳定情况下,物体的运动表现出如下特点
A. 物体振动频率与外力驱动力的频率不同, 振幅呈现有限值; B. 物体振动频率与外力驱动力的频率相同, 振幅呈现有限值; C. 物体振动频率与外力驱动力的频率不同, 振幅趋于无限大; D. 物体振动频率与外力驱动力的频率相同, 振幅趋于无限大;
固有长度l0
3.两飞船,在自己的静止参照系中测得各自的长度均为100m。飞船1上的 仪器测得飞船1的前端驶完飞船2的全长需5/3×10-7s。两飞船的相对速度 的大小是( )
同地钟——固有时间t
0
A.
c/ 6
B.
C.
c/2
l t0
D.
c/ 2
2c / 5
l l0
v2 1 2 c
v
4.光子A的能量是光子B的两倍。则光子A的动量是光子B的( A.1/4 B.1 C. D.2 倍。
l 0 . 5 m m 解:
e e 3 9 0 0 n m 5 2 2
2 2n
l
1 . 71 0r a d
4
4.一平面透射光栅,当用白光垂直照射时,能在30°衍射方向上观察到600nm的第 二级干涉主极大,并能在该处分辨△λ=0.05nm的两条光谱线,但在此30°方向上却 测不到400nm的第三级主极大,计算此光栅的缝宽a和缝距b以及总缝数N 。
大学物理下考试题及答案

大学物理下考试题及答案一、选择题(每题5分,共20分)1. 光在真空中的传播速度是:A. 3×10^8 m/sB. 2×10^8 m/sC. 1×10^8 m/sD. 4×10^8 m/s答案:A2. 根据牛顿第二定律,力和加速度的关系是:A. F=maB. F=mvC. F=m/aD. F=a/m答案:A3. 一个物体从静止开始做匀加速直线运动,其位移与时间的关系为:A. s = 1/2at^2B. s = 1/2vtC. s = 1/2atD. s = vt答案:A4. 在理想气体状态方程中,压强、体积、温度的关系是:A. PV = nRTB. PV = nTC. PV = nRD. PV = n答案:A二、填空题(每题5分,共20分)1. 根据能量守恒定律,一个物体的动能和势能之和在任何情况下都______。
答案:保持不变2. 电场强度的定义式为______。
答案:E = F/q3. 根据库仑定律,两点电荷之间的力与它们电荷量的乘积成正比,与它们距离的平方成反比,其公式为______。
答案:F = kQq/r^24. 光的折射定律表明,入射角和折射角之间的关系为______。
答案:n1sinθ1 = n2sinθ2三、简答题(每题10分,共40分)1. 简述波粒二象性的概念。
答案:波粒二象性是指微观粒子如电子、光子等,既表现出波动性,也表现出粒子性。
在某些实验条件下,它们表现出波动性,如干涉和衍射现象;而在另一些实验条件下,它们表现出粒子性,如光电效应和康普顿散射。
2. 什么是电磁感应定律?请给出其数学表达式。
答案:电磁感应定律描述了变化的磁场在导体中产生电动势的现象。
其数学表达式为ε = -dΦ/dt,其中ε是感应电动势,Φ是磁通量,t是时间。
3. 简述热力学第一定律的内容。
答案:热力学第一定律,也称为能量守恒定律,指出在一个封闭系统中,能量既不能被创造也不能被消灭,只能从一种形式转换为另一种形式。
大学力学专业《大学物理(下册)》期末考试试题 含答案

大学力学专业《大学物理(下册)》期末考试试题含答案姓名:______ 班级:______ 学号:______考试须知:1、考试时间:120分钟,本卷满分为100分。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
一、填空题(共10小题,每题2分,共20分)1、设作用在质量为1kg的物体上的力F=6t+3(SI).如果物体在这一力的作用下,由静止开始沿直线运动,在0到 2.0 s的时间间隔内,这个力作用在物体上的冲量大小I=__________________。
2、图示曲线为处于同一温度T时氦(原子量4)、氖(原子量20)和氩(原子量40)三种气体分子的速率分布曲线。
其中曲线(a)是________气分子的速率分布曲线;曲线(c)是________气分子的速率分布曲线。
3、已知质点的运动方程为,式中r的单位为m,t的单位为s。
则质点的运动轨迹方程,由t=0到t=2s内质点的位移矢量______m。
4、在主量子数n=2,自旋磁量子数的量子态中,能够填充的最大电子数是______________。
5、质点在平面内运动,其运动方程为,质点在任意时刻的位置矢量为________;质点在任意时刻的速度矢量为________;加速度矢量为________。
6、质量为M的物体A静止于水平面上,它与平面之间的滑动摩擦系数为μ,另一质量为的小球B以沿水平方向向右的速度与物体A发生完全非弹性碰撞.则碰后它们在水平方向滑过的距离L=__________。
7、一根无限长直导线通有电流I,在P点处被弯成了一个半径为R的圆,且P点处无交叉和接触,则圆心O处的磁感强度大小为_______________,方向为_________________。
8、气体分子的最可几速率的物理意义是__________________。
9、若静电场的某个区域电势等于恒量,则该区域的电场强度为_______________,若电势随空间坐标作线性变化,则该区域的电场强度分布为 _______________。
大学物理学专业《大学物理(下册)》期末考试试卷A卷 附答案

大学物理学专业《大学物理(下册)》期末考试试卷A卷附答案姓名:______ 班级:______ 学号:______考试须知:1、考试时间:120分钟,本卷满分为100分。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
一、填空题(共10小题,每题2分,共20分)1、图示曲线为处于同一温度T时氦(原子量4)、氖(原子量20)和氩(原子量40)三种气体分子的速率分布曲线。
其中曲线(a)是________气分子的速率分布曲线;曲线(c)是________气分子的速率分布曲线。
2、刚体绕定轴转动时,刚体的角加速度与它所受的合外力矩成______,与刚体本身的转动惯量成反比。
(填“正比”或“反比”)。
3、均匀细棒质量为,长度为,则对于通过棒的一端与棒垂直的轴的转动惯量为_____,对于通过棒的中点与棒垂直的轴的转动惯量_____。
4、两个相同的刚性容器,一个盛有氧气,一个盛氦气(均视为刚性分子理想气体)。
开始他们的压强和温度都相同,现将3J的热量传给氦气,使之升高一定的温度。
若使氧气也升高同样的温度,则应向氧气传递的热量为_________J。
5、四根辐条的金属轮子在均匀磁场中转动,转轴与平行,轮子和辐条都是导体,辐条长为R,轮子转速为n,则轮子中心O与轮边缘b之间的感应电动势为______________,电势最高点是在______________处。
6、长为的匀质细杆,可绕过其端点的水平轴在竖直平面内自由转动。
如果将细杆置与水平位置,然后让其由静止开始自由下摆,则开始转动的瞬间,细杆的角加速度为_____,细杆转动到竖直位置时角加速度为_____。
7、反映电磁场基本性质和规律的积分形式的麦克斯韦方程组为:()。
①②③④试判断下列结论是包含于或等效于哪一个麦克斯韦方程式的.将你确定的方程式用代号填在相应结论后的空白处。
(1) 变化的磁场一定伴随有电场;__________________(2) 磁感线是无头无尾的;________________________(3) 电荷总伴随有电场.__________________________8、一长直导线旁有一长为,宽为的矩形线圈,线圈与导线共面,如图所示. 长直导线通有稳恒电流,则距长直导线为处的点的磁感应强度为___________;线圈与导线的互感系数为___________。
大学物理学(下册)习题答案详解

第十二章 热力学基础一、选择题 12-1 C 12-2 C 12-3 C 12-4 B 12-5 C 12-6 A 二、填空题 12-710000100p V p V p V p V --12-8 260J ,280J - 12-912-10 )(5.21122V p V p -,))((5.01212V V p p -+,)(5.0)(312211122V p V p V p V p -+- 12-11 268J ,732J 三、计算题12-12 分析:理想气体的内能是温度T 的单值函数,内能的增量E ∆由始末状态的温度的增量T ∆决定,与经历的准静态过程无关.根据热力学第一定律可知,在等温过程中,系统从外界吸收的热量全部转变为内能的增量,在等压过程中,系统从外界吸收的热量部分用来转变为内能的增量,同时对外做功. 解:单原子理想气体的定体摩尔热容,32V m C R = (1) 等体升温过程20=A,21333()8.3150623222V V m E Q C T R T R T T J J ∆==∆=∆=-=⨯⨯= (2) 等压膨胀过程,2133()8.315062322V m E C T R T T J J ∆=∆=-=⨯⨯= 2121()()8.3150416A p V V R T T J J =-=-=⨯=1039p Q A E J =+∆=或者,,215()8.315010392p p m p m Q C T C T T J J =∆=-=⨯⨯=12-13 分析:根据热力学第一定律和理想气体物态方程求解. 解:氢气的定体摩尔热容,52V m C R =(1) 氢气先作等体升压过程,再作等温膨胀过程. 在等体过程中,内能的增量为 ,558.3160124622V V m Q E C T R T J J =∆=∆=∆=⨯⨯= 等温过程中,对外界做功为221ln8.31(27380)ln 22033T T V Q A RT J J V ===⨯+⨯= 吸收的热量为3279V T Q Q Q J =+=(2) 氢气先作等温膨胀过程,然后作等体升压过程. 在等温膨胀过程中,对外界做功为211ln8.31(27320)ln 21687T V A RT J J V ==⨯+⨯= 在等体升压过程中,内能的增量为,558.3160124622V m E C T R T J J ∆=∆=∆=⨯⨯= 吸收的热量为2933T Q A E J =+∆=3虽然氢气所经历的过程不同,但由于始末状态的温差T ∆相同,因而内能的增量E ∆相同,而Q 和A 则与过程有关.12-14 分析:卡诺循环的效率仅与高、低温热源的温度1T 和2T 有关.本题中,求出等温膨胀过程吸收热量后,利用卡诺循环效率及其定义,便可求出循环的功和在等温压缩过程中,系统向低温热源放出的热量. 解:从高温热源吸收的热量321110.005ln 8.31400ln 5.35100.001V m Q RT J J M V ==⨯⨯=⨯ 由卡诺循环的效率2113001125%400T A Q T η==-=-= 可得循环中所作的功310.255350 1.3410A Q J J η==⨯=⨯传给低温热源的热量3321(1)(10.25) 5.3510 4.0110Q Q J J η=-=-⨯⨯=⨯12-15 分析:在a b →等体过程中,系统从外界吸收的热量全部转换为内能的增量,温度升高.在b c →绝热过程中,系统减少内能,降低温度对外作功,与外界无热量交换.在c a →等压压缩过程中,系统放出热量,温度降低,对外作负功.计算得出各个过程的热量和功,根据热机循环效率的定义即可得证. 证明:在a b →等体过程中,系统从外界吸收的热量为,,1222()()V m V V m b a C mQ C T T p V p V M R=-=-在c a →等压压缩过程中,系统放出热量的大小为,,2122()()p m P p m c a C mQ C T T p V p V M R=-=- 所以,该热机的循环效率为41,212221,12222(1)()111()(1)p m P V V m V C p V p V Q V p Q C p V p V p ηγ--=-=-=---12-16 分析:根据卡诺定理,在相同的高温热源(1T ),与相同的低温热源(2T )之间工作的一切可逆热机的效率都相等,有221111Q TQ T η=-=-.非可逆热机的效率221111Q T Q T η=-<-. 解:(1) 该热机的效率为21137.4%Q Q η=-= 如果是卡诺热机,则效率应该是21150%c T T η=-= 可见它不是可逆热机.(2) “尽可能地提高效率”是指热机的循环尽可能地接近理想的可逆循环工作方式.根据热机效率的定义,可得理想热机每秒吸热1Q 时所作的功为4410.50 3.3410 1.6710c A Q J J η==⨯⨯=⨯5第十三章 气体动理论一、选择题 13-1 D 13-2 B 13-3 D 13-4 D 13-5 C 13-6 C 13-7 A 二、填空题13-8 相同,不同;相同,不同,相同. 13-9 (1)分子体积忽略不计;(2)分子间的碰撞是完全弹性的; (3)只有在碰撞时分子间才有相互作用.13-10 速率大于p v 的分子数占总分子数的百分比,分子的平均平动动能,()d 1f v v ∞=⎰,速率在∞~0内的分子数占总分子数的百分之百.13-11 氧气,氢气,1T 13-12 3,2,013-13 211042.9-⨯J ,211042.9-⨯J ,1:2 13-14 概率,概率大的状态. 三、计算题13-15 分析:根据道尔顿分压定律可知,内部无化学反应的平衡状态下的混合气体的总压强,等于混合气体中各成分理想气体的压强之和.解:设氦、氢气压强分别为1p 和2p ,则12p p p =+.由理想气体物态方程,得1He He m RTp M V =, 222H H m RT p M V=所以,总压强为62255123334.010 4.0108.31(27230)()()4.010 2.010 1.010H He He H m m RT p p p Pa M M V -----⨯⨯⨯+=+=+=+⨯⨯⨯⨯ 47.5610Pa =⨯13-16 解:(1)=可得 氢的方均根速率3/ 1.9310/s m s ===⨯ 氧的方均根速率483/m s === 水银的方均根速率/193/s m s === (2) 温度相同,三种气体的平均平动动能相同232133 1.3810300 6.211022k kT J J ε--==⨯⨯⨯=⨯13-17 分析:在某一速率区间,分布函数()f v 曲线下的面积,表示分子速率在该速率区间内的分子数占总分子数的百分比.速率区间很小时,这个百分比可近似为矩形面积()Nf v v N∆∆=,函数值()f v 为矩形面积的高,本题中可取为()p f v .利用p v 改写麦克斯韦速率分布律,可进一步简化计算.解: ()Nf v v N∆=∆ 当300T K =时,氢气的最概然速率为1579/p v m s ==== 根据麦克斯韦速率分布率,在v v v →+∆区间内的分子数占分子总数的百分比为232224()2mvkT N m e v v N kTππ-∆=∆7用p v 改写()f v v ∆有223()2222()4()e ()()2pv mv v kTpp mv v f v v v v e kTv v ππ--∆∆=∆=由题意可知,10p v v =-,(10)(10)20/p p v v v m s ∆=+--=.而10p v ,所以可取p v v ≈,代入可得1201.05%1579p N e N-∆=⨯=13-18 解:(1) 由归一化条件204()d 1FF V V dN V AdV f v v N Nπ∞===⎰⎰⎰ 可得 334F NA V π= (2) 平均动能2230143()d d 24FV FV N f v v mv v N V πωωπ∞==⨯⨯⎰⎰423031313d ()2525FV F F F mv v mv E v =⨯==⎰13-19 分析:气体分子处于平衡态时,其平均碰撞次数于分子数密度和分子的平均速率有关.温度一定时,平均碰撞次数和压强成正比.解:(1) 标准状态为50 1.01310p Pa =⨯,0273T K =,氮气的摩尔质量32810/M kg mol -=⨯由公式v =kTp n =可得224Z d nv d d π===5102231.013104(10)/1.3810273s π--⨯=⨯⨯⨯次885.4210/s =⨯次(2) 41.3310p Pa -=⨯,273T K =4102231.331044(10)/1.3810273Z ds ππ---⨯==⨯⨯⨯次0.71/s =次13-20 分析:把加热的铁棒侵入处于室温的水中后,铁棒将向水传热而降低温度,但“一大桶水”吸热后的水温并不会发生明显变化,因而可以把“一大桶水”近似为恒温热源.把铁棒和“一大桶水”一起视为与外界没有热和功作用的孤立系统,根据热力学第二定律可知,在铁棒冷却至最终与水同温度的不可逆过程中,系统的熵将增加.熵是态函数,系统的熵变仅与系统的始末状态有关而与过程无关.因此,求不可逆过程的熵变,可在始末状态之间设计任一可逆过程进行求解. 解:根据题意有 1273300573T K =+=,227327300T K =+=.设铁棒的比热容为c ,当铁棒的质量为m ,温度变化dT 时,吸收(或放出)的热量为dQ mcdT =设铁棒经历一可逆的降温过程,其温度连续地由1T 降为2T ,在这过程中铁棒的熵变为2121d d 300ln 5544ln /1760/573T T T Q mc T S mc J K J K T T T ∆====⨯⨯=-⎰⎰9第十四章 振动学基础一、选择题 14-1 C 14-2 A 14-3 B 14-4 C 14-5 B 二、填空题 14-622 14-7 5.5Hz ,114-82411s ,23π 14-9 0.1,2π14-10 2222mA T π- 三、计算题14-11 解:简谐振动的振幅2A cm =,速度最大值为3/m v cm s =则 (1) 2220.024 4.20.033m A T s s s v ππππω⨯====≈ (2) 222220.03m/s 0.045m/s 4m m m a A v v T ππωωπ===⨯=⨯≈ (3) 02πϕ=-,3rad/s 2ω= 所以 30.02cos()22x t π=- [SI]14-12 证明:(1) 物体在地球内与地心相距为r 时,它受到的引力为2MmF Gr=- 负号表示物体受力方向与它相对于地心的位移方向相反.式中M 是以地心为中心,以r 为半径的球体内的质量,其值为10343M r πρ=因此 43F G m r πρ=-物体的加速度为43F aG r m πρ==- a 与r 的大小成正比,方向相反,故物体在隧道内作简谐振动. (2) 物体由地表向地心落去时,其速度dr dr dv dr v a dt dv dt dv=== 43vdv adr G rdr πρ==-043v r R vdv G rdr πρ=-⎰⎰ 所以v =又因为dr vdt == 所以tRdt =-⎰⎰则得1126721min 4t s ===≈14-13 分析:一物体是否作简谐振动,可从动力学方法和能量分析方法作出判断.动力学的分析方法由对物体的受力分析入手,根据牛顿运动方程写出物体所满足的微分方程,与简谐振动的微分方程作出比较后得出判断.能量法求解首先需确定振动系统,确定系统的机械能是否守恒,然后需确定振动物体的平衡位置和相应的势能零点,再写出物体在任意位置时的机械能表达式,并将其对时间求一阶导数后与简谐振动的微分方程作比较,最后作出是否作简谐振动的判断. 解:(1) 能量法求解取地球、轻弹簧、滑轮和质量为m 的物体作为系统.在物体上下自由振动的过程中,系统不受外力,系统内无非保守内力作功,所以系统的机械能守恒. 取弹簧的原长处为弹性势能零点,取物体受合力为零的位置为振动的平衡位11置,也即Ox 轴的坐标原点,如图14-13(a)所示.图14-13 (a)图14-13 (b)设物体在平衡位置时,弹簧的伸长量为l ,由图14-13(b)可知,有10mg T -=,120T R T R -=,2T kl =得 mgl k=当物体m 偏离平衡位置x 时,其运动速率为v ,弹簧的伸长量为x l +,滑轮的角速度为ω.由系统的机械能守恒,可得222111()222k x l mv J mgx ω+++-=常量 式中的角速度 1v dxR R dt ω==将机械能守恒式对时间t 求一阶导数,得2222d x k x x dt m J Rω=-=-+ 上式即为简谐振动所满足的微分方程,式中ω为简谐振动的角频率2km J R ω=+另:动力学方法求解物体和滑轮的受力情况如图14-13(c)所示.12图14-13 (c)1mg T ma -= (1)12()JT T R J a Rβ-==(2) 设物体位于平衡位置时,弹簧的伸长量为l ,因为这时0a =,可得12mg T T kl ===当物体对平衡位置向下的位移为x 时,2()T k l x mg kx =+=+ (3)由(1)、(2)、(3)式解得2ka x m J R =-+物体的加速度与位移成正比,方向相反,所以它是作简谐振动. (2) 物体的振动周期为222m J R T kππω+==(3) 当0t =时,弹簧无伸长,物体的位移0x l =-;物体也无初速,00v =,物体的振幅22200()()v mgA x l l kω=+=-==00cos 1x kl A mgϕ-===- 则得 0ϕπ=13所以,物体简谐振动的表达式为2cos()mg k x t k m J Rπ=++ 14-14 分析:M 、m 一起振动的固有频率取决于k 和M m +,振动的初速度0m v 由M 和m 的完全非弹性碰撞决定,振动的初始位置则为空盘原来的平衡位置.图14-14解:设空盘静止时,弹簧伸长1l ∆(图14-14),则1Mg k l =∆ (1)物体与盘粘合后且处于平衡位置,弹簧再伸长2l ∆,则12()()m M g k l l +=∆+∆ (2)将(1)式代入得2mg k l =∆与M 碰撞前,物体m 的速度为02m v gh =与盘粘合时,服从动量守恒定律,碰撞后的速度为02m m mv v gh m M m M==++取此时作为计时零点,物体与盘粘合后的平衡位置作为坐标原点,坐标轴方向竖直向下.则0t =时,02mg x l k =-∆=-,02mv v gh m M==+14ω=由简谐振动的初始条件,0000cos , sin x A v A ϕωϕ==-可得振幅A ===初相位0ϕ满足000tan v x ϕω=-== 因为 00x <,00v >所以 032πϕπ<<0ϕπ=+所以盘子的振动表式为cos x π⎤⎫=+⎥⎪⎪⎥⎭⎦14-15 解:(1) 振子作简谐振动时,有222111222k p E E E mv kx kA +==+= 当k p E E =时,即12p E E =.所以 22111222kx kA =⨯0.200.14141x m m ==±=±(2)由条件可得振子的角频率为/2/s rad s ω=== 0t =时,0x A =,故00ϕ=.动能和势能相等时,物体的坐标15x =即cos A t ω=,cos t ω= 在一个周期内,相位变化为2π,故3574444t ππππω=, , , 时间则为1 3.140.3944 2.0t s s πω===⨯ 213330.39 1.24t t s s πω===⨯=315550.39 2.04t t s s πω===⨯=417770.39 2.74t t s s πω===⨯=14-16 解:(1) 合成振动的振幅为A =0.078m== 合成振动的初相位0ϕ可由下式求出110220*********.05sin0.06sin sin sin 44tan 113cos cos 0.05cos 0.06cos 44A A A A ππϕϕϕππϕϕ⨯+⨯+===+⨯+⨯ 084.8ϕ=(2) 当0102k ϕϕπ-=± 0,1,2,k =时,即0103224k k πϕπϕπ=±+=±+时, 13x x +的振幅最大.取0k =,则 031354πϕ== 当020(21)k ϕϕπ-=±+0,1,2,k =时,即020(21)(21)4k k πϕπϕπ=±++=±++时,13x x +的振幅最小.取0k =,则 052254πϕ==(或031354πϕ=-=-) 14-17 分析:质点同时受到x 和y 方向振动的作用,其运动轨迹在Oxy 平面内,16质点所受的作用力满足力的叠加原理.解:(1) 质点的运动轨迹可由振动表达式消去参量t 得到.对t 作变量替换,令12t t '=-,两振动表达式可改写为0.06cos()0.06sin 323x t t πππ''=+=-0.03cos3y t π'=将两式平方后相加,得质点的轨迹方程为222210.060.03x y += 所以,质点的运动轨迹为一椭圆. (2) 质点加速度的两个分量分别为22220.06()cos()3339x d x a t x dt ππππ==-+=-22220.03()cos()3369y d y a t y dt ππππ==--=-当质点的坐标为(,)x y 时,它所受的作用力为22()99x y F ma i ma j m xi yj mr ππ=+=-+=-可见它所受作用力的方向总是指向中心(坐标原点),作用力的大小为223.1499F ma π====⨯=14-18 分析:充电后的电容器和线圈构成LC 电磁振荡电路.不计电路的阻尼时,电容器极板上的电荷量随时间按简谐振动的规律变化.振荡电路的固有振动频率由L 和C 的乘积决定,振幅和初相位由系统的初始状态决定.任意时刻电路的状态都可由振荡的相位决定. 解:(1) 电容器中的最大能量212e W C ε=线圈中的最大能量17212m m W LI =在无阻尼自由振荡电路中没有能量损耗,e m W W =.因此221122m C LI ε=21.4 1.410m I A A -===⨯(2) 当电容器的能量和电感的能量相等时,电容器能量是它最大能量的一半,即22124q C C ε= 因此661.010 1.41.0101.41q C C --⨯⨯==±=±⨯ (3) LC 振荡电路中,电容器上电荷量的变化规律为00cos()q Q t ωϕ=+式中0Q C ε=,ω=.因为0t =时,0q Q =,故有00ϕ=.于是q C ε=当首次q =时有C ε==,4π=53.147.85104t s -===⨯18第十五章 波动学基础一、选择题 15-1 B 15-2 C 15-3 B 15-4 A 15-5 C 15-6 C 二、填空题15-7 波源,传播机械波的介质 15-8B C,2B π,2C π,lC ,lC - 15-9 cos IS θ 15-10 0 15-11 0.45m 三、计算题15-12 分析:平面简谐波在弹性介质中传播时,介质中各质点作位移方向、振幅、频率都相同的谐振动,振动的相位沿传播方向依次落后,以速度u 传播.把绳中横波的表达式与波动表达式相比较,可得到波的振幅、波速、频率和波长等特征量.t 时刻0x >处质点的振动相位与t 时刻前0x =处质点的振动相位相同. 解:(1) 将绳中的横波表达式0.05cos(104)y t x ππ=-与标准波动表达式0cos(22)y A t x πνπλϕ=-+比较可得0.05A m =,52v Hz ωπ==,0.5m λ=,0.55/ 2.5/ u m s m s λν==⨯=. (2) 各质点振动的最大速度为0.0510/0.5/ 1.57/m v A m s m s m s ωππ==⨯=≈各质点振动的最大加速度为192222220.05100/5/49.3/m a A m s m s m s ωππ==⨯=≈(3) 将0.2x m =,1t s =代入(104)t x ππ-的所求相位为10140.29.2ϕπππ=⨯-⨯=0.2x m =处质点的振动比原点处质点的振动在时间上落后0.20.082.5x s s u == 所以它是原点处质点在0(10.08)0.92t s s =-=时的相位. (4) 1t s =时波形曲线方程为x x y 4cos 05.0) 4110cos(05.0πππ=-⨯=1.25t s =时波形曲线方程为)5.0 4cos(05.0) 425.110cos(05.0ππππ-=-⨯=x x y1.50t s =时波形曲线方程为) 4cos(05.0) 45.110cos(05.0ππππ-=-⨯=x x y1t s =, 1.25t s =, 1.50t s =各时刻的波形见图15-12.15-13 解:(1) 由于平面波沿x 轴负方向传播,根据a 点的振动表达式,并以a 点为坐标原点时的波动表达式为0cos[()]3cos[4()]20x xy A t t u ωϕπ=++=+(2) 以a 点为坐标原点时,b 点的坐标为5x m =-,代入上式,得b 点的振动表达式为53cos[4()]3cos(4)20b y t t πππ=-=- 若以b 点为坐标原点,则波动表达式为3cos[4()]20xy t ππ=+-s1s5.12015-14 解:由波形曲线可得100.1A cm m ==,400.4cm m λ==从而0.4/0.2/2u m s m s T λ===,2/rad s Tπωπ==(1) 设振动表达式为 0cos[()]xy A t uωϕ=++由13t s =时O 点的振动状态:2Ot Ay =-,0Ot v >,利用旋转矢量图可得,该时刻O 点的振动相位为23π-,即 10032()33Ot t t ππϕωϕϕ==+=+=-所以O 点的振动初相位为 0ϕπ=-将0x =,0ϕπ=-代入波动表达式,即得O 点的振动表达式为0.1cos()O y t ππ=-(2) 根据O 点的振动表达式和波的传播方向,可得波动表达式0cos[()]0.1cos[(5))]xy A t t x uωϕππ=++=+-(3) 由13t s =时Q 点的振动状态:0Qt y =,0Qt v <,利用旋转矢量图可得,该时刻Q 点的振动相位为2π,即013[()]30.22Q Qt t x x t u πππϕωϕπ==++=+-=可得 0.233Q x m =将0.233Q x m =,0ϕπ=-代入波动表达式,即得Q 点的振动表达式为0.1cos()6Q y t ππ=+(4) Q 点离O 点的距离为0.233Q x m =15-15 分析:波的传播过程也是能量的传播过程,波的能量同样具有空间和时间的周期性.波的强度即能流密度,为垂直通过单位面积的、对时间平均的能流.注意能流、平均能流、能流密度、能量密度、平均能量密度等概念的区别和联系.解:(1) 波中的平均能量密度为32235319.010/ 3.010/2300I w A J m J m u ρω--⨯====⨯最大能量密度为 532 6.010/m w w J m -==⨯ (2) 每两个相邻的、相位差为2π的同相面间的能量为25273000.14() 3.010() 4.621023002u d W wV w S w J v λππ--====⨯⨯⨯⨯=⨯15-16 分析:根据弦线上已知质点的振动状态,推出原点处质点振动的初相位,即可写出入射波的表达式.根据入射波在反射点的振动,考虑反射时的相位突变,可写出反射波的表达式.据题意,入射波和反射波的能量相等,因此,在弦线上形成驻波的平均能流为零.解:沿弦线建立Ox 坐标系,如图15-16所示.根据所给数据可得图15-16/100/u s m s ===,2100 /rad s ωπνπ==,100250u m m v λ===, (1) 设原点处质元的初相位为0ϕ,入射波的表达式为0cos[()]xy A t uωϕ=-+据题意可知,在10.5x m =处质元的振动初相位为103πϕ=,即有110001000.51003x u ωππϕϕϕ⨯=-+=-+=得 05326πππϕ=+=所以,入射波表达式为550.04cos[100()]0.04cos[100()]61006x x y t t u ππππ=-+=-+入考虑半波损失,反射波在2x 处质元振动的初相位为2010511100()10066ππϕππ=-++=反射波表达式为220cos[()]x x y A t uωϕ-=++反 ]611)100(100cos[04.0]611)10010(100cos[04.0ππππ++=+-+=x t x t(2)入射波和反射波的传播方向相反,叠加后合成波为驻波40.08cos()cos(100)23y y y x t ππππ=+=++入反波腹处满足条件 2x k πππ+=即 1()2x k =-因为010x m ≤≤,在此区间内波腹位置为0.5, 1.5, 2.5,,9.5x m = 波节处满足条件 (21)22x k πππ+=+即 x k = 在区间010x m ≤≤,波节坐标为0,1,2,,10x m = (3) 合成为驻波,在驻波中没有能量的定向传播,因而平均能流为零. 15-17 分析:运动波源接近固定反射面而背离观察者时,观察者即接收到直接来自波源的声波,也接收到来自固定反射面反射的声波,两声波在A 点的振动合成为拍.当波源相对于观察者静止,而反射面接近波源和观察者时,观察者接收到直接来自波源的声波无多普勒效应,但反射面反射的频率和观察者接收到的反射波频率都发生多普勒效应,因此,两个不同频率的振动在A 点也将合成为拍. 解:(1) 波源远离观察者而去,观察者接收到直接来自波源声音频率为1R S Suu v νν=+观察者相对反射面静止,接收到来自反射面的声波频率2R ν就是固定反射面接收到的声波频率,这时的波源以S v 接近反射面.2R S Suu v ννν==-反 A 处的观察者听到的拍频为21222S S R R S S S S Suv u uu v u v u v νννννν∆=-=-=-+- 由此可得方程2220S S S v uv u ννν∆+-∆=0.25/S v m s ≈(2) 观察者直接接收到的波的频率就是波源振动频率1RS νν'= 对于波源来说,反射面相当于接收器,它接收到的频率为S u vuνν+'=对于观察者来说,反射面相当于另一波源,观察者接收到的来自反射面的频率为2RS S u u u v u vu v u v u u vνννν++''===--- A 处的观察者听到的拍频为212RR S S S u v vu v u vνννννν+''∆=-=-=-- 所以波源的频率为3400.24339820.4S u v Hz Hz v νν--=∆=⨯= 15-18 解:平面电磁波波动方程的标准形式为222221y y E E x u t ∂∂=∂∂, 222221z zH H x u t ∂∂=∂∂ 与平面电磁波的标准方程相比较,可知波速为82.0010/u m s ==⨯ 所以介质的折射率为1.50cn u== 15-19 解:由电磁波的性质可得00E H =而 000B H μ=, 真空中的光速c =所以0E B c==从而可得 0008703000.8/0.8/310410B E H A m A m c μμπ-====⨯⨯⨯ 磁场强度沿y 轴正方向,且磁场强度和电场强度同相位,所以0.8cos(2)3y H vt ππ=+[SI ]第十六章 几何光学一、选择题 16-1 A 16-2 B 16-3 B 16-4 C 二、填空题16-5 6.0S cm '=,12V = 16-6 80f cm '=16-7 34s cm '=-,2V =- 16-8 左,2R 三、计算题16-9 解:设空气的折射率为n ,玻璃的折射率为n ',则 1n =, 1.5n '= 因为 2r = 所以物方焦距4nrf cm n n=='- 像方焦距6n rf cm n n ''=='- 又因为 1f fs s'+='而 8s cm = 所以 12s cm '=(实像)1ns y V y n s''==-=-' 其中 0.1y cm = 所以 0.1y Vy cm '==-16-10 分析:将球面反射看作n n '=-时球面折射的特例,可由折射球面的成像规律求解。
大学物理下册练习及答案

电磁学 磁力图所示,一电子经过A 点时,具有速率s m /10170⨯=υ。
(1) 欲使这电子沿半圆自A 至C 运动,试求所需的磁场大小和方向;(2) 求电子自A 运动到C 所需的时间。
解:(1)电子所受洛仑兹力提供向心力 Rv m B ev 200=得出T eR mv B 3197310101.105.0106.11011011.9---⨯=⨯⨯⨯⨯⨯== 磁场方向应该垂直纸面向里。
(2)所需的时间为s v R T t 870106.110105.0222-⨯=⨯⨯===ππ eV 3100.2⨯的一个正电子,射入磁感应强度B =0.1T 的匀强磁场中,其速度矢量与B 成B 的方向。
试求这螺旋线运动的周期T 、螺距h 和半径r 。
解:正电子的速率为731193106.21011.9106.110222⨯=⨯⨯⨯⨯⨯==--m E v k m/s 做螺旋运动的周期为101931106.31.0106.11011.922---⨯=⨯⨯⨯⨯==ππeB m T s 螺距为410070106.1106.389cos 106.289cos --⨯=⨯⨯⨯⨯==T v h m半径为3197310105.1.0106.189sin 106.21011.989sin ---⨯=⨯⨯⨯⨯⨯⨯==eB mv rm d =1.0mm ,放在B =1.5T 的磁立方厘米有8.42210⨯个自由电子,每个电子的电荷19106.1-⨯-=-e C ,当铜片中有I =200A 的电流流通时,(1)求铜片两侧的电势差'aa U ;(2)铜片宽度b 对'aa U 有无影响?为什么?解:(1)531928'1023.2100.1)106.1(104.85.1200---⨯-=⨯⨯⨯-⨯⨯⨯==nqd IB U aa V ,负号表示'a 侧电势高。
(2)铜片宽度b 对'aa U =H U 无影响。
(完整版)大学物理下册考题大全

真空中的静电场1、一均匀带电球面,电荷面密度为,球面内电场强度到处为零,球面上边元dS的一个带电量为 ds 的电荷元,在球面内各点产生的电场强度(A)到处为零.(B)不必定都为零.(C)到处不为零.(D)没法判断.2、在边长为a的正方体中心处搁置一电量为Q的点电荷,则正方体顶角处的电场强度的大小为:Q Q(A)120a 2.(B)60 a 2.Q Q(C)30 a2.(D)0 a2.3、如图示,直线MN长为2l,弧OCD是以N点为中心,l 为半径的半圆弧,N点有正电荷+q,M点有负电荷q.今将一试验电荷q0从O点出发沿路径OCDP移到无量远处,设无量远处电势为零,则电场力作功(A)A<0且为有限常量.(B)A>0且为有限常量.(C)A=∞.(D)A=0.第3题图第4题图4、图中实线为某电场中的电力线,虚线表示等势(位)面,由图可看出:(A)E A>E B>E C,U A>U B>U C.(B)E A<E B<E C,U A<U B<U C.(C)E A>E B>E C,U A<U B<U C.(D)E A <E B<E C,U A>U B>U C.5、真空中有两个点电荷M、N,相互间作用力为 F ,当另一点电荷Q移近这两个点电荷时,M、N两点电荷之间的作用力F(A)大小不变,方向改变.(B)大小改变,方向不变.(C)大小和方向都不变.(D)大小和方向都改变.6、电量之比为1∶3∶5的三个带同号电荷的小球A、B、C,保持在一条直线上,相互间距离比小球直径大得多.若固定A、C不动,改变B的地点使B所受电场力为零时,AB 与BC 的比值为(A)5.(B)1/5.(C) 5 .(D)1 5 .7、关于电场强度与电势之间的关系,以下说法中,哪一种是正确的?(A)在电场中,场强为零的点,电必定为零.(B)在电场中,电势为零的点,电场强度必为零.(C)在电势不变的空间,场强到处为零.(D)在场强不变的空间,电势到处相等8、在空间有一非均匀电场,其电力线分布以以下图.在电场中作一半径为R的闭合球面S,已 知经过球面上某一面元 S 的电场强度通量为ΔΦ e ,则经过该球面其他部分的电场强度通量为4 R 2(B)Se(A)e..4R 2S(C)Se.(D) 0第8题图第9题图9、 一电量为-q的点电荷位于圆心O处,A、B、C、D为同一圆周上的四点,以以下图.现将一试验电荷从A点分别挪动到B、C、D各点,则(A)从A到B,电场力作功最大.(B)从A到C,电场力作功最大.(C)从A到D,电场力作功最大.(D)从A到各点,电场力作功相等.10、 在边长为a的正方体中心处搁置一电量为Q的点电荷,设无量远处为电势零点,则在一个侧面的中心处的电势为:Q Q(A)4a.(B)2 0a.QQ(C)0 a . (D) 2 20 a. 11、在边长为a的正方体中心处搁置一点电荷Q,设无量远处为电势零点,则在正方体顶角处的电势为:QQ (A)430a.(B)230a.QQ(C)6a .(D) 12 0 a12. 以以下图,O点是两个相同的点电荷所在处连线的中点,P点为中垂线上的一点,则O、P两点的电势和场强盛小有以下关系:(A) U 0 U P ,E 0 E p . (B)U 0 U P ,E 0E p . (C) U 0U P , E 0 E p . (D)U 0U P , E 0E p .第 12题图第 14题图13、 依据高斯定理的数学表达式 E ds q 0可知下述各种说法中,正确的选项是: S(A)闭合面内的电荷代数和为零时,闭合面上各点场强必定为零.(B)闭合面内的电荷代数和不为零时,闭合面上各点场强必定到处不为零. (C)闭合面内的电荷代数和为零时,闭合面上各点场强不必定到处为零.(D)闭合面上各点场强均为零时,闭合面内必定到处无电荷.14、 一带电量为-q的质点垂直射入开有小孔的两带电平行板之间,以以下图.两平行板之间的电势差为U,距离为d,则此带电质点经过电场后它的动能增量等于(A)-qU /d .(B)+qU.(C)-qU.(D)qU /d15、 真空中有一电量为Q的点电荷,在与它相距为r的a点处有一试验电荷q.现使试验电荷q从a点沿半圆弧轨道运动到b点,以以下图.则电场力作功为Qqr 2 Qq2r(A)40 r 22 .(B)40 r 2.Qq2r(C)40 r.(D) 0.第 15题图第16题图16、一电场强度为 E 的均匀电场, E 的方向与X轴正向平行,以以下图.则经过图中一半径为R的半球面的电场强度通量为(A) R 2E .1 R2 E(B) 2 .(C)2 R 2E . (D)0.17、 关于电场强度定义式E F q 0,以下说法中哪个是正确的? (A)场强 E 的大小与尝试电荷 q 0 的大小成反比.(B)对场中某点,尝试电荷受力 F 与 q 0 的比值不因 q 0 而变.(C)尝试电荷受力F 的方向就是场强 E 的方向.(D)若场中某点不放尝试电荷q 0 ,则 F =0,从而 E =0.18、一带电体可作为点电荷办理的条件是(A)电荷一定呈球形分布. (B)带电体的线度很小.(C)带电体的线度与其他有关长度对比可忽视不计.(D)电量很小.E dsVdV19、高斯定理s(A)合用于任何静电场.(B)只合用于真空中的静电场.(C)只合用于拥有球对称性、轴对称性和平面对称性的静电场.(D)只合用于固然不拥有(C)中所述的对称性、但可以找到适合的高斯面的静电场. 和R (R <R ) 所带电量分别为Q20、两个齐心均匀带电球面,半径分别为Ra a和Q .设某babb点与球心相距r,当Ra <r<Rb 时,该点的电场强度的大小为:1Q aQ b1 Q aQ b(A)4r 2 .(B)4r2.1Q a Q b )1Q a4 0( 224 0 2(C) rb. (D)r .R21、半径为r的均匀带电球面1,带电量为q;其外有一齐心的半径为R的均匀带电球面2,带电量为Q,则此两球面之间的电势差U-U2为:1q(11 ) q(11 ) (A)40 rR .(B)4Rr .4 1 ( qQ )q(C) 0 rR .(D) 4 0 r .22、已知一高斯面所包围的体积内电量代数和∑qi =0,则可必定:(A)高斯面上各点场强均为零.(B)穿过高斯面上每一面元的电通量均为零.(C)穿过整个高斯面的电通量为零.(D)以上说法都不对.23、 有四个等量点电荷在OXY平面上的四种不一样组态,全部点电荷均与原点等距.设无量远处电势为零 , 则原点O处电场强度和电势均为零的组态是 (D)24. 在静电场中,有关静电场的电场强度与电势之间的关系,以下说法中正确的选项是:(A)场强盛的地方电势必定高.(B)场强相等的各点电势必定相等.(C)场强为零的点电势不必定为零.(D)场强为零的点电必定定是零.25、 正方形的两对角上,各置电荷Q,在其他两对角上各置电荷q,若Q所受合力为零,则Q与q的大小关系为(A)Q22q . (B) Q 2q .(C) Q4q .(D) Q2q .有导体和介质的静电场1. 关于高斯定理,以下说法中哪一个是正确的?(A)高斯面内不包围自由电荷,则面上各点电位移矢量 D 为零.(B)高斯面上到处D 为零,则面内必不存在自由电荷.(C)高斯面的 D 通量仅与面内自由电荷有关.(D)以上说法都不正确.2. 关于静电场中的电位移线,以下说法中,哪一种是正确的?(A)起自正电荷,止于负电荷,不形成闭合线,不中断.(B)任何两条电位移线相互平行.(C)起自正自由电荷,止于负自由电荷,任何两条电位移线在无自由电荷的空间不订交.(D)电位移线只出此刻有电介质的空间.3.两个半径相同的金属球,一为空心,一为实心,把二者各自孤即刻的电容值加以比较,则(A)空心球电容值大.(B)实心球电容值大.(C)两球电容值相等.(D)大小关系没法确立.4. C1和C2两空气电容器串通此后接电源充电.在电源保持联接的状况下,在C 2 中插入一电介质板,则(A)C 1 极板上电量增添,C 2 极板上电量增添.(B)C 1 极板上电量减少,C 2 极板上电量增添.(C)C 1 极板上电量增添,C 2 极板上电量减少.(D)C 1 极板上电量减少,C 2 极板上电量减少.第4题图第5题图5. C1和C 2 两空气电容器串通起来接上电源充电.而后将电源断开,再把一电介质板插入C1中,则(A)C 1 上电势差减小,C 2 上电势差增大.(B)C 1 上电势差减小,C 2 上电势差不变.(C)C 1 上电势差增大,C 2 上电势差减小.(D)C 1 上电势差增大,C 2 上电势差不变.6. C1和C2两空气电容器并联此后接电源充电.在电源保持联接的状况下,在C质板,则1 中插入一电介(A)C 1 极板上电量增添,C 2 极板上电量减少.(B)C 1 极板上电量减少,C 2 极板上电量增添.(C)C 1 极板上电量增添,C 2 极板上电量不变.(D)C 1 极板上电量减少,C 2 极板上电量不变.第6题图第7题图7. C1和C2两空气电容器,把它们串通成一电容器组.若在C(A)C 1 的电容增大,电容器组总电容减小.(B)C 1 的电容增大,电容器组总电容增大.(C)C 1 的电容减小,电容器组总电容减小.(D)C 1 的电容减小,电容器组总电容增大.1 中插入一电介质板,则8.有两个带电不等的金属球,直径相等,但一个是空心,一个是实心的.现使它们相互接触,则这两个金属球上的电荷(A)不变化.(C)空心球电量多.(B)均匀分配.(D)实心球电量多.9.在空气平行板电容器中,平行地插上一块各向同性均匀电介质板,以以下图.当电容器充电后,若忽视边沿效应,则电介质中的场强 E 与空气中的场强E0对比较,应有(A)E E0,二者方向相同.(B) E E0,二者方向相同.(C) E E0,二者方向相同.(D) E E0,二者方向相反.第9题图10.两个半径不一样带电量相同的导体球,相距很远.今用一修长导线将它们连接起来,则:(A)各球所带电量不变.(B)半径大的球带电量多.(C)半径大的球带电量少.(D)没法确立哪一个导体球带电量多.真空中的稳固磁场1.一铜条置于均匀磁场中,铜条中电子流的方向以以下图.试问下述哪一种状况将会发生?(A)在铜条上a、b两点产生一小电势差,且U a >U b . (B)在铜条上a、b两点产生一小电势差,且U a <U b .(C)在铜条上产生涡流.(D)电子遇到洛仑兹力而减速.第1题图第2题图2. 边长为 l 的正方形线圈,分别用图示两种方式通以电流I(此中ab、cd与正方形共面),在这两种状况下,线圈在此中心产生的磁感觉强度的大小分别为(A) B 1 0,B 2 0 .(B)B 1 0,B 2 22 0 I / l.(C)B12 2 0 I / l ,B 2 0 .(D)B 1 2 2 0 I / l ,B 2 2 2 0 I / l .3. 一电荷量为q的粒子在均匀磁场中运动,以下哪一种说法是正确的?(A)只要速度大小相同,粒子所受的洛仑兹力就相同.(B)在速度不变的前提下,若电荷q变成-q,则粒子受力反向,数值不变. (C)粒子进入磁场后,其动能和动量都不变.(D)洛仑兹力与速度方向垂直,所以带电粒子运动的轨迹必定是圆.4. 两个齐心圆线圈,大圆半径为R,通有电流I 1;小圆半径为r,通有电流I 图.若 r<<R (大线圈在小线圈处产生的磁场近似为均匀磁场),当它们处在同一平面内时小线 圈所受磁力矩的大小为2,方向如I1I 2 r 20 I 1I 2 r 2(A)2R.(B)2R.0 I 1I 2R 2(C) 2r. (D)0第 4题图第5题图5. 以以下图,在磁感觉强度为B 的均匀磁场中,有一圆形载流导线,a、b、c是其上三个长度相等的电流元,则它们所受安培力大小的关系为(A)F a >F b >F c .(B)F a <F b <F c .(C)F b >F c >F a .(D)F a >F c >F b .6. 电流由长直导线1沿切向经a点流入一个电阻均匀分布的圆环,再由b点沿切向从圆环流出,经长直导线2返回电源 (如图) .已知直导线上电流强度为I,圆环的半径为R,且a、b和圆心O在同向来线上.设长直载流导线1、 2 和圆环分别在O点产生的磁感觉强度为B1 ,B 2 ,B 3,则圆心处磁感觉强度的大小(A)B=0,因为B=B =B =0.123 (B)B=0,因为固然B 1≠0,B 2≠0,但 B 1B 2 0 , B 3=0.(C)B≠0,因为B1≠0,B 2≠0,B 3≠0.(D)B≠0,因为固然B3=0,但B 1 B 2 0 .第6题图 第 7题图7. 在图(a)和(b)中各有一半径相同的圆形回路L、L 2,圆周内有电流I1、I ,其分布12相同,且均在真空中,但在(b)图中L2回路外有电流I,P 1、P2为两圆形回路上的对应3点,则:(A) L 1B dlL 2 B dl , B P 1B P 2(B) L 1 B dl L 2B dl , B P 1 B P 2 .(C) L 1 BdlL 2B dl , B P 1B P 2 .B dlB dl , B P 1BP 2(D)L 1L 2.8. 一电子以速度v 垂直地进入磁感觉强度为B 的均匀磁场中,此电子在磁场中运动轨道所围的面积内的磁通量将(A)正比于B,反比于v 2 .(B)反比于B,正比于v 2 .(C)正比于B,反比于v .(D)反比于B,反比于v .第 8 题图第 9题图9.把轻的正方形线圈用细线挂在载流直导线AB的周边,二者在同一平面内,直导线AB固定,线圈可以活动.当正方形线圈通以以以下图的电流时线圈将(A)不动.(B)发生转动,同时凑近导线AB. (C)发生转动,同时走开导线AB. (D)凑近导线AB.(E)走开导线AB.10. 两根载流直导线相互正交搁置,以以下图.I1 沿Y轴的正方向流动,I2 沿Z轴负方向流动.若载流I 1 的导线不可以动,载流I 2 的导线可以自由运动,则载流I 2 的导线开始运动的趋向是(A)沿X方向平动.(B)以X为轴转动.(C)以Y为轴转动.(D)没法判断.第 10题图第 11题图11. 在匀强磁场中,有两个平面线圈,其面积A1=2A 2,通有电流I1=2I 2,它们所受的最大磁力矩之比M1/M 2 等于(A)1.(B)2.(C)4.(D)1/4.12. 如图,无穷长直载流导线与正三角形载流线圈在同一平面内,若长直导线固定不动,则载流三角形线圈将(A)向着长直导线平移.(B)走开长直导线平移.(C)转动.(D)不动.13. 取一闭合积分回路L,使三根载流导线穿过它所围成的面.现改变三根导线之间的相互间隔,但不越出积分回路,则(A)回路L内的∑I不变,L上各点的 B 不变. (B)回路L内的∑I不变,L上各点的 B 改变. (C)回路L内的∑I改变,L上各点的B 不变.(D)回路L内的∑I改变,L上各点的B 改变.14. 四条平行的无穷长直导线,垂直经过边长为a= 20cm的正方形极点,每条导线中的电流都是I= 20A,这四条导线在正方形中心O点产生的磁感觉强度为-(A) B 0.(B) (C) B 0.8 104T .(D)B104T .B104T .第 14题图 第 15题图15. 如图,匀强磁场中有一矩形通电线圈,它的平面与磁场平行,在磁场作用下,线圈发生转动,其方向是(A)ab边转入纸内,cd边转出纸外.(B)ab边转出纸外,cd边转入纸内.(C)ad边转入纸内,bc边转出纸外.(D)ad边转出纸外,bc边转入纸内.16. 一个电流元idl位于直角坐标系原点,电流沿Z轴方向,空间点P(x,y,z)的磁感应强度沿x轴的重量是:(A)0;(B)(4 )i y dl (x 2 y 2z 2 )3 2 ;(C)(4 )i x dl (x 2 y 2z 2 ) 3 2 ;222(D) ( 0 4 )i y dl (x y z ) .17. 图为四个带电粒子在O点沿相同方向垂直于磁力线射入均匀磁场后的偏转轨迹的照片 . 磁场方向垂直纸面向外,轨迹所对应的四个粒子的质量相等,电量大小也相等,则此中动能最大的带负电的粒子的轨迹是(A)Oa.(B)Ob.(C)Oc.(D)Od.第 17题图第 18题图18. 把轻的导线圈用线挂在磁铁N极周边,磁铁的轴线穿过线圈中心,且与线圈在同一平面内,以以下图.当线圈内通以以以下图方向的电流时,线圈将(A)不动.(B)发生转动,同时凑近磁铁. (C)发生转动,同时走开磁铁. (D)不发生转动,只凑近磁铁.(E)不发生转动,只走开磁铁.19. 磁场由沿空心长圆筒形导体的均匀分布的电流产生,圆筒半径为R,x坐标轴垂直圆筒轴线,原点在中心轴线上,图(A)~(E)哪一条曲线表示B-x的关系? (B)20. 有一由N匝细导线绕成的平面正三角形线圈,边长为a,通有电流I,置于均匀外磁场中,当线圈平面的法向与外磁场同向时,该线圈所受的磁力矩Mm 值为:B(A)3Na 2IB 2 .(B)3Na 2IB 4 . (C) 3Na 2IB sin 60 0. (D)0.21. 如图,两根直导线ab和cd沿半径方向被接到一个截面到处相等的铁环上,稳恒电流I从a端流入而从d端流出,则磁感觉强度B dlB 沿图中闭合路径L的积分L等于(A) I . (B) I/3 .(C) I/4 .(D) 2 I /3.第 21题图第23题图22. 若要使半径为4 10 -3m 的裸铜线表面的磁感觉强度为 7.5 10- 5T ,则铜线中需要经过的电流为(A) A. (B)A. (C) 14A.(D) A.23. 以以下图带负电的粒子束垂直地射入两磁铁之间的水平磁场,则:(A)粒子以原有速度在本来的方向上连续运动.(B)粒子向N极挪动.(C)粒子向S极挪动.(D)粒子向上偏转.(E)粒子向下偏转.24. 若空间存在两根无穷长直载流导线,空间的磁场分布就不拥有简单的对称性,则该磁场分布(A)不可以用安培环路定理来计算. (B)可以直接用安培环路定理求出.(C)只好用毕奥-萨伐尔-拉普拉斯定律求出.(D)可以用安培环路定理和磁感觉强度的叠加原理求出.25. 图示一测定水平方向匀强磁场的磁感觉强度 B (方向见图) 的实验装置.位于竖直面内且横边水平的矩形线框是一个多匝的线圈.线框挂在天平的右盘下,框的下端横边位于待测磁场中.线框没有通电时,将天平调理均衡;通电后,因为磁场对线框的作用力而破坏了天平的均衡,须在天平左盘中加砝码m才能使天平重新均衡.若待测磁场的磁感觉强度增为本来的3倍,而经过线圈的电流减为本来的 1/2,磁场和电流方向保持不变,则要使天平重新均衡,其左盘中加的砝码质量应为(A)6m.(C)2m/3.(B)3m/2.(D)m/6.(E)9m/2.第 25题图有介质时的稳恒磁场1. 关于稳恒磁场的磁场强度 H 的以下几种说法中哪个是正确的?(A) H 仅与传导电流有关.(B)若闭合曲线内没有包围传导电流,则曲线上各点的 H 必为零.(C)若闭合曲线上各点H 均为零,则该曲线所包围传导电流的代数和为零.(D)以闭合曲线L为边沿的任意曲面的H 通量均相等.2. 图示为载流铁芯螺线管,此中哪个图画得正确?(即电源的正负极,铁芯的磁性,磁力 线方向相互不矛盾.)(C)第3题图3. 附图中,M、P、O由软磁资料制成的棒,三者在同一平面内,当K闭合后,(A)M的左端出现N极.(B)P的左端出现N极.(C)O的右端出现N极.(D)P的右端出现N极.4. 磁介质有三种,用相对磁导率 r 表征它们各自的特征时,(A)顺磁质 >0,抗磁质 r <0,铁磁质 r >>1 .r (B)顺磁质 r >1,抗磁质 r =1,铁磁质 r >>1 .(C)顺磁质r >1,抗磁质 r <1,铁磁质r >>1 .(D)顺磁质r >0,抗磁质r <0,铁磁质 r >1.5. 用细导线均匀密绕成长为l 、半径为 a(l>> a)、总匝数为N的螺线管,管内充满相对磁导率为r 的均匀磁介质.若线圈中载有稳恒电流I,则管中任意一点的(A)磁感觉强度大小为 B= 0 r NI .(B)磁感觉强度大小为B= rNI /l(C)磁场强度大小为H=NI /l .(D)磁场强度大小为H=NI /l .电磁感觉1. 在一中空圆柱面上绕有两个完整相同的线圈aa'和bb',当线圈aa'和bb'如图(1)绕制及联系时,ab间自感系数为L1;如图(2)相互重叠绕制及联系时,ab间自感系数为L2.则(A)L 1=L 2=0.(B)L1=L2≠ 0.(C)L 1=0,L 2≠0.(D)L1≠ 0,L2=0.第1题图第2题图2.面积为S和2S的两圆线圈1、2如图搁置,通有相同的电流I.线圈1的电流所产生的经过线圈2的磁通用Φ21 表示,线圈2的电流所产生的经过线圈1的磁通用Φ12 表示,则Φ21和Φ 12 的大小关系为:/2.(A)Φ 21=2Φ 12 .(B)Φ 21 =Φ 12(C)Φ 21 =Φ 12.(D)Φ 21>Φ 12.3. 一根长度为L的铜棒,在均匀磁场 B 中以匀角速度旋转着, B 的方向垂直铜棒转动的平面,如图.设t=0时,铜棒与Ob成角,则在任一时辰t这根铜棒两端之间的感觉电动势是:(A)L2 Bcos(t+).(B) [ L2Bcost ]/2.(C)2L2Bcos(t+).(D)L2 B.(E)L2B /2.第3题图第5题图4.用线圈的自感系数L来表示载流线圈磁场能量的公式W m=LI 2/2(A)只合用于无穷长密绕螺线管.(B)只合用于单匝圆线圈.(C)只合用于一个匝数很多,且密绕的螺线环.(D)合用于自感系数L必定的任意线圈.5. 有甲乙两个带铁芯的线圈以以下图.欲使乙线圈中产生图示方向的感生电流i ,可以采纳下列哪一种方法?(A)接通甲线圈电源.(B)接通甲线圈电源后,减少变阻器的阻值.(C)接通甲线圈电源后,甲乙相互凑近.(D)接通甲线圈电源后,抽出甲中铁芯.旋转(如图所6. 一矩形线框长为a宽为b,置于均匀磁场中,线框绕OO 轴,以匀角速度示).设t=0时,线框平面处于纸面内,则任一时辰感觉电动势的大小为(A) 2abBcos t(B)abB .1abB cos t(C)2.(D)abBcos t(E)abBsin t第 6题图第 7题图7. 以以下图的电路中,A、B是两个完整相同的小灯泡,其内阻r>> R,L是一个自感系数相当大的线圈,其电阻与R相等.当开关K接通和断开时,关于灯泡A和B的状况下边哪一种说法正确?(A)K接通时,I A >I B . (B)K接通时,I (C)K断开时,两灯同时熄灭.(D)K断开时,I8. 两根无穷长平行直导线载有大小相等方向相反的电流I,I以一矩形线圈位于导线平面内(如图),则:A =IB .A =IB .dI/dt的变化率增添,(A)线圈中无感觉电流.(B)线圈中感觉电流为顺时针方向. (C)线圈中感觉电流为逆时针方向.(D)线圈中感觉电流方向不确立.第8题图第9题图9. 如图,两个线圈P和Q并联地接到一电动势恒定的电源上.线圈P的自感和电阻分别是线圈Q的两倍,线圈P和Q之间的互感可忽视不计.当达到稳固状态后,线圈P的磁场能量与Q的磁场能量的比值是(A)4.(B)2.(C)1.(D) 1/2 .10. 如图,M、N为水平面内两根平行金属导轨,ab与cd为垂直于导轨并可在其上自由滑动的两根直裸导线.外磁场垂直水平面向上.当外力使ab向右平移时,cd(A)不动.(B)转动. (C)向左挪动.(D)向右挪动.第10题图第 11题图11. 如图,矩形地域为均匀稳恒磁场,半圆形闭合导线回路在纸面内绕轴O作逆时针方向匀角速转动,O点是圆心且恰好落在磁场的边沿上,半圆形闭合导线完整在磁场外时开始计 时.图(A)─(D)的-t函数图象中哪一条属于半圆形导线回路中产生的感觉电动势?12. 在以以下图的装置中,把静止的条形磁铁从螺线管中按图示状况抽出时(A)螺线管线圈中感生电流方向如A点处箭头所示.(B)螺线管右端感觉呈S极.(C)线框EFGH从图下方粗箭头方向看去将逆时针旋转.(D)线框EFGH从图下方粗箭头方向看去将顺时针旋转.第 12题图第 13题图13. 如图,导体棒AB在均匀磁场B中绕经过C点的垂直于棒长且沿磁场方向的轴OO'转动(角速度与 B 同方向),BC的长度为棒长的1/3 .则 (A)A点比B点电势高. (B)A点与B点电势相等.(C)A点比B点电势低.(D)有稳恒电流从A点流向B点.14. 一个圆形线环,它的一半放在一分布在方形地域的匀强磁场B 中,另一半位于磁场以外,以以下图.磁场 B 的方向垂直指向纸内.欲使圆线环中产生逆时针方向的感觉电流,应使(A)线环向右平移.(B)线环向上平移.(C)线环向左平移.(D)磁场强度减弱.第14题图第 17题图15. 在真空中一个通有电流的线圈a 所产生的磁场内有另一个线圈b,a 和b相对地点固定.若线圈b中没有电流经过,则线圈b与a 间的互感系数:(A)必定为零.(B)必定不为零.(C)可以不为零.(D)是不行能确立的.16. 一块铜板放在磁感觉强度正在增大的磁场中时,铜板中出现涡流(感觉电流),则涡流将(A)加快铜板中磁场的增添. (B)减缓铜板中磁场的增添.(C)对磁场不起作用.(D)使铜板中磁场反向.17. 如图,长度为 l 的直导线ab在均匀磁场B 中以速度 v挪动,直导线ab中的电动势为(A) Blv .(B) Blv sin .(C) Blv cos .(D)0.18. 尺寸相同的铁环与铜环所包围的面积中,通以相同变化率的磁通量,环中:(A) 感觉电动势不一样.(B) 感觉电动势相同,感觉电流相同. (C) 感觉电动势不一样,感觉电流相同.(D) 感觉电动势相同,感觉电流不一样.19. 在无穷长的载流直导线周边搁置一矩形闭合线圈,开始时线圈与导线在同一平面内,且线圈中两条边与导线平行,当线圈以相同的速率作以以下图的三种不一样方向的平动时,线圈中的感觉电流(A)以状况Ⅰ中为最大.(B)以状况Ⅱ中为最大.(C)以状况Ⅲ中为最大.(D)在状况Ⅰ和Ⅱ中相同. 第19题图第22题图20. 一导体圆线圈在均匀磁场中运动,能使此中产生感觉电流的一种状况是(A)线圈绕自己直径轴转动,轴与磁场方向平行.(B)线圈绕自己直径轴转动,轴与磁场方向垂直. (C)线圈平面垂直于磁场并沿垂直磁场方向平移.(D)线圈平面平行于磁场并沿垂直磁场方向平移.21. 自感为 0.25 H的线圈中,当电流在( 1/ 16)s内由2A均匀减小到零时,线圈中自感电动势的大小为:(A) 7.8 × 10-3V.(B) 2.0 V.(C) 8.0 V.(D)× 10-2V.22. 以以下图,一载流螺线管的旁边有一圆形线圈,欲使线圈产生图示方向的感觉电流 i ,以下哪一种状况可以做到?(A)载流螺线管向线圈凑近.(B)载流螺线管走开线圈.(C)载流螺线管中电流增大.(D)载流螺线管中插入铁芯.23. 真空中一根无穷长直细导线上通有电流强度为I的电流,则距导线垂直距离为a的空间某点处的磁能密度为1(0 I) 21(0 I)2(B)202 a(A) 22 a1 2 a21( 0 I22 ()2)(C)0 I(D)2a24. 以以下图,闭合电路由带铁芯的螺线管,电源,滑线变阻器构成.问在以下哪一种状况下可使线圈中产生的感觉电动势与原电流I的方向相反.(A)滑线变阻器的触点A向左滑动.(B)滑线变阻器的触点A向右滑动.(C)螺线管上接点B向左挪动(忽视长螺线管的电阻).(D)把铁芯从螺线管中抽出.25. 将形状完整相同的铜环和木环静止搁置,并使经过两环面的磁通量随时间的变化率相等,则(A)铜环中有感觉电动势,木环中无感觉电动势. (B)铜环中感觉电动势大,木环中感觉电动势小. (C)铜环中感觉电动势小,木环中感觉电动势大.(D)两环中感觉电动势相等.光的干涉1. 在真空中波长为λ的单色光,在折射率为n的透明介质中从A沿某路径流传到B,若A、B两点位相差为3 ,则此路径AB的光程为(A)λ. (B) nλ. (C) 3λ.(D) λ/n2. 在相同的时间内,一束波长为λ的单色光在空气中和在玻璃中(A)流传的行程相等,走过的光程相等.(B)流传的行程相等,走过的光程不相等.(C)流传的行程不相等,走过的光程相等.(D)流传的行程不相等,走过的光程不相等.3.用白光光源进行双缝实验,若用一个纯红色的滤光片掩饰一条缝,用一个纯蓝色的滤光片掩饰另一条缝,则(A)干涉条纹的宽度将发生改变.(B)产生红光和蓝光的两套彩色干涉条纹.(C)干涉条纹的亮度将发生改变.(D)不产生干涉条纹.4.在双缝干涉实验中,为使屏上的干涉条纹间距变大,可以采纳的方法是(A)使屏凑近双缝.(B)使两缝的间距变小.(C)把两个缝的宽度略微调窄.(D)改用波长较小的单色光源5.在迈克耳孙干涉仪的一条光路中,放入一折射率为n,厚度为d的透明薄片,放入后,这条光路的光程改变了(A)2(n-1)d.(B)2nd.(C)2(n-1)d+λ/2.(D)nd.(E)(n-1)d.6. 在双缝干涉实验中,光的波长为600 nm( 1nm= 10-9m),双缝间距为2mm,双缝与屏的间距为 300cm.在屏上形成的干涉图样的明条纹间距为(A)mm.(B)mm.(C) 3.1 mm(D) 1.2 mm.7.在迈克尔逊干涉仪的一支光路中,放入一片折射率为n的透明介质薄膜后,测出两束光的光程差的改变量为一个波长λ,则薄膜的厚度是(A)λ/2.(B)λ/(2n).(C)λ/n.(D)λ /2( n -1)8. 如图,S1、S2是两个相关光源,它们到P点的距离分别为r 1 和r 2.路径S1P垂直穿过一块厚度为t 1,折射率为n 1 的介质板,路径S2P垂直穿过厚度为t 2,折射率为n 2 的另一介质板,其他部分可看作真空,这两条路径的光程差等于(A)(r 2+n 2t 2)-(r 1+n 1t 1)(B) [r2+ (n2- 1)t2]- [r1+ (n1- 1)] t1(C)(r 2-n 2t 2)-(r 1-n 1t 1)(D)n 2t 2-n 1t 1第8题图第9题图9. 在双缝干涉实验中,若单色光源S到两缝SS 1、S 2 距离相等,则观察屏上中央明条纹位于图中O处.现将光源S向下挪动到表示图中的地点,则(A)中央明条纹也向下挪动,且条纹间距不变.(B)中央明条纹向上挪动,且条纹间距不变.(C)中央明条纹向下挪动,且条纹间距增大.(D)中央明条纹向上挪动,且条纹间距增大10.真空中波长为λ的单色光,在折射率为n的均匀透明媒质中,从A点沿某一路径流传到B点,路径的长度为 L .A、B两点光振动位相差记为Δφ,则(A) L=3λ/2,Δφ=3π.(B) L=3λ/(2n),Δφ=3nπ.(C) L=3λ/(2n),Δφ=3π.(D) L =3nλ/2,Δφ=3nπ光的衍射1.丈量单色光的波长时,以下方法中哪一种方法最为正确?。
大学物理(下册)习题与答案

大学物理练习册物理教研室遍热力学(一)一、选择题:1、如图所示,当汽缸中的活塞迅速向外移动从而使汽缸膨胀时,气体所经历的过程(A)是平衡过程,它能用P—V图上的一条曲线表示。
(B)不是平衡过程,但它能用P—V图上的一条曲线表示。
(C)不是平衡过程,它不能用P—V图上的一条曲线表示。
(D)是平衡过程,但它不能用P—V图上的一条曲线表示。
[ ]2、在下列各种说法中,哪些是正确的?[ ](1)热平衡就是无摩擦的、平衡力作用的过程。
(2)热平衡过程一定是可逆过程。
(3)热平衡过程是无限多个连续变化的平衡态的连接。
(4)热平衡过程在P—V图上可用一连续曲线表示。
(A)(1)、(2)(B)(3)、(4)(C)(2)、(3)、(4)(D)(1)、(2)、(3)、(4)3、设有下列过程:[ ](1)用活塞缓慢的压缩绝热容器中的理想气体。
(设活塞与器壁无摩擦)(2)用缓慢地旋转的叶片使绝热容器中的水温上升。
(3)冰溶解为水。
(4)一个不受空气阻力及其它摩擦力作用的单摆的摆动。
其中是逆过程的为(A)(1)、(2)、(4)(B)(1)、(2)、(3)(C)(1)、(3)、(4)(D)(1)、(4)4、关于可逆过程和不可逆过程的判断:[ ](1)可逆热力学过程一定是准静态过程。
(2)准静态过程一定是可逆过程。
(3)不可逆过程就是不能向相反方向进行的过程。
(4)凡有摩擦的过程,一定是不可逆过程。
以上四种判断,其中正确的是(A)(1)、(2)、(3)(B)(1)、(2)、(4)(C)(2)、(4)(D)(1)、(4)5、在下列说法中,哪些是正确的?[ ](1)可逆过程一定是平衡过程。
(2)平衡过程一定是可逆的。
(3)不可逆过程一定是非平衡过程。
(4)非平衡过程一定是不可逆的。
(A)(1)、(4)(B)(2)、(3)(C)(1)、(2)、(3)、(4)(D)(1)、(3)6、置于容器的气体,如果气体各处压强相等,或气体各处温度相同,则这两种情况下气体的状态 [ ](A )一定都是平衡态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. 如图,长载流导线和相互垂直, 它们相距l,固定不动,能绕中点 O 转动,并能靠近或离开 ,当电流 方向如图所示时,导线 将
(A) 顺时针转动同时离开; (B) 顺时针转动同时靠近 ; (C)(C) 逆时针转动同时离开 ; (D)(D) 逆时针转动同时靠近 .
b
d
II
Ov
c
F
a
c
v F
v
b
F
I
大 学 物 理 下 综 合 测 试 题
1. 图中六根无限长导线互相绝缘, 通过电流均为I,区域I、、、 均为相等的正方形,那一个区 域指向纸内的磁通量最大?
(A) I区域; (B) 区域;
(B)(C) 区域; (D) 区域; (E)最大不止一个
载流直导线
B 0I 2 a
I
II
III
IV
2. 一张气泡室照片表明,质子的运动 轨迹是一半径为10cm的圆弧,运动轨 迹平面与磁场垂直,磁感应强度的大 小为0.3Wb/m2。该质子动能的数量级
S1
r1
p
(C) 2 1 2 r 2 r 1/ 2 k ; S 2 (D) 2 1 2 r 1 r 2/ 2 k 。
r2
1
1
2
r1
2
2
2
r2
13. 在双缝干涉实验中,入射光的 波长为 ,用玻璃纸遮住双缝中的 一个,若玻璃纸中光程比相同厚度 的空气的光程大2.5 ,则屏上原来 的明纹处
(A) 仍为明条纹; (B) 变为暗条纹;
;
y m
;0 . 5
u
(D)(Dy)0.50cos14t2,(SI)
。 1 O1 2 3
xm
此题只能逐个检验。
解: 设P的振动方程为:
yoAcos(t0)
已知: A0.5 28
uu
yo0.5cos(8ut0)
由于 t2s,yo0,00
00.5cos(8u20)
8u 0.5sin(8u 20)0
(A) 0
(B) 0 I 4R
(C)(C)2 0 I 4R
(D)(D) 0 I R
;
;
;
; (E) 2 0 I 8R
I
a
b I
。四段导线并联
9. 一沿x轴负方向传播的平面简谐波
在2s时的波形曲线如图所示,则原
点o的振动方程为
(A) y0.50cos(t),(SI) ;
2
(B) y0.50cos12t2,(SI) (C)(Cy)0.50cos12t2,(SI)
11. 一质点作简谐振动,其运动速度 与时间的曲线如图所示。若质点的振 动规律用余弦函数描述,其初相应为 (A) / 6 ; (B) 5 / 6 ;
(B)(C5) / 6 ; (D) / 6 ; (E2) /3 。
yAcos(t0)
vm / s
vA sin(t0)
1 vm
2 vm
t0
v0 Asin0 12vm
r B
vd
I vF FI
(D)(D) 向右移动 。
c
a
bM v
N
阻碍磁通量的变化,即阻碍面积的变化
7. 两个同心圆线圈,大圆半径为R, 通有电流I1;小圆半径为r,通有电 流I2,方向如图。若r<<R(大线圈 在小线圈处产生的磁场近似为均匀 磁场),当它们处在同一平面内时 小线圈所受磁力矩的大小为:
(B)(C) 既非明条纹也非暗条纹;
(C)(D) 无法确定是明条纹还是暗条纹。
r d x d'
k
加强
(2k 1) 2
减弱
14. 如图所示,平板玻璃和凸透镜 构成牛顿环装置,全部浸入1.60 的液体中,凸透镜可沿’移动。用
16. 当一平面简谐机械波在弹性媒质 中传播时,下述结论哪个是正确的?
(A) 媒质质元的振动动能增大时,其 (B) 弹性势能减小,总机械能守恒; (C)(B) 媒质质元的振动动能和弹性势能 (D) 都作周期性变化,但二者的相位不相同; (E)(C) 媒质质元的振动动能和弹性势能的相位 (F) 在任意时刻都相同,但二者的数值不相等; (G)(D) 媒质质元在其平衡位置处弹性势能最大。
y m u
0 .5
1 O 1 2 3
xm
16
u
0
2
0
2
16
u
yo0.5cos(8ut216 u)
10. 当机械波在媒质中传播时, 一媒质质元的最大形变量发生在:
(A) 媒质质元离开其平衡位置最大位移处; (B) 媒质质元离开其平衡位置 2 A / 2 处; (C)(C) 媒质质元在其平衡位置处 ; (D)(D) 媒质质元离开其平衡位置A / 2 处 (E) (A是振动振幅).
m 1 .6 7 1 0 2 7 k g ,e 1 .6 1 0 1 9 C
(A) 0.01MeV; (B) 0.1MeV ;
(B)(C) 1MeV ;
(D) 10MeV; (E) 100MeV.
v
F
eB
2
m
e B R 3106
R
m
v B
1m2 1eBR e10.30.1
22
2
0.045MeV
O
ts
vm
sin 0
1 2
0
6
or
5
6
O
x
vm
12. 如图所示,两列波长为 的相干
波在P点相遇。波在S1点振动的初相
是 1 ,S1到P点的距离是r1;波在S2
点的初相是 2 ,S2到P点的距离是r2 。
以k代表零或正、负整数,则 P 点是
干涉极大的条件为:
(A) r2 r1 k ;
(B) 2 1 2k ;
OI
d
a
4. 顺磁物质的磁导率: (A) 比真空的磁导率略小; (B) 比真空的磁导率略大; (C)(C) 远小于真空的磁导率; (D)(D) 远大于真空的磁导率.
5. 用线圈自感系数L表示载流线圈磁场能量的公式
(A) 只适用于无限长密绕螺线管; (B) 只适用于单匝圆线圈;
Wm
1 2
LI 2
(C)(C) 只适用于一个匝数很多且密绕的螺线管;
(A) 0 I 1 I 2 r 2
2R
(B) 0 I 1 I 2 r 2 2R
(C)(C)0 I 1 I 2 r 2 2r
; ;
;
(D)(D) 0
。
I1 I2 o r
R
M v IS e v n B v m v B v
8. 如图两个半径为R的相同的金属环 在 a、b两点接触(连线为环直径), 并相互垂直放置。电流 I沿连线方 向由a 端流入,b 端流出,则环中心 O点的磁感应强度的大小为
(D)(D) 适用于自感系数L一定的任意线圈.
L d d t dd L tI (L d d I t Id d L t)
6. 如图所示,M、N 为水平面内
两根平行金属导轨,与为垂直于
导轨并可以在其上自由滑动的两
根直裸导线。外磁场垂直水平面
向上,当外力使向右平移时,
(A) 不动; (B) 转动 ; (C)(C) 向左移动;
