大学物理2,13.第十三章思考题
大学课程大二物理第13章(3)课件

部分偏振光
(3)椭圆(圆)偏振光 振动矢量的大小、方向都随时间变化
椭圆偏振光 振动矢量的大小不变、方向随时间变化
圆偏振光
(4)自然光 实际的光源是大量原子发出自然光,包含着无 数多个振动方向,但机会均等。
自然光可分解为两个垂直的、振幅相等 的独立光振动。 自然光的光路
偏振片有起偏与检偏作用
偏振化方向
M
N
M
起偏器
N 检偏器
2.马吕斯定律 研究透射光的强度
I0 A02
I A2
I I0
A2 A02
A02cos2
A02
注意
I I0cos2 ——马吕斯定律
1º若自然光入射前的强度是 I0, 则过a后的强度
是 I0 2 2º由马吕斯定律知
0, 180o 90o, 270o
马吕斯发现:自然光反射时,可以产生部分偏振 光或完全偏振光。
当 i = i0时,反射光为完全偏振光, i0叫“起偏角”。
完
部
ii
分 偏
振
全
i0 i0
偏 振
光
光
2.布儒斯特定律
反射光是完全偏振光时, 实验证明:
i0
i0
2
n1sini0 n2sin
n2sin(2 i0) n2cosi0
布儒斯特定律的实质:
E 的平行分量在iB角入射时, 不反射全部透射。
应用: 1º可由反射获得线偏振光
例如激光器中的布儒斯特窗
布儒斯特窗
iB
最后得到
的线偏振光
2º可测不透明媒质折射率 tgiB tgi0 n
3º若反射光是部分偏振光, 利用偏振片可消去大部
大学物理第十三章课后习题答案

第十三章 热力学基础13 -1 如图所示,bca 为理想气体绝热过程,b1a 和b2a 是任意过程,则上述两过程中气体作功与吸收热量的情况是( )(A) b1a 过程放热,作负功;b2a 过程放热,作负功(B) b1a 过程吸热,作负功;b2a 过程放热,作负功(C) b1a 过程吸热,作正功;b2a 过程吸热,作负功(D) b1a 过程放热,作正功;b2a 过程吸热,作正功分析与解 bca ,b1a 和b2a 均是外界压缩系统,由⎰=V p W d 知系统经这三个过程均作负功,因而(C)、(D)不对.理想气体的内能是温度的单值函数,因此三个过程初末态内能变化相等,设为ΔE .对绝热过程bca ,由热力学第一定律知ΔE =-W bca .另外,由图可知:|W b2a |>|W bca |>|W b1a |,则W b2a <W bca <W b1a .对b1a 过程:Q =ΔE +W b1a >ΔE +W bca =0 是吸热过程.而对b2a 过程:Q =ΔE +W b2a <ΔE +W bca =0 是放热过程.可见(A)不对,正确的是(B).13 -2 如图,一定量的理想气体,由平衡态A 变到平衡态B ,且它们的压强相等,即p A =p B ,请问在状态A 和状态B 之间,气体无论经过的是什么过程,气体必然( )(A) 对外作正功 (B) 内能增加(C) 从外界吸热 (D) 向外界放热分析与解 由p -V 图可知,p A V A <p B V B ,即知T A <T B ,则对一定量理想气体必有E B >E A .即气体由状态A 变化到状态B,内能必增加.而作功、热传递是过程量,将与具体过程有关.所以(A)、(C)、(D)不是必然结果,只有(B)正确.13 -3 两个相同的刚性容器,一个盛有氢气,一个盛氦气(均视为刚性分子理想气体).开始时它们的压强和温度都相同,现将3J 热量传给氦气,使之升高到一定的温度.若使氢气也升高同样的温度,则应向氢气传递热量为( )(A) 6J (B) 3 J (C) 5 J (D) 10 J分析与解 当容器体积不变,即为等体过程时系统不作功,根据热力学第一定律Q =ΔE +W ,有Q =ΔE .而由理想气体内能公式T R i M m E Δ2Δ=,可知欲使氢气和氦气升高相同温度,须传递的热量 ⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=e e e 222e 2H H H H H H H H /:i M m i M m Q Q .再由理想气体物态方程pV =mM RT ,初始时,氢气和氦气是具有相同的温度、压强和体积,因而物质的量相同,则3/5/:e 2e 2H H H H ==i i Q Q .因此正确答案为(C).13 -4 有人想像了四个理想气体的循环过程,则在理论上可以实现的为( )分析与解由绝热过程方程pVγ=常量,以及等温过程方程pV=常量,可知绝热线比等温线要陡,所以(A)过程不对,(B)、(C)过程中都有两条绝热线相交于一点,这是不可能的.而且(B)过程的循环表明系统从单一热源吸热且不引起外界变化,使之全部变成有用功,违反了热力学第二定律.因此只有(D)正确.13 -5一台工作于温度分别为327 ℃和27 ℃的高温热源与低温源之间的卡诺热机,每经历一个循环吸热2 000 J,则对外作功()(A) 2 000J(B) 1 000J(C) 4 000J(D) 500J分析与解热机循环效率η=W/Q吸,对卡诺机,其循环效率又可表为:η=1-T2 /T1,则由W /Q吸=1 -T2 /T1可求答案.正确答案为(B).13 -6根据热力学第二定律()(A) 自然界中的一切自发过程都是不可逆的(B) 不可逆过程就是不能向相反方向进行的过程(C) 热量可以从高温物体传到低温物体,但不能从低温物体传到高温物体(D) 任何过程总是沿着熵增加的方向进行分析与解 对选项(B):不可逆过程应是指在不引起其他变化的条件下,不能使逆过程重复正过程的每一状态,或者虽然重复但必然会引起其他变化的过程.对选项(C):应是热量不可能从低温物体自动传到高温物体而不引起外界的变化.对选项(D):缺少了在孤立系统中这一前提条件.只有选项(A)正确. 13 -7 位于委内瑞拉的安赫尔瀑布是世界上落差最大的瀑布,它高979m.如果在水下落的过程中,重力对它所作的功中有50%转换为热量使水温升高,求水由瀑布顶部落到底部而产生的温差.( 水的比热容c 为4.18×103 J·kg-1·K -1 ) 分析 取质量为m 的水作为研究对象,水从瀑布顶部下落到底部过程中重力作功W =mgh ,按题意,被水吸收的热量Q =0.5W ,则水吸收热量后升高的温度可由Q =mc ΔT 求得.解 由上述分析得mc ΔT =0.5mgh水下落后升高的温度ΔT =0.5gh /c =1.15K13 -8 如图所示,一定量的空气,开始在状态A ,其压强为2.0×105Pa ,体积为2.0 ×10-3m 3 ,沿直线AB 变化到状态B 后,压强变为1.0 ×105Pa ,体积变为3.0 ×10-3m 3 ,求此过程中气体所作的功.分析 理想气体作功的表达式为()⎰=V V p W d .功的数值就等于p -V 图中过程曲线下所对应的面积.解 S ABCD =1/2(BC +AD)×CD故 W =150 J13 -9 汽缸内储有2.0mol 的空气,温度为27 ℃,若维持压强不变,而使空气的体积膨胀到原体积的3s 倍,求空气膨胀时所作的功.分析 本题是等压膨胀过程,气体作功()1221d V V p V p W V V -==⎰,其中压强p 可通过物态方程求得.解 根据物态方程11RT pV v =,汽缸内气体的压强11/V RT p v = ,则作功为 ()()J 1097.92/31112112⨯==-=-=RT V V V RT V V p W v v13 -10 一定量的空气,吸收了1.71×103J 的热量,并保持在1.0 ×105Pa 下膨胀,体积从1.0×10-2m 3 增加到1.5×10-2m 3 ,问空气对外作了多少功? 它的内能改变了多少?分析 由于气体作等压膨胀,气体作功可直接由W =p (V 2 -V 1 )求得.取该空气为系统,根据热力学第一定律Q =ΔE +W 可确定它的内能变化.在计算过程中要注意热量、功、内能的正负取值.解 该空气等压膨胀,对外作功为W =p (V 2-V 1 )=5.0 ×102J其内能的改变为Q =ΔE +W =1.21 ×103J13 -11 0.1kg 的水蒸气自120 ℃加热升温到140℃,问(1) 在等体过程中;(2) 在等压过程中,各吸收了多少热量? 根据实验测定,已知水蒸气的摩尔定压热容C p,m =36.21J·mol -1·K -1,摩尔定容热容C V,m =27.82J·mol -1·K -1. 分析 由量热学知热量的计算公式为T C Q m Δv =.按热力学第一定律,在等体过程中,T C E Q ΔΔm V,V v ==;在等压过程中, T C E V p Q ΔΔd m p,p v =+=⎰.解 (1) 在等体过程中吸收的热量为J 101.3ΔΔ3m V,V ⨯===T C Mm E Q (2) 在等压过程中吸收的热量为 ()J 100.4Δd 312m p,p ⨯=-=+=⎰T T C M m E V p Q 13 -12 如图所示,在绝热壁的汽缸内盛有1mol 的氮气,活塞外为大气,氮气的压强为1.51 ×105 Pa ,活塞面积为0.02m 2 .从汽缸底部加热,使活塞缓慢上升了0.5m.问(1) 气体经历了什么过程? (2) 汽缸中的气体吸收了多少热量? (根据实验测定,已知氮气的摩尔定压热容C p ,m =29.12J·mol -1·K -1,摩尔定容热容C V,m =20.80J·mol -1·K -1 )分析 因活塞可以自由移动,活塞对气体的作用力始终为大气压力和活塞重力之和.容器内气体压强将保持不变.对等压过程,吸热T C Q Δm p,p v =.ΔT 可由理想气体物态方程求出.解 (1) 由分析可知气体经历了等压膨胀过程.(2) 吸热T C Q Δm p,p v =.其中ν =1 mol ,C p,m =29.12J·mol -1·K-1.由理想气体物态方程pV =νRT ,得ΔT =(p 2V 2 -p 1 V 1 )/R =p(V 2 -V 1 )/R =p· S· Δl /R则 J 105.293m p,p ⨯==pS ΔSΔl C Q13 -13 一压强为1.0 ×105Pa,体积为1.0×10-3m 3的氧气自0℃加热到100 ℃.问:(1) 当压强不变时,需要多少热量?当体积不变时,需要多少热量?(2) 在等压或等体过程中各作了多少功?分析 (1) 求Q p 和Q V 的方法与题13-11相同.(2) 求过程的作功通常有两个途径.① 利用公式()V V p W d ⎰=;② 利用热力学第一定律去求解.在本题中,热量Q 已求出,而内能变化可由()12m V,V ΔT T C E Q -==v 得到.从而可求得功W .解 根据题给初态条件得氧气的物质的量为mol 1041.4/2111-⨯===RT V p Mm v 氧气的摩尔定压热容R C 27m p,=,摩尔定容热容R C 25m V,=. (1) 求Q p 、Q V等压过程氧气(系统)吸热()J 1.128Δd 12m p,p =-=+=⎰T T C E V p Q v等体过程氧气(系统)吸热()J 5.91Δ12m V,V =-==T T C E Q v(2) 按分析中的两种方法求作功值解1 ① 利用公式()V V p W d ⎰=求解.在等压过程中,T R Mm V p W d d d ==,则得 J 6.36d d 21p ===⎰⎰T T T R Mm W W 而在等体过程中,因气体的体积不变,故作功为()0d V ==⎰V V p W② 利用热力学第一定律Q =ΔE +W 求解.氧气的内能变化为()J 5.91Δ12m V,V =-==T T C Mm E Q 由于在(1) 中已求出Q p 与Q V ,则由热力学第一定律可得在等压过程、等体过程中所作的功分别为J 6.36Δp p =-=E Q W0ΔV V =-=E Q W13 -14 如图所示,系统从状态A 沿ABC 变化到状态C 的过程中,外界有326J 的热量传递给系统,同时系统对外作功126J.当系统从状态C 沿另一曲线CA 返回到状态A 时,外界对系统作功为52J ,则此过程中系统是吸热还是放热?传递热量是多少?分析 已知系统从状态C 到状态A ,外界对系统作功为W CA ,如果再能知道此过程中内能的变化ΔE AC ,则由热力学第一定律即可求得该过程中系统传递的热量Q CA .由于理想气体的内能是状态(温度)的函数,利用题中给出的ABC 过程吸热、作功的情况,由热力学第一定律即可求得由A 至C 过程中系统内能的变化ΔE AC ,而ΔE AC =-ΔE AC ,故可求得Q CA .解 系统经ABC 过程所吸收的热量及对外所作的功分别为Q ABC =326J , W ABC =126J则由热力学第一定律可得由A 到C 过程中系统内能的增量ΔE AC =Q ABC -W ABC =200J由此可得从C 到A ,系统内能的增量为ΔE CA =-200J从C 到A ,系统所吸收的热量为Q CA =ΔE CA +W CA =-252J式中负号表示系统向外界放热252 J.这里要说明的是由于CA 是一未知过程,上述求出的放热是过程的总效果,而对其中每一微小过程来讲并不一定都是放热.13 -15 如图所示,一定量的理想气体经历ACB 过程时吸热700J ,则经历ACBDA 过程时吸热又为多少?分析 从图中可见ACBDA 过程是一个循环过程.由于理想气体系统经历一个循环的内能变化为零,故根据热力学第一定律,循环系统净吸热即为外界对系统所作的净功.为了求得该循环过程中所作的功,可将ACBDA 循环过程分成ACB 、BD 及DA 三个过程讨论.其中BD 及DA 分别为等体和等压过程,过程中所作的功按定义很容易求得;而ACB 过程中所作的功可根据上题同样的方法利用热力学第一定律去求.解 由图中数据有p A V A =p B V B ,则A 、B 两状态温度相同,故ACB 过程内能的变化ΔE CAB =0,由热力学第一定律可得系统对外界作功W CAB =Q CAB -ΔE CAB =Q CAB =700J在等体过程BD 及等压过程DA 中气体作功分别为()⎰==0d BD V V p W()⎰-=-==J 1200d 12A DA V V P V p W则在循环过程ACBDA 中系统所作的总功为J 500DA BD ACB -=++=W W W W负号表示外界对系统作功.由热力学第一定律可得,系统在循环中吸收的总热量为J 500-==W Q负号表示在此过程中,热量传递的总效果为放热.13 -16 在温度不是很低的情况下,许多物质的摩尔定压热容都可以用下式表示2m p,2--+=cT bT a C式中a 、b 和c 是常量,T 是热力学温度.求:(1) 在恒定压强下,1 mol 物质的温度从T 1升高到T 2时需要的热量;(2) 在温度T 1 和T 2 之间的平均摩尔热容;(3) 对镁这种物质来说,若C p ,m 的单位为J·mol -1·K -1,则a =25.7J·mol -1·K-1 ,b =3.13 ×10-3J·mol -1·K-2,c =3.27 ×105J·mol -1·K.计算镁在300K时的摩尔定压热容C p,m ,以及在200K和400K之间C p,m 的平均值. 分析 由题目知摩尔定压热容C p,m 随温度变化的函数关系,则根据积分式⎰=21d m p,p T T T C Q 即可求得在恒定压强下,1mol 物质从T 1 升高到T 2所吸收的热量Qp .故温度在T 1 至T 2之间的平均摩尔热容()12p m p,/T T Q C -=. 解 (1) 11 mol 物质从T 1 升高到T 2时吸热为()()()()11122122122m p,p d 2d 21----+-+-=-+==⎰⎰T T c T T b T T a T cT bT a T C Q T T (2) 在T 1 和T 2 间的平均摩尔热容为()()21212p m p,//T T c T T a T T Q C -+=-=(3) 镁在T =300 K 时的摩尔定压热容为-1-12m p,K mol J 9.232⋅⋅=-+=-cT bT a C镁在200 K 和400 K 之间C p ,m 的平均值为()-1-12112m p,K mol J 5.23/⋅⋅=-+=T T c T T a C13 -17 空气由压强为1.52×105 Pa ,体积为5.0×10-3m 3 ,等温膨胀到压强为1.01×105 Pa ,然后再经等压压缩到原来的体积.试计算空气所作的功. 解 空气在等温膨胀过程中所作的功为()()2111121T /ln /ln p p V p V V RT Mm W == 空气在等压压缩过程中所作的功为()⎰-==12d V V p V p W利用等温过程关系p 1 V 1 =p 2 V 2 ,则空气在整个过程中所作的功为()J 7.55/ln 11122111=-+=+=V p V p p p V p W W W T p13 -18 如图所示,使1mol 氧气(1) 由A 等温地变到B ;(2) 由A 等体地变到C ,再由C 等压地变到B.试分别计算氧气所作的功和吸收的热量.分析 从p -V 图(也称示功图)上可以看出,氧气在AB 与ACB 两个过程中所作的功是不同的,其大小可通过()V V p W d ⎰=求出.考虑到内能是状态的函数,其变化值与过程无关,所以这两个不同过程的内能变化是相同的,而且因初、末状态温度相同T A =T B ,故ΔE =0,利用热力学第一定律Q =W +ΔE ,可求出每一过程所吸收的热量.解 (1) 沿AB 作等温膨胀的过程中,系统作功()()J 1077.2/ln /ln 31⨯===A B B A A B AB V V V p V V RT Mm W 由分析可知在等温过程中,氧气吸收的热量为Q AB =W AB =2.77 ×103J (2) 沿A 到C 再到B 的过程中系统作功和吸热分别为W ACB =W AC +W CB =W CB =p C (V B -V C )=2.0×103JQ ACB =W A CB =2.0×103 J13 -19 将体积为1.0 ×10-4m 3 、压强为1.01×105Pa 的氢气绝热压缩,使其体积变为2.0 ×10-5 m 3 ,求压缩过程中气体所作的功.(氢气的摩尔定压热容与摩尔定容热容比值γ=1.41)分析 可采用题13-13 中气体作功的两种计算方法.(1) 气体作功可由积分V p W d ⎰=求解,其中函数p (V )可通过绝热过程方程pV C γ= 得出.(2)因为过程是绝热的,故Q =0,因此,有W =-ΔE ;而系统内能的变化可由系统的始末状态求出.解 根据上述分析,这里采用方法(1)求解,方法(2)留给读者试解.设p 、V 分别为绝热过程中任一状态的压强和体积,则由γγpV V p =11得 γγV V p p -=11氢气绝热压缩作功为J 0.231d d 121211121-=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡-===⎰⎰-V V V V γp V V V p V p W V V γγ 13 -20 试验用的火炮炮筒长为3.66 m ,内膛直径为0.152 m ,炮弹质量为45.4kg ,击发后火药爆燃完全时炮弹已被推行0.98 m ,速度为311 m·s -1 ,这时膛内气体压强为2.43×108Pa.设此后膛内气体做绝热膨胀,直到炮弹出口.求(1) 在这一绝热膨胀过程中气体对炮弹作功多少?设摩尔定压热容与摩尔定容热容比值为 1.2γ=.(2) 炮弹的出口速度(忽略摩擦).分析 (1) 气体绝热膨胀作功可由公式1d 2211--==⎰γV p V p V p W 计算.由题中条件可知绝热膨胀前后气体的体积V 1和V 2,因此只要通过绝热过程方程γγV p V p 2211=求出绝热膨胀后气体的压强就可求出作功值.(2) 在忽略摩擦的情况下,可认为气体所作的功全部用来增加炮弹的动能.由此可得到炮弹速度.解 由题设l =3.66 m,D =0.152 m ,m =45.4 kg ,l 1=0.98 m ,v 1=311 m·s -1 ,p 1 =2.43×108Pa ,γ=1.2.(1) 炮弹出口时气体压强为()()Pa 1000.5//7112112⨯===γγl l p V V p p 气体作功J 1000.54π11d 6222112211⨯=--=--==⎰D γl p l p γV p V p V p W (2) 根据分析2122121v v m m W -=,则 -121s m 563⋅=+=v 2W/m v13 -21 1mol 氢气在温度为300K,体积为0.025m 3 的状态下,经过(1)等压膨胀,(2)等温膨胀,(3)绝热膨胀.气体的体积都变为原来的两倍.试分别计算这三种过程中氢气对外作的功以及吸收的热量.分析 这三个过程是教材中重点讨论的过程.在p -V 图上,它们的过程曲线如图所示.由图可知过程(1 ) 作功最多, 过程( 3 ) 作功最少.温度T B >T C >T D ,而过程(3) 是绝热过程,因此过程(1)和(2)均吸热,且过程(1)吸热多.具体计算时只需直接代有关公式即可.解 (1) 等压膨胀()()J 1049.23⨯==-=-=A A B AA AB A p RT V V V RT V V p W v()J 1073.8273,,⨯===-=+=A A m p A B m p p p T R T C T T C E ΔW Q v v (2) 等温膨胀 J 1073.12ln /3⨯===A A RT V W C T vRTlnV对等温过程ΔE =0,所以J 1073.13⨯==T T W Q(3) 绝热膨胀T D =T A (V A /V D )γ-1=300 ×(0.5)0.4=227.4K对绝热过程a 0Q =,则有 ()()J 1051.125Δ3,⨯=-=-=-=D A D A m V a T T R T T C E W v 13 -22 绝热汽缸被一不导热的隔板均分成体积相等的A 、B 两室,隔板可无摩擦地平移,如图所示.A 、B 中各有1mol 氮气,它们的温度都是T0 ,体积都是V0 .现用A 室中的电热丝对气体加热,平衡后A 室体积为B 室的两倍,试求(1) 此时A 、B 两室气体的温度;(2) A 中气体吸收的热量.分析 (1) B 室中气体经历的是一个绝热压缩过程,遵循绝热方程TVγ-1 =常数,由此可求出B 中气体的末态温度TB .又由于A 、B 两室中隔板可无摩擦平移,故A 、B 两室等压.则由物态方程pV A =νRT A 和pV B =νRT B 可知T A =2T B .(2) 欲求A 室中气体吸收的热量,我们可以有两种方法.方法一:视A 、B 为整体,那么系统(汽缸)对外不作功,吸收的热量等于系统内能的增量.即QA =ΔE A +ΔE B .方法二:A 室吸热一方面提高其内能ΔE A ,另外对“外界”B 室作功WA.而对B 室而言,由于是绝热的,“外界” 对它作的功就全部用于提高系统的内能ΔEB .因而在数值上W A =ΔE B .同样得到Q A =ΔE A +ΔE B . 解 设平衡后A 、B 中气体的温度、体积分别为T A ,T B 和V A ,V B .而由分析知压强p A =p B =p .由题已知⎩⎨⎧=+=022V V V V V B A B A ,得⎩⎨⎧==3/23/400V V V V B A (1) 根据分析,对B 室有B γB γT V T V 1010--=得 ()0010176.1/T T V V T γB B ==-;0353.2T T T B A ==(2) ()()0007.312525ΔΔT T T R T T R E E Q B A A A A =-+-=+= 13-23 0.32 kg 的氧气作如图所示的ABCDA 循环,V 2 =2V 1 ,T 1=300K,T 2=200K,求循环效率.分析 该循环是正循环.循环效率可根据定义式η=W /Q 来求出,其中W 表示一个循环过程系统作的净功,Q 为循环过程系统吸收的总热量.解 根据分析,因AB 、CD 为等温过程,循环过程中系统作的净功为()()()J 1076.5/ln /ln 32121211⨯=-==+=V V T T R M m V V RT Mm W W W CD AB由于吸热过程仅在等温膨胀(对应于AB 段)和等体升压(对应于DA 段)中发生,而等温过程中ΔE =0,则AB AB W Q =.等体升压过程中W =0,则DA DA E Q Δ=,所以,循环过程中系统吸热的总量为()()()()J 1081.325/ln /ln Δ42112121,121⨯=-+=-+=+=+=T T R M m V V RT Mm T T C M m V V RT Mm E W Q Q Q m V DAAB DA AB 由此得到该循环的效率为 %15/==Q W η13 -24 图(a)是某单原子理想气体循环过程的V -T 图,图中V C =2V A .试问:(1) 图中所示循环是代表制冷机还是热机? (2) 如是正循环(热机循环),求出其循环效率.分析 以正、逆循环来区分热机和制冷机是针对p -V 图中循环曲线行进方向而言的.因此,对图(a)中的循环进行分析时,一般要先将其转换为p -V 图.转换方法主要是通过找每一过程的特殊点,并利用理想气体物态方程来完成.由图(a)可以看出,BC 为等体降温过程,CA 为等温压缩过程;而对AB 过程的分析,可以依据图中直线过原点来判别.其直线方程为V =CT ,C 为常数.将其与理想气体物态方程pV =m/MRT 比较可知该过程为等压膨胀过程(注意:如果直线不过原点,就不是等压过程).这样,就可得出p -V 图中的过程曲线,并可判别是正循环(热机循环)还是逆循环(制冷机循环),再参考题13-23的方法求出循环效率.解 (1) 根据分析,将V -T 图转换为相应的p -V 图,如图(b)所示.图中曲线行进方向是正循环,即为热机循环.(2) 根据得到的p -V 图可知,AB 为等压膨胀过程,为吸热过程.BC 为等体降压过程,CA 为等温压缩过程,均为放热过程.故系统在循环过程中吸收和放出的热量分别为()A B m p T T C M m Q -=,1 ()()A C A A B m V V V RT Mm T T C M m Q /ln ,2+-= CA 为等温线,有T A =T C ;AB 为等压线,且因V C =2V A ,则有T A =T B /2.对单原子理想气体,其摩尔定压热容C p ,m =5R/2,摩尔定容热容C V ,m =3R/2.故循环效率为()()3/125/2ln 2312/5/2ln 321/112=+-=⎥⎦⎤⎢⎣⎡+-=-=A A A T T T Q Q η 13 -25 一卡诺热机的低温热源温度为7℃,效率为40%,若要将其效率提高到50%,问高温热源的温度需提高多少?解 设高温热源的温度分别为1T '、1T '',则有12/1T T η'-=', 12/1T T η''-=''其中T 2 为低温热源温度.由上述两式可得高温热源需提高的温度为K 3.931111Δ211=⎪⎪⎭⎫ ⎝⎛'--''-='-''=T ηηT T T 13 -26 一定量的理想气体,经历如图所示的循环过程.其中AB 和CD 是等压过程,BC 和DA 是绝热过程.已知B 点温度T B =T 1,C 点温度T C =T 2.(1) 证明该热机的效率η=1-T 2/T 1 ,(2) 这个循环是卡诺循环吗?分析 首先分析判断循环中各过程的吸热、放热情况.BC 和DA 是绝热过程,故Q BC 、Q DA 均为零;而AB 为等压膨胀过程(吸热)、CD 为等压压缩过程(放热),这两个过程所吸收和放出的热量均可由相关的温度表示.再利用绝热和等压的过程方程,建立四点温度之间的联系,最终可得到求证的形式. 证 (1) 根据分析可知 ()()⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛--=---=---=-=B A C D B C A B D CA B m p C D m p AB CD T T T T T T T T T T T T C MT T C M m Q Q η1/11111,, (1) 与求证的结果比较,只需证得BA C D T T T T = .为此,对AB 、CD 、BC 、DA 分别列出过程方程如下V A /T A =V B /T B (2)V C /T C =V D /T D (3) C γC B γB T V T V 11--= (4)A γA D γD T V T V 11--= (5)联立求解上述各式,可证得η=1-T C /T B =1-T 2/T 1(2) 虽然该循环效率的表达式与卡诺循环相似,但并不是卡诺循环.其原因是:① 卡诺循环是由两条绝热线和两条等温线构成,而这个循环则与卡诺循环不同;② 式中T 1、T 2的含意不同,本题中T 1、T 2只是温度变化中两特定点的温度,不是两等温热源的恒定温度.13 -27 一小型热电厂内,一台利用地热发电的热机工作于温度为227℃的地下热源和温度为27℃的地表之间.假定该热机每小时能从地下热源获取1.8 ×1011J的热量.试从理论上计算其最大功率为多少?分析 热机必须工作在最高的循环效率时,才能获取最大的功率.由卡诺定理可知,在高温热源T 1和低温热源T 2之间工作的可逆卡诺热机的效率最高,其效率为η=1-T 2/T 1 .由于已知热机在确定的时间内吸取的热量,故由效率与功率的关系式Q pt Q W η//==,可得此条件下的最大功率.解 根据分析,热机获得的最大功率为()-1712s J 100.2//1/⋅⨯=-==t Q T T t Q ηp13 -28 有一以理想气体为工作物质的热机,其循环如图所示,试证明热()()1/1/12121---=p p V V γη 分析 该热机由三个过程组成,图中AB 是绝热过程,BC 是等压压缩过程,CA 是等体升压过程.其中CA 过程系统吸热,BC 过程系统放热.本题可从效率定义CA BC Q Q Q Q η/1/112-=-=出发,利用热力学第一定律和等体、等压方程以及γ=C p,m 桙C V,m 的关系来证明.证 该热机循环的效率为CA BC Q Q Q Q η/1/112-=-=其中Q BC =m /M C p,m (T C -T B ),Q CA =m/M C V,m (T A -T C ),则上式可写为1/1/11---=---=C A CB C A B C T T T T γT T T T γη 在等压过程BC 和等体过程CA 中分别有T B /V 1 =T C /V 2,T A /P 1 =T C /P 2,代入上式得()()1/1/12121---=p p V V γη 13 -29 如图所示为理想的狄赛尔(Diesel)内燃机循环过程,它由两绝热线AB 、CD 和等压线BC 及等体线DA 组成.试证此内燃机的效率为()()()1//1/12312123---=-V V V V γV V ηγγ证 求证方法与题13-28相似.由于该循环仅在DA 过程中放热、BC 过程中吸热,则热机效率为 ()()BC AD B C m p A D m V BCDA T T T T γT T C M T T C M m Q Q η---=---=-=111/1,, (1) 在绝热过程AB 中,有1211--=γB γA V T V T ,即()121//-=γA B V V T T (2)在等压过程BC 中,有23//V T V T B C =,即23//V V T T B C = (3)再利用绝热过程CD,得1311--=γC γD V T V T (4)解上述各式,可证得()()()1//1/12312123---=-V V V V γV V ηγγ 13 -30 如图所示,将两部卡诺热机连接起来,使从一个热机输出的热量,输入到另一个热机中去.设第一个热机工作在温度为T 1和T 2的两热源之间,其效率为η1 ,而第二个热机工作在温度为T 2 和T 3 的两热源之间,其效率为η2.如组合热机的总效率以η=(W 1 +W 2 )/Q 1 表示.试证总效率表达式为η=(1 -η1 )η2 +η1 或 η=1 -T 3/T 1分析 按效率定义,两热机单独的效率分别为η1=W 1 /Q 1和η2=W 2 /Q 2,其中W 1 =Q 1-Q 2 ,W 2 =Q 2-Q 3 .第一个等式的证明可采用两种方法:(1) 从等式右侧出发,将η1 、η2 的上述表达式代入,即可得证.读者可以一试.(2) 从等式左侧的组合热机效率η=(W 1 +W 2 )/Q 1出发,利用η1、η2的表达式,即可证明.由于卡诺热机的效率只取决于两热源的温度,故只需分别将两个卡诺热机的效率表达式η1=1-T 2 /T 1 和η2=1-T 3 /T 2 代入第一个等式,即可得到第二个等式.证 按分析中所述方法(2) 求证.因η1=W 1 /Q 1 、η2=W 2 /Q 2 ,则组合热机效率12211211121Q Q ηηQ W Q W Q W W η+=+=+= (1) 以Q 2 =Q 1-W 1 代入式(1) ,可证得η=η1 +η2 (1-η1 ) (2) 将η1=1-T 2 /T 1 和η2=1-T 3 /T 2代入式(2),亦可证得η=1-T 2 /T 1 +(1-T 3 /T 2 )T 2 /T 1 =1-T 3 /T 113 -31 在夏季,假定室外温度恒定为37℃,启动空调使室内温度始终保持在17 ℃.如果每天有2.51 ×108 J 的热量通过热传导等方式自室外流入室内,则空调一天耗电多少? (设该空调制冷机的制冷系数为同条件下的卡诺制冷机制冷系数的60%)分析 耗电量的单位为kW·h ,1kW·h =3.6 ×106J.图示是空调的工作过程示意图.因为卡诺制冷机的制冷系数为212T T T e k -=,其中T 1为高温热源温度(室外环境温度),T 2为低温热源温度(室内温度).所以,空调的制冷系数为e =e k · 60% =0.6 T 2/( T 1 -T 2 )另一方面,由制冷系数的定义,有e =Q 2 /(Q 1 -Q 2 )其中Q 1为空调传递给高温热源的热量,即空调向室外排放的总热量;Q 2是空调从房间内吸取的总热量.若Q ′为室外传进室内的热量,则在热平衡时Q 2=Q ′.由此,就可以求出空调的耗电作功总值W =Q 1-Q 2 .解 根据上述分析,空调的制冷系数为7.8%60212=-=T T T e在室内温度恒定时,有Q 2=Q ′.由e =Q 2 /(Q 1-Q 2 )可得空调运行一天所耗电功W =Q 1-Q 2=Q 2/e =Q ′/e =2.89×107=8.0 kW·h13 -32 一定量的理想气体进行如图所示的逆向斯特林循环(回热式制冷机中的工作循环),其中1→2为等温(T 1 )压缩过程,3→4为等温(T 2 )膨胀过程,其他两过程为等体过程.求证此循环的制冷系数和逆向卡诺循环制冷系数相等.(这一循环是回热式制冷机中的工作循环,具有较好的制冷效果.4→1过程从热库吸收的热量在2→3过程中又放回给了热库,故均不计入循环系数计算.)证明 1→2 过程气体放热2111lnV V RT Q v = 3→4 过程气体吸热 2122ln V V RT Q v = 则制冷系数 e =Q 2 /(Q 1-Q 2 )= T 2/( T 1-T 2 ).与逆向卡诺循环的制冷系数相同.13 -33 物质的量为ν的理想气体,其摩尔定容热容C V,m =3R/2,从状态A(p A ,V A ,T A )分别经如图所示的ADB 过程和ACB 过程,到达状态B(p B ,V B ,T B ).试问在这两个过程中气体的熵变各为多少? 图中AD 为等温线.分析 熵是热力学的状态函数,状态A 与B 之间的熵变ΔSAB 不会因路径的不同而改变.此外,ADB 与ACB 过程均由两个子过程组成.总的熵变应等于各子过程熵变之和,即DB AD AB S S S ΔΔΔ+=或CB AC AB S S S ΔΔΔ+=.解 (1) ADB 过程的熵变为()()D B p,m A D B D D A T BD P D A T DBAD AB T T C V V T T C T W T Q T Q S S S /ln /ln /d /d /d /d ΔΔΔm p,v vR v +=+=+=+=⎰⎰⎰⎰ (1)在等温过程AD 中,有T D =T A ;等压过程DB 中,有V B /T B =V D /T D ;而C p ,m =C V ,m +R ,故式(1)可改写为()()()()A B A B A B p,m A B B D ADB V T V V V T C V T V T S /ln 23/ln /ln /ln ΔvR vR v vR +=+=(2) ACB 过程的熵变为()()C B V,m A C p,m CB AC BA ACB T TC V T C S S Q/T S /ln /ln ΔΔd Δv v +=+==⎰ (2)利用V C =V B 、p C =p A 、T C /V C =T A /V A 及T B /p B =T C /p C ,则式(2)可写为()()()()()()()A B A B A A B B V,m A B A B A B V,m ACB V T V V V p V p C V V p p V V R C S /ln 23/ln /ln /ln /ln /ln ΔvR vR v vR v v +=+=++=通过上述计算可看出,虽然ADB 及ACB 两过程不同,但熵变相同.因此,在计算熵变时,可选取比较容易计算的途径进行.13 -34 有一体积为2.0 ×10-2m 3的绝热容器,用一隔板将其分为两部分,如图所示.开始时在左边(体积V 1 =5.0 ×10-3m 3)一侧充有1mol 理想气体,右边一侧为真空.现打开隔板让气体自由膨胀而充满整个容器,求熵变.分析 在求解本题时,要注意⎰=BA T Q S d Δ 的适用条件.在绝热自由膨胀过程中,d Q =0,若仍运用上式计算熵变,必然有ΔS =0.显然,这是错误的结果.由于熵是状态的单值函数,当初态与末态不同时,熵变不应为零.出现上述错误的原因就是忽视了公式的适用条件. ⎰=BA T Q S d Δ 只适用于可逆过程,而自由膨胀过程是不可逆的.因此,在求解不可逆过程的熵变时,通常需要在初态与末态之间设计一个可逆过程,然后再按可逆过程熵变的积分式进行计算.在选取可逆过程时,尽量使其积分便于计算.解 根据上述分析,在本题中因初末态时气体的体积V 1 、V 2 均已知,且温度相同,故可选一可逆等温过程.在等温过程中,d Q =d W =p d V ,而VRT M m p =,则熵变为 ()1-12K J 52.11/ln d 1d d Δ12⋅=====⎰⎰⎰V V R M m V V R M m T V p T Q S V V。
大学物理第13章习题解答(一)2024

大学物理第13章习题解答(一)引言概述:
大学物理第13章习题解答(一)涵盖了该章节习题的解答方法和步骤,旨在帮助读者理解和掌握该章节的重要概念和解题技巧。
本文将按照以下五个大点进行详细阐述每个习题的解答过程。
正文:
1. 运动和力
- 惯性和非惯性系的区别
- 牛顿第一定律的应用
- 各种力的分类和性质
- 牛顿第二定律的推导和应用
- 牛顿第三定律的理解和应用
2. 力的合成和分解
- 力的合成和分解的基本原理
- 合力和分力的定义和计算方法
- 作用在斜面上的分力的计算
- 平衡力和加速度的关系
- 静止物体和运动物体的分力分析
3. 弹力和摩擦力
- 弹簧的钩度系数和拉伸/压缩的关系
- 弹簧构成的力系和力的平衡
- 摩擦力的性质和影响因素
- 静摩擦力和动摩擦力的计算方法
- 摩擦力的方向和大小的分析
4. 圆周运动和万有引力
- 圆周运动的基本概念和特征
- 圆周运动的加速度和角速度的关系
- 圆周运动的向心力和离心力的计算
- 万有引力的定义和万有引力定律
- 行星运动和人造卫星的运动分析
5. 动能和动量
- 动能的定义和计算方法
- 动能定理的推导和应用
- 动量的定义和计算方法
- 动量定理的推导和应用
- 碰撞和弹性碰撞的动量分析
总结:
通过本文对大学物理第13章习题的解答分析,读者可以深入理解运动和力,力的合成和分解,弹力和摩擦力,圆周运动和万有引力,动能和动量等方面的关键概念和解题技巧。
掌握这些知识可以为读者在物理学习和解题过程中提供方法和思路,进一步巩固物理学的基础知识和应用能力。
大学物理下第13章-5

pV 常量
吸收热量
M CV (T2 T1 ) M mol M C p (T2 T1 ) M mol
对外做功 0
内能增量
M CV (T2 T1 ) M mol
等压 C p ( dH ) 等温
0
M V RT ln 2 或 M mol V1 M p RT ln 1 M mol p2
CV (PdV+VdP)= - RPdV
R= Cp - CV
代入
并化简可得
CV PdV+ CV VdP = CV PdV-CpPdV
CVVdP + CpPdV = 0 dP dV 分离变量并应用 = Cp/CV 得 P V
对上式积分可以得到:
PV constan t
利用理想气体的物态方程,可以得到:
张福俊
2013-2014 第一学期
Flash tracking the key points of last lecture
热力学第一定律 Q = U2-U1+A = U +A
系统对外界做功 A>0; 系统从外界吸热 Q>0;
系统内能增加 ΔU>0。 内能、做功、热量
A pdV
V1
V2
Pb Pa ( Va ) 4.98 10 4 ( Pa) Vb
TaVa 1 TbVb 1
压强变小 温度降低
Va 1 Tb Ta ( ) 119 .4 K Vb
绝热过程不吸热
做功等于内能的减少量: U Cv (Ta Tb ) 3.75 10 3 J A
多方
Cn
n Cv n 1
pV n 常量
大学物理第13章习题解答

引言概述:大学物理第13章是力学的一个重要章节,主要介绍了质点系和刚体的运动学和动力学问题。
习题作为巩固章节知识和培养解决问题能力的重要手段,对于学生的学习具有重要的意义。
本文将对大学物理第13章的习题进行解答,以帮助读者更好地理解和掌握力学的相关知识。
正文内容:1.质点系的运动学问题1.1相对位矢和质心位矢的关系1.2质心速度的计算方法1.3质心加速度的计算方法1.4相对位矢和质心位矢之间的关系1.5相对位矢和质心位矢的运动规律2.质点系的动力学问题2.1质点间相互作用力的计算方法2.2质点系受到的合外力和合内力的关系2.3质点系统的动量守恒定律2.4质点系的动量定理2.5质点系的冲量和动量变化的关系3.刚体的运动学问题3.1刚体的转动轴和转动角速度的关系3.2刚体的几何中心和质心的关系3.3刚体的角速度和线速度的关系3.4刚体的力矩和角加速度的关系3.5刚体的运动规律和动能的计算方法4.刚体的动力学问题4.1刚体的力矩和合外力的关系4.2刚体的力矩定理和动力学定理的关系4.3刚体的动量矩定理4.4刚体的角动量守恒定律4.5刚体的角动量定理和动能定理的关系5.刚体的平衡问题5.1刚体的平衡条件5.2刚体的平衡方程的推导和应用5.3刚体的平衡条件和力矩定理的关系5.4刚体的平衡问题和静力学问题的区别和联系5.5刚体的平衡问题和静态平衡问题的应用总结:大学物理第13章习题解答了质点系和刚体的运动学和动力学问题,并深入探讨了质点系和刚体的平衡问题。
通过解答这些习题,我们可以更好地理解和掌握力学的相关知识,提高解决问题的能力和方法。
同时,我们也应该注重理论与实际结合,将所学的知识应用到实际问题中,不断提高自己的应用能力和创新能力。
希望读者通过本文的阐述,能够对大学物理第13章有更深入的理解,并能够在学习和解题中取得更好的成绩。
[工学]大学物理第13章
![[工学]大学物理第13章](https://img.taocdn.com/s3/m/08634bf7b9f3f90f76c61b83.png)
i i i i ( B, n) 90 ( B, n) 90 ( B, n) 90 ( B, n) 90 Bcos ds 0 0 0 0 d d d d 0 若 | | , 0 若, 0 若||, 0 dt dt dt dt 则 i<0 若, 则 i<0 则 >0 则 i>0 i 反向 与假定方向相反 同向 同向
v
共同因素:穿过导体回路的磁通量M发生变化。
d i dt
法拉第电磁感应定律
其中i为回路中的感应电动势 (i为回路中载流子提供能量)
注意:
“–”表示感应电动势的方向, i和都是标量,方向 只是相对回路的绕行方向而言。如下所示: n n n n B B
静电场E不能为闭合回路运动的电荷提供能量! 麦克斯韦 引入 感应电场的概念 非保守场 产生 电场 磁场 Bt 变化的同时
此电场的电力线是闭合的,称为有旋电场—感应电场Ei。
感应电场 E i 的特点: 1)E i 与 E e 一样,对场中的电荷有电场力的作用。 F F qEi Ei q 2) E i 不依赖空间是否有导体存在, 只要有 dB 0 ,则就有Ei的存在。 dt 3) E i 是非保守力场, Ei dl 0 。
为正;成钝角时, i 为负。因此,由上式算出的电动势 有正负之分, i为正时,表示电动势方向顺着 d l 的 方向; i为负时,则表示电动势的方向逆着 d l 的方向。 对于闭合回路
i 由上式可以看出,矢积 v B 与 d l 成锐角时,
L
i v B d l
2
1
磁通计原理
与d/dt无关
大学物理实验课思考题参考答案

大学物理实验思考题参考答案目录一、转动惯量:二、伏安法与补偿法三、混沌思考题四、半导体PN结五、地磁场六、牛顿环七、麦克尔逊干涉仪八、全息照相九、光电效应十、声速测量十一、用电位差计校准毫安表十二、落球法测量液体的黏度十三、电子束偏转与电子比荷测量十四、铁磁材料磁化特性研究十五、光栅衍射十六、电桥十七、电位差计十八、密立根油滴十九、模拟示波器二十、金属杨氏摸量二十一、导热系数二十二、分光计二十三、集成霍尔传感器特性与简谐振动一、转动惯量:1、由于采用了气垫装置,这使得气垫摆摆轮在摆动过程中受到的空气粘滞阻尼力矩降低至最小程度,可以忽略不计。
但如果考虑这种阻尼的存在,试问它对气垫摆的摆动(如频率等)有无影响?在摆轮摆动中,阻尼力矩是否保持不变?答:如果考虑空气粘滞阻尼力矩的存在,气垫摆摆动时频率减小,振幅会变小。
(或者说对频率有影响,对振幅有影响)在摆轮摆动中,阻尼力矩会越变越小。
2、为什么圆环的内、外径只需单次测量?实验中对转动惯量的测量精度影响最大的是哪些因素?答:圆环的内、外径相对圆柱的直径大很多,使用相同的测量工具测量时,相对误差较小,故只需单次测量即可。
(对测量结果影响大小)实验中对转动惯量测量影响最大的因素是周期的测量。
(或者阻尼力矩的影响、摆轮是否正常、平稳的摆动、物体摆放位置是否合适、摆轮摆动的角度是否合适等)3、试总结用气垫摆测量物体转动惯量的方法有什么基本特点?答:原理清晰、结论简单、设计巧妙、测量方便、最大限度的减小了阻尼力矩。
二、伏安法与补偿法1、利用补偿法测量电阻消除了伏安法的系统误差,还可能存在的误差包括:读数误差、计算产生的误差、仪器误差、导线阻值的影响等或其他。
2、能利用电流补偿电路对电流表内接法进行改进:三、混沌思考题1、有程序(各种语言皆可)、K值的取值范围、图 +5分有程序没有K值范围和图 +2分只有K值范围 +1分有图和K值范围 +2分2、(1)混沌具有内在的随机性:从确定性非线性系统的演化过程看,它们在混沌区的行为都表现出随机不确定性。
新编基础物理学第13章习题解答和分析

《新编基础物理学》第13章习题解答和分析(总12页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第13章 电磁场与麦克斯韦方程组13-1 如题图13-1所示,两条平行长直导线和一个矩形导线框共面,且导线框的一个边与长直导线平行,到两长直导线的距离分别为1r ,2r 。
已知两导线中电流都为0sin I I t ω=,其中I 0和ω为常数,t 为时间。
导线框长为a ,宽为b ,求导线框中的感应电动势。
分析:当导线中电流I 随时间变化时,穿过矩形线圈的磁通量也将随时间发生变化,用法拉第电磁感应定律md d i tΦε=-计算感应电动势,其中磁通量m d sB S Φ=⋅⎰, B 为两导线产生的磁场的叠加。
解:无限长直电流激发的磁感应强度为02IB rμ=π。
取坐标Ox 垂直于直导线,坐标原点取在矩形导线框的左边框上,坐标正方向为水平向右。
取回路的绕行正方向为顺时针。
由场强的叠加原理可得x 处的磁感应强度大小00122()2()IIB r x r x μμ=+π+π+方向垂直纸面向里。
通过微分面积d d S a x =的磁通量为00m 12d d d d 2()2()I I B S B S a x r x r x μμΦππ⎡⎤=⋅==+⎢⎥++⎣⎦通过矩形线圈的磁通量为00m 012d 2()2()b I I a x r x r x μμΦ⎡⎤=+⎢⎥π+π+⎣⎦⎰012012ln ln sin 2a r b r b I t r r μω⎛⎫++=+ ⎪π⎝⎭ 感生电动势 0m 12012d ln ln cos d 2i a r b r b I t t r r μωΦεω⎛⎫++=-=-+ ⎪π⎝⎭012012()()ln cos 2ar b r b I t r r μωω⎡⎤++=-⎢⎥π⎣⎦0i ε>时,回路中感应电动势的实际方向为顺时针;0i ε<时,回路中感应电动势的实际方向为逆时针。
大学物理13章习题详细答案
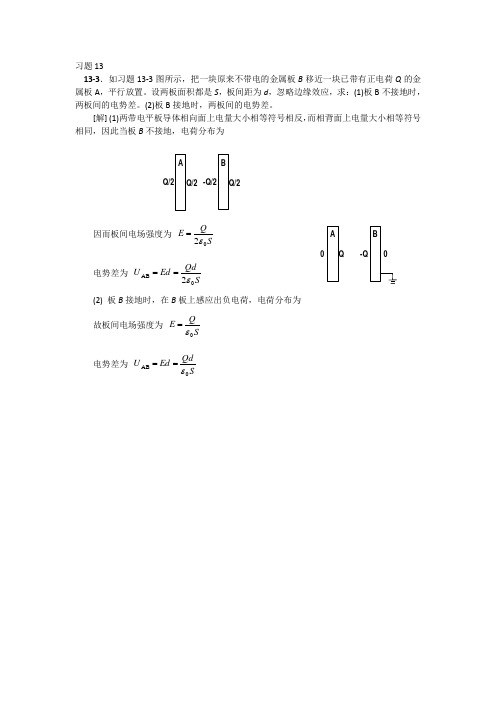
习题1313-3.如习题13-3图所示,把一块原来不带电的金属板B 移近一块已带有正电荷Q 的金属板A ,平行放置。
设两板面积都是S ,板间距为d ,忽略边缘效应,求:(1)板B 不接地时,两板间的电势差。
(2)板B 接地时,两板间的电势差。
[解] (1)两带电平板导体相向面上电量大小相等符号相反,而相背面上电量大小相等符号相同,因此当板B 不接地,电荷分布为因而板间电场强度为 SQ E 02ε=电势差为 SQdEd U 0AB 2ε== (2) 板B 接地时,在B 板上感应出负电荷,电荷分布为 故板间电场强度为 SQ E 0ε=电势差为 SQdEd U 0AB ε== B A-Q/2Q/2Q/2Q/2A B -QQ13-4 两块靠近的平行金属板间原为真空。
使两板分别带上面电荷密度为0的等量异号电荷,这时两板间电压为U 0=300V 。
保持两板上电量不变,将板间空间一半如图习题13-4图所示充以相对电容率为r =5的电介质,试求(1) 金属板间有电介质部分和无电介质部分的E,D 和板上的自由电荷密度; (2) 金属板间电压变为多少电介质上下表面束缚电荷面密度多大13-5.如习题13-5图所示,三个无限长的同轴导体圆柱面A 、B 和C ,半径分别为R A 、R B 、R C 。
圆柱面B 上带电荷,A 和C 都接地。
求B 的内表面上线电荷密度1和外表面上线电荷密度2之比值1/2。
[解] 由A 、C 接地 BC BA U U = 由高斯定理知 r E 01I 2πελ-=rE 02II 2πελ= AB 0101I BA ln 2d 2d ABA BR Rr r U R R R R πελπελ=-==⎰⎰r E IIIB C 0202II BC ln 2d 2d CB CBR R r r U R R R R πελπελ===⎰⎰r EBC 02A B 01ln 2ln 2R R R R πελπελ= 因此 AB BC 21ln :ln:R R R R =λλ13-6.如习题13-6图所示,一厚度为d 的无限大均匀带电导体板,单位面积上两表面带电量之和为。
大学物理(机械工业出版社)第13章课后答案

第十三章 振动#13-1 一质点按如下规律沿x 轴作简谐振动:x = 0.1 cos (8πt +2π/3 ) (SI),求此振动的周期、振幅、初相、速度最大值和加速度最大值。
解:周期T = 2π/ ω= 0.25 s振幅A = 0.1m初相位φ= 2π/ 3V may = ωA = 0.8πm / s ( = 2.5 m / s )a may = ω2 A = 6.4π2m / s ( = 63 m / s 2)13-2 一质量为0.02kg 的质点作谐振动,其运动方程为:x = 0.60 cos( 5 t -π/2) (SI)。
求:(1)质点的初速度;(2)质点在正向最大位移一半处所受的力。
解:(1) )( )25sin(0.3 SI t dt dx v π--==0.3 20x m ma x ω-== (2) 2x m ma F ω-==5.13.052.0,2/ 2N F A x -=⨯⨯-==时13-3 如本题图所示,有一水平弹簧振子,弹簧的倔强系数k = 24N/m ,重物的质量m = 6kg ,重物静止在平衡位置上,设以一水平恒力F = 10 N 向左作用于物体(不计摩擦),使之由平衡位置向左运动了0.05m ,此时撤去力F ,当重物运动到左方最远位置时开始计时,求物体的运动方程。
解:设物体的运动方程为:x = A c o s (ωt +φ)恒外力所做的功即为弹簧振子的能量:F ⨯ 0.05 = 0.5 J当物体运动到左方最位置时,弹簧的最大弹性势能为0.5J ,即:1 /2 kA 2 = 0.5 J ∴A = 0.204 mA 即振幅ω2 = k / m = 4 ( r a d / s )2ω= 2 r a d / s按题目所述时刻计时,初相为φ= π∴ 物体运动方程为x = 0.204 c o s (2 t +π) ( SI ) 13-4 一水平放置的弹簧系一小球。
已知球经平衡位置向右运动时,v =100cm ⋅s -1,周期T =1.0s ,求再经过1/3秒时间,小球的动能是原来的多少倍?弹簧的质量不计。
大学物理实验报告思考题部分答案

实验十三拉伸法测金属丝得扬氏弹性摸量【预习题】1.如何根据几何光学得原理来调节望远镜、光杠杆与标尺之间得位置关系?如何调节望远镜?答:(1)根据光得反射定律分两步调节望远镜、光杠杆与标尺之间得位置关系。
第一步:调节来自标尺得入射光线与经光杠杆镜面得反射光线所构成得平面大致水平。
具体做法如下:①用目测法调节望远镜与光杠杆大致等高。
②用目测法调节望远镜下得高低调节螺钉,使望远镜大致水平;调节光杠杆镜面得仰俯使光杠杆镜面大致铅直;调节标尺得位置,使其大致铅直;调节望远镜上方得瞄准系统使望远镜得光轴垂直光杠杆镜面。
第二步:调节入射角(来自标尺得入射光线与光杠杆镜面法线间得夹角)与反射角(经光杠杆镜面反射进入望远镜得反射光与光杠杆镜面法线间得夹角)大致相等。
具体做法如下:沿望远镜筒方向观察光杠杆镜面,在镜面中若瞧到标尺得像与观察者得眼睛,则入射角与反射角大致相等。
如果瞧不到标尺得像与观察者得眼睛,可微调望远镜标尺组得左右位置,使来自标尺得入射光线经光杠杆镜面反射后,其反射光线能射入望远镜内.(2)望远镜得调节:首先调节目镜瞧清十字叉丝,然后物镜对标尺得像(光杠杆面镜后面2D处)调焦,直至在目镜中瞧到标尺清晰得像。
2。
在砝码盘上加载时为什么采用正反向测量取平均值得办法?答:因为金属丝弹性形变有滞后效应,从而带来系统误差. 【思考题】1。
光杠杆有什么优点?怎样提高光杠杆测量微小长度变化得灵敏度?答:(1)直观、简便、精度高.(2)因为,即,所以要提高光杠杆测量微小长度变化得灵敏度,应尽可能减小光杠杆长度(光杠杆后支点到两个前支点连线得垂直距离),或适当增大D(光杠杆小镜子到标尺得距离为D)。
2。
如果实验中操作无误,得到得数据前一两个偏大,这可能就是什么原因,如何避免?答:可能就是因为金属丝有弯曲。
避免得方法就是先加一两个发码将金属丝得弯曲拉直。
3.如何避免测量过程中标尺读数超出望远镜范围?答:开始实验时,应调节标尺得高低,使标尺得下端大致与望远镜光轴等高,这样未加砝码时从望远镜当中瞧到得标尺读数接近标尺得下端,逐渐加砝码得过程中瞧到标尺读数向上端变化。
大学物理13章-2

n1
d
n1
=
k
(k 1,2, ) 明纹
(2k 1)
(k 0,1,2, ) 暗纹
2
n
薄膜厚度相同的地方光程差相同,从而对应同一级
干涉条纹,故将此类干涉称为等厚干涉。
(演示 V 3.0 劈尖干涉装置和图样)
上页 下页 返回 结束
6
大学
物理学 ➢劈尖干涉条纹的分布特点
第13章 波动光学
2nd
2D
km 141.1
考虑 d = 0 处出现 k = 0 暗条纹,所以共有142条暗纹。
上页 下页 返回 结束
15
大学 物理学
另解:
第13章 波动光学
相邻条纹间距
b
2n
2
L
2D
L =12cm 的长度内呈现的
暗条纹数
L b
2D
141.1
n1
tan
D L
n
n1
n1
d
L
考虑棱边处出现 0 级暗条纹,所以共有142条暗纹。
(2) 检验光学元件 表面的平整度
d
工件表面是上凸的
l N
2
上页 下页 返回 结束
10
大学 物理学
平晶 工件
第13章 波动光学
上页 下页 返回 结束
11
大学
物理学 例13-7 课本P.136 例13-5
第13章 波动光学
利用劈尖干涉可以测量微小角度。折射率n=1.4的 劈尖在单色光垂直照射下,测得两相邻明纹之间的距离
增反膜
利用薄膜上、下表面反射光的光程差满足干涉相长 ,使反射光因干涉而加强,这种膜叫增反膜。
上页 下页 返回 结束
大学物理教程第2章习题答案

⼤学物理教程第2章习题答案思考题2.1 从运动学的⾓度看,什么是简谐振动?从动⼒学的⾓度看,什么是简谐振动?答:从运动学的⾓度看,弹簧振⼦相对平衡位置的位移随时间按余弦函数的规律变化,所作的运动就是简谐振动。
从动⼒学的⾓度看,如果物体受到的⼒的⼤⼩总是与物体对其平衡位置的位移成正⽐,⽽⽅向相反,那么该物体的运动就是简谐振动。
2.2 弹簧振⼦的振幅增⼤到2倍时,其振动周期、振动能量、最⼤速度和最⼤加速度等物理量将如何变化?答:弹簧振⼦的运动⽅程为0cos()x A t ω?=+,速度为0sin()v A t ωω?=-+,加速度的为)cos(02?ωω+-=t A a ,振动周期2T =221kA E =。
所以,弹簧振⼦的振幅A 增⼤到2倍时,其振动周期不变,振动能量为原来的4倍,最⼤速度为原来的2倍,最⼤加速度为原来的2倍。
2.3 下列运动是否为简谐振动?(1)⼩球在地⾯上作完全弹性的上下跳动;(2)⼩球在半径很⼤的光滑凹球⾯底部作⼩幅度的摆动;(3)曲柄连杆机构使活塞作往复运动;(4)⼩磁针在地磁的南北⽅向附近摆动。
答:(2)、(4)为简谐振动,(1)、(3)、不是简谐振动。
2.4 三只相同的弹簧(质量忽略不计)都⼀端固定,另⼀端连接质量为m 的物体,它们放置情况不同,其中⼀个平放,⼀个斜放,另⼀个竖直放。
如果它们振动起来,则三者是否均为简谐振动,它们振动的周期是否相同?答:三者均为简谐振动,它们振动的周期也相同。
2.5 当谐振⼦作简谐振动的振幅增⼤为原来的2倍时,谐振⼦的什么量也增⼤为原来的2倍?答:最⼤速度和最⼤加速度。
2.6 ⼀弹簧振⼦作简谐振动,其振动的总能量为E 1。
如果我们将弹簧振⼦的振动振幅增加为原来的2倍,⽽将重物的质量增加为原来的4倍,则新的振⼦系统的总能量是否发⽣变化?答:弹簧振⼦212E kA = ,所以新的振⼦系统的总能量增加为原来的4倍。
2.7 ⼀质点作简谐振动,振动频率为n,则该质点动能的变化频率是多少?答:该质点动能的变化频率是2n。
湖南大学物理(2)第13章课后习题参考答案

第13章 静电场中的导体和电解质一、选择题1(D),2(A),3(C),4(C),5(C),6(B),7(C),8(B),9(C),10(B)二、填空题(1). 4.55×105 C ;(2). σ (x ,y ,z )/ε0,与导体表面垂直朝外(σ > 0) 或 与导体表面垂直朝里(σ < 0). (3). εr ,1, εr ; (4). 1/εr ,1/εr ;(5). σ ,σ / ( ε 0ε r ); (6).Rq 04επ ;(7). P ,-P ,0; (8) (1- εr )σ / εr ; (9). 452; (10). εr ,εr三、计算题1.如图所示,一内半径为a 、外半径为b 的金属球壳,带有电荷Q ,在球壳空腔内距离球心r 处有一点电荷q .设无限远处为电势零点,试求: (1) 球壳内外表面上的电荷. (2) 球心O 点处,由球壳内表面上电荷产生的电势. (3) 球心O 点处的总电势.解:(1) 由静电感应,金属球壳的内表面上有感生电荷-q ,外表面上带电荷q +Q . (2) 不论球壳内表面上的感生电荷是如何分布的,因为任一电荷元离O 点的 距离都是a ,所以由这些电荷在O 点产生的电势为 adqU q 04επ=⎰-aq04επ-=(3) 球心O 点处的总电势为分布在球壳内外表面上的电荷和点电荷q 在O 点 产生的电势的代数和 q Q q q O U U U U +-++= r q 04επ=a q 04επ-b q Q 04επ++ )111(40b a r q +-π=εbQ04επ+2. 一圆柱形电容器,外柱的直径为4 cm ,内柱的直径可以适当选择,若其间充满各向同性的均匀电介质,该介质的击穿电场强度的大小为E 0= 200 KV/cm .试求该电容器可能承受的最高电压. (自然对数的底e = 2.7183)解:设圆柱形电容器单位长度上带有电荷为λ,则电容器两极板之间的场强分布 为 )2/(r E ελπ= 设电容器内外两极板半径分别为r 0,R ,则极板间电压为⎰⎰⋅π==R rRr r r r E U d 2d ελ 0ln 2r Rελπ=电介质中场强最大处在内柱面上,当这里场强达到E 0时电容器击穿,这时应有002E r ελπ=,000ln r R E r U = 适当选择r 0的值,可使U 有极大值,即令0)/ln(/d d 0000=-=E r R E r U ,得 e R r /0=,显然有22d d r U < 0,故当 e R r /0= 时电容器可承受最高的电压 e RE U /0max = = 147 kV.3. 如图所示,一圆柱形电容器,内筒半径为R 1,外筒半径为R 2 (R 2<2 R 1),其间充有相对介电常量分别为εr 1和εr 2=εr 1 / 2的两层各向同性均匀电介质,其界面半径为R .若两种介质的击穿电场强度相同,问:(1) 当电压升高时,哪层介质先击穿?(2) 该电容器能承受多高的电压?解:(1) 设内、外筒单位长度带电荷为+λ和-λ.两筒间电位移的大小为 D =λ / (2πr ) 在两层介质中的场强大小分别为E 1 = λ / (2πε0 εr 1r ), E 2 = λ / (2πε0 εr 2r ) 在两层介质中的场强最大处是各层介质的内表面处,即E 1M = λ / (2πε0 εr 1R 1), E 2M = λ / (2πε0 εr 2R ) 可得 E 1M / E 2M = εr 2R / (εr 1R 1) = R / (2R 1)已知 R 1<2 R 1, 可见 E 1M <E 2M ,因此外层介质先击穿. (2) 当内筒上电量达到λM ,使E 2M =E M 时,即被击穿,λM = 2πε0 εr 2RE M 此时.两筒间电压(即最高电压)为:r r r r U R R r M RR r M d 2d 221201012⎰⎰+=επελεπελ⎪⎪⎭⎫ ⎝⎛+=R R R R RE r r M r 22112ln 1ln 1εεε4. 一空气平行板电容器,两极板面积均为S ,板间距离为d (d 远小于极板线度),在两极板间平行地插入一面积也是S 、厚度为t (<d )的金属片,如图所示. 试求:(1) 电容C 于多少? (2) 金属片放在两极板间的位置对电容值有无影响?解:设极板上分别带电荷+q 和-q ;金属片与A 板距离为d 1,与B 板距离为d 2;金属片与A 板间场强为 )/(01S q E ε=金属板与B 板间场强为 )/(02S q E ε= 金属片内部场强为 0='E 则两极板间的电势差为2211d E d E U U B A +=- )(210d d S q+=ε)(0t d Sq -=ε 由此得 )/()/(0t d S U U q C B A -=-=ε因C 值仅与d 、t 有关,与d 1、d 2无关,故金属片的安放位置对电容值无影响.O R 1R 2Rεr 2εr 1t S S S d Ad 1t d 2d5. 如图所示,一电容器由两个同轴圆筒组成,内筒半径为a ,外筒半径为b ,筒长都是L ,中间充满相对介电常量为εr 的各向同性均匀电介质.内、外筒分别带有等量异号电荷+Q和-Q .设 (b - a ) << a ,L >> b ,可以忽略边缘效应,求:(1) 圆柱形电容器的电容;(2) 电容器贮存的能量.解:由题给条件 (a a b <<-)和b L >>,忽略边缘效应, 应用高斯定理可求出两 筒之间的场强为: )2/(0Lr Q E r εεπ= 两筒间的电势差 =π=⎰r drL QU bar εε02a b L Q r ln 20εεπ 电容器的电容 )]//[ln()2(/0a b L U Q C r εεπ== 电容器贮存的能量 221CU W =)/ln()]4/([02a b L Q r εεπ=6. 如图所示,一平板电容器,极板面积为S ,两极板之间距离为d ,其间填有两层厚度相同的各向同性均匀电介质,其介电常量分别为ε1和ε2.当电容器带电荷±Q 时,在维持电荷不变下,将其中介电常量为ε1的介质板抽出,试求外力所作的功.解:可将上下两部分看作两个单独的电容器串联,两电容分别为d S C 112ε=,d SC 222ε= 串联后的等效电容为 ()21212εεεε+=d SC带电荷±Q 时,电容器的电场能量为 ()S d Q C Q W 21212242εεεε+== 将ε1的介质板抽去后,电容器的能量为 ()S d Q W 202024εεεε+='外力作功等于电势能增加,即 ⎪⎪⎭⎫⎝⎛-=-'=∆=102114εεS d Q W W W A7. 如图所示,将两极板间距离为d 的平行板电容器垂直地插入到密度为ρ、相对介电常量为εr 的液体电介质中.如维持两极板之间的电势差U 不变,试求液体上升的高度h .解:设极板宽度为L ,液体未上升时的电容为 C 0 = ε0HL / d 液体上升到h 高度时的电容为()d hL dL h H C rεεε00+-=()011C H h r ⎥⎦⎤⎢⎣⎡-+=ε 在U 不变下,液体上升后极板上增加的电荷为()d hLU U C CU Q r /100-=-=∆εε电源作功 ()d hLU QU A r /120-==∆εε液体上升后增加的电能20212121U C CU W -=∆()d hLU r /12120-=εε 液体上升后增加的重力势能 2221gdh L W ρ=∆因 A = ∆W 1+∆W 2,可解出 ()2201gdU h r ρεε-=思考题1. 无限大均匀带电平面(面电荷密度为σ)两侧场强为)2/(0εσ=E ,而在静电平衡状态下,导体表面(该处表面面电荷密度为σ)附近场强为0/εσ=E ,为什么前者比后者小一半?参考解答:关键是题目中两个式中的σ不是一回事。
大学物理2,13.第十三章思考题

1、如图13-9所示,薄膜介质的折射率为n 1,薄膜上下介质的折射率分别为n 1和n 3,并且n 2比n 1和n 3都大。
单色平行光由介质1垂直照射在薄膜上,经薄膜上下两个表面反射的两束光发生干涉。
已知薄膜的厚度为e , λ1为入射光在折射率为n 1的介质中的波长,则两束反射光的光程差等于多少? 【答案:22112λn e n S -=∆】 详解:由于入射光在上表面从光疏介质投射到光密介质上存在半波损失,因此反射光一的光程为21λ=S由于入射光在下表面从光密介质投射到光疏介质上没有半波损失,因此反射光二的光程为e n S 222=两束反射光的光程差为22212λ-=-=∆e n S S S其中λ为光在真空的波长,它与介质1中的波长的关系为λ=n 1λ1,因此22112λn e n S -=∆ 2、在双缝干涉实验中,两缝分别被折射率为n 1和n 2、厚度均为e 的透明薄膜遮盖。
波长为λ的平行单色光垂直照射到双缝上,在屏中央处,两束相干光的相位差等于多少? 【答案:λϕen n )(π212-=∆】详解:设从双缝发出的两束光到屏中央处的距离为r ,依题意它们到达屏中央处的光程分别为)(11e r e n S -+= )(22e r e n S -+=它们的光程差为12S S S -=∆e n n )(12-=因此,在屏中央处两束相干光的相位差为n 3图13-9λϕS∆=∆π2λen n )(π212-=3、在双缝干涉实验中,为使屏上的干涉条纹间距变大,可以采取哪些办法?【答案:增大双缝与屏之间的距离D 、增大入射光波长λ、减小双缝间距d 、减小折射率n 】详解:双缝干涉条纹间距为dnD x λ=∆ 因此,为使屏上的干涉条纹间距变大,可以增大双缝与屏之间的距离D 、改用波长λ较长的光进行实验、将两缝的间距d 变小、将实验装置放在折射率n 较小的透明流体中。
4、如图13-10所示,在双缝干涉实验中,屏幕E 上的P 点处是明条纹。
大学物理_第十三章_课后答案

a sin ϕ = (2k + 1)
λ 2 , k = 1,2,3 ⋅ ⋅ ⋅
x 1.4 = = 3.5 × 10 −3 = tan ϕ ≈ sin ϕ f 400 由 2a sin ϕ 2 × 0.6 λ= = × 3.5 × 10 −3 2k + 1 2k + 1 故 1 = × 4.2 × 10 −3 2k + 1 mm o λ = 6000 A 当 k = 3 ,得 3
得 (2)因第四级缺级,故此须同时满足
0.20(a + b) = 2 × 6000 × 10 −10 0.30(a + b) = 3 × 6000 × 10 −10 a + b = 6.0 × 10 −6 m (a + b) sin ϕ = kλ a sin ϕ = k ′λ a+b a= k ′ = 1.5 × 10 −6 k ′ 4
答:因为衍射角 ϕ 愈大则 a sin ϕ 值愈大,分成的半波带数愈多,每个半波带透过的光通量 就愈小,而明条纹的亮度是由一个半波带的光能量决定的,所以亮度减小. 13-5 若把单缝衍射实验装置全部浸入水中时,衍射图样将发生怎样的变化?如果此时用公
a sin ϕ = ± (2k + 1)
式 在水中的波长?
λ 答: 不矛盾. 单缝衍射暗纹条件为 a sin ϕ = kλ = 2 k 2 , 是用半波带法分析(子波叠加问题). ϕ 相邻两半波带上对应点向 方向发出的光波在屏上会聚点一一相消,而半波带为偶数,故
形成暗纹;而双缝干涉明纹条件为 d sin θ = kλ ,描述的是两路相干波叠加问题,其波程差 为波长的整数倍,相干加强为明纹.
o
a+b =
解:
大学物理课后答案第十三章

第十三章 几何光学一、 基本要求1. 了解光的直线传播定律,光的折射和反射定律及全反射定律。
2. 理解光在平面上的反射和折射成像。
3. 理解光在球面上的反射和折射,掌握在近轴条件下,球面反射成像的物像公式'111s s f +=及球面折射成像的物像公式1221'n n n n s s R-+=,并掌握横向放大率,理解符号法则。
4. 理解薄透镜逐次成像法,掌握薄透镜成像的高斯公式'111s s f+=及磨镜者公式'12111(1)()L f f n R R ==--,掌握透镜的像的横向放大率,会计算一些简单问题。
5. 了解显微镜和放大镜的工作原理及放大倍数。
二、 基本内容1. 几何光学的基本定律(1)光的直线传播定律 光在均匀介质中沿直线传播。
(2)光的反射和折射定律 反射定律 '11i i =折射定律 1122s i n s i n n i n i =(3)光的独立传播定律 光在不太强时,传播过程中与其它光束相遇时,各光束相互不受影响,不改变传播方向,各自独立传播。
2. 全反射定律21arcsinc n i n = 其中,c i 为全反射临界角,2n 为折射空间的折射率,1n 为入射空间的折射率。
3. 光在单球面上的反射近轴成像(1)球面反射近轴物像公式 '111s s f +=,其中2Rf =(R 是单球面的曲率半径),s 是物距,'s 是像距。
(2)符号约定法则a 球面的曲率半径R :若曲率中心C 与出射光在反射面的同侧时,半径R 为正,反之为负。
b 物距s :当物与入射光在反射面的同侧时,物距s 为正,反之为负。
s 为正时,物为实物,s 为负时,物为虚物。
c 像距's :当像与出射光在反射面的同侧时,像距's 为正,反之为负。
's 为正时,像是实像,'s 为负时,像是虚像。
(3)横向放大率 's sβ=-注意:当0β>,像是正立的;0β<,像是倒立的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、如图13-9所示,薄膜介质的折射率为n 1,薄膜上下介质的折射率分别为n 1和n 3,并且n 2比n 1和n 3都大。
单色平行光由介质1垂直照射在薄膜上,经薄膜上下两个表面反射的两束光发生干涉。
已知薄膜的厚度为e , λ1为入射光在折射率为n 1的介质中的波长,则两束反射光的光程差等于多少? 【答案:22112λn e n S -=∆】 详解:由于入射光在上表面从光疏介质投射到光密介质上存在半波损失,因此反射光一的光程为21λ=S由于入射光在下表面从光密介质投射到光疏介质上没有半波损失,因此反射光二的光程为e n S 222=两束反射光的光程差为22212λ-=-=∆e n S S S其中λ为光在真空的波长,它与介质1中的波长的关系为λ=n 1λ1,因此22112λn e n S -=∆ 2、在双缝干涉实验中,两缝分别被折射率为n 1和n 2、厚度均为e 的透明薄膜遮盖。
波长为λ的平行单色光垂直照射到双缝上,在屏中央处,两束相干光的相位差等于多少? 【答案:λϕen n )(π212-=∆】详解:设从双缝发出的两束光到屏中央处的距离为r ,依题意它们到达屏中央处的光程分别为)(11e r e n S -+= )(22e r e n S -+=它们的光程差为12S S S -=∆e n n )(12-=因此,在屏中央处两束相干光的相位差为n 3图13-9λϕS∆=∆π2λen n )(π212-=3、在双缝干涉实验中,为使屏上的干涉条纹间距变大,可以采取哪些办法?【答案:增大双缝与屏之间的距离D 、增大入射光波长λ、减小双缝间距d 、减小折射率n 】详解:双缝干涉条纹间距为dnD x λ=∆ 因此,为使屏上的干涉条纹间距变大,可以增大双缝与屏之间的距离D 、改用波长λ较长的光进行实验、将两缝的间距d 变小、将实验装置放在折射率n 较小的透明流体中。
4、如图13-10所示,在双缝干涉实验中,屏幕E 上的P 点处是明条纹。
如果将缝S 1盖住,并在S 1 S 2连线的垂直平分面处放置一个高折射率玻璃反射面M ,则此时P 点处是明条纹还是暗条纹? 【答案:是暗条纹】详解:设S 1、S 2到P 点的距离分别为r 1和r 2。
由于P 点处原来是明条纹,因此λk r r =-21如果在S 1 S 2连线的垂直平分面处放置一个高折射率玻璃反射面M ,由于从S 2发出的光经M 反射时存在半波损失,因此到达P 点的反射光与直射光的光程差为212r r S -+=∆λ2λλ+=k 2)12(λ+=k即这两束光在P 点处干涉相消,形成暗条纹。
5、如图13-11所示,在双缝干涉实验中,如果单色光源S 到两缝S 1、S 2距离相等,则中央明条纹位于观察屏E 上O 点处。
现在将光源S 向上移动到图中的S ' 位置,中央明条纹将向什么方向移动?此时条纹间距是否发生改变?图13-11S S图13-10P S图13-11S SP【答案:向O 点的下方移动;不发生改变】详解:如图所示,依题意,单色光源S ' 发出的光经S 1、S 2后射到P 点(中央明条纹的新位置)时的光程差为0)()(1122=+-+=∆r l r l S由此解得1221r r l l -=-由于l 1<l 2,因此r 1>r 2,即中央明条纹将向O 点的下方移动。
P 点为明条纹的条件为λk r r l l S =---=∆)()(1212其中x Dd r r =-12 因此λk x Ddl l =--)(12 对k 级和k +1级明条纹而言,有λk x D d l l k =--)(12 λ)1()(112+=--+k x Ddl l k 以上两式相减即得条纹间距为λdDx x x k k =-=∆+1 可见,在将光源S 向上移动时,条纹间距不发生改变。
6、将双缝干涉实验装置放在折射率为n 的水中,两缝间距离为d ,双缝到屏的距离为D (D >>d ),所用单色光在真空中的波长为λ,则屏上干涉条纹中相邻的明纹之间的距离等于多少? 【答案:nd D x λ=∆】 详解:将双缝干涉实验装置放在折射率为n 的水中时,到达光屏上的两束光的光程差为)(12r r n S -=∆由于Dxdr r =-12因此D nxdS =∆ 形成暗条纹的条件为nd D k x 2)12(λ-= 相邻明纹之间的距离为k k x x x -=∆+1n d D k n d D k 2)1(22]1)1(2[λλ---+=nd D λ=7、一双缝干涉装置,在空气中观察时干涉条纹间距为1.5mm 。
如果将整个装置放在水中,干涉条纹的间距将变为多少?已知水的折射率为1.33。
【答案:1.1mm 】详解:在空气和水中观察的双缝干涉条纹间距分别为λd D x =∆0 nd D x λ=∆ 两式相除得n x x 0∆=∆33.15.1=)mm (1.1= 8、如图13-12所示,在双缝干涉实验中SS 1=SS 2,用波长为λ的单色光照射双缝S 1和S 2,通过空气后在屏幕E 上形成干涉条纹。
已知P 点处为第三级明条纹,则S 1和S 2到P 点的光程差等于多少?如果将整个装置放于某种透明液体中,P 点为第四级明条纹,则该液体的折射率等于多少? 【答案:3λ;1.33】详解:由于P 点处为第三级明条纹,因此S 1和S 2到P 点的光程差为λθ3sin =d如果将整个装置放入折射率为n 的液体中,S 1和S 2到P 点的光程差变为θsin nd S =∆由于这时P 点为第四级明条纹,因此λθ4sin =nd与原来的光程差比较,得该液体的折射率为图13-12P33.134==n 9、在双缝干涉实验中,所用单色光波长为562.5nm ,双缝与观察屏的距离为1.5m ,如果测得屏上相邻明条纹的间距为1.7mm ,则双缝的间距等于多少? 【答案:0.50mm 】详解:双缝干涉条纹间距为λdDx =∆ 由此解得双缝间距为xD d ∆=λ36107.1105.5625.1--⨯⨯⨯=(mm)50.0=1、光强均为I 0的两束相干光相遇而发生干涉时,在相遇区域内有可能出现的最大光强是多少? 【答案:4I 0】详解:设光强为I 0的相干光对应的振幅为A 0,在相遇区域内可能出现的最大光振幅为2A 0,其对应的光强设为I 。
由于光强与相应振幅的平方成正比,即4)2(20200==A A I I 因此在相遇区域内有可能出现的最大光强为04I I =2、一束波长为λ的单色光由空气垂直入射到折射率为n 的透明薄膜上,透明薄膜放在空气中,要使反射光干涉加强,则薄膜最小的厚度等于多少? 【答案:ne 4min λ=】详解:反射光干涉加强的光程差条件为λλk ne =+22由此解得干涉加强时的薄膜厚度为nk e 4)12(λ-=当k =1时薄膜厚度最小,其值为ne 4min λ=3、两块平板玻璃构成空气劈形膜,左边为棱边,用单色平行光垂直入射。
如果上面的平板玻璃慢慢地向上平移,则干涉条纹将怎样移动?条纹间距是否变化? 【答案:干涉条纹向棱边方向平移,条纹间距不变】详解:由于劈尖干涉是等厚干涉,当上面的平板玻璃慢慢地向上平移时,各级条纹对应的厚度将向棱边方向平移,因此干涉条纹也向棱边方向平移。
当上面的平板玻璃慢慢地向上平移时,由于劈尖的尖角没有改变,因此条纹间距不变。
4、如图13-32所示,两个直径有微小差别的彼此平行的滚柱之间的距离为L ,夹在两块平板晶体的中间形成空气劈形膜,当单色光垂直入射时,产生等厚干涉条纹.如果滚柱之间的距离L 变大,则在L 范围内干涉条纹的数目怎样变化?条纹间距怎样变化? 【答案:干涉条纹的数目不变,条纹间距变大】详解:当滚柱之间的距离变大时,由于两个滚柱的直径都不变,它们与上面平板晶体相切处的条纹级别不变,因此在在L 范围内干涉条纹的数目也不变。
由于L 变大,而L 范围内干涉条纹的数目不变,因此L 范围内干涉条纹的间距变大。
5、折射率分别为n 1和n 2的两块平板玻璃构成空气劈尖,用波长为λ的单色光垂直照射。
如果将该劈尖装置浸入折射率为n 的透明液体中,并且n 2>n >n 1,则劈尖厚度为e 的地方两反射光的光程差的改变量等于多少? 【答案:2)1(2λ--e n 或 2)1(2λ+-e n 】详解:当该劈尖装置处在空气中时,劈尖厚度为e 的地方两反射光的光程差为221λ+=∆e S 或221λ-=∆e S而当该劈尖装置处在折射率为n (n 2>n >n 1)的透明液体中时,该处的两反射光的光程差变为ne S 22=∆光程差的改变量为2)1(212λ--=∆-∆e n S S 或=∆-∆12S S 2)1(2λ+-e n6、波长为λ的平行单色光垂直照射到劈形膜上,如果劈尖角为θ ,劈形膜的折射率为n ,则在反射光形成的干涉条纹中,相邻明条纹的间距等于多少? 【答案:θλn 2】 详解:如果反射光在劈形膜的一个面有半波损失,则相邻明条纹对应的厚度差为nnk nk e e e k k 24)12(4]1)1(2[11λλλ=---+=-=∆+如果反射光在劈形膜的两个面都有或都没有半波损失,则相邻明条纹对应的厚度差为nnknk e e e k k 222)1(12λλλ=-+=-=∆+图13-32显然,e e e ∆=∆=∆21。
由几何关系容易得到e l ∆=θsin n2λ=由于劈尖尖角θ很小,sin θ ≈θ。
因此相邻明条纹的间距为θλn l 2=7、牛顿环装置的平凸透镜和平板玻璃的折射率都是1.52,如果将这个牛顿环装置由空气中搬入折射率为1.33的水中,则干涉条纹中心暗斑是否会变成亮斑?条纹的疏密程度会发生怎样的变化?【答案:中心暗斑不会变成亮斑;条纹变密集】详解:如果将题目中的牛顿环装置由空气中搬入折射率为1.33的水中,由于水的折射率仍然比玻璃的折射率小,因此干涉条纹中心仍然是暗斑,不会变成亮斑。
设牛顿环装置的薄膜折射率为n ,则第k 级和k +1级暗环半径公式分别为n kR r k λ=2 nR k r k λ)1(21+=+以上两式相减得nRr r k k λ=-+221如果将牛顿环装置由空气中搬入折射率为1.33的水中,折射率n 增大。
由上式可以看出,当n 增大时,221k k r r -+减小,即条纹变密集。
8、如图13-33所示,用单色光垂直照射在牛顿环装置上。
当平凸透镜垂直向上缓慢平移而远离平面玻璃时,这些环状的干涉条纹会发生怎样的变化? 【答案:向中心收缩】详解:由于牛顿环干涉是等厚干涉,当平凸透镜垂直向上上慢慢平移时,各级条纹对应的厚度将向中心收缩,因此各级环状的干涉条纹也向中心收缩。
