振幅、加速度、振动频率三者的关系式

振幅、振速、振动加速度？

振幅、振速、振动加速度？振动一般可以用以下三个单位表示：mm、mm/s、mm/s2。

振幅、振动速度（振速）、振动加速度。

振幅是表象，速度和加速度是转子激振力的程度。

mm振动位移：一般用于低转速机械的振动评定；mm/s振动速度：一般用于中速转动机械的振动评定；mm/s2 振动加速度：一般用于高速转动机械的振动评定。

工程实用的振动速度是速度的有效值，表征的是振动的能量；加速度是用的峰值，表征振动中冲击力的大小。

振幅理解成路程，单位是mm；把振速理解成速度，单位是mm/s；振动加速度理解成运动加速度，单位mm/s2。

速度描述的是运动快慢；振速就是振动快慢，一秒内能产生的振幅。

振幅相同的设备，它的振动状态可能不同，所以引入了振速。

位移、速度、加速度都是振动测量的度量参数。

就概念而言,位移的测量能够直接反映轴承\固定螺栓和其它固定件上的应力状况。

例如:通过分析透平机上滑动轴承的位移,可以知道其轴承内轴杆的位置和摩擦情况。

速度反映轴承及其它相关结构所承受的疲劳应力。

而这正是导致旋转设备故障的重要原因。

加速度则反映设备内部各种力的综合作用。

表达上三者均为正弦曲线,分别有90度,180度的相位差。

现场应用上,对于低速设备(转速小于1000RPM)来说,位移是最好的测量方法。

而那些加速度很小,其位移较大的设备,一般采用折衷的方法,即采用速度测量,对于高速度或高频设备,有时尽管位移很小,速度也适中,但其加速度却可能很高的设备采用加速度测量是非常重要的手段。

另外还需要了解传感器的工作原理及应用选择,提及一点,例如采用涡流传感器测量的位移和应用加速度传感器通过两次积分输出的位移所得到的东西是完全不一样的。

涡流传感器测量轴承与轴杆之间的相对运动,加速度传感器测量轴承顶部的振动,然后转换成位移。

如整个轴承振动的很厉害,轴与轴承的相对运动很小,涡流传感器就不能反应出这样的状态,而加速度传感器则可以。

两种传感器测量两种不同的现象。

振动单位换算表

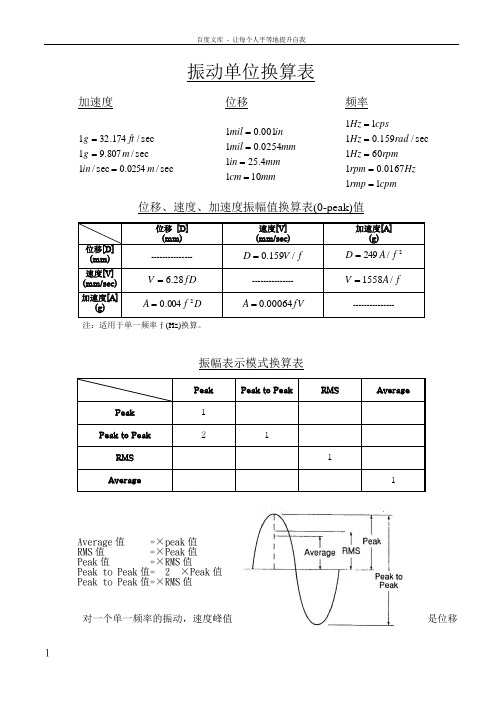
振动单位换算表加速度位移频率sec/0254.0sec /1sec /807.91sec /174.321m in m g ft g ===mmcm mm in mm mil inmil 1014.2510254.01001.01==== cpmrmp Hz rpm rpm Hz rad Hz cpsHz 110167.01601sec/159.0111=====位移、速度、加速度振幅值换算表(0-peak)值位移 [D] (mm) 速度[V] (mm/sec)加速度[A](g)位移[D] (mm) ---------------fV D /159.0=2/249f A D =速度[V] (mm/sec) fD V 28.6= ---------------f A V /1558=加速度[A](g)D f A 2004.0=fV A 00064.0=---------------注：适用于单一频率f (Hz)换算。

振幅表示模式换算表Peak Peak to PeakRMS AveragePeak 1 Peak to Peak2 1 RMS 1 Average1Average 值 =×peak 值 RMS 值 =×Peak 值 Peak 值 =×RMS 值Peak to Peak 值= 2 ×Peak 值 Peak to Peak 值=×RMS 值对一个单一频率的振动，速度峰值是位移峰值的2πf倍，加速度峰值又是速度峰值的2πf倍。

当然要注意位移一般用的峰峰值，速度用有效值，加速度用峰值。

还要注意现场测量的位移是轴和轴瓦的相对振动，速度和加速度测的是轴瓦的绝对振动。

假设一个振动的速度一定，是5mm/s，大家可以自己算下如果是低频振动，其位移会很大，但加速度很小。

高频振动位移则极小，加速度很大。

所以一般在低频区域都用位移，高频区域用加速度，中频用速度。

振动单位换算表

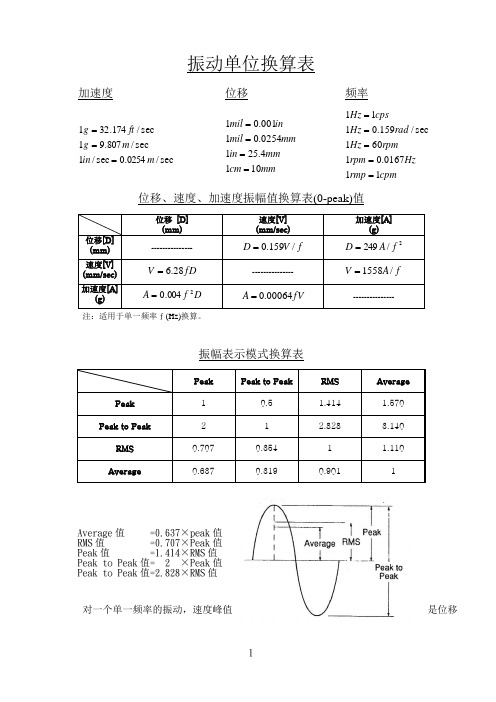
振动单位换算表加速度位移频率sec/0254.0sec /1sec/807.91sec/174.321m in m g ft g ===m mcm m m in m mm il in m il 1014.2510254.01001.01====cpmrmp Hz rpm rpm Hz rad Hz cps Hz 110167.01601sec /159.0111=====位移、速度、加速度振幅值换算表(0-peak)值注：适用于单一频率f (Hz)换算。

振幅表示模式换算表Average 值 =0.637×peak 值 RMS 值 =0.707×Peak 值 Peak 值 =1.414×RMS 值 Peak to Peak 值= 2 ×Peak 值 Peak to Peak 值=2.828×RMS 值对一个单一频率的振动，速度峰值是位移峰值的2πf倍，加速度峰值又是速度峰值的2πf倍。

当然要注意位移一般用的峰峰值，速度用有效值，加速度用峰值。

还要注意现场测量的位移是轴和轴瓦的相对振动，速度和加速度测的是轴瓦的绝对振动。

假设一个振动的速度一定，是5mm/s，大家可以自己算下如果是低频振动，其位移会很大，但加速度很小。

高频振动位移则极小，加速度很大。

所以一般在低频区域都用位移，高频区域用加速度，中频用速度。

但使用范围也有重叠。

位移值体现的是设备在空间上的振动范围，因此取其峰峰值，电力行业一般以位移为评判标准。

速度的有效值和振动的能量是成比例的，其大小代表了振动能量的大小，现在出了电力行业基本上都是以速度有效值为标准的。

加速度和力成正比，一般用其峰值，其大小表示了振动中最大的冲击力，冲击力大设备更容易疲劳损坏，现在没有加速度的标准。

振动幅值的表达式是正弦函数形式的，位移微分得到速度，速度微分得到加速度。

则：振动位移方程式： Y=Asinωt振动速度方程式： V= -Aωcosωt振动速度方程式： G= -Aωωsinωt如果振动频率为f的话，那么ω=2πf 其中π=3.1415926如果是单频率f的振动，位移的幅值为A，则速度幅值为2πfA，加速度幅值为2πf*2πfA。

振动的基础知识

频率
频率f是物体每秒钟振动循环的次数，单位是赫兹[Hz]。频率是一种振动特性，是分析振动故障原因的主要依据。机器发生故障，一般只是某个或某些部件出了故障并产生异常振动，异常振动的频率是由此故障自身机理特性所决定的，也就是说故障与频率存在着对应关系，即“问题严重程度看振幅，什么问题看频率”。
FFT
时间域 IFFT 频率域

之间的相位差，单位是度°。(也是就是转频分量从键相信号起到振动最高峰值之间的时间计算值) （正峰值计算法：第一个正峰值与固定参考点的角位置）无论采取何种相位取值方法，基频信号的相位都是值落后角度。是振动在时间先后关系上或空间位置关系上相互差异的标志。确定相位标记在工程上指转轴上所做的键相谱（光电标）位置。相位主要用于比较不同振动运动之间的关系（时间差及方位差），或确定一个部件相对于另一个部件的振动状况，在区别相同故障频率的不同故障类型时（特别是不平衡）往往起关键作用。

速度振幅反映了分析频段内时间历程的振动能量即振动烈度振动烈度是描述机器振动状态的特征量。通常在各个测量位置的水平、垂直和轴向上都进行测量，得到一组不同的振幅值，所测的宽带最大振幅值定义为振动烈度。由于振动烈度可参照振动标准，评价机器振动状态优劣；因此，在机器壳体上测量振动时要求在靠近轴承位置处的三个方向上都进行测量，最后取最大值作为振动烈度。

机械的支承分类

测量方向上，机器-基础组合分为柔性支承和刚性支承。柔性支承：系统自振转速低于工作转速。刚性支承：系统自振转速高于工作转速。对应基础组合系统的自振转速都有180°的相位变化。其中刚性基础不能承受系统的剪切力；柔性基础能承受系统的剪切力
谢谢大家

振动振动测试基础知识

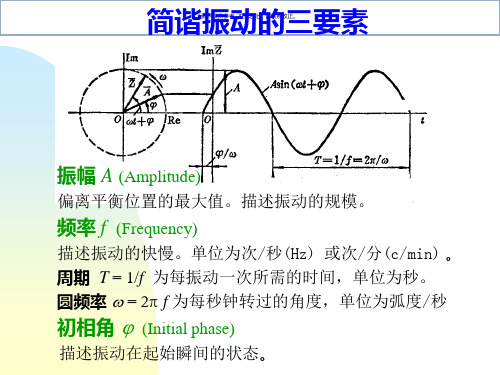
初相角 (Initial phase)
描述振动在起始瞬间的状态。
振动位移、速度、加速度之间的关系资料仅供参考,不当之处，请联系改正。
x
v
vx
a
振动位移
a
位移、速度、加速度都是同
xAs i nt
频率的简谐波。
速度)
vdxAsin t()
dt
2
加速度
三者的幅值相应为A、A、 A 2。
相位关系：加速度领先速度
均值 (Mean value)
又称平均值或直流分量。
x 1
T
x dt
T0
有效值
xrms
1 T x2 dt T0
资料仅供参考,不当之处，请联系改正。
简谐振动的幅值参数
平均绝对值
正峰值
有效值
峰峰值
平均值
负峰值
各幅值参数是常数，彼此间有确定关系
峰值 xp=A; 峰峰值 xp-p=2A
平均绝对值 xav=0.637A
资料仅供参考,不当之处，请联系改正。
旋转机械的振动图示 (变转速)
轴心轨迹阵波德图与极坐标图 (Bode & Polar Plot)
升（降）速时，基频幅值和相位的变化
三维频谱图 (Cascade) 坎贝尔图 (Campber)
各转速下的频谱图的另一种表示
轴心位置
判定轴颈静态工作点和油膜厚度
资料仅供参考,不当之处，请联系改正。
资料仅供参考,不当之处，请联系改正。
振动相位与转子转角的关系
振动信号
参考脉冲
从参考脉冲到第一个正峰值的转角定义振动相位。
振动相位与转子的转动角度一一对应。在平衡和故障诊断中有重要作用。

振动常用术语 (2)

振动常用术语1. 机械振动物体相对于平衡位置所作的往复运动称为机械振动。

简称振动。

例如，机器箱体的颤动、管线的抖动、叶片的摆动等都属于机械振动。

振动用基本参数、即所谓“振动三要素” —振幅、频率、相位加以描述。

3. 振幅3.1 振幅振幅是物体动态运动或振动的幅度。

振幅是振动强度和能量水平的标志，是评判机器运转状态优劣的主要指标。

3.2 峰峰值、单峰值、有效值振幅的量值可以表示为峰峰值（pp）、单峰值（p）、有效值（rms）或平均值（ap）。

峰峰值是整个振动历程的最大值，即正峰与负峰之间的差值；单峰值是正峰或负峰的最大值；有效值即均方根值。

只有在纯正弦波(如简谐振动)的情况下，单峰值等于峰峰值的1/2，有效值等于单峰值的0.707倍，平均值等于单峰值的0.637倍；平均值在振动测量中很少使用。

它们之间的换算关系是：峰峰值＝2×单峰值＝2×21/2×有效值。

此换算关系并无多大的实用价值，只是说明振幅在表示为峰峰值、峰值、有效值时，数值不同、相差很大。

3.3 振动位移、振动速度、振动加速度振幅分别用振动位移、振动速度、振动加速度值加以描述、度量，三者相互之间可以通过微分或积分进行换算。

在振动测量中，除特别注明外，习惯上，振动位移的量值为峰峰值，单位是微米[μm]或密耳[mil]；振动速度的量值为有效值，单位是毫米/秒[mm/s]或英寸/秒[ips]；振动加速度的量值是单峰值，单位是重力加速度[g]或米/秒平方[m/s2]，1[g] = 9.81[m/s2]。

可以认为，在低频范围内，振动强度与位移成正比；在中频范围内，振动强度与速度成正比；在高频范围内，振动强度与加速度成正比。

因为频率低意味着振动体在单位时间内振动的次数少、过程时间长，速度、加速度的数值相对较小且变化量更小，因此振动位移能够更清晰地反映出振动强度的大小；而频率高，意味着振动次数多、过程短，速度、尤其是加速度的数值及变化量大，因此振动强度与振动加速度成正比。

振动单位换算表

振动单位换算表加速度位移频率sec/0254.0sec /1sec /807.91sec /174.321m in m g ft g ===mmcm mm in mm mil inmil 1014.2510254.01001.01==== cpmrmp Hz rpm rpm Hz rad Hz cpsHz 110167.01601sec/159.0111=====位移、速度、加速度振幅值换算表(0-peak)值位移 [D] (mm) 速度[V] (mm/sec)加速度[A](g)位移[D] (mm) ---------------fV D /159.0=2/249f A D =速度[V] (mm/sec) fD V 28.6= ---------------f A V /1558=加速度[A](g)D f A 2004.0=fV A 00064.0=---------------注：适用于单一频率f (Hz)换算。

振幅表示模式换算表Peak Peak to PeakRMS Average Peak 1 0、5 1、414 1、570 Peak to Peak2 1 2、828 3、140 RMS 0、707 0、354 1 1、110 Average0、6370、3190、9011Average 值 =0、637×peak 值 RMS 值 =0、707×Peak 值 Peak 值 =1、414×RMS 值 Peak to Peak 值= 2 ×Peak 值 Peak to Peak 值=2、828×RMS 值对一个单一频率得振动，速度峰值就是位速度峰移峰值得2πf 倍，加速度峰值又就是得峰峰值得2πf 倍。

当然要注意位移一般用值，速度用有效值，加速度用峰值。

还要注意现场测量得位移就是轴与轴瓦得相对振动，速度与加速度测得就是轴瓦得绝对振动。

假设一个振动得速度一定，就是5mm/s，大家可以自己算下如果就是低频振动，其位移会很大，但加速度很小。

加速度频率和振幅的关系公式推算

加速度频率和振幅的关系公式推算说到加速度、频率和振幅的关系，那可是个有趣的话题。

大家可能会想，加速度是什么？频率又是啥？振幅又在哪里跳舞？别担心，咱们慢慢来，轻松聊聊这其中的关系。

加速度就像是你开车时踩油门的感觉，刚开始你是慢悠悠的，突然一脚油门下去，车子嗖的一下就飞起来了，这种变化的速度就叫加速度。

你想想，咱们在生活中是不是经常体验这种“猛然加速”的感觉？比如说，坐过山车的时候，那一瞬间的心跳加速，真是让人既刺激又紧张。

频率就像是乐队里的鼓点，咚咚的节奏在你耳边响起，越快的节奏越让人想跳舞。

频率其实是指单位时间内发生的事情有多少次，就好比你一天要喝几杯咖啡，频率高了，你就得频繁去咖啡机旁边转悠。

生活中的频率就像我们每天的节奏，有些人喜欢慢慢来，有些人则是“快、快、快”的节奏，这个频率决定了你生活的动感。

再说说振幅，听起来像个大词，其实挺简单。

振幅就是你在波动时的幅度，想象一下，你在海边玩水，海浪拍打上岸的高度，这个高度就是振幅。

振幅越大，波动就越厉害，水花四溅，那感觉简直像是在跟大海争风头，真是过瘾！而在生活中，振幅可以用来形容你做事情的激情，有时候你对一件事情充满热情，干劲十足，振幅自然就大；有时候就像天气预报说的“阴天”，动力没那么足，那振幅就小了。

大家一定在想，这三者之间有什么联系呢？嘿嘿，它们就像一对好朋友，紧紧相连。

加速度、频率和振幅就像是三人组，彼此之间有着微妙的互动关系。

比如，加速度大了，频率也会跟着上升，振幅也会随之增加。

就像你坐上了那个过山车，车速越快，感觉越刺激，心跳得也越来越快，手里的饮料都快飞出去了，哈哈！振幅大，频率高时，加速度也会随之增加，简直就像是打开了“超速模式”。

这种状态下，你的身体像是充满了能量，随时准备去征服一切。

你有没有过这样的经历，突然一股激情涌上心头，想要完成某个目标，结果就像火箭一样冲上去，那种感觉真是无与伦比。

反过来说，如果加速度小，那频率和振幅自然也跟着走低。

振幅和频率的关系公式

振幅和频率的关系公式振幅和频率是物理学中重要的概念，它们是描述物体振动特征的两个基本参数。

振幅表示物体振动时偏离平衡位置的最大距离，而频率则表示物体振动的周期性，即每秒钟振动的次数。

在物理学中，振幅和频率的关系可以用一个简单的公式来描述，这个公式是：振幅 = 峰值 / 2其中，峰值表示波形的最大值，也就是振动时物体偏离平衡位置的最大距离。

这个公式表明，振幅和峰值之间的关系是简单的线性关系，只需要将峰值除以2即可得到振幅。

另一方面，频率表示物体每秒钟振动的次数，通常用赫兹（Hz）来表示。

频率和周期的关系是：频率 = 1 / 周期周期是指物体振动一个完整的往复运动所需要的时间，通常用秒（s）来表示。

这个公式表明，频率和周期之间的关系也是简单的倒数关系。

振幅和频率的关系公式可以用来计算物体振动的一些基本参数。

例如，如果我们知道物体振动的频率和振幅，就可以计算出物体振动的最大速度和最大加速度。

最大速度等于振幅乘以频率，最大加速度等于振幅乘以频率的平方。

这些参数对于研究物体振动的性质和应用都非常重要。

振幅和频率的关系公式还可以用来解释一些自然现象。

例如，当我们听到声音时，声音的响度和音调就是由振幅和频率决定的。

响度表示声音的强度，它与声音的振幅成正比。

音调表示声音的高低，它与声音的频率成正比。

因此，当我们听到高音时，声波的频率较高，振幅较小；当我们听到低音时，声波的频率较低，振幅较大。

总之，振幅和频率是物理学中非常重要的概念，它们描述了物体振动的基本特征。

振幅和频率的关系公式可以用来计算物体振动的一些基本参数，也可以用来解释一些自然现象。

在学习物理学和应用物理学中，我们需要深入理解振幅和频率的概念，这将有助于我们更好地理解和应用物理学知识。

正弦振动加速度与速度与振幅与频率关系

正弦振动一共有四个参数来描述,即:加速度（用a表示）m/s A2速度（用v表示）m/s位移（用D表示）行程（2倍振幅）m 频率（用f表示）Hz公式:a=2 n fvv=2 n fc其中d=D/2） a=（2 n f）2d （2 为平方）说明:以上公式中物理量的单位均为国际单位制例如频率为10HZ，振幅为10mmV=2*3.1415926*10*10/1000=0.628m/sa=（2*3.1415926*10）A2*10/1000=39.478/m/sA2正弦运动振幅5mm频率200HZ我想你是在做一个弹簧振子，加速度是变化的，我想你需要的应该是弹簧的弹性系数k首先写出振动方程Y = 5sin（x/200）根据设计要求，弹簧要使振子在1/200s的时候运动距离达到5mm ,速度由最大的V0变为0,在这个过程中属于变力做功，（不知道你会积分不？）如果不会也没有关系，我们知道弹簧的弹性势能为0.5kHA2 （式中H是弹簧的伸长量），在达到振幅时，H = 5mm = 5 X!0A（-3）m应用动能定理：0.5kHA2=1/2mV0A2同时，应满足时间频率要求，应用动量定理，就必须用积分了，弹力在1/800（完成1/4周期需要的时间）时间内的冲量为I，I是以函数kHt为被积函数，对H由0到5，t由0到1/800的定积分，即1 = 6.25 乂10八（-5沐由动量定理 1 = mV1-mV0,得，mV0 = 6.25 X10A（-5）k联立两式解得：k = 256m （式中m不是单位，是振子得质量）而且初速度为400米每秒振动台上放置一个质量n= 10kg的物体，它们一起上下作简谐振动，其3频率V = 10Hz振幅A = 2 X 10-m，求：（1）物体最大加速度的大小；⑵在振动的最高位置、最低位置，物体分别对台面的压力。

解：取x轴竖直向下，以振动的平衡位置为坐标原点，列运动方程x = A cos （2 n V t + ©）于是，加速度2 2a= —4 n V A cos （2 n V t + ©）（1）加速度的最大值2 2 -2I a m |= 4 n V A = 7.9 m・s⑵由于物体在振动过程中仅受重力mg及竖直向上的托力f，按牛顿第二定律在最高位置m g —f = m| a m |f = m（g—| a m|）= 19.1N这时物体对台面的压力最小，其值即19.1N在最低位置m g—f= m(-| a m|)f= m(g+| a m|)= 177N这时物体对台面的压力最大，其值即177N频率为60HZ,振幅为0.15mm 的正弦振动,换算成加速度是多少只要了解一下其物理方法就不难得到结果了。

振幅、加速度、振动频率三者的关系式

振幅、加速度、振动频率三者的关系式在低频范围内，振动强度与位移成正比，而在中频范围内，振动强度与速度成正比。

在高频范围内，振动强度与加速度成正比。

这是因为频率低意味着振动体在单位时间内振动的次数少，过程时间长，速度和加速度的数值相对较小且变化量更小，因此振动位移能够更清晰地反映出振动强度的大小。

而频率高，意味着振动次数多，过程短，速度和尤其是加速度的数值及变化量大，因此振动强度与振动加速度成正比。

也可以认为，振动位移具体地反映了间隙的大小，振动速度反映了能量的大小，振动加速度反映了冲击力的大小。

振动加速度的量值是单峰值，单位是重力加速度[g]或米/秒平方[m/s2]，1[g]=9.81[m/s2]。

最大加速度不可大于20g，最大振幅不可大于5mm。

根据公式最大加速度=0.002×f2（频率Hz的平方）×D（振幅p-pmm），可以举例说明：10Hz最大加速度=0.002×10*10×5=1g。

在任何频率下，最大加速度不可大于20g，最大振幅不可大于5mm。

根据公式最大振幅=20/(0.002×f2)，可以举例说明：100Hz最大振幅=20/(0.002×100*100)=1mm。

在任何频率下，振幅不可大于5mm。

加速度与振幅之间可以通过公式1g=9.8m/s2A=1/2×0.002＊F2＊D进行换算。

其中，A表示加速度(g)，F表示频率(Hz)，D表示位移量(mm)。

举例来说，当13.2Hz振幅为1mm时，加速度为7m/s2A=0.002X(2X2)X1A=0.002X4X1A=0.008g。

可以通过单位转换1g=9.81m/s2A=0. m/s2来得到2Hz频率时的加速度，即0.m/s。

以上公式可以根据对应的参数输入进行计算，得到所需的结果。

大学物理振动波动复习资料

vmax A 0.8 m s 1
(2)
amax
2 2 6 . 4 m s A
2
v 0.8 sin(8t 2 / 3)
a 6.4 cos(8t 2 / 3)
2
(3)
1 2 Ek mv 3.2 10 3 2 sin 2 (8t 2 / 3) 2 1 2 3 2 2 E p kx 3.2 10 cos (8t 2 / 3) 2
x A cos(t )
1
物理学
第五版
2、描述谐振动的物理量（1）振幅
x
A
x t 图
T
T 2
A xmax
（2）周期、频率
o
A
t
周期
T
2π
1 频率 T 2π 2π 2 π 圆频率 T

弹簧振子周期
m T 2π k
周期和频率仅与振动系统本身的物理性质有关
A3
1 A2 2 o
x

4
(2k 1) ,
k 0, 1, 2
(2k 1)

4
A A3 A1 0.02m
24
物理学
第五版
第十章
机械波
教学基本要求一理解描述简谐波的各物理量的意义及各量间的关系. 二理解机械波产生的条件．掌握由已知质点的简谐运动方程得出平面简谐波的波函数的方法．理解波函数的物理意义．理解波的能量传播特征及能流、能流密度概念．
波动的种类：机械波、电磁波、物质波
27
物理学
第五版
一概念：
机械波、横波、纵波、振幅、频率、波长、波速、波函数、波的能量、衍射、干涉、驻波、多普勒效应

正弦振动加速度与速度与振幅与频率关系

正弦振动一共有四个参数来描述,即:加速度(用a表示)m/s^2速度(用v表示) m/s位移(用D表示)行程（2倍振幅）m频率(用f表示)Hz公式:a=2πfvv=2πfd(其中d=D/2)a=(2πf)2d (2为平方)说明:以上公式中物理量的单位均为国际单位制例如频率为10HZ，振幅为10mmV=2*3.1415926*10*10/1000=0.628m/sa=(2*3.1415926*10)^2*10/1000=39.478/m/s^2正弦运动振幅5mm 频率200HZ我想你是在做一个弹簧振子，加速度是变化的，我想你需要的应该是弹簧的弹性系数k首先写出振动方程Y＝5sin(x/200)根据设计要求，弹簧要使振子在1/200s的时候运动距离达到5mm，速度由最大的V0变为0，在这个过程中属于变力做功，（不知道你会积分不？）如果不会也没有关系，我们知道弹簧的弹性势能为0.5kH^2（式中H是弹簧的伸长量），在达到振幅时，H＝5mm＝5×10^(-3)m应用动能定理：0.5kH^2=1/2mV0^2同时，应满足时间频率要求，应用动量定理，就必须用积分了，弹力在1/800(完成1/4周期需要的时间）时间内的冲量为I，I是以函数kHt为被积函数，对H由0到5，t由0到1/800的定积分，即I＝6.25×10^(-5)k由动量定理I＝mV1-mV0,得，mV0＝6.25×10^(-5)k联立两式解得：k＝256m（式中m不是单位，是振子得质量）而且初速度为400米每秒振动台上放置一个质量m＝10kg的物体，它们一起上下作简谐振动，其频率ν＝10Hz、振幅Ａ＝2×10-3ｍ，求：(1)物体最大加速度的大小；(2)在振动的最高位置、最低位置，物体分别对台面的压力。

解：取ｘ轴竖直向下，以振动的平衡位置为坐标原点，列运动方程ｘ＝Ａcos（2πνｔ＋φ）于是，加速度a＝－4π２ν２Ａcos（2πνｔ＋φ）(1)加速度的最大值｜a m｜＝4π２ν２Ａ＝7.9ｍ·ｓ-2(2)由于物体在振动过程中仅受重力mｇ及竖直向上的托力ｆ，按牛顿第二定律在最高位置mｇ－ｆ＝m｜a m｜ｆ＝m（ｇ－｜a｜）＝19.1Nm这时物体对台面的压力最小，其值即19.1N在最低位置mｇ－ｆ＝m（－｜a m｜）ｆ＝m（ｇ＋｜a｜）＝177Nm这时物体对台面的压力最大，其值即177N频率为60HZ,振幅为0.15mm的正弦振动,换算成加速度是多少只要了解一下其物理方法就不难得到结果了。

简谐振动的特性和公式

简谐振动的特性和公式简谐振动是物理学中的一个重要概念，涉及到许多与振动相关的特性和公式。

本文将对简谐振动的特性和公式进行论述，并给出相应的解释和示例。

简谐振动是指一个物体在弹簧的作用下做周期性的振动运动。

它的特性主要包括振幅、周期、频率和相位四个方面。

振幅是指振动的最大偏离位置，用A表示。

周期是指振动完成一个完整循环所需要的时间，用T表示。

频率是指单位时间内振动循环的次数，用f表示。

相位是指振动状态相对于某一特定时刻的位置关系，用Φ表示。

公式方面，简谐振动涉及到的四个重要公式分别是振幅公式、周期公式、频率公式和相位公式。

振幅公式表示振动的最大偏离位置与振幅之间的关系，数学表达式为：A = xmax，其中，A表示振幅，xmax表示最大偏离位置。

周期公式表示振动所需要的时间与周期之间的关系，数学表达式为：T = 1/f，其中，T表示周期，f表示频率。

频率公式表示单位时间内振动循环的次数与频率之间的关系，数学表达式为：f = 1/T，其中，f表示频率，T表示周期。

相位公式表示振动的状态相对于某一特定时刻的位置关系，数学表达式为：Φ = 2πft，其中，Φ表示相位，f表示频率，t表示时间。

除了这些特性和公式之外，简谐振动还具有其他一些重要的特点和规律。

其中，简谐振动的位移与加速度的关系为二次反比关系，位移和速度之间存在90度的相位差，速度和加速度之间存在90度的相位差。

此外，简谐振动的能量是守恒的，振动的总能量等于弹性势能和动能之和。

为了更好地理解简谐振动的特性和公式，我们可以举一个具体的例子来说明。

假设有一个弹簧质量为m，劲度系数为k，振动的最大偏离位置为A。

根据振幅公式，我们可以得到振幅A和最大偏离位置的关系。

对于简谐振动来说，周期和频率是密切相关的。

周期公式和频率公式可以相互转换，通过周期公式可以得到系统的振动频率。

相位是描述振动状态的重要参数，可以用来表示振动的位置和状态。

相位公式可以通过时间来计算振动的位置。