matlab习题第六章

合集下载

控制系统仿真matlab第六章习题答案汇总

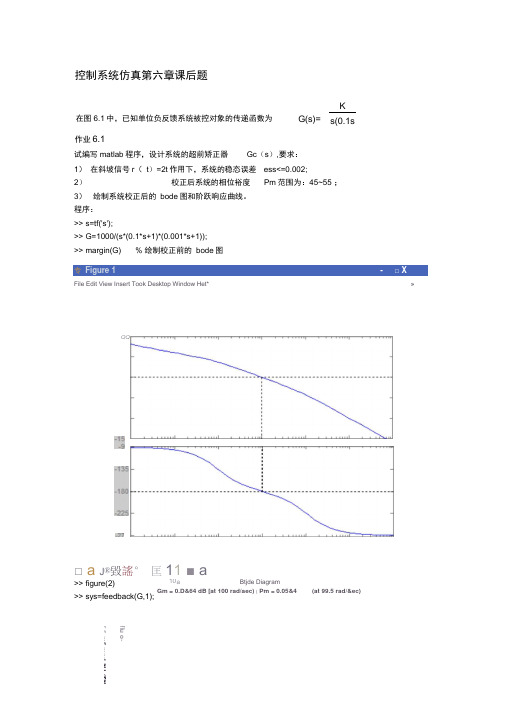
控制系统仿真第六章课后题作业6.1试编写matlab 程序，设计系统的超前矫正器 Gc （s ）,要求：1）在斜坡信号r （ t ）=2t 作用下，系统的稳态误差 ess<=0.002;2）校正后系统的相位裕度 Pm 范围为：45~55 ； 3）绘制系统校正后的 bode 图和阶跃响应曲线。

程序：>> s=tf('s');>> G=1000/(s*(0.1*s+1)*(0.001*s+1));>> margin(G)% 绘制校正前的 bode 图专 Figure 1 - □ X File Edit View Insert Took Desktop Window Het* »□ a J ®毀謠° 匡11 ■ a >> figure(2)>> sys=feedback(G,1); 在图6.1中，已知单位负反馈系统被控对象的传递函数为G(s)= Ks(0.1s 1)(0.0QQo oBtjde Diagram Gm = 0.D&64 dB [at 100 rad/aec) ( Pm = 0.05&4 (at 99.5 rad/&ec)flu o-5 5 mE mprl 左一6『左 a 10>> step(sys) %绘制校正前的单位阶跃响应曲线Figure 2File Edit 过ew Insert Tools Window Help□已鸟|罠4紗®悬乙| 口目| ■回Step Response1.3>> [Gm,Pm]=margin(G); %该句值计算bode图的增益裕量Gm和相位裕量Pm >> [mag,phase,w]=bode(G); %该句只计算bode图上多个频率点w对应的幅值和相位>> QWPm=50; %取矫正后的相位为50>> Flm=QWPm-Pm+5;>> Flm=Flm*pi/180;>> alfa=(1-si n(FIm))/(1+si n( FIm));>> adb=20*log10(mag);>> am=10*log10(alfa);>> wc=spli ne(adb,w,am);>> T=1/(wc*sqrt(alfa));>> alfat=alfa*T;>> Gc=tf([T 1],[alfat 1]) %校正器的传递函数Tran sfer function:0.01794 s + 1Time 330.00179 s + 1>> figure(3)>> margin(Gc*G) %系统矫正后的bode图Ffgure 3Filt gdit yisw ifisert Hcdt Mfimdcw title】I ■回Bode DiagramGm = 17.6 dB (st 69B rad/sec) s Pm = 4S.2 deg (at 176 rad/sec)"I 0 0 N -- 1 1 I I I ! 1 ! | ! ■' I I ' ' I J I I ........... | I I « i i i | i | i f ■ J !!|!|>> figure(4)>> step(feedback(Gc*G ,1)) % 校正后的单位阶跃响应曲线Figure 4n xl Fie Edit 辺足w Insert Tools Desktop Window HelpO t3 J -S □ S ■ Q1010°ID1 1 孑10Frequency (r&fh'see)作业6.2在图6.1中，已知单位负反馈系统被控对象的传递函数为试编写matlab 程序，设计系统的滞后校正器 Gc ( s ),要求:1) 在斜坡信号r(t)=t 作用下，系统的稳态误差ess 乞0.01 ； 2) 校正后系统的相位裕度 Pm 范围为：40~50 ；3) 绘制系统矫正前后的 bode 图和阶跃响应曲线。

数字图像处理及应用（MATLAB）第6章习题答案

第六章习题与思考题参考答案1. 简述飞机红外图像识别中用到的五个红外特征量各自的作用？1）长宽比：反应了目标的几何形状；2）复杂度：反应了红外目标轮廓的情况；3）紧凑度：反应了红外目标在其所在最小外接矩形中所占比重；4）均值对比度：反映了目标的物理特性与背景的物理特性之间的关系；5）部分最亮像素点数与目标总像素数的比值：反应了目标的明暗变化情况；2. 可视密码共享中,如果实现（4 , 5）门限的可视密码分享，程序将做如何编写？clear allclose allM=imread('0.jpg');ss=rgb2gray(M);figureimshow(ss);[m n]=size(ss);for i=1:m*nif ss(i)>250ss(i)=250;endends=double(ss)+1;x=[1 2 3 4 5];g1=zeros(m,n);g2=zeros(m,n);g3=zeros(m,n);g4=zeros(m,n);g5=zeros(m,n);yy1=zeros(m,n);yy2=zeros(m,n);yy3=zeros(m,n);yy4=zeros(m,n);yy5=zeros(m,n);y1=zeros(m,n);y2=zeros(m,n);y3=zeros(m,n);y4=zeros(m,n);y5=zeros(m,n);for j=1:m*na1=mod(2*j,251);a2=mod(3*j,251);a3=mod(5*j,251);f=[a1 a2 a3 s(j)];g1(j)=polyval(f,x(1));yy1(j)=mod(g1(j),251);g2(j)=polyval(f,x(2));yy2(j)=mod(g2(j),251);g3(j)=polyval(f,x(3));yy3(j)=mod(g3(j),251);g4(j)=polyval(f,x(4));yy4(j)=mod(g4(j),251);g5(j)=polyval(f,x(5));yy5(j)=mod(g5(j),251);endy1=uint8(yy1-1)y2=uint8(yy2-1);y3=uint8(yy3-1);y4=uint8(yy3-1);y5=uint8(yy3-1);figure,imshow(y1);figure,imshow(y2)figure,imshow(y3);figure,imshow(y4);figure,imshow(y5);l1=(x(2)*x(3)*x(4)*x(5))/[(x(1)-x(2))*(x(1)-x(3))*(x(1)-x(4))*(x(1)-x(5))];l2=(x(1)*x(3)*x(4)*x(5))/[(x(2)-x(1))*(x(2)-x(3))*(x(2)-x(4))*(x(2)-x(5))];l3=(x(1)*x(2)*x(4)*x(5))/[(x(3)-x(1))*(x(3)-x(2))*(x(3)-x(4))*(x(3)-x(5))];l4=(x(1)*x(2)*x(3)*x(5))/[(x(4)-x(1))*(x(4)-x(2))*(x(4)-x(3))*(x(4)-x(5))];l5=(x(1)*x(2)*x(3)*x(4))/[(x(5)-x(1))*(x(5)-x(2))*(x(5)-x(3))*(x(5)-x(4))];rr1=zeros(m,n);r=zeros(m,n);for j=1:m*nrr1(j)=mod(yy1(j)*l1+yy2(j)*l2+yy3(j)*l3+yy4(j)*l4+yy5(j)*l5,251);endr=uint8(rr1-1);figure,imshow(r);3. 已知图像⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=805020016821024015010017018013070901262068M 。

MATLAB程序设计与应用实验答案第六章刘卫国

1.(1)A=randn(10,5)A =-0.4326 -0.1867 0.2944 -0.3999 -1.6041 -1.6656 0.7258 -1.3362 0.6900 0.2573 0.1253 -0.5883 0.7143 0.8156 -1.0565 0.2877 2.1832 1.6236 0.7119 1.4151 -1.1465 -0.1364 -0.6918 1.2902 -0.8051 1.1909 0.1139 0.8580 0.6686 0.5287 1.1892 1.0668 1.2540 1.1908 0.2193 -0.0376 0.0593 -1.5937 -1.2025 -0.9219 0.3273 -0.0956 -1.4410 -0.0198 -2.1707 0.1746 -0.8323 0.5711 -0.1567 -0.0592 B=mean(A)B =0.0013 0.2310 0.0253 0.3588 -0.4197 C=std(A)C =0.9034 0.8829 1.1898 0.7832 1.0821 (2)D=max(max(A))D =2.1832E=min(min(A))E =-2.1707(3)F=sum(A,2)F =-2.3288-1.32870.01056.2215-1.48953.36024.9201-3.6964-3.3998-0.3025G=sum(sum(A))G =1.9666(4)H=sort(A)H =-1.6656 -0.8323 -1.5937 -1.2025 -2.1707-1.1465 -0.5883 -1.4410 -0.3999 -1.6041-0.4326 -0.1867 -1.3362 -0.1567 -1.0565-0.0376 -0.1364 -0.6918 -0.0198 -0.92190.1253 -0.0956 0.2944 0.6686 -0.80510.1746 0.0593 0.5711 0.6900 -0.05920.2877 0.1139 0.7143 0.7119 0.21930.3273 0.7258 0.8580 0.8156 0.25731.1892 1.0668 1.2540 1.1908 0.52871.19092.1832 1.6236 1.2902 1.4151L=-sort(-A,2,'descend')L =-1.6041 -0.4326 -0.3999 -0.1867 0.2944-1.6656 -1.3362 0.2573 0.6900 0.7258-1.0565 -0.5883 0.1253 0.7143 0.81560.2877 0.7119 1.4151 1.6236 2.1832-1.1465 -0.8051 -0.6918 -0.1364 1.29020.1139 0.5287 0.6686 0.8580 1.19090.2193 1.0668 1.1892 1.1908 1.2540-1.5937 -1.2025 -0.9219 -0.0376 0.0593-2.1707 -1.4410 -0.0956 -0.0198 0.3273-0.8323 -0.1567 -0.0592 0.1746 0.57112.(1)x=[0 15 30 45 60 75 90];y=[0 0.2588 0.5000 0.7071 0.8660 0.9659 1.0000];x1=0:90;y1=interp1(x,y,x1,'spline')y1 =Columns 1 through 110 0.0175 0.0349 0.0524 0.0698 0.0872 0.1045 0.1219 0.1392 0.1564 0.1737Columns 12 through 220.1908 0.2079 0.2249 0.2419 0.2588 0.2756 0.2923 0.3090 0.3255 0.3420 0.3583Columns 23 through 330.3746 0.3907 0.4067 0.4226 0.4384 0.4540 0.4695 0.4848 0.5000 0.5150 0.5299Columns 34 through 440.5446 0.5592 0.5736 0.5878 0.6018 0.6157 0.6293 0.6428 0.6561 0.6691 0.6820Columns 45 through 550.6947 0.7071 0.7193 0.7313 0.7431 0.7547 0.7660 0.7771 0.7880 0.7986 0.8090Columns 56 through 660.8191 0.8290 0.8387 0.8480 0.8571 0.8660 0.8746 0.8829 0.8910 0.8987 0.9062Columns 67 through 770.9135 0.9204 0.9271 0.9335 0.9396 0.9454 0.9510 0.9563 0.9612 0.9659 0.9703Columns 78 through 880.9744 0.9782 0.9817 0.9849 0.9878 0.9904 0.9927 0.9946 0.9963 0.9977 0.9987Columns 89 through 910.9995 0.9999 1.0000x=[0 15 30 45 60 75];y=[0 0.2679 0.5774 1.0000 1.7320 3.7320];x1=0:75;y1=interp1(x,y,x1,'spline')y1 =Columns 1 through 110 0.0184 0.0365 0.0545 0.0724 0.0902 0.1079 0.1255 0.1431 0.1607 0.1784Columns 12 through 220.1961 0.2138 0.2317 0.2497 0.2679 0.2863 0.3048 0.3236 0.3427 0.3620 0.3817Columns 23 through 330.4017 0.4221 0.4429 0.4641 0.4858 0.5079 0.5305 0.5537 0.5774 0.6017 0.6266Columns 34 through 440.6520 0.6780 0.7046 0.7317 0.7593 0.7876 0.8163 0.8456 0.8754 0.9058 0.9367Columns 45 through 550.9681 1.0000 1.0325 1.0658 1.1003 1.1364 1.17431.2145 1.2572 1.3028 1.3516Columns 56 through 661.4041 1.4604 1.5211 1.5863 1.6565 1.7320 1.8131 1.9002 1.99362.0937 2.2008Columns 67 through 762.3152 2.4374 2.5675 2.7060 2.85323.0095 3.17523.3506 3.5361 3.7320x=[0 15 30 45 60 75 90];y=[0 0.2588 0.5000 0.7071 0.8660 0.9659 1.0000];y1=polyfit(x,y,5)y1 =0.0000 0.0000 -0.0000 0.0000 0.0174 0.0000x=[0 15 30 45 60 75];y=[0 0.2679 0.5774 1.0000 1.7320 3.7320];y1=polyfit(x,y,5)y1 =0.0000 -0.0000 0.0000 -0.0010 0.0245 0.0000(2)x=[1 4 9 16 25 36 49 64 81 100];y=1:10;x1=1:100;y1=interp1(x,y,x1,'cubic')y1 =Columns 1 through 111.0000 1.3729 1.71252.0000 2.2405 2.4551 2.64942.82923.0000 3.1636 3.3186Columns 12 through 223.4661 3.6069 3.7422 3.87294.0000 4.1237 4.24354.3599 4.4730 4.5832 4.6907Columns 23 through 334.7958 4.89885.0000 5.0993 5.1966 5.2921 5.38575.4777 5.5681 5.6570 5.7446Columns 34 through 445.8309 5.91606.0000 6.0829 6.1647 6.2454 6.32496.4035 6.4810 6.5577 6.6334Columns 45 through 556.7082 6.7823 6.8556 6.92817.0000 7.0712 7.14167.2113 7.2804 7.3487 7.4164Columns 56 through 667.4835 7.5500 7.6159 7.6812 7.7459 7.8102 7.8739 7.9372 8.0000 8.0623 8.1242Columns 67 through 778.1855 8.2464 8.3068 8.3668 8.4263 8.4854 8.5441 8.6024 8.6603 8.7178 8.7749Columns 78 through 888.8317 8.8881 8.9442 9.0000 9.0555 9.1107 9.16559.2201 9.2744 9.3284 9.3821Columns 89 through 999.4354 9.4884 9.5412 9.5935 9.6456 9.6973 9.7486 9.7996 9.8502 9.9005 9.9505Column 10010.00003.xi=[165 123 150 123 141];yi=[187 126 172 125 148];P=polyfit(xi,yi,3)P =1.0e+003 *-0.0000 0.0013 -0.1779 8.4330线性拟合曲线为：p(x)=1.3x^2—177.9x+84334.(1)P1=[0,3,2];P2=[5,-1,2];P3=[1,0,-0.5];P=conv(P1,conv(P2,P3))P =0 15.0000 7.0000 -3.5000 0.5000 -2.0000 -2.0000 (2)P1=[0,3,2];P2=[5,-1,2];P3=[1,0,-0.5];P=conv(P1,conv(P2,P3));Y=roots(P)Y =0.70710.1000 + 0.6245i0.1000 - 0.6245i-0.7071-0.6667(3)P1=[0,3,2];P2=[5,-1,2];P3=[1,0,-0.5];P=conv(P1,conv(P2,P3));k=0:10;xi=0.2*k;Y=polyval(P,xi)Y =-2.0000 -2.3920 -2.6112 -1.7024 2.7104 15.0000 42.1120 94.1408 184.9056 332.5264 560.00005.(1)[U,fmin]=fminsearch('xiti651',[1,1])U =1.0e-004 *-0.0675 0.1715fmin =1.9920e-010(2)f=inline('-sin(x)-cos(x.^2)');fminbnd(f,0,pi)ans =0.73106.(1)x=[pi/6 pi/4 pi/3 pi/2];f=inline('sin(x).^2+cos(x).^2');dx=diff(f([x,5*pi/12]))/(pi/12)dx =0 0 0 0(2)x=1:3;f=inline('sqrt(x.^2+1)');dx=diff(f([x,4]))dx =0.8219 0.9262 0.96087.(1)g=inline('sin(x).^5.*sin(5*x)');I=quadl(g,0,pi)I =0.0982(2)g=inline('(1+x.^2)./(1+x.^4)');I=quad(g,-1,1)I =2.2214(3)g=inline('(x.*sin(x))./(1+cos(x).^2)'); I=quadl(g,0,pi)I =2.4674(4)f=inline('abs(cos(x+y))');dblquad(f,0,pi,0,pi)ans =6.28329.(1)矩阵求逆法：A=[2,3,5;3,7,4;1,-7,1];b=[10;3;5];x=inv(A)*bx =-1.8060-0.53733.0448矩阵除法：A=[2,3,5;3,7,4;1,-7,1];b=[10;3;5];x=A\bx =-1.8060-0.53733.0448矩阵分解法：A=[2,3,5;3,7,4;1,-7,1];b=[10;3;5];[Q,R]=qr(A);x=R\(Q\b)x =-1.8060-0.53733.0448(2)矩阵求逆法：A=[5,1,-1,0;1,0,3,-1;-1,-1,0,5;0,0,2,4]; b=[1;2;3;-1];x=inv(A)*bx =1.4000-5.90000.1000-0.3000矩阵除法：A=[5,1,-1,0;1,0,3,-1;-1,-1,0,5;0,0,2,4]; b=[1;2;3;-1];x=A\bx =1.4000-5.90000.1000-0.3000矩阵分解法：A=[5,1,-1,0;1,0,3,-1;-1,-1,0,5;0,0,2,4];b=[1;2;3;-1];[Q,R]=qr(A);x=R\(Q\b)x =1.4000-5.90000.1000-0.300010.A=[2 1 -1 1;4 2 -2 1;2 1 -1 -1];b=[1;2;1];[x,y]=line_solution(A,b)原方程组有无穷个解，特解为x，齐次方程组的基础解系为yWarning: Rank deficient, rank = 2, tol = 4.3512e-015. > In line_solution at 11方程组无解x =[]y =-0.5000 0.50001.0000 00 1.00000 011.(1)f=inline('x-sin(x)./x');x=fzero(f,0.5)x =0.8767(2)f=inline('(sin(x).^2).*exp(-0.1.*x)-0.5.*abs(x)');x=fzero(f,1.5)x =1.673812.x=fsolve('xiti612',[0.5,0.5],optimset('Display','off')) x =0.5000y =0.5000f =-0.0509f =-0.0509 0.1173 x =0.5000y =0.5000f =-0.0509f =-0.0509 0.1173 x =0.5000y =0.5000f =-0.0509f =-0.0509 0.1173 x =0.6459y =0.3739f =0.0055f =0.0055 0.0044 x =0.6459y =0.3739f =0.0055f =0.0055 0.0044 x =0.6459y =0.3739f =0.0055f =0.0055 0.0044 x =0.6355y =0.3734f =1.9417e-005f =1.0e-004 *0.1942 0.2589 x =0.6355y =0.3734f =1.9425e-005f =1.0e-004 *0.1942 0.2589x =0.6355y =0.3734f =1.9419e-005f =1.0e-004 *0.1942 0.2591x =0.6354y =0.3734f =2.3754e-010f =1.0e-009 *0.2375 0.2957x =0.6354y =0.3734f =7.9432e-009f =1.0e-008 *0.7943 0.5602x =0.6354y =0.3734f =1.8684e-009f =1.0e-007 *0.0187 0.1936x =0.6354 0.373413.x0=0;xf=20;y1=0;[x,y]=ode45('xiti6131',[x0,xf],y1) x =0.50001.00001.50002.00002.50003.00003.50004.00004.50005.00005.50006.00006.50007.00007.50008.00008.50009.00009.500010.000010.500011.000011.500012.000012.500013.000013.500014.000014.500015.000015.500016.000016.500017.000017.500018.000018.500019.000019.500020.0000 y =NaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaNNaN(2)x0=0;xf=20;[x,y]=ode45('xiti6132',[x0,xf],[-3,2])[x,y]此题结果过长，疑似错误或不会做。

自动控制原理习题全解及MATLAB实验第6章习题解答

系统开环传递函数为 G0 s
s0.1s
K
10.2s
1
，要求：
（1）系统响应斜坡信号 r(t)=t 时，稳态误差 ess 0.01 ；
(2) 系统相位裕量 ' 40 。
试用分析法设计一个串联滞后-超前校正装置。
解：（1）系统为Ⅰ型系统，在单位斜坡信号下
分稳态误差为
essr
1 k
令 essr
稳态性能与动态性能？答：PID 兼有 PI、PD 控制的特点，它相当于提供了一个积分环节与两个一阶微分环节。
积分环节改善稳态性能，两个一阶微分环节改善动态性能。试分别叙述利用比例负反馈和微分负反馈包围振荡环节所起到的作用。
答：二阶振荡环节的频率特性为
1
T 2S 2 2 S 1
用比例负反馈 H(s)=h
0.2s 1 0.0143s 1
（5） Gc (s)
s 1 14s 1
0.2s 1 0.0143s
(6)
G
k
(s)
s(14s
100(s 1) 1)(0.1s 1)(0.0143s
1)
' 180 [90 arctan 7 arctan(14 7) arctan(0.1 7) arctan(0.0143 7)] 41.9 40
10lg( 12)
6dB
,
最后得出 c' m 4.47rad/s>4.4rad/s
(4) 确定校正装置的转折频率
1 m
2.2rad/s ，2 m
8.8rad/s ，T 1 0.45s ， 1
G(s)=
s
2.2 s
1 1
0.45s 0.11s
1 1

Matlab编程 - 第六章 lingo软件基础

第六章
LINGO软件基础
1
第六章 lingo软件简介 LINGO(linear interactive and general optimiuzer) 的基本含义是交互式的线性和离散化求解器。最初是由芝加哥大学的Linus Schrage教授于1980年开发的. 是主要用来求解优化问题的软件。最大特色：允许优化问题中的决策变量为整数，即可求解整数规划，而且执行速度快。
x2+2*x4+x5+3*x6>=20; x3+x5+2*x7>=15; @gin(x1);@gin(x2);@gin(x3); @gin(x4);@gin(x5);@gin(x6); @gin(x7);
x3 x5 2 x7 15,
xi 为整数
结论：按第1种模式切5根，第2种模式切5根，第5种模式切15根，共需切割25根原料钢管。
9
二、LINGO中集集是一群相联系的对象，这些对象也称为集的成员。每个集成员可能有一个或多个与之有关联的特征，这些特征称为属性。 LINGO有两种类型的集：原始集和派生集。原始集是由一些最基本的对象组成的。派生集是用一个或多个其它集来定义的。
10
1.定义原始集 sets: setname/member_list /:attribute_list; endsets
Feasible solution found. Total solver iterations: Variable I1 I2
0 Value 2.000000 3.000000
27
4.集循环函数：@for， @sum, @max, @min 用法：(1) @for(setname: expression_list) 对集合setnane的每个元素独立生成expression_list。 (2) @for(setname(i)|logical_condition:expression_list) 对集合setnane中满足logical_condition的成员独立生成 expression_list。 data: 如： x=3,8,5,7,6,-2; sets: enddata niu/1..6/:x,y,z; @ for(niu:y=x^2+2); endsets @for(niu(i)|i#le#3:z(i)=x(i)-3); @for(niu(i)|i#gt#3:z(i)=x(i)^2-2);

MATLAB基础及其应用教程-周开利-邓春晖课后答案第六章

第6章习题解答1. 在命令窗口中输入，一次只能执行一行命令，脚本文件是命令的集中，只需输入脚本文件名，就可以按顺序一次执行所有命令。

2．脚本文件是命令的集中，只需输入脚本文件名，就可以一次执行所有命令，没有输入参数，没有输出参数。

文件名可任意取，只需符合变量的定义要求即可。

脚本文件中生成的变量是全局变量。

函数文件可以接受参数，也可以返回参数，一般需要由其他语句调用。

首行语句必须以function开始，有函数名，文件名必须与函数名一致。

函数空间中生成的变量是局部变量。

3．function result=project1(year)if mod(year,400)==0 || (mod(year,4)==0 && mod(year,100)~=0)result='是闰年';elseresult='不是闰年';end4．function min=comp(x1,x2)min=x1;if x1>x2min=x2;end5．（1）在命令窗口输入：k=0;for i=-1000:1000;k=k+1;end;k 即可得出：2001步。

（2）方法同上，10步6．（1）循环进行的条件是var不是10的倍数，循环结束时，var必是10的倍数，即10（2）每次循环的结果是：4，16，256，此时，不满足循环条件而退出循环，即var为256（3）循环条件是var>100，而var的值为3，不满足条件，循环不执行，所以var值不变。

7．方法1：clear;A=[1 2 3;4 5 6];fid=fopen('c:\a1.txt','wt');fprintf(fid,'%d ',A(1,:));fprintf(fid,'\n');fprintf(fid,'%d ',A(2,:));fclose(fid);方法2：clear;a=[1 2];A=[1 2 3 4 5 6]B=reshape(A,2,2) dlmwrite('c:\a2.txt',B)。

Matlab第六章作业答案

第六章
6.2 如何进行一下操作：
（1）翻转模块
（2）给模型窗口加标题
（3）指定仿真时间
（4）设置示波器的显示刻度
解：（1）点击模型窗口的Format ，在下拉菜单中中有两个选项：Flip block 和Rotate block 。

Flip block 可使模块旋转180度（快捷键Ctrl+I ），Rotate block 可以模块顺时针旋转90度（快捷键Ctrl+R ）。

（2）在模型窗口的上方双击鼠标左键，会出现的一个文本输入框，编辑输入标题。

（3）单击Simulation ，在下拉菜单中选择configuration parameters ，打开仿真环境参数对话框，在Solver 选项的start time 设置仿真起止时间。

（4）双击示波器Scope 调出显示屏幕，选择Axes properties 选项，改变Y-min 和Y-max 可改变显示刻度。

6.3用Simulink 建立如下控制系统的仿真模型，并对系统进行阶跃响应仿真模型：
22()48
G s s s =++ 解：
6.4在Simulink 环境下，设计一个PID 控制器，实现下面被控制对象的控制，并观察选择不同的PID 参数时对控制效果的影响：
220()212G s s s =++ 其中，系统输入信号分别选择阶跃信号和正弦信号。

解：当输入信号为阶跃信号时：
当输入信号为正弦信号时：。

MATLAB程序设计第6章回归分析和方差分析

参数估计和假设检验
（1）区间估计 ❖例：有一大批糖果，现从中随机地取16袋,称得质量(单位:g)如下: 506 508 499 503 504 510 497 512 514 505 493 496 506 502 509 496
参数估计和假设检验
❖计算的MATLAB程序如下：
x0 = [506 508 499 503 504 510 497 512 514 505 493 496 506 502 509 496]; x0 = x0( : ); alpha = 0.05; mu = mean( x0); sig = std( x0 ); n =length(x0 ); t =[mu -sig/sqrt(n)*tinv(1-alpha /2,n-1),mu+ sig/sqrt(n)*tinv(1 -alpha/2,n-1)]; %以下命令ttest的返回值ci就直接给出了置信区间估计 [h,p,ci] =ttest(x0, mu,0.05)%通过假设检验也可求得置信区间
记
多元线性回归
（2）参数估计理论模型中的参数 β0 ，β1，…，βm用最小二乘法估计，即应选取估计值
， j=0，1，…，m 时，误差平方和达到最小。
，使当
令
得
整理化为正规方程组
多元线性回归
正规方程组的矩阵形式为
，
当矩阵 X列满秩时，XT X 为可逆方阵，
将代回原模型得到 y 的估计值，
而这组数据的拟合值为，
非线性回归
非线性回归是指因变量 y对回归系数 β1 ,…, βm (而不是自变量)是非线性的。 MATLAB统计工具箱中的命令 nlinfit、nlparci、nlpredci、nlintool，不仅可以给出拟合的回归系数及其置信区间，而且可以给出预测值及其置信区间等。

matlab第6章ode

1 L 0
u
i
状态方程以两个状态元件 i和uo作状态变量 21
+S
i
ui
D
-
dT
L
+
C u0 R
-
0
L
di dt
u0
i
C
d u0
dt
u0
R
T
(2)当S=off：时间长度为: （1-d)*T:
di dt
u0
L
du0
dt
i C
u0
RC
22
S=OFF
u
•
i
•
0
0
1 C
1
1. ode23
在MATLAB中，函数ode23采用2-3阶龙格-库塔法求解微分方程。
[t,y]=ode23(odefun,tspan,y0) [t,y]=ode23(odefun,tspan,y0,options) odefun：定义微分方程的形式y’=f(t,y) tspan=[t0,tfinal]：表示微分方程的积分限从t0（始值）到tfinal（终值），该积分限也可以是一些离散的点。 y0:初始状态列向量 options：积分参数，包括‘RelTol’（相对误差）和 ‘AbsTol’（绝对误差），可省略。
IR Vi
L C UC
12
（1）分析：根据电路分析，可以得出微分方程
RI(t) VL(t) VC (t) Vi (t)
I(t) C dVC (t) dt
VL (t)
L
dI(t) dt
LC
d
2VC (t) dt 2
dI(t) L dt RI(t) VC (t) Vi (t)
LC

Matlab 第6章习题A习题具有题解.docx

A 习题（具有题解）A 6-1试判断下述系统的可控性及可观性。

y(k) = [2 —4]x 伙)能否找到一组控制序列，使系统从原点到达[1 1 If,解释为什么。

x(k +1)=0.5 0-0.5 0.25x 伙)+u(k)4C CFT0.5-0.5"[00.25_ 42 -4 1 -2rank= 1,系统不可观。

A 6-2下述连续系统被采样，求离散传递函数，并确定T 为何值时系统不可控，试说明之。

宀、 2（S + 5）G （s ） = ---------------?+105 + 29解：A （5）= 52 4-105 + 25 + 4 = 0 ； 512 =-5± j2；所以込一$2 = /4。

依要求可知，若S\-S2=jk 〒,采样系统不可控。

故有T = k7i/2时系统不可控。

Gd) =2[z~ ~ze 5T cos 2T] z 2-2ze-5T cos2T + e-10r,如当T =冗丨2时心（f 二吕'发生零极对消。

A 6-3给定下述系统「0 1 2「兀1（切'o'x(k + l) = 0 0 3x 2(k) + 10 0 0 x 2(k)（1） (2) 该控制序列最少步数是多少。

解：= [FG G] = <rank=2,系统可控试确定一组控制序列，使系统从%（o ）= [i 1 if 达到原点。

_0 1 2_■f'0_'3_'0_解：1) x(l)=0 0 3 1 + 1 w(0) = 3 + 1 M (0)0 0 1如取u(0)=-3,则如取u(l)=-O,则x(2) = [0] o 表明u(0)=3、u ⑴=0,可使系统从x(0) = [l 1『达到原点。

2) 显然最少步数N=2。

_0 1 03) 因为W R =[F-G FG G]= 0 0 10 0 0移矩阵F 可见，X3(k)不受u(k)影响，且与其他状态无关，所以不能通过u(k)改变其状态。

中南大学matlab课后答案-第六章

实验指导二1，（1）>> A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6];B=[,,]';x=A\B （2）>> A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6];B=[,,]';x=A\B （3）>> cond(A)2，（1）建立函数文件，命令如下;Function fx=funx(x)fx=x^41+x^3+1;$调用fzero函数求根，命令如下;>> z=fzero(@funx,-1)(2) 建立函数文件，命令如下;Function fx=sin(x)fx=x-(sin(x))/x;调用fzero函数求根，命令如下;>> z=fzero(@sin,(3) 建立函数文件，命令如下;function q=myfun(p)x=p(1);、y=p(2);z=p(3);q(1)=sin(x)+y^2+log(z)-7;q(2)=3*x+2^y-z^3+1;q(3)=x+y+z-5;调用fsolve函数求根，命令如下;>> options=optimset('Display','off');x=fsolve(@myfun,[1,1,1]',options) 3,(1) 建立函数文件,命令如下;function yp=funt(t,y)>yp=-y*+sin(10*t));求微分方程，程序如下：>> t0=0;tf=5;y0=1;[t,y]=ode23(@funt,[t0,tf],y0)(2) 建立函数文件,命令如下;function yp=funr(t,y)yp=cos(t)-(y)/(1+t^2);求微分方程，程序如下：>> t0=0;tf=5;y0=1;[t,y]=ode23(@funr,[t0,tf],y0)4,建立函数文件命令如下:{function fx=mymax(x)fx=-1*(1+x^2)/(1+x^4);求最大值，程序如下:>> [x,y]=fminbnd(@mymax,0,2)5,编写目标函数M文件，命令如下:function f=fop(x)f=-1*(x(1)^(1/2)+x(2)^(1/2)+x(3)^(1/2)+x(4)^(1/2));设定约束条件，并调用fmincon函数求解此约束最优化问题，程序如下：>>x0=[200,200,200,200];%A=[1,0,0,0;,1,0,0;,,1,0;,,,1];b=[400,440,484,];Ib=[0,0,0,0];options=optimset('Display','off');[x,y]=fmincon(@fop,x0,A,b,[],[],Ib,[],[],options)思考练习1,(1)矩阵求逆：>> A=[2,3,5;3,7,4;1,-7,1];b=[10,3,5]';x=inv(A)*b矩阵除法：>> A=[2,3,5;3,7,4;1,-7,1];b=[10,3,5]';x=A\b！矩阵分解：>> A=[2,3,5;3,7,4;1,-7,1];b=[10,3,5]';[L,U]=lu(A);x=U\(L\b) (2)矩阵求逆：>>A=[6,5,-2,5;9,-1,4,-1;3,4,2,-2;3,-9,0,2];b=[-4,13,1,11]';x=inv(A)*b矩阵除法：>>A=[6,5,-2,5;9,-1,4,-1;3,4,2,-2;3,-9,0,2];b=[-4,13,1,11]';x=A\b矩阵分解：>> A=[6,5,-2,5;9,-1,4,-1;3,4,2,-2;3,-9,0,2];b=[-4,13,1,11]'; [L,U]=lu(A);x=U\(L\b)2,(1)建立函数文件，命令如下：function fx=fun1(x)fx=3*x+sin(x)-exp(x);调用fzero函数求根，命令如下;>> y=fzero(@fun1,、(2) 建立函数文件，命令如下：function fx=fun2(x)fx=1-(1/x)+5;调用fzero函数求根，命令如下;>> y=fzero(@fun2,1)(3) 建立函数文件，命令如下;function q=fun3(p)x=p(1);y=p(2);q(1)=x^2+y^2-9;'q(2)=x+y-1;调用fsolve函数求根，命令如下;>> options=optimset('Display','off');x=fsolve(@fun3,[1,1]',options) 3,(1)建立函数文件，命令如下：function ydot=fun5(t,y)ydot(1)=(2-3*y(2)-2*t*y(1))/(1+t^2);ydot(2)=y(1);ydot=ydot';求解微分方程，命令如下：'>> t0=0;tf=5;x0=[0,1];[t,y]=ode45(@fun5,[t0,tf],x0);[t,y](2) (1)建立函数文件，命令如下：function ydot=fun6(t,y)ydot(1)=cos(t)+(5*y(1)*cos(2*t))/(t+1)^2-y(2)-y(3)/(3+sin(t)); ydot(2)=y(1);ydot(3)=y(2);ydot=ydot';求解微分方程，命令如下：>> t0=0;tf=5;x0=[0,1];[t,y]=ode45(@fun5,[t0,tf],x0);[t,y]4,】建立函数文件命令如下:function fx=max(x)fx=-1*(sin(x)+cos(x^2));求最大值，程序如下:>> [x,y]=fminbnd(@mymax,0,pi)5,编写目标函数M文件，命令如下:function f=topm(x)f=-1*x*(3-2*x)^2;设定约束条件，并调用fmincon函数求解此约束最优化问题，程序如下：>>x0=[0];A=[1];b=[];Ib=[0];options=optimset('Display','off');[x,y]=fminco n(@top,x0,A,b,[],[],Ib,[],[],options)。

matlab简明教程第六章答案

m a t l a b简明教程第六章答案本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March第6章习题参考答案1. 假设x = [-3, 0, 0, 2, 5, 8]且y = [-5, -2,0, 3, 4, 10]。

通过手算得到以下运算的结果，并使用MATLAB检验计算的结果。

(1) z = y<~x(2)z = x&y(3) z = x|y(4) z = xor(x,y)参考答案： (1) z = [1, 1, 1, 0, 0, 0]；(2) z = [1, 0, 0, 1, 1, 1]；(3) z = [1, 1, 0, 1, 1, 1]；(4) z = [0, 1, 0, 0, 0, 0]2. 在MATLAB中使用一个循环确定：如果用户最初在一个银行帐户中存储$10000，并且在每年的年终再存储$10000(银行每年支付6%的利息)，那么账户上要积累$1000000要需要多长时间。

参考答案： 33年。

3.某个特定的公司生产和销售高尔夫手推车。

每周周末，公司都将那一周所生产的手推车转移到仓库(库存)之中。

卖出的所有手推车都是从库存中提取。

这个过程的一个简单模型为：I (k + 1) = P(k) + I (k) - S(k)其中：P(k) = 第k周所生产的手推车数量；I (k) = 第k周库存中的手推车数量；S(k) = 第k周所卖出的手推车数量；以下为10周计划中的每周销售额；假设每周的产量都基于前一周的销售额，所以有P(k) = S(k - 1)。

假设第一周的产量为50辆手推车：即，P(1) = 50。

编写一个MATLAB程序计算：10周之内每周库存之中的手推车数量或者计算手推车库存数量减少到0为止的时间，并同时绘制图形。

针对以下两种情况运行该程序：（1）初始库存为50辆手推车，所以I(1)= 50；（2）初始库存为30辆手推车，所以I (1) = 30。

matlab(R2010)第六章答案

第 6 章M文件和函数句柄6.1 MATLAB控制流6.1.1if-else-end条件控制【例6.1-1】（1）function y=exm060101(x)%n=length(x);for k=1:nif x(k)<-1y(k)=x(k);elseif x(k)>=1y(k)=exp(1-x(k));elsey(k)=x(k)^3;endend（2）x=[-2,-1.2,-0.4,0.8,1,6]y=exm060101(x)x =-2.0000 -1.2000 -0.4000 0.8000 1.0000 6.0000 y =-2.0000 -1.2000 -0.0640 0.5120 1.0000 0.00676.1.2switch-case控制结构【例6.1-2】clear;%for k=1:10a(k)={89+k};b(k)={79+k};c(k)={69+k};d(k)={59+k};end;c=[d,c];%A=cell(3,5); %A(1,:)={'Jack','Marry','Peter','Rose','Tom'};% <7>A(2,:)={72,83,56,94,100}; % <8>%for k=1:5switch A{2,k} %case 100 %r='满分';case a %r='优秀';case b %r='良好';case c %r='及格';otherwise %r='不及格';endA(3,k)={r};endAA ='Jack' 'Marry' 'Peter' 'Rose' 'Tom'[ 72] [ 83] [ 56] [ 94] [ 100]'及格' '良好' '不及格' '优秀' '满分'6.1.3for循环和while循环【例6.1-3】（1）K=5;A = zeros(K,K) ; %for m = 1:K %for n = 1:K %A(m,n) = 1/(m+n -1);endendformat ratAformat short gA =1 1/2 1/3 1/4 1/5 1/2 1/3 1/4 1/5 1/6 1/3 1/4 1/5 1/6 1/7 1/4 1/5 1/6 1/7 1/8 1/5 1/6 1/7 1/8 1/9 （2）%cleartic %K=1000;for m = 1:Kfor n = 1:KA1(m,n) = 1/(m+n -1);endendt1=toc %t1 =17.434%ticK=1000;A2 = zeros(K,K); %for m = 1:Kfor n = 1:KA2(m,n) = 1/(m+n -1);endendt2=toct2 =2.1895（3）%ticN=1000;n=repmat(1:N,N,1);m=n';A3=1./(n+m-1);t3=toct3 =0.13909【例6.1-4】（1）function [S,N]=exm060104(epsilon)%k=0;s=0;d=inf;S=0;while d>epsilonk=k+1;s=s+k; %d=1/s;S=S+d;endN=k;（2）[S,N]=exm060104(0.0001)S =1.9859N =141syms k n NSINF=limit(symsum(1/symsum(k,1,n),n,1,N),N,inf)SINF =2N=141;SN=vpa(symsum(1/symsum(k,1,n),n,1,N))SN =1.9859154929577464788732394366197【例6.1-5】（1）clearclcwhile 1%<6>n=input('请输入一个能被4整除的正整数！ n = ');if mod(n,4)==0%<8>break%<9>end%<10>end %<11> G=logical(eye(4,4)+rot90(eye(4,4))); %m=n/4;K=repmat(G,m,m); %N=n^2;A=reshape(1:N,n,n);A(K)=N-A(K)+1 %请输入一个能被4整除的正整数！ n = A =144 13 25 108 96 61 73 60 48 109 121 122 131 119 38 50 83 71 86 98 35 23 1343 130 118 39 51 82 70 87 99 34 22 135 141 16 28 105 93 64 76 57 45 112 124 9 140 17 29 104 92 65 77 56 44 113 125 86 127 115 42 54 79 67 90 102 31 19 1387 126 114 43 55 78 66 91 103 30 18 139 137 20 32 101 89 68 80 53 41 116 128 5 136 21 33 100 88 69 81 52 40 117 129 410 123 111 46 58 75 63 94 106 27 15 14211 122 110 47 59 74 62 95 107 26 14 143 133 24 36 97 85 72 84 49 37 120 132 1 （2）s0=round(n*(n*n+1)/2); %disp([int2str(n),' 阶魔方矩阵的标称和是 ',int2str(s0)])Ns0=round(2*(n+1)); %B=A';SC=sum(A); %SR=sum(B); %S d=sum(diag(A)); %S di=sum(diag(B)); %LS=[SC,SR,Sd,Sdi]==s0; %NS=round(sum(LS)); %if NS==Ns0disp('经验证，A是魔方矩阵。

matlab课后习题答案到6章

(6) 将含有 12 个元素的向量 x 转换成3 4 矩阵。

11习题二答： reshape(x,3,4);E|D=1 1 ，11 1.如何理解“矩阵是 MATLAB 最基 (7) 求一个字符串的 ASCII 码。

本的数据对象”？答： abs(‘123'); 或00~E|~D=1 0答：因为向量可以看成是仅有一行或一列 double( ‘ 123 ' );的矩阵，单个数据 (标量) 可以看成是仅 (8) 求一个 ASCII 码所对应的字含一个元素的矩阵，故向量和单个数据都符。

00可以作为矩阵的特例来处理。

答： char(49);find(A>=10&A<25)=[1; 5] 。

因此，矩阵是 MATLAB 最基本、4. 下列命令执行后， L1 、L2 、 L3 、6.当 A=[34, NaN, Inf, -Inf, -pi, eps, 最重要的数据对象。

L4 的值分别是多少？0］时，分析下列函数的执行结果：2.设A 和B 是两个同维同大小的矩 A=1:9;B=10-A;...all(A) ， any(A) ， isnan(A) ， isinf(A)阵，问：L1=A==B;isfinite(A) 。

(1) A*B 和 A.*B 的值是否相L2=A<=5;答： all(A) 的值为 0等？L3=A>3&A<7;any(A) 的值为 1答：不相等。

L4=find(A>3&A<7);isnan(A) 的值为[ 0, 1, 0, 0, 0, 0,(2) A./B 和 B.\A 的值是否相答： L1 的值为 [0, 0, 0, 0, 1, 0, 0, 0, 0]等？0]isinf(A) 的值为[ 0, 0, 1, 1, 0, 0,答：相等。

L2 的值为[1, 1, 1, 1, 1, 0,0](3) A/B 和 B\A 的值是否相0, 0, 0]isfinite(A) 的值为 [1, 0, 0, 0, 1,等？L3 的值为[0, 0, 0, 1, 1, 1, 1, 1]答：不相等。

matlab第二篇第六章考试题及答案

matlab第二篇第六章考试题及答案1. 问题：请解释MATLAB中矩阵的转置操作是如何进行的，并给出一个具体的例子。

答案：在MATLAB中，矩阵的转置操作是通过使用单引号（'）来实现的。

例如，如果有一个矩阵A：```A = [1 2 3; 4 5 6; 7 8 9];```那么A的转置可以通过以下方式获得：```A_transposed = A';```这将输出一个新矩阵，其行变为列，列变为行。

2. 问题：如何使用MATLAB计算矩阵的行列式？答案：在MATLAB中，可以使用`det`函数来计算矩阵的行列式。

例如，对于矩阵A：```A = [1 2; 3 4];```计算其行列式的代码为：```det_A = det(A);```这将返回矩阵A的行列式的值。

3. 问题：描述MATLAB中如何求解线性方程组。

答案：在MATLAB中，求解线性方程组可以使用`\`运算符。

假设我们有方程组Ax = b，其中A是系数矩阵，x是未知数向量，b是常数向量。

求解x的代码如下：```x = A\b;```这将返回方程组的解向量x。

4. 问题：请解释MATLAB中如何实现向量的点积。

答案：在MATLAB中，向量的点积可以通过`dot`函数或者`*`运算符来实现。

例如，对于两个向量u和v：```u = [1 2 3];v = [4 5 6];```计算它们的点积可以使用以下任一方法：```dot_product = dot(u, v);```或者```dot_product = u * v;```两种方法都会返回相同的结果，即u和v的点积。

5. 问题：如何在MATLAB中创建一个3x3的单位矩阵？答案：在MATLAB中，创建一个3x3的单位矩阵可以使用`eye`函数。

代码如下：```I = eye(3);```这将创建一个3x3的单位矩阵I，其中对角线上的元素为1，其余元素为0。

matlab习题6

1
第6章习题
第6_1题：y =f (x )表达式未知，已知该函数在区间[1,4]上6个离散点信息如下，请编写一个M A T L A B 程序(命名为e x 6_1.m )，求出拉格朗日插值多项式,绘制出拉格朗日插值多项式在区间[1,4]内的图形
第6_2题：y =f (x )表达式未知，已知该函数在区间[1,3]上6个离散点信息如下，请编写一个M A T L A B 程
的图像。

第6_3题：y =f (x )表达式未
知，已知该函数上5个离散点信息如下，利用三次样条插值法对x =1.6进
第6_4题：y =f (x )表达式未知，已知该函数在区间[1,3]上6个离散点信息如下，请编写一个M A T L A B 程序(命名为e x 6_4.m )，分别应用拉格朗日插值法、分段线性插值法、三次样条插值法、埃尔米特插
第6_5题：y =f (x )表达式未知，已知该函数上5个离散点信息如下，根据下表所列数据写出基于这5
第6_6题：y =f (x )表达式未知，已知该函数上5个离散点信息如下，根据分段线性插值法写出基于这值（即计算f (1.6)=？）。

第6_7题：y =f (x )表达式未知，已知该函数上4个离散点信息如下，根据埃尔米特插值法写出基于这。

第六章 MATLAB 数值计算

第六章 MATLAB 数值计算6-1 多项式的运算6-1-1 多项式的生成和表达1. 多项式的表达在MA TLAB 环境下多项式是用向量的形式表达的. 向量最右边的元素表示多项式的0阶，向左数依次表示多项式的第1阶、第2阶、第3阶…。

例如多项式425321x x x +++表示为：[5 0 3 2 1]。

2. 多项式的生成语法：P=ploy(MA)说明：1. 若MA 为方阵，则生成的多项式P 为方阵MA 的特征多项式。

2. 若MA 为向量，则向量和多项式满足这样一种关系： []12n MA r r r = ，生成的多项式为：()()()()n n 1n 2123n 012n 1n x r x r x r x r a x a x a x a x a -------=++++3. 直接输入的方式生成多项式。

例6-1利用方阵M=[5 6 7;8 9 1;11 12 13]生成一个多项式（为方阵M 的特征多项式）。

程序设计：>>clearM=[5 6 7;8 9 1;11 12 13];P=poly(M); %产生多项式的向量表达式 Px=poly2str(P, 'x'); %生成常见的多项式表示形式 P,Px运行结果：P =1.0000 -27.0000 90.0000 54.0000Px =x^3 - 27 x^2 + 90 x + 54例6-2利用向量A=[2 3 4 5]生成一个多项式。

程序设计：>>clearA=[2 3 4 5];P=poly(A); %产生多项式的向量表达式Px=poly2str(P, 'x'); %生成常见的多项式表示形式 P,Px运行结果：P =1 -14 71 -154 120Px =x^4 - 14 x^3 + 71 x^2 - 154 x + 1206-1-2 多项式的乘除语法：A. c=conv(a,b)B. [q,r]=decony(c,a)说明：1. a 、b 和c 分别是多项式的向量表示形式。

matlab答案第六章

第六章1. 利用MATLAB提供的randn函数生成符合正态分布的10×5随机矩阵A，进行如下操作：(1) A各列元素的均值和标准方差。

(2) A的最大元素和最小元素。

(3) 求A每行元素的和以及全部元素之和。

(4) 分别对A的每列元素按升序、每行元素按降序排列。

答：clear all; close all; clc;A=randn(10, 5);meanA=mean(A); %(1)A各列元素的均值stdA=std(A); %(1)A各列元素的标准方差maxA=max(max(A)); %(2)A的最大元素minA=min(min(A)); %(2)A的最小元素rowsumA=sum(A, 2); %(3)A每行元素的和sumA=sum(rowsumA); %(3)A全部元素之和sort1=sort(A); %(4)A的每列元素按升序排列sort2=sort(A, 2, 'descend'); %(4)A的每行元素按降序排列2. 按要求对指定函数进行插值和拟合。

(1) 按表6.1用3次样条方法插值计算0~90D范围内整数点的正弦值和0~75D范围内整数点的正切值，然后用5次多项式拟合方法计算相同的函数值，并将两种计算结果进行比较。

表6.1 特殊角的正弦和正切值表α度0 15 30 4560 75 90sinα0 0.2588 0.50000.7071 0.8660 0.9659 1.0000 tanα0 0.2679 0.57741.0000 1.7320 3.7320(2) 按表6.2用3次多项式方法插值计算1~100之间整数的平方根。

表6.2 1~100内特殊值的平方根表N 1 4 9 16 25 36 49 64 81 100N的平方根 1 2 3 4 5 6 7 8 9 10答:(1) 程序设计：clear all; close all; clc;alpha1=0:15:90;sin_alpha1=sin(alpha1*pi/180); %精确正弦值plot(alpha1, sin_alpha1, 'k:p'); hold on; %绘精确正弦曲线alpha2=0:90;sin_Y1=interp1(alpha1, sin_alpha1, alpha2, 'spline'); %3次样条正弦插值plot(alpha2, sin_Y1, 'r-*'); hold on; %绘3次样条插值正弦曲线P1=polyfit(alpha1, sin_alpha1, 5); %5次多项式拟合sin_Y2= polyval(P1, alpha2); %5次多项式求值plot(alpha2, sin_Y2, 'b-o'); %绘5次多项式插值正弦曲线legend('精确正弦值', '3次样条正弦插值', '5次多项式正弦插值'); title('正弦值比较'); alpha3=0:15:75;tan_alpha3=tan(alpha3*pi/180); %精确正切值figure, plot(alpha3, tan_alpha3, 'k:p'); hold on; %绘精确正切曲线alpha4=0:75;tan_Y1=interp1(alpha3, tan_alpha3, alpha4, 'spline'); %3次样条正切插值plot(alpha4, tan_Y1,'r-*'); hold on; %绘3次样条正切曲线P2=polyfit(alpha3, tan_alpha3, 5); %5次多项式拟合tan_Y2= polyval(P2, alpha4); %5次多项式求值plot(alpha4, tan_Y2, 'b-o'); %绘5次多项式插值正弦曲线legend('精确正切值', '3次样条正切插值', '5次多项式正切插值'); title('正切值比较');(2)程序设计：clear all; close all; clc;X=[1, 4, 9, 16, 25, 36, 49, 64, 81, 100]; Y=1:10;X1=1:100; Y1=interp1(X, Y, X1,'cubic');plot(X, Y, 'r:o'); hold on; %绘精确平方根曲线plot(X1, Y1, 'k-x'); %绘3次多项式插值平方根曲线legend('精确平方根', '3次多项式插值');3. 已知一组实验数据如表6.3所示。

matlab习题6答案

matlab习题6答案Matlab习题6答案Matlab是一种广泛应用于科学计算和工程领域的高级编程语言和环境。

它以其强大的数值计算和数据可视化功能而闻名于世。

在Matlab的学习过程中，习题是提高编程技能和理解语言特性的重要方式。

在本文中，我将为大家提供Matlab习题6的答案，帮助大家更好地理解和掌握Matlab编程。

习题1：编写一个Matlab函数，计算给定向量的均值和标准差。

函数的输入参数为一个向量，输出为该向量的均值和标准差。

解答：```matlabfunction [mean_value, std_value] = calculate_stats(vector)mean_value = mean(vector);std_value = std(vector);end```习题2：编写一个Matlab函数，计算给定矩阵的特征值和特征向量。

函数的输入参数为一个矩阵，输出为该矩阵的特征值和特征向量。

解答：```matlabfunction [eigenvalues, eigenvectors] = calculate_eigen(matrix)[eigenvectors, eigenvalues] = eig(matrix);end```习题3：编写一个Matlab函数，计算给定矩阵的逆矩阵。

函数的输入参数为一个矩阵，输出为该矩阵的逆矩阵。

解答：```matlabfunction inverse_matrix = calculate_inverse(matrix)inverse_matrix = inv(matrix);end```习题4：编写一个Matlab函数，实现矩阵的转置操作。

函数的输入参数为一个矩阵，输出为该矩阵的转置矩阵。

解答：```matlabfunction transpose_matrix = calculate_transpose(matrix)transpose_matrix = matrix';end```习题5：编写一个Matlab函数，计算给定向量的累积和。

MATLAB课后答案Prob_chapter6

axis equal, axis off
otherwise
if n==1 | n==2,disp('please input n>=3')
else
t=(0:n)/n*2*pi;
x=sin(t);y=cos(t);
% n The number of sides, while n>=3;
% draw circle, while no parameter;
% not a appropriate "n" ,while n<3 or not natural number.
% edited by zhongguo liu, 12 Dec. 2010
%习题6_2（学生）解
function aa(n)
if nargin==0
t=0:pi/100:2*pi; x=exp(i*t); str='Circle';
else
if(nargin~=0)&(n<=2)
error('输入边数少了')
end
which('smoke') %检查在当前目录下能否看到smoke.m
b_d=b;
b_d(end-4:end)=[]; %在b字符串中去除最后的四个字符，即\work。
str=[b_d,'\toolbox\matlab\elmat\private'];
cd(str) %把smoke.m 所在目录设置为当前目录。
%习题6_3_inline内联函数法
y1=inline('-exp(-x)*abs(sin(cos(x)))'); [x,fval]=fminbnd(y1,-1,1)

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第六章实验指导1、(1)>> A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6]; p=[0.95,0.67,0.52]';x=A\px =1.20000.60000.6000(2)、>> A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6]; p=[0.95,0.67,0.52]';>> A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6]; p=[0.95,0.67,0.53]';>> x=A\px =3.0000-6.60006.6000（3）、>> A=[1/2,1/3,1/4;1/3,1/4,1/5;1/4,1/5,1/6]; p=[0.95,0.67,0.53]';x=A\pcond(A)x =3.0000-6.60006.6000ans =1.3533e+0032、（1）M文件：function fx=funx(x)fx=x^41+x^3+1;运行;>> z=fzero(@funx,-1)z =-0.9525(2)M文件：function fx=funx2(x)fx=x-sin(x)/x;运行：>> x2=fzero(@funx2,0.5)x2 =0.8767（3）M文件：function q=fun3(p)x=p(1);y=p(2);z=p(3);q(1)=sin(x)+y^2+log(z)-7;q(2)=3*x+2^y-z^3+1;q(3)=x+y+z-5;运行：>> options=optimset('Display','off'); x=fsolve(@fun3,[1,1,1]',options)q=fun3(x)x =0.59912.39592.00501.0e-010 *0.2213 0.3804 0.00093、(1)M文件：function yp=fun4(t,y)yp=-(1.2+sin(10*t))*y;运行：>> t0=0;tf=5;y0=1;[t,y]=ode23(@fun4,[t0,tf],y0);t'y'ans =Columns 1 through 90 0.0667 0.1375 0.2003 0.2695 0.3528 0.4362 0.5033 0.5663Columns 10 through 180.6369 0.6913 0.7457 0.8081 0.8738 0.9591 1.0277 1.09631.1600Columns 19 through 271.2246 1.3082 1.3714 1.4347 1.5001 1.5842 1.6530 1.7219 1.7858Columns 28 through 361.8501 1.9319 1.99532.0587 2.1236 2.2053 2.2745 2.34382.4080Columns 37 through 452.4719 2.5501 2.6140 2.6779 2.7419 2.8193 2.9046 2.96853.0323Columns 46 through 543.0959 3.1721 3.2364 3.3007 3.3642 3.4395 3.5328 3.5965 3.6602Columns 55 through 633.7238 3.7998 3.8642 3.9286 3.99204.0671 4.1408 4.21444.2800Columns 64 through 724.3432 4.4159 4.4812 4.5465 4.6094 4.6812 4.7567 4.8322 4.8990Columns 73 through 744.96205.0000ans =Columns 1 through 91.0000 0.9035 0.7822 0.6823 0.5984 0.5402 0.5182 0.5106 0.4976Columns 10 through 180.4656 0.4280 0.3844 0.3355 0.2936 0.2595 0.2469 0.2421 0.2382Columns 19 through 270.2290 0.2054 0.1819 0.1585 0.1387 0.1225 0.1164 0.1140 0.1122Columns 28 through 360.1080 0.0974 0.0864 0.0753 0.0658 0.0581 0.0549 0.0537 0.0529Columns 37 through 450.0511 0.0466 0.0415 0.0361 0.0316 0.0278 0.0258 0.0253 0.0249Columns 46 through 540.0241 0.0221 0.0197 0.0172 0.0150 0.0132 0.0122 0.0119 0.0117Columns 55 through 630.0114 0.0104 0.0093 0.0081 0.0071 0.0062 0.0058 0.0056 0.0055Columns 64 through 720.0054 0.0050 0.0045 0.0039 0.0034 0.0030 0.0027 0.0026 0.0026Columns 73 through 740.0025 0.0025（2）M文件：function yp=fun5(t,y)yp=cos(t)-y/(1+t^2)运行：>> t0=0;tf=5;y0=1;[t,y]=ode23(@fun5,[t0,tf],y0);t'y'yp =yp =0.0277yp =0.0447 yp =0.0659 yp =0.0718 yp =0.0511 yp =0.0177 yp =0.0759 yp =0.0722 yp =0.0647 yp =0.0312 yp =0.0093 yp =-0.0206 yp =-0.0943 yp =-0.1322 yp =-0.1785 yp =-0.2916 yp =-0.3451 yp =-0.4066 yp =-0.5736 yp =-0.6446 yp =-0.7206 yp =-0.8439 yp =-0.8893 yp =-0.9304 yp =-0.8021 yp =-0.8365 yp =-0.8698yp =-0.9247 yp =-0.9452 yp =-0.9626 yp =-0.9811 yp =-0.9855 yp =-0.9872 yp =-0.9763 yp =-0.9810 yp =-0.9845yp =-0.9872 yp =-0.9864 yp =-0.9842 yp =-0.9750 yp =-0.9680 yp =-0.9595 yp =-0.9312 yp =-0.9137 yp =-0.8936yp =-0.8373 yp =-0.8050 yp =-0.7692 yp =-0.6766 yp =-0.6260 yp =-0.5715 yp =-0.4352 yp =-0.3639 yp =-0.2886yp =-0.0993yp =-0.0045yp =0.0927yp =0.2101yp =0.2672yp =0.3242ans =Columns 1 through 90 0.5000 0.8016 1.1033 1.4077 1.7537 2.2301 2.5215 2.8129Columns 10 through 182.97273.1326 3.3001 3.5091 3.75494.0375 4.3637 4.75845.0000ans =Columns 1 through 91.0000 1.0146 1.0363 1.0450 1.0162 0.9157 0.6451 0.4122 0.1437Columns 10 through 18-0.0122 -0.1699 -0.3330 -0.5273 -0.7327 -0.9233 -1.0649 -1.1040 -1.05344、M文件function fx=mymin(x)fx=-(1+x^2)/(1+x^4);运行：>> x=fminbnd(@mymin,0,2);-mymin(x)ans =1.20715、M文件：function f=fun6(x)f=-(sqrt(x(1))+(400-x(1))*1.1+(sqrt(x(2))+(400-x(1))*1.1-x(2))*1.1+sqrt(3)+(((400-x (1))*1.1-x(2))*1.1-x(3))*1.1+sqrt(x(x4)));运行：options=optimset('Display','off');[x,fval]=fmincon(@fun6,[0,0,0],[],[],a,b,lb,ub)-fval思考练习1、（1）>> A=[2,3,5;3,7,4;1,-7,1];B=[10,3,5]';C1=inv(A)*BC2=A\B[L,U]=lu(A);x=U\(L\B)C1 =-1.8060-0.53733.0448C2 =-1.8060-0.53733.0448x =-1.8060-0.53733.0448（2）、>> A=[6,5,-2,5;9,-1,4,-1;3,4,2,-2;3,-9,0,2]; B=[-4,13,1,11]';C1=inv(A)*BC2=A\B[L,U]=lu(A);x=U\(L\B)C1 =0.6667-1.00001.50000.0000C2 =0.6667-1.00001.5000-0.0000x =0.6667-1.00001.5000-0.00002、（1）M文件;function fx=funx1(x)fx=3*x+sin(x)-exp(x);运行：>> x1=fzero(@funx1,1.5)x1 =1.8900(2)M文件：function fx=funx2(x)fx=x-1/x+5;运行;>> x1=fzero(@funx2,1)x1 =0.1926(3)M文件：function q=fun3(p)x=p(1);y=p(2);q(1)=x^2+y^2-9;q(2)=x+y-1;运行：>> options=optimset('Display','off');x=fsolve(@fun3,[3,0]',options)q=fun3(x)x =2.5616-1.5616q =1.0e-013 *0.5684 0.00443、(1)M文件：function ydot=vdpol(t,y);ydot(1)=(2-3*y(2)-2*t*y(1))./(1+t^2); ydot(2)=y(1);ydot=ydot';运行：>> t0=0;tf=5;y0=[0,1];[t,y]=ode45(@vdpol,[t0,tf],y0);[t,y]ans =0 0 1.00000.0001 -0.0001 1.00000.0001 -0.0001 1.00000.0002 -0.0002 1.00000.0002 -0.0002 1.00000.0005 -0.0005 1.00000.0007 -0.0007 1.00000.0010 -0.0010 1.00000.0012 -0.0012 1.00000.0025 -0.0025 1.00000.0037 -0.0037 1.00000.0050 -0.0050 1.00000.0062 -0.0062 1.00000.0125 -0.0125 0.9999 0.0188 -0.0188 0.9998 0.0251 -0.0250 0.9997 0.0313 -0.0313 0.9995 0.0627 -0.0624 0.9980 0.0941 -0.0929 0.9956 0.1255 -0.1226 0.9922 0.1569 -0.1513 0.9879 0.2717 -0.2439 0.9650 0.3864 -0.3127 0.9328 0.5011 -0.3554 0.8943 0.6158 -0.3738 0.8523 0.7408 -0.3721 0.8054 0.8658 -0.3542 0.75990.9908 -0.3263 0.71731.1158 -0.2932 0.6785 1.2408 -0.2584 0.6441 1.3658 -0.2240 0.6139 1.4908 -0.1915 0.5880 1.6158 -0.1616 0.5659 1.7408 -0.1345 0.5475 1.8658 -0.1103 0.53221.9908 -0.0889 0.51982.1158 -0.0702 0.5099 2.2408 -0.0538 0.5021 2.3658 -0.0396 0.4963 2.4908 -0.0273 0.4921 2.6158 -0.0167 0.4894 2.7408 -0.0075 0.4879 2.8658 0.0004 0.48752.9908 0.0071 0.48803.1158 0.0128 0.4892 3.2408 0.0177 0.4911 3.3658 0.0218 0.4936 3.4908 0.0253 0.4966 3.6158 0.0282 0.4999 3.7408 0.0306 0.5036 3.8658 0.0325 0.50753.9908 0.0341 0.51174.1158 0.0354 0.5160 4.2408 0.0364 0.5205 4.3658 0.0371 0.5251 4.4908 0.0376 0.5298 4.6158 0.0380 0.53454.7119 0.0381 0.53824.8079 0.0382 0.54184.9040 0.0382 0.54555.0000 0.0381 0.5492（2）M文件;function ydot=vdpoll(t,y);ydot(1)=cos(t)-y(3)./(3+sin(t))+5*y(1).*cos(2*t)/((t+1).^2)-y(2); ydot(2)=y(1);ydot(3)=y(2);ydot=ydot';运行：t0=0;tf=5;y0=[1;0;2];[t,y]=ode45(@vdpoll,[t0,tf],y0);[t,y]ans =0 1.0000 0 2.00000.0001 1.0003 0.0001 2.00000.0001 1.0005 0.0001 2.00000.0002 1.0008 0.0002 2.00000.0002 1.0011 0.0002 2.00000.0005 1.0024 0.0005 2.00000.0007 1.0038 0.0007 2.00000.0010 1.0051 0.0010 2.00000.0012 1.0064 0.0012 2.00000.0025 1.0132 0.0025 2.00000.0037 1.0199 0.0038 2.00000.0050 1.0267 0.0050 2.00000.0062 1.0335 0.0063 2.00000.0125 1.0680 0.0129 2.00010.0188 1.1030 0.0197 2.00020.0251 1.1386 0.0268 2.00030.0313 1.1749 0.0340 2.00050.0627 1.3647 0.0739 2.00220.0941 1.5677 0.1199 2.00520.1255 1.7822 0.1724 2.00980.1569 2.0058 0.2319 2.01610.2195 2.4683 0.3717 2.03480.2820 2.9334 0.5405 2.0632 0.3445 3.3764 0.7379 2.1030 0.4070 3.7737 0.9617 2.1560 0.5320 4.3485 1.4740 2.3068 0.6570 4.5636 2.0346 2.5252 0.7820 4.4084 2.5980 2.81550.9070 3.9436 3.1228 3.17441.0211 3.3407 3.5396 3.5553 1.13522.64293.8818 3.9796 1.2493 1.90924.1418 4.4381 1.3634 1.1789 4.3176 4.9215 1.4884 0.4072 4.41635.4684 1.6134 -0.3277 4.42106.0218 1.7384 -1.0291 4.3359 6.5699 1.8634 -1.7076 4.16477.10201.9884 -2.37803.9094 7.60752.1134 -3.0529 3.5700 8.0759 2.2384 -3.7425 3.1454 8.4965 2.3634 -4.4523 2.6335 8.8586 2.4884 -5.1832 2.0316 9.1511 2.6134 -5.9286 1.3372 9.3626 2.7384 -6.6747 0.5493 9.4815 2.8634 -7.3993 -0.3307 9.49612.9884 -8.0730 -1.2984 9.39533.1134 -8.6589 -2.3452 9.1683 3.2384 -9.1181 -3.4578 8.8061 3.3634 -9.4112 -4.6179 8.3018 3.4884 -9.5015 -5.8024 7.6508 3.6134 -9.3604 -6.9837 6.8516 3.7384 -8.9696 -8.1318 5.9062 3.8634 -8.3235 -9.2154 4.82103.9884 -7.4281 -10.2026 3.60634.1134 -6.3005 -11.0630 2.2758 4.2384 -4.9650 -11.7689 0.8471 4.3634 -3.4512 -12.2965 -0.6591 4.4884 -1.7921 -12.6257 -2.2190 4.6134 -0.0200 -12.7401 -3.8067 4.7384 1.8334 -12.6274 -5.3945 4.8634 3.7383 -12.2793 -6.9536 4.8976 4.2637 -12.1428 -7.3705 4.9317 4.7902 -11.9882 -7.78254.96595.3174 -11.8157 -8.18885.0000 5.8445 -11.6252 -8.58904、M文件;function fx=mymin(x)fx=sin(x)+cos(x.^2);运行：>> x=fminbnd(@mymin,0,pi);mymin(x) ans =-0.02205、M文件：function fx=mymax(x);fx=-(9*x+4*x.^3-12*x.^2);运行：>> [x,y1]=fminbnd(@mymax,0,1.5);-y1ans =2.0000。