仔猪浓缩料(25%)调好,参考
加工中心常用计算公式

CNC常用计算公式一、三角函数计算1.tanθ=b/aθ=tan-1b/a2.Sinθ=b/c Cos=a/c二、切削速度的计算Vc=(π*D*S)/1000Vc:线速度(m/min) π:圆周率(3.14159) D:刀具直径(mm)S:转速(rpm)例题. 使用Φ25的铣刀Vc为(m/min)25 求S=?rpmVc=πds/100025=π*25*S/1000S=1000*25/ π*25S=320rpm三、进给量(F值)的计算F=S*Z*FzF:进给量(mm/min) S:转速(rpm) Z:刃数Fz:(实际每刃进给)例题.一标准2刃立铣刀以2000rpm)速度切削工件,求进给量(F值)为多少?(Fz=0.25mm)F=S*Z*FzF=2000*2*0.25F=1000(mm/min)四、残料高的计算Scallop=(ae*ae)/8RScallop:残料高(mm) ae:XY pitch(mm) R刀具半径(mm)例题. Φ20R10精修2枚刃,预残料高0.002mm,求Pitch为多少?mmScallop=ae2/8R0.002=ae2/8*10ae=0.4mm五、逃料孔的计算Φ=√2R2X、Y=D/4Φ:逃料孔直径(mm) R刀具半径(mm) D:刀具直径(mm)例题. 已知一模穴须逃角加工(如图),所用铣刀为ψ10;请问逃角孔最小为多少?圆心坐标多少?Φ=√2R2Φ=√2*52Φ=7.1(mm)X、Y=D/4X、Y=10/4X、Y=2.5 mm圆心坐标为(2.5,-2.5)六、取料量的计算Q=(ae*ap*F)/1000Q:取料量(cm3/min)ae:XY pitch(mm) ap:Z pitch(mm)例题. 已知一模仁须cavity等高加工,Φ35R5的刀XY pitch是刀具的60%,每层切1.5mm,进给量为2000mm/min,求此刀具的取料量为多少?Q=(ae*ap*F)/1000Q=35*0.6*1.5*2000/1000Q=63 cm3/min七、每刃进给量的计算Fz=hm * √(D/ap )Fz:实施每刃进给量hm:理论每刃进给量 ap:Z pitch(mm)D:刀片直径(mm)例题 (前提depo XY pitch是刀具的60%)depoΦ35R5的刀,切削NAK80材料hm为0.15mm,Z轴切深1.5mm,求每刃进给量为多少?Fz=hm * √(D/ap )Fz=0.2*√10/1.5Fz=0.5mm冲模刀口加工方法刀口加工深度=板厚-刀口高+钻尖(0.3D)D表示刀径钻头钻孔时间公式T(min)=L(min)/N(rpm)*f(mm/rev)=πDL/1000vfL:钻孔全长N:回转数f:进刀量系数D:钻头直径v:切削速度如图孔深l钻头孔全长L则L=l+D/3T=L/Nf=πDL/1000vf系数表f直径mm进刀mm/rev1.6~3.2 0.025~0.0753.2~6.4 0.05~0.156.4~12.8 0.10~0.2512.8~25 0.175~0.37525以上0.376~0.6251英寸=25.4mm=8分25.4/牙数=牙距管牙计算公式例如25.4/18=1.414牙距为5/16丝攻马力(枪钻)W=Md*N/97.410W:所要动力(KW)Md:扭矩(kg-cm)N:回转数(r.p.m)扭矩计算公式如下:Md=1/20*f*ps*f为进给量mm/rev系数r为钻头半径赛(mm)α:切削抵抗比值ps.在小进给时,一般钢为500kg/m㎡;一般铸铁为300kg/m㎡;。
25届(新教材QG版)数学精练案基础课09幂函数与二次函数

基础课09幕函数与二次函数课时评价提能基础巩固练1. [2024• 吉林模拟]"a>2"是"函数f(x)= (a-1)x 2-2x在(1,+oo)上是2. 增函数”的(A ).A. 充分不必要条件C. 充要条件B. 必要不充分条件D. 既不充分也不必要条件[解析]若a>2, 则f(x)的单调递增区间是[a �l '+oo), 且(1,+oo)豆[a �l '+oo)'所以函数f(x)在(1,+oo)上是增函数,故充分性成立;当a=2时,f(x)= x 2-2x在(1,+oo)上是增函数,故必要性不成立.故"a>2"是“函数f(x)= (a-1)x 2 -2x在(1,+oo )上是增函数”的充分不必要条件故选A.2. [2024• 济南模拟]若二次函数f(x)= ax 2+bx+ c (a < 0), 满足f(1)= f(3), 则下列不等式成立的是(B )A. f (l) < f(4) < f(2) C. f(4) < f (2) < f (1) B. f (4) < f(l) < f(2) D.f (2) < f(4) < f(l) [解析]因为八1)= f(3), 所以二次函数f(x) = ax 2+ b x + c 图象的对称轴为直线x = 2.因为a<0, 所以f(4)< f(3) < f(2), 又f(l)= [(3), 所以f(4)< f(l) < f(2)故选B.3. [2024• 成都模拟]若幕函数f(x)= (矿-3m-3)·产在(0,+ oo )上单调递减,则下列说法正确的是(C )A.m=4B.f(x)是减函数C. f (x)是奇函数D. f(x)是偶函数[解析]因为函数f (x)= (m 2 -3m-3)产为幕函数,所以m 2-3m-3= 1, 解得m =4或m=-1.当m=4时,f (x)= x 4在(0,+ oo)上单调递增,不满足题意,排除A.当m=-1时,f (x)= X -1在(0,+ oo)上单调递减,满足题意函数(x)= X -l在(-oo,0)和(0,+ oo)上单调递减,但不是减函数,排除B .因为函数f (x)的定义域关于原点对称,且八-x)=�= -(x), 所以f (x)是奇函数,不是偶函数,故C正确,D错误.故选C.24. [2024· 新疆模拟]已知函数(x)= (1 X ,X 2:: 0, �,X< 0, g (x) = (-x), 则函数g (x)的图象大致是(B )�yA .y c \XXB .D . 01(X ByXD[解析]因为g (x)=(-x), 所以g (x)的图象与f (x)的图象关于y 轴对称.由f (x)的解析式作出f (x)的大致图象,如图所示,从而可得g (x)的图象大致为B选项.故选B.y\ X5. [2024• i、维坊联考]已知二次函数f(x)= ax2 + b x+ c(a >0)的图象与x轴交点的横坐标分别为-5和3,则该二次函数的单调递减区间为(A).A. (-oo,-1]B.[-1,+oo)C.(-oo,2]D. [2, + oo) [解析]因为二次函数f(x)= ax2 + b x+ c(a >0)的图象与x轴交点的横坐标为-5和3,-s厂=-1, 又a>O, 所以该二次函数的单调递所以其对称轴方程为x=减区间为(-oo,-1].故选A.6. [2024• 东莞模拟]已知函数y= log/x-1) +4(a >0且a-=f=.1)的图象恒过定点P, 点P在幕函数Y= f(x)的图象上,则lg f (2) +l g f (5) =(B) .A.-2B.2C.-1D. 1[解析]·:已知a>O且a*1, 对于函数y= Iog/x-1) +4, 令x-1= 1, 解得x = 2, 此时y= 4, :.定点P(2,4).令点P在幕函数y= f(x) = x a的图象上,:. 2a = 4, :. a= 2, :. f(x) = x2, 则八2)= 4,f(S)= 25,故lg八2)+ l g f(S) = lg [f(2)f(S)] = lg 100 = 2故选B.7. [2024• 苏州模拟]设函数f(x)=卢:二五氧a<0)的定义域为D,若对千任意m,n ED, 所有的点P(m,f(n))构成一个正方形区域,则实数a的值为(D).A.-1B.-2C.-3D.-4[解析]由已知可得ax2-2ax�0.因为a<0, 所以x2-2x :s;0, 解得0:s;x:s; 2, 所以D= [0,2].因为y= x2-2x在[0,1]上单调递减,在[1,2]上单调递增,所以y= x2-2x在x=l处取得最小值,最小值为-1,所以y=a忙-2x)在x=l处取得最大值,最大值为-a,所以函数f(x)=J;l三立立x=l处取得最大值,最大值为Fa.因为八0)= f(2) =o, 且所有的点P(m,f(n))构成一个正方形区域,所以{五三,所以a=-4故选D8. [2024• 绵阳模拟]若函数f(x)= ( 2x-m,x < 1,2 有最小值,则实数m的2x -4mx +3m,x�1取值范围是(B)A. (-oo,0)B.[2,+oo)C. (-oo,0) u [1, +oo)D. (0,1) u [2, +oo)[解析]因为f(x)= 2x -m,x < 1,2x2 -4mx +3m,x�1有最小值,所以当x<l时,f(x)= 2x-m, 显然f(x)在(-oo,1)上单调递增,且f(x)> -m, 即f(x)在(-oo,1)上没有最小值当x�l时,f(x)= 2x2 -4mx +3m, 易知f(x)在[1,+oo)上必有最小值因为f(x)在[1,+oo)上的图象是开口向上,对称轴为直线x=m的抛物线的一部分,所以当m�1时,f(x)mi n= f(l) = 2-m, 易知f(O)= 2°-m = 1-m < 2-m = f(l),故八1)不是八x)在R上的最小值,则f(x)在R上没有最小值,不满足题意;当m>l 时,f(x)min= f(m) = -2m 2+ 3m,2要使得f(m)是八x)在R上的最小值,则f(m)::;-m, 即-2m + 3m::; -m,解得m::;0或m2::2,所以m2:: 2.综上所述,m2:: 2故选B.综合提升练9. [2024• 江苏联考](多选题)若函数f(x)= X 3,且X l < X z , 则(AC ).A. (x 1一心[f 伈)-f 伈)]>0C .f伈)-x 2<f 伈)-XlB. X 1-f 伈)>x z -f 伈)f(x 1) + f 伈)X l + XzD.2>t (2)[解析]由幕函数的性质知,f(x)= x 3在R 上单调递增.因为x 1< X z , 所以f 伈)<f 伈),即X l -X 2< 0, f 伈)-f 伈)< o,所以伈-寸[f 伈)-f 伈)] > 0,故A正确;令x 1= 0,x 2 = 1, 则0-f(O)= 1-f(l) = 0, 故B 错误;11令g(x)= f(x) + x = x 3+ x ,则由函数单调性的性质知,f(x)= X 3在R 上单调递增,y =x在R上单调递增,所以g (x)= f(x) + x = x 3+ x 在R 上单调递增,因为X l < X z ,所以g 伈)<g 伈),即f 伈)+x l<f 伈)+ X z ,则f伈)-X z <f 伈)-X l ,故C 正确;X 1 + Xz令x 1= -1,x 2 = 1,则2= 0,所以f(l) + f(-1)= f(O) = 0, 故D 错误故选AC.10. [2024• 衡阳模拟](多选题)设二次函数f(x ) = a x 2 -4x + c的值域为[O, + oo), 19下列各值(或式子)中一定大千+ 的是(c +l a +9 BD ) .9飞22A 1-532B C. -n 2+ 2n + 8,n E [-2,2]2m +2D .屈, m E R[解析]因为二次函数f(x ) = a x 2-4x+ c的值域为[O ,+ oo), 所以{a> 0, 所以{a >O 4 Ii= 16-4ac= 0 a c = 4, '解得c =—,a 1 9 1 9 a 9 a 2+ 18a + 36所以+ =4 + = + = c +l a +9 a +9 a+4 a +9 2 -+ 1 a + 13a + 36aa 2+ 13a + 36 + Sa SaS2=1+2=1+a + 13a + 36a + 13a + 3636'a+—+ 13a 因为a>O, a+了气2二=12, 36当且仅当a =—即a =6时取等号,a ' 所以1+5636a+了+13::; s ·296对于A ,云<子316对于B —>-, 255'故A 错误;故B正确;对于C,令g (n )= -n 2+ 2n + 8,n E [-2,2], 则0�g (n )�9,故C错误;m2+ 2m2+ 1 + 1212 1 对于D,三=三=五勹+产�2J ✓五二1=2,当且仅当m =O时,等号成立,,6-5> 2故D正确故选BO.(2-3a)x,x 2:: 1I I . [2024• 开封模拟]已知函数f(x)= ( _ix -a . (2)+日-8,x < 11 X 1 , 满足对任意的实数X l 'X 2,且x l* Xz , f伈)-f伈)都有>0成立,X -X123则实数a的取值范围为[l].4立[解析]因为对任意的实数X X , 且x f伈)-f伈)1' 2 1 -=F X z'都有X 1-X 2> Q 成立,所以对任意f伈)-f伈)的实数X l 'X 2,且x l* Xz'x -x < O 恒成立,1 2即函数f(x)= (2-3a)x,x�1, 1 X1 X 1-a .(z ) +日-8,x < 1是R上的减函数令t = (扩,则t>½, 要使f(x )=-a ·(扩+贯-;在(-oo ,1)上单调递减,,,函曰1L , 递文<-a 来女<- 调函单减3-4上为得)171牛俞>-1-纾00义++ , a,。
《数据结构c语言》车厢调度问题解析(经典递归)

车厢调度问题解析(经典递归)博客分类:zhanghonglun算法算法题目假设停在铁路调度站入口处的车厢系列的编号依次为1,2,3,…n。
设计一个程序,求出所有可能由此输出的长度为n 的车厢系列。
解析:一个数的进栈以后,有两种处理方式:要么立刻出栈,或者下一个数的进栈(如果还有下一个元素)其出栈以后,也有两种处理方式:要么继续出栈(栈不为空),或者下一个数的入栈。
该问题有天然的递归性质算法设计:两重递归,下一个元素处理完后返回,再处理出栈的递归,有点像嵌套循环,但比它复杂...进栈的递归跳出条件为最后一个元素进栈出栈的递归跳出条件为栈空附上经典实现代码C代码1.#include<stdafx.h>2.#include<stdio.h>3.#define MaxLen 1004.struct snode{5. int data[MaxLen];6. int top;7.}s;//定义一个栈指针8.int n;//定义输入序列总个数9.void Initstack()10.{11. s.top=-1;12.}13.void push(int q)//元素n进栈14.{15. s.top++;16. s.data[s.top]=q;17.}18.int pop()//出栈19.{20. int temp;21. temp=s.data[s.top];22. s.top--;23. return temp;24.}25.int Emptys()//判断栈空26.{27. if(s.top==-1)28. return 1;29. else30. return 0;31.}32./*33.每次调用求值阶段包含两重递归,只有全部返回,才表示本pos 处理完,可以对上一个元素求值,process 就是找出当前元素进栈后所有可能的操作,即在当前元素进栈后各种情况下,34.包括不出栈,立即出栈,出栈后继续出栈情况(出栈递归)下,继续处理下一个元素(入栈递归)35.36.*/37.void process(int pos,int path[],int curp)//当前处理位置pos的元素38.{39. int m,i;40. if(pos<n)//编号进栈递归41. {42. push(pos+1);//当前元素进栈后下一个元素继续进栈43. process(pos+1,path,curp); //处理下一个元素,返回表明下一个元素进栈的情况处理完了44. pop(); //下一个元素处理完后,pop 掉,准备处理直接出栈45. }46.47. if(!Emptys())//递归处理出栈48. {49. m=pop();50. path[curp]=m;51. curp++;52. process(pos,path,curp);//出栈后处理下一个素继续进栈53. push(m);54. }55. if(pos==n&&Emptys())//输出一种可能的方案56. {57. for(i=0;i<curp;i++)58. printf("%2d",path[i]);59. printf("\n");60. }61.}62.void main()63.{64. int path[MaxLen];65. printf("输入要调度车厢总数:");66. scanf("%d",&n);67. Initstack();68. push(1);69. printf("所有输出序列:\n");70. process(1,path,0); //从1 开始,递归处理所有元素71.}。
计算机网络第四版(课后练习+答案)

第 1 章概述1.假设你已经将你的狗Berníe 训练成可以携带一箱3 盒8mm 的磁带,而不是一小瓶内哇地. (当你的磁盘满了的时候,你可能会认为这是一次紧急事件。
)每盒磁带的窑最为7GB 字节;无论你在哪里,狗跑向你的速度是18km/h 。
请问,在什么距离范围内Berníe的数据传输速率会超过一条数据速率为150Mbps的传输线?答:狗能携带21千兆字节或者168千兆位的数据。
18 公里/小时的速度等于0.005 公里/秒,走过x公里的时间为x / 0.005 = 200x秒,产生的数据传输速度为168/200x Gbps或者840 /x Mbps。
因此,与通信线路相比较,若x<5.6 公里,狗有更高的速度。
6. 一个客户·服务器系统使用了卫星网络,卫星的高度为40 000km. 在对一个请求进行响应的时候,最佳情形下的延迟是什么?答:由于请求和应答都必须通过卫星,因此传输总路径长度为160,000千米。
在空气和真空中的光速为300,000 公里/秒,因此最佳的传播延迟为160,000/300,000秒,约533 msec。
9.在一个集中式的二叉树上,有2n -1 个路出器相互连接起来:每个树节点上都布一个路由器。
路由器i 为了与路由器j 进行通信,它要给树的根发送一条消息。
然后树根将消息送下来给j 。
假设所有的路由器对都是等概率出现的,请推导出当n很大时,每条消息的平均跳数的一个近似表达式。
答:这意味着,从路由器到路由器的路径长度相当于路由器到根的两倍。
若在树中,根深度为1,深度为n,从根到第n层需要n-1跳,在该层的路由器为0.50。
从根到n-1 层的路径有router的0.25和n-2跳步。
因此,路径长度l为:18.OSI 的哪一层分别处理以下问题?答:把传输的比特流划分为帧——数据链路层决定使用哪条路径通过子网——网络层.28.一幅图像的分辨率为1024X 768 像素,每个像素用3 字节来表示。
通用光面钢丝绳规格型号

一般起重光面钢丝绳技术参数,光面钢丝绳规格镀锌钢丝绳型号有两种:热镀锌钢丝绳,电镀锌钢丝绳。
含锌量有 ZAA级,ZAB级,ZBB级(多股股)不旋转钢丝绳规格型号,钢丝绳技术参数18*719x734x718x19s18x19w35x724W*735W*7多层股不旋转钢丝绳技术参数此钢丝绳型号适用于:塔机,吊车,电动葫芦,行车,门机起重机,卷扬机钢丝绳规格型号总共有三种分类:1、表面分类:镀锌钢丝绳,光面钢丝绳,涂塑钢丝绳;2、用途分类:电梯钢丝绳,钻机打井打桩钢丝绳,旋挖钻机钢丝绳,起重机钢丝绳,吊索具钢丝绳,吊装用钢丝绳,吊车钢丝绳,塔机钢丝绳,电动葫芦行车钢丝绳,龙门架卷扬机钢丝绳,吊篮钢丝绳,建筑机械用钢丝绳,索道钢丝绳;3、结构分类:点接触钢丝绳,线接触钢丝绳,面接触钢丝绳,多层股不旋转钢丝绳,三角股钢绳,多层股面接触钢绳,密封钢绳南通力森特种钢丝绳专业生产电梯钢丝绳,提供电梯钢丝绳规格,电梯钢丝绳价格,电梯钢丝绳标准。
电梯钢绳顾名思义,是用在电梯上的钢丝绳,用的最多的小型载人电梯,在商品住宅的小区,电梯钢丝绳规格型号一般用8*19S-FC-8mm,8*19S-10mm。
主要用10mm,8mm主要是辅助绳。
而商场则用稍微大一点的电梯钢绳规格是12mm,13mm,商场载物电梯钢丝绳规格是12mm,13mm,16mm直径。
·钢丝绳电梯无重大事故·电梯钢丝绳断股·电梯绳产国家电梯钢绳行业标准有两种。
一:双钢号双强度,45号钢,65号钢,1370N/mm2,1770Mpa,二:单钢号,单强度,65号钢,1770N/mm2。
电梯钢绳绳芯按国家标准都是剑麻和PPC合成纤维,高速电梯钢丝绳规格型号为8*19S+8*7+pp,8*19S+8*7+1*19通常情况下,新出厂钢丝绳大部分在生产时已经进行了润滑处理,但在使用过程,润滑油脂会流失减少。
鉴于润滑不仅能够对钢丝绳在运输和存储期间起到防腐保护作用,而且能够减少钢丝绳使用过程中各钢丝之间、绳股之间和钢丝绳与曳引轮槽之间的磨损,并且对延长钢丝绳使用寿命也十分有益。
高考数学一轮复习第六章数列课时规范练30等比数列

课时规范练30等比数列基础巩固组1.(2020河南开封定位考试)等比数列{a n}的前n项和为S n,若a3+4S2=0,则公比q=()A.-1B.1C.-2D.22.(2020东北师大附中、重庆一中、吉大附中、长春十一中等高三联合考试)等比数列{a n}各项均为正数,若a1=1,a n+2+2a n+1=8a n,则{a n}的前6项和为()A.1365B.63C.6332D.136510243.(多选)设等比数列{a n}的前n项和为S n,且满足a6=8a3,则()A.数列{a n}的公比为2B.数列{a n}的公比为8C.63=8D.63=94.(2020全国2,理6)数列{a n}中,a1=2,a m+n=a m a n.若a k+1+a k+2+…+a k+10=215-25,则k=()A.2B.3C.4D.55.(2020福建龙岩高三教学质量检查)由实数构成的等比数列{a n}的前n项和为S n,a1=2,且a2-4,a3,a4成等差数列,则S6=()A.62B.124C.126D.1546.(多选)设等比数列{a n}的公比为q,则下列结论正确的是()A.数列{a n a n+1}是公比为q2的等比数列B.数列{a n+a n+1}是公比为q的等比数列C.数列{a n-a n+1}是公比为q的等比数列D.数列1是公比为1的等比数列7.(2020浙大附中模拟)已知数列{a n}的前n项和为S n,且+1=pS n+q(n∈N*,p≠-1),则“a1=q”是“{a n}为等比数列”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件8.设等比数列{a n}的前n项和为S n,若63=3,则96=.9.已知{a n}是递减的等比数列,且a2=2,a1+a3=5,则{a n}的通项公式为;a1a2+a2a3+…+a n+1(n∈N*)=.10.(2018全国3,理17)等比数列{a n}中,a1=1,a5=4a3.(1)求{a n}的通项公式;(2)记S n为{a n}的前n项和,若S m=63,求m.公众号:一枚试卷君11.在①数列{a n}的前n项和S n=12n2+52n;②函数f(x)=sinπx-23cos2π2x+3的正零点从小到大构成数列{x n},a n=x n+83;③2-a n--12−-1=0(n≥2,n∈N*),a n>0,且a1=b2这三个条件中任选一个,补充在下面的问题中,若问题中的M存在,求出M的最小值;若M不存在,说明理由.问题:数列{b n}是首项为1的等比数列,b n>0,b2+b3=12,且,设数列1log3r1的前n项和为T n,是否存在M∈N*,使得对任意的n∈N*,T n<M?综合提升组12.(多选)(2020山东威海模考)设等比数列{a n}的公比为q,其前n项和为S n.前n项积为T n,并且满足条件a1>1,a7·a8>1,7-18-1<0.则下列结论正确的是()A.0<q<1B.a7·a9>1C.S n的最大值为S9D.T n的最大值为T713.(2020辽宁大连第二十四中学模拟)《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何?”题意是:“有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半.”如果墙足够厚,S n为前n天两只老鼠打洞长度之和,则S n=尺.14.设数列{a n}的前n项和为S n,已知a1=1,a2=2,且a n+2=2S n-S n+1+3,记b n=log2a2n-1+log2a2n,则b n=.创新应用组15.(多选)(2020山东青岛高三模拟)在悠久灿烂的中国古代文化中,数学文化是其中的一朵绚丽的奇葩.《张丘建算经》是我国古代有标志性的内容丰富的众多数学名著之一,大约创作于公元五世纪.书中有如下问题:“今有女善织,日益功疾,初日织五尺,今一月织九匹三丈,问日益几何?”.其大意为:“有一女子擅长织布,织布的速度一天比一天快,从第二天起,每天比前一天多织相同数量的布,第一天织5尺,一个月共织了九匹三丈,问从第二天起,每天比前一天多织多少尺布?”.已知1匹=4丈,1丈=10尺,若这一个月有30天,记该女子这一个月中的第n天所织布的尺数为a n,b n=2,对于数列{a n},{b n},下列选项中正确的为()A.b10=8b5B.{b n}是等比数列C.a1b30=105D.3+5+72+4+6=20919316.(2020浙江十校联考)已知数列{a n}满足a1=35,a n+1=32+1,n∈N*.(1)求证:数列1-1为等比数列.(2)是否存在互不相等的正整数m,s,t,使m,s,t成等差数列,且a m-1,a s-1,a t-1成等比数列?如果存在,求出所有符合条件的m,s,t;如果不存在,请说明理由.参考答案课时规范练30等比数列1.C因为a3+4S2=0,所以a1q2+4a1+4a1q=0.因为a1≠0,所以q2+4q+4=0,所以q=-2.故选C.2.B∵等比数列{a n}各项均为正数,且a n+2+2a n+1=8a n,∴a n q2+2a n q=8a n,即q2+2q=8,可得q=2或q=-4(舍去),∴S6=1(1-6)1-=63.故选B.3.AD因为等比数列{a n}的前n项和为S n,且满足a6=8a3,所以63=q3=8,解得q=2,所以63=1-61-3=1+q3=9.故选AD.4.B设该女子第一天织布x尺,则(1-25)1-2=5,得x=531,所以前n天所织布的总尺数为531(2n-1).由531(2n-1)≥30,得2n≥187,则n的最小值为8.故选B.5.C由题意知2a3=a2-4+a4,设{a n}的公比为q,则212=1-4+13,1=2,解得q=2,则S6=2(1-26)1-2=126.故选C.6.AD对于A,由r1-1=q2(n≥2)知,数列{a n a n+1}是公比为q2的等比数列,故A正确;对于B,当q=-1时,数列{a n+a n+1}的项中有0,不是等比数列,故B错误;对于C,当q=1时,数列{a n-a n+1}的项中有0,不是等比数列,故C错误;对于D,1r11=r1=1,所以数列1是公比为1的等比数列,故D正确.故选AD.7.C因为a n+1=pS n +q ,所以当n ≥2时,a n =pS n-1+q ,两式相减得a n+1-a n =pa n ,即当n ≥2时,r1=1+p.当n=1时,a 2=pa 1+q.所以当a 1=q 时,21=1+p ,满足上式,故数列{a n }为等比数列,所以满足充分性;当{a n }为等比数列时,有a 2=pa 1+q=(1+p )a 1,解得a 1=q ,所以满足必要性.故选C .8.73(方法1)由等比数列的性质可知S 3,S 6-S 3,S 9-S 6仍成等比数列,由已知得S 6=3S 3,∴6-33=9-66-3,即S 9-S 6=4S 3,S 9=7S 3,∴96=73.(方法2)因为{a n }为等比数列,由63=3,设S 6=3k ,S 3=k (k ≠0),所以S 3,S 6-S 3,S 9-S 6为等比数列,即k ,2k ,S 9-S 6成等比数列,所以S 9-S 6=4k ,解得S 9=7k ,所以96=73=73.9.a n =4×12n-1323×1-14n由a 2=2,a 1+a 3=5,{a n }是递减的等比数列,得a 1=4,a 3=1,所以q=12,a n =4×12n-1,则a 1a 2+a 2a 3+…+a n +1是首项为8,公比为14的等比数列的前n 项和.故a 1a 2+a 2a 3+…+a n +1=8+2+12+…+8×14n-1=8×[1-(14)]1-14=323×1-14n .10.解(1)设{a n }的公比为q ,由题设得a n =q n-1.由已知得q 4=4q 2,解得q=0(舍去),q=-2或q=2.故a n =(-2)n-1或a n =2n-1.(2)若a n =(-2)n-1,则S n =1-(-2)3.由S m =63得(-2)m =-188,此方程没有正整数解.若a n =2n-1,则S n =2n -1.由S m =63得2m =64,解得m=6.综上,m=6.11.解设数列{b n }的公比为q (q>0),因为数列{b n }是首项为1的等比数列,且b n >0,b 2+b 3=12,所以q 2+q-12=0,解得q=3(q=-4不合题意,舍去),所以b n =3-1.若选①,由S n =12n 2+52n ,可得-1=12(n-1)2+52(n-1)(n ≥2),两式相减可得a n =n+2(n ≥2),又因为a 1=S 1=3也符合上式,所以a n =n+2,所以1log 3r1=1(r2)=121−1r2,则T n =121-13+12−14+13−15+…+1−1r2=34−121r1+1r2.因为1r1+1r2>0,所以T n <34,由题意可得M≥34,又因为M∈N*,所以存在M满足题意,并且M的最小值为1.若选②,f(x)=sinπx-23cos2π2x+3=sinπx-3cosπx=2sinπx-π3,令f(x)=0,可得πx-π3=kπ,k∈Z,解得x=k+13,k∈Z,即x n=n-1+13=n-23,故a n=x n+83=n+2,同上①,则存在M满足题意,并且M的最小值为1.若选③,则由2-a n--12−-1=0,得(a n--1-1)(a n+-1)=0.又因为a n>0,所以a n--1-1=0,即a n-=1,所以数列{a n}是公差为1的等差数列.又因为a1=b2,则a1=3,所以a n=n+2.-1同上①,则存在M满足题意,并且M的最小值为1.12.AD∵a1>1,a7·a8>1,可知q>0,又7-18-1<0,∴a7>1,a8<1,∴0<q<1,故A正确;a7a9=82<1,故B错误;∵a1>1,0<q<1,∴数列{a n}为各项均为正数的递减数列,∴S n无最大值,故C错误;又a7>1,a8<1,∴T7是数列{T n}中的最大项,故D正确.故选AD.13.2n-12-1+1由题意可知,大老鼠每天打洞的距离是以1为首项,2为公比的等比数列,前n天打洞的距离之和为1-21-2=2n-1.小老鼠每天打洞的距离是以1为首项,12为公比的等比数列,前n天打洞的距离之和为1-(12)1-12=2-12-1.所以S n=2n-1+2-12-1=2n-12-1+1.14.2n-1∵a1=1,a2=2,且a n+2=2S n-S n+1+3,∴当n=1时,a3=2-3+3=2.∵a n+2=2S n-S n+1+3,∴当n≥2时,a n+1=2S n-1-S n+3.两式相减可得,a n+2-a n+1=2(S n-S n-1)-(S n+1-S n)(n≥2),即当n≥2时,a n+2-a n+1=2a n-a n+1,即a n+2=2a n.∵a3=2a1,∴数列{a n}的奇数项和偶数项分别成等比数列,公比均为2,∴a2n=2×2n-1=2n,a2n-1=1×2n-1=2n-1,∴b n=log2a2n-1+log2a2n=n-1+n=2n-1.15.BD由题意可知,数列{a n}为等差数列,设数列{a n}的公差为d,a1=5,由题意可得30a1+30×292=390,解得d=1629,∴a n=a1+(n-1)d=16r12929.∵b n=2,∴r1=2r12=2r1-=2d(非零常数),则数列{b n}是等比数列,故B正确;∵5d=5×1629=8029≠3,∴105=(2)5=25d≠23,∴b10≠8b5,故A错误;a30=a1+29d=5+16=21,∴a1b30=5×221>105,故C错误;∵a4=a1+3d=5+3×1629=19329,a5=a1+4d=5+4×1629=20929,∴3+5+72+4+6=3534=54=209193,故D正确.故选BD.16.(1)证明因为a n+1=32+1,所以1r1=13+23,所以1r1-1=131-1.因为a1=35,则11-1=23.所以数列1-1是首项为23,公比为13的等比数列.(2)解不存在.理由如下,由(1)知,1-1=23×13n-1=23,所以a n=33+2.假设存在互不相等的正整数m,s,t满足条件,则有+=2,(-1)2=(-1)(-1).由a n=33+2与(a s-1)2=(a m-1)(a t-1),得33+2-12=33+2-133+2-1.即3m+t+2×3m+2×3t=32s+4×3s.因为m+t=2s,所以3m+3t=2×3s.因为3m+3t≥23r=2×3s,当且仅当m=t时等号成立,这与m,s,t互不相等矛盾.所以不存在互不相等的正整数m,s,t满足条件.。
精品解析:2024年北京高考数学真题(原卷版)(合并)

绝密★本科目考试启用前2024年普通高等学校招生全国统一考试(北京卷)数学本试卷共12页,150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{|31}M x x =-<<,{|14}N x x =-≤<,则M N ⋃=()A.{}11x x -≤< B.{}3x x >-C.{}|34x x -<< D.{}4x x <2.已知1i iz=--,则z =().A.1i --B.1i -+C.1i- D.1i+3.圆22260x y x y +-+=的圆心到直线20x y -+=的距离为()A. B.2 C.3 D.4.在(4x -的展开式中,3x 的系数为()A .6B.6- C.12D.12-5.设a ,b 是向量,则“()()·0a b a b +-= ”是“a b =- 或a b = ”的().A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.设函数()()sin 0f x x ωω=>.已知()11f x =-,()21f x =,且12x x -的最小值为π2,则ω=()A.1B.2C.3D.47.生物丰富度指数1ln S d N-=是河流水质的一个评价指标,其中,S N 分别表示河流中的生物种类数与生物个体总数.生物丰富度指数d 越大,水质越好.如果某河流治理前后的生物种类数S 没有变化,生物个体总数由1N 变为2N ,生物丰富度指数由2.1提高到3.15,则()A.2132N N =B.2123N N =C.2321N N = D.3221N N =8.如图,在四棱锥P ABCD -中,底面ABCD 是边长为4的正方形,4PA PB ==,PC PD ==该棱锥的高为().A.1B.2C.D.9.已知()11,x y ,()22,x y 是函数2x y =的图象上两个不同的点,则()A.12122log 22y y x x ++< B.12122log 22y y x x ++>C.12212log 2y y x x +<+ D.12212log 2y y x x +>+10.已知()(){}2,|,12,01M x y y x t xx x t ==+-≤≤≤≤是平面直角坐标系中的点集.设d 是M 中两点间距离的最大值,S 是M 表示的图形的面积,则()A.3d =,1S <B.3d =,1S >C.d =,1S < D.d =,1S >第二部分(非选择题共110分)二、填空题共5小题,每小题5分,共25分.11.抛物线216y x =的焦点坐标为________.12.在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于原点对称.若ππ,63α⎡⎤∈⎢⎥⎣⎦,则cos β的最大值为________.13.若直线()3y k x =-与双曲线2214x y -=只有一个公共点,则k 的一个取值为________.14.汉代刘歆设计的“铜嘉量”是龠、合、升、斗、斛五量合一的标准量器,其中升量器、斗量器、斛量器的形状均可视为圆柱.若升、斗、斛量器的容积成公比为10的等比数列,底面直径依次为65mm,325mm,325mm ,且斛量器的高为230mm ,则斗量器的高为______mm ,升量器的高为________mm .15.设与是两个不同的无穷数列,且都不是常数列.记集合{}*|,N k k M k a b k ==∈,给出下列4个结论:①若与均为等差数列,则M 中最多有1个元素;②若与均为等比数列,则M 中最多有2个元素;③若为等差数列,为等比数列,则M 中最多有3个元素;④若为递增数列,为递减数列,则M 中最多有1个元素.其中正确结论的序号是______.三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.16.在ABC V 中,内角,,A B C 的对边分别为,,a b c ,A ∠为钝角,7a =,sin 2cos 7B b B =.(1)求A ∠;(2)从条件①、条件②、条件③这三个条件中选择一个作为已知,使得ABC V 存在,求ABC V 的面积.条件①:7b =;条件②:13cos 14B =;条件③:sin c A =注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.17.如图,在四棱锥P ABCD -中,//BC AD ,1AB BC ==,3AD =,点E 在AD 上,且PE AD ⊥,2PE DE ==.(1)若F 为线段PE 中点,求证://BF 平面PCD .(2)若AB ⊥平面PAD ,求平面PAB 与平面PCD 夹角的余弦值.18.某保险公司为了了解该公司某种保险产品的索赔情况,从合同险期限届满的保单中随机抽取1000份,记录并整理这些保单的索赔情况,获得数据如下表:赔偿次数01234单数800100603010假设:一份保单的保费为0.4万元;前3次索赔时,保险公司每次赔偿0.8万元;第四次索赔时,保险公司赔偿0.6万元.假设不同保单的索赔次数相互独立.用频率估计概率.(1)估计一份保单索赔次数不少于2的概率;(2)一份保单的毛利润定义为这份保单的保费与赔偿总金额之差.(i )记X 为一份保单的毛利润,估计X 的数学期望()E X ;(ⅱ)如果无索赔的保单的保费减少4%,有索赔的保单的保费增加20%,试比较这种情况下一份保单毛利润的数学期望估计值与(i )中()E X 估计值的大小.(结论不要求证明)19.已知椭圆E :()222210+=>>x y a b a b,以椭圆E 的焦点和短轴端点为顶点的四边形是边长为2的正方形.过点()(0,t t >且斜率存在的直线与椭圆E 交于不同的两点,A B ,过点A 和()0,1C 的直线AC 与椭圆E 的另一个交点为D .(1)求椭圆E 的方程及离心率;(2)若直线BD 的斜率为0,求t 的值.20.设函数()()()ln 10f x x k x k =++≠,直线l 是曲线()y f x =在点()()(),0t f t t >处的切线.(1)当1k =-时,求()f x 的单调区间.(2)求证:l 不经过点()0,0.(3)当1k =时,设点()()(),0A t f t t >,()()0,C f t ,()0,0O ,B 为l 与y 轴的交点,ACO S 与ABOS 分别表示ACO △与ABO 的面积.是否存在点A 使得215ACO ABO S S =△△成立?若存在,这样的点A 有几个?(参考数据:1.09ln31.10<<,1.60ln51.61<<,1.94ln71.95<<)21.已知集合(){}{}{}{}{},,,1,2,3,4,5,6,7,8,M i j k w i j k w i j k w =∈∈∈∈+++且为偶数.给定数列128:,,,A a a a ,和序列12:,,s T T T Ω ,其中()(),,,1,2,,t t t t t T i j k w M t s =∈= ,对数列A 进行如下变换:将A 的第1111,,,i j k w 项均加1,其余项不变,得到的数列记作()1T A ;将()1T A 的第2222,,,i j k w 项均加1,其余项不变,得到数列记作()21T T A ;……;以此类推,得到()21s T T T A ,简记为()A Ω.(1)给定数列:1,3,2,4,6,3,1,9A 和序列()()():1,3,5,7,2,4,6,8,1,3,5,7Ω,写出()A Ω;(2)是否存在序列Ω,使得()A Ω为123456782,6,4,2,8,2,4,4a a a a a a a a ++++++++,若存在,写出一个符合条件的Ω;若不存在,请说明理由;(3)若数列A 的各项均为正整数,且1357a a a a +++为偶数,求证:“存在序列Ω,使得()A Ω的各项都相等”的充要条件为“12345678a a a a a a a a +=+=+=+”.绝密★本科目考试启用前2024年普通高等学校招生全国统一考试(北京卷)数学本试卷共12页,150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{|31}M x x =-<<,{|14}N x x =-≤<,则M N ⋃=()A.{}11x x -≤< B.{}3x x >-C.{}|34x x -<< D.{}4x x <【答案】C 【解析】【分析】直接根据并集含义即可得到答案.【详解】由题意得{}|34M x x N ⋃=-<<.故选:C.2.已知1i iz=--,则z =().A.1i --B.1i-+ C.1i- D.1i+【答案】C 【解析】【分析】直接根据复数乘法即可得到答案.【详解】由题意得()i 1i i 1z =--=-.故选:C.3.圆22260x y x y +-+=的圆心到直线20x y -+=的距离为()A.B.2C.3D.【答案】D 【解析】【分析】求出圆心坐标,再利用点到直线距离公式即可.【详解】由题意得22260x y x y +-+=,即()()221310x y -++=,则其圆心坐标为()1,3-,则圆心到直线20x y -+==故选:D.4.在(4x -的展开式中,3x 的系数为()A.6B.6- C.12D.12-【答案】A 【解析】【分析】写出二项展开式,令432r-=,解出r 然后回代入二项展开式系数即可得解.【详解】(4x 的二项展开式为(()()442144C C 1,0,1,2,3,4r rrr rr r T xxr --+==-=,令432r-=,解得2r =,故所求即为()224C 16-=.故选:A.5.设a ,b 是向量,则“()()·0a b a b +-=”是“a b =- 或a b = ”的().A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B 【解析】【分析】根据向量数量积分析可知()()0a b a b +⋅-= 等价于a b =,结合充分、必要条件分析判断.【详解】因为()()220a b a b a b +⋅-=-= ,可得22a b = ,即a b = ,可知()()0a b a b +⋅-= 等价于a b = ,若a b = 或a b =- ,可得a b =,即()()0a b a b +⋅-= ,可知必要性成立;若()()0a b a b +⋅-= ,即a b =,无法得出a b = 或a b =- ,例如()()1,0,0,1a b ==,满足a b = ,但a b ≠ 且a b ≠- ,可知充分性不成立;综上所述,“()()0a b a b +⋅-=”是“a b ≠ 且a b ≠- ”的必要不充分条件.故选:B.6.设函数()()sin 0f x x ωω=>.已知()11f x =-,()21f x =,且12x x -的最小值为π2,则ω=()A .1B.2C.3D.4【答案】B 【解析】【分析】根据三角函数最值分析周期性,结合三角函数最小正周期公式运算求解.【详解】由题意可知:1x 为()f x 的最小值点,2x 为()f x 的最大值点,则12minπ22T x x -==,即πT =,且0ω>,所以2π2Tω==.故选:B.7.生物丰富度指数1ln S d N-=是河流水质的一个评价指标,其中,S N 分别表示河流中的生物种类数与生物个体总数.生物丰富度指数d 越大,水质越好.如果某河流治理前后的生物种类数S 没有变化,生物个体总数由1N 变为2N ,生物丰富度指数由2.1提高到3.15,则()A.2132N N =B.2123N N =C.2321N N = D.3221N N =【答案】D 【解析】【分析】根据题意分析可得12112.1,3.15ln ln S S N N --==,消去S 即可求解.【详解】由题意得12112.1, 3.15ln ln S S N N --==,则122.1ln 3.15ln N N =,即122ln 3ln N N =,所以3221N N =.故选:D.8.如图,在四棱锥P ABCD -中,底面ABCD 是边长为4的正方形,4PA PB ==,PC PD ==该棱锥的高为().A.1B.2C.D.【答案】D 【解析】【分析】取点作辅助线,根据题意分析可知平面PEF ⊥平面ABCD ,可知⊥PO 平面ABCD ,利用等体积法求点到面的距离.【详解】如图,底面ABCD 为正方形,当相邻的棱长相等时,不妨设4,PA PB AB PC PD =====,分别取,AB CD 的中点,E F ,连接,,PF EF ,则,PE AB EF AB ⊥⊥,且PE EF E ⋂=,,PE EF ⊂平面PEF ,可知AB ⊥平面PEF ,且AB ⊂平面ABCD ,所以平面PEF ⊥平面ABCD ,过P 作EF 的垂线,垂足为O ,即PO EF ⊥,由平面PEF 平面ABCD EF =,PO ⊂平面PEF ,所以⊥PO 平面ABCD ,由题意可得:2,4PE PF EF ===,则222PE PF EF +=,即PE PF ⊥,则1122PE PF PO EF ⋅=⋅,可得PE PF PO EF⋅==,当相对的棱长相等时,不妨设4PA PC ==,PB PD ==,因为BD PB PD ==+,此时不能形成三角形PBD ,与题意不符,这样情况不存在.故选:D.9.已知()11,x y ,()22,x y 是函数2x y =的图象上两个不同的点,则()A.12122log 22y y x x ++< B.12122log 22y y x x ++>C.12212log 2y y x x +<+ D.12212log 2y y x x +>+【答案】B 【解析】【分析】根据指数函数和对数函数的单调性结合基本不等式分析判断AB ;举例判断CD 即可.【详解】由题意不妨设12x x <,因为函数2x y =是增函数,所以12022x x <<,即120y y <<,对于选项AB :可得121222222x x x x ++>=,即12122202x x y y ++>>,根据函数2log y x =是增函数,所以121212222log log 222x x y y x x+++>=,故B 正确,A 错误;对于选项D :例如120,1x x ==,则121,2y y ==,可得()12223log log 0,122y y +=∈,即12212log 12y y x x +<=+,故D 错误;对于选项C :例如121,x x =-=-,则1211,24y y ==,可得()122223log log log 332,128y y +==-∈--,即12212log 32y y x x +>-=+,故C 错误,故选:B.10.已知()(){}2,|,12,01M x y y x t xx x t ==+-≤≤≤≤是平面直角坐标系中的点集.设d 是M 中两点间距离的最大值,S 是M 表示的图形的面积,则()A.3d =,1S <B.3d =,1S >C.d =,1S <D.d =,1S >【答案】C 【解析】【分析】先以t 为变量,分析可知所求集合表示的图形即为平面区域212y x y x x ⎧≤⎪≥⎨⎪≤≤⎩,结合图形分析求解即可.【详解】对任意给定[]1,2x ∈,则()210xx x x -=-≥,且[]0,1t ∈,可知()222x x t x x x x x x ≤+-≤+-=,即2x y x ≤≤,再结合x 的任意性,所以所求集合表示的图形即为平面区域212y x y x x ⎧≤⎪≥⎨⎪≤≤⎩,如图阴影部分所示,其中()()()1,1,2,2,2,4A B C,可知任意两点间距离最大值d AC ==;阴影部分面积11212ABC S S <=⨯⨯△.故选:C.【点睛】方法点睛:数形结合的重点是“以形助数”,在解题时要注意培养这种思想意识,做到心中有图,见数想图,以开拓自己的思维.使用数形结合法的前提是题目中的条件有明确的几何意义,解题时要准确把握条件、结论与几何图形的对应关系,准确利用几何图形中的相关结论求解.第二部分(非选择题共110分)二、填空题共5小题,每小题5分,共25分.11.抛物线216y x =的焦点坐标为________.【答案】()4,0【解析】【分析】形如()22,0y px p =≠的抛物线的焦点坐标为,02p ⎛⎫⎪⎝⎭,由此即可得解.【详解】由题意抛物线的标准方程为216y x =,所以其焦点坐标为()4,0.故答案为:()4,0.12.在平面直角坐标系xOy 中,角α与角β均以Ox 为始边,它们的终边关于原点对称.若ππ,63α⎡⎤∈⎢⎥⎣⎦,则cos β的最大值为________.【答案】12-##0.5-【解析】【分析】首先得出π2π,Z k k βα=++∈,结合三角函数单调性即可求解最值.【详解】由题意π2π,Z k k βα=++∈,从而()cos cos π2πcos k βαα=++=-,因为ππ,63α⎡⎤∈⎢⎥⎣⎦,所以cos α的取值范围是1,22⎡⎢⎣⎦,cos β的取值范围是1,22⎡⎤--⎢⎥⎣⎦,当且仅当π3α=,即4π2π,Z 3k k β=+∈时,cos β取得最大值,且最大值为12-.故答案为:12-.13.若直线()3y k x =-与双曲线2214x y -=只有一个公共点,则k 的一个取值为________.【答案】12(或12-,答案不唯一)【解析】【分析】联立直线方程与双曲线方程,根据交点个数与方程根的情况列式即可求解.【详解】联立()22143x y y k x ⎧-=⎪⎨⎪=-⎩,化简并整理得:()222214243640k x k x k -+--=,由题意得2140k -=或()()()2222Δ244364140k k k =++-=,解得12k =±或无解,即12k =±,经检验,符合题意.故答案为:12(或12-,答案不唯一).14.汉代刘歆设计的“铜嘉量”是龠、合、升、斗、斛五量合一的标准量器,其中升量器、斗量器、斛量器的形状均可视为圆柱.若升、斗、斛量器的容积成公比为10的等比数列,底面直径依次为65mm,325mm,325mm ,且斛量器的高为230mm ,则斗量器的高为______mm ,升量器的高为________mm .【答案】①.23②.57.5##1152【解析】【分析】根据体积为公比为10的等比数列可得关于高度的方程组,求出其解后可得前两个圆柱的高度.【详解】设升量器的高为1h ,斗量器的高为2h (单位都是mm ),则2222212325325ππ230221065325ππ22h h h ⎛⎫⎛⎫⨯ ⎪ ⎪⎝⎭⎝⎭==⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭,故223mm h =,1115mm 2h =.故答案为:11523mm,mm 2.15.设与是两个不同的无穷数列,且都不是常数列.记集合{}*|,N k k M k a b k ==∈,给出下列4个结论:①若与均为等差数列,则M 中最多有1个元素;②若与均为等比数列,则中最多有2个元素;③若为等差数列,为等比数列,则M 中最多有3个元素;④若为递增数列,为递减数列,则M 中最多有1个元素.其中正确结论的序号是______.【答案】①③④【解析】【分析】利用两类数列的散点图的特征可判断①④的正误,利用反例可判断②的正误,结合通项公式的特征及反证法可判断③的正误.【详解】对于①,因为{}{},n n a b 均为等差数列,故它们的散点图分布在直线上,而两条直线至多有一个公共点,故M 中至多一个元素,故①正确.对于②,取()112,2,n n n n a b --==--则{}{},n n a b 均为等比数列,但当n 为偶数时,有()1122n n n n a b --===--,此时M 中有无穷多个元素,故②错误.对于③,设()0,1nn b AqAq q =≠≠±,()0n a kn b k =+≠,若M 中至少四个元素,则关于n 的方程n Aq kn b =+至少有4个不同的正数解,若0,1q q >≠,则由n y Aq =和y kn b =+的散点图可得关于n 的方程n Aq kn b =+至多有两个不同的解,矛盾;若0,1q q <≠±,考虑关于n 的方程n Aq kn b =+奇数解的个数和偶数解的个数,当n Aq kn b =+有偶数解,此方程即为nA q kn b =+,方程至多有两个偶数解,且有两个偶数解时ln 0Ak q >,否则ln 0Ak q <,因,ny A q y kn b ==+单调性相反,方程nA q kn b =+至多一个偶数解,当n Aq kn b =+有奇数解,此方程即为nA q kn b -=+,方程至多有两个奇数解,且有两个奇数解时ln 0Ak q ->即ln 0Ak q <否则ln 0Ak q >,因,ny A q y kn b =-=+单调性相反,方程nA q kn b =+至多一个奇数解,因为ln 0Ak q >,ln 0Ak q <不可能同时成立,故n Aq kn b =+不可能有4个不同的整数解,即M 中最多有3个元素,故③正确.对于④,因为{}n a 为递增数列,{}n b 为递减数列,前者散点图呈上升趋势,后者的散点图呈下降趋势,两者至多一个交点,故④正确.故答案为:①③④.【点睛】思路点睛:对于等差数列和等比数列的性质的讨论,可以利用两者散点图的特征来分析,注意讨论两者性质关系时,等比数列的公比可能为负,此时要注意合理转化.三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.16.在ABC V 中,内角,,A B C 的对边分别为,,a b c ,A ∠为钝角,7a =,sin 2cos 7B b B =.(1)求A ∠;(2)从条件①、条件②、条件③这三个条件中选择一个作为已知,使得ABC V 存在,求ABC V 的面积.条件①:7b =;条件②:13cos 14B =;条件③:sin c A =注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.【答案】(1)2π3A =;(2)选择①无解;选择②和③△ABC 面积均为1534.【解析】【分析】(1)利用正弦定理即可求出答案;(2)选择①,利用正弦定理得3B π=,结合(1)问答案即可排除;选择②,首先求出33sin 14B =,再代入式子得3b =,再利用两角和的正弦公式即可求出sinC ,最后利用三角形面积公式即可;选择③,首先得到5c =,再利用正弦定理得到sin 14C =,再利用两角和的正弦公式即可求出sin B ,最后利用三角形面积公式即可;【小问1详解】由题意得32sin cos cos 7B B B =,因为A 为钝角,则cos 0B ≠,则32sin 7B b =,则7sin sin sin 37b a BA A ===,解得3sin 2A =,因为A 为钝角,则2π3A =.【小问2详解】选择①7b =,则sin 714142B b ==⨯=,因为2π3A =,则B 为锐角,则3B π=,此时πA B +=,不合题意,舍弃;选择②13cos 14B =,因为B为三角形内角,则33sin 14B ==,则代入32sin 7B b =得3332147b ⨯=,解得3b =,()2π2π2πsin sin sin sin cos cos sin 333C A B B B B⎛⎫=+=+=+ ⎪⎝⎭13121421414⎛⎫=⨯+-⨯=⎪⎝⎭,则11sin 7322144ABC S ab C ==⨯⨯⨯=.选择③sin c A =2c ⨯=,解得5c =,则由正弦定理得sin sin a c A C =5sin 32C =,解得53sin 14C =,因为C 为三角形内角,则11cos 14C ==,则()2π2π2πsin sin sin sin cos cos sin 333B A C C C C ⎛⎫=+=+=+ ⎪⎝⎭3111533321421414⎛⎫=⨯+-⨯=⎪⎝⎭,则11sin 7522144ABC S ac B ==⨯⨯=△17.如图,在四棱锥P ABCD -中,//BC AD ,1AB BC ==,3AD =,点E 在AD 上,且PE AD ⊥,2PE DE ==.(1)若F 为线段PE 中点,求证://BF 平面PCD .(2)若AB ⊥平面PAD ,求平面PAB 与平面PCD 夹角的余弦值.【答案】(1)证明见解析(2)3030【解析】【分析】(1)取PD 的中点为S ,接,SF SC ,可证四边形SFBC 为平行四边形,由线面平行的判定定理可得//BF 平面PCD .(2)建立如图所示的空间直角坐标系,求出平面APB 和平面PCD 的法向量后可求夹角的余弦值.【小问1详解】取PD 的中点为S ,接,SF SC ,则1//,12SF ED SF ED ==,而//,2ED BC ED BC =,故//,SF BC SF BC =,故四边形SFBC 为平行四边形,故//BF SC ,而BF ⊄平面PCD ,SC ⊂平面PCD ,所以//BF 平面PCD .【小问2详解】因为2ED =,故1AE =,故//,=AE BC AE BC ,故四边形AECB 为平行四边形,故//CE AB ,所以CE ⊥平面PAD ,而,PE ED ⊂平面PAD ,故,CE PE CE ED ⊥⊥,而PE ED ⊥,故建立如图所示的空间直角坐标系,则()()()()()0,1,0,1,1,0,1,0,0,0,2,0,0,0,2A B C D P --,则()()()()0,1,2,1,1,2,1,0,2,0,2,2,PA PB PC PD =--=--=-=-设平面PAB 的法向量为(),,m x y z =,则由0m PA m PB ⎧⋅=⎪⎨⋅=⎪⎩可得2020y z x y z --=⎧⎨--=⎩,取()0,2,1m =- ,设平面PCD 的法向量为(),,n a b c =,则由0n PC n PD ⎧⋅=⎪⎨⋅=⎪⎩可得20220a b b c -=⎧⎨-=⎩,取()2,1,1n = ,故cos ,30m n ==-,故平面PAB 与平面PCD 夹角的余弦值为303018.某保险公司为了了解该公司某种保险产品的索赔情况,从合同险期限届满的保单中随机抽取1000份,记录并整理这些保单的索赔情况,获得数据如下表:赔偿次数01234单数800100603010假设:一份保单的保费为0.4万元;前3次索赔时,保险公司每次赔偿0.8万元;第四次索赔时,保险公司赔偿0.6万元.假设不同保单的索赔次数相互独立.用频率估计概率.(1)估计一份保单索赔次数不少于2的概率;(2)一份保单的毛利润定义为这份保单的保费与赔偿总金额之差.(i )记X 为一份保单的毛利润,估计X 的数学期望()E X ;(ⅱ)如果无索赔的保单的保费减少,有索赔的保单的保费增加20%,试比较这种情况下一份保单毛利润的数学期望估计值与(i )中()E X 估计值的大小.(结论不要求证明)【答案】(1)110(2)(i)0.122万元;(ii)这种情况下一份保单毛利润的数学期望估计值大于(i )中()E X 估计值【解析】【分析】(1)根据题设中的数据可求赔偿次数不少2的概率;(2)(ⅰ)设ξ为赔付金额,则ξ可取0,0.8,0.1.6,2.4,3,用频率估计概率后可求ξ的分布列及数学期望,从而可求()E X .(ⅱ)先算出下一期保费的变化情况,结合(1)的结果可求()E Y ,从而即可比较大小得解.【小问1详解】设A 为“随机抽取一单,赔偿不少于2次”,由题设中的统计数据可得()603010180010060301010P A ++==++++.【小问2详解】(ⅰ)设ξ为赔付金额,则ξ可取0,0.8,1.6,2.4,3,由题设中的统计数据可得()()800410010,0.810005100010P P ξξ======,603( 1.6)100050P ξ===,303( 2.4)1000100P ξ===,101(3)1000100P ξ===,故()4133100.8 1.6 2.430.27851050100100E ξ=⨯+⨯+⨯+⨯+⨯=故()0.40.2780.122E X =-=(万元).(ⅱ)由题设保费的变化为410.496%0.4 1.20.403255⨯⨯+⨯⨯=,故()0.1220.40320.40.1252E Y =+-=(万元),从而()()E X E Y <.19.已知椭圆E :()222210+=>>x y a b a b,以椭圆E 的焦点和短轴端点为顶点的四边形是边长为2的正方形.过点()(0,t t >且斜率存在的直线与椭圆E 交于不同的两点,A B ,过点A 和()0,1C 的直线AC 与椭圆E 的另一个交点为D .(1)求椭圆E 的方程及离心率;(2)若直线BD 的斜率为0,求t 的值.【答案】(1)221,422x y e +==(2)2t =【解析】【分析】(1)由题意得b c ==,进一步得a ,由此即可得解;(2)设(:,0,AB y kx t k t =+≠>,()()1122,,,A x y B x y ,联立椭圆方程,由韦达定理有2121222424,1221kt t x x x x k k --+==++,而()121112:y y AD y x x y x x -=-++,令0x =,即可得解.【小问1详解】由题意b c ===,从而2a ==,所以椭圆方程为22142x y +=,离心率为2e =;【小问2详解】直线AB 斜率不为0,否则直线AB与椭圆无交点,矛盾,从而设(:,0,AB y kx t k t =+≠>,()()1122,,,A x y B x y ,联立22142x y y kx t ⎧+=⎪⎨⎪=+⎩,化简并整理得()222124240k x ktx t +++-=,由题意()()()222222Δ1682128420k t k t k t=-+-=+->,即,k t 应满足22420kt +->,所以2121222424,1221kt t x x x x k k --+==++,若直线BD 斜率为0,由椭圆的对称性可设()22,D x y -,所以()121112:y y AD y x x y x x -=-++,在直线AD 方程中令0x =,得()()()()2122112121221121212422214C k t x kx t x kx t kx x t x x x y x y y t x x x x x x kt t-++++++====+==+++-,所以2t =,此时k 应满足222424200k t k k ⎧+-=->⎨≠⎩,即k 应满足22k <-或22k >,综上所述,2t =满足题意,此时22k <-或22k >.20.设函数()()()ln 10f x x k x k =++≠,直线l 是曲线()y f x =在点()()(),0t f t t >处的切线.(1)当1k =-时,求()f x 的单调区间.(2)求证:l 不经过点()0,0.(3)当1k =时,设点()()(),0A t f t t >,()()0,C f t ,()0,0O ,B 为l 与y 轴的交点,ACO S 与ABOS 分别表示ACO △与ABO 的面积.是否存在点A 使得215ACO ABO S S =△△成立?若存在,这样的点A 有几个?(参考数据:1.09ln31.10<<,1.60ln51.61<<,1.94ln71.95<<)【答案】(1)单调递减区间为(1,0)-,单调递增区间为(0,)+∞.(2)证明见解析(3)2【解析】【分析】(1)直接代入1k =-,再利用导数研究其单调性即可;(2)写出切线方程()1()(0)1k y f t x t t t ⎛⎫-=+-> ⎪+⎝⎭,将(0,0)代入再设新函数()ln(1)1tF t t t=+-+,利用导数研究其零点即可;(3)分别写出面积表达式,代入215ACO ABO S S = 得到13ln(1)21501tt t t+--=+,再设新函数15()13ln(1)2(0)1th t t t t t=+-->+研究其零点即可.【小问1详解】1()ln(1),()1(1)11x f x x x f x x x x'=-+=-=>-++,当()1,0x ∈-时,′<0;当∈0,+∞,′>0;()f x ∴在(1,0)-上单调递减,在(0,)+∞上单调递增.则()f x 的单调递减区间为(1,0)-,单调递增区间为(0,)+∞.【小问2详解】()11k f x x '=++,切线l 的斜率为11k t++,则切线方程为()1()(0)1k y f t x t t t ⎛⎫-=+-> ⎪+⎝⎭,将(0,0)代入则()1,()111k k f t t f t t t t ⎛⎫⎛⎫-=-+=+ ⎪ ⎪++⎝⎭⎝⎭,即ln(1)1k t k t t tt ++=++,则ln(1)1t t t +=+,ln(1)01tt t +-=+,令()ln(1)1tF t t t=+-+,假设l 过(0,0),则()F t 在(0,)t ∈+∞存在零点.2211()01(1)(1)t t t F t t t t +-'=-=>+++,()F t ∴在(0,)+∞上单调递增,()(0)0F t F >=,()F t ∴在(0,)+∞无零点,∴与假设矛盾,故直线l 不过(0,0).【小问3详解】1k =时,12()ln(1),()1011x f x x x f x x x+'=++=+=>++.1()2ACO S tf t = ,设l 与y 轴交点B 为(0,)q ,0t >时,若0q <,则此时l 与()f x 必有交点,与切线定义矛盾.由(2)知0q ≠.所以0q >,则切线l 的方程为()()1ln 111y t t x t t ⎛⎫--+=+- ⎪+⎝⎭,令0x =,则ln(1)1t y q y t t ===+-+.215ACO ABO S S = ,则2()15ln(1)1t tf t t t t ⎡⎤=+-⎢⎥+⎣⎦,13ln(1)21501t t t t ∴+--=+,记15()13ln(1)2(0)1th t t t t t=+-->+,∴满足条件的A 有几个即()h t 有几个零点.()()()()()()()()2222221313221152141315294211111t t t t t t t h t t t t t t +-++--+--+-=--=++'==+++,当10,2t ⎛⎫∈ ⎪⎝⎭时,()0h t '<,此时()h t 单调递减;当1,42t ⎛⎫∈⎪⎝⎭时,()0h t '>,此时()h t 单调递增;当()4,t ∞∈+时,()0h t '<,此时()h t 单调递减;因为1(0)0,0,(4)13ln 520131.6200.802h h h ⎛⎫==-⨯-=> ⎪⎝⎭,15247272(24)13ln 254826ln 548261.614820.5402555h ⨯=--=--<⨯--=-<,所以由零点存在性定理及()h t 的单调性,()h t 在1,42⎛⎫⎪⎝⎭上必有一个零点,在(4,24)上必有一个零点,综上所述,()h t 有两个零点,即满足215ACO ABO S S =的A 有两个.【点睛】关键点点睛:本题第二问的关键是采用的是反证法,转化为研究函数零点问题.21.已知集合()}{}{}{}{},,,1,2,3,4,5,6,7,8,M i j k w i j k w i j k w =∈∈∈∈+++且为偶数.给定数列128:,,,A a a a ,和序列12:,,s T T T Ω ,其中()(),,,1,2,,t t t t t T i j k w M t s =∈= ,对数列A 进行如下变换:将A 的第1111,,,i j k w 项均加1,其余项不变,得到的数列记作()1T A ;将()1T A 的第2222,,,i j k w 项均加1,其余项不变,得到数列记作()21T T A ;……;以此类推,得到()21s T T T A ,简记为()A Ω.(1)给定数列:1,3,2,4,6,3,1,9A 和序列()()():1,3,5,7,2,4,6,8,1,3,5,7Ω,写出()A Ω;(2)是否存在序列Ω,使得()A Ω为123456782,6,4,2,8,2,4,4a a a a a a a a ++++++++,若存在,写出一个符合条件的Ω;若不存在,请说明理由;(3)若数列A 的各项均为正整数,且1357a a a a +++为偶数,求证:“存在序列Ω,使得()A Ω的各项都相等”的充要条件为“12345678a a a a a a a a +=+=+=+”.【答案】(1)():3,4,4,5,8,4,3,10A Ω(2)不存在符合条件的Ω,理由见解析(3)证明见解析【解析】【分析】(1)直接按照()ΩA 的定义写出()ΩA 即可;(2)解法一:利用反证法,假设存在符合条件的Ω,由此列出方程组,进一步说明方程组无解即可;解法二:对于任意序列,所得数列之和比原数列之和多4,可知序列Ω共有8项,可知:()()2122128,1,2,3,4n n n n b b a a n --+-+==,检验即可;(3)解法一:分充分性和必要性两方面论证;解法二:若12345678a a a a a a a a +=+=+=+,分类讨论1357,,,a a a a 相等得个数,结合题意证明即可;若存在序列Ω,使得()ΩA 为常数列,结合定义分析证明即可.【小问1详解】因为数列:1,3,2,4,6,3,1,9A ,由序列()11,3,5,7T 可得()1:2,3,3,4,7,3,2,9T A ;由序列()22,4,6,8T 可得()21:2,4,3,5,7,4,2,10T T A ;由序列()31,3,5,7T 可得(321:3,4,4,5,8,4,3,10T T T A ;所以()Ω:3,4,4,5,8,4,3,10A .【小问2详解】解法一:假设存在符合条件的Ω,可知()ΩA 的第1,2项之和为12a a s ++,第3,4项之和为34a a s ++,则()()()()121234342642a a a a sa a a a s⎧+++=++⎪⎨+++=++⎪⎩,而该方程组无解,故假设不成立,故不存在符合条件的Ω;解法二:由题意可知:对于任意序列,所得数列之和比原数列之和多4,假设存在符合条件的Ω,且()128Ω:,,,A b b b ⋅⋅⋅,因为2642824484+++++++=,即序列Ω共有8项,由题意可知:()()2122128,1,2,3,4n n n n b b a a n --+-+==,检验可知:当2,3n =时,上式不成立,即假设不成立,所以不存在符合条件的Ω.【小问3详解】解法一:我们设序列()21...s T T T A 为{}(),18s n a n ≤≤,特别规定()0,18nn aa n =≤≤.必要性:若存在序列12:,,s T T T Ω ,使得()ΩA 的各项都相等.则,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a =======,所以,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a +=+=+=+.根据()21...s T T T A 的定义,显然有,21,21,211,21s j s j s j s j a a a a ----+=++,这里1,2,3,4j =,1,2,...s =.所以不断使用该式就得到12345678,1,2s s a a a a a a a a a a s +=+=+=+=+-,必要性得证.充分性:若12345678a a a a a a a a +=+=+=+.由已知,1357a a a a +++为偶数,而12345678a a a a a a a a +=+=+=+,所以()()24681213574a a a a a a a a a a +++=+-+++也是偶数.我们设()21...s T T T A 是通过合法的序列Ω的变换能得到的所有可能的数列()ΩA 中,使得,1,2,3,4,5,7,8s s s s s s s s a a a a a a a a -+-+--最小的一个.上面已经说明,21,21,211,21s j s j s j s j a a a a ----+=++,这里1,2,3,4j =,1,2,...s =.从而由12345678a a a a a a a a +=+=+=+可得,1,2,3,4,5,6,7,812s s s s s s s s a a a a a a a a a a s +=+=+=+=++.同时,由于t t t t i j k w +++总是偶数,所以,1,3,5,7t t t t a a a a +++和,2,4,6,8t t t t a a a a +++的奇偶性保持不变,从而,1,3,5,7s s s s a a a a +++和,2,4,6,8s s s s a a a a +++都是偶数.下面证明不存在1,2,3,4j =使得,21,22s j s j a a --≥.假设存在,根据对称性,不妨设1j =,,21,22s j s j a a --≥,即,1,22s s a a -≥.情况1:若,3,4,5,6,7,80s s s s s s a a a a a a -+-+-=,则由,1,3,5,7s s s s a a a a +++和,2,4,6,8s s s s a a a a +++都是偶数,知,1,24s s a a -≥.对该数列连续作四次变换()()()()2,3,5,8,2,4,6,8,2,3,6,7,2,4,5,7后,新的4,14,24,34,44,54,64,74,8s s s s s s s s a a a a a a a a ++++++++-+-+-+-相比原来的,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-减少4,这与,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-的最小性矛盾;情况2:若,3,4,5,6,7,80s s s s s s a a a a a a -+-+->,不妨设,3,40s s a a ->.情况2-1:如果,3,41s s a a -≥,则对该数列连续作两次变换()()2,4,5,7,2,4,6,8后,新的2,12,22,32,42,52,62,72,8s s s s s s s s a a a a a a a a ++++++++-+-+-+-相比原来的,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-至少减少2,这与,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-的最小性矛盾;情况2-2:如果,4,31s s a a -≥,则对该数列连续作两次变换()()2,3,5,8,2,3,6,7后,新的2,12,22,32,42,52,62,72,8s s s s s s s s a a a a a a a a ++++++++-+-+-+-相比原来的,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-至少减少2,这与,1,2,3,4,5,7,8s s s s s s s s a a a a a a a a -+-+--的最小性矛盾.这就说明无论如何都会导致矛盾,所以对任意的1,2,3,4j =都有,21,21s j s j a a --≤.假设存在1,2,3,4j =使得,21,21s j s j a a --=,则,21,2s j s j a a -+是奇数,所以,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a +=+=+=+都是奇数,设为21N +.则此时对任意1,2,3,4j =,由,21,21s j s j a a --≤可知必有{}{},21,2,,1s j s j a a N N -=+.而,1,3,5,7s s s s a a a a +++和,2,4,6,8s s s s a a a a +++都是偶数,故集合{},s m m a N =中的四个元素,,,i j k w 之和为偶数,对该数列进行一次变换(),,,i j k w ,则该数列成为常数列,新的1,11,21,31,41,51,61,71,8s s s s s s s s a a a a a a a a ++++++++-+-+-+-等于零,比原来的,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-更小,这与,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-的最小性矛盾.综上,只可能(),21,201,2,3,4s j s j a a j --==,而,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a +=+=+=+,故{}(),Ωs na A =是常数列,充分性得证.解法二:由题意可知:Ω中序列的顺序不影响()ΩA 的结果,且()()()()12345678,,,,,,,a a a a a a a a 相对于序列也是无序的,(ⅰ)若12345678a a a a a a a a +=+=+=+,不妨设1357a a a a ≤≤≤,则2468a a a a ≥≥≥,①当1357a a a a ===,则8642a a a a ===,分别执行1a 个序列()2,4,6,8、2a 个序列()1,3,5,7,可得1212121212121212,,,,,,,a a a a a a a a a a a a a a a a ++++++++,为常数列,符合题意;②当1357,,,a a a a 中有且仅有三个数相等,不妨设135a a a ==,则246a a a ==,即12121278,,,,,,,a a a a a a a a ,分别执行2a 个序列()1,3,5,7、7a 个序列()2,4,6,8可得122712212272778,,,,,,,a a a a a a a a a a a a a a a a ++++++++,即1227122712272712,,,,,,,a a a a a a a a a a a a a a a a ++++++++,因为1357a a a a +++为偶数,即173a a +为偶数,可知17,a a 的奇偶性相同,则*712a a -∈N ,分别执行712a a -个序列()1,3,5,7,()1,3,6,8,()2,3,5,8,()1,4,5,8,可得72172172172172172172173232323232323232,,,,,,,22222222a a a a a a a a a a a a a a a a a a a a a a a+-+-+-+-+-+-+-+,为常数列,符合题意;③若1357a a a a =<=,则2468a a a a =>=,即12125656,,,,,,,a a a a a a a a ,分别执行5a 个()1,3,6,8、1a 个()2,4,5,7,可得1512151215561556,,,,,,,a a a a a a a a a a a a a a a a ++++++++,因为1256a a a a +=+,可得1512151215121512,,,,,,,a a a a a a a a a a a a a a a a ++++++++,即转为①,可知符合题意;④当1357,,,a a a a 中有且仅有两个数相等,不妨设13a a =,则24a a =,即12125678,,,,,,,a a a a a a a a ,分别执行1a 个()2,4,5,7、5a 个()1,3,6,8,可得1512151215561758,,,,,,,a a a a a a a a a a a a a a a a ++++++++,且1256a a a a +=+,可得1512151215121758,,,,,,,a a a a a a a a a a a a a a a a ++++++++,因为13571572a a a a a a a +++=++为偶数,可知57,a a 的奇偶性相同,则()()()()1515151715743a a a a a a a a a a a +++++++=++为偶数,且15151517a a a a a a a a +=+=+<+,即转为②,可知符合题意;⑤若1357a a a a <<<,则2468a a a a >>>,即12345678,,,,,,,a a a a a a a a ,分别执行1a 个()2,3,5,8、3a 个()1,4,6,7,可得1312133415363718,,,,,,,a a a a a a a a a a a a a a a a ++++++++,且1234a a a a +=+,可得1312131215363718,,,,,,,a a a a a a a a a a a a a a a a ++++++++,因为1357a a a a +++为偶数,则()()()()()()131315371313572a a a a a a a a a a a a a a +++++++=+++++为偶数,且13131537a a a a a a a a +=+<+<+,即转为④,可知符合题意;综上所述:若12345678a a a a a a a a +=+=+=+,则存在序列Ω,使得()ΩA 为常数列;(ⅱ)若存在序列Ω,使得()ΩA 为常数列,因为对任意()128Ω:,,,A b b b ⋅⋅⋅,均有()()()()12123434b b a a b b a a +-+=+-+()()()()56567878b b a a b b a a =+-+=+-+成立,若()ΩA 为常数列,则12345678b b b b b b b b +=+=+=+,所以12345678a a a a a a a a +=+=+=+;综上所述:“存在序列Ω,使得()ΩA 为常数列”的充要条件为“12345678a a a a a a a a +=+=+=+”.【点睛】关键点点睛:本题第三问的关键在于对新定义的理解,以及对其本质的分析.。
中微期中前答疑习题汇总(附答案版)

Chapter 1 市场1假设消费者对租房的需求为D(p)=100-2p,如果垄断者有60套出租房,追求利益最大的话垄断者会是用什么价格,出租多少套房子?如果垄断者只有40套房子出租,情况又会怎样呢?Solution:D(p)=100-2p,P=50-q/2TR=p(q)•q=q•(50-q/2)=50q-q2/2MR=50-q=0Q*=50, p*=25Chapter 2 预算约束1税收和补贴问题:假设以消费者只消费土豆(x)和牛肉(y)。
当土豆价格为9元,牛肉价格为5元时,他的所有收入恰好够他买5单位土豆和10单位牛肉。
县政府对购买土豆进行补贴:每单位土豆补贴是消费者5元。
但为了支付这种补贴,政府要向这个消费者征收20元的收入税。
请写出消费者的预算线。
(学会将经济语言翻译成数学语言)Solution:m=p1x+p2y=9*5+5*10=95土豆现价p1’=9-5=4m’=m-20=75所以BL:4x+5y=752食品券问题:一个家庭月收入为300元,只需支付83元即可得到政府补贴的价值153元的食品券。
若政府规定没有用完的食品券可以按照实际金额退款。
请写出预算方程,并图示。
Solution:设购买食品所花费用为x,其他所有花费为y,预算线分类两段(1)当x<153, 食品券的存在,使得食物价格变便宜(相对于153元的其他商品,食品只用83),△y/△x=-p1/p2=-83/153=-0.54,BL: 0.54x+y=300(2)当x>153, △y/△x=-p1/p2=-1/1=-1, BL: x+y=370折凹点为(153,217)3食品券问题:一个家庭月收入为300元,只需支付83元即可得到政府补贴的价值153元的食品券。
若政府规定153元的食品券必须一次性购买且不能退款及转让。
请写出预算方程,并图示。
(注意对比1、2题)Solution:设购买食品所花费用为x,其他所有花费为y,预算线分类三段(1)当家庭月消费食品x<83, 则消费者不会去购买食品券,△y/△x=-p1/p2=-1/1=-1,BL: x+y=300(2)当83<x<153, 消费者一次性购买食品券花费83元,剩余收入217元,此后直到153都不需要再多花钱消费食品。
25_Hz相敏轨道电路与ZPW-2000A结合处的逻辑检查故障分析

25 Hz相敏轨道电路与ZPW-2000A结合处的逻辑检查故障分析贾 鸿,马 樱,张 祺(卡斯柯信号有限公司,北京 100070)摘要:25 H z相敏轨道电路与Z P W-2000A轨道电路特性不同,但在自动闭塞及站内电码化改造过程中两种制式轨道电路常结合应用。
不同的特性会导致结合处的逻辑检查失效。
针对场联进路无法正常解锁、三接近闭塞分区遗留失去分路故障进行分析,介绍故障发生的场景及原因,并讨论计算机联锁、列控中心、区间综合监控系统以及继电逻辑检查电路对于此类故障的解决方案,为后续工程设计及故障处理提供参考。
关键词:25 Hz相敏轨道电路;ZPW-2000A;结合应用;逻辑检查;故障分析中图分类号:U284.2 文献标志码:A 文章编号:1673-4440(2024)03-0101-05Fault Analysis of Logic Check at Junction of 25 Hz Phase Sensitive Track Circuit and ZPW-2000A Track CircuitJia Hong, Ma Ying, Zhang Qi(CASCO Signal Ltd., Beijing 100070, China)Abstract: The 25 Hz phase sensitive track circuit has diff erent characteristics from ZPW-2000A track circuit. However, during the retrofitting of automatic block and station coding systems, these two track circuits are often used together. The diff erent characteristics of these two track circuits may lead to the failure of logic check at their junction. This paper analyzes the failure of normal release of the yard connection route and the loss of shunting kept in the third approach block section, and introduces the scenario and causes of these faults. It also discusses the solutions of the interlocking system, train control center system, integrated section monitoring system and relay logic check circuit for these failures, which provides reference for engineering design and fault handling in the future.Keywords: 25 Hz phase sensitive track circuit; ZPW-2000A track circuit; combined application; logic check; fault analysisDOI: 10.3969/j.issn.1673-4440.2024.03.019收稿日期:2022-10-09;修回日期:2024-01-31基金项目:卡斯柯信号有限公司科研项目(RB_23121022)第一作者:贾鸿(1990-),男,工程师,硕士,主要研究方向:铁路信号,邮箱:*****************.cn。
现代通信原理-曹志刚-答案(很重要)

现代通信原理-曹志刚-答案(很重要)通信原理作业参考答案第三章模拟线性调制3.7证明只要适当选择题图3.7中的放⼤器增益K ,不⽤滤波器即可实现抑制载波双边带调制。
解:tt Af b aK t A t f b aK t A t f b t A t f aK t A t f b t A t f K a t S c c c c c c DSB ωωωωωωcos )(2)(]cos )()[(]cos )([]cos )([]cos )([)]cos )(([)(2222222222?+++-=--+=--+=令 02=-b aK ,则a b K /2=t t bAf t S c DSB ωcos )(4)(=3.13 ⽤90相移的两个正交载波可以实现正交复⽤,即两个载波可分别传输带宽相等的两个独⽴的基带信号)(1t f 和)(2t f ,⽽只占⽤⼀条信道。
试证明⽆失真恢复基带信号的必要条件是:信道传递函数)(f H 必须满⾜W f f f H f f H c c ≤≤-=+0),()(证明:)(]sin )([)(]cos )([)(21t h t t f t h t t f t S c c *+*=ωω)]}()([)()(){(21)(2211c c c c F F j F F H S ωωωωωωωωωω--++++-=以t t C c d ωcos )(=相⼲解调,输出为 )(*)()(t C t S t S d p =)]}()2([)2()(){(41)]}2()([)()2(){(41)]()([21)(22112211ωωωωωωωωωωωωωωωωωωωωωF F j F F H F F j F F H S S S c c c c c c c c p -++++++--++--=++-= 选择适当滤波器,滤掉上式中c ωω2±项,则)]()()[(4)]()()[(41)(21c c c c d H H F jH H F S ωωωωωωωωωωω+--+++-=要⽆失真恢复基带信号,必须=++-+=-常数)()()()(c c c c H H H H ωωωωωωωω此时可恢复)(1t f 。
2024年人教版(2024)高一数学下册月考试卷425

2024年人教版(2024)高一数学下册月考试卷425考试试卷考试范围:全部知识点;考试时间:120分钟学校:______ 姓名:______ 班级:______ 考号:______总分栏题号一二三四五六总分得分评卷人得分一、选择题(共8题,共16分)1、已知数列{a n}满足a1=2,(n∈N*),则连乘积a1a2a3 a2012a2013的值为()A. -6B. 3C. 2D. 12、设集合A={x|2≤x<4};B={x|x≥3},那么A∪B等于()A. {x|x≥2}B. {x|x≥3}C. {x|3≤x<4}D. {x|3<x<4}3、在同一坐标系内作出的两个函数图象如图所示;则这两个函数为()A. y=a x和y=log a(-x)B. y=a x和y=log a x-1C. y=a-x和y=log a x-1D. y=a-x和y=log a(-x)4、若为一个三角形内角,则的值域为()A. (-1,1)B.C.D.5、在△ABC中,a:b:c=3:5:7,则△ABC的最大角的度数为()A. 1200B. 1350C. 450D. 6006、下列函数f(x)中,满足“任意x1, x2∈(0,+∞),且x1≠x2,都有(x1﹣x2)[f(x1)﹣f(x2)]<0”的是()A. f(x)= ﹣xB. f(x)=x3C. f(x)=ln xD. f(x)=2x7、函数f(x)=lg(-x2+x+6)的单调递减区间为()A.B.C.D.8、在鈻�ABC中的内角ABC所对的边分别为abc若b=2ccosAc=2bcosA则鈻�ABC的形状为()A. 直角三角形B. 锐角三角形C. 等边三角形D. 等腰直角三角形评卷人得分二、填空题(共6题,共12分)9、已知幂函数的图象过点10、函数则的值为11、【题文】若函数是偶函数,且在上是减函数,则____.12、【题文】某商店经销一种洗衣粉,年销售总量为6000包,每包进价为2.8元、销售价为3.4元,全年分若干次进货、每次进货均为x包,已知每次进货运输费为62.5元,全年保管费为1.5x元,为使利润最大,则x=______.13、已知一次函数y=x+1与二次函数y=x2﹣x﹣1的图象交于两点A(x1, y1),B(x2, y2),则+=____14、若5a=2b=10c2且abc鈮�0则ca+cb= ______ .评卷人得分三、计算题(共5题,共10分)15、若a、b互为相反数,则3a+3b-2的值为____.16、(2002•宁波校级自主招生)如图,E、F分别在AD、BC上,EFCD是正方形,且矩形ABCD∽矩形AEFB,则BC:AB的值是____.17、已知10a=2,10b=6,则102a-3b=____.18、若不等式|2x+1|-|2x-1|<a对任意实数x恒成立,则a的取值范围是____.19、如图,直角△ABC中,∠BAC=90°,AB=AC=15,AE为过点A的直线,BD⊥AE于D,CE⊥AE于E,CE=9,则DE=____.评卷人得分四、作图题(共1题,共3分)20、如图A、B两个村子在河CD的同侧,A、B两村到河的距离分别为AC=1千米,BD=3千米,且知道CD=3千米,现在要在河边CD上建一水厂,向A、B两村送自来水,铺设管道费用为每千米2000元,请你在CD上选择水厂位置O,使铺设管道的费用最省,并求出其费用.评卷人得分五、证明题(共2题,共4分)21、如图;已知AB是⊙O的直径,P是AB延长线上一点,PC切⊙O于C,AD⊥PC于D,CE⊥AB于E,求证:(1)AD=AE(2)PC•CE=PA•BE.22、AB是圆O的直径,CD是圆O的一条弦,AB与CD相交于E,∠AEC=45°,圆O的半径为1,求证:EC2+ED2=2.评卷人得分六、解答题(共3题,共12分)23、如图;在△ABC中,∠ABC=45°,∠BAC=90°,AD是BC上的高,沿AD把△ABD折起,使∠BDC=90°.(1)若E;F分别为 AB,AC的中点,求证:EF∥平面BDC;(2)证明:平面ADB⊥平面BDC;(3)设BD=1,求三棱锥D-ABC的表面积.24、玻璃盒子里装有各色球12个,其中5红、4黑、2白、1绿,从中任取1球.记事件A为“取出1个红球”,事件B为“取出1个黑球”,事件C为“取出1个白球”,事件D为“取出1个绿球”.已知P(A)= P(B)= P (C)= P(D)=.求:(1)“取出1球为红球或黑球”的概率;(2)“取出1球为红球或黑球或白球”的概率.25、已知函数f(x)=1鈭�42ax+a(a>0且a鈮�1)是定义在(鈭�隆脼,+隆脼)上的奇函数.(1)求a的值;(2)当x隆脢(0,1]时,t?f(x)鈮�2x鈭�2恒成立,求实数t的取值范围.参考答案一、选择题(共8题,共16分)1、C【分析】a1=2;数列的项轮流重复出现;周期是4且a1a2a3a4=1;所以从第一项起每连续四项的乘积为1,又2013=4×503+1所以a1a2a3 a2012a2013=a2013=a1=2故选C【解析】【答案】由于所求是较多项的乘积;逐一求项再作乘积,不太理想.虑数列是否有周期性,可通过求出足够多的项发现周期性,并应用.2、A【分析】∵集合A={x|2≤x<4};B={x|x≥3};∴A∪B={x|x≥2}故选:A.【解析】【答案】直接根据并集的定义得出答案即可.3、D【分析】对于选项A,由图可知y=a x为减函数,故0<a<1,此时y=log a(-x)应为(-∞;0)上的增函数,与图象矛盾,排除A对于选项B,由图可知y=a x为减函数,故0<a<1,此时y=log a()应为(0;+∞)上的增函数,与图象矛盾,排除B对于选项C,由图可知y=a-x为减函数,故a>1,此时y=log a()应为(0;+∞)上的减函数,与图象矛盾,排除C故选D【解析】【答案】先由指数函数的图象确定函数底数的取值范围;再由此推断对数复合函数的图象性质,并与已知图象比较,若矛盾则排除。
第五章 突破1 数列中含绝对值及奇偶项问题-2025年高考数学备考

第五章数列突破1数列中含绝对值及奇偶项问题学生用书P105命题点1数列中含绝对值的求和问题例1[2023全国卷乙]记S n为等差数列{a n}的前n项和,已知a2=11,S10=40.(1)求{a n}的通项公式;(2)求数列{|a n|}的前n项和T n.解析(1)设{a n}的公差为d,则2=1+=11,10=101+45=40,解得a1=13,d=-2.所以{a n}的通项公式为a n=13+(n-1)×(-2)=15-2n.(2)由(1)得|a n|=15-2,≤7,2-15,≥8.当n≤7时,T n=S n=13n+(-1)2×(-2)=14n-n2,当n≥8时,T n=-S n+2S7=-(14n-n2)+2(14×7-72)=98-14n+n2.综上,T n=14-2,≤7,98-14+2,≥8.方法技巧一般地,数列{|a n|}与数列{a n}是两个不相同的数列,只有数列{a n}中的每一项都是非负数时,它们表示的才是同一数列.因此,求数列{|a n|}的前n项和时,应先弄清n取什么值时a n≥0或a n<0,去掉绝对值符号后再求和.训练1[2023长沙一中5月三模]已知数列{a n}满足2a n+1=a n+a n+2(n∈N*),它的前n项和为S n,且a3=-25,S6=-144.(1)求S n的最小值;(2)求数列{|a n|}的前n项和T n.解析(1)由2a n+1=a n+a n+2可得a n+1-a n=a n+2-a n+1,所以{a n}是等差数列.设{a n}的公差为d,由3=-25,6=-144得1+2=-25,61+6×52=-144,解得1=-29,=2.所以S n=-29n+(-1)2×2=n2-30n=(n-15)2-225,所以当n=15时,S n取得最小值-225.(2)由(1)知a n=-29+(n-1)×2=2n-31,则当n≤15时,a n<0,当n≥16时,a n>0.当n ≤15时,T n =-S n =-n 2+30n ,当n ≥16时,T n =-S 15+S n -S 15=n 2-30n +450.综上,T n =-2+30,≤15,2-30+450,≥16.命题点2数列中的奇偶项问题例2[2022天津高考]已知{a n }是等差数列,其前n 项和为S n ,{b n }是等比数列,a 1=b 1=a 2-b 2=a 3-b 3=1.(1)求{a n },{b n }的通项公式.(2)证明:(S n +1+a n +1)b n =S n +1·b n +1-S n ·b n .(3)求∑2J1[a k +1-(-1)k a k ]b k .解析(1)设等差数列{a n }的公差为d ,等比数列{b n }的公比为q ,根据a 1=b 1=a 2-b 2=a 3-b 3=1得1+-=1,1+2-2=1,解得d =q =0(舍)或d =q =2,所以a n =2n -1,b n =2n -1.(2)解法一因为S n 为数列{a n }的前n 项和,所以S n =(1+)2=(1+2-1)2=n 2,则(S n +1+a n +1)b n =[(n +1)2+2(n +1)-1]·2n -1=(n 2+4n +2)·2n -1,S n +1·b n +1-S n ·b n =(n +1)2·2n -n 2·2n -1=2n -1·[2(n +1)2-n 2]=2n -1·(n 2+4n +2),所以(S n +1+a n +1)b n =S n +1·b n +1-S n ·b n .解法二因为S n 为数列{a n }的前n 项和,所以(S n +1+a n +1)b n =(S n +a n +1+a n +1)b n =(S n +2a n +1)b n ,S n +1·b n +1-S n ·b n =(S n +a n +1)·(2b n )-S n ·b n =b n (2S n +2a n +1-S n )=(S n +2a n +1)b n ,所以(S n +1+a n +1)b n =S n +1·b n +1-S n ·b n .(3)令c n =[a n +1-(-1)n a n ]b n ,当n 为奇数时,c n =(a n +1+a n )b n =(2n +1+2n -1)·2n -1=4n ·2n -1=n ·2n +1,当n 为偶数时,c n =(a n +1-a n )b n =(2n +1-2n +1)·2n -1=2×2n -1=2n ,则∑J12[a k +1-(-1)k a k ]b k =(c 1+c 3+c 5+…+c 2n -1)+(c 2+c 4+c 6+…+c 2n ),令T n =c 1+c 3+c 5+…+c 2n -1=1×22+3×24+5×26+…+(2n -1)·22n ,则4T n =1×24+3×26+5×28+…+(2n -1)·22n +2,所以-3T n =22+2(24+26+…+22n )-(2n -1)·22n +2=4+2×24(1-4-1)1-4-(2n -1)·22n +2,所以T n =20+(6-5)·22r29.令A n =c 2+c 4+c 6+…+c 2n =22+24+26+…+22n =4(1-4)1-4=22r2-43.所以∑J12[a k +1-(-1)k a k ]b k =T n +A n =20+(6-5)·22r29+22r2-43=8+(3-1)·22r39.方法技巧解答与奇偶项有关的求和问题的关键(1)弄清n 为奇数或偶数时数列的通项公式.(2)弄清n 为奇数时数列前n 项中奇数项与偶数项的个数.训练2[2023南京六校联考]已知数列{a n }满足a 1=1,a 2=3,数列{b n }为等比数列,且满足b n (a n +1-a n )=b n +1.(1)求数列{a n }的通项公式;(2)已知数列{b n }的前n 项和为S n ,若,记数列{c n }满足c n =,为奇数,,为偶数,求数列{c n }的前2n 项和T 2.在①2S 2=S 3-2,②b 2,2a 3,b 4成等差数列,③S 6=126这三个条件中任选一个,补充在第(2)问中,并对其求解.解析(1)因为b n (+1-a n )=+1,a 1=1,a 2=3,所以令n =1,得2b 1=b 2,又数列{b n }为等比数列,所以+1=2b n ,即数列{b n }的公比为2.则+1-a n =2,所以数列{a n }是以1为首项,2为公差的等差数列,所以a n =2n -1.(2)由(1)知数列{b n }是公比为2的等比数列.若选①,由2S 2=S 3-2得2(b 1+2b 1)=b 1+2b 1+4b 1-2,所以b 1=2,则b n =2n .若选②,由b 2,2a 3,b 4成等差数列得b 2+b 4=4a 3,即2b 1+8b 1=20,所以b 1=2,则b n =2n .若选③,由S 6=126得1(1-26)1-2=126,所以b 1=2,则b n =2n .所以c n =2-1,为奇数,2,为偶数.所以数列{c n }的奇数项是以1为首项,4为公差的等差数列,偶数项是以4为首项,4为公比的等比数列.所以2=(a 1+a 3+…+a 2n -1)+(b 2+b 4+…+b 2n )=n +(-1)2×4+4(1-4)1-4=2n 2-n +4(4-1)3.1.[命题点1]设等比数列{a n }的前n 项和为S n ,a 1=1,S 3=13.(1)求a n ;(2)若{a n }是递增数列,求数列{|a n -n -2|}的前n 项和.解析(1)设等比数列{a n }的公比为q .由题意得a 1+a 1q +a 1q 2=13,即1+q +q 2=13,解得q =3或q =-4.故a n =3n -1或a n =(-4)n -1.(2)由(1)知,a n =3n -1.令b n =|a n -n -2|=|3n -1-n -2|.由3n -1-n -2≥0,得3n -1≥n +2,所以n ≥3.由3n -1-n -2<0,得n ≤2,即n =1,2.设数列{|a n -n -2|}的前n 项和为T n ,则T n =b 1+b 2+b 3+…+b n .当n =1时,T 1=b 1=2;当n =2时,T 2=b 1+b 2=3;当n ≥3时,T n =3+9(1-3-2)1-3-(-2)(r7)2=3-2-5r112.T 1不满足上式,T 2满足上式.综上,T n ≥2.2.[命题点2/2023合肥一中诊断]在等比数列{a n }中,已知a 2=4,a 5=32.(1)求数列{a n }的通项公式;(2)若b n =(-1)n ·log 2a n ,求数列{b n }的前n 项和S n .解析(1)设{a n }的公比为q ,则1=4,14=32,解得1=2,=2,所以数列{a n }的通项公式为a n =2×2n -1=2n .(2)由(1)得b n =(-1)n ·log 2a n =(-1)n ·n ,所以数列{b n }的前n 项和S n =-1+2-3+4-5+6-7+8-…+(-1)n ·n ,当n 为偶数时,S n =-1+2-3+4-5+6-7+8-…+n =2;当n 为奇数时,S n =-1+2-3+4-5+6-7+8-…-n =-12-n =-r12.所以S n r12,为奇数,为偶数.3.[命题点2/2023江苏南京外国语学校、金陵中学三模]已知正项数列{a n }满足a 1=1,r12-2=8n .(1)求{a n }的通项公式;(2)记b n =a n sin π2,数列{b n }的前n 项和为S n ,求S 2023.解析(1)对任意的n ∈N *,r12-2=8n ,当n ≥2时,2=(2--12)+…+(22-12)+12=8(n -1)+…+8×1+1=8[1+2+3+…+(n -1)]+1=8×(-1)2+1=(2n -1)2,因为a n>0,所以a n=2n-1.当n=1时,a1=1符合a n=2n-1,所以a n=2n-1,n∈N*.(2)b n=a n sin(2·π)=(-1)n+1(2n-1),所以当k∈N*时,b2k+b2k+1=-(4k-1)+4k+1=2,故S2023=b1+(b2+b3)+(b4+b5)+…+(b2022+b2023)=1+2×1011=2023.学生用书·练习帮P3131.[2024广州市培英中学校考]若等差数列{a n}的前n项和为S n,且满足S4043>0,S4044<0,对任意正整数n,都有|a n|≥|a m|,则m的值为(C)A.2020B.2021C.2022D.2023解析依题意知S4043=4043(1+4043)2=4043a2022>0,所以a2022>0,又S4044=4044(1+4044)2<0,即a1+a4044<0,所以a2022+a2023<0,则a2023<0,且|a2022|<|a2023|,所以等差数列{a n}是递减数列,a1>a2>…>a2021>a2022>0>a2023>a2024>…,所以对任意正整数n,都有|a n|≥|a m|,则m=2022.故选C.2.[2024福建模拟]如图,九连环是中国从古至今广为流传的一种益智玩具.在某种玩法中,按一定规则移动圆环,用a n表示解下n(n≤9,n∈N*)个圆环所需的最少移动次数,数列{a n}满足a1=1,且a n=2-1,为偶数,2-1+1,为奇数,则解下5个圆环所需的最少移动次数为(C)A.5B.10C.21D.42解析由a1=1,a n=2-1,为偶数,2-1+1,为奇数,得a5=2a4+1=4a3+1=4(2a2+1)+1=8a2+5=16a1+5=21.3.[多选/2024江西抚州模拟]已知数列{a n}满足a n+a n+1=2×(-1)n,n∈N*,且a5=1,则下列表述正确的有(BD)A.a1=-5B.数列{a2n-1}是等差数列C.数列{|a n|}是等差数列D.数列{1r1}的前n项和为14-49解析由a n +a n +1=2×(-1)n ,得r1(-1)r1-(-1)=-2,所以数列{(-1)}是公差为-2的等差数列,所以(-1)=5(-1)5+(n -5)×(-2),即a n =(2n -9)×(-1)n +1.对于选项A ,a 1=(2×1-9)×(-1)1+1=-7,故选项A 不正确;对于选项B ,因为a 2n -1=4n -11,a 2n +1-a 2n -1=4(n +1)-11-(4n -11)=4,故{a 2n -1}是公差为4的等差数列,故选项B 正确;对于选项C ,|a n |=|2n -9|,则|a 3|=3,|a 4|=|a 5|=1,所以{|a n |}不是等差数列,故选项C 不正确;对于选项D ,1r1=1[(2-9)×(-1)r1]×[(2-7)×(-1)r2]=-12(12-9-12-7),所以{1r1}的前n 项和S n =-12(1-7-1-5+1-5-1-3+…+12-9-12-7)=14-49,故选项D 正确.故选BD.4.[多选/2024浙江模拟]已知数列{a n }满足a 1=1,a 2=2,a 3=3,且对任意的正整数m ,n ,都有a 2m +a 2n =2a m +n +|m -n |,则下列说法正确的有(ABD )A.a 4=5B.数列{a 2n +2-a 2n }是等差数列C.a 2n =3n -1D.当n 为奇数时,a n =2+34解析由题意知a 1=1,a 2=2,a 3=3,令m =1,n =2,得a 2+a 4=2a 3+1,解得a 4=5,故A 正确.此时a 4-a 2=3,令m =n +2,得a 2n +4+a 2n =2a 2n +2+2,从而(a 2n +4-a 2n +2)-(a 2n +2-a 2n )=2,所以数列{a 2n +2-a 2n }是以3为首项,2为公差的等差数列,故B 正确.所以a 2n +2-a 2n =3+2(n -1)=2n +1,所以a 2n -a 2=(a 2n -a 2n -2)+(a 2n -2-a 2n -4)+…+(a 4-a 2)=(2n -1)+(2n -3)+…+3=(-1)(2r2)2=n 2-1,所以a 2n =n 2+1,故C 错误.令m =n +1,得a 2n +2+a 2n =2a 2n +1+1,所以a 2n +1=2r2+2-12=n 2+n +1,令k =2n +1,则k 为奇数,则a k =(-12)2+-12+1=2+34,又a 1=1适合上式,所以当n 为奇数时,a n=2+34,故D 正确.故选ABD.5.[2024南京市学情调研]记S n 为数列{a n }的前n 项和,已知a n 为奇数,为偶数,则S 8=169.解析当n为奇数时,a n=2(r2)=1-1r2,当n为偶数时,a n=a n-1,∴S8=2(a1+a3+a5+a7)=2(1-13+13-15+15-17+17-19)=2(1-19)=169.6.[2024重庆八中校考]在数列{a n}中,a1=8,a4=2,且满足a n+2-2a n+1+a n=0(n∈N*).(1)求数列{a n}的通项公式;(2)设T n=|a1|+|a2|+…+|a n|,求T15的值.解析(1)∵a n+2-2a n+1+a n=0,∴a n+2-a n+1=a n+1-a n,∴数列{a n}是等差数列.设{a n}的公差为d,∵a1=8,a4=2,∴d=4-14-1=-2,∴a n=a1+(n-1)d=10-2n,n∈N*.(2)设数列{a n}的前n项和为S n,则由(1)可得,S n=8n+(-1)2×(-2)=9n-n2,n∈N*.由(1)知a n=10-2n,令a n=0,得n=5,当n>5时,a n<0,则T15=|a1|+|a2|+…+|a15|=a1+a2+…+a5-(a6+a7+…+a15)=S5-(S15-S5)=2S5-S15=2×(9×5-25)-(9×15-152)=130.7.[2023广州市二检]设S n是数列{a n}的前n项和,已知a3=0,a n+1+(-1)n S n=2n.(1)求a1,a2;(2)令b n=a n+1+2a n,求b2+b4+b6+…+b2n.解析(1)由a n+1+(-1)n S n=2n,得a2-S1=2,a3+S2=4,即a2-a1=2,a3+a1+a2=4.又a3=0,所以a1=1,a2=3.(2)当n=2k(k∈N*)时,a2k+1+S2k=22k①,当n=2k-1(k∈N*)时,a2k-S2k-1=22k-1②,①+②得a2k+1+a2k+S2k-S2k-1=22k+22k-1,得a2k+1+2a2k=3×22k-1.因为b n=a n+1+2a n,所以b2+b4+b6+…+b2n=(a3+2a2)+(a5+2a4)+(a7+2a6)+…+(a2n+1+2a2n)=3×2+3×23+3×25+…+3×22n-1=3×2×(1-4)1-4=22n+1-2.。
线径电流对照表

1、综述铜芯线的压降与其电阻有关,其电阻计算公式:20℃时:17.5÷截面积(平方毫米)=每千米电阻值(Ω)75℃时:21.7÷截面积(平方毫米)=每千米电阻值(Ω)其压降计算公式(按欧姆定律):V=R×A线损是与其使用的压降、电流有关。
其线损计算公式:P=V×AP-线损功率(瓦特)V-压降值(伏特)A-线电流(安培)2、铜芯线电源线电流计算法1平方毫米铜电源线的安全载流量--17A。
1.5平方毫米铜电源线的安全载流量--21A。
2.5平方毫米铜电源线的安全载流量--28A。
4平方毫米铜电源线的安全载流量--35A6平方毫米铜电源线的安全载流量--48A10平方毫米铜电源线的安全载流量--65A。
16平方毫米铜电源线的安全载流量--91A25平方毫米铜电源线的安全载流量--120A。
单相负荷按每千瓦4.5A(COS&=1),计算出电流后再选导线。
3、铜芯线与铝芯线的电流对比法2.5平方毫米铜芯线等于4平方毫米铝芯线4平方毫米铜芯线等于6平方毫米铝芯线6平方毫米铜芯线等于10平方毫米铝芯线<10平方毫米以下乘以五>即: 2.5平方毫米铜芯线=<4平方毫米铝芯线×5>20安培=4400 瓦; 4平方毫米铜芯线=<6平方毫米铝芯线×5>30安培=6600 瓦;6平方毫米铜芯线=<10平方毫米铝芯线×5>50安培=11000 瓦土方法是铜芯线1个平方1KW,铝芯2个平方1KW.单位是平方毫米就是横截面积(平方毫米)电缆载流量根据铜芯/铝芯不同,铜芯你用2.5(平方毫米)就可以了其标准:0.75/1.0/1.5/2.5/4/6/10/16/25/35/50/70/95/120/150/185/240 /300/400...还有非我国标准如:2.0铝芯1平方最大载流量9A,铜芯1平方最大载流量13.5A二点五下乘以九,往上减一顺号走。
洪铭s一25一24接线法

洪铭s一25一24接线法
输入:"N"接电源零线,"L"接电源火线(相线);开关电源一般输入为单相交流220V的。
输出:“24+”(V+)为输出正极,“24-”(V-)为输出负极。
“GND"为接地端。
注意不能接反!输出为DC24v直流电。
s-25-24开关电源型号含义:25指的是额定输出功率,24指的是输出直流电源电压。
左边第一、二个接线柱L、N:ACINPUT,交流电输入端,分别接交流电的火线和零线;
左边第三个接线柱:GND,接地线,
左边第四、五、六个接线柱:均为COM,DCOUTPUTV-,直流输出端,作为直流电压输出端的负极;
左边第七、八、九个接线柱:均为+V,DCOUTPUTv+,直流输出端,作为直流电压输出端的正极;
左边第十个接线柱:+VADJ,+-10%ADJUSTABLEA,电压调节,用于调节直流电压的值。
小学奥数举一反三A版(六年级)

3�3.75×735�3/8×5730�16.2×62.5
-4-
六年级数学奥数培训资料
第 3 讲 简便运算�二�
一、知识要点 计算过程中�我们先整体地分析算式的特点�然后进行一定的转化�创造条件运用乘 法分配律来简算�这种思考方法在四则运算中用处很大。 二、精讲精练 【例题 1】计算�1234�2341�3412�4123 【思路导航】整体观察全式�可以发现题中的 4 个四位数均由数 1�2�3�4 组成� 且 4 个数字在每个数位上各出现一次�于是有 原式�1×1111�2×1111�3×1111�4×1111 ��1�2�3�4�×1111 �10×1111 �11110 练习 1� 1�23456�34562�45623�56234�62345 2�45678�56784�67845�78456�84567 3�124.68�324.68�524.68�724.68�924.68 【例题 2】计算�2 又 4/5×23.4�11.1×57.6�6.54×28 【思路导航】我们可以先整体地分析算式的特点�然后进行一定的转化�创造条件运 用乘法分配律来简算。所以 原式�2.8×23.4�2.8×65.4�11.1×8×7.2 �2.8×�23.4�65.4��88.8× 7.2 �2.8×88.8�88.8×7.2 �88.8×�2.8�7.2� �88.8×10 �888 练习 2�计算下面各题� 1�99999×77778�33333×66666 2�34.5×76.5�345×6.42�123×1.45 3�77×13�255×999�510 【例题 3】计算�1993×1994�1�/�1993�1992×1994� 【思路导航】仔细观察分子、分母中各数的特点�就会发现分子中 1993×1994 可变 形为 1992�1�×1994=1992×1994�1994�同时发现 1994�1 = 1993�这样就可以把原 式转化成分子与分母相同�从而简化运算。所以 原式�【�1992�1�×1994�1】/�1993�1992×1994�
2024年广东省中考数学真题(学生版+解析版)

2024年广东省中考数学真题满分120分考试用时120分钟注意事项:1. 答题前,考生务必用黑色字迹的签字笔或钢笔将自己的准考证号、姓名、考场号和座位号填写在答题卡上.用2B 铅笔在“考场号”和“座位号”栏相应位置填涂自己的考场号和座位号,将条形码粘贴在答题卡“条形码粘贴处"2. 作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上.3. 非选择题必须用黑色字迹的签字笔或钢笔作答,答案必须写在答题卡各题目指定区域内相应位置上:如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4. 考生必须保持答题卡的整洁.考试结束后,将试卷和答题卡一并交回.一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 计算—5+3的结果是()A. 2B. —2C. 82. 下列几何图形中,既是中心对称图形也是轴对称图形的是()A 6B二c .QD. —8D.3. 2024年6月6日,嫦娥六号在距离地球约384000千米外上演“太空牵手”,完成月球轨道的交会对接.数据384000用科学记数法表示为()A. 3.84xl04B. 3.84xl05C. 3.84xl06D. 38.4xl054. 如图,一把直尺、两个含30°的三角尺拼接在一起,则乙ACE 的度数为()11/三l0三�:'I'IA. 120°B . 90° 5. 下列计算正确的是()A. a 2 . a s= a 10B. a s -;-Q 2 = a 4C . 60°D . 30°C. —2a +5a =7a25D. (a ) = a 106.长江是中华民族的母亲河,长江流域孕育出藏羌文化、巴蜀文化、荆楚文化、吴越文化等区域文化.若从上述四种区域文化中随机选一种文化开展专题学习,则选中“巴蜀文化”的概率是()1 1 3A.—B.—C.—D. —4 3 47.完全相同的4个正方形面积之和是100,则正方形的边长是()A.2B.5C.10D.208.若点(0,Y1),(1, Y2),(2,Y3)都在二次函数y=x2的图象上,则()A.Y3 > Y2 > Y1B.Y2 > Y1 > Y3C.Y1 > Y3> Y2D.Y3 > Y1 > Y22 39.方程=-的解为()X—3 XA.x=3B.X=-9C.x=9D.X=—310.已知不等式kx+b<O的解集是x<2,则一次函数y= kx+b的图象大致是()y,321A.B.I 2 3 xy,321霆3 ,y3,y-2-3D.3.x -3-2-10-1-2-3_、填空题:本大题共5小题,每小题3分,共15分.11.数据2,3, 5, 5, 4的众数是12.关千x的不等式组中,两个不等式的解集如图所示,则这个不等式组的解集是2 -1 fl I13.若关千X的一元二次方程x2+2x+c=O有两个相等的实数根,则c=a 314.计算:- =a-3 a-315.如图,菱形A BCD的面积为24,点E是AB的中点,点F是BC上的动点若D BEF的面积为4,则图中阴影部分的面积为I三、解答题(一):本大题共3小题,每小题7分,共21分.1 16. 计算:2°X-—+✓4-3-13 17. 如图,在AB C 中,乙C=90°.(1)实践与操作:用尺规作图法作乙A的平分线AD交BC 千点D (保留作图痕迹,不要求写作法)(2)应用与证明:在(1)条件下,以点D 为圆心,DC 长为半径作D . 求证:AB 与D 相切.18. 中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图是矩形PQ MN 充电站的平面示意图,矩形A BCD 是其中一个停车位.经测量,缰Q =60°,AB=5.4m , CE=l.6m , GH _l_CD, GH是另一个车位的宽,所有车位的长宽相同,按图示并列划定.,(`,I l,r ·1-` .tI凡根据以上信息回答下列问题:(结果精确到O .lm,参考数据✓3:::::1.73)(1)求PQ 的长;(2)该充电站有20个停车位,求P N 的长.四、解答题(二):本大题共3小题,每小题9分,共27分.19. 端午假期,王先生计划与家人一同前往景区游玩,为了选择一个最合适的景区,王先生对A、B 、C三个景区进行了调查与评估.他依据特色美食、自然风光、乡村民宿及科普基地四个方面,为每个景区评分(10分制).三个景区的得分如下表所示:景区特色美食自然风光乡村民宿科普基地A687 9B 7 7 87C886 6(1)若四项所占百分比如图所示,通过计算回答:王先生会选择哪个景区去游玩?(2)如果王先生认为四项同等重要,通过计算回答:王先生将会选择哪个景区去游玩?(3)如果你是王先生,请按你认为各项“重要程度”设计四项得分的百分比,选择最合适的景区,并说明理由.20. 广东省全力实施“百县千镇万村高质量发展工程", 2023年农产品进出口总额居全国首位,其中荔枝鲜果远销欧美.某果商以每吨2万元价格收购早熟荔枝,销往国外.若按每吨5万元出售,平均每天可售出100吨.市场调查反映:如果每吨降价1万元,每天销售量相应增加50吨.该果商如何定价才能使每天的“利润”或“销售收入“最大?并求出其最大值.(题中“元”为人民币)21. 综合与实践【主题】滤纸与漏斗【素材】如图1所示:少一张直径为10cm的圆形滤纸;@一只漏斗口直径与母线均为7cm的圆锥形过滤漏斗.�7cm叶图l【实践操作】步骤1:取一张滤纸;步骤2:按如图2所示步骤折叠好滤纸;步骤3:将其中一层撑开,围成圆锥形;步骤4:将围成圆锥形滤纸放入如图1所示漏斗中.气_芍c 厂。
12 第11次课(第6章:水流挟沙力)

15
y
4、水流挟沙力的数学表达式
u h s y a
h
距床面y处单位时间、单位断 面面积上通过的悬移质沙量 为u×S
悬移质单宽输沙率数学表达式为 如果上式含沙量用 水流挟沙力表示
h
sa
h
g s u Sdy s uSv dy
a a
h
1 g s uS* dy S* h udy S* hU S* q ha a
AUJ 1 Sv AUJ s s Sv AUJ s C1 s ASv
展开,整理能量平衡方程式
U J J s s S v UJ s C 1 s S v
略去等号左侧相对微小项,则得
Sv
U J J s C 1 s
10
6、床沙质和冲泻质的划分
方法1:若在床沙级配曲线右端P<10%的范围内,如果存在明 显的拐点,也可取这一拐点相应的床沙粒径作为床沙质与冲泻 质的分界粒径。 方法2:将悬移质粒配曲线与相应的床沙粒配曲线进行对比, 取床沙粒配曲线上与纵坐标5%相对应的粒径,作为床沙质 与冲泻质的分界粒径。
11
7、床沙质和冲泻质的区别
此处C1及α分别为正值无量纲系数及指数 所以
E C1 s ASv
22
6、张瑞瑾水流挟沙力公式
(2) 公式推导
c、能量平衡方程式的简化
1 Sv AUJ s s Sv AUJ s AUJ E
E C1 s ASv
(6-26)
s
U3 Sv c agR
m
(6-29)
PP-R_管件名称型号规格

PPR管配件名称型号规格PPR管:作为一种新型的水管材料,PPR管具有得天独厚的优势,它既可以用作冷管,也可以用作热水管,由于其无毒、质轻、耐压、耐腐蚀,正在成为一种推广的材料。
也适用于热水管道,甚至纯净饮用水管道。
PPR管的接口采用热熔技术,管子之间完全融合到了一起,所以一旦安装打压测试通过,而且PPR管不会结垢PP-R管件,采用优质原料注塑而成,产品各项性能均达到或超过国家标准GB/T18742的规定指标。
还具有以下特有的设计和工艺优势:●采用大弧度弯位设计,能有效地减少水锤的形成,杜绝管震现象发生。
●采用45度倒角设计,使熔接更轻松。
产品名称型号规格说明等径直通S20两端接相同规格的PP-R管。
例:S20表示两端均接20PP-R管。
S25S32异径直通S25*20两端接不同规格的PP-R管。
例:S25*20表示一端接25PP-R管,另一端接20PP-R管。
S32*20S32*25堵头D20用于相关规格PP-R管的封堵。
例:D20表示接20PP-R管。
-D25D32等径弯头(90°)L20两端接相同规格的PP-R管。
例:L20表示两端均接20PP-R管。
L25L32等径弯头(45°)L20(45°)两端接相同规格的PP-R管。
例:L20*20(45°)表示两端均接20PP-R管。
L25(45°)L32(45°)异径弯头F12-L25*20两端接不同规格的PP-R管。
例:L25*20表示一端接25PP-R管,另一端接20PP-R管。
F12-L32*20F12-L32*25等径三通T20三端接相同规格的PP-R管。
例:T20表示三端均接20PP-R管。
T25T32异径三通T25*20三端均接PP-R管,其中一端变径。
例:T25表示两端均接25PP-R管,中间接20PP-R管。
T32*20T32*25过桥弯W20两端接相同规格的PP-R管。
(完整版)化学元素周期表(高清)
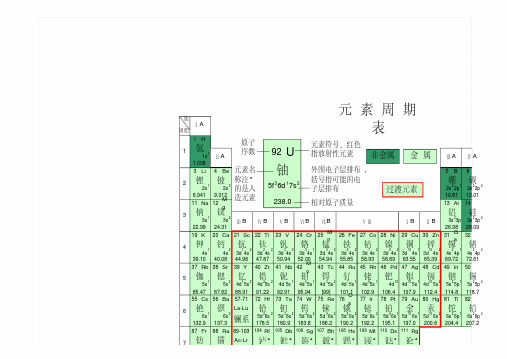
1H3Li4Be5B611Na 12Mg13Al 1419K 20Ca 21Sc 22Ti23V24Cr25M n26Fe 27Co 28Ni29Cu 30Zn 31Ga3237Rb 38Sr 39Y40Zr41Nb 42Mo43Tc44Ru 45Rh 46Pd 47Ag 48Cd 49In5055Cs 56Ba 72Hf 73Ta 74W75Re 76Os77Ir78Pt79Au 80Hg 81Tl8287Fr 88Ra 104Rf 105Db 106Sg 107Bh 108Hs 109Mt 110Ds 111Rg元 素 周 期表氢1s11.008锂铍硼碳2s12s22s 22p12s 22p26.9419.01210.8112.01钠镁铝硅3s13s23s 23p3s 23p222.9924.3126.9828.09钾钙钪钛钒铬锰铁钴镍铜锌镓锗4s14s23d 14s23d 24s23d 34s23d 54s13d 54s23d 64s23d 74s23d 84s23d 104s13d 104s24s 24p14s 24p239.1040.0844.9647.8750.9452.0054.9455.8558.9358.6963.5565.3969.7272.61铷锶钇锆铌钼锝钌铑钯银镉铟锡5s15s24d 15s24d 25s24d 5s14d 55s14d 55s24d 75s14d 85s14d104d 105s14d 105s25s 25p15s 25p285.4787.6288.9191.2292.9195.94[99]101.1102.9106.4107.9112.4114.8118.757-71铯钡La-Lu铪钽钨铼锇铱铂金汞铊铅6s16s25d 26s25d 36s25d 46s25d 56s25d 66s25d 76s25d 96s15d 106s15d 106s26s 26p16s 26p2132.9137.3178.5180.9183.8186.2190.2192.2195.1197.0200.6204.4207.289-103钫镭Ac-Lr1234567镧系周期族ⅠAⅡA ⅢBⅣBⅤB ⅥB ⅦB ⅠB ⅡBⅤⅢⅢA ⅣA U92铀5f 36d 17s 2238.0相对原子质量元素符号,红色指放射性元素外围电子层排布,括号指可能的电子层排布原子序数元素名称注*的是人造元素非金属金属过渡元素杜钅钅卢钅喜钅波钅钅钅钅黑麦达仑********57La 58Ce 59Pr 60Nd 61Pm62S m63Eu 64G d65Tb 66Dy 67Ho 68Er69T m7089Ac 90Th 91Pa 92U93Np 94Pu 95Am96C m97Bk 98Cf99Es 100Fm101M d1027s17s2(6d 27s 2)(6d 37s 2)(6d 47s 2)(6d 57s 2)(6d 67s 2)[223]226.0[261][262][263][262][265][266][269][272]镧铈镨钕钷钐铕钆铽镝钬铒铥镱5d 16s24f 15d 16s4f 36s24f 46s24f 56s 24f 66s24f 76s24f 75d 16s4f 96s24f 106s24f 116s24f 126s24f 136s24f 146s2138.9140.1140.9144.2[147]150.4152.0157.3158.9162.5164.9167.3168.9173.0锕钍镤铀镎钚镅锔锫锎锿镄钔锘6d 17s26d 27s25f 26d 17s 5f 36d 17s 5f 46d 17s5f 67s25f 77s25f 76s 17s5f 97s25f 107s25f 117s25f 127s2(5f 137s2(5f 147s2227.0232.0231.0238.0237.0[244][243][247][247][251][252][257][258][259]7镧系锕系锕系杜钅钅卢钅喜钅波钅钅钅钅黑麦达仑****************电子层2HeC 7N8O9F10NeSi15P16S17Cl18ArG e33As 34Se 35Br36KrSn 51Sb 52Te 53I54Xe Pb 83Bi84Po 85At86Rn 0氦1s24.003碳氮氧氟氖2s 22p22s 22p32s 22p42s 22p52s 22p612.0114.0116.0019.0020.18硅磷硫氯氩3s 23p23s 23p33s 23p43s 23p53s 23p628.0930.9732.0735.4539.95锗砷硒溴氪4s 24p24s 24p34s 24p44s 24p54s 24p672.6174.9278.9679.9083.80锡锑碲碘氙5s 25p25s 25p35s 25p45s 25p55s 25p 6118.7121.8127.6126.9131.3铅铋钋砹氡6s 26p26s 26p36s 26p46s 26p56s 26p6207.2209.0[209][210][222]ⅣAⅤA ⅥA ⅦA 0族电子数KLM N O PK L M N OKL M N K L M KL K 281832188281818828188288282注:Yb 71LuNo 103Lr镱镥4f146s 24f 145d 16173.0175.0锘铹5f 147s2(5f 146d 17s2)[259][260]注:1.相对原子质量录自1995年国际原子量表,并全部取4位有效数字。
进给量(F值)的计算

1,切削量(Fz值)的计算Fz=F/(S*Z)F:进给量(/分) S:转速(rpm) Z:刃数Fz:(实际每刃进给)例题.一标准5刃立铣刀以S100转/分速度切削工件,拖板的进给量(F值)是600mm/分,求Fz实际每刃切削量就是Fz=F/(S*Z)F=600/(100*5)F=1.2(mm/转)2,切削线速度=主轴转速S*3.14/刀具直径刀具进给F=主轴转速S*刃数*每刃进给切削的线速度根据接触部位不同而不同其中S是主轴转速,单位是转/分,F是刀具进给,单位是毫米/分,Vs是切削线速度,单位是米/分3.切削速度的计算Vc=(π*D*S)/1000 Vc:线速度(m/min) π:圆周率(3.14159) D:刀具直径(mm)S:转速(rpm)例题. 使用Φ25的铣刀Vc为(m/min)25 求S=?rpmVc=πds/100025=π*25*S/1000S=1000*25/ π*25S=320rpm4.进给量(F值)的计算F=S*Z*FzF:进给量(mm/min) S:转速(rpm) Z:刃数Fz:(实际每刃进给)例题.一标准2刃立铣刀以2000rpm)速度切削工件,求进给量(F值)为多少?(Fz=0.25mm)F=S*Z*FzF=2000*2*0.25F=1000(mm/min)上图为常见数控刀具各规格的Vs和每刃进给等参数,传统和高速加工中心机参数有所不同,仅供参考,实际要依机床和刀具性能、以及加工材质、加工量、加工工艺等灵活对待。
切削用量——进给量的计算公式进给量有进给速度V f、每转进给量f和每齿进给量f Z3种表示方法。
进给速度V f是单位时间内工件与铣刀沿进给方向的相对位移,单位为mm/min,在数控程序中的代码为F。
每转进给量f是铣刀每转一转,工件与铣刀的相对位移,单位为mm/r。
每齿进给量f Z是铣刀每转过一齿时,工件与铣刀的相对位移,单位为mm/z。
其3种进给量的关系为:V f=f·n=f Z·z·n铣刀转速为n,铣刀齿数为z。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.43 3.57
2.99 4.72 1.90
0.68 1.64 0.97
98.00 78 98
4.29
2.71
2.37 0.62
1.06 0.53
0.73 0.25
1.47 0.30
2.85 0.35
3.36 0.90
0.62 0.24
3.72
2.14
0.61
0.50
0.28
0.37
1.02
1.03
2780.16 13.69 12.71 83.57 16.61 根据25%浓缩4倍,计算添加量时按全价料中添加的四倍 考察赖氨酸+蛋氨酸 苏氨酸和赖氨酸比例
EE(%)
3.50 4.00
CF(%)
1.60 6.80
Ca(%)
0.02 0.10
P(%)
0.27 0.93
AP(%)
0.12 0.24
Nacl(%)
13.01 10.54 15.06 35.15
89.00 90.00 12.55 99.00
46.00 60.00 90.10
94.00 58.00 72.00
13.20 13.39
11.63 12.86
76.08 88.00
41.18 17.80
先调固定值,氯化胆碱,预混料,食盐 再调蛋白 先调磷再调钙 调好的值就不要动了,最好大数为整 调完配方再看成本,降低成本可以通过替代饲料原料
Arg(%)
0.37 0.88
Lys(%)
0.23 0.53
Met(%)
0.15 0.12
1.50 4.90 63.50 98.00
3.30 0.50 5.40
0.34 4.04 1.00 21.00 35.84
0.65 2.90 0.07 16.00
0.22 2.90 0.44 16.00
2.50 0.17
790.00 40.00 15.00 20.00 27.00 38.00 14.00 10.00 2.00 4.00 40.00 1000.00
4.00 10.00 4.5 7.50 2.60 0.13 1.00 8.00 28.00 17 5.00 10.0 4400.6 标准
15.06 12.55 4.50 36.61
0.73 0.52 1.42
0.96
0.00 0.00 0.00 0.00 0.00 98.00
1.85 2.57 2.08
0.65 0.70 0.36
0.03 1.15 0.02 0.18 0.06 39.50
0.05 0.61
0.28 0.16
20.50 0.94 0.35 0.15 0.11
0.51
配方名称:25%仔猪浓缩料配方(8-20kg)
原料名称
玉米 小麦麸
蛋白42
DE(MJ/kg) ME(MJ/kg)
14.18 9.33 13.39 8.66
kg/t
成本(¥)
2.30 1.40
DM(%)
86.00 87.00
CP(%)
8.00 14.30
去皮豆粕 进口鱼粉 玉米蛋白粉 豆油 磷酸氢钙 石粉 食盐 赖氨酸(98%) 蛋氨酸(98%) 苏氨酸 氯化胆碱(50%) 仔猪预混料1%) 合计 全价料
0.19
0.18
0.27
0.19
4.33
1.73
0.47 0.02 59.00
0.80 2.06 0.01
98
0.00 0.00
12.7 1.79 0.58 0.55 0.16 0.63 0.12 0.95 0.10 0.33 0.04 16.25 0.24 0.40 0.10
0.62 0.36
1.21 0.51
0.27
0.53
0.67 0.65
0.27
料中添加的四倍
Cys(%)
0.15 0.24
M+C
0.30 0.36 1.41 2.16
Thr(%)
0.29 0.39
Trp(%)
0.06 0.18
Na(%)
0.02 0.07Fra bibliotekcl(%)
0.04 0.07
Mg(%)
0.12 0.47
K(%)
0.30 1.19
亚油酸 (%)
2.20 1.70
