高频已实现波动率
已实现波动与日内价差条件下的CVaR估计

的C a V R预 测 效 果 更 好 .
关键词 :C p l; oua “已实现 ” 波动 率 ;日内价 差 ; V R C a 中图分类号 : 805 ; 2 13 文献标识码 : 文章编号 : 07— 87 2 1 )8 06 2 F 3.9 0 1 . A 10 9 0 (02 0 — 0O一1 等 则给 出了 应 用 B o t p方 法 的 V R估 计 方 otr sa a
计 方法 . 该方 法 是针 对 高频 时 间序 列而 开 发 的全
于 G R H 模 型 的参 数估 计 方 法 ,a A C Fn和 G 则 u 给 出了基 于半 参 数 方 法 的 V R估 计 方 法 , nl a Eg e 和 Magnll 应 用 分 位 点 回 归 的 思 想 给 出 了 naei l6
V R的度量方 法 , 进行 预测效 果 的检验 . a 并
近年来 , 于存 储 技 术 和 计 算 技 术 的进 步 , 由 “ 高频 ” 金融数 据越 来越 容 易 获得 , 多学 者 就 日 许
内数据 的基 本特征 进行 了大量 研 究 , aoon ¨ D erga
V R估 计 方 法 的 系 a
新 的波 动率 度量 方 法 . 这 种 动 率度 量 方 法 中 在
【国家社会科学基金】_高频数据_基金支持热词逐年推荐_【万方软件创新助手】_20140804

推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
科研热词 研究前沿 知识图谱 沪深300股指期货 可视化分析 高频数据 高频作者 风险值 风险价值 非对称市场冲击 雷曼危机 防碰撞算法 门限预平均实现波动 跳跃显著性检验 跳跃扩散过程 跳跃性波动 跳跃 货币政策 贡献度测算 评价指标体系 股票市场 综述 组合协方差 等风险比例投资组合 稳健分析 科学发展 研究趋势 研究热点 波动率 模型参数 核拟合优度统计量 标签 操作风险 指标体系 拓扑数据模型 情报学 总损失额分布 平均超出量函数图 帧时隙 市场微观结构 已实现波动率 就业质量 小波变换 定量分析 女大学生 大额交易 噪声 品牌生态 分位数回归 全口径评价 保险 价格发现机制 人的全面发展评价
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29
科研热词 风险管理 风险度量 风险价值 隐性手段 跳跃成分 语类 订单差 股价冲击 科技评价指标 科技评价体系 科学发展 甲骨文 流动性 波动率预测 波动率反馈效应 殷商汉字 杠杆效应 期货市场 显性手段 指标体系 态度立场 市场态势 字频 因果关系测量 交易量变化 中国股市波动率 中介语 mcmc方法 c_tz统计量
波动率

波动率研究一、波动率概念波动率是金融资产价格的波动程度,是对资产收益率不确定性的衡量,用于反映金融资产的风险水平。
波动率越高,金融资产价格的波动越剧烈,资产收益率的不确定性就越强;波动率越低,金融资产价格的波动越平缓,资产收益率的确定性就越强。
二、波动率的分类1、隐含波动率隐含波动率是将市场上的权证交易价格代入权证理论价格模型,反推出来的波动率数值。
从理论上讲,要获得隐含波动率的大小并不困难。
由于期权定价模型(如BS模型)给出了期权价格与五个基本参数(标的股价、执行价格、利率、到期时间、波动率)之间的定量关系,只要将其中前4个基本参数及期权的实际市场价格作为已知量代入定价公式,就可以从中解出惟一的未知量,其大小就是隐含波动率。
因此,隐含波动率又可以理解为市场实际波动率的预期。
2、历史波动率历史波动率是指投资回报率在过去一段时间内所表现出的波动率,它由标的资产市场价格过去一段时间的历史数据(即St的时间序列资料)反映。
这就是说,可以根据{St}的时间序列数据,计算出相应的波动率数据,然后运用统计推断方法估算回报率的标准差,从而得到历史波动率的估计值。
显然,如果实际波动率是一个常数,它不随时间的推移而变化,则历史波动率就有可能是实际波动率的一个很好的近似。
3、预测波动率预测波动率又称为预期波动率,它是指运用统计推断方法对实际波动率进行预测得到的结果,并将其用于期权定价模型,确定出期权的理论价值。
因此,预测波动率是人们对期权进行理论定价时实际使用的波动率。
这就是说,在讨论期权定价问题时所用的波动率一般均是指预测波动率。
需要说明的是,预期波动率并不等于历史波动率,因为前者是人们对实际波动率的理解和认识,当然,历史波动率往往是这种理论和认识的基础。
除此之外,人们对实际波动率的预测还可能来自经验判断等其他方面。
4、已实现波动率已实现波动率是针对频率较高的数据计算的一种波动率,又称为日内波动率或高频波动率。
高频数据是指以小时、分钟或秒为采集频率的数据。
我国股市“已实现”波动率最优频率选取研究

() t表示 瞬时波动 率 , 假定 和维纳过 程 w() 且 t独立 。积分波 动率定
rt l +
义 :  ̄s 为I J r ) V 2 (
为 了 对 日 内数 据 进 行 建 模 , 先 假 定 在 t 易 E , 易 价 格 数 首 交 t交 据 是 离 散 的 。 用 , 1 ,… ,t 示 第 t 易 日 的 第 i 交 易 价 格 r表 t 交 个 数 据 是 第 t 易 日所 观 测 的 数 据 总 数 。 以 定 义 “ 实 现 ” 动 交 可 已“ 已实现’ ’ 波动率最优频 率选取研 究
口 罗 意
摘要 : 年来 , 着高频数 据 的可 获取 , 近 随 已实现 波动 率成 为金
融研 究 领 域 的 热 点 . 抽 样 频 率 的 选 择 对 准 确 估 计 已 实现 波 动 率 而
至 关 重 要 最 优 抽 样 频 率 理 论 上 应 能 较 好 的 平 衡 测 量 误 差 和 微 观
来 建 模 和 预 测 . 通 常 需 要 进 行 复 杂 的 参 数 估 计 。 来 来 , 着 计 这 近 随 算 工 具 和 计 算 方 法 的 改 进 以 及 数 据 记 录 和 存 储 成 本 的 降 低 , 融 金 领 域 的 数 据 开 始 以越 来 越 精 细 的 时 间 刻 度 来 收 集 . 得 金 融 高 频 使
误 差
率为金 融资 产 日内高频 收益率 的平方 和 :
R L( v ∑r 1 .)
i: 0
1 引 言 .
其 中 Fl 一 1
为 日 内高 频 收 益 率 。
波 动 率 是 金 融 衍 生 工 具 定 价 、 资 组 合 构 建 以 及 金 融 风 险 管 投 理 的关键 变量 , 直是研 究 的热点 领域 。在低 频领 域一 般采 用 自 一 回 归 条 件 异 方 差 ( CH) 型 和 随 机 波 动 (v) 型 对 金 融 波 动 AR 模 s 模
[论文]高频数据波动率预测
![[论文]高频数据波动率预测](https://img.taocdn.com/s3/m/9878f7e9f605cc1755270722192e453610665bee.png)
高频数据波动率预测论文【摘要】金融市场的交易连续不断,其日内高频数据包含的信息也有一定的差别,除了考虑收盘价这一要素外,日内观测到的最高价、最低价、成交量等因素也要纳入对金融市场的分析中,这样可以获得比单独采用收盘价这一因素进行波动率研究更准确的研究结果。
一、引言随着科技进步尤其是电子计算机技术的发展,对高频数据的记录、收集、存储和操作的时间和金钱成本都大大下降,20实际90年代以来,高频数据的分析与建模得到了迅速的发展,并广泛运用与金融市场微观结构理论的实证研究中。
高频数据能精确到交易日日内分时收盘价,充分保证重要的市场信息不被丢失,使得基于高频数据估计的波动率包含更加丰富的波动信息。
高频波动率与低频波动率的特点不同,呈现出时间序列的负相关性、周期性U型日历效应和长记忆性等,而现有的基于低频数据的ARCH类或SV类模型并不能很好的描述这些统计特征。
对高频波动率的研究已经成为计量经济学领域的一个热点。
深入研究日内高频数据波动率的性质,选择合适的波动率预测模型和金融资产收益率分布来度量中国股票市场的风险,分析市场微观结构对高频波动率的影响,从而为金融机构和监管当局的风险监控提供一种有效的理论方法参考和政策建议具有重大意义。
本文通过选取沪深300指数5分钟交易数据,通过构建目前广泛用于高频数据分析的已实现波动率和已实现极差两个序列,通过R/S法计算Hurst指数,确定两个序列的长记忆性,进而对两者构建了长记忆性的ARFIMA模型,并用这一模型进行了波动率估计,再采用均方根误差和绝对平均误差两个指标对两个模型的预测结果进行了评价。
二、文献综述Engle(2000)为超高频数据或交易的建模应用提供了新的思路。
通过选取的52144条IBM股票的交易数据去为交易的时机建模并测量分析它对价格波动的影响,将ACD模型引入去估计到达比率的相关点过程,同时采用了半参数法去估计调和均数。
实证结果说明对于更长的持续期和更长的预期持续期,其波动会相应的更小。
基于高频数据的已实现波动率模型

02
高频数据概述
高频数据的定义与特点
高频数据定义
高频数据是指在短时间内(如秒、分钟、小时等)收集到的数据,其频率远 高于日度或月度数据。
高频数据特点
高频数据通常具有高分辨率、高时效性、高信息量等特点,能够揭示金融市 场的微观结构和动态变化。
高频数据在金融市场中的应用
01
02
03
交易策略
利用高频数据可以制定更 精确的交易策略,如套利 交易、做市等,从而提高 交易效率和降低风险。
06
参考文献
参考文献
参考文献1
波动率模型在金融领域的应用,作者姓名,出版年 份,期刊名称。
参考文献2
高频数据波动率建模研究,作者姓名,出版年份, 期刊名称。
参考文献3
已实现波动率模型比较研究,作者姓名,出版年份 ,期刊名称。
感谢您的观看
THANKS
研究不足与展望
已实现波动率模型在处理非线性和极端情况下的波动率时还存在一定的 局限性,需要进一步完善和改进。
高频数据的市场稳定性和数据质量对于已实现波动率模型的准确性和可 靠性具有重要影响,需要加强对于数据源和处理技术的研发和应用。
已实现波动率模型在与其他金融统计模型结合使用方面还有待进一步探 索和实践,以实现更全面和准确的金融市场分析和预测。
已实现波动率的计算
利用采集到的数据,采用适当的统计方法计算已实现波动率 。例如,可以采用平方价格变动或交易量的方法来计算已实 现波动率。
基于已实现波动率的模型构建思路
模型构建的基础
基于已实现波动率,通过引入 适当的随机过程或模型来描述 其动态特性,如波动率微笑、
波动率聚集等。
模型参数的估计
利用已实现波动率和价格数据, 采用适当的估计方法对模型的参 数进行估计。例如,可以采用最 大似然估计或矩估计等方法。
交易冲击与资产的非对称波动:基于“已实现波动率”

关键 词 : 已实现 波动 率 非对 称波 动 交 易冲 击
J L分 类 号: 3 G1 G 2 E C0 1 1
一
、
引 言
本文引入“ 已实 现 波 动率 ” ra zdvlti , 称 “ 际波 动 率 ” 来考 察 中 国股 市 A、 ( le o it 也 ei a ly 实 ) B股 的 交 易 冲击 与价格 波 动之 间 的关 系 。尽 管长 期 以来 , 资产 价格 的波动 性一 直是 金 融学 理论 与 实 务所 关 注 的 最基 本 内容 ( E ge 1 8 ) B l rl (9 6 ,hl r 18 ) 及 S h et1 8 ) 等 ) 但 如 n l(9 2 , o es v 1 8 )S ie( 9 1 以 l e l e w r( 9 9 等 , 在 近期 , 随着 计算 机运 算 能力 的提 高 以及 高频分 笔 数据 的普 及 , 学者 们逐 渐 开始 了对 “ 已实 现波 动
以及市 场交 易 活动 的关 系 。波 动与滞 后 收益 率之 间存 在着 负 相关 成为 了一 个 风格 化特 征 , 也就 这
梁 丽 珍 , 建 莆 田学 院 , 教 授 ; 茂 斌 , 外 经 贸 大 学 金 融 学 院 , 士 生 导 师 ; 东 民 , 中 科 技 大 学 经 济 学 院 , 士 生 导 福 副 王 对 硕 孔 华 硕 师 。本研究受到国家 自然科学 基金( 8 3 1)对外经 济贸易大学校科研项 目(7 O o以及华中科技大学人 文社科 青年重点项 7 oO 3、 0 0QD 1) 目 (0 70 ) 助 , 致 谢 意 。 20 0 1的资 谨
是“ 非对称 波 动效应 ” ay e cvl it e et① 在 S h et1 8 ) (smm t oa ly f c) 。 c w r 9 9 之后 , 多学者 的研究都 验证 i r ti f ( 很
【国家自然科学基金】_已实现波动率_基金支持热词逐年推荐_【万方软件创新助手】_20140801
科研热词 推荐指数 已实现波动率 9 高频数据 2 预测 2 燃油 2 波动率预测 2 波动率 2 var 2 spa检验 2 har-rv-cj模型 2 garch模型 2 garch族模型 2 dm检验 2 风险管理 1 预期不足 1 非对称性结构 1 随机波动模型 1 随机波动 1 长记忆性 1 钢材期货 1 金融风险 1 金融市场 1 量价关系 1 跳跃规模细分 1 自适应的不对称性har-d-figarch模型 1 股票信息透明度 1 股指期货 1 结构突变 1 移动窗 1 燃油期货 1 波动率度量方法 1 波动溢出 1 棉花期货 1 样本外预测 1 极差 1 极值理论 1 日历效应 1 成交次数 1 平均交易头寸 1 市场波动性 1 已实现波动率模型 1 已实现极差多幂次变差 1 已实现garch 1 宏观经济指标 1 半参数预测模型 1 区制转移 1 偏t分布 1 下侧已实现半方差 1 上证指数 1 midas模型 1 mcs检验 1 mcmc 1 har 4 5 6 7 8 9 10 11 12
2011年 科研热词 推荐指数 高频波动率 1 非对称性 1 跳跃 1 蒙特卡洛模拟 1 波动预测 1 已实现极差 1 加权已实现极差 1 分整自回归移动平均模型 1 修正的已实现门阀多次幂变差 1 交易量 1 c_tz统计量 1 "已实现"核波动 1
推荐指数 3 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
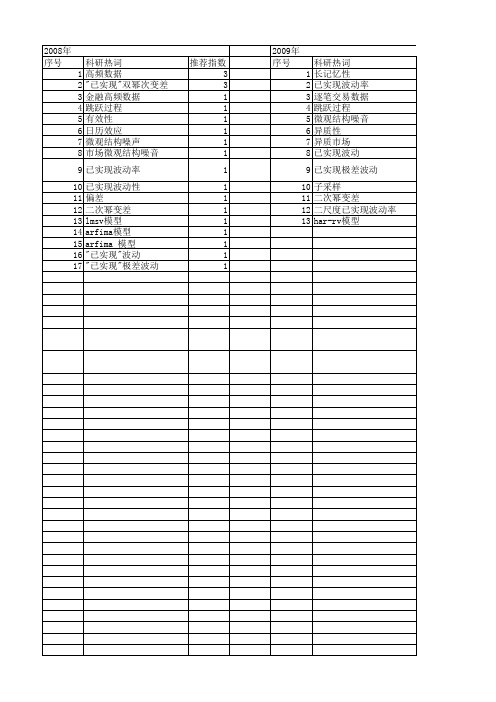
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13
科研热词 长记忆性 已实现波动率 逐笔交易数据 跳跃过程 微观结构噪音 异质性 异质市场 已实现波动 已实现极差波动 子采样 二次幂变差 二尺度已实现波动率 har-rv模型
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1
股票市场波动性研究——基于ARMA-TGARCH-M模型的实证分析

股票市场波动性研究——基于ARMA-TGARCH-M模型的实证分析刘湖;王莹【摘要】通过构建ARMA-TGARCH-M模型,并同时利用上证综合指数和深圳成份指数的低频日收益率和5分钟高频收益率数据,对中国股票市场的波动性问题进行了实证研究.结果表明:中国股票市场存在着大幅度高频率波动,市场总体风险较大,而且收益率波动也存在着波动集群性、尖峰后尾性和非对称分布等特征,深圳股票市场在各方面的特征也都比上海股票市场突出.此外,低频日收益率序列和5分钟高频收益率序列都存在着显著的平稳性、自相关性和ARCH效应,中国股票市场还存在着较长的外部冲击波动持续期,且杠杆效应显著.GARCH族模型能够很好地拟合中国股票市场的波动性问题.【期刊名称】《北京航空航天大学学报(社会科学版)》【年(卷),期】2017(030)004【总页数】11页(P56-66)【关键词】股票市场;价格波动性;ARMA-TGARCH-M模型;高频数据;风险;沪深股市【作者】刘湖;王莹【作者单位】陕西师范大学国际商学院,陕西西安 710100;陕西师范大学国际商学院,陕西西安 710100【正文语种】中文【中图分类】F830.91自深圳宝安县联合投资公司首次公开募股以来,中国的股票市场已走过30年的发展历史。
然而与西方国家发达的资本市场相比,中国的股票市场仍然很不完善,在整个中国都处于制度变迁的大背景下,在某些特定时期中还会出现频繁剧烈的波动。
而保持股票价格及收益率的相对稳定,防止股票价格的大幅度波动,是任何一个股票市场健康运行的内在要求。
因此,一直以来监管机构和各类投资者都十分关注中国股票市场的波动性特征及其影响因素,而掌握股票市场波动性的基本特征与一般规律不仅有利于监管机构的高效规范管理,更有利于各类投资者进行科学的风险防范和理性投资。
鉴于此,股票市场波动性问题研究对于揭示股票市场运行规律,促进中国股票市场健康发展有着积极的促进作用。
投资者情绪、美股波动对A 股市场波动率影响——基于TVP-VAR 模型

投资者情绪、美股波动对A 股市场波动率影响——基于TVP-VAR 模型作者:张宗强戚成飞来源:《东方论坛》 2019年第1期摘要:根据2010至2017年的月度数据,从38个投资者情绪指标中筛选出9个代理指标构造国内投资者情绪变量,并借助状态空间模型及卡尔曼滤波方法得到最终的国内投资者情绪因子。
通过TVP-VAR模型研究发现国内投资者情绪因子、美国股票市场已实现波动率和沪深300已实现波动率三者之间存在相关性。
结果表明:相关关系存在构造的国内投资者情绪可作为我国股票市场波动性的领先指标,且在牛市中的领先期数较熊市中更长;在股市剧烈波动的时期,情绪指标对我国股票市场的影响更大。
美股已实现波动率对我国股票市场的影响长期来说更显著;在我国股票市场剧烈波动的时期,美股市场的影响性较小。
关键词:投资者情绪;已实现波动率;TVP-VAR中图分类号:F832.4文献标识码:A文章编号:1005-7110(2019)01-0104-10一、引言在资本市场中,投资者的买进卖出、赢利亏损也会产生喜怒哀乐的情绪,并反过来影响投资者的交易行为。
通俗地讲,情绪就是投资者对于过往投资成果的感知,以及对后续市场的乐观或者悲观的预期。
投资者情绪是行为金融学的研究热点之一,虽然迄今为止学术界对于投资者情绪并没有统一的定义,但多数学者的研究表明投资者情绪对于投资者行为和股票市场收益率都会产生一定的影响。
从我国资本市场参与者的情况来看,相关调查数据表明2017年账户资金低于50万元的散户投资者所占比例为75.1%,散户化特征依然非常明显。
散户投资者决策随意、追涨杀跌等情绪化交易较多,对市场冲击性较强,更容易造成股票市场的剧烈波动。
因此,现阶段对于国内投资者情绪的研究依然很有意义。
另一方面,根据WIND数据库统计,截止2017年末美国股市上市公司总市值为42.6万亿美元,结合美国经济领头羊的位置,美国股市对其他地区股市的影响是举足轻重的,隔夜美股的较大波动经常给日经指数和恒生指数等带来高开或低开缺口。
基于Cornish-Fisher展开式的中国股市高频数据VaR风险实证研究

基于Cornish-Fisher展开式的中国股市高频数据VaR风险实证研究作者:易莎,胡跃红来源:《经济研究导刊》2012年第05期摘要:实际市场收益率的尾部普遍展现出比正态分布宽大的“厚尾”特征,通过Cornish-Fisher 方法修正正态分布,可使其适合股票市场的实际情况。
用沪深300指数的5分钟高频数据构造已实现波动率,来考察中国股票市场的波动特征,试图将高频金融数据的“已实现”波动率引用到基于Cornish-Fisher的VaR模型当中。
通过与正态分布假设的VaR的返回测试对比,从实证的角度论证Cornish-Fisher扩展方法在VaR估计中的有效性,基于数据特征的Cornish-Fisher扩展方法有效地改善了VaR的估值。
关键词:已实现波动率;高频数据;Cornish-Fisher;VaR中图分类号:F830.92 文献标志码:A 文章编号:1673-291X(2012)05-0161-02引言近十几年来,金融创新加速了金融衍生工具的发展,金融市场危机事件发生也越来越频繁。
异常事件发生的概率虽然很小,却常常隐含着巨大的风险。
目前,国际标准风险管理工具VaR是由J.P.Morgan投资银行在1994年的RiskMetrics系统中提出的。
传统VaR的研究核心是对金融资产收益率统计分布进行分析,利用历史信息对未来的收益分布进行预测。
但是,收益率通常并不服从事先假定分布。
一些学者开始以不假定收益率分布的方法来估计VaR值,比如Koenker和Pack(1996),[1]Engle和Manganelli(2004),[2]Taylor(2000)[3]等等。
Zangari(1996)[4]利用Cornish-Fisher展开式得到修正的VaR。
但是VaR的度量除了与分布有关,还与收益率序列的波动性有关。
由于金融市场的信息是连续影响资产价格运动过程的,所以数据频率越低,损失的信息越多。
基于高频时间序列Anaersen和Bollerslev(2001)[5] 提出了已实现波动(Realized Volatility)。
基于已实现波动率的长记忆性分析

2 1 第 5期 0 0年 ( 总第 9 9期 )
・
2 ・ 7
A FM R I A模型分别对期货 、 汇率和通胀率等不 同 若一个平稳 时间序列 { }的 k阶 自相关 函数 ( ), 即以双曲线 比率随着 时间序列 的长 记 忆性 进 行 了分 析 , 都证 实 了 波动 P k 满足 以负幂指数率 , 中存在 着 长 记忆 性 。【 ‘ 引J ,Ga 6和 V i , 3 】 i 儿 [ n rn e a 滞后 阶数 k的增 加 而 缓 慢 衰 减 下来 , p )满 g 即 (
实上证 指数的 R V序 列具有长记忆性 , 而且 HA R R— V模 型能更好 地对波动进行 预测分析 。
关键词 : 已实 现 波 动 率 ;长记 忆性 ;H R—R A V模 型 中 图 分 类 号 :8 0 F3 文 献 标 识 码 : 文章 编 号 :10 3 2 (0 0 o 0 2 0 A 0 2— 3 1 2 1 )5— 历 史 的 收 益 是无 法 预 测 未 来 收益 的 。换 句 话 说 , 实 生 活 中 经 济 时 间序 列 现 所表 现 出 的长 记 忆 性 , 味着 有效 市 场假 说 的失 意
效 , 也 将导 致 后 续 建 立 在 有效 市 场假 说 基 础 上 这 的一 些 现 代 金 融 理 论 和模 型 , 现 代 投 资 理 论 、 如
易者而不是异质信息流引起的。市场因为具有不 同的参与者 在不 同时间 的 预期 而形 成 了分 形 的市 场结构 , 产生了短期、 中期 和长期交易者 , 既而造
高频金融数据市场微观结构噪音误差

t id fefcie e t to t o f a k tm ir s r cu en iea egv n:u o c v ra c s wo k n so fe t si v ma in me h do r e co tu t r os r ie a t -o a in ee ~ m t to fma k tmir sr cu en iee r ra du i gt e’ e l e ”v ltl y t si t a k tmi i in o r e c o t u t r os ro n sn h ’ ai d oa i t oe tma em r e — ma r z i
维普资讯
第3 1卷 第 3期
20 0 8年 3月
合 肥 工 业 大 学 学 报 (自然科 学版)
J OURNAL EF OF H EIUNI VERS TY I OF TECH NOL OGY
Vo . 1 No 3 13 .
o h o t - ro smu ai nt s , n o rs o d n o cu in r b an d ft eM n eCa l i lt e t a d c re p n ig c n l so sa eo ti e . o
Ke r s h g r q e c i a c a a ’ e l e ’v l tl y;ma k tm ir s r c u e n ie y wo d : i h f e u n y f n e d t ; ’ a i d’ o a i t n r z i r e co tu t r os
h g r qu n y fna c a a i h f e e c i n e d t
Z HA0 i Je
专题研究:波动率的涵义及应用意义

专题研究:波动率的涵义及应⽤意义 导读:⽬前,很多报告、⽂章、⾏情研究中都引⽤了波动率的概念,对⾦融市场波动率的估计和预测是近⼏⼗年来⾦融研究领域的重要课题之⼀。
波动率是个⾮常宽泛的概念,可应⽤的领域也很多,其种类和计算⽅法也颇多。
本⽂就波动率的基本概念、分类、计算⽅法及应⽤意义作了⼀些综合性的介绍,以便有兴趣的研究者对波动率有⼀个基础性的理解。
⼀、波动率的概念 波动率(Volatility),是⼀个统计概念,⼀般⽤来衡量标的资产价格或投资回报率波动的剧烈程度。
⼀般投资者理解的波动率是计算价格或收益率的标准差;波动率也可以指某⼀资产的⼀定时期内最⾼价减去最低价的值再除以最低价所得到的⽐率。
作为资产管理者,更希望能对未来资产波动率进⾏预测从⽽进⾏风险管理。
由于资产价格或投资回报率是⼀个随机过程,实际的波动率永远是⼀个未知数,或者说,实际波动率是⽆法事先精确计算的,⼈们只能通过各种⽅法得到它的估计值,这类似于统计学中总体参数的概念,总体参数⼀般是未知的,需要通过样本统计量去估计。
后⾯⼀系列分类的波动率,实际上都是对实际波动率的⼀种估计。
⼆、波动率的分类 不同的标准下,波动率可以进⾏不同的分类,这⾥按照波动率的计算⽅法与应⽤不同,将波动率分为:隐含波动率、历史波动率和已实现波动率(⾼频波动率/⽇内波动率)等⼏类。
(⼀)隐含波动率 隐含波动率是期权定价理论中的⼀个概念,从理论上讲,隐含波动率是将市场上的权证交易价格代⼊权证理论价格模型,反推出来的波动率数值。
以期权为例,由于期权定价模型给出了期权价格与五个基本参数(标的价格,执⾏价格,利率,到期时间和波动率σ)之间的定量关系,只要将其中前4个基本参数及期权的实际市场价格作为已知量代⼊期权定价模型,就可以从中解出惟⼀的未知量σ—波动率,其⼤⼩就是隐含波动率。
因此,隐含波动率也可以理解为市场实际波动率的预期。
(⼆)历史波动率 历史波动率是指投资回报率(收益率)在过去⼀段时间内所表现出的波动率,它由标的资产市场价格过去⼀段时间的历史时间序列数据({St})反映。
中国股市“已实现”波动率的周期性研究

T eraie oait g o srce l wigtemeh d lg fa d re db l rlv h e l dv ltlyaec ntu tdf l n h to oo yo n esn a ols e .W ef dta h w e e a e z i oo n e n h t et os r sh v i t i
型, 不需要进行复杂的参数估计. () t是满足以下方程的 肠 过程 :
近年来 , 国股票市场的周期性 研究多集 中在 我
指数和收益率低频数据的周期分析 , 本文是对 “ 已实
rt ,)=J +s + () () (+AA +J s d d 1
其 中,∈[ , ] 且 tT 是整数. s 是维纳 t 0T , , 都 W( )
过程.另外 , 把所有时刻 t 到时刻 t 时段都等分成 +l
现” 波动率这一重要参数 的周期性进行分析 , 同时利
用高频数据计算 日波动率 的时间序列 , 这对于研究
我国股市的波动特性有着更为直接的意义.
收稿 日期 :050-3 20—61.
基金项 目: 教育部 中芬合作项 目. 第一作者 : 董 越 (9 7 17 一 ) 男 , , 硕士研究 生
的波动周期做 了实证分析 , 通过 Fu e 谱 分析 , or r i 比较 了沪深两市的波动周期 , 示 了我 国股 市的周期 波动性特 征. 揭 目 前 , 国股票市场的 周期性研 究 多集 中在市场指数和收益 率的低频数据 周期分析 , 文的特 点是利 用高频数 据对 波 我 本
动率这 一重要 参数的周期性进行分析.
维普资讯
第2 2卷 第 6期 20 06年 1 2月
天
津
基于高频数据的沪指波动长记忆性驱动因素分析

(. 1 中国人民大学 应用统计科学研究中心 , 北京 1o 7 ; . o 8 22 山东经济学院 统计与数学学 院,山东 济南 2 0 1 ) 50 4
摘要 : 借助于高频数据 的最优取样法 , 已实现波动率给出的上证指数波动率的有效估计 , 利用 在研究 已实
现波动率特性 的基础上 , 用计量模型探讨沪指波动 的长 记忆特征 。发现 HA R—R V模型 比 F R MA模 型更 AI 能有效地刻画沪指波动的长记忆性 , HA 且 R—R V模型样本外预测效果远远优于 F R MA模型 , AI 这说 明沪指 波动具有伪长记忆性 , 表面特征显示 的长记忆性是 由短期投资 、 中期投资和长期投资形成 的短记忆性叠加 而 成 。同时由于 HA R—R V模型综合考虑 了不 同时 间水平上 的已实现波动率 , 从而在深层次上验证 了中国股票 市场的异质性 和波动率的杠杆效应。 关键词 : 已实现波动率 ; 长记亿性 ; 异质市场 ; A H R—R V模型
作者简介 : 张 波(9 o , , 1 6 一)男 黑龙江人 , 理学博 士 , 教授 , 博士生导 师 , 研究方 向: 随机分析及其在金融与保险中的应用 。
2 1
统计 与信息论坛
d t () ( ) W ( ) p( )= t £十 td t
0≤ t T ≤ () 1 其 中 Ⅳ () 标 准布 朗运 动 过程 , ( ) t是 2 1 t 和 ( ) t 是 可 料过程 , t 具有 有限 变差 , t 严 格正 且平 方 ( ) ( )
中圈分类号 :24 0 F 2 . 文献标志码 : A 文章编号:07—3 1 (0 90 —0 2 —0 10 16 20 )6 0 1 6
长记忆性、结构突变条件下中国股市波动率的高频预测

杂, 都 不 能 直接 应用 于 高 频 金 融 数 据 。随 着 高 频 数 据 可 以 越
来越方便的获得 , 对 于 股 市 波 动 率 的 预 测 有 了 一 些 新 的 方 法
和模型 , 可 以更 加 精 确 地 对 股 市 波 动 率 进 行 模 拟 和 预 测 。其
的 预 测 效 果 比其 他 预 测 模 型 要 好测 效 果 比 A B D L模 型 稍 微 差 ,而 A B D L模 型 在 两种 情 形 下都 是 比 较 稳 健 的 预 测 模 型 。
关 键 词 :已 实现 波 动 率 ;预 测 ;长 记 忆性 ; 结 构 突 变
中 最 有 影 响 的是 A n d e r s e n , B o l l e r s l e v a n d D i e b o d等 ( 后 文 记为 A B D L ) 和B a r n d o r f f - N i e l s e n a n d S h e p h a r d提 出 了 资 产 收
融 资产 收 益 的 波 动 率 的 估 计 和 准 确 预 测 无 疑 迫 在 眉 睫 。 此
外, 金 融 资 产 收益 的 波 动 率 估 计 和 预 测 也 是 金 融 衍 生 品定 价
以及投资组合选择 中一个 非 常重要 的核 心环 节 , 因此 , 如 何 构 建 合 适 的 波 动 率 模 型 来 估 计 和 预 测 金 融 市 场 的 波 动 率 对
于金 融 市 场 的 风 险 监 管 以及 经 济 活 动 中 的 资 产 配 置 等 , 无 疑 都 具 有 极 为 重 要 的理 论 和 现实 意 义 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
i
“已实现”波动率(realized
volatilitiy)模型 该方法构造简单,计算每日已实现波动 时只需要对日内收益平方求和即可。但该方 法具有完备的理论基础:只要日内收益的采 样频率足够高,已实现波动率就能无限逼近 瞬时波动率在样本区间上的积分,而积分波 动率(Integrated Volatility)是对波动率的自然 测度。
xi
2 i
xi 1
i i 1 xi
2 i 1
x
2 i 1
1 i
在均值方程中引入xi 可以验证各种市场微观结 构假说。如果假设无交易意味着坏消息是正确的, 则长的持续期意味着价格将下跌,应该为负。同期 持续期的倒数引入条件方差方程是可以检验持续期 对波动率的影响;如果假设长的持续期意味着没有 消息和较低的波动率,则 为正。 同理,可以根据同样的思想在条件方差方程中 引入其他变量来分析波动率和各变量之间的关系以 检验各种微观结构假说。
推断
标准的GARCH波动率模型运用在高频数据时 的预测能力是很差的,但是ACD-GARCH模 型的预测能力不会比简单的已实现波动率模 型的预测能力差。 但是在金融市场的超高频数据中,调整的已 实现波动率模型的预测能力要高于ACDGARCH模型。
需要做的工作
找实际数据,运用前面所讲的几种模型进行
“已实现”协方差RC模型
当一维变量的“已实现”波动率扩展的多维高频时 间序列时,可以用“已实现”协方差矩阵来计算投 资组合的方差。“已实现”协方差矩阵继承了“已 实现”波动率无需建模,计算简便的优点。
DCC-GARCH模型与“已实现”协方差模 型的比较
DCC-GARCH模型较多元GARCH类模型有较大的 改进,参数估计大大简化,但仍然要进行两阶段估 计,计算成本远远高于“已实现”协方差模型,寻 优时间较长,而且估计结果对初值的选取有一定的 依赖性,另外选取的数据是低频数据,这些都大大 降低了估计的精度。 “已实现”协方差模型基于高频数据,是没有测量 误差的无偏估计,估计精度高。
扩展的ACD-GARCH模型 Engle建议扩展并且提出了更多变量的方程,即允许 观察的和期望的持续期同时引进方程。同时他把一 个更长形式的波动方差用下面的方程定义: xi 2 2 2 1 1 i 1 i 1 i 1 1 xi 2 3i 1 4 i
波动率的估计预测,比较它们的预测精度。
关于投资组合方差的研究
为确定投资组合的风险,不仅要知道投资组合中个 股的风险和率同向变动的程度。协方差和 相关系数可用来测量股票报酬率的共同变动程度。 投资组合的方差等于组合中所有两两配对股票的报 酬率的协方差与他们各自在投资组合中的投资权重 的乘积之和。也就是说,投资组合的总体风险取决 于组合中全部股票之间的总体互动。
问题
在处理投资组合的“已实现”协方差问题时,数据 的采集频率多少为好?是否频率越高越好? DCC-GARCH模型与“已实现”协方差模型的数据 采集时间跨度的比较?(因为DCC-GARCH模型处 理的是低频数据,而“已实现”协方差模型处理的 是高频数据)
可以做的工作
实例分析比较用低频数据建模预测投资组合
波动率估计的模型
波动率是投资组合的构建, 衍生产品定价以及金融风险管
理的关键变量, 对波动率的准确预测一直是现代金融学研 究的热点问题。 低频时间序列领域, 可以直接用GARCH 类模型和SV类模 型进行波动率估计。 而高频金融时间序列通常是指以天、小时、分钟甚至秒 为频率所采集的按时间先后顺序排列的金融类数据。 “已实现”波动率( realized volatility) 是针对高频时间序 列而开发的一种全新的波动率的测度方法。这种波动率 的度量方法中没有模型(model free) , 计算方便, 在金融研 究领域和实际操作领域都有很广阔的应用前景。
vi 1 (ri | xi ) hi
ri 2 Vi 1 ( | xi ) i xi
上面两个方程可以得到:
hi xi
2 i
因此,预测的条件交易方差可以定义为:
Ei1 (hi ) Ei 1 ( xi )
2 i
所以GARCH(1,1)中的方差可以用下面扩展的形式来 ri 1 计算: ri
首先定义p(t)是金融资产的对数价格过程,投资于 该金融资产 时段上的对数收益率为: 其中, >0表示时间间隔。 当 =1时,
r (t , ) p(t ) p(t )
r (t , ) p(t 1) p(t )
表示日间收益率。 定义第t天的“已实现”波动率 1 为
主要内容
数据采集频率对信息的影响
波动率估计模型
高频数据方差模型
投资组合方差的研究
数据采集频率对信息的影响
在金融市场中,信息连续地影响证券市场价格的运 动过程,数据的离散采集必然会造成信息不同程度 的缺失。 无疑,采集频率越高,信息丢失越少;反之,信息 丢失越多。 计算机技术在金融市场的广泛应用,人们更加容易 获得金融市场中每时每刻的价格波动信息,即高频 数据。 为了更深刻的理解金融市场,有必要对更高频率下 的金融市场波动率进行研究。
1
“已实现”波动率模型与GARCH和SV 类模型的比较
GARCH类模型和SV类模型多年来一直是波
动性估计常用的方法,但是扩展到多变量的 情况下, GARCH类模型和SV类模型由于 “维数灾难”问题,很难得到它们参数正确 的估计值。 “已实现”波动率无需建模,计算简便,可 以很好的应用于投资组合风险管理研究中, 因此已经成为学术界研究的新热点。
的波动率与用高频数据建模预测投资组合波 动率的精度
ACD-GARCH模型
ACD-GARCH模型即是在GARCH(1,1)方程中引入ACD 模型中的持续期来作为方差的解释变量。假设 i 表示交易从 i-1时刻到i时刻的收益率,那么每次交易的条件方差定义为:
r
其中 xi 是ACD模型中的调整持续期。条件方差依赖于当前和 过去的收益率以及持续期。每个时间单元的条件波动率是进 行评估的最相关量。可以给出如下表达式:
高频方差模型
高频-GARCH(1,1)模型
如果这些交易的当前持续期没有明确的作为附加的信息源高频 GARCH(1,1)模型可以处理不规则的市场交易数据,。在 这种意义上说,它是在高频数据下定义的最简单的条件方差模 型。模型的表示形式如下:
2 i 2 i 1
2 i 1
t2 rt 21 j, ,
j 1
其中, 是两次采样的时间间隔, 是采样频率。例 1 如,当 =5min时,采样频率 =48.理论上,当 趋 近于0时,意味着连续取样,即“已实现”波动率收 1 2 IVt 0 t 1s ds 敛于积分波动率(Integrated Volatility )。 在GARCH类模型和SV类模型中,使用条件波动 率在t时刻的信息集来度量t+1时刻的波动的预测值。 与它们不同,“已实现”波动率是在t时刻的信息集的 基础上度量t时刻的波动率,基于此,它通常被称为 “已实现”波动( realized volatilitiy),简记为RV。
处理投资组合协方差的模型
DCC-GARCH模型
采用低频时间序列对多个资产收益的时变方差和协 方差建模的主要工具有多元GARCH模型和多元SV 模型,但是多元GARCH模型和多元SV模型的参数 估计由于“维数灾难”问题一直没有很好的解决。 DCC模型比较好的解决了多元GARCH的“维数灾 难”问题。
