不规则三角网DEM建立与应用
土石方计算中不规则三角网的生成及应用

土石方计算中不规则三角网的生成及应用
王威;王卫安
【期刊名称】《南水北调与水利科技》
【年(卷),期】2007(005)005
【摘要】不规则三角网(TIN)作为一种表现三维表面的离散数字形式在很多领域都有广泛的应用,最常见的如数字高程模型(DEM).目前,对由大量离散点组成的地形表面构建TIN最为成熟的方法为基于狄洛尼原则的构网方法.但是该方法并不能很好地顾及"地形特征线".而在实际应用中,设计地形(如交通工程中的设计道路、疏浚工程中的设计航道、吹填工程中的设计堤坝)正是由大量的地形特征线构成,所以该方法并不能解决这类地形的建模问题.在总结狄洛尼三角网构网方法的基础上,结合疏浚工程和吹填工程探讨了基于多边形剖分的设计地形建模方法并给出了应用实例.【总页数】4页(P35-38)
【作者】王威;王卫安
【作者单位】同济大学,测量与国土信息工程系,上海,200092;同济大学,测量与国土信息工程系,上海,200092
【正文语种】中文
【中图分类】TV31
【相关文献】
1.探讨VB环境下不规则三角网在土方计算中的应用 [J], 郭红操;唐斌
2.不规则三角网生成算法及其应用探讨 [J], 李梅;张学雷
3.等高线、平行断面、三角网法在土石方计算中的应用 [J], 韩丽
4.探讨VB环境下不规则三角网在土方计算中的应用 [J], 郭红操;唐斌;崔卫磊
5.Web应用中基于不规则三角网格的Contour图绘制 [J], 古小敏;宋小鹏;何秀锦;吴国珊;王斌武
因版权原因,仅展示原文概要,查看原文内容请购买。
不规则三角网DE
长沙理工大学测绘工程系 谢树春
不规则三角网DEM 不规则三角网DEM
基于张角最大准则的Delaunay三角网建立 五. 基于张角最大准则的 三角网建立
张角最大准则: 张角最大准则:
指一点到基边的张角为最大。 指一点到基边的张角为最大。 张角为最大
与空外接圆准则等价。 与空外接圆准则等价。 等价
长沙理工大学测绘工程系 谢树春
不规则三角网DEM 不规则三角网DEM
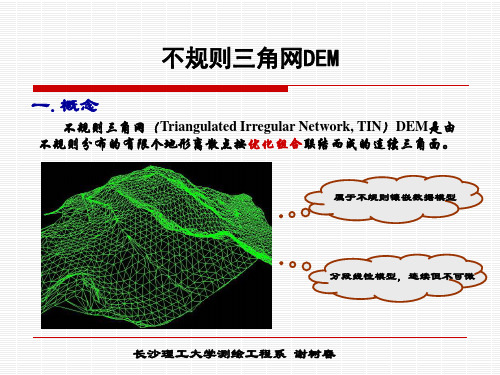
一.概念
不规则三角网( 不规则三角网(Triangulated Irregular Network, TIN)DEM是由 ) 是由 优化组合联结而成的连续三角面 不规则分布的有限个地形离散点按优化组合联结而成的连续三角面。 不规则分布的有限个地形离散点按优化组合联结而成的连续三角面。
长沙理工大学测绘工程系 谢树春
LOP算法实现新点 插入的过程: 算法实现新点p插入的过程 算法实现新点 插入的过程:
求出包含新插入点p 外接圆的三角形; 求出包含新插入点p的外接圆的三角形; 的三角形 删除影响三角形的公共边; 删除影响三角形的公共边; 影响三角形的公共边 与全部影响三角形的顶点连接 将p与全部影响三角形的顶点连接。 与全部影响三角形的顶点连接。
构建TIN比较费时; 比较费时; 构建 比较费时 算法设计比较复杂; 算法设计比较复杂; 复杂 表面分析能力较差。 表面分析能力较差。 能力较差
长沙理工大学测绘工程系 谢树春
不规则三角网DEM 不规则三角网DEM
思考: 思考:
能否结合规则格网 DEM和不规则三角网 和不规则三角网 DEM各自的优点? 各自的优点 各自的优点?
不规则三角网DEM 不规则三角网DEM
基于张角最大准则的Delaunay三角网建立 五. 基于张角最大准则的 三角网建立
实习七:DEM建立与应用

实习七:DEM建立与应用实习七、dem建立与应用一、目的dem是对地形地貌的一种离散的数字表达,是对地面特*进行空间描述的一种数字方法、途径,它的应用可遍及整个地学领域。
通过对本次实习的学习,我们应:1、加深对dem建立过程的原理、方法的认识;2、掌握利用常见空间*值的方法建立dem模型的方法3、熟练掌握利用arcgis或arcview建立dem、tin的技术方法。
4、掌握应用dem解决地学空间分析问题的能力(生成坡度图、坡向图等)。
二、实验准备1、软件准备:arcgis或arcview2、数据准备:(1)stations.shp(一个包含爱达荷州105个气象站点数据和高程数据的shapefile文件(2)idoutl.shp(爱达荷州轮廓图的shapefile文件)(3)高程格网dem数据(plne)(4)河流shapelife文件(stream.shp)(5)?望哨位置的shapefile文件(lookouts.shp)三、实验内容1、由采样点数据station.shp和爱达荷州轮廓图idoutl.shp,建立爱达荷州等高线模型、规则格网dem模型和不规则三角网(tin)模型2、dem的应用:(1)利用dem数据(plne)制作坡度图、坡向图、地貌晕渲图(入*光方位角315度,与地面夹角45度)(2)利用dem数据(plne)创建等高线专题图(等高距200米,基础等高线的高程800米)(3)利用dem数据(plne),创建任意一条线上的断面图,同时利用dem数据(plne)和河流shapelife文件(stream.shp)创建河流代码为“usgh_id=167”这一支流的断面图。
(4)利用高程格网dem数据(plne)和河流shapelife文件(stream.shp),创建本区域立体透视图,把河流信息叠加到数字高程模型上。
(5)视域分析:利用dem数据(plne)和?望哨位置文件lookouts.shp,进行视域分析:(a)分别制作从两个观测点出发的可视区域图及不可视区域图;(b)制作从两个?望哨观测的最大可视区域及不可视区域。
不规则三角网的建立与应用

摘要作为空间数据基础设施中的“4D”产品之一和地理信息系统的核心数据库,数字高程模型(DEM)已在测绘、遥感、农林规划、城市规划、土木水利工程、地学分析等各个领域都有了广泛的应用。
数字高程模型的表示方法主要有规则格网模型、不规则三角网模型和等高线模型三种,而不规则三角网(TIN)是数字高程模型中最基本和最重要的一种模型,它能以不同层次的分辨率来描述地形表面,并可以灵活的处理特殊地形。
因此,围绕基于TIN 的DEM 的构建,本文主要论述了基于 TIN 结构的数字高程模型建模原理和方法,离散点的Delaunay 三角网生成算法,建立有约束条件的约束三角网,最后分析了建立的 TIN模型在土方计算方面的应用。
在本论文论述的过程中,针对传统算法进行了对比和分析后,在逐点插入法的基础之上,提出了一些新的细部改进的实现方法。
局部优化操作和改进的算法实现使得对大容量离散点的三角网构建速度更快,效率更高;对限制条件的嵌入满足由此计算出来的土方量更接近实际期望值。
本论文中主要的研究成果和内容如下: 1)在离散点的 Delaunay 三角网生成方面,本文中在插入点算法的基础上,建立凸包和矩形包容盒,建立虚拟网格,对原始离散点进行一级格网自适应分块,并建立索引关系。
在定位点所在三角形时引入快速点定位算法,简易的空外接圆及圆内测试公式,通过这些改进使得 Delaunay 三角网的剖分更加高效。
2)在约束 Delaunay 三角网理论基础之上,结合上面散点域的剖分方法,对已有的两步算法基础上改进,完成约束 Delaunay 三角网的构建。
在其过程中应用矢量点积等数学工具改善了计算中的凹凸点判断,继续采用上章的快速索引和最速定位方法,并且对约束线相切等特殊情形进行了处理,进一步完善了算法的稳健性。
3)对于在约束三角网构造基础上的 TIN 模型的应用,文中对其在土方量计算方面精度的优越性进行了分析,在可视化表达方面最后结合广东省东莞市某高尔夫球场工程给出了例证。
第五讲 DEM的应用

7)当一条等高线全部跟踪完后,将其光滑输出,方法与前面所 述矩形格网等高线的绘制相同。然后继续三角形的搜索,直至全部 三角形处理完,再改变等高线高程,重复以上过程,直到完成全部 等高线的绘制为止
DEM的应用
1 等高线的生成 2 规则格网DEM的建立 3 不规则三角网TIN的建立 4 DEM编辑处理 5 DEM结构的相互转换
1等高线生成
1)内插等值点的位置
①若三角形的三个顶点的高程相等,则三角形的边上无等值点 ②若三角形三顶点高程值不相等,那么每条边二端点高程满足: (z-z1)*(z-z2)>=0时,则该边无等值点,否则必有等值点; (z-z1)*(z-z3)>=0时,则该边无等值点,否则必有等值点; (z-z2)*(z-z3)>=0时,则该边无等值点,否则必有等值点; ③若三角形三顶点高程不等,其中一点高程等于等值线高程,若有 等值点必在对边。 ④若三角形有两个顶点高程相等,若存在等值点,必位于靠近第三 点两边上。
2.坡度的计算
Z11
tan X
Z10 Z11 Z00 Z01
2
2
X Z01 Z11 Z00 Z10
tan
Y
2
2
Y
R
x 1
Z01
P
Z10
T
(1,1)
O
(0,0)
(1,0)
又:
tan X
PO RO
PO QO QO RO
tan sin 1
Q
y
2 S
tan Y
PO SO
PO QO QO SO
DEM的建立与应用

辽宁工程技术大学本科毕业设计(论文)中期报告题目葫芦岛市数字高程模型的建立与应用指导教师宋伟东院(系、部)测绘与地理科学学院专业班级测绘06-2班学号0604070217姓名王松妍日期2010年5月6日教务处印制内容摘要本文结合葫芦岛市数据库已有数字图像,通过FME软件实现CAD数据与ArcGIS数据的转化,主要研究如何利用转换后的数据在ArcGIS9.2中生成理想的数字高程模型。
同时简单介绍了DEM在葫芦岛市城市规划与建设中的一些应用。
关键词:葫芦岛市 DEM ArcGISABSTRACTBased on the existing digital image database of HuLudao city to Research on how to use the data in ArcGIS9.2 after the conversion of the ideal digital elevation model through the FME software realization CAD data to ArcGIS data transformation。
Also simply introduced DEM urban planning and construction of some applications in HuLudao city.绪论 (4)1、DEM简介 (4)1.1、数字高程模型的定义 (4)1.2、DEM的数字意义 (6)1.3、DEM可视化 (7)2、DEM建立 (7)2.1DEM的基础数据 (7)2.2软件选择 (8)2.2.1 数据格式转换模式 (9)2.2.2 直接数据访问模式 (9)2.2.3 数据语义转换模式 (9)2.3 DEM 的制作思路 (10)2.5 DEM 制作的步骤 (10)2.5.1数据入库 (10)2.5.2 DEM的建立 (11)3、简介DEM在葫芦岛市的应用 (12)结束语 (13)绪论葫芦岛市地处辽宁西南部,是京沈线上重要的城市之一。
不规则三角网DEM的建立与应用

多边形称为泰森多边形。用直线段连接每两个相邻多 边形内的离散点而生成的三角网称为狄洛尼三角网
三角网数字地面模型的存贮
TIN
直接表示网点邻接关系的结构
坐标与高程值表
NO 1 2 3 X Y Z P 1 5 8 NO 2 3 4 5 9 3 1
/ “ 测 绘 信 息 网 ” 网 友 搜 集 版 权 归 原 权 利 人 所 有 ,
搜索该等高线在该三 角形的离去边
基于格网点搜索的等高线绘制
建立一个与邻接关系对应的标志数组
按格网点的顺序进行搜索
坐标与高程值表
NO X Y Z P NO 2 3 Flag() 1
1
2 3
90.0
50.7 67.2
10.0
10.0 23.9
43.5
67.3 62.6
1
5 8
4
5 9
10
10.0
则C为该三角 形第三顶点
示意图
C1
C2
哪个内 角最大
C3
与A点距 离最近的 点
AosCi 2ai bi
2
三角形的扩展
对每一个已生成的三角形的新增加的两 边,按角度最大的原则向外进行扩展, 并进行是否重复的检测。
向外扩展的处理。若从顶点为P1(X1,Y1),
三角网中的内插 格网点的检索:要确定点P落在TIN 的哪个三角形中 。
d ( X X i ) (Y Yi )
2 i 2 2
p
三角网中的内插 高程内插
X X1 X2 X3 Y Y1 Y2 Y3 Z Z1 Z2 Z3 1 1 1 1 0
( X X1 )(Y21Z31 Y31Z 21 ) (Y Y1 )(Z 21 X 31 Z31 X 21 ) Z Z1 X 21 X 31 X 31 X 21
arcgis应用培训材料专题7不规则三角网
专题7 不规则三角网
一、实验目的
1、掌握建立不规则三角网方法,建立地形表面;
2、线要素的邻近区生成方法;
3、点要素的邻近区生成方法;
4、掌握矢量型空间分析方法的实际应用;
二、实验准备
实验数据位置:Training Material | 不规则三角网
预备知识:
1、通过离散点和线数据构建的不规则三角网,可以用于表达地形表面,参与三维分析操作;
三、实验内容与步骤
第1部分建立场景不规则三角网
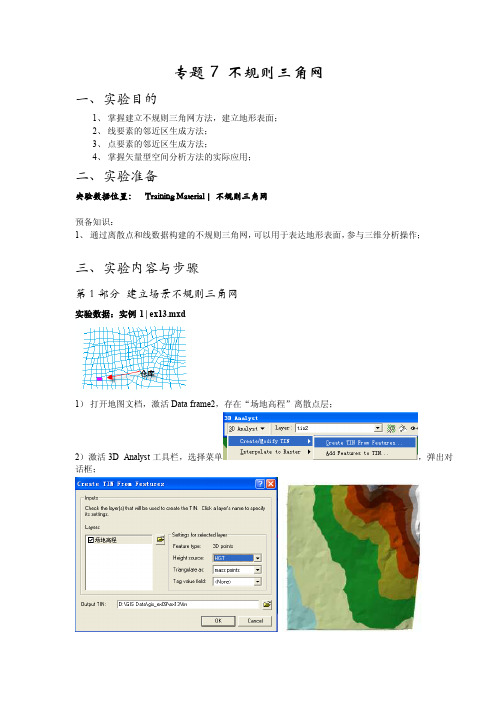
实验数据:实例1 | ex13.mxd
1)打开地图文档,激活Data frame2,存在“场地高程”离散点层;
2)激活3D Analyst工具栏,选择菜单,弹出对话框;
3)选用添加数据工具,加载bldg多边形、road线和water多边形三个CAD地物层;
结果如下:
4)启动ArcScene,加载生成的地形表面,和三个CAD地物层;
5)在导入的三个CAD地物层的属性中的Base Height属性页中,将TIN地形表面设置为基底:
结果如下:
5)在建筑物层的属性对话框的Extrusion属性页,如下设置,将建筑物拉伸;
6)生成三维动画:选择一条道路,然后启动ArcScene中的Animation工具栏,选取菜单Animation/Camera Flyby from Path…,然后选取Open animation Controls工具即可播放路径漫游动画。
作业:
1、请使用上述动画工具栏,并完成该工具栏的详细用户手册,其中需要每个过程的详细抓
图和介绍,并介绍个人使用该工具栏的心得体会。
不规则三角网的算法设计与实现

1 引言地球表面高低起伏,呈现一种连续变化的曲面,这种曲面无法用平面地图来确切表示。
于是我们就利用一种全新的数字地球表面的方法——数字高程模型的方法,这种方法已经被普遍广泛采用。
数字高程模型即DEM(Digital Elevation Model),是以数字形式按一定结构组织在一起,表示实际地形特征空间分布的模型,也是地形形状大小和起伏的数字描述。
由于地理信息系统的普及,DEM作为数字地形模拟的重要成果已经成为国家空间数据基础设施(NSDI)的基本内容之一,并被纳入数字化空间框架(DGDF)进行规模化生产,已经成为独立的标准基础产品[5]。
DEM有三种主要的表示模型:规则格网模型,等高线模型和不规则三角网。
格网(即GRID)DEM在地形平坦的地方,存在大量的数据冗余,在不改变格网大小情况下,难以表达复杂地形的突变现象,在某些计算,如通视问题,过分强调网格的轴方向。
不规则三角网(简称TIN,即Triangulated Irregular Network)是另外一种表示数字高程模型的的方法(Peuker等,1978),它既减少了规则格网带来的数据冗余,同时在计算(如坡度)效率方面又优于纯粹基于等高线的方法。
不规则三角网能随地形起伏变化的复杂性而改变采样点的密度和决定采样点的位置,因而它能够避免地形起伏平坦时的数据冗余,又能按地形特征点如山脊,山谷线,地形变化线等表示数字高程特征。
基于三角形的表面建模可适合所有的数据结构,且三角形在形状和大小方面有很大灵活性,能很容易地融合断裂线,生成线或其他任何数据,因此基于三角形的方法在地形表面建模中得到了越来越多的注意,已经成为表面建模的主要方法之一。
VB语言简洁易学,对于学习GIS的学生来说无疑是接受很容易而且较快的一门计算机编程和开发语言,也是大多数学生最熟悉和了解的语言。
正是基于对生成不规则三角网算法的研究和满足学GIS的学生对VB 语言的喜爱和熟悉的情况下,本文就主要介绍用三角网生长算法生成不规则三角网及其在VB6.0环境下的实现。
【精品】PPT课件 不规则三角网的建立与应用PPT24页

【精品】PPT课件 不规则三角网的建的 ,但是 为了生 存,我 们不得 不为自 己编织 一个笼 子,然 后把自 己关在 里面。 ——博 莱索
•
27、法律如果不讲道理,即使延续时 间再长 ,也还 是没有 制约力 的。— —爱·科 克
•
28、好法律是由坏风俗创造出来的。 ——马 克罗维 乌斯
•
29、在一切能够接受法律支配的人类 的状态 中,哪 里没有 法律, 那里就 没有自 由。— —洛克
•
30、风俗可以造就法律,也可以废除 法律。 ——塞·约翰逊
立与应用
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
浅谈DEM模型的建立及在测绘中的应用

浅谈DEM模型的建立及在测绘中的应用本文介绍数字高程模型的建立及在测绘中的应用标签数字地面模型(DTM);数字高程模型(DEM);不规则三角网(TIN)一、概述数字地面模型DTM(Digital Terrain Model),最初是美国麻省理工学院Miller 教授为了高速公路的自动设计于1956年提出来的。
此后,它被用于各种线路(铁路、公路、输电线路等)的设计及各种工程的面积、体积、坡度的计算,任意两点间可视性判断及绘制任意断面图。
在测绘中被用于绘制等高线、坡度坡向图、立体透视图,制作正射影像图与地形图的修测等。
它也是地理信息系统的基础数据。
数字地面模型DTM是地形表面形态等多种信息的一个数字表示。
严格地说,DTM是定义在某一区域D上的m维向量有限序列:﹛Vi,i=1,2,…,n﹜,其向量Vi=(Vi1,Vi2,…,Vin)的分量为地形((Xi,Yi,Zi),(Xi,Yi)∈D)、资源、环境、土地利用、人口分布等多种信息的定量或定性描述。
DTM是一个地理信息数据库的基本内核,若只考虑DTM的地形分量,我们通常称其为数字高程模型DEM (Digital ElevainModel),其定义如下:数字高程模型DEM是表示区域D上地形的三维向量有限序列:﹛Vi,= Xi,Yi,Zi﹜,i=1,2,…,n),其中(Xi,Yi)∈D是平面坐标,zi是(Xi,Yi)对应的高程。
在实际测绘应用中,许多人习惯将DEM称为DTM,实际上它们是不完全相同的。
DEM有多种表示形式,主要包括规则矩形网格与不规则三角网。
二、数字高程模型的数据获取为了建立DEM,必须测量一些点的三维坐标,这就是DEM数据采集或DEM 数据获取。
被量测的这些点称为数据点或坐标点。
DEM数据点的采集方法主要有以下几种:1、地面测量这是测绘中最常用的DEM点采集方法,利用自动记录的全站仪在野外实测三维坐标点,这种仪器一般都有微处理器,它可以自动记录与显示有关数据,还能进行多种测站上的计算工作。
不规则三角网(tin)的构建与应用-(5313)

第一章绪论1.1研究背景地球是人类生活和活动的承载体。
多年以来,我们为了更充分的认识自然客体和改造自然,总在不懈的努力尝试用不同的方式方法来描述、表达人所处的环境,其中地形图就是一个有代表性的测绘表述变迁的缩影。
从最开始的象形符号抽象的雏形到后来的在二维介质上对三维表面进行地形写景图,地貌写景图等描述是一个进步,但写景方式不具备可量测性,所以还是很局限的。
随着测绘技术发展,地形的表达也由写景式的定性表达过渡到了以等高线为主的矢量化表达。
航空摄影测量,遥感技术提供的影响都在对三维现实世界的模拟。
但是有一个矛盾体,那就是对于地形表面形态而言,一方面我们尽可能的从几何角度去理解和描述以解决实际应用中的可量测性;另外一个方面它本身是一种三维景观现象,对于其表述要考虑生理视觉感受,我们总是希望能够尽可能的直观形象逼真。
从20世纪四十年代开始的计算机图形学、计算机辅助制图等相关学科和理论的发展,使得在测绘领域,在图形表达表述方面发生了从模拟表达时代走向了数字表达时代,有了质的飞跃。
其中地理信息系统(GIS )及数字高程模型(DEM )学科或技术显得尤为重要。
地理信息系统,简称GIS (Geographical Information System ),它源于20世纪60年代初期加拿大测量学家Tomlinson 的“把地图变成数字形式的地图,以便计算机进行处理与分析”的观点,但是在技术工具处理中,则是利用计算机存贮、处理地理信息,并且在计算机软、硬件支持下,把各种资源信息和环境参数按空间分布或地理坐标,以一定的格式或者分类输入、处理、存贮、输出,用以满足其应用需要的人机交互系统。
因此GIS 的本质是在二维地理空间基础上实现对地下、地表和空中诸地理信息的数字化表达和管理。
当然地理信息系统技术发展到当前,功能不再是当初的局限于查询、检索和制图,而是丰富到空间分析、建模、决策等诸多方面,在数据管理上则从简单的栅格数据、矢量数据管理转向多元数据融合,在现实生活中应用的很活跃,也很充分。
武汉大学数字摄影测量课件012不规则三角网的建立与应用

邻接三角形表
NO 1 2 3 … 11 ∆1 2 1 2 … 8 ∆2 4 3 7 … 10 … 6 ∆3
10.0 90.0 81.0
检索效率高,但存贮量较大,编辑不方便。
3.混合表示网点及三角形邻接关系的结构
坐标与高程值表
NO 1 2 3… 10.0 Y 10.0 10.0 23.9 … 90.0 Z 43.5 67.3 62.6 … 81.0 P 1 5 8 … 36 NO
¾
确定第一个三角形
a i2 + bi2 − c 2 cos ∠ C i = 2 a i bi
∠C = max{∠Ci }
C第三顶点
示意图
C1 C2
哪个内 角最大
C3
与A点距 离最近的 点
A
2 i 2 i
B
a +b −c cos ∠Ci = 2ai bi
2
¾三角形的扩展
P1
每个边只能 扩展一次
P4
坐标与高程值表 NO 1 2 3 … 10 X Y Z P 1 5 8 … 36 NO 2 3 4 5 9 3 1 网点邻接的指针链 1 2 3 4 5 6 7
90.0 10.0 43.5 50.7 10.0 67.3 67.2 23.9 62.6 … … … 10.0 90.0 81.0
存贮量小,编辑方便
三角形表
网点邻接的指针链
2 3 4 5 9 3 1 NO 1 2 3 … 11 P1 1 1 4 … 6 P2 2 3 5 … 7 P3 3 4 1 … 8
TIN的压缩存贮
可将TIN转化为规则三角网存贮 方式,从而实现TIN的压缩存贮
P3
P2
F( X ,Y) = (Y2 − Y1)(X − X1) − ( X2 − X1)(Y2 − Y1) = 0
不规则三角网生成算法及其应用探讨

系列相连 的但 不 重叠 的三 角 形 的集 合 , 且 这 些 三角 形 而 的外接 圆不包 含这个 面域 的其 他任 何 点 。构造 TN 的 I
方法一般都归结到 D l ny e ua 三角网, 3 a 1 4年, 9 俄国数学家
B D l ny由 V r o 图 演 化 出 了 更 易 于 分 析 应 用 的 . e ua a o ni o Dl ny三角 网( 图 1 示 )它具 有 以下性 质 : e ua a 如 所 ,
一
图 1 虚线是 V rn i 。 o o o 图 实线是 D lu a ea n y图
Fg 1 V rn i h r d t dl e n i. oo o c at( ot n )a d e i D l n ycat sl n ) e u a h r(o dH e a i
些改进算 法也 陆续 的被提 出 。
本 文在传统算法的基础上总结 了一些改进算法 , 并且提 出了相 关的应用前景。 关键词 :I 生成算 法; e ua TN; D l ny三角网 a 中图分类号 :2 5 1 P 3 . 文献标识码 : B 文章编号 : 7 56 (0 0 0 — 04— 2 1 2— 87 2 1 )2 04 0 6 .
Ab t a t T N sa mp r n t o x r s M , o e t d t n l g r h a e ara y b e pi z d c n tn y a d b e sr c : I i n i o t tmeh d t e p e s DE wh s a i o a o i ms h v e d e n o t a o r i l a t l mie o sa t n e n l as p l dwie y T i a e t d c d s me i rv d ag r h a e n t dt n lo t msa d b u h owad o eaie lo a pi d l . h sp p ri r u e o e no mp o e o i msb s d o a i o a a g r h n r g t r r ss me rlt l t r i l i o f v
基于不规则三角网数字高层模型_DEM_的土方计算方法

第26卷第2期 湖北民族学院学报(自然科学版) Vol.26 No.2 2008年6月 Journal of HubeiUniversity f orNati onalities(Natural Science Editi on) Jun.2008基于不规则三角网数字高层模型(DEM)的土方计算方法吴威龙(湖北民族学院生物科学与技术学院,湖北恩施445000)摘要:提出的基于不规则三角形网数字高程模型(digital evaluati on model,DE M)的土方计算方法———不规则三角形法(Method of Irregular Triangular for Earth Calculate简称M I TEC),分析了DE M误差来源,较好地解决了地面上土方计算精度的问题,是一种实用性较强的方法.关键词:土方计算;不规则三角形法;数字高程模型中图分类号:T B22文献标识码:A文章编号:1008-8423(2008)02-0234-03M ethod of Ca lcul a ti n g Earthwork Ba sed on D i g it a l Eleva ti on M odelWU W ei-l ong(School of B i ol ogical Science and Technol ogy,Hubei University f or Nati onalities,Enshi445000,China)Abstract:This paper put f or ward an earthwork calculating method based on digital elevati on model (DE M),method of irregular triangular net w ork(TI N),and analyzed the err ors of DE M.The results show that the method is higly p recise and feasible.Key words:cubic meter of earth calculating;method of irregular triangulate f or earthcalculati on (M I TEC);digital evaluati on model(DE M)在土方计算过程中,由于地形形状多变,且随着地形图比例尺、工作条件、精度要求等情况的不同而有所变化,所以必须视具体情况而采取不同的方法.根据不同的地形特征,选取不同的计算方法.目前土方计算的基本方法有断面法、方格网法、等高线法及基于数字高程模型(DE M)法.在实际生产应用中,不同方法计算的同一场地土方量数量相差较大,所以不同方法土方计算精度不同,适用范围也不一样.断面法适用于地形起伏较大,场地为狭长形的情况.格网法模型简单,适用于地面平坦的地区.断面法和格网法存在以下两个不足之处[1]:①这两类方法在地形起伏变化大时,计算困难;②两类方法的计算模型都是近似的.DE M可以克服上面两个缺点,适用于所有场地,且精度较高.DE M有多种表示形式,主要包括规则格网DE M和不规则三角网DE M.所谓规则格网DE M,是利用一系列在X、Y方向上都按等间隔排列的地形点的高程值Z表示地形,形成一个矩阵格网DE M.而不规则三角网DE M,是按一定的规则将离散点连接成覆盖整个区域且互不重叠、结构最佳的三角形,实际上是建立离散点之间的空间关系.笔者认为采用三角网理论上比较准确,适用于任何场地[2].相对于规则格网,不规则三角网具有以下优点:利用原始资料作为网格结点,不改变原始数据和精度,能够插入地性线以保存原有关键的地形特征,以及能很好地适应复杂、不规则地形等[3].本文主要介绍基于不规则三角形网数字高程模型(DE M)的土方计算方法———不规则三角形法(M I TEC),该法优点是计算精确度相对较高,模型建立越逼真,精度越高.但建模过程工作难度大,内部计算过程复杂,且对外业特征点测设有一定要求,碎部点应能反映地形细部特征、地形变换特征.该法适用要求较高的工程.收稿日期:2008-03-28.作者简介:吴威龙(1981-),男,主要从事城市规划技术方法及应用研究.1 不规则三角网图1 边长最小二乘法图Fig .1 The length least squares 1.1 基本概念不规则三角形网是一种数字高程模型(DE M )是直接利用测区内野外实测的所有地形特征点(离散数据点),构造出邻接三角形组成的网状结构.不规则三角形网的每个基本单元的核心是组成不规则三角形三个顶点的三维坐标,这些坐标数据完全来自原始测量成果.由于观测采样时选取观测点是由地形决定的,一般是地形坡度的变换点或平面位置的转折点,从而使得离散点在相关区域中形成非规则形状的三角形.1.2 建网原理建立不规则三角形网的基本过程是将最邻近的3个离散点连接成初始三角形,然后以该三角形的每条边为基础向外连接邻近的离散点,组成3个三角形,接着以这3个三角形的每条边为基础连接邻近离散点,组成新的三角形.如此继续下去,直到所有离散点都被连接组成三角形.空间中若干个离散点,在数据点集中以最左下角点为起点,以距此点距离最近点为起始三角形第二个点,以距这两点边线中点最近而不和这两点在一直线上的点作为起始三角形的第三顶点,选取时主要有以下几个原则:①过三角形的外接圆均不含点集中的其余任何点;②三角形中一点到基边两端的距离和最小;③两相邻三角形形成的凸四边形中,这两个三角形中的最小内角一定大于交换凸四边形对角线后形成的两三角形的最小内角;④三角形中第三点到两基边的张角为最大.当起始三角形构建后,以起始三角形的三边作为基边依次向外扩展,直至点集内所有的离散点都构成三角网为止.1.3 形成方法,根据取相邻离散点的准则不同,构造方法有下列几种[4]:泰森多边形法、最近距离法、最小边长法、边长最小二乘法.M I TEC 选用边长最小二乘法形成三角形格网.该方法从离散点集合中选择两个距离最近的A 点和B 点,构成第一条边AB ,再在其余的离散点中选择三角形的另一顶点P,使得AP +BP 最小(如图1),形成第一个三角形;然后用同样的判断条件对第一个三角形△ABP 的各边进行扩展,直到所有的离散点都包含在三角形格网中.2 M I TEC 方案设计首先,将采集到的地貌点的三维坐标(X,Y,H )输入计算机,通过程序形成不规则三角形网,这时整个计算土方的地形就形成了由三棱柱组成的集合,见图4.其次,根据给定设计高程确定零平面(即给定设计高程所在的平面),于是这些三角形被零平面分为两种情况:一种是全挖方或全填方(图3);另一种是既有挖方又有填方(图4).再次,根据数学公式将每个不规则三角形的体积计算出来,以“+”表示挖方,以“-”表示填方.最后,分别统计体积为“+”和体积为“-”的形体的体积总和,这样“-”的体积总和就是该地形内的填方数,“+”的体积总和就是该地形内的挖方数.参阅参考文献[5],根据几何关系可以推导出下列M I TEC 计算公式.(1)对于全挖或全填的三棱柱形AB C 2A 1B 1C 1(图3),可将三棱柱分为C 12A 1A 2B 2B 1与A 2B 2C 12AB C 两部分进行计算,经计算得:V AB CA 1B 1C 1=s 1(h 1+h 2+h 3)/3(1)式中s 1为ΔABC 的面积;h 1,h 2,h 3都是已知地面高程与给定设计高程之间的高差.(2)对于部分挖与部分填的三棱柱(图4),可分解为楔体O 1O 22B 1C 1CB 和三棱锥A 12AO 1O 2两部分.则楔532第2期 吴威龙:基于不规则三角网数字高层模型(DE M )的土方计算方法 体体积V 2为:V 2=s 2h 2/3+s 3(h 2+h 3)/3记三棱锥A 12AO 1O 2的体积V 1为:V 1=s 1h 1/3其中s 2、s 3、s 4分别为△BO 1O 2、△O 2BC 、△AO 1O 2的面积;h 1,h 2,h 3都是已知地面高程与给定设计高程之间的高差.在此不必考虑公式中的符号,因为以“+”表示挖方,“-”表示填方,其中三角形面积计算可采用如下公式:S =6n i =1x i (y k +1-y k -1)/2图5 地面曲线图Fig .5 The gr ound curve 3 D E M 误差的来源与分类[6]为了讨论土方量计算的误差问题,必须首先分析DE M 的建立过程.因为对其计算精度的影响主要也是DE M 的建立过程.DE M 误差的一种来源是对自然真实表面的采样过程.这种误差出现在从原始资料产生地面点的过程中,误差是由原始资料本身的不合适性和使用的仪器引起的.可以采取一些措施尽量减小它,使之达到误差允许的范围内.DE M 误差的另一种来源是重新采样,即在保留了与原始地面较为逼近的情况下,将由原始数据派生的数据压缩成易于管理的过程中.这是一种性质不同的处理,因为提取的信息在很大程度上受采样区间和所用插值方法的影响.DE M 误差的表达和研究涉及到DE M 与实际地面的平均偏差,也涉及误差的分布和误差的非随机空间分量.对于一个实际应用问题,要确定一个合适的DE M ,则基本上依赖于研究对象,所要求的精度,采样方法以及对地形变化的敏感度.总之,DE M 的精度取决于采样密度、测量误差(偶然误差,系统误差和粗差)、地形类别、高程点数目和位置等.影响精度的主要因素是数据获取,通过选择适当的内插法,利用二次曲面进行DE M 内插,提高DE M 模型精度,可以获取基本相同的精度.4 M I TEC 的精度分析M I TEC 的数学模型是将地面抽象成由三棱柱组成的集合,该方法用直线代替了呈现不规则曲面的地面.如图5所示,实际地面可能是曲线ALB ,但计算时却用AB 直线代替了该曲线,这样必然会导致误差,记该项误差为mg .M I TEC 数学模型中除了此项误差外,不存在其它误差,所以可得M I TEC 的数学模型误差为:m m =m g .对于不规则三角形法计算模型误差,由前述推导可知M I TEC 的计算模型中采用全解析法计算,整个计算过程精度高、误差小.因此,由忽略不计原则可认为不规则三角形法的误差为:m =m m =m g .从上述分析可知,若在土方量算区域边界上取足够的点,不规则三角形法也能较好地解决“破格”问题.5 结论M I TEC 优于正方形格网法和断面法,具有容易编程、精度高、计算简便等特点,是一实用性较强的方法.该法优点是计算精确度相对较高,模型建立越逼真,精度越高.但建模过程工作难度大,内部计算过程复杂,且对外业特征点测设有一定要求,碎部点应能反映地形细部特征、地形变换特征.该法适用要求较高的工程.利用M I TEC 计算土方,可以不绘出地形图,由野外测得的离散点的维坐标直接进行计算,减少了工作量.参考文献:[1] 罗德仁,邹自力,汤江龙.工程土方量计算比较分析[J ].东华理工学院学报,2005,28(1):59-64.[2] 李殷,朱益虎.DT M 在土方计算中的应用[J ].地矿测绘,2006,22(4):33-36.[3] 王建雄.CAD 环境下基于不规则三角网的DE M 算法及实现[J ].云南农业大学学报,2005,20(4):573-576.[4] 刘友光,黄桂兰,黄全义,等.工程中数字地面模型的建立与应用及大比例尺数字测图[M ].武汉:武汉测绘科技大学出版社,1987:156-161.[5] 慕永峰,朱昌永,李建.三角网结构DT M 的土方计算及应用[J ].测绘工程,2000,9(1):52-56.[6] 常胜,张前勇.基于全站仪测记法的数字化测图方法[J ].湖北民族学院学报:自然科学版,2007,25(2):165-168.632 湖北民族学院学报(自然科学版) 第26卷。
不规则三角网的原理和应用

不规则三角网的原理和应用1. 引言不规则三角网是一种在地理信息系统(GIS)和计算机图形学中常用的数据结构,用于表示地形、地貌和其他空间数据。
本文将介绍不规则三角网的原理和应用。
2. 不规则三角网的原理不规则三角网是由一组不重叠的三角形组成的网络,其中每个三角形的边都共享一条边。
它可以用于将二维或三维空间上的数据进行离散化表示。
以下是建立不规则三角网的基本原理:•节点选择:首先需要选择一组合适的节点来构建三角网。
节点可以是地理位置、数据采集点或其他感兴趣的位置。
这些节点将成为三角网的顶点。
•三角剖分:根据节点的位置,在节点之间进行三角形的剖分。
通常使用Delaunay三角剖分方法,保证所有三角形的内接圆不包含其他节点,这样可以避免形成过于细长或扭曲的三角形。
•节点连接:将每个三角形的顶点连接起来形成三角网。
每个三角形的边都共享一条边,这样可以保证三角网的连续性。
3. 不规则三角网的应用不规则三角网在地理信息系统和计算机图形学中有广泛的应用。
以下是几个常见的应用场景:3.1 地形分析不规则三角网可以用于对地形进行离散化表示和分析。
通过节点的高程信息,可以计算每个三角形的面积、坡度和曲率等地形属性。
这对于地质学、测绘学和环境科学等领域的地形分析非常重要。
3.2 地理可视化不规则三角网可以用于地理可视化,将地理数据以更直观的方式呈现出来。
通过对三角形进行插值,可以根据节点上的数据对整个区域进行表面重建,从而生成地形模型或地图。
这对于城市规划、区域分析和地理导航等应用非常有用。
3.3 网格生成在计算机图形学中,不规则三角网可以用于网格生成。
根据给定的节点,可以通过插值方法生成一系列网格点,用于绘制曲线、表面或其他图形。
这对于计算机辅助设计、虚拟现实和游戏开发等领域非常重要。
3.4 数据插值不规则三角网可以用于数据插值,将离散的数据点进行填充。
通过插值方法,可以根据已知节点的属性估计其他位置的属性。
这对于气象学、地质学和农业等领域的数据分析非常有用。
DEM分析与可视化-第4章_图文

分割-合并算法(分治算法)
Shamos 和 Hoey 首先提出了分割 - 合并算法的思想 ,Lee 和 Schachter将分治算法思想应用于D-三角网的生成, 并表明该算法的 时间复杂度为O (N logN )。 分割-归并法的基本思路是,递归地分割点集至足够小, 使其易 于生成三角网, 然后把子集中的三角网合并, 经优化生成最终的三角网.
二、Delaunay三角网的性质
1)给定离散点集的D-三角网是唯一的; 2)三角网的外边界构成了点集P的凸多边形“外壳”; 3)空外接圆性质:没有任何点在三角形的外接圆内部,反 之,如果一个三角网满足此条件,那么它就是Delaunay三角网。 4)最大的最小角度性质:在由点集V所能形成的三角
网中,D-三网的建立方法
一、基本准则
Delaunay三角形产生准则的最简明的形式是:任何 一个Delaunay三角形的外接圆的内部不能包含其它任何点 [Delaunay 1934]。
Lawson [1977]提出了一 个 局 部 优 化 过 程 LOP ( Local Optimization Procedure)方法。
第四章 不规则三角网结构DEM的建立
1 2 3 4 5 6 7 8
X Y Z X Y Z X Y Z X Y Z X X X X Y Y Y Y Z Z Z Z
6 1
1 3 2 5 5 6 7 7 4 8
2
顶点
邻接三角形
4 3
1 2 3 4 5 6 7 8
1 5 6 1 4 5 1 2 4 2 5 4 4 3 3 6 5 7 4 4 8 8 8 7
从结构上讲, TIN是一典型的矢量数据结构。它主要通过节 点(地形采样点)、三角形边和三角形面之间的关系来显式或 隐式地表达地形散点的拓扑关系,因此设计一个高效的、结 构紧凑的、维护方便的TIN存储与组织结构对TIN的应用与 库的维护是至关重要的。 TIN的基本单元三角形的几何形状直接决定着TIN应用质量。 由于地形的自相关性,相互愈接近的地形采样点,其之间 的关联程度愈大; 同时,理论与实践均证明,狭长的三角形其插值精度比规 则的三角形插值精度可信度要低。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
NO
网 2点
3邻
4接
5
的 指
9针
3链
10 10.0 90.0 81.0 36
1
第19页/共20页
Flag() 1
1
基于格网点搜索的等高线绘制
对每一格网点,按所记录的与该点
形成格网边的另一端点的顺序搜索,
直接表示三角形及邻接关系的结构
坐标与高程值表
NO X Y Z 1 90.0 10.0 43.5 2 50.7 10.0 67.3 3 67.2 23.9 62.6 10 10.0 90.0 81.0
三角形表
NO P1 P2 P3 1123 2134 3451 11 6 7 8
邻接三角形表
当已知三角形的两个顶点后,利用余 弦定理计算备选第三顶点的三角形内 角的大小,选择最大者对应的点为该 三角形的第三顶点。
•将原始数据分块 检索所处理三角形邻近点
第2页/共20页
• 确定第一个三角形
C3 C2
C1
cosCi
ai2
bi2 c2 2ai bi
A
B
C max Ci
第5页/共20页
P1P2直线方程为
F(X ,Y) (Y2 Y1)( X X1) (X2 X1)(Y2 Y1) 0
p1
若备选点P之坐标为(X,Y)
p3
p2
F ( X ,Y ) F ( X 3,Y3 ) 0
• 重复与交叉的检测。任意一边最多只能是两 个三角形的公共边,
第6页/共20页
权
利 人
所
有
10 10.0 90.0 81.0 36
第10页/共20页
NO
21 网
3
2
点 邻
43 接
5
4
的 指
95 针
36 链
17
直接表示网点邻接关系的结构
最大特点是存贮量小,编 辑方便。但是三角形及邻 接关系都需要实时再生成, 且计算量较大,不便于TIN 的快速检索与显示。
第11页/共20页
NO 1 2 3 124 2136 327 11 8 10
检索网点拓扑关系效率高,便于等高线快速 插绘、TIN快速显示与局部结构分析。但存 贮量较大,编辑不方第1便2页/共。20页
混合表示网点及三角形邻接关系的结构
坐标与高程值表
NO X Y Z P 1 90.0 10.0 43.5 1 2 50.7 10.0 67.3 5 3 67.2 23.9 62.6 8 10 10.0 90.0 81.0 36
则C为该三角 形第三顶点
第3页/共20页
C1
哪个内 角最大
示意图
C2
C3
与A点距 离最近的
点
A
B
cosCi
ai2
bi2 c2 2aibi
第4页/共20页
• 三角形的扩展
对每一个已生成的三角形的新增加的两 边,按角度最大的原则向外进行扩展, 并进行是否重复的检测。
• 向外扩展的处理。若从顶点为P1(X1,Y1), P2(X2,Y2), P3(X3,Y3)的三角形之P1P2边向外扩 展,应取位于直线P1P2与P3异侧的点
0该边有等高线
(Z1
z)(Z 2
z){
0, 该边无等高线点
搜索该等高线在该三 角形的离去边
第18页/共20页
基于格网点搜索的等高线绘制
建立一个与邻接关系对应的标志数组
按格网点的顺序进行搜索
坐标与高程值表
NO X Y Z P 1 90.0 10.0 43.5 1 2 50.7 10.0 67.3 5 3 67.2 23.9 62.6 8
泰森多边形与狄洛尼三角网 区域D上有n个离散点 Pi(Xi,Yi)(i=1,2,…,n),若将D用一组直线 段分成n个互相邻接的多边形,满足:
•每个多边形内含且仅含一个离散点 •D中任意一点P’(X’,Y’)若位于Pi所在的 多边形内,则满足
第7页/共20页
泰森多边形与狄洛尼三角网
X ' Xi 2 Y ' Yi 2 X ' X j 2 Y ' Yj 2
NO
2
网 点
3邻
4接
5的 指
9针
3链
1
三角形表
NO P1 P2 P3 1123 2134 3451 11 6 7 8
存贮量与直接表示三角形及邻接关系 结构相当,但编辑与快速检索较方便
第13页/共20页
TIN的压缩存贮
可将TIN转化为规则三角网存贮 方式,从而实现TIN的压缩存贮
第14页/共20页
ji
•若P’在与所在的两多边形的公共边上,则
X ' Xi 2 Y ' Yi 2 X ' X j 2 Y ' Yj 2 j i
多边形称为泰森多边形。用直线段连接每两个相邻多 边形内的离散点而生成的三角网称为狄洛尼三角网
第8页/共20页
三角网数字地面模型的存贮
TIN
第9页/共20页
/ “
直接表示网点邻接关系的结构
,
坐标与高程值表
测
绘 信
NO X
Y
Z
P
息
网 ”
1 90.0 10.0 43.5 1
网
友
搜 集
2 50.7 10.0 67.3 5
版
权 归 原
3 67.2 23.9 62.6 8
三角网中的内插
格网点的检索:要确定点P落在TIN 的哪个三角形中 。
di2 ( X X i )2 (Y Yi )2
p
第15页/共20页
三角网中的内插
高程内插X Y Z1X1 NhomakorabeaY1
Z1
1 0
X 2 Y2 Z2 1
X 3 Y3 Z3 1
Z
Z1
(X
X1)(Y21Z31
Y31Z21) X 21X 31
(Y Y1)(Z21X31 X 31X 21
Z31X 21)
第16页/共20页
基于三角网的等高线绘制
基于三角形搜索的等高线绘制
设立三角形标志数组 : 每一元素与一个三角形对应,凡处
理过的三角形将标志置为1,以后不 再处理,直至等高线高程改变
第17页/共20页
基于三角网的等高线绘制
按顺序判断每个三角形的三边中两 条边是否有等高线穿过
三角网数字地面模型的构建
可 以 建 立 各 种 非 规 则 网 的 DEM, 最 简 单 是 不 规 则 三 角 网 ( TIN-Triangulated
Irregular Network)
应尽可能保证每个三角形是锐角三角 形或三边的长度近似相等,避免出现 过大的钝角和过小的锐角
第1页/共20页
角度判断法建立TIN
