直方图均衡及分段灰度变换
图像处理6灰度直方图和直方图均衡化

图像处理6灰度直⽅图和直⽅图均衡化灰度直⽅图介绍灰度直⽅图(Gray histogram)是关于灰度级分布的函数,是对图像中灰度级分布的统计。
灰度直⽅图是将数字图像中的所有像素,按照灰度值的⼤⼩,统计其出现的频率。
灰度直⽅图是灰度级的函数,它表⽰图像中具有某种灰度级的像素的个数,反映了图像中某种灰度出现的频率。
如果将图像总像素亮度(灰度级别)看成是⼀个随机变量,则其分布情况就反映了图像的统计特性,这可⽤probability density function (PDF)来刻画和描述,表现为灰度直⽅图。
实现以下代码便于理解灰度直⽅图的计算,其中histogram函数是基于numpy简化的,运⾏结果如下。
# coding: utf8from skimage import dataimport matplotlib.pyplot as pltimport numpy as npdef histogram(a, bins=10, range=None):"""Compute the histogram of a set of data."""import numpy as npfrom numpy.core import linspacefrom numpy.core.numeric import (arange, asarray)# 转成⼀维数组a = asarray(a)a = a.ravel()mn, mx = [mi + 0.0 for mi in range]ntype = np.dtype(np.intp)n = np.zeros(bins, ntype)# 预计算直⽅图缩放因⼦norm = bins / (mx - mn)# 均分,计算边缘以进⾏潜在的校正bin_edges = linspace(mn, mx, bins + 1, endpoint=True)# 分块对于⼤数组可以降低运⾏内存,同时提⾼速度BLOCK = 65536for i in arange(0, len(a), BLOCK):tmp_a = a[i:i + BLOCK]tmp_a_data = tmp_a.astype(float)# 减去Range下限,乘以缩放因⼦,向下取整tmp_a = tmp_a_data - mntmp_a *= normindices = tmp_a.astype(np.intp)# 对indices标签分别计数,标签等于bins减⼀indices[indices == bins] -= 1n += np.bincount(indices, weights=None,minlength=bins).astype(ntype)return n, bin_edgesif__name__ =="__main__":img=data.coffee()fig = plt.figure()f1 = fig.add_subplot(141)f1.imshow(img)f1.set_title("image")f2 = fig.add_subplot(142)arr=img.flatten()n, bins, patches = f2.hist(arr, bins=256, facecolor='red')f2.set_title("plt_hist")f3 = fig.add_subplot(143)hist, others = np.histogram(arr, range=(0, arr.max()), bins=256)f3.plot(others[1:],hist)f3.set_title("np_hist1")f4 = fig.add_subplot(144)hist, others = histogram(arr, range=(0, arr.max()), bins=256)f4.plot(others[1:], hist)f4.set_title("np_hist2")plt.show()关于bincount函数,可以参考Xurtle的博⽂https:///xlinsist/article/details/51346523bin的数量⽐x中的最⼤值⼤1,每个bin给出了它的索引值在x中出现的次数。
直方图均衡化计算
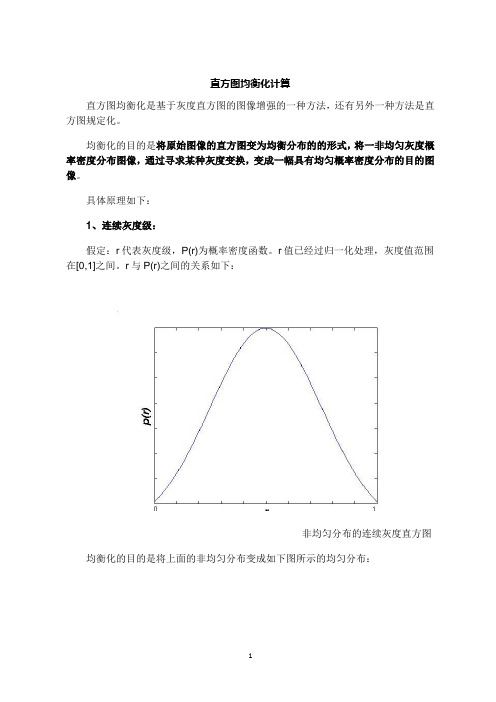
直方图均衡化计算直方图均衡化是基于灰度直方图的图像增强的一种方法,还有另外一种方法是直方图规定化。
均衡化的目的是将原始图像的直方图变为均衡分布的的形式,将一非均匀灰度概率密度分布图像,通过寻求某种灰度变换,变成一幅具有均匀概率密度分布的目的图像。
具体原理如下:1、连续灰度级:假定:r代表灰度级,P(r)为概率密度函数。
r值已经过归一化处理,灰度值范围在[0,1]之间。
r与P(r)之间的关系如下:非均匀分布的连续灰度直方图均衡化的目的是将上面的非均匀分布变成如下图所示的均匀分布:均匀分布的连续灰度直方图我们接下来要做的是要找到一种变换S=T(r)使直方图变平直,为使变换后的灰度仍保持从黑到白的单一变化顺序,且变换范围与原先一致,以避免整体变亮或变暗,需要有如下规定:(1)在0 <= r <= 1中,T(r)是单调递增函数,且0 <= T(r) <= 1;(2)反变换r=(s),(s)也为单调递增函数,且0 <= s <= 1。
直方图均衡化变换公式推导图示因为灰度变换不影响像素的位置分布,而且也不会增减像素数目,所以有如下的推导公式:2、离散灰度级:设一幅图像的像素总数为n,分为L个灰度级,其中::表示第K个灰度级出现的个数。
:第K个灰度级出现的概率。
(0<=<=1, k=0,1,2,...,L-1),公式如下:计算的基本步骤如下:(1)求出图像中所包含的灰度级,一般都经过归一化处理,范围在[0,1]之间,也可以定在[0,L-1]之间。
(2)统计各灰度级的像素数目(k=0,1,2,...,L-1)。
(3)计算图像直方图。
(4)计算变换函数,即:(5)用变换函数计算映射后输出的灰度级。
(6)统计映射后新的灰度级的像素数目。
(7)计算输出图像的直方图。
根据上面推导出来的公式以及计算步骤,我们可以结合栗子来加深理解~~~eg:设图像有64*64=4096的像素,有8个灰度级,灰度分布如下所示:由上图我们知道该图像的,和,下一步我们要做的就是通过变换函数求,即:依次可求得,,,,。
遥感影像灰度值计算

遥感影像灰度值计算遥感影像灰度值是指影像中每个像素点的亮度级别,其反映了被观察物体或地表的特征信息。
灰度值计算对于遥感影像的解译和分析具有重要意义。
本文将介绍遥感影像灰度值的计算方法,并探讨其在不同应用领域中的重要性与指导意义。
一、灰度值的计算方法1. 线性灰度变换:将影像中的原始灰度值转化为可视化的灰度级别。
常用的线性灰度变换方法有线性拉伸、分段线性变换等。
2. 直方图均衡化:通过重新调整影像中各个灰度级别出现的频数,实现亮度的增强和对比度的改善。
直方图均衡化可以提高影像的视觉效果,使各个物体特征更加明显。
3. 比例拉伸:根据影像中最小和最大灰度值,进行线性转换,将原始灰度值映射到特定的范围内。
比例拉伸可以突出影像的细节信息,提高目标的可辨识度。
二、灰度值计算的重要性1. 物体提取与分类:通过计算遥感影像的灰度值,可以帮助识别和分类不同的物体。
不同物体的灰度值往往存在明显差异,可以通过灰度值计算来区分它们,进而实现地物提取和分类。
2. 土地利用与覆盖分析:遥感影像灰度值与地物覆盖类型之间存在一定的关联性。
通过对灰度值的计算和分析,可以了解不同地表特征的分布情况,从而进行土地利用和覆盖分析,为城市规划、环境保护等提供依据。
3. 灾害监测与评估:遥感影像灰度值的变化可以反映灾害事件的发生和演化过程。
通过实时计算和监测灰度值的变化,可以及时发现并评估自然灾害,为灾害管理和救援提供有效支持。
4. 环境变化监测:遥感影像灰度值的变化可以反映自然环境的演变和变化趋势。
通过定期计算和比较灰度值,可以监测和评估气候变化、植被覆盖变化等环境变化情况,为环境保护和可持续发展提供科学依据。
三、灰度值计算的指导意义1. 优化影像解译:灰度值计算可以帮助解译遥感影像,提取目标信息。
根据不同应用领域的需求,灰度值计算可以优化影像的解读和分析过程,提高解译的准确性和效率。
2. 支持决策制定:通过灰度值计算可以获得遥感影像的空间信息和特征参数,为决策制定提供科学依据。
图像增强—灰度变换及直方图均衡化试验目的试验原理及知识点

图像增强—灰度变换及直方图均衡化一、实验目的1、了解图像增强的目的及意义,加深对图像增强的感性认识,巩固所学理论知识。
2、掌握直接灰度变换的图像增强方法。
3、掌握灰度直方图的概念及其计算方法;4、掌握直方图均衡化的计算过程;二、实验原理及知识点1、图像增强是指按特定的需要突出一幅图像中的某些信息,同时,消弱或去除某些不需要的信息的处理方法。
其主要目的是处理后的图像对某些特定的应用比原来的图像更加有效。
图像增强可以在空间域中执行,也可以在变换域中执行。
2、空间域指的是图像平面本身,在空间域内处理图像是直接对图像的像素进行处理。
空间域处理方法分为两种:灰度级变换、空间滤波。
空间域技术直接对像素进行操作,其表达式为g(x,y)=T[f(x,y)]其中f(x,y)为输入图像,g(x,y)为输出图像,T是对图像f进行处理的操作符,定义在点(x,y)的指定邻域内。
定义点(x,y)的空间邻近区域的主要方法是,使用中心位于(x,y)的正方形或长方形区域。
此区域的中心从原点(如左上角)开始逐像素点移动,在移动的同时,该区域会包含不同的邻域。
T应用于每个位置(x,y),以便在该位置得到输出图像g。
在计算(x,y)处的g值时,只使用该领域的像素。
2、灰度变换T的最简单形式是使用领域大小为1×1,此时,(x,y)处的g值仅由f在该点处的亮度决定,T也变为一个灰度变换函数。
由于灰度变换函数仅取决于亮度的值,而与(x,y)无关,所以亮度函数通常可写做如下所示的简单形式:s=T(r)其中,r表示图像f中相应点(x,y)的亮度,s表示图像g中相应点(x,y)的亮度。
灰度拉伸又叫对比度拉伸是最基本的一种灰度变换,使用简单的分段线性变换函数,可以提高灰度的动态范围,适用于低对比度图像的处理,增强对比度。
3、直方图是多种空间城处理技术的基础。
直方图操作能有效地用于图像增强。
除了提供有用的图像统计资料外,直方图固有的信息在其他图像处理应用中也是非常有用的,如图像压缩与分割。
基于直方图均衡和幂次变换的灰度图像增强算法

出一种基于直方 图均衡 化的增强算法 , 该算 法利用 直方 图均衡化算法执行效 率高 、 对低对 比度 图像增 强效果好 的特 点, 结合幂 次 变 换可 以平衡光 照不 均匀 图像 的亮度的特性 , 采 用两种算法分别对原 图进行处 理 , 将结果进行 非线性叠 加后 , 经分段线 性处 理得到最 终结果。实验结果表 明, 对于光 照不均匀 、 暗部信息丰 富的灰度 图像具 有较 好的增强效果。
A b s t r a c t
T r a d i t i o n a l h i s t o g r a m e q u a l i s a t i o n( HE )a l g o r i t h m l o s e s i m a g e d e t a i l s o f b i r g h t r e g i o n s a n d p r o d u c e s n o i s e i n d a r k r e g i o n s w h i l e
第3 0卷 第 4期
2 0 1 3年 4月
计算机 应 用 与软件
Co mp u t e r Ap p l i c a t i o n s a n d S o f t wa r e
Vo I . 3 0 No. 4 Ap r .2 01 3
பைடு நூலகம்
基 于直 方 图均 衡 和 幂 次 变 换 的灰 度 图像 增 强算 法
马士友 付致伟 王晓东 蒯自 强 黄多荣
( 四川大学计算机学院 四川 成都 6 1 0 0 6 5 ) ( 防空兵学院防空导弹系 河南 郑州 4 5 0 0 5 2 )
摘
要
针对传统直 方图均衡 化算法增强光 照不均匀 图像 时出现暗部噪 点过 多 、 亮部细节丢 失, 导致 图像信 息量下 降的问题 , 提
直方图均衡化实验报告
南京信息工程大学实验(实习)报告实验(实习)名称点操作及直方图均衡化实验(实习)日期得分指导教师系计算机系专业软件工程年级三班次 3 姓名学号实验目的:1、理解点操作图像增强方法2、理解直方图均衡化算法的原理,掌握算法的实现实验内容:1、理解图像灰度拉伸,练习imadjust函数的使用;I=imread('pout.tif');K=imadjust(I,[0.2 0.5],[0 1]); figure;subplot(1,2,1),imshow(I);subplot(1,2,2),imshow(K);2、编程实现图像线性灰度变换算法;(全域截取分段 for循环)clear ;clc; I=imread('pout.tif');I=double(I);J=(I-80)*255/70;row=size(I,1);column=size(I,2);for i=1:rowfor j=1:columnif J(i, j)<0J(i,j)=0;endif J(i,j)>255;J(i,j)=255;endendendfigure;subplot(121); imshow(uint8(I)); subplot(122); imshow(uint8(J)); subplot(223),imhist(I);subplot(224),imhist(J);3、编程实现图像二值化算法;直方图选域值clear;clc;i=imread('pout.tif');bw=im2bw(i);subplot(121),imshow(i),subplot(122),imshow(bw);4、编程实现图像灰度对数log变换、指数(三角符号)变换算法;I=imread('pout.tif');J=log(im2double(I)+1);K=fft2(J);n=5;D0=0.1*pi;rh=0.7;rl=0.4;[row, column]=size(J);for i=1:rowfor j=1:columnD1(i,j)=sqrt(i^2+j^2);H(i,j)=rl+(rh/(1+(D0/D1(i,j))^(2*n)));endendL=K.*H;M=ifft2(L); N=exp(M)-1;figure;subplot(121),imshow(I); subplot(122),imshow(real(N));5、在Matlab中编程实现直方图均衡化算法(不使用histeq函数,编程实现其功能)。
实验三、直方图及灰度变换

实验三直方图及灰度变换一,目的熟悉并学会使用MA TLAB中图像增强的相关函数了解图像增强的方法、去噪的方法和效果二,实验条件1)微型计算机:INTEL 奔腾及更高2)MATLAB3)典型的灰度、彩色图像文件三,原理视一幅图像为二维矩阵,用MA TLAB进行图像增强直方图均衡化是通过灰度变换将一幅图像转换为另一幅具有均衡直方图,即在每个灰度级上都具有相同的象素点数的过程。
四,实验内容1.线性变换设计:从灰度区间[a,b]到[a1,b2]cd d:I=imread('test.jpg');J=rgb2gray(I);%imshow(J);figure,subplot(2,2,1)imhist(J);[m n]=size(J);max_=0;min_=255;%for嵌套循环获取最小灰度及最大灰度值,也可两次调用min或max函数for x=1:1:mfor y=1:1:nif J(x,y) < min_min_=J(x,y);endif J(x,y) > max_max_=J(x,y);endendendmin_max_%循环进行函数计算,从而实现变换%原始图像的像素灰度范围【0,255】,变换后的图像像素灰度范围【min_,max_】for x=1:1:mfor y=1:1:nNEW(x,y)=min_+(max_-min_)/255*(J(x,y));endend%imshow(NEW);figure,subplot(2,2,2) imhist(NEW);010020002000400060008000图像变换前 0100200200040006000图像变换后2.直方图,用matlab语言自写一个程序设计并绘出图像直方图cd d:I=imread('test.jpg');J=rgb2gray(I);%imshow(J);figure,subplot(2,2,1)H=zeros(1,256);%zeros(m,n)产生m×n的零矩阵[m n]=size(J);for i=1:mfor j=1:nH(J(i,j)+1)=H(J(i,j)+1)+1;%从第一个开始,并统计灰度值endendplot(H);stem(H); %绘制二维离散数据的火柴杆图3.直方图的均衡化%一,图像的预处理,读入彩色图像将其灰度化cd d:I=imread('test.jpg');H=rgb2gray(I);imshow(H);%二,绘制直方图[m,n]=size(H); %测量图像尺寸参数GL=zeros(1,256); %预创建存放灰度出现概率的向量for k=0:255GL(k+1)=length(find(H==k))/(m*n);%计算每级灰度出现的概率,将其存入GP中相应位置endfigure,bar(0:255,GL,'g') %绘制直方图title('原图像直方图')xlabel('灰度值')ylabel('出现概率')%三,直方图均衡化S1=zeros(1,256); % zeros(m,n)产生m×n的零矩阵for i=1:256for j=1:iS1(i)=GL(j)+S1(i); %计算变换函数SkendendS2=round((S1*256)+0.5); %将Sk归到相近级的灰度for i=1:256GLPeq(i)=sum(GL(find(S2==i))); %计算现有每个灰度级出现的概率endfigure,bar(0:255,GLPeq,'b') %显示均衡化后的直方图title('均衡化后的直方图')xlabel('灰度值')ylabel('出现概率')%四,图像归一化PA=PS;for i=0:255PA(find(PS==i))=S2(i+1); %将各个像素归一化后的灰度值赋给这个像素endfigure,imshow(PA) %显示均衡化后的图像title('均衡化后图像')imwrite(PA,'JUNHENGHUA.bmp');均衡化前的图像-5005010015020025030000.0050.010.0150.020.025原图像直方图灰度值出现概率-5005010015020025030000.0050.010.0150.020.025均衡化后的直方图灰度值出现概率均衡化后图像均衡化后的图像参考:姚静,武文波,康停军. 直方图均衡化的Matlab 实现[J]. 辽宁工程技术大学学报,2007,S2:60-62.仅供参考。
数字图像处理文档-直方图均衡&灰度线性变换&灰度拉伸

技术报告摘要:本文档为数字图像处理程序的技术报告。
程序主要功能为读入8位或24位位图,并可选择性对其进行直方图均衡、灰度线性变换、灰度拉伸等操作。
该文档从算法原理和算法实现两方面,通过对算法的文字表述、函数的功能介绍以及主要代码分析注释,阐述了该程序进行图像处理时的方法,并通过实验测试和分析实验结果,验证了程序的正确性和可靠性。
关键词:直方图均衡灰度线性变换灰度拉伸1、任务说明⏹打开一幅图像,进行直方图均衡。
将灰度线性变化,将灰度拉伸。
⏹用C语言或JAVA编程序读出图像文件,并利用算法进行灰度拉伸。
2、算法原理(背景意义,基本算法,扩展算法)2.1直方图均衡直方图均衡化是将原图像通过某种变换,得到一幅灰度直方图为均匀分布的新图像的方法。
设图像均衡化处理后,图像的直方图是平直的,即各灰度级具有相同的出现频数,那么由于灰度级具有均匀的概率分布,图像看起来就更清晰了。
在离散情况下,共有L个灰度级,其中第k个灰度级rk出现的像素个数为nk,图像的总像素个数为N,则第k个灰度级出现的概率为:P r(r k)=n kN0≤r k≤1,k=0,1,…,L−1进行均匀化处理的变换函数为:s k=T[r k]=∑P r(r j)=kj=0∑n jN kj=0r k=T−1[s k]2.2灰度线性变换灰度的线性变换就是将图像中所有的点按照线性灰度变换函数进行变换。
该线性灰度变换函数f(x)是一个一维线性函数:f(x)=fA*x+fB灰度变换方程为:D2=f(D1)=k*D+d式中参数k为线性函数的斜率,d为线性函数的在y轴上的截距,D1为输入图像的灰度,D2为输出的图像灰度。
当k>1时,输出的图像的对比度增大,图像的像素值在变换后全部增大,整体显示效果增强;当0<k<1时,输出图像的对比度和整体效果都将削弱;当k<0时,原图像较量的区域变暗,较暗的区域则变亮,当k=-1,d=255时,输出图像的灰度正好反转;当k=1且d!=0时,操作仅仅使所有像素的灰度值上移或下移,其效果是使整个图像更亮或更暗;当k=1,d=0时,输出图像和输入图像相同。
直方图均衡化

直方图均衡化
0≤r≤1 • T (r) 满足下列两个条件: (1) 在区间0≤r≤1中为单值且单调递增 (2)当0≤r≤1时,0≤ ≤1 • 条件(1)保证原图各灰度级在变换后仍保
定义(2):
一个灰度级在范围[0,L-1]的数字图像的直 方图是一个离散函数
p(rk ) nk rk / n
n 是图像的像素总数
nk是图像中灰度级为rk的像素个数
rk是第 个灰度级, = 0,1,2,…,L-1
比较两种定义
h(rk ) nk
p(rk ) nk / n
其中,定义(2)
定义(1) 定义(2)
直方图均衡化
对于离散值:
pr
(rk
)
nk n
已知变换函数的离散形式为:
sk 称作直方图均衡化
将输入图像中灰度级为 rk(横坐标)的像素映射到
输出图像中灰度级为 s k(横坐标)的对应像素
得到:
即:
sk
T(rk )
k j0
pr (rj )
k j0
nj n
• 使函数值正则化到[0,1]区间,成为实数函数
• 函数值的范围与象素的总数无关
• 给出灰度级 rk 在图像中出现的概率密度统
计
图像直方图的定义举例
直方图均衡化
• 直方图应用举例——直方图均衡化 • 希望一幅图像的像素占有全部可能的灰度级 且分布均匀,能够具有高对比度
• 使用的方法是灰度级变换:s T (r)
持从黑到白(或从白到黑)的排列次序
• 条件(2)保证变换前后灰度值动态范围的 一致性
图像处理:数字图像的灰度直方图均衡化

图像处理:数字图像的灰度直方图均衡化简介在数字图像处理中,灰度直方图均衡化是一种常用的图像增强技术。
它通过重新分配图像中各个灰度级的像素值,使得最终的灰度直方图呈现出更均匀分布的特点,从而提高图像的对比度和视觉效果。
原理灰度直方图是描述一幅图像中每个灰度级出现频次的统计直方图。
在灰度直方图均衡化过程中,首先需要计算原始图像的累积概率密度函数(CDF),然后利用CDF进行线性变换将原始像素值映射到新的像素值上。
这个线性变换可以通过以下公式表示:G' = (G_max - G_min) \times CDF(G) + G_min其中G'是新的像素值,G是原始的像素值,G_max和G_min分别为像素值范围最大和最小值,而CDF(G)则是原始图像中小于或等于G的累积概率密度函数。
实现步骤1.读取待处理的数字图像。
2.将彩色或多通道图转化为灰度图。
3.计算原始灰度图像的像素值的频次统计,得到原始灰度直方图。
4.计算原始灰度直方图的累积概率密度函数。
5.根据累积概率密度函数进行线性变换,将原始像素值映射到新的像素值上。
6.生成处理后得到的均衡化后的图像。
7.输出均衡化后的图像。
应用场景灰度直方图均衡化在许多领域都有广泛应用,例如医学影像分析、计算机视觉和数字摄影等。
其主要作用是增强图像对比度、改善细节和提升视觉效果。
同时,该技术也能够在一些特定场景下帮助识别和检测对象。
总结通过使用灰度直方图均衡化技术,可以使得数字图像中各个灰度级的像素值更加均匀分布,从而提高图像对比度和视觉效果。
这种方法在数字图像处理中具有广泛的应用,并且简单易实现。
然而,需要注意的是,在某些特定情况下,采用该方法可能会产生过度增强或引入噪声等问题,因此在实际应用中需要谨慎使用并结合其他处理方法进行综合处理。
《灰度直方图变换》PPT课件

pr(r) T(r) ps(s)
2
1.8 1.2
1.6
1.4
1
1.2 0.8
1 0.6
0.8
0.6
0.4
0.4
0.2 0.2
0
0
0.5
1
r
0 0 0.5 1 r
1.2 1
0.8 0.6 0.4 0.2
0 0 0.5 1 s
➢ 离散图像直方图均衡化 对于离散的数字图像,用频率来代替概率,则变换函
数T(rk)的离散形式可表示为:
v4=1/64
12321212
v5=5/64
31231221
v6=8/64
i
v7=5/64
直方图的性质
①灰度直方图只能反映图像的灰度分布情况,而不能反 映图像像素的位置,即丢失了像素的位置信息。
②一幅图像对应唯一的灰度直方图,反之不成立。不同 的图像可对应相同的直方图。下图给出了一个不同的 图像具有相同直方图的例子。
5 5/7 245 0.06 0.95 1
6 6/7 122 0.03 0.98 1
7 1 81 0.02 1 1 1 448 0.11
k rk nk Pr(rk) 0 0 790 0.19 1 1/7 1023 0.25 2 2/7 850 0.21 3 3/7 656 0.16 4 4/7 329 0.08 5 5/7 245 0.06 6 6/7 122 0.03 7 1 81 0.02
ns=zeros(1,8); for i=0:7
idx=find(Tr>=(2*i-1)/14&Tr<(2*i+1)/14); m0=nk(idx); ns(i+1)=sum(m0(:)); end sums=sum(ns(:)); Ps=ns/sums; subplot(133) stem(rk,Ps) xlabel('s_k') ylabel('P_s(s_k)') title('均匀化后的直方图')
图像灰度变换、二值化、直方图

图像灰度变换、⼆值化、直⽅图1、灰度变换1)灰度图的线性变换Gnew = Fa * Gold + Fb。
Fa为斜线的斜率,Fb为y轴上的截距。
Fa>1 输出图像的对⽐度变⼤,否则变⼩。
Fa=1 Fb≠0时,图像的灰度上移或下移,效果为图像变亮或变暗。
Fa=-1,Fb=255时,发⽣图像反转。
注意:线性变换会出现亮度饱和⽽丢失细节。
2)对数变换t=c * log(1+s)c为变换尺度,s为源灰度,t为变换后的灰度。
对数变换⾃变量低时曲线斜率⾼,⾃变量⼤时斜率⼩。
所以会放⼤图像较暗的部分,压缩较亮的部分。
3)伽马变换y=(x+esp)γ,x与y的范围是[0,1], esp为补偿系数,γ为伽马系数。
当伽马系数⼤于1时,图像⾼灰度区域得到增强。
当伽马系数⼩于1时,图像低灰度区域得到增强。
当伽马系数等于1时,图像线性变换。
4)图像取反⽅法1:直接取反imgPath = 'E:\opencv_pic\src_pic\pic2.bmp';img1 = imread(imgPath); % 前景图img0 = 255-img1; % 取反景图subplot(1,2,1),imshow(img1),title('原始图像');subplot(1,2,2),imshow(img0),title('取反图像');⽅法2:伽马变换Matlab:imadjust(f, [low_in, high_in], [low_out, high_out], gamma)[low_in, high_in]范围内的数据映射到 [low_out, high_out],低于low的映射到low_out, ⾼于high的映射到high_out. imgPath = 'E:\opencv_pic\src_pic\pic2.bmp';img1 = imread(imgPath); % 前景图img0 = imadjust(img1, [0,1], [1,0]);subplot(1,2,1),imshow(img1),title('原始图像');subplot(1,2,2),imshow(img0),title('取反图像');2、⼆值化1)rgb2gray⼀般保存的灰度图是24位的灰度,如果改为8bit灰度图。
直方图直方图均衡化增强

直方图均衡化可以改善医学影像的对比度,使医生能够更清晰地观察病变区域,从而提高诊断的准确 性和可靠性。
病理分析
在病理切片分析中,直方图均衡化可以增强细胞核和染色体的细节,有助于病理医生进行更准确的诊 断和分类。
遥感图像增强
土地利用分类
通过直方图均衡化增强遥感图像的对比度,可以更好地区分不同类型的土地利用,如森 林、城市、农田等。
要点二
详细描述
多尺度直方图均衡化的基本思想是将图像分解为多个尺度 的小波系数,每个尺度上的小波系数具有不同的空间分辨 率和频率特性。在每个尺度上进行直方图均衡化,可以增 强图像在该尺度上的细节和边缘信息。通过将多个尺度上 的结果进行融合,可以得到增强后的图像。这种方法能够 更好地处理图像中的高频信息和边缘细节,提高图像的视 觉效果。
联合直方图均衡化
总结词
联合直方图均衡化是一种改进的直方图均衡化方法, 通过联合考虑多个图像或图像的多个通道进行直方图 均衡化,以增强图像的对比度和色彩信息。
详细描述
联合直方图均衡化的基本思想是同时对多个图像或图 像的多个通道进行直方图均衡化。通过联合处理,可 以增强图像的对比度和色彩信息,提高图像的视觉效 果。在实际应用中,可以同时对RGB三个通道进行联 合直方图均衡化,以增强彩色图像的色彩信息;也可 以对相邻帧的图像进行联合直方图均衡化,以提高视 频的清晰度和对比度。
可能会改变原始图像的灰度分布
01
直方图均衡化会改变原始图像的灰度分布,可能导致一些细节
信息的丢失。
对噪声敏感
02
在存在噪声的情况下,直方图均衡化可能会放大噪声,影响增
强效果。
对动态范围较小的图像效果不佳
03
对于动态范围较小的图像,直方图均衡化可能无法显著提高对
实验一 图像的灰度变换及直方图均衡化

实验一:图像灰度变换及直方图均衡化实验一、实验目的:1. 掌握灰度直方图的概念及其计算方法;2. 掌握利用图像灰度变换实现对图像的增强处理;3. 掌握利用直方图直方图均衡化和直方图规定化实现对图像的增强处理;4. 熟悉MA TLAB中图像增强的相关函数。
二、实验设备:1. 硬件设备:计算机;2. 软件环境:Windows+Matlab编程与仿真环境;3. 其他设备:记录用的纸、笔,以及U盘等存储设备。
三、实验原理:灰度直方图(histogram)是灰度级的函数,它表示图像中具有每种灰度级的像素的个数,反映图像中每种灰度出现的频率。
一般来说,灰度直方图的横坐标是灰度级,纵坐标是该灰度级出现的概率,是图像的最基本的统计特性。
从概率论的观点来理解,灰度出现的频率可看作其出现的概率,这样直方图就对应于概率密度函数PDF(Probability Density Function),而概率分布函数就是直方图的累积和,即概率密度函数的积分。
1. 直方图均衡化直方图均衡化是通过灰度变换将一幅图像转换另一幅具有均衡直方图,即在每个灰度级上都具有相同的像素点数的过程。
设灰度变换s=T(r)为斜率有限的非减连续可微函数,它将输入图像A(x,y)转换为输出图像B(x,y),输入图像的直方图为H a(r),输出图像的直方图为H b(s),它们的关系如下:图1.1 输入图像和输出图像直方图之间的关系图直方图均衡化的基本思想是把原始图像的直方图变换成均匀分布的形式图像灰度值的动态范围,从而达到了增强图像整体对比度的效果。
具体方法为:①列出原始图像的灰度级Sk, k=0,1…L-1,其中L是灰度级的个数;②统计原始图像各灰度级的像素数目nk;③计算原始图像直方图各灰度级的频率数;④计算原始图像的累计直方图;⑤取整计算;⑥确定映射关系;⑦统计新直方图各个灰度级的像素数目nk;⑧计算新的直方图。
2. 灰度变换灰度变换是图像增强的另一种重要手段,它可使图像动态范围加大,使图像对比度扩展,图像更加清晰,特征更加明显。
直方图处理(均衡化与匹配)解析

ΣPz(zl)
SML映射(l) 确定映射对应关系(k →l ) 变换后各灰度级像素n'z 变换后直方图
3,4→6 790 0.19 1023 0.25
pr(rk)
Pz(zk) 0.25 0.21 0.19 0.16 0.08 0.06 0.3
0.3 0.2 0.15 0.2 0.15
0.25
0.20 0.15
(3) 计算原始直方图各概率:pk=nk/N; (4) 计算累计直方图:sk=Σpk; (5) 取整Sk=int{(L-1)sk+0.5}; (6) 确定映射对应关系:rksk;
(8) 用pk (sk) =nk'/N计算新直方图。
其中L是灰度层次数, N是图幅总像素数。
直方图的作法
a) 将图像的灰度级归一化
若图象的灰度级为0,1, , L 1, 则令 k rk , k 0,1, , L 1 L 1 则0 rk 1. L为灰度级层次数,Lk rk 1 rk为灰度间隔
b) 计算各灰度级的像素频数(或概率)
设nk 为灰度级为rk的像素的个数,N 为总的像素个数,令 nk pr (rk ) N nk 是像素值为k的像素的频数,pr (rk )为其出现的概率
r 原直方图
s 均衡化后直方图
z
规定直方图
连续图像:设Pr(r)和Pz(z)分别代表原始图像和规定 化处理后图像的灰度概率密度函数. r 对原始直方图进行均衡化处理,有:s T (r ) 0 Pr (r )dr
v G( z ) Pz ( z )dz 对规定化后的直方图均衡化处理,有: 0
0.2
0.1 0.03
6 7
0.10
0.05 0
【数字图像处理】灰度直方图、直方图均衡化、直方图规定化

【数字图像处理】灰度直⽅图、直⽅图均衡化、直⽅图规定化灰度直⽅图 ⼀幅图像由不同灰度值的像素组成,图像中灰度的分布情况是该图像的⼀个重要特征。
图像的灰度直⽅图就描述了图像中灰度分布情况,能够很直观的展⽰出图像中各个灰度级所占的多少。
图像的灰度直⽅图是灰度级的函数,描述的是图像中具有该灰度级的像素的个数:其中,横坐标是灰度级,纵坐标是该灰度级出现的频率。
灰度直⽅图的计算公式如下:p(rk)=nk/MN其中,rk是像素的灰度级,nk是具有灰度rk的像素的个数,MN是图像中总的像素个数。
直⽅图均衡化 Histogram Equalization假如图像的灰度分布不均匀,其灰度分布集中在较窄的范围内,使图像的细节不够清晰,对⽐度较低。
通常采⽤直⽅图均衡化及直⽅图规定化两种变换,使图像的灰度范围拉开或使灰度均匀分布,从⽽增⼤反差,使图像细节清晰,以达到增强的⽬的。
直⽅图均衡化,对图像进⾏⾮线性拉伸,重新分配图像的灰度值,使⼀定范围内图像的灰度值⼤致相等。
这样,原来直⽅图中间的峰值部分对⽐度得到增强,⽽两侧的⾕底部分对⽐度降低,输出图像的直⽅图是⼀个较为平坦的直⽅图。
均衡化算法直⽅图的均衡化实际也是⼀种灰度的变换过程,将当前的灰度分布通过⼀个变换函数,变换为范围更宽、灰度分布更均匀的图像。
也就是将原图像的直⽅图修改为在整个灰度区间内⼤致均匀分布,因此扩⼤了图像的动态范围,增强图像的对⽐度。
通常均衡化选择的变换函数是灰度的累积概率,直⽅图均衡化算法的步骤:计算原图像的灰度直⽅图 P(Sk)=nknP(Sk)=nkn,其中nn为像素总数,nknk为灰度级SkSk的像素个数计算原始图像的累积直⽅图 CDF(Sk)=∑i=0knin=∑i=0kPs(Si)CDF(Sk)=∑i=0knin=∑i=0kPs(Si)Dj=L⋅CDF(Si)Dj=L⋅CDF(Si),其中 DjDj是⽬的图像的像素,CDF(Si)CDF(Si)是源图像灰度为i的累积分布,L是图像中最⼤灰度级(灰度图为255)灰度直⽅图均衡化实现的步骤1.统计灰度级中每个像素在整幅图像中的个数2.计算每个灰度级占图像中的概率分布3.计算累计分布概率4.计算均衡化之后的灰度值5.映射回原来像素的坐标的像素值⽰例说明来看看通过上述步骤怎样实现的拉伸。
灰度图像直方图均衡化变换函数算法

灰度图像直方图均衡化变换函数算法方案一:1) 灰度图像直方图均衡化算法步骤:1、列出原始图像和变换后图像的灰度级I:j=0,1,…L-1,其中L是灰度级的个数;2、统计原始图像个灰度级的像素个数Ni;3、计算原始图像直方图:p(i)=Ni/N,N为原始图像像素总数;4、计算累计直方图Pj=∑p(k),k=0,1…j;5、利用灰度变换函数计算变换后的灰度值,并四舍五入:j=INT[(L-1)Pj+];6、肯定灰度变换关系i—>j,据此将原图像的灰度值f(m,n)=i修正为g(m,n)=j;7、统计变换后各灰度级的像素个数Nj;8、计算变换后图像的直方图p(j)=Nj/N;2) m文件I=imread('');I=I(:,:,1);[m,n]=size(I);num=m*n;pre_mat=zeros(1,256);aft_mat=zeros(1,256);for i=1:mfor j=1:npre_mat(I(i,j)+1)= pre_mat(I(i,j)+1)+1;endendaft_mat(I)=aft_mat(I)/num;for k=2:256s(k)=pre_mat(k)/num;aft_mat(k)=aft_mat(k-1)+s(k);endM=zeros(m,n);aft_mat=aft_mat*255;for i=1:mfor j=1:nM(i,j)=aft_mat(I(i,j)+1);endendJ=uint8(M)subplot(3,2,1)imshow(I);title('1.原始图像');subplot(3,2,2)imhist(I);title('2.原始图像直方图 ');subplot(3,2,3)imshow(J);title('3.均衡化图像');subplot(3,2,4)imhist(J);title('4.均衡化图像直方图');A=histeq(I);subplot(3,2,5)imshow(A);title('5.系统均衡化图像');subplot(3,2,6)imhist(A);title('6.系统均衡化图像直方图')图1 均衡化处置对比经实际验证:该方案对黑白图片均衡化处置有较好的效果。
图像处理——直方图均衡化

图像处理——直⽅图均衡化图像处理——直⽅图均衡化⼀、直⽅图⼀、直⽅图 直⽅图就是之图像中各像素的统计值。
反映图象中每种灰度出现的频率。
直⽅图的性质:直⽅图就是之图像中各像素的统计值。
反映图象中每种灰度出现的频率。
直⽅图的性质:1)表征了图像的⼀维信息。
只反映图像中像素不同灰度值出现的次数(或频数)⽽未反映像素所在位置。
1)表征了图像的⼀维信息。
只反映图像中像素不同灰度值出现的次数(或频数)⽽未反映像素所在位置。
2)与图像之间的关系是多对⼀的映射关系。
⼀幅图像唯⼀确定出与之对应的直⽅图,但不同图像可能有相同的直⽅图。
2)与图像之间的关系是多对⼀的映射关系。
⼀幅图像唯⼀确定出与之对应的直⽅图,但不同图像可能有相同的直⽅图。
3)⼦图直⽅图之和为整图的直⽅图。
3)⼦图直⽅图之和为整图的直⽅图。
⼆、直⽅图均衡化⼆、直⽅图均衡化直⽅图均衡化处理的“中⼼思想”是把原始图像的灰度直⽅图从⽐较集中的某个灰度区间变成在全部灰度范围内的均匀分布。
直⽅图均衡化直⽅图均衡化处理的“中⼼思想”是把原始图像的灰度直⽅图从⽐较集中的某个灰度区间变成在全部灰度范围内的均匀分布。
直⽅图均衡化就是对图像进⾏⾮线性拉伸,重新分配图像像素值,使⼀定灰度范围内的像素数量⼤致相同。
直⽅图均衡化就是把给定图像的直⽅图分布改就是对图像进⾏⾮线性拉伸,重新分配图像像素值,使⼀定灰度范围内的像素数量⼤致相同。
直⽅图均衡化就是把给定图像的直⽅图分布改变成“均匀”分布直⽅图分布。
变成“均匀”分布直⽅图分布。
(I )直⽅图均衡化的过程:(I )直⽅图均衡化的过程:1)列出原始图像和变换后图像的灰度级(L 是灰度级的个数);1)列出原始图像和变换后图像的灰度级(L 是灰度级的个数);2)统计原图像中各灰度级的像素个数;2)统计原图像中各灰度级的像素个数;3)计算原始图像直⽅图P(i)=Ni/N ;3)计算原始图像直⽅图P(i)=Ni/N ;4)计算累计直⽅图P(j)=P(1) + P(2) + P(3) +…+ P(i);4)计算累计直⽅图P(j)=P(1) + P(2) + P(3) +…+ P(i);5)利⽤灰度值变换函数计算变换后的灰度值,并四舍五⼊取整;j=INT[(L-1)Pj+0.5]5)利⽤灰度值变换函数计算变换后的灰度值,并四舍五⼊取整;j=INT[(L-1)Pj+0.5]6)确定灰度变换关系i →j ,据此将原图像的灰度值f (m,n )=i 修正为g (m ,n )=j ;6)确定灰度变换关系i →j ,据此将原图像的灰度值f (m,n )=i 修正为g (m ,n )=j ;7)统计变换后各灰度级的像素个数Nj ;7)统计变换后各灰度级的像素个数Nj ;8)计算变换后图像的直⽅图Pj=Nj/N 8)计算变换后图像的直⽅图Pj=Nj/N(II )图像均衡化后的缺点:(II )图像均衡化后的缺点:1)变换后图像的灰度级减少,某些细节消失;1)变换后图像的灰度级减少,某些细节消失;2)某些图像,如直⽅图有⾼峰,经处理后对⽐度不⾃然的过分增强。
【OpenCV】图像增强---灰度变换、直方图均衡化

【OpenCV】图像增强---灰度变换、直⽅图均衡化图像增强的⽬的:改善图像的视觉效果或使图像更适合于⼈或机器的分析处理。
通过图像增强,可以减少图像噪声,提⾼⽬标与背景的对⽐度,也可以增强或抑制图像中的某些细节。
---------------------------------------------------------------------------------------------------灰度变换:把原图像的像素灰度经过某个函数变换成新图像的灰度。
可分为直线灰度变换法和直⽅图修正法。
直线灰度变换法:线性、分段线性、⾮线性变换。
直⽅图修正法:直⽅图均衡化、直⽅图规定化。
---------------------------------------------------------------------------------------------------图像直⽅图:是对像素的某种属性(如灰度、颜⾊、梯度等)分布进⾏统计分析的重要⼿段。
灰度直⽅图:是灰度级的函数,它反映了图像中每⼀灰度级出现的次数或频率。
直⽅图均衡化:把原始图像的直⽅图变换为均匀分布的形式,从⽽增加图像灰度的动态范围,以达到增强图像对⽐度的效果。
经过均衡化处理的图像,其灰度级出现的概率相同,此时图像的熵最⼤,图像所包含的信息量最⼤。
【注意,离散后是每块区域的概率相等,均衡化后并不是条直线哦。
】 细节概念等省略......---------------------------------------------------------------------------------------------------线性灰度增强、对数变换、指数变换、直⽅图均衡化。
代码见下(代码略粗糙...)【ImageEnhance.cpp部分代码】1//线性灰度增强2bool CImageEnhance::GrayLinearTransform(Mat &src, Mat &dst, uchar c, uchar d)3 {4int b=0,a=255;5 dst = src.clone();6int row = dst.rows, col = dst.cols * dst.channels();7 uchar *cc = dst.data;8for(int i = 0; i < row; ++i) {9for(int j = 0; j < col; ++j) {10int val = *cc;11if(a > val) a = val;12if(b < val) b = val;13 cc++;14 }15 }16 cc = dst.data;17float k = float(d - c)/(b-a);18//CString c1; c1.Format(_T("a=%d,b=%d,c=%d,d=%d,k=%.2f\n"), a,b,c,d,k);MessageBox(c1);19for(int i = 0; i < row; ++i) {20for(int j = 0; j < col; ++j) {21int val = *cc;22int s = (int)(k*(val - a) + c);23 *cc = s;24 cc++;25 }26 }27return true;28 }29//对数变换30bool CImageEnhance::GraynoLinearlog(Mat &src, Mat &dst) {31 dst = src.clone();32int row = dst.rows, col = dst.cols * dst.channels();33 uchar *cc = dst.data;34double k = 255 / log10(256.0);35for(int i = 0; i < row; ++i) {36for(int j = 0; j < col; ++j) {37int val = *cc;38 *cc = k * log10(1.0*(val + 1));39 cc++;40 }41 }42return true;43 }44//指数变换45bool CImageEnhance::GraynoLinearindex(Mat &src, Mat &dst) {46 dst = src.clone();47int row = dst.rows, col = dst.cols * dst.channels();48 uchar *cc = dst.data;49double k = 1.0 / 255;50for(int i = 0; i < row; ++i) {51for(int j = 0; j < col; ++j) {52int val = *cc;53 *cc = k * val * val;54 cc++;55 }56 }57return true;58 }5960 MatND CImageEnhance::getHist1(Mat& image)61 {62 MatND hist;63int channels[] = {0};64int dims = 1;65int histSize[] = {256}; //直⽅图箱⼦的个数66float granges[] = {0, 255};67const float *ranges[] = {granges}; //像素值范围68//计算直⽅图69 calcHist(&image, 1, channels, Mat()/*不使⽤掩码*/, hist, dims/*这是⼀维的直⽅图*/, histSize, ranges);70return hist; //这⾥得到的hiat是256⾏⼀列的Mat71 }7273//直⽅图均衡化74bool CImageEnhance::Equalize_hist(cv::Mat& src,cv::Mat& dst)75 {76//CMFC_Test_lyyDlg pic;77 MatND hist;78int channels[] = {0};79int dims = 1;80int histSize[] = {256}; //直⽅图箱⼦的个数81float granges[] = {0, 255};82const float *ranges[] = {granges}; //像素值范围83//计算直⽅图84 Mat image = src.clone();85 calcHist(&image, 1, channels, Mat()/*不使⽤掩码*/, hist, dims/*这是⼀维的直⽅图*/, histSize, ranges);8687//MatND hist = getHist1(src);//pic.getHist(dst);88float s[256];89float p[256];9091 cv::Mat lookup(cv::Size(1, 256), CV_8U);92int pixNum = src.cols * src.rows;//总像素个数93for (int i =0; i <256; i++) {94 s[i] = hist.at<float>(i) / pixNum;95if (i ==0) {96 p[i] = s[i];97 }98else {99 p[i] = p[i -1] + s[i];100 }101 }102for (int i =0; i <256; i++) {103 lookup.at <uchar>(i) = static_cast<uchar>(p[i]*255.0);104 }105106 cv::LUT(src, lookup, dst);//创建矩阵,把⼀个像素值映射到另⼀个像素值107return true;108 }ImageEnhance.cpp效果如下:原图像:线性灰度增强:我这⾥默认a和b表⽰原图像灰度值的最⼩与最⼤值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图像的直方图均衡与分段灰度变换
F10030255100309018董威
一、基本原理与主要用途;
1.直方图均衡与分段灰度变换的基本原理;
直方图均衡化的目的是将原始图像的直方图变为均衡分布的形式,即将一已知灰度概率密度分布的图像,经过某种变换变成一幅具有均匀灰度概率密度分布的新图像,从而改善图像的灰度层次。
它的基本思想是把原始图像的直方图变换成均匀分布的形式,这样就增加了像素灰度值的动态范围,从而达到了增强图像整体对比度的效果。
MATLAB图像处理工具箱中提供的histeq函数,可以实现直方图的均衡化。
线性变换是指在图像灰度范围内分段对逐个像元进行处理,是将原图像亮度值动态范围按线性关系(线性函数)变换到指定范围或整个动态范围。
在实际运算中给定的是2个亮度区间,即要把输入图像的某个亮度值区间[a,b]映射为输出图像的亮度值区间[c,d]。
即按线性比例对图像每一个象素灰度作灰度线性变换,改善图像视觉效果。
在实际图像处理中,为了突出感兴趣的目标或灰度区域,相对抑制不感兴趣的灰度区域,常常采用分段线性变换来进行图像灰度的处理。
MATLAB图像处理工具箱中提供的imadjust函数,可以实现上述的线性变换。
2.主要用途;
在获取图像的过程中,由于噪声,光照等外界环境或设备本身的原因,原始数字图像质量会退化。
例如一般成像系统只具有一定的响应亮度,常出现对比度不足的弊病,影响视觉效果,在这些情况下需要对图像做增强处理。
图像增强可以提高清晰度,改善图像的视觉效果,突出图像中的有用信息,削弱或消除不需要的信息。
二、实现方案与源码;
1.直方图均衡化;
MATLAB图像处理工具箱的histep函数可以很方便的实现直方图均衡化。
由于原图片是彩色,因而在转换前需要用rgb2gray函数将图片转化为灰度图。
源程序如下:
a=imread('e:\b.bmp');%读取图像
b=rgb2gray(a);%转化为灰度图像
subplot(121),imshow(a);
subplot(122),imhist(b);
实现结果如下:
原图转化为的灰度图像
subplot(121),imshow(b);
subplot(122),imhist(b);%显示灰度图像与其直方图
实现结果如下:
c=histeq(b);%直方图均衡化
subplot(121),imshow(b);
subplot(122),imhist(b);%显示处理后的图像与其直方图
实现结果如下:
不调用histeq函数,利用matlab语言也可直接编程实现图像的直方图均衡化处理。
图像的灰度直方图均衡化公式:
公式中,T(r k)来表示原图像的第k个灰度级的转换函数。
∑表示总和。
∑n j/N表示0~j个灰度级的像素数量总和与像素总数的比值,也就是前面讲过的百分位(当前色阶与前面色阶的所有像素数量÷总像素数量)。
∑P r(r k)表示第0~k的灰度级出现概率累积相加。
因为s是归一化的数值(s∈[0,1]),要转换为0~255的颜色值,需要再乘上255,即S=∑P r(r k)*255。
流程如下:
读取图像——>转换为灰度图像——>计算各灰度出现的概率——>计算新的各灰度出现的概率——>填充各像素点新的灰度值——>显示图像
相应的源程序如下:
a=imread('e:\b.bmp');%读取图像
[m,n,o]=size(a);
grayPic=rgb2gray(a);
figure,imshow(a);
figure,imshow(grayPic);
gp=zeros(1,256);%计算各灰度出现的概率
for i=1:256
gp(i)=length(find(grayPic==(i-1)))/(m*n);
end
figure,bar(0:255,gp);
title('原图像直方图');
xlabel('灰度值');
ylabel('出现概率');
newGp=zeros(1,256);%计算新的各灰度出现的概率
S1=zeros(1,256);
S2=zeros(1,256);
tmp=0;
for i=1:256
tmp=tmp+gp(i);
S1(i)=tmp;
S2(i)=round(S1(i)*256);
end
for i=1:256
newGp(i)=sum(gp(find(S2==i)));
end
figure,bar(0:255,newGp);
title('均衡化后的直方图');
xlabel('灰度值');
ylabel('出现概率');
newGrayPic=grayPic;%填充各像素点新的灰度值
for i=1:256
newGrayPic(find(grayPic==(i-1)))=S2(i);
end
figure,imshow(newGrayPic);
实现结果与调用函数一致。
2.分段线性灰度变换;
通过分段线性变换,原图f (x,y )中灰度值在0到a 和b 到M f 间的动态范围映
射到g(x,y)后被压缩,而a 到b 区间的动态范围增加,从而增强了这个范围内的对比度。
为了实现灰度线性变换在图像处理中的应用,本文以彩色图像"b.bmp"为例,采用MATLAB 语言编制了分段线性变换的实现程序,并获得了变换效果。
编程思路如下:
设原图像f (x,y )灰度范围为[0,M f ],变换后的图像g (x,y )灰度范围为[0,M g ],
通过调整折线拐点的位置及控制分段直线的斜率,可对任一灰度区间进行扩展或压缩。
将感兴趣的灰度范围线性扩展,相对抑制不不感兴趣的灰度区域。
源程序如下:
b=imread('e:\b.bmp');%读取图像
i=rgb2gray(b);%转化为灰度图像
di=double(i);
imhist(i);
a=min(min(di));
b=max(max(di));
c=120.0;d=150.0;
a1=0.0;b1=255.0;
c1=30.0;d1=171.0;
n1=find(di>=a&di<c);
n2=find(di>=c&di<d);
n3=find(di>=d&di<b);
di2=di;
di2(n1)=(di(n1)-a)*(c1-a1)/(c-a)+a1;
di2(n2)=(di(n2)-c)*(d1-c1)/(d-c)+c1;
di2(n3)=(di(n3)-d)*(b1-d1)/(b-d)+d1;
i2=uint8(di2);
subplot(221),imshow(i);
subplot(222),imshow(i2);
subplot(223),imhist(i);
subplot(224),imhist(i2);
实现结果如下:
原图转化为的灰度图像分段灰度变换后图像
三、对实验结果的总结和分析;
直方图均衡化前后对比如下:
原图的灰度图像变换后图像
通过对比可以看出原图动态范围较小,像素集中在图像中间调区域,亮调和暗调几乎没有像素,所以图像平淡,对比度低。
均衡化后直方图扩展到整个图象灰度允许的范围,对比度明显增强。
用直方图均衡化后,图像的直方图的灰度间隔被拉大了,均衡化的图像的一些细节显示了出来,这有利于图像的分析和识别。
分段灰度变换前后对比如下:
原灰度图变换后图像
通过对比可以看出原图经过分段变换前后的对比图可知原图中间得到拉伸,对比度得到增强。
在显示设备的亮度动态范围不足以满足要求时,可以用这种变换再显示,以利于在较大的灰度范围内显示出灰度值的差异。
图像的像素灰度变化是随机的,直方图的图形高低不齐,直方图均衡化就是用一定的算法使直方图大致平和。
灰度变换主要通过对原图像素值进行重新分配,提高图像的对比度;直方图处理是把原始图的直方图变换为均匀分布的形式,增加像素灰度值的动态范围以达到增图像整体对比度的效果;图像增强处理并不能使原始图像信息增加,而只能增强对某种信息的辨别能力,提高了图像的视觉特性。
