锐角三角函数经典总结
最新初三锐角三角函数知识点总结、典型例题、练习(精选)
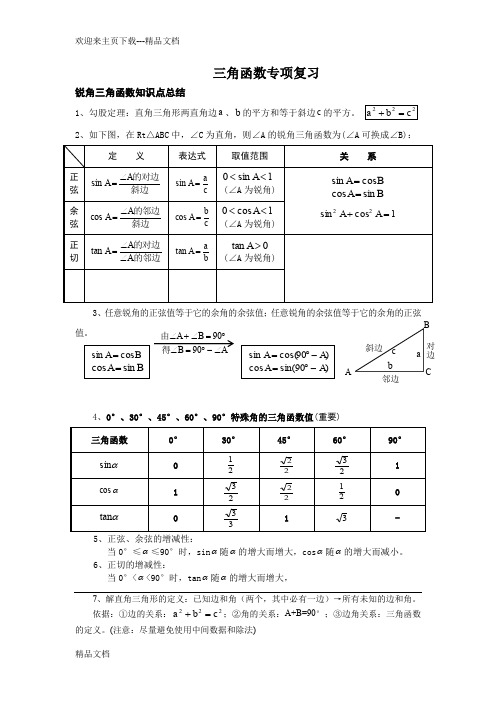
三角函数专项复习锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
222c b a =+2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):定 义表达式取值范围关 系正弦 斜边的对边A A ∠=sin c aA =sin 1sin 0<<A (∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A (∠A 为锐角) 正切 的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A (∠A 为锐角)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、0°、30°、45°、60°、90°特殊角的三角函数值(重要) 三角函数 0° 30°45°60°90° αsin 0 21 22 23 1 αcos1 23 2221 0 αtan33 1 3-5、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
6、正切的增减性:当0°<α<90°时,tan α随α的增大而增大,7、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法) )90cos(sin A A -︒=)90sin(cos A A -︒=BA cos sin =BA sin cos =A90B 90∠-︒=∠︒=∠+∠得由B A对边邻边斜边 ACBba c8、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
锐角三角函数知识点总结大全

锐角三角函数知识点总结大全
1.解直角三角形必备条件:(除直角外)至少知道两条边的
长度或一条边的长度和一个角的度数。
2.近似计算不能用勾股定理求边长,否则误差会很大。
3.解直角三角形解题思路总结:(除直角外)
(1)知一角求另一角题型:已知一个角的度数,用直角三角形中两锐角互余,求出另一角的度数。
(2)知两边求另一边题型:已知两边的边长,用勾股定理求出第三边的长。
(3)锐角三角函数:适用于“知角求边”或“知边求角”
的题型中。
(用sin,cos,tan,cot求出)。
4.仰角和俯角
(1)仰角:视线在水平线上方,与水平线形成的夹角。
(2)俯角:是现在水平线下方,与水平线形成的夹角。
5.锐角三角函数的性质(a为锐角)
(1)正弦的性质:
①取值范围:0<sina<1 ②增减性:a越大,sina越大(2)余弦的性质:
①取值范围:0<cosa<1 ②增减性:a越大,cosa越小联系:sina和cosa互为反函数
(3)正切的性质:
①取值范围:tana可取全体正数②a越大,tana越大
③当a无限接近90度时,tana无穷大。
(4)余切的性质
①取值范围:cota可取全体正数②当a无限接近0度时,cota无穷大③a越大,cota越小
6.锐角三角函数间的关系
(1)平方关系:sina2+cosa2=1
(2)倒数关系:tana=1
cota
(3)比值关系:①tana=sina
cosa ②cota=cosa
sina。
初中锐角三角函数知识点总结

锐角三角函数及其应用榆林第六中学 高启鹏一、锐角三角函数中考考点归纳考点一、锐角三角函数 1、锐角三角函数的定义如图,在 Rt △ ABC 中,/ C 为直角, 有(1) 图表记忆法三角\角 函数、304560si na1 c亡222 cosa爲匹J222tana乜31(2) 规律记忆法:30 °、45 °、60°角的正弦值的分母都是 2,分 子依次为1、. 2、3 ;30°、45°、60°角余弦值恰好是 60°、45°、 30°角的正弦值。
/ A 的正弦: sin A A 的对边a 斜边 c / A 的余弦: cos A A 的邻边b 斜边c / A 的正切: tan AA 的对边a A 的邻边b2、特殊角的三角函数值则/ A ABC 中的一锐角,则(3)口诀记忆法口诀是:“一、二、三,三、二、一,三、九、二十七,弦比二,切比三,分子根号不能删.”前三句中的1,2,3;3,2,1;3,9,27,分别是30°,45 °,60°角的正弦、余弦、正切值中分子根号内的值.弦比二、切比三是指正弦、余弦的分母为2,正切的分母为3.最后一句,讲的是各函数值中分子都加上根号,不能丢掉.如tan60 °二旦 ,3,tan45 =— 1 .这种方法有趣、简单、3 3易记.考点二、解直角三角形1、由直角三角形中的已知元素求出其他未知元素的过程,叫做解直角三角形。
2、解直角三角形的类型和解法如下表:考点二、锐角二角函数的实际应用(咼频考点)仰角、俯角、坡度(坡比)、坡角、方向角仰角、俯角在视线与水平线所成的锐角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角。
坡度(坡比)、坡角坡面的铅直高度h和水平宽度1的比叫坡度(坡比),用字母i表示;坡面与水平线的夹角叫坡角,i tan Pl指北或指南的方向线与目标方向线所成的小于90°的锐角叫做方向角.注意:东北方向指北偏东45方向,东南方向指南偏方向角东45 方向,西北方向指北偏西45方向,西南方向指南偏西45°方向.我们一般画图的方位为上北下南,左西右东.二、锐角三角函数常见考法(一)、锐角三角函数以选择题的形式出现.例1、(2016?陕西)已知抛物线y二-x2-2x+3与x轴交于A B两点,将这条抛物线的顶点记为C,连接AG BC则tan / CAB的值为()A.丄B . ■- C •」D ■ 2【考点】抛物线与x轴的交点;锐角三角函数的定义.CD:【解析】先求出A B、C坐标,作CDL AB于D,根据tan / ACD=-即可计算.o【解答】解:令y=0,则-x —2x+3=0,解得x=—3或1,不妨设A (—3,0),B (1, 0),2 2• y二—x - 2x+3=—( x+1) +4,「•顶点C (- 1, 4),如图所示,作CDL AB于D.故答案为D.(二)、锐角三角函数以填空题的形式出现例2、(2016?陕西)请从以下两个小题中任选一个作答,若多选,则按第一题计分.A. —个多边形的一个外角为45°,则这个正多边形的边数是8 .B. 运用科学计算器计算:3.「sin73 ° 52’〜11.9 .(结果精确到0.1 )【考点】计算器一三角函数;近似数和有效数字;计算器一数的开方;多边形内角与外角.【解析】(1)根据多边形内角和为360°进行计算即可;(2)先分别求得3. 7和sin73 ° 52 '的近似值,再相乘求得计算结果.【解答】解:(1)v正多边形的外角和为360° 二这个正多边形的边数为:360°宁45° =8(2) 3 i sin73 °52’ 〜12.369 x0.961 〜11.9故答案为:8, 11.9例3、(2015?陕西)如图,有一滑梯 AB,其水平宽度AC 为5.3米,铅直高 度BC 为2.8米,则/ A 的度数约为 27.8(用科学计算器计算,结果精【考点】解直角三角形的应用-坡度坡角问题. 【解析】直接利用坡度的定义求得坡角的度数即可. 【解答】 解:T tan / A 」"1〜0.5283 ,AC 5. 3•••/ A=27.8°, 故答案为:27.8 ° .【点评】本题考查了坡度坡角的知识,解题时注意坡角的正切值 等于铅直高度与水平宽度的比值,难度不大.例4、(2014?陕西)用科学计算器计算:一 一;+3tan56 °〜10.02 (结果精确到0.01 ) 计算器一三角函数;计算器一数的开方.先用计算器求出tan56°的值,再计算加减运解:「丨〜5.5678 , tan56 °〜1.4826 , 则-1 +3tan56 °〜5.5678+3 X 1.4826 〜10.02故答案是:10.02 .【点评】 本题考查了计算器的使用,要注意此题是精确到【考点】 【分析】0.01.例5、(2014?陕西)如图,在正方形 ABC [中, AD=1将厶ABD绕点B 顺时针旋转45 °得到△ A BD ,此时A D 与CD 交于【考点】 旋转的性质【分析】 利用正方形和旋转的性质得出 A D=A E ,进而利用 勾股定理得出BD 的长,进而利用锐角三角函数关系得出 DE 的长 即可.【解答】 解:由题意可得出:/ BDC=45,/ DA E=90° , •••/ DEA =45°,••• A D=A E ,•••在正方形ABCD 中AD=1 • AB=A B=1, • BD=:':, • A D 二;:-1,•••在 Rt △ DA E 中,DE备=2-五故答案为:2-血.【点评】此题主要考查了正方形和旋转的性质以及勾股定理、2~41锐角三角函数关系等知识,得出 A D 的长是解题关键.(三) 、锐角三角函数定义以解答题的形式出现例6、( 12分)(2015?陕西)如图,在每一个四边形 ABC 冲,均有AD// BC ;CDL BC / ABC=60 , AD=8 BC=12(1) 如图①,点M 是四边形ABCDi AD 上的一点,则厶BMC 勺面积为 24「;; (2) 如图②,点N 是四边形ABCD* AD 上的任意一点,请你求出△ BNC 周长 的最小值;(3) 如图③,在四边形ABCD 勺边AD 上,是否存在一点P,使得cos / BPC 的 值最小?若存在,求出此时cos / BPC 勺值;若不存在,请说明理由.【考点】四边形综合题.. 【专题】综合题.【解析】(1)如图①,过A 作AE ! BC 可得出四边形AECF 为矩形,得到EC=ADBE 二B G EC 在直角三角形 ABE 中,求出AE 的长,即为三角形 BMC 勺高,求 出三角形BMC 面积即可;(2) 如图②,作点C 关于直线AD 的对称点C ,连接C N, C D, C B 交AD 于点 N ,连接 CN ,贝卩 BN+NC 二BN+NO BC =BN +CN ,可得出厶 BNC 周长的最小值BN C 的周长=BN +CN +BC 二BC+BC 求出即可;(3) 如图③所示,存在点P,使得cos /BPC 的值最小,作BC 的中垂线PQ 交BC 于点Q 交AD 于点P,连接BP CP 作厶BPC 的外接圆Q 圆O 与直线PQ 交于点N,则PB=PC 圆心0在PN 上,根据AD 与BC 平行,得到圆0与AD 相AD圈②图①ACc图③切,根据PQ=DC判断得到PQ大于BQ可得出圆心0在BC上方,在AD上任取一点P',连接P‘ B, P C, P‘ B交圆0于点M连接MC可得/ BPC= / BM OZ BP C,即/ BPC最小,cos/ BPC的值最小,连接0B求出即可.【解答】解:(1)如图①,过A作AE±BC二四边形AEC助矩形,••• EC=AD=8 BE二B G EC=12- 8=4,在Rt△ ABE中, / ABE=60 , BE=4•AB=2BE=8 AE=:・,二=4 二则S A BM千BC? AE=24 -;;故答案为:24. -;;(2)如图②,作点C关于直线AD的对称点C,连接C N, C D, C B交AD于点N,连接CN,贝卩BN+NC二BN+NO BC =BN +CN ,•△ BNC周长的最小值为△ BN C的周长=BN +CN +BC=BC +BCv AD// BC AE! BC / ABC=60 ,•过点A 作AE! BC 则CE=AD=8•BE=4 AE=B? tan60 ° 二酣1,•CC =2CD=2AE=8,v BC=12•BC=血/+防2=4阿,•△ BNC周长的最小值为4 1+12;(3)如图③所示,存在点P,使得cos/ BPC的值最小,作BC的中垂线PQ交BC于点Q交AD于点P,连接BP, CR作厶BPC的外接精品文档圆Q 圆0与直线PQ交于点N,贝S PB=PC圆心0在PN上,v AD// BC•••圆0与AD相切于点P,v PQ=DC=4>6,•PQ> BQ•/BPG 90°,圆心O在弦BC的上方,在AD上任取一点P',连接P‘ B, P‘ C, P‘ B交圆0于点M连接MC•••/ BPC y BM OZ BP C,•/ BPC最大,cos / BPC的值最小,连接0B 贝卩/ BON=/BPN/ BPCv 0B=0P=4 - 0Q在Rt△ B0C中,根据勾股定理得:0Q+62二(砸-0Q 2,解得:0Q二:;,2•0B二:,2•cos / BPC二co/ B0Q==l,P厂则此时cos/ BPC的值为一.【点评】此题属于四边形综合题,涉及的知识有:勾股定理,矩形的判定与性质,对称的性质,圆的切线的判定与性质,以及锐角三角函数定义,熟练掌握定理及性质是解本题的关键.例7、(10分)(2014年陕西省)已知抛物线C: y二-x2+bx+c经过A (- 3, 0)和B (0, 3)两点,将这条抛物线的顶点记为M它的对称轴与x轴的交点记为N.(1)求抛物线C的表达式;(2)求点M的坐标;(3)将抛物线C平移到C,抛物线C的顶点记为M',它的对称轴与x轴的交点记为N'.如果以点M N M、N为顶点的四边形是面积为16的平行四边形,那么应将抛物线C怎样平移?为什么?新课标xk b1. c om【考点】二次函数图象与几何变换;二次函数的性质;待定系数法求二次函数解析式;平行四边形的性质.菁优网版权所有【分析】(1)直接把A(- 3, 0)和B(0, 3)两点代入抛物线y二-x2+bx+c, 求出b, c 的值即可;(2)根据(1)中抛物线的解析式可得出其顶点坐标;(3)根据平行四边形的定义,可知有四种情形符合条件,如解答图所示.需要分类讨论.【解答】解: (1)V抛物线y二-x2+bx+c经过A (- 3, 0)和B (0, 3)两占J \\、’解得仁2,故此抛物线的解析式为:y二-x2- 2x+3;(2)v由(1)知抛物线的解析式为:y二-x2- 2x+3,•••当x=- 一= - = - 1 时,y=4, xKb 1.C omSa 2X ( -1) ,‘,• M(- 1, 4).(3J由题意,以点MN、M、N为顶点的平行四边形的边MN勺对边只能是M‘ N, •MN/ M N 且MN二M N.•MN NN =16,•NN =4.i )当M、N M、N为顶点的平行四边形是? MNN M时,将抛物线C向左或向右平移4个单位可得符合条件的抛物线C ;ii )当M N M、N为顶点的平行四边形是? MNMN时,将抛物线C先向左或向右平移4个单位,再向下平移8个单位,可得符合条件的抛物线C . •上述的四种平移,均可得到符合条件的抛物线C .【点评】本题考查了抛物线的平移变换、平行四边形的性质、待定系数法及二次函数的图象与性质等知识点.第(3)问需要分类讨论,避免漏解.例8、(12分)(2014?陕西)问题探究(1)如图①,在矩形ABCD K AB=3 BC=4如果BC边上存在点巳使厶APD 为等腰三角形,那么请画出满足条件的一个等腰三角形△ APD并求出此时BP 的长;(2)如图②,在△ ABC中,/ ABC=60 , BC=12 AD是BC边上的高,E、F分别为边AB AC的中点,当AD=6时,BC边上存在一点Q 使/ EQF=90,求此时BQ 的长;问题解决(3)有一山庄,它的平面图为如图③的五边形ABCDE山庄保卫人员想在线段CD 上选一点M安装监控装置,用来监视边AB现只要使/ AMB大约为60°, 就可以让监控装置的效果达到最佳,已知/ A二/ E=Z D=90°, AB=270m AE=400mED=285m CD=340m问在线段CD上是否存在点M 使/ AMB=60 ? 若存在,请求出符合条件的DM的长,若不存在,请说明理由.A D團①图②團③【考点】圆的综合题;全等三角形的判定与性质;等边三角形的性质;勾股定理;三角形中位线定理;矩形的性质;正方形的判定与性质;直线与圆的位置关系;特殊角的三角函数值.菁优网版权所有【专题】压轴题;存在型.【分析】(1)由于△ PAD是等腰三角形,底边不定,需三种情况讨论,运用三角形全等、矩形的性质、勾股定理等知识即可解决问题.(2)以EF为直径作。
锐角三角函数单元总结
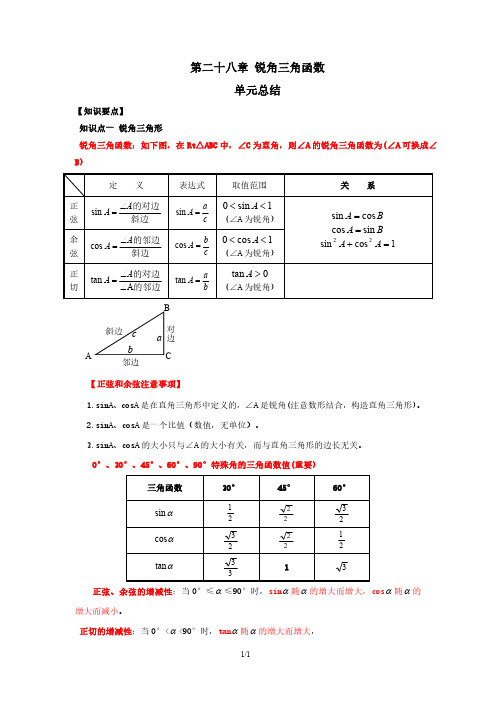
第二十八章锐角三角函数单元总结【知识要点】知识点一锐角三角形锐角三角函数:如下图,在Rt△ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B)定义表达式取值范围关系正弦斜边的对边A A ∠=sin c a A =sin1sin 0<<A (∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A 余弦斜边的邻边A A ∠=cos c b A =cos1cos 0<<A (∠A 为锐角)正切的邻边的对边A tan ∠∠=A A ba A =tan 0tan >A (∠A 为锐角)对边邻边斜边ACBba c 【正弦和余弦注意事项】1.sinA、cosA 是在直角三角形中定义的,∠A 是锐角(注意数形结合,构造直角三角形)。
2.sinA、cosA 是一个比值(数值,无单位)。
3.sinA、cosA 的大小只与∠A 的大小有关,而与直角三角形的边长无关。
0°、30°、45°、60°、90°特殊角的三角函数值(重要)三角函数30°45°60°αsin 212223αcos 232221αtan 3313正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
正切的增减性:当0°<α<90°时,tan α随α的增大而增大,知识点二解直角三角形一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形.直角三角形五元素之间的关系: 1.勾股定理()2.∠A+∠B=90°3.sin A==4.cos A==5.tan A==【考查题型】考查题型一正弦典例1.(2020·陕西西安市·西北工业大学附属中学九年级期中)如图,在54⨯的正方形网格中,每个小正方形的边长都是1,ABC ∆的顶点都在这些小正方形的顶点上,则sin BAC ∠的值为()A .43B .34C .35D .45变式1-1.(2018·西城区·北京四中九年级期中)如图,在Rt ABC ∆中,90C = ∠,10AB =,8AC =,则sin A 等于()A .35B .45C .34D .43变式1-2.(2019·山东淄博市·九年级期中)如图,在Rt △ABC 中,∠C =90°,sin A =45,AC =6cm ,则BC 的长度为()A .6cmB .7cmC .8cmD .9cm考查题型二余弦典例2.(2020·福建省泉州市培元中学九年级期中)如图,△ABC 的顶点都是正方形网格中的格点,则cos ∠ABC 等于()A .55B .255C 5D .23变式2-1.(2016·辽宁铁岭市·九年级期末)在ABC 中,C 90∠= ,AB 6=,1cosA 3=,则AC 等于()A .18B .2C .12D .118变式2-2.(2019·山东滨州市·九年级期末)如图,在平面直角坐标系中,点M 的坐标为M 52),那么cosα的值是()A B .23C .252D .53考查题型三正切典例3.(2020·广东深圳市·深圳中学八年级期中)如图,A 、B 、C 是小正方形的顶点,且每个小正方形的边长为1,则tan ∠BAC 的值为()A .12B .1C .33D 变式3-1.(2018·江苏苏州市·九年级期末)如图,在等腰Rt ABC ∆中,90C ∠=︒,6AC =,D 是AC 上一点,若1tan 5DBA ∠=,则AD 的长为().A .2B C D .1变式3-2.(2020·河北唐山市·九年级期末)如图,有一斜坡AB ,坡顶B 离地面的高度BC 为30m ,斜坡的倾斜角是∠BAC ,若2tan 5BAC ∠=,则此斜坡的水平距离AC 为()A .75mB .50mC .30mD .12m考查题型四特殊角的三角函数值典例4.(2018·南昌市期末)点M(-sin 60°,cos 60°)关于x 轴对称的点的坐标是()A .(32,12)B .(-32,-12)C .(-32,12)D .(-12,-32)变式4-1.(2019·山东淄博市·九年级期中)下列式子错误的是()A .cos40°=sin50°B .tan15°•tan75°=1C .sin 225°+cos 225°=1D .sin60°=2sin30°变式4-2.(2018·河北唐山市·九年级期末)如果△ABC 中,sin A =cos B =22,则下列最确切的结论是()A .△ABC 是直角三角形B .△ABC 是等腰三角形C .△ABC 是等腰直角三角形D .△ABC 是锐角三角形考查题型五同角的三角函数典例5.(2018·山东潍坊市·九年级期末)在Rt △ABC 中,∠C =90°,sinA=45,则cosB 的值等于()A .35B .45C .34D .55变式5-1.(2018·浙江台州市·九年级期末)在Rt △ABC 中,cosA=12,那么sinA 的值是()A .22B .32C .33D .12变式5-2.(2018·湖南岳阳市·九年级期末)在Rt ABC 中,C 90∠= ,如果4cosA 5=,那么tanA 的值是()A .35B .53C .34D .43考查题型六解直角三角形典例6.(2020·东北师大附中明珠学校九年级期中)如图,两根竹竿AB 和AD 斜靠在墙CE 上,量得∠ABC=α,∠ADC=β,则竹竿AB 与AD 的长度之比为()A .tan tan αβB .sin sin βαC .sin sin αβD .cos cos βα变式6-1.(2020·山东枣庄市·九年级期末)如图,在ABC ∆中,144CA CB cosC ==,=,则sinB 的值为()A .102B .3C .4D .104变式6-2.(2019·辽宁沈阳市·九年级期末)如图,甲乙两楼相距30米,乙楼高度为36米,自甲楼顶A 处看乙楼楼顶B 处仰角为30°,则甲楼高度为()A .11米B .(36﹣)米C .D .(36﹣考查题型七利用解直角三角形相关知识解决实际问题典例7.(2019·河南许昌市·九年级期末)如图,某消防队在一居民楼前进行演习,消防员利用云梯成功救出点B 处的求救者后,又发现点B 正上方点C 处还有一名求救者.在消防车上点A 处测得点B 和点C 的仰角分别是45°和65°,点A 距地面2.5米,点B 距地面10.5米.为救出点C 处的求救者,云梯需要继续上升的高度BC 约为多少米?(结果保留整数.参考数据:≈1.4)变式7-1.(2018·江苏无锡市·九年级期末)如图,为了测量出楼房AC的高度,从距离楼底C 处603D(点D与楼底C在同一水平面上)出发,沿斜面坡度为3的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈43,计算结果用根号表示,不取近似值).变式7-2.(2018·山西晋中市期末)“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB 的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)。
锐角三角函数的比例性质总结

锐角三角函数的比例性质总结一、正弦函数的比例性质1.正弦函数的定义:在直角三角形中,正弦函数是对于一个锐角,其对边与斜边的比值。
2.正弦函数的周期性:正弦函数的值域为[-1,1],且每隔2π,函数值重复一次。
3.正弦函数的奇偶性:sin(-x) = -sin(x),所以正弦函数是奇函数。
4.正弦函数的单调性:在0°到90°之间,正弦函数是增函数。
二、余弦函数的比例性质1.余弦函数的定义:在直角三角形中,余弦函数是对于一个锐角,其邻边与斜边的比值。
2.余弦函数的周期性:余弦函数的值域为[-1,1],且每隔2π,函数值重复一次。
3.余弦函数的奇偶性:cos(-x) = cos(x),所以余弦函数是偶函数。
4.余弦函数的单调性:在0°到90°之间,余弦函数是减函数。
三、正切函数的比例性质1.正切函数的定义:在直角三角形中,正切函数是对于一个锐角,其对边与邻边的比值。
2.正切函数的周期性:正切函数的值域为R,且每隔π,函数值重复一次。
3.正切函数的奇偶性:tan(-x) = -tan(x),所以正切函数是奇函数。
4.正切函数的单调性:在0°到90°之间,正切函数是增函数。
四、三角函数的相互关系1.和角公式:sin(α+β) = sinαcosβ + cosαsinβ,cos(α+β) = cosαcosβ - sinαsinβ,tan(α+β) = (tanα + tanβ) / (1 - tanαtanβ)2.差角公式:sin(α-β) = sinαcosβ - cosαsinβ,cos(α-β) = cosαcosβ + sinαsinβ,tan(α-β) = (tanα - tanβ) / (1 + tanαtanβ)3.倍角公式:sin2α = 2sinαcosα,c os2α = cos^2α - sin^2α = 2cos^2α - 1 = 1 - 2sin^2α,tan2α = (2tanα) / (1 - tan^2α)五、三角函数的图像和性质1.正弦函数的图像:一条波浪线,周期为2π,振幅为1,对称轴为y 轴。
锐角三角函数知识点

锐角三角函数知识点总结
1、 勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):
3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)
6、正弦、余弦的增减性:
当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
7、正切、余切的增减性:
A
90B 90∠-︒=∠︒=∠+∠得由B A 对边
邻边 C A
90B 90∠-︒=∠︒
=∠+∠得由B A
当0°<α<90°时,tanα随α的增大而增大,cotα随α的增大而减小。
8、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
完整版)锐角三角函数超经典讲义

完整版)锐角三角函数超经典讲义锐角三角函数锐角三角函数是三角函数的一种,包括正弦、余弦和正切。
在一个锐角三角形中,锐角的对边、邻边和斜边之间的比例就是锐角三角函数。
具体来说,对于锐角A,其正弦、余弦和正切分别表示为sinA、cosA和XXX。
其中,XXX表示A的对边与斜边的比,cosA表示A的邻边与斜边的比,XXX表示A的对边与邻边的比。
这些符号都是完整的,单独的“sin”没有意义。
在用大写字母表示角度时,一般省略“∠”符号。
在求解锐角三角函数时,关键在于构造以此锐角所在的直角三角形。
例如,在一个直角三角形ABC中,如果已知∠C=90°,cosB=4/5,则AC:BC:AB=3:4:5.另外,需要注意的是,正弦、余弦和正切是实数,没有单位,它们的大小只与角的大小有关,而与所在直角三角形无关。
例1:在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE。
证明△ABE≌△DFA,并求sin∠EDF的值。
解:首先,连接AC,易得△ABC为等腰直角三角形,∠BAC=45°。
又因为AE=BC,所以△ABE和△ACD相似,即∠ABE=∠ACD,∠XXX∠ADC。
又因为∠ADC=90°,所以∠AEB=90°。
因此,△ABE和△DFA是全等三角形。
接下来,求sin∠EDF的值。
由于∠BAC=45°,所以∠AED=45°。
由于△ABE和△DFA全等,所以∠XXX∠BAE=45°。
因此,sin∠EDF=sin45°=1/√2.例2:在△ABC中,∠A=60°,∠B=45°,AB=8,求△ABC面积(结果可保留根号)。
解:由于∠A=60°,∠B=45°,所以∠C=75°。
根据三角函数的定义,可以得到:sin75°=cos15°=(sin60°cos45°+cos60°sin45°)/2=√6+√2/4cos75°=sin15°=(sin60°cos45°-cos60°sin45°)/2=√6-√2/4因此,△ABC面积为S=(1/2)AB·BC·sin75°=4(√6+√2)。
锐角三角函数、概率、圆总结

锐角三角函数 一、锐角三角函数 1、正弦:在△ABC 中,∠C=90°,我们把锐角A 的对边与斜边的叫做∠A 的正弦,记做sinA 。
2、余弦:在△ABC 中,∠C=90°,我们把锐角A 的邻边与斜边的叫做∠A 的余弦,记做cosA 。
3、正切:在△ABC 中,∠C=90°,我们把锐角A 的对边与邻边的叫做∠A 的正切,记做tanA 。
4、余切:在△ABC 中,∠C=90°,我们把锐角A 的邻边与对边的叫做∠A 的余切,记做cotA 。
[注]:0°、30°、45°、60°、90°特殊角的三角函数值二、解直角三角形1、定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
2、依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法) [注]:(1)三角形面积公式:111sin sin sin 222S ab C bc A ca B ===. (2)正弦定理 :2sin sin sin a b cR A B C ===. (3)余弦定理:2222cos a b c bc A =+-;2222cos b c a ca B =+-;2222cos c a b ab C =+-三、实际应用1、仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示,即hi l=。
把坡面与水平面的夹角记作α(叫做坡角),那么tan hi lα==。
概率一、随机事件和概率 1、 事件的分类:(1)不可能事件:事件一定不会发生 (2)必然事件:事件一定会发生(2)随机事件:事件有可能发生,也有可能不发生2、概率:对于一个事件A ,我们把刻画其发生可能性的大小的数值叫做事件A 的概率,记做:P(A)特点:每次试验结果只有有限个;各种结果出现的可能性相等。
九年级数学《锐角三角函数》知识点总结归纳

一、三角函数的定义1. 正弦函数sinx:对于任意实数x,将x的终边与x轴正方向的夹角的终点的纵坐标就是sinx。
2. 余弦函数cosx:对于任意实数x,将x的终边与x轴正方向的夹角的终点的横坐标就是cosx。
3. 正切函数tanx:对于任意实数x,将sinx除以cosx就是tanx。
4. 余切函数cotx:对于任意实数x,将cosx除以sinx就是cotx。
5. 正割函数secx:对于任意实数x,将1除以cosx就是secx。
6. 余割函数cscx:对于任意实数x,将1除以sinx就是cscx。
二、三角函数的性质1. 基本关系式:sin^2x + cos^2x = 12. 周期性:sin(x+2kπ) = sinx,cos(x+2kπ) = cosx,其中k为任意整数。
3. 奇偶性:奇函数有sinx、tanx和cotx,偶函数有cosx、secx和cscx。
4. 正函数和负函数:在单位圆上,sinx和cscx为正函数,cosx和secx为负函数。
5. 三角函数的范围:sinx、cosx和tanx的范围是[-1,1],cotx、secx和cscx的范围是(-∞,∞)。
三、特殊角的三角函数值1.0°、30°、45°、60°和90°的三角函数值。
2.30°、45°、60°和90°的三角函数值的推导。
四、角度的度量转换1.度和弧度之间的转换:π弧度=180°,1°=π/180弧度。
2.角度的换算:1°=60',1'=60''。
五、倍角、半角和三倍角公式1. 倍角公式:sin2x = 2sinxcosx,cos2x = cos^2x - sin^2x,tan2x = 2tanx / (1 - tan^2x)。
2. 半角公式:sin(x/2) = ±√[(1-cosx)/2],cos(x/2) =±√[(1+cosx)/2],tan(x/2) = ±√[(1-cosx) / (1+cosx)]。
(完整版)锐角三角函数超经典学习资料

(完整版)锐角三角函数超经典学习资料锐角三角函数是数学中重要的概念之一,它们在几何、物理和工程等领域都有广泛的应用。
通过研究锐角三角函数,我们可以更好地理解和解决各种相关问题。
一、正弦函数正弦函数是锐角三角函数中最基本的函数之一,在数学中常记作sin。
正弦函数的定义如下:$$ \sin(\theta) = \frac{opposite}{hypotenuse} $$其中,$\theta$ 表示角度,$opposite$ 表示对边的长度,$hypotenuse$ 表示斜边的长度。
正弦函数有许多重要的性质和关系,比如:- 正弦函数的取值范围是[-1, 1]:即对于任意角度 $\theta$,$-1 \leq \sin(\theta) \leq 1$。
- 正弦函数是一个周期函数:即 $\sin(\theta)$ 的周期是 $2\pi$,即在每个 $2\pi$ 的区间内,$\sin(\theta)$ 的值重复。
二、余弦函数余弦函数也是锐角三角函数中的一种重要函数,在数学中常记作cos。
余弦函数的定义如下:$$ \cos(\theta) = \frac{adjacent}{hypotenuse} $$其中,$\theta$ 表示角度,$adjacent$ 表示邻边的长度,$hypotenuse$ 表示斜边的长度。
余弦函数同样有许多重要的性质和关系,比如:- 余弦函数的取值范围是[-1, 1]:即对于任意角度 $\theta$,$-1 \leq \cos(\theta) \leq 1$。
- 余弦函数也是一个周期函数:即 $\cos(\theta)$ 的周期是$2\pi$,即在每个 $2\pi$ 的区间内,$\cos(\theta)$ 的值重复。
三、正切函数正切函数是锐角三角函数中的另一种常见函数,它经常用于计算角度的斜率。
正切函数的定义如下:$$ \tan(\theta) = \frac{opposite}{adjacent} $$其中,$\theta$ 表示角度,$opposite$ 表示对边的长度,$adjacent$ 表示邻边的长度。
初中锐角三角函数知识点总结

锐角三角函数及其应用XX 第六中学高启鹏一、锐角三角函数中考考点归纳考点一、锐角三角函数1、锐角三角函数的定义如图,在Rt △ABC 中,∠C 为直角,则∠A 为△ABC 中的一锐角,则有 ∠A的正弦:斜边的对边A A ∠=sin c a=∠A 的余弦:斜边的邻边A A ∠=cos cb=∠A的正切:的邻边的对边A tan ∠∠=A A ba =2、特殊角的三角函数值(1)图表记忆法(2)规律记忆法:30°、45°、60°角的正弦值的分母都是2,分子依次为1、2、3;30°、45°、60°角余弦值恰好是60°、45°、30°角的正弦值。
对边b a c(3)口诀记忆法口诀是:“一、二、三,三、二、一,三、九、二十七,弦比二,切比三,分子根号不能删.”前三句中的1,2,3;3,2,1;3,9,27,分别是30°,45°,60°角的正弦、余弦、正切值中分子根号内的值.弦比二、切比三是指正弦、余弦的分母为2,正切的分母为3.最后一句,讲的是各函数值中分子都加上根号,不能丢掉.如tan60°=273=,tan45°=91=.这种方法有趣、简单、易记.考点二、解直角三角形1、由直角三角形中的已知元素求出其他未知元素的过程,叫做解直角三角形。
2、解直角三角形的类型和解法如下表:考点三、锐角三角函数的实际应用(高频考点)仰角、俯角、坡度(坡比)、坡角、方向角仰角、俯角在视线与水平线所成的锐角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角。
坡度(坡比)、坡角坡面的铅直高度h和水平宽度l的比叫坡度(坡比),用字母i表示;坡面与水平线的夹角α叫坡角,方向角指北或指南的方向线与目标方向线所成的小于90°的锐角叫做方向角.注意:东北方向指北偏东45°方向,东南方向指南偏东45°方向,西北方向指北偏西45°方向,西南方向指南偏西45°方向.我们一般画图的方位为上北下南,左西右东.二、锐角三角函数常见考法(一)、锐角三角函数以选择题的形式出现.例1、(2016•XX)已知抛物线y=﹣x2﹣2x+3与x轴交于A、B两点,将这条抛物线的顶点记为C,连接AC、BC,则tan∠CAB的值为()A.B.C.D.2【考点】抛物线与x轴的交点;锐角三角函数的定义.【解析】先求出A、B、C坐标,作CD⊥AB于D,根据tan∠ACD=即可计算.lhi==αtan【解答】解:令y=0,则﹣x2﹣2x+3=0,解得x=﹣3或1,不妨设A(﹣3,0),B(1,0),∵y=﹣x2﹣2x+3=﹣(x+1)2+4,∴顶点C(﹣1,4),如图所示,作CD⊥AB于D.在RT△ACD中,tan∠CAD===2,故答案为D.(二)、锐角三角函数以填空题的形式出现.例2、(2016•XX)请从以下两个小题中任选一个作答,若多选,则按第一题计分.A.一个多边形的一个外角为45°,则这个正多边形的边数是8.B.运用科学计算器计算:3sin73°52′≈11.9.(结果精确到0.1)【考点】计算器—三角函数;近似数和有效数字;计算器—数的开方;多边形内角与外角.【解析】(1)根据多边形内角和为360°进行计算即可;(2)先分别求得3和sin73°52′的近似值,再相乘求得计算结果.【解答】解:(1)∵正多边形的外角和为360°∴这个正多边形的边数为:360°÷45°=8(2)3sin73°52′≈12.369×0.961≈11.9故答案为:8,11.9例3、(2015•XX)如图,有一滑梯AB,其水平宽度AC为5.3米,铅直高度BC为2.8米,则∠A的度数约为27.8°(用科学计算器计算,结果精确到0.1°).【考点】解直角三角形的应用-坡度坡角问题.【解析】直接利用坡度的定义求得坡角的度数即可.【解答】解:∵tan∠A==≈0.5283,∴∠A=27.8°,故答案为:27.8°.【点评】本题考查了坡度坡角的知识,解题时注意坡角的正切值等于铅直高度与水平宽度的比值,难度不大.例4、(2014•XX)用科学计算器计算:+3tan56°≈10.02(结果精确到0.01)【考点】计算器—三角函数;计算器—数的开方.【分析】先用计算器求出′、tan56°的值,再计算加减运算.【解答】解:≈5.5678,tan56°≈1.4826,则+3tan56°≈5.5678+3×1.4826≈10.02故答案是:10.02.【点评】本题考查了计算器的使用,要注意此题是精确到0.01.例5、(2014•XX)如图,在正方形ABCD中,AD=1,将△ABD绕点B顺时针旋转45°得到△A′BD′,此时A′D′与CD交于点E,则DE的长度为2﹣.【考点】旋转的性质【分析】利用正方形和旋转的性质得出A′D=A′E,进而利用勾股定理得出BD的长,进而利用锐角三角函数关系得出DE的长即可.【解答】解:由题意可得出:∠BDC=45°,∠DA′E=90°,∴∠DEA′=45°,∴A′D=A′E,∵在正方形ABCD中,AD=1,∴AB=A′B=1,∴BD=,∴A′D=﹣1,∴在Rt△DA′E中,DE==2﹣.故答案为:2﹣.【点评】此题主要考查了正方形和旋转的性质以及勾股定理、锐角三角函数关系等知识,得出A′D的长是解题关键.(三)、锐角三角函数定义以解答题的形式出现例6、(12分)(2015•XX)如图,在每一个四边形ABCD中,均有AD∥BC,CD⊥BC,∠ABC=60°,AD=8,BC=12.(1)如图①,点M是四边形ABCD边AD上的一点,则△BMC的面积为24;(2)如图②,点N是四边形ABCD边AD上的任意一点,请你求出△BNC周长的最小值;(3)如图③,在四边形ABCD的边AD上,是否存在一点P,使得cos∠BPC 的值最小?若存在,求出此时cos∠BPC的值;若不存在,请说明理由.【考点】四边形综合题..【专题】综合题.【解析】(1)如图①,过A作AE⊥BC,可得出四边形AECF为矩形,得到EC=AD,BE=BC﹣EC,在直角三角形ABE中,求出AE的长,即为三角形BMC 的高,求出三角形BMC面积即可;(2)如图②,作点C关于直线AD的对称点C′,连接C′N,C′D,C′B 交AD于点N′,连接′,则BN+NC=BN+NC′≥BC′=BN′+′,可得出△BNC 周长的最小值为△BN′C的周长=BN′+′+BC=BC′+BC,求出即可;(3)如图③所示,存在点P,使得cos∠BPC的值最小,作BC的中垂线PQ 交BC于点Q,交AD于点P,连接BP,CP,作△BPC的外接圆O,圆O与直线PQ交于点N,则PB=PC,圆心O在PN上,根据AD与BC平行,得到圆O 与AD相切,根据PQ=DC,判断得到PQ大于BQ,可得出圆心O在BC上方,在AD上任取一点P′,连接P′B,P′C,P′B交圆O于点M,连接MC,可得∠BPC=∠BMC≥∠BP′C,即∠BPC最小,cos∠BPC的值最小,连接OB,求出即可.【解答】解:(1)如图①,过A作AE⊥BC,∴四边形AECD为矩形,∴EC=AD=8,BE=BC﹣EC=12﹣8=4,在Rt△ABE中,∠ABE=60°,BE=4,∴AB=2BE=8,AE==4,则S △BMC=BC•AE=24;故答案为:24;(2)如图②,作点C关于直线AD的对称点C′,连接C′N,C′D,C′B 交AD于点N′,连接′,则BN+NC=BN+NC′≥BC′=BN′+′,∴△BNC周长的最小值为△BN′C的周长=BN′+′+BC=BC′+BC,∵AD∥BC,AE⊥BC,∠ABC=60°,∴过点A作AE⊥BC,则CE=AD=8,∴BE=4,AE=BE•tan60°=4,∴CC′=2CD=2AE=8,∵BC=12,∴BC′==4,∴△BNC周长的最小值为4+12;(3)如图③所示,存在点P,使得cos∠BPC的值最小,作BC的中垂线PQ交BC于点Q,交AD于点P,连接BP,CP,作△BPC的外接圆O,圆O与直线PQ交于点N,则PB=PC,圆心O在PN上,∵AD∥BC,∴圆O与AD相切于点P,∵PQ=DC=4>6,∴PQ>BQ,∴∠BPC<90°,圆心O在弦BC的上方,在AD上任取一点P′,连接P′B,P′C,P′B交圆O于点M,连接MC,∴∠BPC=∠BMC≥∠BP′C,∴∠BPC最大,cos∠BPC的值最小,连接OB,则∠BON=2∠BPN=∠BPC,∵OB=OP=4﹣OQ,在Rt△BOQ中,根据勾股定理得:OQ2+62=(4﹣OQ)2,解得:OQ=,∴OB=,∴cos∠BPC=cos∠BOQ==,则此时cos∠BPC的值为.【点评】此题属于四边形综合题,涉及的知识有:勾股定理,矩形的判定与性质,对称的性质,圆的切线的判定与性质,以及锐角三角函数定义,熟练掌握定理及性质是解本题的关键.例7、(10分)(2014年XX省)已知抛物线C:y=﹣x2+bx+c经过A(﹣3,0)和B(0,3)两点,将这条抛物线的顶点记为M,它的对称轴与x轴的交点记为N.(1)求抛物线C的表达式;(2)求点M的坐标;(3)将抛物线C平移到C′,抛物线C′的顶点记为M′,它的对称轴与x 轴的交点记为N′.如果以点M、N、M′、N′为顶点的四边形是面积为16的平行四边形,那么应将抛物线C怎样平移?为什么?【考点】二次函数图象与几何变换;二次函数的性质;待定系数法求二次函数解析式;平行四边形的性质.菁优网所有【分析】(1)直接把A(﹣3,0)和B(0,3)两点代入抛物线y=﹣x2+bx+c,求出b,c的值即可;(2)根据(1)中抛物线的解析式可得出其顶点坐标;(3)根据平行四边形的定义,可知有四种情形符合条件,如解答图所示.需要分类讨论.【解答】解:(1)∵抛物线y=﹣x2+bx+c经过A(﹣3,0)和B(0,3)两点,∴,解得,故此抛物线的解析式为:y=﹣x2﹣2x+3;(2)∵由(1)知抛物线的解析式为:y=﹣x2﹣2x+3,∴当x=﹣=﹣=﹣1时,y=4,xKb 1.C om∴M(﹣1,4).(3)由题意,以点M、N、M′、N′为顶点的平行四边形的边MN的对边只能是M′N′,∴MN∥M′N′且MN=M′N′.∴MN•NN′=16,∴NN′=4.i)当M、N、M′、N′为顶点的平行四边形是▱MNN′M′时,将抛物线C 向左或向右平移4个单位可得符合条件的抛物线C′;ii)当M、N、M′、N′为顶点的平行四边形是▱MNM′N′时,将抛物线C 先向左或向右平移4个单位,再向下平移8个单位,可得符合条件的抛物线C′.∴上述的四种平移,均可得到符合条件的抛物线C′.【点评】本题考查了抛物线的平移变换、平行四边形的性质、待定系数法及二次函数的图象与性质等知识点.第(3)问需要分类讨论,避免漏解.例8、(12分)(2014•XX)问题探究(1)如图①,在矩形ABCD中,AB=3,BC=4,如果BC边上存在点P,使△APD为等腰三角形,那么请画出满足条件的一个等腰三角形△APD,并求出此时BP的长;(2)如图②,在△ABC中,∠ABC=60°,BC=12,AD是BC边上的高,E、F分别为边AB、AC的中点,当AD=6时,BC边上存在一点Q,使∠EQF=90°,求此时BQ的长;问题解决(3)有一山庄,它的平面图为如图③的五边形ABCDE,山庄保卫人员想在线段CD上选一点M安装监控装置,用来监视边AB,现只要使∠AMB大约为60°,就可以让监控装置的效果达到最佳,已知∠A=∠E=∠D=90°,AB=270m,AE=400m,ED=285m,CD=340m,问在线段CD上是否存在点M,使∠AMB=60°?若存在,请求出符合条件的DM的长,若不存在,请说明理由.【考点】圆的综合题;全等三角形的判定与性质;等边三角形的性质;勾股定理;三角形中位线定理;矩形的性质;正方形的判定与性质;直线与圆的位置关系;特殊角的三角函数值.菁优网所有【专题】压轴题;存在型.【分析】(1)由于△PAD是等腰三角形,底边不定,需三种情况讨论,运用三角形全等、矩形的性质、勾股定理等知识即可解决问题.(2)以EF为直径作⊙O,易证⊙O与BC相切,从而得到符合条件的点Q唯一,然后通过添加辅助线,借助于正方形、特殊角的三角函数值等知识即可求出BQ长.(3)要满足∠AMB=60°,可构造以AB为边的等边三角形的外接圆,该圆与线段CD的交点就是满足条件的点,然后借助于等边三角形的性质、特殊角的三角函数值等知识,就可算出符合条件的DM长.【解答】解:(1)①作AD的垂直平分线交B C于点P,如图①,则PA=PD.∴△PAD是等腰三角形.∵四边形ABCD是矩形,∴AB=DC,∠B=∠C=90°.∵PA=PD,AB=DC,∴Rt△ABP≌Rt△DCP(HL).∴BP=CP.∵BC=4,∴BP=CP=2.②以点D为圆心,AD为半径画弧,交BC于点P′,如图①,.则DA=DP′.∴△P′AD是等腰三角形.∵四边形ABCD是矩形,∴AD=BC,AB=DC,∠C=90°.∵AB=3,BC=4,∴DC=3,DP′=4.∴CP′==.∴BP′=4﹣.③点A为圆心,AD为半径画弧,交BC于点P″,如图①,则AD=AP″.∴△P″AD是等腰三角形.同理可得:BP″=.综上所述:在等腰三角形△ADP中,若PA=PD,则BP=2;若DP=DA,则BP=4﹣;若AP=AD,则BP=.(2)∵E、F分别为边AB、AC的中点,∴EF∥BC,EF=BC.∵BC=12,∴EF=6.以EF为直径作⊙O,过点O作OQ⊥BC,垂足为Q,连接EQ、FQ,如图②.∵AD⊥BC,AD=6,∴EF与BC之间的距离为3.∴OQ=3∴OQ=OE=3.∴⊙O与BC相切,切点为Q.∵EF为⊙O的直径,∴∠EQF=90°.过点E作EG⊥BC,垂足为G,如图②.∵EG⊥BC,OQ⊥BC,∴EG∥OQ.∵EO∥GQ,EG∥OQ,∠EGQ=90°,OE=OQ,∴四边形OEGQ是正方形.∴GQ=EO=3,EG=OQ=3.∵∠B=60°,∠EGB=90°,EG=3,∴BG=.∴BQ=GQ+BG=3+.∴当∠EQF=90°时,BQ的长为3+.(3)在线段CD上存在点M,使∠AMB=60°.理由如下:以AB为边,在AB的右侧作等边三角形ABG,作GP⊥AB,垂足为P,作AK⊥BG,垂足为K.设GP与AK交于点O,以点O为圆心,OA为半径作⊙O,过点O作OH⊥CD,垂足为H,如图③.则⊙O是△ABG的外接圆,∵△ABG是等边三角形,GP⊥AB,∴AP=PB=AB.∵AB=270,∴AP=135.∵ED=285,∴OH=285﹣135=150.∵△ABG是等边三角形,AK⊥BG,∴∠BAK=∠GAK=30°.∴OP=AP•tan30°=135×=45.∴OA=2OP=90.∴OH<OA.∴⊙O与CD相交,设交点为M,连接MA、MB,如图③.∴∠AMB=∠AGB=60°,OM=OA=90..∵OH⊥CD,OH=150,OM=90,∴HM===30.∵AE=400,OP=45,∴DH=400﹣45.若点M在点H的左边,则DM=DH+HM=400﹣45+30.∵400﹣45+30>340,∴DM>CD.∴点M不在线段CD上,应舍去.若点M在点H的右边,则DM=DH﹣HM=400﹣45﹣30.∵400﹣45﹣30<340,∴DM<CD.∴点M在线段CD上.综上所述:在线段CD上存在唯一的点M,使∠AMB=60°,此时DM的长为(400﹣45﹣30)米.X|k | B| 1 . c |O |m【点评】本题考查了垂直平分线的性质、矩形的性质、等边三角形的性质、正方形的判定与性质、直线与圆的位置关系、圆周角定理、三角形的中位线定理、全等三角形的判定与性质、勾股定理、特殊角的三角函数值等知识,考查了操作、探究等能力,综合性非常强.而构造等边三角形及其外接圆是解决本题的关键.三、三角函数易错点解析三角函数是初中数学的重要内容,三角函数是学生在初中阶段第一次接触角函数,这部分知识的学习对于学生来说有一定的难度,下面就三角函数教学中容易出现的几种“错误”进行分析: 1.对应关系混淆【1】如图9,先进村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为a 米,那么这两树在坡面上的距离AB 为() A. a a cos 米B. αcos a米 C. a a sin 米D.αsin a米 解析:分别过点B ,A 作平行水平面的直线和垂直于水平面的直线相交于点C 。
《锐角三角函数》 知识清单

《锐角三角函数》知识清单一、锐角三角函数的定义在直角三角形中,锐角的正弦、余弦和正切统称为锐角三角函数。
1、正弦(sin)对于锐角 A,它的对边与斜边的比值叫做角 A 的正弦,记作 sinA。
即:sinA =角 A 的对边/斜边。
例如,在一个直角三角形 ABC 中,∠C = 90°,∠A 为锐角,其对边为 a,斜边为 c,则 sinA = a / c 。
2、余弦(cos)角 A 的邻边与斜边的比值叫做角 A 的余弦,记作 cosA。
即:cosA =角 A 的邻边/斜边。
在上述直角三角形 ABC 中,∠A 的邻边为 b,则 cosA = b / c 。
3、正切(tan)角 A 的对边与邻边的比值叫做角 A 的正切,记作 tanA。
即:tanA =角 A 的对边/角 A 的邻边。
对于直角三角形 ABC ,tanA = a / b 。
二、特殊锐角的三角函数值1、 30°角sin30°= 1/2 ,cos30°=√3/2 ,tan30°=√3/3 。
2、 45°角sin45°=√2/2 ,cos45°=√2/2 ,tan45°= 1 。
3、 60°角sin60°=√3/2 ,cos60°= 1/2 ,tan60°=√3 。
这些特殊角的三角函数值需要牢记,在解题中经常会用到。
三、锐角三角函数的关系1、平方关系sin²A + cos²A = 1 。
这意味着,对于一个锐角 A,其正弦的平方加上余弦的平方等于 1 。
2、商数关系tanA = sinA / cosA 。
即正切等于正弦除以余弦。
四、锐角三角函数的应用锐角三角函数在解决实际问题中有广泛的应用,比如:1、测量问题在测量物体的高度、距离等时,可以通过构建直角三角形,利用锐角三角函数来计算。
例如,要测量一座塔的高度,可以在塔的附近选择一个测量点,测量出测量点到塔底部的距离,以及在测量点观测塔顶的仰角,然后通过正切函数计算出塔的高度。
28.1锐角三角函数(1)(知识点总结和典型例题汇总)

28.1锐角函数(一)知识点1:当锐角A 的大小确定后,它所在的直角三角形每两边所构成的角都有唯一的确定的值。
观察图的Rt △AB 1C 1、Rt △AB 2C 2和Rt △AB 3C 3,它们之间有什么关系?Rt △AB 1C 1∽Rt △AB 2C 2∽Rt △AB 3C 3所以 =__________=__________.可见,在Rt △ABC 中,对于锐角A 的每一个确定的值,其对边与斜边的比值是惟一确定的.同时: =__________=__________; =__________=__________. 所以当锐角A 的大小确定后,它所在的直角三角形每两边所构成的比都有唯一确定的值。
知识点2:正弦和余弦的定义:由知识点1可知,当锐角A 固定时,∠A 的对边和斜边的比值是一个固定 的值,∠A 的邻边与斜边的比值也是一个固定的值。
(1)在Rt △ABC 中,∠C=900,把锐角A 的对边与斜边的比叫做∠A 的正弦(sine),记作sinA ( sin ∠BAC ) 即 sinA= =(2)我们把锐角A 的邻边与斜边的比叫做∠A 的余弦(cosine ),记作cosA , 即注意:(1)正弦、余弦都是一个比值,是没有单位的数值;(2)正弦、余弦只与角的大小有关,而与三角形的大小无关 (3)sinA ,cosA 是整体符号,不能写成sinA,cosA 。
(4)每用三个字母表示角时,角的符号“∠”不能省略,如 sin ∠BAC图19.3.2 A BC 对边邻边 ┌斜边ab c 在图中 ∠A 的对边记作a ∠B 的对边记作b ∠C 的对边记作cc b A A =∠=斜边的邻边cos(5)sin 2A 表示(sinA )2,而不能写成sinA 2(6)三角函数还可以写成sin α,cos β。
知识点3正切的定义: 由知识点1可知,当锐角A 固定时,∠A 的对边与邻边的比值是一个固定的值。
我们把锐角A 的对边与邻边的比叫做∠A 的正切(tangent ),记作tanA , 即注意:(1)正切是一个比值,是没有单位的数值;(2)正切只与角的大小有关,而与三角形的大小无关 (3)tanA 是整体符号,不能写成sin 。
锐角三角函数知识点总结与复习

锐角三角函数知识点总结与复习1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方;2、如下图,在Rt △ABC 中,∠C 为直角, 则∠A 的锐角三角函数为∠A 可换成∠B :3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值;4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值;5、0°、30°、45°、60°、90°特殊角的三角函数值重要A 90B 90∠-︒=∠︒=∠+∠得由B A邻边A90B 90∠-︒=∠︒=∠+∠得由B A直角三角形中 的边角关系解直角三角形当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小; 7、正切、余切的增减性:当0°<α<90°时,tan α随α的增大而增大,cot α随α的增大而减小;一、知识性专题专题1:锐角三角函数的定义例 1 在Rt △ABC 中,∠ACB =90°,BC =1,AB =2,则下列结论正确的是 A .sin A B .tan A =12C .cos BD .tan B 分析 sin A =BC AB =12,tan A =BC AC ,cos B =BCAB =12.故选D.例2 在△ABC 中,∠C =90°,cos A =35,则tan A 等于 ; 分析 在Rt △ABC 中,设AC =3k ,AB =5k ,则BC =4k ,由定义可知tan A =4433BC k AC k ==. 分析 在Rt △ABC 中,BC =3,∴sin A =35BC AB =.故填35.例312·哈尔滨在Rt △ABC 中,∠C=900,AC=4,AB=5,则sinB 的值是 ; 解析本题考查了锐角三角函数的意义.解题思路:在直角三角形中,锐角的正弦等于对边比邻边,故sinB=54. 例42012内江如图4所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为 ;解析欲求sinA,需先寻找∠A 所在的直角三角形,而图形中∠A 所在的△ABC 并不是直角三角形,所以需要作高.观察格点图形发现连接CD 如下图所示,恰好可证得CD ⊥AB,于是有图4图4sinA =CD AC =210=55.例5 2012宁波,Rt △ABC,∠C=900,AB=6,cosB=错误!,则BC 的长为 ;解析cosB=错误!=错误!,又∵AB=6∴BC=4例62012贵州铜仁如图,定义:在直角三角形ABC 中,锐角α的邻边与对边的比叫做角α的余切,记作ctan α, 即ctan α=BCAC=的对边角的邻边角αα,根据上述角的余切定义,解下列问题:1ctan30◦= ;2如图,已知tanA=43,其中∠A 为锐角,试求ctanA 的值.分析1可先设最小边长为一个特殊数这样做是为了计算方便,然后在计算出其它边长,根据余切定义进而求出ctan30◦;2由tanA=43,为了计算方便,可以设BC=3 AC=4根据余切定义就可以求出ctanA 的值.解析1设BC=1, ∵α=30◦∴AB=2∴由勾股定理得:AC=3ctan30◦=BCAC=32 ∵tanA=43∴设BC=3 AC=4∴ctanA =BC AC =34例72012山东滨州把△ABC 三边的长度都扩大为原来的3倍,则锐角A 的正弦函数值 A .不变B .缩小为原来的13C .扩大为原来的3倍D .不能确定 解析因为△ABC 三边的长度都扩大为原来的3倍所得的三角形与原三角形相似,所以锐角A 的大小没改变,所以锐角A 的正弦函数值也不变.答案选A .例82012湖南观察下列等式 ①sin30°= cos60°=②sin45°=cos=45°=③sin60°= cos30°=根据上述规律,计算sin 2a+sin 290°﹣a= .解析:根据①②③可得出规律,即sin 2a+sin 290°﹣a=1,继而可得出答案. 答案:解:由题意得,sin 230°+sin 290°﹣30°=1;sin 245°+sin 290°﹣45°=1; sin 260°+sin 290°﹣60°=1;故可得sin 2a+sin 290°﹣a=1.故答案为:1.点评:此题考查了互余两角的三角函数的关系,属于规律型题目,注意根据题意总结,另外sin 2a+sin 290°﹣a=1是个恒等式,同学们可以记住并直接运用.例9 2012山东德州为了测量被池塘隔开的A ,B 两点之间的距离,根据实际情况,作出如下图形,其中AB BE ⊥,EF BE ⊥,AF 交BE 于D ,C 在BD 上.有四位同学分别测量出以下四组数据:22题图①BC ,∠ACB ; ②CD ,∠ACB ,∠ADB ;③EF ,DE ,BD ;④DE ,DC ,BC .能根据所测数据,求出A ,B 间距离的有哪 组解析对于①,可由公式AB=BC ×tan ∠ACB 求出A 、B 两点间的距离;对于②,可设AB 的长为x,则BC=x tan ACB ∠,BD=xtan ADB ∠,BD-BC=CD,可解出AB .对于③,易知△DEF ∽△DBA,则DE BDEF AB=,可求出AB 的长;对于④无法求得,故有①、②、③三组点评此题考查解直角三角形和三角形相似的性质与判定.在直角三角形中至少要有已知一边和一角才能求出其他未知元素;判定两三角形相似的方法有:AA,SAS,SSS,两直角三角形相似的判定还有HL . 例102012江苏泰州18如图,在边长相同的小正方形组成的网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,AB 、CD 相交于点P,则tan ∠APD 的值是 .解析 要求tan ∠APD 的值,只要将∠APD 放在直角三角形中,故过B 作CD 的垂线,然后利用勾股定理计算出线段的长度,最后利用正切的定义计算出结果即可. 答案作BM ⊥CD,DN ⊥AB 垂足分别为M 、N,则2,易得:10,设PM=x,则PD=22-x,由△DNP ∽△BMP,得:PN DN PM BM =,即10102PN x =,∴PN=55x,由DN 2+PN 2=PD 2,得:110+15x 2=22-x 2,解得:x 1=24,x 2=2舍去,∴tan ∠APD=2224BM PM ==2.例11. 2011江苏苏州如图,在四边形ABCD 中,E 、F 分別是AB 、AD 的中点,若EF=2,BC=5,CD=3,则tanC 等ABCDEFF于 .分析:根据三角形的中位线定理即可求得BD 的长,然后根据勾股定理的逆定理即可证得△BCD 是直角三角形,然后根据正切函数的定义即可求解.解答:解:连接BD .∵E 、F 分別是AB 、AD 的中点.∴BD=2EF=4∵BC=5,CD=3∴△BCD是直角三角形.∴tanC= 43例122011山东日照在Rt△ABC 中,∠C=90°,把∠A 的邻边与对边的比叫做∠A 的余切,记作cotA=ab.则下列关系式中不成立的是A .tanA•cotA=1B .sinA=tanA•cosAC .cosA=cotA•sinAD .tan 2A+cot 2A=1解答:解:根据锐角三角函数的定义,得 A 、tanA•c otA=a b b a ⋅=1,关系式成立;B 、sinA=c a ,tanA•cosA=cac b b a =⋅,关系式成立; C 、cosA=,cotA•sinA=c b a b c a =⋅,关系式成立;D 、tan 2A+cot 2A=b a 2+ab 2≠1,关系式不成立.故选D .点评:本题考查了同角三角函数的关系.1平方关系:sin 2A+cos 2A=1 2正余弦与正切之间的关系积的关系:一个角的正切值等于这个角的正弦与余弦的比,即tanA=BAcos sin 或sinA=tanA•cosA.3正切之间的关系:tanA•tanB=1. 例132011•贵港如图所示,在△ABC 中,∠C=90°,AD 是BC 边上的中线,BD=4,AD=2,则tan∠CAD 的值是 .解答:解:∵AD 是BC边上的中线,BD=4,∴CD=BD=4,在Rt△ACD中,AC===2,∴tan∠CAD===2.故选A .例142011烟台如果△ABC 中,sin A =cos B 2,则下列最确切的结论是 A. △ABC 是直角三角形 B. △ABC 是等腰三角形C. △ABC 是等腰直角三角形D. △ABC 是锐角三角形 解:∵sinA=cosB=22,∴∠A =∠B =45°,∴△ABC 是等腰直角三角形.故选C . 例152011四川如图所示,在数轴上点A 所表示的数x 的范围是A 、330sin 602sin x ︒︒<< B 、3cos302x ︒︒<<cos45C 、3tan 302x ︒︒<<tan45D 、3cot 4502x ︒︒<<cot3 解答:故选D .同步练习12011甘肃如图,A 、B 、C 三点在正方形网格线的交点处,若将△ACB 绕着点A 逆时针旋转得到△AC ’B ’,则tanB ’的值为 .解答:解:过C 点作CD ⊥AB ,垂足为D .根据旋转性质可知,∠B′=∠B .在Rt△BCD 中,tanB= CD :BD =13,∴tan B′=tan B = 13. 2 2011甘肃兰州点M -sin60°,cos60°关于x 轴对称的点的坐标是 . 解:∵sin60°=32,cos60°= 12,∴点M -32,12.∵点P m ,n 关于x 轴对称点的坐标P′m ,-n ,∴M 关于x 轴的对称点的坐标是-32,-12.故选B . 32011广东已知:45°<A <90°,则下列各式成立的是A 、sinA =cosAB 、sinA >cosAC 、sinA >tanAD 、sinA <cosA解答:解:∵45°<A <90°,∴根据sin 45°=cos 45°,sinA 随角度的增大而增大,cosA 随角度的增大而减小,当∠A >45°时,sinA >cosA ,故选:B .4、2011•宜昌教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=33,则边BC 的长为 .cm解:在直角三角形ABC 中,根据三角函数定义可知:tan ∠BAC=BCAC,又AC=30cm,tan ∠3则BC=ACtan 33cm .故选C . 5、 2011福建莆田如图,在矩形ABCD 中,点E 在AB 边上,沿CE 折叠矩形ABCD ,使点B 落在AD 边上的点F 处,若AB =4,BC=5,则tan ∠AFE 的值为 .ABCC ’ B ’解答:解:∵四边形ABCD 是矩形,∴∠A =∠B =∠D =90°,CD =AB =4,AD =BC =5,由题意得:∠EFC =∠B =90°,CF =BC =5,∴∠AFE +∠DFC =90°,∠DFC +∠FCD =90°, ∴∠DCF =∠AFE ,∵在Rt △DCF 中,CF =5,CD =4,∴DF =3,∴tan ∠AFE =tan ∠DCF =DFDC =34 .6、2012连云港小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD 沿过点B的直线折叠,使点A 落在BC 上的点E 处,还原后,再沿过点E 的直线折叠,使点A 落在BC 上的点F 处,这样就可以求出°的角的正切值是 .EC DA BF答案设AB=x,则BE=x,在直角三角形ABE 中,用勾股定理求出AE=EF=2x,于是2在直角三角形ABF 中,tan ∠FAB=21)BF xAB x=2°.选B; 7、2012福州如图15,已知△ABC,AB=AC=1,∠A=36°,∠ABC 的平分线BD 交AC 于点D,则AD 的长是 ,cosA 的值是 .结果保留根号解析:由已知条件,可知△BDC 、△ADB 是等腰三角形,且DA=DB=BC,可证△BDC ∽△ABC,则有BC DC AC BC =,设BC=x,则DC=1-x,因此21,101x xx x x -=+-=即,解方程得, 125151x x ---==,舍去,即AD=512;又cosA=512451512AB AD===--⨯答案:5151,24 8、2012南京如图,将45°的∠AOB 按下面的方式放置在一把刻度尺上:顶点O 与尺下沿的端点重合,OA 与尺下沿重合.OB 与尺上沿的交点B 在尺上的读书恰为2厘米,若按相同的方式将37°的∠AOC 放置在该刻度尺上,则OC 与尺上沿的交点C 在尺上的读数为 厘米.结果精确到厘米,参考数据sin370≈,cos370≈,tan370≈C B AO4321解析:由于∠AOB=45°,B 点读书为2厘米,则直尺的宽为2厘米,解直角三角形得点C 的读数为2÷tan370≈2÷≈厘米.答案:9、2012·湖南张家界黄岩岛是我国南海上的一个岛屿,其平面图如图甲所示,小明据此构造出该岛的一个数学模型如图乙所示,其中∠A=∠D=90°,AB=BC=15千米,CD=23千米,请据此解答如下问题:1 求该岛的周长和面积结果保留整数,参考数据2≈ 73.13≈45.26≈ 2 求∠ACD 的余弦值.解答1结AC,∵AB=BC=15千米,∠B=90°,∴∠BAC=∠ACB=45°,AC=152千米. 又∵∠D=90°, ∴AD=2222)23()215(-=-CD AC =123千米∴周长=AB+BC+CD+DA=30+32+123=30++≈55千米. 面积=S △ABC +S △ADC =21×15×15+21×123×32=2225+186≈157平方千米. 2cos ∠ACD=5121523==AC CD . 10、2012甘肃兰州在建筑楼梯时,设计者要考虑楼梯的安全程度;如图1,虚线为楼梯的倾斜度,斜度线与地面的夹角为倾角θ,一般情况下,倾角越小,楼梯的安全程度越高;如图2,设计者为了提高楼梯的安全程度,要把楼梯的倾角1θ减至2θ,这样楼梯占用地板的长度由d 1增加到d 2 ,已知d 1=4米,140θ∠=,236θ∠=,楼梯占用地板的长度增加了多少米 计算结果精确到米;参考数据:tan40°=,tan36°=AC解析:根据在Rt△ACB中,AB=d1tanθ1=4tan40°,在Rt△ADB中,AB=d2tanθ2=d2tan36°,即可得出d2的值,进而求出楼梯占用地板增加的长度.解:由题意可知可得,∠ACB=∠θ1,∠ADB=∠θ2在Rt△ACB中,AB=d1tanθ1=4tan40°,在Rt△ADB中,AB=d2tanθ2=d2tan36°,得4tan40°=d2tan36°,∴d2=4tan40tan36≈,∴d2-d1==≈,答:楼梯占用地板的长度增加了米.11、2012贵州为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长.参考数据:sin54°≈,cos54°≈,tan54°≈,≈,精确到个位解析:首先过点C作CD⊥AB于D,然后在Rt△BCD中,利用三角函数的知识,求得BD,CD的长,继而在Rt△ACD 利用∠CAB的正切求得AD的长,继而求得答案.答案:解:过点C作CD⊥AB于D∵BC=200m,∠CBA=30°,∴在Rt△BCD中,CD=BC=100m,BD=BC•cos30°=200×=100≈173m,∵∠CAB=54°,在Rt△ACD中,AD=≈≈74m,∴AB=AD+BD=173+74=247m.答:隧道AB的长为247m.12、2011新疆建设兵团如图,在△ABC中,∠A=90°.1用尺规作图的方法,作出△ABC绕点A逆时针旋转45°后的图形△AB1C1保留作图痕迹;2若AB=3,BC=5,求tan∠AB1C1.第22题图d2解答:解:1作∠CAB 的平分线,在平分线上截取AB 1=AB ,作C 1A ⊥AB 1,在AC 1上截取AC 1=AC ,如图所示即是所求.2∵AB =3,BC =5,∴AC =4,∴AB 1=3,AC 1=4,tan∠AB 1C 1=错误!=错误!. 专题2 特殊角的三角函数值例12012,湖北孝感计算:cos 245°+tan30°·sin60°=________.答案1例22012陕西计算:(02cos 45-38+1-2=︒ .解析原式2=2-322+1=-52+12⨯⨯答案-52+1 例32012广安计算:---)32(218cos45o +13- ; 解析:1182()cos 4533---︒+=322212323+-+21 例4 计算|-3|+2cos 45310. 解:原式=3+22-122. 例5 计算-12⎛⎫- ⎪⎝⎭9+-12007-cos 60°.解:原式=12+3+-1-12=3-1=2. 例6 计算|2+cos 60°-tan 30°08 21十+221. 例7 计算312-⎛⎫ ⎪⎝⎭-π-0-|1-tan 60°|32-.解:原式=8-13132=10. 例82012呼和浩特计算:11|122sin 45--+︒解析三角函数、绝对值、乘方答案11|12sin 45--+︒11)2211232=-+=+=例92011天水计算:si n 230°+tan 44°tan 46°+si n 260°= . 分析:根据特殊角的三角函数值计算.tanA •tan 90°﹣A =1. 解答:解:原式=14+1+34=2.故答案为2. 例102011•莱芜若a=3﹣tan60°,则196)121(2-+-÷--a a a a = ;33-解答:解:a=3﹣tan60°=3﹣3,∴原式=23-a 1-a 121)(⨯---a a =31-a =33313331-=-=--故答案为:33-. 练习1、2011浙江计算:|-1|5-π0+4cos45°. 解原式=1-122练习2、2011浙江衢州1计算:|﹣2|﹣3﹣π0+2c os45°;解答:解:1原式=2122-+⨯,=1 练习3、计算:20110+8-2sin45°;原式=1+22-2=1+2;练习3、观察下列各式:①sin 59°>sin 28°;②0<cos α<1α是锐角;③tan 30°+tan 60°=tan 90°;④tan 44°<1.其中成立的有A .1个B .2个C .3个D .4个 练习3、C 提示:sin 59°>sin 28°成立,0<cos α<1α是锐角成立,tan 30°+tan 60tan 90°,tan 44°<tan 45°,即tan 44°<1.练习4、计算2sin 30°-tan 60°+tan 45°= .练习5、如图28-146所示,在△ABC 中,∠A =30°,tan B =13,BC 10则AB 的长为 . 练习6、当x =sin 60°时,代数式2242x x x -+·22244x x x x +-++42xx-的值是 .练习7、已知cos 59°24′≈,则sin 30°36′≈ .练习8、若∠A ,∠B 互余,且tan A -tan B =2,则tan 2A +tan 2B = .练习9、如图28-147所示,在菱形ABCD 中,AE ⊥BC 于E ,EC =1,cos B=513,则这个菱形的面积是 . 10.已知正方形ABCD 的边长为1,若将线段BD 绕着点B 旋转后,点D落在DC 延长线上的点D ′处,则∠BAD ′的正弦值为 . 11.如图28-148所示,若将四根木条钉成的矩形木框变为平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角等于 .12.在△ABC 中,∠B =30°,tan C =2,AB =2,则BC = .13.设θ为锐角,且x 2+3x +2sin θ=05.则θ= . 14.如图28-149所示,在△ABC 中,∠C =90°,点D 在BC 边上,BD =4,AD =BC ,cos ∠ADC =35. 1求DC 的长;2求sin B 的值.练习4、23 提示:2sin 30°-tan 60°+tan 45°=2×1231=23 练习5、33提示:过点C 作CD ⊥AB ,垂足为D ,在Rt △BDC 中,tan B =13.∴13CD BD =,∴BD =3CD ,∵BC 10∴CD 2+3CD 210,∴CD =1,BD =3.在Rt △ADC 中,tan A =CDAD,∴AD 3∴AB =AD +BD =33 练习632242x x x -+·22244x x x x +-++42xx-=2x ,∴原式=2sin 603练习7、提示:sin 30°36′=cos 59°24′.练习8、6提示:∵∠A ,∠B 互余,∴tan A ·tan B =1,tan 2A +tan 2B =tan A -tan B 2+2tan A ·tan B =22+2=6. 练习9、3916提示:∵cos B =513,设BE =5x ,则AB =13x ,∴AE 22AB BE -12x .∵AB =BC =BE +CE ,∴13x =5x +1,∴x =18,则AE =12x =12×18=32,BC =5x +1=5×18+1=138,∴S =32×138=3916.10.5提示:如图28-155所示,根据题意得DD ′=2DC ,设正方形的边长为x ,则AD =x ,DD ′=2x .∵∠ADD ′=90°,根据勾股定理得AD 22AD DD '+5x .∵AD =x ,∴sin ∠AD ′D =ADAD '=555x x=.∵AB ∥DD ′,∴∠BAD ′=∠AD ′D ,∴sin ∠BAD ′=55.11.30°提示:如图28=156所示,∵S ABCD=12S 矩形BEFC ,且BC =BC 底相同, ∴GC =12FC .∵CF =DC ,∴GC =12DC ,12CG DC =.∵∠DGC =90°,sin 30°=12,∴∠CDG =30°,即这个平行四边形的一个最小内角为30°. 12.12+3 13.30°提示:x 1·x 2=2sin θ,x 1+x 2=-3,则x 1-x 22=x 1+x 22-4x 1x 2=9-8sin θ=52,∴sin θ=12,∴θ=30°. 14.解:1∵cos ∠ADC =35,∴设CD =3x ,则AD =5x ,AC =4x ,∴BC =AD =5x .∵BD =BC-CD ,∴5x -3x =4,∴x =2,∴CD =3x =6. 2∵AC =4x =8,BC =5x =10,∴AB =2222810241AC BC +=+=,∴sin B =844141241AC AB ==. ★ 专题三:题型一俯角与仰角仰角:视线在水平线上方的角;★ 俯角:视线在水平线下方的角;仰角铅垂线水平线视线视线俯角例1、2012湖北襄阳在一次数学活动中,李明利用一根拴有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD .如图5,已知李明距假山的水平距离BD 为12m,他的眼睛距地面的高度为,李明的视线经过量角器零刻度线OA 和假山的最高点C,此时,铅垂线OE 经过量角器的60°刻度线,则假山的高度为 m .解析如下图,过点A 作AF⊥CD 于F,则AF =BD =12m,FD =AB =.再由OE∥CF 可知∠C=∠AOE=60°.所以,在Rt△ACF 中,CF =tan 60AF=43,那么CD =CF +FD =43+m .例2、2012珠海如图,水渠边有一棵大木瓜树,树干DO 不计粗细上有两个木瓜A 、B 不计大A O BE D CF图5 CDA BO E小,树干垂直于地面,量得AB=2米,在水渠的对面与O 处于同一水平面的C 处测得木瓜A 的仰角为45°、木瓜B 的仰角为30°.求C 处到树干DO 的距离CO.结果精确到1米参考数据:41.12,73.13≈≈第16题图D BA OC解析如图,根据题意,得∠COD =90°, ∠ACO =45°, ∠BCO =30°, AB =2,求CO.设CO 为x 米, 根据AO =CO,列方程,解得即可.答案解:设CO 为x 米在Rt △BCO 中,tan30°=BO CO ,则BO =33x 在Rt △ACO 中,AO =CO,得方程33x +2=x 解得x ≈5.答: CO 长大约是5米. 例3、2012江苏盐城如图所示,当小华站立在镜子EF 前A 处时,他看自己的脚在镜中的像的俯角为450 :如果小华向后退米到B 处,这时他看自己的脚在镜中的像的俯角为300.求小华的眼睛到地面的距离;结果精确到米,参考数据:3≈.答案设AC=BD=x,在Rt △ACA 1中,∠AA 1C=450,∴AA 1=x,在Rt △DBB 1中,BB 1=tan30x=3x ,又∵12BB 1-12AA 1=12,即12×3x -12x=12,解得:x=312+≈米. 例4、2012山西如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A .B 的距离,飞机在距海平面垂直高度为100米的点C 处测得端点A 的俯角为60°,然后沿着平行于AB 的方向水平飞行了500米,在点D 测得端点B 的俯角为45°,求岛屿两端A .B 的距离结果精确到米,参考数据:解析解:过点A 作AE⊥CD 于点E,过点B 作BF⊥CD 于点F,∵AB∥CD,∴∠AEF=∠EFB=∠ABF=90°,∴四边形ABFE 为矩形.第24题图∴AB=EF,AE=BF.由题意可知:AE=BF=100米,CD=500米.…2分 在Rt△AEC 中,∠C=60°,AE=100米.∴CE===米. …4分在Rt△BFD中,∠BDF=45°,BF=100. ∴DF===100米.…6分∴AB=EF=CD+DF﹣CE=500+100﹣≈600﹣×≈600﹣≈米. …8分答:岛屿两端A .B 的距离为米.例5、2012呼和浩特22如图,线段AB 、DC 分别表示甲、乙两建筑物的高;某初三课外兴趣活动小组为了测量两建筑物的高,用自制测角仪在B 处测得D 点的仰角为α,在A 处测得D 点的仰角为β;已知甲、乙两建筑物之间的距离BC 为m ;请你通过计算用含α、β、m 的式子分别表示出甲、乙两建筑物的高度;答案解:过点A 作AM ⊥CD 于M在Rt △BCD 中,tan α=CD BC ∴CD =BC ·tan α=m tan α在Rt △AMD 中,tan β=DMAM∴DM =AM ·tan β=m tan β∴AB =CD –DM =mtan α–tan β例6、2012湖北随州,20在一次暑假旅游中,小亮在仙岛湖的游船上A 处,测得湖西岸的山峰太婆尖C 处和湖东岸的山峰老君岭D 处的仰角都是45°,游船向东航行100米后B 处,测得太婆尖、老君岭的高度为多少米3 1.732 ,结果精确到米;解析:设太婆尖高h 1米,老君岭高h 2米;可分别在直角三角形中利用正切值表示出水平线段的长度,再利用移动距离为AB=100米,可建立关于h 1、h 2的方程组,解这个方程组求得两山峰高度;答案:设太婆尖高h 1米,老君岭高h 2米,依题意,有FE第20题图60304545D (老君岭)C (太婆尖)BAβα乙甲ADB M C⇒⎪⎪⎩⎪⎪⎨⎧=-=-10060tan 45tan 10045tan 30tan 2211h h h h 1376.136)1732.1(50)13(5045tan 60tan 1001≈=+=+=-=h 米33110030tan 45tan 1002-=-=h 2376.236)732.13(50)33(50)13(350≈=+=+=+=米答:太婆尖高度为137米,老君岭高度为237米;题型二方位角问题1、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角;如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°;2、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角;如图4:OA 、OB 、OC 、OD 的方向角分别是:北偏东30°东北方向,南偏东45°东南方向,南偏西60°西南方向,北偏西60°西北方向;例1、2011山东省潍坊轮船从B 处以每小时海里的速度沿男偏东30°方向匀速航行,在B 处观测灯塔A 位于南偏东75°方向上,轮船航行半小时到达C 处,在观测灯塔A 北偏东60°方向上,则C 处与灯塔A 的距离是 .海里解答: BC=50×=25海里;根据方位角知识得,∠BCD=30°,=75°-30°;CB=∠BCD+∠ACD=30°+60°=90°;∠A=∠CBD=45°所以CA=CB 所以CB=25海里例2、2012年四川德阳某时刻海上点P 处有一客轮,测得灯塔A 位于客轮P 的北偏东30°方向,且相距20海里.客轮以60海里/小时的速度沿北偏西60°方向航行32小时到达B 处,那么tan ∠ABP=A.21 C.55 D.552解析如图6所示,根据题意可知∠APB=90°.且AP=20, PB=60×23=40. 所以tan ∠ABP=201402PA PB ==例3、2012连云港已知B 港口位于A 观测点北偏东°方向,且其到A 观测点正北方向的距离BD 的长为16km;一艘货轮从B 港口以40km/h 的速度沿如图所示的BC 方向航行,15min 后到达C 处;现测得C 处位于A观测点北偏东°方向;求此时货轮与A 观测点之间的距离AC 的长精确到.25东北CBDCBH解析过点B 作AC 的垂线,把所求线段AC 换为两线段的差;利用Rt △ABH 和Rt △BCH 求线段AH 、CH 的长,利用AH -CH 确定AC 的长; 答案BC=40×1560=10.在Rt△ADB 中,sin ∠DAB=DB AB , °≈;所以AB=DAB DB ∠sin ≈1.60.8=20.如图,过点B 作BH⊥AC,交AC 的延长线于H;在Rt△AHB 中,∠BAH=∠DAC -∠DAB=°―37°=°,tan∠BAH=BH AH ,=BH AH,AH =+CH 2=AB 2,BH 2+2BH 2=2025所以AH=85,在Rt△AHB 中, BH 2+CH 2=BC 2,CH=2108025-=所以第22题图APCB °°AC=AH―CH=85―25=65≈.例4、2012四川攀枝花如图6,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B 处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.答案作CD⊥AB于D,设BD=x,∵∠BCD=30°,∴CD=3x,因为∠CAD=45°,∴AD=CD3,AB3–x,依据题意3x–x=,x 31+,31+小时,离渔船C的距离最近;例5、2012山东东营如图某天上午9时,向阳号轮船位于A处,观测到某港口城市P位于轮船的北偏西°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到城市P位于该船的南偏西°方向,求此时轮船所处位置B 与城市P的距离参考数据:°≈35,°≈34,°≈1213,°≈125解析过点P作PC⊥AB,构造直角三角形,设PC=x海里,用含有x的式子表示AC,BC的值,从而求出x的值,再根据三角函数值求出BP的值即可解答.答案过点P作PC⊥AB,垂足为C,设PC=x海里.在Rt△APC中,∵tan∠A=PCAC,∴AC=5tan67.512PC x=︒.在Rt△PCB中,∵tan∠B=PCBC,∴BC=4tan36.93x x=︒.∵AC+BC=AB=21×5,∴54215123x x+=⨯,解得60x=.∵sinPCBPB∠=,∴60560100sin sin36.93PCPBB===⨯=∠︒海里.∴向阳号轮船所处位置B与城市P的距离为100海里.例6、2012山东省青岛如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE ;而当光线与地面夹角是45°时,教学楼顶A 在地面上的影子F 与墙角C 有13米的距离B 、F 、C 在一条直线上 ⑴求教学楼AB 的高度;⑵学校要在A 、E 之间挂一些彩旗,请你求出A 、E 之间的距离结果保留整数.参考数据:sin22°≈错误!,cos22°≈错误!,tan22°≈错误! 答案解:⑴过点E 作EM ⊥AB,垂足为M.设AB 为x.Rt △ABF 中,∠AFB=45°,∴BF=AB=x,∴BC=BF+FC=x+13在Rt △AEM 中,∠AEM=22°,AM=AB-BM=AB-CE=x-2,∴tan22°= 错误!, 错误!=错误!,x=12.即教学楼的高12m.⑵由1可得ME=BC=x+13=12+13=25.在Rt △AME 中,cos22°= 错误!, ∴AE= 错误!≈ 错误!≈27.即AE之间的距离约为27m.题型三、坡比是垂直高度与水平距离的比值,即是坡角的正切值应用举例: 坡面的铅直高度h 和水平宽度l 的比叫做坡度坡比;用字母i 表示,即hi l=;坡度一般写成1:m 的形式,如1:5i =等;把坡面与水平面的夹角记作α叫做坡角,那么tan hi lα==;例1、2012广安如图2,某水库堤坝横断面迎水坡AB 的坡比是1:3,堤坝高BC=50m,则迎水坡面AB 的长度是 .m解:tan∠BAC=13,∠BAC=30°,sin∠BAC=12, sin∠BAC=BC AB ,AB=2BC=100m例2、小强在教学楼的点P 处观察对面的办公大楼.为了测量点P 到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A 的仰角为45°,测得办公大楼底部点B 的俯角为60°,已知办公大楼高46米,CD =10米.求点P 到AD 的距离用含根号的式子表示.图2:i h l=hlαABCDPN M解析连结PA 、PB ,过点P 作PM ⊥AD 于点M ;延长BC ,交PM 于点N则∠APM =45°,∠BPM =60°,NM =10米………1分设PM =x 米 在Rt △PMA 中,AM =PM ×tan ∠APM =x tan 45°=x 米…3分在Rt △PNB 中,BN =PN ×tan ∠BPM =x -10tan 60°=x -103米…5分 由AM +BN =46米,得x +x -103 =46……6分解得,4610313x +=+ ,∴点P 到AD 的距离为4610313++米.结果分母有理化为()1838-米也可……8分答案4610313++结果分母有理化为()1838-米也可例3、2012湖北如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A ,斜坡的起始点为C ,现设计斜坡BC 的坡度1:5i =,则AC 的长度是 cm .解析如图,过点B 作BD ⊥AC 于D,依题意可求得AD =60cm,BD =54cm ;由斜坡 BC 的坡度i =1:5,求得CD =270cm,故AC =CD -AD =270-60=210cm .例4、2012浙江省绍兴,19如图1,某超市从一楼到二楼的电梯AB 的长为米,按坡角∠BAC 为32°.1求一楼与二楼之间的高度BC 精确到米;2电梯每级的水平级宽均是米,如图2.小明跨上电梯时,该电梯以每少上升2级的高度运行,10秒后他上升了多少米精确到米 备用数据:sin 32°=,cos 32°=,tan 32°=.解析1在Rt△ABC 中,已知∠B AC=32°,斜边AB 的长为米,根据锐角三角函数的定义即可求得第20题图MPDCBA第12题A BC3018一楼与二楼之间的高度BC .2先计算1级电梯的高,再根据10秒钟电梯上升了20级可计算10秒后他上升的高度.答案解:1∵sin ∠BAC =ABBC ,∴BC =AB ×sin32°=×≈米. 2∵tan32°= 级高级宽,∴级高=级宽×tan32°=×=,∵10秒钟电梯上升了20级,∴小明上升的高度为:20×米. 例5、2012浙江丽水,19学校校园内有一小山坡,经测量,坡角∠ABC=30°,斜坡AB 长为12米.为方便学生行走,决定开挖小山坡,使斜坡BD 的坡比是1:3即为CD 与BC 的长度之比,A,D 两点处于同一铅垂线上,求开挖后小山坡下降的高度AD.解析:∴AD=AC-CD=6-23.答:开挖后小山坡下降的高度AD 为6-23米.例6、2012深圳小明想测一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图3,此时测得地面上的影长为8米,坡面上的影长为4米,已知斜坡的坡角为30,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为 .米解答:如图3—1,根据坡角易求树的下半部分的高为2米,树的上半部分所在直角三角形的水平距离为(+823米,由两个直接三角形相似易求树的上半部分高度为(43米,知树的高度为()63米,选择A例72012江苏泰州24如图,一居民楼底部B 与山脚P 位于同一水平线上,小李在P 处测得居民楼顶A 的仰角为60°,然后他从P 处沿坡角为45°的山坡上走到C 处,这时,PC=30m,点C 与点A 在同一水平线上,A 、B 、P 、C 在同一平面内.1求居民楼AB 的高度;2求C 、A 之间的距离.精确到,参考数据:2≈,3≈,6≈60° CA B 45°图330°21图3-1第24题图解析过C作BP的垂线,垂足为G,利用特殊Rt△PCG和Rt△ABP中的边角关系,我们容易计算出CG即AB的长,最后用AC=BP+PG,就是C、A之间的距离.答案1过C作BP的垂线,垂足为G,在Rt△PCG中,CG=PCsin450=30×2所以=m2PG= PCcos450=30×2=所以C、A之间的距离例82012四川水务部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD.如图9所示,已知迎水坡面AB的长为16米,∠B=60°,背水坡面CD的长为,加固后大坝的横截面为梯形ABED,CE的长为8米.1已知需加固的大坝长为150米,求需要填土石方多少立方米2求加固后大坝背水坡面DE的坡度.解析1求出横截面△DCE的面积,然后乘以坝堤长度即可得出体积.可以分别过点A,D 作BC边上的高将问题转化为解直角三角形问题.2求大坝背水坡面DE的坡度就是求坡面DE上一点到BE的铅直高度与它到点E的水平宽度的比,这一点通常取梯形的顶点.答案解:1过点A作AG⊥BC于G,过点D作DH⊥BC于H,∴AG=DH.在Rt△ABG中,AG=sin60°·AB×16=∴DH=S△DCE=12·DH·CE=12×8=∴需要填土石方150=3.2在Rt△DHC中,HC24,∴HE=HC+CE=24+8=32.∴加固后大坝背水坡面DE的坡度=DHHE.AB CD图9E例9 2012江苏苏州如图,已知斜坡AB 长60米,坡角即∠BAC 为30°,BC⊥AC,现计划在斜坡中点D 处挖去部分坡体用阴影表示修建一个平行于水平线CA 的平台DE 和一条新的斜坡BE .请讲下面2小题的结果都精确到米,参考数据:≈.1若修建的斜坡BE 的坡角即∠BEF 不大于45°,则平台DE 的长最多为 米;2一座建筑物GH 距离坡角A 点27米远即AG=27米,小明在D 点测得建筑物顶部H 的仰角即∠HDM 为30°.点B 、C 、A 、G 、H 在同一个平面内,点C 、A 、G 在同一条直线上,且HG⊥CG,问建筑物GH 高为多少米解答: 解:1∵修建的斜坡BE 的坡角即∠BEF 不大于45°,∴∠BEF 最大为45°当∠BEF=45°时,EF 最短,此时ED 最长,∵∠DAC=∠BDF=30°,AD=BD=30,∴BF=EF=BD=15,DF=15,故:DE=DF ﹣EF=15﹣1≈;2过点D 作DP⊥AC,垂足为P .在Rt△DPA中,DP=AD=×30=15,PA=AD•cos30°=×30=15. 在矩形DPGM 中,MG=DP=15,DM=PG=15+27,在Rt△DMH 中,HM=DM•tan30°=×15+27=15+9. GH=HM+MG=15+15+9≈.答:建筑物GH 高为米.A B C DE GH。
(完整)锐角三角函数题型分类总结,推荐文档

锐角=角函数∙知识点一:钦角三角国数的≡x≡ 一、 锐角三角函数定义:在 RiAABC 中,ZC=9O 0, ZAS ZBX ZC 的对边分别为 a 、b 、c, 则ZA 的正弦可表示为;S ilLX= _________ JZA 的余弦可表示为CoSA= _________厶的正切:Tan-A= ________ ,它们弦称为ZA 的锐角三角函数2、取値范围—<¾inA< Co i⅛< __________ tanA>______1例如图所示,在RlA^C 中〉乙C=9Q° .例2.锐角三角函数束值;在 RtΔ,45C 中,ZC= 90° ,若 σ=9, B= 12,则 C= ___________SilL a l — _______ , COSU I f- __________ 9 taiL -l — __________ SSin^= _____ ; CQ ∖B= ____ ; tan.例3∙已知;如图,RI0∙∖M r 中,Z∏I ∖r =90o …⑷丄ZV 于出点,Zy=4, Hv=3• 求:SinZ732KxCOSZrVC?、tanZ∏IK .典型m :类型一:直角三角形求值31 .已知 RtQUBC 中丿 ZC≡90Q 5 taπJ= ,5C≡1⅞ 求.4C ∖∙3 和 8田・② CoSJ = ® tan.4∙=第1题團① sin J( ) 软边 an 5【an 方=ZB 旳对边( )2. 如朗 OO 的半径θA = 16cm, OC 丄貝B 于C 点,an ΛAOC =-.求肋及OC 的长•3. 已知:0。
中,OC 丄朋于 C 点;J5= 16cm ; dnZA0C (1) 求OQ 的半径OA 的长及弦心距& (2) 求 COSz4 OC 及 ta∏ZJθC∙g4. 已知ZJ 是锐角,SitIW=—;求COSA > tan J 的值17对应ill 练二1. 在RtA^C 中7 ZC=90C 7 若5C=1, .15-√5 ;则Ianj 的值为5B.巫5C.丄 2D. 22.在ABC 中,ZC=90o ,S inA=- >那么tanA 的值等于( ).53G 4 C 3 c 4 A.-5 B.— 5 C. 一4D. 一 3类型二利用角度转化求值,2. 如團,直径为10的CU 经过点C(Oo)和点O(Qo);与X 轴的正半釉交于点D, B 是》轴右侧圆弧上一点〉则C O SZ^C 的值为〈)C.-D-I1.已知;如图,RtZUBC 中,ZC= 90o ∙ Q 是Je 边上一点'DE 丄曲于E 点.^≡s⅛E3.如图,角α的顶点为0,它的一边在工轴的正半轴上J另一边Od上有一点Pd 4),则3丄如團,菱形九5CD的边长为IQCm,DE1AB, SinJ =-,则遗个菱形的面积二.5.如國06>是^iBC的外接圆,AD杲©O的直径,AC = I,则sin5的值是(7 \A. -B.-3 26.如图6,沿川E折蠡矩形纸片曲CQ ,c.£⅞□-4B=8, BC =10, AB=⅛ 则tan NEFC 的值为(A.- C.-57.如图7,在等腰直角三角形C中'ZC =90o , JC = 6, Z)为AC±—点,若tan ZDA.! = -,则-Q 的长为()5A・近B・2 C・1 D・2√21 ^rIS.如图S,在RtA-LffC 中,Z090°,AOS, Ad的平分线/D=」一求ZB的度数及边BC. AB的长.类型三化斜三角形为直角三角形例1 如图,在A ABC中,Z A=30C,Z B=45% AC=2√3、求AB 的长.Cn T •353.正方形网格中, ZHoB 如團放乱则tanZJ (95的值是(√L例 2∙已知:如團,在 AABC 中,ZBAC=I 20° , ∠S=10, AC=5 .对应岷1.如图,在RlAABC 中,ZBAC=90=,点D 在BC 边上,且AABD 是等边三甬形.若.43=2, 求AABC 的周长•〈结果保留根号)2. 已知:如虱 AABC 中「3=9, BC=G,厶4恥的面枳尊于9丿求血^3. ABC 中,乙4=60° …4方=6 Cm , AC=4 Clrb 则A-45C 的面积是求:siik^ABC 的值..4 羽 CnrDllcm 2类型四;利用 构造直角三角形例1如图所示,AABC 的顶点杲正方形网格的格点,则SinA 的值为<对应练习:1. ________________________________________________ 如图,AABC 的顶点都在方格纸的格点上,则Sir I A= ____________ .点厘逆吋针旋转得到AC8,则tanF 的值为D∙ 110D.IR特殊角的三角函数值锐角C30s45060。
锐角三角函数 知识点总结+典型例题

AB= BC = 5,
sin A
4 5
,求
B
解:作BD⊥AC于点D, ∵ sin A 4
∴ BD AB sin A 5 4 4,
5
5
AD AB2 BD2 52 42 3.
,
5 A
5
C D
又∵ △ABC 为等腰三角形, BD⊥AC, ∴ AC=2AD=6,
∴S△ABC=AC×BD÷2=12.
斜边c
B ∠A的对边a
sin A=∠A斜的边对边 cos A=∠A斜的边邻边
A ∠A的邻边b C
tan A=∠∠AA的的对邻边边
锐角A的正弦、余弦、和正切统称∠A的锐角三角函数.
已知直角三角形两边求锐角三角函数的值
例 如图,在 Rt△ABC 中,∠C=90°,AB=10, BC=6,求sinA,cosA,tanA的值.
解:由勾股定理,得
B
因此 sin A BC = 6 = 3,
AB 10 5
10
6
A
C
cos A AC 8 4 , tan A BC = 6 = 3 .
AB 10 5
AC 8 4
已知一边及一锐角三角函数值求函数值
如图,在Rt△ABC中,∠C=90°,
求sinB的值.
sin A 5, AC=12.
13
B
解:在Rt △ABC中,
13 5
设AB=13x,BC=5x,;122=(13x)2.
C 12
解得x=1.所以AB=13,BC=5.
因此 sin B AC 12. AB 13
如图,在 △ABC中, △ABC 的面积.
正弦:
sin
A
A的对边 斜边
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
锐角三角函数与特殊角专题训练【基础知识精讲】一、 正弦与余弦:1、 在ABC ∆中,C ∠为直角,我们把锐角A 的对边与斜边的比叫做A ∠的正弦,记作A sin , 锐角A 的邻边与斜边的比叫做A ∠的余弦,记作A cos .斜边的邻边斜边的对边A A A A ∠=⋅∠=cos sin .若把A ∠的对边BC 记作a ,邻边AC 记作b ,斜边AB 记作c ,则ca A =sin ,c bA =cos 。
2、当A ∠为锐角时, 1sin 0<<A ,1cos 0<<A (A ∠为锐角)。
二、 特殊角的正弦值与余弦值:2130sin =, 2245sin = , 2360sin =.2330cos = , 2245cos =, 2160cos = .三、 增减性:当00900<<α时,sin α随角度α的增大而增大;cos α随角度α的增大而减小。
四、正切概念:(1) 在ABC Rt ∆中,A ∠的对边与邻边的比叫做A ∠的正切,记作A tan 。
即 的邻边的对边A A A ∠∠=tan (或ba A =tan )五、特殊角的正弦值与余弦值:3330tan =; 145tan = ; 360tan =六、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值.)90sin(cos ),90cos(sin A A A A -︒=-︒=.七、任意锐角的正切值等于它的余角的余切值,任意锐角的余切值等于它的余角的正切值。
即 ()A A -=90cot tan , ()A A -=90tan cot .八、同角三角函数之间的关系:⑴、平方关系:1cos sin 22=+A A ⑵商的关系AAA cos sin tan =A AA sin cos cot =⑶倒数关系tana ·cota=1b【典型例题】【基础练习】 一、填空题:1. =︒+︒30sin 30cos ___________,2.sin 21= cos = 。
3.若21sin =θ,且︒<<︒900θ,则θ=_______,已知23sin =α,则锐角α=__________。
4.在_________cos ,,60,90,==∠=∠B A C ABC Rt 则中∆5.在ABC ∆,_________cos ,5,3,90====∠B AB AC C 则6._________sin ,5,3,90,====∠A AB BC C ABC Rt 则中∆7.在ABC ∆Rt 中,︒=∠90C ,b a 33=,则A ∠=_________,A sin =_________ 8.在ABC ∆Rt 中,如果各边长度都扩大2倍,则锐角A 的正弦值和余弦值( ) 9.在ABC ∆中,若0cos 2322sin 2=⎪⎪⎭⎫⎝⎛-+-B A ,A ∠,B ∠都是锐角,则C ∠的度数是( )10.(1) 如果α是锐角,且154sin sin 22=+ α,那么α的度数为( )(2).如果α是锐角,且54cos =α,那么)90cos(α-的值是( ) 11. 将︒21cos ,︒37cos ,︒41sin ,︒46cos 的值,按由小到大的顺序排列是_____________________12.在ABC ∆中,︒=∠90C ,若51cos =B ,则B 2sin =________ 13. 30cos 30sin 22+的值为__________, ________18sin 72sin 22=+14.一个直角三角形的两条边长为3、4,则较小锐角的正切值是( ) 15.计算22)31(45tan 60sin ---⋅,结果正确的是( ) 16.在_________,1,2tan ,,===∠=∠∆b a B Rt C ABC Rt 则若中17.等腰梯形腰长为6,底角的正切为42,下底长为212,则上底长为 ,高为 。
18.在ABC ∆Rt 中,︒=∠90C ,3cot =A ,则2tan sin cot CB A ++的值为____________。
19.比较大小(用>、<、=号连接):(其中︒=+90B A )A A tan _____sin ,B A cos ______sin ,A A Atan _____cos sin20.在Rt ABC ∆中,︒=∠90C ,则B A tan tan ⋅等于( )ADEBC二、【计算】21︒⋅︒+︒⋅︒45sin 30cos 45cos 30sin 22.︒⋅︒+︒+︒30cos 30sin 45sin 2260sin 21。
23.)45cos 60)(sin 45sin 30)(cos 45sin 230sin 2(︒-︒︒+︒︒+︒ 24. 21+12--)(+2sin60°—︒60tan 1—【能力提升】1、如图,在AB CD Rt ACB ABC Rt ⊥∠=∠,,中∆于点D ,AD =4,,54sin =∠ACD CD 求、BC 的值。
2、比较大小:sin23°______sin33°;cos67.5°_________cos76.5°。
3、若30°<α<β<90°,化简αβαβcos 123cos )cos (cos 2-+---4、已知1sin 40sin 22=+︒α,则锐角α=_________。
5、在54sin ,51cos ,90-===∠n B A C ABC Rt 中,∆那么n 的值是___________。
6、已知,cos sin ,cos sin n m ==+αααα 则m 、n 的关系是( )A .n m =B .12+=n nC .122+=n mD .n m 212-= 7、如图,在等腰Rt △ABC 中,∠C =90o,AC =6,D 是AC 上一点,若tan ∠DBA =5,则AD 的长为( )A.2 B.3 C.2 D.1 8、如图,矩形ABCD 中,AB >AD ,AB =a ,AN 平分∠DAB ,DM ⊥AN 于点M ,CN ⊥AN 于点N .则DM +CN 的值为(用含a 的代数式表示)( ) A .a B .a 54C .a 22D .a 23 9、已知AD 是等腰△ABC 底边上的高,且tan ∠B=43, aNMCDABAC 上有一点E ,满足AE:CE=2:3则tan ∠ADE 的值是( )A E ⊥BC 于E ,BC=1,cosB=135,求这个菱形的面积。
11、(北京市中考试题) 在中ABC ∆Rt ,︒=∠90C ,斜边5=c ,两直角边的长b a 、是关于x 的一元二次方程0222=-+-m mx x 的两个根,求ABC ∆Rt 较小锐角的正弦值. 12、(上海中考模拟)如图ΔABC 中,AD 是BC 边上的高,tan ∠B=cos ∠DAC 。
(1)求证:AC=BD (2)若sin ∠C=1312,BC=12,求AD 的长.14、(上海中考模拟)已知:如图,在BC D B ACB ABC Rt 是中,,53sin ,90==∠ ∆边上一点,且︒=∠45ADC ,DC = 6 。
求.的正切值BAD ∠。
DC[思维拓展训练]1、如图,已知P为∠AOB的边OA上的一点,以P为顶点的∠MPN的两边分别交射线OB 于M、N两点,且∠MPN=∠AOB=α(α为锐角).当∠MPN以点P为旋转中心,PM边与PO重合的位置开始,按逆时针方向旋转(∠MPN保持不变)时,M、N两点在射线OB上同时以不同的速度向右平行移动.设OM=x,ON=y(y>x>0),△POM的面积为S.若sinα=二分之根号三。
oP=2.(1)当∠MPN旋转30°(即∠OPM=30°)时,求点N移动的距离;(2)求证:△OPN∽△PMN;(3)写出y与x之间的关系式;(4)试写出S随x变化的函数关系式,并确定S的取值范围.2题图2、如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P 从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).(1)设△BPQ的面积为S,求S与t之间的函数关系式;(2)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形;(3)当线段PQ与线段AB相交于点O,且2AO=OB时,求∠BQP的正切值;(4)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由.3、如图:直角坐标系中,梯形ABCD 的底边AB 在x 轴上,底边CD 的端点D 在y 轴上.直线CB 的表达式为y =-43x +163,点A 、D 的坐标分别为(-4,0),(0,4).动点P 自A 点出发,在AB 上匀速运行.动点Q 自点B 出发,在折线BCD 上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P 运动t (秒)时,△OPQ 的面积为s (不能构成△OPQ 的动点除外).(1)求出点B 、C 的坐标;(2)求s 随t 变化的函数关系式; (3)当t 为何值时s 有最大值?并求出最大值.4、如图,将矩形OABC 放置在平面直角坐标系中,点D 在边0C 上,点E 在边OA 上,把矩形沿直线DE 翻折,使点O 落在边AB 上的点F 处,且tan ∠BFD=34.若线段OA 的长是一元二次方程x 2—7x 一8=0的一个根,又2AB=30A .请解答下列问题: (1)求点B 、F 的坐标: (2)求直线ED 的解析式:(3)在直线ED 、FD 上是否存在点M 、N ,使以点C 、D 、M 、N 为顶点的四边 形是平行四边形,若存在,请直接写出点M 的坐标;若不存在,请说明理由. OxyABCDPQ6题图5、如图,在直角梯形ABCD 中,∠D=∠BCD=90°,∠B=60°, AB=6,AD=9, 点E 是CD 上的一个动点(E 不与D 重合),过点E 作EF ∥AC ,交AD 于点F(当E 运动到C 时,EF 与AC 重合巫台).把△DEF 沿EF 对折,点D 的对应点是点G ,设DE=x , △GEF 与梯形ABCD 重叠部分的面积为y 。
(1) 求CD 的长及∠1的度数;(2) 若点G 恰好在BC 上,求此时x 的值;(3) 求y 与x 之间的函数关系式。
