代数几何综合问题(2)课后练习
(7)代数几何综合题
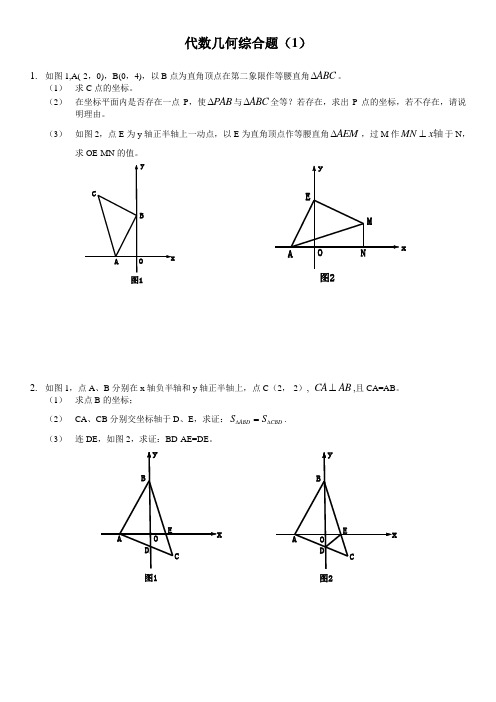
1. 如图1,A(-2,0),B(0,4),以B 点为直角顶点在第二象限作等腰直角ABC ∆。
(1) 求C 点的坐标。
(2) 在坐标平面内是否存在一点P ,使PAB ∆与ABC ∆全等?若存在,求出P 点的坐标,若不存在,请说明理由。
(3) 如图2,点E 为y 轴正半轴上一动点,以E 为直角顶点作等腰直角AEM ∆,过M 作MN x ⊥轴于N ,求OE-MN 的值。
2. 如图1,点A 、B 分别在x 轴负半轴和y 轴正半轴上,点C (2,-2), CA AB ⊥,且CA=AB 。
(1) 求点B 的坐标;(2) CA 、CB 分别交坐标轴于D 、E ,求证:ABD CBD S S ∆∆=. (3) 连DE ,如图2,求证:BD-AE=DE 。
图1图2x图2图11. 如图1,已知(0,)A a ,(,0)B b ,点P 为ABO ∆的角平分线的交点。
(1) 若,a b 满足2440a b a a ++-+=,求A 、B 的坐标。
(2) 连OP ,在(1)的条件下,求证:OP+OB=AB.(3) 如图2,PM PA ⊥交x 轴于M ,PN AB ⊥于N ,试探究:AO -OM 与PN 之间的数量关系。
2. 已知ABC ∆中,90ABC ∠=︒,AB=AC ,点A 、B 分别是x 轴和y 轴上的一动点。
(1) 如图1,若点C 的横坐标为-4,求点B 的坐标;(2) 如图2,BC 交x 轴于D ,AD 平分BAC ∠,若点C 的纵坐标为3,A(5,0),求点D 的坐标。
(3) 如图3,分别以OB 、AB 为直角边在第三、第四象限作等腰直角OBF ∆和等腰直角ABE ∆,EF 交y轴于M ,求:BEM ABO S S ∆∆。
图2图1x图3图2x图1x。
九年级数学练习题之代数几何综合题

九年级数学练习题之代数几何综合题Ⅰ、综合问题精讲:代数几何综合题是初中数学中覆盖面最广、综合性最强的题型,近几年中考试题中的综合题大多以代数几何综合题的形式出现,其解题关键点是借助几何直观解题,运用方程、函数的思想解题,灵活运用数形结合,由形导数,以数促形,综合运用代数几何知识解题.Ⅱ、典型例题剖析【例1】(温州,12分)如图,已知四边形ABCD内接于⊙O,A是的中点,AEAC于A,与⊙O及CB的延长线分别交于点F、E,且,EM切⊙O于M。
⑴ △ADC∽△EBA;⑵ AC2=BC⑶如果AB=2,EM=3,求cotCAD的值。
解:⑴∵四边形ABCD内接于⊙O,CDA=ABE,∵,DCA=BAE,△CAD∽△AEB⑵ 过A作AHBC于H(如图)∵A是中点,HC=HB=BC,∵CAE=900,AC2=CHCE=BCCE⑶∵A是中点,AB=2,AC=AB=2,∵EM是⊙O的切线,EBEC=EM2 ①∵AC2=BCCE,BCCE=8 ②①+②得:EC(EB+BC)=17,EC2=17∵EC2=AC2+AE2,AE=∵△CAD∽△ABE,CAD=AEC,cotCAD=cotAEC=点拨:此题的关键是树立转化思想,将未知的转化为已知的.此题表现的非常突出.如,将CAD转化为AEC就非常关键. 【例2】(自贡)如图 2-5-2所示,已知直线y=2x+2分别与x 轴、y轴交于点A、B,以线段AB为直角边在第一象限内作等腰直角△ABC,BAC=90○。
过C作CDx轴,D为垂足.(1)求点 A、B的坐标和AD的长;(2)求过B、A、C三点的抛物线的解析式。
解:(1)在y=2x+2中分别令x=0,y=0.得 A(l,0),B(0,2).易得△ACD≌△BAO,所以 AD=OB=2.(2)因为A(1,0),B(0,2),且由(1),得C(3,l).设过过B、A、C三点的抛物线为所以所以点拨:此题的关键是证明△ACD≌△BAO.【例3】(重庆,10分)如图,在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.(1) 求直线AB的解析式;(2) 当t为何值时,△APQ与△AOB 相似?(3) 当t为何值时,△APQ的面积为个平方单位?解:(1)设直线AB的解析式为y=kx+b由题意,得解得所以,直线AB的解析式为y=-x+6.(2)由AO=6, BO=8 得AB=10所以AP=t ,AQ=10-2t1 当APQ=AOB时,△APQ∽△AOB.所以 = 解得 t=(秒)2 当AQP=AOB时,△AQP∽△AOB.所以 = 解得 t=(秒)(3)过点Q作QE垂直AO于点E.在Rt△AOB中,SinBAO==在Rt△AEQ中,QE=AQSinBAO=(10-2t)=8 -t所以,S△APQ=APQ E=t(8-t)=-+4t= 解得t=2(秒)或t=3(秒).(注:过点P作PE垂直AB于点E也可,并相应给分)点拨:此题的关键是随着动点P的运动,△APQ的形状也在发生着变化,所以应分情况:①APQ=AOB=90○②APQ=ABO.这样,就得到了两个时间限制.同时第(3)问也可以过P作PEAB.【例4】(南充,10分)如图2-5-7,矩形ABCD中,AB=8,BC=6,对角线AC上有一个动点P(不包括点A和点C).设AP=x,四边形PBCD的面积为y.(1)写出y与x的函数关系,并确定自变量x的范围.(2)有人提出一个判断:关于动点P,⊿PBC面积与⊿PAD面积之和为常数.请你说明此判断是否正确,并说明理由. 解:(1)过动点P作PEBC于点E.在Rt⊿ABC中,AC=10, PC=AC-AP=10-x.∵ PEBC,ABBC,⊿PEC∽⊿ABC.故,即⊿PBC面积=又⊿PCD面积=⊿PBC面积=即 y,x的取值范围是0(2)这个判断是正确的.理由:由(1)可得,⊿PAD面积=⊿PBC面积与⊿PAD面积之和=24.点拨:由矩形的两边长6,8.可得它的对角线是10,这样PC=10-x,而面积y是一个不规则的四边形,所以可以把它看成规则的两个三角形:△PBC、△PCD.这样问题就非常容易解决了.Ⅲ、综合巩固练习(100分 90分钟)1、如图2-5-8所示,在直角坐标系中,△ABC各顶点坐标分别为A (0,),B(-1,0)、C(0,1)中,若△DEF各顶点坐标分别为D(,0)、E(0,1)、F(0,-1),则下列判断正确的是( )A.△DEF由△ABC绕O点顺时针旋转90○得到;B.△DEF由△ABC绕O点逆时针旋转90○得到;C.△DEF由△ABC绕O点顺时针旋转60○得到;D.△DEF由△ABC绕O点顺时针旋转120○得到2.如图2-5-9,已知直线 y=2x+1与x轴交于A点,与y轴交于B点,直线y=2x1与x轴交于C点,与y轴交于D点,试判断四边形ABCD的形状.3.如图2-5-10所示,在矩形ABCD中,BD=20,ADAB,设ABD=,已知sin是方程25z2-35z+ 12=0的一个实根.点E、F分别是BC、DC上的点,EC+CF=8,设BE=x,△AEF面积等于y.⑴ 求出y与x之间的函数关系式;⑵ 当E、F两点在什么位置时y有最小值?并求出这个最小值.4.(10分)如图2-5-11所示,直线y=-x+ 4与x 轴、y轴分别交于点M、N.(1)求M、N两点的坐标;(2)如果点P在坐标轴上,以点P为圆心,为半径的圆与直线y=-x+ 4相切,求点P的坐标.5.(10分)如图2-5-12所示,已知等边三角形ABC中,AB=2,点P是AB边上的任意一点(点P可以与点A重合,但不与点B重合),过点P作PEBC.垂足为E;过点E作EFAC,垂足为F;过点F作FQAB,垂足为Q.设BP=x,AQ=y.⑴ 写出y与x之间的函数关系式;⑵ 当BP的长等于多少时,点P与点Q重合;⑶ 当线段 PE、FQ相交时,写出线段PE、EF、FQ所围成三角形的周长的取值范围(不必写出解题过程)6.(12分)如图2-5-13所示,已知A由两点坐标分另为(28,0)和(0,28),动点P从A点开始在线段AO上以每秒3个长度单位的速度向原点O运动,动直线 EF从 x轴开始以每秒1个长度单位的速度向上平行移动(即EF∥x轴)并且分别交y轴,线段AB交于E、F点.连接FP,设动点P与动直线EF 同时出发,运动时间为t秒.⑴ 当t=1秒时,求梯形OPFE的面积,t为何值时,梯形OPFE 的面积最大,最大面积是多少?⑵ 当梯形OPFE的面积等于△APF的面积时,求线段 PF的长.⑶ 设t的值分别取t1,t2时(t1t2),所对应的三角形分别为△AF1P1和△AF2P2 ,试判断这两个三角形是否相似,请证明你的判断.7.(12分)如图2-5-14所示,在直角坐标系中,矩形ABCD的顶点,A的坐标为(1,0),对角线的交点P的坐标为(,1)⑴ 写出B、C、D三点的坐标;⑵ 若在AB上有一点 E作,入过 E点的直线将矩形ABCD的面积分为相等的两部分,求直线l的解析式;⑶ 若过C点的直线将矩形ABCD的面积分为4:3两部分,并与y轴交于点M,求过点C、D、M三点的抛物线的解析式.8.(10分)已知矩形ABCD在平面直角坐标系中,顶点A、B、D的坐标分别为A(0,0),B(m,0),D(0,4)其中m0.⑴ 写出顶点C的坐标和矩形ABCD的中心P点的坐标(用含m 的代数式表示)⑵ 若一次函数y=kx-1的图象把矩形ABCD分成面积相等的两部分,求此一次函数的解析式(用含m的代数式表示)⑶ 在⑵的前提下,又与半径为1的⊙M相切,且点 M(0,1),求此矩形ABCD的中心P点的坐标.9.(10分)如图2-5-15所示,等边三角形ABC的边长为6,点D、E分别在边AB,AC上,且AD=AE=2,若点F从点B开始以每秒二个单位长度的速度沿射线BC方向运动,设点F运动的时间为t秒,当t0时,直线FD与过点A且平行于BC 的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.⑴ 设△EGA的面积为S,写出S与 t的函数解析式;⑵ 当t为何值时,AB⑶ 请你证明△GFH的面积为定值.10. (10分)如图2-5-16,在矩形ABCD中,AB=10。
省市公开课专题六 代数几何综合题 精编作业本

∴△MBD≌△NCD, ∴BM=CN,DM=DN.在△EMD和△FND中,
EMD FND
DM
DN
MDE NDF
首页
末页
∴△EMD≌△FND,∴EM=FN,
∴BE+CF=BM+EM+CF=BM+FN+CF=BM+CN
∵PQ∥AB, ∴∠DPE=∠PEB. ∵∠CPQ=∠DPE, ∠CPQ=∠B, ∴∠B=∠PEB, ∴PB=PE=5x,
∴3x+5x=9,解得x= 9
①当0<x≤
9 8
时,
8
T=PD+DE+PE=3x+4x+5x= 1②2当x,此9 <时x0<<3T时≤ ,227 设
8
PE交AB于点G,DE交AB 于F,作GH⊥FQ,垂足 为H, ∴HG=DF,FG=DH, Rt△PHG∽Rt△PDE,
在Rt△BMD中,DM=BM•tanB= 3 BM,
∴BE+CF= 3 (BE﹣CF).
首页
末页
首页
末页
(2)解:连接AD,
∵PQ∥AB,
∴∠ADQ=∠DAB.
∵点D在∠BAC的平分线
上,
∴∠DAQ=∠DAB,
∴∠ADQ=∠DAQ,
∴AQ=DQ.
在Rt△CPQ中,PQ=5x,
∵PD=PC=3x,
首页
末页
∴DQ=2x. ∵AQ=12﹣4x, ∴12﹣4x=2x,解得x=2, ∴CP=3x=6. (3)解:当点E在AB上 时,
∴F5G=DH= 3x 3(9 3x) ∴T=PG+PD+DF5 +FG = (9 3x) 3x 4 (9 3x) [3x 3 (9 3x)]
初中数学代数几何综合问题

代数几何综合问题一、选择题1.如图,是一对变量满足的函数关系的图象,有下列3个不同的问题情境:①小明骑车以400米/分的速度匀速骑了5分,在原地休息了4分,然后以500米/分的速度匀速骑回出发地,设时间为x分,离出发地的距离为y千米;②有一个容积为6升的开口空桶,小亮以1.2升/分的速度匀速向这个空桶注水,注5分后停止,等4分后,再以2升/分的速度匀速倒空桶中的水,设时间为x分,桶内的水量为y升;③矩形ABCD中,AB=4,BC=3,动点P从点A出发,依次沿对角线AC、边CD、边DA运动至点A停止,设点P的运动路程为x,当点P与点A不重合时,y=S△ABP;当点P与点A重合时,y=0.其中,符合图中所示函数关系的问题情境的个数为【】A.0 B.1 C.2 D.32.如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于12MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为【】A.a=b B.2a+b=﹣1 C.2a﹣b=1 D.2a+b=13.若a,b为实数,且a1b10++-=,则(ab)2013的值是【】A、0B、1C、﹣1D、±14.一个三角形的两边长分别为3和6,第三边的边长是方程(x﹣2)(x﹣4)=0的根,则这个三角形的周长是【】A.11 B.11或13 C.13 D.以上选项都不正确5.若平行四边形的一边长为2,面积为46】A .3与4之间B .4与5之间C .5与6之间D .6与7之间6.已知()2x y 32x y 0-+++=,则x +y 的值为【 】A .0B .﹣1C .1D .57.一条直线y =kx +b ,其中k +b =﹣5、kb =6,那么该直线经过【 】A .第二、四象限B .第一、二、三象限C .第一、三象限D .第二、三、四象限 8.已知实数x ,y ,m 满足x 2|3x y m |0++++=,且y 为负数,则m 的取值范围是【 】A .m >6B .m <6C .m >﹣6D .m <﹣6二、填空题9.若a 2b 30-+-=,则a b = ▲ .10.如图,正方形ODBC 中,OC =1,OA =OB ,则数轴上点A 表示的数是 ▲ .11.若实数a 、b 满足a 2b 40++-=,则2a b= ▲ . 12.无论x 2x 6x m -+都有意义,则m 的取值范围为 ▲ .13a 1a b 10-+++=,则a b = ▲ .14.已知点P (3,﹣1)关于y 轴的对称点Q 的坐标是(a +b ,1﹣b ),则a b 的值为 ▲ .15.函数3x y -=x 的取值范围是 ▲ . 16.函数y x 3=-x 的取值范围是 ▲ ;若分式2x 3x 1-+的值为0,则x = ▲ . 17.若直角三角形的两直角边长为a 、b 2a 6a 9b 40-+-=,则该直角三角形的斜边长为 ▲ .1822a 3a 1b 2b 10-+++=,则221a b a +-= ▲ 。
代数几何综合问题

代数几何综合问题题1、(北京丰台)如图,已知平面直角坐标系中三点A (2,0),B (0,2),P (x ,0))0(<x ,连结BP ,过P 点作PC PB ⊥交过点A 的直线a 于点C (2,y ) (1)求y 与x 之间的函数关系式;(2)当x 取最大整数时,求BC 与PA 的交点Q 的坐标。
解:(1) PC PB BO PO ⊥⊥, ∴∠+∠=︒∠+∠=︒∴∠=∠CPA OPB PBO OPB CPA PBO 9090, A (2,0),C (2,y )在直线a 上 ∴∠=∠=︒BOP PAC 90 ∴∆∆B O P PAC ~∴=PO AC BO PA ,∴=+||||||x y x 22, x y x y x <<∴=-0022,,∴=-+y x x 122 (2) x <0,∴x 的最大整数值为-1 , 当x =-1时,y =-32,∴=CA 32BO a BOQ CAQ OQ AQ BOCA//~,,∴∴=∆∆ 设Q 点坐标为()m ,0,则AQ m =-2∴-=∴=m m m 223287, ∴Q 点坐标为()870,说明:利用数形结合起来的思想,考查了相似三角形的判定及应用。
关键是搞清楚用坐标表示的数与线段的长度的关系。
题2、(2006、徐州)在平面直角坐标系中,已知矩形ABCD 中,边2AB =,边1AD =,且AB 、AD 分别在x 轴、y 轴的正半轴上,点A 与坐标原点重合.将矩形折叠,使点A 落在边DC 上,设点A '是点A 落在边DC 上的对应点.(1)当矩形ABCD 沿直线12y x b =-+折叠时(如图1),求点A '的坐标和b 的值;(2)当矩形ABCD 沿直线y kx b =+折叠时,① 求点A '的坐标(用k 表示);求出k 和b 之间的关系式; ② 如果我们把折痕所在的直线与矩形的位置分 为如图2、3、4所示的三种情形, 请你分别写出每种情形时k 的取值范围. (将答案直接填在每种情形下的横线上)k 的取值范围是 ; k 的取值范围是 ;k 的取值范围是 ;【分析:】1、对折是一个操作性名词,它的数学实质就是轴对称。
初中数学几何综合-含答案
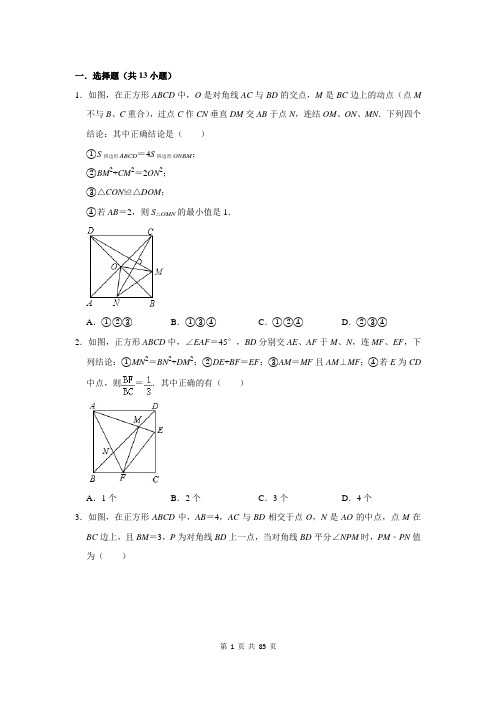
一.选择题(共13小题)1.如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M 不与B、C重合),过点C作CN垂直DM交AB于点N,连结OM、ON、MN.下列四个结论:其中正确结论是()①S四边形ABCD=4S四边形ONBM;②BM2+CM2=2ON2;③△CON≌△DOM;④若AB=2,则S△OMN的最小值是1.A.①②③B.①③④C.①②④D.②③④2.如图,正方形ABCD中,∠EAF=45°,BD分别交AE、AF于M、N,连MF、EF,下列结论:①MN2=BN2+DM2;②DE+BF=EF;③AM=MF且AM⊥MF;④若E为CD 中点,则=.其中正确的有()A.1个B.2个C.3个D.4个3.如图,在正方形ABCD中,AB=4,AC与BD相交于点O,N是AO的中点,点M在BC边上,且BM=3,P为对角线BD上一点,当对角线BD平分∠NPM时,PM﹣PN值为()A.1B.C.2D.4.如图,在正方形ABCD内一点E连接BE、CE,过C作CF⊥CE与BE延长线交于点F,连接DF、DE.CE=CF=1,DE=,下列结论中:①△CBE≌△CDF;②BF⊥DF;③点D到CF的距离为2;④S四边形DECF=+1.其中正确结论的个数是()A.1B.2C.3D.45.如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M.则下列结论:①∠AME=90°,②∠BAF=∠EDB,③AM=MF,④ME+MF=MB.其中正确结论的有()A.4个B.3个C.2个D.1个6.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,EH与CF交于点O.则HE的长为()A.2B.C.2D.或27.如图,在正方形ABCD中,E为BC上一点,过点E作EF∥CD,交AD于F,交对角线BD于G,取DG的中点H,连结AH,EH,FH.下列结论:①FH∥AE;②AH=EH且AH⊥EH;③∠BAH=∠HEC;④△EHF≌△AHD;⑤若,则.其中哪些结论是正确()A.①②④⑤B.②③④C.①②③D.②③④⑤8.如图,在正方形ABCD中,AC、BD相交于点O,E、F分别为BC、CD上的两点,BE =CF,AE、BF分别交BD、AC于M、N两点,连OE、OF.下列结论:①AE=BF;②AE⊥BF;③CE+CF=BD;④S四边形OECF=S正方形ABCD,其中正确的是()A.①②B.①④C.①②④D.①②③④9.如图,在正方形ABCD中,M是对角线BD上的一点,点E在AD的延长线上,连接AM、EM、CM,延长EM交AB于点F,若AM=EM,∠E=30°,则下列结论:①FM=ME;②BF=DE;③CM⊥EF;④BF+MD=BC,其中正确的结论序号是()A.①②③B.①②④C.②③④D.①②③④10.如图,在正方形ABCD中,对角线AC,BD交于点O,AG平分∠BAC交BD于G,DE ⊥AG于点H.下列结论:①AD=2AE:②FD=AG;③CF=CD:④四边形FGEA是菱形;⑤OF=BE,正确的有()A.2个B.3个C.4个D.5个11.如图,以正方形ABCD的顶点A为圆心,以AD的长为半径画弧,交对角线AC于点E,再分别以D,E为圆心,以大于DE的长为半径画弧,两弧交于图中的点F处,连接AF并延长,与BC的延长线交于点P,则∠P=()A.90°B.45°C.30°D.22.5°12.如图,正方形ABCD中,点E在边CD上,连接AE,过点A作AF⊥AE交CB的延长线于点F,连接EF,AG平分∠F AE,AG分别交BC,EF于点G,H,连接EG,DH.则下列结论中:①AF=AE;②∠EGC=2∠BAG;③DE+BG=EG;④AD+DE=DH;⑤若DE=CE,则CE:CG:EG=3:4:5,其中正确的结论有()A.2个B.3个C.4个D.5个13.如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC=2,则下列结论:①FB⊥OC;②△EOB≌△CMB;③四边形EBFD是菱形;④MB=2.其中正确结论的个数是()A.1个B.2个C.3个D.4个二.填空题(共3小题)14.如图,点E为正方形ABCD外一点,且ED=CD,连接AE,交BD于点F.若∠CDE =40°,则∠DFC的度数为.15.如图,正方形ABCD中,在AD的延长线上取点E,F,使DE=AD,DF=BD,连接BF分别交CD,CE于H,G,下列结论:①EC=2DG;②∠GDH=∠GHD;③S△CDG=S四边形DHGE;④图中只有8个等腰三角形.其中正确的有(填番号).16.如图,在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE、BE、F A⊥AE交DP于点F,连接BF,FC.若AE=2,则FC=.三.解答题(共24小题)17.如图,在直线l上将正方形ABCD和正方形ECGF的边CD和边CE靠在一起,连接DG,过点A作AH∥DG,交BG于点H.连接HF,AF,其中FH交DG于点M.(1)求证:△AHF为等腰直角三角形.(2)若AB=3,EC=4,求DM的长.18.如图,已知正方形ABCD的面积是8,连接AC、BD交于点O,CM平分∠ACD交BD 于点M,MN⊥CM,交AB于点N,(1)求∠BMN的度数;(2)求BN的长.19.如图示,正方形ABCD的对角线交于点O,点E、F分别在AB,BC的延长线上,且∠EOF=90°,OE与BC交于点M,连接EF,G是EF的中点,连接OG.(1)求证:OE=OF(2)若∠BOG=65°,求∠BOE的度数;(3)是否存在点M是BC中点,且使(1)的结论成立,若存在,请给予证明;若不存在,请说明理由.20.如图,正方形ABCD中,AB=,在边CD的右侧作等腰三角形DCE,使DC=DE,记∠CDE为α(0°<α<90°),连接AE,过点D作DG⊥AE,垂足为G,交EC的延长线于点F,连接AF.(1)求∠DEA的大小(用α的代数式表示);(2)求证:△AEF为等腰直角三角形;(3)当CF=时,求点E到CD的距离.21.如图1,在正方形ABCD中,点E在边CD上(不与点C,D重合),AE交对角线BD 于点G,GF⊥AE交BC于点F.(1)求证:AG=FG.(2)若AB=10,BF=4,求BG的长.(3)如图2,连接AF,EF,若AF=AE,求正方形ABCD与△CEF的面积之比.22.在正方形ABCD中,点E是DC上一点,连结AC,AE.(1)如图1,若AC=8,AE=10,求△ACE的面积.(2)如图2,EF⊥AC于点F,连结BF.求证:AE=BF.23.如图1,正方形ABCD中,点E是边BC延长线上一点,连接DE,过点B作BF⊥DE,垂足为点F,BF与CD相交于点G.(1)求证:△BCG≌△DCE;(2)如图2,连接BD,若,求BG的长.24.如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(不与O、C 重合),作AF⊥BE,垂足为G,分别交BC、OB于F、H,连接OG、CG.(1)求证:△AOH≌△BOE;(2)求∠AGO的度数;(3)若∠OGC=90°,BG=,求△OGC的面积.25.如图,O为正方形ABCD对角线的交点,E为AB边上一点,F为BC边上一点,△EBF 的周长等于BC的长.(1)若AB=24,BE=6,求EF的长;(2)求∠EOF的度数;(3)若OE=OF,求的值.26.如图,正方形ABCD中,E为BC上一点,过B作BG⊥AE于G,延长BG至点F使∠CFB=45°(1)求证:∠BAG=∠CBF;(2)求证:AG=FG;(3)若GF=2BG,CF=,求AB的长.27.如图1,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且P A=PE,PE交CD于点F,(1)证明:PC=PE;(2)求∠CPE的度数;(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.28.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.(1)试说明EO=FO;(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.29.如图,已知平行四边形ABCD中,对角线AC、BD交于点O,E是DB延长线上一点,且△ACE是等边三角形.(1)求证:四边形ABCD是菱形;(2)若∠AEB=2∠EAB,求证:四边形ABCD是正方形.30.如图1,在正方形ABCD中,G为线段BD上一点,连接AG,过G作AG⊥GE交BC 于E,连接AE.(1)求证:BG=DG+BE;(2)如图2,AB=4,E为BC中点,P,Q分别为线段AB,AE上的动点,满足QE=AP,则在P,Q运动过程中,当以PQ为对角线的正方形PRQS的一边恰好落在△ABE的某一边上时,直接写出正方形PRQS的面积.31.如图,在平行四边形ABCD中,AC⊥AD,延长DA于点E,使得DA=AE,连接BE.(1)求证:四边形AEBC是矩形;(2)过点E作AB的垂线分别交AB,AC于点F,G,连接CE交AB于点O,连接OG,若AB=6,∠CAB=30°,求△OGC的面积.32.如图,在四边形ABCD中,AD∥BC,AB=BC,对角线AC、BD交于点O,BD平分∠ABC,过点D作DE⊥BC,交BC的延长线于点E,连接OE.(1)求证:四边形ABCD是菱形;(2)若DC=2,AC=4,求OE的长.33.如图,在菱形ABCD中,对角线AC、BD交于点O,过点A作AE⊥BC于点E,延长BC至F,使CF=BE,连接DF.(1)求证:四边形AEFD是矩形;(2)若BF=8,DF=4,求CD的长.34.已知:如图,点E为▱ABCD对角线AC上的一点,点F在线段BE的延长线上,且EF =BE,线段EF与边CD相交于点G.(1)求证:DF∥AC;(2)如果AB=BE,DG=CG,联结DE、CF,求证:四边形DECF是矩形.35.如图,▱ABCD的对角线AC,BD交于点O,过点D作DE⊥BC于E,延长CB到点F,使BF=CE,连接AF,OF.(1)求证:四边形AFED是矩形.(2)若AD=7,BE=2,∠ABF=45°,试求OF的长.36.如图,平行四边形ABCD中,AC⊥BC,过点D作DE∥AC交BC的延长线于点E,点M为AB的中点,连接CM.(1)求证:四边形ADEC是矩形;(2)若CM=5,且AC=8,求四边形ADEC的周长.37.如图,已知△OAB中,OA=OB,分别延长AO、BO到点C、D.使得OC=AO,OD =BO,连接AD、DC、CB.(1)求证:四边形ABCD是矩形;(2)以OA、OB为一组邻边作▱AOBE,连接CE,若CE⊥BD,求∠AOB的度数.38.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.(1)求证:四边形AEFD是矩形;(2)连接OE,若AD=10,EC=4,求OE的长度.39.如图,在平行四边形BPCD中,点O为BD中点,连接CO并延长交PB延长线于点A,连接AD、BC,若AC=CP,(1)求证:四边形ABCD为矩形;(2)在BA的延长线上取一点E,连接OE交AD于点F,若AB=9,BC=12,AE=3,则AF的长为.40.如图,菱形ABCD中,AC与BD交于点O,DE∥AC,DE=AC.(1)求证:四边形OCED是矩形;(2)连结AE,交OD于点F,连结CF,若CF=CE=1,求AC长.2021年01月06日杨莲莲的初中数学组卷参考答案与试题解析一.选择题(共13小题)1.如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M 不与B、C重合),过点C作CN垂直DM交AB于点N,连结OM、ON、MN.下列四个结论:其中正确结论是()①S四边形ABCD=4S四边形ONBM;②BM2+CM2=2ON2;③△CON≌△DOM;④若AB=2,则S△OMN的最小值是1.A.①②③B.①③④C.①②④D.②③④【分析】根据正方形的性质,依次判定△CNB≌△DMC,△AON≌△BOM,根据全等三角形的性质以及勾股定理进行计算即可得出结论.【解答】解:∵四边形ABCD是正方形,∴AC⊥BD,AO=AC,BO=BD,AC=BD,∴AO=BO,∠OAN=∠OBM=45°,∠AOB=90°,∵CN⊥DM,∴∠MCN+∠CMD=∠CMD+∠CDM=90°,∴∠CDM=∠BCN,∵CD=BC,∠DCM=∠CBN,∴△CDM≌△BCN(AAS),∴CM=BN,∴AN=BM,∴△AON≌△BOM(SAS),∴S△AON=S△BOM,∴S四边形ONBM=S△AOB=S正方形ABCD,∴S四边形ABCD=4S四边形ONBM;故①正确;∵△AON≌△BOM,∴ON=OM,∠AON=∠BOM,∴∠NOM=∠AOB=90°,∴△NOM是等腰直角三角形,∴MN2=2ON2,∵BN2+BM2=MN2,∴CM2+BM2=2ON2,故②正确;∵∠MON=∠COD=90°,∴∠NOC=∠MOD,∵OD=OC,ON=OM,∴△CON≌△DOM(SAS),故③正确;∵AB=2,∴S正方形ABCD=4,∵△AON≌△BOM,∴四边形BMON的面积=△AOB的面积=1,即四边形BMON的面积是定值1,∴当△MNB的面积最大时,△MNO的面积最小,设BN=x=CM,则BM=2﹣x,∴△MNB的面积=x(2﹣x)=﹣x2+x=﹣(x﹣1)2+,∴当x=1时,△MNB的面积有最大值,此时S△OMN的最小值是1﹣=,故④不正确,故选:A.【点评】本题主要考查了正方形的性质、全等三角形的判定与性质,二次函数的最值以及勾股定理的综合应用,解题时注意二次函数的最值的运用.2.如图,正方形ABCD中,∠EAF=45°,BD分别交AE、AF于M、N,连MF、EF,下列结论:①MN2=BN2+DM2;②DE+BF=EF;③AM=MF且AM⊥MF;④若E为CD 中点,则=.其中正确的有()A.1个B.2个C.3个D.4个【分析】①过B作BD的垂线,截取BH=MD,连接AH,HN,如图,易证△ADM≌△ABH,△AHN≌△AMN,得MN=HN,最后根据勾股定理可作判断;②延长CB,截取BI=DE,连接AI,如图,易证△ADE≌△ABI,△AIF≌△AEF,得IF=EF,即DE+BF=EF,成立.③作辅助线,则可证△AFJ为等腰直角三角形,CK=BF=KJ,证明∠JCK=45°,推出四边形BCJK为平行四边形,所以GJ=BC=AD,可证△GJM≌△DAM,则M为AJ的中点,又∠AFJ=90°,故AM=MF且AM⊥MF,成立.④延长CB,截取BL=DE,连接AL,可设DE=a,BF=x,则EF=LF=a+x,CF=2a﹣x,CE=a,由勾股定理可知:3x=2a,则==,成立.【解答】解:①过B作BD的垂线,截取BH=MD,连接AH,HN,如图,∵四边形ABCD是正方形,∴AD=AB,∠ADB=∠ABD=45°,∠BAD=90°,∴∠ABH=45°=∠ADM,在△ADM和△ABM中,∵,∴△ADM≌△ABH(SAS),∴∠DAM=∠BAH,AM=AH,∵∠EAF=45°,∠BAD=90°,∴∠DAM+∠BAN=∠BAH+∠BAN=45°,∴∠MAN=∠HAN=45°,在△AHN和△AMN中,∵,∴△AHN≌△AMN(SAS),∴MN=HN,Rt△BHN中,HN2=BH2+BN2,∴MN2=BN2+DM2,成立.②延长CB,截取BI=DE,连接AI,如图,在△ADE和△ABI中,∵∴△ADE≌△ABI(SAS),同理得△AIF≌△AEF(SAS),∴IF=EF,即DE+BF=EF,成立;③如图,过F作FJ⊥AF交AE的延长线于J,过J作JK⊥BC于K,连接CJ,过J作JG ∥BC交BD于G,∴∠AFJ=∠AFB+∠JFK=90°,∵∠AFB+∠BAF=90°,∴∠BAF=∠JFK,∵∠EAF=45°,∠AFJ=90°,∴△AFJ是等腰直角三角形,在△ABF和△FKJ中,∵,∴△ABF≌△FKJ(SAS),∴AB=FK=BC,BF=KJ,∴CK=BF=KJ,∴∠JCK=45°,∴∠DBC=∠JCK,∴BG∥CJ,∵JG∥BC,∴四边形BCJK为平行四边形,∴GJ=BC=AD,∵AD∥BC∥GJ,∴∠DAM=∠MJK,在△GJM和△DAM中,∵,∴△GJM≌△DAM(AAS),∴AM=MJ,则M为AJ的中点,又∠AFJ=90°,故AM=MF且AM⊥MF,成立.④延长CB,截取BL=DE,连接AL,可设DE=a,BF=x,则EF=LF=a+x,∵E为CD中点,∴CD=BC=2a,∴CF=2a﹣x,CE=a,在Rt△EFC中,由勾股定理得:EF2=CE2+CF2∴(a+x)2=a2+(2a﹣x)2解得:3x=2a,则==,成立.故选:D.【点评】本题考查了正方形的性质,全等三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.3.如图,在正方形ABCD中,AB=4,AC与BD相交于点O,N是AO的中点,点M在BC边上,且BM=3,P为对角线BD上一点,当对角线BD平分∠NPM时,PM﹣PN值为()A.1B.C.2D.【分析】作以BD为对称轴作N的对称点N',连接MN',PN',根据PM﹣PN=PM﹣PN'≤MN',当P,M,N'三点共线时,取“=”,再证得△MCN'∽△BCA,从而推得△MCN'为等腰直角三角形,结合BM=3.正方形的边长为4,求得CM,即为MN',问题可解.【解答】解:如图所示,∵对角线BD平分∠NPM,∴作以BD为对称轴N的对称点N',连接MN',PN',根据轴对称性质可知,PN=PN',∠NPO=N′PO,NO=N′O∵在正方形ABCD中,AB=4∴AC=AB=4,∵O为AC中点∴OA=OC=2∵N为OA的中点∴ON=∴ON'=CN'=∴AN'=3∵BM=3∴CM=4﹣3=1∴==∵∠MCN'=∠BCA∴△MCN'∽△BCA∴∠CMN'=∠ABC=90°∵∠MCN'=45°∴△MCN'为等腰直角三角形∴MN'=CM=1∴PM﹣PN的值为1.故选:A.【点评】本题主要考查了正方形的性质,明确正方形的相关性质及相似三角形的判定、勾股定理等知识点,是解题的关键.4.如图,在正方形ABCD内一点E连接BE、CE,过C作CF⊥CE与BE延长线交于点F,连接DF、DE.CE=CF=1,DE=,下列结论中:①△CBE≌△CDF;②BF⊥DF;③点D到CF的距离为2;④S四边形DECF=+1.其中正确结论的个数是()A.1B.2C.3D.4【分析】根据正方形的性质、全等三角形的判定和性质、勾股定理等知识逐项判断即可.【解答】解:∵四边形ABCD是正方形,∴BC=CD,∠BCD=90°,∵CF⊥CE,∴∠ECF=∠BCD=90°,∴∠BCE=∠DCF,在△BCE与△DCF中,,∴△BCE≌△DCF(SAS),故①正确;∵△BCE≌△DCF,∴∠CBE=∠CDF,∴∠DFB=∠BCD=90°,∴BF⊥DF,故②正确,过点D作DM⊥CF,交CF的延长线于点M,∵∠ECF=90°,FC=EC=1,∴∠CFE=45°,∵∠DFM+∠CFB=90°,∴∠DFM=∠FDM=45°,∴FM=DM,∴由勾股定理可求得:EF=,∵DE=,∴由勾股定理可得:DF=2,∵EF2+BE2=2BE2=BF2,∴DM=FM=,故③错误,∵△BCE≌△DCF,∴S△BCE=S△DCF,∴S四边形DECF=S△DCF+S△DCE=S△ECF+S△DEF=+,故④错误,故选:B.【点评】本题考查四边形的综合问题,涉及正方形的性质、全等三角形的性质与判定、勾股定理、三角形面积公式等知识内容,综合程度高,需要学生灵活运用知识解答.5.如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M.则下列结论:①∠AME=90°,②∠BAF=∠EDB,③AM=MF,④ME+MF=MB.其中正确结论的有()A.4个B.3个C.2个D.1个【分析】根据正方形的性质可得AB=BC=AD,∠ABC=∠BAD=90°,再根据中点定义求出AE=BF,然后利用“边角边”证明△ABF和△DAE全等,根据全等三角形对应角相等可得∠BAF=∠ADE,然后求出∠ADE+∠DAF=∠BAD=90°,从而求出∠AMD =90°,再根据邻补角的定义可得∠AME=90°,得出①正确;根据中线的定义判断出∠ADE≠∠EDB,然后求出∠BAF≠∠EDB,判断出②错误;设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM=MF,判断出③正确;过点M作MN⊥AB于N,由相似三角形的性质得出==,解得MN=a,AN=a,得出NB=AB﹣AN=2a﹣a=a,根据勾股定理得BM=a,求出ME+MF=+a=a,MB=a,得出ME+MF=MB,故④正确.于是得到结论.【解答】解:在正方形ABCD中,AB=BC=AD,∠ABC=∠BAD=90°,∵E、F分别为边AB,BC的中点,∴AE=BF=BC,在△ABF和△DAE中,,∴△ABF≌△DAE(SAS),∴∠BAF=∠ADE,∵∠BAF+∠DAF=∠BAD=90°,∴∠ADE+∠DAF=∠BAD=90°,∴∠AMD=180°﹣(∠ADE+∠DAF)=180°﹣90°=90°,∴∠AME=180°﹣∠AMD=180°﹣90°=90°,故①正确;∵DE是△ABD的中线,∴∠ADE≠∠EDB,∴∠BAF≠∠EDB,故②错误;设正方形ABCD的边长为2a,则BF=a,在Rt△ABF中,AF===a,∵∠BAF=∠MAE,∠ABC=∠AME=90°,∴△AME∽△ABF,∴=,即=,解得:AM=a,∴MF=AF﹣AM=a﹣a=a,∴AM=MF,故③正确;如图,过点M作MN⊥AB于N,则MN∥BC,∴△AMN∽△AFB,∴==,即==,解得MN=a,AN=a,∴NB=AB﹣AN=2a﹣a=a,根据勾股定理得:BM===a,∵ME+MF=+a=a,MB=a,∴ME+MF=MB,故④正确.综上所述,正确的结论有①③④共3个.故选:B.【点评】本题考查了正方形的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理等知识;仔细分析图形并作出辅助线构造出直角三角形与相似三角形是解题的关键.6.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,EH与CF交于点O.则HE的长为()A.2B.C.2D.或2【分析】利用直角三角形斜边上的中线等于斜边的一半,分别求得HO和OE的长后即可求得HE的长.【解答】解:∵AC、CF分别是正方形ABCD和正方形CGFE的对角线,∴∠ACD=∠GCF=45°,∴∠ACF=90°,又∵H是AF的中点,∴CH=HF,∵EC=EF,∴点H和点E都在线段CF的中垂线上,∴HE是CF的中垂线,∴点H和点O是线段AF和CF的中点,∴OH=AC,在Rt△ACD和Rt△CEF中,AD=DC=1,CE=EF=3,∴AC=,∴CF=3,又OE是等腰直角△CEF斜边上的高,∴OE=,∴HE=HO+OE=2.故选:C.【点评】本题考查了正方形的性质、直角三角形的性质及勾股定理的知识,综合性较强,难度较大.7.如图,在正方形ABCD中,E为BC上一点,过点E作EF∥CD,交AD于F,交对角线BD于G,取DG的中点H,连结AH,EH,FH.下列结论:①FH∥AE;②AH=EH且AH⊥EH;③∠BAH=∠HEC;④△EHF≌△AHD;⑤若,则.其中哪些结论是正确()A.①②④⑤B.②③④C.①②③D.②③④⑤【分析】①根据正方形对角线互相垂直、过一点有且只有一条直线与已知直线垂直即可得结论;②根据矩形的判定和性质、直角三角形的性质,证明三角形全等即可得结论;③根据全等三角形性质、矩形的性质进行角的计算即可得结论;④根据边边边证明三角形全等即可得结论;⑤根据割补法求四边形的面积,再求等腰直角三角形的面积,即可得结论.【解答】证明:①在正方形ABCD中,∠ADC=∠C=90°,∠ADB=45°,∵EF∥CD∴∠EFD=90°,得矩形EFDC.在Rt△FDG中,∠FDG=45°,∴FD=FG,∵H是DG中点,∴FH⊥BD∵正方形对角线互相垂直,过A点只能有一条垂直于BD的直线,∴AE不垂直于BD,∴FH与AE不平行.所以①不正确.②∵四边形ABEF是矩形,∴AF=EB,∠BEF=90°,∵BD平分∠ABC,∴∠EBG=∠EGB=45°,∴BE=GE,∴AF=EG.在Rt△FGD中,H是DG的中点,∴FH=GH,FH⊥BD,∴∠AFH=∠AFE+∠GFH=90°+45°=135°,∠EGH=180°﹣∠EGB=180°﹣45°=135°,∴∠AFH=∠EGH,∴△AFH≌△EGH,∴AH=EH,∠AHF=∠EHG,∴∠AHF+AHG=∠EHG+∠AHG,即∠FHG=∠AHE=90°,∴AH⊥EH.所以②正确.③∵△AFH≌△EGH,∴∠F AH=∠GEH,∵∠BAF=CEG=90°,∴∠BAH=∠HEC.所以③正确.④∵EF=AD,FH=DH,EH=AH,∴△EHF≌△AHD所以④正确.⑤如图,过点H作HM⊥AD于点M,设EC=FD=FG=x,则BE=AF=EG=2x,∴BC=DC=AB=AD=3x,HM=x,AM=x,∴AH2=(x)2+(x)2=x2,S四边形DHEC=S梯形EGDC﹣S△EGH=(2x+3x)•x﹣×=2x2S△AHE=AH•EH=AH2=x2∴==.所以⑤不正确.故选:B.【点评】本题考查了正方形的性质、矩形的判定和性质、全等三角形的判定和性质、直角三角形的性质、三角形和梯形的面积等内容,解题关键是综合利用以上知识解决问题.8.如图,在正方形ABCD中,AC、BD相交于点O,E、F分别为BC、CD上的两点,BE =CF,AE、BF分别交BD、AC于M、N两点,连OE、OF.下列结论:①AE=BF;②AE⊥BF;③CE+CF=BD;④S四边形OECF=S正方形ABCD,其中正确的是()A.①②B.①④C.①②④D.①②③④【分析】①易证得△ABE≌△BCF(ASA),则可证得结论①正确;②由△ABE≌△BCF,可得∠FBC=∠BAE,证得AE⊥BF,选项②正确;③证明△BCD是等腰直角三角形,求得选项③错误;④证明△OBE≌△OCF,根据正方形被对角线将面积四等分,即可得出选项④正确.【解答】解:①∵四边形ABCD是正方形,∴AB=BC,∠ABE=∠BCF=90°,在△ABE和△BCF中,∵,∴△ABE≌△BCF(SAS),∴AE=BF,故①正确;②由①知:△ABE≌△BCF,∴∠FBC=∠BAE,∴∠FBC+∠ABF=∠BAE+∠ABF=90°,∴AE⊥BF,故②正确;③∵四边形ABCD是正方形,∴BC=CD,∠BCD=90°,∴△BCD是等腰直角三角形,∴BD=BC,∴CE+CF=CE+BE==BC,故③错误;④∵四边形ABCD是正方形,∴OB=OC,∠OBE=∠OCF=45°,在△OBE和△OCF中,∵,∴△OBE≌△OCF(SAS),∴S△OBE=S△OCF,∴S四边形OECF=S△COE+S△OCF=S△COE+S△OBE=S△OBC=S正方形ABCD,故④正确;故选:C.【点评】此题属于四边形的综合题.考查了正方形的性质,全等三角形的判定与性质、勾股定理以及等腰直角三角形的性质.注意掌握全等三角形的判定与性质是解此题的关键.9.如图,在正方形ABCD中,M是对角线BD上的一点,点E在AD的延长线上,连接AM、EM、CM,延长EM交AB于点F,若AM=EM,∠E=30°,则下列结论:①FM=ME;②BF=DE;③CM⊥EF;④BF+MD=BC,其中正确的结论序号是()A.①②③B.①②④C.②③④D.①②③④【分析】①证明△AFM是等边三角形,可判断;②③证明△CBF≌△CDE(ASA),可作判断;④设MN=x,分别表示BF、MD、BC的长,可作判断.【解答】解:①∵AM=EM,∠AEM=30°,∴∠MAE=∠AEM=30°,∴∠AMF=∠MAE+∠AEM=60°,∵四边形ABCD是正方形,∴∠F AD=90°,∴∠F AM=90°﹣30°=60°,∴△AFM是等边三角形,∴FM=AM=EM,故①正确;②连接CE、CF,∵四边形ABCD是正方形,∴∠ADB=∠CDM,AD=CD,在△ADM和△CDM中,∵,∴△ADM≌△CDM(SAS),∴AM=CM,∴FM=EM=CM,∴∠MFC=∠MCF,∠MEC=∠ECM,∵∠ECF+∠CFE+∠FEC=180°,∴∠ECF=90°,∵∠BCD=90°,∴∠DCE=∠BCF,在△CBF和△CDE中,∵,∴△CBF≌△CDE(ASA),∴BF=DE;故②正确;③∵△CBF≌△CDE,∴CF=CE,∵FM=EM,∴CM⊥EF,故③正确;④过M作MN⊥AD于N,设MN=x,则AM=AF=2x,AN=x,DN=MN=x,∴AD=AB=x+x,∴DE=BF=AB﹣AF=x+x﹣2x=x﹣x,∴BF+MD=(x﹣x)+x=x,∵BC=AD=x+x x,故④错误;所以本题正确的有①②③;故选:A.【点评】本题考查了正方形的性质,全等三角形的判定与性质,等腰三角形的性质和判定,熟记正方形的性质确定出△AFM是等边三角形是解题的关键.【点评】此题考查的是正方形的性质,等腰直角三角形的性质和判定以及菱10.如图,在正方形ABCD中,对角线AC,BD交于点O,AG平分∠BAC交BD于G,DE⊥AG于点H.下列结论:①AD=2AE:②FD=AG;③CF=CD:④四边形FGEA是菱形;⑤OF =BE,正确的有()A.2个B.3个C.4个D.5个【分析】①根据正方形的性质和角平分线的定义得:∠BAG=∠CAG=22.5°,由垂直的定义计算∠AED=90°﹣22.5°=67.5°,∠EAD=∠EAD=22.5°,得ED是AG的垂直平分线,则AE=EG,△BEG是等腰直角三角形,则AD=AB>2AE,可作判断;②证明△DAF≌△ABG(ASA),可作判断;③分别计算∠CDF=∠CFD=67.5°,可作判断;④根据对角线互相平分且垂直的四边形是菱形可作判断;⑤设BG=x,则AF=AE=x,表示OF和BE的长,可作判断.【解答】解:①∵四边形ABCD是正方形,∴∠BAD=90°,∠BAC=45°,∵AG平分∠BAC,∴∠BAG=∠CAG=22.5°,∵AG⊥ED,∴∠AHE=∠EHG=90°,∴∠AED=90°﹣22.5°=67.5°,∴∠ADE=22.5°,∵∠ADB=45°,∴∠EDG=22.5°=∠ADE,∵∠AHD=∠GHD=90°,∴∠DAG=∠DGA,∴AD=DG,AH=GH,∴ED是AG的垂直平分线,∴AE=EG,∴∠EAG=∠AGE=22.5°,∴∠BEG=45°=∠ABG,∴∠BGE=90°,∴AE=EG<BE,∴AD=AB>2AE,故①不正确;②∵四边形ABCD是正方形,∴AD=AB,∠DAF=∠ABG=45°,∵∠ADF=∠BAG=22.5°,∴△DAF≌△ABG(ASA),∴DF=AG,故②正确;③∵∠CDF=45°+22.5°=67.5°,∠CFD=∠AFE=90°﹣22.5°=67.5°,∴∠CDF=∠CFD,∴CF=CD,故③正确;④∵∠EAH=∠F AH,∠AHE=∠AHF,∴∠AEF=∠AFE,∴AE=AF,∴EH=FH,∵AH=GH,AG⊥EF,∴四边形FGEA是菱形;故④正确;⑤设BG=x,则AF=AE=x,由①知△BEG是等腰直角三角形,∴BE=x,∴AB=AE+BE=x+x=(+1)x,∴AO==,∴OF=AO﹣AF=﹣x=,∴==,∴OF=BE;故⑤正确;本题正确的结论有:②③④⑤;故选:C.形的判定与性质等知识.此题综合性较强,难度较大,注意掌握正方形的性质,注意数形结合思想的应用.11.如图,以正方形ABCD的顶点A为圆心,以AD的长为半径画弧,交对角线AC于点E,再分别以D,E为圆心,以大于DE的长为半径画弧,两弧交于图中的点F处,连接AF并延长,与BC的延长线交于点P,则∠P=()A.90°B.45°C.30°D.22.5°【分析】根据正方形的性质得到∠DAC=∠ACD=45°,由作图知,∠CAP=∠DAC =22.5°,根据三角形的内角和即可得到结论.【解答】解:∵四边形ABCD是正方形,∴∠DAC=∠ACD=45°,由作图知,∠CAP=∠DAC=22.5°,∴∠P=180°﹣∠ACP﹣∠CAP=22.5°,故选:D.【点评】本题考查了正方形的性质,角平分线定义,正确的理解题意是解题的关键.12.如图,正方形ABCD中,点E在边CD上,连接AE,过点A作AF⊥AE交CB的延长线于点F,连接EF,AG平分∠F AE,AG分别交BC,EF于点G,H,连接EG,DH.则下列结论中:①AF=AE;②∠EGC=2∠BAG;③DE+BG=EG;④AD+DE=DH;⑤若DE=CE,则CE:CG:EG=3:4:5,其中正确的结论有()A.2个B.3个C.4个D.5个【分析】①正确.证明△ADE≌△ABF(ASA)可得结论.②正确.证明△AGF≌△AGE(SAS),推出∠AGF=∠AGE=90°﹣∠BAG,推出∠EGF =180°﹣2∠BAG可得结论.③正确.证明△GAF≌△GAE,推出GF=GE可得结论.④正确.过点H作HM⊥AD于M,HN⊥CD于N,证明△HMA≌△HNE(AAS),推出AM=EN,HM=HN,再证明四边形HMDN是正方形可得结论.⑤正确.当DE=EC时,设DE=EC=a,BG=x,则EG=a+x,GC=2a﹣x,利用勾股定理构建方程求出x即可解决问题.【解答】解:∵四边形ABCD是正方形,∴AB=AD,∠ABC=∠ABF=∠ADE=∠BAD=90°,∵AE⊥AF,∴∠EAF=∠BAD=90°,∴∠BAF=∠DAE,∴△ADE≌△ABF(ASA),∴AE=AF,故①正确,∵AG平分∠EAF,∴∠GAF=∠GAE,∵AF=AE,AG=AG,∴△AGF≌△AGE(SAS),∴∠AGF=∠AGE=90°﹣∠BAG,∴∠EGF=180°﹣2∠BAG,∵∠EGF=180°﹣∠EGC,∴∠EGC=2∠BAG,故②正确,∵△ADE≌△ABF,∴DE=BF,∵△GAF≌△GAE,∴GF=GE,∵FG=BF+BG=DE+BG,∴EG=BG+DE,故③正确,过点H作HM⊥AD于M,HN⊥CD于N,∵AE=AF,∠EAF=90°,AH平分∠EAF,∴AH⊥EF,HF=HE,∴HA=HE=HF,∵∠ADE+∠AHE=180°,∴∠HAD+∠DEH=180°,∵∠DEH+∠HEN=180°,∴∠HAM=∠HEN,∵∠AMH=∠ENH=90°,∴△HMA≌△HNE(AAS),∴AM=EN,HM=HN,∵∠HMD=∠HND=∠MDN=90°,∴四边形HMDN是矩形,∵HM=HN,∴四边形HMDN是正方形,∴DM=DN=HM=HN,DH=DM,∴DA+DE=DM+AM+DN﹣EN=2DM=DH,故④正确,当DE=EC时,设DE=EC=a,BG=x,则EG=a+x,GC=2a﹣x,在Rt△ECG中,∵EG2=EC2+CG2,∴(x+a)2=a2+(2a﹣x)2,解得x=a,∴CG=a,EG=a,∴CE:CG:EG=a:a:=3:4:5,故⑤正确,故选:D.【点评】本题考查正方形的性质,全等三角形的判定和性质,勾股定理等知识,解题的关键是正确寻找全等三角形解决问题,学会利用参数构建方程解决问题,属于中考选择题中的压轴题.13.如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB、CD交于点E、F,连接BF交AC于点M,连接DE、BO.若∠COB=60°,FO=FC=2,则下列结论:①FB⊥OC;②△EOB≌△CMB;③四边形EBFD是菱形;④MB=2.其中正确结论的个数是()A.1个B.2个C.3个D.4个【分析】连接BD,先证明△BOC是等边三角形,得FO=FC,BO=BC,故①正确;因为△EOB≌△FOB≌△FCB,故△EOB不会全等于△CBM,故②错误;再证明四边形EBFD是平行四边形,由OB⊥EF推出四边形EBFD是菱形故③正确,先判断出CM=,再由∠CBM=30°,判断出BC=2,进而判断出④,由此不难得到答案.【解答】解:连接BD,∵四边形ABCD是矩形,∴AC=BD,AC、BD互相平分,∵O为AC中点,∴BD也过O点,∴OB=OC,∵∠COB=60°,OB=OC,∴△OBC是等边三角形,∴OB=BC=OC,∠OBC=60°,在△OBF与△CBF中,,∴△OBF≌△CBF(SSS),∴△OBF与△CBF关于直线BF对称,∴FB⊥OC,OM=CM;∴①正确,∵∠OBC=60°,∴∠ABO=30°,∵△OBF≌△CBF,∴∠OBM=∠CBM=30°,∴∠ABO=∠OBF,∵AB∥CD,∴∠OCF=∠OAE,∵OA=OC,∠AOE=∠FOC∴△AOE≌△COF(ASA),∴OE=OF,∴OB⊥EF,∴四边形EBFD是菱形,∴③正确,∵△EOB≌△FOB≌△FCB,∴△EOB≌△CMB错误.∴②错误;∵FO=FC=2,FM⊥OC,∠FCM=30°,∴CM=,∵∠CBM=30°,∴BC=2,∴BM=3,∴④错误.综上可知其中正确结论的个数是2个,故选:B.【点评】本题属于四边形的综合题,考查矩形的性质、等边三角形的判定和性质.全等三角形的判定和性质、菱形的判定、勾股定理等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.二.填空题(共3小题)14.如图,点E为正方形ABCD外一点,且ED=CD,连接AE,交BD于点F.若∠CDE =40°,则∠DFC的度数为110°.【分析】根据正方形性质和已知得:AD=DE,利用等腰三角形性质计算∠DAE=25°,由三角形的内角和定理得:∠AFD=110°,证明△ADF≌△CDF(SAS),∠DFC=∠AFD =110°.【解答】解:∵四边形ABCD是正方形,∴AD=DC,∠ADC=90°,∴∠ADB=∠BDC=45°,∵DC=DE,∴AD=DE,∴∠DAE=∠DEA,∵∠ADE=90°+40°=130°,∴∠DAE==25°,∴∠AFD=180°﹣25°﹣45°=110°,在△ADF和△CDF中,∵,∴△ADF≌△CDF(SAS),∴∠DFC=∠AFD=110°,故答案为:110°.【点评】本题考查了正方形的性质、三角形全等的性质和判定、等腰三角形的性质、三角形内角和定理,属于基础题,熟练掌握正方形的性质是关键.15.如图,正方形ABCD中,在AD的延长线上取点E,F,使DE=AD,DF=BD,连接BF分别交CD,CE于H,G,下列结论:①EC=2DG;②∠GDH=∠GHD;③S△CDG=S四边形DHGE;④图中只有8个等腰三角形.其中正确的有②③(填番号).【分析】根据正方形的性质和已知推出四边形DECB是平行四边形,得到BD=CE,BD ∥CE,无法证出G为CE的中点;得到BD∥CE,推出∠DCG=∠BDC=45°,求出∠BGC=∠GBC,得到BC=CG=CD,求出∠CDG=∠DHG即可;根据三角形的面积公式推出△CDG和四边形DHGE的面积相等;可得有9个等腰三角形.【解答】解:∵正方形ABCD,DE=AD,∴AD∥BC,DE=BC,∠EDC=90°,∴四边形DECB是平行四边形,∴BD=CE,BD∥CE,∵DE=BC=AD,∴∠DCE=∠DEC=45°,要使CE=2DG,只要G为CE的中点即可,但DE=DC,DF=BD,∴EF≠BC,即△EFG和△BCG不全等,∴G不是CE中点,∴①错误;∵∠ADB=45°,DF=BD,∴∠F=∠DBH=∠ADB=22.5°,∴∠DHG=180°﹣90°﹣22.5°=67.5°,∵BD∥CE,∴∠DCG=∠BDC=45°,∵∠DHG=67.5°,∴∠HGC=22.5°,∠DEC=45°,∵∠BGC=180°﹣22.5°﹣135°=22.5°=∠GBC,∴BC=CG=CD,∴∠CDG=∠CGD=(180°﹣45°)=67.5°=∠DHG,∴②正确;∵CG=DE=CD,∠DCE=∠DEC=45,∠HGC=22.5°,∠GDE=90﹣∠CDG=90﹣67.5=22.5°,∴△DEG≌△CHG,要使△CDG和四边形DHGE的面积相等,只要△DEG和△CHG的面积相等即可,根据已知条件△DEG≌△CHG,∴③S△CDG=S四边形DHGE;正确,等腰三角形有△ABD,△CDB,△BDF,△CDE,△BCG,△DGH,△EGF,△CDG,△DGF;∴④错误;故答案为:②③.【点评】本题主要考查对三角形的内角和定理,等腰三角形的性质和判定,正方形的性质,平行四边形的性质和判定等知识.综合运用这些性质进行推理是解此题的关键.16.如图,在正方形ABCD中,P为AB的中点,BE⊥PD的延长线于点E,连接AE、BE、F A⊥AE交DP于点F,连接BF,FC.若AE=2,则FC=2.【分析】根据正方形的性质可得AB=AD,再求出∠BAE=∠DAF,∠ABE=∠ADF,然后利用“角边角”证明△ABE和△ADF全等,根据全等三角形对应边相等可得AE=AF,从而判断出△AEF是等腰直角三角形,根据AE的长度求出EF,过点A作AH⊥EF于H,连接BH,根据等腰直角三角形的性质可得AH=EH=FH,利用“角边角”证明△APH 和△BPE全等,根据全等三角形对应边相等可得BE=AH,然后求出△BEH是等腰直角三角形,根据等腰直角三角形的性质可得∠EHB=45°,然后求出∠AHB=∠FHB,再利用“边角边”证明△ABH和△FBH全等,根据全等三角形对应边相等可得AB=BF,再根据全等三角形对应边相等求出BE=DF,全等三角形对应角相等求出∠BAH=∠BFE,然后求出∠BFE=∠ADF,根据等角的余角相等求出∠EBF=∠FDC,再利用“边角边”证明△BEF和△DFC全等,根据全等三角形对应边相等可得FC=EF.【解答】解:在正方形ABCD中,AB=AD,∠BAD=90°,∵F A⊥AE,∴∠EAF=90°,∴∠BAE=∠DAF,∵∠ABE+∠BPE=∠ADF+∠APD=90°,∴∠ABE=∠ADF,在△ABE和△ADF中,,∴△ABE≌△ADF(ASA),∴AE=AF,BE=DF,∵F A⊥AE,∴△AEF是等腰直角三角形,∴EF=AE=2,过点A作AH⊥EF于H,连接BH,。
解析几何综合问题圆与椭圆双曲线抛物线等课后限时作业(二)带答案人教版新高考分类汇编

高中数学专题复习《解析几何综合问题圆与椭圆双曲线抛物线等》单元过关检测经典荟萃,匠心巨制!独家原创,欢迎下载!注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人得分一、选择题1.(汇编福建理2)以抛物线24y x =的焦点为圆心,且过坐标原点的圆的方程为( ) A .22x +y +2x=0 B .22x +y +x=0C .22x +y -x=0D .22x +y -2x=0第II 卷(非选择题)请点击修改第II 卷的文字说明 评卷人得分二、填空题2.已知椭圆221:12x C y +=和圆222:1C x y +=,椭圆1C 的左顶点和下顶点分别为A ,B ,且F 是椭圆1C 的右焦点.(1) 若点P 是曲线2C 上位于第二象限的一点,且△APF 的面积为12,24+求证:;AP OP ⊥(2) 点M 和N 分别是椭圆1C 和圆2C 上位于y 轴右侧的动点,且直线BN 的斜率是直线BM 斜率的2倍,求证:直线MN 恒过定点.3.椭圆21)0,0(12222=>>=+e b a by ax 的离心率,右焦点F (c,0),方程02=-+c bx ax 的两个根分别为x 1,x 2,则点P (x 1,x 2)在与圆222=+y x 的位置关系是▲ . 评卷人得分三、解答题4.已知椭圆22221x y a b += ()0a b >>的右焦点为1(20)F ,,离心率为e .(1)若22e =,求椭圆的方程; (2)设A ,B 为椭圆上关于原点对称的两点,1AF 的中点为M ,1BF 的中点为N ,若原点O 在以线段MN 为直径的圆上. ①证明点A 在定圆上;②设直线AB 的斜率为k ,若3k ≥,求e 的取值范围. 关键字:求椭圆方程;证明点在定圆上;求点的轨迹方程;5.已知,A B 分别是直线33y x =和33y x =-上的两个动点,线段AB 的长为23是AB 的中点,点P 的轨迹为.C(1)求轨迹C 的方程;(2)过点(1,0)Q 任意作直线l (与x 轴不垂直),设l 与轨迹C 交于,M N 两点,与y 轴交于R 点。
代数几何综合题

1.如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0),与过A点的直线相交于另一点D(3,),过点D作DC⊥x轴,垂足为C. (1)求抛物线的表达式; (2)点P在线段OC上(不与点O、C重合),过P作PN⊥x轴,交直线AD于M,交抛物线于点N,连接CM,求△PCM面积的最大值;
(3)若P是x轴正半轴上的一动点,设OP的长为t,是否存在t,使以点M、C、D、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由. 2.如图1,抛物线y=ax2+2x+c与x轴交于A(﹣4,0),B(1,0)两点,过点B的直
线y=kx+分别与y轴及抛物线交于点C,D.
(1)求直线和抛物线的表达式; (2)动点P从点O出发,在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动,设运动时间为t秒,当t为何值时,△PDC为直角三角形?请直接写出所有满足条件的t的值;
(3)如图2,将直线BD沿y轴向下平移4个单位后,与x轴,y轴分别交于E,F两点,在抛物线的对称轴上是否存在点M,在直线EF上是否存在点N,使DM+MN的值最小?若存在,求出其最小值及点M,N的坐标;若不存在,请说明理由. 3.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(﹣1,0),C(2,3)两点,与y轴交于点N.其顶点为D.
(1)抛物线及直线AC的函数关系式; (2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值. (3)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由; 4.如图1,抛物线y=ax2+bx+c关于y轴对称,它的顶点在坐标原点O,点
B
4
(2)3,
和点C(-3,-3)均在抛物线上,点F3(0)4,在y轴上,过点3(0)4,作直线l与x轴平行.
代数几何综合问题经典

代数几何综合问题新题赏析
新题赏析
题一:如图,在平面直角坐标系中,已知矩形AOBC的顶点C的坐标是(2,4),动点P从点A出发,沿线段AO向终点O运动,同时动点Q从点B出发,沿线段BC向终点C运动.点P、Q的运动速度均为每秒1个单位,运动时间为t秒.过点P作PE⊥AO交AB于点E.
(1)求直线AB的解析式;
(2)设△PEQ的面积为S,求S与t时间的函数关系,并指出自变量t的取值范围;
(3)在动点P、Q运动的过程中,点H是矩形AOBC内(包括边界)一点,且以B、Q、E、H为顶点的四边形是菱形,直接写出t值和与其对应的点H的坐标.
题二:如图,在平面直角坐标系中,顶点为(4, 1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3).
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴l与⊙C有怎样的位置关系,并给出证明.
参考答案
新题赏析
题一:(1)y = -2x +4;(2)S =222(02)22(24)2
t t t t t t ⎧-+<⎪⎪⎨-⎪≤⎪⎩<<; (3)t 1=2013,H 1 (1013,1213
),t 2
=20-,H 2
(10-,4). 题二:(1)21
234y x x =-+;(2)相交.。
代数几何综合问题

(2)当矩形ABCD沿直线折叠时, ① 求点的坐标(用k表示);求出k和b之间的关系式; ② 如果我们把折痕所在的直线与矩形的位置分 为如图2、3、4所示的三种情形, 请你分别写出每种情形时k的取值范围. (将答案直接填在每种情形下的横线上)
(图4) (图2) (图3)
k的取值范围是 ; k的取值范围是
;k的取值范围是
;
【分析:】
1、对折是一个操作性名词,它的数学实质就是轴对称。
2、能掌握轴对称的性质,把握好这两点就不难解决这个问题了。
[解] (1)如图答5,设直线与OD交于点E,与OB交于点F,连结,则
OE = b,OF = 2b,设点的坐标为(a,1)
因为,
所以.所以.
在图答6和图答7中求解参照给分. (3)图13﹣2中:; 图13﹣3中:≤≤;
图13﹣4中: (图答6) (图答5) (图答7)
【点评:】 这是一道有关折叠的问题,主要考查一次函数、四边形、相似形等
知识,试题中贯穿了方程思想和数形结合的思想,请注意体会。
题3、(吉林长春课改卷)如图①,正方形的顶点的坐标分别为,
代数几何综合问题
题1、(北京丰台)如图,已知平面直角坐标系中三点A(2,
0),B(0,2),P(x,0),连结BP,过P点作交过点A的直线a于点 C(2,y)
(1)求y与x之间的函数关系式; (2)当x取最大整数时,求BC与PA的交点Q的坐标。
解:(1) A(2,0),C(2,y)在直线a上
,, (2),的最大整数值为 , 当时,,
是x轴上一动点(n<0)以AO为一边作矩形AOBC,点C在第二象限, 且OB=2OA.矩形AOBC绕点A逆时针旋转90o得矩形AGDE.过点A的直 线y=kx+m 交y轴于点F,FB=FA.抛物线y=ax2+bx+c过点E、F、G且 和直线AF交于点H,过点H作HM⊥x轴,垂足为点M. (1)求k的值;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
代数几何综合问题(2)专项练习1. 如图,已知二次函数23y x bx =++与x 轴交于点B (3,0),与y 轴交于点A ,O 为坐标原点,P 是二次函数23y x bx =++图象上的一个动点,点P 的横坐标是m ,且m >3,过点P 作PM 垂直x 轴,PM 交直线AB 于点M 。
(1)求二次函数的解析式;(2)若以AB 为直径的⊙N 恰好与直线PM 相切,求此时点M 的坐标;(3)在点P 的运动过程中,△APM 能否为等腰三角形?若能,求出点P 的坐标;若不能,请说出理由。
2. 如图,已知二次函数()20y x bx c c =-++>的图象与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,且OB=OC=3,顶点为M 。
(1)求二次函数的解析式;(2)点P 为线段BM 上的一个动点,过点P 作x 轴的垂线PQ ,垂足为Q ,若OQ=m ,四边形ACPQ 的面积为S ,求S 关于m 的函数解析式,并写出m 的取值范围;(3)探索:线段BM 上是否存在点N ,使△NMC 为等腰三角形?如果存在,求出点N 的坐标;如果不存在,请说明理由。
3. 将抛物线c 1:y=2+x 轴翻折,得抛物线c 2,如图所示。
(1)请直接写出抛物线c 2的表达式.(2)现将抛物线c 1向左平移m 个单位长度,平移后得到的新抛物线的顶点为M ,与x 轴的交点从左到右依次为A ,B ;将抛物线c 2向右也平移m 个单位长度,平移后得到的新抛物线的顶点为N ,与x 轴交点从左到右依次为D ,E 。
①当B ,D 是线段AE 的三等分点时,求m 的值;②在平移过程中,是否存在以点A ,N ,E ,M 为顶点的四边形是矩形的情形?若存在,请求出此时m的值;若不存在,请说明理由。
代数几何综合问题(2)专项练习参考答案1. 解:(1)将点B (3,0)代入y=x 2+bx+3得:0=9+3b+3,解得b=-4, ∴二次函数的解析式为y=x 2-4x+3;(2)令x=0,则y=3,∴A 点坐标为A (0,3), 直线AB 的解析式为y=-x+3,C 为⊙C 的圆心,CA=CB=∴D 点坐标为(331,22⎛⎫ ⎪⎝⎭(312M x =+将(312M x =+代入y=-x+3得(312M y =∴点M 的坐标为((331,122⎛⎫+ ⎪⎝⎭(3)若△APM 为等腰三角形,进行分类讨论:若()243P m m m -+,,则()3M m m -+,,23PM m m =-,PA =,AM ==;①当PA=PM 时,可得23m m -=,解得m=4,2433m m -+=,则P 点坐标为()43P ,②当PA=AM =,解得m=3,或m=5,当m=3时,m 2-4m+3=0,由题意可知m >3,故m=3不合题意;[来源:学科网]当m=5时,2438m m -+=,故点P 坐标为()58P ,,③当PA=AM 时,23m m -=,解得3m =+或3m =由题意可知m >3,故3m =当3m =时,2432m m -+=,故点P 坐标为(3P +。
综上所述:()43P ,、()58P ,、(32P ++ 2. 解:(1)∵OB=OC=3, ∴B(3,0),C (0,3)∴0933b cc =-++⎧⎨=⎩解得23b c =⎧⎨=⎩∴二次函数的解析式为y=-x 2+2x+3;[来源:学。
科。
网Z 。
X 。
X 。
K](2)()11••22AOCACPQ PQOC AO CO PQ CO OQ S SS ++=+=四边形梯形()()2119313263132222m m mm m =⨯⨯+-++⋅=-++≤<(3)设N 点坐标为(),x yCM =,CN =,MN =[来源:]①当CM=NC 时,此时71655N ⎛⎫⎪⎝⎭,②当CM=MN 时,此时14N +⎛⎝③当CN=MN 时,此时()22N ,。
综上所述:71655N ⎛⎫⎪⎝⎭,、14N +⎛⎝、()22N ,3. (1)2y = (2)①令20+=,得1211x x =-=,则拋物线c 1与x 轴的两个交点坐标为()()1010-,,,。
∴()()1010A m B m ---,,,。
同理可得:()()1010D m E m -++,,,。
当13AD AE =时,[来源:学|科|网Z|X|X|K]()()()()111113m m m m -+---=+---⎡⎤⎣⎦,∴12m =。
当13AB AE =时,()()()()111113m m m m ---+=+---⎡⎤⎣⎦,∴m=2。
故当B ,D 是线段AE 的三等分点时,12m =或2。
②存在。
连接AN ,NE ,EM ,MA 。
依题意可得:((M m N m -,,。
即M ,N关于原点O 对称,∴OM=ON。
[来源:学科网ZXXK] ∵()()1010A m E m --+,,,,∴A,E 关于原点O 对称,∴OA=OE∴四边形ANEM 为平行四边形。
∵()22214AM m m =-+++=,()22221444ME m m m m =+++=++,()22211484AE m m m m =+++=++,若222AM ME AE +=,则224444484m m m m +++=++,∴m=1,此时△AME 是直角三角形,且∠AME=90°。
∴当m=1时,以点A ,N ,E ,M 为顶点的四边形是矩形。
2019-2020学年数学中考模拟试卷一、选择题1.下列运算正确的是( ) A.a 5﹣a 3=a 2 B.6x 3y 2÷(﹣3x )2=2xy 2 C.2212a2a -=D.(﹣2a )3=﹣8a 32.如图,已知抛物线y =x 2﹣2x ﹣3与x 轴相交于点A ,B ,若在抛物线上有且只有三个不同的点C 1,C 2,C 3,使得△ABC 1,△ABC 2,△ABC 3的面积都等于a ,则a 的值是( )A .6B .8C .12D .16 3.如图,已知一次函数的图像与轴分别交于点,与反比例函数的图像交于点,且,则的值为( )A. B. C. D.4.一个圆锥的轴截面是一个边长为2cm 的等边三角形,则它的侧面积是( ). A .4πB .2πC .πD.5.若整数a 使关于x 的不等式组()222233a xx x x +⎧≥-⎪⎪⎨⎪-->⎪⎩的解为2x <,且使关于x 的分手方程15444x a x x -++=---的解为正整数,则满足条件a 的的值之和为( ) A .12 B .11 C .10 D .96.已知抛物线y =ax 2+bx+c (a≠0)的对称轴为直线x =2,与x 轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:①抛物线一定过原点②方程ax 2+bx+c =0(a≠0)的解为x =0或x =4,③a ﹣b+c <0;④当0<x <4时,ax 2﹣bx+c <0;⑤当x <2时,y 随x 增大而增大,其中结论正确的个数( )A .1B .2C .3D .47.如图,在菱形ABCD 中,60ABC ∠=︒,E 为BC 边的中点,M 为对角线BD 上的一个动点。
则下列线段的长等于12AM BM +最小值的是( )A .ADB .AEC .BD D .BE8.一个个“刻度”,印证着中国高铁的不断前行.截至2017年底,全国铁路营业里程达到127000千米,其中高铁里程为25000千米,占世界高铁里程总量的66.3%,是当之无愧的“世界冠军”,其中25000千米用科学记数法表示为( ) A .25×107米B .2.5×107米C .C.2.5×104米D .D.0.25×108米9 ) A .πB .3πC .4πD .12π10.如图,矩形ABCD 中,AB =5,BC =12,点E 在边AD 上,点G 在边BC 上,点F 、H 在对角线BD 上,若四边形EFGH 是正方形,则AE 的长是( )A .5B .11924C .13024D .1692411.把边长相等的正六边形ABCDEF 和正五边形GHCDL 的CD 边重合,按照如图所示的方式叠放在一起,延长LG 交AF 于点P ,则∠APG =( )A .141°B .144°C .147°D .150°12.如图,在正方形ABCD 中,E 是边BC 上一点,且BE :CE =1:3,DE 交AC 于点F ,若DE =10,则CF 等于( )A .7B .CD .二、填空题13.如图,在边长为3的正方形ABCD 的外部作等腰Rt AEF ,AE 1=,连接DE ,BF ,BD ,则22DE BF +=______.14.在矩形ABCD 中,AB=3cm ,BC=4cm ,则点A 到对角线BD 的距离为___________15.我们用[m]表示不大于m 的最大整数,如:[2]=2,[4.1]=4,[3.99]=3.(1)=_____;(2)若6=,则x 的取值范围是_____.16.某校规定学生的期末学科成绩由三部分组成,将课堂、作业和考试三项得分按1:3:6的权重确定每个人的期末成绩.小明同学本学期数学这三项得分分别是:课堂98分,作业95分,考试85分,那么小明的数学期末成绩是_____分.17.如图,在△ABC 中,DE ∥BC ,AD :DB=1:2,DE=2,则BC 的长是 .18.如图,四边形ABCD 内接于⊙O ,E 为CD 的延长线上一点.若110B ∠=°,则ADE ∠的大小为____________.三、解答题19.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一条直线上.已知纸板的两条边DE=70cm,EF=30cm,测得AC=78 m,BD=9m,求树高AB.20.某商场将进价为1800元的电冰箱以每台2400元售出,平均每天能售出8台,为了配合国家"家电下乡”政策的实施,商场决定采取适当的降价措施,调查表明:这种冰箱的售价每降价50元,平均每天就能多售出4台(1)设每台冰箱降价x元,商场每天销售这种冰箱的利润为y元,求y与x之间的函数关系式(不要求写自变量的取值范围)(2)商场想在这种冰箱的销售中每天盈利8000元,同时又要使顾客得到实惠,每台冰箱应降价多少元?(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少元?21.如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=18°,∠ACD=14°.求电子警察安装在悬臂灯杆上的高度AD的长.(参考数据:sin14°≈0.242,cos14°≈0.97,tan14°≈0.25,sin18°≈0.309,cos18°≈0.951,tan18°≈0.325)22.已知锐角△ABC,∠ABC=45°,AD⊥BC于D,BE⊥AC于E,交AD于F.(1)求证:△BDF≌△ADC;(2)若BD=4,DC=3,求线段BE的长度.23.河南省开封市铁塔始建于公元1049年(北宋皇祐元年),是国家重点保护文物之一,在900多年中,历经了数次地震、大风、水患而巍然屹立,素有“天下第一塔”之称.如图,小明在铁塔一侧的水平面上一个台阶的底部A 处测得塔顶P 的仰角为45°,走到台阶顶部B 处,又测得塔顶P 的仰角为38.7°,已知台阶的总高度BC 为3米,总长度AC 为10米,试求铁塔的高度.(结果精确到1米,参考数据:sin38.7°≈0.63,cos38.7°≈0.78,tan38.7°≈0.80)24.解方程:123132x x --=+. 25.如图,在Rt △ABC 中,∠ACB =90°,以点A 为圆心,AC 为半径,作⊙A ,交AB 于点D ,交CA 的延长线于点E ,过点E 作AB 的平行线交⊙A 于点F ,连接AF ,BF ,DF . (1)求证:△ABC ≌△ABF ; (2)填空:①当∠CAB = °时,四边形ADFE 为菱形;②在①的条件下,BC = cm 时,四边形ADFE 的面积是cm 2.【参考答案】*** 一、选择题二、填空题 13.2014.125cm 15.916x ≤<16.3 17. 18.110°三、解答题19 【解析】【分析】先判定△DEF 和△DBC 相似,然后根据相似三角形对应边成比例列式求出BC 的长,再加上AC 即可得解.【详解】解:在直角△DEF 中,DE =70cm ,EF =30cm ,则由勾股定理得到DF ==在△DEF 和△DBC 中,∠D =∠D ,∠DEF =∠DCB ,∴△DEF ∽△DCB , ∴DF EF DB BC=, 又∵EF =30cm ,BD =9m ,∴BC =58EF DB DF ⋅==(m ) ∵78AC m =,∴AB =AC+BC =78+=m . 【点睛】本题考查了相似三角形的应用,主要利用了相似三角形对应边成比例的性质,比较简单,判定出△DEF 和△DBC 相似是解题的关键.20.(1)y=-2240480025x x ++(2)400(3)每台冰箱降价250元时,商场利润最高.最高利润是9800元 【解析】【分析】(1)根据升降价问题,表示出每台冰箱的利润=(2400-1800-x)与总的销量(8+50x ⨯4),两者之积,即可求出, (2)结合函数解析式y=8000,即可表示出,然后解方程求出,(3)二次函数最值问题,求出结果【详解】(1) 设每台冰箱降价x 元,商场每天销售这种冰箱的利润是y 元则y=(2400-1800-x) (8+50x ⨯4)=-2240480025x x ++ (2)由题意得:- 2240480025x x ++=8000 解得:x 1 =100,x 2 =400要使顾客得到实惠,取x=400答: 每台冰箱应降价400元 (3)y=2240480025x x ++=22(250)980025x -+ ∵a=2025< ∴y 有最大值・∴当x=250时y 最大=9800 ∴每台冰箱降价250元时,商场利润最高.最高利润是9800元【点睛】此题考查二次函数的应用,解题关键在于列出方程21.AD 的长为6.5 m .【解析】【分析】设电子警察安装在悬臂灯杆上的高度AD 的长为xm .通过解Rt △ADB 和Rt △ACD 求得BD 、CD 的长度,然后结合BC =CD ﹣BD 列出方程,并解答.【详解】设电子警察安装在悬臂灯杆上的高度AD 的长为x m .在Rt △ADB 中,tan ∠ABD =AD BD , ∴BD =0tan tan18AD x ABD =∠, 在Rt △ACD 中,tan ∠ACD = AD CD, ∴CD =0tan tan14AD x ACD =∠, ∵BC =CD ﹣BD , ∴0tan14x ﹣0tan18x =6, ∴4x ﹣4013x =6. 解这个方程,得x =6.5.答:电子警察安装在悬臂灯杆上的高度AD 的长为6.5 m .【点睛】本题考查的是解直角三角形的应﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.22.(1)见解析;(2)BE =285. 【解析】【分析】(1)由题意可得AD=BD ,由余角的性质可得∠CBE=∠DAC ,由“ASA”可证△BDF ≌△ADC ;(2)由全等三角形的性质可得AD=BD=4,CD=DF=3,BF=AC ,由三角形的面积公式可求BE 的长度.【详解】解:(1)∵AD ⊥BC ,∠ABC =45°∴∠ABC =∠BAD =45°,∴AD=BD,∵DA⊥BC,BE⊥AC∴∠C+∠DAC=90°,∠C+∠CBE=90°∴∠CBE=∠DAC,且AD=BD,∠ADC=∠ADB=90°∴△BDF≌△ADC(ASA)(2)∵△BDF≌△ADC∴AD=BD=4,CD=DF=3,BF=AC∴BF=5∴AC=5,∵S△ABC=12×BC×AD=12×AC×BE∴7×4=5×BE∴BE=285.【点睛】本题考查了全等三角形的判定和性质,等腰三角形的性质,利用三角形面积公式可求BE的长度. 23.铁塔约高55米.【解析】【分析】如图,过点B作BE⊥DP于点E,由题可知,∠EBP=38.7°,∠DAF=45°,BE=CD,DP=AD,设铁塔高度DP为x米,则BE=CD=x+10,解直角三角形即可得到结论.【详解】如图,过点B作BE⊥DP于点E,由题可知,∠EBP=38.7°,∠DAF=45°,BE=CD,DP=AD,设铁塔高度DP为x米,则BE=CD=x+10,EP=DP﹣DE=AD﹣BC=x﹣3,在Rt△BEP中∵EP=x﹣3,BE=x+10,∴tan∠EBP=EPBE,x﹣3=(x+10)×tan38.7°,解得x=55,答:铁塔约高55米.【点睛】本题考查了解直角三角形的应用﹣仰角俯角问题,还考查的知识点有三角函数、直角三角形的性质以及勾股定理等,解题的关键是纷杂的实际问题中整理出直角三角形并解之.24.57x = 【解析】【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解【详解】解:2(1-2x)=3(x -3)+62-4x =3x -9+6-4x -3x =-9+6-2-7x =-557x = 【点睛】此题考查解分式方程,掌握运算法则是解题关键25.(1)证明见解析;(2)60;(3)6.【解析】【分析】(1)首先利用平行线的性质得到∠FAB=∠CAB ,然后利用SAS 证得两三角形全等即可;(2)当∠CAB=60°时,四边形ADFE 为菱形,根据∠CAB=60°,得到∠FAB=∠CAB=∠CAB=60°,从而得到EF=AD=AE ,利用邻边相等的平行四边形是菱形进行判断四边形ADFE 是菱形;(3)设菱形AEFD 的边长为a ,易知△AEF 、△AFD 都是等边三角形,列出方程求出a ,再在RT △ACB 中,利用勾股定理即可解决问题.【详解】(1)证明:∵EF ∥AB ,∴∠E =∠CAB ,∠EFA =∠FAB ,∵∠E =∠EFA ,∴∠FAB =∠CAB ,在△ABC 和△ABF 中,AF AC FAB CAB AB AB =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△ABF ;(2)当∠CAB =60°时,四边形ADFE 为菱形,证明:∵∠CAB =60°,∴∠FAB =∠CAB =∠CAB =60°,∴EF =AD =AE ,∴四边形ADFE 是菱形,故答案为60.(3)∵四边形AEFD 是菱形,设边长为a ,∠AEF =∠CAB =60°,∴△AEF、△AFD都是等边三角形,a2=∴a2=12,∵a>0,∴a=∴AC=AE=,在RT△ACB中,∠ACB=90°,AC=CAB=60°,∴∠ABC=30°,∴AB=2AC=,BC6.故答案为6.【点睛】本题考查了菱形的判定、全等三角形的判定与性质及圆周角定理的知识,解题的关键是了解菱形的判定方法及全等三角形的判定方法,难度不大,记住等边三角形面积公式a2(a是边长)2019-2020学年数学中考模拟试卷一、选择题1.如图,点B是直线l外一点,在l的另一侧任取一点K,以B为圆心,BK为半径作弧,交直线l与点M、N;再分别以M、N为圆心,以大于12MN为半径作弧,两弧相交于点P;连接BP交直线l于点A;点C是直线l上一点,点D、E分别是线段AB、BC的中点;F在CA的延长线上,,8,6FDA B AC AB∠=∠==则四边形AEDF的周长为()A.8B.10C.16D.182.估6的值应在()A.3和4之间B.4和5之间C.5和6之间D.6和7之间3.在刚刚结束的中考英语听力、口语测试中,某班口语成绩情况如图所示,则下列说法正确的是()A.中位数是9 B.众数为16 C.平均分为7.78 D.方差为24.如图,将△ABC绕C顺时针旋转,使点B落在AB边上的点B′处,此时,点A的对应点A′恰好落在BC边的延长线上,则下列结论中错误的是()A.∠BCB′=∠ACA′B.∠ACB=2∠BC.B′C平分∠BB′A′D.∠B′CA=∠B′AC5.下列图形中,的是( )A. B.C. D.6.如图所示的四边形,与选项中的一个四边形相似,这个四边形是( )A .B .C .D .7.如图,用四个直角边分别是6和8的全等直角三角形拼成“赵爽弦图”,随机往大正方形区域内投针一次,则针扎在小正方形EFGH 内的概率是()A .14B .16C .124D .1258.如图,抛物线()()142L y x t x t =---+:(常数0t >),双曲线6(0)y x x=>.设L 与双曲线有个交点的横坐标为0x ,且满足034x <<,在L 位置随t 变化的过程中,t 的取值范围是( )A .322t <<B .34t <<C .45t <<D .57t <<9.如图,小山岗的斜坡AC 的坡度是tan α=34,在与山脚C 距离200米的D 处,测得山顶A 的仰角为26.6°,则小山岗的高AB 是( )(结果取整数,参考数据:sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50)A.300米B.250米C.400米D.100米10,则它的外接圆的面积为()A.πB.3πC.4πD.12π11.直线y=﹣2x+5分别与x轴,y轴交于点C、D,与反比例函数y=3x的图象交于点A、B.过点A作AE⊥y轴于点E,过点B作BF⊥x轴于点F,连结EF;下列结论:①AD=BC;②EF∥AB;③四边形AEFC是平行四边形;④S△EOF:S△DOC=3:5.其中正确的个数是( )A.1 B.2 C.3 D.412.如图,在⊙O中,弦AB=10,PA=6㎝,OP=5㎝,则⊙O的半径R等于()A.7㎝B㎝C.49㎝D㎝二、填空题13.在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2014个正方形的面积为_________。
