第03章 正弦交流电路
合集下载
电路基础第3章 正弦交流电路共109页

3-1 正弦交流电的基本概念 正弦交流电
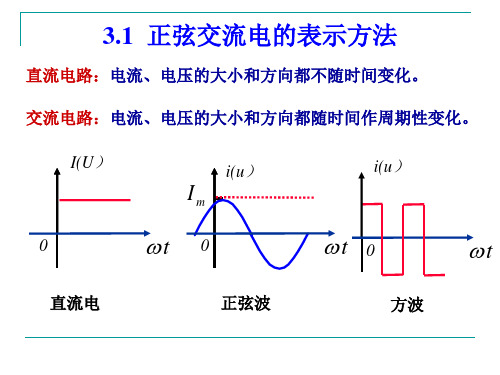
一、正弦交流电的特征
i
iImsi nt
Im
t
特征量:
I m : 电流幅值(最大值)
: 角频率(弧度/秒)
: 初相
1.频率与周期
i
t
T
几种描述:
▪周期 T:变化一周所需的时间 单位:秒(s)…
▪频率 f:每秒变化的次数 单位:赫兹(Hz) ...
▪角频率 ω:每秒变化的弧度 单位:弧度/秒(rad/s)
或 u3s 1i3 1 nt1 (1 4 2 )V0
例 3-2 已知二正弦电压 u 1 1s 4i3 1 nt1 (94 )0 V u 2 3s 1i3 1 nt1 (14 5 )V 0
求二者的相位差,并指出二者的关系。
解: 相位差 12=- 90°-150°= -240°
由于 12 180 ,故 12=-240 °+360 °=120°
3.相位差
i
u
t
u i
▪相位差 :两个同频率 正弦量间的初相位之差。
如: uUmsintu iImsinti
t u t i u i
两个正弦信号的相位关系
▪ 若ui 0,
称 u 超前 i 角;
u u,i
▪ 若ui 0,
称 u 滞后 i 角;
u,i i u
i
o
t
o
t
波形图
两个正弦信号的相位关系
三者间的关系: f 1 T
2 2 f
T
关于单位:
★国际单位制(SI)中,周期的单位为秒(s) ;频率的单位为1/秒,又称为赫兹(Hz); 角频率的单位为弧度/秒(rad/s)。 ★单位换算:
第3章正弦交流电路

+
_ C u_ C
设:i Im sinω t
u Umsin(ω t )
p u i Um sin(ω t ) Imsinω t
UmImcos sin2 ω t UI sin sin2ω t
耗能元件上 的瞬时功率
储能元件上 的瞬时功率
在每一瞬间,电源提供的功率一部 分被耗能元件消耗掉,一部分与储能 元件进行能量交换。
U
( < 0 容性)
U X 由电压三角形可得:
U Rຫໍສະໝຸດ 电压 三角形UR Ucos U x Usin
总目录 章目录 返回 上一页 下一页
2) 相量图
U
U L U C U X
U R
电压 三角形
Z
X XL XC 阻抗
R
三角形
由阻抗三角形:
R Z cos X Z sin
i 16.8 2 sin( 314 t 10.9 ) A
有效值 I =16.8 A
总目录 章目录 返回 上一页 下一页
例3: 图示电路是三相四线制电源, 已知三个电源的电压分别为:
uA 220 2 sin 314 t V
uB 220 2 sin (314 t 120 )V uC 220 2 sin (314 t 120 )V
RLC串联交流电路中
设:i 2 I sinω t
+
_ C u_ C
U?=IR + IL + I 1/ C
交流电路、U I与参数R、L、C、 间的关系如何?
总目录 章目录 返回 上一页 下一页
3.7 RLC串联的交流电路
1. 电流、电压的关系
第3章 正弦交流电路

3.3.2 功率消耗与能量转换
1.瞬时功率 2.平均功率 3.能量转换
1.瞬时功率
在任一瞬间,某元件瞬时电压u与瞬时电流i的乘 积,称为该元件的瞬时功率,并用小写的p表示, 即 p=UmImsin2ωt=UmIm1-cos2ωt2=UI(1-cos2ωt)
2.平均功率
ห้องสมุดไป่ตู้
3.能量转换
电阻元件是消耗功率的,吸取电源提供的电能转 换为热能散发掉,是一种不可逆转换。在一周期 内转换成的热能为 WR=UIT=I2RT=U2RT
3.5 电容元件的正弦交流电路
3.5.1 伏安关系
3.5.2 功率消耗与能量转换
3.5 电容元件的正弦交流电路
图3-9 电容元件的正弦交流电路
3.5.1 伏安关系
1)i与u是同频率的正弦量。
2)i超前u相位角90°。 3)u与i的有效值(或最大值)之比称为容抗,记作 4)电压u与电流i的波形如图3-9b所示。 5)电压与电流相量之比称为复容抗,用ZC表示,即 6)u与i的相量图如图3-9c所示。
2.线性电感L的平均功率
瞬时功率PL在一周期内的平均值即为平均功率 PL=1T∫T0pLdt=1T∫T0UIsin2ωtdt=0 可见理想电感在正弦交流电路中是不消耗能量的。
3.无功功率
电感L虽不消耗有功功率,但要求与电源间进行 能量交换,这种能量交换的规模,用u与i的有效 值乘积来衡量,称为无功功率,并记作 QL=UI=I2XL=U2XL 为与有功功率区别,无功功率的单位是乏或千乏。 储能元件(L或C),虽本身不消耗能量,但需占用 电源容量并与之进行能量交换,对电源是一种负 担。
3.6.3 正弦交流电路中的功率
1.瞬时功率
2.平均功率 3.无功功率 4.视在功率
正弦交流电路课件

θ
+1
22
j
ω
u
+1
Um
wt
ωt + u
u
有向线段与横轴的夹角为 ( w t + u ) 有向线段在纵轴上的投影为Um Sin ( w t + u ) 旋转的有向线段在纵轴上的投影是正弦电量: u = Um Sin ( w t + u )
23
概念 :一个正弦量的瞬时值可以用一个旋转的有
Ub
u1 40 2 sin w t 60 o U2 u2 30 2 sin w t - 30 o
b
U1
Ua U2
60 o a 30 o 23o
ua = u1 + u2
ua 50 2 sin w t 23 o Ub = U1 - U2 = 5097o ub 50 2 sin w t 97 o
wt
Um
u
u U m sin(wt )
有效值:
与交流热效应相等的直流 定义为交流电的有效值
10
热效应相当
有 效 值 概 念
T
0
i R dt I RT
2
2
交流
直流 (方均根值)
1 T 2 I i dt T 0
可得,
当
i I m sin w t 时,
Im I 2
用符号:
I
U
E
表示。
包含幅度与相位信息。
26
例1
有效值
i1 = 8 2 sin (w t + 60 i2 = 6 2 sin (w t -
) 30 o )
o
I1
初相位
60 o 30 o
+1
22
j
ω
u
+1
Um
wt
ωt + u
u
有向线段与横轴的夹角为 ( w t + u ) 有向线段在纵轴上的投影为Um Sin ( w t + u ) 旋转的有向线段在纵轴上的投影是正弦电量: u = Um Sin ( w t + u )
23
概念 :一个正弦量的瞬时值可以用一个旋转的有
Ub
u1 40 2 sin w t 60 o U2 u2 30 2 sin w t - 30 o
b
U1
Ua U2
60 o a 30 o 23o
ua = u1 + u2
ua 50 2 sin w t 23 o Ub = U1 - U2 = 5097o ub 50 2 sin w t 97 o
wt
Um
u
u U m sin(wt )
有效值:
与交流热效应相等的直流 定义为交流电的有效值
10
热效应相当
有 效 值 概 念
T
0
i R dt I RT
2
2
交流
直流 (方均根值)
1 T 2 I i dt T 0
可得,
当
i I m sin w t 时,
Im I 2
用符号:
I
U
E
表示。
包含幅度与相位信息。
26
例1
有效值
i1 = 8 2 sin (w t + 60 i2 = 6 2 sin (w t -
) 30 o )
o
I1
初相位
60 o 30 o
第3部分正弦交流电路

【例3-7】 把电容量为40μF的电 容器接到交流电源上,通过电容 •••器解的则:由的电通I=过电流2.7电I压为5容A2瞬器.,A75的ω,时30电=试值3流14求表解r析a电达d式/容式sA,可器。φ以=两3得0端°到
• 电容器的X 容C 抗1 C 为31441 010680
U j X C I 1 9 0 8 0 2 . 7 5 3 0 2 2 0 6 0
• 正弦量 :正弦交流电路中的正弦电压和电流等 20物20/9理/5 量
二、正弦交流电三要素
• 频率、幅值和初相位是正弦交流电的三要素。
• 设 i=Imsin(ωt+φ) • 1.瞬时值、最大值和有效值
• 瞬时值:用小写字母表示,如i 表示电流
• 最大值:I用 带I m 下标 m的大写字母表示,如Im 表
• 相位角 :(ωt+φ) • 初相位 :t=0时的相位角
• 相位差 :两个同频率正弦量的相位角之差或初 相位角之差 .用
• φ表示
• 同相: φ=0° • 反相: φ=180°
2020/9/5
3.2 正弦量的相量表示法 • 1.复数的实部、虚部和模
• 2.复数的A表 r达ej方式 A r • A=a+ j b=r cosφ+ j r sinφ=r(cosφ+ j sinφ)
示电流的最大2 值
•
有效值
:U
U
m
2
2
2020/9/5
2.频率与周期
• 周期T:正弦量变化一次所需的时间(秒)。
• 频率f:每秒内变化的次数称为,单位赫兹
(Hz)。 f
1 T
• 工频:我国采2 用f 520 Hz作为电力标准频率。
第3章 正弦交流电路

3.3.1 单一参数的正弦交流电路
1.纯电阻电路 (1) 电压与电流的关系
+
u iR
u
i I m sin t
_
u iR I m R sin t U m sin t
i R
对于正弦交流电路中的电阻电路(又称纯电阻 电路),一般结论为:
1)电压、电流均为同频率的正弦量。
2)电压与电流初相位相同,即两者同相。
y
i
ω
Im
i1
ωt1 φ
Im
i0
90
o
x
o
ωt1
ωt
φ
t t1 i1 I m sin(t 1)
对于一个正弦量可以找到一个与其对应的旋转矢量,反之, 一个旋转矢量也都有一个对应的正弦量。
3.2.2 复数及复数的运算 1、复数
A a jb
A r cos r sin
e j cos j sin
作相量图时要注意: 只有同频率的正弦量才 能画在一个相量图上,不 同频率的正弦量不能画在 一个相量图上。
+j
U
Φu
o
Φi
+1
I
3.3正弦交流电路的简单分析与运算
电阻元件、电感元件与电容元件都是组成 电路模型的理想元件。
所谓理想元件,就是突出元件的主要电磁 性质,而忽略其次要因素。如电阻元件具 有消耗电能的性质(电阻性),其它的电 磁性质如电感性、电容性等忽略不计。。
f = 1/T T = 1/f
i
角频率是指交流电在1s内变化的电 Im
角度。正弦量每经过一个周期T,
o
对应的角度变化了2π弧度,所以
φ
ωt
T
2f 2
电工电子技术第3章 正弦交流电路

最大值相量
U m Um
U U
相量图
U
有效值相量
I
u i
3.3 交流电路基本元件与基本定律
3.3.1交流电路基本元件
1.电容元件
电容的单位为法拉(F),
i
常采用微法(μF)和皮法
C
(pF)作为其单位。
+
u
-
当电压、电流为关联参考方向时 i C du
dt
电容元件储存的电场ห้องสมุดไป่ตู้量为
wC
(t)
1 2
Cu2 (t)
2.电感元件
iL
+
u
电感单位为亨利L( HLi)。 - 通 微常亨还(有μH毫)亨。u(mdH)L 和d (
dt d
当电压、电流为关联参考方向时 u L di
dt
电感元件储存的磁场能量为
L
(t)
1 2
Li2 (t)
3.3.2交流电路基本定律的相量形式
I U Z
220 30o 5053.1o
A
4.4 23.1o A
电路的平均功率
P UI cos (220 4.453.1o )W 58W
电路的无功功率
Q UI sin (220 4.4sin 53.1o )Var 774 Var
电路的视在功率
A A1 A2 (a1 a2 ) j(b1 b2 )
乘除运算
实部和虚部分别 相加减
A1 r11
A2 r22
A1A2 r1r21 2
两模相乘,辐 角相加。
A1 A2
r1 r2
-第3章 正弦交流电路

30
I 2
总电流瞬时值表达式:
I I12 I22
82 62A10A ψ arctanb 30
a 23.1
i102si(n ω t23.1)A
有效值 I =10 A
33
第二节、正弦量的相量表示法
计算正弦交流电的一般步骤
1.将正弦交流电化成相量式。 2.运算出结果。
ψ ω t1
ωt
若:有向线段长度 = I m
初相位
有向线段与横轴夹角
角频率
有向线段按逆时针方向旋转角速度
瞬时值i
有向线段每一瞬时在纵轴上的投影
t=0时, i0 Imsinψ
t=t1时, i1Im si(ntψ 2)1
第二节、正弦量的相量表示法
二、复数
复数常见的表达形式: ●代数形式 ●三角函数形式 ●指数形式 ●极坐标形式
+1
-jA1
26
三、相量
第二节、正弦量的相量表示法
实质:用复数表示正弦量。
正弦交流电
矢量
复数
+j
b r
O
A a +1
可见:正弦交流电可用矢量表示,矢量又可用复数 表示,所以,正弦交流电也可用复数表示。
相量: 表示正弦量的复数称相量。
27
第二节、正弦量的相量表示法
相量表示: 设正弦量: iIm si(n ω tψ )
二、相位差
相位差:两个同频率的正弦量相位之差。用
表示。
如:uU (ω t ψ u) (ω t ψ i)
ψu ψi
ui u i
若 ψ1ψ20 O
ωt
电压超前电流
13
ψuψi 0
I 2
总电流瞬时值表达式:
I I12 I22
82 62A10A ψ arctanb 30
a 23.1
i102si(n ω t23.1)A
有效值 I =10 A
33
第二节、正弦量的相量表示法
计算正弦交流电的一般步骤
1.将正弦交流电化成相量式。 2.运算出结果。
ψ ω t1
ωt
若:有向线段长度 = I m
初相位
有向线段与横轴夹角
角频率
有向线段按逆时针方向旋转角速度
瞬时值i
有向线段每一瞬时在纵轴上的投影
t=0时, i0 Imsinψ
t=t1时, i1Im si(ntψ 2)1
第二节、正弦量的相量表示法
二、复数
复数常见的表达形式: ●代数形式 ●三角函数形式 ●指数形式 ●极坐标形式
+1
-jA1
26
三、相量
第二节、正弦量的相量表示法
实质:用复数表示正弦量。
正弦交流电
矢量
复数
+j
b r
O
A a +1
可见:正弦交流电可用矢量表示,矢量又可用复数 表示,所以,正弦交流电也可用复数表示。
相量: 表示正弦量的复数称相量。
27
第二节、正弦量的相量表示法
相量表示: 设正弦量: iIm si(n ω tψ )
二、相位差
相位差:两个同频率的正弦量相位之差。用
表示。
如:uU (ω t ψ u) (ω t ψ i)
ψu ψi
ui u i
若 ψ1ψ20 O
ωt
电压超前电流
13
ψuψi 0
电工学课件:第3章 正弦交流电路

(1) i1 5sin(314t 600 )
(2) i2 5sin(314t 600 )
I1 5 600 2.5 2600 2
I 2 5 600 2.5 2 600 2
(3) i3 5sin(314t 600 )
i3 5sin(314t 600 1800 ) = 5sin(314t 1200 )
振幅相量的关系:
Im
2 I
U m 2U
例:1、写出下列正弦电压的相量(用直角坐标式表示):
(1) u 10 2 sint V
2
解:(1)
U
j
10e 2V
10
V
2
(2) u 10 2 sint 3 V
4
(2)
U
j 3
10e 4 V
10
3
V
4
2.将下述正弦量用相量表示:
相量图: 相量也可以在复平面上用矢量表示。
图中相量Ė 的长度为E代表正弦量的有效值,与实
轴夹角 0 等于正弦量的初相位。
五、用相量法求同频率正弦量的代数和..
例3-1 已知 u1 (t) 20 2 sin( 100t 1200 ) V
u2 (t) 15 2 cos(100t 600 ) V
式中 U m U me ju U mu
称为u(t)的相量
同理,设i(t) Im sin( t i )
则 Im I me ji I m i 称为i(t)的相量
从式子: Um sin(t ) Im[U me j t ]
说明一个三角函数等于一个旋转向量在虚轴上的投 影。考虑正弦交流线性电路中,电压和电流的频率 是不会改变的,为化简计算,将旋转向量的投影中 的旋转因子去掉,剩下相量部分代表一个三角函数 。且为了与数学上的复数区别开来,将相量符号上 方加˙标号。即:
正弦交流电路

第3 章
正弦交流电路
第 3 章 正弦交流电路
3.1 正弦电压与电流 3.2 正弦量旳相量表达法 3.3 电阻元件、电感元件、电容元件 3.4 电阻元件旳交流电路 3.5 电感元件旳交流电路 3.6 电容元件旳交流电路
3.7 电阻、电感与电容元件旳交流电路 3.8 阻抗旳串联与并联 3.10 交流电路旳频率特征 3.11 功率因数旳提升
三相交流电路:三种电压初相位各差120。
uA uB uC
t
第三章习题
例2 已知: i sin1000t 30
幅度: 频率:
Im 1A
I 1 0.707A 2
1000 rad/s f 1000 159 Hz
2 2
初相位: 30
3.2 正弦量旳相量表达法
正弦量旳表达措施:
阐明: 设:任一相量
A
90°旋转因子。+j逆时针 转90°,-j顺时针转90°
则:A e j90 ( j)A
3. 除法运算
设: U1 U1e j1 U 2 U 2e j 2
则:
U1 U 2
U1 U2
e j 1 2
复数运算应用举例
例1:已知瞬时值,用相量表达。
已知: 解:
i 141.4sin314t A
u 5 2 sin( t 126 9 )
u 5 2 sin( t 126 9 )
符号阐明
瞬时值 --- 小写
u、i
有效值 --- 大写
U、I
最大值 --- 大写带下标
Um
复数、相量 --- 大写,头上加 U
“.”
正误判断
u 100sin t U ?
瞬时值
复数
正误判断
U 50 e j15 50 2 sin( t 15 )?
正弦交流电路
第 3 章 正弦交流电路
3.1 正弦电压与电流 3.2 正弦量旳相量表达法 3.3 电阻元件、电感元件、电容元件 3.4 电阻元件旳交流电路 3.5 电感元件旳交流电路 3.6 电容元件旳交流电路
3.7 电阻、电感与电容元件旳交流电路 3.8 阻抗旳串联与并联 3.10 交流电路旳频率特征 3.11 功率因数旳提升
三相交流电路:三种电压初相位各差120。
uA uB uC
t
第三章习题
例2 已知: i sin1000t 30
幅度: 频率:
Im 1A
I 1 0.707A 2
1000 rad/s f 1000 159 Hz
2 2
初相位: 30
3.2 正弦量旳相量表达法
正弦量旳表达措施:
阐明: 设:任一相量
A
90°旋转因子。+j逆时针 转90°,-j顺时针转90°
则:A e j90 ( j)A
3. 除法运算
设: U1 U1e j1 U 2 U 2e j 2
则:
U1 U 2
U1 U2
e j 1 2
复数运算应用举例
例1:已知瞬时值,用相量表达。
已知: 解:
i 141.4sin314t A
u 5 2 sin( t 126 9 )
u 5 2 sin( t 126 9 )
符号阐明
瞬时值 --- 小写
u、i
有效值 --- 大写
U、I
最大值 --- 大写带下标
Um
复数、相量 --- 大写,头上加 U
“.”
正误判断
u 100sin t U ?
瞬时值
复数
正误判断
U 50 e j15 50 2 sin( t 15 )?
第3章正弦交流电路
A=a+jb = r(cos jsin) 式中,r叫做复数A的模,又称为A的绝对值, 叫做复数A的辐角 。
3)指数形式
A =r (cos jsin) = re j
4)极坐标形式
A=r∠
从图中可以看出,复数A的实部a、虚部b与模r构成一个直角三角形。
三者之间的关系为
r a2 b2
arctan b
个正弦量同相,如图4.2 (b)所示;
(4) 当 12 = 时,一个正弦量到达正最大值时,另一个正弦量到达
负最大值,此时称第1个正弦量与第2个正弦量反相,如图4.2 (c)所示;
(5) 当 12 = /2时,一个正弦量到达零时,另一个正弦量到达正最
大值(或负最大值),此时称第1个正弦量与第2个正弦量正交。如图4.2 (d) 所示。
U1 U1 1
U U1 U 2
U 2 U 2 2
u(t ) 2 U cos( t )
故同频正弦量相加减运算变成对 应相量的相加减运算。
i1 i2 = i3
I1 I2 I3
3.2 单一参数正弦交流电路的分析
一、纯电阻元件电路
1. 电阻元件 在正弦电路中,电流、电压虽然都是随时间变化
= 311sin(30°)= 115.5V
i= 5sin(314t 90°) = 5sin(314×0.00333 90°) = 5sin(150°)
= 2.5A
可见,当两个同频率正弦量的计时起点变化时,各自的相位将发生
变化,但其相位差不变。说明相位的大小与计时起点的选择有关,
而相位差与计时起点的选择无关。
(2)、 乘除运算——极坐标为例
若 A1= r1 1 ,若A2= r2 2
则
A 1
3)指数形式
A =r (cos jsin) = re j
4)极坐标形式
A=r∠
从图中可以看出,复数A的实部a、虚部b与模r构成一个直角三角形。
三者之间的关系为
r a2 b2
arctan b
个正弦量同相,如图4.2 (b)所示;
(4) 当 12 = 时,一个正弦量到达正最大值时,另一个正弦量到达
负最大值,此时称第1个正弦量与第2个正弦量反相,如图4.2 (c)所示;
(5) 当 12 = /2时,一个正弦量到达零时,另一个正弦量到达正最
大值(或负最大值),此时称第1个正弦量与第2个正弦量正交。如图4.2 (d) 所示。
U1 U1 1
U U1 U 2
U 2 U 2 2
u(t ) 2 U cos( t )
故同频正弦量相加减运算变成对 应相量的相加减运算。
i1 i2 = i3
I1 I2 I3
3.2 单一参数正弦交流电路的分析
一、纯电阻元件电路
1. 电阻元件 在正弦电路中,电流、电压虽然都是随时间变化
= 311sin(30°)= 115.5V
i= 5sin(314t 90°) = 5sin(314×0.00333 90°) = 5sin(150°)
= 2.5A
可见,当两个同频率正弦量的计时起点变化时,各自的相位将发生
变化,但其相位差不变。说明相位的大小与计时起点的选择有关,
而相位差与计时起点的选择无关。
(2)、 乘除运算——极坐标为例
若 A1= r1 1 ,若A2= r2 2
则
A 1
正弦交流电路

2. 平均功率(有功功率)P:一个周期内的平均值
i
P=UI
=I2R=i U2/2RI
sint
Uu =IRR
u 2U sint
P1 Tpd t1Tuidt
T0
T0
大写 1 T 2UIsin2t dt
T0
1
T
UI(1cos2t)dtUI
T0
§ 3.4 理想电感元件上的正弦稳态响应
一、电压电流关系
即:瞬时值和相量满足基尔霍夫定律,有效值不满足
I1I2I30
I1
I3
I1-I2+I3= 0
I2
U 3
U 4
U 2 U 1 U 2 U 3 U 4 U 5 U 6 0 U 1
U 5
U 6
例: i162si nt (3)0
i282si nt (6)0
求i=i1+i2
i
解: I 1 6 3 0 5 .1 9 j3 6
Im[Ime ji e jt ]
复指数函数中的一个复常数
复常数定义为正弦量的相量,记
为
Im
相量 的表示
Im 为“最大值”相量
Im Im eji Im i
I 为“有效值”相量 IIeji Ii
相量是一个复数
注意
1)相量可以代表一个正弦量,但不等于该
正弦量。
U 50ej15° 50
2
sin(
实部是余弦量 虚部是正弦量
则 I[ m Im e j( t i)] Im sitn ( i)
正弦量可以用上述形式复数函数描述
I[ m Im e j( t i)] Im sitn ( i)
正弦量可以用上述形式复数函数描述
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、已知电路中的电阻与电抗, 求解复阻抗时,有:
z R 2 ( X L X C )2 XL XC arctan R 2、已知电路的复阻抗,求解电路中的电阻与电抗时,有:
R z cos X L X C z sin
33
第3章 正弦交流电路
由复阻抗的定义式:
2)平均功率 1 T 1 P p d t UI sin 2t d t 0 T 0 T 0 3)无功功率
QL UI I 2 X L 0(VAR)
25
第3章 正弦交流电路
二、C元件正弦交流电路
1、电压-电流关系 令:u U m sin t
i C
du d C (U m sin t ) CU m cos t I m sin(t 90 ) dt dt
原矢量数值大小不变,方向旋转α 角度,根据欧拉公式有
e cos jsin
90 ,代入上式有 若
j
e
j90
cos(90 ) jsin(90 ) j
由此可得,虚数号j也是旋转因子,矢量与j相乘,该 矢量将逆时针旋转90度,矢量与-j相乘,矢量将顺时针 旋转90度
2、功率
1)瞬时功率
p iu I m sin t U m sin I mU m sin 2 t IU (1 cos 2t )t
2)平均功率
1 T 1 T U2 2 P p d t IU (1 cos 2t ) d t IU I R T 0 T 0 R
12
第3章 正弦交流电路
二、矢量图
定义:由几个表示同频率正弦量的矢量构成的 几何图形
注意: 1、矢量图中的各矢量频率相同,不同频率的矢量 不能够画在同一个矢量图中 2、矢量图中的各矢量满足平行四边形法则 3、选取了参考矢量后,矢量图中可以省略坐标轴
13
第3章 正弦交流电路
三、矢量的复数表示
复平面中的矢量表示有四种方法
比较电压-电流表示式,有: 1) 0 90 90
u i
即:电容电压滞后电流 2)
Um U 1 1 XC Im I C 2 fC
26
容抗 Xc:C元件对电流流过时的阻力,量纲(欧姆)
第3章 正弦交流电路
3)欧姆定律的向量式及向量图
I U j XC
一、周期与频率 1、名词:
周期 T :正弦量变化一周所需的时间(s) 频率 f : 单位时间内正弦量变化的次数(Hz) 角频率ω :单位时间内正弦量变化的弧度数 (rad/s)
2、三者之间的关系:
1 f T
2 2 f T
3
第3章 正弦交流电路
二、幅值与有效值
瞬时值u、i:正弦量在任一瞬时的数值 初始值u(0):正弦量在t=0时的数值 最大值Um:瞬时值中数值最大的值 有效值U、I:方均根值
1、代数式
OA a j b
j OA re
2、三角函数式 OA r cos j r sin
3、指数式 4、极坐标式
OA r
14
第3章 正弦交流电路
四、旋转因子 e j
若矢量与旋转因子相乘有
j OA e re j e j re j( ) OB
22
第3章 正弦交流电路
二、L元件的正弦交流电路
1、电压-电流关系 令: i I m sin t
uL di d L ( I m sin t ) L I m cos t U m sin(t 90 ) dt dt
比较电压-电流表示式,有: 1) u i 90 0 90 即:电感电压超前电流 90° 角
复阻抗:电压向量与电流向量的比值 XL XC U 2 2 Z R j( X L X C ) R ( X L X C ) arctan z I R
上式中 Z 是阻抗,φ 是阻抗角
复阻抗是复数,在复平面中 可以画出复阻抗
32
第3章 正弦交流电路
由复阻抗的复平面表示可以得到阻抗三角形
Ψ >0
Ψ <0
8
第3章 正弦交流电路
2)相位差
在数学中,相位差是任意两个同频率正弦量 的初相位之差,在工程电学中,相位差的定义是:
u i
当φ >0时,正弦电压超前于电流; 当φ <0时,正弦电压滞后于电流。
9
第3章 正弦交流电路
3)相位差不同时的正弦波形
10
第3章 正弦交流电路
A B r r r r r
A r r r B r r
17
第3章 正弦交流电路
注意:
1、向量是表示正弦量的复数,但向量不是正弦量,即向 量代表正弦量,向量不等于正弦量 2、如果一个电路参数是复数,但不是正弦量,则该电路 参数不可以使用向量表示 3、根据公式 1 1 1 j j ,所以在正弦函数的 表示式中没有负号,电路运算出现的负号按照180度角 折算记入正弦量的相位角中。
34
第3章 正弦交流电路
在正弦交流电路中
1、如果 >0, u i >0 电路就称为感性电路,电路中电压超前电流
2、如果 <0, u i <0 电路就称为容性电路,电路中电压滞后电流
3、如果 =0, u i =0 电路就称为阻性电路,电路中电压与电流同相位
三、相位与初相位
1、名词 相:正弦量的状态称为相 相位角(ω t+ψ ):决定正弦量状态的角度 初相位(ψ ):t=0时的相位 相位差(φ ):两个同频率正弦量的初相位之差
(t 1 ) (t 2 ) 1 2
7
第3章 正弦交流电路
2、注意
1)初相位Ψ 的取值范围 规定:Ψ 的数值在 –π— +π之间
1 T 2 I i dt T 0
4
第3章 正弦交流电路
2、最大值与有效值的关系
将正弦函数式代入有效值的计算公式,可以 得到最大值与有效值之间的关系式:
1 T 0 T 0
T T
I T Im T 2 2
2 m
即:
Im I 2
2 R 2
29
第3章 正弦交流电路
以串联电流为参考向量,在复平面中可以画 出电压向量的向量图
30
第3章 正弦交流电路
由向量图可以得到串联电路的电压三角形
1、已知分电压求解总电压时,有:
U U (U L U C )
2 R
2
UL UC arctan UR
2、已知总电压求解分电压时,有:
§6 功率因数的提高........................54
1
第3章 正弦交流电路
§1 正弦函数的表示方法
正弦函数的表示有三要素:
频率:表示正弦函数变化的快慢 幅值:表示正弦函数的数值大小 初相位:表示正弦函数在t=0时的状态
i I m sin(t )
2
第3章 正弦交流电路
比较电压-电流表示式,有: 1)在R元件电路中,电压与电流同相位 u i 0
Um U 2) R Im I
20
1、电压-电流关系 令: u U sin t
m
第3章 正弦交流电路
3) R元件电路欧姆定律的向量表示式与向量图为
U I R
4)正弦波形
21
第3章 正弦交流电路
I Ie j
I I
16
第3章 正弦交流电路
六、向量运算
设两个向量分别为
A a j b r
则向量运算式如下
B a j b r
A B (a j b) (a j b) (a a) j(b b) a j b r
U R U cos (U L U C ) U sin
31
第3章 正弦交流电路
二、阻抗三角形
由欧姆定律可以得到串联电路电压-电流的关系式:
U U R U L U C RI j X L I j X C I I R j( X L X C )
5
第3章 正弦交流电路
3、有效值的物理意义
定义:一个正弦电流流过一个定值电阻,在一个 周期时间内产生的热量与一个直流电流流过同一 个电阻在同样时间内产生的热量相同,这个直流 电流的数值即为正弦电流的有效值。
即:
T
0
i R d t I RT
2 2
1 T 2 I 0 i d t T
6
第3章 正弦交流电路
4)波形图
27
第3章 正弦交流电路
2、功率
1)瞬时功率
p ui U m sin t I m sin(t 90 ) I mU m sin t cos t IU sin 2t
2)平均功率
1 T 1 P pdt T 0 2
3)无功功率
2
0
UI sin 2t d t 0
§2 正弦量的向量表示
一、旋转矢量的建立 条件:
1.矢量的长度=正弦量的幅值 2.矢量与坐标轴正方向的夹角=正弦量的初相 3.矢量按照逆时针方向旋转的角速度=正弦量的角频率
结论:
满足上述条件的旋转矢量在任一瞬时在坐标纵轴上的 投影=正弦量的瞬时值
11
第3章 正弦交流电路
旋转矢量的图示
表示正弦量的旋转矢量
第3章 正弦交流电路
§1 正弦电压与电流........................02 §2 正弦量的相量表示方法.............11 §3 R、L、C元件的正弦交流电路....20
z R 2 ( X L X C )2 XL XC arctan R 2、已知电路的复阻抗,求解电路中的电阻与电抗时,有:
R z cos X L X C z sin
33
第3章 正弦交流电路
由复阻抗的定义式:
2)平均功率 1 T 1 P p d t UI sin 2t d t 0 T 0 T 0 3)无功功率
QL UI I 2 X L 0(VAR)
25
第3章 正弦交流电路
二、C元件正弦交流电路
1、电压-电流关系 令:u U m sin t
i C
du d C (U m sin t ) CU m cos t I m sin(t 90 ) dt dt
原矢量数值大小不变,方向旋转α 角度,根据欧拉公式有
e cos jsin
90 ,代入上式有 若
j
e
j90
cos(90 ) jsin(90 ) j
由此可得,虚数号j也是旋转因子,矢量与j相乘,该 矢量将逆时针旋转90度,矢量与-j相乘,矢量将顺时针 旋转90度
2、功率
1)瞬时功率
p iu I m sin t U m sin I mU m sin 2 t IU (1 cos 2t )t
2)平均功率
1 T 1 T U2 2 P p d t IU (1 cos 2t ) d t IU I R T 0 T 0 R
12
第3章 正弦交流电路
二、矢量图
定义:由几个表示同频率正弦量的矢量构成的 几何图形
注意: 1、矢量图中的各矢量频率相同,不同频率的矢量 不能够画在同一个矢量图中 2、矢量图中的各矢量满足平行四边形法则 3、选取了参考矢量后,矢量图中可以省略坐标轴
13
第3章 正弦交流电路
三、矢量的复数表示
复平面中的矢量表示有四种方法
比较电压-电流表示式,有: 1) 0 90 90
u i
即:电容电压滞后电流 2)
Um U 1 1 XC Im I C 2 fC
26
容抗 Xc:C元件对电流流过时的阻力,量纲(欧姆)
第3章 正弦交流电路
3)欧姆定律的向量式及向量图
I U j XC
一、周期与频率 1、名词:
周期 T :正弦量变化一周所需的时间(s) 频率 f : 单位时间内正弦量变化的次数(Hz) 角频率ω :单位时间内正弦量变化的弧度数 (rad/s)
2、三者之间的关系:
1 f T
2 2 f T
3
第3章 正弦交流电路
二、幅值与有效值
瞬时值u、i:正弦量在任一瞬时的数值 初始值u(0):正弦量在t=0时的数值 最大值Um:瞬时值中数值最大的值 有效值U、I:方均根值
1、代数式
OA a j b
j OA re
2、三角函数式 OA r cos j r sin
3、指数式 4、极坐标式
OA r
14
第3章 正弦交流电路
四、旋转因子 e j
若矢量与旋转因子相乘有
j OA e re j e j re j( ) OB
22
第3章 正弦交流电路
二、L元件的正弦交流电路
1、电压-电流关系 令: i I m sin t
uL di d L ( I m sin t ) L I m cos t U m sin(t 90 ) dt dt
比较电压-电流表示式,有: 1) u i 90 0 90 即:电感电压超前电流 90° 角
复阻抗:电压向量与电流向量的比值 XL XC U 2 2 Z R j( X L X C ) R ( X L X C ) arctan z I R
上式中 Z 是阻抗,φ 是阻抗角
复阻抗是复数,在复平面中 可以画出复阻抗
32
第3章 正弦交流电路
由复阻抗的复平面表示可以得到阻抗三角形
Ψ >0
Ψ <0
8
第3章 正弦交流电路
2)相位差
在数学中,相位差是任意两个同频率正弦量 的初相位之差,在工程电学中,相位差的定义是:
u i
当φ >0时,正弦电压超前于电流; 当φ <0时,正弦电压滞后于电流。
9
第3章 正弦交流电路
3)相位差不同时的正弦波形
10
第3章 正弦交流电路
A B r r r r r
A r r r B r r
17
第3章 正弦交流电路
注意:
1、向量是表示正弦量的复数,但向量不是正弦量,即向 量代表正弦量,向量不等于正弦量 2、如果一个电路参数是复数,但不是正弦量,则该电路 参数不可以使用向量表示 3、根据公式 1 1 1 j j ,所以在正弦函数的 表示式中没有负号,电路运算出现的负号按照180度角 折算记入正弦量的相位角中。
34
第3章 正弦交流电路
在正弦交流电路中
1、如果 >0, u i >0 电路就称为感性电路,电路中电压超前电流
2、如果 <0, u i <0 电路就称为容性电路,电路中电压滞后电流
3、如果 =0, u i =0 电路就称为阻性电路,电路中电压与电流同相位
三、相位与初相位
1、名词 相:正弦量的状态称为相 相位角(ω t+ψ ):决定正弦量状态的角度 初相位(ψ ):t=0时的相位 相位差(φ ):两个同频率正弦量的初相位之差
(t 1 ) (t 2 ) 1 2
7
第3章 正弦交流电路
2、注意
1)初相位Ψ 的取值范围 规定:Ψ 的数值在 –π— +π之间
1 T 2 I i dt T 0
4
第3章 正弦交流电路
2、最大值与有效值的关系
将正弦函数式代入有效值的计算公式,可以 得到最大值与有效值之间的关系式:
1 T 0 T 0
T T
I T Im T 2 2
2 m
即:
Im I 2
2 R 2
29
第3章 正弦交流电路
以串联电流为参考向量,在复平面中可以画 出电压向量的向量图
30
第3章 正弦交流电路
由向量图可以得到串联电路的电压三角形
1、已知分电压求解总电压时,有:
U U (U L U C )
2 R
2
UL UC arctan UR
2、已知总电压求解分电压时,有:
§6 功率因数的提高........................54
1
第3章 正弦交流电路
§1 正弦函数的表示方法
正弦函数的表示有三要素:
频率:表示正弦函数变化的快慢 幅值:表示正弦函数的数值大小 初相位:表示正弦函数在t=0时的状态
i I m sin(t )
2
第3章 正弦交流电路
比较电压-电流表示式,有: 1)在R元件电路中,电压与电流同相位 u i 0
Um U 2) R Im I
20
1、电压-电流关系 令: u U sin t
m
第3章 正弦交流电路
3) R元件电路欧姆定律的向量表示式与向量图为
U I R
4)正弦波形
21
第3章 正弦交流电路
I Ie j
I I
16
第3章 正弦交流电路
六、向量运算
设两个向量分别为
A a j b r
则向量运算式如下
B a j b r
A B (a j b) (a j b) (a a) j(b b) a j b r
U R U cos (U L U C ) U sin
31
第3章 正弦交流电路
二、阻抗三角形
由欧姆定律可以得到串联电路电压-电流的关系式:
U U R U L U C RI j X L I j X C I I R j( X L X C )
5
第3章 正弦交流电路
3、有效值的物理意义
定义:一个正弦电流流过一个定值电阻,在一个 周期时间内产生的热量与一个直流电流流过同一 个电阻在同样时间内产生的热量相同,这个直流 电流的数值即为正弦电流的有效值。
即:
T
0
i R d t I RT
2 2
1 T 2 I 0 i d t T
6
第3章 正弦交流电路
4)波形图
27
第3章 正弦交流电路
2、功率
1)瞬时功率
p ui U m sin t I m sin(t 90 ) I mU m sin t cos t IU sin 2t
2)平均功率
1 T 1 P pdt T 0 2
3)无功功率
2
0
UI sin 2t d t 0
§2 正弦量的向量表示
一、旋转矢量的建立 条件:
1.矢量的长度=正弦量的幅值 2.矢量与坐标轴正方向的夹角=正弦量的初相 3.矢量按照逆时针方向旋转的角速度=正弦量的角频率
结论:
满足上述条件的旋转矢量在任一瞬时在坐标纵轴上的 投影=正弦量的瞬时值
11
第3章 正弦交流电路
旋转矢量的图示
表示正弦量的旋转矢量
第3章 正弦交流电路
§1 正弦电压与电流........................02 §2 正弦量的相量表示方法.............11 §3 R、L、C元件的正弦交流电路....20
