第八章-第1节 多元函数的基本概念
(整理)81 第八章 多元函数微分法及其应用 第一节.多元函数的基本概念.

第八章.多元函数微分法及其应用 第一节 多元函数的基本概念教学目标:掌握多元函数的概念,掌握二元函数的几何表示、极限、连续的概念,以及有界闭区域上连续函数的性质. 课时安排:2课时重点:多元函数的极限、多元函数的连续性 难点:多元函数的连续性 教学法:讲授法一. 平面点集 n 维空间⒈ 平面点集 (){}2R R R=x,y x R,y R =∈∈,坐标系平面; ① Def :坐标平面上具有某种性质的点的集合。
记为()(){}E x,y x,y p =是具有某种性质如 :圆内:(){}222x,y x +y r<② 邻域:设()000p x ,y 为xoy 平面上一点,0δ>。
与0p 的距离小于的点()p x,y 的全体称为点0p 的邻域,记为:(){}({}00U p ,p pp x,y δδδ=<=<注:⑴几何上:圆内部的点全体; ⑵()()o00U p ,U p 。
③ 内点,外点,边界点ⅰ内点:若∃点P 的某个邻域()()U p s.t.U p E ⊂,则称P 为E 的内点; ⅱ外点:若点P 的某个邻域()()U p s.t.U p E=⋂∅,则称P 为E 的外点; ⅲ边界点:若点P 的任一邻域内既含有属于E 的点,又含有不属于E 的点,则称P 为E 的边界点注:⑴E 的边界点的全体,称为E 的边界,记作E ∂; ⑵内点E ∈,外点E ∉,不边界点不一定; ⑶22p R E R ∀∈⊂和,三种关系必具之一。
④ 聚点:如果()o0,U p,δδ∀>内总有E 中的点,称P 为E 的聚点; 注:⑴聚点可以E ∈,也可以E ∉,如E=(){}22x,y /x y 2+≤; ⑵例中边界点都是聚点,但边界点不总是聚点;⑶聚点P 的()oU p,δ中有无穷多个E 中的点。
⑤ 开集 闭集 连通集ⅰ开集:E 的点全是的内点,称E 为开集; ⅱ闭集:E 的余集C E 为开集,E 为闭集; 开集:(){}22x,y 1<x y <2+;闭集 :(){}22x,y 1x y 2≤+≤; 非开非闭集:(){}22x,y 1<x y 2+≤。
8-1多元函数基本概念

20
lim f ( x, y)
念多
x x0 y y0
元 函 数
说明
的 基
本
(1) 定义中 P P0的方式是任意的;
概
(2) 二元函数的极限也叫二重极限. (double limit)
21
例2
求证lim( x2 x0
y2 )sin
x2
1
y2
0
y0
证
(x2
y2 )sin
x2
1
必有以下三种关系中的一种:
念多
元
(1) 内点 设E为一平面点集,点P E, 若存在
函 数
0,使U(P) E, 称P为E的 内点.(P1)
的 基
显然, E的内点属于E.
本
P3
P1
概
(2) 外点 如果存在点P的某个邻域 U(P),
E
使U(P) ∩ E = , 则称P为E的外点.(P2 )
y2
0
x2
y2
sin
x2
1
y2
x2 y2
0, ,
当 0 ( x 0)2 ( y 0)2 时,
(x2
y2 )sin
x2
1
y2
0
原结论成立.
22
多元函数的极限与一元函数的极限的
念多
元
相同点和差异是什么
函 数
相同点 定义相同.
研究单值函数
z
z f (x, y)
M
念多 元 函 数 的 基 本 概
y
O
第一节多元函数的基本概念

(2)找 两 种 不 同 趋 使l向 imf(方 x,y)式 存, 在 , 但 xx0 yy0 两 者 不 相 等 , lim 则 f(x,可 y)不 断存 言 .在 xx0 yy0
定义 2 设n元函数 z f(P)的定义域为D点 , P0集
函数z f (x, y)当x x0, y y0 时的极限, 记作 lim f (x, y) A.
xx0 y y0
或记为 ( f (x, y) A,( 0),这里 PP0 ) .
说明:
义P中 P0的方式是
(2) 二元函数的极 二限 重也 极 lim 叫 限 f(x,做 y); xx0 yy0
U(P,)P|P|P
0
0
• P0
( x , y ) |( x x ) 2 ( y y ) 2 .
0
0
2. 区域
设 E 是平面上的一个点集, P 是平面上的 一个点.如果存在点 P 的某一邻域 U(P) 蘿E , 则称 P 为 E 的内点 . E 的内点属于E .
如果点集E的点都是内点,
x2y2
例 3求 极li限 m sinx(2y).
x y x 0
2
2
y 0
解
lim
x0
sin( x x2
2 y) y2
y0
limsin(x2 y) x 2 y ,
x0 y0
x2 y
x2 y2
其中
limsin(x2 y)
x0 y0
x2 y
ux2y
lim
u0
sin u u
1,
x2y x2 y2
第一节 多元函数的基本概念

第八章 多元函数微分法及其应用大纲要求1.理解多元函数的概念2.了解二元函数的极限和连续的概念3.理解偏导数和全微分的概念,了解全微分存在的必要条件和充分条件,以及全微分在近似计算中的应用4.理解方向导数和梯度的概念并掌握其计算方法5.掌握复合函数一阶、二阶偏导数的求法;会求隐函数的偏导数6.了解曲线的切线和法平面及曲面的切平面和法线的概念,会求它们的方程7.理解多元函数极值和条件极值的概念,掌握多元函数极值的必要条件,了解二元函数极值的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值、最小值并会解决一些简单的应用问题第一节 多元函数的基本概念㈠本课的基本要求理解多元函数的概念,了解二元函数的极限和连续的概念㈡本课的重点、难点多元函数的有关概念为重点、难点是二元函数的极限和连续性的概念㈢教学内容前面我们研究了一元函数(一个自变量的函数)及其微积分。
但在自然科学与工程技术的实际问题中,往往涉及到多个因素之间的关系,这在数学上就表示为一个变量依赖于多个变量的情形,这种关系就相应地导出多元函数的概念。
本章的目的是在一元函数微分学的基础上,讨论多元函数的微分法及其应用。
我们以二元函数为主,但所得到的概念、性质与结论都可以很自然地推广到二元以上的多元函数。
同时,我们还须注意与一元函数微分学中有区别的地方,不要把概念、方法与记号弄混淆。
一.平面点集、n 维空间在讨论一元函数时,一些概念、理论和方法,都是基于1R 中的点集、两点间的距离、区间和邻域等概念。
为了将一元函数微积分推广到多元的情形,首先需要将上述一些概念加以推广,同时还需涉及一些其他概念。
为此我们先引入n 维空间,以便推广到一般的n R 中。
1.平面点集我们知道二元有序实数组),(y x 的全体,即},|),{(2R y x y x R R R ∈=⨯=就表示坐标平面。
(请思考:n 维空间?)坐标平面上具有某种性质P 的点的集合,称为平面点集,记作),(|),{(y x y x E =具有性质P}。
8-1 多元函数的基本概念

其中:D称为定义域 f ( D)称为值域 ,
w 类似地可定义三元函数. f ( x , y , z )
n元函数 y f ( x ) f ( x1 , x2 ,, xn )
多元函数两点说明:
(1)多元函数uf(x)定义域指自然定义域
arcsin( 3 x 2 y 2 ) f ( x, y) 例1 求定义域 x y2 的. 3 x2 y2 1 解 x y2 0 2 x 2 y 2 4 2 x y
n U n维空间邻域: ( P0 , ) P | PP0 | , P R
内点、边界点、区域、聚点等概念也可定义.
1.4 二元函数的定义
定义:设区域 R 2 D 映射f : D R称为二元函数 记为:z f ( P ) f ( x, y ) P ( x , y ) D
lim
x3 y4
xy 1 x y
2 2
2
闭区域上连续函数的性质
(1)最大值和最小值D
使得:f(P1) max{f(P )|PD }
f(P2) min{f(P )|PD } .
(2)介值定理
有界闭区域D上的多元连续函数,必取得介于最大值 和最小值之间的任何值
2 2
去心邻域:( P , ) { P | 0 | PP0 | } U
不需要考虑邻域半径时 简记为: (P ) U
0
P
1.2 区域
E
P
P
(1)设 E 是平面 点集,点 E P 如果存 在U ( P ) E , 则称 P 为 E 的内点 . ( 2)设 E 是平面点集,点 E P 如果存在U ( P ) E , 则称 P 为 E 的外点 . ( 3)如 果 U ( P ) E 且U ( P ) E E 称P 为 E 的 边 界 点 .
第八章多元函数微分学课件

四.多元函数的连续性
习题
返回
第一节 多元函数的基本概念
一、区域
1.邻域 设 P0(x0, y0) 是xOy平面上的一个点,δ是某一
正数.与点 P0(x0, y0) 距离小于δ的点 P(x, y) 的全体 称为P0 的邻域,记为U (P0, ),即
U (P0, ) {P PP0 }
也就是
U (P0, ) {(x, y) (x x0 )2 ( y y0 )2 }
也称为因变量,数集
{z z f (x, y),(x, y)D}
称为该函数的值域.
把定义1中的平面点集D换成n维空间内的点集 D.则可类似的定义n元函数 u f (x1, x2, , xn ) .当 n=1时,n元函数就是一元函数.当n≥2时n元函 数统称为多元函数.
上一页 下一页 返 回
三、多元函数的极限
M 0Tx 对y轴的斜率.
上一页 下一页 返 回
x
z y
2z yx
fyx (x,
y), y
z y
2z y2
fyy (x,
y)
其中第二、第三两个偏导数称为混合偏导数.同 样可得三阶、四阶、···以及n阶偏导数.二阶及 二阶以上的偏导数统称为高阶偏导数.
例题
定理 如果函数z=f(x,y)的两个二阶混合偏
,
x
x x0 y y0
,
zx
xx0 或fx (x0, y0 )
y y0
如果函数 z f (x, y) 在区域D内每一点(x,y)
处对x的偏导数都存在,那么这个偏导数就是
x、y函数,它就称为函数 z f (x, y) 对自变量x
的偏导函数,记作
上一页 下一页 返 回
多元函数的基本概念

| f ( x, y) A |
成立,则称常数A为二元函数f (x, y)当PP0 (或xx0, yy0)时的极限,记作
P P0
lim f ( P) A或 lim f ( x, y ) A
x x0 y y0
首页
上页
下页
注1:二元函数的极限称为二重极限;
二重极限存在是指点P(x, y)以任何方式趋于
首页 上页
下页
3. 多元初等函数 (1) 二元基本初等函数 考虑一个变量x或y的基本初等数,将它们当成 二元函数. 如:C, x , y , sinx, siny,…… 称为二元基本初等函数.
首页
上页
下页
(2) 二元初等函数 将二元基本初等函数经有限次四则运算与复合 所组成的函数,称为二元初等函数.
U(P) E
则称点P为点集E的内点.
o
P
E
x y o
1 x
下页
注: 若点集E的点都是内点, 则称E为开集.
例如: 点集 E1= {(x,y)| x2 + y2 < 1}是开集.
点集 E2= {(x,y)| x2 + y2 1}不是开集.
首页 上页
(2) 边界点: 设E为一平面点集, P1为一点, 不论P1点 是否属于 E, 如果 P1 的任何邻域内 , 既 有属于E的点, 也有不属于E的点, 则称 点P1为点集E的边界点.y P1 注: 点集E的全体边界点
所成的点集, 称为点 集E的边界. 例如: 点集 E= {(x, y)| 1 x2 + y2 < 4} 的边界点是圆 x2 + y2 = 1和 x2 + y2 = 4 .
首页
多元函数的基本概念课件

曲面积分是计算曲面上的函数值累积的 数学工具,分为第一类曲面积分和第二 类曲面积分。
曲线积分和曲面积分在物理、工程等领 域有广泛应用,如计算力矩、功等物理 量。
06 多元函数的应用
在物理中的应用
热力学
多元函数可以用来描述热力学中的状态方程,如压力、温度和体 积之间的关系。
多元函数的基本概念课件
目录
• 多元函数的定义与表示 • 多元函数的极限与连续性 • 多元函数的导数与微分 • 多元函数的极值与最值 • 多元函数的积分 • 多元函数的应用
01 多元函数的定义与表示
定义与性质
定义
多元函数是指定义在两个或更多 个变量上的数学函数。例如,三 维空间中的函数f(x, y, z)定义了x 、y和z的每一个值对。
多元函数的最值
定义
多元函数的最值是指函数在某个 区域内的最大值和最小值。
求解方法
通过求导数找到可能的极值点, 然后通过比较这些点的函数值来
找到最大值和最小值。
应用
在优化问题中,最值的概念被用 来确定某个目标函数的最大或最
小值。
条件极值与无约束最值问题
定义
条件极值是指在满足某些约束条件下求函数的极值;无约束最值问 题则没有约束条件。
02
二重积分的计算通常通 过直角坐标系或极坐标 系进行。
03
04
二重积分可以应用于面 积、体积、质量等的计 算。
二重积分的计算公式为: ∫∫D f(x,y) dxdy,其中 D是积分区域。
三重积分
01
02
03
04
三重积分是计算三维空间区域 上的函数值累积的数学工具。
高等数学 多元函数的微分学 (8.1.1)--多元函数的基本概念

为E 的边界点
内点
·
·
外点
若集合 E 中每个点都是
·
边 界点
E 的内点,称 E 为开集;开集 E 的余集 R2-E 称为 闭集
若集合 E 中任意两点都能用完全属于 E 的折 连接线起来,则称 E 是连通的;连通的开集称为区 域 E 的所有的边界点组成的集合称为 E 的边 区域连界同其边 界称为 闭 区域
若存在 R ,集 E {(x, y) x2 y2 R2}, 称 E 有界 合例 下列集合是否开集、区域、连通、有界
D1 {(x, y) x2 y2 4}, D2 {(x, y) x2 y2 4},
D3 {(x, y) | xy 0}, D4 {x 0, y 0}
称为 P0 的 δ 邻域(不强调半径时为邻域U (P0 )
)
U (P0, P) {P(x, y) 0 d (P, P0 ) }
称为 P0 的去心 δ 邻域
二 . 开集与区域
E 是平面 R2 中的集合, P0 是平面中的点
若存在 δ>0 , U (P0, ) E, 称 P0 为 E 的内点 若使对任意 δ , U (P0, ) 内既;有属于 E 的点又有不 在属于 E 的点,称 P0
例 已知f (x y, xy) x3 y3, 求 f (x, y)
例 z y f ( x y), 且 z y1 x 1, 求函数 z 的表达式
例 求 z ln[x ln(y x)] 的定义域
二元函数图形 (图象 )
集合 {(x,y,z) z f (x,y),(x, y) D} 所对应
D5
{(x, y)
x2 4
高等数学8.1多元函数的基本概念ppt课件

函数的间断点: 若函数f(x,y)在点P0(x0,y0)不连续,则P0 称为函数f(x,y)的
间断点. 注:间断点可能是孤立点也可能是曲线上的点.
例
f(x,y)
xy
x2
y
2
,
x2
y2
0,
点(0,0)是f(x,y)的间断点;
0 , x2 y2 0.
z
sin
x2
1 y2
1
,
x2y21上的点是其间断点.
E的边界点的全体称为E的边 界.
开集: E{(x,y)|1<x2 +y2<4}
E
P
边界 :x2 +y2 1和x2y24
连通性:
设D是开集.如果对于D 内
任何两点,都可用属于D的折线
连结起来,则称开集D 是连通
的区域:
.
连通的开集称为区域或开区 域.
闭区域:
开区域连同它的边界称为闭 区域.
E1 P1
时,总有
|(x2y2)sin 1 0|<e
x2 y2 成立,所以 lim f (x, y) 0 .
x0 y0
必须注意: (1) 二重极限存在,是指P以任何方式趋于P0时,函数都无
限接近于A (2) 如果当P以两种不同方式趋于P0时,函数趋于不同的值,
则函数的极限不存在.
例
函数f(x,y)
xy x2 y2
z=f(x,y)(或z=f(P))
其中D称为定义域,x,y 称为自变量,z 称为因变量.
例 函数z=ln(x+y)的定义域为
y x2y21
{(x,y)|x+y>0}(无界开区域);
函数zarcsin(x2y2)的定义域为
《高等数学教学课件》高数-第八章-多元函数微分学
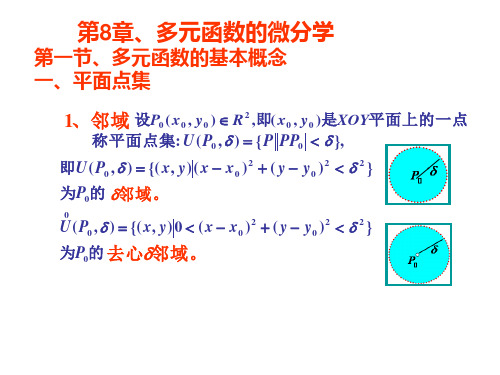
称点P为E的 外点。
边界点的定义:
若点P的任意的邻域内,既有属于E的点
也 有 不 属 于E的 点, 则 称 点P是E的 边 界 点 。
边界的定义:
E的边界点的全体称为E的 边 界 。
3、聚点、孤立点
设E是一个平面点集
聚点的定义:
若点P的任意邻域都含有E的无穷多个点,
为P0的 邻域。
0
U(P0 , ) {( x, y) 0 ( x x0 )2 ( y y0 )2 2 }
为P0的 去心邻域。
2、内点、外点、边界点
设E是一个平面点集.
内点的定义:
若点P E,并且存在P点的一个
邻域U(P, ), 使U(P, ) E,则称点P
为E的内点。
外点的定义: 若点P E,并且存在P点的一个
一切多元初等函数在其定义区域内是连续的。
例6、讨论下列函数的连续性
(1)、f
(
x,
y)
x
3 xy 2 2
y
2
x2 y2 0
解 0
x2 y2 0
当x 2 y 2 0时, f ( x, y) 3xy 是初等函数, x2 2y2
且 有 定 义, 连 续.
3kx 2
lim f ( x, y) lim
lim
x0
x2 2y4
02 2(1)4
. 2
y1
在有界闭区域上连续的多元函数的重要性质如下:
定理1、(最大最小值定理)
在有界闭区域D上连续的多元函数f , 在D上必有
最大值和最小值,亦即在D上有点P1和P2 , 使对D上任意
点P,恒有 f P1 f P f P2 , P D
课件8-1多元函数的基本概念.ppt

图形为 空间中的超曲面.
三、多元函数的极限
D
lim f ( x)=A
P
P0
x x0
lim
( x , y )( x0 , y0 )
f ( x, y)=A
(其中P( x,
y), P0( x0 , y0 ))
定义设n元函数 f (P), P D Rn, P0 是D的聚点,
若存在常数A , 对任意正数,总存在正数 ,
Rn R R R
2. 邻域
U( x0, ) x x x0
在平面上,
x0
x
P0
(
x0
,
y0
)
U( P0 , δ) ( x, y) ( x x0)2 ( y y0)2 δ (圆邻域)
在空间中, (球邻域)
U( P0 , ) (x, y, z ) (x x0)2 ( y y0)2 (z z0)2 δ
对一切 P D U (P0,δ), 都有 则称A为函数
记作
lim f (P)=A (也称为 n 重极限)
P P0
lim f (P)=A
P P0
当n =2时, 记 PP0 ( x x0 )2 ( y y0 )2
二元函数的极限可写作:
lim f ( x, y) A lim f ( x, y) A
引言
上册中讨论的函数是一元函数问题.但在 许多实际问题中往往涉及到多方面的因素, 反映在数学上就是多元函数以及多元函数 的微分和积分问题.多元函数微积分的基本 概念、理论和方法是一元函数微积分中相 应概念、理论和方法的推广与发展,它们既 有许多相似之处,又有很多本质上的不同. 学习时注意比较和区分.
2. 二重极限 lim f ( x, y) 与累次极限: x x0 y y0
多元函数的基本概念

多 元 函 数 的 基 本 概 念
纯数学问题的函数: 定义域为使运算有意义的 定义域为使运算有意义 运算有意义的
自变量取值的全体. 自变量取值的全体
10
例 求下面函数的定义域
多 元 函 数 的 基 本 概 念
1. z =
xy
x ≥ 0 x ≤ 0 解 xy ≥ 0, 即定义域为 和 y ≥ 0 y ≤ 0
•M
多 元 函 数 的 基 本 概 念
y
O
y
P
x
x
D
二元函数的图形通常是一张曲面 曲面.
13
由空间解析几何知, 由空间解析几何知 函数 如,
多 元 函 数 的 基 本 概 念
z = R2 − x2 − y2
的图形是以原点为中心, 为半径的上半球面 的图形是以原点为中心 R为半径的上半球面 为半径的上半球面. 最后指出, 从一元函数到二元函数, 在内容 最后指出 从一元函数到二元函数 和方法上都会出现一些实质性的差别, 和方法上都会出现一些实质性的差别 而多元 函数之间差异不大. 因此研究多元函数时, 函数之间差异不大 因此研究多元函数时 将以 二元函数为主. 二元函数为主
25
多
同一元函数一样, 多元函数的和、 同一元函数一样 多元函数的和、差、 积、商(分母不为零)及复合仍是连续的. 分母不为零)及复合仍是连续的 每个自变量的基本初等函数经有限次四则 运算和有限次复合, 运算和有限次复合, 由一个式子表达的函数 称为多元初等函数, 在它们的定义域的内点 称为多元初等函数 处均连续. 处均连续
P → P0
0 , y0 )
f ( x , y ) = A 或 lim f ( x, y )
x → x0 y → y0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
去心邻域的概念也可搬过来。
中去心邻域的定义空间n
R
0 ) ,3 ,2 ( 0为实数,则称集合,设>=∈δ⋯n R X n
}
),d(0 | {),U(00δδ<<=X X X X
),(U ˆ 00。
去心邻域,记为的中点为δδX X R n
2. 开集、闭集、有界集、无界集
聚点
O
E
E 中的有界集
2
R
) U(O,E r ⊂
无界集
},|),{(E +∞<<∞−≤≤=y b x a y x
单连通集
分为
连通集
复连通集
单连通 复连通
不连通
区域是连通开集. 区域是连通开集.
区域 Ω 的内点及边界点都是它的聚点. 区域 Ω 的内点及边界点都是它的聚点.
, 则称为一连通开集若非空集n
R ⊂Ω
. 中的区域为n
R Ω注意:集合的聚点
不一定属于集合.
二元函数 的图形
),(y x f z = 设函数
的定义域为,对于任意取定的
y x P ∈),(,对应的函数值为
,(y
x f z =,这样,以为横坐标、为纵坐
标、为竖坐标在空间就确定一点,
当取遍上一切点时,得一个空间点集,这个点集称
为二元函数的图形.
(如下页图)
二元函数的图形通常是一张曲面.
x
y
z
o
xy
z sin =例如,图形如右图.
2
222a
z y x =++例如,如右图,为球面.
}.
),{(2
2
2
a y x y x D ≤+=2
2
2
y
x a z −−=.
2
2
2
y x a z −−−=单值分支:
三. 多元函数的极限及极限的运算
x
x
y
a
y =ε
+=a y ε
−=a y ()
..
()
a
)
(x f .
x O
)
(x f y =P
),(U ˆ0
δx )
,U(εa 0
x x →.
x
x
y
a
y =ε
+=a y ε
−=a y ()
..
()
a
)
(x f .
x O
)
(x f y =P
),(U ˆ0
δx )
,U(εa 0
x x →.
),(U ˆ0δx x ∈
x
x
y
a
y =ε
+=a y ε
−=a y ()
..
(
)
a )
(x f .
x O
)
(x f y =P
),(U ˆ0
δx ),U(εa 0
x x →.
),(U ˆ0δx x ∈),U(
)(εa x f ∈
二元函数极限的定义
该例还说明一个问题
对此你有什么想法 ?
对此你有什么想法 ?,
2
x k y =虽然沿无穷多个方向:,
, )0,0(),( 函数均有极限时当→y x . ),( lim 00不存在但函数的极限y x f y x →→
“无穷多个方向”不等于“任意方向”.
可利用方向性来判别
多元函数的极限不存在.。
