直角坐标系下牛顿法潮流计算
牛顿法最优潮流

最优潮流
总结分析
综上所述,若一个电力系统含有N个节点,选取第N个作平衡节点, 剩余n=N-1各节点中有r个节点是PV节点,有n-r个节点是PQ节点,因 此出平衡节点外,有n个节点注入有功P,有n-r个节点注入无功Q,有 r个节点的电压是已知的。在直角坐标系下,待求未知数共有2n个,
x 代求变量 e f e1e2 e2 ...en f1 f 2 ... f 3 P P sp e a f b i 1, 2, 3,...n i i i i i 潮流方程线性化 sp Qi Q f i ai ei bi i 1, 2, 3,...n r 2 sp 2 2 2 Vi Vi ei f i i n r 1,......n
其近似解与精确解分别相差
x1 , x2 ,..., xn
f1 ( x1 0 x1 , x2 0 x2 ,....... xn 0 xn ) y1 0 0 0 f 2 ( x1 x1 , x2 x2 ,....... xn xn ) y2 ........ 0 0 0 f ( x x , x x ,....... x x ) y n 1 1 2 2 n n n
数学描述
潮流计算
最优潮流
总结分析
为了便于用迭代法解方程组,需要将上述功率方程改 写成功率平衡方程,并对功率平衡方程求偏导,得出 对应的雅可比矩阵,给未知节点赋电压初值,一般为 额定电压,将初值带入功率平衡方程,得到功率不平 衡量,这样由功率不平衡量、雅可比矩阵、节点电压 平衡量(未知的)构成了误差方程,解误差方程,得 到节点电压不平衡量,节点电压加上节点电压不平衡 量构成新的节点电压初值,将新的初值带入原来的功 率平衡方程,并重新形成雅可比矩阵,然后计算新的 电压不平衡量,这样不断迭代,不断修正,一般迭代 三到五次就能收敛。
直角坐标系下牛顿法潮流计算

直角坐标系下牛顿法潮流计算1电力系统潮流计算潮流计算是电力系统分析中的一种最基本的计算,它的任务是对给定的运行条件确定系统的运行状态,如母线上的电压(幅值及相角)、网络中的功率分布及功率损耗等。
在电力系统规划设计和现有电力系统运行方式的研究中,都需要利用潮流计算来定量地分析比较供电方案或运行方式的合理性.可靠性和经济性。
此外,电力系统潮流计算也是计算系统动态稳定和静态稳定的基础。
2节点导纳矩阵的形成在图1(a )的简单电力系统中,若略去变压器的励磁功率和线路电容,负荷用阻抗表示,便可以得到一个有5个节点(包括零电位点)和7条支路的等值网络,如图1(b )所示。
将接于节点1和4的电势源和阻抗的串联组合变换成等值的电流源和导纳的并联组合,变得到图1(c )的等值网络,其中1101I y E =和4404I y E =分别称为节点1和4的注入电流源。
(a)24İİ4(c)图1 电力系统及其网络以零电位点作为计算节点电压的参考点,根据基尔霍夫定律,可以写出4个独立节点的电流平衡方程如下:1011212112212022323242423323434244234434044()()()()0()()0()()y U y U U I y U U y U y U U y U U y U U y U U y U U y U U y U I ⎫+-=⎪-++-+-=⎪⎬-+-=⎪⎪-+-+=⎭ (2-1) 上述方程组经过整理可以写成1111221211222233244322333344422433444400Y U Y U I Y U Y U Y U Y U Y U Y U Y U Y U Y U Y U I ⎫+ =⎪+++=⎪⎬++=⎪⎪ ++=⎭ (2-2)式中,111012Y y y =+;2220232412Y y y y y =+++;332334Y y y =+;44402434Y y y y =++;122112Y Y y ==-;233223Y Y y ==-;244224Y Y y ==-;344334Y Y y ==-。
C语言潮流计算-牛顿-拉夫逊法(直角坐标)

(k )
计算平衡节点功率 S s 和线路功率
~
停止
1 / 20
程序代码如下:
#include<stdio.h> #include<stdlib.h> #include<math.h> #include<string.h> #include<conio.h> struct linetype // 线路参数 { int jiedian[2]; // 若为变压器,则 左端为“低”压侧(换算成Π型等值电路),变压器的阻抗在“低”压侧 double R,X,K,B0; }line[30]; struct Nodetype // 节点功率 { int lei; // PQ 定义 1,PV 定义 2,平衡节点 定义 3 int jie; // 节点编号 double P,Q; double y1,y2; // 初始电压 }poin[30]; int point,road; // 节点数 point 支路数 road int p1,p2; // PQ PV 节点数目 //************************************************* 自定义 函数 *************************************************************** void chargescreen() // 调节屏幕 { int mode; printf("\t 请选择界面模式: ①. 106*45 ②. 134*45\n\t>>"); a: scanf("%d",&mode); if(mode!=1 && mode!=2) { printf("\n\t 错误,请重新输入...\n\t>>"); goto a; } printf("\n\t"); system("pause"); if(mode==1) system("mode con:cols=106 lines=45"); // 调整屏幕大小 else system("mode con:cols=134 lines=45"); } void pqpv() // 统计 PQ、PV 节点 数目
关于直角坐标牛拉法系统潮流分布计算的答辩

关于直角坐标牛拉法系统潮流分布计算的答辩关于直角坐标牛拉法系统潮流分布计算的答辩一、引言直角坐标牛拉法是一种常用的电力系统潮流计算方法,用于计算电力系统中各节点的电压和功率分布。
本文将从算法原理、计算步骤、应用场景等方面进行阐述和答辩。
二、算法原理直角坐标牛拉法基于功率平衡方程和节点电压方程,通过迭代求解的方式,逐步逼近系统的潮流分布。
其核心思想是将电压和功率分别表示为实部和虚部,通过复数运算来求解未知量。
具体而言,直角坐标牛拉法将电流和导纳分别表示为复数形式,利用复数的乘法和除法运算,将节点电流和导纳联系起来,从而得到节点电压和功率的计算结果。
三、计算步骤直角坐标牛拉法的计算步骤包括以下几个部分:1. 初始化:给定电网拓扑结构、节点导纳和负荷信息,初始化节点电压和功率。
2. 潮流计算:根据功率平衡方程和节点电压方程,通过迭代计算节点电压和功率。
具体而言,每次迭代中,首先根据节点电压和导纳计算节点电流;然后,根据节点电流和导纳计算节点电压;再根据节点电压和导纳计算节点功率。
通过多次迭代,直到收敛为止。
3. 收敛判断:判断节点电压和功率的迭代计算是否收敛。
一般来说,可以通过判断节点电压和功率的变化量是否小于设定的收敛阈值来进行判断。
若满足收敛条件,则停止迭代;否则,继续迭代。
4. 输出结果:输出最终的节点电压和功率分布结果。
根据需要,还可以输出其他相关信息,如潮流方向、线路功率损耗等。
四、应用场景直角坐标牛拉法广泛应用于电力系统潮流计算和分析。
具体而言,它可以用于以下几个方面:1. 网络规划:通过潮流计算,可以评估电力系统的稳定性和可靠性,为电网规划提供依据。
例如,可以通过潮流计算来确定新建变电站的容量和位置,优化电网结构。
2. 运行调度:在电力系统的日常运行中,潮流计算可以用于实时监测和调度。
通过潮流计算,可以了解各节点的电压和功率情况,及时发现问题并采取措施,确保电力系统的安全稳定运行。
3. 短路分析:在电力系统发生短路故障时,潮流计算可以用于分析故障电流的分布情况,确定故障点和故障线路,为故障处理和保护调整提供参考。
直角坐标牛顿-拉夫逊潮流算法的简化

直角坐标牛顿-拉夫逊潮流算法的简化
杨道驰;周步祥;杜小兵
【期刊名称】《沈阳工程学院学报(自然科学版)》
【年(卷),期】2008(004)001
【摘要】根据电力系统的运行特征提出新的假设,改进了牛顿-拉夫逊潮流算法中修正方程式的建立,继而对直角坐标下牛顿-拉夫逊潮流算法的雅可比矩阵进行简化,并提出用最优乘子解决病态系统.13节点算例计算结果表明,该法具有良好的收敛性,可减少内存占有量并具有较高的计算速度.
【总页数】4页(P37-40)
【作者】杨道驰;周步祥;杜小兵
【作者单位】四川大学,电气信息学院,成都,610065;蚌埠坦克学院,安徽,蚌
埠,233013;四川大学,电气信息学院,成都,610065;四川大学,电气信息学院,成
都,610065
【正文语种】中文
【中图分类】TM744
【相关文献】
1.简化的牛顿——拉夫逊潮流计算法 [J], 李宝国;巴金祥;鲁宝春
2.直角坐标牛顿——拉夫逊法潮流计算新解法 [J], 陈恳
3.直角坐标牛顿拉夫逊潮流计算的简化方法 [J], 屈思毅
4.直角坐标牛顿——拉夫逊法潮流计算的改进算法 [J], 曹春阳
5.对直角坐标型牛顿—拉夫逊法潮流计算的几点探讨 [J], 陈恳
因版权原因,仅展示原文概要,查看原文内容请购买。
例4牛顿拉夫逊法潮流例题

例3-5利用牛顿-拉夫逊法直角坐标方式计算例3-3所示网络潮流分布情况。
解:确定例3-3系统雅可比矩阵的维数。
系统有n = 5条母线(节点),采用直角坐标方法求解时组成2(n -1) =8个方程,J(i )维数为8×8。
按题意要求,该系统中,节点1为平衡节点,保持U 1=1+j0为定值,2,4,5为PQ 节点,3为PU 节点,U 3=1.05+j0。
(1)赋初值由已知可知平衡节点:111.0,0e f == 对PQ、PU节点赋电压初值:(0)(0)(0)(0)(0)(0)(0)(0)245245331.0,0, 1.05,0e e e f f f e f ========(2)求PQ 节点有功、无功不平衡量,PU 节点有功、电压不平衡量()()(){}55(0)(0)(0)(0)(0)(0)(0)(0)222222222211()()8.0 1.00 2.6783 1.0000.8928 1.00 1.7855 1.0008.0s s j jj j jj j j j j P P P P e GeB f f Gf B e ==∆=-=---+=--⨯+⨯-++-⨯-+-⨯-+=-⎡⎤⎣⎦∑∑()()(){}55(0)(0)(0)(0)(0)(0)(0)(0)222222222211(0)(0)(0)(0)(0)(0)333333333()()2.80 1.00028.4590 1.0009.9197 1.0019.8393 1.0 1.5()(s s j jj j jj j j j j s s j jj j jQ Q Q Q f GeB f e Gf B e P P P P e GeB f f G==∆=-=--++=---⨯+-⨯+++⨯++⨯=-⎡⎤⎣⎦∆=-=---∑∑()(){}()()55(0)(0)311(0)22(0)22(0)2(0)222333333(0)(0)(0)(0)(0)(0)(0)4444444444)4.4 1.05007.4580 1.0507.4580 1.0000 4.00851.05 1.0500()(j j j j j s s s s j jj j jj j f B e U U U U e f P P P P e GeB f f Gf B e ==+=-⨯++⨯-+-⨯-++=⎡⎤⎣⎦∆=-=-+=-+=∆=-=---+∑∑()()()(){}()55(0)1155(0)(0)(0)(0)(0)(0)(0)(0)444444444411)0 1.000.8928 1.007.4580 1.05011.9219 1.00 3.57111.0000.3729()()00 1.0009.9197 1.009j j j s s j jj j jj j j j j Q Q Q Q f GeB f e Gf B e =====-⨯+-⨯-+-⨯-+⨯-+-⨯-+=⎡⎤⎣⎦∆=-=--++=--⨯++⨯++∑∑∑∑()()(){}()()()(){}55(0)(0)(0)(0)(0)(0)(0)(0)5555555555119.4406 1.050147.9589 1.0039.6768 1.0 6.052()()0 1.0 3.7290 1.00 1.7855 1.000 3.57111.009.0856 1.000s s j jj j jj j j j j P P P P e GeB f f Gf B e ==⨯+-⨯++⨯=⎡⎤⎣⎦∆=-=---+=-⨯-⨯-+-⨯-++-⨯-+⨯-+=⎡⎤⎣⎦∑∑()()()(){}55(0)(0)(0)(0)(0)(0)(0)(0)5555555555110()()00 1.0049.7203 1.0019.8393 1.00039.6786 1.00108.5782 1.00.66s s j jj j jj j j j j Q Q Q Q f GeB f e Gf B e ==∆=-=--++=--⨯+⨯++⨯+++⨯+-⨯=⎡⎤⎣⎦∑∑(3)计算雅可比矩阵以节点2(PQ )有功、无功功率和节点3(PU )电压幅值分别对各节点电压实部、虚部求导为例,其他节点的求解过程略。
潮流计算直角坐标andPQ

n
n (2Gii GijfBii eiBe j ) (GBf je Gii )f Bii ei U i2 ( f i j ) ij ij ii i Bij e j i 2 f i j G 1(Gij e j Bij f j ) 1 ii ei Bii f i j f
当i=j时
n Pi e (Gij e j Bij f j ) ( Gii ei Bii f i ) j 1 i n Pi (Gij f j Bij e j ) Bii ei Gii f i f i j 1 n Q i (Gij f j Bij e j ) Gij f i Bii ei e i j 1 n Qi (G e B f ) B f G e ij j ij j ii i ii i f i j 1 2 U i e 2ei i U i2 2 f i f 1
F J X ( k 1) X X ( k ) X ( k )
迭代收敛条件:
max(| Fi |)
四、 直角坐标下的牛顿拉夫逊法潮流计算
计算 i j 时雅可比矩阵各元素
n n Pi PGi PLi ei (Gij e j Bij f j ) f i (Gij f j Bij e j ) 0 j 1 j 1 n Qi QGi QLi f i (Gij e j Bij f j ) ei (Gij f j Bij e j ) 0 j 1 U 2 U 2 U U 2 e 2 f 2 0 si i si i i i
2 U m 1 f 1
牛顿-拉夫逊算法(极坐标)潮流计算算例

极坐标系下的潮流计算
潮流计算
在电力系统中,潮流计算是一种常用的计算方法,用于确定在给定网络结构和参数下,各节点的电压 、电流和功率分布。在极坐标系下进行潮流计算,可以更好地描述和分析电力系统的电磁场分布和变 化。
极坐标系下的潮流计算特点
在极坐标系下进行潮流计算,可以更直观地描述电力线路的走向和角度变化,更好地反映电力系统的 复杂性和实际情况。此外,极坐标系下的潮流计算还可以方便地处理电力系统的非对称性和不对称故 障等问题。
03
CATALOGUE
极坐标系下的牛顿-拉夫逊算法
极坐标系简介
极坐标系
一种二维坐标系统,由一个原点(称为极点)和一条从极点出发的射线(称为 极轴)组成。在极坐标系中,点P的位置由一个角度θ和一个距离r确定。
极坐标系的应用
极坐标系广泛应用于物理学、工程学、经济学等领域,特别是在电力系统和通 信网络中,用于描述电场、磁场、电流和电压等物理量的分布和变化。
极坐标形式
将电力系统的节点和支路参数以极坐 标形式表示,将实数问题转化为复数 问题,简化计算过程并提高计算效率 。
02
CATALOGUE
牛顿-拉夫逊算法原理
算法概述
牛顿-拉夫逊算法是一种迭代算法,用于求解非线性方程组。在电力系统中,它 被广泛应用于潮流计算,以求解电力网络中的电压、电流和功率等参数。
准确的结果。
通过极坐标系的处理,算法 能够更好地处理电力系统的 复杂结构和不对称性,提高 了计算的准确性和适应性。
算例分析表明,该算法在处理 大规模电力系统时仍具有较好 的性能,能够满足实际应用的
需求。
展望
进一步研究牛顿-拉夫逊算法在极坐标 系下的收敛性分析,探讨收敛速度与电 力系统规模、结构和参数之间的关系, 为算法的优后的电压、电流和功 率等参数。
极坐标的牛顿拉夫逊法潮流计算

%主程序"PowerFlow_NR.m"function [bus_res,S_res] = PowerFlow_NR_2 % 牛顿-拉夫逊法解潮流方程的主程序[bus,line] = OpDF_; % 打开数据文件的子程序,返回bus(节点数据)和line(线路数据)回主程序[nb,mb]=size(bus);[nl,ml]=size(line); % 计算bus和line矩阵的行数和列数[bus,line,nPQ,nPV,nodenum] = Num_(bus,line); % 对节点重新排序的子程序Y = y_(bus,line); % 计算节点导纳矩阵的子程序myf = fopen('Result.m','w');fprintf(myf,'\n\n');fclose(myf); % 在当前目录下生成“Result.m”文件,写入节点导纳矩阵format longEPS = 1.0e-10; % 设定误差精度for t = 1:100 % 开始迭代计算,设定最大迭代次数为100,以便不收敛情况下及时跳出[dP,dQ] = dPQ_(Y,bus,nPQ,nPV); % 计算功率偏差dP和dQ的子程序J = Jac_(bus,Y,nPQ); % 计算雅克比矩阵的子程序UD = zeros(nPQ,nPQ);for i = 1:nPQUD(i,i) = bus(i,2); % 生成电压对角矩阵enddAngU = J \ [dP;dQ];dAng = dAngU(1:nb-1,1); % 计算相角修正量dU = UD*(dAngU(nb:nb+nPQ-1,1)); % 计算电压修正量bus(1:nPQ,2) = bus(1:nPQ,2) - dU; % 修正电压bus(1:nb-1,3) = bus(1:nb-1,3) - dAng; % 修正相角if (max(abs(dU))<EPS)&(max(abs(dAng))<EPS)breakend % 判断是否满足精度误差,如满足则跳出,否则返回继续迭代endbus = PQ_(bus,Y,nPQ,nPV); % 计算每个节点的有功和无功注入的子程序[bus,line] = ReNum_(bus,line,nodenum); % 对节点恢复编号的子程序YtYm = YtYm_(line); % 计算线路的等效Yt和Ym的子程序,以计算线路潮流bus_res = bus_res_(bus); % 计算节点数据结果的子程序S_res = S_res_(bus,line,YtYm); % 计算线路潮流的子程序myf = fopen('Result.m','a');fprintf(myf,'---------------牛顿-拉夫逊法潮流计算结果----------\n\n 节点计算结果:\n节点节点电压节点相角(角度)节点注入功率\n');for i = 1:nbfprintf(myf,'%2.0f ',bus_res(i,1));fprintf(myf,'.6f ',bus_res(i,2));fprintf(myf,'.6f ',bus_res(i,3));fprintf(myf,'.6f + j .6f\n',real(bus_res(i,4)),imag(bus_res(i,4)));endfprintf(myf,'\n线路计算结果:\n节点I 节点J 线路功率S(I,J)线路功率S(J,I) 线路损耗dS(I,J)\n');for i = 1:nlfprintf(myf,'%2.0f ',S_res(i,1));fprintf(myf,'%2.0f ',S_res(i,2));fprintf(myf,'.6f + j .6f ',real(S_res(i,3)),imag(S_res(i,3)));fprintf(myf,'.6f + j .6f ',real(S_res(i,4)),imag(S_res(i,4)));fprintf(myf,'.6f + j .6f\n',real(S_res(i,5)),imag(S_res(i,5)));endfclose(myf); % 迭代结束后继续在“Result.m”写入节点计算结果和线路计算结果程序结束bus = [1 1.00 0.00 -0.30 -0.18 1;2 1.00 0.00 -0.55 -0.13 1;3 1.10 0.00 0.50 0.00 2;4 1.05 0.00 0.00 0.00 3]line = [1 2 0.10 0.40 0.0 0.01528 0;4 2 0.08 0.40 0.0 0.01413 0;1 4 0.12 0.50 0.0 0.0192 0;3 1 0.00 0.3 0.0 0.0 -1.1]----------------------------------------牛顿-拉夫逊法潮流计算结果-------------------------------------------- 节点计算结果:节点节点电压节点相角(角度)节点注入功率1 0.984674906330845 -0.500170385513657 -0.300000000000000 - 0.180000000000000i2 0.964797665550885 -6.450305258622626 -0.550000000000000 - 0.130000000000000i3 1.100000000000000 6.732349388989963 0.500000000000000 + 0.093411003244513i4 1.050000000000000 0 0.367882692523292 + 0.264698252215732i 线路计算结果:节点I 节点J 线路功率S(I,J) 线路功率S(J,I) 线路损耗dS(I,J)1 2 0.246244-j0.014651 -0.239990+j0.010627 0.006254- j0.0040241 3 -0.500001-j0.029264 0.500000+j0.093409 -0.000001+j0.0641451 4 -0.046244-j0.136088 0.048216+j0.104522 0.001972-j0.0315662 4 -0.310010-j0.140627 0.319666+j0.160176 0.009656+j0.019549%子程序1 "OpDF_.m" 作用为打开数据文件function [bus,line] = OpDF_[dfile,pathname]=uigetfile('*.m','Select Data File'); % 数据文件类型为m文件,窗口标题为“Select Data File”if pathname == 0error(' you must select a valid data file') % 如果没有选择有效文件,则出现错误提示elselfile =length(dfile); % 读取文件字符串长度eval(dfile(1:lfile-2)); % 去除后缀,打开文件!注意!新浪博客中"eval"函数会自动加上"_r"后缀,此处的函数名是"eval"而不是"eval_r",拷贝后请去除"_r"后缀end%子程序2 "Num.m" 作用为对节点重排序,并修改相应的线路数据function [bus,line,nPQ,nPV,nodenum] = Num_(bus,line)[nb,mb]=size(bus);[nl,ml]=size(line);nSW = 0; % nSW为平衡节点个数nPV = 0; % nPV为PV节点个数nPQ = 0; % nPQ为PQ节点个数for i = 1:nb, % nb为总节点数type= bus(i,6);if type == 3,nSW = nSW + 1;SW(nSW,:)=bus(i,:); % 计算并储存平衡节点elseif type == 2,nPV = nPV +1;PV(nPV,:)=bus(i,:); % 计算并储存PV节点elsenPQ = nPQ + 1;PQ(nPQ,:)=bus(i,:); % 计算并储存PQ节点endendbus=[PQ;PV;SW]; % 对bus矩阵按PQ、PV、平衡节点的顺序重新排序nodenum=[[1:nb]' bus(:,1)];% 生成新旧节点对照表for i=1:nlfor j=1:2for k=1:nbif line(i,j)==nodenum(k,2)line(i,j)=nodenum(k,1);breakendendendend % 按排序以后的节点顺序对line矩阵重新编号%子程序3 "y_.m" 作用为计算节点导纳矩阵function Y = y_(bus,line)[nb,mb]=size(bus);[nl,ml]=size(line);Y=zeros(nb,nb); % 对导纳矩阵赋初值0for k=1:nlI=line(k,1);J=line(k,2);Zt=line(k,3)+j*line(k,4); % 读入线路参数if Zt~=0Yt=1/Zt; % 接地支路不计算YtendYm=line(k,5)+j*line(k,6);K=line(k,7);if (K==0)&(J~=0) % 普通线路: K=0Y(I,I)=Y(I,I)+Yt+Ym;Y(J,J)=Y(J,J)+Yt+Ym;Y(I,J)=Y(I,J)-Yt;Y(J,I)=Y(I,J);endif (K==0)&(J==0) % 对地支路: K=0,J=0,R=X=0Y(I,I)=Y(I,I)+Ym;endif K>0 % 变压器线路: Zt和Ym为折算到i侧的值,K在j侧Y(I,I)=Y(I,I)+Yt+Ym;Y(J,J)=Y(J,J)+Yt/K/K;Y(I,J)=Y(I,J)-Yt/K;Y(J,I)=Y(I,J);endif K<0 % 变压器线路: Zt和Ym为折算到K侧的值,K在i侧Y(I,I)=Y(I,I)+Yt+Ym;Y(J,J)=Y(J,J)+K*K*Yt;Y(I,J)=Y(I,J)+K*Yt;Y(J,I)=Y(I,J);endend%子程序4 "dPQ_.m" 作用为计算功率偏差function [dP,dQ] =dPQ_(Y,bus,nPQ,nPV) % nPQ、nPV为相应节点个数n = nPQ + nPV +1; % 总节点个数dP = bus(1:n-1,4);dQ = bus(1:nPQ,5); % 对dP和dQ赋初值PV节点不需计算dQ 平衡节点不参与计算for i = 1:n-1for j = 1:ndP(i,1) =dP(i,1)-bus(i,2)*bus(j,2)*(real(Y(i,j))*cos(bus(i,3)-bus(j,3))+imag(Y(i,j))*sin(bus(i,3)-bus(j,3)));if i<nPQ+1dQ(i,1) = dQ(i,1)-bus(i,2)*bus(j,2)*(real(Y(i,j))*sin(bus(i,3)-bus(j,3))-imag(Y(i,j))*cos(bus(i,3)-bus(j,3)));endendend % 利用循环计算求取dP和dQ%子程序5 "Jac_.m" 作用为计算雅克比矩阵function J = Jac_(bus,Y,nPQ)[nb,mb]=size(bus);H = zeros(nb-1,nb-1);N = zeros(nb-1,nPQ);K = zeros(nPQ,nb-1);L = zeros(nPQ,nPQ); % 将雅克比矩阵分块,即:J = [H N; K L],并初始化Qi = zeros(nb-1,1);Pi = zeros(nb-1,1);for i = 1:nb-1for j = 1:nbPi(i,1)=Pi(i,1)+bus(i,2)*bus(j,2)*(real(Y(i,j))*cos(bus(i,3)-bus(j,3))+imag(Y(i,j))*sin(bus(i,3)-bus(j,3) ));Qi(i,1)=Qi(i,1)+bus(i,2)*bus(j,2)*(real(Y(i,j))*sin(bus(i,3)-bus(j,3))-imag(Y(i,j))*cos(bus(i,3)-bus(j,3) ));endend % 初始化并计算Qi和Pifor i = 1:nb-1for j = 1:nb-1if i~=jH(i,j)=-bus(i,2)*bus(j,2)*(real(Y(i,j))*sin(bus(i,3)-bus(j,3))-imag(Y(i,j))*cos(bus(i,3)-bus(j,3)));elseH(i,j)=Qi(i,1)+imag(Y(i,j))*((bus(i,2))^2);end % 分别计算H矩阵的对角及非对角元素if j < nPQ+1if i~=jN(i,j)=-bus(i,2)*bus(j,2)*(real(Y(i,j))*cos(bus(i,3)-bus(j,3))+imag(Y(i,j))*sin(bus(i,3)-bus(j,3)));elseN(i,j)=-Pi(i,1)-real(Y(i,j))*((bus(i,2))^2);endend % 分别计算N矩阵的对角及非对角元素if i < nPQ+1if i~=jK(i,j)=bus(i,2)*bus(j,2)*(real(Y(i,j))*cos(bus(i,3)-bus(j,3))+imag(Y(i,j))*sin(bus(i,3)-bus(j,3)));elseK(i,j)=-Pi(i,1)+real(Y(i,j))*((bus(i,2))^2);end % 分别计算K矩阵的对角及非对角元素if j < nPQ+1if i~=jL(i,j)=-bus(i,2)*bus(j,2)*(real(Y(i,j))*sin(bus(i,3)-bus(j,3))-imag(Y(i,j))*cos(bus(i,3)-bus(j,3)));elseL(i,j)=-Qi(i,1)+imag(Y(i,j))*((bus(i,2))^2);endend % 分别计算L矩阵的对角及非对角元素endendendJ = [H N; K L]; % 生成雅克比矩阵%子程序6 "PQ_.m" 作用为计算每个节点的功率注入function bus = PQ_(bus,Y,nPQ,nPV)n = nPQ+nPV+1; % n为总节点数for i = nPQ+1:n-1for j = 1:nbus(i,5)=bus(i,5)+bus(i,2)*bus(j,2)*(real(Y(i,j))*sin(bus(i,3)-bus(j,3))-imag(Y(i,j))*cos(bus(i,3)-bus(j, 3)));endend % 利用公式计算PV节点的无功注入for j =1:nbus(n,4)=bus(n,4)+bus(n,2)*bus(j,2)*(real(Y(n,j))*cos(bus(n,3)-bus(j,3))+imag(Y(n,j))*sin(bus(n,3)-b us(j,3)));bus(n,5)=bus(n,5)+bus(n,2)*bus(j,2)*(real(Y(n,j))*sin(bus(n,3)-bus(j,3))-imag(Y(n,j))*cos(bus(n,3)-b us(j,3)));end % 计算平衡节点的无功及有功注入%子程序7 "ReNum_.m" 作用为对节点和线路数据恢复编号function [bus,line] = ReNum_(bus,line,nodenum)[nb,mb]=size(bus);[nl,ml]=size(line);bus_temp = zeros(nb,mb); % bus_temp矩阵用于临时存放bus矩阵的数据k = 1;for i = 1 :nbfor j = 1 : nbif bus(j,1) == kbus_temp(k,:) = bus(j,:);k = k + 1;endendend % 利用bus矩阵的首列编号重新对bus矩阵排序并存入bus_temp矩阵中bus = bus_temp; % 重新赋值回bus,完成bus矩阵的重新编号for i=1:nlfor j=1:2for k=1:nbif line(i,j)==nodenum(k,1)line(i,j)=nodenum(k,2);breakendendendend % 恢复line的编号%子程序8 "YtYm_.m" 作用为计算线路的等效Yt和Ym,以计算线路潮流function YtYm = YtYm_(line)[nl,ml]=size(line);YtYm = zeros(nl,5); % 对YtYm矩阵赋初值0YtYm(:,1:2) = line(:,1:2); % 矩阵前两列为线路两段节点编号,后三列分别为线路等效Yt,i侧的等效Ym,j侧的等效Ymj = sqrt(-1);for k=1:nlI=line(k,1);J=line(k,2);Zt=line(k,3)+j*line(k,4);if Zt~=0Yt=1/Zt;endYm=line(k,5)+j*line(k,6);K=line(k,7);if (K==0)&(J~=0) % 普通线路: K=0YtYm(k,3) = Yt;YtYm(k,4) = Ym;YtYm(k,5) = Ym;endif (K==0)&(J==0) % 对地支路: K=0,J=0,R=X=0YtYm(k,4) = Ym;endif K>0 % 变压器线路: Zt和Ym为折算到i侧的值,K在j侧YtYm(k,3) = Yt/K;YtYm(k,4) = Ym+Yt*(K-1)/K;YtYm(k,5) = Yt*(1-K)/K/K;endif K<0 % 变压器线路: Zt和Ym为折算到K侧的值,K在i侧YtYm(k,3) = -Yt*K;YtYm(k,4) = Ym+Yt*(1+K);YtYm(k,5) = Yt*(K^2+K);endend%子程序9 "bus_res_.m" 计算并返回节点数据结果function bus_res = bus_res_(bus);[nb,mb]=size(bus);bus_res = zeros(nb,4); % bus_res矩阵储存着节点计算结果bus_res(:,1:2) = bus(:,1:2);bus_res(:,3) = bus(:,3) *180 / pi; % 相角采用角度制bus_res(:,4) = bus(:,4) + (sqrt(-1))*bus(:,5); % 注入功率%子程序10 "S_res_.m" 计算并返回线路潮流function S_res = S_res_(bus,line,YtYm)[nl,ml]=size(line);S_res = zeros(nl,5); % S_res矩阵储存着线路潮流计算结果S_res(:,1:2) = line(:,1:2); % 前两列为节点编号for k=1:nlI = S_res(k,1);J = S_res(k,2);if (J~=0)&(I~=0)S_res(k,3)=bus(I,2)^2*(conj(YtYm(k,3))+conj(YtYm(k,4)))-bus(I,2)*bus(J,2)*(cos(bus(I,3))+j*sin(bu s(I,3)))*(conj(cos(bus(J,3))+j*sin(bus(J,3))))*conj(YtYm(k,3));S_res(k,4)=bus(J,2)^2*(conj(YtYm(k,3))+conj(YtYm(k,5)))-bus(I,2)*bus(J,2)*(conj(cos(bus(I,3))+j*s in(bus(I,3))))*(cos(bus(J,3))+j*sin(bus(J,3)))*conj(YtYm(k,3));S_res(k,5)=S_res(k,3) + S_res(k,4); % 利用公式计算非接地支路的潮流elseif J==0S_res(k,3)=bus(I,2)^2*conj(YtYm(k,4));S_res(k,5)=S_res(k,3)+S_res(k,4);elseS_res(k,4)=bus(J,2)^2*conj(YtYm(k,5));S_res(k,5)=S_res(k,3)+S_res(k,4); % 利用公式计算接地支路的潮流endend。
直角坐标与极坐标牛顿法潮流计算速度的比较

况下 ,尽管极 坐标 牛顿法 中的方程数和迭代次数可能均少 于直角 坐标牛顿法 ,但无论 系统 中 PV节点数 多少 ,直角
坐标 牛顿法的潮流计算速度均快于极坐标 牛顿法。对 IEEE一30、一57、一118节点 系统进行 编程计算结 果表 明 ,直
角坐标牛顿法 的计算效率远高 于极 坐标 牛顿法 ,尤其 在运 用稀 疏矩阵技术后 。
第 38卷第 1期 2016年 3月
南昌大学学报 (工科版 ) Jour nal of Nanchang University(Engineer ing& Technology)
文 章 编 号 :1006—0456(2016)01—0098—05
Vo1.38 No.1 M ar.2016
SHAO Weizhe,WANG Yujun,WAN Xinru,GONG Jiawei,CHEN Ken
(School of Information Engineer ing,Nanchang University,Nanchang 33003 1,China)
Abstract:The comparison of the calculating speeds on Newton—Raphson power flow method in rectangular and polar coordinates was presented in the paper,which included the amount of the equations solved,the calculating a— mount of the elements in Jacobian matrix,the calculation of tr iangle function,the iteration number,the amount of PV buses in the system and SO on.It was obvious that the number of PV buses in the system played a vital role in deci- ding the calculating speeds with Newton method in rectangular and polar coordinates.W ithout considering the ele— ments’ sparsity,if the supposing that the amount of PV buses in the system was low ,the calculating speed of Newton method in rectangu lar coordinates would be faster than the speed in polar coordinates.On the contrary,suppose that the am ount of PV buses in the system was high,then it would lead to a opposite result.W ith the elements’ sparsity considered,even though the amount of the equations solved and the iteration num ber with Newton m ethod in polar coordinates was less than with Newton method in rectangular coordinates.But whatever the amount of PV buses in the system was more or less,the calculating speed with Newton m ethod in rectangular coordinates was always faster than the speed in polar coordinates.The results of programming and calculating the systems of IEEE 一30、一57、
牛顿拉夫逊法潮流计算(直角坐标)

function PowerFlowNRRec(linedatabusdataerror)%节点标号无特殊要求clcif nargin < 1% linedata = [% 1 2 0.1 0.4 0.01528 1;% 1 3 0 0.3 0 1.1;% 1 4 0.12 0.5 0.01920 1;% 2 4 0.08 0.40 0.01413 1];% busdata = [% 1 0 -0.30 -0.18 1 0;% 2 0 -0.55 -0.13 1 0;% 3 2 0.5 0 1.10 0;% 4 1 0 0 1.05 0;];linedata = [1 4 0.1 0.4 0.01528 1;1 3 0 0.3 0 1.1;1 2 0.12 0.5 0.01920 1;4 2 0.08 0.40 0.01413 1];busdata = [1 0 -0.30 -0.18 1 0;4 0 -0.55 -0.13 1 0;3 2 0.5 0 1.10 0;2 1 0 0 1.05 0;];endif nargin < 3error = 10^-5;endclc%优化节点排序pqbus = find(busdata(:2)==0);pvbus = find(busdata(:2)==2);baxxxxsebus = find(busdata(:2)==1);bussort = [pqbus' pvbus' baxxxxsebus'];Num = busdata(bussort1);%对节点进行重新排列,使其排列顺序为 PQ节点->PV节点->平衡节点linedata = NumResort(linedataNum);P = busdata(:3);Q = busdata(:4);U = busdata(:5);Us = U;deta = busdata(:6);e = U.*cos(deta);f = U.*sin(deta);busnum = length(busdata(bussort1));pqnum = length(pqbus);%生成节点导纳矩阵Y = BuildY(linedata);for k = 1:100[dPdQdU2] = CalcCollection(PQUsefYbusnumpqnum); if max(abs([dP dQ]))<errorbreak;endJ = CalcJ(efYbusnumpqnum)dPQU = zeros(busnum-11);for ii = 1:pqnumdPQU(2*ii-1) = dP(ii);dPQU(2*ii) = dQ(ii);endfor ii = pqnum+1:busnum-1dPQU(2*ii-1) = dP(ii);dPQU(2*ii) = dU2(ii);enddef = Jordan(JdPQU);for ii = 1:busnum-1f(ii) = f(ii)+def(2*ii-1);e(ii) = e(ii)+def(2*ii);endendif k >= 100disp('不收敛!');return;end[SbusSijSvc] = CalcS(linedataefYbusnum);disp('编号:');disp(Num');disp('节点电压:');disp(e'+1j*f');disp('平衡节点功率:');disp(Svc);disp('线路功率');for n = 1:length(Sij(:1))fprintf('%o %o 'Num(Sij(n1))Num(Sij(n2)))disp(Sij(n3))enddisp('节点功率');for n = 1:busnumfprintf('%o 'Num(n))disp(Sbus(n))endendfunction [SbusSijSvc] = CalcS(linedataefYbusnum)Sbus = zeros(1busnum);Qi = zeros(1busnum);Ud = e+1j*f;%公式11-57for ii = 1:busnumfor jj = 1:busnumSbus(ii) = Sbus(ii)+Ud(ii)*conj(Y(iijj))*conj(Ud(jj));endendSvc = Sbus(busnum);Sij = zeros(length(linedata(:1))3);for n=1:length(linedata(:1))ii=linedata(n1);jj=linedata(n2);Sij(2*n-11) = ii;Sij(2*n-12) = jj;Sij(2*n-13) = Ud(ii)*(conj(Ud(ii))...*conj(1j*linedata(n5)+linedata(n6)*(linedata(n6)-1)/(linedata(n3)+1j*linedata(n4)))... +(conj(Ud(ii))-conj(Ud(jj)))*conj(-Y(iijj)));ii=linedata(n2);jj=linedata(n1);Sij(2*n1) = ii;Sij(2*n2) = jj;Sij(2*n3) = Ud(ii)*(conj(Ud(ii))...*conj(1j*linedata(n5)+(1-linedata(n6))/(linedata(n3)+1j*linedata(n4)))...+(conj(Ud(ii))-conj(Ud(jj)))*conj(-Y(iijj)));endendfunction linedata1 = NumResort(linedataNum) %对节点进行重排linedata1 = linedata;for n = 1:length(Num)n1 = find(linedata(:1)==Num(n));n2 = find(linedata(:2)==Num(n));linedata1(n11) = n*ones(length(n1)1);linedata1(n22) = n*ones(length(n2)1);endendfunction J = CalcJ(efYbusnumpqnum)%计算雅可比矩阵G = real(Y);B = imag(Y);J = zeros(2*(busnum-1));H = zeros(pqnumpqnum);N = H;M = H;L = H;for ii = 1:pqnumfor jj = 1:pqnumif ii~=jjH(iijj) = -B(iijj)*e(ii)+G(iijj)*f(ii); N(iijj) = G(iijj)*e(ii)+B(iijj)*f(ii); M(iijj) = -N(iijj);L(iijj) = H(iijj);J(2*ii-12*jj-1) = H(iijj);J(2*ii-12*jj) = N(iijj);J(2*ii2*jj-1) = M(iijj);J(2*ii2*jj) = L(iijj);endendIii = G(iiii)*e(ii)-B(iiii)*f(ii)...+1j*(G(iiii)*f(ii)+B(iiii)*e(ii));for jj = 1:busnumif ii~=jjIii = Iii+G(iijj)*e(jj)-B(iijj)*f(jj)... +1j*(G(iijj)*f(jj)+B(iijj)*e(jj));endendH(iiii) = -B(iiii)*e(ii)+G(iiii)*f(ii)+imag(Iii); N(iiii) = G(iiii)*e(ii)+B(iiii)*f(ii)+real(Iii); M(iiii) = -G(iiii)*e(ii)-B(iiii)*f(ii)+real(Iii); L(iiii) = -B(iiii)*e(ii)+G(iiii)*f(ii)-imag(Iii); J(2*ii-12*ii-1) = H(iiii);J(2*ii-12*ii) = N(iiii);J(2*ii2*ii-1) = M(iiii);J(2*ii2*ii) = L(iiii);endH = zeros(pqnumbusnum-pqnum-2);N = H;M = H;L = H;for ii = 1:pqnumfor jj = pqnum+1:busnum-1if ii~=jjH(iijj) = -B(iijj)*e(ii)+G(iijj)*f(ii);N(iijj) = G(iijj)*e(ii)+B(iijj)*f(ii);M(iijj) = -N(iijj);L(iijj) = H(iijj);J(2*ii-12*jj-1) = H(iijj);J(2*ii-12*jj) = N(iijj);J(2*ii2*jj-1) = M(iijj);J(2*ii2*jj) = L(iijj);endendendH = zeros(busnum-pqnum-2pqnum);N = H;R = H;S = H;for ii = pqnum+1:busnum-1for jj = 1:pqnumif ii~=jjH(iijj) = -B(iijj)*e(ii)+G(iijj)*f(ii);N(iijj) = G(iijj)*e(ii)+B(iijj)*f(ii);R(iijj) = 0;S(iijj) = 0;J(2*ii-12*jj-1) = H(iijj);J(2*ii-12*jj) = N(iijj);J(2*ii2*jj-1) = R(iijj);J(2*ii2*jj) = S(iijj);endendendH = zeros(busnum-pqnum-2);N = H;R = H;S = H;for ii = pqnum+1:busnum-1for jj = pqnum+1:busnum-1if ii~=jjH(iijj) = -B(iijj)*e(ii)+G(iijj)*f(ii);N(iijj) = G(iijj)*e(ii)+B(iijj)*f(ii);R(iijj) = 0;S(iijj) = 0;J(2*ii-12*jj-1) = H(iijj);J(2*ii-12*jj) = N(iijj);J(2*ii2*jj-1) = R(iijj);J(2*ii2*jj) = S(iijj);endendIii = G(iiii)*e(ii)-B(iiii)*f(ii)...+1j*(G(iiii)*f(ii)+B(iiii)*e(ii));for jj = 1:busnumif ii~=jjIii = Iii+G(iijj)*e(jj)-B(iijj)*f(jj)...+1j*(G(iijj)*f(jj)+B(iijj)*e(jj));endendH(iiii) = -B(iiii)*e(ii)+G(iiii)*f(ii)+imag(Iii);N(iiii) = G(iiii)*e(ii)+B(iiii)*f(ii)+real(Iii);R(iiii) = 2*f(ii);S(iiii) = 2*e(ii);J(2*ii-12*ii-1) = H(iiii);J(2*ii-12*ii) = N(iiii);J(2*ii2*ii-1) = R(iiii);J(2*ii2*ii) = S(iiii);endendfunction [dPdQdU2] = CalcCollection(PQUsefYbusnumpqnum) %计算修正值G = real(Y);B = imag(Y);Pt = P;Qt = Q;dP = zeros(1busnum);dQ = zeros(1busnum);dU2 = zeros(1busnum);for ii = 1:pqnumPi = 0;Qi = 0;for jj = 1:busnumPi = Pi+e(ii)*(G(iijj)*e(jj)-B(iijj)*f(jj))... +f(ii)*(G(iijj)*f(jj)+B(iijj)*e(jj));Qi = Qi+f(ii)*(G(iijj)*e(jj)-B(iijj)*f(jj))... -e(ii)*(G(iijj)*f(jj)+B(iijj)*e(jj));enddP(ii) = P(ii)-Pi;dQ(ii) = Q(ii)-Qi;Pt(ii) = Pi;Qt(ii) = Qi;endfor ii = pqnum+1:busnum-1Pi = 0;for jj = 1:busnumPi = Pi+e(ii)*(G(iijj)*e(jj)-B(iijj)*f(jj))... +f(ii)*(G(iijj)*f(jj)+B(iijj)*e(jj));enddP(ii) = P(ii)-Pi;Pt(ii) = Pi;dU2(ii) = Us(ii)^2-(e(ii)^2+f(ii)^2);endendfunction Y = BuildY(linedata)if nargin < 1linedata = [1 4 0.1 0.4 0.01528 1;1 3 0 0.3 0 1.1;1 2 0.12 0.5 0.01920 1;4 2 0.08 0.40 0.01413 1];endnf = linedata(:1);nt = linedata(:2);r = linedata(:3);x = linedata(:4);b = linedata(:5);k = linedata(:6);branchnum = length(nf);busnum = max([nf'nt']);y = ones(branchnum1)./(r+1j*x);Y = zeros(busnum);for n = 1:branchnumY(nf(n)nt(n)) = Y(nf(n)nt(n))-k(n)*y(n);Y(nt(n)nf(n)) = Y(nf(n)nt(n));Y(nf(n)nf(n)) = Y(nf(n)nf(n))+k(n)^2*y(n)+1j*b(n);Y(nt(n)nt(n)) = Y(nt(n)nt(n))+y(n)+1j*b(n);endendfunction s = Jordan(Ab)%约当消元if nargin < 1A=[1 2 3;2 7 5;1 4 9];b=[1 6 -3]';endif rank(A)~=rank([Ab])error('A矩阵的秩和增广矩阵的秩不相同方程不存在唯一解'); end[~n]=size(A);A(:n+1) = b;for k = 1:nA(kk:end) = A(kk:end)/A(kk);% 规格化for q = 1:k-1% 消上三角if A(qk)~=0A(qk:end) = A(qk:end)-A(kk:end).*A(qk);endendfor p = k+1:n% 消下三角if A(pk)~=0A(pk:end) = A(pk:end)-A(kk:end).*A(pk);endendends = A(:end);end。
牛顿拉夫逊法极坐标下的计算流程

牛顿拉夫逊法极坐标下的计算流程下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor. I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!1. 初始化:给定电力系统的网络拓扑结构和参数,包括节点数、支路数、节点导纳矩阵等。
4-3 n-l潮流计算

PQ节点
H2 p N2 p H2n
PV节点
H pp N pp H pn Rpp S pp Rpn Hnp Nnp Hnn Rnp Snp Rnn
2(n-m)
5
2(n-m)
2(m-1)
4-3牛顿-拉夫逊迭代法潮流计算
一、潮流计算时的修正方程式
1. 用直角坐标表示的修正方程
∂Pi H ij = ∂f j ∂Qi J ij = ∂f j
13
当j = i时:
n ∂ Pi ⎧ ⎪ H ii = ∂ δ = −U i ∑ U j ( G ij sin δ ij -Bij cos δ ij ) j =1, j ≠ i i ⎪ n ⎪ ∂ Pi N ii = U i = U i ∑ U j ( G ij cos δ ij + Bij sin δ ij ) +2 U i 2 G ii ⎪ ∂U i j =1, j ≠ i ⎪ ⎨ n ∂ Qi ⎪J = = U i ∑ U j ( G ij cos δ ij -Bij sin δ ij ) ii ⎪ ∂δ i j =1, j ≠ i ⎪ n ∂ Qi ⎪L = U i = U i ∑ U j ( G ij sin δ ij + Bij cos δ ij ) -2 U i 2 Bii ⎪ ii ∂ U j =1, j ≠ i i ⎩
17
4-4 P-Q分解法潮流计算
一、修正方程式
⎡ ΔP ⎤ ⎡ H11 1 ⎢ ΔP ⎥ ⎢ H ⎢ 2 ⎥ ⎢ 21 ⎢ ⎥ ⎢ ⎢ ⎥ ⎢ ⎢ ΔPp ⎥ ⎢H p1 ⎢ ΔP ⎥ = ⎢ Hn1 n ⎢ ⎥ ⎢ ⎢ ⎥ ⎢ ⎢ ΔQ ⎥ ⎢ J ⎢ 1 ⎥ ⎢ 11 ⎢ΔQ2 ⎥ ⎢ J21 ⎢ ⎥ ⎢ ⎣ ⎦ ⎣
10潮流计算的牛顿—拉夫逊法

Qgi min Qgi Qgi max
ijmin ij ijmax
21
三、极坐标下的牛拉法潮流 计算
n m nm1 1 m
PQ
n
Pi Vi Vj (Gij cosij Bij sin ij ) j 1
n
Qi Vi Vj (Gij sinij Bij cosij ) j 1
⑦ 引入修正系数; ⑧ 初值、平值电压启动。
19
计算步骤
输入原始数据
形成节点导纳矩阵
给定节点电压初值
e(0) i
,
f (0) i
k 0
用公式计算 Pi(k ) , Qi(k )及Vi2(k )
是
max{| Pi(k) , Qi(k) , Vi2(k) |} ?
否
按公式计算雅可比矩阵各元素
解修正方程式,求ei(
已知
x(0) 1
,
x(0) 2
,与真解的差为
x1(0) , x2(0)
f1 (
x(0) 1
x1(0)
,
x(0) 2
x2(0)
)
0
f2(
x(0) 2
x2(0) ,
x(0) 2
x2(0)
)
0
8
一、牛顿一拉夫逊法的基本原理
展开:
f1
(
x(0) 1
,
x(0) 2
)
f1 x1
x1( 0 )
0
f1 x2
0
x2( 0 )
10.954526
x4
x3
f ( x3 ) f ( x3 )
10.954526 0.00163988 2 10.954526
直角坐标系牛顿拉夫逊算法毕业设计论文

基于直角坐标系的牛顿—拉夫法潮流计算摘要潮流计算是电力网络设计及运行中最基本的计算,对电力网络的各种设计方案及各种运行方式进行潮流计算,可以得到各种电网各节点的电压,并求得网络的潮流及网络中各元件的电力损耗,进而求得电能损耗。
因此,网络通过潮流计算可以分析该网络的电压水平高低,功率分布与电力损耗的合理性及经济性等,从而对该网络的设计及运行做出评价。
本文主要章节内容包括节点导纳矩阵,电力系统潮流计算数学模型,直角坐标的牛顿拉夫逊法,以及程序设计和算例结果分析。
牛顿—拉夫逊法潮流计算主要采用C语言编写潮流计算程序,首先编写原始数据的输入程序,将原始数据形成一个目标文件,打开文件取出数据,根据电力网络连接图列写节点电压方程,编写计算节点导纳矩阵各个元素的程序,计算各个节点的不平衡量,进行校验,如不收敛则编写计算雅克比矩阵元素的程序,列写修正方程,利用高斯消去法,对增广矩阵进行消去,从而解出修正量的值。
经过多次迭代,如果经校验节点电压的不平衡量已收敛,则结束迭代,转入编写计算平衡节点的功率和线路的潮流分布程序。
最后,编写潮流计算的输出程序,输出节点电压的近似值。
关键词:潮流计算,牛顿——拉夫逊法,C语言,节点导纳矩阵,雅克比矩阵Newton – Laphson flow calculation based on Cartesiancoordinate systemABSTRACTFlow calculation is the most basic calculation in the design of the electricity network and the various ways of the operation. Flow calculation is used to calculation of all kinds of designs and the various ways of operation. So we can acquire a variety of nodal voltage and achieve the power loss in the network and the trend and various components in the network. Then can seek power loss. Therefore, the network can be calculated through the analysis of the level of voltage, power distribution and power losses and the reasonableness, the economy in the network.Node admittance matrix,Digital Analog Function Table ,Newton – Raphson of Rectangular coordinates , formula design and results analysis are the main chapter of this article Newton- Raphson flow calculation method is main program through C-language. First of all, write input the program of the raw data and make raw data form a target file. Open the file and retrieve data, according to the electricity network plan to write out he raw data to form a target file, according to the power network, plan to write out nodal voltage equation, computing various elements of nodal Admittance matrix, calculated the imbalance of each node, to check, if the imbalance isn’t convergence, then calculate various elements of Jacques matrix and write that equation, use Gaussian elimination method to eliminate broaden matrix, answer the equation. After several rounds iteration, if the imbalance of nodal voltage is convergence, then end the iteration, turn into calculate the power of balance nodes and the distribution of power in various branches. Finally, write the output program, output approximation of nodal voltage.KEY WORDS:Flow calculation;Newton - Laphson method;C language;Node admittance matrix;Jacques matrix毕业设计(论文)原创性声明和使用授权说明原创性声明本人郑重承诺:所呈交的毕业设计(论文),是我个人在指导教师的指导下进行的研究工作及取得的成果。
直角坐标系
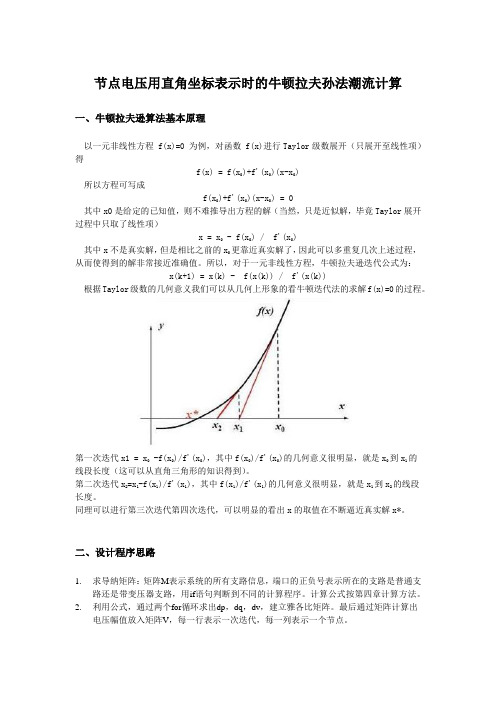
节点电压用直角坐标表示时的牛顿拉夫孙法潮流计算一、牛顿拉夫逊算法基本原理以一元非线性方程 f(x)=0 为例,对函数 f(x)进行Taylor级数展开(只展开至线性项)得f(x) = f(x0)+f'(x0)(x-x0)所以方程可写成f(x0)+f'(x0)(x-x0) = 0其中x0是给定的已知值,则不难推导出方程的解(当然,只是近似解,毕竟Taylor展开过程中只取了线性项)x = x0 - f(x0) / f'(x0)其中x不是真实解,但是相比之前的x0更靠近真实解了,因此可以多重复几次上述过程,从而使得到的解非常接近准确值。
所以,对于一元非线性方程,牛顿拉夫逊迭代公式为:x(k+1) = x(k) - f(x(k)) / f'(x(k))根据Taylor级数的几何意义我们可以从几何上形象的看牛顿迭代法的求解f(x)=0的过程。
第一次迭代x1 = x0 -f(x0)/f'(x0),其中f(x0)/f'(x0)的几何意义很明显,就是x0到x1的线段长度(这可以从直角三角形的知识得到)。
第二次迭代x2=x1-f(x1)/f'(x1),其中f(x1)/f'(x1)的几何意义很明显,就是x1到x2的线段长度。
同理可以进行第三次迭代第四次迭代,可以明显的看出x的取值在不断逼近真实解x*。
二、设计程序思路1.求导纳矩阵:矩阵M表示系统的所有支路信息,端口的正负号表示所在的支路是普通支路还是带变压器支路,用if语句判断到不同的计算程序。
计算公式按第四章计算方法。
2.利用公式,通过两个for循环求出dp,dq,dv,建立雅各比矩阵。
最后通过矩阵计算出电压幅值放入矩阵V,每一行表示一次迭代,每一列表示一个节点。
三、程序代码%节点电压用直角坐标表示时的牛顿-拉夫逊潮流计算clear;N=input('请输入节点数:N=')L=input('请输入支路数:L=')M=input('请输入支路信息:M=') %第一列表示支路端口,第二列表示支路另一端口第三列表示支路的电阻R,第四列表示支路的电抗X,第五列表示支路的对地电容或变比Y=zeros(N);G=zeros(N);B=zeros(N);for n=1:NI=M(n,1)J=M(n,2)R=M(n,3)X=M(n,4)K=M(n,5)if I*J>0G(I,I)=G(I,I)+R/(R^2+X^2);G(J,J)=G(J,J)+R/(R^2+X^2);G(J,I)=-(R/(R^2+X^2));G(I,J)=G(J,I);B(I,I)=B(I,I)+K-(X/(R^2+X^2));B(J,J)=B(J,J)+K-(X/(R^2+X^2));B(J,I)=(X/(R^2+X^2));B(I,J)=B(J,I);elseJ=abs(J)G(I,I)=G(I,I)+(1/K^2)*(R/(R^2+X^2)); G(J,J)=G(J,J)+R/(R^2+X^2);G(I,J)=-1/(K*(R/(R^2+X^2))) ;G(I,J)=G(J,I);B(I,I)=B(I,I)-(1/K^2)*(X/(R^2+X^2)); B(J,J)=-(X/(R^2+X^2));B(J,I)=-(-1/K)*(X/(R^2+X^2));B(I,J)=B(J,I);endY=G+i.*B;endYp1s=-0.30;q1s=-0.18;p2s=-0.55;q2s=-0.13;p3s=0.5;u3s=1.10;u4s=1.05;e=[1 1 1.1 1.05 ]f=[0 0 0 0 ]W(1,:)=e(1,:)k=1;for k=1:10;I=[0 0;0 0;0 0;0 0];for m=1:4I(1,1)= I(1,1)+G(1,m)*e(1,m)-B(1,m)*f(1,m);I(1,2)= I(1,2)+G(1,m)*f(1,m)+B(1,m)*e(1,m);endfor m=1:4I(2,1)=I(2,1)+G(2,m)*e(1,m)-B(2,m)*f(1,m);I(2,2)=I(2,2)+G(2,m)*f(1,m)+B(2,m)*e(1,m);endfor m=1:4I(3,1)= I(3,1)+G(3,m)*e(1,m)-B(3,m)*f(1,m);I(3,2)= I(3,2)+G(3,m)*f(1,m)+B(3,m)*e(1,m);endfor m=1:4I(4,1)= I(4,1)+G(4,m)*e(1,m)-B(4,m)*f(1,m);I(4,2)= I(4,2)+G(4,m)*f(1,m)+B(4,m)*e(1,m);enddp1=p1s-e(1)*I(1,1)-f(1)*I(1,2)dq1=q1s-f(1)*I(1,1)+e(1)*I(1,2);dp2=p2s-e(2)*I(2,1)-f(2)*I(2,2);dq2=q2s-f(2)*I(2,1)+e(2)*I(2,2);dp3=p3s-e(3)*I(3,1)-f(3)*I(3,2);dv3=0;M=[dp1 dq1 dp2 dq2 dp3 dv3]d(k,:)=M(1,:)h=[abs(dp1) abs(dp2) abs(dp3) abs(dq1) abs(dq2) abs(dv3)] a=max(h)if a<10^(-5)break;endC=[];%p eD=[];%p fE=[];%q eF=[];%q fH=[];L=[];J=[];for m=1:3for n=1:3if(m==n)C(m,m)=I(m,1)+G(m,m)*e(m)+B(m,m)*f(m);D(m,m)=I(m,2)-B(m,m)*e(m)+G(m,m)*f(m);E(m,m)=-I(m,2)-B(m,m)*e(m)+G(m,m)*f(m);F(m,m)=I(m,1)-G(m,m)*e(m)-B(m,m)*f(m);H(m,m)=2*e(m);L(m,m)=-2*f(m);elseC(m,n)=G(m,n)*e(m)+B(m,n)*f(m);D(m,n)=-B(m,n)*e(m)+G(m,n)*f(m);F(m,n)=-C(m,n);E(m,n)=D(m,n);H(m,n)=0;L(m,n)=0;endendendJ=[C(1,1) D(1,1) C(1,2) D(1,2) C(1,3) D(1,3);E(1,1) F(1,1) E(1,2) F(1,2) E(1,3) F(1,3);C(2,1) D(2,1) C(2,2) D(2,2) C(2,3) D(2,3);E(2,1) F(2,1) E(2,2) F(2,2) E(2,3) F(2,3);C(3,1) D(3,1) C(3,2) D(3,2) C(3,3) D(3,3);H(3,1) L(3,1) H(3,2) L(3,2) H(3,3) L(3,3)];disp('雅各比矩阵J=');JR=[];T=[dp1;dq1;dp2;dq2;dp3;dv3]R=J\Te(1)=e(1)+R(1,1);f(1)=f(1)+R(2,1);e(2)=e(2)+R(3,1);f(2)=f(2)+R(4,1);e(3)=e(3)+R(5,1);f(3)=f(3)+R(6,1);W(k+1,:)=e(1,:)V(k+1,:)=f(1,:)U=W.^2+V.^2;V/WU=U.^(0.5)O=atan(V./W)k=k+1endP=[];Q=[];S=[];P(4,4)=e(4)*(G(4,1)*e(1)+G(4,2)*e(2)+G(4,3)*e(3)+G(4,4)*e(4)) Q(4,4)=e(4)*(B(4,1)*e(1)+B(4,2)*e(2)+B(4,3)*e(3)+B(4,4)*e(4))S(4,4)=P(4)+j.*Q(4)x=1:kfigure(1)plot(x,U(x,1),x,U(x,2),x,U(x,3))title('电压幅值与迭代次数')hold onfigure(2)plot(x,O(x,1),x,O(x,2),x,O(x,3))title('相角与迭代次数')四、运行结果>> NEWTON请输入节点数:N=4N =4请输入支路数:L=4L =4请输入支路信息:M=[1 2 0.1 0.4 0.01528;1 -3 0 0.3 1.1;1 4 0.12 0.50 0.01920;2 4 0.08 0.4 0.01413]M =1.00002.0000 0.1000 0.4000 0.01531.0000 -3.0000 0 0.3000 1.10001.0000 4.0000 0.1200 0.5000 0.01922.0000 4.0000 0.0800 0.4000 0.0141I =1J =2R =0.1000 X =0.4000 K =0.0153I =1J =-3R =X =0.3000 K =1.1000 J =3I =1J =4R =0.1200 X =0.5000 K =0.0192I =2J =4R =0.0800X =0.4000K =0.0141Y =1.0421 - 6.9644i -0.5882 +2.3529i 0.0000 +3.0303i -0.4539 + 1.8911i -0.5882 + 2.3529i 1.0690 -4.7274i 0.0000 + 0.0000i -0.4808 + 2.4038i 0.0000 + 3.0303i 0.0000 + 0.0000i 0.0000 - 3.3333i 0.0000 + 0.0000i -0.4539 + 1.8911i -0.4808 + 2.4038i 0.0000 + 0.0000i 0.9346 - 4.2616ie =1.0000 1.0000 1.1000 1.0500f =0 0 0 0W =1.0000 1.0000 1.1000 1.0500dp1 =-0.2773M =-0.2773 0.5275 -0.5260 0.0196 0.5000 0d =-0.2773 0.5275 -0.5260 0.0196 0.5000 0h =0.2773 0.5260 0.5000 0.5275 0.0196 0a =0.5275雅各比矩阵J=J =1.0194 7.6719 -0.5882 -2.3529 0 -3.0303 6.2568 -1.0648 -2.3529 0.5882 -3.0303 0 -0.5882 -2.3529 1.04504.8770 0 0 -2.3529 0.5882 4.5778 -1.0930 0 0 0 -3.3333 0 0 0 3.0303 0 0 0 0 2.2000 0T =-0.27730.5275-0.52600.01960.5000R =0.1023-0.03230.0328-0.11810.1295W =1.0000 1.0000 1.1000 1.05001.1023 1.0328 1.1000 1.0500V =0 0 0 0-0.0323 -0.1181 0.1295 0ans =0 00.9763 -0.9484U =1.0000 1.0000 1.1000 1.05001.1027 1.0395 1.1076 1.0500O =0 0 0 0-0.0293 -0.1139 0.1171 0k =2dp1 =0.0064M =0.0064 -0.0694 0.0141 -0.0607 -0.0401 0d =-0.2773 0.5275 -0.5260 0.0196 0.5000 0 0.0064 -0.0694 0.0141 -0.0607 -0.0401 0h =0.0064 0.0141 0.0401 0.0694 0.0607 0a =0.0694雅各比矩阵J=J =1.0989 7.7512 -0.7244 -2.5745 -0.0979 -3.3402 7.5344 -1.6485 -2.5745 0.7244 -3.3402 0.0979 -0.8855 -2.3606 1.13104.8840 0 0 -2.3606 0.8855 4.6281 -2.1940 0 0 0.3923 -3.3333 0 0 0.0979 3.3402 0 0 0 0 2.2000 -0.2589T =0.0064-0.06940.0141-0.0607-0.0401R =-0.0176-0.0034-0.02020.0027-0.0016-0.0133W =1.0000 1.0000 1.1000 1.0500 1.1023 1.0328 1.1000 1.0500 1.0846 1.0126 1.0984 1.0500V =0 0 0 0 -0.0323 -0.1181 0.1295 0 -0.0357 -0.1154 0.1162 0ans =0 0 0-0.6583 -9.2392 9.9642-0.6096 -8.7860 9.4558U =1.0000 1.0000 1.1000 1.0500 1.1027 1.0395 1.1076 1.0500 1.0852 1.0192 1.1046 1.0500O =0 0 0 0 -0.0293 -0.1139 0.1171 0 -0.0329 -0.1135 0.1054 0k =3dp1 =2.8761e-04M =0.0003 -0.0011 0.0000 -0.0012 -0.0007 0d =-0.2773 0.5275 -0.5260 0.0196 0.5000 0 0.0064 -0.0694 0.0141 -0.0607 -0.0401 0 0.0003 -0.0011 0.0000 -0.0012 -0.0007 0h =0.0003 0.0000 0.0007 0.0011 0.0012 0a =0.0012雅各比矩阵J=J =1.1079 7.6903 -0.7221 -2.5310 -0.1082 -3.2867 7.3426 -1.6502 -2.5310 0.7221 -3.2867 0.1082 -0.8672 -2.3147 1.10624.8503 0 0 -2.3147 0.8672 4.4770 -2.1500 0 0 0.3520 -3.3286 0 0 0.1082 3.2867 0 0 0 0 2.1969 -0.2323T =0.0003-0.00110.0000-0.0012-0.0007R =1.0e-03 *-0.3169-0.0408-0.41400.0256-0.0230-0.2176W =1.0000 1.0000 1.1000 1.0500 1.1023 1.0328 1.1000 1.0500 1.0846 1.0126 1.0984 1.0500 1.0843 1.0122 1.0984 1.0500V =0 0 0 0 -0.0323 -0.1181 0.1295 0 -0.0357 -0.1154 0.1162 0 -0.0358 -0.1154 0.1159 0ans =1.0e+04 *0 0 0 0 0.0007 0.0270 -1.3516 1.3238 0.0006 0.0244 -1.2203 1.1953 0.0006 0.0243 -1.2182 1.1932U =1.0000 1.0000 1.1000 1.05001.1027 1.0395 1.1076 1.05001.0852 1.0192 1.1046 1.05001.0849 1.0188 1.1045 1.0500O =0 0 0 0-0.0293 -0.1139 0.1171 0-0.0329 -0.1135 0.1054 0-0.0330 -0.1135 0.1052 0k =4dp1 =1.1759e-07M =1.0e-06 *0.1176 -0.3410 -0.0486 -0.5219 -0.2062 0d =-0.2773 0.5275 -0.5260 0.0196 0.5000 0 0.0064 -0.0694 0.0141 -0.0607 -0.0401 0 0.0003 -0.0011 0.0000 -0.0012 -0.0007 0 0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0h =1.0e-06 *0.1176 0.0486 0.2062 0.3410 0.5219 0a =5.2187e-07雅各比矩阵J=J =1.1081 7.6892 -0.7220 -2.5303 -0.1084 -3.2858 7.3393 -1.6499 -2.5303 0.7220 -3.2858 0.1084 -0.8669 -2.3138 1.10564.8497 0 0 -2.3138 0.8669 4.4738 -2.1495 0 0 0.3514 -3.3285 0 0 0.1084 3.2858 0 0 0 0 2.1968 -0.2319T =1.0e-06 *0.1176-0.3410-0.0486-0.5219-0.2062R =1.0e-06 *-0.1092-0.0090-0.16910.0047-0.0063-0.0600W =1.0000 1.0000 1.1000 1.05001.1023 1.0328 1.1000 1.05001.0846 1.0126 1.0984 1.05001.0843 1.0122 1.0984 1.05001.0843 1.0122 1.0984 1.0500V =0 0 0 0-0.0323 -0.1181 0.1295 0-0.0357 -0.1154 0.1162 0-0.0358 -0.1154 0.1159 0-0.0358 -0.1154 0.1159 0ans =1.0e+04 *0 0 0 0 0 0.0007 0.0270 -1.3506 0 1.3228 0.0006 0.0244 -1.2194 0 1.1944 0.0006 0.0243 -1.2172 0 1.1923 0.0006 0.0243 -1.2172 0 1.1923U =1.0000 1.0000 1.1000 1.05001.1027 1.0395 1.1076 1.05001.0852 1.0192 1.1046 1.05001.0849 1.0188 1.1045 1.05001.0849 1.0188 1.1045 1.0500O =0 0 0 0-0.0293 -0.1139 0.1171 0-0.0329 -0.1135 0.1054 0-0.0330 -0.1135 0.1052 0-0.0330 -0.1135 0.1052 0k =5dp1 =1.3392e-14M =1.0e-13 *0.1339 -0.3425 -0.1493 -0.9284 -0.1969 0d =-0.2773 0.5275 -0.5260 0.0196 0.5000 0 0.0064 -0.0694 0.0141 -0.0607 -0.0401 0 0.0003 -0.0011 0.0000 -0.0012 -0.0007 0 0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0 0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0h =1.0e-13 *0.1339 0.1493 0.1969 0.3425 0.9284 0a =9.2842e-14图一电压幅值-迭代次数图二相角特性-迭代次数分析与讨论:运行结果表明,当迭代次数达到3的时候,电压幅值和相角收敛。
基于MATLAB的直角坐标下牛顿拉夫逊法潮流计算

基于MATLAB的直角坐标下牛顿拉夫逊法潮流计算基于MATLAB的直角坐标下牛顿-拉夫逊法潮流计算摘要潮流计算,指在给定电力系统网络拓扑、元件参数和发电、负荷参量条件下,计算有功功率、无功功率及电压在电力网中的分布。
潮流计算是根据给定的电网结构、参数和发电机、负荷等元件的运行条件,确定电力系统各部分稳态运行状态参数的计算。
通常给定的运行条件有系统中各电源和负荷点的功率、枢纽点电压、平衡点的电压和相位角。
待求的运行状态参量包括电网各母线节点的电压幅值和相角,以及各支路的功率分布、网络的功率损耗等。
它是基于配电网络特有的层次结构特性,论文提出了一种新颖的分层前推回代算法。
该算法将网络支路按层次进行分类,并分层并行计算各层次的支路功率损耗和电压损耗,因而可大幅度提高配电网潮流的计算速度。
论文在MATLAB环境下,利用其快速的复数矩阵运算功能,实现了文中所提的分层前推回代算法,并取得了非常明显的速度效益。
另外,论文还讨论发现,当变压器支路阻抗过小时,利用Π型模型会产生数值巨大的对地导纳,由此会导致潮流不收敛。
为此,论文根据理想变压器对功率和电压的变换原理,提出了一种有效的电压变换模型来处理变压器支路,从而改善了潮流算法的收敛特性。
关键词:电力系统;潮流分析;MATLABAbstractFlow calculation is an important analysis function of power system and is the necessary facility of fault analysis, relay protection setting and security analysis. In addition, the traditional design method is a structured program design method based on functional decomposition, the entire software engineering as a combination of objects, as the domain of a particular issue, the composition of the object will remain basically unchanged Therefore, this decomposition methodbased on object design software structure relatively stable, easy to maintain and expand. . Combine the characteristics of power systems, software running on the use of MATLAB language WINDOWS OS graphical flow calculation software. The main features of the system are simple and intuitive graphical interface and stable operation. Calculated accurately Calculations, the algorithm has done a number of improvements to enhance the computing speed, the various types of effective package makes the procedure has good modularity maintainability and reusability. The MATLAB language is used to calculate flow distribution of power system in this paper. The typical examples explain that the method has the characteristics of simple programming high calculation efficiency and matching people habit the calculation result can satisfy the engineering calculation needs and at the same time verify the usefulness of the method.Key words: Electric power system; flow calculation; MATLAB 第一章电力系统潮流计算概述1.1电力系统潮流概述潮流计算是电力系统分析中的一种最基本的计算,它的任务是在给定的接线方式和运行条件下,确定系统的运行状态,如各母线上的电压(幅值和相角)、网络中的功率分布及功率损耗等,是电力系统的稳态计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直角坐标系下牛顿法潮流计算1电力系统潮流计算潮流计算是电力系统分析中的一种最基本的计算,它的任务是对给定的运行条件确定系统的运行状态,如母线上的电压(幅值及相角)、网络中的功率分布及功率损耗等。
在电力系统规划设计和现有电力系统运行方式的研究中,都需要利用潮流计算来定量地分析比较供电方案或运行方式的合理性.可靠性和经济性。
此外,电力系统潮流计算也是计算系统动态稳定和静态稳定的基础。
2节点导纳矩阵的形成在图1(a )的简单电力系统中,若略去变压器的励磁功率和线路电容,负荷用阻抗表示,便可以得到一个有5个节点(包括零电位点)和7条支路的等值网络,如图1(b )所示。
将接于节点1和4的电势源和阻抗的串联组合变换成等值的电流源和导纳的并联组合,变得到图1(c )的等值网络,其中1101I y E =&&和4404I y E =&&分别称为节点1和4的注入电流源。
(a)24İİ4(c)图1 电力系统及其网络以零电位点作为计算节点电压的参考点,根据基尔霍夫定律,可以写出4个独立节点的电流平衡方程如下:1011212112212022323242423323434244234434044()()()()0()()0()()y U y U U I y U U y U y U U y U U y U U y U U y U U y U U y U I ⎫+-=⎪-++-+-=⎪⎬-+-=⎪⎪-+-+=⎭&&&&&&&&&&&&&&&&&&&&& (2-1)上述方程组经过整理可以写成1111221211222233244322333344422433444400Y U Y U I Y U Y U Y U Y U Y U Y U Y U Y U Y U Y U I ⎫+ =⎪+++=⎪⎬ ++=⎪⎪ ++=⎭&&&&&&&&&&&&&& (2-2)式中,111012Y y y =+;2220232412Y y y y y =+++;332334Y y y =+;44402434Y y y y =++;122112Y Y y ==-;233223Y Y y ==-;244224Y Y y ==-;344334Y Y y ==-。
一般的,对于有n 个独立节点的网络,可以列写n 个节点方程11112211211222221122n n n n n n nn n n Y U Y U Y U I Y U Y U Y U I Y U Y U Y U I ⎫+++=⎪+++=⎪⎬⎪⎪+++=⎭&&&&L &&&&L M &&&&L (2-3)也可以用矩阵写成1111121212222212n n n n nn n n U I Y Y Y Y Y Y U I Y Y Y U I ⎡⎤⎡⎤ ⎡⎤⎢⎥⎢⎥⎢⎥ ⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥ ⎢⎥⎢⎥⎢⎥ ⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦&&L &&L M M M &&L (2-4)或缩写为YU I = (2-5)矩阵Y 称为节点导纳矩阵。
它的对角线元素ii Y 称为节点i 的自导纳,其值等于接于节点i 的所有支路导纳之和。
非对角线元素ijY 称为节点i 、j 间的互导纳,它等于直接接于节点i 、j 间的支路导纳的负值。
若节点i 、j 间不存在直接支路,则有ij Y =。
由此可知节点导纳矩阵是一个稀疏的对称矩阵。
3牛顿-拉夫逊法潮流计算牛顿-拉夫逊法的基本原理牛顿—拉夫逊法(Newton —Raphson 法)是求解非线性方程代数方程组的有效迭代计算方法。
在牛顿—拉夫逊法的每一次迭代过程中,对非线性方程通过线性化处理逐步近似。
下面以单变量加以说明。
设有单变量非线性方程()0f x = (3-1)求解此方程时。
先给出解的近似值(0)x它与真解的误差为(0)x∆,则(0)(0)x x x=+∆将满足方程,即(0)(0)()0f x x +∆= (3-2)将(3-8)式左边的函数在(0)x附近展成泰勒级数,于是便得2'''()(0)(0)(0)(0)(0)(0)(0)(0)(0)()()()()......()....2!!()()nn f f n x x fffx x x x x x x +∆=+∆++++∆∆ (3-3)式中'(0)()f x,……()(0)()n fx 分别为函数()f x 在(0)x 处的一阶导数,….,n阶导数。
如果差值(0)x∆很小,3-9式右端(0)x∆的二次及以上阶次的各项均可略去。
于是,3-9便简化为'(0)(0)(0)(0)(0)()()()f f f xx x xx+∆=+∆=0 (3-4)这是对于变量的修正量(0)x∆的现行方程式,亦称修正方程式。
解此方程可得修正量(0)(0)'(0)()()f x xf x∆=-(3-5)用所求的(0)x∆去修正近似解,变得(0)(1)(0)(0)(0)'(0)()()f x xx xx f x=+∆=-(3-6)由于3-10是略去高次项的简化式,因此所解出的修正量(0)x∆也只是近似值。
修正后的近似解(1)x 同真解仍然有误差。
但是,这样的迭代计算可以反复进行下去,迭代计算的通式是()(1)()'()()()k k k k f x xxf x+=-(3-7)迭代过程的收敛判据为()1()k f x ε< (3-8)或()2k xε∆< (3-9)式中1ε,2ε为预先给定的小正数。
这种解法的几何意义可以从图3-1得到说明。
函数y =f(x)为图中的曲线。
f(x)=0的解相当于曲线与x 轴的交点。
如果第k 次迭代中得到()k x,则过()()(),()k k k f y x x ⎡⎤=⎢⎥⎣⎦点作一切线,此切线同x 轴的交点便确定了下一个近似值(1)k x+。
由此可见,牛顿-拉夫逊法实质上就是切线法,是一种逐步线性化的方法。
应用牛顿法求解多变量非线性方程组3-1时,假定已给出各变量的初值1(0)x ,2(0)x…. (0)nx ,令1(0)x ∆,2(0)x∆,…..(0)nx∆分别为各变量的修正量,使其满足方程3-2即11122211221122(0)(0)(0)(0)(0)(0)(,,....,)0(0)(0)(0)(0)(0)(0)(,,....,)0......(0)(0)(0)(0)(0)(0)(,,....,)0n n n n nn n f x x x x x x f x x x x x x f x x x x x x ⎧+∆+∆+∆=⎪⎪+∆+∆+∆=⎪⎨⎪⎪+∆+∆+∆=⎪⎩(3-10)将上式中的n 个多元函数在初始值附近分别展成泰勒级数,并略去含有)0(1x ∆,)0(2x ∆,……,)0(n x ∆二次及以上阶次的各项,便得111001121212111002121212101211(0)(0)(0)(0)(0)(0)(,,...,)...0(0)(0)(0)(0)(0)(0)(,,...,) 0......(0)(0)(0)(0)(,,...,)|||||||nnn n nnnnf f f f x x x x x x x xx f f f f x x x x x x x xxf fx x x x x ∂∂∂+∆+∆++∆=∂∂∂∂∂∂+∆+∆++∆=∂∂∂∂∂+∆+∂110022(0)(0) 0||nnf f x x xx⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪∂⎪∆++∆=⎪∂∂⎩.(3-11)方程式3-17也可以写成矩阵形式1110001211222221200121200012...(0)(0)(0)(,,...,)(0)(0)(0)(,,...,).....................(0)(0)(0)(,,...,)...|||||||||nn n nn n n n n n f f f x x x f x x x f f f f x x x x xx fx x x f f f x xx ⎡∂∂∂⎢∂∂∂⎢⎡⎤⎢⎢⎥∂∂∂⎢⎢⎥⎢⎢⎥=-∂∂∂⎢⎢⎥⎢⎥⎢⎥⎣⎦∂∂∂∂∂∂⎣12(0)(0)...(0)n x x x ⎤⎥⎥⎡⎤∆⎥⎢⎥⎥⎢⎥∆⎥⎢⎥⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥∆⎢⎥⎣⎦⎢⎥⎢⎥⎦(3-12)方程式3-18是对于修正量)0(1x ∆,)0(2x ∆,……,)0(n x ∆ 的线性方程组,称为牛顿法的修正方程式.利用高斯消去法或三角分解法可以解出修正量)0(1x ∆,)0(2x ∆,……,)0(n x ∆。
然后对初始近似值进行修正(1)(0)(0)iiix x x=+∆ (i=1,2,….,n) (3-13)如此反复迭代,在进行k +1次迭代时,从求解修正方程式11112112222212121212...()()()(,,...,)()()()(,,...,).....................()()()(,,...,)...|||||||||k kk nn n k kknn n n n n k kk n k k k k k k k k k f ff x x x f x x x f f f f x x x x xx fx x x f f f x xx ⎡∂∂∂⎢∂∂∂⎢⎡⎤⎢⎢⎥∂∂∂⎢⎢⎥⎢⎢⎥=-∂∂∂⎢⎢⎥⎢⎥⎢⎥⎣⎦∂∂∂∂∂∂⎣12()()...()n k k k x x x ⎤⎥⎥⎡⎤∆⎥⎢⎥⎥⎢⎥∆⎥⎢⎥⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥∆⎢⎥⎣⎦⎢⎥⎢⎥⎦(3-14)得到修正量1()k x ∆,2()k x ∆,()nk x ∆,并对各变量进行修正(1)()()iiik k k x x x+=+∆ (i=1,2,…,n) (3-15) 式3-20和3-21也可以缩写为())()()(k k k x J x F ∆-= (3-16)和)()()1(k k k x x x ∆+=+ (3-17)式中的X 和X ∆分别是由n 个变量和修正量组成的n 维列向量;F(X)是由n 个多元函数组成的n 维列项量;J 是n 阶方阵,称为雅可比矩阵,它的第i 、j 个元素i ijif Jx=∂∂是第n 个函数12(,,...,,)nif x x x 对第j 个变量jx的偏导数;上角标(k)表示J 阵的每一个元素都在点,,,()()()(...,)12ik k k n f x x x 处取值。
