灰色预测模型实验以及例题分析实验报告
统计专业实验-实验9-灰色预测分析

19
400
25311
28713.56
1167.833
767.8332
191.9583
20
4647
29958
29849.15
1135.584
3511.4159
75.5631
21
22
23
24
25
表四
-2854.5
2187
系数
-5269
2642
-6895
610
-8768
3136
μ/α
69836.26
1702
22959
23839.45
1306.252
395.7479
23.2519
16
592
23551
25109.63
1270.181
678.1805
114.5575
17
952
24503
26344.73
1235.105
283.1051
29.7379
18
408
24911
27545.73
1200.998
792.9982
5.得到预测模型X^(k+1)=(X(0)(1) -μ/a )e-ak+μ/a
X^(k+1)=3662.905e0.1305k– 3094.7149
6.残差检验
(1)由预测公式,计算X^(1),
(2)累减生成X^(0),
(3)计算绝对残差和相对残差
在G2中输入=ABS(C2-F2),往下复制到G7;
在H2中输入=G2/C2,往下复制到H7中;
计算平均相对残差,在H8中输入=SUM(H2:H13)/12。
最新灰色预测实验.pdf

实验五灰色预测模型
姓名:XXX
学号:15086666
班级:150866班
实验时间:2018年6月11日实验地点:天津XX大学
一、实验目的
1.理解灰色系统的基本概念
2.掌握灰色关联系数和关联度的计算方法
3.掌握GM(1,1)模型的建模、参数估计和检验方法
4.熟练运用Excel进行灰色预测的操作
5.熟练运用Excel进行灾变预测的操作
6.综合运用所学模型进行预测分析
二、实验内容
1.GM(1,1)模型预测
2.灾变预测
3.综合运用
三、实验过程与步骤
某市第三产业从业人数如表4所示,试建立GM(1,1)模型并进行残差检验,预测其2006年的从业人数。
表4 第三产业从业人数
(单位:万人)年份2000 2001 2002 2003 2004 2005
人数 2.97 3.23 3.29 3.46 3.59 3.71
x(0)(i) x(0)(1) x(0)(2) x(0)(3) x(0)(4) x(0)(5) x(0)(6)。
灰色预测模型论文

GM(1,1)灰色预测模型摘要灰色理论认为系统的行为现象尽管是朦胧的,数据是复杂的,但它毕竟是有序的,是有整体功能的。
灰数的生成,就是从杂乱中寻找出规律。
同时,灰色理论建立的是生成数据模型,不是原始数据模型,因此,灰色预测的数据是通过生成数据的gm(1,1)模型所得到的预测值的逆处理结果。
本文利用灰色预测对重庆市的人均收入进行模拟,容易理解,操作简单灵活,直接面向用户,精度较高。
一、GM(1,1)预测模型的基本原理:灰色预测的基本原理时间序列预测是采用趋势预测原理进行的.然而时间序列预测存在以下问题:(1)时间序列变化趋势不明显时,很难建立起较精确的预测模型.(2)它是在系统按原趋势发展变化的假设下进行预测的,因而未考虑对未来变化产生影响的各种不确定因素.为克服上述缺点,邓聚龙教授引入了灰色因子的概念,采用“累加”和“累减”的方法创立了灰色预测理论.1.1 GM(1,1)模型的基本原理当一时间序列无明显趋势时,采用累加的方法可生成一趋势明显的时间序列.如时间序列X(0)={32,38,36,35,40,42}的趋势并不明显,但将其元素进行“累加”所生成的时间序列X(1)={32,70,106,141,181,223}则是一趋势明显的数列,按该数列的增长趋势可建立预测模型并考虑灰色因子的影响进行预测,然后采用“累减”的方法进行逆运算,恢复原时间序列,得到预测结果,这就是灰色预测的基本原理.数据来源:重庆市统计年鉴重庆城市居民家庭人均可支配收入:收入4375.435022.965302.05表1二、利用软件对数据进行模拟:模拟值残差相对误差4375.432 3910.0859 -1112.8741 -22.1557433 4368.869126 -933.180874 -17.6003794 4881.482893 -561.357107 -10.313685 5454.243318 -374.186682 -6.4200256 6094.207607 -82.092393 -1.3291527 6809.261006 236.961006 3.605458 7608.213972 370.143972 5.1138499 8500.910713 407.240713 5.03159510 9498.350496 277.390496 3.0082611 10612.823165 368.833165 3.60048312 11858.060575 288.320575 2.49202313 13249.40578 -465.84422 -3.39654214 14804.00209 -904.73791 -5.75945615 16541.004292 -650.095708 -3.78158316 18481.814669 -617.915331 -3.235205三、实验结果表21995200020052010x 104时间(年)人均收入(元)图1所得预测值与实测值折线比较 如图 1。
火灾灰色预测实验报告

火灾灰色预测实验报告引言火灾是一种常见的灾害,给人们的生命财产安全带来了严重威胁。
因此,能够准确预测火灾的发生时间和程度对于火灾管理和防控具有重要的意义。
灰色预测模型是一种有效的预测方法,它通过建立灰色微分方程来预测未来的发展趋势。
本实验旨在通过对火灾数据的分析和建模,利用灰色预测模型对火灾发生的趋势进行预测。
实验数据本实验选择了某市过去10年的火灾数据作为实验数据,数据包括每年火灾发生次数和火灾严重程度两个指标。
年份火灾发生次数火灾严重程度-2010 500 32011 460 22012 510 42013 540 32014 480 22015 470 12016 520 32017 550 42018 510 32019 490 2数据分析与建模首先,对实验数据进行可视化分析,以了解数据的分布和规律。
pythonimport matplotlib.pyplot as pltyears = [2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019] fires = [500, 460, 510, 540, 480, 470, 520, 550, 510, 490]severity = [3, 2, 4, 3, 2, 1, 3, 4, 3, 2]绘制火灾发生次数折线图plt.figure(figsize=(12, 6))plt.plot(years, fires, marker='o', linestyle='-', color='r', label='Fire Frequency')plt.xlabel('Year')plt.ylabel('Frequency')plt.title('Fire Frequency in the Past 10 Years')plt.legend()plt.show()绘制火灾严重程度折线图plt.figure(figsize=(12, 6))plt.plot(years, severity, marker='o', linestyle='-', color='b', label='Fire Severity')plt.xlabel('Year')plt.ylabel('Severity')plt.title('Fire Severity in the Past 10 Years')plt.legend()plt.show()根据可视化分析结果,可以看出火灾发生次数和火灾严重程度都呈现一定的趋势,难以通过直接观察来预测未来的发展情况。
灰色预测模型GM(1_1)及其应用

灰色预测模型GM(1,1)的应用一、问题背景:蠕变是材料在高温下的一个重要性能。
处于高温状态下的材料长期受到载荷作用时,即使其载荷较低,并且在短时间的高温拉伸试验中材料不发生变形,但在此情况下仍会有微小的蠕变,极端的情况下,甚至会使材料发生破坏。
高温材料多应用于各种车辆的发动机及冶金厂中各种设备上,如果因蠕变引起破坏,可能造成很大的事故。
为了保证设备的安全可靠,在某一使用温度下,预先知道该材料对不同载荷应力下断裂的时间是很重要的。
过去,人们都是通过蠕变试验测量断裂时间。
而做蠕变试验时,需要很长时间才能得到结果,即使通过试验得出的数据,也只是对某几个具体试样而言,存在很大的偶然性,不能代表普遍的规律。
如果将实测的数据用灰色系统理论来处理,可以预测在某一温度下的任何载荷应力的断裂时间。
二、低合金钢铸件蠕变性能的灰色预测下面是对Cr-mo-0.25V 低合金钢铸件高温蠕变情况利用灰色系统理论进行研究。
在500℃的高温下,已测得此铸件在载荷分别为37,36,35,34,33(kg/mm 2)情况下的蠕变断裂时间见下表。
数 列 序 数 K1 2 3 4 5载荷应力(kg/mm 2) 37 36 35 34 33 断裂时间()(100)0(K X ⨯小时)2.38 2.80 4.25 6.85 11.30 一次累加数列)()1(K X 2.38 5.18 9.43 16.28 27.581、建立GM (1,1)模型(1)数据处理:将同一数据列的前k 项元素累加后生成新数据列的第k 项元素。
即根据断裂时间数列)()0(k X 由∑==kn n X k X 1)0()1()()(得到 )()1(k X 。
(2)建立矩阵B,y:根据⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+--+-+-=1)]()1([5.01)]3()2([5.01)]2()1([5.0)1()1()1()1()1()1(N X N X X X X X B 得到 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=19.2118.12130.7178.3B根据 T N N X X X Y )](,),3(),2([)0()0()0( =,得到 T N Y ]3.11,85.6,25.4,80.2[=(3)求出逆矩阵1()T BB - (4)作最小二乘估计,求参数u a ,N T T Y B B B u a 1)(ˆ-=⎪⎪⎭⎫⎝⎛=α 可得,⎪⎪⎭⎫ ⎝⎛-=97.05.0ˆα a = -0.5, u=0.97(5)建立时间响应函数,计算拟合值把a 和u 分别代入au e a u X t X at +-=+-))1(()1(ˆ)0()1(可得到解为2.24.4)1(ˆ5.0)1(-=+t e t X, 取t 为应力序数k 时,即得到时间响应方程为:2.24.4)1(ˆ5.0)1(-=+k e k X即可得到生成累加数列),2,1()1(ˆ)1( =+k k X 。
灰色预测GM(1,1)模型分析

SPSS分析SPSS教程SPSSAU 灰色预测模型GM11 灰色模型灰色预测GM(1,1)模型分析Contents1背景 (2)2理论 (2)3操作 (3)4 SPSSAU输出结果 (3)5文字分析 (4)6剖析 (5)灰色预测模型可针对数量非常少(比如仅4个),数据完整性和可靠性较低的数据序列进行有效预测,其利用微分方程来充分挖掘数据的本质,建模所需信息少,精度较高,运算简便,易于检验,也不用考虑分布规律或变化趋势等。
但灰色预测模型一般只适用于短期预测,只适合指数增长的预测,比如人口数量,航班数量,用水量预测,工业产值预测等。
灰色预测模型有很多,GM(1,1)模型使用最为广泛,第1个数字表示进行一阶微分,第2个数字1表示只包含1个数据序列。
特别提示:GM(1,1)模型仅适用于中短期预测,不建议进行长期预测;GM(1,1)模型适用于数量少(比如20个以内)时使用,大量数据时不适合。
灰色预测模型案例Contents1背景 (2)2理论 (2)3操作 (3)4 SPSSAU输出结果 (3)5文字分析 (4)6剖析 (5)1背景当前某城市1986~1992共7年的道路交通噪声平均声级数据,现希望预测出往后一期器械声平均声级数据。
数据如下:年份城市交通噪声/dB(A)198671.10198772.40198872.40198972.10199071.40199172.00199271.602理论灰色预测GM(1,1)模型一般针对数据量少,有一定指数增长趋势的数据。
在进行模型构建时,通常包括以下步骤:第一步:级比值检验;此步骤目的在于数据序列是否有着适合的规律性,是否可得到满意的模型等,该步骤仅为初步检验,意义相对较小。
级比值=当期值/上一期值。
一般情况下级比值介于[0.982,1.0098]之间则说明很可能会得到满意的模型,但并不绝对。
第二步:后验差比检验;在进行模型构建后,会得到后验差比C值,该值为残差方差/ 数据方差;其用于衡量模型的拟合精度情况,C值越小越好,一般小于0.65即可。
23实验二十三灰色预测模型

实验二十三灰色预测模型一、实验目的了解灰色系统基本理论,理解灰色预测模型的基本概念。
掌握灰色预测模型的步骤和方法。
学会用MATLAB编程解决灰色预测中的计算问题.二、实验的理论与内容客观世界在不断发展变化的同时,往往通过事物之间及因素之间相互制约、相互联系而构成一个整体,我们称之为系统。
按事物内涵的不同,人们已建立了工程技术系统、社会系统、经济系统等。
人们试图对各种系统所外露出的一些特征进行分析,从而弄清楚系统内部的运行机理。
从信息的完备性与模型的构建上看,工程技术等系统具有较充足的信息量,其发展变化规律明显,定量描述较方便,结构与参数较具体,人们称之为白色系统;对另一类系统诸如社会系统、农业系统、生态系统等,人们无法建立客观的物理原型,其作用原理亦不明确,内部因素难以辨识或之间关系隐蔽,人们很难准确了解这类系统的行为特征,因此对其定量描述难度较大,带来建立模型的困难。
这类系统内部特性部分已知的系统称之为灰色系统。
一个系统的内部特性全部未知,则称之为黑色系统。
灰色系统理论首先基于对客观系统的新的认识。
尽管某些系统的信息不够充分,但作为系统必然是有特定功能和有序的,只是其内在规律并未充分外露。
有些随机量、无规则的干扰成分以及杂乱无章的数据列,从灰色系统的观点看,并不认为是不可捉摸的。
相反地,灰色系统理论将随机量看作是在一定范围内变化的灰色量,按适当的办法将原始数据进行处理,将灰色数变换为生成数,从生成数进而得到规律性较强的生成函数。
例如,某些系统的数据经处理后呈现出指数规律,这是由于大多数系统都是广义的能量系统,而指数规律是能量变化的一种规律。
灰色系统理论的量化基础是生成数,从而突破了概率统计的局限性,使其结果不再是过去依据大量数据得到的经验性的统计规律,而是现实性的生成律。
这种使灰色系统变得尽量清晰明了的过程被称为白化。
目前,灰色系统理论已成功地应用于工程控制、经济管理、未来学研究、生态系统及复杂多变的农业系统中,并取得了可喜的成就。
灰色预测模型案例

1.1.5 两岸间液体化工品贸易前景预测从上述分析可见,两岸间液体化工品贸易总体上呈现上升的增长趋势。
然而,两岸间的这类贸易受两岸关系、特别是台湾岛内随机性政治因素影响很大。
因此,要对这一贸易市场今后发展的态势做出准确的定量判断是相当困难的;但从另一方面来说,按目前两岸和平交往的常态考察,贸易作为两岸经济与贸易交往的一个有机组成部分,其一般演化态势有某些规律可寻的。
故而,我们可以利用其内在的关联性,通过选取一定的数学模型和计算方法,对之作一些必要的预测。
鉴此,本研究报告拟采用一定的预测技术,借助一定的计算软件,对今后10余年间大陆从台湾进口液化品贸易量作一个初步的预测。
(1) 模型的选择经认真考虑,我们选取了灰色系统作为预测的技术手段,因为两岸化工品贸易具有的受到外界的因素影响大和受调查条件限制数据采集很难完全的两大特点,正好符合灰色系统研究对象的主要特征,即“部分信息已知,部分信息未知”的不确定性。
灰色系统理论认为,对既含有已知信息又含有未知信息或不确定信息的系统进行预测,就是在一定方位内变化的、与时间有关的灰色过程进行的预测。
尽管这一过程中所显示的现象是随机的,但毕竟是有序的,因此这一数据集合具有潜在的规律。
灰色预测就是利用这种规律建立灰色模型对灰色系统进行预测。
本报告以灰色预测模型,对两岸间化工品贸易进行的预测如下: 灰色预测模型预测的一般过程为: ① 一阶累加生成(1-AGO ) 设有变量为)0(X的原始非负数据序列)0(X =[)1()0(x ,)2()0(x ,…)()0(n x ] (1.1)则)0(X的一阶累加生成序列)1(X =[)1()1(x ,)2()1(x …)()1(n x ] (1.2)式中)()(1)0()1(i x k x ki ∑== k=1,2…n② 对)0(X进行准光滑检验和对进行准指数规律检验设)1()()()1()0(-=k x k x k ρ k=2,3…n (1.3) 若满足)(k ρ<1、)(k ρ∈[0,ε](ε<0.5),)(k ρ呈递减趋势,则称)0(X 为准光滑序列,则)1(X具有准指数规律。
实验指导书-实验09 灰色预测方法
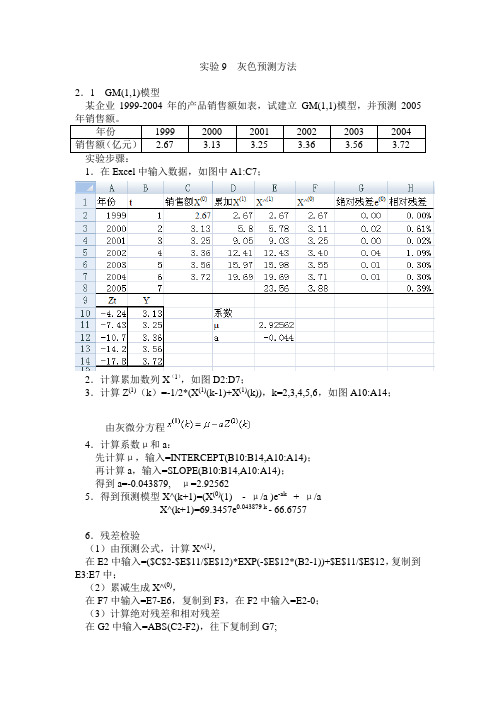
实验9 灰色预测方法2.1 GM(1,1)模型某企业1999-2004年的产品销售额如表,试建立GM(1,1)模型,并预测20051.在Excel中输入数据,如图中A1:C7;2.计算累加数列X(1),如图D2:D7;3.计算Z(1)(k)=-1/2*(X(1)(k-1)+X(1)(k)),k=2,3,4,5,6,如图A10:A14;由灰微分方程4.计算系数μ和a:先计算μ,输入=INTERCEPT(B10:B14,A10:A14);再计算a,输入=SLOPE(B10:B14,A10:A14);得到a=-0.043879, μ=2.925625.得到预测模型X^(k+1)=(X(0)(1) - μ/a )e-ak + μ/aX^(k+1)=69.3457e0.043879 k - 66.67576.残差检验(1)由预测公式,计算X^(1),在E2中输入=($C$2-$E$11/$E$12)*EXP(-$E$12*(B2-1))+$E$11/$E$12,复制到E3:E7中;(2)累减生成X^(0),在F7中输入=E7-E6,复制到F3,在F2中输入=E2-0;(3)计算绝对残差和相对残差在G2中输入=ABS(C2-F2),往下复制到G7;在H2中输入=G2/C2,往下复制到H7中;计算平均相对残差,在H8中输入=SUM(H2:H7)/6。
由平均相对残差为0.39%,而第6期残差为0.3%,均小于1%,因此模型优秀,预测精度高。
7.预测2005年时,k=7,X(1)(8)=23.56X(0)(8)=X(1)(8)-X(1)(7)=3.88亿元。
2.2 灾变预测某地区年降水量数据小于390mm为旱灾年,由历史数据得到第1,9,15,16,18,23年发生了旱灾,先建立旱灾灰色预测模型,并预测下一次旱灾出现到年份。
实验步骤:1.在Excel中输入数据,如图中A1:B7;2.计算累加数列X(1),如图C2:C7;3.计算Z(1)=-1/2*(X(1)(k-1)+X(1)(k)),k=2,3,4,5,6,由灰微分方程4.计算系数μ和a:先计算μ,输入=INTERCEPT(B11:B15,A11:A15);再计算a,输入=SLOPE(B11:B15,A11:A15);得到a=-0.043879, μ=2.925625.得到预测模型X^(k+1)=(X(0)(1) - μ/a )e-ak + μ/aX^(k+1)=51.6772e0.188422 k – 50.67736.残差检验(1)由预测公式,计算X^(1),在D2中输入=($B$2-$F$23/$F$22)*EXP(-$F$22*(A2-1))+$F$23/$F$22,复制到D3:D7中;(2)累减生成X^(0),在E7中输入=D7-D6,复制到D3,在E2中输入=D2-0;(3)计算绝对残差和相对残差在F2中输入=ABS(B2-D2),往下复制到F7;在G2中输入=F2/B2,往下复制到G7中;计算平均相对残差,在G8中输入=SUM(G3:G7)/5。
灰色模型建模例题

灰色模型建模例题灰色模型是一种基于时间序列数据的预测方法,通过对序列数据的灰度化和建模,可以对未来的趋势进行预测和分析。
下面是一个灰色模型建模的例题:假设有一家服装公司,过去3年的销售额数据如下:年份销售额2018 100万2019 120万2020 135万现在需要利用灰色模型对2021年的销售额进行预测。
解答步骤如下:1. 灰度化处理:将原始数据进行一次累加得到累加数据:100, 220, 355。
可以发现累加数据的增长幅度不稳定,不适合直接进行建模,因此需要进行灰度化处理。
利用紧邻平均法进行灰度化处理,得到灰度数据:100, (100+220)/2 = 160, (220+355)/2 = 287.5。
2. 建立灰色模型:根据得到的灰度数据,可以建立灰色模型进行预测。
常用的灰色模型有GM(1,1)模型和GM(0,1)模型。
假设选取GM(1,1)模型,根据灰度数据建立差分方程:x(k+1) + a * x(k) = b,其中x(k)为累加数据,a为发展系数,b为灰色作用量。
代入灰度数据可得:160 + a * 100 = b,287.5 + a * 160 = b。
解上述方程组可以得到a ≈ 0.5754,b ≈ 100.0128。
进一步求取预测模型:x(k+1) = (x(0) - b/a) * exp(-a * k) + b/a。
代入x(0) = 355,k = 3,a ≈ 0.5754,b ≈ 100.0128可得:x(4) = (355 - 100.0128 / 0.5754) * exp(-0.5754 * 3) + 100.0128 / 0.5754 ≈ 140.36。
3. 预测销售额:根据建立的灰色模型,将k取为4进行预测,可以得到2021年的销售额预测值为140.36万。
通过灰色模型建模分析,得出2021年的销售额预测为140.36万。
灰色预测模型相关技术研究的开题报告

灰色预测模型相关技术研究的开题报告一、选题背景近年来,随着社会经济发展水平不断提高,我们的生活中出现的许多问题都越来越复杂,需要采用更多的技术手段去解决。
在这种情况下,灰色预测模型作为一种非参数、小样本预测方法,逐渐引起了学术界和工业界的广泛关注。
灰色预测模型不仅具有运算简便、计算速度快、适用性广等优点,而且在预测结果精度方面也表现出了突出的特点,因此在可靠性要求不是过高的情况下,灰色预测模型也可以取得较好的预测效果。
由于灰色预测模型涉及到的理论较为复杂,所以在实际应用中需要针对具体问题进行适当的模型改进、参数选择等处理。
因此,对灰色预测模型相关技术进行研究,对于提升其在实际应用环境中的准确性和可靠性具有重要意义。
二、研究内容本次研究将主要关注以下内容:1. 灰色预测模型的基本原理及其推导过程。
2. 对现有的灰色预测模型进行系统的分类与整理,包括灰色模型GM(1,1)、灰色马尔科夫模型等。
3. 对于每种灰色预测模型,详细研究其参数选择方法和模型修正方法,并通过实例进行验证和分析。
4. 结合实际问题,针对灰色预测模型在实际应用中所遇到的问题进行研究。
例如,如何应对样本量较小、数据质量低、误差累积等问题。
5. 利用R、MATLAB等工具对灰色预测模型进行实现和分析,并对比灰色预测模型与其他预测模型的预测准确性。
三、研究意义通过对灰色预测模型相关技术的深入研究,对于解决实际问题具有重要意义,具体表现在以下几个方面:1. 对于那些数据量较小、具有一定规律性但又不够规律的问题,灰色预测模型能够提供一种较为可靠的预测方法,可以更好地实现分析与决策。
2. 研究灰色预测模型的参数选择方法和模型修正方法,可以更好地提高灰色预测模型的应用范围和预测准确性。
3. 对比灰色预测模型与其他预测模型的预测准确性,可以更好地了解灰色预测模型的优点和缺点,并选用最优的预测模型。
4. 通过改进和优化灰色预测模型,在实际应用中提高其准确性和可靠性,从而更好地为社会经济发展提供支撑和保障。
统计专业实验实验9-灰色预测分析-叶勇
-11682
966
-12844
1358
-15544
4042
-18201.5
1273
-19198
720
-19835
554
-20343.5
463
-20916
682
-22108
1702
-23255
592
-24027
952
-24707
408
-25111
400
-27634.5
4647
1999
667.01
2005
1215.76
2011
3487.81
2000
719.95
2006
1403.58
2012
3961.19
2001
782.31
2007
1661.23
2013
4511.77
2002
853.60
2008
2064.09
2014
5096.2
2015
6424.02
实验步骤:
1.在Excel中A1:C8输入数据
万立方米。再通过累减可得预测的径流量小于1000万立方米的年份为2008年其值为:987.2146
结果如下表:
序号
年份
径流量X(0)
累加X(1)
X^(1)
X^(0)
绝对残差e(0)
相对残差
1
1984
1761
1761
1761
1761
0
0
2
1985
2187
3948
3640.867
1879.867
307.1334356
预测的灰色模型用于食品质量安全检查数据分析

食品质量安全抽检数据分析摘要针对问题一,对深圳市这三年各主要食品领域微生物、重金属、添加剂含量等安全情况的变化趋势做出定量的综合评价,首先对数据处理按季节分为17个子样本点的抽样值进行分析,得到各子样本食品安全情况。
运用分层抽样决定食品安全单位指标在综合评价中权重,得到深圳市近三年来的食品质量情况应是明显提高。
针对问题二,我们先通过MATLAB对原始数据进行检验,运用MATLAB进行编程,得到各因素的偏回方和。
可以得到,在食品质量影响因素中食品产地影响最大,食品加工次之,季节影响最小,抽查地点几乎无影响。
针对问题三,由问题一、二结果可以通过建立抽检模型,即改进后的规准型抽样检验模型,并以蒙特卡罗法对抽检的全过程进行模拟。
可以得到相对误差逐渐趋向于0。
本文运用多种数学模型,在研究气象预报、地震预报、自动控制等,都可以用到此模型,而且通过它可以对食品安全质量进行预报和分析,有利于城市的食品安全质量监控,真正让百姓吃得放心,用得开心,生活舒心。
关键字:统计最小二乘法拟合分层抽样1 问题重述“民以食为天”,食品安全关系到千家万户的生活与健康。
随着人们对生活质量的追求和安全意思的提高,食品安全已成为社会关注的热点,也是政府民生工程的一个主题。
城市食品的来源越来越广泛,人们消费加工好的食品的比例也越来越高,因此除食材的生产收获外,食品的运输、加工、包装、贮存、销售以及餐饮等每一个环节皆可能影响食品的质量与安全。
另一方面,食品质量与安全又是一个专业性很强的问题,其标准的制定和抽样检测及评价都需要科学有效的方法。
深圳是食品抽检、监督最统一、最规范、最公开的城市之一。
请下载2010年、2011年和2012年深圳市的食品抽检数据(注意蔬菜、鱼类、鸡鸭等抽检数据的获取),并根据这些资料来讨论:◆如何评价深圳市这三年各主要食品领域微生物、重金属、添加剂含量等安全情况的变化趋势;◆从这些数据中能否找出某些规律性的东西:如食品产地与食品质量的关系;食品销售地点(即抽检地点)与食品质量的关系;季节因素等等;◆能否改进食品抽检的办法,使之更科学更有效地反映食品质量状况且不过分增加监管成本(食品抽检是需要费用的),例如对于抽检结果稳定且抽检频次过高的食品领域该作怎样的调整?2 问题分析第一问根据2010,2011,2012年的数据统计综合来看,由于每次的数据统计项目不同,从而导致了不同领域的合格产品统计有所难度,而且期数也不同,导致了数据拟合有难度。
灰色系统预测模型实验

实验四1. 实验项目名称 灰色系统预测模型 2.实验目的要求掌握灰色系统检验方法,尤其是GM(1.1)模型 2. 实验环境使用灰色系统理论建模软件 4.实验内容与实验步骤1.灰色预测时关于残差、关联度、方差比和小误差概率的检验准则M(1,1)模型的检验分为三个方面:残差检验;关联度检验;后验差检验。
(1)残差检验:对模型值和实际值的残差进行逐点检验。
首先按模型计算(1)ˆ(1)xi +,将(1)ˆ(1)xi +累减生成(0)ˆ()x i ,最后计算原始序列(0)()x i 与(0)ˆ()x i 的绝对残差序列及相对残差序列,并计算平均相对残差。
给定α,当φα<,且n φα<成立时,称模型为残差合格模型。
(2)关联度检验:即通过考察模型值曲线和建模序列曲线的相似程度进行检验。
按前面所述的关联度计算方法,计算出(0)ˆ()x i 与原始序列(0)()x i 的关联系数,然后算出关联度,根据经验,关联度大于0.6便是满意的。
(3)后验差检验:即对残差分布的统计特性进行检验。
若对于给定的00C >,当0C C <时,称模型为均方差比合格模型;如对给定的00P >,当0P P >时,称模型为小残差概率合格模型。
若相对残差、关联度、后验差检验在允许的范围内,则可以用所建的模型进行预测,否则应进行残差修正。
2.实验的基本程序、基本步骤和运行结果现在已知我国从2002年-2013年的每年的专利申请量的数据,试建立灰色预测模型并且预测2014年我国的专利申请量的情况。
2.1在excel 表格中输入以下数据2.2计算并累加设时间序列为X(0)=(x(0)(1), x(0)(2), x(0)(3),x(0)(4)………………………………. x(0)(12))=(205396,251238,278943,345074…………… 1505574)计算并累加X(0)的1-AGO序列为(累加)(1)(1)(1)(1)(1)x(1)(12))得到下图2.3对X(1)做紧邻均值生成令Z(1)(k)=(0.5x(1)(K)+0.5X(1)(K-1)),k=1,2,3,4…….13;2.4计算灰微分方程打开灰色系统理论建模软件,找到GM(1.1)模型,在第一行输入205396,251238,278943,345074,383157,470342,586734,717144,877611,1109428,1411080, 1792177,2083483得到方程X (0)(K)-0.2099Z (1)(K)=138316.4494即模型的方程为X^(k+1)=1044777.462*e 0.2140k-839381.4621 2.5估计值运算(1)由预测公式,计算X^(1),在E2中输入=($C$2-$E$11/$E$12)*EXP(-$E$12*(B2-1))+$E$11/$E$12,复制到E3:E7中;(2)累减生成X^(0),在F7中输入=E7-E6,复制到F3,在F2中输入=E2-0;3.模型检验3.1检验一:残差和相对残差检验 原始序列X (0)=(x (0)(1), x (0)(2), x (0)(3),x (0)(4)………………………………. x (0)(12)) 相应的银行模拟序列(0)(0)(0)(0)(0)ˆˆˆˆˆ(1)(2)(3)..............(12)XX X X X =+++ 残差为X (0)-(0)ˆX,得出残差序列如下相对残差(X (0)-(0)ˆX)/X (0)由平均相对残差为0.7551%,而第12期残差为1.2707%,均远小于5%,因此模型较好,预测精度高。
灰色预测模型实验以及例题分析实验报告

1.0691 1.2371
预测数据与实际数据的比较图如下:
2.P3-2(P34)
结果如下:
a=-0.0624
b =156.6162
预测数据与实际数据的比较图如下:
3.预测与会代表人数”(P35)
结果如下:
G=
Columns 1 through 9
0.1810 0.1980 0.1735 0.1520 0.1331 0.1166 0.1021 0.0895 0.0784
实验名称
灰色预测模型实验
实验目的
用MATLAB编程验证程序P3-1(P32)及P3-2(P34),并用其解决“预测与会代表人数”(P35)问题。
学会使用matlab编程做灰色预测实验。
实验内容(算法、程序、步骤和方法)
实验内容(算法、程序、步骤和方法)
实验内容(算பைடு நூலகம்、程序、步骤和方法)
1.P3-1(P32)
D=A;D(1)=[];
D=D';
E=[-C;ones(1,n-1)];
c=inv(E*E')*E*D;
c=c';
a=c(1);b=c(2); %预测后续数据
F=[];F(1)=A(1);
for i=2:(n+10)
F(i)=(A(1)-b/a)/exp(a*(i-1))+b/a;
end
G=[];G(1)=A(1);
for i=2:(n+10)
G(i)=F(i)-F(i-1); %得到预测出来的数据
end
t1=1:4;
t2=1:14;
G
plot(t1,A,'o',t2,G) %原始数据与预测数据的比较
例题灰色预测

某开发区2007年四个季度的用电量如下表:试用灰色预测模型进行预测,并进行模型精度的后验差检验与预测结果的相对误差检验。
解:第一步,计算原始数列)0(x 的累加生成值。
(0)(0)(0)(0)(0)(1),(2),(3),(4)x x x x x ⎡⎤=⎣⎦=(19.67,18.22,18.56,19.22)则)0(x 的1—AGO 为(1)(0)(1)(1)19.67x x ==(1)(1)(0)(2)(1)(2)37.89x x x =+=(1)(1)(0)(3)(2)(3)56.45x x x =+=(1)(1)(0)(4)(3)(4)75.67x x x =+= (3分)第二步,计算数据矩阵B 和数据向量Yn 。
采用GM (1,1)模型所对应的数据矩阵为(1)(1)(1)(1)(1)(1)1(1)(2)1228.7811(2)(3)147.171266.0611(3)(4)12x x B x x x x ⎛⎫⎡⎤-+ ⎪⎣⎦-⎛⎫ ⎪ ⎪ ⎪⎡⎤=-+=-⎣⎦ ⎪ ⎪ ⎪- ⎪⎝⎭ ⎪⎡⎤-+ ⎪⎣⎦⎝⎭18.2218.5619.22Yn ⎛⎫⎪= ⎪ ⎪⎝⎭ (3分)第三步,计算GM (1,1)微分方程的参数aˆ和u ˆ。
将B 、Yn 代入式可得0.02686ˆ17.39515A -⎡⎤=⎢⎥⎣⎦(3分)第四步,建立灰色预测模型至此,可求解白化微分方程,首先得到累加数列)1(x 的灰色预测模型为a u e a u x k x k a ˆˆˆˆ)1()1(ˆˆ)0()1(+⎥⎦⎤⎢⎣⎡-=+- (k=0,1,2,…) 将有关数据代入后得(1)0.02686ˆ(1)667.2936647.6236k xk e +=- 再由)(ˆ)1(ˆ)1(ˆ)1()1()0(k x k x k x-+=+得原始数列的灰色预测模型为 (0)0.026860.02686ˆ(1)667.2936(1)k xk e e -+=- (k=0,1,2,…) (5分) )(ˆ)1(ˆ)1(ˆ)1()1()0(k x k x k x-+=+ k a a e au x e ˆ)0(ˆ)ˆˆ)1()(1(---= (k=0,1,2,…) 由此两模型可得)(ˆ)0(k x的模型值)(ˆ)0(k x模型值计算表第五步,模型精度的后验差检验。
灰色预测模型案例

2006
644.3
2007
736.2
2008
805.4
数据来自表 2-1 ① 累加生成 对数列 X
(0)
=[166.7 214.6,256.3,342.8,406.4,644.3,736.2,805.4]累加生成
X (1) =[166.7 381.3 637.6 980.4 1386.4 2030.7 2766.9 3572.3]
预测,依次递补,直到完成预测的目标为之。
(2) 以总进口量为例预测 表 1-4 年份 进口总量 1995 22.8 1996 30.5 祖国大陆从台湾地区进口有机化学品贸易统计量 1997 21.7 1998 22.1 1999 40.8 2000 93.1 2001 166.7 2002 214.6 2003 256.3 单位:万吨 2004 342.8 2005
S x2
则后验差比值 越好。
表 1-3 指标 一级 二级 三级 四级 ⑥ 等维新信息递推 去掉 X
(0)
精度检验等级参考表 评价 好 合格 勉强 不合格 c 0.35 0.50 0.65 0.80 p 0.95 0.80 0.70 0.60
的首值,增加 x
ˆ ( 0 ) (k 1) 为 X ( 0 ) 的末值,保持数列的等维,新陈代谢,逐个
x '( 0 ) ( k )
并且将 x
(0)
1 ( x(k ) x(k 1) ... x(n)) n k 1
k=1,2…n
(1.4)
(k ) = x'( 0 ) (k ) ,即 X ( 0 ) 由 X '( 0 ) 所替代。
(1)
③ 由第 2 步可知, X 一阶线性微分方程
灰色预测方法实验报告

灰色预测方法实验报告实验报告:灰色预测方法一、实验目的通过使用灰色预测方法,对某个问题进行预测,并分析预测结果的准确性。
二、实验原理灰色预测方法是一种基于数据的预测方法,用于在缺乏足够数据的情况下对未来趋势进行预测。
该方法主要基于灰色系统理论,通过对数据序列进行灰色分析,找出其内在规律,并建立预测模型。
三、实验步骤1. 收集相关数据:首先,需要收集与要预测的问题相关的数据,包括历史数据和现有数据。
2. 数据预处理:对收集到的数据进行清洗和处理,确保数据的准确性和可靠性。
3. 灰色分析:使用灰色分析方法对数据进行处理,包括建立灰色模型、计算关联度等步骤。
4. 模型建立:基于灰色分析的结果,建立预测模型。
5. 验证模型:使用部分历史数据进行模型验证,评估模型的准确性和可靠性。
6. 进行预测:根据建立的模型,对未来一段时间内的数据进行预测。
7. 分析结果:对预测结果进行分析,并评估预测的准确性和可行性。
四、实验结果通过实验,我们成功应用了灰色预测方法对某个问题进行了预测,并得到了如下结果:1. 在灰色分析过程中,我们找到了数据序列的内在规律,并建立了预测模型。
2. 模型验证结果显示,该模型在部分历史数据上具有较高的准确性和可靠性。
3. 根据建立的模型,我们对未来一段时间内的数据进行了预测,并取得了一定的准确性。
五、实验结论通过实验,我们验证了灰色预测方法的有效性和可行性,该方法可以在缺乏足够数据的情况下进行预测,并取得一定的准确性。
在实际应用中,我们可以根据实际问题的特点,选择适当的灰色预测方法,并进行合理的预测。
六、实验总结通过本次实验,我们对灰色预测方法有了更深入的了解,并且验证了其在预测问题上的有效性。
实验过程中,我们还需要注意数据的质量和预处理的准确性,以及模型的验证过程,确保预测结果的准确性和可靠性。
灰色预测方法在实际应用中有很大的潜力,可以帮助我们做出合理的预测和决策。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.0691 1.2371
预测数据与实际数据的比较图如下:
2.P3-2(P34)
结果如下:
aห้องสมุดไป่ตู้-0.0624
b =156.6162
预测数据与实际数据的比较图如下:
3.预测与会代表人数”(P35)
结果如下:
G=
Columns 1 through 9
0.1810 0.1980 0.1735 0.1520 0.1331 0.1166 0.1021 0.0895 0.0784
程序如下:
clear
syms a b;
c=[a b]';
A=[89677,99215,109655,120333,135823,159878,182321,209407,246619,300670];
B=cumsum(A);
n=length(A);
for i=1:(n-1);
C(i)=(B(i)+B(i+1))/2;
G;a,b
plot(t1,A,'o',t2,G) %原始数据与预测数据的比较
3.预测与会代表人数”(P35)
由题目可知,本届发来回执的数量为755。根据以往的数据,我们可以得出前四届缺席率(=法拉回执但未与会的代表数/发来回执的代表数)以及未知与会率(=未发来回执但与会的代表数的数量/发来回执的代表数),见下表
end
D=A;D(1)=[];
D=D';
E=[-C;ones(1,n-1)];
c=inv(E*E')*E*D;
c=c';
a=c(1);b=c(2);
F=[];F(1)=A(1);
for i=2:(n+10)
F(i)=(A(1)-b/a)/exp(a*(i-1))+b/a;
end
G=[];G(1)=A(1);
clear
syms a b;
c=[a b]';
A=[0.180952 0.193820 0.183824 0.146273];
B=cumsum(A); %原始数据累加
n=length(A);
for i=1:(n-1);
C(i)=(B(i)+B(i+1))/2; %生成累加矩阵
end %计算待定参数的值
Columns 10 through 14
0.0687 0.0601 0.0527 0.0461 0.0404
z =
628.9942
预测数据与实际数据的比较图如下:
求出第五届预测与会代表数为628.9942人,保守考虑记为629个人。
小结(对本次实验的思考和建议)
使用灰色模型预测得出的结果比较稳定,不仅适用于大量数据的预测,在数据量较少时,也可以进行预测,而且结果也较为准确。灰色预测中很多是关于矩阵的运算,所以使用matlab编程是灰色预测的首选。
指导教师总评:
签名:日期:
for i=2:(n+10)
G(i)=F(i)-F(i-1);
end
t1=1999:2008;
t2=1999:2018;
G
plot(t1,A,'o',t2,G)
2.P3-2(P34)
程序如下:
clear
syms a b;
c=[a b]';
A=[174 179 183 189 207 234 220.5 256 270 285];
结论
(结果)
结论
(结果)
结论
(结果)
1.P3-1(P32)
结果如下:
G=1.0e+006 *
Columns 1 through 9
0.0897 0.0893 0.1034 0.1196 0.1385 0.1602 0.1854 0.2146 0.2483
Columns 10 through 18
0.2873 0.3325 0.3847 0.4452 0.5152 0.5962 0.6899 0.7984 0.9239
F=[];F(1)=A(1);
for i=2:(n+10)
F(i)=(A(1)-b/a)/exp(a*(i-1))+b/a;
end
G=[];G(1)=A(1);
for i=2:(n+10)
G(i)=F(i)-F(i-1); %得到预测出来的数据
end
t1=1995:2004;
t2=1995:2014;
for i=2:(n+10)
G(i)=F(i)-F(i-1); %得到预测出来的数据
end
t1=1:4;
t2=1:14;
G
plot(t1,A,'o',t2,G) %原始数据与预测数据的比较
z=755*(1+G(5)-0.3)
假设求出的未知与会率为x,则可以求出第五届预测与会代表数为z=755×(1+x-0.3)人。
备注或说明(成功或失败的原因、实验后的心得体会)
用matab编写灰色预测程序时,可以完全按照预测模型的求解步骤:1.对原始数据进行累加2.构造累加矩阵和常数向量3.求解灰参数4.将参数带入预测模型进行数据预测。
在对与会代表人数进行预测时,由于数据量较少,所以模型需要改进。
指导教师评分(包括对实验的预习、操作和结果的综合评分):
B=cumsum(A); %原始数据累加
n=length(A);
for i=1:(n-1);
C(i)=(B(i)+B(i+1))/2; %生成累加矩阵
end %计算待定参数的值
D=A;D(1)=[];
D=D';
E=[-C;ones(1,n-1)];
c=inv(E*E')*E*D;
c=c';
a=c(1);b=c(2); %预测后续数据
届数
第一届
第二届
第三届
第四届
缺席率
0.282540
0.323034
0.296569
0.299578
未知与会率
0.180952
0.193820
0.183824
0.146273
由上表可知,缺席率保持在0.3左右,未知与会率变化较大,故假定第五届的缺席率为0.3,对未知与会率用灰色预测模型进行预测,程序如下:
实验名称
灰色预测模型实验
实验目的
用MATLAB编程验证程序P3-1(P32)及P3-2(P34),并用其解决“预测与会代表人数”(P35)问题。
学会使用matlab编程做灰色预测实验。
实验内容(算法、程序、步骤和方法)
实验内容(算法、程序、步骤和方法)
实验内容(算法、程序、步骤和方法)
1.P3-1(P32)
D=A;D(1)=[];
D=D';
E=[-C;ones(1,n-1)];
c=inv(E*E')*E*D;
c=c';
a=c(1);b=c(2); %预测后续数据
F=[];F(1)=A(1);
for i=2:(n+10)
F(i)=(A(1)-b/a)/exp(a*(i-1))+b/a;
end
G=[];G(1)=A(1);
