高中化学竞赛经典讲义晶体结构
高中化学奥赛 晶体结构 专题讲义

高中化学奥赛 晶体结构 专题讲义8. 晶胞的划分将空间点阵划分为晶格,用晶格切割实际晶体,得到一个个并置堆砌的平行六面体,这些平行六面体不再是抽象的几何体,而是包括了晶体的具体组成物质,称为晶胞。
晶胞是晶体结构中的基本重复单位。
素晶胞 复晶胞。
♦ 晶胞不等同于结构基元,它不一定是最小的重复单位,只有素晶胞才是最小的重复单位。
♦ 晶胞一定是平行六面体,不能为六方柱或其它形状,否则不满足并置堆砌的要求。
9. 晶胞的基本要素 晶胞有两个基本要素:①晶胞参数:晶胞的大小和形状。
晶胞参数和点阵参数一致,由a,b,c,α,β,γ规定,即边长和各边间夹角。
②坐标参数:晶胞内部各个原子的坐标位置。
原点指向原子的向量r =xa +yb +zc ,原子坐标参数(x, y, z )。
【例】CsCl 晶胞。
八个顶点上只贡献一个原子,内部一个原子,因此晶胞中含有两个原子。
中心Cs +的坐标参数为:(1/2, 1/2, 1/2)。
如果坐标参数的差别是加1或减1,则这些参数指的是同一种原子,所以对顶点上的Cl-只需用0,0,0表示,不必写出(0,1,0);(0,0,1)。
2. 晶体的宏观对称性① 宏观对称元素 8个是独立的,分别为:1, 2, 3, 4, 6;m ;i (=1);4 ③ 晶系 晶体32个点群分为七类,7个晶系,每个晶系包含若干个点群。
⑴ 立方晶系 晶胞形状:立方体晶胞参数:a =b =c , α=β=γ=90︒特征对称元素:立方体对角线方向上的4个3。
⑵ 六方晶系 晶胞形状:六方晶胞参数:a =b ≠c , α=β=90︒, γ=120︒特征对称元素:上图红色虚线所示方向上的1个6或1个6 ⑶ 四方晶系晶胞参数:a =b ≠c , α=β=γ=90︒ 晶胞形状:四方特征对称元素:上图红色虚线所示方向上的1个4位序的方向:c (4次轴), a (与4次轴垂直), a+b (与4次轴垂直并与第二位方向成45︒)。
高中化学竞赛经典讲义——晶体结构

第五章晶体结构§5-1晶体的点阵理论1. 晶体的结构特征人们对晶体的印象往往和晶莹剔透联系在一起。
公元一世纪的古罗马作家普林尼在《博物志》中,将石英定义为“冰的化石”,并用希腊语中“冰”这个词来称呼晶体。
我国至迟在公元十世纪,就发现了天然的透明晶体经日光照射以后也会出现五色光,因而把这种天然透明晶体叫做"五光石"。
其实,并非所有的晶体都是晶莹剔透的,例如,石墨就是一种不透明的晶体。
日常生活中接触到的食盐、糖、洗涤用碱、金属、岩石、砂子、水泥等都主要由晶体组成,这些物质中的的晶粒大小不一,如,食盐中的晶粒大小以毫米计,金属中的晶粒大小以微米计。
晶体有着广泛的应用。
从日常电器到科学仪器,很多部件都是由各种天然或人工晶体而成,如,石英钟、晶体管,电视机屏幕上的荧光粉,激光器中的宝石,计算机中的磁芯等等。
晶体具有按一定几何规律排列的内部结构,即,晶体由原子(离子、原子团或离子团)近似无限地、在三维空间周期性地呈重复排列而成。
这种结构上的长程有序,是晶体与气体、液体以及非晶态固体的本质区别。
晶体的内部结构称为晶体结构。
晶体的周期性结构,使得晶体具有一些共同的性质:(1) 均匀性晶体中原子周期排布的周期很小,宏观观察分辨不出微观的不连续性,因而,晶体内部各部分的宏观性质(如化学组成、密度)是相同的。
(2) 各向异性在晶体的周期性结构中,不同方向上原子的排列情况不同,使得不同方向上的物理性质呈现差异。
如,电导率、热膨胀系数、折光率、机械强度等。
(3) 自发形成多面体外形无论是天然矿物晶体还是人工合成晶体,在一定的生长条件下,可以形成多面体外形,这是晶体结构的宏观表现之一。
晶体也可以不具有多面体外形,大多数天然和合成固体是多晶体,它们是由许多取向混乱、尺寸不一、形状不规则的小晶体或晶粒的集合。
(4) 具有确定的熔点各个周期内部的原子的排列方式和结合力相同,到达熔点时,各个周期都处于吸热溶化过程,从而使得温度不变。
化学竞赛专题辅导资料——晶体结构

郴州市二中高一化奥班辅导资料——晶体结构(2008-05-28)【涉及概念和内容】根据《化学课程标准》和中学化学教材以及《物质结构与性质》选修教材,晶体结构涉及的内容包括:(1)基本概念:周期性有序排列、晶胞及晶胞类型、晶胞中粒子数的计算、配位数、空隙、堆积方式、晶格能、并置碓砌;(2)堆积方式:面心立方、六方、体心立方和简单立方堆积;(3)晶体种类和性质:金属晶体、离子晶体、分子晶体、原子晶体,自范性、各向异性、金属晶体的导电导热和延展性、X-射线衍射。
这些内容看似零碎,实际上它们有着密切的内在联系,了解和建立它们的关系,对于晶体结构的教与学,深刻理解晶体结构和性质,掌握核心、突出重点都是很重要的。
它们的联系可以用下面的结构表示,其中堆积类型是联系晶体基本概念、基本结构与不同晶体类型的结构和性质的桥梁。
面心立方最密堆积(A1)最密堆积六方最密堆积(A3)体心立方密堆积(A2)简单立方堆积金刚石型堆积(四面体堆积)(A4)一、晶体的结构1、晶体的概念晶体是质点(原子、分子、离子)在空间有规律周期性地重复排列,是具有规则的多面体固体物质。
2自范性:在一定条件下晶体能自动地呈现具有一定对称性的多面体的外形(晶体的形貌)。
非晶体不能呈现多面体的外形。
晶态石英的谱图非晶态石英的谱图3、晶体的点阵结构概念:在晶体内部原子或分子周期性地排列的每个重复单位的相同位置上定一个点,这些点按一定周期性规律排列在空间,这些点构成一个点阵。
点阵是一组无限的点,连结其中任意两点可得一矢量,将各个点阵按此矢量平移能使它复原。
点阵中每个点都具有完全相同的周围环境。
晶体结构= 点阵+ 结构基元结构基元:在晶体的点阵结构中每个点阵所代表的具体内容,包括原子或分子的种类和数量及其在空间按一定方式排列的结构。
(1)直线点阵(2)平面点阵(3)晶胞(晶胞是人为划定的,为平行六面体)空间点阵必可选择3个不相平行的连结相邻两个点阵点的单位矢量a,b,c,它们将点阵划分成并置的平行六面体单位,称为点阵单位。
化学竞赛教程第九讲:晶体结构

几种典型结构型式
干冰(CO2)结构 范德华力型 每个晶胞中CO2的数目为 8×1/8+6×1/2=4 每个CO2周围距离最近且相等的 CO2分子有 个 12
冰(H2O)结构 氢鍵型 四面体骨架结构
空间利用率的计算
• 空间利用率:指构成晶体的原子、离子或分子在整个晶体空间中
所占有的体积百分比。 球体积
空间利用率=
晶胞体积
100%
單位晶格個數
單位晶格含有
2 個原子
1 4
1 8 1 2 8
(1)晶格邊長a與原子半徑r
斜邊長為
a 2
邊長為 a
邊長為 a
(2)晶格邊長a與原子半徑r
斜邊長為 a
2 2
邊長為 a
3a 4 r 3 r a 4
3
對角邊長為
a =3 4r
竞赛大纲 要求
晶体结构。晶胞。原子坐标。晶胞中原子数目或分子数的 计算及与化学式的关系。分子晶体、原子晶体、离子晶体 和金属晶体。原子堆积与晶胞的关系。晶体的堆积与填隙 模型。常见的晶体结构类型,如:NaCl、CsCl、闪锌矿 (ZnS)、萤石(CaF2),低温石英,金刚石,石墨,硒、 冰、干冰、尿素、方解石、钙铁矿、钾、镁、铜等。
求(A2)体心立方晶胞中金属原子的空间利用率
•(1)计算每个晶胞含有几个原子: •• 1 + 8 × 1/8 = 2 • (2)原子半径r 与晶胞边长a 的关系: • 勾股定理: 2a 2 + a 2 = (4r) 2 • 底面对角线平方 垂直边长平方 斜边平方 • 得: 3a 2 16 r 2
配位数为4,空间利用率为34.01%,不是密堆积。这种堆积方式的存在因为 原子间存在着有方向性的共价键力。如Si、Ge、Sn等。边长为a的单位晶胞 含半径
高中化学竞赛课程 无机化学第三章 晶体结构

c. 附加极化:某些含有d电子的阳离子容易被极化变形, 增加了极化作用。
3. 离子极化对化合物性质的影响
(1) 对键型和溶解度的影响
Hale Waihona Puke AgF AgClAgBr
离子型 过渡型 过渡型
极化作用逐渐增强
共价性逐渐增强
颜色加深
AgI 共价型
晶胞: 面心立方晶胞, 含4个(60.5 + 8 (1/8))原子. 配位数:12 空间利用率: 74%
被第二层掩盖的四面体空隙
A
面
心
C
立
方
B
密
A
堆 积
没被第二层掩盖的八面体空隙, 被 第三层掩盖
(b) 六方密堆积 (ABAB…)
晶胞: 六方晶胞, 含6个 (12(1/6) + 2 (1/2) + 3)原子 空间利用率: 74%
堆
体心立方堆积
积
方
式
面心立方密堆积
密置堆积
六方密堆积
(1) 非密置堆积
(a) 简单立方堆积
重叠堆积 简单立方堆积
晶胞: 简单立方晶胞 配位数 : 6 每个角上的原子被8个晶胞共用 晶胞内的原子数:8(1/8)= 1
空间利用率 = 一个原子的体积/立方体的体积 = (4/3 r3)/(2r)3 = 52%
晶胞:在晶体中能代表晶格一切特征的最小单元为晶 胞,晶胞在三维空间中无限重复形成了晶格。
由六个常数描述: 代表长度的a,b,c 代表角度的α ,β,
γ
七种晶系
立方
四方
正交
三方
Cubic
单斜
高中化学竞赛晶体结构课件

• 晶格能越大: 晶格能 q1 q2
r
– 形成的离子晶体越稳定;(离子键越强)
– 熔点越高;
– 硬度越大。
5
离子晶体总结
• 熔点较高 • 沸点较高 • 易脆性 • 溶解性 Some are soluble, some not.
离子晶体的性质还跟离子键的极化有关,极 化越强,离子键越弱,熔沸点越低,溶解性越小。
18
按照液晶的形成条件分类
热致液晶
熔致液晶
采用降温的方法,既将 熔融的液体降温, 当降温到一定程度 后分子的取向有序 化,从而获得液晶 态.
有机分子溶解在溶剂
中,使溶液中溶质 的浓度增加,溶剂 的浓度减小,有机 分子的排列有序而 获得液晶.
19
液晶的三种结构类型(近晶型)
• 近晶型: 由棒状或片状分子组
16
层状结构晶体-石墨 石墨晶体结构
17
液晶
液晶的发现
• 1888年,奥地利植物学家莱尼茨尔在做加
热胆甾醇苯甲酸脂结晶的实验时发现:在 145.5摄氏度时,结晶凝结成浑浊粘稠的液体, 加热到178.5摄氏度时,形成了透明的液体. • 德国物理学家莱曼用偏光显微镜观察时, 发现这种材料有双折射现象,他阐明了这一 现象并提出了“液晶”这一学术用语.
• 某些非金属化合物:
– 碳化硅(SiC)晶体、氮化硼(BN)晶体
• 某些氧化物:
– 二氧化硅( SiO2)晶体、Al2O3
9
3、分子晶体
• 概念
– 分子间以分子间作用力(范德华力,氢 键)相结合的晶体叫分子晶体。
– 构成分子晶体的粒子是分子,粒子间的 相互作用是分子间作用力。
10
分子晶体特点
(1)较低的熔点和沸点 (2)较小的硬度 (3)一般都是绝缘体,熔融状态
高中化学竞赛辅导 第6讲 晶体结构

二、离子晶体
(一)离子晶体的基本特征 1. 占据晶格结点的质点:正、负离子;
质点间互相作用力:静电引力(离子键) 2. 整个晶体的无限分子:
NaCl、CaF2 、 KNO3…为最简式。 3. 晶格能U↑,熔、沸点↑
U =[NAA Z +Z –e 2 (1 – 1/n)] / 40r0
U Z +Z – /r0 (掌握玻恩-哈伯计算) 4. 熔融或溶于水导电。
据勾股定理: ab2 bc2 ac2 得:
2(2 2r )2 42
r 0.414
NaCl(面心立方)晶体
(三)半径比规则(续)
即 r+ / r - = 0.414 / 1= 0.414 时: ① 正、负离子互相接触 ② 负离子两两接触
1. 若 r+ / r - = 0.414 - 0.732 , 6 : 6配位 (NaCl型面心立方)
=
3 a3
34 a3
100% 68%
密度与金属固体的结构
(a) 简单立方:d = m/a3 = (1M/NA)/(2r)3 = M/(8NAr3) (b) 体心立方: d = m/a3 = (2M/NA)/(4r/31/2)3 = 33/2M/(32NAr3) (c) 面心立方: d = m/a3 = (4M/NA)/(81/2r)3 = 4M/(83/2NAr3)
9.1.2 晶体结构的实验测定
2dsinθ=nλ
Sir William (Henry) Bragg 1915 Nobel Prize in Physics
ccd单晶x射线衍射仪
9.2 晶体的基本类型及其结构
按质点种类及质点互相间作用力划分为4类。
全国化学竞赛初赛讲义——晶体结构

全国化学竞赛初赛讲义——晶体结构晶体结构是化学竞赛中的重要内容之一、晶体是指由具有有序排列的原子,分子或离子组成的固态物质,具有规则的几何形状。
晶体结构的了解对于理解物质的性质和反应机理非常重要。
下面是晶体结构的讲义。
一、晶体结构的基本概念晶体的结构由最小的重复单元所组成,这个最小重复单元称为晶胞。
晶体结构中的重复单元之间的关系是平移关系,即晶胞通过平移操作得到整个晶体。
晶体结构可以分为离子晶体结构、共价晶体结构和金属晶体结构三种。
离子晶体由阳离子和阴离子组成,通常具有高熔点和硬度,如NaCl、CaF2等。
共价晶体由原子通过共价键相连形成,通常具有高熔点和硬度,如钻石、石墨等。
金属晶体由金属离子通过金属键相连形成,通常具有良好的导电性和延展性,如Cu、Al等。
二、晶体结构的表示方法1.点阵表示法:用数学点阵表示晶体中原子的相对位置关系。
有三种常见的点阵表示方法:简单立方点阵、面心立方点阵和体心立方点阵。
(1)简单立方点阵:晶胞内只含一个原子,每个原子都在晶体的角落上。
(2)面心立方点阵:晶胞内含有4个原子,每个原子都在晶体的角落和晶胞的中心。
(3)体心立方点阵:晶胞内含有2个原子,其中一个原子在晶体的角落上,另一个原子在晶胞的中心。
2.坐标表示法:用坐标系表示晶体中原子的位置。
在二维平面上,可以使用直角坐标系或斜坐标系表示晶体中原子的位置。
直角坐标系中,原子的位置可以用x和y两个坐标表示;斜坐标系中,原子的位置可以用a和b两个坐标表示。
在三维空间中,晶体中原子的位置通常用直角坐标系表示,即通过x、y和z三个坐标来确定原子的位置。
三、晶体的常见缺陷与晶体的生长晶体中常见的缺陷有点缺陷、线缺陷和面缺陷。
1.点缺陷:晶体中原子在其位置上发生的缺失、置换、插入或附加等现象。
(1)缺失缺陷:晶体中缺少一个原子。
(2)置换缺陷:晶体中一个原子被其他原子所替代。
(3)插入缺陷:晶体中多了一个原子。
(4)附加缺陷:晶体中多了一个原子,同时缺少一个原子。
高中化学竞赛经典讲义——晶体结构

高中化学竞赛经典讲义——晶体结构晶体结构是高中化学竞赛中一个非常重要的知识点。
晶体是由一定数量的离子、分子或原子按照一定的几何排列方式所组成的固体,其最具有代表性的性质就是具有规则的几何形状。
晶体结构的了解对于理解晶体的性质、结构与合成具有重要意义。
晶体结构的揭示是通过实验技术以及理论研究来实现的。
其中最重要的实验手段是X射线衍射。
当X射线穿过晶体时,会产生衍射现象,出现一系列亮斑,这些亮斑的位置和强度依赖于晶体结构。
通过对衍射图像的解析,可以确定晶胞参数,揭示出晶体内部的几何排列。
理论上,可以使用动力学理论计算晶体的结构,得出一系列理论結构参数。
实验与理论的比较可以验证理论的正确性,并进一步完善理论模型。
晶体结构是有一定规律的,可以分为离子晶体和共价晶体两种类型。
离子晶体是由正离子和负离子通过离子键结合而成的晶体。
离子晶体的结构稳定,离子之间的排列有一定的规则。
若正离子与负离子的离子半径比较接近,离子晶体的结构会较紧密,例如氯化钠、氟化钙等。
若离子半径比差异较大,离子晶体的结构则会较为散松,例如氧化银、氧化铅等。
共价晶体是由原子通过共价键结合而成的晶体。
共价晶体的原子之间的键长和键角与几何排列有密切关系。
晶体结构可以通过晶胞参数来描述。
晶胞是晶体的最小重复单元,其正六面体的两边长度为a,与该边垂直的四棱面间的夹角为90°,而与该边相邻的两棱面间的夹角为120°。
晶胞参数a、b、c分别代表了晶体沿三个坐标轴方向的长度,而α、β、γ代表了晶体坐标轴之间的夹角。
晶体结构的描述还需要引入晶体结构中的间隙。
间隙是晶胞中没有原子、离子或分子占据的空隙,可以是正交的,也可以是六角形的。
晶胞中间隙的存在对于许多晶体性质有着重要影响,例如导电性、光学性质等。
为了更好的理解晶体结构,可以引入晶体结构分类的一些基本概念。
首先是晶格点的概念,晶格点是描述晶体排列的重要参考点。
晶格参数是晶体中两个晶格点之间的最短距离,而晶格的基元则是指两个相邻晶格点之间的最短距离。
化学竞赛——晶体结构

化学竞赛——晶体结构化学竞赛,晶体结构晶体结构是化学竞赛中的一个重要知识点,它涉及到晶体的组成、结构、性质等方面。
下面我将详细介绍晶体结构的相关知识。
晶体是由原子、离子或分子按照一定的几何规律排列而形成的具有固定形状和结构的物质。
晶体的结构可以分为晶格和晶胞两个层面。
晶格是指晶体中的原子、离子或分子的排列方式。
晶格可以分为三种类型:点阵、空间点阵和布拉维格子。
点阵是指晶体中原子、离子或分子的周期性排列形式,可以分为平面点阵、体心点阵、面心点阵等。
空间点阵是三维空间中具有平移对称性的点的集合,它可以由平面点阵通过添加一个垂直于平面的平移矢量得到。
布拉维格子是指空间中按照一定的几何规律分布的点,它由空间点阵通过移动原点所得到。
晶胞是晶体中一个最小的、具有完整晶体结构的单位。
晶胞可以分为简单晶胞、面心立方晶胞、体心立方晶胞等。
简单晶胞是指由一个或多个原子组成,没有原子在晶体内的重合部分的晶胞。
面心立方晶胞是指在体心立方晶胞的基础上,在每个体心加入了一个原子的晶胞。
体心立方晶胞是指在每个面心和一个体心分别加入一个原子的晶胞。
晶体结构可以通过X射线衍射、电子衍射等实验手段进行研究。
通过这些实验可以确定晶体中原子、离子或分子的位置和排列方式,从而揭示晶体的结构和性质。
晶体结构还可以用来解释化学反应的发生过程。
例如,固态反应与气态反应相比,通常速度较慢。
原因是固态反应需要克服晶体结构的稳定性,使反应物分子能够进入晶体内部,而气态反应则不受晶体结构的限制。
除了晶体结构,晶体中还存在一些缺陷,如点缺陷、线缺陷和面缺陷。
点缺陷是晶体中原子或离子位置的缺陷,如空位、空隙等。
线缺陷是晶体中原子或离子位置的缺陷,如缺陷线、螺旋线等。
面缺陷是晶体中晶面的缺陷,如晶界、孪晶等。
总之,晶体结构是化学竞赛中的一个重要知识点。
它涉及到晶体的组成、结构、性质等方面,对于理解物质的性质和变化过程具有重要意义。
同时,晶体结构的研究也为合成新材料、开发新技术提供了重要的理论基础。
高中化学竞赛-晶体结构,晶胞
高中化学奥林匹克竞赛辅导晶体结构【学习要求】晶胞中原子数或分子数的计算及化学式的关系(均摊法)。
分子晶体、原子晶体、离子晶体和金属晶体。
配位数。
晶体的堆积与填隙模型。
常见的晶体结构类型,如NaCl 、CsCl 、闪锌矿(ZnS)、萤石(CaF 2)、金刚石、石墨、硒、冰、干冰、尿素、金红石、钙钛矿、钾、镁、铜等。
点阵的基本概念。
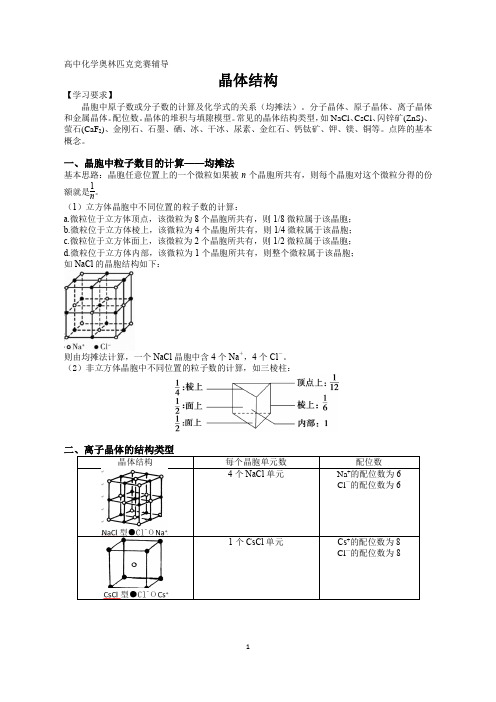
一、晶胞中粒子数目的计算——均摊法基本思路:晶胞任意位置上的一个微粒如果被n 个晶胞所共有,则每个晶胞对这个微粒分得的份额就是1n。
(1)立方体晶胞中不同位置的粒子数的计算:a.微粒位于立方体顶点,该微粒为8个晶胞所共有,则1/8微粒属于该晶胞;b.微粒位于立方体棱上,该微粒为4个晶胞所共有,则1/4微粒属于该晶胞;c.微粒位于立方体面上,该微粒为2个晶胞所共有,则1/2微粒属于该晶胞;d.微粒位于立方体内部,该微粒为1个晶胞所共有,则整个微粒属于该晶胞; 如NaCl 的晶胞结构如下:则由均摊法计算,一个NaCl 晶胞中含4个Na +,4个Cl -。
(2)非立方体晶胞中不同位置的粒子数的计算,如三棱柱:晶体结构离子的电子组态在一定程度上也会影响它的晶体结构,这三个性质综合起来还会决定离子键的共价性成分,后者过分强烈时,将使离子晶体转变为原子晶体,其间存在离子晶体到原子晶体的过渡型。
+-堆积方式简单立方堆积体心立方堆积面心立方最密堆积六方最密堆积四、原子晶体1.金刚石、晶体硅的结构:金刚石的晶体结构如下图所示,每个碳原子以sp3杂化与相邻的4个碳原子形成4个共价键,把晶体内所有的C原子连结成一个整体,形成空间网状结构,这种结构使金刚石具有很大的硬度和熔沸点。
由金刚石晶胞得,在一个金刚石晶胞中,含有8个C原子。
晶体硅具有金刚石型的结构。
只需将金刚石中的C原子换成Si原子即得到硅的结构。
常见的原子晶体有:金刚石(C)、晶体硅(Si)、SiO2、SiC、Si3N4、晶体硼(B)、晶体锗(Ge)、氮化硼(BN)等。
安徽安徽高中化学竞赛无机化学第六章晶体结构基础

安徽安徽高中化学竞赛无机化学第六章晶体结构基础6. 0. 01 晶体的四种差不多类型:依照晶体中微粒之间相互作用的性质,能够将晶体分成4种差不多类型:离子晶体、金属晶体、分子晶体和原子晶体。
6. 1. 01 分子晶体及其物理性质:分子之间以分子间作用力结合成的晶体称为分子晶体。
由于熔、沸点较低,因此分子晶体一样要在较低的温度下才能形成,而在常温时多以气体形式存在。
分子晶体的硬度较小,导电性能一样较差,因为电子从一个分子传导到另一个分子专门不容易。
6. 1. 02 极性分子:分子的正电荷重心和负电荷重心不重合,则为极性分子。
6. 1. 03 偶极矩:极性分子的极性能够用偶极矩m 来度量。
若正电荷(或负电荷)重心上的电荷量为q,正、负电荷重心之间距离即偶极长为d,则偶极矩m = q d6. 1. 04 偶极矩的单位:当d = 1.0 ´10-10 m,即d 为 1 ,q = 1.602 ´10-19 C,即q 为电子的电荷量时,偶极矩m = 4.8 D。
D 为偶极矩单位,称为德拜。
在国际单位制中,偶极矩m以C•m(库仑•米)为单位,当q = 1 C,d = 1 m时,m = 1 C•m。
C•m 与D 这两种偶极矩单位的换算关系为= 3.34 ´10-30 C•m6. 1. 05 永久偶极:极性分子的偶极矩称为永久偶极,偶极矩的矢量方向由正极指向负极。
多原子分子中的大p 键及孤电子对,有时也阻碍分子的偶极矩。
6. 1. 06 诱导偶极:非极性分子在外电场的作用下,能够变成具有一定偶极矩的极性分子,如下面左图所示。
而极性分子在外电场作用下,其偶极矩也能够增大,如下面右图所示。
在电场的阻碍下产生的偶极称为诱导偶极。
6. 1. 07 阻碍诱导偶极的因素:诱导偶极强度大小与电场强度成正比,也与分子的变形性成正比。
所谓分子的变形性,即分子的正、负电荷重心的可分程度。
分子体积越大,电子越多,变形性越大。
全国化学竞赛初赛讲义——晶体结构

全国化学竞赛初赛讲义——晶体结构汕头市潮阳第一中学 谢新民 xxmmy@【初赛要求】晶胞。
原子坐标。
晶格能。
晶胞中原子数或分子数的计算及化学式的关系。
分子晶体、原子晶体、离子晶体和金属晶体。
配位数。
晶体的堆积与填隙模型。
常见的晶体结构类型,如NaCl 、CsCl 、闪锌矿(ZnS )、萤石(CaF 2)、金刚石、石墨、硒、冰、干冰、尿素、金红石、钙钛矿、钾、镁、铜等。
点阵的基本概念。
1.晶胞晶体的外表特征是有一定的、整齐的、有规则的凸多面体外形。
晶体的这种外形是晶体中的原子在微观空间里呈周期性整齐排列的结果,为了表达晶体的微观结构,可以从晶体的微观空间中取出一个基本单位,这种基本单位通常是一个平行六面体(如果只研究二维平面则取平行四边形),称为晶胞。
晶胞是晶体微观结构的代表物,这就决定了:一个晶胞的上下左右前后都有与之完全无隙且并置的形状与内容完全相同的晶胞,或者说整个晶体就是晶胞按一定方式并置而成的。
晶胞是晶体中最小的结构单元,但不是最基本的实体,最基本的实体可以看成是原子、分子、离子或原子团。
简而言之,晶胞是晶体中最小的结构单元,它是一个平行六面体,它按一定方式并置就可以得到整个晶体。
晶胞的最基本特征:【问题与思考】下图中的氯化钠晶胞和金刚石晶胞是分别指实线的小立方体还是虚线的大立方体?【分析与归纳】作为晶胞最基本的特征就是顶角、棱、面之间的无差别性,或者说从一个晶胞平移到另一个晶胞,不会察觉是否平移过了。
因此上图中的实线小立方体不是氯化钠晶胞和金刚石的晶胞,因为它们的顶角不同,图中的虚线大立方体才是。
晶胞有两个基本要素:一是晶胞的大小和形状,二是晶胞的内容(晶胞中有哪些微粒以及它们在晶胞中的分布位置)。
晶胞的大小和形状可用晶胞参数来描述。
晶胞的边长a 、b 、c 及它们之间的夹角α、β、γ就规定了晶胞的大小和形状,这些总称晶胞参数(符号定义如下图所示)。
顶角(8个):每个顶角为8个晶胞共用,8个顶角无任何差别。
全国化学竞赛初赛讲义——晶体结构

全国化学竞赛初赛讲义——晶体结构一、晶体结构的概念和基本特点1.晶体结构的定义:晶体是由重复排列的原胞构成的固体。
2.晶体结构的基本特点:(1)有序性:晶体具有一定的有序性,原子、离子或分子排列有规律。
(2)三维性:晶体结构在三个维度上都有周期性重复性。
(3)稳定性:晶体结构对外界条件的变化具有较高的稳定性。
二、晶体结构的描述和表示方法1.晶胞:晶胞是由原胞重复平移所得到的一个最小重复单元,可以完全描述晶体的结构。
2.原胞:原胞是晶体中重复出现的、具有最简单结构的单元。
3.晶体参数:晶体参数包括晶胞的长度和夹角,用来描述晶体的形状和结构特征。
4.晶格:晶格是由原胞构成的、具有无限重复的空间点阵。
晶格可以用晶面和晶轴来表示。
三、晶体的结构类型和晶系分类1.结构类型:晶体的结构类型有离子晶体、共价晶体、金属晶体和分子晶体等。
2.晶系:晶系是根据晶格的对称性将晶体分为不同的类型。
晶系包括立方系、四方系、单斜系、正交系、斜方系、菱方系和三斜系。
四、晶体的基本结构单元1.离子晶体的基本结构单元是离子。
(1)离子晶体的特点:离子晶体由正、负离子通过电荷吸引力相互结合而成。
(2)离子晶体的类型:离子晶体包括简单离子晶体和复式离子晶体。
2.共价晶体的基本结构单元是原子。
(1)共价晶体的特点:共价晶体由共享电子键结合而成,键强较大。
(2)共价晶体的类型:共价晶体包括晶体分子、网络共价晶体和金刚石型晶体。
3.金属晶体的基本结构单元是金属离子。
(1)金属晶体的特点:金属晶体由金属阳离子和自由移动的电子云组成。
(2)金属晶体的类型:金属晶体包括简单金属晶体和合金。
4.分子晶体的基本结构单元是分子。
(1)分子晶体的特点:分子晶体由分子之间的相互作用力相互结合而成。
(2)分子晶体的类型:分子晶体包括极性分子晶体和非极性分子晶体。
五、晶体的性质与应用1.晶体的性质:晶体具有各向异性、光学性、热学性、电学性等特点。
2.晶体的应用:(1)光学应用:晶体在光学领域有着广泛的应用,如光学仪器、激光技术等。
高中化学竞赛培训晶体结构

立方面心(F)
68
四方简单(P)
四方体心(I)
六方简单 (H)
三方简单 (R)
69
正交简单(P)
正交底心(C)
正交体心(I)
正交面心(F)
70
三斜简单P
单斜简单P
单斜底心C
71
3 晶胞中质点个数的计算
73
4 晶胞的划分深化
• 对称性
晶系
正当晶胞
正当晶胞
素晶胞:含1个结构基元 复晶胞:含2个以上结构基元
74
“晶体的最小重复单位是晶胞” ??? 晶胞的取用条件的先后性:
(1)必须反映晶体的微观对称性 (2)选取尽可能小的体积。
75
4个NaCl!!!
76
2个NaCl!!!
77
体心晶胞
• 体心晶胞中的任何一个原子均可发生体心平移 • 在它的原子坐标 x, y, z 上 分 别 加 ½, ½,½, 所
其中任意两点可得一矢量,将各个点阵按此
矢量平移能使它复原。点阵中每个点都具有
完全相同的周围环境。
25
晶体结构 = 点阵 + 结构基元
结构基元: 在晶体的点阵结构中每个点
阵所代表的具体内容,包括原子或 分子的种类和数量及其在空间按一 定方式排列的结构。
26
27
28
例1、2002年江苏夏令营选拔赛
22
• ⑸有特定的对称性
23
(6)
晶体的周期性结构使它成为天然的三维光
晶
栅,周期与X光波长相当, 能够对X光产生衍射:
体
的
X
射
线
衍
射
效
应
24
三、晶体的点阵结构
高中化学竞赛辅导无机化学8.3晶体结构知识点素材

§8-3 晶体结构The Structures of Crystalline Solids一、基本概念(The Basic Concepts):1.晶体(Crystals):(1)物质的质点(分子、离子或原子)在空间有规则地排列而成的、具有整齐外形的、以多面体出现的固体物质,称为晶体。
(2) 晶体有同质多象性由同样的分子(或原子)可以以不同的方式堆积成不同的晶体,这种现象叫做同质多象性,例如由ZnS组成的闪锌矿和纤维锌矿。
但同一种物质的气态、液态只存在一种结构。
因此在研究晶体时,确定化学成份仅仅是第一步,只有进一步确定其结构,才能深入探讨晶体的性质。
(3) 晶体的几何度量和物理效应常随方向不同而表现出量上的差异,这种性质称为各向异性。
2.晶格(Crystal lattices)(1) 以确定位置的点在空间作有规则的排列所具有一定的几何形状,称为晶体格子,简称为晶格。
Fig. 8.10 The 14 Bravais unit cells(2) 格子分类成平面格子(无数并置的平行四边形)和空间格子(无数并置的平行六面体)。
3.晶胞(Unit cells )(1) 在晶格中,含有晶体结构,具有代表性的最小单元,称为单元晶胞,简称晶胞。
(2) 在晶胞中的各结点上的内容必须相同。
例如:铝是面心立方结构,其晶胞中的六个面心和八个顶点都是铝原子(或铝离子),而NaCl 晶体也是面心立方结构,则六个面心和八个顶点都必须是Na +离子,或都必须是Cl -离子。
(3) 晶胞参数 晶胞参数:a 、b 、c 、α、β、γ根据不同的晶胞参数,Cubic a = b = c ,α = β = γ = 90︒,即晶胞参数为aTetragonal a = b ≠ c ,α = β = γ = 90︒,即晶胞参数为a 、c Orthorhombic a ≠ b ≠ c ,α = β = γ = 90︒,cTrigonal a = b = c ,α = β = γ ≠ 90︒,即晶胞参数为a 、b 、c 、ααβγbc aHexagonal a = b ≠ c ,α = β = 90︒,γ = 120︒,即晶胞参数为a 、cMonoclinic a ≠ b ≠ c ,α = β = 90︒,γ ≠ 90︒,即晶胞参数为a 、b 、c 、γ Tric linic a ≠ b ≠ c ,α ≠ β ≠ γ ≠ 90︒,即晶胞参数为a 、b 、c 、α、β、γ(4) 分数坐标 用来表示晶胞中质点的位置例如: 简单立方 立方体心 立方面心(0, 0, 0),(0, 0, 0) (0, 0, 0), (21,21,21) (21,21,0), (21,0,21), (0,21,21) Fig. 8.11 The coordinates of atoms in the unit cell在分数坐标中,绝对不能出现1,因为1即0。
高中化学竞赛——常见金属晶体的结构

高中化学竞赛——常见金属晶体的结构金属是一种特殊的物质,不像非金属那样具有明确的原子、分子结构,而是由大量的金属离子组成的。
金属晶体是由金属离子通过静电力相互吸引、排列而成的有序三维排列结构。
金属晶体具有许多独特的性质,如良好的导电性、导热性、延展性和机械性能等。
以下是几种常见金属的晶体结构的介绍。
1.面心立方结构(FCC)面心立方结构是一种常见的金属晶体结构,也称为充分面心立方结构。
在FCC晶体中,金属离子位于一个面心立方格子的顶点和面心上,形成四方紧密堆积的结构。
银(Ag)、铝(Al)、铜(Cu)和金(Au)都具有FCC结构。
2.体心立方结构(BCC)体心立方结构是另一种常见的金属晶体结构,也称为充分体心立方结构。
在BCC晶体中,金属离子位于一个体心立方格子的顶点和体心上,形成六方紧密堆积的结构。
铁(Fe)、钴(Co)、钨(W)和钠(Na)都具有BCC结构。
3.紧密堆积结构(HCP)紧密堆积结构是一种相对稳定的金属晶体结构。
在HCP晶体中,金属离子位于六方密排的顶点和六角面上,形成堆积的结构。
锌(Zn)、钛(Ti)和镁(Mg)都具有HCP结构。
4.单斜结构单斜结构是一种稀有的金属晶体结构,通常在少数金属中存在。
在单斜结构中,金属离子位于不同的位置上,形成不规则的结构。
例如,铬(Cr)和钽(Ta)具有单斜结构。
5.其他结构除了上述常见的金属晶体结构外,还存在一些特殊的金属晶体结构。
例如,钻石(C)具有金刚石结构,锌矿石(ZnS)具有闪锌矿结构。
这些结构更加复杂,但仍然是由金属离子有序排列而成的。
总结起来,金属晶体的结构多种多样,常见的包括面心立方结构、体心立方结构和紧密堆积结构。
每种结构都具有不同的特点和性质,这些特点和性质决定了金属的物理、化学性质和用途。
通过研究和了解金属晶体结构,可以更好地理解金属材料的性质和应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章晶体结构§5-1晶体的点阵理论1. 晶体的结构特征人们对晶体的印象往往和晶莹剔透联系在一起。
公元一世纪的古罗马作家普林尼在《博物志》中,将石英定义为“冰的化石”,并用希腊语中“冰”这个词来称呼晶体。
我国至迟在公元十世纪,就发现了天然的透明晶体经日光照射以后也会出现五色光,因而把这种天然透明晶体叫做"五光石"。
其实,并非所有的晶体都是晶莹剔透的,例如,石墨就是一种不透明的晶体。
日常生活中接触到的食盐、糖、洗涤用碱、金属、岩石、砂子、水泥等都主要由晶体组成,这些物质中的的晶粒大小不一,如,食盐中的晶粒大小以毫米计,金属中的晶粒大小以微米计。
晶体有着广泛的应用。
从日常电器到科学仪器,很多部件都是由各种天然或人工晶体而成,如,石英钟、晶体管,电视机屏幕上的荧光粉,激光器中的宝石,计算机中的磁芯等等。
晶体具有按一定几何规律排列的内部结构,即,晶体由原子(离子、原子团或离子团)近似无限地、在三维空间周期性地呈重复排列而成。
这种结构上的长程有序,是晶体与气体、液体以及非晶态固体的本质区别。
晶体的内部结构称为晶体结构。
晶体的周期性结构,使得晶体具有一些共同的性质:(1) 均匀性晶体中原子周期排布的周期很小,宏观观察分辨不出微观的不连续性,因而,晶体内部各部分的宏观性质(如化学组成、密度)是相同的。
(2) 各向异性在晶体的周期性结构中,不同方向上原子的排列情况不同,使得不同方向上的物理性质呈现差异。
如,电导率、热膨胀系数、折光率、机械强度等。
(3) 自发形成多面体外形无论是天然矿物晶体还是人工合成晶体,在一定的生长条件下,可以形成多面体外形,这是晶体结构的宏观表现之一。
晶体也可以不具有多面体外形,大多数天然和合成固体是多晶体,它们是由许多取向混乱、尺寸不一、形状不规则的小晶体或晶粒的集合。
(4) 具有确定的熔点各个周期内部的原子的排列方式和结合力相同,到达熔点时,各个周期都处于吸热溶化过程,从而使得温度不变。
(5) 对称性晶体的理想外形和内部结构具有对称性。
(6) X射线衍射晶体结构的周期和X射线的波长差不多,可以作为三维光栅,使X射线产生衍射现象。
X 射线衍射是了解晶体结构的重要实验方法。
2. 周期性(a)(b)上面两个图形均表现出周期性:沿直线方向,每隔相同的距离,就会出现相同的图案。
如果在图形中划出一个最小的重复单位(阴影部分所示),通过平移,将该单位沿直线向两端周期性重复排列,就构成了上面的图形。
最小重复单位的选择不是唯一的,例如,在图(a)中,下面任何一个图案都可以作为最小的重复单位。
确定了最小的重复单位后,为了描述图形的周期性,可以不考虑重复单位中的具体内容,抽象地用一个点表示重复单位。
点的位置可以任意指定,可以在单位中或边缘的任何位置,但一旦指定后,每个单位中的点的位置必须相同。
如,不论点的位置如何选取,最后得到的一组点在空间的取向以及相邻点的间距不会发生变化。
对图(b)也用同样的方法处理,可以得到完全相同的一组周期性排列的点。
这样的一组抽象的点集中反映了2个图形中重复周期的大小和规律。
以上是一维周期性排列的例子,如果图案在二维的平面上不断重复,也可以用相同的方式处理。
还可以进一步推广的三维的情况。
3. 结构基元在晶体中,原子(离子、原子团或离子团)周期性地重复排列。
上面我们在图形找出了最小的重复单位,类似的,可以在晶体中划出结构基元。
结构基元是指晶体中能够通过平移在空间重复排列的基本结构单位。
【例】一维实例:在直线上等间距排列的原子。
一个原子组成一个结构基元,它同时也是基本的化学组成单位。
结构基元必须满足如下四个条件:化学组成相同;空间结构相同;排列取向相同;周围环境相同。
【例】一维实例:在伸展的聚乙烯链中,-CH2-CH2-组成一个结构基元,而不是-CH2-。
注意,上图所示的聚乙烯链结构中,红色和蓝色的球虽然均表示-CH2-,可它们各自的周围环境并不相同。
上图右侧画出了两种CH2-CH2-CH2片段,其组成和结构相同,但从空间位置关系来看,两者的取向不同,其中一个可由另一个通过旋转180 而得,这表明相邻-CH2-的周围环境不同,因而,-CH2-只是基本的化学组成,而不是结构基元。
【例】二维实例:层状石墨分子,其结构基元由两个C原子组成(相邻的2个C原子的周围环境不同)。
结构基元可以有不同的选法,但其中的原子种类和数目应保持不变。
上图用阴影部分标出了3种选法,但在每种选法中结构基元均含有2个C原子。
如,在第三个图中,六边形的每个角上只有1/3的C原子位于六边形之内,所以平均有2个C原子属于一个六边形。
【例】二维实例:NaCl晶体内部的一个截面。
一个Na+和一个Cl-组成一个结构基元(四边形内部有1个Na+,顶角上的每个Cl-只有1/4属于结构基元)。
【例】二维实例:Cu晶体内部的一个截面。
一个Cu原子组成一个结构基元。
【例】三维实例:Po晶体。
结构基元含1个Po原子。
【例】三维实例:CsCl晶体。
结构基元含1个Cs+和Cl-。
【例】三维实例:金属Na。
每个Na原子的周围环境都相同,结构基元应只含有1个Na原子。
左侧的立方体中含有2个Na原子(每个顶点提供1/8个Na原子,中心提供1个Na原子),它不是结构基元,右侧图中虚线部分包围的平行六面体给出了一种正确的选法。
【例】三维实例:金属Cu (左图所示立方体的每个顶点和每个面的中心有一个Cu原子)。
每个Cu原子的周围环境都相同,结构基元只含有1个Cu原子。
右侧图中虚线部分所示平行六面体为一个结构基元。
【例】三维实例:金刚石。
结构基元含2个C原子(红色和蓝色分别表示周围环境不同的2种C原子)。
这是因为:如右图所示,每个C原子虽然都是以正四面体的形式和周围原子成键,但相邻C原子周围的4个键在空间取向不同,周围环境不同。
4. 点阵确定了结构基元后,可以不管它的具体内容和具体结构,用一个抽象的几何点来表示它,这个点可以是每个结构基元中某个原子的中心、或某个键的中心、或其它任何指定的点,但每个结构基元中点的位置应相同。
这样就抽象出来一组点。
从晶体中无数结构单元中抽象出来的一组几何点形成一个点阵。
每个点称为点阵点(简称阵点)。
点阵反映了晶体中结构基元的周期排列方式。
(二维)层状石墨分子平面点阵(抽象的几何点)点阵:点阵是按周期性规律在空间排布的一组无限多个点,按照连接其中任意两点的向量(矢量)进行平移时,能使点阵复原。
或者说当向量的一端落在任意一个点阵点上时,另一端也必定落在点阵点上。
点阵中每个点具有相同的周围环境。
5. 点阵和晶体结构如前所述,结构基元表示晶体中周期性变化的具体内容,它可以是一个原子,也可以是若干相同或不同的原子,取决于具体的晶体结构;点阵代表重复周期的大小和规律,点阵点是由结构基元抽象出来的几何点。
因此,晶体结构可表示为晶体结构 点阵结构基元=+6. 点阵单位(1) 直线点阵:分布在同一直线上的点阵。
在直线点阵中,连接相邻两个点阵点的向量,称为直线点阵的素向量,用a 表示(晶体学中往往用字母加下划线代表向量)。
2a 、3a 、3a 等称为复向量。
素向量a 的长度a 称为直线点阵的点阵参数。
以任何一个阵点为原点,所有点阵点都落在下式所表示的向量的端点上。
a m T m = (m =0, ±1, ±2, …)上式称为平移群。
这是因为这些向量的集合满足群的定义,构成了一个群,群的乘法规则是向量加法。
按照任何一个向量移动阵点,点阵能与原来位置完全重合。
平移群是点阵的代数形式。
(2) 平面点阵:分布在平面上的点阵。
选择任意一个阵点作为原点,连接两个最相邻的两个阵点作为素向量a ,再在其它某个方向上找到最相邻的一个点,作素向量b 。
素向量b 的选择有无数种方式,如下图中的b 1和b 2均可作为素向量。
素向量a 和b 的长度a 、b ,以及两者的夹角γ=a ∧b ,称为平面点阵的点阵参数。
平面点阵的平移群可表示为b n a m T n m +=, (m,n =0, ±1, ±2, …) 根据所选择的素向量,将各点阵点连上线,平面点阵划分为一个个并置堆砌的平行四边形,平面点阵形成由线连成的格子,称为平面格子。
其中的每个平行四边形称为一个单位。
所谓并置堆砌,是指平行四边形之间没有空隙,每个顶点被相邻的4个平行四边形共用。
下面两种图形都不满足并置堆砌的定义。
由于素向量的选择方式有无数种,因此,平面格子也有无数种,下图为对同一平面点阵画出的2种平面格子。
相应的单位分别为下图所示的平行四边形。
平行四边形单位顶点上的阵点,对每个单位的平均贡献为1/4;内部的阵点,对每个单位的贡献为1。
因此,上图左侧所示的单位只含有一个阵点,这种单位称为素单位;右侧所示的单位含有2个阵点,这种含有2个或2个以上阵点的单位称为复单位。
注意:素向量不一定构成素单位,如上面例子中的复单位就是由素向量构成的。
为方便研究,常采用正当单位,即,在考虑对称性尽量高的前提下,选取含点阵点尽量少的单位。
这要求:①素向量之间的夹角最好是90︒,其次是60︒,再次是其它角度;②选用的素向量尽量短。
对于平面格子,正当单位只有4种形状(5种型式):正方形、矩形、带心矩形、六方和平行四边形。
aa =ba ∧b =90ºa ¹b a ∧b =90ºa ¹b a ∧b =90ºa =b a ∧b =120ºa ¹b a ∧b ¹120º♦ 只有矩形正当单位有带心的(复单位),其它的都是素单位。
如,如果正方形格子带心,一定可以取出更小的正方形素单位。
带心的正方形复单位(非正当单位)更小的正方形素单位(正当单位)(2) 空间点阵:分布在三维空间的点阵。
选择任一点阵点为原点,分别和邻近的3个点阵点相连,构成三个素向量a 、b 、c ,这3个素向量要求互相不平行。
3个素向量的长度a 、b 、c 以及彼此间的夹角α=b ∧ c 、β=a ∧ c 、γ=a ∧ b 称为空间点阵的点阵参数。
空间点阵的平移群可表示为c p b n a m T p n m ++=,, (m,n,p =0, ±1, ±2, …)按照选择的素向量,将点阵点连上线,把空间点阵划分并置堆砌的平行六面体 (这时,每个顶点被八个平行六面体共有),空间点阵形成的由线连成的格子称为晶格。
划分出的每个平行六面体为一个单位。
平行六面体单位顶点上的点阵点,对每个单位的平均贡献为1/8;面上的点阵点对每个单位的贡献为1/2,内部的点阵点,对每个单位的贡献为1。
根据平行六面体单位中包含的点阵点的数目,分为素单位和复单位。
空间点阵的正当单位有七种形状(十四种型式),具体讨论见“晶体的对称性”一节。
