阵列信号处理答案
阵列信号处理的基本知识分析

加性噪声。
将整个阵列的输出信号写成矩阵形式为:
x(t ) As(t ) n(t )
A [a( ),, a( )] 为阵列流行矩阵、空间信 号方向矢量、阵列响应矩阵。
1 P
a( ) [1 e
1 P
j 2 d sin /
,, e
j 2 ( M 1 ) d sin /
式中L为阵列最大口径,F和 为信号中心频率 和该频率对应的波长。 远场假设 即辐射源到阵列的距离远大于阵列的最大口 径,从而入射到阵列的信号波前可近似为平 面波前(d ).
L2
入射信号统计特性 空间入射信号平稳且各态历经,可以用时 间平均代替集合平均。一般还假定各入射 信号统计独立。 E{s(t ) s (t )} diag{ ,, } 噪声统计特性 空时白高斯噪声;色噪声环境下需要稳健 的算法。 E{n(t )n (t )} I
阵元之间的互藕 有关因素:阵元之间的间距大小,系统工作 频段,采用的传感器类型等。 设所有阵元之间的藕合系数矩阵为C,则考 虑到阵元间互藕的阵列输出信号模型为:
x(t ) CAs (t ) n(t )
阵元位置 阵元测向的关键信息是空间信号入射到各阵 元的相对延迟相位,而这一相位依赖于阵元 之间的空间位置,阵元位置误差直接导致延 迟相位估计误差,从而影响信号参数估计。 阵列模糊 阵元间距大于 / 2 时,影响空间信号到达角 的可辨识性和确定性,需要解决阵列模糊问 题。
H 2 2 s1 sP
H 2
信号数目 属于信号检测问题(AIC,MDL,etc),一般 假定先验已知。
二、阵列信号处理的主要内容
信号参数估计(DOA,频率,极化参数,距离, 时延等): 谱估计方法(子空间方法,波束形成 方法),参数化方法(最大似然,基于子空间逼 近方法)。
阵列信号处理
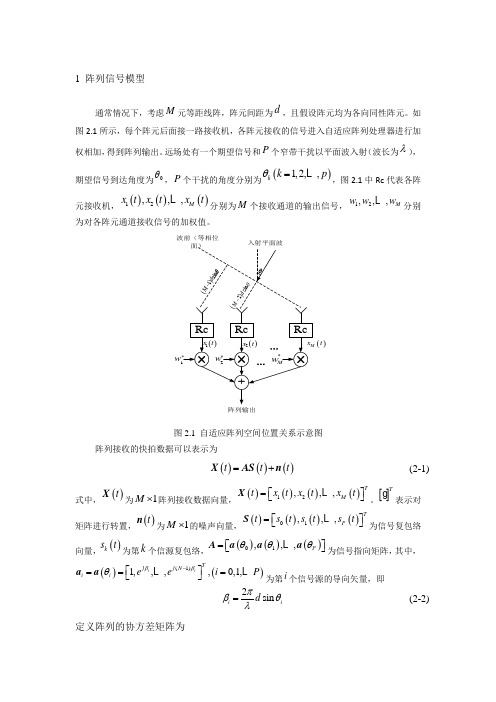
1 阵列信号模型通常情况下,考虑M 元等距线阵,阵元间距为d ,且假设阵元均为各向同性阵元。
如图2.1所示,每个阵元后面接一路接收机,各阵元接收的信号进入自适应阵列处理器进行加权相加,得到阵列输出。
远场处有一个期望信号和P 个窄带干扰以平面波入射(波长为λ),期望信号到达角度为0θ,P 个干扰的角度分别为()1,2,,k k p θ= ,图2.1中Rc 代表各阵元接收机,()()()12,,,M x t x t x t 分别为M 个接收通道的输出信号,12,,,M w w w 分别为对各阵元通道接收信号的加权值。
()t w 阵列输出波前(等相位图2.1 自适应阵列空间位置关系示意图阵列接收的快拍数据可以表示为()()()t t t =+X AS n(2-1)式中,()t X 为1M ⨯阵列接收数据向量,()()()()12,,,TM t x t x t x t =⎡⎤⎣⎦X 。
[]T表示对矩阵进行转置,()t n 为1M ⨯的噪声向量,()()()()01,,,TP t s t s t s t =⎡⎤⎣⎦S 为信号复包络向量,()k s t 为第k 个信源复包络,()()()01,,,P θθθ=⎡⎤⎣⎦A a a a 为信号指向矩阵,其中,()()(1)1,,,,0,1,i iTj j N i i e e i P ββθ-⎡⎤===⎣⎦a a 为第i 个信号源的导向矢量,即2sin i i d πβθλ=(2-2)定义阵列的协方差矩阵为()()2H H x s n E t t σ⎡⎤==+⎣⎦R X X AR A I (2-3)式中,()()H s E t t ⎡⎤=⎣⎦R S S 为信号的协方差矩阵,I 为M 维单位矩阵,2n σ为阵元的噪声功率,本文中约定,[]T表示转置,[]*表示共轭,[]H表示共轭转置。
式(2-3)常由接收数据采样协方差矩阵ˆx R 代替,即()()11ˆNH xiii t t N==∑R x x(2-4)如图2.1所示的自适应阵列模型,阵列的M 个通道接收信号经加权处理后,最后的输出信号为()()()1MH i i i y t w x t t *===∑w x(2-5)阵列的方向图()p θ定义为()()H p θθ=w a(2-6)调整自适应阵列的权矢量w ,可以改变阵列的方向图,即改变各个方向上入射信号增益。
阵列信号处理 psf 点扩散函数 反卷积

阵列信号处理(Array Signal Processing)1. 简介阵列信号处理是一种利用多个传感器或微phones接收到的信号进行处理的技术。
这些传感器通常以阵列的形式排列在一起,可以在空间上对信号进行采样。
阵列信号处理技术可以用于各种应用,包括无线通信、雷达、声音定位和语音增强等领域。
在阵列信号处理中,经常会使用到点扩散函数(Point Spread Function,PSF)和反卷积(Deconvolution)等概念。
本文将详细介绍这些特定函数的定义、用途和工作方式。
2. 点扩散函数(Point Spread Function,PSF)2.1 定义点扩散函数(PSF)是指在观察到一个点源时,系统输出的响应。
点源可以是一个理想的点光源、点声源或点热源等。
PSF描述了系统对于一个点源的感知能力,可以用于评估系统的分辨率和信号传输特性。
2.2 用途PSF在阵列信号处理中具有广泛的应用,主要用于以下几个方面:2.2.1 分辨率评估PSF可以用于评估系统的分辨率,即系统能够分辨并显示的最小特征尺寸。
通过分析PSF的形状和尺寸,可以确定系统的分辨率限制,进而优化系统设计和参数设置。
2.2.2 反卷积PSF还可以用于图像或信号的反卷积处理。
在实际应用中,由于传感器和系统的限制,观测到的信号往往受到模糊和失真的影响。
通过将观测到的信号与PSF进行卷积运算的逆过程,可以恢复出原始信号的更清晰的图像或声音。
2.2.3 信号重构PSF在阵列信号处理中也可以用于信号重构。
通过对多个传感器接收到的信号进行处理和分析,可以利用PSF将信号的不同成分分离出来,从而实现信号的重构和定位。
2.3 工作方式PSF的工作方式可以通过以下几个步骤来理解:2.3.1 系统建模首先,需要对阵列系统进行建模。
这包括确定阵列的几何结构、传感器的位置和响应特性等。
通过建模,可以得到系统的传递函数,即系统对于输入信号的响应。
2.3.2 点源输入接下来,将一个点源输入到系统中,观察系统的输出。
传感器阵列设计与信号处理考核试卷

3. MUSIC算法基于信号子空间和噪声子空间的正交性,通过搜索峰值确定信号源位置。其优势在于高分辨率和抗干扰能力。
4.融合层次包括传感器级、特征级和决策级。传感器级融合提供原始数据集成,特征级融合对提取的特征进行处理,决策级融合进行最终决策。选择取决于系统需求和计算复杂度。例如,对于实时性要求高的系统,可选用决策级融合。
B.逆波束形成
C.频域分析
D.时间域分析
18.传感器阵列中的互模糊函数与以下哪个参数无关?()
A.时间延迟
B.频率偏移
C.传感器间距
D.信号波长
19.在阵列信号处理中,如何定义“旁瓣”现象?()
A.波束图中的主要波瓣
B.波束图中的次要波瓣
C.波束图中的最小值
D.波束图中的零点
20.下列哪种技术通常用于增加传感器阵列的动态范围?()
A.独立成分分析
B.最小方差无畸变响应
C.卡尔曼滤波
D.波束形成
13.哪些因素会影响传感器阵列的波束宽度?()
A.传感器的尺寸
B.阵列的孔径
C.传感器的数量
D.信号的波长
14.以下哪些方法可以用于提高传感器阵列的信号处理速度?()
A.并行处理
B.快速傅立叶变换
C.滤波器组设计
D.硬件加速
15.以下哪些传感器类型适用于温度测量?()
A.电感式传感器
B.压电传感器
C.磁电传感器
D.光电传感器
5.在信号处理中,以下哪些是时间域分析的特点?()
A.对信号的时间历程进行分析
B.对信号的频率成分进行分析
阵列信号考试复习题(全)

H 2
Nd
,利用倍
角公式化简,得到
sin
H 4
,当 Nd
2Nd
,可以得到第一零点位置为
null
H 2
2
。
Nd
10.阵元数较少时(N=4,5,6),波束图怎么画?(最大值,零点)
对于均匀加权的均匀线列阵, B
(
)
1 N
sin( N ) 2
Nd
d
出第一个零点位置为 Nd ,零点-零点波束宽度 BWNN 2 Nd 。
计算第一旁瓣:
Bu (u)
的分子逼近极大值,即
sin( Nd u) 1
,所以
Nd u ( m2 1 )m , 1, ,得2到 ,u 2m 1 , m 1, 2, , 第 一 旁 瓣 出 现 在
7.任意结构阵列,对于远场信号,其Vk 如何推导?
坐标原点的接收信号为: f (t)
阵列接收到的信号向量: f (t, p) [ f (t 0), f (t 1), , f (t N1)]T
sin cos 其中信号入射方向向量: a sin sin , u a
P
V
1 H ununHV
影响算法性能的因素:噪声和信号的相关性,两两阵元之间噪声的相关性,每个阵元的噪声方差是否相同,
阵列本身的流行向量在实际中很难于理论完全相符, S f 是否非奇异,信号个数是否已知,若信号个数位
置,对信号的个数如果判断少于实际源个数,会影响其正交关系(信源个数 Dmax N 1),是否为均匀
分布的直线阵,接受信号是否为远场平面波,采样点个数影响性能,在保证信号方向不变的情况下,越多 越好。
第四章 阵列信号处理

通常信号的频带B比载波 ω 小很多,即s(t)变化 相对 ω 缓慢,则延时
1 c
r α <<
T
1 B
则可以认为 s (t − r α ) ≈ s (t ) 即信号包络 在各阵元上差异可忽略——窄带信号。
4.2 等距线阵与均匀圆阵
一、等距线阵 M个阵元等距排成一直线,阵元间距为d,到达波 的方向角定义为与阵列法线的夹角 θ ,称为波 达方向(DOA)。 在三维空间中还可以 θ θ 确定信源方位角 ψ
d
5
4
y
ψ
2
1
x
等距线阵(ULA)的方向向量
aULA (θ ) = [1, e = [1, e
−j 2π − j k d sin θ −j
,L, e
2π
− j k ( M −1) d sin θ T
]
λ
d sin θ
,L, e
λ
( M −1) d sin θ
]T
若有多个信源(p个),波达方向分别为 θ i (i − 1, L, p) 方向矩阵为
A = [a(θ1 ), a(θ 2 ),L, a(θ p )] = 1 ⎡ ⎢ e − j 2λπ d sin θ1 =⎢ ⎢ L ⎢ − j 2λπ ( M −1) d sin θ1 ⎣e ⎤ π − j 2λ d sin θ p ⎥ L e ⎥ ⎥ L L π − j 2λ ( M −1) d sin θ p ⎥ L e ⎦ L 1
θ
d sin θ
Vandermonde矩阵
阵列结构不允许其方向向量和空间角之间模糊, 等距线阵阵元间距不能大于 λ ,则可以保证 2 方向矩阵中各个列向量线性独立。 二、等距线阵的阵列响应与方向图 在单个信源情况下,阵列输出为各阵元信号的加 权和(不考虑噪声),
阵列信号处理(知识点)

信号子空间:设N 元阵接收p 个信源,则其信号模型为:()()()()1piiii x t s t a N t θ==+∑在无噪声条件下,()()()()()12,,,P x t span a a a θθθ∈L称()()()()12,,,P span a a a θθθL 为信号子空间,是N 维线性空间中的P 维子空间,记为P N S 。
P N S 的正交补空间称为噪声子空间,记为N P N N -。
正交投影设子空间m S R ∈,如果线性变换P 满足,()1),,,2),,,0m mx R Px S x S Px x x R y S x Px y ∀∈∈∀∈=∀∈∀∈-=且则称线性变换P 为正交投影。
导向矢量、阵列流形设N 元阵接收p 个信源,则其信号模型为:()()()()1piiii x t s t a N t θ==+∑,其中矢量()i ia θ称为导向矢量,当改变空间角θ,使其在空间扫描,所形成的矩阵称为阵列流形,用符号A 表示,即(){|(0,2)}a A θθπ=∈波束形成波束形成(空域滤波)技术与时间滤波相类似,是对采样数据作加权求和,以增强特定方向信号的功率,即()()()()HHy t W X t s t W a θ==,通过加权系数W 实现对θ的选择。
最大似然已知一组服从某概率模型()f X θ的样本集12,,,N X X X K ,其中θ为参数集合,使条件概率()12,,,N f X X X θK 最大的参数θ估计称为最大似然估计。
不同几何形态的阵列的阵列流形矢量计算问题假设有P 个信源,N 元阵列,则先建立阵列的几何模型求第i 个信源的导向矢量()i i a θ 选择阵元中的一个作为第一阵元,其导向矢量()1[1]i a θ=然后根据阵列的几何模型求得其他各阵元与第一阵元之间的波程差n ∆,则确定其导向矢量()2jn i a eπλθ∆=最后形成N 元阵的阵列流形矢量()11221N j j N Pe A e πλπλθ-∆∆⨯⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦M 例如各向同性的NxM 元矩形阵,阵元间隔为半个波长,当信源与阵列共面时:首先建立阵列几何模型:对于第m 行、第n 列的阵元,其与第1行、第1列阵元之间的波程差为(1)sin()(1)cos()mn i i n d m d θθ∆=---故:()1122(sin()cos())22((1)sin()(1)cos())11N j j d j j d N M NM P NM Pe e A e e ππθθλλππθθλλθ-∆-∆---⨯⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦M M而当信源与阵列不共面时: 首先将信源投影到阵列平面然后建立阵列模型对于第m 行、第n 列的阵元,其与第1行、第1列阵元之间的波程差为[(1)sin()(1)cos()]sin()mn i i i n d m d θθϕ∆=-+-故:()1122(sin()cos())cos()22((1)sin()(1)cos())cos()11N j j d j j d N M NM P NM Pe e A e e ππθθϕλλππθθϕλλθ-∆-∆---⨯⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦M M线性约束最小方差准则(LCMV )的自适应波束形成算法: 对于信号模型:()()()0X t s t a J N θ=++, 波束形成输出:()()()()0()H H H yt W X t s t W a W J N θ==++LCMV 准则实际上是使()0HW a θ为一个固定值的条件下,求取使得()HWJ N +方差最小的W 作为最有权值,即:()0min .H X W HW R Ws t W a Fθ⎧⎪⎨⎪=⎩,其中F 为常数利用拉格朗日乘子法可解得:()10X opt W R a μθ-=当取1F =时,则()()11H X a R a μθθ-=,μ的取值不影响SNR 和方向图。
阵列信号处理(知识点)

信号子空间:设N 元阵接收p 个信源,则其信号模型为:()()()()1piiii x t s t a N t θ==+∑在无噪声条件下,()()()()()12,,,P x t span a a a θθθ∈称()()()()12,,,P span a a a θθθ 为信号子空间,是N 维线性空间中的P 维子空间,记为P NS 。
PN S 的正交补空间称为噪声子空间,记为N P N N -。
正交投影设子空间m S R ∈,如果线性变换P 满足,()1),,,2),,,0m mx R Px S x S Px x x R y S x Px y ∀∈∈∀∈=∀∈∀∈-=且则称线性变换P 为正交投影。
导向矢量、阵列流形设N 元阵接收p 个信源,则其信号模型为:()()()()1piiii x t s t a N t θ==+∑,其中矢量()i ia θ称为导向矢量,当改变空间角θ,使其在空间扫描,所形成的矩阵称为阵列流形,用符号A 表示,即(){|(0,2)}a A θθπ=∈波束形成波束形成(空域滤波)技术与时间滤波相类似,是对采样数据作加权求和,以增强特定方向信号的功率,即()()()()HHy t W X t s t W a θ==,通过加权系数W实现对θ的选择。
最大似然已知一组服从某概率模型()f X θ的样本集12,,,N X X X ,其中θ为参数集合,使条件概率()12,,,N f X X X θ 最大的参数θ估计称为最大似然估计。
不同几何形态的阵列的阵列流形矢量计算问题假设有P 个信源,N 元阵列,则先建立阵列的几何模型求第i 个信源的导向矢量()i i a θ 选择阵元中的一个作为第一阵元,其导向矢量()1[1]i a θ=然后根据阵列的几何模型求得其他各阵元与第一阵元之间的波程差n ∆,则确定其导向矢量()2jn i a eπλθ∆=最后形成N 元阵的阵列流形矢量()11221N j j N Pe A e πλπλθ-∆∆⨯⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦ 例如各向同性的NxM 元矩形阵,阵元间隔为半个波长,当信源与阵列共面时:首先建立阵列几何模型:对于第m 行、第n 列的阵元,其与第1行、第1列阵元之间的波程差为(1)sin()(1)cos()mn i i n d m d θθ∆=---故:()1122(sin()cos())22((1)sin()(1)cos())11N j j d j j d N M NM P NM Pe e A e e ππθθλλππθθλλθ-∆-∆---⨯⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦而当信源与阵列不共面时: 首先将信源投影到阵列平面然后建立阵列模型对于第m 行、第n 列的阵元,其与第1行、第1列阵元之间的波程差为[(1)sin()(1)cos()]sin()mn i i i n d m d θθϕ∆=-+-故:()1122(sin()cos())cos()22((1)sin()(1)cos())cos()11N j j d j j d N M NM P NM Pe e A e e ππθθϕλλππθθϕλλθ-∆-∆---⨯⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦线性约束最小方差准则(LCMV )的自适应波束形成算法: 对于信号模型:()()()0X t s t a J N θ=++, 波束形成输出:()()()()0()H H H yt W X t s t W a W J N θ==++LCMV 准则实际上是使()0HW a θ为一个固定值的条件下,求取使得()HWJ N +方差最小的W 作为最有权值,即:()0min .H X WHW R Ws t W a Fθ⎧⎪⎨⎪=⎩,其中F 为常数利用拉格朗日乘子法可解得:()10X opt W R a μθ-=当取1F =时,则()()11H X a R a μθθ-=,μ的取值不影响SNR 和方向图。
阵列信号处理的基本知识分析

diag{g ej1 ,, g e } jM
1
M
阵元之间的互藕 有关因素:阵元之间的间距大小,系统工作 频段,采用的传感器类型等。 设所有阵元之间的藕合系数矩阵为C,则考 虑到阵元间互藕的阵列输出信号模型为:
x(t) CAs(t) n(t)
阵元位置 阵元测向的关键信息是空间信号入射到各阵 元的相对延迟相位,而这一相位依赖于阵元 之间的空间位置,阵元位置误差直接导致延 迟相位估计误差,从而影响信号参数估计。
信号参数估计(DOA,频率,极化参数,距离, 时延等): 谱估计方法(子空间方法,波束形成 方法),参数化方法(最大似然,基于子空间逼 近方法)。
Ref[1] H.krim and M.Viberg, Two decdees of array processing research: the parametric approach, IEEE signal processing Magazine, Vol.13, Vol.4, 1996. Ref.[2] D.H.Johnson, D.E.Dudgeon, Array signal processing, Prentice-Hall,1993. Ref.[3] IEE Proc. 1991. Ref.[4] Vaccaro, R.J, The past, present, and the future of underwater acoustic signal processing, IEEE Signal Processing Magazine, Vol.15 , No.4 , 1998.
-25
-30
-35
-40
-45
-50
-80 -60 -40 -20
0
20
现代信号处理讲义讲义

子空间:向量组 a1, ,ap 的线性组合的集合,称为 a1, ,ap 张成的空间。
p
span a1, ,a p close a1, ,a p ja j , j C
j1
信号子空间: span s1, ,sp span u1, ,up 噪声子空间: span g1, ,g p span up1, ,um
J (w) 0
w*
wopt Rxx1a(k )
又
wH opt
a(k
)
1
aH
(k
)wopt
,代入上式
aH
(k
1
)R xx1a( k
)
wopt
Rxx1a(k ) aH (k )Rxx1a(k )
最佳滤波器
由Capon提出,称为最小方差无畸变(MVDR)波束形成器
MVDR: minimum variance distortionless response
期望信号 干扰信号 加性噪声
E z(n) 2 lim 1 N z(n) 2 wH E x(n)xH (n) w
N N
n1
E sk (n) 2 wH a(k ) 2 p E si (n) 2 wH a(i ) 2 2 w 2 i 1,i k
wH a(k ) 1
(波束形成条件)
现代信号处理讲义
3.5 MUSIC方法
1. 阵列信号处理问题 2. 最优波束形成器 3. 子空间方法 4. MUSIC方法 5. 改进的MUSIC方法
3.5 MUSIC方法
MUSIC: Multiple Signal Classification 1. 阵列信号处理问题 (array signal processing)
2024年考研数学信号处理中的数学题目详解与答案

2024年考研数学信号处理中的数学题目详解与答案在2024年的考研数学信号处理科目中,数学题目是重点考察的内容之一。
下面将对信号处理数学题目进行详解,并提供答案供大家参考。
一、题目一题目描述:给定一个信号处理系统的传输函数H(z),要求计算系统的频率响应。
解答:在信号处理中,系统的传输函数常用以描述信号输入和输出之间的关系。
频率响应则反映了系统对不同频率信号的响应情况。
根据题目给定的传输函数H(z),我们可以将其转换为z域表达式。
接下来,将z域表达式转换为频率域表达式,即可得到系统的频率响应。
最后,我们可以根据频率响应的表达式,计算系统在不同频率下的响应值。
答案:根据传输函数H(z)计算频率响应,并列出不同频率下的响应值。
二、题目二题目描述:信号处理系统中的数字滤波器具有一个单位冲激响应h(n),要求计算该滤波器的频率响应。
解答:单位冲激响应是数字滤波器的重要性质之一。
频率响应则描述了滤波器对不同频率的信号的响应情况。
根据题目给出的单位冲激响应h(n),我们可以通过对其进行傅里叶变换,得到滤波器的频率响应。
最后,我们可以绘制出频率响应的图像或列出不同频率下的响应值,以便进一步分析滤波器的性能。
答案:通过对单位冲激响应h(n)进行傅里叶变换,计算得到滤波器的频率响应,并展示该频率响应的图像或者列出不同频率下的响应值。
三、题目三题目描述:信号处理系统中的数字滤波器具有一个差分方程y(n) =x(n) + 0.8y(n-1),其中x(n)为输入信号,y(n)为输出信号。
要求计算该滤波器的单位冲激响应。
解答:差分方程是描述数字滤波器行为的数学公式。
通过求解差分方程得到单位冲激响应,可以帮助我们了解滤波器的特性。
根据题目给出的差分方程y(n) = x(n) + 0.8y(n-1),我们需要对其进行求解。
首先,我们可以采用Z变换的方法,将差分方程转化为滤波器的传输函数H(z)。
然后,根据传输函数H(z)进行反变换,得到滤波器的单位冲激响应。
阵列信号

2010 年春季学期研究生课程考核(读书报告、研究报告)考核科目: 阵列信号处理报告题目: 阵列信号处理习题与实验学生所在院(系): 电子与信息工程学院学生所在学科: 信息与通信工程学生姓名: 崔岩学号: 09S005068学生类别: 非委培考核结果:阅卷人:实验一 自适应波束形成一 实验目的1、 掌握自适应波束形成的方法2、 了解影响自适应波束形成性能的因素二 实验内容假设阵元个数M=12,阵元间距为半波长,信号方向为0度,2个与信号不相关的干扰,方向分别为-30度和50度,仿真:(1)不同信噪比(SNR )下的窗函数;(2)不同干噪比(INR )下的窗函数;(3)不同快拍数下的窗函数。
三 实验原理3.1最小无失真方差响应最小无失真方差响应(MVDR )波束形成器阵列输出的最小均方值使波束受到限制,从而在给定信号的方向到来的波形产生无畸变的响应。
采样矩阵求逆(SMI )方法。
有:其中是数据的协方差矩阵的最大似然估计,s 是目标的导向向量。
11ˆNH jjj R L x x=⎛⎫= ⎪⎝⎭∑其中,表示阵列模型在某一时刻的快拍矢量。
3.2最小均方波束形成器最小均方准则条件下的权重每经过一个采样间隔都要增加一个增量。
这个增量是与输出剩余功率的变化率成正比的。
最小均方准则的自适应方法计算较为简单,并是慢慢收敛的。
LMS 算法如下图:图2.1 LMS 算法方框图下面将要具体的介绍一下最小均方波束形成器的发展情况。
假设为一个N 元阵接收到的的向量信号,波束形成器的输出是由一个复杂的权和每个阵元的输出相乘得到的,再将所有阵元相加,得到:1()w a Rθ-=HqWHB()H a W k X(k)Z(k)D(k)+-Y(k)E(k)通过权使阵列的输出功率最小,同时还要受到:的限制,其中C 为的限制矩阵,f 为的限制向量。
为了在后面得到最小均方准则的结果,设:,需要解决的最优化问题就可以表示成:其约束条件为,这里表示协方差矩阵。
阵列信号处理的基本知识

a
பைடு நூலகம்11
各通道同步采集假设
阵列接收信号需要进行采样和A/D变换 为数字信号后进入DSP处理器进行算法处 理。
Nyquist采样率
宽频段信号:采用欠采样率(空时欠采 样),需要解模糊算法。
a
12
对信号和噪声的假设
窄带假设
信号带宽远小于信号波前跨越阵列最大口径 所需要的时间的倒数,即有如下假设:
1
P
波传播的方向信息含于载波上,而不是复包络上, 即与波形无关(这与时域信号处理不同),空间信 息含于载波上,时域信息含于信号包络上。
a
7
对阵列及其通道的假设 阵元的方向性:
空间入射信号示意图
a ( ) [ f ( ) e , ,f( ) e] 1
j k • p 1
a
j k • p M T
B L 1
F
式中L为阵列最大口径,F和为信号中心频率 和该频率对应的波长。
远场假设
即辐射源到阵列的距离远大于阵列的最大口
径,从而入L2射到阵列的信号波前可近似为平
面波前(d ).
a
13
入射信号统计特性
空间入射信号平稳且各态历经,可以用时
间平均代替集合平均。一般还假定各入射
信号统计独立。
E { s ( t) s H ( t) } d{ i2 , a ,2 g }
6
将整个阵列的输出信号写成矩阵形式为:
x (t) A (t) sn (t)
A [a () ,,a ()]为阵列流行矩阵、空间信
1
P
号方向矢量、阵列响应矩阵。
a ( ) [ 1 e , ,e ] j2 d si /n
j2( M 1 ) d si /n T
阵列信号处理1-2

2 2 T
+ W (t ) RXX (t )W (t )
T
(2.2.3 )
将上式对变量 W(t)求导数并使之等于零
ξ[W (t )] = 2rXd (t ) + 2RXX (t )W (t ) Wopt = RXX rXd
多径信号:有用信号经过多次反(散)射进入接收机的信号. 2,信号模型:
① 随机信号 例如:舰船发动机的噪声,推进器的噪声,未知的通信 信号,传感器热噪声,环境噪声,干扰信号,本质上都是随 机的.这些噪声都典型地来自大量独立微弱源的合成效应, 故应用统计学中心极限定理,可取合成噪声信号的数学模型 为高斯(Gauss)随机过程(通常是平稳高斯随机过程). 高斯信号的统计学性质特别有利于分析计算,因为高斯随机 过程的一阶矩和二阶矩给出了这种随机信号的全部信息特征. 来源:大量独立微弱源的合成效应.(未知的通信信号传感 器热噪声,环境噪声,干扰……等) 模型:Gauss平稳随机过程 参数:均值,方差
(2.1.1) (2.1.2) (2.1.3)
T 方向图形成网络: W = [ w1 , w 2 , L , w N ]
(形成最优权 和系统输出) 自适应处理器:
y (t ) = W T X = X T W
( 例如MVDR:Minimum Variance Distortionless Response) 求解约束性问题: min s.t
4,有利于多目标远距离的检测和跟踪 (Multiple targets detection and traction) 阵元数越多,天线孔径越大,波束及空间谱分辨率越高. 同时自由度增大.增加形成的主波束数量,实现对多目标的跟 踪.另一方面,也可以增加抑制干扰的数量. 三,自适应阵列信号处理的发展历史 自适应波束形成技术的研究主要在六十年代到七十年代, 到七十年代末已经基本成熟. 空间谱估计:主要是超/高分辨空间谱估计技术,从七 十年代到八十年代末期. 八十年代到九十年代,主要研究如何在实际系统中应用
哈工大阵列信号处理答案2

1.设一个辐射源距接收阵列的距离为r 0(该距离远大于天线的孔径),天线阵由M 个感应器构成,辐射源辐射的功率为P s ,噪声的平均功率为P n 。
设阵列的时延可以使阵列的主瓣与信号的传播方向匹配,且阵列的加权系数为1。
1) 在信号源处,信噪比是多少? 2) 在感应器处,信噪比是多少?3) 当阵列的主瓣方向与传播方向匹配时,阵列输出的信噪比是多少?4) 如信号源在接收阵列附近,发射的平均功率为P t ,信号以球面波的方式传播,到物体后备物体反射,且仍以球面波的方式传播,被物体反射的信号P s 为入射功率的ρ倍,物体到阵列中心位置的距离为r 0,计算阵列输出信号的信噪比(阵列的最大方向与目标反射信号的传播方向相同)? 解:1) 在信号源处,信噪比为0snP SNR P =2) 在感应器处,信噪比为0204s n P SNR SNR P r π''== 3) 当阵列主瓣方向匹配时,感应器处信噪比被加强,加强倍数为阵列增益。
阵列输出的信噪比是 0204s n P SNR SNR SNR G G M P r π''=⋅=⋅=⋅ 4) 近场时,位于阵列中心的感应器处接收到的信号功率为()2220044s t P P P r r ρππ⋅'==,噪声功率仍为n P 。
因此,该出的信噪比为:()2204t n n P PSNR P P r ρπ⋅==⋅计算得到阵列的输出信噪比为,中心点处信噪比乘以阵列增益G '。
()2204t n P G SNR SNR G P r ρπ'⋅⋅'=⋅=⋅阵列2.阵列的增益在频域可以表示为:⎰⎰⎰⎰⎰⎰⎰⎰∞∞-∞∞-∞∞-∞∞-∞∞-∞∞-∞∞-∞∞-=ωωωωωωωωωωd k d k S d k d k H k S d k d k S d k d k H k S G n n 222222),(/),(),(),(/),(),( 这里),(ωk S为信号的空时付氏变换,),(ωk H 为阵列的空时滤波函数,),(ωk S n 为噪声的空时付氏变换。
阵列信号处理答案

1.(1)关于接收天线阵列的假设。
接收阵列由位于空间已知坐标处的无源阵元按一定的形式排列而成。
假设阵元的接收特性仅与其位置有关而与其尺寸无关(认为其是一个点),并且阵元都是全向阵元,增益均相等,相互之间的互耦忽略不计。
阵元接收信号时将产生噪声,假设其为加性高斯白噪声,各阵元上的噪声相互统计独立,且噪声与信号是统计独立的。
(2)关于空间源信号的假设。
假设空间信号的传播介质是均匀且各向同性的,这时空间信号在介质中按直线传播,同时又假设阵列处在空间信号辐射的远场中,所以空间源信号到达阵列时可以看做是一束平行的平面波,空间源信号到达阵列各阵元在时间上的不同延时,可由阵列的几何结构和空间波的来向所决定。
空间波的来向在三维空间中常用仰角和方位角来表征。
其次,在建立阵列信号模型时,还常常要区分空间源信号是窄带信号还是宽带信号。
所谓窄带信号是指相对于信号(复信号)的载频而言,信号包络的带宽很窄(包络是慢变的),因此在同一时刻,该类信号对阵列各阵元的不同影响仅在于因其到达各阵元的波程不同而导致的相位差异。
2.自适应波束形成亦称空域滤波,是阵列处理的一个主要方面,逐步成为阵列信号处理的标志之一,其实质是通过对各阵元加权进行空域滤波,来达到增强期望信号、抑制干扰的目的;而且可以根据信号环境的变化自适应嘚改变各阵元的加权因子。
虽然阵列天线的方向图是全方向的,但阵列的输出经过加权求和后,可以被调整到阵列接收的方向增益聚集在一个方向,相当于形成了一个波束,这就是波束形成的物理意义所在。
波束形成技术的基本思想是:通过将各阵元输出进行加权求和,将天线阵列波束导向到一个方向上,对期望信号得到最大输出功率的导向位置即给出波达方向估计。
3. ULA :()1exp(2sin )exp(2(1)sin )Tk k k d dj j M θπθπθλλ⎡⎤=---⎢⎥⎣⎦αL 阵:(,)[(,),(,)]T x y a a a θφθφθφ=,其中2sin cos 2(1)sin cos (,)[1,...],,T j d j M x a e e πθφπθφθφ---=2s i n s i n 22s i ns i n 2(1...(,)[,,,]j d jd jM T y a ee e πθφπθφπθφθφ----=面阵: 12()()()M D D D ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦x y x y x y A A A A A A A ,其中112211222cos sin /2cos sin /2cos sin /2(1)cos sin /2(1)cos sin /2(1)cos sin /111K K K K j d j d j d x j d M j d M j d M e e e e e e πθφλπθφλπθφλπθφλπθφλπθφλ---------⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦A112211222sin sin /2sin sin /2sin sin /2(1)sin sin /2(1)sin sin /2(1)sin sin /111K K K K j d j d j d y j d M j d M j d M e ee ee e πθφλπθφλπθφλπθφλπθφλπθφλ---------⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦A4. 输公式烦死了,详见张老师写的书《阵列信号处理的理论和应用》38页和45页(应该是,挑一个写,这玩意我也不懂)5. MUSIC: 利用信号子空间和噪声子空间的正交性,通过谱峰搜索得到DOA 估计,适用任意阵列结构。
最优阵列处理技术答案

最优阵列处理技术答案
1、阵列配置:阵元的天线方向图(全向性各方向均匀,实际非全向性),阵列的几何结构包括线性、平面和立体阵列,线性阵列分为均匀间隔、非均匀间隔和随机间隔。
2、信号的空域和时域结构。
时域结构包括已知信号、具有位置参数的信号、具有已知结构的信号和随机信号。
空域包括从已知方向入射的平面波、从未知方向入射的平面波和空域扩展信号。
3、噪声(或干扰)的空域和时域结构。
来自外部源的噪声必须同时在时域和空域内进行表征。
时域包括具有未知参数的信号、随机信号。
空域包括从已知方向入射的一个或多个平面波、从未知方向入射的一个或多个平面波和空域扩展干扰。
4、阵列处理问题的目标。
在存在噪声和干扰的情况下,检测一个信号是否存在;在存在噪声和干扰的情况下,对信号实现解调,并估计信息波形;在一个二元通信信号通过多径到达阵列,检测信息序列;对存在噪声的情况下,估计多个平面波信号的波达方向角;对入射的信号和噪声场进行时域和空域的谱估计;把发射信号指向空间一个特定的位置。
第五章 阵列信号的高分辨处理解析

N
N N
P)投影矩阵为
P(s 或
Pn
)
Ps a a 则 a spana1,a2 , ,aP
反证:假设, i , i 1 ~ P
即 a , a1, , aP 线性相关(P+1个导向
矢量)。
而当 P 1 N 时,a , a1, , aP 应线性独
立。矛盾。
1
P P N 1
西安电子科技大学雷达信号处理实验室
精度提高,这是因为
3dB
0.886 L cos0
(rad )
西安电子科技大学雷达信号处理实验室
2. 波束扫描 波束形成: yt W H xt
普通波束形成(匹配滤波)W a0
y t aH 0 x t aH 0 s t a 1 s t aH 0 a 1
扫描指: 0 变化在[0,180]范围内,画出输出功 率随扫描角度变化的图形。
对于等距线阵(ULA)
j 2 d sin
a 1 e
j 2 d N 1sin T
e
1 Z
Z N 1 T
j 2 d sin
其中 Z e
范德蒙矩阵:
1 x1
1 x2
M
x12
x22
x1N 1
xN 1 2
1
xN
xN2
xNN 1
是满秩的充要条件为 xi x j ,当i j。
西安电子科技大学雷达信号处理实验室
➢问题:虽可测多个信源,但当多个信源的夹角小 于一个波束宽度时,无法分辨。 ➢波束宽度与阵列孔径成反比,又称为瑞利限。
西安电子科技大学雷达信号处理实验室
§ 5.2正交子空间投影与高分辨处理
1. 信号子空间与噪声子空间的定义
西工大阵列信号处理考点整理

西工大《阵列信号处理》复习考点整理考试形式:一、8道问答题,每道题5分;二、六道大题,包括PPT 上老师给出的那一道。
一1. 均匀线列阵在波束扫描时,波束图怎么变化?当波束指向法线方向时,波束图具有最窄的主瓣宽度;随着阵元指向逐渐远离法线方向,主瓣一直指向所调方向并且展宽;除了指向法线方向外,主瓣都关于波束倾角轴不对称;当达到某一临界角时不能形成波束,但是在端射方向又可以形成波束。
且在端射方向形成一个较宽的主瓣。
2.DI 是什么?DI 表示指向性指数,其表达式为D 为方向性,是阵列和孔径的一个常用性能度量。
⎰⎰⋅=ππφθθφθπφθ200),(sin 41),(P d d P D T T 3. DC 加权的特点(1)旁瓣级给定时,主瓣宽度最小; (2)主瓣宽度给定时,旁瓣级最低; (3)等旁瓣级。
4. 频域快拍模型是什么,步骤是什么,常用的频域快拍取的时间有什么关系? (1)记住《最优阵列处理技术》245页图5.1 (2)步骤:①把总的观测时间T 分为K 个不重叠的时间区域,区域长度为△T ; ②对时域快拍进行FT ;③对频域向量(频域快拍)进行窄带波束形成; ④对上述频域信号进行IFT 。
(3)△T 的选择准则①△T 必须远大于平面波通过阵列的传播时间;②△T 依赖于输入信号的带宽和信号的时域谱,16≥∆⋅T B (B*△T 足够大,选用频域快拍模型)。
5. 什么是均匀阵的瑞利限?常规波束形成分辨率的极限。
表达式为6. 空间白噪声的阵增益的相关计算。
阵列增益ωA 的定义为阵列的输出SNR 和一个阵元上的输入SNR 的比值。
下标“ω”表示空域不相关的噪声输入。
表达式如下:22101)()(--====∑nN n nin o SNR SNR A ωωωωω对于一个标准线阵(阵元间距为d=λ/2),白噪声阵列增益等于阵列的方向性D ; 对于一个均匀加权阵列,有ωn =1/N(n=0,…,N-1),N A =ω(或单位为dB 时,为N log 10) 7. N 元ULA 可以分辨有多少来波?可以分辨N-1个来波个数(N 元阵有1个参考元,所以自由度为N-1).二1. 对于阵元数N =5和N =6两种情况,推导并绘制标准均匀线列阵指向阵列法线方向,均匀加权得到的波束图)(u B ,注意旁瓣个数以及端射方向的波束形状。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.(1)关于接收天线阵列的假设。
接收阵列由位于空间已知坐标处的无源阵元按一定的形式排列而成。
假设阵元的接收特性仅与其位置有关而与其尺寸无关(认为其是一个点),并且阵元都是全向阵元,增益均相等,相互之间的互耦忽略不计。
阵元接收信号时将产生噪声,假设其为加性高斯白噪声,各阵元上的噪声相互统计独立,且噪声与信号是统计独立的。
(2)关于空间源信号的假设。
假设空间信号的传播介质是均匀且各向同性的,这时空间信号在介质中按直线传播,同时又假设阵列处在空间信号辐射的远场中,所以空间源信号到达阵列时可以看做是一束平行的平面波,空间源信号到达阵列各阵元在时间上的不同延时,可由阵列的几何结构和空间波的来向所决定。
空间波的来向在三维空间中常用仰角和方位角来表征。
其次,在建立阵列信号模型时,还常常要区分空间源信号是窄带信号还是宽带信号。
所谓窄带信号是指相对于信号(复信号)的载频而言,信号包络的带宽很窄(包络是慢变的),因此在同一时刻,该类信号对阵列各阵元的不同影响仅在于因其到达各阵元的波程不同而导致的相位差异。
2.自适应波束形成亦称空域滤波,是阵列处理的一个主要方面,逐步成为阵列信号处理的标志之一,其实质是通过对各阵元加权进行空域滤波,来达到增强期望信号、抑制干扰的目的;而且可以根据信号环境的变化自适应嘚改变各阵元的加权因子。
虽然阵列天线的方向图是全方向的,但阵列的输出经过加权求和后,可以被调整到阵列接收的方向增益聚集在一个方向,相当于形成了一个波束,这就是波束形成的物理意义所在。
波束形成技术的基本思想是:通过将各阵元输出进行加权求和,将天线阵列波束导向到一个方向上,对期望信号得到最大输出功率的导向位置即给出波达方向估计。
3. ULA :()1exp(2sin )
exp(2(1)sin )T
k k k d d
j j M θπθπθλλ⎡⎤
=---⎢⎥⎣⎦
α
L 阵:(,)[(,),(,)]T x y a a a θφθφθφ=,其中
2sin cos 2(1)sin cos (,)[1,...],,T j d j M x a e e πθφπθφθφ---=
2s i n s i n 22s i n
s i n 2(1
...(,)[,,,]
j d j
d j
M T y a e
e e πθφπθφπθφθφ----=
面阵: 12()()()M D D D ⎡⎤
⎢⎥
⎢⎥=⎢⎥⎢⎥⎢⎥⎣
⎦x y x y x y A A A A A A A ,其中1
1
2
2
1
1
2
2
2cos sin /2cos sin /2cos sin /2(1)cos sin /2(1)cos sin /2(1)cos sin /111
K K K K j d j d j d x j d M j d M j d M e e e e e e πθφλπθφλπθφλ
πθφλ
πθφλπθφλ---------⎡⎤
⎢⎥⎢⎥=⎢
⎥
⎢⎥⎣⎦
A
112211222sin sin /2sin sin /2sin sin /2(1)sin sin /2(1)sin sin /2(1)sin sin /111
K K K K j d j d j d y j d M j d M j d M e e
e e
e e πθφλ
πθφλ
πθφλ
πθφλπθφλ
πθφλ---------⎡
⎤⎢⎥⎢
⎥=⎢
⎥⎢⎥
⎣⎦
A
4. 输公式烦死了,详见张老师写的书《阵列信号处理的理论和应用》38页和45页(应该是,挑一个写,这玩意我也不懂)
5. MUSIC: 利用信号子空间和噪声子空间的正交性,通过谱峰搜索得到DOA 估计,适用任意
阵列结构。
Root-music :利用信号子空间和噪声子空间的正交性,通过求解多项式的根来避免谱峰
搜索。
Smooth-music: 处理相关信号的DOA 估计问题。
ESPRIT :利用信号子空间通过协方差分解来得到DOA 估计,对阵列流型要求较高。
PM :不需要协方差矩阵的特征值分解得到信号子空间和噪声子空间的同构矩阵,进而得
到DOA 估计,复杂度低于esprit 。
%%% DOA estimation by ESPRIT clear all close all clc
derad = pi/180; radeg = 180/pi;
twpi = 2*pi; kelm = 8; dd = 0.5; d=0:dd:(kelm-1)*dd; iwave = 3; theta = [-10 0 20]; snr = 10; n = 500;
A=exp(-j*twpi*d.'*sin(theta*derad)); S=randn(iwave,n); X=A*S;
X1=awgn(X,snr,'measured');
Rxx=X1*X1'/n;
[EV,D]=eig(Rxx);%%%%
EVA=diag(D).';
[EVA,I]=sort(EVA);
EVA=fliplr(EVA);
EV=fliplr(EV(:,I));
%ESPRIT
L=iwave;
Us=EV(:,1:L);
U1=Us(1:kelm-1,:);
U2=Us(2:kelm,:);
InvU1=inv(U1'*U1)*U1';
q=InvU1*U2;
[EVq,Dq]=eig(q);
Dq=diag(Dq).';
theta_esprit=asin(-angle(Dq)/(twpi*dd))*radeg
Dq=log(Dq)*(-j);
theta_esprit0=asin(-Dq/(twpi*dd))*radeg
8. 阵列信号处理是信号处理领域的一个重要分支,用传感器阵列来接收空间信号,与传统的单个定向传感器相比,具有灵活的波束控制、高的信号增益、极强的干扰抑制能力以及高的空间分辨能力等优点,直接导致阵列信号处理具有重要的军事、民事应用价值和广阔的应用前景,具体来说已涉及雷达、声纳、通信、地震勘探、射电天文以及医学诊断等多种领域。
