ANSYS邓肯-张材料模型
044三维邓肯-张变形应力模拟
3D 非线性简单算例
1、问题描述 模拟土体在逐渐被压的过程中,应力应变变化过程。在本算例中,本构模型 采用非线性弹性 Duncan-Chang 模型。 其中,Duncan-Chang 模型计算参数取值,见下表: K n
(4)点击“Meshing”—〉 “Generate” ,划分出图示网格。
(5)把前处理数据转化为SciFEA 所需计算格式。点击【Files】-【Save】 菜单,保存为GID 文件。点击菜单【Calculate】-【Calculate】,弹出“process info”消息框,如图所示,点击“ok”按钮,然后退出Gid,至此前处理工作结 束。
(。 )
c
Rf
G
F
D
2.0e2 0.2
32 5e4 0.8 0.3 0.15 3.0
2、求解步骤 2.1 选择项目 (1)启动 SciFEA,选择“项目”-> “新建项目” 菜单或者选择新建项目按 钮“ ” ,弹出如下对话框。
(2)在“项目名称”后输入该项目的名称,再点击“问题类型”栏中的“二 维 Duncan”选项。如图所示。 (3)点击“OK”按钮完成项目类型的选择。
第二步,点击鼠标右键,再点击“Contextual”—〉 “Join C-a”
第三步,在图示的平面内点击一点,就可以显示出这一点的应力应变变 化曲线图,如下图所示。
第四步,同时画出第二主应力S2和第三主应力S3的曲线,如图所示。
本例中,S2的曲线和S3的曲线重合。 第五步,画出剪应力的变化曲线,点击“View results”—〉 “Graphs” —〉 “Point Analysis”—〉 “unodm0”—〉 “tr”,如图所示。
邓肯_张E_B模型的ANSYS二次开发及应用_孙明权 (1)

Vol. 34 No. 2 Apr. 2013
邓肯 - 张 E - B 模型的 ANSYS 二次开发及应用
孙明权,陈姣姣,刘运红
( 华北水利水电学院,河南 郑州 450045)
摘 要: 随着土石坝坝体高度的增加,土石坝的应力和变形分析已成为大型土石坝设计中不可缺少的一部分,有限
元法是进行应力和变形分析的一种有效方法. 在土石坝有限元计算中,难点主要是 ANSYS 中并不包含土
写的邓肯 - 张 E - B 模型的宏命令如下:
* create,Duncan-Chang
! 建立宏文件
* afun,deg
! 设置角度单位为度
* set,Pa,1e5 * set,P1,- ArrS3( num)
! 定义 Pa = 1e5
! 注意: 岩土工程中为拉负压正
* set,P3,- ArrS1( num)
式中: γ 为填土的重度; h 为单元形心在土层表面以
下的深度; K0 为土的静止侧压力系数; φ 为此种材 料的内摩擦角.
32
华北水利水电学院学报
2013 年 4 月
1. 2. 5 计算步骤 首先建立土石坝三维模型; 然后通过控制单元
生死来模拟土石坝的分层施工,在每一层施工完成 后通过编制的宏命令来提取各个活单元的最大、最 小主应力,执行宏修改每个单元的弹性常数; 再把当 前填筑高度所计算的结果作为下次继续计算的初始 条件进行重启动计算. 从而可动态模拟土石坝的施 工过程,并在每一层填筑的过程中动态修改土石坝 的弹性常数,进而可实现邓肯 - 张本构模型在土石 坝中的应用. 1. 2. 6 对结果进行后处理
准大气压; σ1 ,σ3 分别为单元的大主应力、小主应
力; Rf 为破坏比; K 为弹性模量系数; n 为弹性模量
邓肯张本构模型在FLAC3D中的开发与实现

邓肯张本构模型在FLAC3D中的开发与实现一、本文概述随着计算机技术的不断发展和数值模拟方法的日益成熟,岩土工程领域的数值模拟分析已成为研究岩土工程问题的重要手段。
邓肯张本构模型(Duncan-Chang Constitutive Model)作为一种能够描述岩土材料非线性、弹塑性行为的本构模型,在岩土工程领域具有广泛的应用。
然而,在岩土工程数值模拟软件FLAC3D中,邓肯张本构模型并未直接内置,因此需要对其进行开发与实现。
本文旨在探讨邓肯张本构模型在FLAC3D中的开发与实现过程。
将介绍邓肯张本构模型的基本原理和特点,包括其应力-应变关系、屈服准则、硬化法则等。
然后,将详细阐述如何在FLAC3D中通过用户自定义本构模型(User-Defined Constitutive Model)接口实现邓肯张本构模型,包括模型的初始化、应力更新、应变更新等关键步骤。
还将讨论邓肯张本构模型在FLAC3D中的数值实现方法,如如何设置模型参数、如何处理模型的非线性问题等。
通过本文的研究,旨在为FLAC3D用户提供一种在岩土工程数值模拟中应用邓肯张本构模型的有效方法,也为其他岩土工程数值模拟软件的本构模型开发与实现提供借鉴和参考。
本文的研究成果将有助于提高岩土工程数值模拟的准确性和可靠性,推动岩土工程领域的数值模拟研究向更高水平发展。
二、邓肯张本构模型基本理论邓肯张本构模型(Duncan-Chang Model)是一种广泛使用的岩土工程材料本构模型,主要用于描述土的应力-应变关系。
该模型基于土的弹塑性理论,能够模拟土的非线性、弹塑性和剪胀性等行为。
邓肯张本构模型的基本假设包括土的应力-应变关系是非线性的,土的应力路径对其后续行为有影响,以及土的体积变化与其应力状态有关。
模型的核心在于其应力-应变关系的数学描述,其中包括弹性部分和塑性部分。
在弹性部分,邓肯张模型采用了切线弹性模量来描述土的弹性行为,这个模量随着应力的变化而变化,体现了土的非线性弹性特性。
基于邓肯-张模型的软土路基沉降变形的数值模拟分析

基于邓肯-张模型的软土路基沉降变形的数值模拟分析唐坤尧【摘要】针对位于沼泽地中的某高铁站软土路基采用预应力管桩加固后的工后沉降的计算,通过室内饱和土固结不排水三轴试验(CU),取得了不同围压条件下现场土试样的力学参数。
在此基础上将邓肯张模型引入 FLAC3D软件中,对某高铁站软土路基工后沉降的稳定性进行了系统数值模拟研究,分析了不同土体参数对管桩路基沉降的影响,确定了各参数敏感顺序,为分析不同软体路基工程沉降分析提供了技术支持,为今后同类工程的设计计算提供了参考。
%In order to calculate post-construction settlement of soft roadbed with prestressed pipe reinforcement in a high-speed railway station,we depended on saturated soil consolidated undrained triaxial test(CU),and got the soil mechanical parameters under different confining pressures.Based on this,we introduced the Duncan-Chang Model into FLAC3D soft-ware,and conducted a system numerical simulation of post-construction settlement of soft roadbed,then analyzed the effect of different soil parameters to pipe roadbed settlement and determined the sensitive order of each parameter.According to the study, this paper could provide technical support for settlement analysis of soft roadbed and references for similar projects in future.【期刊名称】《铁道建筑技术》【年(卷),期】2016(000)003【总页数】4页(P104-107)【关键词】工后沉降;三轴试验;数值模拟;软土路基【作者】唐坤尧【作者单位】中国铁建大桥工程局集团有限公司天津 300300【正文语种】中文【中图分类】U213.157路基作为道路交通工程建设中的重点,是路面荷载的承载主体。
邓肯-张模型公式推导 高土

邓肯-张模型是一个非线性本构模型,既然是一个本构模型,可想而之他反应的是应力与应变之间的关系。
说它是非线性的,那么反映应力应变关系的模量就不是一个常数E那么简单。
在介绍该模型之前,先要介绍一个概念,就是反映非线性关系的增量广义胡克定律: 1123()tt tv d d d d E E σεσσ=-+ (1) 1963年,康纳(Kondner )根据大量土的三轴试验的应力应变关系曲线,提出可以用双曲线拟合出一般土的三轴试验13()~a σσε-曲线,即:13aaa b εσσε-=+ (2)其中,a 、b 为试验常数。
对于常规三轴压缩试验,1a εε=。
邓肯等人根据这一双曲线应力应变关系提出了一种目前被广泛的增量弹性模型,一般被称为邓肯-张(Duncan-Chang )模型。
在常规三轴压缩试验中,13aaa b εσσε-=+可以写成:1113a b εεσσ=+- (3)将常规三轴压缩试验的结果按1113~εεσσ-的关系进行整理,则二者近似成线性关系(见图1)。
其中,a 为直线的截距;b 为直线的斜率。
在常规三轴压缩试验中,由于230d d σσ==,所以切线模量为ε1/(σ1-σ3)1-σ3)ult图11113~εεσσ-线性关系图13211()()t d aE d a b σσεε-==+ (4) 在试验的起始点,10ε=,t i E E =,则:1i E a=,这表明a 表示的是在这个试验中的起始变形模量E i 的倒数。
如果1ε→∞,则: 131()ult bσσ-=(5) 由此可以看出b 代表的是双曲线的渐近线所对应的极限偏差应力13()ult σσ-的倒数。
在土的试样中,如果应力应变曲线近似于双曲线关系,则往往是根据一定的应变值(如115%ε=)来确定土的强度13()f σσ-,而不可能在试验中使1ε无限大,求取13()ult σσ-;对于有峰值点的情况,取1313()()f σσσσ-=-峰,这样1313()()f σσσσ--ult <。
邓肯张模型模拟

研究生课程作业邓肯张模型参数计算学生姓名李俊学科专业岩土工程学号201420105614任课教师周小文教授作业提交日期2014年12月1.计算轴向应变ch h∆∑=1ε式中 1ε-轴向应变;h ∆∑-固结下沉量,由轴向位移计测得0h -土样初始高度c h —按实测固结下沉的试样高度c h ∆—试样固结下沉量2.计算按实测固结下沉的试样高度,面积:式中 Ac -按实测固结下沉的试样面积0V -土样初始体积3.计算剪切过程中试样的平均面积:式中 a A -剪切过程中平均断面积c V -按实测固结下沉的试样的体积i V ∆-排水剪中剪切时的试样体积变化 按体变管或排水管读数求得1h ∆-固结下沉量,由轴向位移计测得 3. 计算主应力差cic h V V A ∆-=01h h V V A c i c a ∆-∆-=Cc c A h V ⨯=1031⨯=-aA CR σσ 式中 31σσ- - 主应力差 1σ―大主应力 3σ-小主应力 C -测力计率定系数 R -测力计读数2 数据处理2.1 3σ=100kPa 数据初步计算当3σ=100kPa 时,各数据初步计算如表1所示。
围压100kPa 数据初步计算表 表12.1.1 由切线模量计算数据 对公式)(311σσε-=a +b 1ε进行直线拟合,如图1所示。
图11131/()~εσσε-拟合曲线 a =0.0002,1i E a==5000kPa b ==0.0028,()131ult bσσ-==263.16kPa ()13f σσ-=204.26kPa ,()()1313f fultR σσσσ-=-=0.77622.1.2 由泊松比计算数据对公式()313/f D εεε-=+-进行直线拟合,如图2所示。
图2 313/~εεε--拟合曲线f=i ν=0.2122 D=2.72972.2 3σ=200kPa 数据初步计算当3σ=200kPa 时,各数据初步计算如表2所示。
由实验到邓肯-张模型的参数

lg (σଷ) pୟ
−εଷ εୟ
v୧
图 3.3
图中εଷ表示侧向应变,εଷ
=
க౬ିக。
ଶ
4、F 与 G 的确定。
v୧
α D=tanα
−εଷ
F G
图 3.4
lg (σଷ) pୟ
每一个围压都对应一个 Vi 和
lg (య),因此通过图 3.4 我们可以得到 G 和 F。
୮
5、Kur 的确定 Kur 卸载表示卸载模量通常取 2-3 倍的 K。 (二)、邓肯-张 E-B 模型参数的确定 K、n、Rf、Kur 的确定与 E-v 模型中的确定方法相同,这里就不在赘述。 1、m 和 Kb 的确定 首先求出每一级围压σଷ情况下的 B。
B = (σଵ − σଷ)% 3(εୟ)%
然后根据图 3.5 确定 m 和 Kb。
B lg ( )
Pୟ
α m=tanα
lgKୠ
(三)、关于 C、∆φ、φ的确定
图 3.5
lg ( σଷ) Pୟ
C、∆φ、φ有两种表示方法,一种是用线性的邓肯张参数表示,参数有 C 和φ。另 外一种是用大小随围压σଷ不断变化的φ表示,参数有∆φ和φ。
验 b 也可以这样确定。
b
=
ቀσଵ
εୟ −
σଷቁଽହ%
−
ቀσଵ
εୟ −
σଷቁ%
(εୟ)ଽହ% − (εୟ)%
其中,下标 95%、70%分别代表σଵ − σଷ等于(σଵ − σଷ)的 95%及 70%时有关的
数据。后面遇到此种情况亦同。
2、K 与 n 的确定。
从图 3.1 中,我们可得到每一级围压σଷ下的 a,或者用公式
①主应力
邓肯-张E-B模型的ANSYS二次开发及应用

邓肯-张E-B模型的ANSYS二次开发及应用
孙明权;陈姣姣;刘运红
【期刊名称】《华北水利水电学院学报》
【年(卷),期】2013(034)002
【摘要】随着土石坝坝体高度的增加,土石坝的应力和变形分析已成为大型土石坝设计中不可缺少的一部分,有限元法是进行应力和变形分析的一种有效方法.在土石坝有限元计算中,难点主要是ANSYS中并不包含土石坝材料的本构关系.利用ANSYS提供的APDL语言二次开发平台,开发出了在土石坝工程中应用广泛的邓肯-张E-B模型,并应用于安宁水电站沥青混凝土心墙堆石坝的应力与变形计算,结果较好地反映了土石坝的实际应力变形规律.
【总页数】5页(P30-34)
【作者】孙明权;陈姣姣;刘运红
【作者单位】华北水利水电学院,河南郑州450045
【正文语种】中文
【中图分类】TV314
【相关文献】
1.基于ABAQUS邓肯张E-B模型的坝体变形分析 [J], 路强
2.堆石体邓肯-张E-B模型反演参数的敏感性分析 [J], 秦瑞;涂小龙;李烈
3.基于邓肯-张E-B模型的边坡稳定性强度折减法的研究及应用 [J], 张铭;戴磊
4.堆石体邓肯-张E-B模型反演参数的敏感性分析 [J], 秦瑞;涂小龙;李烈;;;
5.考虑颗粒破碎的钙质砂修正邓肯-张E-B模型 [J], 曾凯锋; 刘华北
因版权原因,仅展示原文概要,查看原文内容请购买。
邓肯-张模型参数求取
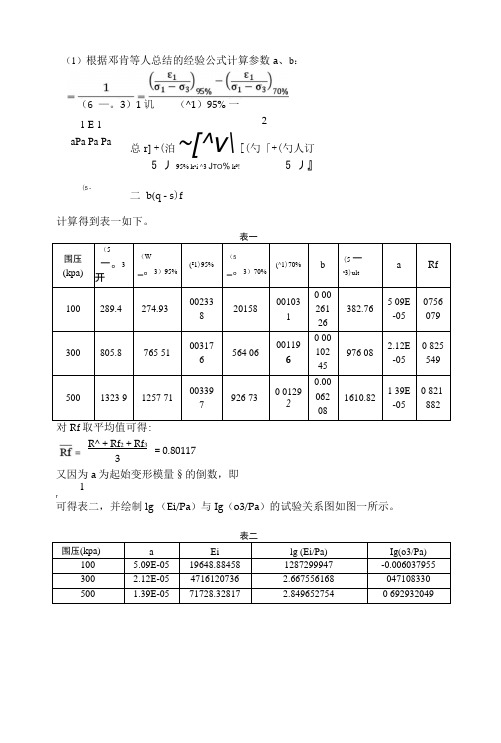
(1)根据邓肯等人总结的经验公式计算参数a 、b :总r] +(泊~[^v\[(勺「+(勺人订5 丿95% k a i ^3 J TO % k 0!5 丿』计算得到表一如下。
表一围压(kpa)(5一。
3开(W_。
3)95%(£1)95%(5_。
3)70%(^1)70%b (5 一a3)ulta Rf100289.4274.9300233 8 2015800103 1 0 00 261 26 382.765 09E -05 0756 079300 805.8 765 51 00317 6 564 060011960 00 102 45 976 082.12E -05 0 825 549500 1323 9 1257 71 00339 7926 730 0129 20.00 062 081610.821 39E -05 0 821882对Rf 取平均值可得:又因为a 为起始变形模量§的倒数,即1r可得表二,并绘制lg (Ei/Pa )与Ig (o3/Pa )的试验关系图如图一所示。
表二围压(kpa)a Eilg (Ei/Pa) Ig(o3/Pa) 100 5.09E-05 19648.88458 1287299947 -0.006037955 3002.12E-054716120736 2.667556168 047108330 500 1.39E-0571728.328172.8496527540 692932049(5 -二 b(q - s )f1 E 1 aPa Pa PaR^ + Rf 2 + Rf 33 = 0.80117(6 —。
3)1讥 (^1)95% 一(“)70%2At对图一中的试验点进行拟合,得到lg (Ei/Pa)与Ig(o3/Pa)的直线关系: 尸0.8033X+2.2914.根据公式:E=5③可知K、n分别代表lg (Ei/Pa)与lg(a 3/Pa)直线的截距和斜率,故可得K=2.2914: n=0.8033oE-v 法在常规三轴试验中,轴向应变£ 1与侧向应变一£ 3之间也存在双曲线关系,经 变换之后可得如下公式:由上式知一£ 3/8 1与一£ 3为直线关系,但实际上,二者并不是严格的直线关 系,需先对试验结果进行収舍,然后选取某一区间进行拟合。
由实验到邓肯-张模型的参数

参数 ∆φ
φ
C K n R Kୠ m K୳୰
单位 度
度
Pa 无 无 无 无 无 无
E-B 模型的参数特性 性质
说明
C、∆φ、φ有两种表示方法,一种是用 线性的摩尔库伦参数表示,参数只有 C 和 φ。另外一种是用大小随围压σଷ不断变化的 φ表示,参数有∆φ和φ。对于粘性土,最 好用 C 和φ表示。
K 的基数 反映 K 随σଷ增长的速率
同 E-u 模型中论述 同 E-u 模型中论述 同 E-u 模型中论述 当σଷ = Pa时,K = KୠPa 当 m=0 时,K = kୠpୟ 当 m=1 时E୧= kୠσଷ 同 E-u 模型中论述
三、邓肯-张模型中各个参数的计算 (一)、邓肯-张 E-v 模型参数的确定 1、Rf 的确定。 Rf 表示破坏比,其计算公式为:
R
无
反映(σଵ − σଷ)与
(σଵ − σଷ)୳之间的关系。
G
无 初始泊松比v୧的基数
σଷ = pୟ,则v୧= G
F
无
反映初始泊松比v୧随围压σଷ 增长而降低的速率
F = 0,则v୧= G
D
无 反映v୧随εୟ增长的关系
K୳୰
无 反映土体卸载的参数
D = 0 ,则泊松比大小不变,为v୧ 一般取 2-3 倍的 K
B = (σଵ − σଷ)% 3(εୟ)%
然后根据图 3.5 确定 m 和 Kb。
B lg ( )
Pୟ
α m=tanα
lgKୠ
(三)、关于 C、∆φ、φ的确定
图 3.5
lg ( σଷ) Pୟ
C、∆φ、φ有两种表示方法,一种是用线性的邓肯张参数表示,参数有 C 和φ。另 外一种是用大小随围压σଷ不断变化的φ表示,参数有∆φ和φ。
邓肯_张模型研究现状和在工程中的应用讨论

按照初始切线模量 Ei 的定义 ,当ε1 →0 时 ,由 (1)
式得 :
Ei
=
d (σ1
- σ3 ) /
dε1
|
ε 1
→0
= 1/ a
(3)
而当ε1
→∞时
, (σ1
- σ3 )
u
=ε1 /
(a
+bLeabharlann ·ε1)|
ε 1
→∞
=
1/ b
至此 ,康 得纳 ( Kandner ) 和柴 拉 斯 高 ( Zelasko )
压缩试验所得的 e - p 曲线在一定程度上体现了土 体的非线性特性 ,可考虑用它来确定非线性变形参数 K、n 。在压缩试验中. 土体处于无侧向变形状态 ,静止 侧压力系数近似表示为 :
掌握在 2~4 次间 。在河槽段浆体 ,相邻各孔均出现串 通 ,浆体主脉基本沿轴线连续形成 。二序打 21 孔 ,进尺 334. 6m 、注入干土量 7363kg 。二序孔施灌与一序孔相 隔 1 个月左右 。此次灌浆河槽段浆脉厚度理论计算可 达到 27cm ,两岸坡段接触不良的沉降量达 6~9cm 。这 说明灌浆效果较好 。 3. 2 某( 2) 水库土坝劈裂灌浆
本构模型之邓肯张模型可编辑全文

将式(4)、式(8)、式(10)和式(18)代入式 (19),则得到任一应力(σ1,σ3)时的泊松比的 邓肯-张计算公式:
vt
GFlg(3 / pa)
2
1
Kpa(pa3
)n
1DR(2fc(1co1s3)3)2(13ssiinn)
(20)
• 这样在切线泊松比 v t 的计算公式中又
引人了
等3种材料常数,加上 E t
13 (13)f
(12)
根据莫尔-库仑强度准则,有
(13)f
2cc出lg(Ei / pa)与lg(3 / pa)直线,则其截距等于lgK, 斜率等于n,
lgEi/Pa
n
3
1
/Pa成为无量纲数
lgk
lg 3/Pa
Pa为大气压,单位与Ei相同,以便使Ei/Pa、 3 /Pa成为无量纲数
力( 1 , 3 )时的切线模量的邓肯-张计算公式:
Et Kpa(pa 3)n1R2fc(co1s3)2(1 3ssiinn)2
可见切线变形模量的公式中共包括5个材料常
数
这样我们就求出了切线变形模量 E t
下面我们切线泊松比 v i
邓肯等人根据一些试验资料,发现在常规三轴压缩 试验中,轴向应变与侧向应变之间也存在双曲线
K、n为无因次基数和无因次指数,是决定于土质的
试验常数,由lg(Ei/Pa)与lg(σ3/Pa)直线关系确定,
其截距为lgK、斜率为n。Ei为初始切线模量,Ei=
1/a, Pa大气压力。
lgEi lgknlg3
Pa
Pa
Ei KPa(Pa3 )n
(14)
将式(13)和式(14)代入式(12)则得到任一应
中的5个常数,共有8个常数。其中可
邓肯-张非线性模型研究及其在ANSYS中的实现

文章编号:100722284(2010)0320076204邓肯2张非线性模型研究及其在ANSYS 中的实现宿 辉1,2,党承华2,崔佳佳2(1.北京科技大学土木与环境学院,北京100083;2.河北工程大学水电学院,河北邯郸056021) 摘 要:对工程领域使用广泛的邓肯2张非线性本构模型进行了研究,总结了国内外的研究现状及理论成果,针对其无法判定因结压力降低时的加载情况,提出了相应的变形模量的计算方法,同时考虑中主应力、土体抗拉强度的影响对模型进行了修正。
利用A PDL 编写程序实现了ANSYS 的材料本构模型的二次开发,运用重启动方法实现单元应力修正后数据重写入数据库,通过试验模拟对比分析验证了模型的适用性。
关键词:邓肯2张模型;抗拉强度;中主应力;应力分析 中图分类号:TU470+.3 文献标识码:ADuncan 2Chang Nonlinear Elastic Model and R ealization in ANSYSSU H ui 1,2,DANG Cheng 2hua 2,CUI Jia 2jia 2(1.School of Civil and Environmen Engineering ,Beijing University of Science and Technology ,Beijing 100083,China ;2.School of Water Resources and Hydropower ,Hebei University of Engineering ,Handan 056021,Hebei Province ,China )Abstract :Based on the present research situation and theoretical results ,research is done on Duncan 2Chang nonlinear elastic model ,which is applied widely in engineering ,.According to the fact that Duncan 2Chang model can ’t judge the loading situation while con 2solidation pressure decreases .The model is modified cosidering the effect of intermediate principal stress and tensile strength of soil.The secondary development of material constitutive model in ANSYS is accomplished by utilizing the A PDL language.Then the re 2start method is used to modify element stress ,the corrected data is database rewritten.A series of compliance tests verify the accura 2cy and applicability of the modified Duncan 2Chang nonlinear elastic model embedded ANSYS.K ey w ords :Duncan 2Chang nonlinear elastic model ;tensile strength ;intermediate principal stress ;stress analysis收稿日期:2009205218作者简介:宿 辉(19722),男,副教授,博士研究生,主要从事岩土工程及水工结构教学及研究工作。
邓肯-张EB模型参数求解的二次优化法

邓肯-张EB模型参数求解的二次优化法陈立宏【摘要】邓肯-张非线性弹性模型是土石坝工程中最常用的本构模型.水利行业《土工试验规程》中根据应力水平75%和90%两点法进行计算时,得到的结果往往并不合理,有时n值还可能出现负数.一般的适线法仅仅对单个试样结果进行优化,而并不是针对整组试验结果,因此无法得到最优结果.提出了一种二步优化的参数计算方法,首先对每级围压下单个试样的试验成果采用适线法优化,得到每级围压下的参数a、b.在此基础上,计算得到参数K、n、Rf的初值.然后以邓肯-张理论为基础,根据获得的参数初值针对整组试验成果进行二次优化,以理论计算与试验的应力应变曲线差的平方和最小为目标函数,从而得到EB模型的主要参数.该方法简单实用,能够快速和准确地获得邓肯-张模型参数,并结合糯扎渡大坝堆石料三轴试验数据,对方法进行了验证.%Duncan-Chang nonlinear elastic constitutive model is the most used one in embankment dam engineering.The Specification of Soil Test in hydraulic industry proposes a computational method based on the values of two points from the stress-axial strain curve of the triaxial testing results.The stress levels of these two points are 75% and 90%respectively.However the proposed method cannot obtain reasonable results all the times,and sometimes even the parameter n maybe negative.Curve fitting methods make some progress,but still could not gain the optimal value for the parameters because these methods only based on single sample result.A two step optimization method for acquiring the optimal values of Duncan-Chang model is presented herein.First,the traditional curve fitting method is adopted to obtain thevalues of parameters a and b under each confining pressure.Then the parameters K,n and Rf are ing these parameters as initial values,a second optimization procedure is carried out to fit all the resultsof triaxial test to gain the parameters of Duncan-Chang model,in which,the minimum square sum of the differences of stress and strain curves of theoretical calculation and experiment is taken as the objectivefunction.The method is simple and practical,and can quickly and accurately obtain the parameters of DuncanZhang model.The method is validated based on the triaxial test data of Nuozhadu Dam.【期刊名称】《水力发电》【年(卷),期】2017(043)008【总页数】5页(P52-55,75)【关键词】堆石料;邓肯-张模型;优化方法;土石坝【作者】陈立宏【作者单位】北京交通大学土建学院,北京100044【正文语种】中文【中图分类】TU413堆石料作为高土石坝工程的主体填料,其工程特性和本构模型参数一直为大家所关注。
Duncan-Chang模型第四章本构模型

第四章本构模型第一节邓肯-张(Duncan—Chang)模型(1)(2)复合地基的数值解法主要以有限元方法为主,因为有限元法可以较方便地模拟桩土之间的相互作用,较灵活的处理复杂边界条件,而且还比较容易与其他方法相耦合,因此受到学术界的青睐。
(3)(4)复合地基有限元方法大致可以分为两类,一类是采用增强体单元+界面单元+土体单元进行计以()31/σσε-a 为纵坐标,a ε为横坐标,构成新的坐标系,则双曲线转换成直线。
见图4-2。
其斜率为b ,截距为a 。
有增量广义虎克定律,如果只沿某一方向,譬如Z 方向,给土体施加应力增量ΔZ σ,而保持其他方向的应力不变,可得:Ez x σεΔΔ=(4-3) Ev z x σεΔΔ-= (4-4) 则 xz E εσΔΔ= (4-5) z x v εεΔΔ-= (4-6) 邓肯和张利用上述关系推导出弹性模量公式。
由式(4-5)得:()()aa E εσσεσσεσ∂-∂=-==313111ΔΔΔ (4-7) 由此可见虎克定律中所用的弹性模量实际上是常规三轴试验()a εσσ~31-曲线的切线斜率。
这样的模量叫做切线弹性模量,可用t E 表示,见图4-1。
将式(4-1)代入式(3-7),得到:()2a t b a a E ε+=(4-8) 由式(4-2)可得: b aa --=311σσε (4-9)式(4-9)代入式(4-8),得:()[]23111σσ--=b aE t (4-10) 由式(4-2)可得:当0→a ε时031→⎪⎪⎭⎫ ⎝⎛-=a a a εσσε (4-11)而双曲线的初始切线模量i E 为:31→⎪⎪⎭⎫ ⎝⎛-=a a i E εεσσ (4-12) 见图4-1。
因此:iE a 1= (4-13) 这里表示a 是初始切线模量的倒数。
在双对数纸上点绘⎪⎭⎫⎝⎛a i P E lg 和⎪⎭⎫ ⎝⎛a P 3lg σ的关系,则近似的为一直线,如图4-3所示。
土体邓肯—张非线性弹性模型参数反演分析

土体邓肯—张非线性弹性模型参数反演分析近年来,随着科学技术的发展,经过精心设计的弹性模型和参数反演算法技术开始被广泛应用于土体力学中。
英国科学家邓肯(Duncan)和张(Zhang)的非线性弹性模型参数反演分析方法为土体力学研究奠定了坚实的理论基础。
线性弹性模型参数反演分析旨在研究土体的弹性本构模型,决土体的动态参数反演问题,从而更好地控制和解释土体力学行为。
首先,非线性弹性模型是一种普遍适用的土体力学模型,描述了土体的应力应变关系,其中包括受力弹性部分,恢复弹性部分和弹性非线性部分.述应力应变关系的函数可以用地质、浅层力学等参数表示。
其中包括材料参数,比如弹性模量、泊松比、抗拉强度极限等;空间参数,比如等效平面应力变化率等;时间参数,比如历史负荷重复次数等。
然后,非线性弹性参数反演分析是一种专门用于研究土体动态参数变化特性和土体弹性本构模型确定的非线性优化算法。
主要包括反演算法和参数估计算法。
演算法可以从提供的土体动态应力应变数据中恢复弹性本构参数的值,而参数估计算法则可以从实验测量数据中精确估计土体实际弹性参数的值。
此外,非线性弹性模型参数反演分析具有许多优点,到的结果有助于深入理解土体动态变化特性,有助于开发新的土体力学理论,有助于实现高精度的土体力学分析及模拟,为现有土体力学分析方法提供了更为准确的理论支撑。
最后,非线性弹性模型参数反演分析技术对土体力学研究有重要意义。
管技术刚刚起步,但有望在解决实际问题上发挥重要作用。
此,有必要加强相关技术的研究,加强详细计算,改进参数反演算法,并在非线性弹性本构分析的理论和实验研究方面进行深入挖掘,以及在实际工程中对该技术的实际应用。
综上所述,非线性弹性模型参数反演分析是一种新的、有效的土体力学分析方法,从理论和实践上都有重要意义,为土体力学研究和工程实践提供了有用的理论和技术支持。
邓肯_张非线性模型研究及其在ANSYS中的实现

文章编号:1007-2284(2010)03-0076-04邓肯-张非线性模型研究及其在ANSYS 中的实现宿 辉1,2,党承华2,崔佳佳2(1.北京科技大学土木与环境学院,北京100083;2.河北工程大学水电学院,河北邯郸056021)摘 要:对工程领域使用广泛的邓肯-张非线性本构模型进行了研究,总结了国内外的研究现状及理论成果,针对其无法判定因结压力降低时的加载情况,提出了相应的变形模量的计算方法,同时考虑中主应力、土体抗拉强度的影响对模型进行了修正。
利用AP DL 编写程序实现了A N SYS 的材料本构模型的二次开发,运用重启动方法实现单元应力修正后数据重写入数据库,通过试验模拟对比分析验证了模型的适用性。
关键词:邓肯-张模型;抗拉强度;中主应力;应力分析 中图分类号:T U 470+.3 文献标识码:ADuncan -Chang Nonlinear Elastic Model and Realization in ANSYSSU Hui 1,2,DANG Cheng -hua 2,CUI Jia -jia2(1.Schoo l of Civ il and Env iro nmen Engineering ,Beijing U niver sity o f Science and T echnolog y,Beijing 100083,China;2.Scho ol o f Water Resources and H ydropow er,Hebei U niv ersity of Engineering ,H andan 056021,H ebei Pro vince ,China)Abstract:Based on the pr esent research situation and theor etical r esults,research is do ne o n Duncan -Chang no nlinear elastic mo del,w hich is applied w idely in engineer ing,.A cco rding t o the fact that Duncan -Chang model can't judg e the lo ading situatio n w hile co n -solidat ion pressure decr eases .T he model is mo dified cosidering the effect of int ermediate principal stress and tensile strength of so il.T he seco ndar y dev elo pment of mater ial co nstitut ive model in A N SYS is accomplished by utilizing the A PDL lang uag e.T hen t he r e -start method is used to modify element str ess,the co rrected data is database rew ritten.A ser ies of compliance tests verify the accur a -cy and applicability of the modified Duncan -Chang nonlinear elastic mo del embedded AN SY S.Key words:Duncan -Chang no nlinear elastic mo del;tensile str eng th;inter mediat e pr incipal stress;str ess analy sis 收稿日期:2009-05-18作者简介:宿 辉(1972-),男,副教授,博士研究生,主要从事岩土工程及水工结构教学及研究工作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
!用APDL得到初步成果,贴于此供感兴趣的朋友参考,不当之处敬请指正,
!欢迎加以完善。
!基本思路:
!邓肯-张模型的关键点是材料的弹性模量随大小主应力差
!及小主应力(围压)的变化而变化,用APDL实现之的基本思路是:
!给每个单元定义一个材料号,分级施加荷载,在每个荷载步结束时提取出各
blc4,0,0,0.08,0.15 !建立几何模型
/PNUM,AREA,1
/REPLOT
aesize,all,0.01 !网格划分
mat,1
amesh,all
nsel,s,loc,y,0 !边界条件
d,all,Uy !底边界竖向约束
nsel,s,loc,x,0
*set,P3,-ArrS1(i)
*if,P3,LT,0.1*Pa,then
P3=0.1*Pa !围压最小取值
*endif
Sf0=2*(c0*cos(Fai)+P3*sin(Fai))/(1-sin(Fai)) !Mohr-Coulomb破坏强度(p1-p3)f
Ds=(P1-P3)/Sf0 !应力水平,
MaxPs(i)=P1-P3 !保存历史最大应力
*elseif,MaxPs(i),GE,P1-P3
Et0=Kur*Pa*(P3/Pa)**n0 !卸荷模量
*endif
mp,ex,i,Et0 !修改材料i的Et
mp,nuxy,i,Mu0
mp,dens,I,1800 !重新定义第I种材料的密度
*dim,MaxDs,array,120 !Max history Ds
!*dim,EEt,array,50 !Et of elememt
!!!Duncan-Chang Model
!!!Symbols:c-粘滞力,Fai-内摩擦角,Sf-破坏强度(p1-p3)f,
!Ds-应力水平,Pa-大气压,P3-围压
ETABLE,EtabS3,S,3 !取各单元第三主应力
*dim,ArrS1,array,120
*dim,ArrS3,array,120
*do,Num,1,120 !Num为单元编号
*get,ArrS1(Num),elem,Num,etab,EtabS1 !将单元结果存入数组
楼主给的在ANSYS上实现邓肯-张模型的方法很有用,但其中还有几点需要修正的,这也是楼上的兄弟们有疑问的原因。我把楼主的代码运行了一下,然后对照作了修改,现在上传一下,有问题的兄弟可以仔细对照一下,在这里我对其中几个比较明显的问题说明一下:
*if,Ds,GT,0.95,then
Ds=0.95 !应力水平最大取值
*endif
!判断加卸荷,如果(P1-P3)小于历史最大值视为卸荷-再加荷过程
*if,MaxPs(i),LT,P1-P3,then
Ei=k0*Pa*(P3/Pa)**n0
Et0=Ei*(1-Rf*Ds)**2 !加荷情况的切线模量
*get,ArrS3(Num),elem,Num,etab,EtabS3
*enddo
/PREP7
c0=0
Fai=35
Rf=0.7
k0=400
n0=0.6
Mu0=0.33
Kur=326.7 !修改砂土单元的Et,单元号1-120
*do,i,1,120 !各单元循环计算
*DO,ti,1,2 !取出计算结果,修改弹性模量
/POST1
*get,SUy(ti),node,29,u,y !Settlement record of time ti
ETABLE,EtabS1,S,1 !取各单元第一主应力
!*********************以下定义材料初始模量*************************
mp,ex,1,3.728e7 !砂土的弹性模量
mp,nuxy,1,0.33
mp,dens,1,1800
!******************************************************************
*END
!***********************单元类型***********************************
et,1,42
!平面四节点单元
KEYOPT,1,3,2 !平面应变
!**********************************************************************
*CREATE,Duncan-Chang !Creat Macro file
*afun,deg !Unit of angle
*set,Pa,1e5
*set,P1,-ArrS3(i) !注意:岩土工程中应力为拉负压正
/CLEAR
/TITLE,Numerical Simulation of three axes testing of soils
/PREP7
*dim,SUy,array,50 !Settlement records
*dim,MaxPs,array,120 !Max history p1-p3
*use,Duncan-Chang,c0,Fai,Rf,k0,n0,Mu0,Kur !调用Duncan-Chang宏文件
mpchg,i,i
!!!!!!注意,这个命令是把第I种材料施加给第I个单元
*enddo
/SOLU !EEt(ti)=ET !保存第120单元之ET
1.MP命令不能直接给单元加材料,ቤተ መጻሕፍቲ ባይዱ是对的。在这里,楼主遗漏了一下命令:MPCHG,具体见下面的修改过的代码。
2.关于密度的问题。这些要在宏中定义,每修改一种材料(即调用一次邓肯-张子程序)就要修改一次材料的密度,其他有关材料的问题可以类推。
3.关于施加重力的问题。要在调用宏后,在同一个循环中重新定义一下重力。
time,ti
sfl,3,pres,2e5+1e4*ti !施加荷载,增量1e4
ACEL,0,9.8,0 !重新施加重力
solve !对ti级荷载情况求解
*ENDDO
!单元的大小主应力,据此计算出下个荷载步的弹性模量Et,修改各单元之MP,
!用于下一步计算。
!以下是一个简单算例,copy出去可直接运行。
!!!常规三轴试验模拟
!**********************************************************
FINISH
d,all,Ux !左侧边界水平向约束
nsel,all
/replot
fini
/SOLU
time,0.01 !施加围压
ACEL,0,9.8,0
sfl,all,pres,2e5 !200kPa
solve
!********分级施加荷载,实现非线性计算,荷载增量10kPa,共50级********
