第二章习题答案讲解
第二章习题及答案

思考与练习1.名词解释SNA 国内生产总值名义变量实际变量净出口间接税国内生产净值国民收入个人可支配收入绿色GDP2.试述六大经济总量包括哪些项目?各个经济量之间有何关系?4.国民收入核算方法有哪几种?5.简述两部门经济、三部门经济以及四部门经济具体如何循环的?6.在统计中,社会保险税增加对GDP、GNP、NNP、NI、PI和PDI这六个经济总量中那个总量有影响?为什么?7.如果甲乙两国并成一个国家,对GDP总和会有什么影响(假定两国产出不变)?8.储蓄-投资恒等式为什么不意味着计划的储蓄恒等于计划的投资?9.经济国民经济核算时要遵循社么样的平衡原则。
10.以中国国民经济核算体系为例介绍SNA的基本内容。
11.试用收入法说明GDP的构成。
11.如何理解产出等于收入,产出等于支出两个等式?12.假定国内生产总值是10000亿美元,个人可支配收入是8200亿美元,政府预算赤字是400亿美元,消费是7600亿美元,贸易赤字是200亿美元。
计算储蓄、投资、政府支出。
13.假定某国各项经济指标如下:消费支出:3000亿;总投资:2000亿;政府支出:900亿;进口:300亿;出口:150亿;工资:4200亿;间接税未知;利息:200亿,租金:250亿;利润:400亿;折旧:100亿;非企业收入:400亿‘根据所给资料进行:(1)用支出法计算该国国内生产总值;(2)该国间接税为多少?(3)该国国内生产净值为多少?14.假定某经济社会有A、B、C三个厂商,A厂商年产出5000美元,卖给B、C和消费者。
其中B买A的产出200美元,C买2000美元,其余2800美元卖给消费者。
B年产出500美元,直接卖给消费者,C年产出6000美元,其中3000美元由A买,其余由消费者买。
(1)假定投入在生产中用光,计算价值增加;(2)计算GDP为多少;(3)如果只有C有500美元折旧,计算国民收入。
1.名词解释(1)SNA: 即国民账户体系。
(完整版)第二章货币资金习题及答案解析

第二章货币资金一、单项选择题1.甲股份有限公司2010年度正常生产经营过程中发生的下列事项中,不影响其2010年度利润表中营业利润的是( )。
A.有确凿证据表明存在某金融机构的款项无法收回,该款项已计提过准备。
B.期末计提带息应收票据利息C.外币应收账款发生汇兑损失D.无法查明原因的现金短缺2.下列情形中,不违背《内部会计控制规范——货币资金》规定的“确保办理货币资金业务的不相容岗位相互分离、制约和监督”原则的是( )。
A.由出纳人员兼任会计档案保管工作B.由出纳人员兼任固定资产明细账及固定资产总账的登记工作C.由出纳人员兼任收入总账和明细账的登记工作D.由出纳人员保管签发支票所需全部印章3.下列经济业务中,企业不得动用库存现金支付的是( )。
A.支付职工奖金65000元B.购买办公用品付款300元C.预付出差人员携带的差旅费5000元D.支付购买设备款1200元4.企业用于办理日常转账结算和现金收付的银行存款户是( )。
A.临时存款户B.基本存款户C.专用存款户D.一般存款户5.企业将准备用于有价证券投资的现金存入证券公司指定的账户时,应借记的会计科目是( )。
A.银行存款B.其他货币资金C.其他应收款D.短期投资6.企业发现现金短缺属于无法查明的其他原因,按照管理权限经批准处理时,应在以下科目核算( )。
A.其他应收款B.管理费用C.其他应付款D.财务费用7.企业采用托收承付方式销售商品,其销售收入确认的时间是( )。
A.发出商品时B.发出商品时并向银行办妥托收手续时C.发出商品时并办妥托运手续时D.购买单位承付全部货款8.企业进行外币存款核算时,使用的会计科目是 ( )。
.A.其他货币资金B.银行存款C.备用金D.其他应收款9.下列各项中,不通过“其他货币资金”科目核算的是( )。
A.信用证存款B.银行本票存款C.信用卡存款D.备用金10.下列款项中,可以采用托收承付方式结算的有()。
A.商品交易的货款B.提供劳务的款项C.代销商品的款项D.赊销商品的款项11.企业将款项汇往外地开立采购专用账户时,应借记的会计科目是()。
高等工程数学第二章习题及答案

第2章 线性代数方程组数值解法 研究n 阶线性方程组Ax b =的数值解法.()ij A a =是n n⨯矩阵且非奇异,12(,,,)Tn x x x x = ,12(,,,)Tn b b b b =两类数值方法:(1) 直接法:通过有限次的算术运算,若计算过程中没有舍入误差,可以求出精确解的方法.Ax b Gx d == 等价变换G 通常是对角矩阵、三角矩阵或者是一些结构简单的矩阵的乘积.(2) 迭代法:用某种极限过程去逐次逼近方程组的解的方法.(1)()i i Ax b x Bx k x Bx k +==+−−−−−→=+ 等价变换建立迭代格式,0,1,i =一、向量范数与矩阵范数 1. 向量范数【定义】 若对nK 上任一向量x ,对应一个非负实数x ,对任意,nx y R ∈及K α∈,满足如下条件(向量范数三公理) (1) 非负性:0x ≥,且0x =的充要条件是0x =;(2)齐次性:x xαα=;(3)三角不等式:x y x y+≤+.则称x为向量x的范数.常用的向量范数: (1) 1—范数11nii x x ==∑(2) 2—范数12221()ni i x x ==∑(3) ∞—范数1max ii nxx ∞≤≤=(4) 一般的p —范数11()pnpi pi xx ==∑2. 矩阵范数【定义】 若n nK ⨯上任一矩阵()ij n n A a ⨯=,对应一个非负实数A ,对任意的,n nA B K ⨯∈和K α∈,满足如下条件(矩阵范数公理):(1) 非负性:0A ≥,且0A =的充要条件是0A =;(2)齐次性:A Aαα=;(3)三角不等式:A B A B +≤+;(4)乘法不等式:AB A B≤.则称A为矩阵A的范数.矩阵范数与向量范数是相容的:Ax A x≤向量范数产生的从属范数或算子范数:10max maxx x AxA Ax x=≠==常见从属范数:(1) 1—范数111max ||nij j ni A a ≤≤==∑(2) ∞—范数11max ||nij i nj A a ∞≤≤==∑(3) 2—范数2A =谱半径1()max ||H i i n A A ρλ≤≤=,iλ为H A A 的特征值.H A 为A 的共轭转置. 注:矩阵A 的谱半径不超过A 的任一范数,即()A A ρ≤范数等价性定理:,s t x x为n R 上向量的任意两种范数,则存在常数12,0c c >,使得12,ns t s c x x c x x R ≤≤ ∀∈.注:矩阵范数有同样的结论. 【定理2.1】是任一向量范数,向量序列()k x 收敛于向量*x 的充要条件是()*0,k x x k -→ →∞二、 Gauss 消去法 1.顺序Gauss 消去法 将方程Ax b =写成如下形式11112211,121122222,11122,1n n n n n n n n nn n n n a x a x a x a a x a x a x a a x a x a x a ++++++=⎧⎪+++=⎪⎨⎪⎪+++=⎩其中记,1,1,2,,.i n i a b i n +==消元过程:第一次消元:设110a ≠,由第2,3,,n 个方程减去第一个方程乘以1111/(2,3,,)i i m a a i n == ,则将方程组中第一个未知数1x消去,得到同解方程11112211,1(1)(1)(1)22222,1(1)(1)(1)22,1n n n n n n n nn n n n a x a x a x a a x a x a a x a x a ++++++=⎧⎪ ++=⎪⎨⎪⎪ ++=⎩其中, (1)11,2,3,,;2,3,,,1ijij i j a a m a i n j n n =-==+ . 1111/i i m a a =,2,3,,i n = .第二次消元:设(1)220a ≠,.由第2,3,,n 个方程减去方程组中的第2个方程乘以(1)(1)2222/(3,4,,)i i m a a i n == ,则将方程组第2个未知数2x 消去,得到同解方程11112213311,1(1)(1)(1)(1)2222322,1(2)(2)(2)33333,1(2)(2)(2)33,1n n n n n n n n n nnn n n n a x a x a x a x a a x a a x a a x a x a a x a x a ++++++++=⎧⎪ +++=⎪⎪ ++=⎨⎪⎪⎪ ++=⎩其中(2)(1)(1)22, 3,4,,; 3,4,,,1ij ij i j a a m a i n j n n =-==+ . (1)(1)2222/i i m a a =,3,4,,i n = .经过1n -次消元后,原方程组变成等价方程组11112213311,1(1)(1)(1)(1)2222322,1(2)(2)(2)33333,1(1)(1),1n n n n n n n n n n n nn n n n a x a x a x a x a a x a a x a a x a x a a x a +++--+++++=⎧⎪ +++=⎪⎪ ++=⎨⎪⎪⎪ =⎩其中()(1)(1), 1,2,,k k k ij ij ik ij a a m a i k k n --=-=++ , 1,2,,,1j k k n n =+++ .(1)(1)/k k ik ik kkm a a --=,1,2,,i k k n =++ ;1,2,,1k n =- .回代过程:(1)(1),1(1)(1)(1),1,,1/[]/,1,2,,2,1.n n n n n m n i i i ii n i j j i j j i x a a x a a x a i n n --+---+=+⎧=⎪⎨=-=--⎪⎩∑计算量:按常规把乘除法的计算次数合在一起作为Gauss 消去法总的计算量,而略去加减法的计算次数. 在消去过程中,对固定的消去次数(1,2,,1)k k n =- ,有:除法(1)(1),,/,1,1,,k k ik i k k k m a a i k k n --= =++ 共计n k -次;乘法(1),,1,2,,;1,2,,,1k ik k j m a i k k n j k k n n - =++ =+++ 共计()(1)n k n k --+次.因此,消去过程总的计算量为1311[()(1)]3n k M n k n k n k n-==--++-≈∑ 回代过程的乘除法计算次数为21()2n n +.与消去法计算量相比可以略去不计.所以, Gauss 消去法总的计算量大约为313n .2. Gauss-Jordan 消去法Gauss-Jordan 消去法是Gauss 消去法的一种变形.此方法的第一次消元过程同Gauss 消去法一样,得到(1)(1)(1)(1)11112213311,1(1)(1)(1)(1)22223322,1(1)(1)(1)(1)32233333,1(1)(1)(1)(1)2233,1,,,,n n n n n n n n n nn nn n n n a x a x a x a x a a x a x a x a a x a x a x a a x a x a x a ++++⎧++++=⎪ +++=⎪ +++=⎨ +++= ⎪⎪⎪⎪⎩其中,(1)11,2,,,1jj a a j n n ==+ . 第二次消元:设(1)220a ≠,由第1,3,4,,n 个方程减去第2个方程乘以(1)(1)2222/(1,3,4,,)i i m a a i n == ,则得到同解方程组(2)(2)(2)11113311,1(1)(2)(2)(2)22223322,1(2)(2)(2)33333,1(2)(2)33,1,,,n n n n n n n n n nnn n n n a x a x a x a a x a x a x a a x a x a a x a x a +++++ +++= +++= ++= ++= (2),⎧⎪⎪⎪⎨⎪⎪⎪⎩继续类似的过程,在第k 次消元时,设(1)k kk a -,将第i 个方程减去第k 个方程乘以(1)(1)/k k ik ik kk m a a --=,这里1,3,4,1,1,,i k k n =-+ .经过1n -次消元,得到(2)1111,1(1)(2)2222,1(2)(2)33,1,,,n n n n n a x a a x a a x a +++⎧ =⎪ =⎪⎪ ⎨⎪⎪⎪ =⎩其中()(1)(1),1,2,,1,1,,k k k ij ij ik kj a a m a i k k n --=-=-+ ;1,2,,,1; 1,2,,1j n n k n =+=- .此时,求解回代过程为(1)(1),1/,1,2,,n i i i n iix a a i n --+= = 经统计,总的计算量约为312M n ≈次乘除法. 从表面上看Gauss-Jordan 消去法似乎比Gauss 消去法好,但从计算量上看Gauss -Jordan 消去法明显比Gauss消去法的计算量要大,这说明用Gauss-Jordan 消去法解线性方程组并不可取.但用此方法求矩阵的逆却很方便. 3.列选主元Gauss 消去法在介绍Gauss 消去法时,始终假设(1)0k kk a -≠,称(1)k kka -为主元.若(1)0k kka -=,显然消去过程无法进行.实际上,既使(1)0k kka -≠,但(1)k kka -很小时,用它作除数对实际计算结果也是很不利的.称这样的(1)k kka -为小主元.【例2.2】设计算机可保证10位有效数字,用消元法解方程1112120.3100.7,0.9,x x x x -⎧⨯+=⎪⎨ +=⎪⎩【解】经过第一次消元:第2个方程减去第1个方程乘以212111/m a a =得1112(1)(1)222230.3100.7x x a x a -⎧⨯+=⎪⎨ =⎪⎩其中(1)1222222111/0.333333333310a a a a =-=-⨯,(1)123323211113(/)0.233333333310a a a a a =-⋅=-⨯于是解得(1)(1)223221/0.7000000000,0.0000000000,x a a x ⎧==⎪⎨=⎪⎩而真解为120.2,0.7x x = =注:造成结果失真的主要因素是主元素11a太小,而且在消元过程中作了分母,为避免这个情况发生,应在消元之前,作行交换.【定义】 若 (1)(1)||max ||k k k r k ik k i na a --≤≤=,则称(1)||k k r k a - 为列主元素. k r 行为主元素行,这时可将第 k r行与第k 行进行交换,使(1)||k k r k a - 位于交换后的等价方程组的 (1)k kk a - 位置,然后再施实消去法,这种方法称为列选主元Gauss 消去法或部分主元Gauss 消去法.【例2.3】 应用列选主元Gauss 消去法解上述方程. 【解】 因为2111a a >,所以先交换第1行与第2行,得1211120.9,0.3100.7,x x x x -⎧+=⎪⎨⨯+=⎪⎩ 然后再应用Gauss 消去法,得到消元后的方程组为1220.9,0.7.x x x ⎧+=⎨=⎩回代求解,可以得到正确的结果.即120.2,0.7x x = =.三、三角分解法 设方程组Ax b =的系数矩阵A 的顺序主子式不为零.即1112121222110,1,2,,.kk k k k kka a a a a a k n a a a ∆=≠=在Gauss 消去法中,第一次消元时,相当于用单位下三角阵211131111010010n m L m m -⎡⎤⎢⎥- ⎢⎥⎢⎥=- ⎢⎥ ⎢⎥⎢⎥- ⎢⎥⎣⎦ ,左乘方程组Ax b =,得11A x b =,其中11121(1)(1)122211(1)200n n n nn a a a a a A L a a -(1)⎡⎤⎢⎥ ⎢⎥==⎢⎥ ⎢⎥⎢⎥ ⎣⎦ ,1(1)(1)111,11,1,1(,,,)Tn n n n b L b a a a -+++== .第二次消元时,相当于用单位下三角阵1232210101001n L m m - ⎡⎤⎢⎥ ⎢⎥⎢⎥= - ⎢⎥⎢⎥⎢⎥ - ⎢⎥⎣⎦0 ,左乘方程组11A x b =,得22A x b =其中11121(1)(1)22211(2)(2)221333(2)(2)300000n n n n nn a a a a a A L L A a a a a --⎡⎤ ⎢⎥ ⎢⎥⎢⎥== ⎢⎥⎢⎥ ⎢⎥ ⎢⎥⎣⎦ ,11(1)(2)(2)2211,12,13,1,1(,,,,).Tn n n n n b L L b a a a a --++++==经过1n -次消元,最后得到等价方程组11n n A x b --=其中11121(1)222111111221(1)n n n n n n nn a a a a a A L L L L A a (1)--------⎡⎤⎢⎥ ⎢⎥==⎢⎥⎢⎥⎢⎥ ⎣⎦1111(1)(1)112221,12,1,1(,,,)n Tn n n n n n n b L L L L b a a a --------+++==注意到1n A -是一个上三角阵,记111111221n n n U A L L L L A -------==则121()n A L L L U LU -==其中,121n L L L L -= . 不难验证21313212_1111n n nn m L m m m m m ⎡⎤⎢⎥ ⎢⎥⎢⎥= ⎢⎥ ⎢⎥⎢⎥ 1 ⎢⎥⎣⎦是单位下三角阵.于是解线性方程组Ax b =,就转化为解方程 LUx b =,若令Ux y =就得到一个与 Ax b =等价的方程组Ly b Ux y =⎧⎨=⎩【定理2.2】 若 A 为 n 阶方阵,且 A 的所有顺序主子式0k ∆≠,1,2,,k n = .则存在唯一的一个单位下三角矩阵 L 和一个上三角矩阵 U ,使A LU =.在上述过程中,若不假设A 的顺序主子式都不为零,只假设A 非奇异,那么Gauss 消去法将不可避免要应用两行对换的初等变换.第一次消元,将第1行与第1r 行交换,相当于将方程组Ax b =左乘矩阵11r P :1111r r P Ax P b=经第一次消元得11111111r r L P Ax L P b--=即系数矩阵为11111r A L P A-=,其中110111r P ⎡⎢ ⎢ 1= 1 0 1 ⎣0 0 ⎤⎥⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎦1 列 1r列 类似地,经1n -次消元,有121111111,22,11n n n n n r n n r r A L P L P L P A----------= .如果预先知道每一个(1,2,,1)iir P i n =- ,则在消元之前就全部作交换,得 1211,2,1,n n n r n r r A P P P A PA----== ,其中,1211,2,1,n n n r n r r P P P P ----= .即原方程变为PAx Pb =然后再消元,相当于对PA 做三角分解PA LU =由以上讨论,可得结论 【定理2.3】 若A 非奇异,则一定存在排列矩阵 P ,使得 PA 被分解为一个单位下三角阵和一个上三角1 行1行r阵的乘积,即PA LU =成立.这时,原方程组Ax b = 等价于 PAx Pb =,即等价于求解LUx Pb =令Ux y =则Ly Pb =实际求解时,先解方程组Ly Pb =,再根据 y 求解 Ux y =,即得原方程组Ax b =的解. 这种求解方法称为三角分解法.常用三角分解方法有以下几种. 1.Doolittle 分解方法 假设系数矩阵A 不需要进行行交换,且三角分解是唯一的. 记21121110n n l L l l ⎡⎤⎢⎥ ⎢⎥=⎢⎥ ⎢⎥ ⎢⎥⎣⎦ , 11121222n n nn u u u u u U u ⎡⎤⎢⎥ ⎢⎥=⎢⎥ ⎢⎥ 0 ⎣⎦ 于是有1112111121222212222112111110n n n n n n n n nn a a a u u u u u a a a l l l a a a ⎡⎤ ⎡⎤⎢⎥⎢⎥ ⎢⎥⎢⎥=⎢⎥⎢⎥ ⎢⎥⎢⎥ ⎢⎥⎢⎥ ⎣⎦⎣⎦ nn u ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥0 ⎣⎦从前面讨论A 的LU 分解过程可看出,L 、U 的元素都是用有关的(1)k ij a -来表示的,而它们的计算较麻烦.现在给出直接从系数矩阵A ,通过比较等式的两边逐步把L 和U 构造出来的方法,而不必利用Gauss 消去法的中间结果(1)k ij a -.计算步骤: (1) 由L 阵的第1行分别乘U 阵的各列,先算出U 阵的第1行元素 11,1,2,,j j u a j n = = .然后,由L 阵的各行分别去乘U 阵的第1列,算出L 阵的第1列元素1111/,2,3,,i i l a a i n = = .(2)现假设已经算出U 阵的前1r -行元素,L 阵的前1r -列元素,下面来算U 阵的第r 行元素,L 阵的第r 列元素.由L 阵的第r 行分别乘U 阵的第j 列(,1,,)j r r n =+ ,得11r ij rk kj rjk a l u u -==+∑所以,得U 阵的第r 行元素11,,1,,r rj rj rk kj k u a l u j r r n-==- =+∑ .再由L 阵的第i 行(1,2,,)i r r n =++ 分别去乘U 阵的第r 列,得11r ir ik kr ir rrk a l u l u -==+∑,所以,得L 阵的第r 列元素11[]/,1,2,,.r ir ir ik kr rr k l a l u u i r r n -==- =++∑取1,2,,r n = 逐步计算,就可完成三角分解A LU =;(3)解与Ax b = 等价的方程组Ly b Ux y =⎧⎨=⎩逐次用向前代入过程先解Ly b = 得1111,2,3,,.i i i ij j j y b y b l y i n -==⎧⎪⎨=- =⎪⎩∑然后再用逐次向后回代过程解Ux y =得1/,()/,1,2,,2,1.n n nn n i i ij j ii j i x y u x y u x u i n n =+=⎧⎪⎨=- =--⎪⎩∑2.Crout 分解方法仍假设系数矩阵A 不需要进行行交换,且三角分解是唯一的.即ˆA L=ˆU .与Doolittle 分解方法的区别在111212122211n n n n nn a a a a a a a a a ⎡⎤ ⎢⎥ ⎢⎥=⎢⎥ ⎢⎥⎢⎥ ⎣⎦ 1122ˆˆl l ⎡⎤ 0⎢⎥ ⎢⎥⎢⎥ ⎢⎥⎢⎥⎣⎦ 122ˆ1ˆ10n u u ⎡⎤⎢⎥ ⎢⎥⎢⎥ ⎢⎥ 1 ⎣⎦ 比较两边,则可推导出与Doolittle 分解方法类似的公式,不过Crout 分解方法是先算ˆL 的第r 列,然后再算ˆU的第r 行.3.Cholesky 分解方法若 A 为对称正定矩阵,则有 ˆT U L =,即11()()TT T A LDL LD LD LL ===其中L 为下三角阵. 进一步展开为1121111211112122221222221212n n n n n n nn n n nn a a a l l l l a a a l l l l l l l a a a ⎡⎤⎡⎤ ⎢⎥⎢⎥ 0 ⎢⎥⎢⎥=⎢⎥⎢⎥ ⎢⎥⎢⎥ ⎢⎥ ⎢⎥⎣⎦⎣⎦ 0nn l ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥ ⎣⎦ 比较两边对应元素,容易得到12121()r rr rr rk k l a l -==-∑ ,11()/r ir ir ik rk rrk l a l l l -==-∑ 1,2,,;1,2,,.r n i r r n ==++Cholesky 分解的优点:不用选主元. 由21rrr rk k a l ==∑ 可以看出||1,2,,.rk l k r ≤=这表明中间量rk l得以控制,因此不会产生由中间量放大使计算不稳定的现象. Cholesky 分解的缺点:需要作开方运算. 改进的Cholesky 分解: 改为使用分解T A LDL =即11121121121221222121111n n n n n n n n nn a a a d l l l d a a a l l d a a a ⎡⎤ 1 ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥ 1 1 ⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥ ⎢⎥⎢⎥⎢⎥ ⎢⎥ ⎣⎦⎣⎦⎣⎦ 2n l ⎡⎤⎢⎥ ⎢⎥⎢⎥ ⎢⎥ 1⎣⎦其中21ˆl 1ˆn l 2ˆn l ˆnn l 1ˆn u12111()/r r rr rk k k r ir ir ik k rk rk d a l d l a l d l d-=-=⎧=-⎪⎪⎨⎪=-⎪⎩∑∑,1,2,,;1,2,,.r n i r r n ==++Cholesky 分解方法或平方根法:应用Cholesky 分解可将Ax b =分解为两个三角形方程组T Ly b L x y ⎧= ⎪⎨= ⎪⎩分别可解得111111/,()/.i i i ik k ii k y b l y b l y l i n -=⎧=⎪⎨=-, =2,3,,⎪⎩∑和1/,()/1,.n n nn n i i ki k ii k i x y l x y l x l i n n =+⎧=⎪⎨=-, =--2,,2,1⎪⎩∑改进的Cholesky 分解方法或改进的平方根法:应用改进的Cholesky 分解,将方程组Ax b =分解为下面两个方程组1,,T Ly b L x D y -= ⎧⎨= ⎩同理可解得1111,,2,3,,.i i i ik k k y b y b l y i n ==⎧=⎪⎨=- =⎪⎩∑和1/,/,1,2,,2,1.n n n n i i i ki k k i x y d x y d l x i n n =+⎧=⎪⎨=- =--⎪⎩∑ 4.解三对角方程组的追赶法若()ij n n A a ⨯=满足1||||,1,2,,.nii ij j j ia a i n =≠> =∑则称A 为严格对角占优矩阵.若A 满足1||||,1,2,,.nii ij j j ia a i n =≠≥ =∑且其中至少有一个严格不等式成立,则称A 为弱对角占优矩阵.现在考虑Ax d = 的求解,即11112222211111n n n n n n n n n b c x d a b c x d a b c x d d a b x -----⎡⎤⎡⎤⎡⎤ ⎢⎥⎢⎥⎢⎥ ⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥ = ⎢⎥⎢⎥⎢⎥ ⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 系数矩阵A 满足条件11||||0,||||||,,0,2,3,, 1.||||0,i i i i i n n b c b a c a c i n b a ⎧>>⎪≥+ ≠=-⎨⎪>>⎩采用Crout 分解方法11112222221111n n n n n n n b c a b c a b c a b βαβγαγα---⎡⎤ ⎡⎤⎢⎥ 1 ⎢⎥⎢⎥ ⎢⎥⎢⎥ = ⎢⎥⎢⎥ ⎢⎥ ⎢⎥ ⎢⎥⎢⎥⎣⎦ ⎣⎦ 1n β-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥1 ⎢⎥⎢⎥ 1 ⎣⎦其中,,,i i i αβγ为待定系数.比较上式两边可得到111111,;,,2,3,,;,2,3,, 1.i i i i i i i i i b c a b i n c i n ααβγγβααβ-= == =+ == =-进而可导出1111111,2,3,,.,/,,2,3,,./(),2,3,, 1.i i i i i i ii i i i a i n b c b b i n c b i n γαβααββαβ--⎧= =⎪= =⎪⎨=- =⎪⎪=- =-⎩由此可看出,真正需要计算的是(1,2,,1)i n β=- ,而i α可由,i i b a 和1i β-产生.因此,实现了A 的Crout 分解后,求解Ax d =就等价于解方程组Ly dUx y =⎧⎨=⎩从而得到解三对角方程组的追赶法公式: (1) 计算i β的递推公式:1111/,/(),2,3,, 1.i i i i i c b c b i n ββαβ-⎧=⎪⎨=- =-⎪⎩(2) 解方程组Ly d =:11111/()/(),2,3,,.i i i i i i i y d b y d a y b a i n β--⎧=⎪⎨=-- =⎪⎩(3) 解方程组Ux y =:1,1,2,,2,1.n n i i i i x y x y x i n n β+⎧=⎪⎨=- =--⎪⎩追赶法的乘除法次数是66n -次.将计算121n βββ-→→→ 及12n y y y →→→ 的过程称之为“追”的过程,将计算方程组Ax d =的解121n n x x x x -→→→→ 的过程称之为“赶”的过程.四、迭代法 将Ax b =改写为一个等价的方程组 x Bx k =+建立迭代公式 (1)(),0,1,2,.i i x Bx k i +=+ =称矩阵B 为迭代矩阵.【定义】 如果对固定的矩阵B及向量k,对任意初始猜值向量(0)x ,迭代公式(1)()i i +()i()*lim i i x x →+∞=成立,其中*x 是一确定的向量,它不依赖于(0)x 的选取.则称此迭代公式是收敛的,否则称为发散的.如果迭代收敛,则应有**,x Bx k =+1. 收敛性()()*,0,1,2,i i x x i ε=- =为第i步迭代的误差向量.则有(1)(1)*()*()(),0,1,2,.x x B x x B i εε++=-=-==所以,容易推出()(0),0,1,2,,i i B i εε= =其中,(0)(0)*xxε=-为初始猜值的误差向量.设n nB K ⨯∈,lim 0i i B →+∞=⇔ ()1B ρ<.迭代法收敛基本定理: 下面三个命题是等价的 (1) 迭代法(1)()i i x Bx k +=+收敛;(2)()1B ρ<;(3) 至少存在一种矩阵的从属范数⋅,使1B <注:当条件()1B ρ<难以检验时,用1B 或B ∞等容易求出的范数,检验11B <或1B∞<来作为收敛的充分条件较为方便.常用迭代法如下. 2.Jacob 迭代 考察线性方程组Ax b =,设A 为非奇异的n 阶方阵,且对角线元素0ii a ≠(1,2,,)i n = .此时,可将矩阵A 写成如下形式A D L U =++,1122(,,,)nn D diag a a a = ,21313212000n n a L a a a a ⎡⎤⎢⎥ ⎢⎥⎢⎥= ⎢⎥ ⎢⎥⎢⎥ 0 ⎢⎥⎣⎦ ,12131232000n n a a a a a U ⎡⎤ ⎢⎥ ⎢⎥⎢⎥= 0 ⎢⎥ ⎢⎥⎢⎥ ⎢⎥⎣⎦ ,建立Jacobi 迭代公式(1)1()1(),i i x D L U x D b +--=-++迭代矩阵11()J B D L U I D A --=-+=-J B 的具体元素为112111122122221200n n J n n nn nn a a a a a a B a a a a a a ⎡⎤ - -⎢⎥⎢⎥⎢⎥- - ⎢⎥=⎢⎥⎢⎥ ⎢⎥⎢⎥- - 0 ⎢⎥⎣⎦ Jacobi 迭代法的分量形式如下1(1)()()111(),j n i i i jj jm m jm m m m j jj xb a x a x a -+==+=--∑∑1,2,,;0,1,2,.j n i = =3.Gauss-Seidel 迭代容易看出,在Jacobi 迭代法中,每次迭代用的是前一次迭代的全部分量()(1,2,,)i jx j n = .实际上,在计算(1)i j x +时,最新的分量(1)(1)(1)121,,,i i i j x x x +++- 已经算出,但没有被利用.事实上,如果Jacobi 迭代收敛,最新算出的分量一般都比前一次旧的分量更加逼近精确解,因此,若在求(1)i j x+时,利用刚刚计算出的新分量(1)(1)(1)121,,,i i i j x x x+++- ,对Jacobi 迭代加以修改,可得迭代公式1(1)(1)()111(),j ni i i jj jm m jm m m m j jj xb a x a x a -++==+=--∑∑1,2,,;0,1,2,.j n i = =矩阵形式(1)1()1()(),0,1,2,.i i x D L Ux D L b i +--=-++-+=1()G B D L U -=--+注:(1)两种迭代法均收敛时,Gauss-Seidt 迭代收敛速度更快一些.(2)但也有这样的方程组,对Jacobi 迭代法收敛,而对Gauss-Seidel 迭代法却是发散的. 【例2.4】 分别用Jacobi 迭代法和Gauss-Seidel 迭代法求解下面的方程组121232342,46,4 2.x x x x x x x ⎧- =⎪-+-=⎨⎪-+=⎩初始猜值取0(0,0,0)x =. 【解】 Jacobi 迭代公式为(1)()12(1)()()213(1)()321(2),41(6),0,1,2,41(2),4i i i i i i i x x x x x i x x +++⎧=+⎪⎪⎪=++=⎨⎪⎪=+⎪⎩迭代计算4次的结果如下 (1)(2)(3)(4)(0.5,1.5,0.5),(0.875,1.75,0.875),(0.938,1.938,0.938),(0.984,1.969,0.984).T T T T x x x x ====Gauss-Seidel 迭代公式为(1)()12(1)(1)()213(1)(1)321(2),41(6),0,1,2,41(2),4i i i i i i i x x x x x i x x +++++⎧=+⎪⎪⎪=++=⎨⎪⎪=+⎪⎩迭代计算4次的结果如下(1)(2)(3)(4)(0.5,1.625,0.9063),(0.9063,1.9532,0.9883),(0.9883,2.0,0.9985),(0.9985,1.999,0.9998).T T T T x x x x ====从这个例子可以看到,两种迭代法作出的向量序列(){}i x 逐步逼近方程组的精确解*(1,2,1)T x =,而且Gauss-Seidel 迭代法收敛速度较快.一般情况下,当这两种迭代法均收敛时,Gauss-Seidt 迭代收敛速度更3.超松弛迭代法为了加快迭代的收敛速度,可将Gauss-Seidel 迭代公式改写成1(1)()(1)()11(),j ni i i i jjj jm m jm m m m jjj xx b a x a x a -++===+--∑∑ 1,2,,;0,1,2,.j n i = =并记1(1)(1)()11(),j ni i i jj jm m jm m m m jjj rb a x a x a -++===--∑∑称 (1)i j r + 为 1i + 步迭代的第 j 个分量的误差向量.当迭代收敛时,显然有所有的误差向量(1)0(),1,2,,.i j r i j n +→→∞=为了获得更快的迭代公式,引入因子R ω∈,对误差向量 (1)i j r + 加以修正,得超松弛迭代法(简称SOR 方法)(1)()(1),0,1,2,.i i i j j j x x r i ω++=+ =即1(1)()(1)()1(),j ni i i i jjj jm mjm m m m jjjxx b a xa x a ω-++===+--∑∑1,2,,;0,1,2,.j n i = =适当选取因子ω,可望比Gauss-Seidel 迭代法收敛得更快.称ω为松弛因子.特别当1ω=时,SOR 方法就是Gauss-Seidel 迭代法.写成矩阵向量形式(1)1()1()[(1)](),j i x D L D U x D L b ωωωωω+--=+--++0,1,2,.i =迭代矩阵为1()[(1)].B D L D U ωωωω-=+--实际计算时,大部分是由计算经验或通过试算法来确定opt ω的近似值.所谓试算法就是从同一初始向量出发,取不同的松驰因子ω迭代相同次数(注意:迭代次数不应太少),然后比较其相应的误差向量()()i i r b Ax =-(或()(1)i i x x --),并取使其范数最小的松弛因子ω作为最佳松弛因子opt ω的近似值.实践证明,此方法虽然简单,但往往是行之有效的. 4.迭代收敛其它判别方法:用迭代法收敛基本定理来判断收敛性时,当n 较大时,迭代矩阵的谱半径计算比较困难,因此,人们试图建立直接利用矩阵元素的条件来判别迭代法的收敛定理. (1) 若方程组Ax b =中的系数矩阵A 是对称正定阵,则 Gauss-Seidel 迭代法收敛. 对于SOR 方法,当02ω<< 时迭代收敛(2)若A 为严格对角占优阵,则解方程组 Ax b = 的Jacobi 迭代法,Gauss -Seidel 迭代法均收敛. 对于SOR 方法,当01ω<< 时迭代收敛.【例2.5】 设线性方程组为121221,32,x x x x ⎧+=-⎪⎨+=⎪⎩建立收敛的Jacobi 迭代公式和Gauss -Seidel 迭代公式. 【解】 对方程组直接建立迭代公式,其Jacobi 迭代矩阵为0230J B -⎡⎤=⎢⎥- ⎣⎦,显见谱半径()1J B ρ=>,故Jacobi 迭代公式发散.同理Gauss -Seidel 迭代矩阵为0206G B -⎡⎤=⎢⎥ ⎣⎦,谱半径()61G B ρ=>,故Gauss -Seidel 选代公式也发散. 若交换原方程组两个方程的次序,得一等价方程组121232,21,x x x x ⎧+=⎪⎨+=-⎪⎩其系数矩阵显然对角占优,故对这一等价方程组建立的Jacobi 迭代公式,Gauss -Seidel 迭代公式皆收敛. (3)SOR 方法收敛的必要条件是 02ω<<【定理2.5】 如果A 是对称正定阵,且02ω<<,则解Ax b =的SOR 方法收敛.注:当(0,2)ω∈ 时,并不是对任意类型的矩阵A ,解线性方程组Ax b =的SOR 方法都是收敛的.当SOR 方法收敛时,通常希望选择一个最佳的值opt ω使SOR 方法的收敛速度最快.然而遗憾的是,目前尚无确定最佳超松弛因子opt ω的一般理论结果.实际计算时,大部分是由计算经验或通过试算法来确定opt ω的近似值.所谓试算法就是从同一初始向量出发,取不同的松驰因子ω迭代相同次数(注意:迭代次数不应太少),然后比较其相应的误差向量()()i i r b Ax =-(或()(1)i i x x --),并取使其范数最小的松弛因子ω作为最佳松弛因子opt ω的近似值.实践证明,此方法虽然简单,但往往是行之有效的.【例2.6】 求解线性方程组Ax b =,其中10.3000900.308980.30009100.4669110.274710.30898A - -- -0.46691 0= - -- 00.274711(5.32088,6.07624,8.80455,2.67600).T b ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥ - ⎣⎦ =-分别利用Jacobi 迭代法,Gauss -Seidel 迭代法,SOR 迭代法求解. 【解】其结果列入下表中,方程组精确解(五位有效数字)为*(8.4877,6.4275, 4.7028,4.0066).T x =-Jacobi 迭代法计算结果i()1i x()2i x ()3i x ()4i x ()2||||i r0 012.3095 1 5.3209 6.0762 -8.8046 2.6760 5.3609 27.97113.5621 -5.2324 1.90143.631820 8.4872 6.4263 -4.7035 4.0041 0.0041 218.48606.4271 -4.7050 4.0063 0.0028Gauss-Seidel 迭代法计算结果i()1i x()2i x()3i x()4i x()2||||i r0 012.3095 1 5.3209 7.6730 -5.2220 2.8855 3.6202 28.51506.1933 -5.1201 3.90040.49098 8.4832 6.4228 -4.7064 4.0043 0.0078 98.48556.4252-4.70554.00550.0038SOR 迭代法计算结果(1.16ω=)i()1i x()2i x()3i x()4i x()2||||i r0 012.3095 1 6.1722 9.1970 -5.2320 3.6492 3.6659 29.69416.1177 -4.8999 4.43351.33136 8.4842 6.4253 -4.7005 4.4047 0.0051 78.48686.4288-4.70314.00650.0016计算结果表明,若求出精确到小数点后两位的近似解,Jacobi 迭代法需要21次,Gauss -Seidel 迭代法需要9次,而SOR 迭代法(选松弛因子 1.16ω=)仅需要7次,起到加速作用.5.误差分析 【定理2.6】设 *x 是方程 Ax b = 的惟一解,v ⋅ 是某一种向量范数,若对应的迭代矩阵其范数1v B <,则迭代法(1)(),0,1,2,.i i xBx k i +=+ = 收敛,且产生向量序列(){}i x 满足()*()(1)||||||||||||1||||i i i vv vvB x x x x B --≤--()*(1)(0)||||||||||||1||||i i vv vvB x x x x B -≤--【证明】 由迭代收敛基本定理的(3)知,迭代法(1)(),0,1,2,.i i x Bx k i +=+ =收敛到方程的解*x .于是,由迭代公式立即得到(1)*()*(1)()()(1)(),().i i i i i i x x B x x x x B x x ++--=--=-为书写方便把v 范数中v 略去,有估计式(1)*()*||||||||||||,i i x x B x x +-≤⋅-(1)()()(1)||||||||||||.i i i i x x B x x +--≤⋅-再利用向量范数不等式||||||||||||x y x y -≥-于是得第一个不等式()(1)(1)()()*(1)*()*||||||||||||||||||||(1||||)||||,i i i i i i i B x x x x x x x x B x x -++ -≥-≥--- ≥--再反复递推即第二个不等式.注:(1)若事先给出误差精度ε,利用第二个不等式可得到迭代次数的估计(1)(0)(1||||)ln ln ||||||||v v v B i B x x ε⎡⎤->⎢⎥-⎣⎦ (2)在||||v B 不太接近1的情况下,由第一个不等式,可用()(1)||||i i v x x ε--<作为控制迭代终止的条件,并取 ()i x 作为方程组 Ax b = 的近似解.但是在||||v B 很接近1时,此方法并不可靠.一般可取1,2,v =∞或F .【例2.7】 用Jacobi 迭代法解方程组123123123202324,812,231530.x x x x x x x x x ⎧++=⎪++=⎨⎪-+=⎩问Jacobi 迭代是否收敛?若收敛,取(0)(0,0,0)T x =,需要迭代多少次,才能保证各分量的误差绝对值小于610-?【解】 Jacobi 迭代的分量公式为(1)()()123(1)()()213(1)()()3121(2423)201(12),0,1,2,81(3022),15i i i i i i i i i x x x x x x i x x x +++⎧=--⎪⎪⎪=-- =⎨⎪⎪=-+⎪⎩Jacobi 迭代矩阵J B 为130102011088210155J B ⎡⎤ - -⎢⎥⎢⎥⎢⎥=- -⎢⎥⎢⎥⎢⎥- ⎢⎥⎣⎦,由5251||||max ,,1208153J B ∞⎧⎫==<⎨⎬⎩⎭知,Jacobi 迭代收敛. 因设(0)(0,0,0)Tx =,用迭代公式计算一次得(1)(1)(1)12363,, 2.52x x x = = =而(1)(0)|||| 2.x x ∞-=于是有6110(1)13ln ln 13.23i -⎡⎤⋅-⎢⎥>=⎢⎥⎢⎥⎣⎦所以,要保证各分量误差绝对值小于610-,需要迭代14次.【例2.8】 用Gauss -Seidel 迭代法解例2.11中的方程组,问迭代是否收敛?若收敛,取(0)(0,0,0)Tx =,需要迭代多少次,才能保证各分量误差的绝对值小于610-?【解】 Gauss -Seidel 迭代矩阵G B 为102403601()03025524000G B D L U - - ⎡⎤⎢⎥=-+= -⎢⎥⎢⎥ 38 -3⎣⎦显然1||||14G B =<,所以迭代收敛. Gauss -Seidel 迭代分量公式为(1)()()123(1)(1)()213(1)(1)(1)3121(2423),201(12),0,1,2,81(3022),15i i i i i i i i i x x x x x x i x x x ++++++⎧=--⎪⎪⎪=-- =⎨⎪⎪=-+⎪⎩因取(0)(0,0,0)T x =,故迭代一次得(1)(1)(1)1231.2, 1.35, 2.11x x x = = =于是有(1)(0)|||| 2.11x x ∞-=,计算得6110(1)14ln ln 10.2.114i -⎡⎤⋅-⎢⎥>=⎢⎥⎢⎥⎣⎦所在,要保证各分量误差绝对值小于610-,需要迭代11次.。
第二章传递函数习题与答案

第二章习题课一. 求图示系统结构图的传递函数)()(s R s C ,)()(s N s C ,)()(s R s E ,)()(s N s E 。
二.T 型网络如下图所示,试绘出其动态结构图,并求出传递函数)()(s U s U i o 。
1i三.系统的微分方程组为)()()(1t c t r t x -=)()()(21121t x t x k dtt dx T -=)()()(323t c k t x t x -=)()()(322t x k t c dtt dc T =+式中32121,,,,k k k T T 均为正的常数,系统的输入量为)(t r ,输出量为)(t c ,试画出动态结构图,并求)()(s R s C 。
四.求下图所示系统的传递函数。
五.用结构图化简法求系统传递函数)()(s R s Y 。
)(s六.系统动态结构图如图所示,试确定系统的闭环传递函数)()(s R s C第二章习题课一. 求图示系统结构图的传递函数)()(s R s C ,)()(s N s C ,)()(s R s E ,)()(s N s E 。
1、求)()(s R s C )1(1)1()()(5412152545421G G H G G G G G G G G GG s R s C -++--=2、求)()(s N s C))1)(1()1)(()()(5221545432G G H G G G G G G G G s N s C ++--+=)1(11)()(5412152545254G G H G G G G G G G G G G s R s E -++-+-=)1(1))(1()()(5412152543254G G H G G G G G G G G G G H s N s E -++-+--=二.T 型网络如下图所示,试绘出其动态结构图,并求出传递函数)()(s U s U i o 。
材料化学第二章习题参考答案与解析

第二章参考答案1.原子间的结合键共有几种?各自特点如何?2.为什么可将金属单质的结构问题归结为等径圆球的密堆积问题?答:金属晶体中金属原子之间形成的金属键即无饱和性又无方向性, 其离域电子为所有原子共有,自由流动,因此整个金属单质可看成是同种元素金属正离子周期性排列而成,这些正离子的最外层电子结构都是全充满或半充满状态,电子分布基本上是球形对称,由于同种元素的原子半径都相等,因此可看成是等径圆球。
又因金属键无饱和性和方向性, 为使体系能量最低,金属原子在组成晶体时总是趋向形成密堆积结构,其特点是堆积密度大,配位数高,因此金属单质的结构问题归结为等径圆球的密堆积问题.3.计算体心立方结构和六方密堆结构的堆积系数。
(1) 体心立方 a :晶格单位长度 R :原子半径a 34R = 34R a =,n=2, ∴68.0)3/4()3/4(2)3/4(23333===R R a R bccππζ (2)六方密堆 n=64. 试确定简单立方、体心立方和面心立方结构中原子半径和点阵参数之间的关系。
解:简单立方、体心立方和面心立方结构均属立方晶系,点阵参数或晶格参数关系为90,=====γβαc b a ,因此只求出a 值即可。
对于(1)fcc(面心立方)有a R 24=, 24R a =, 90,=====γβαc b a(2) bcc 体心立方有:a 34R = 34R a =; 90,=====γβαc b a(3) 简单立方有:R a 2=, 90,=====γβαc b a74.0)3(3812)3/4(6)2321(6)3/4(633hcp =⋅=⋅R R R R a a c R ππξ=R a a c 238==5. 金属铷为A2型结构,Rb 的原子半径为0.2468 nm ,密度为1.53g·cm-3,试求:晶格参数a 和Rb 的相对原子质量。
解:AabcN nM=ρ 其中, ρ为密度, c b a 、、为晶格常数, 晶胞体积abc V =,N A 为阿伏加德罗常数6.022×1023 mol -1,M 为原子量或分子量,n 为晶胞中分子个数,对于金属则上述公式中的M 为金属原子的原子量,n 为晶胞中原子的个数。
物理性污染控制习题答案解析第二章

解:物理性污染控制习题答案 第二章噪声污染及其控制1. 什么是噪声?噪声对人的健康有什么危害?答:噪声是声的一种,是妨碍人们正常活动的声音;具有声波的一切特性;主要来源 于固体、液体、气体的振动;产生噪声的物体或机械设备称为噪声源。
噪声对人的健康危害有:弓I 起耳聋、诱发疾病、影响生活、影响工作。
2. 真空中能否传播声波?为什么?答:声音不能在真空中传播,因为真空中不存在能够产生振动的弹性介质。
3. 可听声的频率范围为 20〜20000Hz,试求出500 Hz 、5000 Hz 、10000 Hz 的声波波长。
L L ' L 20lg 2 6(dB)PPP5. 一声源放在刚性面上,若该声源向空间均匀辐射半球面波,计算该声源的指向性指数和指向性因数。
解:c=340m/s, 340 500 0.68m 340 50000.068m 340 0.0034m 4. 声压增大为原来的两倍时,声压级提高多少分贝?解:L 20lg 巴, P P20lg 2 I L P20lg 空P 04.9 10 3m/sWI Q - IS 半s 仝/ 2.半=J =4 r 2 2, DI=10lg Q 10lg2 3.01占沖 2 r '全6. 在一台机器半球辐射面上的5个测点,测得声压级如下表所示。
计算第 5测点的指向性指数和指向性因数。
测点 1 2 3 4 5 声压级/dB 8587868489解:7. 已知某声源均匀辐射球面波,在距声源4m 处测得有效声压为2Pa,空气密度1.2 kg / m 3 使计算测点处的声强、质点振动速度有效值和声功率。
I 电0c22 9.8 10 3(W/m 2)1.2 340u UA PA2pePe 2Ue 恵20C2 0c0c 1.2 340W IS9.8 10 3 4 42 1.97(W)DI ioig(P 2^2 P10lg Qn 0.1L . n10 pi 10.1L10 P旦0.1L 10 pp 2 010lg1.74 2.410lg !(108-5 108.7 108-6 108-4 108-9) 86.6(dB)50.1L 0.1L 10 P P 100.1(89 86.6)1.74I 解:DV S tS0cP 0cu f Sue,u 0cDc, D IS,W8. 在半自由声场空间中离点声源2 m处测得声压的平均值为88 dB , (1)求其声功率级和声功率;(2)求距声源5m处的声压级解:(1)按球面波考虑L p L I L W 20lgr 11L W L p 20lg r 11 88 20lg 2 11 105(dB)0.1L W12 0.1 105 1.5W W0 10 W 10 10 10 0.032(W)(2)L p L W 20lg r 11 105 20lg 5 11 80(dB)9. 已知空气密度0=1.21 kg/m3、空气声速c=340m/s。
物理化学 答案 第二章_习题解答

=
(0.3 × 48.66 +
0.7 ×12) KJ·mol-1
=
23.0KJ·mol-1
B
∑ ∑ ∑ S
2-2 已知当 NaCl 溶液在 1kg 水中含物质的量为 n(单位为 mol)的 NaCl 时,体积 V 随 n 的变化关系为:
V/m3 = 1.00138×10-3 + 1.66253×10-5n/mol +1.7738×10-3(n/mol)3/2 + 1.194×10-7(n/mol)2
求当 n 为 2mol 时 H2O 和 NaCl 的偏摩尔体积为多少? 解:设水用“A”表示,NaCl 用“B”表示,由题意得:
1
⎜⎜⎝⎛
∂V ∂n B
⎟⎟⎠⎞ = 1.66253 ×10−5
+ 1.7738 ×10−3
×
3 2
1
× (n / mol) 2
+ 1.194 × 10−7
× 2(n / mol)
那么当 n=2 时,NaCl 的偏摩尔体积
VB
= 1.66253 × 10−5
+ 1.7738 × 10−3
×
3
×
2
1 2
mol·dm3 = 0.547mol·dm-3
bB
=
nB mA
=
wB M (1 − wB )
=
0.095 0.18 × (1 − 0.095)
mol·kg-1 = 0.583mol·kg-1
2-4 若将 25℃、101.325KPa 纯理想气体的状态定为气体的标准状态,则氧气的标准
熵 S1O =205.03J·K-1·mol-1,现改为 25℃、100Kpa 的纯理想气体作为气体的标准态,氧气
大学物理第二章质点动力学习题答案

习题二2-1质量为m 的子弹以速率0v 水平射入沙土中,设子弹所受阻力与速度反向,大小与速度成正比,比例系数为k ,忽略子弹的重力,求:(1)子弹射入沙土后,速度大小随时间的变化关系;(2)子弹射入沙土的最大深度。
[解]设任意时刻子弹的速度为v ,子弹进入沙土的最大深度为s ,由题意知,子弹所受的阻力f =-kv (1)由牛顿第二定律tv mma f d d == 即tv mkv d d ==- 所以t mk v v d d -=对等式两边积分⎰⎰-=tvv t m k v v 0d d 0得t mkv v -=0ln因此t mke v v -=0(2)由牛顿第二定律xv mv t x x v m t v m ma f d d d d d d d d ==== 即xvmv kv d d =- 所以v x mkd d =-对上式两边积分⎰⎰=-000d d v sv x mk 得到0v s m k-=-即kmv s 0=2-2质量为m 的小球,在水中受到的浮力为F ,当它从静止开始沉降时,受到水的粘滞阻力为f =kv (k 为常数)。
若从沉降开始计时,试证明小球在水中竖直沉降的速率v 与时间的关系为[证明]任意时刻t 小球的受力如图所示,取向下为y 轴的正方向,开始沉降处为坐标原点。
由牛顿第二定律得即tvm ma kv F mg d d ==--整理得mtkv F mg v d d =--对上式两边积分⎰⎰=--t vmt kv F mg v00d dy得mktF mg kv F mg -=---ln即⎪⎪⎭⎫ ⎝⎛--=-m kte kFmg v 1 2-3跳伞运动员与装备的质量共为m ,从伞塔上跳出后立即张伞,受空气的阻力与速率的平方成正比,即2kv F =。
求跳伞员的运动速率v 随时间t 变化的规律和极限速率T v 。
[解]设运动员在任一时刻的速率为v ,极限速率为T v ,当运动员受的空气阻力等于运动员及装备的重力时,速率达到极限。
第二章80C51的结构和原理习题及答案

第⼆章80C51的结构和原理习题及答案第⼆章80C51的结构和原理习题及答案1、80C514单⽚机在功能上、⼯艺上、程序存储器的配置上有哪些种类?答:80C51单⽚机在功能上有两种⼤类:(1)、基本型;(2)、增强型;80C51单⽚机在⽣产⼯艺上有两种:(1)、HMOS⼯艺(即⾼密度短沟道MOS ⼯艺);(2)、CHMOS⼯艺(即互补⾦属氧化物的HMOS⼯艺);80C51单⽚机在程序存储器的配置上有三种形式:(1)、掩膜ROM;(2)、EPROM;(3)、ROMLess(⽆⽚内程序存储器)。
2、80C51单⽚机存储器的组织采⽤何种结构?存储器地址空间如何划分?各地址空间的地址范围和容量如何?在使⽤上有何特点?答:80C51单⽚机存储器的组织采⽤哈佛结构:存储器在物理上设计成程序存储器和数据存储器两个独⽴的空间。
基本型单⽚机⽚内程序存储器容量为4KB,地址范围是0000H~0FFFH。
增强型单⽚机⽚内程序存储器容量为8KB,地址范围是0000H~0FFFH。
基本型单⽚机⽚内数据存储器均为128字节,地址范围是00H~7FH,⽤于存放运算的中间结果、暂存数据和数据缓冲。
这128字节的低32个单元⽤作⼯作寄存器,在20H~2FH共16个单元是位寻址区,然后是80个单元的他通⽤数据缓冲区。
增强型单⽚机⽚内数据存储器为256字节,地址范围是00H~FFH。
低128字节的配置情况与基本型单⽚机相同,⾼128字节为⼀般RAM,仅能采⽤寄存器间接寻址⽅式访问(⽽与该地址范围重叠的SFR空间采⽤直接寻址⽅式访问)。
3、80C51单⽚机的P0~P3⼝在结构上有何不同?在使⽤上有何特点?答:80C51单⽚机各⼝均由接⼝锁存器、输出驱动器和输⼊缓冲器组成,但是结构存在差异:P0、P1⼝有转换开关MUX,P2、P3⼝没有;P1~P3⼝都有上来电阻,但是P0没有。
4个I/O⼝的使⽤特点:(1)、P0:P0⼝是⼀个多功能的8位⼝,可按字节访问也可以按位访问。
中北大学概率统计习题册第二章完整答案(详解)说课讲解

中北大学概率统计习题册第二章完整答案(详解)收集于网络,如有侵权请联系管理员删除1.设X 的分布函数为⎪⎩⎪⎨⎧>≤<≤=111000)(2x x Ax x x F确定A 并求{}7.03.0≤<X P 。
解:由()F x 的右连续性得()11lim ()1x A F F x →+==={}()()220.30.70.70.30.70.30.4P X F F <≤=-=-=2. 检查下面数列,指出哪个是分布律,并说明理由,若是分布律,写出其分布函数. (1)5,4,3,2,1,0,15)(==x xx p ; 解:由55()115x x xp x ====∑∑及 ()()00,1,,515xp x x =≥=L 知5,4,3,2,1,0,15)(==x xx p 是分布律。
分布函数为0,11/15,123/1523()6/153410/154515x x x F x x x x <⎧⎪≤<⎪⎪≤<=⎨≤<⎪⎪≤<⎪≥⎩(2)3,2,1,0,65)(2=-=x x x p 。
解:由253(3)06p -=<知 3,2,1,0,65)(2=-=x x x p 不是分布律。
3. 设离散型随机变量X 的分布列为⎪⎪⎭⎫ ⎝⎛-3.04.03.0101,求:(1)X 的分布函数;解:010.310()0.70111x x F x x x <-⎧⎪-≤<⎪=⎨≤<⎪⎪≥⎩(2) }21{≤≤-X P 。
解:{12}P X -≤≤()()()21110.30.31F F P X =-+=-=-+=4.某射手的射击命中率为p ,现对一目标连续射击,直到第一次击中为止。
令X 表示到第一次击中为止所用的射击次数,试求X 的概率分布。
解:设i A ={第i 击中目标},1,2,i =L()()11P X P A p === ()()()12111,1,2,k k k P X k P A A A A p p k --===-=L L5. 已知随机变量X 的密度函数为,01,()(2),12,0,kx x f x k x x <<⎧⎪=-≤≤⎨⎪⎩其它.试求:收集于网络,如有侵权请联系管理员删除(1)常数k ; 解:1211()d d (2)d f x x kx x k x x +∞-∞==+-⎰⎰⎰22k kk =+= 即 1k =(2)X 的分布函数; 解: ()()dt x F x f t -∞=⎰()()010112100dt01dt 2dt 12dt 2dt 2xxx t x t t x t t x ≤⎧⎪<≤⎪⎪=⎨+-<≤⎪⎪⎪+->⎩⎰⎰⎰⎰⎰ 22000122112212x x x x x x x ≤⎧⎪⎪<≤⎪=⎨⎪--<≤⎪⎪>⎩(3)13{}22P X <<。
随机信号分析(常建平,李林海)课后习题答案第二章习题讲解
A与 B独立 , f AB (a, b) f A (a) fB (b)
X (t) A Bt Y(t) A
A Y(t) X (t) Y (t)
B t
01 J1 1 1
t tt
1
xy 1
xy
f XY (x, y; t ) J f AB (a,b) t f AB ( y, t ) t f A ( y) f B ( t )
E X (t) E A cost XH cost EA XH
D X (t) E X 2 (t ) E2 X (t )
方法 2:
D X (t)
D Acost XH D Acost cos2 t DA cos2 t
12
D XH
公式: D aX+ bY a2 D X b2 D Y 2abC XY
RX (t1, t2 )=E Acost1 XH A cost2 XH
f X (x1;0)
1
x12 e 2,
2Байду номын сангаас
A
1
X (t)
~ N (0, )
t 30
2
4
f X ( x2; 3
)=
0
2 2
e
2
x2
2
,
X (t) t
=0,
f ( x3;2
)
0
20
( x3)
(离散型随机变量分布律 )
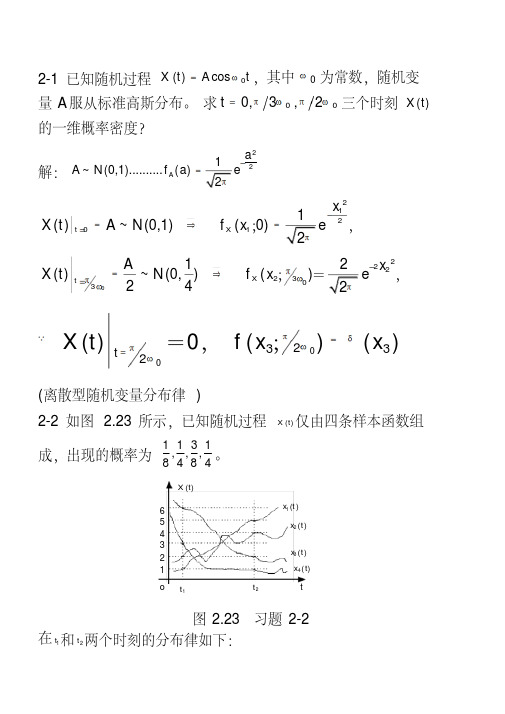
2-2 如图 2.23 所示,已知随机过程 X (t) 仅由四条样本函数组
成,出现的概率为
数 RX (t1, t2 ) ?②若已知随机变量相 A, B 互独立,
它们的概率密度分别为 f A (a) 和 f B (b) ,求 X (t) 的一
操作系统第二章作业讲解

操作系统第二章作业讲解第二章习题讲解1、进程之间存在着哪几种制约关系?各是什么原因引起的?下列活动分别属于哪种制约关系?(1)若干同学去图书馆借书;(2)两队举行篮球比赛;(3)流水线生产的各道工序;(4)商品生产和社会消费。
答:进程之间存在着直接制约与间接制约这两种制约关系,其中直接制约(同步)是由于进程间的相互合作而引起的,而间接制约(互斥)则是由于进程间共享临界资源而引起的。
(1)若干同学去图书馆借书,是间接制约,其中书是临界资源;(2)两队举行篮球比赛,是间接制约,其中蓝球是临界资源;(3)流水线生产的各道工序,是直接制约,各道工序间需要相互合作,每道工序的开始都依赖于前一道工序的完成;(4)商品生产和社会消费,是直接制约,两者也需要相互合作:商品生产出来后才可以被消费;商品被消费后才需要再生产。
2、试写出相应的程序来描述下图所示的前趋图vara,b,c,d,e,f:semaphore:=0,0,0,0,0,0;begin S1; signal(a); signal(b);signal(c); end;begin wait(a); S2; end;begin wait(b); S3; signal(d); end; begin wait(c); S4; end;begin wait(d); S5; signal(e); signal(f); end; begin wait(e); S6; end;begin wait(f); S7; end;3、已知一个求值公式(A2+3B)/(B+5A),若A、B已赋值,试画出该公式求值过程的前趋图,并使用信号量描述这些前趋关系。
答:根据求值公式,假设:S1: X1=A*AS2: X2=3*BS3: X3=5*AS4: X4=X1+X2S5: X5=B+X3S6: X6=X4/X5var a,b,c,d,e:semaphore:=0,0,0,0,0;begin S1; signal(a); end;begin S2; signal(b); end;begin S3; signal(c); end;begin wait(a); wait(b); S4; signal(d); endbegin wait(c); S5; signal(e); endbegin wait(d); wait(e); S6; end4、桌上有一只能容纳一个水果的盘子;爸爸专向盘子中放苹果(apple),妈妈专向盘子中放桔子(orange),一个儿子专等吃盘子中的桔子,一个女儿专等吃盘子里的苹果,1)试用信号量实现他们的同步关系;2)如果有两个家庭的爸爸、妈妈、儿子、女儿和二只盘子呢?会需要专门的实现吗?var empty,apple,orange:semaphore:= 1,0,0;说明:empty与apple表示盘子为空与盘子中放入了苹果,用于表示爸爸与女儿间的同步关系;empty与orange表示盘子为空与盘子中放入了桔子,用于表示妈妈与儿子间的同步关系;答案:1)使用记录型信号量father:beginrepeatproducer an apple;wait(empty);Put an apple to the dish;signal(apple);Until falseend daughter:beginrepeatwait(apple);Get an apple from dish;signal(empty);Eat an apple; Until falseendmother:beginrepeatproducer an orange;wait(empty);Put an orange to the dish;signal(orange); Until falseend son:beginrepeatwait(orange);Get an orange from dish;signal(empty);Eat an orange; Until falseend2)使用记录型信号量varmutex,empty,apple,orange:semaphore:=1,2,0,0;dish: array[0,1] of fruit;in, out:integer:= 0,0;father:beginrepeatproducer an apple;wait(empty);wait(mutex);if dish[in]==apple or dish[in]==orange thenin:=(in+1) mod 2;disk[in]:=apple;in:=(in+1) mod 2;signal(mutex);signal(apple);Until falseend daughter:begin repeatwait(apple);wait(mutex);ifdish[out]==orange thenout:=(out+1) mod 2;get an apple from dish[out];out:=(out+1) mod 2;signal(mutex);signal(empty);Eat an apple; Until falseEndmother:beginrepeatproducer an orange;wait(empty);wait(mutex);if dish[in]==apple or dish[in]==orange thenin:=(in+1) mod 2;disk[in]:=orange;in:=(in+1) mod 2;signal(mutex);signal(orange);Until falseend son:beginrepeatwait(orange);wait(mutex);ifdish[out]==apple thenout:=(out+1) mod 2;get an orange from dish[out];out:=(out+1) mod 2;signal(mutex);signal(empty);Eat an apple; Until falseend5、试用信号量实现课件92页,司机与售票员进程的同步关系var stop, door :semaphore:=0,0;driver:beginrepeatdrive a bus; arrive at bus station; signal(stop);rest;wait(door);Until falseend conductor:begin repeatsell tickets;wait(stop);Open the door;Close the doorsignal(door); Until falseend6、试用信号量解决读者—写者问题,使得写者与读者优先级根据到达顺序确定。
第二章习题解答及参考答案

2 I λz Is = 0 π d
∫
∞
0
J1 (ψ ) ψ ψdψ
2 2 2 2
∞J ( ∞J ( ψ J ( I (r ) ψ J (ψ ) ψ ) ψ ) 1 ψ ) 故: F (r0 ) = i 0 = ∫ 1 ψdψ / ∫ 1 ψ dψ = ∫ 1 dψ dψ / ∫0 0 0 0 Is ψ ψ ψ ψ
第二章 标量衍射理论
部分习题解答及参考答案
[2-1] 在基尔霍夫衍射公式(2-2-16)或(2-2-20)中,同时对光场及其法向导数施加了边 界条件,从而导致了理论本身的不自恰性。为了消除这种不自恰性,索末菲选择了换用格林 函数的办法,使新的格林函数或其法向导数在表面 S1 上为 0,这时就不必同时对光场及其法 向导数施加边界条件。例如,可以选择 G 同时由观察点 P0 及其对衍射屏的镜对称点 P0 各
1 ikz i 2 z (x0 2 + y 0 2 ) U ( x0 , y0 ) = e e F {t (x1 , y1 )} iλ z k 1 ikz i 2 z (x0 2 + y 0 2 ) 2 = [a sinc (af x , af y ) − b 2sinc (bf x ,bf y )] e e iλ z
解:方形环带的透过率函数为:
当用单位振幅的单色平面波垂直照明时,其透过此环带的光场 U t ( x1 , y1 ) = t ( x1 , y1 ) ,故观察 面上的光场分布为:
x y x y t ( x1 , y1 ) = rect 1 , 1 − rect 1 , 1 a a b b
按极值条件,令 x J 0 (x ) − 2 J1 (x ) x = 0 = 0, εx J 0 (εx ) − 2 J1 (εx ) x = 0 = 0 求得:
通信原理第二章(信道)习题及其答案

第二章(信道)习题及其答案【题2-1】设一恒参信道的幅频特性和相频特性分别为0()()d H K t ωϕωω⎧=⎨=-⎩其中,0,d K t 都是常数。
试确定信号()s t 通过该信道后的输出信号的时域表达式,并讨论之。
【答案2-1】 恒参信道的传输函数为:()0()()d j t j H H e K e ωϕωωω-==,根据傅立叶变换可得冲激响应为:0()()d h t K t t σ=-。
根据0()()()i V t V t h t =*可得出输出信号的时域表达式:000()()()()()()d d s t s t h t s t K t t K s t t δ=*=*-=-讨论:题中条件满足理想信道(信号通过无畸变)的条件:()d d H ωωφωωτττ⎧=⎨⎩常数()=-或= 所以信号在传输过程中不会失真。
【题2-2】设某恒参信道的幅频特性为[]0()1cos d j t H T e ωω-=+,其中d t 为常数。
试确定信号()s t 通过该信道后的输出表达式并讨论之。
【答案2-2】 该恒参信道的传输函数为()0()()(1cos )d j t j H H e T e ωϕωωωω-==+,根据傅立叶变换可得冲激响应为:0011()()()()22d d d h t t t t t T t t T δδδ=-+--+-+根据0()()()i V t V t h t =⊗可得出输出信号的时域表达式:0000011()()()()()()()2211 ()()()22d d d d d d s t s t h t s t t t t t T t t T s t t s t t T s t t T δδδ⎡⎤=⊗=⊗-+--+-+⎢⎥⎣⎦=-+--+-+讨论:和理想信道的传输特性相比较可知,该恒参信道的幅频特性0()(1cos )H T ωω=+不为常数,所以输出信号存在幅频畸变。
其相频特性()d t ϕωω=-是频率ω的线性函数,所以输出信号不存在相频畸变。
应用多元统计分析课后习题答案详解北大高惠璇(第二章部分习题解答)

x22
2x1x2
22x1
14x2
65)
1 2 1 2
1
2
exp
1
212
2 2
(1
2
)
[
2 2
(
x1
1 ) 2
21 2(x1
1)(x2
2
)
2 1
(
x2
2
)
2
]
比较上下式相应的系数,可得:
1 2
2 2
1 2
2
1
2 1
1
1 2 1
2 1
1
2
1/
21
2 2
2
2
2 1
21 22 21 21
X
X X
(1) (2)
~
N2 p
(1) (2)
,
1 2
2 1
,
其中μ(i) (i=1,2)为p维向量,Σi (i=1,2)为p阶矩阵,
(1) 试证明X(1) +X(2)和X(1) -X(2) 相互独立.
(2) 试求X(1) +X(2) 和X(1) -X(2) 的分布.
解 :(1) 令
Y
因2x12
2x1x2
x22
(x1,
x2
)
2 1
11
x1 x2
,
而
2 1
11 11
1011
10 BB,
令y
y1 y2
11
1 0
x1 x2
x1
x2 x1
4 3
u1u2
1
2
exp[
1 2
(2u12
u22
2u1u2 )]du1du2
高等数学第二章习题详细解答答案

1 ⎧ 2 1 ⎪ x sin , x ≠ 0 (2)∵ y = ⎨ ,而 lim y = lim x 2 sin = 0 = y x = 0 ,所以函数在 x = 0 处连续 x x →0 x →0 x ⎪ x=0 ⎩ 0,
1 x = 0 ,所以函数在 x = 0 点处可导. 而 lim x →0 x−0 x 2 sin
−2 sin cos (x + Δx) − cos x 3.解: ( cos x)′ = lim = lim Δx → 0 Δx →0 Δx Δx sin 2 x + Δx 2 = − sin x = - lim sin ⋅ lim Δx → 0 Δx → 0 Δx 2 2
4. 解:(1)不能,(1)与 f ( x ) 在 x0 的取值无关,当然也就与 f ( x ) 在 x0 是否连续无关, 故是 f ′( x0 ) 存在的必要条件而非充分条件. (2)可以,与导数的定义等价. (3)可以, 与导数的定义等价. 5. 解:(1) 5 x
9 −1 = 4 ,而 y′ = (x 2 )′ = 2 x ,令 2 x = 4 , 3 −1
得: x = 2 ,所以该抛物线上过点 (2, 4) 的切线平行于此割线. 10.解:(1)连续,但因为
f (0+ h )− f (0 ) = h
因而 lim
h→0
3
h −0 1 = 2/ 3 h h
f (0 + h) − f (0) 1 = lim 2 / 3 = +∞ ,即导数为无穷大。 → h 0 h h
∴ f +′(0) ≠ f −′(0) = −1 ,所以 f ′(0) 不存在.
13. 解 : 当 x > 0 时 , f ( x) = x 是 初 等 函 数 , 所 以 f ′( x) = 3 x ; 同 理 , 当 x < 0 时
《电路分析教程(第三版》第二章习题与答案解析

解按等效概念,图(a)、(b)的等效电压源如题2-26解图所示。
题2-26解图
2-27(略)
2-28(略)
第3章习题解析
3-1如图示电路,试用网孔法求电压u1。
题3-1图
解在各网孔中设网孔电流i1,i2,i3,可列各网孔方程如下:
2i1–i3= 10 – 5
2i2–i3= 5
2i3–i1–i2= –2u1
(2)全电路消耗功率为多少?说明什么规律?
题2-2图
解(1)根据所标示的电流、电压的参考方向,有
P1=u1i1=9 × 1W= 9W
P2=u2(i1)=5 × (1 )W=5W
P3=u3i2=(4 ) × 2W=8W
P4=u4i3=6 × (1 )W=6W
P5=u5(i3)=10 × 1W= 10W
(2)全电路消耗的功率为
P=P1+P2+P3+P4+P5= 0
该结果表明,在电路中有的元件产生功率,有的元件消耗功率,但整个电路的功率守恒。
2-3如图示电路,(1)求图(a)中电压uAB;(2)在图(b)中,若uAB=6V,求电流i。
题2-3图
解对于图(a),由KVL,得
uAB=(8 +3 × 16 + 2 × 1)V= 7V
I5= = 0.5mA
由KCL,得
I2=I4+I5= 1.5mA
设流过2k电阻的电流为I,得
I=I1+I5= 3.5mA
由KVL,有
US2I= 3I3
解得
US= 13V
2-15对图示电路,试求uAB。
题2-15图
解由KVL,可得
uAB=( × 12 + 56)V= 5V
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⑥ 任何绝热过程
W=ΔU
2019/6/8
4
(ⅱ)热量Q的计算:
QV= ∫nCV,m dT= ΔU Qp = ∫nCp,mdT= ΔH
相变热 Qp = ΔH (定温、定压)
ΔvapHm(T) Δfus Hm(T) …
2019/6/8
5
1.试写出实际气体的范德华方程
。
2.封闭系统的热力学第一定律的数学表达式为
凝聚相 W≈0
相变化: W=-p(Vβ-Vα) Β为理气 W=-pVβ=-nR T
ν 化学反应:W
=-p(V
产-V
气态为理气
反)
-RT
∑
B(g)
⑤可逆过程
理气,定温, W=-nRT ㏑(V2/V1)= nRT ㏑(V1/V2)
psu =p-d p
理气,绝热,W =ΔU=nCV,m (T 2-T 1)用绝热可逆方程算 T 2 或 pVr=k
(封闭、W'= 0 )
试将不同过程的体积功计算公式归纳如下:
①向真空自由膨胀 psu= 0,W=0
②psu= 常数(恒外压) W= -psu(V2-V1)
③定容过程
ΔV=0,W=0
2019/6/8
3
④定压过程
理想气体: W=-psu(V2-V1)=-p(V2-V1)=-nR(T2-T1)
p1=p2=psu =常数
)7 。
15. 恒温100oC,在一个带有活塞的气缸中装有3.5mol的水蒸气
H2O(g),在平衡条件下,缓慢的压缩到压力p=( 103.125 )kPa 时,才
可能有水滴H 2O(l) 出现。
17. 在n,T 一定时,任何种类气体,当压力趋近于零时:
lim( pV ) ? (nRT
)
p? 0
18. 封闭系统过程的体积功为零的条件是( dV=0或者p外=0
(升高,降低) 。
,
12. dU ? nCv,mdT式 适用于理想气体的一切变温过程。
(对)
(。 对,错)
14、物理量Q、W、U、H、V、T、p属于状态函数的有(
U、H 、V、T、p );
属于途径函数的有( Q、W )。状态函数中属于强度性质的有
(2019/6/8 T、p );属于广度性质的有( U、H、V
2019/6/8
11
解:
n ? pV ? 4.403 mol RT
He(g)
n= 4.403mol
T1=273K p1=1.0×106 Pa
V1=0.01m 3
(1) Q = 0, 可逆
(2) Q = 0 p外= p2
He(e)
n=4.403mol
T2=? P2=1.0×105Pa
V2=?
2019/6/8
= 80.129 kJ ( 2 )Q = 0,
? U2 = ? U1 = 56.6 kJ ,
? H2 = ? H1 = 80.129 kJ
W = ? U2 = 56.6 kJ ( 3 )dp = 0,? U3 = ? U1 = 56.6 kJ
Qp = ? H = 80.129 kJ
? W ? ?
V2 V1
2019/6/8
6
7.理想气体的微观模型是 分子间无相互作用 力, 分子无体
积
。
8.为使气体经恒温压缩液化,其温度必须 低于 临界温度。
(低于、高于)
9. ? H ? Q p 的适用条件是
0
。。
恒压,非体积功为
10.
Δ
f
H
?
m
(H 2
O,
g)
?
Δ
C
H
?
m
(H
2
,
g)
。
错 (对,错)
11.随着温度的升高,物质的标准摩尔蒸发焓 降低 。
得功(+) W 环境对系统做功
对环境做功(-)
2019/6/8
1
⑵ 特点:Q、W之值随过程发生而产生,因过程而异 其微小量用差分符号δW,δQ。
∮δQ ≠ 0 ;∮δW ≠ 0
Q ≠ Q1+Q2 ! (因过程而异)
只有在特定条件下, (a)封闭、W'=0 ,ΔV=0, (b)封闭、W'=0 ,Δp=0, (c)封闭、绝热
12
(1) Q ? 0
? ? C p,m ? 2.5 ? 1.67
一、小结:
热力学第一定律: 能量守恒
封闭物系: dU = δQ + δW 封闭物系,W'=0 : dU = δQ - psudV
ΔU = Q - ∫psudV 主要讨论了两个过程变量,二个状态函数 (U、H )及状 态函数法。
㈠ 过程变量 Q、W
⑴ 正负号规定(以系统为立足点):
吸热(+) Q
放热(-)
( 1 )体积保持不变; ( 2 )系统与环境无热交换; ( 3 )压力保持不变。
2019/6/8
9
解:( 1 )dV = 0,W = 0。
QV = ? U = n CV,m( T2-T1 ) = ( 10×20×283 ) J = 56.6 kJ ? H = n C p,m( T2-T1 ) = {10×(20+8.314)×283} J
△U=W+Q
。
3.
在孤立系统中发生一化学反应,则其△U = 0。(
>,=,<)
4.
对理想气体其Cp,m -Cv,m=R。 对 (对,错)
5.
SO2 (g) ?
1 2
O2
(
g
)
?
SO3 (g)
反应的标准摩尔反应焓就是 SO 2(g)
的标准摩尔燃烧焓。 错 (对,错)
6. 焦耳—汤姆逊过程也称节流过程,它的基本特征是 恒焓 。
恒容热QV=ΔU 恒压热 Qp=ΔH 绝热功 W= ΔU
这时,恒容热QV ,恒压热 Qp=ΔH ,绝热功 W= ΔU才 能借助于热力学状态函数法进行计算。 (最典型的如反
应热效应计算…)
2019/6/8
2
⑶ Q、W的计算
关键要弄清楚过程性质
(ⅰ)体积功 W = -∫ psudV 也可用 W = -ΔU-Q
19.封闭系统过程的? U ? 0 的条件是( 理想气体的恒温过程 )
或( 绝热恒容过程
).
20.封闭系统下列三个不同类型过程的 ? H ? 0 皆为零:(节流过程
、理想气体恒温过程、绝热恒压 )
2019/6/8
8
例1. 某理想气体,其 CV,m = 20 J·mol?1·K?1,现有 该气体10 mol 处于283 K ,采取下列不同途径升温 至566 K 。试计算各个过程的 Q,W,? U,? H, 并比较之。
pdV
?
-p(V 2-V 1)
= -nRT2
?
nRT1
?
nR(T1
?
T2 )
= -23.529 kJ
2019/6/8
10
例2:273K,1.0MPa,0.01m 3的He(g) 经(1)绝 热可逆过程; (2)绝热且外压恒定在 100kPa 的过程膨胀到末态压力为 100kPa ,分别求 此二过程的 Q,W, ΔU 和ΔH。
