水稻水肥耦合田间试验的设计、方差分析及多重比较
水稻“3414”测土配方施肥田间试验总结

水稻“3414”测土配方施肥田间试验总结作者:李德双来源:《农家科技下旬刊》2015年第01期水稻测土配方施肥试验,主要是探索水稻氮磷钾施用量与产量的相关关系,为测土配方、配肥、施肥提供理论依据,提高粮食单产水平,降低生产成本,提高肥料利用率,减少化肥投放不均造成的环境污染,促进农民增收,保护农民种植积极性,特做此肥料田间试验。
一、材料与方法1.试验地选在洗马镇新场村田维全的责任田里,面积4.2亩,地势平整,交通方便,前作洋芋,土种为鸭泥屎田,肥力下等,海拔900米。
2.供试材料试验选用赤天化尿素,含N量为46%、50%的硫酸钾、14%的开阳普钙,施用量严格按“3414”方案进行,供试水稻品种为福优325。
3.试验设计试验采用“3414”方案设计,共14个处理,两次重复,处理间、重复间用土埂相隔,并用薄膜包埂,试验区四周设保护行,每小区长5cm,宽4cm。
4.栽培管理(1)育苗移栽采用两段育秧方式育秧,4月9日播种,6月20日大田移栽,秧龄71天,行距0.8尺;窝距0.6尺,每小区375窝,每亩栽12500窝,移栽后及时查苗补缺。
(2)施肥整个试验各小区化肥严格按方案进行投入,6月20日大田移栽时,尿素50%作基肥,普钙全部作基肥一次性施用,硫酸钾60%作基肥,6月27日施分蘖肥30%的尿素,8月1日施穗肥,尿素20%、硫酸钾40%。
(3)田间管理适时进行田间常规观察记载和病虫害防治,9月28日进行田间抽样考种,10月7日各小区产量实测。
二、结果分析1.生育期调查和经济性状考查随着氮肥施用量的增大,水稻生育期也延长。
施用量最多的11处理生育期比对照长5天,比6处理长2天;氮肥施用量适中,而磷钾肥的增大,生育期也相应增加,如:磷肥施用量最大的7处理,钾肥施用量最大的10处理,生育期均为162天,比对照多4天,比6处理多1天。
随着氮、磷、钾肥施用量的增加,水稻分蘖数,有效穗增加,但成穗率相应降低,氮肥施用量最多的11处理最高分蘖数比对照多7.93万/亩,亩有效穗多5.5万穗,成穗率比对照降低17.5个百分点;磷肥施用量最多的7处理,最多分蘖数比对照多6.18万/亩,有效穗比对照多4.81万穗,成穗率比对照降低4.3%,钾肥施用量最多的10处理,最高分蘖数比对照多6万/,亩有效穗多4.13万穗,而结实率的高低与氮、磷的施用量关系密切,施用量过大,结实率会降低,而钾肥的影响不很明显,如:处理7、10、11与其它处理相比较。
水稻品种比较试验方差分析

水稻品种比较试验方差分析作者:周晓芳来源:《现代农业科技》2016年第02期摘要进行水稻品比试验,对结果进行方差分析。
结果表明:F优498可列为主导品种,宜香4245、德香4103、乐优198、蓉18优188等可列为示范品种。
关键词水稻;品种;对比试验;变量分析中图分类号 S511 文献标识码 A 文章编号 1007-5739(2016)02-0052-021 材料与方法1.1 试验材料供试水稻品种8个,分别为德香4103、川优6203、蓉18优188、宜香4245、F优498、宜香优2115、内5优39、乐优198。
1.2 试验设计试验设8个处理,即每个品种为一个处理。
分别为德香4103(A)、川优6203(B)、蓉18优188(C)、宜香4245(D)、F优498(E)、宜香优2115(F)、内5优39(G)、乐优198(H)。
4次重复,随机区组排列。
水稻品比试验田间分布见图1。
小区面积20 m2,走道宽区组间2 m,小区间0.5 m,周边保护行宽4 m(D优527)。
1.3 技术规程1.3.1 适宜播期。
3月25日至4月5日。
1.3.2 旱育壮秧。
本田与苗床1∶30,床土培肥、调酸,播前施肥,做厢,分厢匀播。
严格苗床水分管理[1]。
1.3.3 施足底肥。
施农家肥15 t/hm2、碳铵600 kg/hm2、过磷酸钙600 kg/hm2、氯化钾75 kg/hm2。
1.3.4 中苗直插。
5~6叶[2]。
1.3.5 合理稀植。
规格23.31 cm×13.32 cm,30窝/m2,每窝1苗,基本苗30万株/hm2。
1.3.6 田间管理。
具体包括:①水浆管理。
湿润为主。
时到苗足晒田,及时复水。
②追肥。
栽后7 d,施尿素75 kg/hm2。
有效分蘖终止期后(6月25日左右)施穗肥,氯化钾75kg/hm2(长势弱的稻田+尿素40 kg/hm2[3-6])。
谢花后喷施0.5%磷酸二氢钾,每7 d进行1次,共3~4次。
六安市金安区水稻肥料效应田间试验
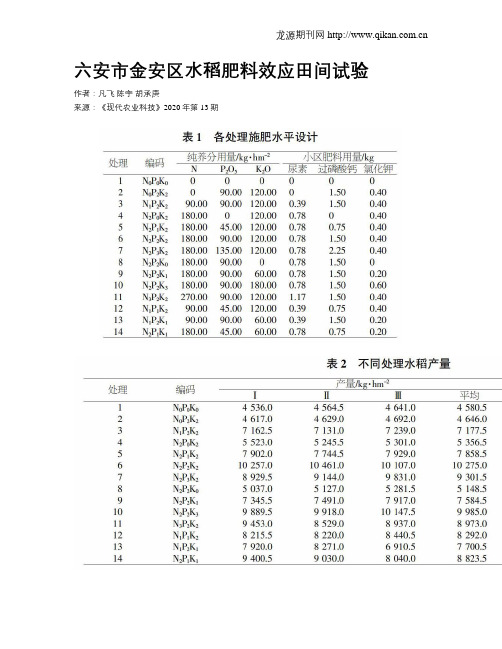
六安市金安区水稻肥料效应田间试验作者:凡飞陈宇胡承庚来源:《现代农业科技》2020年第13期摘要 ; ;通过采用“3414”肥效试验方案,以水稻品种Ⅱ优084为材料,在安徽省六安市金安区开展了氮、磷、钾肥肥效试验研究。
结果表明,水稻最佳产量为11 656.1 kg/hm2,氮、磷、钾肥建议推荐量分别为278.0、185.3、266.8 kg/hm2。
关键词 ; ;水稻;“3414”试验;产量;安徽六安;金安区中图分类号 ; ;S511;S147.5 ; ; ; ;文献标识码 ; ;A文章编号 ; 1007-5739(2020)13-0020-02 ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; 开放科学(资源服务)标识码(OSID)水稻是我国重要的粮食作物。
根据国家统计年鉴数据分析,我国水稻播种面积占粮食作物播种面积的27.5%左右,水稻产量占粮食总产的37.3%以上[1]。
当前水稻的施肥量主要依靠农户的经验来判定,易出现某种养分施用不足而造成减产的现象,或因施用过量造成肥料浪费[2]。
特别是当前农村人居环境综合整治下,农业面源污染已经成为人居环境综合整治的重点和难点。
因此,合理有效施肥,避免浪费和污染,成为水稻生产过程中必须解决的问题[3]。
1 ; ;材料与方法1.1 ; ;试验地概况试验田位于六安市金安区孙岗镇境内,黄白土田,耕层厚度20 cm,pH值5.3,土壤含速效钾96 mg/kg、缓效钾173 mg/kg、有效磷10.3 mg/kg、全磷0.65 g/kg、碱解氮108 mg/kg、全氮1.48 g/kg、有机质24.8 g/kg、硫31.45 mg/kg、硼0.52 mg/kg、锌1.89 mg/kg、铜4.34mg/kg、锰34.63 mg/kg、铁61.56 mg/kg。
控制灌溉条件下水肥耦合对水稻叶面积指数及产量的影响

控制灌溉条件下水肥耦合对水稻叶面积指数及产量的影响魏永华;何双红;徐长明
【期刊名称】《农业系统科学与综合研究》
【年(卷),期】2010(26)4
【摘要】采用控制灌溉技术,通过不同的水肥配合比,研究水肥耦合对水稻的叶面积指数的影响,并进一步探究叶面积指数与腾发量、产量之间的相关关系.试验采用D-最优饱和设计方法设计水肥配合比,试验小区根据随机区组原理进行布置.通过试验得出以下结论:水分和氮肥对叶面积指数具有主要的促进作用,钾肥和磷肥次之;叶面积指数与腾发量、水分利用率呈正相关;叶面积指数的增加可以提高产量.图3,表8,参6.
【总页数】6页(P500-505)
【作者】魏永华;何双红;徐长明
【作者单位】黑龙江省农垦总局,佳南水政水资源管理办公室,黑龙江,佳木
斯,154007;东北农业大学,水利与建筑学院,黑龙江,哈尔滨,150030;黑龙江省农垦总局,佳南农场水利科,黑龙江,佳木斯,154007
【正文语种】中文
【中图分类】S511
【相关文献】
1.滴灌条件下水肥耦合对花生干物质积累和产量的影响 [J], 刘欣婷;王娟;候献飞;陈跃华;兰海燕;李强
2.滴灌条件下水肥耦合对春玉米光合速率及产量的影响 [J], 王雯;张雄;白盼盼;刘远超
3.控制灌溉条件下水肥耦合对水稻产量及其构成因子的影响 [J], 魏永霞;何双红;魏永华
4.膜下滴灌水肥耦合对寒地水稻产量构成因素及产量的影响 [J], 吕艳东;郭晓红;李猛;陈立强;牛同旭;赵海成;孙嵩;姚琪;周云峰;郑桂萍;周健
5.水肥耦合条件下水稻株高及其与产量关系组成分析 [J], 何双红;魏永霞
因版权原因,仅展示原文概要,查看原文内容请购买。
水稻肥料田间试验总结

水稻肥料田间试验总结作者:焦玉刚来源:《农业开发与装备》 2018年第9期摘要:通过严格的田间小区试验,明确供试肥料与习惯性施肥处理、推荐施肥处理间的施肥效果差异,为供试肥料登记提供科学依据。
关键词:水稻施肥;试验方法;试验结果1试验目的通过严格的田间小区试验,明确供试肥料与习惯性施肥处理、推荐施肥处理间的施肥效果差异,为供试肥料登记提供科学依据。
2材料与方法2.1试验作物与品种水稻品种吉大898。
2.2供试肥料掺混肥料,由吉林农利肥料有限公司生产。
主要养分指标为:26-12-12总养分≥50%。
2.3设计与田间排列试验采用随机区组小区试验,试验设三个处理,三次重复,小区15行区,面积30m2,实行单排单灌。
2.4试验处理处理1为供试肥料处理。
用量550kg/hm2,60%翻地前施入,40%耙地时施入,免追肥。
处理2为习惯施肥处理。
施水稻专用肥500kg/hm2作底肥,100kg/hm2尿素作追肥。
处理3为推荐施肥处理。
施尿素145kg/hm2,65kg/hm2作基肥,80kg/hm2作追肥分四次施入;施磷酸二铵196.5kg/hm2,156.5kg/hm2作基肥,40kg/hm2作追肥分蘖期施入;施硫酸钾120kg/hm2,88kg/hm2作基肥,32kg/hm2作追肥穗肥施入;施硫酸锌20kg/hm2,作基肥施入。
2.5试验地基本情况试验设于吉林省九台市九郊办事处马家岗子村四社试验基地,土壤类型为水稻土,土壤肥力中等,前茬作物水稻。
4月5日浸种,4月12日播种,5月26日插秧。
2.6调查内容及方法作物性状调查:①生物性状:株高、茎粗、、叶片数、叶色、发病情况、倒伏情况。
②产量性状:穴数/m2、穗数/穴、粒数/穗、千粒重、空秕率、小区产量、公顷产量、增产率。
调查时间:生物性状在拔节期、灌浆期2次调查,产量性状在成熟期调查。
3结果与分析3.1掺混肥对水稻生物学性状的影响从水稻株高调查结果(详见表1、2、3)看出:拔节期供试肥料处理水稻株高高于习惯施肥处理8.7cm,高于推荐施肥处理1.9cm;灌浆期供试肥料处理水稻株高高于习惯施肥处理11cm,高于推荐施肥处理2cm。
水稻肥料利用率田间试验总结

水稻肥料利用率田间试验总结发布时间:2022-07-08T06:30:09.320Z 来源:《科学与技术》2022年第3月5期作者:韦强、贾毓杨[导读] 为进一步验证水稻肥料利用率参数完善测土配方施肥技术指标体系韦强、贾毓杨融水苗族自治县农业农村局广西融水 545300为进一步验证水稻肥料利用率参数完善测土配方施肥技术指标体系,以及为融水县测土配方施肥决策系统提供技术支撑,在融水镇东良村陆村屯实施了水稻肥料利用率小区试验。
1 试验材料与方法1.1试验时间与地点2020年4月~8月该试验在融水镇东良村陆村屯的稻田实施,试验田位于东经109度 12 分04.2秒,北纬:25度 00 分57.2秒,海拔111.8m,属于低丘平坝。
1.2试验材料试验田土壤为潴育黄泥田,质地为中壤。
0~20厘米耕层土壤主要养分含量为土壤有机质33.9g/kg,全氮2.17g/kg,有效磷53.0mg/kg,速效钾51mg/kg,缓效钾40mg/kg,pH5.39。
所用杂交水稻品种为莱两优华占。
供试肥料品种分别为折合纯N含量为46%的河池尿素,P2O5含量为15%的福泉钙镁磷肥,K2O含量为60%的加拿大氯化钾。
1.3试验设计与施肥1.4样品的采集与分析试验地块试验前严格按“测土配方施肥技术规范”中的采样方法采集不少于2公斤的耕层混合样,进行分析化验并保存样品。
收获时各小区按要求取植株样测试籽粒、秸秆氮磷钾含量、籽秆比以便计算氮磷钾肥料利用率。
2.结果与分析2.1田间生育期及生长情况2.1.1生育期各处理生育期在117—120天之间,各施肥处理间的成熟期,其中处理3(N0P2K2)成熟稍早,于7月30日成熟,全生育期117天,其他处理于8月2日成熟(见表1)。
2.2 不同施肥处理经济性状比较不同施肥处理水稻的植株性状见表4。
从表4中可以看出,各施肥处理间的株高、亩有效穗、每穗总粒数、每穗实粒数存在一定差异,其中株高在80.7—94.4cm之间,以处理2、4最高;亩有效穗在10.338万穗—12.719万穗之间,各施肥处理以处理3最少,处理2最多;每穗总粒数以处理3最少,处理2最多。
水稻肥密耦合试验

水稻肥密耦合试验发表时间:2020-07-03T14:57:50.040Z 来源:《基层建设》2020年第8期作者:陶鑫[导读]黑龙江省云山农场黑龙江 158420前言获得水稻高产高效,最有效的途径就是提高水稻产量,不同的施肥水平、不同的插秧密度直接影响水稻的生长及产量结构的形成。
为了实现增产、高效,设计了三个施肥水平,11叶品种三个插秧规格,12叶品种两个插秧规格进行对比试验,从中探寻合理的施肥水平及栽培密度,为生产提供依据。
1 试验地基本情况试验地设在云山农场水田科技园区,土壤属草甸白浆土,有机质含量64.8㎎/㎏,碱解氮299.5㎎/㎏,有效磷55.5㎎/㎏,速效钾173.3㎎/㎏,PH值5.71。
地势平坦,灌排方便,供试品种为11叶品种龙粳31和12叶品种龙粳21。
2 气象条件日平均气温4月份较历年低2.0℃,5月份较历年高1℃,7、8、9月份气温接近历年。
播种后因气温较低,所以水稻出苗较慢,致使插秧时水稻不足3.5叶,5月份气温仍然较低,水稻缓苗速度慢,不扎根,使水稻生育期延迟,7、8、9月份气温正常,日照充足,有利于水稻的生长发育,对前期不利的自然条件做出了补偿,使水稻的生长发育趋于正常。
3 试验设计及处理采用小区试验,每个处理为120平方米,不设重复。
处理一:亩施肥纯量20公斤,即亩施尿素18公斤、二铵11公斤、硫酸钾(50%)9公斤。
插秧规格:龙粳31为30×10厘米,每平方米28穴,每穴6株;龙粳21为30×12厘米,每平方米25穴,每穴6株。
处理二:亩施肥纯量20公斤,即亩施尿素18公斤、二铵11公斤、硫酸钾(50%)9公斤。
插秧规格:龙粳31为30×10厘米,每平方米27穴,每穴6株;龙粳21为30×12厘米,每平方米23穴,每穴6株。
处理三:亩施肥纯量18公斤,即亩施尿素16公斤、二铵10公斤,硫酸钾(50%)8公斤。
插秧规格:龙粳31为30×10厘米,每平方米28穴,每穴6株;龙粳21为30×12厘米,每平方米25穴,每穴6株。
水稻品种比较试验方差分析

农艺学现代农业科技2016年第2期1材料与方法1.1试验材料供试水稻品种8个,分别为德香4103、川优6203、蓉18优188、宜香4245、F 优498、宜香优2115、内5优39、乐优198。
1.2试验设计试验设8个处理,即每个品种为一个处理。
分别为德香4103(A )、川优6203(B )、蓉18优188(C )、宜香4245(D )、F 优498(E )、宜香优2115(F )、内5优39(G )、乐优198(H )。
4次重复,随机区组排列。
水稻品比试验田间分布见图1。
小区面积20m 2,走道宽区组间2m ,小区间0.5m ,周边保护行宽4m (D 优527)。
1.3技术规程1.3.1适宜播期。
3月25日至4月5日。
1.3.2旱育壮秧。
本田与苗床1∶30,床土培肥、调酸,播前施肥,做厢,分厢匀播。
严格苗床水分管理[1]。
1.3.3施足底肥。
施农家肥15t/hm 2、碳铵600kg/hm 2、过磷酸钙600kg/hm 2、氯化钾75kg/hm 2。
1.3.4中苗直插。
5~6叶[2]。
1.3.5合理稀植。
规格23.31cm×13.32cm ,30窝/m 2,每窝1苗,基本苗30万株/hm 2。
1.3.6田间管理。
具体包括:①水浆管理。
湿润为主。
时到苗足晒田,及时复水。
②追肥。
栽后7d ,施尿素75kg/hm 2。
有效分蘖终止期后(6月25日左右)施穗肥,氯化钾75kg/hm 2(长势弱的稻田+尿素40kg/hm 2[3-6])。
谢花后喷施0.5%磷酸二氢钾,每7d 进行1次,共3~4次。
③病虫害绿色防控。
2结果与分析分小区、同时收获、计重,计入《水稻品比试验产量比较表》,具体见表1。
处理A 、B 、C 、D 、E 、F 、G 、H 的折合产量分别为8280、7710、8175、8460、8925、7470、7785、8205kg/hm 2。
编制产量比较表,进行统计计算:(1)分解自由度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
水稻水肥耦合田间试验的设计、方差分析及多重比较戴琳1,金春明21河海大学农业工程学院,南京 (210098)2 南京市苏地源土地整理规划设计有限公司,南京 (210029)E-mail :darling.1983@摘 要:正确合理的试验设计和统计方法,对于提高田间试验水平,科学分析田间试验结果,以及为读者提供准确信息和增加试验的重演性等均有重要意义。
目前,绝大多数田间试验结果都利用各种分析软件(如DPSS 、DPS 、SAS 、EXCEL 等)进行分析,虽然方便易行,但是许多人对其中含义并不了解,不能很好地达到寻求规律、指导生产的目的。
本文分别用随机区组和裂区设计水稻水肥耦合田间试验,并用二因素随机区组试验和裂区试验的统计分析方法进行方差分析和多重比较。
关键词:田间试验;试验设计;方差分析;多重比较;水稻1. 引言试验在江苏省南京市蔬菜花卉科学研究所内修建的蒸渗仪中进行。
研究水氮耦合对水稻的影响,设灌溉定额和氮肥用量两个因素,其中,灌溉定额设3个水平:300 mm 、450 mm 、600 mm ;氮肥用量设4个水平:150 kg/hm 2、200 kg/hm 2、250 kg/hm 2、300 kg/hm 2。
试验过程中,除施肥和灌水因素外,其它栽培管理措施同一般大田。
2. 试验设计设W 因素为灌溉定额,分别用A1、A2、A3来表示300 mm 、450 mm 、600 mm 三个水平(a=3)。
设N 因素为施加氮肥量,分别用B1、B2、B3、B4来表示:150 kg/hm 2、200 kg/hm 2、250 kg/hm 2、300 kg/hm 2四个水平 (b=4)。
共ab=3×4=12个处理,重复3次(r=3),共abr=3×4×3=36个试验数据。
土壤肥力南北向变化。
2.1 用随机区组的方法对试验进行设计随机区组设计是随机排列设计中最常用而最基本的设计,其特点是根据“局部控制”的原则,将试验地按肥力程度划分为等于重复次数的区组,一个区组亦即一个重复,区组内各处理都独立地随机排列[1,2]。
本试验土壤肥力南北向变化,设三次重复。
借助于随机数字表对三个区组内各小区进行随机排列,设计结果如图1所示:图1 水稻水肥耦合试验的随机区组设计Ⅰ A 1B 1 A 3B 4 A 2B 3A 1B 2A 3B 3A 3B 2A 1B 3A 2B 1A 1B 4 A 2B 2 A 3B 1 A 2B 4Ⅱ A 1B 3 A 2B 1 A 1B 2A 3B 4A 2B 2A 1B 1A 2B 3A 2B 4A 3B 2 A 1B 4 A 3B 1 A 3B 3土壤肥力Ⅲ A 1B 2 A 1B 4 A 3B 4A 2B 4A 2B 2A 3B 3A 1B 1A 2B 3A 2B 1 A 3B 1 A 1B 3 A 3B 22.2 用裂区的方法对试验进行设计裂区设计是多因素试验的一种设计形式,本试验有灌溉定额和施氮肥量两个因素,以水分控制作为主处理划分主区,以施加氮肥量作为副处理划分副区。
先对主处理进行随机排列,后对副处理进行随机排列,每一重复的主、副处理的随机皆独立进行[1,2]。
裂区设计的排列可如图2所示。
图2 水稻水肥耦合试验的裂区设计ⅠⅡⅢB3 B1 B4 B2B2 B3 B1 B4B1 B3 B2 B4B1B2B3B4 B4B1B3B2B2B4B3B1B2B4B1B3B3 B2 B4 B1B1 B4B2B3 A3A2A1A1A3A2A2A1A33.根据各小区内水稻的产量资料,对本试验进行方差分析和多重比较3.1 随机区组试验结果的分析3.1.1结果整理将所得水稻产量资料按处理和区组作两向分组整理成表1;按灌溉定额和氮肥施量做两向分组整理成表2[1-3]。
表1 区组和处理产量的两向表(产量单位为t/hm2)处理区组Ⅰ区组Ⅱ区组Ⅲ总和TABA1B1 11.8 10.6 11.3 33.7 A1B2 12.6 13.0 11.5 37.1 A1B3 15.6 14.8 16.0 46.4 A1B4 12.3 13.2 12.6 38.1 A2B1 14.3 13.7 15.4 43.4 A2B2 16.6 15.6 17.6 49.8 A2B3 18.5 20.3 22.2 61.0 A2B4 22.1 23.8 21.9 67.8 A3B1 16.5 16.8 14.8 48.1 A3B2 16.8 17.5 18.2 52.5 A3B3 13.5 14.2 12.8 40.5 A3B4 15.4 14.3 15.6 45.3 总和Tr 186 187.8 189.9 T=563.7表2 灌溉定额(A)和氮肥施量(B)的两向表B1 B2 B3 B4 TA33.7 37.1 46.4 38.1 155.3A143.4 49.8 61.0 67.8 222A2A348.1 52.5 40.5 45.3 186.4 TB 125.2 139.4 147.9 151.2 T=563.73.1.2 自由度和平方和的分解自由度的分解可按表3直接填入表4。
表3 二因素随机区组试验自由度的分解以下分解各变异来源的平方和:28826.6T C rab ===××2(563.7)334由表1按单因素随机区组的分析方法可得:218826.6381.05abrT jklSS y C =−=+++−=∑"22211.810.615.6C ab T SS rR −∑=20.64C ++=−=×222186187.8189.934Cr T SS ABt −∑=2=8826.6360.17+++−="222(33.737.145.3)3 SSe=SST-SSt-SSR=381.5-360.17-0.64=20.24由表2对SSt=360.17进行再分解:C rb T SS AA −∑=2=C ++−=×222155.3222186.4185.6534 Cra T SS BB −∑=2=2125.2151.28826.644.87+++−=×222139.4147.933=360.17-185.65-44.87=129.65AB t A B SS SS SS SS =−−3.1.3 方差分析表和F 测验将上述结果列于表4。
这里对A 和B 两因素皆取固定模型,区组则取随机模型,因此各项变异来源的MS 均可用对误差项MS 的比进行F 测验。
表4 水稻品种与密度二因素试验的方差分析变 异 来 源 DF SS MS F F0.05 F0.01 区 组 间 2 0.64 0.32 0.35 3.44 5.72 处理(组合)间11 360.17 32.74 35.59**2.263.19灌 溉 定 额 2 185.65 92.83 100.90** 3.44 5.72 氮 肥 施 量 3 44.87 14.96 16.26** 3.05 4.82 灌溉定额×氮肥施量6 129.65 21.61 23.49** 2.55 3.76 误 差 22 20.24 0.92 总 变 异 35 381.05 10.89表4的F 测验说明:该试验区组间差异不显著,而灌溉定额间、氮肥效应间及灌溉与氮肥的交互作用间的差异都是极显著的。
所以需进一步测验灌溉定额间、氮肥效应间及灌溉与氮肥的交互作用间的差异显著性。
3.1.4 差异显著性测验 3.1.4.1 灌溉定额间比较以各灌溉定额处理的水稻产量平均数(将表2的各个TA 值除以rb=12)进行新复极差测验。
假设为H0: 1A µ= 2A µ= 3A µ对HA :1A µ、2A µ、3A µ不全相等。
算得各灌溉定额下水稻产量平均数的标准误:0.277SE ===根据ν=22,在新复级差检验的SSR 表中查得不同p 值所对应的SSR0.05 和SSR0.01,并根据公式p LSR SE SSR αα=⋅,计算出相应的LSR0.05和LSR0.01的值于列于表5。
并根据表5对各灌溉定额处理的水稻产量平均数进行新复极差测验,测验结果于表6所示。
表5 不同灌水量下水稻产量平均数的LSR 值p SSR0.05 SSR0.01 LSR0.05 LSR0.01 2 2.93 3.99 0.81 1.113 3.08 4.17 0.85 1.16表6 不同灌水量下水稻产量平均数的新复极差测验差 异 显 著 性灌溉定额平 均 数(t/hm2)0.05 0.01A2 18.5 a A A3 15.5 b B A1 12.9 c C由表6可见,A2的灌溉定额处理的水稻产量最高,其次是A3和A1 ;A2与A3、A1灌溉定额的处理均有极显著的差异,且A3与A1也有极显著差异。
3.1.4.2 不同氮肥施用量下水稻产量平均数的比较求得各氮肥施用量下水稻产量平均数的标准误:0.320SE ===故有各不同氮肥施量所对应的水稻产量平均数的LSR 值于表7,显著性测验结果于表8。
表7 不同氮肥施用量下水稻产量平均数的LSR 值p SSR0.05 SSR0.01 LSR0.05 LSR0.01 2 2.93 3.99 0.94 1.17 3 3.08 4.17 0.99 1.33 43.174.28 1.01 1.37表8 不同氮肥施用量下水稻产量平均数的新复极差测验差 异 显 著 性氮肥用量平 均 数(t/hm2)0.05 0.01B4 16.8 a A B3 16.4 ab A B2 15.5 b A B1 13.9 c B由表8可知,B4处理的水稻产量最高,其次是B3、B2和B1,即施加氮肥越多水稻产量越高;B4与B3无显著的差异;B4与B3和B2均无极显著差异;但B1与B2 、B3 、B4均有极显著差异。
3.1.4.3灌溉定额×氮肥施量的互作由于灌溉定额×氮肥施量的互作是极显著的,说明各灌溉定额所要求的最适合的氮肥施量可能不相同。
因此,可分别计算各灌溉定额不同氮肥施量的简单效应,以分析互作的具体情形。
将表1各个TAB 值除以r=3,即得各灌溉定额在不同氮肥施量下的小区平均产量(t/hm2)。
求得标准误:SE ==根据ν=22,在新复级差检验的SSR 表中查得不同p 值所对应的SSR0.05 和SSR0.01,并根据公式p LSR SE SSR αα=⋅,计算出相应的LSR0.05和LSR0.01的值于列于表9。
表9 各处理组合平均数的LSR 值p 2 3 4 5 6 7 8 9 10 11 12 SSR0.05 2.93 3.08 3.17 3.24 3.29 3.32 3.35 3.37 3.39 3.40 3.42SSR0.01 3.99 4.17 4.28 4.36 4.42 4.48 4.53 4.57 4.60 4.62 4.65LSR0.05 1.62 1.71 1.76 1.79 1.82 1.84 1.86 1.87 1.88 1.88 1.89LSR0.01 2.21 2.31 2.37 2.42 2.45 2.482.512.532.55 2.56 2.57以表9的显著尺度测验表1中各处理组合的平均数,并将差异显著性列于表10。
