相图的边界理论及其应用 相区及其边界构成相图的规律(赵慕愚,宋利珠著)思维导图
第四章-相平衡PPT课件

综述:
1、在SiO2的多晶转变中,
同级转变:-石英 -鳞石英-方石英
转变很慢,要加 快转变,必须加入矿化剂。
同类转变:-、-和 -型晶体,转变速度非常快。
2、不同的晶型有不同的比重, -石英的最大。 3、 SiO2的多晶转变的体积效应(见表6-1)
-鳞石英,在117℃转变为介稳态的-鳞石英。加热时-鳞石英仍在原转变温
度以同样的速度先后转变为-鳞石英和.-鳞石英。
24
P
R
S
T
U
β-方石英
β-鳞石英
γ-鳞石英
M
L
β-石英
N α -石 英
石英玻璃 V
熔体
N' D'
C
O
α-方石英 D
α-鳞石英
120 163 230
573
870
1200-1350 1470 1600 1670 1713 °C T
石英; 3、在配方中适当加入Fe2O3、MnO2、CaO或Ca(OH)2
等矿化剂,在1000℃左右产生一定量的液相, α石英、α- 方石英在此液相中的溶解度大,而α-鳞 石英的溶解度小,因而 α- 石英、α- 方石英不断 溶入液相,而α-鳞 石英则不断从液相中析出。 4、烧成后降温加快,使其在磷石英间同类转变 5、相变点附近缓慢进行。适用温度870~1470℃
SiO2在自然界储量很大,以多种矿物的形态出现。如水晶、玛瑙、 砂岩、蛋白石、玉髓、燧石等。 在常压和有矿化剂存在的条件下,固 态有7种晶型,其转变温度如下:
熔体(1600℃) 熔体 (1670℃)
相图与相平衡全解

相图的作用:
? 预示不同条件下可能出现的各种组态以及条件 改变时, 各种组态可能发生转变的方向和限度;
? 了解体系在不同条件下的相转变及相平衡存在 的状态;
? 为提高已有材料的性能及设计、开发和研制新 材料提供重要依据;
? 预测材料的性能,为制定材料的制备、合成和 加工工艺提供参考依据。
§1 相图中的点、线、面
F ? C? P?n
ⅰ)相
相:指物质系统中具有稳定和相同的
化学组成、晶体结构、聚集状态以及相同 物理、化学性质的 完全均匀 一致的所有部 分的总和。相可以是单质,也可以是由几 种物质组成的均匀液相或化合物。
“完全均匀”是指物质在分子或离子 水平上的均匀混合状态。
特点:不同相之间有明显界面;机械
方法可分开;通过不同相的宏观界面性质 发生突变;与数量多少无关;与是否连续 无关。
无论溶质原子是以何种方式进入晶格,总会 对溶剂晶格造成一定程度的畸变。这种点阵畸变 会使晶体能量升高,即晶格畸变能。
畸变能越高,晶格越不稳定。单位体积畸变 能的大小与溶质原子溶入的数量以及溶质、溶剂 原子的相对尺寸差别有关。
此外,溶解度还与晶体结构类型、电负性和 电子浓度等因素有关。
§3 平衡态与平衡凝固
在没有外界影响的条件下,系统各部分的宏 观性质长时间内不发生变化的状态。没有外界影 响,是指系统与外界之间不通过作功或传热的方 式交换能量,否则系统就不能达到并保持平衡态。
实际中并不存在完全不受外界影响、宏观性 质绝对保持不变的系统,所以平衡态只是一个理 想化的概念,它是在一定条件下对实际情况的抽 象和概括。只要系统状态的变化很小而可以忽略, 就可以近似看成平衡态。
? 从一种结构转变为另一种结构; ? 化学成分的不连续变化; ? 更深层次序结构的变化并引起物理性质的突变。
第五章 相图
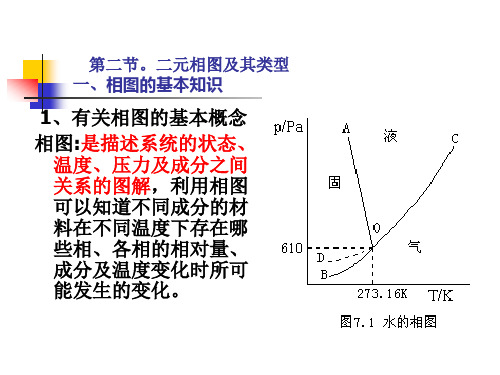
第三节 二元共晶相图及合金凝固
(2)共晶合金(分析要点) ① 凝固过程(冷却曲线、相变、组织示意图)。 ② 共晶线上两相的相对量计算。 ③ 室温组织(α+β)及其相对量计算。
2h
图4-28 Pb-Sn共晶合金平衡凝固过程示意图
1) 在液体中α 和β 同时具有析出条件,都可以析出。
2) 由于α 和β 析出过程在成分上可以互相补充和促进, 共同析出。
二元匀晶相图
一、匀晶相图及其分析 (1)匀晶转变:由液相直接结晶出单相固溶体的 转变。 (2)匀晶相图:具有匀晶转变特征的相图。 Cu-
Ni、 Cu-Au、 Au-Ag、Fe-Cr等
(3)相图分析(以Cu-Ni相图为例) 两点:纯组元的熔点; 两线:L, S相线; 三区:L, α, L+α。
固溶体合金的平衡结晶
金相法
膨胀法 电阻法
热分析法(以Cu-Ni系相图为例):
配制一系列成分不同的Cu-Ni合金; 测定上述合金的冷却曲线 找出各合金的临界点 以温度为纵坐标、以成分为横坐标的图中,将各临 界点连接起来即得到Cu-Ni合金相图
二.相图的建立
名称 晶格类型 熔点 合金1 合金2 合金3 …….. 合金9 合金10 合金11 A金属 fcc 高 100% 90% 80% …….. 20% 10% 0% B金属 fcc 低 0% 10% 20% ……. 80% 90% 100%
二、包晶体转变
过程
成分为P点合金的凝固 β 相的形核在α 相晶体和液体 的边界处,由于β 相的成分介于 液体和α 相之间,所以它是靠消 耗部分已有的α 相和部分液体来 实现。 β 相的生长在液体和α 相的交 界面处最有利,沿边界同时消耗 液体和α 相来长大,形成的β 相 包围在α 相外围,将α 相与液体 分隔开,所以把这种转变称为包 晶转变。
相图中各相成分随体系总成分变化而变化的规律

的影响 。
总结起来 ,在一定温度 、压力下 ,若体系中第 k相含有组元 i且 k相中组元 i的浓度可变 ,
当增加体系中组元 i的量或当另一个 j相中组元 i的浓度增加时 ,则第 k相中组元 i的浓度将
增加 ;而不含组元 i的其他相或含组元 i的定组成的相在一定范围内可以不受影响 。
上面讨论的原则对于电解质溶液或熔融盐也是适用的 。只是因为电解质溶液 (或熔融
图 2 Ag2Ho相图
2. 3 Gupta等人论文中的不足 Gup ta等人在 1986年发表了《用交叉 ZPF ( Zero Phase Fraction,零相分区 )线来构筑多元相 图 》的论文 [5 ] 。论文中叙述了根据有限的信息用交叉 ZPF线的方法来构筑恒压恒温的多元水 平截面图的方法 ,该论文被国际相图界广泛引用 ,所介绍的构筑水平截面图的方法也被国际相 图计算工作者频繁利用 ,但该论文有一些不足 。 在该文图 4中加了如下图注 :“从同样的数据 ( x, y, z)构成 4 个不同的截面 ,在这种情况 下 ,必须进行补充实验 。”Gup ta还指出这些图形在拓扑学上都是正确的 。为了讨论方便起见 , 本文重新给出了图序 ,但没有改变图形的形状 ,见图 3[ 5 ] 。 该文令人难以理解的是为什么要画成这样的图形 。按一般情况 , x、y、z应分别代表富 A、 富 B 和富 C相 ,但这样整个截面图就不可理解了 。这里按常规将图 3 ( a)和图 3 ( b)分别改画 成合理的图 4 ( a)和图 4 ( b) ,并把相区 ( x + y + z)简化为相区 ( xyz) ,其他相区的标识与此类 似。 首先看图 4 ( a) ,这样画是合理的 。靠近左侧腰的边线处 ,体系含组元 C的量较多 ,而含组 元 B 的量很少甚至没有 。从只含 x相的单相区出发 ,使体系中组元 C的量增加 ,按本文前面 讨论过的原理 ,当组元 C增加到一定程度时 ,应该从 x相中析出 z相 ,即形成 xz相区 。 其次看图 4 ( b)的 x相区中靠近底边的部分 。体系中含组元 B 的量较多而含组元 C的量 较少甚至没有 ,从只含 x相的单相区出发 ,使体系的组元 B 的含量增加 ,同理 ,当组元 B 增加 到一定程度时 ,应该从 x相中析出 y相 ,即得 xy相区 。 同样 ,把图 3 ( c)和图 3 ( d)合起来 ,只能画出一个合理的图 4 ( c) 。从只含 x相的单相区出 发 ,若向体系中增加组元 C的量 ,则应析出 z相即得 xz相区 ;若向体系中增加组元 B 的量 ,则 应析出 y相即得 xy相区 。 总起来说 ,根据热力学原理 ,图 4有关相区中所含的相都可以确定 ,不必再做补充的实验 。
相图边界理论与相区接触定律及Gupta方法的比较

中国科学 B 辑 化学 2006, 36 (2): 101~109 101相图边界理论与相区接触定律及Gupta 方法的比较万 强 宋利珠 冯守华* 赵慕愚*(吉林大学化学学院, 长春 130061)摘要 综述了恒压相图中与相邻相区及其边界关系有关的经验规则和理论法则, 重点比较了相图的边界理论和相区接触定律, 着重指出相区接触定律的不足, 并显示相图边界理论的确是一个比较基本的相理论. 还比较了Gupta 方法和相图边界理论的方法在根据有限的信息构筑多元复杂恒压水平截面图上的优劣.关键词 相图边界理论 相区接触定律 Gupta 方法收稿日期: 2005-07-01; 接受日期: 2005-07-22* 联系人, E-mail: shfeng@, muyuzhao@1 引言Gibbs 相平衡理论, 特别是相律构成了相平衡和相图的理论基础. 但相律不能解决相图中相邻相区及其边界的相互关系, 因而在这以后, 国际相图界出现了有关处理这些问题的许多经验规则和理论法则. 1915年, Schreinemakers 提出了Schreinemakers 规则[1]. Vogel-Masing 规则与此类似, 这个规则指出N 个相的相区与(N +1)个相的相区以边界线相邻, 或者与(N +2)个相的相区以边界点对顶相交[1]. 现在有时候又把这个规则叫交叉规则. Gordon 从经验总结出一个不成熟的边界规则[2]. 1955年, Палатник-Ландау(英译名Palatnik-Landau, 或简写为P-L)根据相平衡原理导出了一个理论法则即相区接触定律[3]. 1956年,Rhines 总结了构成复杂三元相图所必须遵循的十条经验规则[4]. 1986年, Gupta 等人提出ZPF(zero phase fraction, 零相分区)线的概念, 并由此出发, 根据有限的信息即可构成复杂的多元水平截面图[5]. 目前, 在国际相图界, P-L 相区接触定律和Gupta 的工作得到了普遍的认可和广泛的应用, 特别是Gupta 方法.赵慕愚从1981年研究了P-L 相区接触定律, 发现它有许多不足之处. 赵慕愚通过多年的研究, 提出了一套完整的系统的相图边界理论[1]. 在一些根本性的问题上, 和P-L 相区接触定律相比, 相图的边界理论有明显的优点. 在构筑多元复杂的水平截面图方面, 与Gupta 方法相比, 相图边界理论的方法也有一些优点.102中国科学 B 辑 化学第36卷2 相图的边界理论与P-L 相区接触定律的比较2.1 P-L 相区接触定律[3]Palatnik-Landau 系统地研究了多元体系的相平衡关系[2], 其中最重要的是相区接触定律. P-L 理论对相邻相区之间的边界仅理解为边界上体系点的集合. Palatnik-Landau 通过复杂的相平衡关系式, 推导出相区接触定律. 边界的维数以1R ′表示, 在两个相邻相区转变过程中, 行将消失的相的相数为D −, 新形成的相的相数为D +, 相图或其截面的维数为R , 则P-L 相区接触定律的公式表述如下:1().R R D D +−′=−+ (1) Palatnik-Landau 的相平衡研究有许多贡献, 其中相区接触定律能解释相邻相区及其边界的相当多的关系, 因而受到人们的重视. 相区接触定律被认为是对相图理论的一个重要贡献. 但应指出的是, 相区接触定律仅能讨论边界的维数.2.2 相图边界理论的重要内容及三个主要公式2.2.1 相边界的概念相边界的概念是一个重要的概念. 过去没有相边界的概念时, 对于图1来说, 处于边界线aE 线上的体系, 只有L 相存在. 按相律, 对于N 元恒压相图中, 若体系中有p 个相, 则:f = N – p + 1.此处N =2, p =1(液相L), 则自由度f 为2. 但aE 是一维的, 仅只有一个自由度, 为什么? 有了相边界的概念, 这个问题就比较容易理解了.众所周知, 一个平衡体系处于任一相区, 均有体系点和一个或几个平衡相点; 边界是相邻相区的共同部分, 当然也是每个相邻相区的一部分. 那么处于边界上的平衡体系也应该有体系点和一个或几个平衡相点.因此, 边界概念应该包含两层意思: 边界和相边界. 边界是划分相邻相区的分界线, 由体系点的集合组成. 其维数以1R ′表之. 而相边界是处于边界上平衡体系的平衡相点的集合. 其维数以R 1表之. 边界和相边界既有相互联系, 又相互区别. 曾有许多文献用到相边界这个词, 但它通常是指一个相或者一个单相区的边界, 与上面定义的相边界的含义是不同的. 对于相平衡来说, 相边界比边界更为重要. 相图的边界理论之所以能提出, 主要是因为区分了边界和相边界这两个不同的概念, 并认识到了相边界的重要性.边界和相边界的不同可以用图1的二元恒压相图的两个相邻相区(L +S 1)/(S 1+S 2)的边界为例来说明. 这两个相邻相区的边界是cE 线, 1R ′=1, 而相边界却是c , E , d 三个平衡相点, R 1=0. 1R ′≠R 1.图1 典型的等压二元相图2.2.2 相图的边界理论的三个主要公式由相边界的基本概念出发, 结合相图所固有的特征, 可以导出相图的边界理论的三个主要公式.(ⅰ) 对应关系定理如两个或多个相邻相区的相的组合(即每个相区包含哪些相)已知, 则Φ (两个或多个相区中所有不同相的总数)和p c (两个或多个相区中每一个相区中都具有的相, 即共同相的数目)为已知. 从相边界的基本概念出发, 根据相平衡和化学平衡的原理可以导出R 1和N 元相图中相邻相区中所有不同相的总数Φ的对应关系定理(the theory of corresponding relation, 简写为TCR):1()2,R N Z r Φ=−−−+ (2)第2期万 强等: 相图边界理论与相区接触定律及Gupta 方法的比较 103其中r 是平衡体系中实际进行的独立化学反应数, Z 是平衡体系中的诸组元的浓度之间的其他独立限制条件数(不包括1Ni i X ==∑,11Ni j i x ==∑的条件在内); X i 为整个体系中组元i 的摩尔分数, x ij 为组元i 在j 相中的摩尔分数, (N −Z −r )在相律中被称为独立组元数. 这是大家熟知的. 在一般恒压相图中, Z =r =0, 在恒压条件下,1 1.R N Φ=−+ (3)有了对应关系定理, 图1中aE 线的相边界维数为R 1=N −Φ+1=2−2+1=1. 这与事实符合, 也很容易理解.推导公式(3)的思路是这样的: 边界(此处是一个通称)是两个(或多个)相邻相区的共同部分, 处于边界上的平衡体系应同时满足相邻的第一个相区和第二个相区中体系的相平衡条件, 写出两个相区的平衡体系的相平衡方程. 即在一定压力P 和温度T 下, 每一个组元在各个相中化学势应相等. 找出两个相区中独立的相平衡方程的总数目, 同时找出相边界上体系的诸平衡相点的物理参数的总数目. 二者相减, 再经过一系列推导, 即可以找出处于边界上平衡体系的平衡相点的独立可变的参数(如T , x ij 等等)的数目, 也就是N 元相图的N 维空间中平衡相点可以独立变动的维数. 即R 1. 在N 元恒压相图中, R 1的数值就等于(N −Φ+1), 也就是公式(3). 它确定了R 1和Φ的一一对应的关系, 故称之为TCR. TCR 的导出思路和相律的导出思路是相似的, 因而大家容易理解.但应着重指出TCR 是不同于相律的一个独立的定理. 文献[2]对此有详尽的论证, 对于多个相区的相边界的TCR 推导方法, 与上述推导过程相似, 此处从略.(ⅱ) 1R ′与R 1和p c 之间的关系 相边界虽然重要, 但显示在相图中的边界(此处指通称)通常是边界而不是相边界, 因此还要求出1R ′和R 1, p c 之间关系. 在两个相区过度过程中, 根据对各类相图进行分析, 有两类不同的情况, 因而1R ′和R 1, p c 之间有两种不同的关系.a)11c .R R p ′=+ (4) 在两个相区过渡过程中, 体系的质量不仅可以分布在共同相中, 同时也可以分布在非共同相中, 在各类相图中只有一种情况是这样的.当R 1=0, 两个相邻相区分别处于边界线的高温和低温上下两侧, 如图1的(L +S 1)/(S 1+S 2). 此时, 在两个相区过度过程, 即相变过程中, 共有Φ=(N +1)个相(二元相图中N +1=3)均可以一定比例同时存在, 即体系的质量既可分布于共同相(此例是S 1相)也可以分布在非共同相(此例是行将消失的L 相和新形成的S 2相)中, 而且它们的比例在相变过程中是不断变化的. 我们把这类情况简称之为当R 1=0, 两个相邻相区间有(N +1)个相同时存在的共存区的情况.通过质量守恒原理, 可以建立起整个体系中每一个组元的摩尔分数X i (i =1, 2, …, N )和第一相区中各相的诸平衡相点的摩尔分数x ij (i =1, 2, …, N ; j =1, 2, …, p c , p c+1, p c+2, …, p c+m1)或第二相区中各相的诸平衡相点的摩尔分数x ij (i =1, 2, …, N ; j =1, 2, …, p c , p c+1′, p c+2′, …, p c+m2)之间的关系式.相变刚刚开始时, 体系的质量全分布在第一个相区, m j 为第j 个相中的物质的量, M 为整个体系的物质的量.c c c c c c c c 112212211.i i ij j ip p ip p ip p p m p m i x m x m x m x m x m x m x m X M ++++++++++++++="""相变完成后, 体系的质量全分布在第二个相区中.c c c c c c 1122112222.i i ij j ip p ip p ip m p m i x m x m x m x m x m x m X M ′′′′++++++++++++++="""经过一系列推导, 可以找到边界维数1R ′和R 1及p c 的关系式. 即当R 1=0, 两个相区间存在(N +1)个相的共存区, 在这些条件下,11c .R R p ′=+ b)11c 1.R R p ′=+− (5) 在所有的其他情况下, 包括R 1≥1, 或R 1=0两个相邻相区虽然总共有Φ=(N +1)个相, 但处于边界上的平衡体系的质量全分布在共同相中(如图1, R 1=1时的L/(L+S 1)中的L 相以及R 1=0时的(L +S 1)/(L +S 2)中的L 相), 体系的质量分布在非共同相(如L/(L+S 1)中的S 1相)的质量只是无限小量: 这就是除了a)的情104中国科学 B 辑 化学第36卷况之外的所有情况. 在这些情况下, 通过质量守恒原理, 可以找到体系点上整个体系中各组元的摩尔分数X i 和各个平衡共同相中各个组元的摩尔分数x ij (i =1, 2, …, N ; j =1, 2, …, p c )之间关系式:c c 1122c (1,2,,;1,2,,),i i ij j ip p i x m x m x m x m X M i N j p +++++===""""式中m j 和M 的含义同前, 注意, 此处质量守恒的等式只有一个. 经过一系列推导, 最后可以得到公式(5).注意, (4), (5)两式的差别不是简单的−1, 而是a)的情况中, 体系质量既可以分布在共同相, 也可以分布在非共同相中, 这是公式(4), (5)二式不同的根本原因所在.公式(3)~(5)就是恒压相图边界理论中最主要的三个公式. 根据上述思路, 可写出它们的完整的推导过程.由两个相邻相区中相的组合, 可以求Φ和p c . 根据式(3), 由Φ可以求R 1. 根据(4)式或(5)式, 可以由R 1及p c 求出1R ′, 有了Φ, p c , R 1和1R ′的值, 恒压相图中相邻相区及其边界的关系就很清楚了. 反之, 若已知一个相邻相区的相的组合以及其边界性质(即已知R 1和1R ′), 则可以求出相邻的第二个相区中相的组合. 总之, 根据相图边界理论, 可以求出Φ, p c R 1, 和1R ′等物理量的数值. 有了这些物理量的数值, 可以系统说明各类恒压相图中相邻相区及其边界的关系. 从相图边界理论可以得到有关这方面的信息比相区接触定律为多.公式(3)~(5)这三个公式和前面所引出的主要基本概念一起, 就构成了恒压相图边界理论的基本内容.2.3 相图中的边界理论和相区接触定律的比较2.3.1 相图边界理论与相区接触定律的关系从相图边界理论的主要公式出发, 可以简捷地导出相区接触定律. 相反, 从P-L 相区接触定律出发, 不能导出相图边界理论中的任何一个主要公式.根据相区接触定律中的D +和D -的定义, 则(D ++D -)实际上就是两个相邻相区中互不相同相的数目(不包括共同相的相数在内). 而Φ既包括(D ++D -),又包括p c , 即.c D D p Φ+−=++ (6)在一般恒压相图中, 有式(3). 很容易证明, 也很容易理解: N 元恒压相图的维数R =N (恒压二、三元相图的维数是2或3等). 将这个关系式和(6)式代入(3)式, 整理可得11().c R p R D D +−+−=−+ (7)再根据公式(5), 可得式(1). 这样就把相区接触定律推导出来了.而P-L 理论以及相区接触定律均无相边界的概念, 也无R 1这个物理量. 因而由它们出发, 不可能导出相图边界理论中三个主要公式中的任何一个.由此可见, 和相区接触定律相比, 相图边界理论是一个更基本的理论.2.3.2 相区接触定律和相图边界理论的适用范围在由相图边界理论推导出相区接触定律的过程中, 引入了下列条件:Z =r =0, 压力恒定. N ≥2, R 1≥1或N ≥2, R 1=0, 但在两个相邻相区转变过程中不存在(N +1)个相的共存区的情况. 因此, 在下列情况下相区接触定律均是无效的:①当Z ≠0或r ≠0, ②N =1,③当N ≥2, R 1=0而在两个相邻相区的相的转变过程中, 存在(N +1)个相的共存区.把相区接触定律应用于实际相图时, 在这些情况下, 相区接触定律的确无效. 此时, Palatnik-Landau 引入了退化区概念以及其他人们难以接受的方法来处理. 例如把图1画成图2的形式.又如把正确的图3画成令人不能接受的与实际不符的图4的形状, 才能应用P-L 相区接触定律.我们认为这样做, 是不合适的. 而相图边界理论对所有前述三种情况都是适用的, 请参见文献[2]第三章.2.3.3 相图边界理论对多元体系的恒温截面和等成分截面的处理比P-L 理论全面而且深刻相图边界理论的处理如下所述:N 元体系的恒压相图维数为N , 相邻相区的边界第2期万 强等: 相图边界理论与相区接触定律及Gupta 方法的比较 105图2 Palatnik-Landau 所画的二元相图图3 有最低共熔点的二元相图图4 Palatnik-Landau 所画的具有最低共熔点的二元相图维数为1R ′, 为了把N 维恒压相图表现在二维平面上就必须把N 维相图进行多次切割, 总共要切割(N −2)次, 即减少(N −2)维, 因此11()(2).s R R N ′′=−− (8) 同理11()(2),s R R N =−− (9)其中S 代表截面(Section). 凡是符合(8), (9)两式的截面叫规则截面.相图边界理论完全能处理三元乃至更多元的体系的规则二维截面图, 为节省篇幅, 在此只讨论三元体系的恒压二维截面图.将公式(3)~(5)以及公式(8)和(9)应用于三元体系的二维水平或垂直截面, 可以得到这个二维截面上表1 三元体系二维水平截面中Φ, p c , R 1,1R ′, (R 1)S 和(1R ′)S 的变化规律a)Φ2 34 R 1 21 0 p c 1 2≥p c ≥1 2≥p c ≥01R ′2 R 1+p c −1= p cR 1+p c =p c(R 1)S =R 1−11 0−1 (1R ′)S =1R ′ −1 1p c −1p c −1p c =2, (1R ′)S =1(f i +f j )/(f i +f j +f m )p c =2, (1R ′)V =1(f i +f j +f k )/ (f j +f k +f m )两个相邻相区中相的组合i , j , k , m =1, 2, 3, 4i ≠ j ≠ k ≠ mf i /(f i +f j )p c =1, (1R ′)S =0f j /(f i +f j +f k ) (f i +f j )/(f j +f k )p c =1, (1R ′)V =0 (f i +f j )/ (f j +f k +f m )a) 在规则三元等压水平截面上没有Φ =4的情况. 方框内的情况只出现在垂直截面. 垂直截面的边界维数用(1R ′)v 表示106中国科学B辑化学第36卷的Φ, p c , R1, 1R′, (R1)S和(1R′)S的变化规律, 如表1所示.根据这个表完全可以阐明各类三元恒压水平截面图和垂直截面图上相邻相区及其边界的情况. 这个表实际上把这两类截面图的规律统一起来了. 图形互不相同的两类截面, 相图边界理论发现它们在相邻相区及其边界的关系上, 有基本相同的规律, 这也是相图边界理论的一个成功之处. 更复杂的其他类型的水平截面图和垂直截面图也可以用相图边界理论来说明. 对于非规则截面, 直接应用相图的边界理论的三个主要公式就可以讨论.Palatnik-Landau只是分门别类地讨论了若干水平截面图和垂直截面图上相邻相区及其边界的关系, 而且主要只涉及了共晶体系[3].2.3.4 P-L理论仅讨论了恒压相图, 而相图的边界理论还进一步延伸到了P-T-X i均可变化的多元相图赵慕愚还将恒压相图边界理论推广到P-T-X i均可变化的相图, 找出了这类复杂相图中相邻相区及其边界的关系[6], 赵慕愚和肖平进一步找出了这类复杂相图(高压相图)的计算的热力学关系式[7], 由宋利珠和周维亚理论计算和实验测定了Cd-Pb-Sn和Cd-Sn-Zn的各二元系和三元系的合金相图, 计算相图和实验相图符合得很好[8~12].这一系列的开创性的工作在国际上得到了很高的评价. 但是由于高温高压相图测定所需仪器太复杂、太昂贵, 国际上继续进行这种工作的学者为数不多.3 根据有限的信息, 构筑多元水平截面图—Gupta方法和根据相图边界理论的方法的比较Gupta等人提出了交叉ZPF(zero phase fraction)线构筑多元水平截面图的方法[5]. 这个方法可以根据有限的信息构筑复杂多元的水平截面图. 这个方法原理是这样的: 事先必须知道相图上若干体系点的相的组合(即一定成分的体系中包含哪几个相), 然后在相图上划ZPF线. 线的一边含有某一个相, 线的另一边不含有这个相. 若相图上总共有p个相, 则可以画出p条ZPF线, 这些ZPF线的交叉, 可以把相图分成若干区域. 若某一个区域包含某几个相, 则可以得出这一个相区包含这几个相. 同样若另一个区域包含另外几个相, 于是又得到包含这几个相的另一相区. 如此等等, 最后可以把整个水平截面图粗略构筑出来. Gupta等人以A, B, C, D, E五个组元包括α, β, γ, δ, ε五个相的体系为例, 说明了他们的方法. 根据他们的方法所划出来的水平截面图可有两个. 但哪一个水平截面图是正确的呢?他们指出: 需要有补充的实验数据才能判断[5].根据相图边界理论, 对Gupta所述的五元体系也可以处理, 也可以勾画出符合条件的水平截面图. 其原理如下[2,13]:两个相邻相区共用一条边界线, 则二者之间只有一个不同的相; 两个相邻相区彼此间相差两个相, 则二者必共同交于一个边界点, 即对顶相交; 如果已知有三个相邻相区相交于一个点, 则很容易推出相邻的第四个相区中包含哪些相. 不相邻的相区与其间的诸边界之间也有一定规律可循, 这可以帮助构筑复杂多元的水平截面图[1]. 赵慕愚详细讨论了构筑的方法见文献[2]第五章及文献[13]. 在划边界线的走向时, 已经考虑了下列法则: 四条边界线交于一点, 其中两条夹角较小的边界线的延长线必延伸到夹角较大的两条边界线所夹的相区中. 对于Gupta所给的五元体系和条件, 同样也可以得到彼此略有差别的两个水平截面图. 但我们不需要补充实验数据, 仅根据热力学原理就可以论证其中的一个水平截面图是正确的, 另一个水平截面图是错误的[2,13].Gupta等人还将他们的方法用到一个实际体系的水平截面图上[5]. 这个体系的5个组元的成分固定(Fe, 62%; Mn, 15%; Cr, 12%; Mo, 2%; Nb, 1%), 另外3个组元的成分(Al+Si+C)%=8%(均为质量百分比); 温度固定为700℃. 事先测定了45个合金体系的相的组合, 整个相图中共有α-Fe, Cr, 石墨(用G表示), β-Mn, MSi(M为金属), M3Si, Fe5Si3, Mn5Si3, M2C, M3C和M23C6等相. 因α-Fe和Cr在所有样品中均存在, 所以在图5中各相区中均未标出. Gupta等人用交叉ZPF线的方法得到图5. 我们根据相图边界理论同样可以构筑上述八元体系的水平截面图, 如图6.比较图5和6, 可以看出用相图边界理论的方法第2期万 强等: 相图边界理论与相区接触定律及Gupta 方法的比较 107图5 用交叉ZPF 线勾画的Fe-Mn-Cr-Mo-Nb-Al-Si-C 体系在700℃时的二维截面构筑的八元水平截面图的形状与一般书籍和文献所给的其他水平截面图较相像, 也有可能与将要用实验测定出来的相图形状比较接近. 这有利于在以后的相图测定过程中的实验点布置, 以准确测定有关相区之间的边界线的位置, 从而得到准确的信息完全的八元水平截面图. 人们很难根据Gupta 等人用ZPF 线方法所构筑的水平截面图(图5)来布置新的实验点.图6是完全根据相图边界理论推导出来的, 而且不论从哪个角的两个相邻相区及其边界出发, 进一步推导其他相区组合, 所推导出来的相图雏形都是一样的, 没有任意性.图5根据ZPF 线来粗略构筑相图的截面的方法, 实际上是很复杂的. 我们曾按Gupta 方法, 根据他们所给的相区组合, 进行多次相图的截面的粗略构筑, 我们发现他们的ZPF 线的曲线形状有相当的任意性. 按图5, 用相图边界理论推算第14, 15两个相区的相的组合, 所得结果是第14相区和第15相区分别包含(MSi+M 3Si+Fe 5Si 3+M 23C 6+Mn 5Si 3)和(MSi+M 3Si+ Fe 5Si 3). 这就是说, 从第13相区出发, 到第14相区然后再到第15相区; 而第15相区的相区组合(MSi+ M 3Si+Fe 5Si 3)和第13相区的相区组合(MSi+M 3Si+ Fe 5Si 3)却完全一样. 即第13相区通过第14相区, 到第15相区又回到了和第13相区一样的相区组合. 这是不符合相图的一般原理的. 实际上若把图5上的23/6-23/6的ZPF 曲线的中间部分向左偏, 把Mn 5Si 3- Mn 5Si 3的ZPF 曲线的中间部分向右偏, 则可使这两条ZPF 曲线不相交. 即可使第13相区直接与第21相区相连, 这样就没有第14和第15两个相区了. 这正是我们根据相图边界理论所推导出来的结果. 文献 [2]第103页指出“Gupta 所构成的图中的个别相区即相区14,15是不必要的”. 实际上, 应该说这是错误的. 我们将在另外一篇文章中, 从热力学原理证明它的确是错误的, 因篇幅较大, 此处从略. 在我们所推导出的图6上就没有这两个相区. 另外相图边界理论还讨论了水平截面图上不相邻相区以及它们之间的诸108中国科学 B 辑 化学第36卷图6 用相图边界理论勾画的 Fe-Mn-Cr-Mo-Nb-Al-Si-C 体系在700℃时的二维截面边界之间的关系. 两个相区即使不相邻, 却仍可以计算这两个不相邻相区中的不同相的总数Φ以及这两个相区都共同具有的相的数目p c , 则(Φ−p c )就是这两个相区之间互不相同的相的数目. 有了这个数目就可以计算出这两个相区之间有几条边界线, 或者有几条边界线和几个边界点.以上的规律有助于根据有限信息构筑复杂的多元水平截面图(文献[2]第五章第二节).由上可见, 在根据不完全的信息构筑粗略的多元水平截面图时, 应用相图边界理论的方法, 有其特点. 把Gupta 方法和相图边界理论的方法结合起来, 可能是有益的.4 总结和展望和Palatnik-Landau 的相区接触定律相比, 相图的边界理论是一个更基本的相平衡理论. 这个理论深入地研究了边界的性质, 从而引入了相边界的概念. 在这基础上根据相转变过程的特性、相平衡热力学原理和质量守恒原理, 导出了相图边界理论的三个主要公式. 利用这些公式, 可以阐述各种不同类型的相图中的相邻相区及其边界的关系, 实际上也就是阐明了相区及其边界如何构成复杂相图的规律. 因而这个理论可以应用于相图的计算, 相图的测定和相图的评估[2].相图的边界理论在相图的教学上也有重要的应用, 因为相图的边界理论阐述了相区及其边界如何构成相图的规律, 从而使学生能更好地了解不同类型的相图之间的内在联系. 这有利于相图的讲授与学习.在根据有限信息来构筑多元复杂恒压水平截面图方面, 和Gupta 方法相比, 相图边界理论的方法也有其特点. 把这两种方法结合起来应用, 可能更为有益.在相图中相邻相区及其边界的关系方面, Palat-第2期万强等: 相图边界理论与相区接触定律及Gupta方法的比较109nik-Landau的相区接触定律和Gupta用交叉ZPF线构筑多元水平截面图的方法是国际相图界应用得最多的两个工作, 而相图边界理论与它们相比, 确有许多优点或特点. 因此, 相图边界理论是一个有一定意义的基本性质的理论.参考文献1 Schreinemakers, F A H. Proc K Akad Wetenschappen Amsterdam(Section of Sciences), 1915, 18, 1162 赵慕愚, 宋利珠. 相图的边界理论及其应用, 北京: 科学出版社, 20043 Palatnik L S, Landau A I. Phase Equilibria in MulticomponentSystems. New York: Holt, Rinehart and Winston, Inc, 19644 Rhines F N. Phase Diagrams in Metallurgy. New York: McGrawhill, 19565 Gupta H, Morral J E, Nowotny H. Constructing mutlicomponentphase diagrams by overlapping ZPF lines. Scripta Metallurgica, 1986, 20: 889~8946 赵慕愚. 对应关系定理及其推论在温度、压强、组成均可变化的多元相图的应用. 中国科学, B辑, 1982, 6: 540~5477 Zhao M Y, Xiao P. The principles of calculation of high pressuremulticomponent phase diagrams. High Pressures-High Tempera-tures, 1987, 19: 513~5188 Zhou W Y, Shen Z Y, Zhao M Y. Calculation of high pressurephase diagrams of binary system. J Less Common Metals, 1990, 160: 237~2459 Zhao M Y, Zhou W Y, Song L Z. Calculation of high pressurephase diagrams of alloy systems. J Phys Chem Solid, 1992, 51: 92110 Zhou W Y, Shen Z Y, Zhao M Y. Optimization of thermodynamicproperties and calculation of phase diagrams for the Cd-Sn system at high pressure. High Pressures-High Temperatures, 1992, 24: 511~51811 Zhou W Y, Shen Z Y, Zhao M Y. The determination of high pres-sure vertical sections of Cd-Pb-Sn ternary system. High Pres-sures-High Temperatures, 1988, 20: 56112 Song L Z, Hua Y, Zhao M Y. Determination of the phase diagramof the Cd-Sn(0.2)-Zn ternary system at high pressure. J Alloys and Components, 1992, 187: 13713 赵慕愚, 王子忱, 肖平. 应用相图边界理论勾画多元恒温截面相图. 高等学校化学学报, 1990, 11(6): 622~627。
《材料科学基础教学课件》第一章-相图

在化学工业中的应用
化工过程控制
相图可以用来预测不同成分和温 度下的相态和物性,为化工过程 的控制提供依据,确保生产过程
的稳定性和安全性。
化学反应研究
相图可以用来研究化学反应过程中 物质的状态和性质变化,有助于深 入理解化学反应机理和反应条件的 选择。
分离技术应用
相图可以用来指导分离技术的选择 和应用,例如利用相图的溶解度曲 线进行萃取分离或结晶分离。
04
相图的应用
在材料科学中的应用
合金设计
相图是合金设计的基础,通过相 图可以确定合金的成分范围以及 各相的组成和性质,从而优化合 金的性能。
热处理工艺制定
利用相图可以确定合金在不同温 度下的相变过程,从而制定合理 的热处理工艺,优化材料的显微 组织和力学性能。
新材料研发
相图为新材料研发提供了理论指 导,通过研究不同成分和温度下 的相变规律,可以发现具有优异 性能的新型材料。
实验法是绘制相图最直接和可靠的方 法,但需要耗费大量的时间和资源。
实验法通常需要使用精密的实验仪器 和设备,如热分析仪、X射线衍射仪、 扫描电子显微镜等,以获得精确的数 据。
计算法
计算法是根据物质的分子或原 子模型,通过计算机模拟计算 物质之间的相平衡关系。
计算法可以快速地预测物质的 相平衡关系,但需要建立准确 的分子或原子模型,且对计算 资源的要求较高。
在冶金工业中的应用
钢铁冶金
01
钢铁冶金过程中涉及大量的相变和相分离,相图是指导钢铁冶
金工艺的重要工具,有助于优化炼钢和连铸连轧工艺。
有色金属冶金
02
在有色金属冶金中,相图可以用来确定合金的成分和温度范围,
优化熔炼、浇注和凝固工艺,提高产品的质量和性能。
聊城大学材料物理化学-第五章 相平衡5

三元系统的等温截面
2020/7/28
熔体M L p=1 f=3
C/
M/
L C
L1 [S1 , (C)]
S1
L1
B/
p=2 f=2
E2
L C+B L3[S3 , C+(B)]
S2
L2
p=3 f=1
A/
E’[S4, B+C+(A)]
S3
E3 L3
E1
L A +B+C
S4
S
E/
p=4 f=0
D[C , C+(B)]
p=1 f=3
p=2 f=2
p=3 f=1
E [F ,B+C+(A)]
L A +B+C E(L消失)[M ,A+B+C]
p=4 f=0
2020/7/28
小结:
从以上析晶过程的讨论,可以总结出在具有一个低共 熔点的三元系统投影图上表示熔体冷却析晶过程的规律: 1)初晶区规则; 2)杠杆规则; 3)液相组成点、固相组成点的变化规律; 4)三元低共熔点一定是结晶结束终点。
的方向背向顶点。
N B
2020/7/28
3、杠杆规则
在三元系统中,一种混合物分解为两种物质(或两种物质合成为 一种混合物)时,它们的组成点在一条直线上,它们的重量比与其 它组成点之间的距离成反比。 C
P M o
b1 A
b b2
B GO MP GP MO
物推质导的:分GM解=和G合O+成G实P 际上就是物相的变化。对于三元系统中有 混用合两物次分杠解杆为规GM三则×种求b%物出=质。G,O或×有b1三%种+G物P×质b生2%成一种物质,其重量比需
第03章-相图

体系成分固定后(设为xB),在T1温度参与平衡的两相的相对量 由杠杆规则确定。杠杆规则表达为
β α ( xα ) x ( x B B B)
T = T1
α相和β相所占的摩尔分数为 β xB − xB α α A ( xB ) = β xB − xα B
PDF 文件使用 "pdfFactory Pro" 试用版本创建
三相平衡 三相平衡(φ=3,F=0),三相平衡只能在固定温度下平衡相固定的 成分共存,即在一条恒温线上的3个点。这恒温线就是三相区。三 相区必和由这3个相两两组成的3个两相区连接 ,连接的方式只能 有两种 :
下面分析一些整体的二元相图的例子
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
PDF 文件使用 "pdfFactory Pro" 试用版本创建
根据吉布斯−杜亥姆方程
SdT − Vdp +
∑ n dµ
i i =1
C
i
=0
沿α−β平衡的相线可以写出:
SdT + (− Vdp ) = −nα dµ SdT + (− Vdp ) = − n β dµ
上两式相除消去dµ,得
S −S dp n n ΔS m = = dT V β V α ΔVm − n n
PDF 文件使用 "pdfFactory Pro" 试用版本创建 炣
F = C −φ + 2 相律: 对于凝聚态系统中的相平衡,通常每改变105Pa压力,其平衡温度改 变约为10-2Κ的数量级,因此,当压力变化不大的情况下,压力的 影响可以忽略。此时相律为: F = C −φ +1
相图及其应用
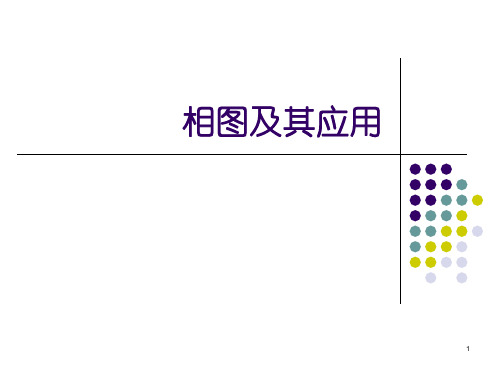
一元系统相图
三相点是严格的单组分体系,而通常的水的冰点则是暴露
在101.325 kPa空气中的冰-水两相平衡体系。其中水已
被空气中的其它组分(如CO2,O2,N2等)所饱和,严格地说 已不是单组分体系。由于空气中其它组分溶于水中要使单
物质,在平衡时这三种物质建立了一个化学平衡:
CaCO3 (s) CaO (s) + CO2 (g)
这时的组分数应为:
C=SR=31=2
而不是 3
因为三相平衡时,只要两个组分确定,第三个也就定
了。
12
组分数(组元,Component)
说明:
1.
究竟选择哪些物质作为独立组分是任意的,从
上例看,可取 CaCO3 和 CO2 ,也可取 CaO 和
CO2,或CaCO3 和 CaO 作为独立组分。
2.
减去的化学平衡数必须是独立的化学平衡数, 否则将会得出荒谬的结论。
13
14
组分数(组元,Component)
某些特殊情况下的特殊限制条件,会使独立组 分数减少。
例如 NH4Cl 分解体系: NH4Cl (s) NH3 (g) + HCl (g) 当起始体系中没有 NH3 (g) 和 HCl (g) 存在,或存在的 NH3 (g) 和 HCl (g) 的物质量相等,则达到平衡时,NH3 (g) 和 HCl (g) 之间有一定的比例关系。 因此,表示气相的组成时,有关系式: PNH3 = PHCl(或 c NH3 = c HCl) 所以这时的组分数既不是 3 也不是 2,而是: C=311=1
同理,在一定温度下,水的压力不能小于该温度时水的饱和蒸汽压,否 则将转化成蒸汽相。
教你如何学习相图的相关知识(详细版本)

2.5 生成异分熔点化合物的三元相图
2.5.1 异分熔点二元化合物
化合物发生相变时,生成的异相成份与原成份不同,则这种化合物为异分熔点化合物。如
图 2-19
ቤተ መጻሕፍቲ ባይዱ
图2-20
图 2-19,中组元 A 与 B 形成一化合物 AB,在其熔点时将从液相析出固相组元 A 和液相 Lg, 而液相 Lg 的组成并非化合物 AB 的化学组成。实质上,这类化合物是由包晶反应生成的, 即 Lg+a=ab。
2.5.2 生成异分熔点二元化合物的的三元相图的特点分析
以 2-19,2-20 图所示的异分熔点二元化合物的的三元相图为例,在组元 A 与 B 除形成 一共晶 e1 外,还生成一异分熔点二元化合物 AB;组元 C 与 A 和组元 B 与 C 之间形成共晶 e3、e2。这一相图的特点主要表现在浓度三角形 ABC 中面、线和点的特点 不同,现讨论 分析如下: (1) 面
一、 相律
相律是体系平衡条件的数学表示式它表示了一个体系中自由度、组元数和相数之间的 关系。
设体系有 C 个独立组元,有 P 个相,则体系的自由度数 F 可表示为 F=C-P+2
其中 2 是体系的压力和温度两个因素。 对冶金过程而言,由于所研究的体系一般都是由凝聚相组成的,压力的影响很小,所 以相律可表示为
Ws /W1 11 / a1
又因固相是由固相 A 和 AB 组成的,则固相总量 WS 为 A 和 AB 的量 WA 和 WAB 之和, 即
WS=WA+WAB 平衡的固相量 WA 和 WAB 的关系可由重心规则确定,即
WA /WAB Aa / a AB
当冷却至 J 点,将发生四元共晶反应: LJ+A=AB+C 在 J 点为三个 组元(A+AB+C)和四个相(LJ+A+AB+C),所以其自由度 f=3-4+1=0, 即 J 点为一个特定点,表现在冷却曲线上出现平台。 又因为原始物系点 1 在组元 A,AB 和 C 组成的小浓度三角形中,故在 J 点处液相 LG 全部耗尽后,最后平衡的固相为 A+AB+C,而不会沿 JE 线冷却至 E 点。
相图及其应用2

9
第二节 二元系统相图
溶剂蒸气压与浓度之间的关系式可表示为: p1=x1p10 x1 表示溶液中溶剂的物质的量分数,恒小于 1 ;所以 p1<p10, 这是拉乌尔定律 若是含有非挥发性溶质的溶液,由于降低了溶剂 的蒸气压,也就降低了溶液的总蒸气压,这必然导致沸 点上升和凝固点下降.
10
第二节 二元系统相图
20
第二节 二元系统相图
◆泰曼三角形: 从冷却过程的分析可以知道,各种不同的组成冷却时,在低共 熔温度处停留的时间是不一样的,愈靠近纯组分则在低共熔温度停留 时间愈短,愈靠近低共熔点则停留时间愈长。如果我们将各组分在低 共熔温度处停留的时间垂直地画在相应的组成上,将这些线段的末端 连起来,所形成的三角形,叫泰曼三角形。三角形的高,相当于低 共熔物xe的位置。 泰曼三角形法亦可求得同成分或异成分熔融化合物的准确组成, 因为这些组成位置在三角形上的高度等于零或最大。
4
第二节 二元系统相图
3.二元系统中的相律及相图表示法
二元体系中的组分数C=2,据相律得: f=4-P
当体系仅有一相时,最大自由度为 3,也就是说,体系的状态由 三个可变因素完全确定。这三个可变因素是温度、压力和组成。所以 二元体系的相图必须通过三维空间坐标才能作出。 组成这一变量可以用作图法表示,如果在这基础之上再加上温度 轴和压力轴,这样,就可成一个三维坐标系。如果我们把各种组成在 不同温度、压力下的相平衡关系用作图的方法描绘出来就得到一个立 体的二元系统相图。组成轴的两个垂直侧面,即是组分 A 和组分 B的 单元相图。
3
第二节 二元系统相图
原始组成物中 B 的含量与 E 、 F中B的含量之和相等。
AE AF AD d =e +g AB AB AB
相变贮能第06讲相律和相图

6
第三章 相律和相图
相图的应用案例 钢的含硫量
硫是钢铁中十分有害的 杂质元素,根据Fe-FeS 系统相图,假设钢液中 含FeS在C点以右,即大 于0.02%wtFeS,则冷却 时先析出固溶体。当冷 却到985℃时,开始析出 +固溶体共晶(组成点 E),这些共晶分布在先 前析出的晶粒边界上。
pv RT U U(S,V) dp Q dT T v
(1) (2)
(3)
同样可知O点(三相点)时水、汽、冰三相 平衡点,自由度为0。即欲维持三相平衡,则 系统的温度和压力都只能各为某以确定值。 (610pa,273.16K)
三相点和普通所说的冰点并不相同。通常 水的冰点是暴露在空气中的冰水两相平衡 的温度,其中水已经被空气中的各种气体 所饱和,而且气相总压为101.325kPa, 因此体系已经不是单元系了。
当母相失稳而新相具有较高的稳定性时,就会发生相变。
13
第三章 相律和相图
以水的相图为例讨论自由度的概念 当室温和大气压为101325Pa时(M),只有
一个液相。在M点的区域内,可以任意改变 系统的温度和压力不致产生新相或消失旧相, 因此自由度为2; 在N点,系统有两个相,水和蒸汽建立了平衡。 若要使系统保持这两相平衡,系统的压力就 由温度确定或温度由压力确定,物系点必须 在OC线上变化,自由度为1;
p*
(17) (18)
(19)
17
第三章 相律和相图
非理想气体
✓ 范德瓦耳方程
RT a p V b V2
RT 2a b
ln
f
ln V
b RTV 2
V
b
18
第六章 相平衡与相图1
二、相 律
对于系统中的固体,则有以下几种情况: ① 形成机械混合物——有几种物质就有几相。 ② 生成化合物——一种新的固态物质,是一个 新相。 ③ 形成固熔体——几个物质间形成固熔体为一 个相。 ④ 同质多晶现象 同一物质的不同晶型(变体) 虽具有相同的化学组成,但由于其晶体结构 和物理性质不同,因而分别各自成相。有几 种变体就由度
定义: 温度、压力、组分浓度等可能影响系统平衡状态的变量中, 定义 温度、压力、组分浓度等可能影响系统平衡状态的变量中,可 以在一定范围内改变而不会引起旧相消失新相产生的独立变量的 数目 具体看一个二元系统的自由度。 具体看一个二元系统的自由度。
L
f=2
L+A + f=1 A+B + A
压 强 S
L
解释线的 斜率!气相区、 COB:固相区、BOA:气相区、 :固相区、 :
AOC:液相区 : 特点:相数为1,自由度数为2。 特点:相数为 ,自由度数为 。 即在单相区范围内, 即在单相区范围内,温度和压力 均可以自由变化。 均可以自由变化。
是固相( 溶解曲线; 线:OC:液相-固相共存曲 线,是固相(冰)溶解曲线; OC:液相 固相共存曲 OB:固相-气相共存曲线 是固相( 气相共存曲线, 升华曲线; OB:固相 气相共存曲线,是固相(冰)升华曲线; OA:液相-气相共存曲线 是液相( 气相共存曲线, 蒸发曲线。 OA:液相 气相共存曲线,是液相(水)蒸发曲线。 特点:这些线上是两相平衡共存, ,根据相率F=3-P=1, , 特点:这些线上是两相平衡共存,P=2,根据相率 所以在线上温度和压力只有一个是独立可变的。 所以在线上温度和压力只有一个是独立可变的。
压 强 S
C 溶解
L 蒸发 O
临 界 A点
第十三章 相图

1 画出含有两个化合物并包含共晶反应和包晶反应的二元相图,注明相应的共晶和包晶反应的成分点和温度,写出共晶和包晶反应式。
2简述相图在晶体生长中的应用相图用途:1.由材料的成分和温度预知平衡相;2.材料的成分一定而温度发生变化时其他平衡相变化的规律;3.估算平衡相的数量。
预测材料的组织和性能3写出相律的表达式及其各参数的意义。
Gibbs 相律热力学平衡条件下,系统的组分数、相数和自由度数之间的关系:P + F = C + 2式中P----在所选系统中共存相的数目;F----自由度;C----系统中的组元数。
C 组元(组分) 系统中每一个能够单独分离出来并能够独立存在的化学纯物质。
如元素、化合物或溶液。
自由度 F 是当系统为平衡状态时,在不改变相的数目情况下,可独立改变的因素(如温度和压力)。
注意事项:1. 相律是根据热力学平衡条件推导而得,因而只能处理真实的热力学平衡体系,不能预告反应动力学(即反应速度问题)。
2. 相律表达式中的“2”是代表外界条件温度和压强。
如果电场、磁场或重力场对平衡状态有影响,则相律中的“2”应为“3”、“4”、“5”。
如果研究的系统为固态物质,可以忽略压强的影响,相律中的“2”应为“1”。
3. 必须正确判断独立组分数、独立化学反应式、相数以及限制条件数,才能正确应用相律。
4.只表示系统中组分和相的数目,不能指明组分和相的类型和含量。
5. 自由度只取“0”以上的正值。
如果出现负值,则说明系统可能处于非平衡态。
三、相律的一般推导:假设一个平衡系统中有C个组分、P个相,对于每一个相来说,温度、压力及其相成分(即所含各组分的浓度)可变。
确定每个相的成分,需要确定(C-1)个组分浓度,因为C个组分浓度之和为100%。
现有P个相,故有P(C-1)个浓度变量。
所有描述整个系统的状态有P(C-1)+2个变量。
但这些变量并不是彼此独立的,由热力学可知,平衡时每个组分在各相中的化学势都必须彼此相等。
