(完整版)第二章热力学第一定律
第2章 热力学第一定律
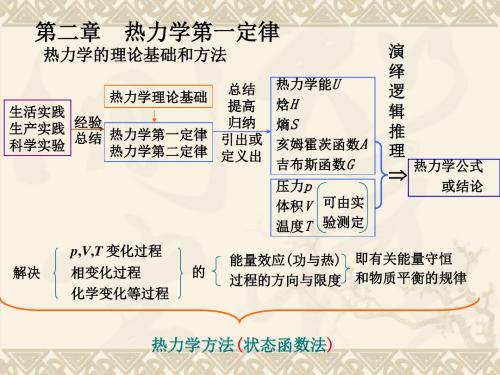
四、热力学第一定律
对封闭系统当系统与环境同时有功W及热Q交换时,则
U =U2-U1 = Q + W 微小的变化 dU=δQ+δW
上式即为封闭系统的热力学第一定律的数学表达式。 力学第热一定律的实质 能量守恒。
Q 与W 都是途径函数,而U 是状态函数, U = Q + W ,
说明了两个途径函数的代数和,为一个状态函数的变化值。
途径I C 始态1 B 途径II 状态函数的改变量只决定于系统的始态和终态,而与变化 的过程或途径无关。即 如 ΔT = T2-T1, Δp = p2-p1 ;ΔV= V2-V1 终态2
这套处理方法是热力学中的重要方法,通常称为状态函数法。
第二节 热力学第一定律
1. 热 定义: 由于系统与环境间存在温度差,而引起的能量传递形式。
宏观性质也称为系统的状态函数。 (i) 对于一定量组成不变的理想气体系统,系统的任意宏观
性质是另外两个独立的宏观性质的函数: V=f(T,p),如 nRT V 理想气体 p (ii) 状态函数的改变量只决定于系统的始态和终态,而与 变化的过程或途径无关。即 状态函数的改变量=系统终态的函数值-系统始态的函数值 如 ΔT = T2-T1, ΔU = U2-U1
的反应进度必然相同)。反应进度的单位是mol。
反应进度的积分表示形式可以如下理解: 若反应进度为 0 时,B的物质的量为nB(0) ,反应进度 时, B的物质的量为nB() ,积分得:
nB 0 νB
若反应开始时,0 = 0 ,则: = nB/ B
六、 状态函数法
② 反应进度 :
定义: 表示化学反应进行的程度。符号 。 对于反应: 0 νBB 反应进度定义为: dξ dnB /ν B 其中, nB为反应方程式中,任何一种物质的物质的量,B 为 该物质在方程式中的化学计量数。一个化学反应的反应进度,
工程热力学 第二章 热力学第一定律

wt
1 2
cf22
cf21
gz2
z1 ws
(2-11)
将轴功的表达式代入上式,即有:
2
1 d ( pv)
2
2
1 pdv 1 vdp
wt 12 pdv p2v2 p1v1 12 vdp (2-11a)
由上式可知,准静态过程的 技术功的大小可用过程线左边的 面积来表示。
准静态 pdv d( pv) wt
wt pdv d( pv) pdv ( pdv vdp) vdp
wt vdp wt vdp
准静态
q du pdv
q dh vdp
热一律解析式之一 热一律解析式之二
技术功在示功图上的表示
q12 (u2 u1) w12
Q dU pdV (2-4)
2
Q12
(U2
U1)
pdV
1
(2-4a)
q du pdv (2-4b)
2
q12
(u2 u1)
pdv
1
(2-4c)
2-3 开口系统能量方程 Energy balance for open system
式中各项的正负号规定为:系统吸热为正,放热为负; 系统对外作功为正,外界对系统作功为负。
上式既适用于准静态过程,也适用于非准静态过程。
对于无耗散的准静态过程, w pdv
因此上述诸式可写为:
Q dU W
Q12 (U2 U1) W12
对1kg工质,有:
q du w
所以有:
h1 h2
1 2
热工流体第二章 热力学第一定律

第二章 热力学第一定律第一节 第一定律的实质及热力学能和总能能量守恒与转换定律是自然界的基本规律之一,它指出:自然界中的一切物质都具有能量,能量不可能被创造,也不能被消灭;但能量可以从一种形态转变为另一种形态,且在能量的转化过程中能量总量不变。
热力学第一定律是能量守恒与转换定律在热现象中的应用。
它确定了热力过程中热力系统与外界进行能量交换时,各种形态能量数量上的守恒关系。
一、热力学能热力学能是与物质内部粒子的微观运动和粒子的空间位置有关的能量。
它包括分子移动、转动、粒子震动运动的内动能和分子间由于相互作用力的存在而具有的内位能,故又称内能。
内动能取决于分子热运动,是温度的函数,而内位能取决于分子间的距离,是比体积的函数,即u = f ( T, v )二、总能除热力学能外,工质的总能量还包括工质在参考坐标系中作为一个整体,因有宏观运动速度而具有动能、因有不同高度而具有位能。
前一种能量称之为内部储存能,后两种能量则称之为外部储存能。
我们把内部储存能和外部储存能的总和,即热力学能与宏观运动动能和位能的总和,叫做工质的总储存能,简称总能。
即p k E U E E =++ (2-1)E---总能; U---热力学能; E k ---宏观动能; E p ---宏观位能。
第二节 第一定律的基本能量方程及工质的焓一、焓在有关热力计算总时常有U+pV 出现,为了简化公式和计算,把它定义为焓,用符号H 表示,即H=U+pV (2-2)1kg工质的焓值称为比焓,用h表示,即h=u+pv (2-3)焓的单位是J,比焓的单位是J/kg。
焓是一个状态参数,在任一平衡状态下,u、p和v都有一定得值,因而焓h也有一定的值,而与达到这一状态的路径无关。
当1kg工质通过一定的界面流入热力系统时,储存于它内部的热力学能当然随着也进入到系统中,同时还把从外部功源获得的推动功pv带进了系统。
因此系统中因引进1kg工质而获得的总能量是热力学能与推动功之和(u+pv),即比焓。
(完整版)哈工大工程热力学习题答案——杨玉顺版

(完整版)哈⼯⼤⼯程热⼒学习题答案——杨⽟顺版第⼆章热⼒学第⼀定律思考题1. 热量和热⼒学能有什么区别?有什么联系?答:热量和热⼒学能是有明显区别的两个概念:热量指的是热⼒系通过界⾯与外界进⾏的热能交换量,是与热⼒过程有关的过程量。
热⼒系经历不同的过程与外界交换的热量是不同的;⽽热⼒学能指的是热⼒系内部⼤量微观粒⼦本⾝所具有的能量的总合,是与热⼒过程⽆关⽽与热⼒系所处的热⼒状态有关的状态量。
简⾔之,热量是热能的传输量,热⼒学能是能量?的储存量。
⼆者的联系可由热⼒学第⼀定律表达式 d d q u p v δ=+ 看出;热量的传输除了可能引起做功或者消耗功外还会引起热⼒学能的变化。
2. 如果将能量⽅程写为d d q u p v δ=+或d d q h v p δ=-那么它们的适⽤范围如何?答:⼆式均适⽤于任意⼯质组成的闭⼝系所进⾏的⽆摩擦的内部平衡过程。
因为 u h pv =-,()du d h pv dh pdv vdp =-=-- 对闭⼝系将 du 代⼊第⼀式得q dh pdv vdp pdv δ=--+ 即 q dh vdp δ=-。
3. 能量⽅程δq u p v =+d d (变⼤)与焓的微分式 ()d d d h u pv =+(变⼤)很相像,为什么热量 q 不是状态参数,⽽焓 h 是状态参数?答:尽管能量⽅程 q du pdv δ=+与焓的微分式 ()d d d h u pv =+(变⼤)似乎相象,但两者的数学本质不同,前者不是全微分的形式,⽽后者是全微分的形式。
是否状态参数的数学检验就是,看该参数的循环积分是否为零。
对焓的微分式来说,其循环积分:()dh du d pv =+蜒? 因为0du =??,()0d pv =??所以0dh =??,因此焓是状态参数。
⽽对于能量⽅程来说,其循环积分:q du pdv δ=+蜒?虽然: 0du =?? 但是: 0pdv ≠?? 所以: 0q δ≠?? 因此热量q 不是状态参数。
第二章 热力学第一定律

令
u pv h
U pV H
,h 称为比焓。
, H 称为焓
焓的定义:焓=热力学能+推动功。
2-4 开口系统的稳定流动能量方程式
由于p、v 、u都是状态参数,所以焓也是工质的一个
1 2 Ws m u2 cf2 gz2 mp2v2 2 1 2 Ws m u2 cf2 gz2 p2v2 2
2-4 开口系统的稳定流动能量方程式
根据热力学第一定律可得
1 2 Q m u1 p1v1 2 cf1 gz1
本章主要内容
1 2 3 4 5
热力系统的储存能 热力学第一定律的实质 闭口系统的热力学第一定律表达式 开口系统的稳定流动能量方程式 稳定流动能量方程式的应用
2-1 热力系统的储存能
热力学能
热力学储存能
U
宏观动能与宏观位能
热力学能的定义:
Ek , E p
物体因热运动而具有的能量 , 是存储于物体内部的能量 。 内动能 内位能 原子能 化学能
对于单位质量工质的可逆过程 ,
q du pdv
q u pdv
1
2
2-3 闭口系统的热力学第一定律表达式
适用条件:
闭口系;可逆、不可逆; 理想和实际气体;初、终态为平衡态
符号规定:
吸热q为正,放热为负 系统对外作功为正,反之为负
系统内能增大 U为正,反之为负
2-3 闭口系统的热力学第一定律表达式
热力学能(内能)
2-3 闭口系统的热力学第一定律表达式
Q ΔU
热力学第一定律 (5)精选全文完整版

可编辑修改精选全文完整版第二章 热力学第一定律 一、基本概念1. 系统与环境;状态与状态函数;过程与途径2. PVT 、相变化及化学变化独特的基本概念(略)3. 状态函数:内能、焓 →(H=U+pV )4. 途径函数:功、热★热——恒容热:Q V =ΔU →适用条件:封闭系统、恒容过程、W ’=0; 恒压热:Q p =ΔH →适用条件:封闭系统、恒压过程、W ’=0。
★功——W =-∫p amb d V :真空膨胀过程W =0 恒容过程W =0恒压过程W =-p ΔV ; 恒外压过程:W =-p amb ΔV5. pVT 变化基础热数据热容:C→C p , C V →C p,m ,C V ,m (理想气体的C p,m -C V ,m =R )6. 可逆相变化基础热数据摩尔相变焓:(),m p m pH T C βα∂∆∂=∆; ΔC p,m =C p,m (β)-C p,m (α) 7. 化学变化基础热数据:θθr m B f m B Δ(B)H H ν∆∑=; θθr m B c m BΔ(B)H H ν∆∑=-二、热力学第一定律:ΔU =Q + W 三、基本过程热数据计算 1. 理想气体pVT 变化过程恒容过程:W =0;,;V V m Q U nC T =∆=∆ ΔH=nC p,m ΔT恒压过程:,;P p m Q H nC T =∆=∆ ΔU=nC V ,m ΔT ;(W =ΔU — Q = — p ΔV ) 恒温可逆过程:ΔU=ΔH=0;—Q= W (可逆)=—nR T ln(V 2/V 1)=nR T ln(p 2/p 1) 恒温恒外压过程:ΔU=ΔH=0;—Q= W (不可逆)=—p amb ΔV绝热可逆过程:过程方程式(重要,自行总结,);Q=0;W =ΔU=nC V ,m ΔT ;ΔH=nC p,m ΔT绝热恒外压过程:Q=0;W =—p amb ΔV=ΔU=nC V ,m ΔT ;ΔH=nC p,m ΔT 节流膨胀:自行总结2. 相变化过程: 可逆相变(平衡温度及其平衡压力下的相变化过程):凝聚相相变化:W=0;ΔU =Q p =ΔH =m n H βα∆ 含气相相变化:Q p =ΔH = m n H βα∆;W =-p ΔV=-p (V 末-V 始);ΔU =Q p + W 不可逆相变:状态函数法设计途径。
第二章 热力学第一定律

进入系统的能量-离开系统的能量=系统能量的增加 (2-9) 进入系统的能量-离开系统的能量= - )
1 2 Q = m2 (u2 + cf 2 + gz2 ) + m2 p2 v2 2 1 2 − m1 (u1 + cf 1 + gz1 ) − m1 p1v1 + Wi 2
1 2 wt = (cf 2 − cf21 ) + g ( z 2 − z1 ) + wi 2
比较式(2-10b)和(2-16) 比较式( - 和 - )
(2 − 19)
q = ∆u + w q = ∆h + wt = ∆u + ∆( pv) + wt 1 2 w = ∆( pv) + wt = ∆( pv) + ∆cf + g∆z + wi 2
由于m 由于 1=m2=m, 整理上式得
1 2 Q = m(u2 + p2 v2 + cf 2 + gz2 ) 2 1 2 − m(u1 + p1v1 + cf 1 + gz1 ) + Wi 2 令 H = U + pV 代入上式得
1 Q = ∆H + m∆cf2 + mg∆z + Wi 2 1 2 δQ = dH + mdcf + mgdz + δWi 2
m1 = m2 = m
∆ECV = 0
稳定系统的能量分析: 稳定系统的能量分析: 进入系统的能量: 进入系统的能量:
1 2 Q + E1 + p1V1 = Q + m1 (u1 + cf 1 + gz1 ) + m1 p1v1 2 离开系统的能量: 离开系统的能量: 1 2 E2 + p2V2 + Wi = m2 (u 2 + cf 2 + gz 2 ) + m2 p2 v2 + Wi 2
(完整版)第二章热力学第一定律.doc
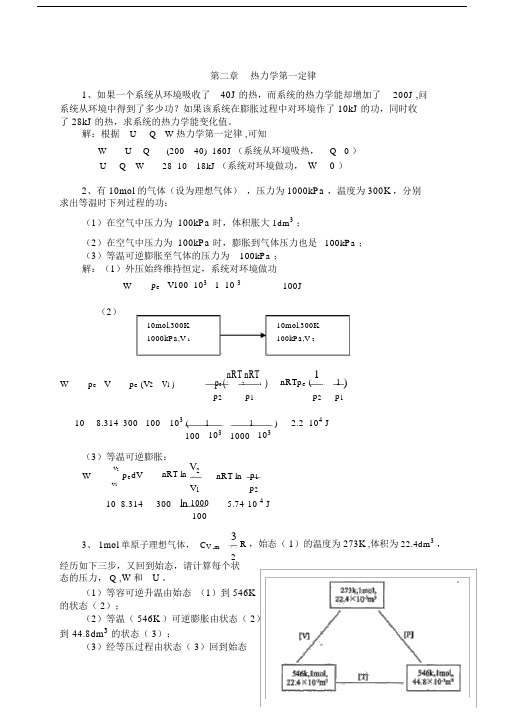
第二章热力学第一定律1、如果一个系统从环境吸收了40J 的热,而系统的热力学能却增加了200J ,问系统从环境中得到了多少功?如果该系统在膨胀过程中对环境作了 10kJ 的功,同时收了 28kJ 的热,求系统的热力学能变化值。
解:根据U Q W 热力学第一定律,可知W U Q (200 40) 160J (系统从环境吸热,Q 0 )U Q W 28 10 18kJ (系统对环境做功,W 0 )2、有 10mol 的气体(设为理想气体),压力为 1000kPa ,温度为 300K ,分别求出等温时下列过程的功:(1)在空气中压力为 100kPa 时,体积胀大1dm3;(2)在空气中压力为 100kPa 时,膨胀到气体压力也是100kPa ;(3)等温可逆膨胀至气体的压力为100kPa ;解:(1)外压始终维持恒定,系统对环境做功W p e V100 103 1 10 3 100J(2)10mol,300K10mol,300K1000kPa,V 1100kPa,V 2W p e V p e (V2 V1 ) p e(nRT2nRT1) nRTp e (11 )p2 p1 p2 p110 8.314 300 100 103 ( 1 1103 ) 2.2 104 J100 103 1000(3)等温可逆膨胀:V2p e dV nRT ln V2 nRT ln p1WV1 V1 p210 8.314 300 ln 1000 5.74 10 4 J1003、 1mol 单原子理想气体,C V ,m 3R ,始态(1)的温度为273K ,体积为 22.4dm3,2经历如下三步,又回到始态,请计算每个状态的压力, Q ,W和U 。
(1)等容可逆升温由始态(1)到 546K 的状态( 2);(2)等温( 546K )可逆膨胀由状态( 2)到44.8dm3的状态( 3);(3)经等压过程由状态( 3)回到始态( 1);解:(1)等容可逆升温过程:W P e V 0UQ WQ VT 2 nC V ,m dT 138.314 546 273 3404.58 JT 12(2)等温可逆膨胀过程:U 0WnRT lnV 21 8.314 546ln 44.83146.50JV 122.4Q W 3146.50J(3)等压过程 :WP e VnRT V 1 V 2 1 8.314 273 22.4 44.8 10 3 2269.72 JV 1 22.4 10 3Q pH T 2nC P ,m dT n 3 R 273 546 5 8.314 273 5674.31J T 1 R 12 2UQ W 5674.31 2269.72 3404.59 J4、在 291K 和 100kPa 下, 1molZn (s) 溶于足量稀盐酸中, 置换出 1molH 2 ( g) ,并放热 152kJ 。
(完整版)第二章热力学第一定律习题

第二章热力学第一定律选择题1. 热力学第一定律厶U=Q+W只适用于(A) 单纯状态变化(B) 相变化(C) 化学变化(D) 封闭物系的任何变化答案:D2. 关于热和功, 下面的说法中, 不正确的是(A) 功和热只出现于系统状态变化的过程中, 只存在于系统和环境间的界面上(B) 只有在封闭系统发生的过程中, 功和热才有明确的意义(C) 功和热不是能量, 而是能量传递的两种形式, 可称之为被交换的能量(D) 在封闭系统中发生的过程中, 如果内能不变, 则功和热对系统的影响必互相抵消答案:B3. 关于焓的性质, 下列说法中正确的是(A) 焓是系统内含的热能, 所以常称它为热焓(B) 焓是能量, 它遵守热力学第一定律(C) 系统的焓值等于内能加体积功(D) 焓的增量只与系统的始末态有关答案:D。
因焓是状态函数。
4. 涉及焓的下列说法中正确的是(A) 单质的焓值均等于零(B) 在等温过程中焓变为零(C) 在绝热可逆过程中焓变为零(D) 化学反应中系统的焓变不一定大于内能变化答案:D。
因为焓变厶HM U+A (pV),可以看出若△ (pV) V 0则厶H VA Uo5. 下列哪个封闭体系的内能和焓仅是温度的函数(A) 理想溶液(B) 稀溶液(C) 所有气体(D) 理想气体答案:D6. 与物质的生成热有关的下列表述中不正确的是(A) 标准状态下单质的生成热都规定为零(B) 化合物的生成热一定不为零(C) 很多物质的生成热都不能用实验直接测量(D) 通常所使用的物质的标准生成热数据实际上都是相对值答案:A。
按规定,标准态下最稳定单质的生成热为零。
7. dU=CvdT及dUm=Cv,md■适用的条件完整地说应当是(A) 等容过程(B) 无化学反应和相变的等容过程(C) 组成不变的均相系统的等容过程(D) 无化学反应和相变且不做非体积功的任何等容过程及无反应和相变而且系统内能只与温度有关的非等容过程答案:D8.下列过程中, 系统内能变化不为零的是(A) 不可逆循环过程(B) 可逆循环过程(C) 两种理想气体的混合过程(D) 纯液体的真空蒸发过程答案:0因液体分子与气体分子之间的相互作用力是不同的故内能不同。
(完整版)《物理化学》第二章热力学第一定律练习题(含答案)

(完整版)《物理化学》第⼆章热⼒学第⼀定律练习题(含答案)第⼆章练习题⼀、填空题1、根据体系和环境之间能量和物质的交换情况,可将体系分成、、。
2、强度性质表现体系的特征,与物质的数量⽆关。
容量性质表现体系的特征,与物质的数量有关,具有性。
3、热⼒学平衡状态同时达到四种平衡,分别是、、、。
4、体系状态发⽣变化的称为过程。
常见的过程有、、、、。
5、从统计热⼒学观点看,功的微观本质是,热的微观本质是。
6、⽓体各真空膨胀膨胀功W= 07、在绝热钢瓶中化学反应△U= 08、焓的定义式为。
⼆、判断题(说法对否):1、当体系的状态⼀定时,所有的状态函数都有⼀定的数值。
(√)2、当体系的状态发⽣变化时,所有的状态函数的数值也随之发⽣变化。
(χ)3.因= ΔH, = ΔU,所以与都是状态函数。
(χ)4、封闭系统在压⼒恒定的过程中吸收的热等于该系统的焓。
(χ)错。
只有封闭系统不做⾮膨胀功等压过程ΔH=Q P5、状态给定后,状态函数就有定值;状态函数确定后,状态也就确定了。
(√)6、热⼒学过程中W的值应由具体过程决定( √ )7、1mol理想⽓体从同⼀始态经过不同的循环途径后回到初始状态,其热⼒学能不变。
( √ )三、单选题1、体系的下列各组物理量中都是状态函数的是( C )A 、T、P、V、QB 、m、W、P、HC、T、P、V、n、D、T、P、U、W2、对于内能是体系的单值函数概念,错误理解是( C )A体系处于⼀定的状态,具有⼀定的内能B对应于某⼀状态,内能只能有⼀数值不能有两个以上的数值C状态发⽣变化,内能也⼀定跟着变化D对应于⼀个内能值,可以有多个状态3下列叙述中不具有状态函数特征的是(D )A体系状态确定后,状态函数的值也确定B体系变化时,状态函数的改变值只由体系的始终态决定C经循环过程,状态函数的值不变D状态函数均有加和性4、下列叙述中正确的是( A )A物体温度越⾼,说明其内能越⼤B物体温度越⾼,说明其所含热量越多C凡体系温度升⾼,就肯定是它吸收了热D凡体系温度不变,说明它既不吸热也不放热5、下列哪⼀种说法错误( D )A焓是定义的⼀种具有能量量纲的热⼒学量B只有在某些特定条件下,焓变△H才与体系吸热相等C焓是状态函数D焓是体系能与环境能进⾏热交换的能量6、热⼒学第⼀定律仅适⽤于什么途径(A)A同⼀过程的任何途径B同⼀过程的可逆途径C同⼀过程的不可逆途径D不同过程的任何途径7. 如图,将CuSO4⽔溶液置于绝热箱中,插⼊两个铜电极,以蓄电池为电源进⾏电解,可以看作封闭系统的是(A)(A) 绝热箱中所有物质; (B) 两个铜电极;(C) 蓄电池和铜电极;(D) CuSO4⽔溶液。
热力学第一定律精选全文完整版

可编辑修改精选全文完整版热力学第一定律科技名词定义中文名称:热力学第一定律英文名称:first law of thermodynamics其他名称:能量守恒和转换定律定义:热力系内物质的能量可以传递,其形式可以转换,在转换和传递过程中各种形式能源的总量保持不变。
概述热力学第一定律热力学第一定律:△U=Q+W。
系统在过程中能量的变化关系英文翻译:the first law of thermodynamics简单解释在热力学中,系统发生变化时,设与环境之间交换的热为Q(吸热为正,放热为负),与环境交换的功为W(对外做功为负,外界对物体做功为正),可得热力学能(亦称内能)的变化为ΔU = Q+ W或ΔU=Q-W物理中普遍使用第一种,而化学中通常是说系统对外做功,故会用后一种。
定义自然界一切物体都具有能量,能量有各种不同形式,它能从一种形式转化为另一种形式,从一个物体传递给另一个物体,在转化和传递过程中能量的总和不变。
英文翻译:The first explicit statement of the first law of thermodynamics, byRudolf Clausiusin 1850, referred to cyclic thermodynamic processes "In all cases in which work is produced by the agency of heat, a quantity of heat is consumed which is proportional to the work done; and conversely,by the expenditure of an equal quantity of work an equal quantity of heat is produced."基本内容能量是永恒的,不会被制造出来,也不会被消灭。
(完整版)物理化学课后答案-热力学第一定律

欢迎共阅第二章热力学第一定律【复习题】【1】判断下列说法是否正确。
(1)状态给定后,状态函数就有一定的值,反之亦然。
(2)状态函数改变后,状态一定改变。
(3)状态改变后,状态函数一定都改变。
(4)因为△ U=Q v, △H =Q p,所以Q v,Q p是特定条件下的状态函数。
(5)恒温过程一定是可逆过程。
(6)汽缸内有一定量的理想气体,反抗一定外压做绝热膨胀,则△H= Q p=0。
(7)根据热力学第一定律,因为能量不能无中生有,所以一个系统若要对外做功,必须从外界吸收热量。
(8)系统从状态Ⅰ变化到状态Ⅱ,若△T=0 ,则Q=0 ,无热量交换。
(9)在等压下,机械搅拌绝热容器中的液体,使其温度上升,则△H = Q p = 0。
(10)理想气体绝热变化过程中,W=△U,即W R=△U=C V△T,W IR=△U=C V△T,所以W R=W IR 。
(11)有一个封闭系统,当始态和终态确定后;(a)若经历一个绝热过程,则功有定值;(b)若经历一个等容过程,则Q 有定值(设不做非膨胀力);(c)若经历一个等温过程,则热力学能有定值;(d)若经历一个多方过程,则热和功的代数和有定值。
(12)某一化学反应在烧杯中进行,放热Q1,焓变为△ H 1,若安排成可逆电池,使终态和终态都相同,这时放热Q2,焓变为△ H2,则△ H1=△H 2。
【答】(1)正确,因为状态函数是体系的单质函数,体系确定后,体系的一系列状态函数就确定。
相反如果体系的一系列状态函数确定后,体系的状态也就被惟一确定。
(2)正确,根据状态函数的单值性,当体系的某一状态函数改变了,则状态函数必定发生改变。
(3)不正确,因为状态改变后,有些状态函数不一定改变,例如理想气体的等温变化,内能就不变。
(4)不正确,ΔH=Qp,只说明Qp 等于状态函数H 的变化值ΔH,仅是数值上相等,并不意味着Qp 具有状态函数的性质。
ΔH=Qp 只能说在恒压而不做非体积功的特定条件下,Qp 的数值等于体系状态函数H 的改变,而不能认为Qp 也是状态函数。
(完整版)物理化学作业答案

第二章 热力学第一定律2.11 1 mol 理想气体于27°C ,101.325kPa 的始态下,先受某恒定外压温压缩至平衡态,再恒容 升温至97.0°C ,250.0 kPa ,求过程的W ,Q , U , H,已知气体的C v,m =20.92J 。
mol -1•K -1。
解:111325.10115.3001V kPa p K T mol n ===−−→−=0dT 22215.3001V p K T moln ==−−→−=0dV 233300.25015.3701V V kPap K T moln ====因为23V V =,有3322T p T p=,kPa kPa T T p p 72.20215.37015.30000.2503232=⨯==02=WkJJ p pnRT p nRT p nRT V V p W 497.2)]1325.10172.202(15.300314.81[)1()(12111211221=-⨯⨯⨯=-=+-=--=所以 kJ W W W 497.221=+=()()()kJkJ W U Q kJ J T T R Cn T TnC H kJJ T T nC U mV mp m V 033.1497.2464.1(046.2)]15.30015.370()314.892.20(1[)(464.1)15.30015.370(92.201[13,13,13,-=-=-∆==-⨯+⨯=-+=-=∆=-⨯⨯=-=∆2.39 某双原子理想气体1 mol 从始态350K ,200kPa 经过如下五个不同过程达到各自的平衡态,求各过程的功W1) 恒温可逆膨胀到50kPa ;2) 恒温反抗50kPa 恒外压不可逆膨胀; 3) 恒温向真空膨胀到50kPa ; 4) 绝热可逆膨胀到50kPa ;5) 绝热反抗50kPa 恒外压不可逆膨胀; 解:(1)kJ J p p nRT W 034.4)20050ln 350314.81(ln12-=⨯⨯⨯== (2)kJj p nRTp nRT p V V p V p W 182.2)]200350314.8150350314.81(50[)()(1212-=⨯⨯-⨯⨯⨯=--=--=∆-=(3)0=amb p ,0=∆-=V p W amb(4)对绝热可逆过程:R C m p 5.3,=,R C m V 5.2,=()K K T p p T R R C R T m p 5.235]350)20050[()(5.3/1/12,=⨯=⨯= 因为Q=0,所以()()[]kJJ T T nC Q U W m V 380.23505.235314.85.21012,-=-⨯⨯⨯=--=-∆=(5)Q=0,所以 ()12,T T nC U Q U W m V -=∆=-∆=而 )(11222p nRT p nRT p V p W --=∆-= 联合上述二式可得)350(314.85.21350314.8120050314.8)1(22K T K T -⨯⨯=⨯⨯⨯+⨯- 解出 K T 2752=于是()()[]kJ J T T nC U W m V 559.13505.235314.85.2112,-=-⨯⨯⨯=-=∆= 第三章 热力学第二定律 3.1 卡诺热机在的高温热源和的低温热源间工作。
02章 热力学第一定律

3. 几种典型可逆过程: (1)可逆膨胀和可逆压缩:力学平衡 (2)可逆传热:热平衡 (3)可逆相变:相平衡 (4)可逆化学反应:A + B
E反=E-dE + 电 池(E) A+B C -
C
§ §2 2- -4 4 热的计算 热的计算 (How (How to to calculate calculate heat) heat)
§2-1 基本概念 (Important concepts)
一、系统和环境 (System and surroundings) ¾ 定义:系统——研究对象(也称体系) 环境——与系统有相互作用的外界 ¾ 系统的分类 敞开系统 系统 封闭系统 孤立系统
二、热力学平衡状态 (Thermodynamic equilibrium state)
V1 V1 V1
V2
V2
V2
= −∫
V2
V1
nRT V dV = − nRT ln 2 V V1
等温膨胀 W=? H2(1000Pa, 3m3)
例:1mol H2 (3000Pa, 1m3)
(1) 若 p外=0 (自由膨胀):W=0 (2) 若 p外=1000 Pa (一次膨胀):W=-1000×(3-1) J =-2000 J (3) 可逆膨胀:
∆U = ∫ CV dT
T1
T2
¾ 理气 H = U + pV = U + nRT = f(T)
⎛ ∂H ⎜ ⎜ ∂p ⎝
⎞ ⎟ ⎟ =0 ⎠T
对任意物质的任意(p V T)过程 ⎛ ∂H ⎞ d H = C p dT + ⎜ ⎜ ∂p ⎟ ⎟ dp ⎝ ⎠T 理想气体
dH = C p dT
T2
(完整版)物理化学热力学第一定律习题答案..

第二章 热力学第一定律2-1 1mol 理想气体于恒定压力下升温1℃,试求过程中气体与环境交换的功W 。
解:体系压力保持恒定进行升温,即有P 外=P ,即反抗恒定外压进行膨胀,JT nR nRT nRT pV pV V V p W amb 314.8)(121212-=∆-=+-=+-=--=2-2 系统由相同的始态经过不同途径达到相同的末态。
若途径a 的Q a =2.078kJ ,W a = -4.157kJ ;而途径b 的Q b = -0.692kJ 。
求W b 。
解:应用状态函数法。
因两条途径的始末态相同,故有△U a =△U b ,则 bb a a W Q W Q +=+所以有,kJQ W Q W b a a b 387.1692.0157.4078.2-=+-=-+=2-3 4mol 某理想气体,温度升高20℃,求△H -△U 的值。
解: 方法一: 665.16J208.3144 )20()( 2020,,20,20,=⨯⨯=-+==-=-=∆-∆⎰⎰⎰⎰++++T K T nR nRdT dT C C n dTnC dT nC U H K T TKT Tm V m p KT Tm V KT T m p 方法二:可以用△H=△U+△(PV)进行计算。
2-4 某理想气体。
今有该气体5 mol 在恒容下温度升高50℃,求过, 1.5V m C R =程的W ,Q ,△H 和△U 。
解:恒容:W=0;kJJ K nC T K T nC dT nC U m V m V K T Tm V 118.33118503145.823550 )50(,,50,==⨯⨯⨯=⨯=-+==∆⎰+kJJ KR C n T K T nC dT nC H m V m p KT Tm p 196.55196503145.8255 50)()50(,,50,==⨯⨯⨯=⨯+==-+==∆⎰+根据热力学第一定律,:W=0,故有Q=△U=3.118kJ2-5某理想气体。
(完整版)第二章热力学第一定律习题

第二章热力学第一定律选择题1.热力学第一定律ΔU=Q+W 只适用于(A) 单纯状态变化 (B) 相变化(C) 化学变化 (D) 封闭物系的任何变化答案:D2.关于热和功, 下面的说法中, 不正确的是(A) 功和热只出现于系统状态变化的过程中, 只存在于系统和环境间的界面上(B) 只有在封闭系统发生的过程中, 功和热才有明确的意义(C) 功和热不是能量, 而是能量传递的两种形式, 可称之为被交换的能量(D) 在封闭系统中发生的过程中, 如果内能不变, 则功和热对系统的影响必互相抵消答案:B3.关于焓的性质, 下列说法中正确的是(A) 焓是系统内含的热能, 所以常称它为热焓(B) 焓是能量, 它遵守热力学第一定律(C) 系统的焓值等于内能加体积功(D) 焓的增量只与系统的始末态有关答案:D。
因焓是状态函数。
4.涉及焓的下列说法中正确的是(A) 单质的焓值均等于零(B) 在等温过程中焓变为零(C) 在绝热可逆过程中焓变为零(D) 化学反应中系统的焓变不一定大于内能变化答案:D。
因为焓变ΔH=ΔU+Δ(pV),可以看出若Δ(pV)<0则ΔH<ΔU。
5.下列哪个封闭体系的内能和焓仅是温度的函数(A) 理想溶液 (B) 稀溶液 (C) 所有气体 (D) 理想气体答案:D6.与物质的生成热有关的下列表述中不正确的是(A) 标准状态下单质的生成热都规定为零(B) 化合物的生成热一定不为零(C) 很多物质的生成热都不能用实验直接测量(D) 通常所使用的物质的标准生成热数据实际上都是相对值答案:A。
按规定,标准态下最稳定单质的生成热为零。
7.dU=CvdT及dUm=Cv,mdT适用的条件完整地说应当是(A) 等容过程(B)无化学反应和相变的等容过程(C) 组成不变的均相系统的等容过程(D) 无化学反应和相变且不做非体积功的任何等容过程及无反应和相变而且系统内能只与温度有关的非等容过程答案:D8.下列过程中, 系统内能变化不为零的是(A) 不可逆循环过程 (B) 可逆循环过程(C) 两种理想气体的混合过程 (D) 纯液体的真空蒸发过程答案:D 。
物理化学02热力学第一定律

§2.1 热力学基本概念及术语
一、系统与环境 二、系统的性质 三、状态和状态函数 四、平衡态 五、过程和途径 六、过程函数 七、热力学能
一、系统与环境 1. 系统 系统(System): 研究的对象, 研究的对象,即我们感兴趣的那部 分物质或空间,也称物系或体系。 分物质或空间,也称物系或体系。 2. 环境 环境(Surroundings): 系统之外与之有直接联系的那部分 物质或空间
五、过程与途径
1. 过程 过程(process):系统状态发生的任何变化 : 2. 途径 途径(Path):系统状态发生变化过程的具体步骤 : 3. 热力学常见过程: 热力学常见过程: (1) 纯pVT变化、相变化、化学变化过程 变化、 变化 相变化、 (2)可逆过程与不可逆过程 可逆过程与不可逆过程 (3)循环与非循环过程 循环与非循环过程 (4)恒温、恒压、恒容、恒外压、绝热过程 : 体积功:系统由于体积变化与环境交换的能量 δW=Fdl=(F/A)(A dl)= p环dV
活塞,面积 活塞,面积A 气体
pamb dl
pamb < p: : dV>0,膨胀, ,膨胀, 系统对外作功 δW<0 pamb > p: : dV<0,压缩, ,压缩, 系统得到功 δW>0
l
图2.2.1 体积功示意图
2.4 变温过程热的计算
与恒容热Q 一、定容摩尔热容CV,m与恒容热 V 定容摩尔热容 与恒压热Q 二、定压摩尔热容Cp,m与恒压热 p 定压摩尔热容 三、CV,m与Cp,m的关系 四、 Cp,m与T的关系 的关系 五、平均摩尔定压热容 六、气体恒容变温和恒压变温过程热的计算 七、液体和固体变温过程热的计算
4.经验规律: .经验规律: 对组成不变的系统 两个强度性质确定 则所有强度性质确定; 确定, 强度性质确定 ①两个强度性质确定,则所有强度性质确定; ②两个强度性质和一个广延性质确定,则所有 两个强度性质和一个广延性质确定, 确定 性质都确定。 性质都确定。 由此可见: 由此可见: 对组成及数量不变的系统, 对组成及数量不变的系统,某一状态函数 可表示为另外两个状态函数的函数。 两个状态函数的函数 可表示为另外两个状态函数的函数。 如:压力可表示为体积和温度的函数 p = f (T,V)
第二章 热力学第一定律

第二章热力学第一定律基本公式功: δW = -P外dV热力学第一定律: dU =δQ + δW ΔU = Q + W焓的定义: H ≡ U + PV热容的定义: C=limΔT→0δQ/ ΔT等压热容的定义: C P =δQ P /dT =(∂H/∂T)P等容热容的定义: C V =δQ V /dT =(∂U/∂T)V任意体系的等压热容与等容热容之差: C P - C V = [P + (∂U/∂V)T] (∂V/∂T)P 理想气体的等压热容与等容热容之差: C P - C V = nR理想气体绝热可逆过程方程: γ = C P / C VPVγ-1 =常数T Vγ-1 =常数P1-γTγ=常数理想气体绝热功: W =C V(T1 – T2 ) W = P1V1 – P2V2 /γ-1热机效率: η = W/Q2可逆热机效率: η = T2 – T1 / T2冷冻系数: β= Q1′/W可逆制冷机冷冻系数: β = T1 / T2 – T1焦汤系数: μ = ( ∂T/ ∂P)H = - (∂H/∂P)/C P反应进度: ξ= n B – n B0 / νB化学反应的等压热效应与等容热效应的关系: Q P = Q V + ΔnRT当反应进度ξ= 1 mol 时Δr H m= Δr U m +ΣBνB RT化学反应等压热效应的几种计算方法:Δr H m⊖=ΣBνBΔf H m⊖(B)Δr H m⊖=ΣB (єB )反应物 - ΣB(єB )产物Δr H m⊖= -ΣBνBΔC H m⊖(B)反应热与温度的关系: Δr H m(T2) =Δr H m(T1) + ∫21T TΔr C P dT表 1-1 一些基本过程的W 、Q、△U 、△H 的运算过程W Q △U △H 理想气体自由膨胀0 0 0 0 理想气体等温可逆 -nRTLnV2/V1 -nRTLnV2/V10 0任意物质等容可逆理想气体0∫C V dT∫C V dTQ v∫C V dT△U + V△P∫C P dT任意物质等压可逆理想气体-P外△V-P外△V∫C P dT∫C p dTQ P - P△V∫C V dTQ P∫C P dT理想气体绝热过程C V(T2 – T1)1/γ-1(P2V2-P1V1) 0 ∫C V dT ∫C P dT理想气体多方可逆过程PVδ=常数n R/1-δ(T2-T1) △U + W ∫C V dT ∫C P dT 可逆相变(等温等压) -P外△V Q P Q P -W Q P化学反应(等温等压) -P外△VQ PQ P – WΔr H m=Δr U m+ΣBνB RTQ PΔr H m⊖=ΣBνBΔf H m⊖(B) 例题例1 0.02Kg 乙醇在其沸点时蒸发为气体。
热力学第二章第一定律

对于式:
q
h
1 2
cf2
gz
wi
注意:q和wi分别是1kg工质进入系统后,系统从外界吸入的
热量和在系统内部所作的功。除的m不是系统的质量。
对于微元过程 ,稳定流动能量方程写成
δQ
dH
1 2
mdcf2
mgdz
δWi
δq
dh
1 2
dcf2
gdz
δwi
焓
焓:H=U+pV ,单位:J或kJ
注意:区分各截面间参数可不同。
设在τ时间段内有m1千克工质流进系统,同时 m2千克的工质流出系统。
mCV 0 qm1 qm2 m1 m2 m
在 时间段内进入系统的能量
在 时间段内离开系统的能量
Wi
m
u2
1 2
cf22
gz2
mp 2 v2
Wi
m
分析开口系统时,除了能量平衡外,还必须考虑质量平衡:
进入系统的质量-离开系统的质量=系统质量的变化
推动功
因工质出、入开口系统而 传递的功,叫推动功(推进 功) 。
W推 = p A l = pV w推= pv
A p pV
l
对推动功的说明
1、与宏观流动有关,流动停止,推动功不存在;
2、作用过程中,工质仅发生位置变化,无状态变化;
δQ δW
7. 热力学第一定律解析式的适用条件:
q u w
①闭口系统;②任何工质;③任何过程
δq δw
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 热力学第一定律1、如果一个系统从环境吸收了J 40的热,而系统的热力学能却增加了J 200,问系统从环境中得到了多少功?如果该系统在膨胀过程中对环境作了kJ 10的功,同时收了kJ 28的热,求系统的热力学能变化值。
解:根据W Q U +=∆热力学第一定律,可知J Q U W 160)40200(=-=-∆=(系统从环境吸热,0>Q ) kJ W Q U 181028=-=+=∆(系统对环境做功,0<W )2、有mol 10的气体(设为理想气体),压力为kPa 1000,温度为K 300,分别求出等温时下列过程的功:(1)在空气中压力为kPa 100时,体积胀大31dm ;(2)在空气中压力为kPa 100时,膨胀到气体压力也是kPa 100; (3)等温可逆膨胀至气体的压力为kPa 100; 解:(1)外压始终维持恒定,系统对环境做功 J V p W e 1001011010033-=⨯⨯⨯-=∆-=-(2))11()()(12112212p p nRTp p nRT p nRT p V V p V p W e e e e --=--=--=∆-=343311108.31430010010() 2.21010010100010J =-⨯⨯⨯⨯-=-⨯⨯⨯(3)等温可逆膨胀:2112ln ln21p p nRT V V nRT dV p W V V e -=-=-=⎰J 41074.51001000ln 300314.810⨯-=⨯⨯⨯-=3、1mol 单原子理想气体,,32V m C R =,始态(1)的温度为273K ,体积为322.4dm ,经历如下三步,又回到始态,请计算每个状态的压力,Q ,W 和U ∆。
(1)等容可逆升温由始态(1)到546K 的状态(2);(2)等温(546K )可逆膨胀由状态(2)到44.8dm 3的状态(3);(3)经等压过程由状态(3)回到始态10mol,300K 1000kPa,V 1 10mol,300K 100kPa,V 2(1);解:(1)等容可逆升温过程:()21,0318.3145462733404.582e T V V m T W P V U Q W Q nC dT J=-∆=∆=+===⨯⨯⨯-=⎰ (2)等温可逆膨胀过程:0U ∆=2144.8ln 18.314546ln 3146.5022.43146.50V W nRT JV Q W J=-=⨯⨯⨯=-=-=(3)等压过程:()()()()()2131231,18.31427322.444.8102269.7222.4103527354618.3142735674.31225674.312269.723404.59e T p P m T nRT W P V V V J V Q H nC dT n R R J U Q W J--⨯⨯=-∆=--=-⨯-⨯=⨯⎛⎫=∆=+⨯-=⨯⨯⨯-=- ⎪⎝⎭∆=+=-+=-⎰4、在K 291和kPa 100下,)(1s molZn 溶于足量稀盐酸中,置换出)(12g molH ,并放热kJ 152。
若以Zn 和盐酸为系统,求该反应所做的功及系统热力学能的变化。
解: )()()(2)(22g H l ZnCl l HCl s Zn +=+在K 291和kPa 100下的条件下发生以上反应,生成)(2g HnRT pnRTp V p V V p W eg H e e -=-=-=--=)(122)( J .2419291314.81-=⨯⨯-=该反应为放热反应, 0<Q , J Q 310152⨯-=J W Q U 5310544.1241910152⨯=-⨯-=+=∆5、在K 298时,有)(22g molN ,始终态体积为体积为315dm ,保持温度不变,经下列三个过程膨胀到350dm ,计算各过程的,,U H W ∆∆和Q 的值。
设气体为理想气体。
(1)自由膨胀;(2)反抗恒定外压kPa 100膨胀; (3)可逆膨胀; 解:(1)自由膨胀过程,因为理想气体的U 和H 都只是温度的函数,所以在等温下0U ∆=,0H ∆=, 由于0=e p , 0=∆-=V p W e又根据U Q W ∆=+可知0=Q 。
(2)反抗恒定外压膨胀J V V p V p W e e 350010)1550(10100)(3312-=⨯-⨯-=--=∆-=- 因为理想气体的U 和H 都只是温度的函数,所以在等温下0U ∆=,0H ∆=,J W Q 3500=-=。
(3)等温可逆膨胀,等温过程0U ∆=,0H ∆=12ln 21V VnRT dV p W V V e -=-=⎰J 86.59651550ln 298314.82-=⨯⨯⨯-=U Q W ∆=+,J W Q 86.5965=-=6、在水的正常沸点(373.15K ,101.325kPa ),有21()molH O l 变为同温同压的2()H O g ,已知水的摩尔汽化焓变值为140.69vap m H kJ mol -∆=⋅,请计算该变化的Q ,U ∆,H ∆的值各为多少?解:相变在373.15K ,101.325kPa 等温等压下进行,p H Q n ∆==40.69140.69()vap m H kJ ∆=⨯=()18.314373 3.1()g l W p V V nRT kJ =--=-=-⨯⨯=-40.69 3.137.59()U Q W kJ ∆=+=-=7.理想气体等温可逆膨胀,体积从1V 膨胀大到101V ,对外作了41.85kJ 的功,系统的起始压力为202.65 kPa 。
(1)求始态体积1V ;(2)若气体的量为mol 2,试求系统的温度。
解:(1)等温可逆过程21lnV W nRT V =- 理想气体状态方程pV nRT = 两式联合求解121ln WpV V V =-3313211141.85100.08910ln 202.6510lnW V m V V p V V ⨯=-=-=⨯(2)同理根据等温可逆过程21lnV W nRT V =-可得3211141.8510109310ln 28.314lnWT K V V nR V V ⨯=-=-=⨯8、在kPa 100及K 423时,将)(13g molNH 等温压缩到体积等于31dm ,求最少需做多少功?(1) 假定是理想气体;(2)假定符合van der Waals 方程式。
已知van der Waals 常数a=0.417Pa m 6mol -2解:(1)假定是理想气体,那么气体在等温可逆压缩中做功最小2133133W nRT ln 10101mol 8.314mol 423ln 35104405.74VV m J K m J-----=-⨯=-⨯⨯⨯⨯=可根据理想气体状态方程113133nRT 1mol 8.314mol 423 100103510J K V P Pa m ----⨯⨯==⨯=⨯代入上式方可求解。
(2)假定符合van der Waals 方程,方程整理后,可得320m m m RT a ab V V b V P P P ⎛⎫-++-= ⎪⎝⎭ 代入数据 3226103.47210 4.1710 1.547100mm m V V V ----⨯+⨯-⨯= 解三次方程后得 33 3510m V m -=⨯2122V V nRT an W dV V nb V ⎛⎫=-- ⎪-⎝⎭⎰2212111n lnV nbRT an V nb V V ⎛⎫-=--- ⎪-⎝⎭3353113353110101 3.711018.314300ln35101 3.7110m mol m mol mol J mol K m mol m mol -----------⨯-⨯⨯⋅=-⨯⨯⨯⨯-⨯⨯⋅61233110.41714385.210.010.35Pa m mol J m m -⎛⎫=⋅⋅⨯⨯-= ⎪⎝⎭9、已知在373K 和100kPa 压力时,21()kgH O l 的体积为31.043dm ,21()kgH O g 的体积为31677dm ,2()H O l 的摩尔汽化焓变值140.69Vap H kJ mol -∆=⋅,当21()molH O l 在373K和100kPa 压力时完全蒸发成2()H O g ,求:(1)蒸发过程中系统对环境所做的功;(2)假定液态水的体积可忽略不计,试求蒸发过程中系统对环境所做的功; (3)假定把蒸汽看作理想气体,且略去液态水的体积,求系统所做的功; (4)求(1)中变化的Vap m U ∆和Vap m H ∆; (5)解释何故蒸发的焓变大于系统所做的功。
解:(1)蒸发过程中系统对环境所做的功()e g l W p V V =--33331310010(167710 1.04310)(1810)Pa m kg kg ----=-⨯⨯⨯-⨯⋅⨯⨯ 3016.72J =-(2)假定液态水的体积可忽略不计,0l V =3331001016771018103018.60e g W p V nRT J --=-=-=-⨯⨯⨯⨯⨯=- 3018.63016.72100%0.062%3016.72-+⨯=-(3)蒸汽看作理想气体,则pV nRT = 液态水的体积可忽略不计,0l V =1118.3143733101.12e g W p V nRT mol J mol K K J --=-=-=-⨯⋅⋅⨯=- (4)1,40.69p m Vap m Q H kJ mol -=∆=⋅33140.69110(3016.72)37.67101Vap Q W U J mol n -+⨯⨯+-∆===⨯⋅3137.6710J mol -=⨯⋅(5)在蒸发过程中,用于系统对环境做膨胀功的部分很少,吸收的大部分热量用于提高系统的热力学能。
10、1mol 单原子理想气体,从始态: 273K 、200kPa ,到终态:323K 、100kPa ,通过两个途径:(1)先等压加热至323K ,再等温可逆膨胀至100kPa ; (2)先等温可逆膨胀至100kPa ,再等压加热至323K 。
请分别计算两个途径的Q ,W ,U ∆和H ∆,试比较两种结果有何不同,说明为什么?解:(1)因为单原子理想气体,3V m C R =,,5p m C R =过程如图所示。
① 等压升温21121()()e nRT nRT W p V V p p p=--=-- 21()18.314(323273)415.7()nR T T J =--=-⨯⨯-=-2111,518.314(323273)1039()2T p p m T H Q nC dT J ∆===⨯⨯⨯-=⎰211,318.314(323273)623.6()2T v m T U nC dT J ∆==⨯⨯⨯-=⎰② 等温可逆21212200lnln 18.314323ln 1861()100V p W nRT RT J V p =-=--⨯⨯⨯=- 20U ∆=,20H ∆= 221861()Q W J =-=122277()W W W J =+=- 122900()Q Q Q J =+=12623.6()U U U J ∆=∆+∆= 121039()H H H J ∆=∆+∆=①等温可逆21112200lnln 18.314273ln 1573()100V p W nRT RT J V p =-=-=-⨯⨯⨯=- 10U ∆=,10H ∆= 111573()Q W J =-=②等压升温21221()()e nRT nRT W p V V p p p=--=-- 21()18.314(323273)415.7()nR T T J =--=-⨯⨯-=2112,518.314(323273)1039()2T p p m T H Q nC dT J ∆===⨯⨯⨯-=⎰212,318.314(323273)623.6()2T v m T U nC dT J ∆==⨯⨯⨯-=⎰121989()W W W J =+=- 122613()Q Q Q J =+=12623.6()U U U J ∆=∆+∆= 121039()H H H J ∆=∆+∆=比较两种结果,U ∆和H ∆的值相同,而Q 和W 值不同,说明Q 和W 不是状态函数,它们的数值与所经过的途径和过程有关,而U 和H 是状态函数,无论经过何种途径,只要最终状态相同,U ∆和H ∆的数值必然相同。
