51单片机PID算法程序(三)增量式PID控制算法

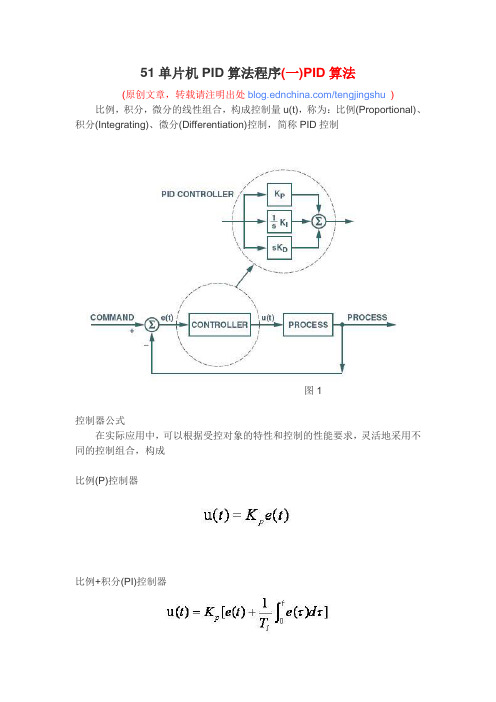
51单片机PID算法程序(一)PID算法(原创文章，转载请注明出处/tengjingshu) 比例，积分，微分的线性组合，构成控制量u(t)，称为：比例(Proportional)、积分(Integrating)、微分(Differentiation)控制，简称PID控制图1控制器公式在实际应用中，可以根据受控对象的特性和控制的性能要求，灵活地采用不同的控制组合，构成比例(P)控制器比例+积分(PI)控制器比例+积分+微分(PID)控制器式中或式中控制系统中的应用在单回路控制系统中，由于扰动作用使被控参数偏离给定值，从而产生偏差。

自动控制系统的调节单元将来自变送器的测量值与给定值相比较后产生的偏差进行比例、积分、微分(PID)运算，并输出统一标准信号，去控制执行机构的动作，以实现对温度、压力、流量、也为及其他工艺参数的自动控制。

比例作用P只与偏差成正比；积分作用I是偏差对时间的积累；微分作用D 是偏差的变化率；比例(P)控制比例控制能迅速反应误差，从而减少稳态误差。

除了系统控制输入为0和系统过程值等于期望值这两种情况，比例控制都能给出稳态误差。

当期望值有一个变化时，系统过程值将产生一个稳态误差。

但是，比例控制不能消除稳态误差。

比例放大系数的加大，会引起系统的不稳定。

图2比例(P)控制阶跃响应积分(I)控制在积分控制中，控制器的输出与输入误差信号的积分成正比关系。

为了减小稳态误差，在控制器中加入积分项，积分项对误差取决于时间的积分，随着时间的增加，积分项会增大。

这样，即使误差很小，积分项也会随着时间的增加而加大，它推动控制器的输出增大使稳态误差进一步减少，直到等于零。

积分(I)和比例(P)通常一起使用，称为比例+积分(PI)控制器，可以使系统在进入稳态后无稳态误差。

如果单独用积分(I)的话，由于积分输出随时间积累而逐渐增大，故调节动作缓慢，这样会造成调节不及时，使系统稳定裕度下降。

图3积分(I)控制和比例积分(PI)控制阶跃相应微分(D)控制在微分控制中，控制器的输出与输入误差信号的微分（即误差的变化率）成正比关系。

由于自动控制系统有较大的惯性组件（环节）或有滞后（delay）组件，在调节过程中可能出现过冲甚至振荡。

解决办法是引入微分(D)控制，即在误差很大的时候，抑制误差的作用也很大；在误差接近零时，抑制误差的作用也应该是零。

图4微分(D)控制和比例微分(PD)控制阶跃相应总结：PI比P少了稳态误差，PID比PI反应速度更快并且没有了过冲。

PID比PI 有更快的响应和没有了过冲。

图5增益常数（系数）上升时间过冲建立时间稳态误差Kp 减少增大很小变化减小K I减少增大增加消除K D很小变化减小减少很小变化表1注意，这里的图6 典型的PID控制器对于阶跃跳变参考输入的响应参数的调整应用PID控制，必须适当地调整比例放大系数K P，积分时间T I和微分时间T D，使整个控制系统得到良好的性能。

最好的寻找PID参数的办法是从系统的数学模型出发，从想要的反应来计算参数。

很多时候一个详细的数学描述是不存在的，这时候就需要实际地调节P ID的参数.Ziegler-Nichols方法Ziegler-Nichols方法是基于系统稳定性分析的PID整定方法．在设计过程中无需考虑任何特性要求，整定方法非常简单，但控制效果却比较理想。

具体整定方法步骤如下：1. 先置I和D的增益为0,逐渐增加K P直到在输出得到一个持续的稳定的振荡。

2. 记录下振荡时的P部分的临界增益Kc,和振荡周期Pc，代到下表中计算出K P，Ti，Td。

Ziegler-Nichols整定表表2Tyreus-Luyben 整定表:表3Tyreus-Luyben的整定值减少了振荡的作用和增强了稳定性。

自动测试方法：为了确定过程的临界周期Pc和临界增益Kc，控制器会临时使它的PID算法失效，取而代之的是一个ON/OFF的继电器来让过程变为振荡的。

这两个参数很好的将过程行为进行了量化以决定PID控制器应该如何整定来得到理想的闭环回路性能。

图6参考资料1）Mixed-Signal Control Circuits Use Microcontroller for Flexibility in Impl ementing PID Algorithms，By Eamon Neary（图1，表1）2）Atmel 8-bit AVR Microcontrollers Application Note:AVR221: Discrete PI D controller（图2，图3，图4，图5，表2）3）使用Ziegler-Nichols方法的自整定控制/2007-03/200733042815.htm（图6）4）Ziegler-Nichols Method/~tbco/cm416/zn.html（表3）5）Ziegler-Nichols方法PID参数整定--随风的blog/u/4/archives/2007/97.htm6) PID控制原理教程，胡晓若编制51单片机PID算法程序(二)位置式PID控制算法(转载请注明出处/tengjingshu) 由51单片机组成的数字控制系统控制中，PID控制器是通过PID控制算法实现的。

51单片机通过AD对信号进行采集，变成数字信号，再在单片机中通过算法实现PID运算，再通过DA把控制量反馈回控制源。

从而实现对系统的伺服控制。

位置式PID控制算法位置式PID控制算法的简化示意图上图的传递函数为：（2-1）在时域的传递函数表达式（2-2）对上式中的微分和积分进行近似（2-3）式中n是离散点的个数。

于是传递函数可以简化为：（2-4）其中u(n)——第k个采样时刻的控制；K P ——比例放大系数；K i ——积分放大系数；K d ——微分放大系数；T ——采样周期。

如果采样周期足够小，则（2-4）的近似计算可以获得足够精确的结果，离散控制过程与连续过程十分接近。

（2-4）表示的控制算法直接按（2-1）所给出的PID控制规律定义进行计算的，所以它给出了全部控制量的大小，因此被称为全量式或位置式PID控制算法。

缺点：1）由于全量输出，所以每次输出均与过去状态有关，计算时要对e(k)(k=0, 1,…n)进行累加，工作量大。

2）因为计算机输出的u(n)对应的是执行机构的实际位置，如果计算机出现故障，输出u(n)将大幅度变化，会引起执行机构的大幅度变化，有可能因此造成严重的生产事故，这在实际生产中是不允许的。

位置式PID控制算法C51程序具体的PID参数必须由具体对象通过实验确定。

由于单片机的处理速度和r am资源的限制，一般不采用浮点数运算，而将所有参数全部用整数，运算到最后再除以一个2的N次方数据（相当于移位），作类似定点数运算，可大大提高运算速度，根据控制精度的不同要求，当精度要求很高时，注意保留移位引起的“余数”，做好余数补偿。

这个程序只是一般常用pid算法的基本架构，没有包含输入输出处理部分。

=========================================================== ==========================================*/#include <reg52.h>#include <string.h> //C语言中memset函数头文件/*========================================================== ==========================================PID FunctionThe PID (比例、积分、微分) function is used in mainlycontrol applications. PIDCalc performs one iteration of the PID algorithm.While the PID function works, main is just a dummy program showinga typical usage.=========================================================== ==========================================*/typedef struct PID {double SetPoint; // 设定目标Desired valuedouble Proportion; // 比例常数Proportional Constdouble Integral; // 积分常数Integral Constdouble Derivative; // 微分常数Derivative Constdouble LastError; // Error[-1]double PrevError; // Error[-2]double SumError; // Sums of Errors} PID;/*========================================================== ==========================================PID计算部分=========================================================== ==========================================*/double PIDCalc( PID *pp, double NextPoint ){double dError, Error;Error = pp->SetPoint - NextPoint; // 偏差pp->SumError += Error; // 积分dError = Error - pp->LastError; // 当前微分pp->PrevError = pp->LastError;pp->LastError = Error;return (pp->Proportion * Error // 比例项+ pp->Integral * pp->SumError // 积分项+ pp->Derivative * dError // 微分项);}/*========================================================== ==========================================Initialize PID Structure PID参数初始化=========================================================== ==========================================*/void PIDInit (PID *pp){memset ( pp,0,sizeof(PID));}/*========================================================== ==========================================Main Program 主程序=========================================================== ==========================================*double sensor (void)// Dummy Sensor Function{return 100.0;}void actuator(double rDelta) // Dummy Actuator Function{}void main(void){PID sPID;// PID Control Structuredouble rOut; // PID Response (Output)double rIn; // PID Feedback (Input)PIDInit ( &sPID ); // Initialize StructuresPID.Proportion = 0.5; // Set PID CoefficientssPID.Integral = 0.5;sPID.Derivative = 0.0;sPID.SetPoint = 100.0; // Set PID Setpointfor (;;) {// Mock Up of PID ProcessingrIn = sensor (); // Read InputrOut = PIDCalc ( &sPID,rIn ); // Perform PID Interationactuator ( rOut ); // Effect Needed Changes}参考资料：1）Atmel 8-bit AVR Microcontrollers Application Note:AVR221: Discrete PI D controller2）茶壶- pid C程序，好东西- 腾讯博客–Qzone/blog/38162254-12259767773）PID 调节控制做电机速度控制，SUNPLUS凌阳科技51单片机PID算法程序(三)增量式PID控制算法(转载请注明出处/tengjingshu) 当执行机构需要的不是控制量的绝对值，而是控制量的增量（例如去驱动步进电动机）时，需要用PID的“增量算法”。