(完整版)所有计量经济学检验方法(全)
2024版计量经济学全册课件(完整)pptx

REPORTING
2024/1/28
23
EViews软件介绍及操作指南
EViews软件概述
EViews是一款功能强大的计量经济学 软件,提供数据处理、统计分析、模型
估计和预测等功能。
统计分析与检验
2024/1/28
详细讲解EViews中的统计分析工具, 包括描述性统计、假设检验、方差分
析等。
数据导入与预处理 介绍如何在EViews中导入数据,进行 数据清洗、转换和预处理等操作。
随着大数据时代的到来,机器学 习算法在数据挖掘、预测和分类 等方面展现出强大的能力,为计 量经济学提供了新的研究工具和 方法。
机器学习在计量经济 学中的应用领域
机器学习在计量经济学中的应用 领域广泛,如变量选择、模型选 择、非线性模型估计、高维数据 处理等。
机器学习在计量经济 学中的常用算法
机器学习在计量经济学中常用的 算法包括决策树、随机森林、支 持向量机(SVM)、神经网络等。 这些算法可以用于分类、回归、 聚类等任务,提高模型的预测精 度和解释力。
面板数据特点
同时具有时间序列和截面数据的特征,能够提供更多的信息、更多的变化、更少共 线性、更多的自由度和更高的估计效率。
2024/1/28
20
固定效应模型与随机效应模型
固定效应模型(Fixed Effects Model)
对于特定的个体而言,其截距项是固定的,不随时间变化而变化。
随机效应模型(Random Effects Mode…
经典线性回归模型
REPORTING
2024/1/28
7
一元线性回归模型
模型设定与参数估计
介绍一元线性回归模型的基本形式, 解释因变量、自变量和误差项的含义, 阐述最小二乘法(OLS)进行参数估 计的原理。
所有计量经济学检验方法

所有计量经济学检验方法
1、回归分析:回归分析是用来确定两个变量之间相关关系的一种统计方法,它能够推断出一个变量对另一个变量的影响程度。
常用的回归检验包括偏直斜率检验、R平方检验、Durbin-Watson检验、自相关检验、Box-Cox检验等。
2、主成分分析:主成分分析(PCA)是一种统计分析方法,用于消除随机变量之间的相关性,从而简化数据分析过程。
常用的方法有二元主成分分析(BPCA)、多元主成分分析(MPCA)
3、因子分析:因子分析是一种统计学方法,用于确定从多个离散观测变量中提取的隐含变量。
常用的因子分析检验包括KMO检验、Bartlett 统计量检验、条件双侧门限统计量检验等。
4、多元分析:多元分析是一种统计学方法,用于探索随机变量之间的关系,常用的多元分析检验包括多元弹性网络(MANOVA)、多元回归(MR)以及结构方程模型(SEM)。
5、聚类分析:聚类分析是一种用于探索研究数据中的结构和特征的统计学方法。
它主要是将数据集分组,以便对数据集中的每组信息单独进行分析。
常用的聚类分析检验有K均值聚类、层次聚类、嵌套聚类等。
6、特征选择:特征选择是一种数据分析技术,用于从大量可能的特征中,选择有效的特征变量。
计量经济学协整检验方法

三、协整检验协整性的检验方法主要有两个: (一) EG 两步法以两个变量y 和x 为例。
在检验协整性之前,首先要对变量的单整性进行检验,只有当两个变量的单整阶数相同时,才可能存在协整关系。
不妨设y 和x 都是一阶单整序列,即y 、x 均)1(~I ,则EG 两步法的具体检验步骤为:第一步:利用最小二乘法估计模型:t t t x y εββ++=10 (5-1) 并计算相应的残差序列:)ˆˆ(10tt t x y e ββ+-= 第二步:检验残差序列的平稳性,可以使用的检验方程有: t mi i t i t t e e e εγδ+∆+=∆∑=--11(5-2) t m i i t i t t e e e εγδα+∆++=∆∑=--11(5-3)t mi i t i t t e e t e εγδβα+∆+++=∆∑=--11(5-4)如果经过DF 检验(或ADF 检验)拒绝了原假设0:0=δH ,残差序列是平稳序列,则意味着y 和x 存在着协整关系,称模型(5-1)为协整回归方程;如果接受了存在单位根的原假设,则残差序列是非平稳的,y 和x 之间不可能存在协整关系,模型(5-1)是虚假回归方程。
说明: 1.在检验方程中加上差分的滞后项是为了消除误差项的自相关性,检验也相应称为AEG 检验;其中滞后阶数一般用SIC 或AIC 准则确定,EViews 5中增加了根据SC 等准则自动确定滞后阶数的功能。
2.检验残差序列的平稳性时,可以在检验方程中加上常数项和趋势项,即使用方程(5-3)、(5-4)进行检验,也可以加在原始回归方程(5-1)中,但在两个方程中只能加一次,不能重复加入。
3.在检验残差序列的平稳性时,虽然检验统计量与DF (或ADF )检验中的相同,但是检验统计量的分布已不再是DF 或ADF 分布,所以临界值也发生了变化,而且还与回归方程中变量个数、样本容量和协整检验方程的不同有关。
麦金农(Mackinnon )给出了协整检验临界值的计算公式,EViews 软件也可以直接输出Mackinnon 临界值(或伴随概率)。
(超全)计量经济学框架图
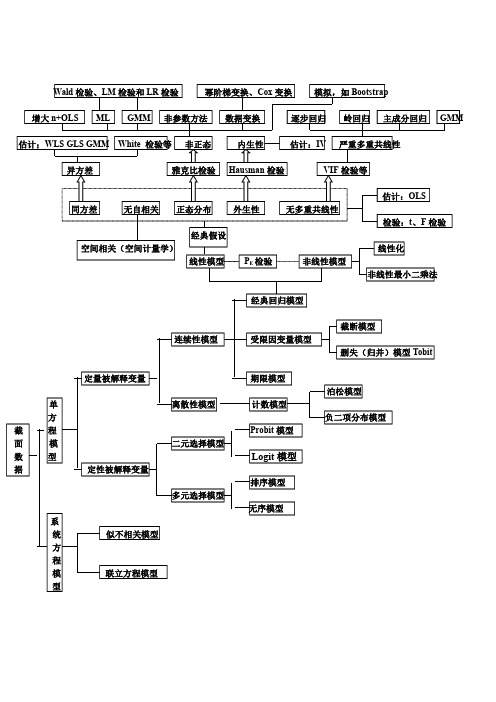
面
模
二元选择模型
数
型
Logit 模型
据
定性被解释变量
排序模型
多元选择模型
无序模型
系
统
似不相关模型
方
程
模
联立方程模型
型
泊松模型 负二项分布模型
平稳序列 ARMA 模型
单变量序列
非平稳序列
ARIMA 模型 SARMA 模型
单方程模型
平稳序列 建模方法同截面数据
多变量序列 单位根检验
时
协整(同阶单整)
间
Wald 检验、LM 检验和 LR 检验
幂阶梯变换、Cox 变换 模拟,如 Bootstrap
增大 n+OLS ML GMM 非参数方法 数据变换
逐步回归 岭回归 主成分回归 GMM
估计;WLS GLS GMM White 检验等 非正态
内生性
估计:IV 严重多重共线性
异方差
雅克比检验 Hausman 检验
VIF 检验等
同方差
无自相关 正态分布 外生性
无多重共线性
空间相关(空间计量学)
经典假设 线性模型
PE 检验
非线性模型
估计:OLS 检验:t、F 检验 线性化 非线性最小二乘法
经典回归模型
连续性模型
受限因变量模型
截断模型 删失(归并)模型 Tobit
定量被解释变量
期限模型
单
离散性模型
计数模型
方
截
程
Probit 模型
随机效应模型
面
时间效应模型
板
数
据
PVAR
类似时间序列数据的方法
面板单位根
所有计量经济学检验方法(全)

所有计量经济学检验方法(全)计量经济学所有检验方法一、拟合优度检验 可决系数TSSRSSTSS ESS R -==12 TSS 为总离差平方和,ESS为回归平方和,RSS 为残差平方和该统计量用来测量样本回归线对样本观测值的拟合优度。
该统计量越接近于1,模型的拟合优度越高。
调整的可决系数)1/()1/(12----=n TSS k n RSS R 其中:n-k-1为残差平方和的自由度,n-1为总体平方和的自由度。
将残差平方和与总离差平方和分别除以各自的自由度,以剔除变量个数对拟合优度的影响。
二、方程的显著性检验(F 检验)方程的显著性检验,旨在对模型中被解释变量与解释变量之间的线性关系在总体上是否显著成立作出推断。
原假设与备择假设:H 0:β1=β2=β3=…βk =0 H 1:βj 不全为0 统计量)1/(/--=k n RSS kESS F 服从自由度为(k , n-k-1)的F分布,给定显著性水平α,可得到临界值Fα(k,n-k-1),由样本求出统计量F的数值,通过F>Fα(k,n-k-1)或F≤Fα(k,n-k-1)来拒绝或接受原假设H,以判定原方程总体上的线性关系是否显著成立。
三、变量的显著性检验(t检验)对每个解释变量进行显著性检验,以决定是否作为解释变量被保留在模型中。
原假设与备择假设:H0:βi=0 (i=1,2…k);H1:βi≠0给定显著性水平α,可得到临界值tα/2(n-k-1),由样本求出统计量t的数值,通过|t|> tα/2(n-k-1) 或|t|≤tα/2(n-k-1)来拒绝或接受原假设H0,从而判定对应的解释变量是否应包括在模型中。
四、参数的置信区间参数的置信区间用来考察:在一次抽样中所估计的参数值离参数的真实值有多“近”。
统计量)1(~1ˆˆˆ----'--=k n t k n c S t iiii iiie e βββββ在(1-α)的置信水平下βi 的置信区间是( , ) ββααββi i t s t s ii-⨯+⨯22,其中,t α/2为显著性水平为α、自由度为n-k-1的临界值。
计量模型检验方法(谢第斌)

y x x x
t
1 1t
2 2t
3 3t
t
检验线性约束条件
2
3
是否成立,则约束模型表示为
y x (x x
)
t
1 1t
2 2t
3t
t
如果约束条件成立则无约束估计量
(
)
应该近似为零,定义W统计量
2
3
为: 通常
W ( ) Var( ) ~ N (0,1)
2
3
2
3
Var(
参数,求出残差项,以残差项作为随机项的估计值,再描绘残
差项的散点图并以此判断残差的相关性。
检验步骤——将残差对时间作图
ut
ut
O
t
ut-1
(a)
如a图所示,扰动项的估计值呈循环型,并不频繁地改变符号(一 个正接一个负),而是相继若干个正的以后跟着几个负的,表 明存在正自相关。
二、回归检验法
检验思想 以 e~t 为被解释变量,以各种可能的相关量,诸如以e~t1 、 e~t2 、 e~t2 等为解释变量,建立各种方程:
三格兰杰因果检验三格兰杰因果检验44格兰杰因果检验的讨论格兰杰因果检验的讨论格兰杰因果关系检验的结论只是一种预测是统计意义上格兰杰因果关系检验的结论只是一种预测是统计意义上的的格兰杰格兰杰因果性而不是真正意义上的因果关系不能作因果性而不是真正意义上的因果关系不能作为肯定或否定因果关系的根据
计量模型中的检验方法
变量,做对其他解释变量的回归,称为辅助回归。以 X j 为被解释变量做对
其他解释变量辅助回归的可决系数,用
R2 j
表示,则解释变量
X j 参数估计
计量经济学的三种检验

38
从模型中删除不重要的解释变量
• 对待严重的多重共线性问题,最简单的 解决方法就是删除一个或多个共线性变 量。
– 导致“模型设定误差”,参数估计量可能是 有偏的。 – 建议不要仅仅因为共线性很严重就从一个经 济上可行的模型中删除变量。所选模型是否 符合经济理论是一个重要的问题。
39
获取额外的数据或者新的样本
42
消费支出对于收入和财富的回归方程
• • • •
40个观察值: Y=2.0907+0.7299 X1 +0.0605 X2 t= (0.8713) (6.0014) (2.0641) R2 =0.9672
43
重新考虑模型
• 模型的不恰当设定可能是回归模型存在共 线性的原因。
– 省略一些重要的变量 – 没有正确选择模型的函数形式
计量经济学检验
一、多重共线性 二、异方差 三、自相关
1
一:多重共线性
• • • • •
多重共线性的性质 多重共线性的原因 多重共线性的后果 多重共线性的诊断 多重共线性的补救措施
2
回顾多元线性回归模型的若干假定
• • • • •
零均值假定 同方差假定 无自相关假定 随机项与自变量不相关 非多重共线性
24
例:消费函数
• Y 只对收入回归:
– Y = 24.45 + 0.51X1 (3.81) (14.24) R2= 0.96
– 收入变量是高度显著的,但是在前一个模型中 是不显著的
25
例:消费函数
• Y 只对财富回归:
– Y = 24.41 + 0.05X2 – t (3.55) (13.29) R2 = 0.96
• 假设在过去估计过的对《wideget》需求函 数中,收入系数为0.9,并且是统计显著的。 如果收入系数的过去值没有多少改变的话, 我们可以重新估计方程 • 需求量=b0+b1*价格+b2*收入+u = b0+b1*价格+0.9*收入+u • 需求量- 0.9*收入= b0+b1*价格+u
u检验

u检验、t检验、F检验、X2检验常用显著性检验1.t检验适用于计量资料、正态分布、方差具有齐性的两组间小样本比较。
包括配对资料间、样本与均数间、两样本均数间比较三种,三者的计算公式不能混淆。
2.t'检验应用条件与t检验大致相同,但t′检验用于两组间方差不齐时,t′检验的计算公式实际上是方差不齐时t检验的校正公式。
3.U检验应用条件与t检验基本一致,只是当大样本时用U检验,而小样本时则用t检验,t检验可以代替U检验。
4.方差分析用于正态分布、方差齐性的多组间计量比较。
常见的有单因素分组的多样本均数比较及双因素分组的多个样本均数的比较,方差分析首先是比较各组间总的差异,如总差异有显著性,再进行组间的两两比较,组间比较用q检验或LST检验等。
5.X2检验是计数资料主要的显著性检验方法。
用于两个或多个百分比(率)的比较。
常见以下几种情况:四格表资料、配对资料、多于2行*2列资料及组内分组X2检验。
6.零反应检验用于计数资料。
是当实验组或对照组中出现概率为0或100%时,X2检验的一种特殊形式。
属于直接概率计算法。
7.符号检验、秩和检验和Ridit检验三者均属非参数统计方法,共同特点是简便、快捷、实用。
可用于各种非正态分布的资料、未知分布资料及半定量资料的分析。
其主要缺点是容易丢失数据中包含的信息。
所以凡是正态分布或可通过数据转换成正态分布者尽量不用这些方法。
8.Hotelling检验用于计量资料、正态分布、两组间多项指标的综合差异显著性检验。
计量经济学检验方法讨论计量经济学中的检验方法多种多样,而且在不同的假设前提之下,使用的检验统计量不同,在这里我论述几种比较常见的方法。
在讨论不同的检验之前,我们必须知道为什么要检验,到底检验什么?如果这个问题都不知道,那么我觉得我们很荒谬或者说是很模式化。
检验的含义是要确实因果关系,计量经济学的核心是要说因果关系是怎么样的。
那么如果两个东西之间没有什么因果联系,那么我们寻找的原因就不对。
所有计量经济学检验方法

所有计量经济学检验方法1. OLS回归分析:OLS(Ordinary Least Squares)是一种常用的回归分析方法,它通过最小二乘估计来计算自变量对因变量的影响。
OLS回归分析可用于检验两个或多个变量之间的关系。
2.t检验:t检验用于检验样本均值与总体均值之间的差异是否显著。
在计量经济学中,常常用t检验来检测回归系数的显著性,即判断自变量对因变量的影响是否显著。
3.F检验:F检验用于检验回归模型的整体显著性。
通过F检验可以判断回归模型中自变量的组合对因变量的影响是否显著。
4.残差分析:残差分析用于检验回归模型的拟合优度。
它通过对回归模型的残差进行统计分析,判断残差是否符合正态分布、是否存在异方差等,并据此评估回归模型的合理性。
5.雅克-贝拉检验:雅克-贝拉检验用于检验时间序列数据的自相关性。
自相关性是指时间序列数据中的随机误差项之间存在相关性,为了使回归模型的估计结果有效,需要排除自相关性的影响。
6. ARIMA模型:ARIMA(Autoregressive Integrated Moving Average)模型是一种常用的时间序列分析模型,用于分析和预测时间序列数据。
ARIMA模型可以用于检验时间序列数据的平稳性和趋势。
7. Granger因果检验:Granger因果检验用于检验两个时间序列变量之间的因果关系。
通过检验一个变量的过去值对另一个变量的当前值的预测能力,可以判断两个变量之间是否存在因果关系。
8.卡方检验:卡方检验用于检验两个或多个分类变量之间是否存在显著差异。
在计量经济学中,卡方检验常用于检验变量之间的相关性和拟合优度。
9.随机效应模型和固定效应模型:随机效应模型和固定效应模型是面板数据分析中常用的方法。
它们通过考虑个体特征对经济现象的影响,帮助研究人员解决面板数据中存在的个体特征和时间特征之间的内生性问题。
10.引导变量法:引导变量法用于解决因果关系中的内生性问题。
通过引入其他变量作为工具变量,可以将内生性引起的估计偏误消除或减小。
(完整版)计量经济学简答

1. 模型的检验包括哪几个方面?具体含义是什么?模型的检验主要包括:经济意义检验、统计检验、计量经济学检验、模型的预测检验。
①在经济意义检验中,需要检验模型是否符合经济意义,检验求得的参数估计值的符号、大小、参数之间的关系是否与根据人们的经验和经济理论所拟订的期望值相符合; ②在统计检验中,需要检验模型参数估计值的可靠性,即检验模型的统计学性质,有拟合优度检验、变量显著检验、方程显著性检验等;③在计量经济学检验中,需要检验模型的计量经济学性质,包括随机扰动项的序列相关检验、异方差性检验、解释变量的多重共线性检验等;④模型的预测检验,主要检验模型参数估计量的稳定性以及对样本容量变化时的灵敏度,以确定所建立的模型是否可以用于样本观测值以外的范围。
2. 计量经济学研究的基本步骤是什么?包括四个步骤:理论模型的设定、模型参数的估计、模型的检验、模型的应用。
3. 总体回归函数和样本回归函数之间有哪些区别与联系?样本回归函数是总体回归函数的一个近似。
总体回归函数具有理论上的意义,但其具体的参数不可能真正知道,只能通过样本估计。
样本回归函数就是总体回归函数的参数用其估计值替代之后的形式,即01ˆˆββ,为01ββ,的估计值。
4. 为什么用可决系数2R 评价拟合优度,而不是用残差平方和作为评价标准? 可决系数R 2=ESS/TSS=1-RSS/TSS ,含义为由解释变量引起的被解释变量的变化占被解释变量总变化的比重,用来判定回归直线拟合的优劣,该值越大说明拟合的越好;而残差平方和与样本容量关系密切,当样本容量比较小时,残差平方和的值也比较小,尤其是不同样本得到的残差平方和是不能做比较的。
此外,作为检验统计量的一般应是相对量而不能用绝对量,因而不能使用残差平方和判断模型的拟合优度。
5. 根据最小二乘原理,所估计的模型已经使得拟合误差达到最小,为什么还要讨论模型的拟合优度问题?普通最小二乘法所保证的最好拟合是同一个问题内部的比较,即使用给出的样本数据满足残差的平方和最小;拟合优度检验结果所表示的优劣可以对不同的问题进行比较,即可以辨别不同的样本回归结果谁好谁坏。
(完整版)计量经济学(第四版)习题及参考答案详细版

计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3什么是时间序列和横截面数据? 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4估计量和估计值有何区别?估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2请用例2.2中的数据求北京男生平均身高的99%置信区间NSS x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
计量经济学第八讲

三、多重共线性的检验 (一) 相关系数检验利用相关系数可以分析解释变量之间的两两相关情况。
在EViews 软件中可以直接计算(解释)变量的相关系数矩阵: [命令方式]COR 解释变量名[菜单方式]将所有解释变量设置成一个数组,并在数组窗口中点击View\Correlations. (二) 辅助回归模型检验相关系数只能判断解释变量之间的两两相关情况,当模型的解释变量个数多于两下、并且呈现出较为复杂的相关关系时,可以通过每个解释变量对其他解释变量的辅助回归模型来检验多重共线性,即依次建立k 个辅助回归模型:k i x a x a x a x a a x kki i i i i,,1111111=++++++=++--ε如果,其中某些方程显著,则表明存在多重共线性,所对应的变量可以近似地用其他解释变量线性表示。
辅助回归模型检验不仅能检验多元回归模型的多重共线性,而且可以得到多重共线性的具体形式;如果再结合偏相关关系检验,还能进一步判定是哪些解释变量引起了多重共线性,这有助于分析如何消除多重共线性的影响。
(三) 方差膨胀因子检验对于多元线性回归模型,ib ˆ的方差可以表示成:iijiiijiVIF x x R x x b D ∙∑-=-∑-=22222)(11)()ˆ(σσ其中,i i x R 为2关于其他解释变量辅助回归模型的判定系数,i VIF 为方差膨胀因子。
随着多重共线性程度的增强,VIF 以及系数估计误差都在增大。
因此,可以用VIF 作为衡量多重共线性的一个指标;一般当10>VIF 时,(此时9.02>iR ),认为模型存在较严重的多重共线性。
另一个与VIF 等价的指标是“容许度”(Tolerance ),其定义为:iiiVIF R TOL /1)1(2=-=显然,10≤≤TOL ,当i x 与其他解释变量高度相关时,0→TOL 。
因此,一般当1.0<TOL 时,认为模型存在较严重的多重共线性。
计量经济学课件全完整版

自回归移动平均模型,适用于平 稳和非平稳时间序列的预测,通 过识别、估计和诊断模型参数来 实现预测。
05
面板数据分析方法及应用
面板数据基本概念及特点
面板数据定义
面板数据,也叫时间序列截面数据或混合数 据,是指在时间序列上取多个截面,在这些 截面上同时选取样本观测值所构成的样本数 据。
介绍空间滞后模型(SLM)、空间误差模型(SEM)等空间计量经济模型的建立与估 计方法,包括极大似然估计、广义矩估计等。
贝叶斯计量经济学原理及应用
01
02
贝叶斯统计推断基础
阐述贝叶斯统计推断的基本原理和方法, 包括先验分布、后验分布、贝叶斯因子 等概念。
贝叶斯计量经济模型 的建立与估计
介绍贝叶斯线性回归模型、贝叶斯时间 序列模型等贝叶斯计量经济模型的建立 与估计方法,包括马尔科夫链蒙特卡罗 (MCMC)模拟等。
模型假设
广义线性模型假设响应变量与解释变量之间存在一 种可通过链接函数转化的线性关系,而非线性模型 则不受此限制,可以拟合任意复杂的非线性关系。
模型诊断与检验
对于广义线性模型,常用的诊断方法包括残差分析、 拟合优度检验等;对于非线性模型,由于模型的复 杂性,诊断方法可能更加多样化,包括交叉验证、 可视化分析等。
与其他社会科学的关系 计量经济学也可以应用于其他社会科学领域,如 社会学、政治学等,对社会科学现象进行定量分 析。
计量经济学发展历史及现状
发展历史
计量经济学起源于20世纪初,随着计算机技术的发展和普及,计量经济学得到 了广泛的应用和发展。
现状
目前,计量经济学已经成为经济学领域的重要分支,广泛应用于宏观经济、微 观经济、金融、国际贸易等领域。同时,随着大数据和人工智能技术的发展, 计量经济学面临着新的机遇和挑战。
计量经济学步骤总结

OLS 过程:1 数据收集2 画图(是为了观察是否呈线性~如果不是线性,观察数据的趋势)3 稳定性检验(注意:只在老师给出的数据是时间序列时,采用这一步,横切面数据不用)4 线性化处理(既然确定数据趋势,可以对线性方程t t t u bX a Y ++=左右两边同时Ln, 或者左右两边同时指数化e 变量 或者出去线性要求,可以对左边或右边进行单变换,不需要对称)5 检验自变量的多重共线性:12t x x x 方法:2 种1种: 12t x x x 求两两相关系数(缺陷:只可以确定两两是否相关) 2种: 1122t t t t x a x a x u --=++6 线性方程拟合EVIEWS (注意:若果方程的X 是随机确定的,EIVEWS 拟合时方法选用TSLS 两阶段最小方差法)拟合以后 观察参数 T 值, 和adjusted square注意 排序标准:首先根据经济意义排序其次根据数据的相关性排序虚拟变量问题:如果存在需要,要加虚拟变量,譬如数据中途出现大的转折之类的可能有特殊事件发生。
()11t t t t t Y a a D bX b DX u =++++7 找到残差t u ,观察是否线性相关(对应于OLS 的假设u 是独立的),也就是1122t t t t u a u a u e --=++,检验方法和改正方法不再叙述,老师的给的OLS 模板里面已经有了。
8 找到残差t u ,检验是否存在异方差(对应于假设2var()t u σ=) 检验方法:1散点图判断:大样本情况下,均方差分布的残差分布为矩形。
2 F -检验法步骤:分组;分别进行OLS 回归并计算残差平方和;进行F 检验;23210:σσ=H ;23211:σσ≠H ()()332312311211211131k n ek n e F n t t n t t----=∑∑==σσ ()33111,1~k n k n F ----计算得到的F 与()33111,1k n k n F ----α比较3 回归法:t t t bX a e η++=2t tt bX a e η++=22t t tX b a e η++=12 异方差的修正方法 t t X e 018.0ˆ2=22001.0ˆtt X e =t t X e 5.0001.0ˆ= 选择原则:2R 最大的尽量避免产生多重共线性目标模型:t t t u bX a Y ++=t t t t tt t X u X bX X a X Y ////++= t t t t u X b X a Y ++=*)/1(*t t t t tt t X u X bX X a X Y ////++= *****++=tt t u X b a Y在确认*t u 为均方差的情况下,对新的模型 *****++=tt t u X b a Y 进行参数估计,得到*a 和*b ;注意: OLS 基本是上述步骤,中间可能会有循环,但是为了节省时间,大家表明即可,就像老师在给我们的样本中写的那样~时间序列:1 平稳性检验也就是检验单位根( 千万注意:带有时间趋势t 的单位根检验,千万不要用,那个即使合格只是说明趋势平稳,不是真正的数据平稳,所以只可以选用 带截距和不带截距的单位根检验)2 确定采用AR, MA,或者ARMA 模型检验前,要确定滞后阶数(老师样本里有,不叙述) AR,MA,或者ARMA 怎么实现,HELP 里有Var 模型后面说明3建模4 ARCH 检验( 必然满足arch 模型)5 构建arch 模型 ,比如什么ARCH , GARCH , TGARCH , EGARCH稍稍解释一下TGARCH 模型和EGARCH 模型TGARCH 模型是描述2t σ变化时,加虚拟变量,譬如测定星期一效应,星期五效应的时候应用。
(完整版)所有计量经济学检验方法(全)

计量经济学所有检验方法一、拟合优度检验可决系数TSS RSS TSS ESS R -==12 TSS 为总离差平方和,ESS 为回归平方和,RSS 为残差平方和 该统计量用来测量样本回归线对样本观测值的拟合优度。
该统计量越接近于1,模型的拟合优度越高。
调整的可决系数)1/()1/(12----=n TSS k n RSS R 其中:n-k-1为残差平方和的自由度,n-1为总体平方和的自由度。
将残差平方和与总离差平方和分别除以各自的自由度,以剔除变量个数对拟合优度的影响。
二、方程的显著性检验(F 检验) 方程的显著性检验,旨在对模型中被解释变量与解释变量之间的线性关系在总体上是否显著成立作出推断。
原假设与备择假设:H 0:β1=β2=β3=…βk =0 H 1: βj 不全为0统计量)1/(/--=k n RSS kESS F 服从自由度为(k , n-k-1)的F 分布,给定显著性水平α,可得到临界值F α(k,n-k-1),由样本求出统计量F 的数值,通过F>F α(k,n-k-1)或F ≤F α(k,n-k-1)来拒绝或接受原假设H 0,以判定原方程总体上的线性关系是否显著成立。
三、变量的显著性检验(t 检验)对每个解释变量进行显著性检验,以决定是否作为解释变量被保留在模型中。
原假设与备择假设:H0:βi =0 (i=1,2…k );H1:βi ≠0给定显著性水平α,可得到临界值t α/2(n-k-1),由样本求出统计量t 的数值,通过 |t|> t α/2(n-k-1) 或 |t|≤t α/2(n-k-1)来拒绝或接受原假设H0,从而判定对应的解释变量是否应包括在模型中。
四、参数的置信区间参数的置信区间用来考察:在一次抽样中所估计的参数值离参数的真实值有多“近”。
统计量)1(~1ˆˆˆ----'--=k n t k n c S t iiii ii ie e βββββ在(1-α)的置信水平下βi 的置信区间是( , ) ββααββi i t s t s ii-⨯+⨯22,其中,t α/2为显著性水平为α、自由度为n-k-1的临界值。
计量经济学试验完整版--李子奈

计量经济学试验完整版--李子奈计量经济学试验??李子奈目录实验一一元线性回归5一实验目的 5二实验要求 5三实验原理 5四预备知识 5五实验内容 5六实验步骤 51.建立工作文件并录入数据 52.数据的描述性统计和图形统计: 73.设定模型,用最小二乘法估计参数: 84.模型检验: 85.应用:回归预测: 9实验二可化为线性的非线性回归模型估计、受约束回归检验及参数稳定性检验12一实验目的: 12二实验要求12三实验原理12四预备知识12五实验内容12六实验步骤13实验三多元线性回归14一实验目的14三实验原理15四预备知识15五实验内容15六实验步骤156.1 建立工作文件并录入全部数据 15 6.2 建立二元线性回归模型156.3 结果的分析与检验166.4 参数的置信区间166.5 回归预测176.6 置信区间的预测18实验四异方差性20一实验目的20二实验要求20三实验原理20四预备知识20五实验内容20六实验步骤206.1 建立对象: 206.2 用普通最小二乘法建立线性模型216.3 检验模型的异方差性216.4 异方差性的修正24实验五自相关性28一实验目地28二实验要求28三实验原理28四预备知识28五实验内容28六实验步骤286.1 建立Workfile和对象 296.2 参数估计、检验模型的自相关性296.3 使用广义最小二乘法估计模型 336.4 采用差分形式作为新数据,估计模型并检验相关性35 实验六多元线性回归和多重共线性37一实验目的37二实验要求37三实验原理37四预备知识37五实验内容37六实验步骤376.1 建立工作文件并录入数据386.2 用OLS估计模型386.3 多重共线性模型的识别386.4 多重共线性模型的修正39实验七分布滞后模型与自回归模型及格兰杰因果关系检验 41 一实验目的41二实验要求41三实验原理41四预备知识41五实验内容41六实验步骤426.1 建立工作文件并录入数据426.2 使用4期滞后2次多项式估计模型426.3 格兰杰因果关系检验45实验八联立方程计量经济学模型49一实验目的49二实验要求49三实验原理49四预备知识49五实验内容49六实验步骤506.1 分析联立方程模型。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计量经济学所有检验方法一、拟合优度检验可决系数TSS RSS TSS ESS R -==12 TSS 为总离差平方和,ESS 为回归平方和,RSS 为残差平方和 该统计量用来测量样本回归线对样本观测值的拟合优度。
该统计量越接近于1,模型的拟合优度越高。
调整的可决系数)1/()1/(12----=n TSS k n RSS R 其中:n-k-1为残差平方和的自由度,n-1为总体平方和的自由度。
将残差平方和与总离差平方和分别除以各自的自由度,以剔除变量个数对拟合优度的影响。
二、方程的显著性检验(F 检验) 方程的显著性检验,旨在对模型中被解释变量与解释变量之间的线性关系在总体上是否显著成立作出推断。
原假设与备择假设:H 0:β1=β2=β3=…βk =0 H 1: βj 不全为0统计量)1/(/--=k n RSS kESS F 服从自由度为(k , n-k-1)的F 分布,给定显著性水平α,可得到临界值F α(k,n-k-1),由样本求出统计量F 的数值,通过F>F α(k,n-k-1)或F ≤F α(k,n-k-1)来拒绝或接受原假设H 0,以判定原方程总体上的线性关系是否显著成立。
三、变量的显著性检验(t 检验)对每个解释变量进行显著性检验,以决定是否作为解释变量被保留在模型中。
原假设与备择假设:H0:βi =0 (i=1,2…k );H1:βi ≠0给定显著性水平α,可得到临界值t α/2(n-k-1),由样本求出统计量t 的数值,通过 |t|> t α/2(n-k-1) 或 |t|≤t α/2(n-k-1)来拒绝或接受原假设H0,从而判定对应的解释变量是否应包括在模型中。
四、参数的置信区间参数的置信区间用来考察:在一次抽样中所估计的参数值离参数的真实值有多“近”。
统计量)1(~1ˆˆˆ----'--=k n t k n c S t iiii ii ie e βββββ在(1-α)的置信水平下βi 的置信区间是( , ) ββααββi i t s t s ii-⨯+⨯22,其中,t α/2为显著性水平为α、自由度为n-k-1的临界值。
五、异方差检验1. 帕克(Park)检验与戈里瑟(Gleiser)检验 试建立方程:iji i X f e ε+=)(~2 或iji i X f e ε+=)(|~|选择关于变量X的不同的函数形式,对方程进行估计并进行显著性检验,如果存在某一种函数形式,使得方程显著成立,则说明原模型存在异方差性。
如:帕克检验常用的函数形式:ieXXfjijiεασ2)(=或ijiiXeεασ++=lnln)~ln(22若α在统计上是显著的,表明存在异方差性。
Glejser检验类似于帕克检验。
Glejser建议:在从OLS回归取得误差项后,使用e i的绝对值与被认为密切相关的解释变量再做LS估计,并使用如右的多种函数形式。
若解释变量的系数显著,就认为存在异方差。
如下函数形式:2. 戈德菲尔德-匡特(Goldfeld-Quandt)检验G-Q检验以F检验为基础,适用于样本容量较大、异方差递增或递减的情况。
G-Q检验的步骤:①将n对样本观察值(Xi,Yi)按观察值Xi的大小排队②将序列中间的c=n/4个观察值除去,并将剩下的观察值划分为较小与较大的相同的两个子样本,每个子样样本容量均为(n-c)/2③对每个子样分别进行OLS回归,并计算各自的残差平方和④在同方差性假定下,构造如下满足F分布的统计量)12,12(~)12(~)12(~2122------------=∑∑kcnkcnFkcnekcneFii⑤给定显著性水平α,确定临界值Fα(v1,v2),若F> Fα(v1,v2),则拒绝同方差性假设,表明存在异方差。
3、怀特(White)检验怀特检验不需要排序,且适合任何形式的异方差iiiiXXYμβββ+++=2211做如下辅助回归iiiiiiiiXXXXXXeεαααααα++++++=21522421322112~在同方差假设下R2为辅助方程的可决系数,h为辅助方程解释变量的个数。
iiiiiiiiiiiiiiiXbbeXbbeXbbeXbbeXbbeμμμμμ++=++=++=++=++=2111111六、序列相关检验 1. 回归检验法以t e ~为被解释变量,以各种可能的相关量,诸如以1~-t e 、2~-t e 、2~t e 等为解释变量,建立各种方程:tt t e e ερ+=-1~~tt t t e e e ερρ++=--2211~~~ …如果存在某一种函数形式,使得方程显著成立,则说明原模型存在序列相关性。
2. 杜宾-瓦森(Durbin-Watson )检验法杜宾和瓦森针对原假设:H 0: ρ=0,即不存在一阶自回归,构如下造统计量:∑∑==--=nt tnt t tee eW D 12221~)~~(..(1)计算DW 值(2)给定α,由n 和k 的大小查DW 分布表,得临界值dL 和dU (3)比较、判断若 0<D.W.<dL 存在正自相关 dL<D.W.<dU 不能确定 dU <D.W.<4-dU 无自相关 4-dU <D.W.<4- dL 不能确定 4-dL <D.W.<4 存在负自相关 当D.W.值在2左右时,模型不存在一阶自相关。
3. 拉格朗日乘数(Lagrange multiplier )检验 拉格朗日乘数检验克服了DW 检验的缺陷,适合于高阶序列相关以及模型中存在滞后被解释变量的情形。
对于模型iki k i i i X X X Y μββββ+++++= 22110如果怀疑随机扰动项存在p 阶序列相关:tp t p t t t εμρμρμρμ+++=--- 2211 GB 检验可用来检验如下受约束回归方程tp t p t kt k t t X X Y εμρμρβββ+++++++=-- 11110约束条件为: H 0: ρ1=ρ2=…=ρp =0约束条件H0为真时,大样本下 其中,n 、R2为如下辅助回归的样本容量和可决系数给定α,查临界值χα2(p),与LM 值比较,做出判断,实际检验中,可从1阶、2阶、…逐次向更高阶检验。
)(~22p nR LM χ=tp t p t kt k t t e e X X e ερρβββ+++++++=--~~~11110七、多重共线性检验 1.综合统计检验法当模型的拟合优度(R 2)很高,F 值很高,而每个回归参数估计值的方差Var(βj ) 又非常大(即t 值很低)时,说明解释变量间可能存在多重共线性。
2.简单相关系数法求出任意两个解释变量的简单相关系数,若接近于1,则说明两变量存在较强的多重共线性。
3.判定系数检验法统计量F j =R j 2/(k-1)/(1-R j 2)/(n-k)服从自由度为(k-1 , n-k)的F 分布,原假设为X j 与其他解释变量间不存在显著的线性关系,给定显著性水平α,通过计算的F 值与相应的临界值的比较来判断。
4.逐步回归法以Y 为被解释变量,逐个引入解释变量,构成回归模型,进行估计。
如果拟合优度变化显著,则说明新引入的变量是一个独立解释变量;如果拟合优度变化很不显著,则说明新引入的变量不是一个独立解释变量,即它与其他变量之间存在共线性的关系。
八、格兰杰因果关系检验对两变量Y 与X ,格兰杰因果关系检验要求估计:ti t mi i m i i t i t Y X Y 111μβα++=-==-∑∑ (1)ti t mi i m i i t i t X Y X 211μδλ++=-==-∑∑ (2)可能存在有四种检验结果:(1)X 对Y 有单向影响,表现为(*)式X 各滞后项前的参数整体不为零,而(**) Y 各滞后项前的参数整体为零;(2)Y 对X 有单向影响,表现为(**)式Y 各滞后项前的参数整体不为零,而(*)X 各滞后项前的参数整体为零;(3)Y 与X 间存在双向影响,表现为Y 与X 各滞后项前的参数整体不为零; (4)Y 与X 间不存在影响,表现为Y 与X 各滞后项前的参数整体为零。
格兰杰检验是通过受约束的F 检验完成的。
如:针对ti t mi i m i i t i t Y X Y 111μβα++=-==-∑∑中X 滞后项前的参数整体为零的假设(X 不是Y 的格兰杰原因) 分别做包含与不包含X 滞后项的回归,记前者与后者的残差平方和分别为RSSU 、RSSR ;再计算F 统计量:)/(/)(k n RSS mRSS RSS F U U R --=k 为无约束回归模型的待估参数的个数如果: F>F α(m,n-k) ,则拒绝原假设,认为X 是Y 的格兰杰原因。
九、时间序列平稳性检验 1.DF 检验随机游走序列 X t =X t-1+μt 是非平稳的,其中μt 是白噪声。
而该序列可看成是随机模型X t =ρX t-1+μt 中参数ρ= 1时的情形。
也就是说,我们对式 X t =ρX t-1+μt (1) 做回归,如果确实发现ρ=1,就说随机变量X t 有一个单位根。
可变形式成差分形式:X t =(ρ-1)X t-1+μ t =δX t-1+ μt (2) 检验(1)式是否存在单位根ρ=1,也可通过(2)式判断是否有 δ=0。
检验一个时间序列Xt 的平稳性,可通过检验带有截距项的一阶自回归模型 X t =α+ ρX t-1 +μt (*)中的参数ρ是否小于1。
或者:检验其等价变形式Xt=α+ δX t-1+μt (**)中的参数δ是否小于0 。
零假设 H 0:δ= 0;备择假设 H 1:δ< 0 可通过OLS 法估计Xt=α+ δX t-1+μt 并计算t 统计量的值,与DF 分布表中给定显著性水平下的临界值比较:如果:t < 临界值,则拒绝零假设H0:δ= 0 ,认为时间序列不存在单位根,是平稳的。
2.ADF 检验 在DF 检验中,实际上是假定了时间序列是由具有白噪声随机误差项的一阶自回归过程AR(1)生成的。
但在实际检验中,时间序列可能由更高阶的自回归过程生成的,或者随机误差项并非是白噪声,为了保证DF 检验中随机误差项的白噪声特性,Dicky 和Fuller 对DF 检验进行了扩充,形成了ADF (Augment Dickey-Fuller )检验。
ADF 检验是通过下面三个模型完成的:模型1: t mi it i t t XX X εβδ+∆+=∆∑=--11 (*)模型2: t mi it i t t XX X εβδα+∆++=∆∑=--11 (**)模型3: t mi it it t XX t X εβδβα+∆+++=∆∑=--11 (***)模型3 中的t 是时间变量,代表了时间序列随时间变化的某种趋势(如果有的话)。
