平行四边形基础练习(全章)
上海曲阳第二中学八年级数学下册第十八章《平行四边形》基础练习(答案解析)

一、选择题1.如图,在平行四边形ABCD 中,DE 平分,6,2ADC AD BE ∠==,则平行四边形ABCD 的周长是( )A .16B .18C .20D .242.如图,在等腰直角ABC 中,AB BC =,点D 是ABC 内部一点, DE BC ⊥,DF AB ⊥,垂足分别为E ,F ,若3CE DE =, 53DF AF =, 2.5DE =,则AF =( )A .8B .10C .12.5D .15 3.已知正方形ABCD 中,对角线4AC =,这个正方形的面积是( ) A .8 B .16 C .82 D .162 4.如图,将菱形纸片ABCD 折叠,使点A 恰好落在菱形的对称中心O 处,折痕为EF .若菱形ABCD 的边长为4,120B ∠=︒,则EF 的值是( )A .3B .2C .23D .45.如图,在ABC 中,点D 在边BC 上,过点D 作//DE AC ,//DF AB ,分别交AB ,AC 于E ,F 两点.则下列命题是假命题的是( )A .四边形AEDF 是平行四边形B .若90BC ∠+∠=︒,则四边形AEDF 是矩形C .若BD CD =,则四边形AEDF 是菱形D .若AD BD =,则四边形AEDF 是矩形6.已知四边形ABCD 是平行四边形,下列结论中不正确的是( )A .当AB BC =时,四边形ABCD 是菱形B .当AC BD ⊥时,四边形ABCD 是菱形C .当90ABC ∠=时,四边形ABCD 是矩形D .当AC BD =时,四边形ABCD 是正方形7.下列条件中不能判定一定是平行四边形的有( )A .一组对角相等,一组邻角互补B .一组对边平行,另一组对边相等C .两组对边相等D .一组对边平行,且另一组对边也平行8.如果平行四边形ABCD 的对角线相交于点O ,那么在下列条件中,能判断平行四边形ABCD 为菱形的是( )A .OAB OBA ∠=∠;B .OAB OBC ∠=∠; C .OAB OCD ∠=∠;D .OAB OAD ∠=∠. 9.四边形ABCD 中,对角线AC BD 、交于点O .给出下列四组条件:①AB ∥CD ,AD ∥BC ;②AB CD =,AD BC =;③AO CO =,BO DO =;④AB ∥CD ,AD BC =. 其中一定能判定这个四边形是平行四边形的条件共有( )A .1组;B .2组;C .3组;D .4组. 10.如图,己知四边形ABCD 是平行四边形,下列说法正确..的是( )A .若AB AD =,则平行四边形ABCD 是矩形B .若AB AD =,则平行四边形ABCD 是正方形C .若AB BC ⊥,则平行四边形ABCD 是矩形D .若AC BD ⊥,则平行四边形ABCD 是正方形11.如图,以平行四边形ABCD 的边AB 、BC 、CD 、DA 为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E 、F 、G 、H ,顺次连结这四个点,得四边形EFGH ,当()090ADC αα∠=︒<<︒时,有以下结论:①180GCF α∠=︒-;②90HAE α∠=︒+;③HE HG =;④ EH GH ⊥;⑤四边形EFGH 是平行四边形.则结论正确的是( )A .①③④B .②③⑤C .①③④⑤D .②③④⑤ 12.如图,在平行四边形ABCD 中,DE 平分∠ADC ,AD =6,BE =2,则平行四边形ABCD的周长是( )A .60B .30C .20D .16 13.如图,直线L 上有三个正方形,,a b c ,若,a c 的边长分别为1和3,则b 的面积为( )A .8B .9C .10D .11 14.如图,将矩形ABCD 折叠,使点C 和点A 重合,折痕为EF .若5AF =,3BE =,则EF 的长为( )A .23B .17C .25D .3515.如图,已知平行四边形ABCD 中,4B A ∠=∠,则C ∠=( )A .18°B .36°C .72°D .144°二、填空题16.如图,四边形ABCD 为菱形,以AD 为斜边的Rt AED △的面积为3,2DE =,点E ,C 在BD 的同侧,点P 是BD 上的一动点,则PE PC +的最小值是_____________.17.如图,在平行四边形ABCD 中,10,AB BAD =∠的平分线与BC 的延长线交于点E 、与DC 交于点F ,且点F 为边DC 的中点,ADC ∠的平分线交AB 于点M ,交AE 于点N ,连接DE .若6DM =,则DE 的长为_______.18.如图,在平行四边形ABCD 中,2AD CD =,F 是AD 的中点,CE AB ⊥,垂足E 在线段AB 上.下列结论①DCF ECF ∠=∠;②EF CF =;③3DFE AEF ∠=∠;④2BEC CEF S S <中,一定成立的是_________.(请填序号)19.如图,在矩形ABCD 中,连接AC ,按以下步骤作图:分别以点A ,C 为圆心,以大于12AC 的长为半径作弧,两弧分别相交于点M ,N ,作直线MN 交BC 于点E ,连接AE .若AB =1,BC =2,则BE =_____.20.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理,如图所示的图形就用了这种分割方法若5AE =,正方形ODCE 的边长为1,则BD 等于___________.21.如图,在四边形ABCD 中,AC a =,BD b =,且AC BD ⊥顺次连接四边形ABCD 各边的中点,得到四边形1111D C B A ,再顺次连接四边形1111D C B A 各边中点,得到四边形2222A B C D …如此进行下去,得到四边形n n n n A B C D ,下列结论正确的有__________.①四边形2222A B C D 是矩形;②四边形4444A B C D 是菱形;③四边形5555A B C D 的周长是4a b +.22.如图,在ABC ∆中,点,D E 分别在边,AB AC 上,且BD CE =,连接,CD DE ,点,,M N P 分别是,,DE BC CD 的中点,34PMN ∠=,则MPN ∠的度数是_______.23.如图,正方形ABCD 中,5AD =,点E 、F 是正方形ABCD 内的两点,且4AE FC ==,3BE DF ==,则EF 的平方为________.24.如图,在ABCD 中,AC 与BD 相交于点O ,(1)若18cm,24cm AC BD ==,则AO =_______,BO =_______.又若13AB =厘米,则COD △的周长为________.(2)若AOB 的周长为30cm ,12cm AB =,则对角线AC 与BD 的和是________. 25.如图,B ,E ,F ,D 四点在一条直线上,菱形ABCD 的面积为2120cm ,正方形AECF 的面积为250cm ,则菱形的边长为___cm .26.如图,在Rt △ABC 中,∠ACB =90°,D 是斜边AB 中点,若∠B =30°,AC =2,则CD =_____.三、解答题27.如图,平行四边形ABCD 中,,AP BP 分别平分DAB ∠和CBA ∠,交于DC 边上点P , 2.5AD =.(1)求线段AB 的长.(2)若3BP =,求ABP △的面积.28.已知:AB ⊥CD 于点O ,AB=AC=CD ,点I 是∠BAC ,∠ACD 的平分线的交点,连接IB ,ID(1)求证:IA ID =且IA ID ⊥;(2)填空:①∠AIC+∠BID=_________度;②S IBD ∆______S AIC ∆(填“﹥”“﹤”“=”)(3)将(2)小题中的第②结论加以证明.29.如图,在△ABC 中,AB =AC ,DE 垂直平分AC ,CE ⊥AB ,AF ⊥BC , (1)求证:CF =EF ;(2)求∠EFB 的度数.30.如图,点E 在正方形ABCD 的边AB 上,点F 在边BC 的延长线上,且90EDF ∠=︒.求证:DE DF =.。
平行四边形练习题(含答案)

第十八章平行四边形18.1 平行四边形1.在ABCD中,对角线AC,BD相交于点O,若△AOB的面积为3,则ABCD的面积为A.6 B.9 C.12 D.182.若平行四边形中两个内角的度数比为1∶2,则其中较小的内角是A.90°B.60°C.120°D.45°3.如果四边形ABCD是平行四边形,AB=6,且AB的长是四边形ABCD周长的316,那么BC的长是A.6 B.8 C.10 D.164.如图,在四边形ABCD中,∠DAC=∠ACB,要使四边形ABCD成为平行四边形,则应增加的条件不能是A.AD=BC B.OA=OCC.AB=CD D.∠ABC+∠BCD=180°5.如图,AB∥CD,AD不平行于BC,AC与BD相交于点O,写出三对面积相等的三角形是__________.6.如图,A、B两处被池塘隔开,为了测量A、B两处的距离,在AB外选一适当的点C,连接AC、BC,并分别取线段AC、BC的中点E、F,测得EF=22 m,则AB=__________m.7.如图,在△ABC中,AD⊥BC于点D,E,F,G分别是BC,AC,AB的中点.若AB=23BC=3DE=12,DG=12AB,求四边形DEFG的周长.8.如图,在△ABC中,∠BAC=90°,∠B=45°,BC=10,过点A作AD∥BC,且点D在点A的右侧.点P 从点A出发沿射线AD方向以每秒1个单位长度的速度运动,同时点Q从点C出发沿射线CB方向以每秒2个单位长度的速度运动,在线段QC上取点E,使得QE=2,连接PE,设点P的运动时间为t秒.(1)若PE⊥BC,求BQ的长;(2)请问是否存在t的值,使以A,B,E,P为顶点的四边形为平行四边形?若存在,求出t的值;若不存在,请说明理由.9.已知ABCD的对角线AC,BD的长分别为10,6,则AB长的范围是A.AB>2 B.AB<8 C.2<AB<8 D.2≤AB≤810.平行四边形ABCD与等边三角形AEF按如图所示的方式摆放,如果∠B=45°,则∠BAE的大小是A.75°B.80°C.100°D.120°11.如图,已知四边形ABCD中,AD∥BC,∠A=∠BCD=∠ABD,DE平分∠ADB,下列说法:①AB∥CD;②ED⊥CD;③∠DFC=∠ADC–∠DCE;④S△EDF=S△BCF,其中正确的结论是A.①②③B.①②④C.①③④D.①②③④12.如图,点A,B为定点,定直线l∥AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PMN的面积;③△PAB的周长;④∠APB的大小;⑤直线MN,AB之间的距离.其中会随点P的移动而不改变的是A.①②③B.①②⑤C.②③④D.②④⑤13.如图,在△ABC中,∠ACB=90°,AC=3,BC=4,点D是边AB的中点,将△ABC沿着AB平移到△DEF 处,那么四边形ACFB的面积等于__________.14.如图,DE 是ABC △的中位线,M 是DE 的中点,CM 的延长线交AB 于点N ,:DMN CEM S S △△等于_________.15.如图,在ABCD 中,对角线AC ,BD 相交于点O ,OA =5cm ,E ,F 为直线BD 上的两个动点(点E ,F 始终在ABCD 的外面),且DE =12OD ,BF =12OB ,连接AE ,CE ,CF ,AF . (1)求证:四边形AFCE 为平行四边形. (2)若DE =13OD ,BF =13OB ,上述结论还成立吗?由此你能得出什么结论? (3)若CA 平分∠BCD ,∠AEC =60°,求四边形AECF 的周长.16.(2018·贵州黔东南、黔南、黔西南)如图在ABCD 中,已知AC =4 cm ,若△ACD 的周长为13 cm ,则ABCD 的周长为A .26 cmB .24 cmC .20 cmD .18 cm17.(2018·甘肃兰州)如图,将ABCD 沿对角线BD 折叠,使点A 落在点E 处,交BC 于点F ,若48ABD ∠=︒,40CFD ∠=︒,则E ∠为A .102︒B .112︒C .122︒D .92︒18.(2018·黑龙江绥化)下列选项中,不能判定四边形ABCD 是平行四边形的是A .AD BC ∥,AB CD ∥ B .AB CD ∥,AB CD =C .AD BC ∥,AB DC =D .AB DC =,AD BC =19.(2018·内蒙古呼和浩特)顺次连接平面上A 、B 、C 、D 四点得到一个四边形,从①AB ∥CD ②BC =AD③∠A =∠C ④∠B =∠D 四个条件中任取其中两个,可以得出“四边形ABCD 是平行四边形”这一结论的情况共有 A .5种B .4种C .3种D .1种20.(2018·广西玉林)在四边形ABCD 中:①AB ∥CD ;②AD ∥BC ;③AB =CD ;④AD =BC ,从以上选择两个条件使四边形ABCD 为平行四边形的选法共有 A .3种B .4种C .5种D .6种21.(2018·四川德阳)如图,四边形AOEF 是平行四边形,点B 为OE 的中点,延长FO 至点C ,使3FO OC =,连接AB 、AC 、BC ,则在ABC ∆中::ABO AOC BOC S S S △△△A .621∶∶B .321∶∶C .632∶∶D .432∶∶ 22.(2018·安徽)ABCD 中,E 、F 是对角线BD 上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是 A .BE =DF B .AE =CF C .AF ∥CED .∠BAE =∠DCF23.(2018·广西梧州)如图,已知在△ABC 中,D 、E 分别是AB 、AC 的中点,BC =6 cm ,则DE 的长度是__________cm .24.(2018·湖北十堰)如图,已知ABCD 的对角线AC ,BD 交于点O ,且AC =8,BD =10,AB =5,则△OCD的周长为__________.25.(2018·江苏泰州)如图,ABCD 中,AC 、BD 相交于点O ,若AD =6,AC +BD =16,则△BOC 的周长为__________.26.(2018·辽宁抚顺)如图,ABCD 中,AB =7,BC =3,连接AC ,分别以点A 和点C 为圆心,大于12AC 的长为半径作弧,两弧相交于点M ,N ,作直线MN ,交CD 于点E ,连接AE ,则△AED 的周长是__________.27.(2018·山东淄博)在如图所示的平行四边形ABCD中,AB=2,AD=3,将△ACD沿对角线AC折叠,点D落在△ABC所在平面内的点E处,且AE过BC的中点O,则△ADE的周长等于__________.28.(2018·福建)如图,ABCD的对角线AC,BD相交于点O,EF过点O且与AD,BC分别相交于点E,F.求证:OE=OF.29.(2018·广西梧州)如图,在ABCD中,对角线AC,BD相交于点O,过点O的一条直线分别交AD,BC于点E,F.求证:AE=CF.30.(2018·辽宁大连)如图,ABCD的对角线AC,BD相交于点O,点E、F在AC上,且AF=CE.求证:BE =DF .31.(2018·湖北孝感)如图,B ,E ,C ,F 在一条直线上,已知AB DE ∥,AC DF ∥,BE CF ,连接AD .求证:四边形ABED 是平行四边形.32.(2018·江苏无锡)如图,平行四边形ABCD 中,E 、F 分别是边BC 、AD 的中点,求证:∠ABF =∠CDE .33.(2018·湖北恩施州)如图,点B 、F 、C 、E 在一条直线上,FB =CE ,AB ∥ED ,AC ∥FD ,AD 交BE于O .求证:AD 与BE 互相平分.34.(2018·浙江衢州)如图,在ABCD中,AC是对角线,BE⊥AC,DF⊥AC,垂足分别为点E,F,求证:AE=CF.35.(2018·江苏宿迁)如图,在ABCD中,点E、F分别在边CB、AD的延长线上,且BE=DF,EF分别与AB、CD交于点G、H,求证:AG=CH.36.(2018·青海)如图,在平行四边形ABCD中,E为AB边上的中点,连接DE并延长,交CB的延长线于点F.;(1)求证:AD BF(2)若平行四边形ABCD的面积为32,试求四边形EBCD的面积.37.(2018·云南曲靖)如图:在平行四边形ABCD的边AB,CD上截取AF,CE,使得AF=CE,连接EF,点M,N是线段EF上两点,且EM=FN,连接AN,CM.(1)求证:△AFN≌△CEM;(2)若∠CMF=107°,∠CEM=72°,求∠NAF的度数.38.(2018·黑龙江大庆)如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.(1)证明:四边形CDEF是平行四边形;(2)若四边形CDEF的周长是25 cm,AC的长为5 cm,求线段AB的长度.1.【答案】C【解析】∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∴S△AOD=S△COD=S△BOC=S△AOB.∵△AOB的面积为3,∴ABCD的面积为4×3=12.故选C.2.【答案】B【解析】如图所示:∵四边形ABCD是平行四边形,∴AB∥CD,∴∠B+∠C=180°,∵∠B∶∠C=1∶2,∴∠B=13×180°=60°,故选B.3.【答案】C【解析】∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∵AB=6,且AB的长是四边形ABCD周长的316,∴四边形ABCD周长为:6÷316=32,∴AB+BC=12×32=16,∴BC=10.故选C.5.【答案】△ADC和△BDC;△ADO和△BCO;△DAB和△CAB【解析】根据AB∥CD可得:△ABC和△ABD的面积相等,△ACD和△BCD的面积相等,则△ACD的面积减去△OCD的面积等于△BCD的面积减去△OCD的面积,即△AOD和△BOC的面积相等.【解析】∵E、F是AC,CB的中点,∴EF是△ABC的中位线,∴EF=12AB,∵EF=22m,∴AB=44m,故答案为44.7.【解析】∵AB=23BC=3DE=12,∴BC=18,DE=4,∴DG=12AB=6,∵E,F,G分别是BC,AC,AB的中点,∴FG=12BC=9,EF=12AB=6,∴四边形DEFG的周长为4+6+9+6=25.8.【解析】(1)作AM⊥BC于M,如图所示:∵∠BAC=90°,∠B=45°,∴∠C=45°=∠B,∴AB=AC,∴BM=CM,∴AM=12BC=5,∵AD∥BC,∴∠PAN=∠C=45°,∵PE⊥BC,∴PE=AM=5,PE⊥AD,∴△APN和△CEN是等腰直角三角形,∴PN=AP=t,CE=NE=5–t,∵CE=CQ–QE=2t–2,∴5–t=2t–2,解得:t=73,BQ=BC–CQ=10–2×71633;(2)存在,t=4;理由如下:若以A,B,E,P为顶点的四边形为平行四边形,则AP=BE,∴t=10–2t+2,解得:t=4,∴存在t的值,使以A,B,E,P为顶点的四边形为平行四边形,t=4.【解析】如图,在平行四边形ABCD中,AO=CO=5,BO=DO=3,∴2<AB<8.故选C.10.【答案】A【解析】∵四边形ABCD是平行四边形,∴AD∥BC,∴∠BAD=180°–∠B=180°–45°=135°,∵△AEF是等边三角形,∴∠EAF=60°,∴∠BAE=∠BAD–∠EAF=75°.故选A.11.【答案】D【解析】∵AD∥BC,∴∠A+∠ABC=180°,∠ADC+∠BCD=180°,∵∠A=∠BCD,∴∠ABC=∠ADC,∵∠A=∠BCD,∴四边形ABCD是平行四边形,∴AB∥CD.∴①正确;∵∠A=∠ABD,DE平分∠ADB,∴DE⊥AB,∴DE⊥CD,∴②正确;∵∠A=∠ABD,四边形ABCD是平行四边形,∴AD=BD=BC,∴∠BDC=∠BCD,∵AD∥BC,∴∠ADB=∠DBC,∵∠ADC=∠ADB+∠BDC,∴∠ADC=∠DBC+∠BCD,∴∠ADC–∠DCE=∠DBC+ ∠BCD–∠DCE=∠DBC+∠BCF,∵∠DFC=∠DBC+BCF,∴∠DFC=∠ADC–∠DCE;∴③正确;∵AB∥CD,∴△BED的边BE上的高和△EBC的边BE上的高相等,∴由三角形面积公式得:S△BED= S△EBC,都减去△EFB的面积得:S△EDF=S△BCF,∴④正确;综上得①②③④都正确,故选D.12.【答案】B【解析】∵点A,B为定点,点M,N分别为PA,PB的中点,∴MN是△PAB的中位线,∴MN=12 AB,即线段MN的长度不变,故①正确;∵MN的长度不变,点P到MN的距离等于l与AB的距离的一半,∴△PMN的面积不变,故②正确;PA、PB的长度随点P的移动而变化,所以,△PAB的周长会随点P的移动而变化,故③错误;∠APB的大小点P的移动而变化,故④错误.直线MN,AB之间的距离不随点P的移动而变化,故⑤正确;综上所述,随点P的移动而不变化的是①②⑤.故选B.13.【答案】9【解析】∵将△ABC沿AB方向向右平移到△DEF,∴四边形ADFC是平行四边形,四边形ACFB是是梯形.∵∠ACB =90°,AC =3,BC =4,∴22345AB =+=.∵点D 是边AB 的中点,∴AD =BD =15522⨯=,∴CF =AD =12AB 52=, 设AB 边上的高为x .∵AB =5,AC =3,BC =4,AB 边上的高为x ,∴12AC ·BC =12AB ·x ,∴125x =.∴S 梯形ACFB =1512(5)9225⨯+⨯=. 14.【答案】1∶3【解析】如图,作EF AD ∥,M 是DE 的中点,则△DMN ≌△EMF ,得MN =MF ,E 是AC 的中点,则FC =NF ,所以13MF MC =,得13FEM CEMS S =△△,得:DMN CEM S S △△=1∶3.16.【答案】D【解析】∵AC =4 cm ,若△ADC 的周长为13 cm ,∴AD +DC =13-4=9(cm ).又∵四边形ABCD 是平行四边形,∴AB =CD ,AD =BC ,∴平行四边形的周长为2(AB +BC )=18 cm .故选D . 17.【答案】B【解析】∵AD BC ∥,∴ADB DBC ∠=∠,由折叠可得ADB BDF ∠=∠,∴DBC BDF ∠=∠,又∵40DFC ∠=︒,∴20DBC BDF ADB ∠=∠=∠=︒,又∵48ABD ∠=︒,∴ABD △中,1802048112A ︒︒-︒∠=-=︒,∴112E A ∠∠==︒,故选B .18.【答案】C【解析】A 、由AD BC ∥,AB CD ∥可以判断四边形ABCD 是平行四边形,故本选项不符合题意; B 、由AB CD ∥,AB CD =可以判断四边形ABCD 是平行四边形,故本选项不符合题意; C 、由AD BC ∥,AB DC =不能判断四边形ABCD 是平行四边形,故本选项符合题意;D 、由AB DC =,AD BC =可以判断四边形ABCD 是平行四边形,故本选项不符合题意,故选C . 19.【答案】C【解析】当①③时,四边形ABCD 为平行四边形;当①④时,四边形ABCD 为平行四边形;当③④时,四边形ABCD 为平行四边形,故选C . 20.【答案】B【解析】(1)①②,利用两组对边平行的四边形是平行四边形判定; (2)③④,利用两组对边相等的四边形是平行四边形判定;(3)①③或②④,利用一组对边平行且相等的四边形是平行四边形判定,共4种组合方法,故选B . 21.【答案】B【解析】如图,连接BF .设平行四边形AFEO 的面积为4m .∵FO :OC =3:1,BE =OB ,AF ∥OE ,∴S △OBF =S △AOB =m ,S △OBC =13m ,S △AOC =23m ,∴S △AOB ∶S △AOC ∶S △BOC =m ∶23m ∶13m =3∶2∶1,故选B . 22.【答案】B【解析】A 、如图,∵四边形ABCD 是平行四边形,∴OA =OC ,OB =OD ,∵BE =DF ,∴OE =OF ,∴四边形AECF 是平行四边形,故不符合题意;B、如图所示,AE=CF,不能得到四边形AECF是平行四边形,故符合题意;C、如图,∵四边形ABCD是平行四边形,∴OA=OC,∵AF∥CE,∴∠FAO=∠ECO,又∵∠AOF=∠COE,∴△AOF≌△COE,∴AF=CE,∴AF//CE,∴四边形AECF是平行四边形,故不符合题意;D、如图,∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠ABE=∠CDF,又∵∠BAE=∠DCF,∴△ABE≌△CDF,∴AE=CF,∠AEB=∠CFD,∴∠AEO=∠CFO,∴AE∥CF,∴AE//CF,∴四边形AECF是平行四边形,故不符合题意,故选B.23.【答案】3【解析】∵D、E分别是AB、AC的中点,∴DE是△ABC的中位线,∴DE=12BC=162=3 cm,故答案为:3.24.【答案】14【解析】∵四边形ABCD是平行四边形,∴AB=CD=5,OA=OC=4,OB=OD=5,∴△OCD的周长=5+4+5=14,故答案为:14.25.【答案】14【解析】∵四边形ABCD是平行四边形,∴AD=BC=6,OA=OC,OB=OD,∵AC+BD=16,∴OB+OC=8,∴△BOC的周长=BC+OB+OC=6+8=14,故答案为14.26.【答案】10【解析】∵四边形ABCD是平行四边形,AB=7,BC=3,∴AD=BC=3,CD=AB=7,∵由作图可知,MN 是线段AC的垂直平分线,∴AE=CE,∴△ADE的周长=AD+(DE+AE)=AD+CD=3+7=10,故答案为:10.27.【答案】10【解析】∵四边形ABCD是平行四边形,∴AD∥BC,CD=AB=2,由折叠,∠DAC=∠EAC,∵∠DAC=∠ACB,∴∠ACB=∠EAC,∴OA=OC,∵AE过BC的中点O,∴AO=12BC,∴∠BAC=90°,∴∠ACE=90°,由折叠,∠ACD=90°,∴E、C、D共线,则DE=4,∴△ADE的周长为:3+3+2+2=10,故答案为:10.28.【解析】∵四边形ABCD是平行四边形,∴OA=OC,AD∥BC,∴∠OAE=∠OCF,在△OAE和△OCF中,OAE OCF OA OCAOE COF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AOE≌△COF(ASA),∴OE=OF.29.【解析】∵ABCD的对角线AC,BD交于点O,∴AO=CO,AD∥BC,∴∠EAC=∠FCO,在△AOE和△COF中,EAO FCO AO OCAOE COF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△AOE≌△COF(ASA),∴AE=CF.31.【解析】∵AB∥DE,AC∥DF,∴∠B=∠DEF,∠ACB=∠F.∵BE=CF,∴BE+CE=CF+CE,∴BC=EF.在△ABC和△DEF中,B DEF BC EFACB F ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABC≌△DEF(ASA),∴AB=DE.又∵AB∥DE,∴四边形ABED是平行四边形.32.【解析】在ABCD中,AD=BC,∠A=∠C,∵E、F分别是边BC、AD的中点,∴AF=CE,在△ABF与△CDE中,AB CDA C AF CE=⎧⎪∠=∠⎨⎪=⎩,∴△ABF≌△CDE(SAS),∴∠ABF=∠CDE.33.【解析】如图,连接BD,AE,∵FB=CE,∴BC=EF,又∵AB∥ED,AC∥FD,∴∠ABC=∠DEF,∠ACB=∠DFE,在△ABC和△DEF中,ABC DEF BC EFACB DFE ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ABC≌△DEF(ASA),∴AB=DE,又∵AB∥DE,∴四边形ABDE是平行四边形,∴AD与BE互相平分.34.【解析】∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠BAE=∠DCF.又BE⊥AC,DF⊥AC,∴∠AEB=∠CFD=90°.在△ABE与△CDF中,AEB CFDBAE DCF AB CD∠=∠⎧⎪∠=∠⎨⎪=⎩,∴得△ABE≌△CDF(AAS),∴AE=CF.35.【解析】∵四边形ABCD是平行四边形,∴AD ∥BC ,AD =BC ,∠A =∠C , ∴∠E =∠F , 又∵BE =DF , ∴AD +DF =CB +BE , 即AF =CE ,在△CEH 和△AFG 中,E F EC FA C A ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△CEH ≌△AFG , ∴CH =AG .36.【解析】(1)∵E 是AB 边上的中点,∴AE BE =, ∵AD BC ∥, ∴ADE F ∠=∠,在ADE △和BFE △中,ADE F ∠=∠,DEA FEB ∠=∠,AE BE =, ∴ADE △≌BFE △, ∴AD BF =.(2)如图,过点D 作DM AB ⊥于点M ,∵AB ∥DC ,∴DM 同时也是平行四边形ABCD 的高, ∴11113282244AED S AB DM AB DM =⋅⋅=⋅=⨯=△, ∴32824EBCD S =-=四边形.37.【解析】(1)∵四边形ABCD 是平行四边形,∴CD∥AB,∴∠AFN=∠CEM,∵FN=EM,AF=CE,∴△AFN≌△CEM(SAS).(2)∵△AFN≌△CEM,∴∠NAF=∠ECM,∵∠CMF=∠CEM+∠ECM,∴107°=72°+∠ECM,∴∠ECM=35°,∴∠NAF=35°.38.【解析】(1)∵D、E分别是AB、AC的中点,F是BC延长线上的一点,∴ED是Rt△ABC的中位线,∴ED∥F C.BC=2DE,又EF∥DC,∴四边形CDEF是平行四边形.(2)∵四边形CDEF是平行四边形;∴DC=EF,∵DC是Rt△ABC斜边AB上的中线,∴AB=2DC,∴四边形DCFE的周长=AB+BC,∵四边形DCFE的周长为25 cm,AC的长5 cm,∴BC=25-AB,∵在Rt△ABC中,∠ACB=90°,∴AB2=BC2+AC2,即AB2=(25-AB)2+52,解得AB=13 cm.。
昆山市八年级数学下册第十八章《平行四边形》基础练习(专题培优)(1)

一、选择题1.已知正方形ABCD 中,对角线4AC =,这个正方形的面积是( )A .8B .16C .82D .162 2.如图,在ABC 中,D ,E 分别是,AB AC 的中点,12BC =,F 是DE 的上任意一点,连接,AF CF ,3DE DF =,若90AFC ∠=︒,则AC 的长度为( )A .4B .5C .8D .103.如图,M 是ABC 的边BC 的中点AN 平分BAC ∠.且BN AN ⊥,垂足为N 且6AB =,10BC =.2MN =,则ABC 的周长是( )A .24B .25C .26D .28 4.如图,把长方形纸片ABCD 沿对角线折叠,设重叠部分为EBD △.下列说法错误的是( )A .AE CE =B .12AE BE =C .EBD EDB ∠=∠ D .△ABE ≌△CDE 5.已知四边形ABCD 中,90A B C ∠=∠=∠=,如果添加一个条件,即可判定该四边形是正方形,那么所添加的这个条件可以是( )A .90D ∠=;B .AB CD =;C .AD BC =; D .BC CD =. 6.如果平行四边形ABCD 的对角线相交于点O ,那么在下列条件中,能判断平行四边形ABCD 为菱形的是( )A .OAB OBA ∠=∠; B .OAB OBC ∠=∠;C .OAB OCD ∠=∠; D .OAB OAD ∠=∠.7.在矩形ABCD 中,对角线AC 、BD 相交于点O ,AE 平分BAD ∠交BC 于点E ,15CAE ∠=︒.连接OE ,则下面的结论:①DOC 是等边三角形;②BOE △是等腰三角形;③2BC AB =;④150∠=︒AOE ;⑤AOE COE S S =,其中正确的结论有( )A .2个B .3个C .4个D .5个8.如图,已知四边形ABCD 中,R 、P 分别为BC 、CD 上的点,E 、F 分别为AP 、RP 的中点.当点P 在CD 上从点C 向点D 移动而点R 不动时,那么下列结论成立的是( )A .线段EF 的长逐渐增大B .线段EF 的长不变C .线段EF 的长逐渐减小D .线段EF 的长与点P 的位置有关 9.如图,已知ABC ∆的面积为24,点D 在线段AC 上,点F 在线段BC 的延长线上,且4,BC CF =四边形DCFE 是平行四边形,则图中阴影部分的面积为( )A .6B .8C .3D .410.如图,以平行四边形ABCD 的边AB 、BC 、CD 、DA 为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E 、F 、G 、H ,顺次连结这四个点,得四边形EFGH ,当()090ADC αα∠=︒<<︒时,有以下结论:①180GCF α∠=︒-;②90HAE α∠=︒+;③HE HG =;④ EH GH ⊥;⑤四边形EFGH 是平行四边形.则结论正确的是( )A .①③④B .②③⑤C .①③④⑤D .②③④⑤ 11.如图,在Rt ABC 中,90C =∠,30A ∠=,D 是 AC 边的中点,DE AC ⊥于点D ,交AB 于点E ,若83AC =,则DE 的长是( )A .8B .6C .4D .212.如图,将长方形ABCD 沿对角线BD 折叠,使点C 落在点C ′处,BC ′交AD 于E ,AD =8,AB =4,则重叠部分(即BDE )的面积为( )A .6B .7.5C .10D .2013.如图,已知在正方形ABCD 中,E 是BC 上一点,将正方形的边CD 沿DE 折叠到DF ,延长EF 交AB 于点G ,连接DG .现有如下4个结论:①AG =GF ;②AG 与EC 一定不相等;③45GDE ∠=︒;④BGE △的周长是一个定值.其中正确的个数为( )A .1B .2C .3D .414.如图,矩形纸片ABCD 中,6AB =,10AD =,折叠纸片,使点A 落在BC 边上的点A 处,折痕为PQ ,当点1A 在BC 边上移动时,折痕的端点P 、Q 分别在AB 、AD 边上移动,则当1A B 最小时其值为( )A .2B .3C .4D .515.如图在ABCD 中,对角线,AC BD 相交于点O ,AOD △与AOB 的周长相差3,8AB =,那么AD 为( )A .5B .8C .11或5D .11或14二、填空题16.如图,Rt ABC △中,90,5∠=︒=B AB ,D 为AC 的中点, 6.5=BD ,则BC 的长为__________.17.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理,如图所示的图形就用了这种分割方法若5AE =,正方形ODCE 的边长为1,则BD 等于___________.18.如图:在ABC ∆中,13,12,AB BC ==点D E 、分别是,AB BC 的中点,连接DE CD 、,如果 2.5,DE =那么ABC ∆的周长是___.19.如图,在平行四边形ABCD 中,BE 平分ABC ∠,CF BE ⊥,连接AE ,G 是AB 的中点,连接GF ,若4AE =,则GF =_____.20.如图,在ABC 中,45BAC ∠=︒,4AB AC ==,点D 是AB 上一动点,以AC 为对角线的所有平行四边形ADCE 中,DE 的最小值是________.21.如图,在四边形ABCD 中,150ABC ∠=︒,BD 平分ABC ∠,过A 点作//AE BC 交BD 于点E ,EF BC ⊥于点F 若6AB =,则EF 的长为________.22.如图,将长方形纸片ABCD 沿着对角线BD 翻折,点C 落在点C '处,BC '与AD 交于点E .若20AD cm =,5AB cm =,则DE =_______cm .23.如图,90MON ∠=︒,矩形ABCD 的顶点A ,B 分别在边OM ,ON 上,当点B 在边ON 上移动时,点A 随之在边OM 上移动,2AB =,1BC =,运动过程中,点D 到点O 的最大距离为______.24.如图,AC 是ABCD 的对角线,点E 在AC 上,AD AE BE ==,102D =︒,则BAC ∠的度数是______.25.如图,长方形ABCD 中,4=AD ,3AB =,点P 是AB 上一点,1AP =,点E 是BC 上一动点,连接PE ,将BPE 沿PE 折叠,使点B 落在B ',连接DB ',则PB DB ''+的最小值是________.26.如图,正方形ABCD 的顶点B 在直线l 上,作AE l ⊥于E ,连结CE ,若4BE =,3AE =,则BCE 的面积________.三、解答题27.如图,六个完全相同的小长方形拼成了一个大长方形,A 、B 是如图所示小长方形的顶点,请在大长方形中按下列要求完成画图:(1)请你仅用无刻度直尺在图1中画一个等腰Rt ABC △,其中90ABC ∠=︒; (2)请你仅用无刻度直尺在图2作出线段AB 的垂直平分线.28.(1)如图,已知线段a ,c ,求作Rt ABC ,使得90C ∠=︒,BC a =,AB c =;(2)在Rt ABC 中,斜边AB 边上的中线长为5,7BC =,试比较AC ,BC 的大小. 29.(问题提出)小颖发现某座房屋的侧面是一种特殊的五边形,她决定好好研究一下它的特点,并计算它的面积.(问题探究)定义:如图()1,我们把满足,,90AB AE CB DE C D ︒==∠=∠=的五边形ABCDE 叫做屋形.其中,AB AE 叫做脊,,BC DE 叫做腰,CD 叫做底.性质:边:屋形的腰相等,脊相等;角:①屋形腰与底的夹角相等;②脊与腰的夹角相等;对角线:①②屋形有两组对角线分别相等,且其中一组互相平分.对称性:屋形是以底的垂直平分线为对称轴的轴对称图形;(1)请直接填写屋形对角线的性质①;(2)请你根据定义证明“屋形的脊与腰的夹角相等”;己知:如图,五边形ABCDE 是屋形.求证:证明:(问题解决)(3)如图,在屋形ABCDE 中,若5,8,6AB BC CD ===,试求出屋形ABCDE 的面积.30.“半角型”问题探究:如图1,在四边形ABCD 中,AB =AD ,∠BAD =120°,∠B =∠ADC =90°,且∠EAF =60°,探究图中线段BE ,EF ,FD 之间的数量关系.(1)小明同学的方法是将△ABE 绕点A 逆时针旋转120°到△ADG 的位置,然后再证明△AFE ≌△AFG ,从而得出结论:(2)如图2,在四边形ABCD 中,AB =AD ,∠B+∠D =180°,E ,F 分别是边BC ,CD 上的点,且∠EAF =12∠BAD ,上述结论是否仍然成立,并说明理由. (3)如图3,边长为4的正方形ABCD 中,点E 、F 分别在AB 、CD 上,AE =CF =1,O 为EF 的中点,动点G 、H 分别在边AD 、BC 上,EF 与GH 的交点P 在O 、F 之间(与O 、F 不重合),且∠GPE =45°,设AG =m ,求m 的取值范围.。
平行四边形全章练习题

平行四边形的性质演习题【1 】1.平行四边形得周长为50cm,两邻边之差为5cm,求各边长.2.平行四边形ABCD 的周长为40cm,两邻边AB.AC 之比为2:3,则AB=_______,BC=________.3.四边形ABCD 是平行四边形,∠BAC=90°,AB=3,AC=4,求AD 的长.4.平行四边形ABCD 中,∠A-∠B=20°,∠A=______∠B=______∠C=______∠D=______5.四边形ABCD 是平行四边形,AB=6cm,BC=8cm,∠B=70°,则AD=________,CD=______,∠D=_______,∠A=______,∠C=_______.6.平行四边形ABCD 的周长为50,个中AB=15,∠ABC=60°,则平行四边形面积=_______7.在平行四边形ABCD 中,∠BAC=34°, ∠ACB=26°,则∠DAC=________,∠D=________8.如图,在平行四边形ABCD 中,CE ⊥AD,CF ⊥BA 交BA 的延伸线于F,∠FBC=30°,CE=3cm,CF=5cm,则平行四边形ABCD 的周长=_______9.平行四边形得周长为50cm,两邻边之差为5cm,则长边是________ ,短边是__________. 10.平行四边形 ABCD 中,∠A+∠C=200°.则:∠A= _______,∠B= _________ . 11.如图,在ABCD 中,DE ⊥AB,E 是垂足,假如∠C=40°,求∠A 与∠ADE 的度数.12 .如图,在ABCD 中,已知对角线AC 和BD 订交于点O,△BOC 的周长为24,BC=10, 求对角线AC 与BD 的和是若干?13.如图所示,在ABCD 中,AB=10cm,AB 边上的高DH=4cm,BC=6cm,求BC 边上的高DF 的长.14.如图,ABCD 的周长为60㎝,△AOB 的周长比△BOC 大8㎝,求AB.BC 的长.平行四边形的剖断演习题ABCDOABCDOABC D EA BCDFEOM ABCD4321F ED CBA 1. 如图, 已知:E.F 是平行四边形ABCD 对角线AC 上的两点,并且AE=CF.求证:四边形BFDE 是平行四边形变式一:在□ABCD 中,E,F 为AC 上两点,BE//DF . 求证:四边形BEDF 为平行四边形.变式二:在□ABCD 中,E,F 分离是AC 上两点,BE ⊥AC 于E,DF ⊥AC 于F. 求证:四边形BEDF 为平行四边形2.如图,平行四边形ABCD 中,AF =CH,DE =BG 求证:EG 和HF 互相等分.3.如图所示,在四边形ABCD 中,M 是BC 中点,AM.BD 互相等分于点O,那么请解释AM=DC 且AM ∥DC4.如图所示,已知□ABCD 中,AE.CF 分离是∠DAB.∠BCD 的等分线, 求证:四边形AFCE 是平行四边形.H G图20.1.3-1FED CBA图4GFEDCBAABCDEF5.如图,在△ABC 中,BD 等分∠ABC,DE ∥BC 交AB 于点E,EF ∥AC 交BC 于点F, 那么BE=CF,请你解释来由.6.已知,如图4,△ABC 是等边三角形,过AC 边上的点D 作DG ∥BC,交AB 于点G, 在GD 和延伸线上取点E,使DE =DC,衔接AE.BD. (1)求证:△AGE ≌△DAB;(2)过点E 作EF ∥DB,交BC 于点F,贯穿连接AF,求∠AFE 的度数.7.已知如图所示,点O 为平行四边形ABCD 的对角线BD 的中点,直线EF 经由点O, 分离交BA.DC 的延伸线于E.F 两点, 求证:AE=CF .8. 已知:如图,四边形ABCD 是平行四边形,且∠=∠E A D B A F . (1)解释∆C E F 是等腰三角形.(2)∆C E F 的哪双方之和等于平行四边形ABCD 的周长,为什么9.已知:如图所示,平行四边形ABCD的对角线AC.BD•订交于点O,EF经由点O并且分离和AB.CD订交于点E.F,又知G.H分离为OA.OC的中点.求证:四边形EHFG是平行四边形.EA DF B C10.等边三角形ABC的边长为a,P为△ABC内一点,且PD∥AB,PE∥BC,PF∥AC,那么,PD+PE+PF的值为一个定值.这个定值是若干?请你说出这个定值的来历.矩形的性质与剖断演习题QPMNABCDR1.下列前提中,能断定一个四边形是矩形的是( )(填序号)A .对角相等且有一个角是直角 B. 对角线互相垂直且相等C. 对角线互相等分且相等 D.一组对边平行,另一组对边相等.且两条对角线相等 E. 一组对边平行且相等,有一个内角是直角2. 若矩形的一条角等分线分一边为3cm 和5cm 两部分,则矩形的周长为 ( ) A .22B .26C .22或26D .283.已知一矩形的周长是24cm,相邻双方之比是1:2,那么这个矩形的面积是 () A .24cm 2B .32cm 2C .48cm 2D .128cm 24.由矩形的一个极点向其所对的对角线引垂线,该垂线分直角为1:3两部分,则该垂线与另一条对角线的夹角为( )° B.45° C.30° D.60°5.如图,在矩形ABCD 中,DE ⊥AC,∠ADE= ∠CDE,那么∠BDC 等于 ( )A .60°B .45°C .30°D °6.如图,矩形ABCD 中,E 是BC 的中点,且∠AED=90°.当AD=10cm 时,AB 等于( )7.如图,过矩形ABCD 的对角线BD 上一点R 分离作矩形双方的平行线MN 与PQ,那么图中矩形AMRP 的面积S 1,与矩形QCNR 的面积S 2的大小关系是 ( )A. S 1> S 2B. S 1= S 2C. S 1< S 2D. 不克不及肯定8.下面的图形中,既是轴对称图形,又是中间对称图形的是( )A. 角B. 随意率性三角形C. 矩形D. 等腰三角形9.若按序贯穿连接一个四边形的四边中点所构成的四边形是矩形,则原四边形必定是( ) A .一般平行四边形 B .对角线互相垂直的四边形 C .对角线相等的四边形 D .矩形 10.下列前提中,不克不及剖断四边形ABCD 为矩形的是( ). A .AB ∥CD,AB=CD,AC=BD B .∠A=∠B=∠D=90° C .AB=BC,AD=CD,且∠C=90° D .AB=CD,AD=BC,∠A=90°11.矩形ABCD 的两条对角线订交于O,∠AOB =60o,AB =8,则矩形对角线的长___12.矩形的两条对角线的夹角为60°,若一条对角线与短边的和为15,则短边的长是,对角线的长是 ;若较短的边长为5cm .则这个矩形的面积是_____cm 2.13.如图,在矩形ABCD 中,E 是BC 的中点,且EA ⊥ED .•若矩形ABCD•的周长为48cm,• 则矩形ABCD 的面积为_______cm 2.14.矩形一个角的等分线分矩形一边成2cm 和3cm,则这个矩形的面积为. 15.矩形ABCD 的对角线订交于O,AC=2AB,则△COD 为________三角形16.如图,将矩形纸片折叠,先折出折痕(对角线)BD,再折使AD 边与对角线BD 重合,得折痕DG,若AB=2,BC=1, 求AG 的长17.如图:矩形ABCD 中,AB=2 cm , BC=3 cm . M 是BC 的中点,求D 点到AM 的距离.18.如图,在矩形ABCD 中,AE 等分∠BAD,∠1=15°. (1)求∠2的度数.(2)求证:BO =BE19.已知:如图,在平行四边形ABCD 中,O 为边AB 的中点,且∠AOD=∠BOC . 求证:平行四边形ABCD 是矩形.BACDOPDODACB20.已知:如图,四边形ABCD 是由两个全等的正三角形ABD 和BCD 构成的,M.N•分离为BC.AD 的中点. 求证:四边形BMDN 是矩形.21.已知:如图,AB=AC,AE=AF,且∠EAB=∠FAC,EF=BC .求证:四边形EBCF 是矩形.22.如图,已知平行四边形ABCD 的对角线AC.BD 订交于点O,△AOB 是等边三角形, AB=4cm.(1)平行四边形ABCD 是矩形吗?解释来由. (2)求平行四边形ABCD 的面积.NM DCBAF ECBA23.如图,在梯形ABCD 中,AD BC AB DE AF DC E F ∥,∥,∥,、两点在边BC 上, 且四边形AEFD 是平行四边形. (1)AD 与BC 有多么量关系?请解释来由;(2)当AB DC 时,求证:□AEFD 是矩形.24.如图,在△ABC 中,点O 是AC 边上的一个动点,过点O 作直线MN ∥BC, 设MN 交∠BCA 的等分线于点E,交∠BCA 的外角等分线于点F.①求证:EO=FO;②当O 点活动到何处时,四边形AECF 是矩形?并证实你的结论.菱形的性质和剖断温习1.下面性质中菱形有而矩形没有的是( )(A )邻角互补 (B )内角和为360° (C )对角线相等 (D )对角线互相垂直2.如图,在菱形ABCD 中,∠BAD=60°,BD=4,则菱形ABCD 的周长是_______.ADCFEB3.如图,菱形ABCD的边长是2cm,E是AB的中点,且DE丄AB,则菱形ABCD的面积为cm2.4.已知菱形两条对角线的长分离为5cm和8cm,则这个菱形的面积是______cm.5.如图,菱形ABCD的对角线AC.BD订交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点O到边AB的距离6.如图,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四边形ABCD,若AD=6cm,∠ABC=60°,则四边形ABCD的面积等于cm2.2题 3题5题 6题7.如图,依次贯穿连接第一个矩形各边的中点得到一个菱形,再依次贯穿连接菱形各边的中点得到第二个矩形,按照此办法持续下去.已知第一个矩形的面积为1,则第n个矩形的面积为.……7题8.P为菱形ABCD的对角线上一点,PE⊥AB于点E,PF⊥AD于点 F,PF=3cm,则P点到AB的距离是_____ cm9.如图,菱形ABCD的两条对角线分离长6和8,点P是对角线AC上的一个动点,点M.N分离是边AB.BC的中点,则PM+PN的最小值是_______.二.选择;10.小明和小亮在做一道习题,若四边形ABCD是平行四边形,请填补前提,使得四边形ABCD是菱形.小明填补的前提是AB=BC;小亮填补的前提是AC=BD,你以为下列说法准确的是()A.小明.小亮都准确B.小明准确,小亮错误C.小明错误,小亮准确D.小明.小亮都错误11.已知四边形ABCD是平行四边形,下列结论不准确的是()A. 当AB=BC时,它是菱形;B. 当AC⊥BD时,它是菱形;C. 当∠ABC=90°时,它是矩形;D. 当AC=BD时,它是菱形12.用直尺和圆规作一个菱形,如图,能得到四边形ABCD是菱形的根据是()A.一组临边相等的四边形是菱形B.每条对角线等分一组对角的平行四边形是菱形C.对角线互相垂直的平行四边形是菱形D.四边相等的四边形是菱形三.求证题13.如图,在已知平行四边形ABCD中,AE等分∠BAD,与BC订交于点E,EF//AB,与AD订交于点F. 求证:四边形ABEF是菱形.14.如图,已知矩形ABCD的两条对角线订交于O,∠ACB=30°,AB=2.(1)求AC的长.(2)求∠AOB的度数.(3)以OB.OC为邻边作菱形OBEC,求菱形OBEC的面积.15.如图,在平行四边形ABCD中,∠DAB=60°,AB=2AD,点 E.F分离是CD的中点,过点A作AG∥BD,交CB的延伸线于点G.(1)求证:四边形DEBF是菱形;(2)请断定四边形AGBD是什么特别四边形?并加以证实.16.如图,在△ABC中,∠ACB=90°,BC的垂直等分线DE交BC于D,交AB于E,F在DE上,且AF=CE=AE.(1)解释四边形ACEF是平行四边形;(2)当∠B知足什么前提时,四边形ACEF是菱形,并解释来由.17.如图,矩形ABCD的对角线订交于点O,DE∥CA,AE∥BD.(1)求证:四边形AODE是菱形;(2)若将题设中“矩形ABCD”这一前提改为“菱形ABCD”,其余前提不变,则四边形AODE是如何的四边形?第11页,共11页。
2021年八年级数学下册第十八章《平行四边形》基础练习(答案解析)(1)
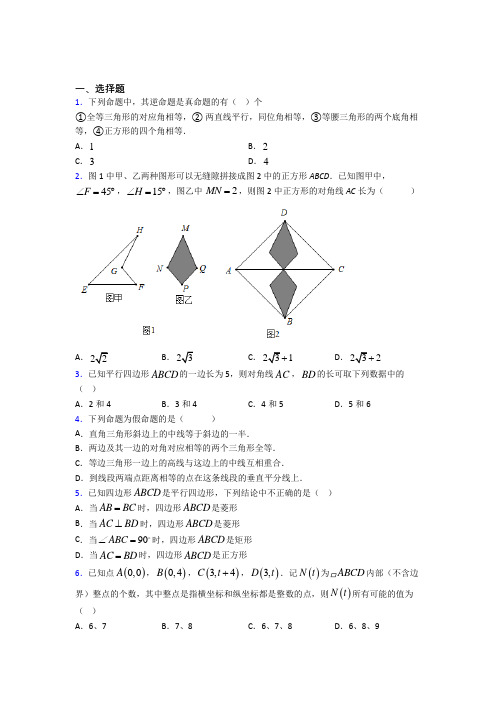
一、选择题1.下列命题中,其逆命题是真命题的有( )个①全等三角形的对应角相等,② 两直线平行,同位角相等,③等腰三角形的两个底角相等,④正方形的四个角相等.A .1B .2C .3D .42.图1中甲、乙两种图形可以无缝隙拼接成图2中的正方形ABCD .已知图甲中,45F ∠=︒,15H ∠=︒,图乙中 2MN =,则图2中正方形的对角线AC 长为( )A .2B .3C .231D .232 3.已知平行四边形ABCD 的一边长为5,则对角线AC ,BD 的长可取下列数据中的( )A .2和4B .3和4C .4和5D .5和6 4.下列命题为假命题的是( )A .直角三角形斜边上的中线等于斜边的一半.B .两边及其一边的对角对应相等的两个三角形全等.C .等边三角形一边上的高线与这边上的中线互相重合.D .到线段两端点距离相等的点在这条线段的垂直平分线上.5.已知四边形ABCD 是平行四边形,下列结论中不正确的是( )A .当AB BC =时,四边形ABCD 是菱形B .当AC BD ⊥时,四边形ABCD 是菱形C .当90ABC ∠=时,四边形ABCD 是矩形D .当AC BD =时,四边形ABCD 是正方形6.已知点()0,0A ,()0,4B ,()3,4C t +,()3,D t .记()N t 为ABCD 内部(不含边界)整点的个数,其中整点是指横坐标和纵坐标都是整数的点,则()N t 所有可能的值为( )A .6、7B .7、8C .6、7、8D .6、8、97.如图,在菱形ABCD 中,对角线BD =4,AC =3BD ,则菱形ABCD 的面积为( )A .96B .48C .24D .68.如图,以平行四边形ABCD 的边AB 、BC 、CD 、DA 为斜边,分别向外侧作等腰直角三角形,直角顶点分别为E 、F 、G 、H ,顺次连结这四个点,得四边形EFGH ,当()090ADC αα∠=︒<<︒时,有以下结论:①180GCF α∠=︒-;②90HAE α∠=︒+;③HE HG =;④ EH GH ⊥;⑤四边形EFGH 是平行四边形.则结论正确的是( )A .①③④B .②③⑤C .①③④⑤D .②③④⑤ 9.矩形ABCD 与ECFG 如图放置,点B ,C ,F 共线,点C ,E ,D 共线,连接AG ,取AG 的中点H ,连接EH .若4AB CF ==,2BC CE ==,则EH =( )A .2B .2C .3D .510.如图,以AB 为斜边的Rt ABC 和Rt ABD △位于直线AB 的同侧,连接CD .若135,6BAC ABD AB ∠+∠=︒=,则CD 的长为( )A .3B .4C .32D .3311.如图,把一张长方形纸片沿对角线折叠,若△EDF 是等腰三角形,则∠BDC ( )A .45ºB .60ºC .67.5ºD .75º12.如图,已知在正方形ABCD 中,E 是BC 上一点,将正方形的边CD 沿DE 折叠到DF ,延长EF 交AB 于点G ,连接DG .现有如下4个结论:①AG =GF ;②AG 与EC 一定不相等;③45GDE ∠=︒;④BGE △的周长是一个定值.其中正确的个数为( )A .1B .2C .3D .413.如图,在平行四边形ABCD 中,DE 平分ADC ∠,6AD =,2BE =,则平行四边形ABCD 的周长是( )A .16B .14C .20D .2414.如图,在矩形ABCD 中,3AB =,4=AD ,ABC ∠的平分线BE 交AD 于点E .点F ,G 分别是BC ,BE 的中点,则FG 的长为( )A .2B .52C .102D .32215.如图,矩形纸片ABCD 中,6AB =,10AD =,折叠纸片,使点A 落在BC 边上的点A 处,折痕为PQ ,当点1A 在BC 边上移动时,折痕的端点P 、Q 分别在AB 、AD 边上移动,则当1A B 最小时其值为( )A.2 B.3 C.4 D.5二、填空题16.如图,平行四边形ABCD中,CE AD⊥于点E,点F为边AB的中点,连接EF,CF,若12AD CD=,38CEF∠=︒,则AFE∠=_____________.17.如图,直线a过正方形ABCD的顶点A,点B、D到直线a的距离分别为1、3,则正方形的边长为_______.18.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理,如图所示的图形就用了这种分割方法若5AE=,正方形ODCE的边长为1,则BD 等于___________.19.如图,点O 是菱形ABCD 对角线的交点,DE //AC ,CE //BD ,连接OE ,设AC =12,BD =16,则OE 的长为_____.20.如图,在平面直角坐标系中,点A 、点B 分别在x 轴和y 轴的正半轴上运动,且AB =4,若AC =BC =5,△ABC 的形状始终保持不变,则在运动的过程中,点C 到原点O 的最小距离为____________.21.如图,在长方形纸片ABCD 中,12AB =,5BC =,点E 在AB 上,将DAE △沿DE 折叠,使点A 落在对角线BD 上的点A '处,则AE 的长为______.22.如图,点D 、E 分别是边AB 、AC 上的点,已知点F 、G 、H 分别是DE 、BE 、BC 的中点,连接FG 、GH 、FH ,若BD =8,CE =6,∠FGH =90°,则FH 长为____.23.如图,在四边形ABCD 中,150ABC ∠=︒,BD 平分ABC ∠,过A 点作//AE BC 交BD 于点E ,EF BC ⊥于点F 若6AB =,则EF 的长为________.24.在△ABC 中, AD 是BC 边上的高线,CE 是AB 边上的中线,CD =AE ,且CE <AC .若AD =6,AB =10,则CE =___________25.如图,将Rt △ABC 沿着点B 到A 的方向平移到△DEF 的位置,BC =8,FO =2,平移距离为4,则四边形AOFD 的面积为__.26.如图,长方形ABCD 中,4=AD ,3AB =,点P 是AB 上一点,1AP =,点E 是BC 上一动点,连接PE ,将BPE 沿PE 折叠,使点B 落在B ',连接DB ',则PB DB ''+的最小值是________.三、解答题27.如图,四边形ABCD 是矩形,对角线AC 与BD 相交于点O ,∠AOD =60°,AD =2,求AC 的长度.28.如图,已知点E 是ABCD 的边CD 延长线上的一点;连接AE ,BD ,且//AE BD ;过点E 作EF BC ⊥,交BC 的延长线于点F ,连接DF ;求证:DF DE =29.如图,平行四边形ABCD 中,,AP BP 分别平分DAB ∠和CBA ∠,交于DC 边上点P , 2.5AD =.(1)求线段AB 的长.(2)若3BP =,求ABP △的面积.30.如图,CD 是线段AB 的垂直平分线,M 是AC 延长线上一点.(1)在图中补充完整以下作图,保留作图痕迹:作∠BCM 的角平分线CN ,过点B 作CN 的垂线,垂足为E ;(2)求证:四边形BECD 是矩形;(3)AB 与AC 满足怎样的数量关系时,四边形BECD 是正方形?证明你的结论.。
平行四边形全章复习练习题.docx

平行四边形总复习1.利用基本图形结构使本章内容系统化.教2.对比掌握各种特殊四边形的概念,性质和判定方法.学3.总结常用添加辅助线的方法.目4.总结本章常用的数学思想方法,提高逻辑思维能力.标教学重点平行四边形与特殊平行四边形的从属关系及它们的概念、性质和判定方法.教学难点提高数学思维能力教学准备课件教学过程教教学内容学环节一第一步:全章知识线索. 1. 平行四边形与特殊的平行四边形的关系:全矩形章知识有一个角是直角,线索平行四边形且有一组邻边相等正方形菱形用集合表示为:2.平行四边形与特殊的平行四边形的性质与判定:平行四边形矩形菱形正方形对边平行且相对边平行,四边对边平行,四边边对边平行且相等性等相等相等质四个角都是直对角相等四个角都是直角角对角相等角对互相平分且相互相垂直平分,互相垂直平分且角互相平分且每条对角线平相等 , 每条对角等线分一组对角线平分一组对角1两组对边分别行;有三个角是直四边相等的四边2两组对边分别等;角;形;3一组对边平行且是平行四边形是平行四边形且是矩形,且有一相等;且有一个角是有一组邻边相组邻边相等;判定直角 ;4两组对角分别相等;是菱形,且有一等;是平行四边形是平行四边形且个角是直角 .5两条对角线互相且两条对角线两条对角线互相平分 .相等 .垂直 .对称只是中心对称图形既是轴对称图形,又是中心对称图形性面积S= ah S=ab S=1d1d 2S= a2 23. 三角形中位线定理 . 、二类型一、平行四边形的性质与判定、例 1. 如图, ABCD为平行四边形, E、 F 分别为 AB、CD的中点,①求证: AECF也是平例行四边形;②连接 BD,分别交 CE、AF于 G、H,求证:BG=DH;③连接 CH、AG,则 AGCH 题也是平行四边形吗?选讲例 2.如图,已知在平行四边形ABCD中, AE⊥BC于 E, AF⊥CD于 F,若∠ EAF=60 o,CE=3cm,FC=1cm,求 AB、BC的长及 ABCD面积 .类型二、矩形、菱形的性质与判定例 3.如图,在矩形ABCD中,对角线交于点O,DE平分∠ ADC,∠AOB=60°,则∠ COE =.例4. 如图,矩形 ABCD中的长 AB= 8 cm,宽 AD=5 cm,沿过 BD的中点 O的直线对折,使 B 与 D 点重合,求证: BEDF为菱形,并求折痕 EF的长.类型三、正方形的性质与判定例 6.如图,已知E、F分别是正方形ABCD的边BC、CD上的点,AE、AF分别与对角线 BD相交于M、N,若∠ EAF=50°,则∠CME+∠ CNF=.类型四、与三角形中位线定理相关的问题例7. 如图, BD=AC, M、 N 分别为 AD、 BC的中点, AC、BD交于 E, MN与 BD、AC分别交于点 F、 G,求证: EF=EG.1.在菱形 ABCD中, AC、BD相交于点 O,DE⊥ BC于点 E,且 DE= OC,OD=2,则 AC 三=.、能2.如图,正方形 OMNP的一个顶点与正方形 ABCD的对角线交点 O重合,且正方形 ABCD、力OMNP的边长都是 acm,则图中重合部分的面积是2 cm.训练 3. 如图,设 M、N 分别是正方形 ABCD的边 AB、AD的中点,MD与 NC相交于点 P,若△ PCD 的面积是 S,则四边形 AMPN的面积是.4.如图, M为边长为 2 的正方形 ABCD对角线上一动点, E 为 AD中点,则 AM+EM的最小值为.5.边长为 1 的正方形 ABCD绕点 A 逆时针旋转 30 o到正方形AB C D,图中阴影部分的面积为.6.菱形的两条对角线长为 6 和 8,则菱形的边长为 ______,面积为 _______.7.在平行四边形 ABCD中,对角线 AC、 BD相交于点 O, AF⊥BD,CE⊥ BD,垂足分别为E、 F;连结 AE、CF,得四边形 AFCE,求证: AFCE是平行四边形 .8.□ABCD中, AE、CF、 BF、DE分别为四个内角平分线,求证: EGFH是矩形 .9.如图,∠ BAC=90 o, BF平分∠ ABC交 AC于 F,EF⊥BC于 E,AD⊥BC于 D,交 BF于G.求证:四边形AGEF为菱形.10. 如图,正方形 ABCD中,E 为 BC上一点, DF=CF,DC+CE=AE,求证: AF 平分∠ DAE.教学反思。
平行四边形基础练习

四边形基础知识1.平行四边形的一条边长是12cm,那么它的两条对角线的长可能是()A.8cm和16cm B.10cm和16cm C.8cm和14cm D.8cm和12cm2.如图,M,N分别是平行四边形ABCD的对边AD,BC的中点,且AD=2AB,连接AN,BM,交于点P,连接DN,CM,交于点Q,则以下结论错误的是()A.AP=PN B.NQ=QD C.四边形PNQM是矩形 D.△ABN是等边三角形3.菱形的两条对角线长分别为18与24,则此菱形的周长为()A.15 B.30 C.60 D.1204.如图,四边形ABCD是菱形,对角线AC=8cm,BD=6cm,DH⊥AB,则DH的长为()A.cm B.cm C.cm D.4cm5.如图,过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE、CF.若AB=,∠DCF=30°,则EF的长为(A.2 B.3 C.D.第2题第4题第5题6.正方形具有而菱形不一定具有的性质是()A.对角线相等B.对角线互相垂直平分C.对角线平分一组对角D.四条边相等7.四边形ABCD的对角线AC,BD相交于点O,能判定它为正方形的条件是()A.AO=CD B.AO=CO=BO=DOC.AO=CO,BO=DO,AC⊥BD D.AO=BO=CO=DO,AC⊥BD8.如图所示,在矩形ABCD中,AB=,BC=2,对角线AC、BD相交于点O,过点O作OE 垂直AC交AD于点E,则AE的长是()A.B.C.1 D.1.59.如图,要使▱ABCD成为菱形,则需添加的一个条件是()A.AC=AD B.BA=BC C.∠ABC=90°D.AC=BD10.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是()A.AB=BE B.BE⊥DC C.∠ADB=90°D.CE⊥DE第8题第9题第10题11.已知四边形ABCD,下列说法正确的是()A.当AD=BC,AB∥DC时,四边形ABCD是平行四边形B.当AD=BC,AB=DC时,四边形ABCD是平行四边形C.当AC=BD,AC平分BD时,四边形ABCD是矩形D.当AC=BD,AC⊥BD时,四边形ABCD是正方形12.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC 交于点F,且点F为边DC的中点,DG⊥AE,垂足为G.若DG=1,则AE的边长为.13.如图,在四边形ABCD中,∠ABC=90°,对角线AC、BD交于点O,AO=CO,∠AOD=∠ADO,E是DC边的中点,下列结论中,错误的是()A.OE=AD B.OE=OB C.OE=OC D.OE=BC14.已知:如图,在▱ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是()A.菱形 B.矩形 C.平行四边形D.正方形第12题第13题第14题16.如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,动点P从点A出发,沿AB方向以每秒cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C 运动,将△PQC沿BC翻折,点P的对应点为点P′.设Q点运动的时间为t秒,若四边形QP′CP 为菱形,则t的值为()A.B.2 C. D.317.如图,菱形ABCD和菱形ECGF的边长分别为2和4,∠A=120°.则阴影部分面积是.(结果保留根号)18.如图,点D、E、F分别为△ABC各边中点,下列说法正确的是()A.DE=DF B.EF=AB C.S△ABD=S△ACD D.AD平分∠BAC19.如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为()A.24 B.12 C.6 D.320.如图,菱形中,对角线AC、BD交于点O,E为AD边中点,菱形ABCD的周长为28,则OE的长等于()A.3.5 B.4 C.7 D.1421.如图,在△ABC中,AB=AC,M,N分别是AB,AC的中点,D,E为BC上的点,连接DN,EM.若AB=13cm,BC=10cm,DE=5cm,求图中阴影部分的面积.第19题第20题第21题24.如图,AD是△ABC的中线,AE∥BC,BE交AD于点F,且AF=DF.(1)求证:四边形ADCE是平行四边形;(2)当AB、AC之间满足时,四边形ADCE是矩形;(3)当AB、AC之间满足时,四边形ADCE是正方形.25.如图,已知BD平分∠ABF,且交AE于点D,(1)求作:∠BAE的平分线AP(要求:尺规作图,保留作图痕迹,不写作法);(2)设AP交BD于点O,交BF于点C,连接CD,当AC⊥BD时,求证:四边形ABCD是菱形.。
【学生卷】初中八年级数学下册第十八章《平行四边形》基础练习(课后培优)(1)

一、选择题1.如图,ABC 中,//DE BC ,//EF AB ,要判定四边形DBFE 是菱形,可添加的条件是( )A .BD EF =B .AD BD =C .BE AC ⊥D .BE 平分ABC ∠ 2.如图为某城市部分街道示意图,四边形ABCD 为正方形,点G 在对角线BD 上,GE CD ⊥,GF BC ⊥,1500m AD =,小敏行走的路线为B AG E →→→,小聪行走的路线为B A D E F →→→→.若小敏行走的路程为3100m ,则小聪行走的路程为( )A .3100mB .4600mC .5500mD .6100m 3.如图,在ABC 中,90ACB ∠=︒,点D 在AC 边上且AD BD =,M 是BD 的中点.若16AC =,8BC =,则CM 等于( )A .5B .6C .8D .104.在平面直角坐标系中,长方形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,OA =3,OB =4,D 为边OB 的中点,若E 为x 轴上的一个动点,当△CDE 的周长最小时,求点E 的坐标( )A .(一3,0)B .(3,0)C .(0,0)D .(1,0) 5.如图,在平行四边形ABCD 中,100B D ︒∠+∠=,则B 等于( )A .50°B .65°C .100°D .130° 6.如图,在平行四边形ABCD 中,对角线,AC BD 交于点O ,2BD AD =,E ,F ,G 分别是,,OA OB CD 的中点,EG 交FD 于点H .下列结论:①ED CA ⊥;②EF EG =;③12EH EG =;成立的个数有( )A .3个B .2个C .1个D .0个 7.已知四边形ABCD 是平行四边形,下列结论中不正确的是( )A .当AB BC =时,四边形ABCD 是菱形B .当AC BD ⊥时,四边形ABCD 是菱形C .当90ABC ∠=时,四边形ABCD 是矩形D .当AC BD =时,四边形ABCD 是正方形8.如图,在ABC 中,90A ∠=,D 是AB 的中点,过点D 作BC 的平行线,交AC 于点E ,作BC 的垂线交BC 于点F ,若AB CE =,且DFE △的面积为1,则BC 的长为( )A.25B.5 C.45D.109.如图,已知四边形ABCD中,R、P分别为BC、CD上的点,E、F分别为AP、RP的中点.当点P在CD上从点C向点D移动而点R不动时,那么下列结论成立的是()A.线段EF的长逐渐增大B.线段EF的长不变C.线段EF的长逐渐减小D.线段EF的长与点P的位置有关10.如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD 的周长是()A.60 B.30 C.20 D.1611.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,若OA=6,S菱形ABCD=48,则OH的长为()A.4 B.8 C13D.612.如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边的中线,点D,E分别在边AC 和BC上,DB=DE,EF⊥AC于点F,则以下结论;①∠DBM=∠CDE;②BN=DN;③AC=2DF;④S BDE﹤S BMFE四边形其中正确的结论是()A .①②③B .②③④C .①②④D .①③ 13.如图,矩形ABCD 的对角线AC ,BD 相交于点O ,30ACD ∠=︒,若ABC 的周长比AOB 的周长大10,则AB 的长为( ).A .103B .53C .10D .2014.如图,在矩形ABCD 中,3AB =,4=AD ,ABC ∠的平分线BE 交AD 于点E .点F ,G 分别是BC ,BE 的中点,则FG 的长为( )A .2B .52C .102D .32215.如图在ABCD 中,对角线,AC BD 相交于点O ,AOD △与AOB 的周长相差3,8AB =,那么AD 为( )A .5B .8C .11或5D .11或14二、填空题16.菱形的周长为20cm ,一条对角线长为8cm ,则菱形的面积为______cm 2. 17.如图,在ABCD 中,AC 与BD 相交于点O ,(1)若18cm,24cm AC BD ==,则AO =_______,BO =_______.又若13AB =厘米,则COD △的周长为________.(2)若AOB 的周长为30cm ,12cm AB =,则对角线AC 与BD 的和是________. 18.如图,在正方形ABCD 中,有面积为4的正方形EFGH 和面积为2的正方形PQMN 、点E F P Q 、、、分别在边AB BC CD AD 、、、上,点M N 、在边HG 上,且组成的图形为轴对称图形,则正方形ABCD 的面积为__________.19.如图,BD 是矩形ABCD 的对角线,在BA 和BD 上分别截取BE ,BF ,使BE =BF ;分别以E ,F 为圆心,以大于12EF 的长为半径作弧,两弧在∠ABD 内交于点G ,作射线BG 交AD 于点P ,若AP =3,则点P 到BD 的距离为_______.20.如图,在矩形ABCD 中,AD =2.将∠A 向内翻折,点A 落在BC 上,记为A ',折痕为DE .若将∠B 沿EA '向内翻折,点B 恰好落在DE 上,记为B ',则AB =_______.21.如图,将Rt △ABC 沿着点B 到A 的方向平移到△DEF 的位置,BC =8,FO =2,平移距离为4,则四边形AOFD 的面积为__.22.如图,矩形ABCD 中,2AB =,4=AD ,点E 是边AD 上的一个动点;把BAE △沿BE 折叠,点A 落在A '处,如果A '恰在矩形的对称轴上,则AE 的长为______.23.如图,在Rt △ABC 中,∠ACB =90°,D 是斜边AB 中点,若∠B =30°,AC =2,则CD =_____.24.如图所示,在ABCD 中,AC 与BD 相交于点O ,若DAC EAC ∠=∠,4AE =,3AO =,则AEC S ∆的面积为____.25.如图,在正方形ABCD 中,AB=6,E 是CD 上一点,BE 交AC 于点F ,连接DF .过点D 且垂直于DF 的直线,与过点A 且垂直于AC 的直线交于点G .∠ABE 的平分线交AD 于点M ,当满足四边形AGDF 面积2BCE S =△时,线段AM 的长度是_______.26.如图,△ABC 是边长为1的等边三角形,取BC 边中点E ,作ED ∥AB ,EF ∥AC ,得到四边形EDAF ,它的周长记作C 1;取BE 中点E 1,作E 1D 1∥FB ,E 1F 1∥EF ,得到四边形E 1D 1FF 1,它的周长记作C 2.照此规律作下去,则C 2020=__.参考答案三、解答题27.如图,已知点E 是ABCD 的边CD 延长线上的一点;连接AE ,BD ,且//AE BD ;过点E 作EF BC ⊥,交BC 的延长线于点F ,连接DF ;求证:DF DE =28.如图,四边形ABCD 中,//AD BC ,90A D ∠=∠=︒,点E 是AD 的中点,连接BE ,将ABE △沿BE 折叠后得到GBE ,且点G 在四边形ABCD 内部,延长BG 交DC 于点F ,连接EF .(1)求证:EGF EDF △△≌;(2)求证:BG CD =;(3)若点F 是CD 的中点,8BC =,求CD 的长.29.已知:如图,菱形ABCD 的对角线AC 与BD 相交于点O ,若CAD DBC ∠=∠. (1)求证:四边形ABCD 是正方形.(2)E 是OB 上一点,DH CE ⊥,垂足为H ,DH 与OC 相交于点F ,求证:OE OF =.30.如图,平行四边形ABCD 中,BD 是它的一条对角线,过A 、C 两点作,AE BD CF BD ⊥⊥,垂足分别为E 、F ,延长AE 、CF 分别交CD 、AB 于M 、N .(1)求证:四边形CMAN 是平行四边形; (2)已知4,3DE FN ==.求BN 的长.。
北师大二附中汇才国际学校八年级数学下册第十八章《平行四边形》基础练习(含解析)

一、选择题1.下列命题中,其逆命题是真命题的有( )个①全等三角形的对应角相等,② 两直线平行,同位角相等,③等腰三角形的两个底角相等,④正方形的四个角相等.A .1B .2C .3D .4 2.如图,正方形ABCD 的边长为4,点E 在对角线BD 上,且∠BAE =22.5°,EF ⊥AB ,垂足为F ,则EF 的长为( )A .4﹣22B .32﹣4C .1D .23.如图,在等腰直角ABC 中,AB BC =,点D 是ABC 内部一点, DE BC ⊥,DF AB ⊥,垂足分别为E ,F ,若3CE DE =, 53DF AF =, 2.5DE =,则AF =( )A .8B .10C .12.5D .154.如图,点E 、F 分别在正方形ABCD 的边BC 、CD 上,45EAF ∠=︒,已知6AD =(正方形的四条边都相等,四个内角都是直角),2DF =.则AEF 的面积AEF S =( )A .6B .12C .15D .305.在ABCD 中AB BC ≠.F 是BC 上一点,AE 平分FAD ∠,且E 是CD 的中点,则下列结论:①AB BF =;②AF CF CD =+;③AF CF AD =+;④AE EF ⊥,其中正确的是( )A .①②B .②④C .③④D .①②④ 6.下列说法正确的是( )A .有一个角是直角的平行四边形是正方形B .对角线互相垂直的矩形是正方形C .有一组邻边相等的菱形是正方形D .各边都相等的四边形是正方形 7.如果平行四边形ABCD 的对角线相交于点O ,那么在下列条件中,能判断平行四边形ABCD 为菱形的是( )A .OAB OBA ∠=∠;B .OAB OBC ∠=∠; C .OAB OCD ∠=∠; D .OAB OAD ∠=∠.8.如图,在ABC 中,90A ∠=,D 是AB 的中点,过点D 作BC 的平行线,交AC 于点E ,作BC 的垂线交BC 于点F ,若AB CE =,且DFE △的面积为1,则BC 的长为( )A .25B .5C .45D .109.如图,已知ABC ∆的面积为24,点D 在线段AC 上,点F 在线段BC 的延长线上,且4,BC CF =四边形DCFE 是平行四边形,则图中阴影部分的面积为( )A .6B .8C .3D .410.在菱形ABCD 中,∠ABC=60゜,AC=4,则BD=( )A .3B .23C .33D .43 11.下列命题中,正确的命题是( )A .菱形的对角线互相平分且相等B .顺次联结菱形各边的中点所得的四边形是矩形C .矩形的对角线互相垂直平分D .顺次连结矩形各边的中点所得的四边形是正方形12.如图,把一张长方形纸片沿对角线折叠,若△EDF 是等腰三角形,则∠BDC ( )A .45ºB .60ºC .67.5ºD .75º13.如图,Rt Rt ABC BAD △≌△,BC 、AD 交于点E ,M 为斜边的中点,若CMD α∠=,AEB β∠=.则α和β之间的数量关系为( )A .2180βα-=︒B .60βα-=︒C .180αβ+=︒D .2βα=14.如图,已知平行四边形ABCD 中,4B A ∠=∠,则C ∠=( )A .18°B .36°C .72°D .144° 15.矩形不一定具有的性质是( ) A .对角线互相平分 B .是轴对称图形 C .对角线相等 D .对角线互相垂直参考答案二、填空题16.如图,在矩形ABCD 中,连接AC ,按以下步骤作图:分别以点A ,C 为圆心,以大于12AC 的长为半径作弧,两弧分别相交于点M ,N ,作直线MN 交BC 于点E ,连接AE .若AB =1,BC =2,则BE =_____.17.在正方形ABCD 中,点E 在对角线BD 上,点P 在正方形的边上,若∠AEB=105°,AE=EP ,则∠AEP 的度数为_________.18.在Rt ABC 中,∠C =90°,点D 是AB 边的中点,若AB =8,则CD =______. 19.如图,在长方形纸片ABCD 中,12AB =,5BC =,点E 在AB 上,将DAE △沿DE 折叠,使点A 落在对角线BD 上的点A '处,则AE 的长为______.20.生活中,有人喜欢把传送的便条折成形状,折叠过程如图所示(阴影部分表示纸条的反面):已知由信纸折成的长方形纸条(图①)长为25cm ,宽为cm x .如果能折成图④的形状,且为了美观,纸条两端超出点P 的长度相等,即最终图形是轴对称图形,则在开始折叠时起点M 与点A 的距离(用x 表示)为______cm .21.在平面直角坐标系xOy 中,OABC 的三个顶点的坐标分别为()()()0,0,3,0,4,3O A B ,则其第四个顶点C 的坐标为______.22.如图,矩形纸片ABCD 的长AD =6cm ,宽AB =2cm ,将其折叠,使点D 与点B 重合,那么折叠后DE 的长______cm .23.如图,在平行四边形ABCD 中,过点C 的直线CE ⊥AB ,垂足为E ,若∠BAD =127°,则∠BCE =____.24.在△ABC 中, AD 是BC 边上的高线,CE 是AB 边上的中线,CD =AE ,且CE <AC .若AD =6,AB =10,则CE =___________25.如图,将两个边长为1的小正方形,沿对角线剪开,重新拼成一个大正方形,则大正方形的边长是______.26.如图(1)所示为长方形纸带,将纸带沿EF 折叠成图(2),再沿BF 折叠成图(3),继续沿EF 折叠成图(4),按此操作,最后一次折叠后恰好完全盖住EFG ;整个过程共折叠了8次,问图(1)中DEF ∠的度数是_________.三、解答题27.如图,BD 为ABC 的角平分线,E 为AB 上一点,BE BC =,连结DE . (1)求证:BDC BDE ≅△△;(2)若7AB =,2CD =,90︒∠=C ,求ABD △的面积.28.如图,矩形ABCD 中,4AB =,6AD =,E ,F 分别是AD 和AB 上的点,2AE =,F 是AB 的中点,请使用无刻度的直尺,分别按下列要求作图.(1)在图1中,作一个以EF 为直角边的直角三角形;(2)在图2中,作一个以EF 为边的平行四边形.29.如图,在四边形ABCD 中,BD 为一条对角线,//AD BC ,2AD BC =,90ABD ∠=︒,E 为AD 的中点,连接BE .(1)求证:四边形BCDE 为菱形;(2)连接AC ,若AC 平分BAD ∠,1BC =,求AC 的长.30.如图,将矩形ABCD 沿DE 折叠,连接CE 使得点A 的对应点F 落在CE 上.(1)求证:CEB DCF ≅;(2)若2AB BC =,求CDE ∠的度数.。
(完整版)平行四边形练习题附答案

平行四边形测试题一、选择题1.若平行四边形ABCD 的周长是40cm ,△ABC 的周长是27cm ,则AC 的长为( ) A .13cm B .3cm C .7cm D .11.5 cm 2.根据下列条件,不能判定四边形是平行四边形的是( )A .一组对边平行且相等的四边形B .两组对边分别相等的四边形C .对角线相等的四边形D .对角线互相平分的四边形 3.已知平行四边形周长为28cm ,相邻两边的差是4cm ,则两边的长分别为( ) A .4cm 、10cm B .5cm 、9cm C .6cm 、8cm D .5cm 、7cm 4.下列条件中,能判定一个四边形是平行四边形的是( )A .一组对边平行,另一组对边相等B .一组对边平行,一组对角相等C .一组邻边相等,一组对角相等D .一组对边平行,一组对角互补 5.若A 、B 、C 三点不在同一条直线上,则以其为顶点的平行四边形共有( )个 A .1 B .2 C .3 D .4 6.能够判定四边形是平行四边形的条件是( )A .一组对角相等B .两条对角线互相垂直C .两条对角线互相平分D .一条邻角互补7.已知平行四边形的一条边长为14,下列各组数中能分别作它的两条对角线长的是( ) A .10与6 B .12与16 C .20与22 D .10与18 8.四边形ABCD 中,AD ∥BC ,当满足条件( )时,四边形ABCD 是平行四边形 A .∠A +∠C =︒180 B .∠B +∠D =︒180 C .∠A +∠B =︒180 D .∠A +∠D =︒180 9.已知下列三个命题⑴两组对角分别相等的四边形是平行四边形 ⑵一个角与相邻两角都互补的四边形是平行四边形 ⑶一组对角相等,一组对边平行的四边形是平行四边形 其中错误的命题的个数是( )A .0个B .1个C .2个D .3个10.平行四边形ABCD 中,对角线AC 、BD 交于点O ,AC = 10,BD = 8,则AD 的取值范围是( ) A .AD >1 B . AD <9 C .1<AD <9 D .AD >9 二、填空题11.一个平行四边形的周长为40,两邻边的比为3∶5,则四边形的长为_________.12.一个平行四边形的一个内角比它的邻角大︒24,则这个四边形的四个内角分别是________.13.在平行四边形ABCD 中,EF 过对角线交点O ,交CD 、AB 于E 、F ,若AB = 4cm ,AD = 3cm ,OF = 1.3cm ,则四边形BCEF 周长为_____________.14.已知平行四边形的面积是144,相邻两边上的高分别为8和9,则它的周长为_____.15.在平行四边形ABCD 中,对角线BD = 7cm ,∠DBC =︒30,BC = 5cm ,则平行四边形ABCD 的面积为___________.16.从平行四边形的一锐角顶点引另两条边的垂线,两垂线夹角︒135,则此四边形的四个角分别为_____________.三、解答题:17.平行四边形周长等于68cm ,被两条对角线分成两个不同的三角形的周长和等于80cm ,两对角线的长度之比是2∶3,求两条对角线的长度.18.如图,AD 、BC 垂直相交于点O ,AB ∥CD ,又BC = 8,AD = 6,求:AB +CD 的长.19.如图,某村有一口呈四边形的池塘,在它的四个角A 、B、C 、D 处均种有一棵大核桃树,这村准备开挖池塘建养鱼池,想使池塘面积扩大一倍,又想保持核桃树不动,并要求扩建后的池塘成平行四边形形状,请问这村能否实现这一设想?若能,请你设计并画出图形;若不能,请说明理由.20.已知如图,在平行四边形ABCD 中,∠A =︒60,E 、F 分别为AB 、CD 的中点,AB = 2AD ,求证:BD=3EF .参考答案:一、选择题:C .C .B . B . C .C .C .D .A .C . 二、填空题:11.7.5、12.5、7.5、12.5 12.︒102、︒78、︒102、︒7813.9.6 cm 14.68 15.17.5 cm 216. ︒45,︒135,︒45,︒135ADC B AB OCDEEC三、解答题:17.设一条对角线长为2a ,则另一条对角线长为3a . ∵平行四边形周长等于68cm ,∴相邻两边的长为 34cm , ∴34+2a +3a = 80,解得a = 9.2, 2a = 18.4,3a = 27.6.即两条对角线的长度分别为18.4 cm 和3a = 27.6 cm . 18.过点C 作CE ∥AD 交BA 延长线于E , ∵AB ∥CD ,∴四边形AECD 是平行四边形, ∴AE = CD ,∠BCE =∠BOA =︒90,CE = AD = 6, BE =22CE BC +=2268+= 10. ∵ BE = AB +AE =AB +CD , ∴AB +CD = 10.19.这村能实现他们的设想.① 分别过点A 、C 作BD 的平行线1l 、2l ,② 分别过点B 、D 作AC 的平行线3l 、4l ,3l 交1l 、2l 于点M 、N ;4l 交1l 、2l 于点P 、Q ,则四边形MNPQ 就是所求的平行四边形.20.连结DE ,在平行四边形ABCD 中,AB =//CD ,DF =21CD ,AE =21AB ,∴DF =//AE , ∴四边形AEFD 是平行四边形,∴EF = AD . 又∵AB = 2AD ,AB = 2AE , ∴AD = AE ,且∠A =︒60, ∴DE = AE = BE ,ADCB AQDPCNB M 1l2l3l4lABOCDABOCDEEC∴∠1 =21∠2 =21×︒30,∴∠ADB =︒90,BD =22AD AB -=22)2(AD AD -=3AD ,∴BD =3EF .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形基础练习
一、选择题
1、下列条件中,能判定四边形是平行四边形的是()
A.一组对角相等
B.对角线互相平分
C.一组对边相等
D.对角线互相垂直
2、如图,□ABCD中,E,F是对角线BD上的两点,如果添加一个条件使△ABE≌△CDF,则添加的条件不能是()
(A)AE=CF(B)BE=FD(C)BF=DE(D)∠1=∠2
3、如图,在□ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是()
A.AB∥CD,AD∥BC
B.OA=OC,OB=OD
C.AD=BC,AB∥CD
D.AB=CD,AD=BC
第2题第3题第4题
4、如图,已知四边形ABCD中,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是()A.线段EF的长逐渐增大 B.线段EF的长逐渐减小
C.线段EF 的长不变
D.线段EF 的长与点P 的位置有关
5、若平行四边形的两条对角线长分别是x ,y ,一边长为12,则x ,y 的值可能是( )
A .8和14
B .10和14
C .18和20
D .10和34
6、在四边形ABCD 中,对角线AC 、BD 相交于点O ,给出下列四组条件:
①AB ∥CD AD ∥BC ②AB=CD AD=BC ③AO=CO BO=DO ④AB ∥CD AD=BC 其中一定能判断这个四边形是平行四边形的共有( ).
A.1组
B.2组
C.3组
D.4组
7、能判断四边形是平行四边形的是( )
A.一组对边平行,另一组对边相等
B.一组对边平行,一组对角相等
C.一组对边平行,一组邻角互补
D.一组对边相等,一组邻角相等
8、下面性质中,平行四边形不一定具备的是( )
A 、对角相等
B 、邻角互补
C 、对角互补
D 、对角线互相平分
9、如图所示,长方形ABCD 的面积为10,它的两条对角线交于点O 1,以AB 、AO 1为邻边作平行四边形ABC 1O 1,平行四边形ABC 1O 1的对角线交于点O 2,同样以AB 、AO 2为邻边作平行四边形A BC 2O 2,……,依次类推,则平行四边形ABC 5O 5的面积为( )
A 、1
B 、2
C 、85
D 、165
10、如图,在平面直角坐标系中,□ABCD的顶点A、B、D的坐标分别是(0,0),(5,0)(2,3),则顶点C的坐标是()
A、(3,7)
B、(5,3)
C、(7,3)
D、(8,2)
11、四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:①AD∥BC,②AD=BC,
③OA=OC,④OB=OD.从中任选两个条件,能使四边形ABCD为平行四边形的选法有()
A.3种
B.4种
C.5种
D.6种
12、一个四边形的三个内角的度数依次如下,那么其中是平行四边形的是()A.88°, 108°, 88°B.88°,104°,88°C.88°,92°,92°D.88°,92°,88°
二、填空题
1.一个三角形的周长是36 cm,则以这个三角形各边中点为顶点的三角形的周长是cm.
2、如图,▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为
3、如图,□ABCD中,,,AC的垂直平分线交AD于点E,则△CDE的周长是
4、如图,□ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是
5、在□ABCD中,∠A=2∠B,则∠B的度数是
6、如图,在□ABCD中,DE平分∠ADC,AD=6,BE=2,则□ABCD的周长是
7、如图,▱ABCD绕点A逆时针旋转30°,得到▱AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则
∠C= 度
第2题第3题第4题
第6题第7题第8题
8、如图,□ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是
9、如图,在平行四边形纸片上作随机扎针试验,针头扎在阴影区域内的概率为
10、如图所示,平行四边形ABCD中,DE⊥AB于E,DF⊥BC于F,若□ABCD的周长为48,DE=5,DF=10,则□ABCD的面积等于
11、如图,在四边形ABCD中,对角线AC、BD交于点O,AD∥BC,请添加一个条件:,使四边形ABCD为平行四边形(不添加任何辅助线).
12、□ABCD的周长为30,对角线AC、BD相交于点O,若△AOB的周长比△BOC的周长少3,则AB= .
三、简答题
1、如图,在四边形ABCD 中,点E,F,G,H 分别为AB,CD,AC,BD 的中点. 四边形EGFH 是平行四边形吗?请证明你的结论.
第9题第10题第11题
2、如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.
已知:在四边形ABCD中,__________,__________;
求证:四边形ABCD是平行四边形.
3、如图,AD∥BC,AE∥CD,BD平分∠ABC,求证AB=CE.
4. 如图,在四边形 ABCD 中,AB ∥CD ,AB > CD. E ,F 分别是 AC ,BD 的中点. 求证:EF = 21(AB - CD )
5、(选做)如图,D 、E 分别是△ABC 边AB 、BC 上的点,AD=2BD ,
BE=CE ,设△ADF 的面积为S 1,△CEF 的面积为S 2,若S △ABC =6,
则S 1-S 2的值为______.
THANKS !!!
致力为企业和个人提供合同协议,策划案计划书,学习课件等等
打造全网一站式需求
欢迎您的下载,资料仅供参考。
