数据结构与算法分析课后习题答案

合集下载

Mark Allen Weiss 数据结构与算法分析课后习题答案9

This ﬂow is not unique. For instance, two units of the ﬂow that goes from G to D to A to E could go by G to H to E.
-47-
9.12 Let T be the tree with root r , and children r 1, r 2, ..., rk , which are the roots of T 1, T 2, ..., Tk , which have maximum incoming ﬂow of c 1, c 2, ..., ck , respectively. By the problem statement, we may take the maximum incoming ﬂow of r to be inﬁnity. The recursive function FindMaxFlow( T, IncomingCap ) ﬁnds the value of the maximum ﬂow in T (ﬁnding the actual ﬂow is a matter of bookkeeping); the ﬂow is guaranteed not to exceed IncomingCap . If T is a leaf, then FindMaxFlow returns IncomingCap since we have assumed a sink of inﬁnite capacity. Otherwise, a standard postorder traversal can be used to compute the maximum ﬂow in linear time. _ ______________________________________________________________________________ FlowType FindMaxFlow( Tree T, FlowType IncomingCap ) { FlowType ChildFlow, TotalFlow; if( IsLeaf( T ) ) return IncomingCap; else { TotalFlow = 0; for( each subtree Ti of T ) { ChildFlow = FindMaxFlow( Ti , min( IncomingCap, ci ) ); TotalFlow += ChildFlow; IncomingCap -= ChildFlow; } return TotalFlow; } } _ ______________________________________________________________________________ 9.13 (a) Assume that the graph is connected and undirected. If it is not connected, then apply the algorithm to the connected components. Initially, mark all vertices as unknown. Pick any vertex v , color it red, and perform a depth-ﬁrst search. When a node is ﬁrst encountered, color it blue if the DFS has just come from a red node, and red otherwise. If at any point, the depth-ﬁrst search encounters an edge between two identical colors, then the graph is not bipartite; otherwise, it is. A breadth-ﬁrst search (that is, using a queue) also works. This problem, which is essentially two-coloring a graph, is clearly solvable in linear time. This contrasts with three-coloring, which is NP-complete. (b) Construct an undirected graph with a vertex for each instructor, a vertex for each course, and an edge between (v ,w ) if instructor v is qualiﬁed to teach course w . Such a graph is bipartite; a matching of M edges means that M courses can be covered simultaneously. (c) Give each edge in the bipartite graph a weight of 1, and direct the edge from the instructor to the course. Add a vertex s with edges of weight 1 from s to all instructor vertices. Add a vertex t with edges of weight 1 from all course vertices to t . The maximum ﬂow is equal to the maximum matching.

数据结构与算法分析习题与参考答案

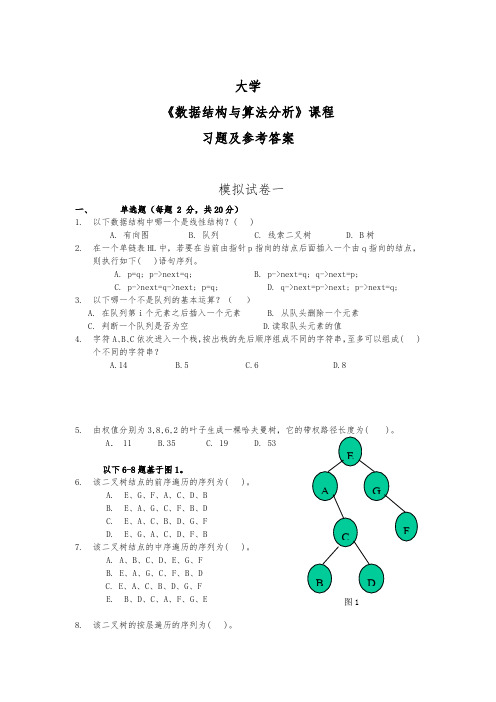
大学《数据结构与算法分析》课程习题及参考答案模拟试卷一一、单选题（每题 2 分，共20分）1.以下数据结构中哪一个是线性结构？( )A. 有向图B. 队列C. 线索二叉树D. B树2.在一个单链表HL中，若要在当前由指针p指向的结点后面插入一个由q指向的结点，则执行如下( )语句序列。

A. p=q; p->next=q;B. p->next=q; q->next=p;C. p->next=q->next; p=q;D. q->next=p->next; p->next=q;3.以下哪一个不是队列的基本运算？（）A. 在队列第i个元素之后插入一个元素B. 从队头删除一个元素C. 判断一个队列是否为空D.读取队头元素的值4.字符A、B、C依次进入一个栈，按出栈的先后顺序组成不同的字符串，至多可以组成( )个不同的字符串？A.14B.5C.6D.85.由权值分别为3,8,6,2的叶子生成一棵哈夫曼树，它的带权路径长度为( )。

以下6-8题基于图1。

6.该二叉树结点的前序遍历的序列为( )。

A.E、G、F、A、C、D、BB.E、A、G、C、F、B、DC.E、A、C、B、D、G、FD.E、G、A、C、D、F、B7.该二叉树结点的中序遍历的序列为( )。

A. A、B、C、D、E、G、FB. E、A、G、C、F、B、DC. E、A、C、B、D、G、FE.B、D、C、A、F、G、E8.该二叉树的按层遍历的序列为( )。

A．E、G、F、A、C、D、B B. E、A、C、B、D、G、FC. E、A、G、C、F、B、DD. E、G、A、C、D、F、B9.下面关于图的存储的叙述中正确的是( )。

A．用邻接表法存储图，占用的存储空间大小只与图中边数有关，而与结点个数无关B．用邻接表法存储图，占用的存储空间大小与图中边数和结点个数都有关C. 用邻接矩阵法存储图，占用的存储空间大小与图中结点个数和边数都有关D．用邻接矩阵法存储图，占用的存储空间大小只与图中边数有关，而与结点个数无关10.设有关键码序列(q，g，m，z，a，n，p，x，h)，下面哪一个序列是从上述序列出发建堆的结果?( )A. a，g，h，m，n，p，q，x，zB. a，g，m，h，q，n，p，x，zC. g，m，q，a，n，p，x，h，zD. h，g，m，p，a，n，q，x，z二、填空题（每空1分，共26分）1.数据的物理结构被分为_________、________、__________和___________四种。

Mark Allen Weiss 数据结构与算法分析课后习题答案11

Chapter11:Amortized Analysis11.1When the number of trees after the insertions is more than the number before.11.2Although each insertion takes roughly log N ,and each DeleteMin takes2log N actualtime,our accounting system is charging these particular operations as2for the insertion and3log N −2for the DeleteMin. The total time is still the same;this is an accounting gimmick.If the number of insertions and DeleteMins are roughly equivalent,then it really is just a gimmick and not very meaningful;the bound has more signiﬁcance if,for instance,there are N insertions and O (N / log N )DeleteMins (in which case,the total time is linear).11.3Insert the sequence N ,N +1,N −1,N +2,N −2,N +3,...,1,2N into an initiallyempty skew heap.The right path has N nodes,so any operation could takeΩ(N )time. 11.5We implement DecreaseKey(X,H)as follows:If lowering the value of X creates a heaporder violation,then cut X from its parent,which creates a new skew heap H 1with the new value of X as a root,and also makes the old skew heap H smaller.This operation might also increase the potential of H ,but only by at most log N .We now merge H andH 1.The total amortized time of the Merge is O (log N ),so the total time of theDecreaseKey operation is O (log N ).11.8For the zig −zig case,the actual cost is2,and the potential change isR f ( X )+ R f ( P )+ R f ( G )− R i ( X )− R i ( P )− R i ( G ).This gives an amortized time bound ofAT zig −zig =2+ R f ( X )+ R f ( P )+ R f ( G )− R i ( X )− R i ( P )− R i ( G )Since R f ( X )= R i ( G ),this reduces to=2+ R f ( P )+ R f ( G )− R i ( X )− R i ( P )Also,R f ( X )> R f ( P )and R i ( X )< R i ( P ),soAT zig −zig <2+ R f ( X )+ R f ( G )−2R i ( X )Since S i ( X )+ S f ( G )< S f ( X ),it follows that R i ( X )+ R f ( G )<2R f ( X )−2.ThusAT zig −zig <3R f ( X )−3R i ( X )11.9(a)Choose W (i )=1/ N for each item.Then for any access of node X ,R f ( X )=0,andR i ( X )≥−log N ,so the amortized access for each item is at most3log N +1,and the net potential drop over the sequence is at most N log N ,giving a bound of O (M log N + M + N log N ),as claimed.(b)Assign a weight of q i /M to items i .Then R f ( X )=0,R i ( X )≥log(q i /M ),so theamortized cost of accessing item i is at most3log(M /q i )+1,and the theorem follows immediately.11.10(a)To merge two splay trees T 1and T 2,we access each node in the smaller tree andinsert it into the larger tree.Each time a node is accessed,it joins a tree that is at leasttwice as large;thus a node can be inserted log N times.This tells us that in any sequence of N −1merges,there are at most N log N inserts,giving a time bound of O (N log2N ).This presumes that we keep track of the tree sizes.Philosophically,this is ugly since it defeats the purpose of self-adjustment.(b)Port and Moffet[6]suggest the following algorithm:If T 2is the smaller tree,insert itsroot into T 1.Then recursively merge the left subtrees of T 1and T 2,and recursively merge their right subtrees.This algorithm is not analyzed;a variant in which the median of T 2is splayed to the rootﬁrst is with a claim of O (N log N )for the sequence of merges.11.11The potential function is c times the number of insertions since the last rehashing step,where c is a constant.For an insertion that doesn’t require rehashing,the actual time is 1,and the potential increases by c ,for a cost of1+ c .If an insertion causes a table to be rehashed from size S to2S ,then the actual cost is 1+ dS ,where dS represents the cost of initializing the new table and copying the old table back.A table that is rehashed when it reaches size S was last rehashed at size S / 2, so S / 2insertions had taken place prior to the rehash,and the initial potential was cS / 2.The new potential is0,so the potential change is−cS / 2,giving an amortized bound of(d − c / 2)S +1.We choose c =2d ,and obtain an O (1)amortized bound in both cases.11.12We show that the amortized number of node splits is1per insertion.The potential func-tion is the number of three-child nodes in T .If the actual number of nodes splits for an insertion is s ,then the change in the potential function is at most1− s ,because each split converts a three-child node to two two-child nodes,but the parent of the last node split gains a third child(unless it is the root).Thus an insertion costs1node split,amor-tized.An N node tree has N units of potential that might be converted to actual time,so the total cost is O (M + N ).(If we start from an initially empty tree,then the bound is O (M ).)11.13(a)This problem is similar to Exercise3.22.Theﬁrst four operations are easy to imple-ment by placing two stacks,S L and S R ,next to each other(with bottoms touching).We can implement theﬁfth operation by using two more stacks,M L and M R (which hold minimums).If both S L and S R never empty,then the operations can be implemented as follows:Push(X,D):push X onto S L ;if X is smaller than or equal to the top of M L ,push X onto M L as well.Inject(X,D):same operation as Push ,except use S R and M R .Pop(D):pop S L ;if the popped item is equal to the top of M L ,then pop M L as well.Eject(D):same operation as Pop ,except use S R and M R .FindMin(D):return the minimum of the top of M L and M R .These operations don’t work if either S L or S R is empty.If a Pop or E j ect is attempted on an empty stack,then we clear M L and M R .We then redistribute the elements so that half are in S L and the rest in S R ,and adjust M L and M R to reﬂect what the state would be.We can then perform the Pop or E j ect in the normal fashion.Fig. 11.1shows a transfor-mation.Deﬁne the potential function to be the absolute value of the number of elements in S L minus the number of elements in S R .Any operation that doesn’t empty S L or S R can3,1,4,6,5,9,2,61,2,63,1,4,65,9,2,6 1,4,65,2S L S R M L RL S RM L M R Fig.11.1.increase the potential by only1;since the actual time for these operations is constant,so is the amortized time.To complete the proof,we show that the cost of a reorganization is O (1)amortized time. Without loss of generality,if S R is empty,then the actual cost of the reorganization is | S L | units.The potential before the reorganization is | S L | ;afterward,it is at most1. Thus the potential change is1− | S L | ,and the amortized bound follows.。

数据结构与算法课后习题解答

数据结构与算法课后习题解答数据结构与算法课后习题解答第一章绪论（参考答案）1.3 (1) O(n)(2) (2) O(n)(3) (3) O(n)(4) (4) O(n1/2)(5) (5) 执行程序段的过程中，x,y值变化如下：循环次数x y0（初始）91 1001 92 1002 93 100。

9 100 10010 101 10011 9112。

20 9921 91 98。

30 101 9831 91 97到y=0时，要执行10*100次，可记为O（10*y）=O（n）数据结构与算法课后习题解答1.5 2100 , (2/3)n , log2n , n1/2 , n3/2 , (3/2)n , nlog2n , 2 n , n! , n n第二章线性表(参考答案)在以下习题解答中，假定使用如下类型定义：（1）顺序存储结构：#define ***** 1024typedef int ElemType;// 实际上，ElemTypetypedef struct{ ElemType data[*****];int last; // last}sequenlist;（2*next；}linklist;（3）链式存储结构（双链表）typedef struct node{ElemType data;struct node *prior,*next；数据结构与算法课后习题解答}dlinklist;（4）静态链表typedef struct{ElemType data;int next;}node;node sa[*****];2.1 la，往往简称为“链表la”。

是副产品）2.2 23voidelenum个元素，且递增有序，本算法将x插入到向量A中，并保持向量的{ int i=0,j;while (ielenum A[i]=x) i++; // 查找插入位置for (j= elenum-1;jj--) A[j+1]=A[j];// 向后移动元素A[i]=x; // 插入元素数据结构与算法课后习题解答} // 算法结束24void rightrotate(ElemType A[],int n,k)// 以向量作存储结构，本算法将向量中的n个元素循环右移k位，且只用一个辅助空间。

数据结构与算法设计课后习题及答案详解

数据结构与算法设计课后习题及答案详解1. 习题一：数组求和题目描述：给定一个整数数组，编写一个函数来计算它的所有元素之和。

解题思路：遍历数组，将每个元素累加到一个变量中，最后返回累加和。

代码实现：```pythondef sum_array(arr):result = 0for num in arr:result += numreturn result```2. 习题二：链表反转题目描述：给定一个单链表，反转它的节点顺序。

解题思路：采用三指针法，依次将当前节点的下一个节点指向上一个节点，然后更新三个指针的位置，直到链表反转完毕。

代码实现：```pythonclass ListNode:def __init__(self, val=0, next=None):self.val = valself.next = nextdef reverse_list(head):prev = Nonecurr = headwhile curr:next_node = curr.nextcurr.next = prevprev = currcurr = next_nodereturn prev```3. 习题三：二叉树的层序遍历题目描述：给定一个二叉树，返回其节点值的层序遍历结果。

解题思路：采用队列来实现层序遍历，先将根节点入队，然后循环出队并访问出队节点的值，同时将出队节点的左右子节点入队。

代码实现：```pythonclass TreeNode:def __init__(self, val=0, left=None, right=None): self.val = valself.left = leftself.right = rightdef level_order(root):if not root:return []result = []queue = [root]while queue:level = []for _ in range(len(queue)):node = queue.pop(0)level.append(node.val)if node.left:queue.append(node.left)queue.append(node.right)result.append(level)return result```4. 习题四：堆排序题目描述：给定一个无序数组，使用堆排序算法对其进行排序。

《数据结构与算法分析》(C++第二版)【美】Clifford A.Shaffer著课后习题答案二

《数据结构与算法分析》（C++第二版）【美】Clifford A.Shaffer著课后习题答案二5Binary Trees5.1 Consider a non-full binary tree. By definition, this tree must have some internalnode X with only one non-empty child. If we modify the tree to removeX, replacing it with its child, the modified tree will have a higher fraction ofnon-empty nodes since one non-empty node and one empty node have been removed.5.2 Use as the base case the tree of one leaf node. The number of degree-2 nodesis 0, and the number of leaves is 1. Thus, the theorem holds.For the induction hypothesis, assume the theorem is true for any tree withn − 1 nodes.For the induction step, consider a tree T with n nodes. Remove from the treeany leaf node, and call the resulting tree T. By the induction hypothesis, Thas one more leaf node than it has nodes of degree 2.Now, restore the leaf node that was removed to form T. There are twopossible cases.(1) If this leaf node is the only child of its parent in T, then the number ofnodes of degree 2 has not changed, nor has the number of leaf nodes. Thus,the theorem holds.(2) If this leaf node is the child of a node in T with degree 2, then that nodehas degree 1 in T. Thus, by restoring the leaf node we are adding one newleaf node and one new node of degree 2. Thus, the theorem holds.By mathematical induction, the theorem is correct.32335.3 Base Case: For the tree of one leaf node, I = 0, E = 0, n = 0, so thetheorem holds.Induction Hypothesis: The theorem holds for the full binary tree containingn internal nodes.Induction Step: Take an arbitrary tree (call it T) of n internal nodes. Selectsome internal node x from T that has two leaves, and remove those twoleaves. Call the resulting tree T’. Tree T’ is full and has n−1 internal nodes,so by the Induction Hypothesis E = I + 2(n − 1).Call the depth of node x as d. Restore the two children of x, each at leveld+1. We have nowadded d to I since x is now once again an internal node.We have now added 2(d + 1) − d = d + 2 to E since we added the two leafnodes, but lost the contribution of x to E. Thus, if before the addition we had E = I + 2(n − 1) (by the induction hypothesis), then after the addition we have E + d = I + d + 2 + 2(n − 1) or E = I + 2n which is correct. Thus,by the principle of mathematical induction, the theorem is correct.5.4 (a) template <class Elem>void inorder(BinNode<Elem>* subroot) {if (subroot == NULL) return; // Empty, do nothingpreorder(subroot->left());visit(subroot); // Perform desired actionpreorder(subroot->right());}(b) template <class Elem>void postorder(BinNode<Elem>* subroot) {if (subroot == NULL) return; // Empty, do nothingpreorder(subroot->left());preorder(subroot->right());visit(subroot); // Perform desired action}5.5 The key is to search both subtrees, as necessary.template <class Key, class Elem, class KEComp>bool search(BinNode<Elem>* subroot, Key K);if (subroot == NULL) return false;if (subroot->value() == K) return true;if (search(subroot->right())) return true;return search(subroot->left());}34 Chap. 5 Binary Trees5.6 The key is to use a queue to store subtrees to be processed.template <class Elem>void level(BinNode<Elem>* subroot) {AQueue<BinNode<Elem>*> Q;Q.enqueue(subroot);while(!Q.isEmpty()) {BinNode<Elem>* temp;Q.dequeue(temp);if(temp != NULL) {Print(temp);Q.enqueue(temp->left());Q.enqueue(temp->right());}}}5.7 template <class Elem>int height(BinNode<Elem>* subroot) {if (subroot == NULL) return 0; // Empty subtreereturn 1 + max(height(subroot->left()),height(subroot->right()));}5.8 template <class Elem>int count(BinNode<Elem>* subroot) {if (subroot == NULL) return 0; // Empty subtreeif (subroot->isLeaf()) return 1; // A leafreturn 1 + count(subroot->left()) +count(subroot->right());}5.9 (a) Since every node stores 4 bytes of data and 12 bytes of pointers, the overhead fraction is 12/16 = 75%.(b) Since every node stores 16 bytes of data and 8 bytes of pointers, the overhead fraction is 8/24 ≈ 33%.(c) Leaf nodes store 8 bytes of data and 4 bytes of pointers; internal nodesstore 8 bytes of data and 12 bytes of pointers. Since the nodes havedifferent sizes, the total space needed for internal nodes is not the sameas for leaf nodes. Students must be careful to do the calculation correctly,taking the weighting into account. The correct formula looks asfollows, given that there are x internal nodes and x leaf nodes.4x + 12x12x + 20x= 16/32 = 50%.(d) Leaf nodes store 4 bytes of data; internal nodes store 4 bytes of pointers. The formula looks as follows, given that there are x internal nodes and35x leaf nodes:4x4x + 4x= 4/8 = 50%.5.10 If equal valued nodes were allowed to appear in either subtree, then during a search for all nodes of a given value, whenever we encounter a node of that value the search would be required to search in both directions.5.11 This tree is identical to the tree of Figure 5.20(a), except that a node with value 5 will be added as the right child of the node with value 2.5.12 This tree is identical to the tree of Figure 5.20(b), except that the value 24 replaces the value 7, and the leaf node that originally contained 24 is removed from the tree.5.13 template <class Key, class Elem, class KEComp>int smallcount(BinNode<Elem>* root, Key K);if (root == NULL) return 0;if (KEComp.gt(root->value(), K))return smallcount(root->leftchild(), K);elsereturn smallcount(root->leftchild(), K) +smallcount(root->rightchild(), K) + 1;5.14 template <class Key, class Elem, class KEComp>void printRange(BinNode<Elem>* root, int low,int high) {if (root == NULL) return;if (KEComp.lt(high, root->val()) // all to leftprintRange(root->left(), low, high);else if (KEComp.gt(low, root->val())) // all to rightprintRange(root->right(), low, high);else { // Must process both childrenprintRange(root->left(), low, high);PRINT(root->value());printRange(root->right(), low, high);}}5.15 The minimum number of elements is contained in the heap with a single node at depth h − 1, for a total of 2h−1 nodes.The maximum number of elements is contained in the heap that has completely filled up level h − 1, for a total of 2h − 1 nodes.5.16 The largest element could be at any leaf node.5.17 The corresponding array will be in the following order (equivalent to level order for the heap):12 9 10 5 4 1 8 7 3 236 Chap. 5 Binary Trees5.18 (a) The array will take on the following order:6 5 3 4 2 1The value 7 will be at the end of the array.(b) The array will take on the following order:7 4 6 3 2 1The value 5 will be at the end of the array.5.19 // Min-heap classtemplate <class Elem, class Comp> class minheap {private:Elem* Heap; // Pointer to the heap arrayint size; // Maximum size of the heapint n; // # of elements now in the heapvoid siftdown(int); // Put element in correct placepublic:minheap(Elem* h, int num, int max) // Constructor{ Heap = h; n = num; size = max; buildHeap(); }int heapsize() const // Return current size{ return n; }bool isLeaf(int pos) const // TRUE if pos a leaf{ return (pos >= n/2) && (pos < n); }int leftchild(int pos) const{ return 2*pos + 1; } // Return leftchild posint rightchild(int pos) const{ return 2*pos + 2; } // Return rightchild posint parent(int pos) const // Return parent position { return (pos-1)/2; }bool insert(const Elem&); // Insert value into heap bool removemin(Elem&); // Remove maximum value bool remove(int, Elem&); // Remove from given pos void buildHeap() // Heapify contents{ for (int i=n/2-1; i>=0; i--) siftdown(i); }};template <class Elem, class Comp>void minheap<Elem, Comp>::siftdown(int pos) { while (!isLeaf(pos)) { // Stop if pos is a leafint j = leftchild(pos); int rc = rightchild(pos);if ((rc < n) && Comp::gt(Heap[j], Heap[rc]))j = rc; // Set j to lesser child’s valueif (!Comp::gt(Heap[pos], Heap[j])) return; // Done37swap(Heap, pos, j);pos = j; // Move down}}template <class Elem, class Comp>bool minheap<Elem, Comp>::insert(const Elem& val) { if (n >= size) return false; // Heap is fullint curr = n++;Heap[curr] = val; // Start at end of heap// Now sift up until curr’s parent < currwhile ((curr!=0) &&(Comp::lt(Heap[curr], Heap[parent(curr)]))) {swap(Heap, curr, parent(curr));curr = parent(curr);}return true;}template <class Elem, class Comp>bool minheap<Elem, Comp>::removemin(Elem& it) { if (n == 0) return false; // Heap is emptyswap(Heap, 0, --n); // Swap max with last valueif (n != 0) siftdown(0); // Siftdown new root valit = Heap[n]; // Return deleted valuereturn true;}38 Chap. 5 Binary Trees// Remove value at specified positiontemplate <class Elem, class Comp>bool minheap<Elem, Comp>::remove(int pos, Elem& it) {if ((pos < 0) || (pos >= n)) return false; // Bad posswap(Heap, pos, --n); // Swap with last valuewhile ((pos != 0) &&(Comp::lt(Heap[pos], Heap[parent(pos)])))swap(Heap, pos, parent(pos)); // Push up if largesiftdown(pos); // Push down if small keyit = Heap[n];return true;}5.20 Note that this summation is similar to Equation 2.5. To solve the summation requires the shifting technique from Chapter 14, so this problem may be too advanced for many students at this time. Note that 2f(n) − f(n) = f(n),but also that:2f(n) − f(n) = n(24+48+616+ ··· +2(log n − 1)n) −n(14+28+316+ ··· +log n − 1n)logn−1i=112i− log n − 1n)= n(1 − 1n− log n − 1n)= n − log n.5.21 Here are the final codes, rather than a picture.l 00h 010i 011e 1000f 1001j 101d 11000a 1100100b 1100101c 110011g 1101k 11139The average code length is 3.234455.22 The set of sixteen characters with equal weight will create a Huffman coding tree that is complete with 16 leaf nodes all at depth 4. Thus, the average code length will be 4 bits. This is identical to the fixed length code. Thus, in this situation, the Huffman coding tree saves no space (and costs no space).5.23 (a) By the prefix property, there can be no character with codes 0, 00, or 001x where “x” stands for any binary string.(b) There must be at least one code with each form 1x, 01x, 000x where“x” could be any binary string (including the empty string).5.24 (a) Q and Z are at level 5, so any string of length n containing only Q’s and Z’s requires 5n bits.(b) O and E are at level 2, so any string of length n containing only O’s and E’s requires 2n bits.(c) The weighted average is5 ∗ 5 + 10 ∗ 4 + 35 ∗ 3 + 50 ∗ 2100bits per character5.25 This is a straightforward modification.// Build a Huffman tree from minheap h1template <class Elem>HuffTree<Elem>*buildHuff(minheap<HuffTree<Elem>*,HHCompare<Elem> >* hl) {HuffTree<Elem> *temp1, *temp2, *temp3;while(h1->heapsize() > 1) { // While at least 2 itemshl->removemin(temp1); // Pull first two treeshl->removemin(temp2); // off the heaptemp3 = new HuffTree<Elem>(temp1, temp2);hl->insert(temp3); // Put the new tree back on listdelete temp1; // Must delete the remnantsdelete temp2; // of the trees we created}return temp3;}6General Trees6.1 The following algorithm is linear on the size of the two trees. // Return TRUE iff t1 and t2 are roots of identical// general treestemplate <class Elem>bool Compare(GTNode<Elem>* t1, GTNode<Elem>* t2) { GTNode<Elem> *c1, *c2;if (((t1 == NULL) && (t2 != NULL)) ||((t2 == NULL) && (t1 != NULL)))return false;if ((t1 == NULL) && (t2 == NULL)) return true;if (t1->val() != t2->val()) return false;c1 = t1->leftmost_child();c2 = t2->leftmost_child();while(!((c1 == NULL) && (c2 == NULL))) {if (!Compare(c1, c2)) return false;if (c1 != NULL) c1 = c1->right_sibling();if (c2 != NULL) c2 = c2->right_sibling();}}6.2 The following algorithm is Θ(n2).// Return true iff t1 and t2 are roots of identical// binary treestemplate <class Elem>bool Compare2(BinNode<Elem>* t1, BinNode<Elem* t2) { BinNode<Elem> *c1, *c2;if (((t1 == NULL) && (t2 != NULL)) ||((t2 == NULL) && (t1 != NULL)))return false;if ((t1 == NULL) && (t2 == NULL)) return true;4041if (t1->val() != t2->val()) return false;if (Compare2(t1->leftchild(), t2->leftchild())if (Compare2(t1->rightchild(), t2->rightchild())return true;if (Compare2(t1->leftchild(), t2->rightchild())if (Compare2(t1->rightchild(), t2->leftchild))return true;return false;}6.3 template <class Elem> // Print, postorder traversalvoid postprint(GTNode<Elem>* subroot) {for (GTNode<Elem>* temp = subroot->leftmost_child();temp != NULL; temp = temp->right_sibling())postprint(temp);if (subroot->isLeaf()) cout << "Leaf: ";else cout << "Internal: ";cout << subroot->value() << "\n";}6.4 template <class Elem> // Count the number of nodesint gencount(GTNode<Elem>* subroot) {if (subroot == NULL) return 0int count = 1;GTNode<Elem>* temp = rt->leftmost_child();while (temp != NULL) {count += gencount(temp);temp = temp->right_sibling();}return count;}6.5 The Weighted Union Rule requires that when two parent-pointer trees are merged, the smaller one’s root becomes a child of the larger one’s root. Thus, we need to keep track of the number of nodes in a tree. To do so, modify the node array to store an integer value with each node. Initially, each node isin its own tree, so the weights for each node begin as 1. Whenever we wishto merge two trees, check the weights of the roots to determine which has more nodes. Then, add to the weight of the final root the weight of the new subtree.6.60 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15-1 0 0 0 0 0 0 6 0 0 0 9 0 0 12 06.7 The resulting tree should have the following structure:42 Chap. 6 General TreesNode 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15Parent 4 4 4 4 -1 4 4 0 0 4 9 9 9 12 9 -16.8 For eight nodes labeled 0 through 7, use the following series of equivalences: (0, 1) (2, 3) (4, 5) (6, 7) (4 6) (0, 2) (4 0)This requires checking fourteen parent pointers (two for each equivalence),but none are actually followed since these are all roots. It is possible todouble the number of parent pointers checked by choosing direct children ofroots in each case.6.9 For the “lists of Children” representation, every node stores a data value and a pointer to its list of children. Further, every child (every node except the root)has a record associated with it containing an index and a pointer. Indicatingthe size of the data value as D, the size of a pointer as P and the size of anindex as I, the overhead fraction is3P + ID + 3P + I.For the “Left Child/Right Sibling” representation, every node stores three pointers and a data value, for an overhead fraction of3PD + 3P.The first linked representation of Section 6.3.3 stores with each node a datavalue and a size field (denoted by S). Each child (every node except the root)also has a pointer pointing to it. The overhead fraction is thusS + PD + S + Pmaking it quite efficient.The second linked representation of Section 6.3.3 stores with each node adata value and a pointer to the list of children. Each child (every node exceptthe root) has two additional pointers associated with it to indicate its placeon the parent’s linked list. Thus, the overhead fraction is3PD + 3P.6.10 template <class Elem>BinNode<Elem>* convert(GTNode<Elem>* genroot) {if (genroot == NULL) return NULL;43GTNode<Elem>* gtemp = genroot->leftmost_child();btemp = new BinNode(genroot->val(), convert(gtemp),convert(genroot->right_sibling()));}6.11 • Parent(r) = (r − 1)/k if 0 < r < n.• Ith child(r) = kr + I if kr +I < n.• Left sibling(r) = r − 1 if r mod k = 1 0 < r < n.• Right sibling(r) = r + 1 if r mod k = 0 and r + 1 < n.6.12 (a) The overhead fraction is4(k + 1)4 + 4(k + 1).(b) The overhead fraction is4k16 + 4k.(c) The overhead fraction is4(k + 2)16 + 4(k + 2).(d) The overhead fraction is2k2k + 4.6.13 Base Case: The number of leaves in a non-empty tree of 0 internal nodes is (K − 1)0 + 1 = 1. Thus, the theorem is correct in the base case.Induction Hypothesis: Assume that the theorem is correct for any full Karytree containing n internal nodes.Induction Step: Add K children to an arbitrary leaf node of the tree withn internal nodes. This new tree now has 1 more internal node, and K − 1more leaf nodes, so theorem still holds. Thus, the theorem is correct, by the principle of Mathematical Induction.6.14 (a) CA/BG///FEDD///H/I//(b) CA/BG/FED/H/I6.15 X|P-----| | |C Q R---| |V M44 Chap. 6 General Trees6.16 (a) // Use a helper function with a pass-by-reference// variable to indicate current position in the// node list.template <class Elem>BinNode<Elem>* convert(char* inlist) {int curr = 0;return converthelp(inlist, curr);}// As converthelp processes the node list, curr is// incremented appropriately.template <class Elem>BinNode<Elem>* converthelp(char* inlist,int& curr) {if (inlist[curr] == ’/’) {curr++;return NULL;}BinNode<Elem>* temp = new BinNode(inlist[curr++], NULL, NULL);temp->left = converthelp(inlist, curr);temp->right = converthelp(inlist, curr);return temp;}(b) // Use a helper function with a pass-by-reference // variable to indicate current position in the// node list.template <class Elem>BinNode<Elem>* convert(char* inlist) {int curr = 0;return converthelp(inlist, curr);}// As converthelp processes the node list, curr is// incremented appropriately.template <class Elem>BinNode<Elem>* converthelp(char* inlist,int& curr) {if (inlist[curr] == ’/’) {curr++;return NULL;}BinNode<Elem>* temp =new BinNode<Elem>(inlist[curr++], NULL, NULL);if (inlist[curr] == ’\’’) return temp;45curr++ // Eat the internal node mark.temp->left = converthelp(inlist, curr);temp->right = converthelp(inlist, curr);return temp;}(c) // Use a helper function with a pass-by-reference// variable to indicate current position in the// node list.template <class Elem>GTNode<Elem>* convert(char* inlist) {int curr = 0;return converthelp(inlist, curr);}// As converthelp processes the node list, curr is// incremented appropriately.template <class Elem>GTNode<Elem>* converthelp(char* inlist,int& curr) {if (inlist[curr] == ’)’) {curr++;return NULL;}GTNode<Elem>* temp =new GTNode<Elem>(inlist[curr++]);if (curr == ’)’) {temp->insert_first(NULL);return temp;}temp->insert_first(converthelp(inlist, curr));while (curr != ’)’)temp->insert_next(converthelp(inlist, curr));curr++;return temp;}6.17 The Huffman tree is a full binary tree. To decode, we do not need to know the weights of nodes, only the letter values stored in the leaf nodes. Thus, we can use a coding much like that of Equation 6.2, storing only a bit mark for internal nodes, and a bit mark and letter value for leaf nodes.7Internal Sorting7.1 Base Case: For the list of one element, the double loop is not executed and the list is not processed. Thus, the list of one element remains unaltered and is sorted.Induction Hypothesis: Assume that the list of n elements is sorted correctlyby Insertion Sort.Induction Step: The list of n + 1 elements is processed by first sorting thetop n elements. By the induction hypothesis, this is done correctly. The final pass of the outer for loop will process the last element (call it X). This isdone by the inner for loop, which moves X up the list until a value smallerthan that of X is encountered. At this point, X has been properly insertedinto the sorted list, leaving the entire collection of n + 1 elements correctly sorted. Thus, by the principle of Mathematical Induction, the theorem is correct.7.2 void StackSort(AStack<int>& IN) {AStack<int> Temp1, Temp2;while (!IN.isEmpty()) // Transfer to another stackTemp1.push(IN.pop());IN.push(Temp1.pop()); // Put back one elementwhile (!Temp1.isEmpty()) { // Process rest of elemswhile (IN.top() > Temp1.top()) // Find elem’s placeTemp2.push(IN.pop());IN.push(Temp1.pop()); // Put the element inwhile (!Temp2.isEmpty()) // Put the rest backIN.push(Temp2.pop());}}46477.3 The revised algorithm will work correctly, and its asymptotic complexity will remain Θ(n2). However, it will do about twice as many comparisons, since it will compare adjacent elements within the portion of the list already knownto be sorted. These additional comparisons are unproductive.7.4 While binary search will find the proper place to locate the next element, it will still be necessary to move the intervening elements down one position in the array. This requires the same number of operations as a sequential search. However, it does reduce the number of element/element comparisons, and may be somewhat faster by a constant factor since shifting several elements may be more efficient than an equal number of swap operations.7.5 (a) template <class Elem, class Comp>void selsort(Elem A[], int n) { // Selection Sortfor (int i=0; i<n-1; i++) { // Select i’th recordint lowindex = i; // Remember its indexfor (int j=n-1; j>i; j--) // Find least valueif (Comp::lt(A[j], A[lowindex]))lowindex = j; // Put it in placeif (i != lowindex) // Add check for exerciseswap(A, i, lowindex);}}(b) There is unlikely to be much improvement; more likely the algorithmwill slow down. This is because the time spent checking (n times) isunlikely to save enough swaps to make up.(c) Try it and see!7.6 • Insertion Sort is stable. A swap is done only if the lower element’svalue is LESS.• Bubble Sort is stable. A swap is done only if the lower element’s valueis LESS.• Selection Sort is NOT stable. The new low value is set only if it isactually less than the previous one, but the direction of the search isfrom the bottom of the array. The algorithm will be stable if “less than”in the check becomes “less than or equal to” for selecting the low key position.• Shell Sort is NOT stable. The sublist sorts are done independently, andit is quite possible to swap an element in one sublist ahead of its equalvalue in another sublist. Once they are in the same sublist, they willretain this (incorrect) relationship.• Quick-sort is NOT stable. After selecting the pivot, it is swapped withthe last element. This action can easily put equal records out of place.48 Chap. 7 Internal Sorting• Conceptually (in particular, the linked list version) Mergesort is stable.The array implementations are NOT stable, since, given that the sublistsare stable, the merge operation will pick the element from the lower listbefore the upper list if they are equal. This is easily modified to replace“less than” with “less than or equal to.”• Heapsort is NOT stable. Elements in separate sides of the heap are processed independently, and could easily become out of relative order.• Binsort is stable. Equal values that come later are appended to the list.• Radix Sort is stable. While the processing is from bottom to top, thebins are also filled from bottom to top, preserving relative order.7.7 In the worst case, the stack can store n records. This can be cut to log n in the worst case by putting the larger partition on FIRST, followed by the smaller. Thus, the smaller will be processed first, cutting the size of the next stacked partition by at least half.7.8 Here is how I derived a permutation that will give the desired (worst-case) behavior:a b c 0 d e f g First, put 0 in pivot index (0+7/2),assign labels to the other positionsa b c g d e f 0 First swap0 b c g d e f a End of first partition pass0 b c g 1 e f a Set d = 1, it is in pivot index (1+7/2)0 b c g a e f 1 First swap0 1 c g a e f b End of partition pass0 1 c g 2 e f b Set a = 2, it is in pivot index (2+7/2)0 1 c g b e f 2 First swap0 1 2 g b e f c End of partition pass0 1 2 g b 3 f c Set e = 3, it is in pivot index (3+7/2)0 1 2 g b c f 3 First swap0 1 2 3 b c f g End of partition pass0 1 2 3 b 4 f g Set c = 4, it is in pivot index (4+7/2)0 1 2 3 b g f 4 First swap0 1 2 3 4 g f b End of partition pass0 1 2 3 4 g 5 b Set f = 5, it is in pivot index (5+7/2)0 1 2 3 4 g b 5 First swap0 1 2 3 4 5 b g End of partition pass0 1 2 3 4 5 6 g Set b = 6, it is in pivot index (6+7/2)0 1 2 3 4 5 g 6 First swap0 1 2 3 4 5 6 g End of parition pass0 1 2 3 4 5 6 7 Set g = 7.Plugging the variable assignments into the original permutation yields:492 6 4 0 13 5 77.9 (a) Each call to qsort costs Θ(i log i). Thus, the total cost isni=1i log i = Θ(n2 log n).(b) Each call to qsort costs Θ(n log n) for length(L) = n, so the totalcost is Θ(n2 log n).7.10 All that we need to do is redefine the comparison test to use strcmp. The quicksort algorithm itself need not change. This is the advantage of paramerizing the comparator.7.11 For n = 1000, n2 = 1, 000, 000, n1.5 = 1000 ∗√1000 ≈ 32, 000, andn log n ≈ 10, 000. So, the constant factor for Shellsort can be anything less than about 32 times that of Insertion Sort for Shellsort to be faster. The constant factor for Shellsort can be anything less than about 100 times thatof Insertion Sort for Quicksort to be faster.7.12 (a) The worst case occurs when all of the sublists are of size 1, except for one list of size i − k + 1. If this happens on each call to SPLITk, thenthe total cost of the algorithm will be Θ(n2).(b) In the average case, the lists are split into k sublists of roughly equal length. Thus, the total cost is Θ(n logk n).7.13 (This question comes from Rawlins.) Assume that all nuts and all bolts havea partner. We use two arrays N[1..n] and B[1..n] to represent nuts and bolts. Algorithm 1Using merge-sort to solve this problem.First, split the input into n/2 sub-lists such that each sub-list contains twonuts and two bolts. Then sort each sub-lists. We could well come up with apair of nuts that are both smaller than either of a pair of bolts. In that case,all you can know is something like:N1, N2。

《数据结构与算法》习题与答案

《数据结构与算法》习题与答案（解答仅供参考）一、名词解释：1. 数据结构：数据结构是计算机存储、组织数据的方式，它不仅包括数据的逻辑结构（如线性结构、树形结构、图状结构等），还包括物理结构（如顺序存储、链式存储等）。

它是算法设计与分析的基础，对程序的效率和功能实现有直接影响。

2. 栈：栈是一种特殊的线性表，其操作遵循“后进先出”（Last In First Out, LIFO）原则。

在栈中，允许进行的操作主要有两种：压栈（Push），将元素添加到栈顶；弹栈（Pop），将栈顶元素移除。

3. 队列：队列是一种先进先出（First In First Out, FIFO）的数据结构，允许在其一端插入元素（称为入队），而在另一端删除元素（称为出队）。

常见的实现方式有顺序队列和循环队列。

4. 二叉排序树（又称二叉查找树）：二叉排序树是一种二叉树，其每个节点的左子树中的所有节点的值都小于该节点的值，而右子树中的所有节点的值都大于该节点的值。

这种特性使得能在O(log n)的时间复杂度内完成搜索、插入和删除操作。

5. 图：图是一种非线性数据结构，由顶点（Vertex）和边（Edge）组成，用于表示对象之间的多种关系。

根据边是否有方向，可分为有向图和无向图；根据是否存在环路，又可分为有环图和无环图。

二、填空题：1. 在一个长度为n的顺序表中，插入一个新元素平均需要移动______个元素。

答案：(n/2)2. 哈希表利用______函数来确定元素的存储位置，通过解决哈希冲突以达到快速查找的目的。

答案：哈希（Hash）3. ______是最小生成树的一种算法，采用贪心策略，每次都选择当前未加入生成树且连接两个未连通集合的最小权重边。

答案：Prim算法4. 在深度优先搜索（DFS）过程中，使用______数据结构来记录已经被访问过的顶点，防止重复访问。

答案：栈或标记数组5. 快速排序算法在最坏情况下的时间复杂度为______。

Mark Allen Weiss 数据结构与算法分析课后习题答案1

k +1 i =1
Σ Fi =
sum on the right is Fk +2 − 2 + Fk +1 = Fk +3 − 2, where the latter equality follows from the deﬁnition of the Fibonacci numbers. This proves the claim for N = k + 1, and hence for all N. (b) As in the text, the proof is by induction. Observe that φ + 1 = φ2. This implies that φ−1 + φ−2 = 1. For N = 1 and N = 2, the statement is true. Assume the claim is true for N = 1, 2, ..., k . Fk +1 = Fk + Fk −1 by the deﬁnition and we can use the inductive hypothesis on the right-hand side, obtaining Fk +1 < φk + φk −1 < φ−1φk +1 + φ−2φk +1 Fk +1 < (φ−1 + φ−2)φk +1 < φk +1 and proving the theorem. (c) See any of the advanced math references at the end of the chapter. The derivation involves the use of generating functions. 1.10 (a) (2i −1) = 2 Σ i − Σ 1 = N (N +1) − N = N 2. Σ i =1 i =1 i =1

数据结构与算法分析课后习题解答

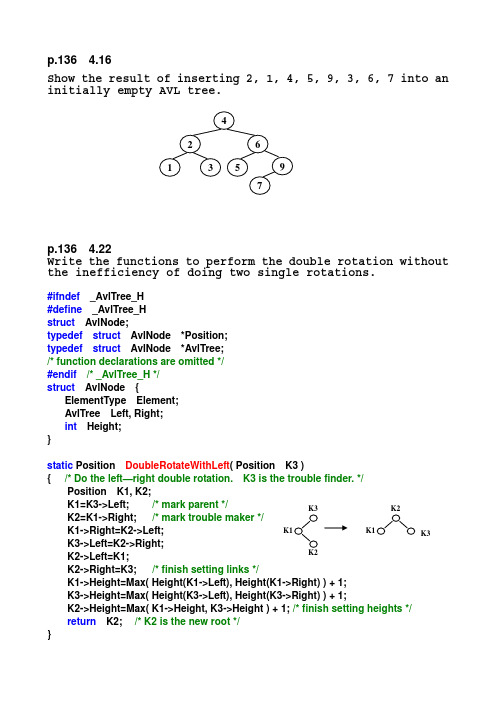
p.136 4.16Show the result of inserting 2, 1, 4, 5, 9, 3, 6, 7 into an initially empty AVL tree.p.136 4.22Write the functions to perform the double rotation without the inefficiency of doing two single rotations.#ifndef _AvlTree_H #define _AvlTree_H struct AvlNode;typedef struct AvlNode *Position; typedef struct AvlNode *AvlTree; /* function declarations are omitted */ #endif /* _AvlTree_H */ struct AvlNode { ElementType Element; AvlTree Left, Right; int Height; }static Position DoubleRotateWithLeft ( Position K3 ){ /* Do the left—right double rotation. K3 is the trouble finder. */ Position K1, K2;K1=K3->Left; /* mark parent */ K2=K1->Right; /* mark trouble maker */K1->Right=K2->Left;K3->Left=K2->Right;K2->Left=K1;K2->Right=K3; /* finish setting links */ K1->Height=Max( Height(K1->Left), Height(K1->Right) ) + 1; K3->Height=Max( Height(K3->Left), Height(K3->Right) ) + 1; K2->Height=Max( K1->Height, K3->Height ) + 1; /* finish setting heights */ return K2; /* K2 is the new root */ }K3static Position DoubleRotateWithRight( Position K1 ){ /* Do the right--left double rotation. K1 is the trouble finder. */Position K2, K3; /* Similar to the above function */K3=K1->Right;K2=K3->Left;K1->Right=K2->Left;K3->Left=K2->Right;K2->Left=K1;K2->Right=K3;K1->Height=Max( Height(K1->Left), Height(K1->Right) ) + 1;K3->Height=Max( Height(K3->Left), Height(K3->Right) ) + 1;K2->Height=Max( K1->Height, K3->Height ) + 1;return K2;}p.136 4.23Show the result of accessing the keys 3, 9, 1, 5 in order in the splay tree in Figure 4.61.Figure 4.61Result for 3:Result for 9:Result for 1:Result for 5:。

数据结构与算法分析java课后答案

数据结构与算法分析java课后答案【篇一：java程序设计各章习题及其答案】>1、 java程序是由什么组成的？一个程序中必须有public类吗？java源文件的命名规则是怎样的？答：一个java源程序是由若干个类组成。

一个java程序不一定需要有public类：如果源文件中有多个类时，则只能有一个类是public类；如果源文件中只有一个类，则不将该类写成public也将默认它为主类。

源文件命名时要求源文件主名应与主类（即用public修饰的类）的类名相同，扩展名为.java。

如果没有定义public类，则可以任何一个类名为主文件名，当然这是不主张的，因为它将无法进行被继承使用。

另外，对applet小应用程序来说，其主类必须为public，否则虽然在一些编译编译平台下可以通过（在bluej下无法通过）但运行时无法显示结果。

2、怎样区分应用程序和小应用程序？应用程序的主类和小应用程序的主类必须用public修饰吗？答：java application是完整的程序，需要独立的解释器来解释运行；而java applet则是嵌在html编写的web页面中的非独立运行程序，由web浏览器内部包含的java解释器来解释运行。

在源程序代码中两者的主要区别是：任何一个java application应用程序必须有且只有一个main方法，它是整个程序的入口方法；任何一个applet小应用程序要求程序中有且必须有一个类是系统类applet的子类，即该类头部分以extends applet结尾。

应用程序的主类当源文件中只有一个类时不必用public修饰，但当有多于一个类时则主类必须用public修饰。

小应用程序的主类在任何时候都需要用public来修饰。

3、开发与运行java程序需要经过哪些主要步骤和过程？答：主要有三个步骤（1）、用文字编辑器notepad（或在jcreator,gel, bulej,eclipse, jbuilder等）编写源文件；(2)、使用java编译器（如javac.exe)将.java源文件编译成字节码文件.class；(3)、运行java程序：对应用程序应通过java解释器（如java.exe)来运行，而对小应用程序应通过支持java标准的浏览器(如microsoft explorer)来解释运行。

数据结构与算法分析课后习题答案

数据结构与算法分析课后习题答案【篇一：《数据结构与算法》课后习题答案】>2.3.2 判断题2．顺序存储的线性表可以按序号随机存取。

（√）4．线性表中的元素可以是各种各样的，但同一线性表中的数据元素具有相同的特性，因此属于同一数据对象。

（√）6．在线性表的链式存储结构中，逻辑上相邻的元素在物理位置上不一定相邻。

（√）8．在线性表的顺序存储结构中，插入和删除时移动元素的个数与该元素的位置有关。

（√）9．线性表的链式存储结构是用一组任意的存储单元来存储线性表中数据元素的。

（√）2.3.3 算法设计题1．设线性表存放在向量a[arrsize]的前elenum个分量中，且递增有序。

试写一算法，将x 插入到线性表的适当位置上，以保持线性表的有序性，并且分析算法的时间复杂度。

【提示】直接用题目中所给定的数据结构（顺序存储的思想是用物理上的相邻表示逻辑上的相邻，不一定将向量和表示线性表长度的变量封装成一个结构体），因为是顺序存储，分配的存储空间是固定大小的，所以首先确定是否还有存储空间，若有，则根据原线性表中元素的有序性，来确定插入元素的插入位置，后面的元素为它让出位置，（也可以从高下标端开始一边比较，一边移位）然后插入x ，最后修改表示表长的变量。

int insert (datatype a[],int *elenum,datatype x) /*设elenum为表的最大下标*/ {if (*elenum==arrsize-1) return 0; /*表已满，无法插入*/else {i=*elenum;while (i=0 a[i]x)/*边找位置边移动*/{a[i+1]=a[i];i--;}a[i+1]=x;/*找到的位置是插入位的下一位*/ (*elenum)++;return 1;/*插入成功*/}}时间复杂度为o(n)。

2．已知一顺序表a，其元素值非递减有序排列，编写一个算法删除顺序表中多余的值相同的元素。

数据结构与算法分析-C++版答案

Data Structures and Algorithm 习题答案Preface ii1 Data Structures and Algorithms 12 Mathematical Preliminaries 53 Algorithm Analysis 174 Lists, Stacks, and Queues 235 Binary Trees 326 General Trees 407 Internal Sorting 468 File Processing and External Sorting 54 9Searching 5810 Indexing 6411 Graphs 6912 Lists and Arrays Revisited 7613 Advanced Tree Structures 82iii Contents14 Analysis Techniques 8815 Limits to Computation 94PrefaceContained herein are the solutions to all exercises from the textbook A Practical Introduction to Data Structures and Algorithm Analysis, 2nd edition.For most of the problems requiring an algorithm I have given actual code. Ina few cases I have presented pseudocode. Please be aware that the code presented in this manual has not actually been compiled and tested. While I believe the algorithmsto be essentially correct, there may be errors in syntax as well as semantics. Most importantly, these solutions provide a guide to the instructor as to the intendedanswer, rather than usable programs.1Data Structures and AlgorithmsInstructor’s note: Unlike the other chapters, many of the questions in this chapter are not really suitable for graded work. The questions are mainly intended to get students thinking about data structures issues.1.1This question does not have a specific right answer, provided the student keeps to the spirit of the question. Students may have trouble with the concept of “operations.”1.2This exercise asks the student to expand on their concept of an integer representation.A good answer is described by Project 4.5, where a singly-linkedlist is suggested. The most straightforward implementation stores each digitin its own list node, with digits stored in reverse order. Addition and multiplicationare implemented by what amounts to grade-school arithmetic. Foraddition, simply march down in parallel through the two lists representingthe operands, at each digit appending to a new list the appropriate partial sum and bringing forward a carry bit as necessary. For multiplication, combine the addition function with a new function that multiplies a single digitby an integer. Exponentiation can be done either by repeated multiplication (not really practical) or by the traditional Θ(log n)-time algorithm based on the binary representation of the exponent. Discovering this faster algorithm will be beyond the reach of most students, so should not be required.1.3A sample ADT for character strings might look as follows (with the normal interpretation of the function names assumed).Chap. 1 Data Structures and Algorithms// Concatenate two stringsString strcat(String s1, String s2);// Return the length of a stringint length(String s1);// Extract a substring, starting at ‘start’,// and of length ‘length’String extract(String s1, int start, int length);// Get the first characterchar first(String s1);// Compare two strings: the normal C++ strcmp function.Some// convention should be indicated for how to interpretthe// return value. In C++, this is 1for s1<s2; 0 for s1=s2;// and 1 for s1>s2.int strcmp(String s1, String s2)// Copy a stringint strcpy(String source, String destination)1.4The answer to this question is provided by the ADT for lists given in Chapter 4.1.5One’s compliment stores the binary representation of positive numbers, and stores the binary representation of a negative number with the bits inverted. Two’s compliment is the same, except that a negative number has its bits inverted and then one is added (for reasons of efficiency in hardware implementation).This representation is the physical implementation of an ADTdefined by the normal arithmetic operations, declarations, and other support given by the programming language for integers.1.6An ADT for two-dimensional arrays might look as follows.Matrix add(Matrix M1, Matrix M2);Matrix multiply(Matrix M1, Matrix M2);Matrix transpose(Matrix M1);void setvalue(Matrix M1, int row, int col, int val);int getvalue(Matrix M1, int row, int col);List getrow(Matrix M1, int row);One implementation for the sparse matrix is described in Section 12.3 Another implementationis a hash table whose search key is a concatenation of the matrix coordinates.1.7Every problem certainly does not have an algorithm. As discussed in Chapter 15, there are a number of reasons why this might be the case. Some problems don’t have a sufficiently clear definition. Some problems, such as the halting problem, are non-computable. For some problems, such as one typically studied by artificial intelligence researchers, we simply don’t know a solution.1.8We must assume that by “algorithm” we mean something composed of steps a reof a nature that they can be performed by a computer. If so, than any algorithm can be expressed in C++. In particular, if an algorithm can be expressed in any other computer programming language, then it can be expressed in C++, since all (sufficiently general) computer programming languages compute the same set of functions.1.9The primitive operations are (1) adding new words to the dictionary and (2) searching the dictionary for a given word. Typically, dictionary access involves some sort of pre-processing of the word to arrive at the “root” of the word.A twenty page document (single spaced) is likely to contain about 20,000 words. A user may be willing to wait a few seconds between individual “hits” of mis-spelled words, or perhaps up to a minute for the whole document to be processed. This means that a check for an individual word can take about 10-20 ms. Users will typically insert individual words into the dictionary interactively, so this process cantake a couple of seconds. Thus, search must be much more efficient than insertion.1.10The user should be able to find a city based on a variety of attributes (name, location,perhaps characteristics such as population size). The user should also be able to insertand delete cities. These are the fundamental operations of any database system: search, insertion and deletion.A reasonable database has a time constraint that will satisfy the patience of a typicaluser. For an insert, delete, or exact match query, a few seconds is satisfactory. If thedatabase is meant to support range queries and mass deletions, the entire operation may be allowed to take longer, perhaps on the order of a minute. However, the time spent to process individual cities within the range must be appropriately reduced.Inpractice, the data representation will need to be such that it accommodates efficient processing to meet these time constraints. In particular, it may be necessary to supportoperations that process range queries efficiently by processing all cities in the range as a batch, rather than as a series of operations on individual cities.1.11Students at this level are likely already familiar with binary search. Thus, they should typically respond with sequential search and binary search. Binary search should be described as better since it typically needs to make fewer comparisons (and thus is likely to be much faster).1.12The answer to this question is discussed in Chapter 8. Typical measures of cost will be number of comparisons and number of swaps. Tests should include running timings on sorted, reverse sorted, and random lists of various sizes.Chap. 1 Data Structures and Algorithms1.13The first part is easy with the hint, but the second part is rather difficult to do withouta stack.a) bool checkstring(string S) {int count = 0;for (int i=0; i<length(S); i++)if (S[i] == ’(’) count++;if (S[i] == ’)’) {if (count == 0) return FALSE;count--;}}if (count == 0) return TRUE;else return FALSE;}b) int checkstring(String Str) {Stack S;int count = 0;for (int i=0; i<length(S); i++)if (S[i] == ’(’)S.push(i);if (S[i] == ’)’) {if (S.isEmpty()) return i;S.pop();}if (S.isEmpty()) return -1;else return S.pop();}1.14Answers to this question are discussed in Section 7.2.1.15This is somewhat different from writing sorting algorithms for a computer, since person’s “working space” is typically limited, as is their ability to physically manipulatethe pieces of paper. Nonetheless, many of the common sorting algorithms have their analogs to solutions for this problem. Most typical answers will be insertion sort, variations on mergesort, and variations on binsort.1.16Answers to this question are discussed in Chapter 8.2Mathematical Preliminaries2.1(a) Not reflexive if the set has any members. One could argue it is symmetric, antisymmetric, and transitive, since no element violate any ofthe rules.(b)Not reflexive (for any female). Not symmetric (consider a brother and sister). Not antisymmetric (consider two brothers). Transitive (for any3 brothers).(c)Not reflexive. Not symmetric, and is antisymmetric. Not transitive(only goes one level).(d)Not reflexive (for nearly all numbers). Symmetric since a+ b= b+ a,so not antisymmetric. Transitive, but vacuously so (there can be nodistinct a, b,and cwhere aRband bRc).(e)Reflexive. Symmetric, so not antisymmetric. Transitive (but sort of vacuous).(f)Reflexive – check all the cases. Since it is only true when x= y,itis technically symmetric and antisymmetric, but rather vacuous. Likewise,it is technically transitive, but vacuous.2.2In general, prove that something is an equivalence relation by proving that it is reflexive, symmetric, and transitive.(a)This is an equivalence that effectively splits the integers into odd andeven sets. It is reflexive (x+ xis even for any integer x), symmetric(since x+ y= y+ x) and transitive (since you are always adding twoodd or even numbers for any satisfactory a, b,and c).(b)This is not an equivalence. To begin with, it is not reflexive for any integer.(c)This is an equivalence that divides the non-zero rational numbers into positive and negative. It is reflexive since x˙x>0. It is symmetric sincexy˙= yx˙. It is transitive since any two members of the given class satisfy the relationship.5Chap. 2 Mathematical Preliminaries(d)This is not an equivalance relation since it is not symmetric. For example,a=1and b=2.(e)This is an eqivalance relation that divides the rationals based on their fractional values. It is reflexive since for all a, a.a=0. It is symmetricsince if a.b=xthen b.a=.x. It is transitive since any two rationalswith the same fractional value will yeild an integer.(f)This is not an equivalance relation since it is not transitive. For example, 4.2=2and 2.0=2,but 4.0=4.2.3A relation is a partial ordering if it is antisymmetric and transitive.(a)Not a partial ordering because it is not transitive.(b)Is a partial ordering bacause it is antisymmetric (if ais an ancestor ofb, then bcannot be an ancestor of a) and transitive (since the ancestorof an ancestor is an ancestor).(c)Is a partial ordering bacause it is antisymmetric (if ais older than b,then bcannot be older than a) and transitive (since if ais older than band bis older than c, ais older than c).(d)Not a partial ordering, since it is not antisymmetric for any pair of sisters.(e)Not a partial ordering because it is not antisymmetric.(f)This is a partial ordering. It is antisymmetric (no violations exist) and transitive (no violations exist).2.4A total ordering can be viewed as a permuation of the elements. Since there are n!permuations of nelements, there must be n!total orderings.2.5This proposed ADT is inspired by the list ADT of Chapter 4.void clear();void insert(int);void remove(int);void sizeof();bool isEmpty();bool isInSet(int);2.6This proposed ADT is inspired by the list ADT of Chapter 4. Note that while it is similiar to the operations proposed for Question 2.5, the behaviour is somewhat different.void clear();void insert(int);void remove(int);void sizeof();7bool isEmpty();// Return the number of elements with a given valueintcountInBag(int);2.7The list class ADT from Chapter 4 is a sequence.2.8long ifact(int n) { // make n <= 12 so n! for long intlong fact = 1;Assert((n >= 0) && (n <= 12), "Input out of range");for (int i=1; i<= n; i++)fact = fact * i;return fact;}2.9void rpermute(int *array, int n) {swap(array, n-1, Random(n));rpermute(array, n-1);}2.10(a) Most people will find the recursive form natural and easy to understand. The iterative version requires careful examination to understand whatit does, or to have confidence that it works as claimed.(b)Fibr is so much slower than Fibi because Fibr re-computes thebulk of the series twice to get the two values to add. What is muchworse, the recursive calls to compute the subexpressions also re-computethe bulk of the series, and do so recursively. The result is an exponential explosion. In contrast, Fibicomputes each value in the seriesexactly once, and so its running time is proportional to n.2.11// Array curr[i] indicates current position of ring i.void GenTOH(int n, POLE goal, POLE t1, POLE t2,POLE* curr) {if (curr[n] == goal) // Get top n-1 rings set upGenTOH(n-1, goal, t1, t2, curr);else {if (curr[n] == t1) swap(t1, t2); // Get names right// Now, ring n is on pole t2. Put others on t1.GenTOH(n-1, t1, goal, t2, curr);move(t2, goal);GenTOH(n-1, goal, t1, t2, curr); // Move n-1 back}}2.12At each step of the way, the reduction toward the base case is only half asfar as the previous time. In theory, this series approaches, but never reaches, 0, so it will go on forever. In practice, the value should become computationally indistinguishable from zero, and terminate. However, this is terrible programming practice.Chap. 2 Mathematical Preliminaries2.13void allpermute(int array[], int n, int currpos) {if (currpos == (n-1)} {printout(array);return;}for (int i=currpos; i<n; i++) {swap(array, currpos, i);allpermute(array, n, currpos+1);swap(array, currpos, i); // Put back for next pass}}2.14In the following, function bitposition(n, i) returns the value (0 or1) at the ith bit position of integer value n. The idea is the print out the elements at the indicated bit positions within the set. If we do this for values in the range 0 to 2n.1, we will get the entire powerset.void powerset(int n) {for (int i=0; i<ipow(2, n); i++) {for (int j=0; j<n; j++)if (bitposition(n, j) == 1) cout << j << " ";cout << endl;}2.15 Proof: Assume that there is a largest prime number. Call it Pn,the nth largest prime number, and label all of the primes in order P1 =2, P2 =3,and so on. Now, consider the number Cformed by multiplying all of the nprime numbers together. The value C+1is not divisible by any of the nprime numbers. C+1is a prime number larger than Pn, a contradiction.Thus, we conclude that there is no largest prime number. .2.16Note: This problem is harder than most sophomore level students can handle.√Proof: The proof is by contradiction. Assume that 2is rational. By definition, there exist integers pand qsuch that√p2=,qwhere pand qhave no common factors (that is, the fraction p/qis in lowestterms). By squaring both sides and doing some simple algebraic manipulation, we get2p2=2q222q= pSince p2 must be even, p must be even. Thus,9222q=4(p)222q=2(p)2This implies that q2 is also even. Thus, pand qare both even, which contra√dicts the requirement that pand qhave no common factors. Thus, 2mustbe irrational. .2.17The leftmost summation sums the integers from 1 to n. The second summation merely reverses this order, summing the numbers from n.1+1=ndown to n.n+1=1. The third summation has a variable substitution ofi.1for i, with a corresponding substitution in the summation bounds. Thus, it is also the summation of n.0=n.(n.1)=1.2.18 Proof:(a) Base case.For n=1, 12 = [2(1)3 +3(1)2 +1]/6=1. Thus, the formula is correct for the base case. (b) Induction Hypothesis.n.12(n.1)3 +3(n.1)2 +(n.1)i2 =.6i=1(c) Induction Step.nn.1i2 i2 +n2=i=1 i=12(n.1)3 +3(n.1)2 +(n.2=+n62n3 .6n2 +6n.2+3n2 .6n+3+n.1 2=+n62n3 +3n2 +n=.6Thus, the theorem is proved by mathematical induction. .2.19 Proof:(a) Base case.For n=1, 1/2=1.1/2=1/2. Thus, the formula iscorrect for the base case.(b) Induction Hypothesis.n.111=1.2in.1 2i=1Chap. 2 Mathematical Preliminaries(c) Induction Step.nn.11 11=+iin222i=1 i=111=1.+n.1 n221=1..n2Thus, the theorem is proved by mathematical induction. .2.20 Proof:(a) Base case. For n=0, 20 =21 .1=1. Thus, the formula is correctfor the base case.(b) Induction Hypothesis.n.12i=2n.1.i=0(c) Induction Step.nn.12i=2i+2ni=0 i=0n=2n.1+2n+1 .1=2.Thus, the theorem is proved by mathematical induction. .2.21 The closed form solution is 3n+1.3, which I deduced by noting that 3F (n).2n+1 .3F(n)=2F(n)=3. Now, to verify that this is correct, use mathematicalinduction as follows.For the base case, F(1)=3=32.3 .n.1The induction hypothesis is that =(3n.3)/2.i=1So,nn.13i=3i+3ni=1 i=13n.3n= +32n+1 .33= .2Thus, the theorem is proved by mathematical induction.11n2.22 Theorem 2.1 (2i)=n2 +n.i=1(a) Proof: We know from Example 2.3 that the sum of the first noddnumbers is n2.The ith even number is simply one greater than the ith odd number. Since we are adding nsuch numbers, the sum must be n greater, or n2 +n. .(b) Proof: Base case: n=1yields 2=12 +1, which is true.Induction Hypothesis:n.12i=(n.1)2 +(n.1).i=1Induction Step: The sum of the first neven numbers is simply the sum of the first n.1even numbers plus the nth even number.nn.12i=( 2i)+2ni=1 i=1=(n.1)2 +(n.1)+2n=(n2 .2n+1)+(n.1)+2n= n2 .n+2n= n2 +n.nThus, by mathematical induction, 2i=n2 +n. .i=12.23 Proof:52Base case. For n=1,Fib(1) = 1 <3.For n=2,Fib(2) = 1 <(5).3Thus, the formula is correct for the base case. Induction Hypothesis. For all positive integers i<n,5 iFib(i)<().3Induction Step. Fib(n)=Fib(n.1)+Fib(n.2)and, by the InductionHypothesis, Fib(n.1)<(5)n.1 and Fib(n.2)<(5)n.2.So,3355 n.2Fib(n) < ()n.1 +()3355 5 n.2<()n.2 +()333Chap. 2 Mathematical Preliminaries85 n.2= ()3355 n.2<()2()33n5= .3Thus, the theorem is proved by mathematical induction. .2.24 Proof:12(1+1)23 =(a) Base case. For n=1, 1=1. Thus, the formula is correct4for the base case.(b) Induction Hypothesis.n.122(n1)ni3 = .4i=0(c) Induction Step. n2(n.1)n2i33=+n4i=02n4 .2n3 +n3=+n4n4 +2n3 +n2=4n2(n2 +2n+2)=2n2(n+1)=4Thus, the theorem is proved by mathematical induction..2.25(a) Proof: By contradiction. Assume that the theorem is false. Then, each pigeonhole contains at most 1 pigeon. Since there are nholes, there isroom for only npigeons. This contradicts the fact that a total of n+1pigeons are within the nholes. Thus, the theorem must be correct. .(b) Proof:i. Base case.For one pigeon hole and two pigeons, there must betwo pigeons in the hole.ii. Induction Hypothesis.For npigeons in n.1holes, some holemust contain at least two pigeons.13iii. Induction Step. Consider the case where n+1pigeons are in nholes. Eliminate one hole at random. If it contains one pigeon, eliminate it as well, and by the induction hypothesis some otherhole must contain at least two pigeons. If it contains no pigeons, then again by the induction hypothesis some other hole must contain at least two pigeons (with an extra pigeon yet to be placed). Ifit contains more than one pigeon, then it fits the requirements of the theorem directly..2.26 (a)When we add the nth line, we create nnew regions. But, we startwith one region even when there are no lines. Thus, the recurrence is F(n)=F(n.1)+n+1.(b) This is equivalent to the summation F(n)=1+ i=1 ni.(c) This is close to a summation we already know (equation 2.1).2.27 Base case: T(n.1)=1=1(1+1)/2.Induction hypothesis: T(n.1)=(n.1)(n)/2.Induction step:T(n)= T(n.1)+n=(n1)(n)/2+n= n(n+1)/2.Thus, the theorem is proved by mathematical induction.2.28 If we expand the recurrence, we getT(n)=2T(n.1)+1=2(2T(n.2)+1)+1)=4T(n.2+2+1.Expanding again yieldsT(n)=8T(n.3)+4+2+1.From this, we can deduce a pattern and hypothesize that the recurrence is equivalent tonT(n)= .12i=2n.1.i=0To prove this formula is in fact the proper closed form solution, we use mathematical induction.Base case: T(1)=21 .1=1.14Chap. 2 Mathematical PreliminariesInduction hypothesis: T(n.1)=2n.1 .1.Induction step:T(n)=2T(n.1)+1= 2(2n.1 .1) + 1=2n.1.Thus, as proved by mathematical induction, this formula is indeed the correct closed form solution for the recurrence.2.29 (a)The probability is 0.5 for each choice.(b)The average number of “1” bits is n/2, since each position has 0.5probability of being “1.”(c)The l eftmost “1” will be the leftmost bit (call it position 0) with probability 0.5; in position 1 with probability 0.25, and so on. The numberof positions we must examine is 1 in the case where the leftmost “1” isin position 0; 2 when it is in position 1, and so on. Thus, the expectedcost is the value of the summationni.2ii=1The closed form for this summation is 2 .n+2, or just less than two.2nThus, we expect to visit on average just less than two positions. (Students at this point will probably not be able to solve this summation,and it is not given in the book.)2.30There are at least two ways to approach this problem. One is to estimate the volume directly. The second is to generate volume as a function of weight. This is especially easy if using the metric system, assuming that the human body is roughly the density of water. So a 50 Kilo person has a volumeslightly less than 50 liters; a 160 pound person has a volume slightly less than 20 gallons.2.31(a) Image representations vary considerably, so the answer will vary as a result. One example answer is: Consider VGA standard size, full-color(24 bit) images, which is 3 ×640 ×480, or just less than 1 Mbyte perimage. The full database requires some 30-35 CDs.(b)Since we needed 30-35 CDs before, compressing by a factor of 10 isnot sufficient to get the database onto one CD.[Note that if the student picked a smaller format, such as estimating the size of a “typical” gif image, the result might wel l fit onto a single CD.]2.32(I saw this problem in John Bentley’s Programming Pearls.) Approach 1:The model is Depth X Width X Flow where Depth and Width are in milesand Flow is in miles/day. The Mississippi river at its mouth is about 1/4 mile wide and 100 feet (1/50 mile) deep, with a flow of around 15 miles/hour =360 miles/day. Thus, the flow is about 2 cubic miles/day.Approach 2: What goes out must equal what goes in. The model is Area XRainfall where Area is in square miles and Rainfall is in (linear) miles/day. The Mississipi watershed is about 1000 X 1000 miles, and the average rainfalis about 40 inches/year ≈.1 inches/day ≈.000002 miles/day (2 X 10.6).Thus, the flow is about 2 cubic miles/day.2.33Note that the student should NOT be providing answers that look like theywere done using a calculator. This is supposed to be an exercise in estimation! The amount of the mortgage is irrelevant, since this is a question about rates. However, to give some numbers to help you visualize the problem, pick a$100,000 mortgage. The up-front charge would be $1,000, and the savingswould be 1/4% each payment over the life of the mortgage. The monthlycharge will be on the remaining principle, being the highest at first and gradually reducing over time. But, that has little effect for the first few years.At the grossest approximation, you paid 1% to start and will save 1/4% each year, requiring 4 years. To be more precise, 8% of $100,000 is $8,000, while7 3/4% is $7,750 (for the first year), with a little less interest paid (and therefore saved) in following years. This will require a payback period of slightlyover 4 years to save $1000. If the money had been invested, then in 5 yearsthe investment would be worth about $1300 (at 5would be close to 5 1/2years.2.34Disk drive seek time is somewhere around 10 milliseconds or a little lessin 2000. RAM memory requires around 50 nanoseconds – much less thana microsecond. Given that there are about 30 million seconds in a year, a machine capable of executing at 100 MIPS would execute about 3 billionbillion (3 .1018) instructions in a year.2.35Typical books have around 500 pages/inch of thickness, so one million pages requires 2000 inches or 150-200 feet of bookshelf. This would be in excess of 50 typical shelves, or 10-20 bookshelves. It is within the realm of possibility that an individual home has this many books, but it is rather unusual.2.36A typical page has around 400 words (best way to derive this is to estimate the number of words/line and lines/page), and the book has around 500 pages, so the total is around 200,000 words.16Chap. 2 Mathematical Preliminaries2.37An hour has 3600 seconds, so one million seconds is a bit less than 300 hours.A good estimater will notice that 3600 is about 10% greater than 3333, so the actual number of hours is about 10% less than 300, or close to 270. (The real value is just under 278). Of course, this is just over 11 days.2.38Well over 100,000, depending on what you wish to classify as a city or town. The real question is what technique the student uses.2.39(a) The time required is 1 minute for the first mile, then 60/59 minutesfor the second mile, and so on until the last mile requires 60/1=60minutes. The result is the following summation.60 6060/i=60 1/i=60H60.i=1 i=1(b)This is actually quite easy. The man will never reach his destination,since his speed approaches zero as he approaches the end of the journey.。

【精编】数据结构与算法分析C版答案

【精编】数据结构与算法分析-C++版答案数据结构与算法是计算机科学的核心内容之一，它为解决实际问题提供了有效的方法和技巧。

C++是一种常用的编程语言，具有强大的功能和灵活性，因此在数据结构和算法的学习与实践中被广泛应用。

1. 什么是数据结构？数据结构是组织和存储数据的方式，它涉及到数据的逻辑关系和物理存储方式。

常见的数据结构有数组、链表、栈、队列、树、图等。

2. 什么是算法？算法是解决问题的方法和步骤的描述，它是一个有限的指令集合。

算法包括输入、输出和执行步骤，可以用来解决各种问题。

3. 什么是时间复杂度和空间复杂度？时间复杂度是衡量算法执行时间的度量，表示算法的运行时间与输入规模之间的关系。

空间复杂度是衡量算法所需存储空间的度量，表示算法的存储空间与输入规模之间的关系。

4. 数组和链表的区别是什么？数组是一种连续存储的数据结构，可以通过下标访问元素，但插入和删除元素时需要移动其他元素。

链表是一种非连续存储的数据结构，每个节点包含数据和指向下一个节点的指针，插入和删除元素时只需要修改指针。

5. 栈和队列的区别是什么？栈是一种后进先出（LIFO）的数据结构，只能在栈顶插入和删除元素。

队列是一种先进先出（FIFO）的数据结构，只能在队尾插入元素，在队头删除元素。

6. 二叉树和二叉搜索树的区别是什么？二叉树是一种每个节点最多有两个子节点的树结构。

二叉搜索树是一种二叉树，其中左子树的值小于根节点的值，右子树的值大于根节点的值。

7. 图的遍历算法有哪些？图的遍历算法包括深度优先搜索（DFS）和广度优先搜索（BFS）。

DFS以深度为优先级，沿着图的某一分支尽可能深地搜索，直到无法继续为止。

BFS以广度为优先级，按照距离从近到远的顺序搜索。

8. 动态规划和贪心算法的区别是什么？动态规划和贪心算法都是求解最优化问题的方法。

动态规划通过将问题划分为子问题，并保存已解决子问题的解来求解整个问题。

贪心算法则根据每个子问题的局部最优解，选择当前最优解，而不考虑整体最优解。

Mark Allen Weiss 数据结构与算法分析课后习题答案2

Chapter 2:Algorithm Analysis2.12/N ,37,√ N ,N ,N log log N ,N log N ,N log (N 2),N log 2N ,N 1.5,N 2,N 2log N ,N 3,2N / 2,2N .N log N and N log (N 2)grow at the same rate.2.2(a)True.(b)False.A counterexample is T 1(N ) = 2N ,T 2(N ) = N ,and f (N ) = N .(c)False.A counterexample is T 1(N ) = N 2,T 2(N ) = N ,and f (N ) = N 2.(d)False.The same counterexample as in part (c)applies.2.3We claim that N log N is the slower growing function.To see this,suppose otherwise.Then,N ε/ √ log N would grow slower than log N .Taking logs of both sides,we ﬁnd that,under this assumption,ε/ √ log N log N grows slower than log log N .But the ﬁrst expres-sion simpliﬁes to ε√ logN .If L = log N ,then we are claiming that ε√ L grows slower than log L ,or equivalently,that ε2L grows slower than log 2 L .But we know that log 2 L = ο (L ),so the original assumption is false,proving the claim.2.4Clearly,log k 1N = ο(log k 2N )if k 1 < k 2,so we need to worry only about positive integers.The claim is clearly true for k = 0and k = 1.Suppose it is true for k < i .Then,by L’Hospital’s rule,N →∞lim N log i N ______ = N →∞lim i N log i −1N _______The second limit is zero by the inductive hypothesis,proving the claim.2.5Let f (N ) = 1when N is even,and N when N is odd.Likewise,let g (N ) = 1when N is odd,and N when N is even.Then the ratio f (N ) / g (N )oscillates between 0and ∞.2.6For all these programs,the following analysis will agree with a simulation:(I)The running time is O (N ).(II)The running time is O (N 2).(III)The running time is O (N 3).(IV)The running time is O (N 2).(V) j can be as large as i 2,which could be as large as N 2.k can be as large as j ,which is N 2.The running time is thus proportional to N .N 2.N 2,which is O (N 5).(VI)The if statement is executed at most N 3times,by previous arguments,but it is true only O (N 2)times (because it is true exactly i times for each i ).Thus the innermost loop is only executed O (N 2)times.Each time through,it takes O ( j 2) = O (N 2)time,for a total of O (N 4).This is an example where multiplying loop sizes can occasionally give an overesti-mate.2.7(a)It should be clear that all algorithms generate only legal permutations.The ﬁrst two algorithms have tests to guarantee no duplicates;the third algorithm works by shufﬂing an array that initially has no duplicates,so none can occur.It is also clear that the ﬁrst two algorithms are completely random,and that each permutation is equally likely.The third algorithm,due to R.Floyd,is not as obvious;the correctness can be proved by induction.SeeJ.Bentley,"Programming Pearls,"Communications of the ACM 30(1987),754-757.Note that if the second line of algorithm 3is replaced with the statementSwap(A[i],A[RandInt(0,N-1)]);then not all permutations are equally likely.To see this,notice that for N = 3,there are 27equally likely ways of performing the three swaps,depending on the three random integers.Since there are only 6permutations,and 6does not evenly divide27,each permutation cannot possibly be equally represented.(b)For the ﬁrst algorithm,the time to decide if a random number to be placed in A [i ]has not been used earlier is O (i ).The expected number of random numbers that need to be tried is N / (N − i ).This is obtained as follows:i of the N numbers would be duplicates.Thus the probability of success is (N − i ) / N .Thus the expected number of independent trials is N / (N − i ).The time bound is thusi =0ΣN −1N −i Ni ____ < i =0ΣN −1N −i N 2____ < N 2i =0ΣN −1N −i 1____ < N 2j =1ΣN j 1__ = O (N 2log N )The second algorithm saves a factor of i for each random number,and thus reduces the time bound to O (N log N )on average.The third algorithm is clearly linear.(c,d)The running times should agree with the preceding analysis if the machine has enough memory.If not,the third algorithm will not seem linear because of a drastic increase for large N .(e)The worst-case running time of algorithms I and II cannot be bounded because there is always a ﬁnite probability that the program will not terminate by some given time T .The algorithm does,however,terminate with probability 1.The worst-case running time of the third algorithm is linear -its running time does not depend on the sequence of random numbers.2.8Algorithm 1would take about 5days for N = 10,000,14.2years for N = 100,000and 140centuries for N = 1,000,000.Algorithm 2would take about 3hours for N = 100,000and about 2weeks for N = 1,000,000.Algorithm 3would use 1⁄12minutes for N = 1,000,000.These calculations assume a machine with enough memory to hold the array.Algorithm 4solves a problem of size 1,000,000in 3seconds.2.9(a)O (N 2).(b)O (N log N ).2.10(c)The algorithm is linear.2.11Use a variation of binary search to get an O (log N )solution (assuming the array is preread).2.13(a)Test to see if N is an odd number (or 2)and is not divisible by 3,5,7,...,√N .(b)O (√ N ),assuming that all divisions count for one unit of time.(c)B = O (log N ).(d)O (2B / 2).(e)If a 20-bit number can be tested in time T ,then a 40-bit number would require about T 2time.(f)B is the better measure because it more accurately represents the size of the input.2.14The running time is proportional to N times the sum of the reciprocals of the primes lessthan N .This is O (N log log N ).See Knuth,Volume2,page394.2.15Compute X 2,X 4,X 8,X 10,X 20,X 40,X 60,and X 62.2.16Maintain an array PowersOfX that can beﬁlled in a for loop.The array will contain X ,X 2,X 4,up to X 2 log N .The binary representation of N (which can be obtained by testing even or odd and then dividing by2,until all bits are examined)can be used to multiply the appropriate entries of the array.2.17For N =0or N =1,the number of multiplies is zero.If b (N )is the number of ones in thebinary representation of N ,then if N >1,the number of multiplies used islog N + b (N )−12.18(a)A .(b)B .(c)The information given is not sufﬁcient to determine an answer.We have only worst-case bounds.(d)Yes.2.19(a)Recursion is unnecessary if there are two or fewer elements.(b)One way to do this is to note that if theﬁrst N −1elements have a majority,then the lastelement cannot change this.Otherwise,the last element could be a majority.Thus if N is odd,ignore the last element.Run the algorithm as before.If no majority element emerges, then return the N th element as a candidate.(c)The running time is O (N ),and satisﬁes T (N )= T (N / 2)+ O (N ).(d)One copy of the original needs to be saved.After this,the B array,and indeed the recur-sion can be avoided by placing each B i in the A array.The difference is that the original recursive strategy implies that O (log N )arrays are used;this guarantees only two copies. 2.20Otherwise,we could perform operations in parallel by cleverly encoding several integersinto one.For instance,if A=001,B=101,C=111,D=100,we could add A and B at the same time as C and D by adding00A00C+00B00D.We could extend this to add N pairs of numbers at once in unit cost.2.22No.If Low =1,High =2,then Mid =1,and the recursive call does not make progress. 2.24No.As in Exercise2.22,no progress is made.。

数据结构与算法分析课后习题答案

数据结构与算法分析课后习题答案第一章：基本概念一、题目：什么是数据结构与算法？数据结构是指数据在计算机中存储和组织的方式，如栈、队列、链表、树等；而算法是一系列解决问题的清晰规范的指令步骤。

数据结构和算法是计算机科学的核心内容。

二、题目：数据结构的分类有哪些？数据结构可以分为以下几类：1. 线性结构：包括线性表、栈、队列等，数据元素之间存在一对一的关系。

2. 树形结构：包括二叉树、AVL树、B树等，数据元素之间存在一对多的关系。

3. 图形结构：包括有向图、无向图等，数据元素之间存在多对多的关系。

4. 文件结构：包括顺序文件、索引文件等，是硬件和软件相结合的数据组织形式。

第二章：算法分析一、题目：什么是时间复杂度？时间复杂度是描述算法执行时间与问题规模之间的增长关系，通常用大O记法表示。

例如，O(n)表示算法的执行时间与问题规模n成正比，O(n^2)表示算法的执行时间与问题规模n的平方成正比。

二、题目：主定理是什么？主定理（Master Theorem）是用于估计分治算法时间复杂度的定理。

它的公式为：T(n) = a * T(n/b) + f(n)其中，a是子问题的个数，n/b是每个子问题的规模，f(n)表示将一个问题分解成子问题和合并子问题的所需时间。

根据主定理的不同情况，可以得到算法的时间复杂度的上界。

第三章：基本数据结构一、题目：什么是数组？数组是一种线性数据结构，它由一系列具有相同数据类型的元素组成，通过索引访问。

数组具有随机访问、连续存储等特点，但插入和删除元素的效率较低。

二、题目：栈和队列有什么区别？栈和队列都是线性数据结构，栈的特点是“先进后出”，即最后压入栈的元素最先弹出；而队列的特点是“先进先出”，即最先入队列的元素最先出队列。

第四章：高级数据结构一、题目：什么是二叉树？二叉树是一种特殊的树形结构，每个节点最多有两个子节点。

二叉树具有左子树、右子树的区分，常见的有完全二叉树、平衡二叉树等。

Mark Allen Weiss 数据结构与算法分析课后习题答案3Mark Allen Weiss 数据结构与算法分析课后习题答案3

List Intersect( List L1, List L2 ) {
List Result; Position L1Pos, L2Pos, ResultPos;
L1Pos = First( L1 ); L2Pos = First( L2 ); Result = MakeEmpty( NULL ); ResultPos = First( Result ); while( L1Pos != NULL && L2Pos != NULL ) {
(b) The bound can be improved by multiplying one term by the entire other polynomial, and then using the equivalent of the procedure in Exercise 3.2 to insert the entire sequence. Then each sequence takes O (MN ), but there are only M of them, giving a time bound of O (M 2N ).
if( L1Pos->Element < L2Pos->Element ) L1Pos = Next( L1Pos, L1 );
else if( L1Pos->Element > L2Pos->Element ) L2Pos = Next( L2Pos, L2 );
else {
Insert( L1Pos->Element, Result, ResultPos ); L1 = Next( L1Pos, L1 ); L2 = Next( L2Pos, L2 ); ResultPos = Next( ResultPos, Result ); } } return Result; } _______________________________________________________________________________

数据结构与算法习题含参考答案

数据结构与算法习题含参考答案一、单选题（共100题，每题1分，共100分）1、要为 Word 2010 格式的论文添加索引，如果索引项已经以表格形式保存在另一个 Word文档中，最快捷的操作方法是：A、在 Word 格式论文中，逐一标记索引项，然后插入索引B、直接将以表格形式保存在另一个 Word 文档中的索引项复制到 Word 格式论文中C、在 Word 格式论文中，使用自动插入索引功能，从另外保存 Word 索引项的文件中插D、在 Word 格式论文中，使用自动标记功能批量标记索引项，然后插入索引正确答案：D2、下面不属于计算机软件构成要素的是A、文档B、程序C、数据D、开发方法正确答案：D3、JAVA 属于：A、操作系统B、办公软件C、数据库系统D、计算机语言正确答案：D4、在 PowerPoint 演示文稿中,不可以使用的对象是：A、图片B、超链接C、视频D、书签第 6 组正确答案：D5、下列叙述中正确的是A、软件过程是软件开发过程和软件维护过程B、软件过程是软件开发过程C、软件过程是把输入转化为输出的一组彼此相关的资源和活动D、软件过程是软件维护过程正确答案：C6、在 Word 中，不能作为文本转换为表格的分隔符的是：A、@B、制表符C、段落标记D、##正确答案：D7、某企业为了建设一个可供客户在互联网上浏览的网站，需要申请一个：A、密码B、门牌号C、域名D、邮编正确答案：C8、面向对象方法中，将数据和操作置于对象的统一体中的实现方式是A、隐藏第 42 组B、抽象C、结合D、封装正确答案：D9、下面属于整数类 I 实例的是A、-919B、0.919C、919E+3D、919D-2正确答案：A10、定义课程的关系模式如下：Course (C#, Cn, Cr，prC1#, prC2#)（其属性分别为课程号、课程名、学分、先修课程号 1和先修课程号 2），并且不同课程可以同名，则该关系最高是A、BCNFB、2NFC、1NFD、3NF正确答案：A11、循环队列的存储空间为 Q(1:100)，初始状态为 front=rear=100。

数据结构与算法分析c语言描述中文答案

数据结构与算法分析c语言描述中文答案【篇一：数据结构(c语言版)课后习题答案完整版】选择题：ccbdca6．试分析下面各程序段的时间复杂度。

（1）o（1）（2）o（m*n）（3）o（n2）（4）o（log3n）（5）因为x++共执行了n-1+n-2+??＋1= n(n-1)/2，所以执行时间为o（n2）（6）o(n)第2章线性表1．选择题babadbcabdcddac 2．算法设计题（6）设计一个算法，通过一趟遍历在单链表中确定值最大的结点。

elemtype max (linklist l ){if(l-next==null) return null;pmax=l-next; //假定第一个结点中数据具有最大值 p=l-next-next; while(p != null ){//如果下一个结点存在if(p-data pmax-data) pmax=p;p=p-next; }return pmax-data;（7）设计一个算法，通过遍历一趟，将链表中所有结点的链接方向逆转，仍利用原表的存储空间。

void inverse(linklist l) { // 逆置带头结点的单链表 l p=l-next; l-next=null; while ( p) {q=p-next; // q指向*p的后继p-next=l-next;l-next=p; // *p插入在头结点之后p = q; }}（10）已知长度为n的线性表a采用顺序存储结构，请写一时间复杂度为o(n)、空间复杂度为o(1)的算法，该算法删除线性表中所有值为item的数据元素。

[题目分析] 在顺序存储的线性表上删除元素，通常要涉及到一系列元素的移动（删第i个元素，第i+1至第n个元素要依次前移）。

本题要求删除线性表中所有值为item的数据元素，并未要求元素间的相对位置不变。

因此可以考虑设头尾两个指针（i=1，j=n），从两端向中间移动，凡遇到值item的数据元素时，直接将右端元素左移至值为item的数据元素位置。

《数据结构与算法》课后习题答案

《数据结构与算法》课后习题答案一、算法分析和复杂度1.1 算法复杂度的定义算法的复杂度是指算法所需资源的度量，包括时间复杂度和空间复杂度。

时间复杂度描述了算法的执行时间随输入规模增长的增长速度，空间复杂度描述了算法执行期间所需的存储空间随输入规模增长的增长速度。

1.2 时间复杂度的计算方法时间复杂度可以通过估算算法的执行次数来计算。

对于循环结构，通常可以通过循环体内代码的执行次数来估算时间复杂度。

对于递归算法，则可以通过递归的深度和每次递归的复杂度来计算时间复杂度。

1.3 常见的时间复杂度在算法分析中，常见的时间复杂度有：O(1)、O(log n)、O(n)、O(n log n)、O(n^2)、O(n^3)等。

其中，O(1)表示算法的执行时间与输入规模无关，即常数时间复杂度；O(log n)表示算法的执行时间随输入规模呈对数增长；O(n)表示算法的执行时间随输入规模呈线性增长；O(nlog n)表示算法的执行时间随输入规模呈线性对数增长；O(n^2)表示算法的执行时间随输入规模呈平方增长；O(n^3)表示算法的执行时间随输入规模呈立方增长。

1.4 空间复杂度的计算方法空间复杂度可以通过估计算法执行过程中所需要的额外存储空间来计算。

对于递归算法，通常使用递归的深度来估算空间复杂度。

1.5 算法复杂度的应用算法的复杂度分析在实际应用中非常重要，可以帮助我们选择合适的算法来解决问题。

在时间复杂度相同的情况下，可以通过比较空间复杂度来选择更优的算法。

在实际开发中，我们也可以根据算法的复杂度来进行性能优化，减少资源的消耗。

二、搜索算法2.1 线性搜索算法线性搜索算法是一种简单直观的搜索算法，逐个比较待搜索元素和数组中的元素，直到找到匹配的元素或遍历完整个数组。

其时间复杂度为O(n)，空间复杂度为O(1)。

2.2 二分搜索算法二分搜索算法是一种高效的搜索算法，前提是数组必须是有序的。

算法首先取数组的中间元素进行比较，如果相等则返回找到的位置，如果大于中间元素则在右半部分继续搜索，如果小于中间元素则在左半部分继续搜索。

数据结构与算法分析-C++版答案

数据结构与算法分析-C++版答案Data Structures and Algorithm 习题答案Preface ii1 Data Structures and Algorithms 12 Mathematical Preliminaries 53 Algorithm Analysis 174 Lists, Stacks, and Queues 235 Binary Trees 326 General Trees 407 Internal Sorting 468 File Processing and External Sorting 54 9Searching 5810 Indexing 6411 Graphs 6912 Lists and Arrays Revisited 7613 Advanced Tree Structures 82iii Contents14 Analysis Techniques 8815 Limits to Computation 94PrefaceContained herein are the solutions to all exercises from the textbook A Practical Introduction to Data Structures and Algorithm Analysis, 2nd edition.For most of the problems requiring an algorithm I have given actual code. Ina few cases I have presented pseudocode. Please be aware that the code presented in this manual has not actually been compiled and tested. While I believe the algorithmsto be essentially correct, there may be errors in syntax as wellas semantics. Most importantly, these solutions provide a guide to the instructor as to the intendedanswer, rather than usable programs.1Data Structures and AlgorithmsInstructor’s note: Unlike the other chapters, many of the questions in this chapter are not really suitable for graded work. The questions are mainly intended to get students thinking about data structures issues.1.1This question does not have a specific right answer, provided the student keeps to the spirit of the question. Students may have trouble with the concept of “operations.”1.2This exercise asks the student to expand on their concept of an integer representation.A good answer is described by Project 4.5, where a singly-linkedlist is suggested. The most straightforward implementation stores each digitin its own list node, with digits stored in reverse order. Addition and multiplicationare implemented by what amounts to grade-school arithmetic. Foraddition, simply march down in parallel through the two lists representingthe operands, at each digit appending to a new list the appropriate partial sum and bringing forward a carry bit as necessary. For multiplication, combine the addition function with a new function that multiplies a single digitby an integer. Exponentiation can be done either by repeated multiplication (not really practical) or by the traditional Θ(log n)-time algorithm based on the binary representation of the exponent. Discovering this faster algorithm will be beyond the reach of most students, so should not be required.1.3A sample ADT for character strings might look as follows (with the normal interpretation of the function names assumed).Chap. 1 Data Structures and Algorithms// Concatenate two stringsString strcat(String s1, String s2);// Return the length of a stringint length(String s1);// Extract a substring, starting at ‘start’,// and of length ‘length’String extract(String s1, int start, int length);// Get the first characterchar first(String s1);// Compare two strings: the normal C++ strcmp function.Some// convention should be indicated for how to interpretthe// return value. In C++, this is 1for s1// and 1 for s1>s2.int strcmp(String s1, String s2)// Copy a stringint strcpy(String source, String destination)1.4The answer to this question is provided by the ADT for listsgiven in Chapter 4.1.5One’s compliment stores the binary representation of positive numbers, and stores the binary representation of a negative number with the bits inverted. Two’s compliment is the same, except that a negative number has its bits inverted and then one is added (for reasons of efficiency in hardware implementation).This representation is the physical implementation of an ADT defined by the normal arithmetic operations, declarations, and other support given by the programming language for integers.1.6An ADT for two-dimensional arrays might look as follows.Matrix add(Matrix M1, Matrix M2);Matrix multiply(Matrix M1, Matrix M2);Matrix transpose(Matrix M1);void setvalue(Matrix M1, int row, int col, int val);int getvalue(Matrix M1, int row, int col);List getrow(Matrix M1, int row);One implementation for the sparse matrix is described in Section 12.3 Another implementationis a hash table whose search key is a concatenation of the matrix coordinates.1.7Every problem certainly does not have an algorithm. As discussed in Chapter 15, there are a number of reasons why this might be the case. Some problems don’t have a sufficiently clear definition. Some problems, such as the halting problem, are non-computable. For some problems, such as one typicallystudied by artificial intelligence researchers, we simply don’t know a solution.1.8We must assume that by “algorithm” we mean something composed of steps areof a nature that they can be performed by a computer. If so, than any algorithm can be expressed in C++. In particular, if an algorithm can be expressed in any other computer programming language, then it can be expressed in C++, since all (sufficiently general) computer programming languages compute the same set of functions.1.9The primitive operations are (1) adding new words to the dictionary and (2) searching the dictionary for a given word. Typically, dictionary access involves some sort of pre-processing of the word to arrive at the “root” of the word.A twenty page document (single spaced) is likely to contain about 20,000 words. A user may be willing to wait a few seconds between individual “hits” of mis-spelled words, or perhaps up to a minute for the whole document to be processed. This means that a check for an individual word can take about 10-20 ms. Users will typically insert individual words into the dictionary interactively, so this process cantake a couple of seconds. Thus, search must be much more efficient than insertion.1.10The user should be able to find a city based on a variety of attributes (name, location,perhaps characteristics such as population size). The user should also be able to insertand delete cities. These are the fundamental operations of any database system: search, insertion and deletion.A reasonable database has a time constraint that will satisfy the patience of a typicaluser. For an insert, delete, or exact match query, a few seconds is satisfactory. If thedatabase is meant to support range queries and mass deletions, the entire operation may be allowed to take longer, perhaps on the order of a minute. However, the time spent to process individual cities within the range must be appropriately reduced.Inpractice, the data representation will need to be such that it accommodates efficient processing to meet these time constraints. In particular, it may be necessary to support operations that process range queries efficiently by processing all cities in the range as a batch, rather than as a series of operations on individual cities.1.11Students at this level are likely already familiar with binary search. Thus, they should typically respond with sequential search and binary search. Binary search should be described as better since it typically needs to make fewer comparisons (and thus is likely to be much faster).1.12The answer to this question is discussed in Chapter 8. Typical measures of cost will be number of comparisons and number of swaps. Tests should include running timings on sorted, reverse sorted, and random lists of various sizes.Chap. 1 Data Structures and Algorithms1.13The first part is easy with the hint, but the second part is rather difficult to do withouta stack.a) bool checkstring(string S) {int count = 0;for (int i=0; i<="" p="">if (S[i] == ’(’) count++;if (S[i] == ’)’) {if (count == 0) return FALSE;count--;}}if (count == 0) return TRUE;else return FALSE;}b) int checkstring(String Str) {Stack S;int count = 0;for (int i=0; i<="" p="">if (S[i] == ’(’)S.push(i);if (S[i] == ’)’) {if (S.isEmpty()) return i;S.pop();}if (S.isEmpty()) return -1;else return S.pop();}1.14Answers to this question are discussed in Section 7.2.1.15This is somewhat different from writing sorting algorithms for a computer, since person’s “working space” is typically limited, as is their ability to physically manipulatethe pieces of paper. Nonetheless, many of the common sorting algorithms have their analogs to solutions for this problem. Most typical answers will be insertion sort, variations on mergesort, and variations on binsort.1.16Answers to this question are discussed in Chapter 8.2Mathematical Preliminaries2.1(a) Not reflexive if the set has any members. One could argue it is symmetric, antisymmetric, and transitive, since no element violate any ofthe rules.(b)Not reflexive (for any female). Not symmetric (consider a brother and sister). Not antisymmetric (consider two brothers). Transitive (for any3 brothers).(c)Not reflexive. Not symmetric, and is antisymmetric. Not transitive(only goes one level).(d)Not reflexive (for nearly all numbers). Symmetric since a+ b+ a,so not antisymmetric. Transitive, but vacuously so (there can be nodistinct a, b,and cwhere aRband bRc).(e)Reflexive. Symmetric, so not antisymmetric. Transitive (but sort of vacuous).(f)Reflexive – check all the cases. Since it is only true when x= y,itis technically symmetric and antisymmetric, but rather vacuous. Likewise,it is technically transitive, but vacuous.2.2In general, prove that something is an equivalence relation by proving that it is reflexive, symmetric, and transitive.(a)This is an equivalence that effectively splits the integers into odd andeven sets. It is reflexive (x+ xis even for any integer x), symmetric(since x+ y= y+ x) and transitive (since you are always adding twoodd or even numbers for any satisfactory a, b,and c).This is not an equivalence. To begin with, it is not reflexive for any integer.(c)This is an equivalence that divides the non-zero rational numbers into positive and negative. It is reflexive since x ˙x>0. It is symmetric sincexy˙= yx˙. It is transitive since any two members of the given class satisfy the relationship.5Chap. 2 Mathematical Preliminaries(d)This is not an equivalance relation since it is not symmetric. For example,a=1and b=2.(e)This is an eqivalance relation that divides the rationals based on their fractional values. It is reflexive since for all a, a.a =0. It is symmetricsince if a.b=xthen b.a=.x. It is transitive since any two rationalswith the same fractional value will yeild an integer.(f)This is not an equivalance relation since it is not transitive. For example, 4.2=2and 2.0=2,but 4.0=4.2.3A relation is a partial ordering if it is antisymmetric and transitive.(a)Not a partial ordering because it is not transitive.(b)Is a partial ordering bacause it is antisymmetric (if ais an ancestor ofb, then bcannot be an ancestor of a) and transitive (since the ancestor of an ancestor is an ancestor).(c)Is a partial ordering bacause it is antisymmetric (if ais older than b,then bcannot be older than a) and transitive (since if ais older than band bis older than c, ais older than c).(d)Not a partial ordering, since it is not antisymmetric for any pair of sisters.(e)Not a partial ordering because it is not antisymmetric.(f)This is a partial ordering. It is antisymmetric (no violations exist) and transitive (no violations exist).2.4A total ordering can be viewed as a permuation of the elements. Since there are n!permuations of nelements, there must be n!total orderings.2.5This proposed ADT is inspired by the list ADT of Chapter 4.void clear();void insert(int);void remove(int);void sizeof();bool isEmpty();bool isInSet(int);2.6This proposed ADT is inspired by the list ADT of Chapter 4. Note that while it is similiar to the operations proposed for Question 2.5, the behaviour is somewhat different.void clear();void insert(int);void remove(int);void sizeof();7bool isEmpty();// Return the number of elements with a given valueintcountInBag(int);2.7The list class ADT from Chapter 4 is a sequence.2.8long ifact(int n) { // make n <= 12 so n! for long intlong fact = 1;Assert((n >= 0) && (n <= 12), "Input out of range");for (int i=1; i<= n; i++)fact = fact * i;return fact;}2.9void rpermute(int *array, int n) {swap(array, n-1, Random(n));rpermute(array, n-1);}2.10(a) Most people will find the recursive form natural and easy to understand. The iterative version requires careful examination to understand whatit does, or to have confidence that it works as claimed.(b)Fibr is so much slower than Fibi because Fibr re-computes thebulk of the series twice to get the two values to add. What is muchworse, the recursive calls to compute the subexpressions also re-computethe bulk of the series, and do so recursively. The result is an exponential explosion. In contrast, Fibicomputes each value in the seriesexactly once, and so its running time is proportional to n.2.11// Array curr[i] indicates current position of ring i.void GenTOH(int n, POLE goal, POLE t1, POLE t2,POLE* curr) {if (curr[n] == goal) // Get top n-1 rings set upGenTOH(n-1, goal, t1, t2, curr);else {if (curr[n] == t1) swap(t1, t2); // Get names right// Now, ring n is on pole t2. Put others on t1.GenTOH(n-1, t1, goal, t2, curr);move(t2, goal);GenTOH(n-1, goal, t1, t2, curr); // Move n-1 back}}2.12At each step of the way, the reduction toward the base case is only half asfar as the previous time. In theory, this series approaches, but never reaches, 0, so it will go on forever. In practice, the value should become computationally indistinguishable from zero, and terminate. However, this is terrible programming practice.Chap. 2 Mathematical Preliminaries2.13void allpermute(int array[], int n, int currpos) {if (currpos == (n-1)} {printout(array);return;}for (int i=currpos; i<="">swap(array, currpos, i);allpermute(array, n, currpos+1);swap(array, currpos, i); // Put back for next pass}}2.14In the following, function bitposition(n, i) returns the value (0 or1) at the ith bit position of integer value n. The idea is the print out the elements at the indicated bit positions within the set. If we do this for values in the range 0 to 2n.1, we will get the entire powerset.void powerset(int n) {for (int i=0; i<="">for (int j=0; j<="" p="">if (bitposition(n, j) == 1) cout << j << " ";cout << endl;}2.15 Proof: Assume that there is a largest prime number. Call it Pn,the nth largest prime number, and label all of the primes in order P1 =2, P2 =3,and so on. Now, consider the number Cformed by multiplying all of the nprime numbers together. The value C+1is not divisible by any of the nprime numbers. C+1is a prime number larger than Pn, a contradiction.Thus, we conclude that there is no largest prime number. .2.16Note: This problem is harder than most sophomore level students can handle.√Proof: The proof is by contradiction. Assume that 2is rational. By definition, there exist integers pand qsuch that√p2=,qwhere pand qhave no common factors (that is, the fraction p/qis in lowestterms). By squaring both sides and doing some simple algebraic manipulation, we get2p2=2q222q= pSince p2 must be even, p must be even. Thus,。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

数据结构与算法分析课后习题答案【篇一：《数据结构与算法》课后习题答案】>2.3.2 判断题2．顺序存储的线性表可以按序号随机存取。

（√）4．线性表中的元素可以是各种各样的，但同一线性表中的数据元素具有相同的特性，因此属于同一数据对象。

（√）6．在线性表的链式存储结构中，逻辑上相邻的元素在物理位置上不一定相邻。

（√）8．在线性表的顺序存储结构中，插入和删除时移动元素的个数与该元素的位置有关。

（√）9．线性表的链式存储结构是用一组任意的存储单元来存储线性表中数据元素的。

（√）2.3.3 算法设计题1．设线性表存放在向量a[arrsize]的前elenum个分量中，且递增有序。

试写一算法，将x 插入到线性表的适当位置上，以保持线性表的有序性，并且分析算法的时间复杂度。

2．已知一顺序表a，其元素值非递减有序排列，编写一个算法删除顺序表中多余的值相同的元素。

【提示】对顺序表a，从第一个元素开始，查找其后与之值相同的所有元素，将它们删除；再对第二个元素做同样处理，依此类推。

void delete(seqlist *a){i=0;while(ia-last)/*将第i个元素以后与其值相同的元素删除*/{k=i+1;while(k=a-lasta-data[i]==a-data[k])k++;/*使k指向第一个与a[i]不同的元素*/ n=k-i-1;/*n表示要删除元素的个数*/for(j=k;j=a-last;j++)a-data[j-n]=a-data[j]; /*删除多余元素*/a-last= a-last -n;i++;}}3．写一个算法，从一个给定的顺序表a中删除值在x~y(x=y)之间的所有元素，要求以较高的效率来实现。

【提示】对顺序表a，从前向后依次判断当前元素a-data[i]是否介于x和y之间，若是，并不立即删除，而是用n记录删除时应前移元素的位移量；若不是，则将a-data[i]向前移动n位。

n用来记录当前已删除元素的个数。

void delete(seqlist *a,int x,int y){i=0;n=0;while (ia-last){if (a-data[i]=x a-data[i]=y)n++; /*若a-data[i] 介于x和y之间，n 自增*/ else a-data[i-n]=a-data[i];/*否则向前移动a-data[i]*/i++;}a-last-=n;}4．线性表中有n个元素，每个元素是一个字符，现存于向量r[n]中，试写一算法，使r中的字符按字母字符、数字字符和其它字符的顺序排列。

要求利用原来的存储空间，元素移动次数最小。

【提示】对线性表进行两次扫描，第一次将所有的字母放在前面，第二次将所有的数字放在字母之后，其它字符之前。

int fch(char c) /*判断c是否字母*/{if(c=ac=z||c=ac=z) return (1);elsereturn (0);}int fnum(char c) /*判断c是否数字*/{if(c=0c=9)return (1);elsereturn (0);}void process(char r[n]){low=0;high=n-1;while(lowhigh) /*将字母放在前面*/{while(lowhighfch(r[low])) low++;while(lowhigh!fch(r[high])) high--;if(lowhigh){k=r[low];r[low]=r[high];r[high]=k;}}low=low+1;high=n-1;while(lowhigh) /*将数字放在字母后面，其它字符前面*/{while(lowhighfnum(r[low])) low++;while(lowhigh!fnum(r[high])) high--;if(lowhigh){k=r[low];r[low]=r[high];r[high]=k;}}}5．线性表用顺序存储，设计一个算法，用尽可能少的辅助存储空间将顺序表中前m个元素和后n个元素进行整体互换。

即将线性表：（a1, a2, … , am, b1, b2, … , bn）改变为：（b1, b2, … , bn , a1, a2, … , am）。

【提示】比较m和n的大小，若mn，则将表中元素依次前移m次；否则,将表中元素依次后移n次。

void process(seqlist *l,int m,int n){if(m=n)for(i=1;i=m;i++){x=l-data[0];for(k=1;k=l-last;k++)l-data[k-1]=l-data[k];l-data[l-last]=x;}else for(i=1;i=n;i++){x=l-data[l-last];for(k=l-last-1;k=0;k- -)l-data[k+1]=l-data[k];l-data[0]=x; }}6．已知带头结点的单链表l中的结点是按整数值递增排列的，试写一算法，将值为x 的结点插入到表l中，使得l仍然递增有序，并且分析算法的时间复杂度。

linklist insert(linklist l, int x){p=l;while(p-next xp-next-data)p=p-next;/*寻找插入位置*/ s=(lnode *)malloc(sizeof(lnode)); /*申请结点空间*/ s-data=x;/*填装结点*/s-next=p-next;p-next=s; /*将结点插入到链表中*/ return(l);}7．假设有两个已排序（递增）的单链表a和b，编写算法将它们合并成一个链表c而不改变其排序性。

linklist combine(linklist a, linklist b){c=a;rc=c;pa=a-next; /*pa指向表a的第一个结点*/pb=b-next; /*pb指向表b的第一个结点*/free(b); /*释放b的头结点*/while (pa pb) /*将pa、pb所指向结点中，值较小的一个插入到链表c的表尾*/if(pa-datapb-data){rc-next=pa;rc=pa;pa=pa-next;}else{rc-next=pb;rc=pb;pb=pb-next;}if(pa) rc-next=pa;else rc-next=pb;/*将链表a或b中剩余的部分链接到链表c的表尾*/return(c);}8．假设长度大于1的循环单链表中，既无头结点也无头指针，p为指向该链表中某一结点的指针，编写算法删除该结点的前驱结点。

【提示】利用循环单链表的特点，通过s指针可循环找到其前驱结点p及p的前驱结点q，然后可删除结点*p。

viod delepre(lnode *s){lnode *p, *q;p=s;while (p-next!=s){q=p;p=p-next;}q-next=s;free(p);}9．已知两个单链表a和b分别表示两个集合，其元素递增排列，编写算法求出a和b的交集c，要求c同样以元素递增的单链表形式存储。

【提示】交集指的是两个单链表的元素值相同的结点的集合，为了操作方便，先让单链表c带有一个头结点，最后将其删除掉。

算法中指针p用来指向a中的当前结点，指针q用来指向b中的当前结点，将其值进行比较，两者相等时，属于交集中的一个元素，两者不等时，将其较小者跳过，继续后面的比较。

linklist intersect(linklist a, linklist b){lnode *q, *p, *r, *s;linklist c;c= (lnode *)malloc(sizeof(lnode));c-next=null;r=c;p=a;q=b;while (p q )if (p-dataq-data) p=p-next;else if (p-data==q-data){s=(lnode *)malloc(sizeof(lnode));s-data=p-data;r-next=s;r=s;p=p-next;q=q-next;}else q=q-next;r-next=null;c=c-next;return c;}10．设有一个双向链表，每个结点中除有prior、data和next域外，还有一个访问频度freq域，在链表被起用之前，该域的值初始化为零。

每当在链表进行一次locata(l,x)运算后，令值为x的结点中的freq域增1，并调整表中结点的次序，使其按访问频度的非递增序列排列，以便使频繁访问的结点总是靠近表头。

试写一个满足上述要求的locata(l,x)算法。

【提示】在定位操作的同时，需要调整链表中结点的次序：每次进行定位操作后，要查看所查找结点的freq域，将其同前面结点的freq域进行比较，同时进行结点次序的调整。

typedef structdnode【篇二：数据结构课后习题答案】lass=txt>高等学校精品资源共享课程绪论第 1 章1.1 什么是数据结构？【答】：数据结构是指按一定的逻辑结构组成的一批数据，使用某种存储结构将这批数据存储于计算机中，并在这些数据上定义了一个运算集合。

1.2 数据结构涉及哪几个方面？【答】：数据结构涉及三个方面的内容，即数据的逻辑结构、数据的存储结构和数据的运算集合。

1.3 两个数据结构的逻辑结构和存储结构都相同，但是它们的运算集合中有一个运算的定义不一样，它们是否可以认作是同一个数据结构？为什么？【答】：不能，运算集合是数据结构的重要组成部分，不同的运算集合所确定的数据结构是不一样的，例如，栈与队列它们的逻辑结构与存储结构可以相同，但由于它们的运算集合不一样，所以它们是两种不同的数据结构。

数据结构与算法分析课后习题答案

Mark Allen Weiss 数据结构与算法分析 课后习题答案9

数据结构与算法分析习题与参考答案

Mark Allen Weiss 数据结构与算法分析 课后习题答案11

数据结构与算法课后习题解答

数据结构与算法设计课后习题及答案详解

《数据结构与算法分析》(C++第二版)【美】Clifford A.Shaffer著 课后习题答案 二

《数据结构与算法》习题与答案

Mark Allen Weiss 数据结构与算法分析 课后习题答案1

数据结构与算法分析课后习题解答

数据结构与算法分析java课后答案

数据结构与算法分析课后习题答案

数据结构与算法分析-C++版答案

【精编】数据结构与算法分析C版答案

Mark Allen Weiss 数据结构与算法分析 课后习题答案2

数据结构与算法分析课后习题答案

Mark Allen Weiss 数据结构与算法分析 课后习题答案3Mark Allen Weiss 数据结构与算法分析 课后习题答案3

数据结构与算法习题含参考答案

数据结构与算法分析c语言描述中文答案

《数据结构与算法》课后习题答案

数据结构与算法分析-C++版答案

Mark Allen Weiss 数据结构与算法分析课后习题答案9

Mark Allen Weiss 数据结构与算法分析课后习题答案11

《数据结构与算法分析》(C++第二版)【美】Clifford A.Shaffer著课后习题答案二

Mark Allen Weiss 数据结构与算法分析课后习题答案1

Mark Allen Weiss 数据结构与算法分析课后习题答案2

Mark Allen Weiss 数据结构与算法分析课后习题答案3Mark Allen Weiss 数据结构与算法分析课后习题答案3