制动器设计的计算过程
制动器的设计与计算.

第四节 制动器的设计与计算一、鼓式制动器的设计计算1.压力沿衬片长度方向的分布规律除摩擦衬片因有弹性容易变形外,制动鼓、蹄片和支承也有变形,所以计算法向压力在摩擦衬片上的分布规律比较困难。
通常只考虑衬片径向变形的影响,其它零件变形的影响较小而忽略不计。
制动蹄有一个自由度和两个自由度之分。
首先计算有两个自由度的紧蹄摩擦衬片的径向变形规律。
如图8-8a 所示,将坐标原点取在制动鼓中心O 点。
1y 坐标轴线通过蹄片的瞬时转动中心1A 点。
制动时,由于摩擦衬片变形,蹄片一面绕瞬时转动中心转动,同时还顺着摩擦力作用的方向沿支承面移动。
结果蹄片中心位于1O 点,因而未变形的摩擦衬片的表面轮廓(11E E 线),就沿1OO 方向移动进入制动鼓内。
显然,表面上所有点在这个方向上的变形是一样的。
位于半径1OB 上的任意点1B 的变形就是11B B '线段,所以同样一些点的径向变形1δ为 111C B =δ≈111cos ψB B '考虑到︒-+=90)(111αϕψ和max 1111δ=='OO B B ,所以对于紧蹄的径向变形1δ和压图8—8 计算摩擦衬片径向变形简图a)有两个自由度的紧蹄 b)有一个自由度的紧蹄力1p 为:⎭⎬⎫+=+=)sin()sin(11max 1111max 11ϕαϕαδδp p (8-1)式中,1α为任意半径1OB 和1y 轴之间的夹角;1ψ为半径1OB 和最大压力线1OO 之间的夹角;1ϕ为1x 轴和最大压力线1OO 之间的夹角。
其次计算有一个自由度的紧蹄摩擦衬片的径向变形规律。
如图8-8b 所示,此时蹄片在张开力和摩擦力作用下,绕支承销1A 转动γd 角。
摩擦衬片表面任意点1B 沿蹄片转动的切线方向的变形就是线段11B B ',其径向变形分量是这个线段在半径1OB 延长线上的投影,即为11C B 线段。
由于γd 很小,可认为︒='∠90111B B A ,故所求摩擦衬片的变形应为 γγγδd B A B B C B 111111111sin sin ='==考虑到1OA ≈R OB =1,那么分析等腰三角形11OB A ,则有γαsin sin 11RB A =,所以表面的径向变形和压力为⎭⎬⎫==αγαδsin sin max 11p p d R (8-2)综上所述可知,新蹄片压力沿摩擦衬片长度的分布符合正弦曲线规律,可用式(8-1)和式(8-2)计算。
制动器的设计计算

制动器的设计计算制动器是用来减速和停止运动物体的一种装置。
在设计制动器时,需要考虑以下几个因素:制动力的大小、制动距离的要求、制动器材料的选型、热力学效应以及制动器的结构设计等等。
首先,要确定所需的制动力大小。
制动力是指制动器施加在运动物体上的力,它的大小决定了物体的减速度和停止的时间。
根据实际需求和应用场景,可以通过以下公式计算制动力:制动力=质量×减速度其中,质量是指运动物体的质量,减速度是要达到的减速度。
根据这个制动力,可以选择适当的制动器结构和材料。
其次,要确定制动距离的要求。
制动距离是指从开始制动到停止的距离,它的大小决定了制动器制动的效果和占用的空间。
制动距离可以通过以下公式计算:制动距离=初始速度²/(2×减速度)其中,初始速度是运动物体开始制动时的速度,减速度是物体的减速度。
根据这个制动距离,可以调整制动器结构和制动参数的设计。
然后,要选择适当的制动器材料。
制动器材料需要具备一定的强度、硬度和耐磨性,以保证制动效果和使用寿命。
常见的制动器材料包括金属、陶瓷和复合材料等。
选择合适的材料还需要考虑制动温度的影响,因为制动过程中会产生大量的热量,可能导致制动器材料的热膨胀、软化或者燃烧。
最后,要进行制动器的结构设计。
制动器的结构设计包括选择合适的制动器类型(如摩擦制动器、液力制动器和电磁制动器等),确定制动器的安装位置和方式,设计制动器的摩擦面积和接触面形状等。
结构设计需要考虑制动器的尺寸、重量和安装方便性,以保证制动器能够稳定可靠地工作。
在制动器设计的过程中,还需要考虑一些其他的因素,如制动器的可靠性、维修性以及制动器和运动物体之间的适配性。
制动器的设计是一个综合考虑各种因素的过程,需要进行合理的计算和模拟分析,并结合实际的试验验证。
制动器设计及计算实例汇总

等效压力:
或
方向通过 ,
以上是固定销式求合力的方法(含合力的角度 )
摩擦力矩:
,c为常数;(另外,摩擦力矩T还可以用积分方法求: = )
=
力矩:
由制动器的几何尺寸( 、 )确定。
总等效压力:
由P与输入力F的关系可作图求出(力平衡)
故可得出:
式中BEF为制动器效率因数。
车型
制动鼓
直径
(前桥)
(前桥)
为蹄片与制动鼓间磨擦系数。
2.求制动效能系数的几个要点
1)制动时磨擦片与制动鼓全面接触,单位压力的大小呈正弦曲线分布,如图2, 位于蹄片轴中心---毂中心连线的垂线方向,其它各点的单位压力 ;
2)通过微积分计算,将制动鼓
与磨擦片之间的单位压
力换算成一个等效压力,
求出等效压力的方向
和力的作用点 、
( 、 ),等效力
0.576
0.621
0.574
0.571
0.58
0.568
0.416
0.35
0.292
0.263
0.285
0.286
0.295
摩擦片上最大单位压力位于 角处:
摩擦片上单位压力的分配:
位于与x-x成 角处。
单位压力在x、y方向上分解:
P分解为:
对整个蹄片x-x方向上合力为:
同样y-y方向上合力为:
合力角度
P所产生的摩擦力
(等于 )即扭矩(需建
立M和蹄片平台受力F之间的关系);实际计算必须找出M与F之间的关系式:
3)制动扭矩计算
蹄片受力如图3:
a.三力平衡
领蹄:
从蹄:
b.通过对蹄片受力平衡分析(对L点取力矩)
制动器设计及计算实例

制动器设计及计算实例制动器是一种用于车辆或机械设备上的重要安全装置,用于减速、停止或保持其运动状态。
其设计和计算涉及到多个方面的因素,包括制动力的大小、刹车盘的尺寸和材料、制动液的压力等。
下面将通过一个实例来介绍制动器的设计及计算。
假设我们需要设计一个汽车的制动器,首先我们需要确定以下几个参数:1. 汽车的质量:假设汽车的质量为1500kg;2.最大限制加速度:假设最大限制加速度为4m/s^2;3.停车的时间:假设停车的时间为3秒。
基于以上参数,我们可以计算出汽车需要的制动力:制动力=汽车质量×最大限制加速度= 1500kg × 4m/s^2=6000N接下来,我们需要设计制动盘的尺寸和材料。
制动盘的直径和厚度会影响其散热性能和制动力的传递效果。
一般而言,制动盘的直径越大,制动力就越好,但也会增加重量和成本。
制动盘的材料通常选择具有良好耐磨性和散热性能的金属材料,如铸铁或复合材料。
假设我们选择了铸铁制动盘,并给定以下参数:1. 制动盘的直径:假设制动盘的直径为300mm;2. 制动盘的厚度:假设制动盘的厚度为40mm;根据制动盘的直径和厚度,我们可以计算制动盘的转动惯量:转动惯量=(1/2)×制动盘的质量×(制动盘的直径/2)^2=(1/2)×制动盘的质量×(0.15m)^2根据实际情况,制动盘的质量需要根据制动盘的材料、直径和厚度来选择。
为了方便计算,假设制动盘的质量为20kg。
转动惯量= (1/2) × 20kg × (0.15m)^2= 0.45kg·m^2接下来,我们需要选择适当的制动液和计算所需的制动液压力。
制动液在制动器中起到传递力和控制制动器放松的作用。
制动液需要具有良好的抗压性、稳定性和耐高温性能。
假设我们选择了常用的DOT4制动液,并给定以下参数:1.制动液的抗压性比:假设制动液的抗压性比为10:1;2.需要的制动力:假设需要的制动力为6000N。
制动器的设计与计算

比摩擦力f0 每单位衬片(衬块)摩擦面积的制动器摩擦力
在j=0.6g时,鼓式制动器的比摩擦力f0以不大于0.48N/mm2为宜。与之相应的衬片与制动 鼓之间的平均单位压力pm=f0/f=1.37~1.60N/mm2(设摩擦因数f=0.3~0.35)。
4.制动器中心到张开力F0作用线的距离e
使距离e(图8-7)尽可能大, 初步设计时可暂定e=0.8R左右。 5.制动蹄支承点位置坐标a和c
使a尽可能大而c尽可能小。初步设计时,也可暂定a=0.8R左右。
二、盘式制动器主要参数的确定
1.制动盘直径D 通常选择为轮辋直径70%~79%
2.制动盘厚度h 实心制动盘厚度可取为10~20mm; 通风式制动盘厚度取为20~50mm; 采用较多的是20~30mm
对于紧蹄的径向变形δ1和压力p1为:
p11p11mmaaxsxsiinna(a(1111))
一个自由度的紧蹄摩擦衬片的径向变形规律
1 B 1 C 1 B 1 B 1 si 1 n A 1 B 1 si 1 d n
表面的径向变形和压力为:
1
p1
Rsinad
pmax sina
新蹄片压力沿摩擦衬片长度的分布符合正弦曲线规律
2.计算蹄片上的制动力矩 法向力 制动力矩
对于紧蹄 对于松蹄
液力驱动
自锁条件 领蹄表面的最大压力
不会自锁
二、盘式制动器的设计计算
单侧制动块加于制动盘的制动力矩 单侧衬块加于制动盘的总摩擦力 有效半径
m值一般不应小于0.65。 平面度允差为0.012mm,表面粗糙度为Ra0.7~1.3μm,两摩擦表面的平行度不应 大于0.05mm,制动盘的端面圆跳动不应大于0.03mm。
制动器设计的计算过程

制动器设计的计算过程钳盘式制动器在液力助力下制动力大且稳定,而且空气直接通过盘式制动盘,故盘式制动器的散热性很好,在各种路面都有良好的制动表现。
将越来越多地应用于轮式装载机的制动系统设计中。
目前,轮式装载机制动系统的设计有两大发展有两大发展趋势。
其一是行车制动起向封闭式湿式全盘式发展。
这种制动器全封闭防水防尘,制动性能稳定,耐磨损使用寿命长,不需调整。
散热效果良好,摩擦副温度显著降低。
不增大径向尺寸的前提下改变摩擦盘数量,可调节制动力矩,实现系列化标准化。
其二是制动传动装置由气推油向全液压动力制动发展。
这种制动装置的制动踏板直接操纵制动液压阀,可省去气动元件,结构简单紧凑,冬季不会冻结,不需放水保养,阀和管路不会锈蚀,制动可靠性提高。
所以在轮式装载机的制动系统中被越来越多地得到应用。
本文对此系统的设计计算方法和步骤简单介绍。
1假设条件和制动性能要求1.1假设条件忽略空气阻力,并假定四轮的制动器制动力矩相等且同时起作用;驻车制动器制动力矩作用于变速器的输出端或驱动桥的输入端。
1.2制动性能要求1.2.1对制动距离的要求根据GB8532-87 (与ISO 3450-85等效),非公路行驶机械的制动距离的(水平路面)要求如表1。
表1非公路行驶机械的制动距离最高车速(km/h)最大质量(kg)行车制动系统的制动距离(m)辅助制动系统的制动距离(m)二32/ 0 W32000 V2/68+(V2/124) . (G/32000) V2/39+ (V2/130). (G/32000)三32000 V2/44 V2/30W32 / 0 W32000 V2/68+(V2/124) . (G/32000) +0.1(32-V) V2/39+ (V2/130) . (G/32000) +0.1(32-V)三32000 V2/44+0.1(32-V) V2/30+0.1(32-V)* V——制动初速度(Km/h) G——整机工作质量(kg)1.2.2对行车系统的性能要求除了满足制动距离要求外,还要求行车制动系统能满足装载机空载在25% (14.0)的坡度上停住。
制动器的设计计算

§3 制动器的设计计算3.3制动蹄上的压力分布规律与制动力矩的简化计算1.沿蹄片长度方向的压力分布规律用解析方法计算沿蹄片长度方向的压力分布规律比较困难,因为除了摩擦衬片有弹性容易变形外,制动鼓、制动蹄以及支承也都有弹性变形。
通常在近似计算中只考虑衬片径向变形的影响,其他零件变形的影响较小,可以忽略不计。
制动蹄可设计成一个自由度和两个自由度的(见图37)形式。
首先计算有两个自由度的增势蹄摩擦衬片的径向变形规律。
为此,取制动鼓中心O点为坐标原点,如图37所示,并让y 1坐标轴通过制动蹄的瞬时转动中心A 1点。
制动时,由于摩擦衬片变形,制动蹄在绕瞬时转动中心A 1转动的同时,还顺着摩擦力作用方向沿支承面移动。
结果使制动蹄中心位于点,因而可以想象未变形的摩擦衬片的表面轮廓(EE 1O l 线)就沿方向移人制动鼓体内。
显然,衬片表面上所有点在这个方向上的变形是相同的。
例如,位于半径,上的任意点的变形就是线段。
因此,对于该点的径向变形为1OO 1OB 1B '11B B 1'11111cos Ψ≈=B B C B δ由于 和ο90)(111−+=Ψαϕmax 11'11δ==OO B B 于是得到增势蹄的径向变形1δ和压力为1q )sin(11max 11ϕαδδ+≈)sin(11max 1ϕα+=q q (43)式中 1α——任意半径1OB 和轴之间的夹角;1y 1ϕ——最大压力线与轴之间的夹角;1OO 1x 1ψ——半径和线之间的夹角。
1OB 1OO 下面再计算有一个自由度的增势蹄摩擦衬片的径向变形规律。
此时摩擦衬片在张开力和摩擦力的作用下,绕支承销中心A 1转动γd 角(见图37(b))。
摩擦衬片表面任意点沿制动蹄转动的切线方向的变形即为线段,其径向变形分量是线段,在半径延长线上的投影,即线段。
由于1B '11B B '11B B 1OB 1BB γd 角很小,可以认为,则所求的摩擦衬片径向变形为°=∠90'111B B Aγγγδd B A B B C B ⋅===sin sin 11'11111 考虑到,则由等腰三角形可知R OB OA =≈1111OB A γαsin /sin /11R B A = 代入上式,得摩擦衬片的径向变形和压力分别为γαδd R sin 1=αsin max 11q q = (44)综合上述可以认为:对于尚未磨合的新制动蹄衬片,沿其长度方向的压力分布符合正弦曲线规律,可用式(43)和式(44)计算。
汽车-汽车鼓式制动器设计

第一章制动参数选择及计算第一节汽车参数(符号以汽车设计为准)制动器设计中需要的重要参量:汽车轴距:L=1370mm车轮滚动半径:r r=295mm汽车满载质量:m a=4100Kg汽车空载质量:m o=2600Kg满载时轴荷的分配:前轴负荷39%,后轴负荷61%空载时轴荷的分配:前轴负荷47%,后轴负荷53%满载时质心高度:hg=745mm空载时质心高度:hg'=850mm质心距前轴的距离:L1=835mm L1'=726mm 质心距后轴的距离:L2=535mm L2'=644mm 对汽车制动性有影响的重要参数还有:制动力及其分配系数、同步附着系数、制动强度、附着系数利用率、最大制动力矩与制动因数等。
第二节制动器的设计与计算一制动力与制动力矩分配系数0水平路面满载行驶时,前、后轴的负荷计算对于后轴驱动的移动机械和车辆,在水平路面满载行驶时前后轴的最大负荷按下式计算(g=9.8N/kg)前轴的负荷F1=Ga(L2-ϕhg)/(L-ϕhg)=3830.8N 后轴的负荷F2=GaL1/(L-ϕhg)=36349.2Nϕ---附着系数,沥青.混凝土路面,取0.6轴荷转移系数:前轴:m ,1=F Z 1/G1=0.24后轴:m ,2=F Z 1/G2=1.481、(汽车理论108页)水平路面满载行驶制动时,地面对前后车轮的法向反作用力(满载)F Z 1=GL(L 2+ϕgh )=4100×9.8÷1.370×(0.535+0.6×0.745)=28800.55N F Z 2=GL(L 1-ϕgh)=4100×9.8÷1.370×(0.835-0.6×0.745)=11379.45N式中:G--汽车所受重力;L--汽车轴距;1L --汽车质心离前轴距离;L 2--汽车质心离后轴距离;gh--汽车质心高度;g --重力加速度;(取9.80N/kg)2(汽车理论8,22)汽车制动时,如果不记车轮的滚动阻力矩和汽车的回转质量的惯性力矩,则任何角速度ω﹥0的车轮,其力矩平衡方程为Mμ-F b ×R e =0(4-2)式中:Mμ--制动器对车轮作用的制动力矩,即制动器的摩擦力矩,其方向与车轮旋转方向相反,N﹒m;F b --地面作用于车轮上的制动力,即地面与轮胎之间的摩擦力,又称地面制动力,其方向与汽车行驶方向相反,N ;R e --车轮有效半径,m令F B =Mμ/R e并称之为制动器的制动力,它是在轮胎周缘克服制动器的摩擦力矩所需的力,因此又称为制动周缘力。
制动器的设计计算部分

制动器的设计计算部分制动器是用来控制或减速机械设备运动的装置。
它通常由摩擦垫、压力单元、驱动装置和控制装置组成。
制动器的设计计算部分包括静态设计与动态设计两个方面。
静态设计主要涉及计算所需的制动力和摩擦垫的尺寸,而动态设计则涉及制动器在运行期间的热量分布和冷却。
在进行静态设计计算之前,首先需要确定制动器所需的制动力。
制动器的制动力通常由下述式子计算:制动力=需要减速度×机械设备的质量其中,需要减速度是由系统要求或运行条件决定的。
机械设备的质量可以通过实际测量或通过计算机辅助设计软件进行估算。
此外,制动器还需要考虑一些额外的因素,如摩擦系数和安全系数,以确保制动器的可靠性和安全性。
在确定制动力后,需要计算摩擦垫的尺寸。
摩擦垫的尺寸取决于制动器的类型和具体应用。
常见的制动器类型包括盘式制动器和鼓式制动器。
对于盘式制动器,摩擦垫通常由摩擦面的直径和宽度来确定。
对于鼓式制动器,摩擦垫的尺寸通常由鼓面的直径和摩擦面的长度来决定。
与摩擦垫尺寸相关的参数还包括摩擦垫的摩擦系数和最大摩擦温度。
摩擦系数表示摩擦垫在制动时的摩擦性能,其数值通常由摩擦材料的选择决定。
最大摩擦温度是指制动器在运行期间可能达到的最高温度,该温度主要取决于摩擦材料和运行工况。
在动态设计方面,制动器的热量分布和冷却是设计中的重要考虑因素。
当制动器运行一段时间后,摩擦垫会产生大量热量,如果不能及时散热,可能会导致制动性能下降、摩擦垫老化或甚至引发火灾。
因此,制动器的设计需要考虑散热系统,以保持摩擦垫的正常工作温度。
散热系统通常包括散热片或散热鳍片,以增加散热面积,帮助热量的有效传递。
此外,制动器还可以采用风冷式冷却系统,通过引入外部冷气来加速热量的散发。
冷却系统的设计需要考虑风量、风速和冷却材料的选择等因素。
综上所述,制动器的设计计算部分涉及静态设计和动态设计两个方面。
静态设计主要包括计算制动力和摩擦垫尺寸,而动态设计则涉及制动器的热量分布和冷却。
制动器的设计与计算(图片高清)

第四节制动器的设计与计算一、鼓式制动器的设计计算1.压力沿衬片长度方向的分布规律除摩擦衬片因有弹性容易变形外,制动鼓、蹄片和支承也有变形,所以计算法向压力在摩擦衬片上的分布规律比较困难。
通常只考虑衬片径向变形的影响,其它零件变形的影响较小而忽略不计。
制动蹄有一个自由度和两个自由度之分。
首先计算有两个自由度的紧蹄摩擦衬片的径向变形规律。
如图8—8a所示,将坐标原点取在制动鼓中心O点。
y I坐标轴线通过蹄片的瞬时转动中心A1点。
制动时,由于摩擦衬片变形,蹄片一面绕瞬时转动中心转动,同时还顺着摩擦力作用的方向沿支承面移动。
结果蹄片中心位于O1点,因而未变形的摩擦衬片的表面轮廓(E1E1线),就沿OO1方向移动进入制动鼓内。
显然,表面上所有点在这个方向上的变形是一样的。
位于半径OB l上的任意点B1的变形就是B1B’1线段,所以同样一些点的径向变形δ1为δ1=B1C1≈B1B’1cosψ1考虑到ψ1≈(φ1+α1—90º)和B1B’1=001=δ1max所以对于紧蹄的径向变形δ1和压力p1为:式中,α1为任意半径OB l和y1轴之间的夹角;Ψl为半径OBi和最大压力线001之间的夹角;φ1为х1轴和最大压力线001之间的夹角。
其次计算有一个自由度的紧蹄摩擦衬片的径向变形规律。
如图8—8b 所示,此时蹄片在张开力和摩擦力作用下,绕支承销A 1转动d γ角。
摩擦衬片表面任意点B l 沿蹄片转动的切线方向的变形就是线段B 1B ’1,其径向变形分量是这个线段在半径OB 1延长线上的投影,即为B 1C 1线段。
由于d γ很小,可认为∠A 1B 1B ’1=90º,故所求摩擦衬片的变形应为δ1=B 1C 1=B 1B’1sin γ1=A 1B 1sin γ1d γ考虑到OA l ~OB 1=R.那么分析等腰三角形A l OB 1,则有A 1月l /sin α=R /sin7,所以表面的径向变形和压力为γαδd R sin 1=αsin max 1p p = (8—2)综上所述可知,新蹄片压力沿摩擦衬片长度的分布符合正弦曲线规律,可用式(8—1)和式(8—2)计算。
制动器的设计计算资料

制动器的设计计算资料制动器是控制机械设备的停止和稳定的主要装置之一,是重要的机械工程设计内容之一、制动器设计计算资料主要包括制动器类型选择、制动器工作原理、主要性能参数计算、热弹性计算和其他相关计算等。
一、制动器类型选择根据工作原理和应用需求,可以选择摩擦制动器、电磁制动器、液压制动器等不同类型的制动器。
制动器的类型选择应根据具体的工作条件、负荷情况、速度要求、空间限制等因素进行合理选择。
二、制动器工作原理制动器工作原理主要包括静摩擦制动、动摩擦制动、电磁制动、液压制动等。
根据具体应用要求,选择合适的工作原理,确保制动器的稳定性和可靠性。
三、主要性能参数计算1.制动力矩计算:根据所需的制动力矩和工作条件,通过力矩平衡计算或摩擦因数计算等方法,确定制动器所需的力矩大小和设计参数。
2.制动器转矩计算:根据所需的转矩大小和工作条件,通过摩擦副转矩平衡计算或材料强度计算等方法,确定制动器所需的转矩大小和设计参数。
3.制动器制动时间计算:根据物体的质量、速度、制动距离和制动器的工作特性等参数,通过运动学方程和力学方程计算,确定制动器的制动时间。
4.制动器制动压力计算:根据制动器的工作特性、制动力矩和材料强度等参数,通过流体力学原理和弹性力学原理计算,确定制动器所需的制动压力。
四、热弹性计算在制动器工作过程中,由于摩擦产生的热量会引起制动器温升,并且制动器会受热膨胀的影响。
为确保制动器的稳定性和可靠性,需要进行热弹性计算,包括热传导计算、热膨胀计算和热应力计算等。
五、其他相关计算除了上述主要计算外,还需要进行其他相关的计算,如制动器的材料选择和强度计算、制动器的寿命估算和可靠性分析等。
总之,制动器的设计计算资料包括制动器类型选择、制动器工作原理、主要性能参数计算、热弹性计算和其他相关计算等内容。
制动器的设计应根据具体的工作条件和要求,经过合理的计算和分析,确保制动器的性能稳定和可靠性,满足机械设备的工作要求。
制动器的设计计算资料

§3 制动器的设计计算3.1制动蹄摩擦面的压力分布规律从前面的分析可知,制动器摩擦材料的摩擦系数及所产生的摩擦力对制动器因数有很大影响。
掌握制动蹄摩擦面上的压力分布规律,有助于正确分析制动器因数。
在理论上对制动蹄摩擦面的压力分布规律作研究时,通常作如下一些假定:(1)制动鼓、蹄为绝对刚性;(2)在外力作用下,变形仅发生在摩擦衬片上;(3)压力与变形符合虎克定律。
1.对于绕支承销转动的制动蹄如图29所示,制动蹄在张开力P 作用下绕支承销点转动张开,设其转角为,则蹄片上某任意点A 的位移AB 为 AB =A O '·θ∆由于制动鼓刚性对制动蹄运动的限制,则其径向位移分量将受压缩,径向压缩为AC AC =AB COS β即 AC =A O 'θ∆COS β从图29中的几何关系可看到A O 'COS β=D O '=O O 'Sin ϕAC =O O 'Sin ϕθ∆⋅ 因为θ∆⋅'O O 为常量,单位压力和变形成正比,所以蹄片上任意一点压力可写成 q=q 0Sin ϕ (36)亦即,制动器蹄片上压力呈正弦分布,其最大压力作用在与O O '连线呈90°的径向线上。
2.浮式蹄在一般情况下,若浮式蹄的端部支承在斜支座面上,如图30所示,则由于蹄片端部将沿支承面作滚动或滑动,它具有两个自由度运动,而绕支承销转动的蹄片只有一个自由度的运动,因此,其压力分布状况和绕支承销转动的情况有所区别。
现分析浮式蹄上任意一点A 的运动情况。
今设定蹄片和支座面之间摩擦足够大,制动蹄在张开力作用下,蹄片将沿斜支座面上作滚动,设Q 为其蹄片端部圆弧面之圆心,则蹄片上任意一点A 的运动可以看成绕Q 作相对转动和跟随Q 作移动。
这样A 点位移由两部分合成:相对运动位移AB 和牵连运动位移BC ,它们各自径向位移分量之和为AD (见图30)。
AD =AB COS β+BC COS(ϕ-α)根据几何关系可得出AD =(θ∆·OQ +BC Sin α) Sin ϕ+BC COS αCOS ϕ式中θ∆为蹄片端部圆弧面绕其圆心的相对转角。
汽车制动器计算原则归纳

汽车制动器设计计算步骤1.文中的一些命名方式以及符号可能不是很适应你们的习惯,希望能根据你们的习惯用红色字体进行修改。
2.鉴于口头形式或许会遗漏很多细节,所以将汽车制动器计算部分进行了一个归纳,里面有些处理的方法不是很清楚,希望能进一步进行文本上的完善。
3.有些参数是不是有常用的默认值,或者是取值范围,请在参数名称的后面表明。
4.其他错误也望能一同更正5.由于上个星期忙于期末汇报没能及时提交这份总结望见谅1.车型部分:输入:车满载质量:M max(Kg)车空载质量:M min(Kg)初速度:V0(Km/h)刹车距离:S0(m)轴距:L(m)前轮轴距:L1(m)后轮轴距:L2(m)满载质心高:Hg1(m)空载质心高::Hg2(m)前/后轮滚动半径:Rg(m)地面附着力系数:u轮辋规格:(内径和深度)(mm)输出:最大减速度:a max=g*u(m/s2)必要减速度:a mu=V02/(2*S0)(m/s2)制动盘的最大直径D max: (mm)(受轮辋内部空间限制,包括内径和深度)前轮分配比:dt1=(L2+a max*Hg1/g)/L满载时的情况:(按地面能够提供的最大减速度计算)后轮分配比:dt2=(L1-a max*Hg1/g)/L地面总制动力矩:M=a max*g*u*Rg(N.m)前轮所需制动力矩:M1=M*dt1后轮所需制动力矩:M2=M*dt2空载时的情况: (按地面能够提供的最大减速度计算)前轮分配比:dt1、=(L2+a max*Hg2/g)/L后轮分配比:dt2、=(L1-a max*Hg2/g)/L地面总制动力矩:M、= M min *g*u*R g(N·m)前轮所需制动力矩:M1、=M*dt1、(N·m)后轮所需制动力矩:M2、=M*dt2、(N·m)约束1:A mu<A max满足:继续设计不满足:怎么处理?(车型设计的减速度是由法律规定的,设计车型时,应该是由法律规定的减速度,确定车辆的初速以及停车距离,不可能会出现设定的减速度大于地面能够提供的最大减速度,如果出现这种可能,只能是车型设计有问题。
制动系统设计与计算

从上述计 算和图表 中可以看 到,该车 的制动器 附着系数 利用曲线 负荷ECE 标准。
空载
附着系数利用法规线 GB21670
GB21670 -2008中要求:在车辆所有载荷状态下,当制动强度z处于0.15~0.80之间时,后轴附着系数利用 于前轴上方;当附着系数ψ在0.2~0.8之间时,制动强度z≥0.1+0.7(ψ-0.2)。
G* (b+z*hg )/L 10457.36 N
φ*Fz1
8124.393 N 2372.323 N.m G*(az*hg)/L 7079.145 φ*Fz2 5499.833 N 1605.951 N.m
空载
G*
汽车前轮最大法向反作用力Fz1‘
(b+z*hg )/L
8768.286 N
汽车前轮空载最大地面附着力Fxb1' φ*Fz1
7077.212377 3255.907623
0.9
2.46178968
8266.739706 3358.020294
1
2.807471264
9524.017208 3392.382792
β曲线(与制动系统的参数有关,制动系统参数定义完成后,β曲线就定义完成)
前制动器所能提供的最大制动力
后制动器所能提供的最大制动力
制动强度 前轴的利用附着系数 0
后轴的利用附着系数
0.1
0.2
0.3
0.4
0.5
0.6
同上
0.7
0.8
0.9
同上 空载
1
1.1
满载 制动强度 前轴的利用附着系数
0 0.1
0.2
0.3
0.4
阜新市中考满分作文-制动器的设计计算
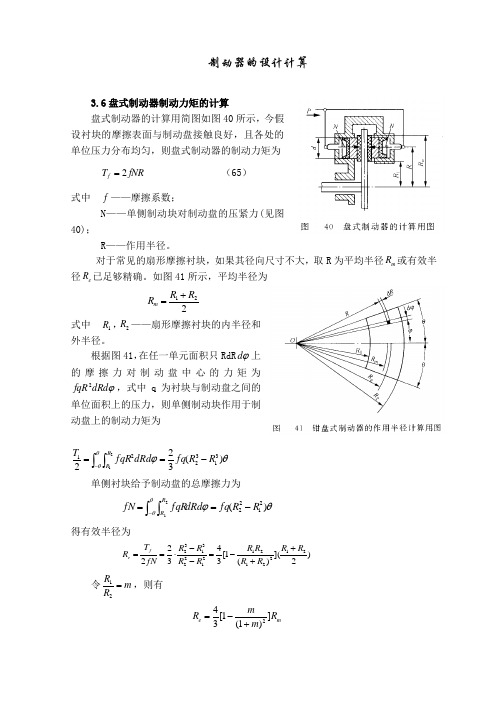
制动器的设计计算3.6盘式制动器制动力矩的计算盘式制动器的计算用简图如图40所示,今假设衬块的摩擦表面与制动盘接触良好,且各处的单位压力分布均匀,则盘式制动器的制动力矩为fNR T f 2= (65)式中 f ——摩擦系数;N ——单侧制动块对制动盘的压紧力(见图40);R ——作用半径。
对于常见的扇形摩擦衬块,如果其径向尺寸不大,取R 为平均半径m R 或有效半径e R 已足够精确。
如图41所示,平均半径为 221R R R m += 式中 1R ,2R ——扇形摩擦衬块的内半径和外半径。
根据图41,在任一单元面积只RdR ϕd 上的摩擦力对制动盘中心的力矩为ϕdRd fqR 2,式中q 为衬块与制动盘之间的单位面积上的压力,则单侧制动块作用于制动盘上的制动力矩为θϕθθ)(32231322121R R fq dRd fqR T R R -==⎰⎰- 单侧衬块给予制动盘的总摩擦力为θϕθθ)(212221R R fq dRd fqR fN R R -==⎰⎰- 得有效半径为 )2]()(1[34322212212121223132R R R R R R R R R R fN T R fe ++-=--⋅== 令m R R =21,则有 m e R m m R ])1(1[342+-=因121<=R R m ,41)1(2<+m m ,故m e R R >。
当21R R →,1→m ,m e R R →。
但当m 过小,即扇形的径向宽度过大,衬块摩擦表面在不同半径处的滑磨速度相差太大,磨损将不均匀,因而单位压力分布将不均匀,则上述计算方法失效。
3.7 驻车计算图42为汽车在上坡路上停驻时的受力情况,由此可得出汽车上坡停驻时的后轴车轮的附着力为: )sin cos (12ααϕϕg a h L Lg m Z += 同样可求出汽车下坡停驻时的后轴车轮的附着力为: )sin cos (12ααϕϕg a h L Lg m Z -=' 根据后轴车轮附着力与制动力相等的条件可求得汽车在上坡路和下坡路上停驻时的坡度极限倾角α,α',即由 αααϕsin )sin cos (1g m h L Lg m a g a =+ 求得汽车在上坡时可能停驻的极限上坡路倾角为 gh L L ϕϕα-=1arctan (66) 汽车在下坡时可能停驻的极限下坡路倾角为 gh L L ϕϕα+='1arctan 一般对轻型货车要求不应小于25%,中型货车不小于20%,汽车列车的最大停驻坡度约为12%左右。
制动器的设计计算

§3 制动器的设计计算3.1制动蹄摩擦面的压力分布规律从前面的分析可知,制动器摩擦材料的摩擦系数及所产生的摩擦力对制动器因数有很大影响。
掌握制动蹄摩擦面上的压力分布规律,有助于正确分析制动器因数。
在理论上对制动蹄摩擦面的压力分布规律作研究时,通常作如下一些假定:(1)制动鼓、蹄为绝对刚性;(2)在外力作用下,变形仅发生在摩擦衬片上;(3)压力与变形符合虎克定律。
1.对于绕支承销转动的制动蹄如图29所示,制动蹄在张开力P 作用下绕支承销O '点转动张开,设其转角为θ∆,则蹄片上某任意点A 的位移AB 为 AB =A O '·θ∆由于制动鼓刚性对制动蹄运动的限制,则其径向位移分量将受压缩,径向压缩为AC AC =AB COS β即 AC =A O 'θ∆COS β从图29中的几何关系可看到A O 'COS β=D O '=O O 'Sin ϕAC =O O 'Sin ϕθ∆⋅ 因为θ∆⋅'O O 为常量,单位压力和变形成正比,所以蹄片上任意一点压力可写成 q=q 0Sin ϕ (36)亦即,制动器蹄片上压力呈正弦分布,其最大压力作用在与O O '连线呈90°的径向线上。
2.浮式蹄在一般情况下,若浮式蹄的端部支承在斜支座面上,如图30所示,则由于蹄片端部将沿支承面作滚动或滑动,它具有两个自由度运动,而绕支承销转动的蹄片只有一个自由度的运动,因此,其压力分布状况和绕支承销转动的情况有所区别。
现分析浮式蹄上任意一点A 的运动情况。
今设定蹄片和支座面之间摩擦足够大,制动蹄在张开力作用下,蹄片将沿斜支座面上作滚动,设Q 为其蹄片端部圆弧面之圆心,则蹄片上任意一点A 的运动可以看成绕Q 作相对转动和跟随Q 作移动。
这样A 点位移由两部分合成:相对运动位移AB 和牵连运动位移,它们各自径向位移分量之和为AD (见图30)。
制动器设计~计算说明书

三、课程设计过程(一)设计制动器的要求:1、具有良好的制动效能—其评价指标有:制动距离、制动减速度、制动力和制动时间。
2、操纵轻便—即操纵制动系统所需的力不应过大。
对于人力液压制动系最大踏板力不大于(500N )(轿车)和700N (货车),踏板行程货车不大于150mm ,轿车不大于120mm 。
3、制动稳定性好—即制动时,前后车轮制动力分配合理,左右车轮上的制动力矩基本相等,汽车不跑偏、不甩尾;磨损后间隙应能调整!4、制动平顺性好—制动力矩能迅速而平稳的增加,也能迅速而彻底的解除。
5、散热性好—即连续制动好,摩擦片的抗“热衰退”能力要高(指摩擦片抵抗因高温分解变质引起的摩擦系数降低);水湿后恢复能力快。
6、对挂车的制动系,还要求挂车的制动作用略早于主车;挂车自行脱钩时能自动进行应急制动。
(二)制动器设计的计算过程:设计条件:车重2t ,重量分配60%、40%,轮胎型175/75R14,时速70km/h ,最大刹车距离11m 。
1. 汽车所需制动力矩的计算根据已知条件,汽车所需制动力矩:M=G/g ·j ·r k (N ·m ) 206.321j )(v S ⋅=(m/s 2) 式中:r k — 轮胎最大半径 (m);S — 实际制动距离 (m);v 0 — 制动初速度 (km/h)。
217018211 3.6j ⎛⎫=⋅= ⎪⋅⎝⎭(m/s 2) m=G/g=2000kg查表可知,r k 取0.300m 。
M=G/g ·j ·r k =2000·18·0.300=10800(N ·m )前轮子上的制动器所需提供的制动力矩:M ’=M/2⋅60%=3240(N ·m )为确保安全起见,取安全系数为1.20,则M ’’=1.20M ’=3888(N ·m )2. 制动器主要参数的确定(1)制动盘的直径D制动盘直径D 希望尽量大些,这时制动盘的有效半径得以增大,就可以降低制动钳的夹紧力,降低摩擦衬块的单位压力和工作温度。
制动器制动力矩的计算

制动器制动力矩的计算制动器是汽车制动系统中的关键组成部分,它负责将车轮的动能转化为热能,并通过与摩擦盘接触产生的摩擦力来减慢汽车运动。
制动器制动力矩的计算是评估制动器性能的重要指标之一,本文将从制动器的工作原理、制动力矩的定义和计算公式等方面进行详细介绍。
一、制动器的工作原理制动器主要由刹车盘(或鼓)和制动钳组成。
当驾驶员踩下制动踏板时,制动液被压缩并传递到制动钳中,使制动钳内的活塞发生运动。
制动钳的活塞会通过制动片将摩擦力传递到刹车盘上,从而减慢车辆的运动。
制动器的制动力矩是指制动器对车轮的制动力矩。
在制动过程中,制动器产生的摩擦力会产生一个力矩,从而减慢车轮的转速。
制动力矩的大小决定了车轮的制动效果。
二、制动力矩计算公式制动力矩的计算公式如下:制动力矩=制动力×刹车半径。
1.制动力的计算制动力是指制动器产生的摩擦力,其大小取决于刹车系统的设计和制动器的性能。
制动力的计算通常基于以下几个因素:-车辆的质量:车辆的质量越大,所需的制动力就越大。
-刹车系统的设计:刹车系统的设计决定了制动力的输出方式和传递效率。
-刹车片材料和状态:刹车片的摩擦系数与制动力密切相关。
另外,刹车片的磨损状态也会影响制动力。
-刹车系统的液压压力:制动液的压力越大,制动力越大。
2.刹车半径的计算刹车半径是指刹车盘(或鼓)的半径。
刹车半径的大小决定了制动力矩的大小。
刹车盘(或鼓)的半径可以通过测量得到,或者根据制动器的设计参数确定。
三、制动力矩计算的实例假设一个汽车质量为1000千克,制动力为3000牛顿,刹车盘的半径为0.3米,测算制动力矩。
首先,根据制动力的计算公式,制动力=3000牛顿。
然后,根据刹车半径的计算公式,刹车半径=0.3米。
最后,根据制动力矩的计算公式,制动力矩=制动力×刹车半径=3000牛顿×0.3米=900牛顿·米。
因此,这个汽车的制动力矩为900牛顿·米。
制动器设计说明书

一、汽车总体设计(纸上) 二.制动器的设计计算2.1 地面对车轮的法向反作用力B F ——地面作用于车轮上的制动力,即地面与轮胎之间的摩擦力,又称为地面制动力,其方向与汽车行驶方向相反,N ;e r ——车轮有效半径,m 。
令 ef f r T F =并称之为制动器制动力,它是在轮胎周缘克服制动器摩擦力矩所需的力,因此又称为制动周缘力。
f F 与地面制动力B F 的方向相反,当车轮角速度ω>0时,大小亦相等,且f F 仅由制动器结构参数所决定。
即f F 取决于制动器的结构型式、尺寸、摩擦副的摩擦系数及车轮有效半径等,并与制动踏板力即制动系的液压或气压成正比。
当加大踏板力以加大f T ,f F 和B F 均随之增大。
但地面制动力B F 受着附着条件的限制,其值不可能大于附着力ϕF ,即B F ≤ϕϕZ F = 或ϕϕZ F F B ==max 式中 ϕ——轮胎与地面间的附着系数; Z ——地面对车轮的法向反力。
当制动器制动力f F 和地面制动力B F 达到附 着力ϕF 值时,车轮即被抱死并在地面上滑 移。
此后制动力矩f T 即表现为静摩擦力矩, 而e f f r T F /=即成为与B F 相平衡以阻止车轮制动力与踏板力的关系再旋转的周缘力的极限值。
当制动到ω=0以后,地面制动力B F 达到附着力ϕF 值后就不再增大,而制动器制动力f F 由于踏板力P F 的增大使摩擦力矩f T 增大而继续上升(见图2-2)。
根据汽车制动时的整车受力分析,考虑到制动时的轴荷转移,可求得地面对前、后轴车轮的法向反力Z 1,Z 2为:)(21dtdu g h L L G Z g +==20008.9*1680(640+8.9600x6.86)=8725N)(12dtdu g h L LG Z g -==20008.9*1680(1360-8.9600x6.86)=7738N式中 G ——汽车所受重力; L ——汽车轴距;1L ——汽车质心离前轴距离; 2L ——汽车质心离后轴距离;g h ——汽车质心高度; g ——重力加速度;dtdu -——汽车制动减速度。
制动器设计参数与计算方法

第一章制动器设计参数与计算方法根据制动原理,制动器分为摩擦式和非摩擦式。
按摩擦元件的结构有外抱块式、内张蹄式、带式和盘式;非摩擦式有磁粉式、磁涡流式和水涡流式。
制动器的主要设计步骤如下:(!)计算制动轴上的转矩;(")确定制动安全因数,计算制动转矩;(#)选定制动器类型和结构;($)求出驱动推力,设计驱动装置。
!"!制动转矩的确定!"!"!载荷转矩的计算(!)在时间!(")内将制动轴的转速从#!降至#%,要求完全制动时,#%&%$!%&’()(#!*#%)+(’#()*!)(+·,)(!*!)(")在制动转角!(-./)内将制动轴的转速从#!降至#%,要求完全制动时,#%&%$!%&’()(#"!*#"%)+(!)’%!)(+·,)(!*")(#)在车辆等行走,(,)距离内将制动轴的转速从#!降至#%,要求完全制动时,#%&%$!%&’()(#"!*#"%)+(!)’%,-)(+·,)(!*#)上述三式中,$0———载荷转矩(+·,);&———重力加速度(,12");’34———等效转动惯量(56,");.———车轮半径(,);-———制动轴到车轮轴的传动比。
!"!"#制动转矩的计算(!)水平制动:被制动的只是惯性质量,如车辆的制动。
其制动转矩为$%$0*$7(!*$)式中$7———换算到制动轴上的总摩擦阻力矩。
(")垂直制动:被制动的有惯性质量和垂直载荷,且垂直载荷是主要的。
如提升设备的制动。
其制动转矩为$%/$0(!**)式中/———保证重物可靠悬吊的制动安全因数,见表89!9!。
w w w.bz f x w.c om表!"#"#制动安全因数!的推荐值设备类型矿井提升机起重机械的提升机构手动、机动的轻级工作制机动的中级工作制机动的重级工作制机动的特重级工作制双制动中的每一台制动器!!"#$"#%$&#’&#$"#&$ ()值!"$*&$*+’*,’*注:()值为工作率,在"’-./内机构的工作时间与整个工作周期之比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
制动器设计的计算过程
钳盘式制动器在液力助力下制动力大且稳定,而且空气直接通过盘式制动盘,故盘式制动器的散热性很好,在各种路面都有良好的制动表现。
将越来越多地应用于轮式装载机的制动系统设计中。
目前,轮式装载机制动系统的设计有两大发展有两大发展趋势。
其一是行车制动起向封闭式湿式全盘式发展。
这种制动器全封闭防水防尘,制动性能稳定,耐磨损使用寿命长,不需调整。
散热效果良好,摩擦副温度显著降低。
不增大径向尺寸的前提下改变摩擦盘数量,可调节制动力矩,实现系列化标准化。
其二是制动传动装置由气推油向全液压动力制动发展。
这种制动装置的制动踏板直接操纵制动液压阀,可省去气动元件,结构简单紧凑,冬季不会冻结,不需放水保养,阀和管路不会锈蚀,制动可靠性提高。
所以在轮式装载机的制动系统中被越来越多地得到应用。
本文对此系统的设计计算方法和步骤简单介绍。
1 假设条件和制动性能要求
1.1 假设条件
忽略空气阻力,并假定四轮的制动器制动力矩相等且同时起作用;驻车制动器制动力矩作用于变速器的输出端或驱动桥的输入端。
1.2 制动性能要求
1.2.1 对制动距离的要求
根据GB8532-87(与ISO 3450-85等效),非公路行驶机械的制动距离的(水平路面)要求如表1。
表1 非公路行驶机械的制动距离最高车速
(km/h) 最大质量
(kg) 行车制动系统的制动距离
(m) 辅助制动系统的制动距离
(m)
≥32
/ θ≤32000 V2/68+(V2/124).(G/32000) V2/39+(V2/130).(G/32000)
≥32000 V2/44 V2/30
≤32 / θ≤32000 V2/68+(V2/124).(G/32000)+0.1(32-V) V2/39+(V2/130).(G/32000)+0.1(32-V)
≥32000 V2/44+0.1(32-V) V2/30+0.1(32-V)
* V——制动初速度(Km/h) G——整机工作质量(kg)
1.2.2 对行车系统的性能要求
除了满足制动距离要求外,还要求行车制动系统能满足装载机空载在25%(14.0)的坡度上停住。
1.2.3 对辅助制动系统的性能要求
满载时,应在15%(8.5)的坡道上驻车无滑移;空载时,应在18%(10.2)的坡道上无滑移。
行车制动系统失效时,应能作为紧急制动。
2 制动力矩计算
2.1 按所需制动距离计算
在水平路面上四轮制动的轮式装载机的,其行车制动总制动力矩MB1:
MB1=δ.G.a1.rk (N.m)
a1=V02/[25.92(S0-V0.t1/3.6)] (m/S2)
式中 G—整机工作质量(kg)
a1 —制动减速度(m/s2)
rk—车轮滚动工半径(m)
δ—回转质量换算系数
δ=1+[4Jk+∑(Jm.Im2)]/(rk2.G)
Jk—轮胎和轮辋的转动惯量(kg.m2)
Jm__m转动件转动惯量(kg.m2)
Im—m转动件到车轮的传动比
若Jk、Jm尚未可知,可取近似δ=1.1
V0——制动初速度(km/h)
轮式装载机V0=20km/h
S0——表1中V=V0时的制动距离(m)
t1——制动系统滞后时间(s)
对全液压制动系统,取t1=0.2
2.2 按坡道上驻车计算总制动力矩
(1)用行车制动器时总制动力矩
Mp1=G.g.sin14o.rk)(N.m)
式中g——重力加速度(m/s2)
(2)空载驻车用制动器时总制动力矩
Mp2=G.g.sin10.2o.rk)(N.m)
(3)满载驻车用制动器时总制动力矩
Mp3=(G+W).g.sin8.5o.rk)(N.m)
式中W——装载机额定载质量(kg)
根据2.1和2.2的计算,所需行车制动总制动力矩 M'B=max{MB1,Mp3};
所需驻车制动总制动力矩
M'P=max{MP1,Mp3};
2.3 按附着长件校核总制动力矩
(1)水平路面行车制动
MBu=G.g.δ.u.rk(N.m)
u——轮胎与水泥路面的滑动磨擦系数一般取u=0.6 (2)坡道空载驻车制动
MPu1=G.g.f.rkcos10.2o/(Id.If)(N.m)
f——轮胎与水泥路面的静磨擦系数
Id——桥主传动传动化
If——桥终传动传动化
(3)坡道满载驻车制动
Mpu2=(G+W).g.f.rkcos8.5/(Id.If)(N.m)
事实上,MPu1<Mpu2
2.4 制动力矩确定
综合考虑2.1、2.2和2.3的计算结果,则行车制动总力矩MB应满足
MB=min{M'B,MBu}
驻车制动总力矩Mp应满足:
Mp=min{MP,MPu1}
确定MB2后,再重新计算制动减速度a和制动距离S:
a=MB/(G.δ.rk)=(0.32-0.37)g (m/s2)
S=V02/(25.92a)+V0.t/3.6 (m)
确定Mp后,还可计算停车制动器作为紧急制动用的制动减速度ae和制动器距离Se:
ae=Mp.Id.If/(G.δ.u.rk)0.25g (m/s2)
Se=V02/(25.92ae)+V0.t/3.6 (m)
S和Se要满足表1的要求。
3 制动器设计计算
四轮制动器所能产生的制动力矩应大于或等于总制动力矩,即
4F.(nj+nd-1).ud.re≥MB
nj——每个制动器中静磨擦盘片数
nd——每个制动器中动磨擦盘片数一般nj=nd+1
ud——动、静磨擦盘间的磨擦系数
F——磨擦盘上的压紧力(N)
F=Pd.Ad-Fs
Pd——作用在磨擦衬块上的压力(Mpa)
Pd/ θ≤[Pd]
[Pd] ——磨擦衬块许用压力(Mpa)
Ad——磨擦盘有效面积(m)
Ad=3.14(R22-R2)
R1、R2——分别为磨擦衬块的内径、外径(m),由结构布置和磨擦盘生产厂家产品的尺寸系列决定。
Fs——制动器活塞回位弹簧作用力(N)一般取Fs=0 .1F re——磨擦盘当量磨擦半径(m)
假设磨擦盘均匀受力,可按下式计算:
re=R1(1-γ)2/[6(1+γ)]+(R1+R2)/2
式中γ=R1/R2
4 一次制动单个制动器用油量V1计算
V1=Ap.Lp (L)
式中 Ap——受油压侧活塞环面积(m2)
活塞环的平均半径应与磨擦盘的当量半径一致
Lp ——一次制动活塞总行程(mm)
Lp =(E+0.05).nj+(Ed+0.05).nd
Ej、Ed——静、动磨擦盘的平面度误差(mm)
根据单个制动器用油量可计算时滞控制阀和制动传动装置的用油量。
5 温升校核
5.1 制动能量计算
一次制动产生的总能量:
E=G.V2/25.92 (J)
单根驱动桥中制动器所要耗散的能量为
E1=E.β
式中β——前(后)桥制动器制动力分配比按前述假设β=0.5
5.2 温升计算A
△t=E1/(C1m1+C2m2)
=G.V2β/[25.92(C1m1+C2m2)]/ θ≤[△t/ θ]
式中C>1/ θ、——前(后)桥中制动器金属部件和冷却液的热容量[J/(kg./ θK)]
m1/ θ、m2/ θ——前(后)桥中邻接磨擦表面的金属部件质量和冷却液的质量(kg)
/ θ[△t]/ θ——一次制动最大允许温升(K)
[△t]/ θ的计算,是按制动器和驱动桥所产生的热量与所能散发的热量相平衡的原则,以及磨擦材料、油液和密封件所能承受的温度来决定的原则,以及磨擦材料、油液和密封件所能承受的温度来决定。
一般一次制动温度上升不应超过18oC,纸基磨擦材料表面温度经常高于200oC,将导致其迅速摩损。
