matlab第4章
第4章-MATLAB符号运算

simplify与simple命令
• simplify普遍使用于表达式化简。此外,还可以 使用simple函数进行化简; • simplify 函数可以对包含和式、根式、分数、 乘方、指数、对数、三角函数等的表达式化简; • 而simple 函数的目标是寻找最少字符的表达式。 • 例:Jacobi矩阵的Jacobian行列式。
findsym函数的例
syms a b c x >> f=sym('a*x^2+b*x+c'); >> findsym(f,1) %确定符号表达式首选的一个 变量 ans = x >> findsym(f,2) %确定符号表达式首选、次选 的2个变量 ans = x,c
符号微积分运算
• diff(f) 对符号表达式f进行微分运算,符号变量由前面 的规则确定; • diff(f,a) f对指定变量a进行微分运算; • diff(f,n)或diff(f,a,n) 计算f对默认变量或指定变量a 的n 阶导数,n是正整数; • int(f) 对于符号变量f代表的符号表达式,求f关于默认 变量的不定积分; • int(f,v) 计算f关于变量v的不定积分; • int(f,a,b)或int(f,v,a,b) 量v从a到b的定积分。 计算f关于默认变量或指定变
符号变量的定义
使用符号变量之前,应先对其予以声明,命令格式如下: • syms 变量名列表(其中各个变量名用空格分隔,不能 用逗号分隔) 如: syms x a • sym (‘变量名’) • 随后输入的 y = ax和y = a*sin(x) 就成了符号函数; f= ' sin(y)^2 ' 则定义了f为一个符号表达式; eq = ' a-y^2 =0 ' 定义了eq为一个符号方程。 如: sym(' y ' ) 经上述定义后,x, y, a已成为符号变量。
MATLAB-第4章

v
i 1
n
2 i
。
max { vi } 。
1 ≤i ≤n
设 A 是一个 m ×n 的矩阵,矩阵的 3 种常用范数如下。 1-范数: A 1 max { aij } 。
1 ≤ j ≤n i 1 m
2-范数: A 2 1 ,其中 λ 1 为 A'A 最大特征值。 ∞-范数: A max { aij } 。
【例4.6】先建立5 × 5矩阵A,然后将A的第一行元素乘以1, 第二行乘以2,…,第五行乘以5。 用一个对角矩阵左乘一个矩阵时,相当于用对角阵的第一个 元素乘以该矩阵的第一行,用对角阵的第二个元素乘以该 矩阵的第二行……依此类推,因此,只需按要求构造一个 对角矩阵D,并用D左乘A即可。命令如下: A=[1:5;2:6;3:7;4:8;5:9] D=diag(1:5); D*A %用D左乘A,对A的每行乘以一个指定常数
(2)构造对角矩阵 设V为具有m个元素的向量,diag(V,k)的功能是产生一个 n × n(n = m + k|)对角阵,其第k条对角线的元素即为 向量V的元素。 例如: diag(1:3,-1) ans = 0 0 0 0 1 0 0 0 0 2 0 0 0 0 3 0 省略k时,相当于k为0,其主对角线元素即为向量V的元素。
2.矩阵的秩与迹 (1)矩阵的秩 rank(A) (2)矩阵的迹 矩阵的迹即矩阵的对角线元素之和。 trace(A)。
3.向量和矩阵的范数
设向量 V = (v1 ,v2 ,…,vn ),向量的 3 种常用范数如下。 1-范数: V 2-范数: V ? -范数: V
1
vi 。
i 1
n
2
3.矩阵的转置 所谓转置,即把源矩阵的第一行变成目标矩阵第一列,第二 行变成第二列……依此类推。显然,一个m行n列的矩阵 经过转置运算后,变成一个n行m列的矩阵。MATLAB中, 转置运算符是单撇号(')。
第4章MATLAB程序流程控制-习题答案

第4章M A T L A B程序流程控制-习题答案第4章MATLAB程序流程控制习题4一、选择题1.下列关于脚本文件和函数文件的描述中不正确的是()。
AA.函数文件可以在命令行窗口直接运行B.去掉函数文件第一行的定义行可转变成脚本文件C.脚本文件可以调用函数文件D.函数文件中的第一行必须以function开始2.下列程序的输出结果是()。
Dy=10;ify==10y=20;elseify>0y=30enddisp(y)A.1B.30C.10D.203.有以下语句:a=eye(5);forn=a(2:end,:)for循环的循环次数是()。
CA.3B.4C.5D.104.设有程序段k=10;whilekk=k-1end则下面描述中正确的是()。
AA.while循环执行10次B.循环是无限循环C.循环体语句一次也不执行D.循环体语句执行一次5.有以下程序段:x=reshape(1:12,3,4);m=0;n=0; fork=1:4ifx(:,k)<=6m=m+1; elsen=n+1; end end则m 和n 的值分别是()。
CA .66B .21C .22D .126.调用函数时,如果函数文件名与函数名不一致用()。
A A .函数文件名B .函数名 C .函数文件名或函数名均可D .@函数名 7.如果有函数声明行为“f unction[x,y,z]=f1(a,b,c)”,则下述函数调用格式中错误的是 ()。
B A .x=f1(a,b,c)B .[x,y,z,w]=f1(a,b,c) C .[x,b,z]=f1(a,y,c)D .[a,b]=f1(x,y,z) 8.执行语句“f n=@(x)10*x;”,则fn 是()。
A A .匿名函数B .函数句柄C .字符串D .普通函数 9.执行下列语句后,变量A 的值是()。
D >>f=@(x,y)log(exp(x+y)); >>A=f(22,3); A .22,3B .22C .3D .25 10.程序调试时用于设置断点的函数是()。
第4章MATLAB在信号处理中的应用ppt课件

4.5.1 线性时不变系统的时域响应
1.连续LTI系统的响应
y (t) T x (t) x (t)* h (t) x ( )h (t )d
用MATLAB中的卷积函数conv( )来实现。
2.离散LTI系统的响应
y(n)x(n)h(n)x(m )h(nm )
m
x(n) e(j)n
直接实现:n=[ns:nf]; x=exp((sigema+jw)*n); 5.正(余)弦序列
x(n)co n s()
直接实现:n=[ns:nf]; x=cos(w*n+sita);
第 4 章 MATLAB在信号处理中的应用
4.2 信号的基本运算
4.2.1信号的相加与相乘
y(n)=x1(n)+x2(n) y(n)=x1(n)×x2(n) MATLAB实现:y=x1+x2; y=x1.*x2
功能 产生冲激串 产生非周期的方波信号 产生非周期的三角波信号 产生Dirichlet或周期sinc函数 产生高斯单脉冲信号
第 4 章 MATLAB在信号处理中的应用
第 4 章 MATLAB在信号处理中的应用
第 4 章 MATLAB在信号处理中的应用
3.实指数序列
x(n) an
n aR
直接实现:n=[ns:nf]; x=a.^n; 4.复指数序列
用MATLAB中的卷积函数conv( )来实现。
第 4 章 MATLAB在信号处理中的应用
3.时域响应函数 (1)对任意输入的连续LTI系统响应函数lsim( )
格式:[y,x]=lsim(a,b,c,d,u,t) 功能:返回连续LTI系统 x'(t)ax(t)bu(t)
matlab课后习题答案第四章
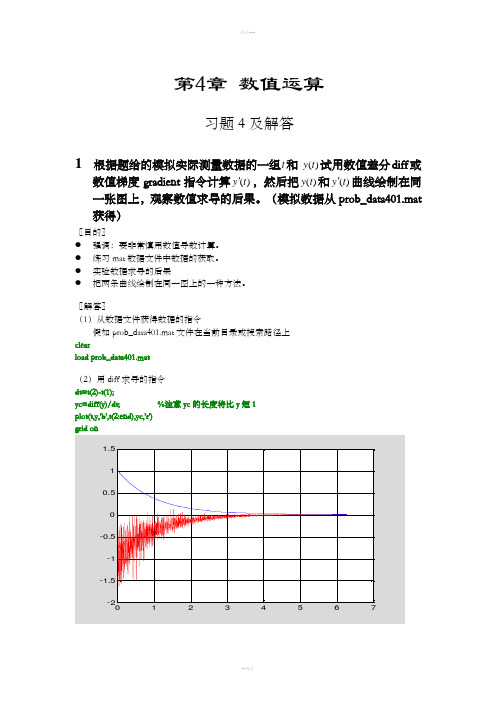
第4章数值运算习题 4 及解答1 根据题给的模拟实际测量数据的一组t和)(t y试用数值差分diff或数值梯度gradient指令计算)(t y',然后把)(t y和)(t y'曲线绘制在同一张图上,观察数值求导的后果。
(模拟数据从prob_data401.mat 获得)〖目的〗●强调:要非常慎用数值导数计算。
●练习mat数据文件中数据的获取。
●实验数据求导的后果●把两条曲线绘制在同一图上的一种方法。
〖解答〗(1)从数据文件获得数据的指令假如prob_data401.mat文件在当前目录或搜索路径上clearload prob_data401.mat(2)用diff求导的指令dt=t(2)-t(1);yc=diff(y)/dt; %注意yc的长度将比y短1plot(t,y,'b',t(2:end),yc,'r')grid on(3)用gradent 求导的指令(图形与上相似)dt=t(2)-t(1);yc=gradient(y)/dt;plot(t,y,'b',t,yc,'r')grid on〖说明〗● 不到万不得已,不要进行数值求导。
● 假若一定要计算数值导数,自变量增量dt 要取得比原有数据相对误差高1、2个量级以上。
● 求导会使数据中原有的噪声放大。
2 采用数值计算方法,画出dt tt x y x ⎰=0sin )(在]10 ,0[区间曲线,并计算)5.4(y 。
〖提示〗● 指定区间内的积分函数可用cumtrapz 指令给出。
● )5.4(y 在计算要求不太高的地方可用find 指令算得。
〖目的〗● 指定区间内的积分函数的数值计算法和cumtrapz 指令。
● find 指令的应用。
〖解答〗dt=1e-4;t=0:dt:10;t=t+(t==0)*eps;f=sin(t)./t;s=cumtrapz(f)*dt;plot(t,s,'LineWidth',3)ii=find(t==4.5);s45=s(ii)s45 =1.65413 求函数x ex f 3sin )(=的数值积分⎰=π0 )(dx x f s ,并请采用符号计算尝试复算。
第4章 MATLAB 非线性方程(组)的求解

x*k
=
g(x* ),即x* 是 g 的不动点,也就是f 的根。
fixpt.m
逐次逼近: 将隐式方程归结为显式计 算
y
y=x
p1 p0
y=g(x)
✓
x
x0
x1 x*
y
y=x
y=g(x)
p0
p1
x x1 x0 x*
y p0
y=x
✓
y=g(x) p1
x0
x*
y
y=g(x) p0
x x1
y=x
是函数表达式中附加的参数x是返回的根fval是根x处的目标函数的值exitflag表明解存在的情况正数表明解存在负数表示解不存在遇到复数nan或者无穷大等
第4章 非线性方程(组)的求解
本章目标:求 f (x) = 0 的根
4.1 二分法 4.2 简单迭代法 4.3 Newton法 4.4 抛物线法 4.5 非线性方程组的求解 4.6 实例解析
p1
x x0 x* x1
4.3 Newton法
原理:将非线性方程线性化 —— Taylor 展开
取 x0 x*,将 f (x)在 x0 做一阶Taylor展开:
f (x)
f ( x0 )
f ( x0 )(x x0 )
f
(
2!
)
(
x
x0
)2,
在
x0
和
x
之间.
将 (x* x0)2 看成高阶小量,则有:
x = g (x)
f (x) 的根
g (x) 的不动点
从一个初值 x0 出发,计算 x1 = g(x0), x2 = g(x1), …,
第4章 MATLAB程序流程控制

第4章 MATLAB程序流程控制
2.switch语句 switch语句根据表达式的取值不同,分别执行不 同的语句,其语句格式为:
第4章 MATLAB程序流程控制
(3) 多分支if语句: if 条件1 语句组1 elseif 条件2 语句组2 …… elseif 条件m 语句组m else 语句组n end
第4章 MATLAB程序流程控制
第4章 MATLAB程序流程控制
例4-4 输入一个字符,若为大写字母,则输出其对应 的小写字母;若为小写字母,则输出其对应的大写 字母;若为数字字符则输出其对应的数值,若为其 他字符则原样输出。
age is 17>> >> fprintf('age is %d\n',17); age is 17
第4章 MATLAB程序流程控制
例4-2 求一元二次方程ax2 +bx+c=0的根。 程序如下: a=input('a=?'); b=input('b=?'); c=input('c=?'); delta=b*b-4*a*c; x=[(-b+sqrt(delta))/(2*a),(-b-sqrt(delta))/(2*a)]; disp(['x1=',num2str(x(1)),',x2=',num2str(x(2))]);
M文件的扩展名为.mFra bibliotek第4章 MATLAB程序流程控制
1.建立新的M文件 为建立新的M文件,启动MATLAB编辑器有3种方法。 ① 在MATLAB主窗口选择“主页”选项卡,在“文件” 命令组中单击“新建脚本”命令按钮。 ② 在MATLAB命令行窗口输入命令: edit 文件名 启动MATLAB编辑器后,输入M文件的内容并存盘。 ③ 在命令历史窗口选中一些命令(按住Ctrl可同时选 择多条命令),然后从右键快捷菜单中选择“创建 脚本”命令,将会启动MATLAB编辑器,并在编辑 区中加入所选中的命令。
Matlab基础及其应用 第4章 图形绘制

'MarkerIndices',[1 31 61 91 121],... %在4个点显示标记
'MarkerEdgeColor','r',...
%设置曲线标记外框为红色
'MarkerFaceColor','y',...
%设置曲线标记内填充黄色
'MarkerSize',8)
%设置曲线标记大小为8
用法:
fplot(funx, funy, lims)
其中,funx、funy代表函数,通常采用函数句柄的形式。li
ms为参数函数funx和funy的自变量的取值范围,用二元向量
[tmin,tmax]描述。例如,例4.1也可以用以下命令实现:
>> fplot(@(t)sin(t)+sin(2*t), @(t)cos(t)-cos(2*t), [0,2*pi])
t1=linspace(0,3*pi,90);
x=cos(t1)+t1.*sin(t1);
t2=linspace(0,2*pi,50);
y=sin(t2)-t2.*cos(t2);
plot(t1,x,t2,y);
4.1 二维曲线的绘制
MATLAB基础与应用教程
4.1.1 绘制二维曲线
2.fplot函数
支持的TeX字符串中,用\bf、\it、\rm标识符分别定义字形
为加粗、倾斜和常规字体。
表4.5中的各个字符既可以单独使用,又可以和其他字符及
命令联合使用。为了将控制字符串、TeX标识符与输出字符
分隔开来,可以用大括号界定控制字符串以及受控制字符串
MATLAB程序设计基础教程(刘国良)-第4章

函数
体
第4章 M脚本与M函数
2.脚本M文件 脚本文件也叫命令文件,是独立执行的文件,它不接受输 入参数,不返回任何值,而是代码的结合,该方法允许用户将 一系列MATLAB命令输入到一个简单的脚本“.m”文件中,只 要在MATLAB命令窗口中执行该文件,则会依次执行该文件中 的命令。 脚本M文件中包含一族由MATLAB语言所支持的语句,它类 似于DOS下的批处理文件,它的执行方式很简单,用户只需在 MATLAB 的提示符“>>”下键入该M文件的文件名,这样 MATLAB就会自动执行该M文件中的各条语句,并将结果直接返 回到MATLAB 的工作空间。
第4章 M脚本与M函数
3.块注释 在 MATLAB 5以前的版本中,注释是逐行进行的,采用百 分号(%)进行标记。逐行注释不利于用户增加和修改注释内容。 在MATLAB 5及以后的版本中,用户可以使用“%{”和“%}” 符号进行块注释,“%{”和“%}”分别代表注释块的起始和 结束。
第4章 M脚本与M函数
第4章 M脚本与M函数
在使用脚本文件时需要注意一点:如果当前工作区中存在 与该脚本同名的变量,则当输入该文件名时,系统将其作为变 量名执行。
MATLAB中有一个专门用于寻找“.m”文件的路径搜索器。 “.m”文件是以目录和文件夹的方式分布于文件系统中的,一 部分“.m”文件的目录是MATLAB的子目录,由于MATLAB的一 切操作都是在它的搜索路径,包括当前路径中进行的,因此如 果调用的函数在搜索路径之外,MATLAB就会认为此函数不存 在。
第4章 M脚本与M函数
4.1.2 M文件的建立、运行与命名规则 M文件的语法类似于一般高级语言,是一种程序化的编程
语言,但是与传统的高级语言相比,M文件又有其特点。它只 是一个简单的ASCII码型文本文件,因此,它的语法比一般的 高级语言要简单,程序也容易调试,并具有很好的交互性。
matlab第4章

行向量元素为按降幂排列的多项式系数。
1.多项式乘法函数 conv ( )
格式:C= conv (A, B) %求多项式A和B的乘积
A、B是两个多项式的系数向量,按降幂排列。 conv( ) 把两个多项式相乘合并成一个多项式。
2
p1 2s 3;
2
p2 s 2 4
3 2
A (2s 3)(s 4) 2s 3s 8s 12
x:操作点处的状态向量
u:操作点处的输入向量
x,u缺省值为0。
20
( s 1)(s 2 2s 6) 2 【例4.4】 求传递函数 G(s) 2 s (s 3)(s 3 2s 2 3s 4)
的分子和分母多项式,并求传递函数的特征 根。
21
% num 分子多项式 % conv( ) 采用嵌套形式
G (s)
5s 3 s 3 6 s 2 11s 6
13
3.部分分式展开函数residue ( ) 功能:对两个多项式的比进行部分展开。 格式:[r, p, k]=residue(b, a) 求B(s)/A(s)的部分分式展开式 向量b和a是按s降幂排列的多项式系数。
14
B( s) bn s n bn1s n1 ...b0 F ( s) A( s) an s n an1s n1 ...a0
38
2.并联 G(s)=G1(s)+G2(s) 模型并联函数 parallel 格式:[num, den]=parallel(num1, den1, num2, den2) num1, den1:G1(s) 的分子、分母多项式 num2, den2:G2(s)的分子、分母多项式 num, den:G(s) 的分子、分母多项式
《MATLAB程序设计》第4章数组及应用

0x0012FF68 a[0] 0x0012FF6C a[1] 0x0012FF70 a[2] 0x0012FF74 a[3]
数组元素
0x0012FF78 a[4]
0x0012FF7C a[5]
8
一维数组在内存中的存储形式
说明:
(1)数组名a表示内存首地址,是地址常量。
(2)数组a中每个数组元素占的内存空间根据 数组类型确定,整个数组占的内存为:数组元 素个数乘以每个元素所占内存空间如: int a[10]; 4×10=40 float b[20]; 4×20=80 double c[5]; 8×5=40 char d[8]; 1×8=8
第4章 数组
教学内容
数组的定义及应用
字符串处理函数
几个常用算法:排序算法(选择排序、
冒泡排序)
1
第4章 数组
重点、难点
数组的定义及应用
常用算法的设计(选择排序、
冒泡排序)
2
第4章 数组
教学目标
熟练掌握数组的定义及应用
掌握字符数组的定义及应用
掌握常用的字符串处理函数
熟练掌握几个常用算法:排序
算法(选择排序、冒泡排序)
分析:所谓转置就是将矩阵的行列互换,即将 a矩阵 的a[i][j]元素变成b矩阵的b[j][i]。
24
#include <iostream> using namespace std; int main() { int a[3][4] ={{1,2,3,4},{3,4,5,6},{5,6,7,8}}; int b[4][3],i,j; for(i=0;i<3;i++) //输出二维数组a[3][4] { for(j=0;j<4;j++) cout<<a[i][j]<<" "; cout<<endl; } for(i=0;i<4;i++) //将矩阵a转置给矩阵b for(j=0;j<3;j++) b[i][j]=a[j][i]; for(i=0;i<4;i++) //输出二维数组b[4][3] { for(j=0;j<3;j++) cout<<b[i][j]<<" "; cout<<endl; } return 0;}
第4章MATLAB程序设计

例 求一个值n,使n!最大但小于1050。 MATLAB程序如下: %初始化 r=1;k=1; 执行后结果如下: %做循环 The 41!Is while r<1e50 3.345253e+049 r=r*k; k=k+1; end k=k-1;r=r/k;k=k-1; % 输出结果 disp(['The',num2str(k),'!is',num2str(r)])
4.2.3 循环结构 for 循环:可完成指定次重复的循环,且在循环开 始之前,就知道代码重复的次数。
while 循环:while语句可完成不定次重复的循 环,与for语句不同,每次循环前要先判断条件 是否满足,再决定循环是否进行。
例 利用rand函数产生10个随机数,然后利用嵌套 for循环进行从小到大排序。
2 1.5 1 0.5 0 150 100 50
然后通过调用函数fun计算出z, 并利用mesh绘制出网格线。 编写的脚本文件如下: % 坐标系准备 x=[0:.02:2]; y=[-2:.02:0]; % 调用函数计算函数值 z=fun(x,y); % 绘图 figure mesh(z)
150 100 50
4.3.2 函数的调用 函数调用的一般格式如下: [输出实参表] = 函数名(输入实参表) 要注意的是,函数调用时各实参出现的顺 序、个数,应与函数定义时形参的顺序、 个数一致,否则会出错。函数调用时,先 将实参传递给相应的形参,从而实现参数 传递,然后再执行函数的功能。
例 对于函数
z ( x 1)2 ( y 1)2
fprintf函数中,format字符中常常会使用到一些特 殊字符来灵活的实现一些显示功能 format string 结果 %d %e %f %g 把值作为整数来处理 用科学记数法来显示数据 用于格式化浮点数,并显示这个 数 用科学记数格式,或浮点数格式, 根据那个表示的数位短,显示那 个 转到新的一行
(完整版)第4章MATLAB程序流程控制_习题答案

第4章 MATLAB程序流程控制习题4一、选择题1.下列关于脚本文件和函数文件的描述中不正确的是()。
AA.函数文件可以在命令行窗口直接运行B.去掉函数文件第一行的定义行可转变成脚本文件C.脚本文件可以调用函数文件D.函数文件中的第一行必须以function开始2.下列程序的输出结果是()。
Dy=10;if y==10y=20;elseif y>0y=30enddisp(y)A.1 B.30 C.10 D.203.有以下语句:a=eye(5);for n=a(2:end,:)for循环的循环次数是()。
CA.3 B.4 C.5 D.104.设有程序段k=10;while kk=k-1end则下面描述中正确的是()。
AA.while循环执行10次B.循环是无限循环C.循环体语句一次也不执行D.循环体语句执行一次5.有以下程序段:x=reshape(1:12,3,4);m=0;n=0;for k=1:4if x(:,k)<=6m=m+1;elsen=n+1;endend则m和n的值分别是()。
CA.6 6 B.2 1 C.2 2 D.1 26.调用函数时,如果函数文件名与函数名不一致,则使用()。
A A.函数文件名B.函数名C.函数文件名或函数名均可D.@函数名7.如果有函数声明行为“function [x,y,z]=f1(a,b,c)”,则下述函数调用格式中错误的是()。
BA.x=f1(a,b,c) B.[x,y,z,w]=f1(a,b,c)C.[x,b,z]=f1(a,y,c) D.[a,b]=f1(x,y,z)8.执行语句“fn=@(x) 10*x;”,则fn是()。
AA.匿名函数B.函数句柄C.字符串D.普通函数9.执行下列语句后,变量A的值是()。
D>> f=@(x,y) log(exp(x+y));>> A=f(22,3);A.22,3B.22 C.3 D.2510.程序调试时用于设置断点的函数是()。
MATLAB教程-第4章

4.6 稀疏矩阵
本小节的主要内容包括: 稀疏矩阵与全矩阵 创建与转换稀疏矩阵 操作稀疏矩阵
4.7 小结
本章主要讲解如何在MATLAB中进行矩阵分析。矩阵运算 和分析是MATLAB的基础应用,几乎所有的高等应用都 需要使用到矩阵分析的内容。矩阵分析包括的范围很广 ,本章讲解最基本的内容
本章讲解的知识点包括: 矩阵运算 线性方程组 特征值和特征向量 矩阵分解 矩阵函数 稀疏矩阵
4.1 矩阵运算
本小节的主要内容包括: 矩阵加减运算 矩阵乘法 矩阵除法 矩阵的幂 矩阵的按位运算
4.2 线性方程组
本小节的主要内容包括: 线性方程的形式 计算矩阵行列式 计算矩阵的逆 计算条件数 计算范数 计算矩阵的秩
EVD分解 Schur分解 Cholesky分解 LU分解 QR分解 SVD分解
MATLAB函数 eig、eigs schur chol、cholinc lu、luinc qr svd、svds
4.5 矩阵函数
矩阵函数是以矩阵为参变量的函数。虽然MATLAB中有很 多函数都支持矩阵作为输入参数,但是这其中大部分是 对矩阵进行按位运算。
4.3 特征值和特征向量
MATLAB中的eig函数用于求矩阵特征值和特征向量,其调 用格式为:
D = eig(A) [V, D] = eig(A)
4.4 矩阵分解
矩阵分解通过将复杂矩阵表示成形式简单矩阵的组合,以进 行理论分析或数值计算。通常矩阵分解将复杂矩阵分解 为几个简单矩阵的乘积。下表列出了一些常用的矩阵分 解及其对应的MATLAB实现函数。
第4章 MATLAB 绘图

4.图例标注
菜单Insert---legend 命令legend('string1','string2',...)
4.1.6 一个图形窗口多个子图的绘制
subplot(m,n,i)把图形窗口分为m*n个子图,并在第i个子图 中画图 例 4-11 在同一坐标系中画出两个函数,y=cos2x,y=sinxsin6x 的图形,自变量的范围为0≤ x ≤π,函数y=cos2x用红色星号,函数 y=sinxsin6x用蓝色实线,并加图名、坐标轴、图形、图例标注 解 MATLAB命令为: x=0:pi/50:pi; y1=cos(2*x);y2=sin(x).*sin(6*x); plot(x,y1,'r*',x,y2,'b-'),grid on title(‘曲线y1=cos(2x)曲线y2=sin(x)sin(6x)') xlabel('x轴'),ylabel('y轴') gtext('y1=cos(2x)'),gtext('y2=sin(x)sin(6x)') legend('y1=cos(2x)','y2=sin(x)sin(6x)')
group 8 6 4 2 0 10 30 20
stack
1
2
3
4 stack
5
6
0
1
2
3
4 stack
5
6
8 6 5 4 3 2 1 0 10 20 30 6 4 2 0
其它特殊绘图略(见教科书 )
1
2
3
4
5
6
4.3 三维曲线绘图
第四章 MATLAB符号计算

Ezpolar函数实现极坐标中二维曲 线图象的绘制,它的调用格式:
ezpolar(f,[a,b])
说明: 绘图表达式为rho=f(theta)极坐标曲线,
theta的取值范围为,缺省时为[0,2*pi]
例:p83
4.5.2三维绘图函数
ezplot3是实现三维绘图的函数,它的 调用格式:
ezplot3(x,y,z,[tmin,tmax]) ezplot3(x,y,z,[tmin,tmax ],'animate')
3.符号表达式的提取分子和分母运算
在matlab中可利用numden函数来提取符号表达式 中的分子或分母。其一般调用格式为:
[n,d]=numden(s)
说明:
参数s是符号表达式是一个 有理分式或可以展开为有理
例: s=sym('2/5+3/7')
n= 29
分式,numden函数把有理分 式的分子返回给n,分母返回
dsolve在求常微分方程组时 的调用格式为:
dsolve('eq1,eq2,...','cond1,cond2...','v')
说明: 该函数求解常微分方程组eq1,…,eqn在初值条件或边界 条件为cond1,…,condn下的符号特解,若不给出初值 条件,则求方程组的通解,v为指定的返回值中的变量 表示。
例4-9解超越方程组
sin(x+y)-y*exp(x)=0 x^2-y=2
syms x y
[x,y]=solve('sin(x+y)-y*exp(x)=0','x^2-y=2')
x =-.66870120500236202933135901833637
第4章MATLAB数据分析与多项式计算

第4章MATLAB数据分析与多项式计算MATLAB是一种强大的数值计算和数据分析工具,能够帮助用户高效地进行各种数据处理和分析操作。
本章将介绍MATLAB在数据分析和多项式计算方面的应用。
1.数据分析数据分析是指通过对大量数据进行整理、分析和挖掘,从中获取有价值的信息和知识。
MATLAB提供了丰富的数据分析函数和工具箱,可以帮助用户进行各种统计分析、数据可视化和模型拟合等操作。
1.1统计分析MATLAB中的统计工具箱提供了丰富的统计分析函数,可以进行各种统计指标的计算,如均值、方差、标准差等。
同时,还可以进行假设检验、置信区间估计等统计推断分析。
1.2数据可视化MATLAB提供了强大的数据可视化工具,可以通过绘制统计图表来展示数据的分布和趋势。
用户可以利用MATLAB绘制条形图、散点图、线图等各种图表,帮助理解数据的特点和关系。
1.3模型拟合MATLAB中的曲线拟合工具可以帮助用户根据已知数据拟合出合适的数学模型。
通过拟合曲线,可以对数据进行预测和推断,从而为后续的决策和分析提供依据。
多项式计算是指对多项式进行各种运算,如多项式乘法、求导、积分等。
在MATLAB中,多项式计算可以利用多项式系数和多项式对象来实现。
2.1多项式乘法MATLAB中提供了polyval函数,可以根据给定的多项式系数和x值计算多项式的值。
此外,还提供了conv函数,可以实现多项式的乘法运算。
2.2多项式求导MATLAB中提供了polyder函数,可以根据给定的多项式系数计算多项式的导数。
用户可以利用该函数计算多项式导函数的值,从而研究多项式的变化规律。
2.3多项式积分MATLAB中提供了polyint函数,可以根据给定的多项式系数计算多项式的积分。
用户可以利用该函数计算多项式在给定区间上的积分值,求解多项式面积和曲线长度等问题。
总结:MATLAB是一种功能强大的数据分析和多项式计算工具,能够帮助用户进行各种数据分析和多项式运算操作。
第4章MATLAB程序设计

第4章MATLAB程序设计在当今科技飞速发展的时代,计算机编程成为了许多领域中不可或缺的工具。
而 MATLAB 作为一款功能强大的数学计算和编程软件,在科学研究、工程设计、数据分析等众多领域都发挥着重要的作用。
MATLAB 具有丰富的函数库和简洁易懂的语法,这使得它对于初学者来说相对容易上手。
它提供了直观的操作界面,让用户能够轻松地进行各种复杂的计算和绘图。
在 MATLAB 程序设计中,变量的定义和使用是基础。
变量可以存储各种类型的数据,如数值、字符串、数组等。
与其他编程语言类似,变量的命名需要遵循一定的规则,通常使用有意义的名称能够提高程序的可读性。
比如,我们要计算一个圆形的面积,就可以定义半径变量`r` ,然后通过公式`S = pi r^2` 来计算面积。
在这个简单的例子中,清晰的变量名`r` 让人一眼就能明白它代表的是半径。
数组是 MATLAB 中常用的数据结构之一。
它可以是一维的、二维的甚至多维的。
通过数组,我们能够方便地处理大量相关的数据。
例如,要存储一个班级学生的成绩,我们可以创建一个一维数组来存放每个学生的分数。
而如果要表示一个矩阵,比如一个图像的像素值,就可以使用二维数组。
控制流语句在 MATLAB 程序中也非常重要。
像`ifelse` 语句用于条件判断,根据不同的条件执行不同的代码块。
假设我们要判断一个数是奇数还是偶数,就可以使用以下代码:```matlabnum = 5;if mod(num, 2) == 0disp('偶数');elsedisp('奇数');end````for` 循环用于重复执行一段代码特定的次数,而`while` 循环则在条件为真时持续执行。
函数的定义和调用是 MATLAB 程序设计中的重要环节。
通过将一段具有特定功能的代码封装成函数,可以提高代码的复用性和可读性。
例如,我们定义一个计算阶乘的函数:```matlabfunction result = factorial(n)if n == 0 || n == 1result = 1;elseresult = n factorial(n 1);endend```在需要计算阶乘的时候,直接调用这个函数就可以得到结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
fac(i)=factor(i);
end
fac 3 .函数所传递参数的可调性
MATLAB在函数调用上有一个与众不同之处:函数所传递参数数目的可调性。凭借这一
点,一个函数可完成多种功能。
在调用函数时,MATLAB用两个永久变量nargin和nargout分别记录调用该函数时的输入
实参和输出实参的个数。只要在函数文件中包含这两个变量,就可以准确地知道该函数文件
if rem(m,i)==0 flag=0;
end i=i+1;
end %while循环结束
4.3 函数文件 函数文件是另一种形式的M文件,每一个函数文件都定义一个函数。MATLAB提供
的标准函数大部分都是由函数文件定义的。 从使用的角度看,函数是一个“黑箱”,把一些数据送进去,经加工处理,把结果
送出来。
【例8】 编写函数文件求小于任意自然数n的Fibonacci数列各项。
function f = ffib(n) % 用于求Fibonacci数列的函数文件
f=[1,1];
% f(1)=1, f(2)=1
i=1;
while f(i)+f(i+1)<n
f(i+2)=f(i)+f(i+1);
i=i+1;
end 【例9】 利用函数文件,实现直角坐标(x,y)与极坐标(γ,θ)之间的转换。
switch num case -1 disp('I am a teacher.'); case 0 disp('I am a student.'); case 1 disp('You are a teacher.'); otherwise disp('You are a student.');
end (三)循环结构的实现 Matlab提供两种实现循环结构的语句:for语句和while语句。 1. for语句: 格式: for 循环变量 = 表达式1 : 表达式2 : 表达式3
max(x)
求x各列的最大元素
mean(x)
求x各列的平均值
median(x)
求x各列的中值
min(x)
求x各列的最小元素
std(x)
求x各列元素的标准差
prod(x)
求x各列元素之积
sum(x)
求x各列元素之和
cumsum(x)
求x各列元素累计和
cumprod(x)
求x各列元素累计积
roots(A)
重循环结构。 多重循环的嵌套层数可以是任意的。可以按照嵌套层数,分别叫做二重循环、三
重循环等。处于内部的循环叫作内循环,处于外部的循环叫作外循环。 【例7】求[100,1000]以内的全部素数。
n=0; for m=100:1000
flag=1; i=2; j=m-1; while i<=j & flag
end x x=
i=1:n x(i)=i.^2;
% i=1:1:n
1 4 9 16 25 36 49 64 81 100 【例6】利用while循环,求解使n!达到100位数的第一个n是多少?
n=1; while prod(1:n)<1e100
n=n+1; end n
3. 循环的嵌套 如果一个循环结构的循环体又包括一个循环结构,就称为循环的嵌套,或称为多
[gam,the]=tran(x,y);
gam
the 【例10】利用函数的递归调用,求n!。
function f = factor(n)
if n<=1
f=1;
else
f=factor(n-1)*n;
end return;
%返回
在命令文件 main2.m 中调用函数文件factor.m:
for i=1:10
被调用时的输入输出参数个数,从而决定函数如何进行处理。
【例11】 nargin用法示例
函数文件examp.m:
function fout=examp(a,b,c)
if nargin= =1 fout=a;
elseif nargin= =2 fout=a+b;
elseif nargin= =3 fout=(a*b*c)/2;
.txt .dat等ASCII码数据文件 用load或save命令进行读入与存储。
.bmp .jpg .tif等图像文件 用imread和imwrite命令进行读入与存储。
.wav声音文件 用wavread和wavwrite命令进行读入与存储。
还有其它的数据文件
数据的输出
在MATLAB中,全局变量用命令global定义。函数文件的内部变量是局部的,与其他 函数文件及MATLAB工作空间相互隔离。但是,如果在若干函数中,都把某一变量定义为全局 变量,那么这些函数将公用这一个变量。全局变量的作用域是整个MATLAB工作空间,即全程 有效。所有的函数都可以对它进行存取和修改。因此,定义全局变量是函数间传递信息的一种 手段。
求多项式的根
poly(A)
建立多项式
polyval(A,x) 求多项式的值
conv(A,B) 求多项式的乘积
deconv(A,B)求多项式的商和余数多项式
4.1 M文件 用MATLAB语言编写的程序,称为M文件。 M文件的扩展名是 ‘ .m’ M文件有两类:命令文件和函数文件。
建立M文件以及运行M文件的步骤及方法 4.2 程序结构及实现
elseif 条件2 语句组2
…… elseif 条件m 语句组m
else 语句组m+1
end 【例3】 输入三角形的三条边,求面积。要求判断三条边是否能构成一个三角形。
a=input('请输入三角形的三条边:');
if a(1)+a(2)>a(3) & a(1)+a(3)>a(2) & a(2)+a(3)>a(1) p=(a(1)+a(2)+a(3))/2; s=sqrt(p*(p-a(1))*(p-a(2))*(p-a(3))); disp(s);
循环体语句
end 注:其中表达式1的值为循环变量的初值,表达式2的值为步长,表达式3的值为循环变量的终 值。步长为1时,表达式2可以省略。
2. while语句
格式为: while
end
表达式 循环体语句
只要表达式的值非零,循环体就重复执行。直到表达式的值为零时停止。
【例5】对1~10的数求平方
n=10; for
for j=1:4 if rem(k(j),2)~=0 s=s+k(j); end
end end s
max(x) mean(x) median(x) min(x) std(x) prod(x) sum(x) cumsum(x) cumprod(x) roots(A) poly(x) polyval(A,x) conv(A,B) deconv(A,B)
输出为: s= 5 习题
1. 输入20个数,求其中最大数和最小数。要求分别用循环结构和调用MATLAB的max函数、min 函数来实现。 2. 求Fibonacci数列
(1)大于4000的最小项。 (2)5000之内的项数。
3. 写出下列程序的输出结果: s=0;
a=[12,13,14;15,16,17;18,19,20;21上看,函数文件与命令文件的区别在于:函数文件以function开头,而命令文 件则没有。
从变量的存储看:命令文件的变量在文件执行完成后保留在工作空间中,而函数文
件内定义的变量只在函数文件内部起作用,当函数文件执行完后,这些内部变量将被清除。
2.函数调用 函数调用的一般格式是:
[输出实参表]=函数名(输入实参表)
else disp('不能构成一个三角形。')
end
运行:
请输入三角形的三条边:[4 5 6] 9.9216
2. switch语句-分支语句 switch语句根据变量或表达式的取值不同,分别执行多种不同的语句。 其具体格式为:
【例4】 根据变量 num 的值来决定显示的内容。 num=input('请输入一个数');
disp函数的功能:在命令窗口输出数据。
调用格式:
disp(输出项)
注:输出项可以是字符串或矩阵。
【例2】 建立一个命令文件将变量a,b的值互换。
(二)选择结构的实现 实现选择结构的语句有if语句和switch语句。
1. if语句-条件语句 格式一: if 条件 语句组
end
格式三: if 条件1 语句组1
求x各列的最大元素 求x各列的平均值 求x各列的中值
求x各列的最小元素 求x各列元素的标准差 求x各列元素之积 求x各列元素之和 求x各列元素累计和 求x各列元素累计积 求多项式的根 建立多项式 求多项式的值 求多项式的乘积 求多项式的商和余数多项式
【例12】 全局变量应用示例先建立函数文件wadd.m,该函数将输入的参数加权相加。 function f=wadd(x,y) % add two variable global ALPHA BETA f=ALPHA*x+BETA*y;
在命令窗口中输入:
global ALPHA BETA ALPHA=1; BETA=2; s=wadd(1,2)
函数文件tran.m:
function [gama, theta]=tran(x, y)
gama=sqrt(x*x+y*y);
theta=atan(y/x); 调用tran.m的命令文件main1.m:
x=input('Please input x=:');
