实验七SIMULINK 仿真单回路控制系统及PID控制器参数整定
Simulink中系统PID控制调节

PID控制实现:
1)离散时间域 2Байду номын сангаас考虑硬件条件 3)控制算法生成代码
3.在PID Controller的Data Types页,可 以对每个PID参数进行定标处理
4.右击PID Controller,C/C++ Code->Buid This Subsystem生成 PID控制算法对应的c代码,或者生 成S-function进行软件在回路测试
3.点击Select Blocks...选择调节的模块, 完成后点击Tune Blocks进行参数调优
动态调节Simulink系统响 应:
4.选择系统动态调节图像
6.点击Finish输出图像
动态调节图可以拖 动图像改变系统特 性,同时改变变量 的值
5.点击Next选择系统分析图像
分析图只能做分析 用
动态调节Simulink系统响 应:
9.在窗口Compensator页选项,选择要调 节的项目,在窗口Design Requirements 页,点击Add new design requirement 添加设计要求
10.点击OK会在分析图像上显示出设 计要求区间。点击Start Optimization, 软件会开始自动迭代寻找符合要求的 参数
动态调节Simulink系统响 应:
7.在补偿设计窗口选Compensator Editor页选项,可以手动调节PID系 数,完成后点击Update Simulink Block Parameters更新参数
8.在补偿设计窗口选Automated Tuning页选项,可以自动调节最优系 统PID系数,点击Optimize Compensators...开始自动调节
动态调节Simulink系统响 应:
matlab simulink pid参数设定技巧

matlab simulink pid参数设定技巧
在Simulink中进行PID参数设定时,可以采用以下技巧:
1. 使用PID自动调节工具箱:Simulink提供了PID自动调节工具箱,可以根据系统的特性自动计算PID参数。
使用该工具
箱可以简化参数设定过程,提高调节效果。
2. 使用试控制法:试控制法是一种通过观察系统响应来调节PID参数的方法。
可以通过设置比例增益Kp,观察系统的响
应特性,根据实际需求调整Kp的大小。
3. 逐步调节参数:可以通过逐步调节参数的方式获取最佳结果。
首先调节比例增益Kp,观察系统响应;然后调节积分时间Ti,观察系统稳态误差;最后调节微分时间Td,观察系统对变化
的响应。
4. 增加反馈路径:在PID控制器中增加反馈路径,可以减小
系统误差。
可以使用仿真结果和实验数据来进行参数调整,并优化PID参数。
5. 使用频域分析:通过分析系统的频域特性,可以更好地调节PID参数。
可以使用Bode图来观察系统的稳定性和幅频响应
特性,调整PID参数以获得更好的控制效果。
6. 考虑系统时间常数:系统的时间常数是影响PID参数设定
的重要因素之一。
根据具体的系统响应特性,合理选择PID
参数的大小和调整范围。
7. 进行参数整定实验:通过设计合适的实验,观察系统响应,可以更准确地确定PID参数。
可以通过改变输入信号的大小、频率等,观察系统的稳态误差、超调量等指标,调整PID参
数以达到设计要求。
MATLAB_Simulink_PID参数整定

·674·
哈 尔 滨 商 业 大 学 学 报 ( 自 然 科 学 版 ) 第 23卷
性 ,直接在闭合的调节回路中进行整定 ,方法简单 、 计算方便 、容易掌握 ,适合在工程实际中应用. 控制 工程中常用的工程整定方法有稳定边界法 、4∶1衰 减 法 、鲁 棒 P ID 参 数 整 定 法 和 ISTE ( Integral Squared Time - weighted Errors)最优参数整定法. 这四种方法各有优缺点 ,稳定边界法和 4∶1衰减法 上升时间短 、调节过程较快 ;而鲁棒 P ID 参数整定 法和 ISTE最优参数整定法超调量小 ,调节过程比 较平稳 ,鲁棒性好. 4种方法中 ,稳定边界法简单方 便 、容易掌握 ; 4∶1衰减法超调量大 ,在一些特殊情 况下 ,可能得不到 4∶1衰减比时的比例度和操作周 期 ,有一定的局限性 ,此外其鲁棒性也差 ; ISTE调 节时间长 ;鲁棒 P ID 参数整定法在被控对象的有 关过程参数比较准确时 ,该法整定的参数就比较偏 保守一些. 通过对上述 4 种 P ID 参数整定方法的 比较 ,我们可以体会到 ,控制系统的快速性和鲁棒 性是相互矛盾和相互制约的. 4 种方法各有优缺 点 ,在工程整定法中都有着各自的生命力.
Abstract: The p rocess of P ID parameters turning is comp licated and time2consum ing to engi2 neering technician. To solve this p roblem , simulating the Z—N method of engineering turn2 ing, based on the MATLAB / simulink, a simp le and efficient method for P ID parameters turning is p resented in this paper. Compares w ith the general methods, it has many advanta2 ges, such as simp licity, visual manipulation, leaving out the workload of p rogram and so on. The simulation results show the effectiveness of this method and be fit for app lication in the enginee ring. Key words: P ID control; MATLAB / Simulink; param eters turning; Z—N m ethod
基于Matlab_Simulink的PID参数整定方法

信息与电气工程学院 自动化系 2013
例 2:
单回路控制系统的传递函数如下,设计PID参数
基于Matlab/Simulink的PID 参数整定方法
信息与电气工程学院 自动化系 2013
解决如下问题:
如何利用Matlab/Simulink中的控制系统分析工 具完成单输入单输出系统的PID参数整定。
例 1:
单回路控制系统的传递函数如下,设计PID参数
1 W 0 (s) (1100s)3
信息与电气工程学院 自动化系 2013
步骤一:
在Simulink环境下建立被控对象的数学模型,该 数学模型可以为传递函数,也可以是状态空间表达式。
步骤制设计工具,完成模型的线性化, 并将线性化后的模型导入工作空间。
信息与电气工程学院 自动化系 2013
步骤四:
1 2 .5 s W ( s ) e 0 2 0 s 1
信息与电气工程学院 自动化系 2013
PID控制系统的Simulink仿真实验报告

自动控制原理实验报告PID 控制系统的Simulink 仿真1.实验目的1)掌握PID 控制规律及控制器的实现。
控制规律及控制器的实现。
2)对给定系统合理地设计PID 控制器。
控制器。
3)掌握对给定系统进行PID 控制器参数在线实验工程整定的方法。
控制器参数在线实验工程整定的方法。
2.实验原理在串联校正中,比例控制可提高系统开环增益,减少系统稳态误差,提高系统的控制精度,但会降低系统的相对稳定性,甚至可能造成系统闭环系统不稳定,积分控制可以提高系统的型别,有利于提高系统稳定性能,有利于提高系统稳定性能,但积分控制增加了一个位于原点的开环极点,但积分控制增加了一个位于原点的开环极点,但积分控制增加了一个位于原点的开环极点,使信号产生使信号产生90度的相位滞后,对系统的稳定不利,故不宜采用单一的积分控制器;微分控制规律能反映输入信号的变化趋势,映输入信号的变化趋势,产生有效的早期修正信号,产生有效的早期修正信号,产生有效的早期修正信号,以增加系统的阻尼程度,以增加系统的阻尼程度,以增加系统的阻尼程度,从而改善系统从而改善系统的稳定性,但微分控制增加了一个(-1/t)的开环极点,使系统的相角裕度提高,因此有助于系统动态性能的改善。
系统动态性能的改善。
在串联校正中,PI 控制器增加了一个位于原点的开环极点,同时也增加了一个位于s 左半平面的开环零点。
位于原点的开环极点可以提高系统的型别(无差度),减小稳态误差,有利于提高系统稳定性能;负的开环零点可以减小系统的阻尼,缓和PI 极点对系统产生的不利影响。
只要积分时间常数Ti 足够大,PI 控制器对系统的不利影响可大大减小。
PI 控制器主要用来改善控制系统的稳态性能。
主要用来改善控制系统的稳态性能。
在串联校正中,PID 控制器增加了一个位于原点的开环极点和两个位于s 左半平面的开环零点。
除了具有PI 控制器的优点外,还多了一个负实零点,动态性能比PI 更具有优越性。
单回路控制系统整定实验报告

单回路控制系统整定实验报告一、实验目的(1)掌握动态模型的创建方法.。
(2)掌握单回路控制系统的理论整定方法和工程整定方法。
(3)了解调节器参数对控制品质的影响。
二、实验仪器计算机一台三、实验步骤(1)启动计算机,运行MATLAB应用程序。
(2)在MATLAB命令窗口输入Smulink,启动Simulink。
(3)在Simulink库浏览窗口中,单击工具栏中的新建窗口快捷按钮或在Simulink库窗口中选择菜单命令File→New→Modeel,打开一个标题为“Untitled”的空白模型编辑窗口。
(4)用鼠标双击信号源模块库(Source)图标,打开信号源模块库,将光标移动到阶跃信号模块(Step)的图标上,按住鼠标左键,将其拖放到空白模型编辑窗口中。
用鼠标双击附加模块库(Simulink Extra)图标,打开A到底提哦哪里Liner模块库,将光标移到PID Controller 图标上,按住鼠标左键,将其拖放到空白模块编辑窗口中。
(5)用同样的方法从连续系统模块库(Continuous)、接受模块库(Sinks)和数学运算模块库(Math Operations)中把传递函数模块(Transfer Fcn)、示波器模块(Scope)和加法器模块(Sum)拖放到空白模型编辑窗口中。
(6)用鼠标单击一个模块的输出端口并用鼠标拖放到另一模块的输入端口,完成模块间的连接,如图1,图二。
图1图二(7)构造图1所示的单回路反馈系统的仿真模型。
其中控制对象由子系统创建,如图2。
(8)设调节器为比例调节器,对象传递函数为:0(1)nK T s (其中:0K =1,0T =10,n=4),用广义频率特性法按衰减率0.75计算调节器的参数;根据计算结果设置PID 调节其参数,启动仿真,通过示波器模块观测并记录系统输出的变化曲线(9)用响应曲线法整定调节器的参数。
1)求出对象的阶跃响应曲线2)根据响应曲线求取对象的动态特性参数。
控制系统pid参数整定报告
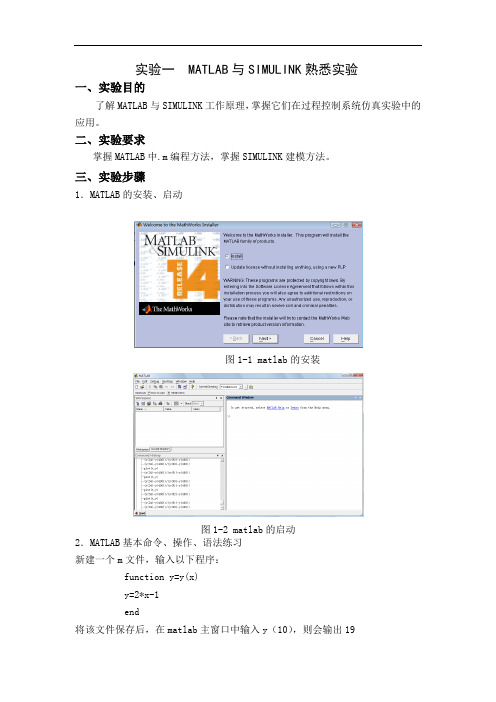
实验一 MATLAB与SIMULINK熟悉实验一、实验目的了解MATLAB与SIMULINK工作原理,掌握它们在过程控制系统仿真实验中的应用。
二、实验要求掌握MATLAB中.m编程方法,掌握SIMULINK建模方法。
三、实验步骤1.MATLAB的安装、启动图1-1 matlab的安装图1-2 matlab的启动2.MATLAB基本命令、操作、语法练习新建一个m文件,输入以下程序:function y=y(x)y=2*x-1end将该文件保存后,在matlab主窗口中输入y(10),则会输出19图1-3 m文件编译窗口图1-4 matlab主窗口3. SIMULINK建模练习新建一个model,在元件库中找出所需元件,并设置好元件参数,之后再用线段连接好系统并进行仿真。
图1-5 仿真模型四、思考题1、MATLAB中的HELP有什么作用?Help为用户提供了一些函数、工具箱具体用法及例子以及matlab的一些功能介绍。
2、MATLAB的特点是什么?1.Matlab有强大的自带的帮助手册,基于HTML的完整的帮助功能;2.运算符丰富。
由于MATLAB是用C语言编写的,MATLAB提供了和C语言几乎一样多的运算符,灵活使用MATLAB的运算符将使程序变得极为简短。
3.高级但简单的程序环境,与其它语言编写的程序结合和输入输出格式化数据的能力;MATLAB既具有结构化的控制语句(如for循环,while循环,break 语句和if语句),又有面向对象编程的特性。
4. 程序限制不严格,程序设计自由度大。
例如,在MATLAB里,用户无需对矩阵预定义就可使用。
有大量事先定义的数学函数,并且有很强的用户自定义函数的能力;5.程序的可移植性很好,基本上不做修改就可以在各种型号的计算机和操作系统上运行。
6. MATLAB的图形功能强大。
在FORTRAN和C语言里,绘图都很不容易,但在MATLAB里,数据的可视化非常简单。
单回路控制系统的整定实验

W s
1
20s 1
3
四、实验要求
1、在MATLAB软件的Simulink工具箱中,打开一个Simulink控制系统仿真界 面,在其中建立如图1-17所示的单回路控制系统方框图。 2、在图1-7所示的单回路控制系统中,采用书中介绍的临界比例带法对比 例积分调节器(PI)和比例积分微分调节器(PID)的各参数进行整定,并通过
在图1-2所示的Simulink工具箱主窗口的功能模块组列表中点击Math Operations功能模块组,会在窗口右边出现对应的各功能模块,用鼠标选择 其中的加(减)法模块(Sum)并按住左键将其拖到图1-3所示的Simulink 控制系统仿真界面中,即可以得到一个加(减)法模块(Sum)。双击加 (减)法模块(Sum),可以打开加(减)法模块(Sum)的参数设置对话 框如下图所示:
制系统为例,首先在Simulink控制系统仿真界面中建立控制系统的方
框图如下:
图1-14 单回路比例控制系统方框图
点击Simulink控制系统仿真界面中的Simulation下拉菜单,在下 拉菜单中点击Configuration Parameters„,出现下图所示的仿真 参数设置对话框:
仿真开始时间
三、实验原理
本实验利用MATLAB软件中Simulink工具箱中的功能模块组成具有 不同调节规律的单回路控制系统,并对其进行仿真研究,控制系统方 框图如下图ቤተ መጻሕፍቲ ባይዱ示:
图1-17 单回路控制系统方框图
被控对象
在图1-17所示的单回路控制系统中,由三个一阶惯性环节仿真模块 (Transfer Fcn1~Transfer Fcn3)串联组成一个三阶惯性被控对象,其传递 函数为:
点击右键,按住右键拖动鼠标指针,在需要转弯出松开右键,即出现一
基于MATLAB_Simulink环境下的PID参数整定

•
6、意志坚强的人能把世界放在手中像 泥块一 样任意 揉捏。 2020年 12月14 日星期 一上午 12时49 分10秒 00:49:1 020.12. 14
•
7、最具挑战性的挑战莫过于提升自我 。。20 20年12 月上午 12时49 分20.1 2.1400: 49Dece mber 14, 2020
• 13、无论才能知识多么卓著,如果缺乏热情,则无异 纸上画饼充饥,无补于事。Monday, December 14, 2020
14-Dec-2020.12.14
• 14、我只是自己不放过自己而已,现在我不会再逼自 己眷恋了。20.12.1400:49:1014 December 202000:49
•
8、业余生活要有意义,不要越轨。20 20年12 月14日 星期一 12时49 分10秒 00:49:1 014 December 2020
•
9、一个人即使已登上顶峰,也仍要自 强不息 。上午 12时49 分10秒 上午12 时49分 00:49:1 020.12. 14
• 10、你要做多大的事情,就该承受多大的压力。12/14/
放大坐标观察两个波峰之间的距离,比15多一点,因此T可取15.2 ,此时Kp=12.5。按照稳定边界法表格里的计算方法,我们很容易就 可以得到整定的PID参数。
在MATLAB Command Window中输入Kp=12.5;T=15.2;Ki=1.2*Kp/T; Kd=0.075*Kp*T;Kp=0.6*Kp;
2)积分时间常数TI
积分控制通常与比例控制或比例微分控制联合使用,构成 PI或PID控制,增大积分时间常数(积分变弱)有利于减小 超调,减小振荡,使系统更稳定,但同时会延长系统消除静 差的时间。积分时间常数太小又会降低系统的稳定性,增大 系统的振荡次数。
单回路控制系统的参数整定

单回路控制系统的参数整定
实验要求:
(1)了解调节器特性的实验测试方法
(2)掌握依据飞升特性曲线求取对象动态特性参数和调节器参数的方法
(3)熟悉单回路控制系统的工程整定方法
实验内容:
(1)在 Simulink 中搭建含该被控对象的单回路控制系统,其中输入为单位阶跃信号、单位负反馈、调节器选用 PID控制规律 (提示:PID环节用 Simulink 库中自带的)
(2)采用稳定边界法整定调节器参数,并给出 P、PI、PID三种调节规律下的单回路控制系统的输出曲线
Kp=4.78 Pm=0.2092 (Kp=1/Pm)
Tm=156.1-84.11=71.99s
P调节:
Kp=1/(2*Pm)=1/2*4.78=2.39
PI调节:
Kp=1/(2.2*Pm)=1/2.2*4.78=2.173
Ki=Kp/Ti=2.173/(0.85*71.99)=0.0355
PID调节:
Kp=1/(1.7*Pm)=1/1.7*4.78=2.81
Ki=Kp/Ti=2.81/(0.5*71.99)=0.078 Kd=Kp*Ti=2.81*0.125*71.99=25.286
(3)比较、分析实验结果
(4)加分项目:采用衰减曲线法整定调节器参数衰减比为4:1 时。
过程控制-单回路PID控制、PID的参数整定、实用数字PID及相关技术-文档资料

如何确定PID参数?
PID控制器的 参数整定与应用
PID参数对控制性能的影响
控制器增益 Kc或比例度δ
增 定益性下Kc降的;增大(或比例度δ下降),使系统的调节作用增强,但稳
积分时间Ti
积 制分系作统用的的稳增定强性(下即降;Ti 下降),使系统消除余差的能力加强,但控
电流转变为气压来操纵阀门
数字计算和通讯
手动操作
信号在局域网中传输, 传感器和阀门也可带有微处理器!
机械装置
气动设备 电动设备
数字PID
数字计算
数字计算 和通讯
信号采用数字传输
电流转变为气压来操纵阀门
数字控制
为什么?
数字控制采用分布式网络结构
操作站
操作站
数字通讯
(s)
Kc
(1
1 Ti s
)
积分时间Ti 对系统性能的影响
引入积分作用的根本目的是为了消除稳态余差,但使控制 系统的稳定性下降。当积分作用过强时(即Ti 过小),可 能使控制系统不稳定。
积分作用Ti对控制性能的影响
理想的比例积分微分PID控制器
u
Kc
(e
1 Ti
t
edt
0
Td
d ቤተ መጻሕፍቲ ባይዱt)
Kd
Td s 1
+
u (t)
Kv Tvs 1
K p exp( s) + Tps 1
y (t)
Km
z (t)
Tms 1
假设控制输入u (t)与干扰输入d (t)均为阶跃信号,要求显示 输入对被控变量y (t)及其测量z (t)的动态响应。
利用Simulink进行PID控制器的参数分析

利用Simulink搭建PID控制系统模型及分析——201706527曾庆松在参考了《过程控制系统》一书中PID调节原理相关章节的基础上,利用Matlab的Simulink仿真器搭建PID控制系统模型,并进行仿真,对PID控制器的三个参数Kp,Ki,Kd与控制性能(稳态误差,上升时间,峰值时间,调节时间,超调量等)之间的关系进行分析,其完整过程如下。
一、搭建模型搭建好的PID控制系统模型如图1所示,其中输入为阶跃响应,被控对象为二阶惯性环节。
其输出响应曲线如图2所示。
图 1 PID控制系统模型图2系统输出响应曲线二、参数对性能影响的分析1、Kp的影响。
图 3 调整Kp时输出响应曲线的变化从图中可以看出对于一个已经设计好的PID控制器,当Kp的值变小时系统的峰值时间、上升时间变长,超调量增加,甚至造成系统不稳定;而当Kp的值变大时则会造成系统震荡加剧。
2、Ki的影响。
图 4 调整Ki时输出响应曲线的变化从曲线的变化情况可以看出,当Ki的值变大时将导致系统产生减幅震荡,Ki过小时又会使系统的稳态误差增大。
3、Kd的影响。
图 5 调整Kd时输出响应曲线的变化从输出响应曲线的变化情况来看,当Kd的值减小时系统的超调量明显增加,调节时间、上升时间等参数也受到影响;当Kd的值增加时系统的调节时间大大增加,并且稳态误差较大,系统反应速度满且调节效果很差。
三、总结1、比例增益Kp的作用比例控制是一种最简单的控制方式。
其控制器的输出与输入误差信号成比例关系。
增大Kp就等于加大系统的开环增益,结果导致系统剧烈震荡甚至不稳定。
2、积分时间Ki的作用在积分控制中,控制器的输出与输入误差信号的积分成正比关系,所以主要用于消除静差,提高系统的无差度。
增大Ki将造成系统稳定性下降,直到出现发散的震荡过程。
3、微分时间Kd的作用在微分控制中,控制器的输出与输入误差信号的微分(即误差的变化率)成正比关系。
所以微分控制可以减小超调量,克服振荡,使系统的稳定性提高,同时加快系统的动态响应速度,减小调节时间,从而改善系统的动态性能。
基于MATLABSimulink的PID参数整定

基于MATLABSimulink的PID参数整定基于MATLAB/Simulink的PID参数整定摘要:针对PID参数整定过程的复杂性,基于MATLAB/Simulink仿真环境,模拟临界⽐例度法PID参数整定的⽅法和步骤,给出了⼀种简单有效的PID参数整定⽅法。
与通常的整定⽅法⽐较,其优点是⾮常直观、可以随意修改仿真参数,节省了⼤量的计算和编程⼯作量。
通过仿真实例验证了该⽅法的有效性。
关键词:PID控制;参数整定;MATLAB/Simulink;临界⽐例度法Abstract:The PID tuning is a complicated process.To solve the problem,a method of critical gain is presented based on the MATLAB/Simulink simulationenvironment.The simulation examples are also given.Key words:PID control;parameter tuning;MATLAB/Simulink;critical gain method 1 引⾔PID控制是最早发展起来且⽬前在⼯业过程控制中仍然是应⽤最为⼴泛的控制策略之⼀。
据统计,在⼯业过程控制中95%以上的控制路都具有PID结构,⽽且许多⾼级控制都是以PID控制为基础的。
PID控制能被⼴泛应⽤和发展,根本原因在于PID控制具有以下优点:原理简单,使⽤⽅便,PID参数K p、T i和T d可以根据过程动态特性及时调整,适应性强。
鲁棒性强,即其控制品质对控对象特性的变化不太敏感。
采⽤不同的PID参数,对控制系统的性能将会不—样,因此PID参数的调节和优化决定了控制系统最终能达到的控制性能,PID参数整定是控制系统设计的核⼼内容。
综观各种PID参数整定⽅法,可以有如下分类:根据研究⽅法来划分,可分为基于频域的PID参数整定⽅法和基于时域的PID参数整定⽅法;根据发展阶段来划分,可分为常规PID参数整定⽅法和智能PID 参数整定⽅法根据被控对象个数来划分,可分为单变量PID参数整定⽅法和多变量PID参数整定⽅法;根据控制量的组合形式来划分,可分为线性PID参数整定和⾮线性PID参数整定⽅法。
在Simulink下实现PID控制器的设计与仿真

基于MATLAB_Simulink的机电一体化系统的仿真分析
一、实验目的 二、实验内容 三、实验报告 四、实验过程
五、实验操作
《机电一体化系统设计》课程实验
一、实验目的和要求
目的:
机电一体化系统建模是进行机电一体化系统分析与设计的基础,通过对系 统的简化分析建立描述系统的数学模型,进而研究系统的稳态特性和动态 特性,为机电一体化系统的物理实现和后续的系统调试工作提供数据支持, 而仿真研究是进行系统分析和设计的有利方法。 本实验目的在于通过实验使同学对机电一体化系统建模方法和仿真方法有初步 的了解,初步掌握在MATLAB/ SIMULINK环境下对机电一体化系统数学模 型进行仿真的方法。 (1)掌握机电一体化系统数学建模的基本方法; (2)掌握对机电一体化系统进行数学仿真的基本方法和步骤; (3)在初步掌握在MATLAB/ SIMULINK环境下对机电一体化系统数学模 型进行仿真的方法。
《机电一体化系统设计》课程实验
二、实验内容
2 PID控制系统的设计 Ziegler- Nichols法是一种基于频域设计 PID 控制器的方法。此法首先通过 实验获取控制对象单位阶跃响应,获得K、L 和 T 参数。令a=KL/T,我们可以通 过下表给出的Ziegler- Nichols经验公式确定P、PI 和 PID 控制器的参数。
《机电一体化系统设计》课程实验
二、实验内容
3 PID 控制系统MATLAB/Simulink仿真分析 3.1 在MATLAB 下实现PID 控制器的设计与仿真 elseif length(vars)==3, K=vars(1); Tc=vars(2); N=vars(3); if key==1, Kp=0.5*K; elseif key==2, Kp=0.4*K; Ti=0.8*Tc; elseif key==3 | key==4, Kp=0.6*K; Ti=0.5*Tc; Td=0.12*Tc; end elseif length(vars)==5, K=vars(1); Tc=vars(2); rb=vars(3); N=vars(5);pb=pi*vars(4)/180; Kp=K*rb*cos(pb); if key==2, Ti=-Tc/(2*pi*tan(pb)); elseif key==3|key==4, Ti=Tc*(1+sin(pb))/(pi*cos(pb)); Td=Ti/4; end end
Simulink仿真之PID控制

因此,控制作用u常用的表示 形式为:
式中的Kc是控制器的比例增益, Ti和Td都具有时间量纲,分别 称为积分时间和微分时间。
PID控制器具有以下优点:
(1)原理简单,使用方便。
(2)适应性强。
(3)鲁棒性强,即其控制 品质对被控制对象特性的变 化不太敏感。
精选ppt课件
3
5.2 PID控制算法
(3)增加的负实部零点则可减小系统的阻尼程度, 缓和PI控制器极点对系统稳定性及动态过程产生的 不利影响。
(4)在实际工程中,PI控制器通常用来改善系统的 稳态性能。
精选ppt课件
5
PI控制举例
精选ppt课件
6
5.2.3 比例微分(PD)控制
PD控制作用举例
精选ppt课件
7
5.2.4 比例积分微分(PID)控制
5.3.2 临界比例度法
精选ppt课件
12
临界比例度法整定举例
精选ppt课件
13
5.3.3 衰减曲线法
精选ppt课件
按“先P后I最后D”的操作 程序,将求得的整定参数设 置在调节器上,再观察运行 曲线,若不太理想,还可作 适当调整。
衰减曲线法的注意事项: (1)对于反应较快的控制
系统,要认定41衰减曲线和 读出Ts比较困难,此时,可 认为记录指针来回摆动两次 就达到稳定是41衰减过程。 (2)在生产过程中,负荷 变化会影响过程特性。当负 荷变化较大时,必须重新整 定调节器参数值。 (3)若认为41衰减太慢, 可采用101衰减过程。对于 101衰减曲线法整定调节器 参数的步骤与上述完全相同, 仅仅所用计算公式有些不同。
(3)增大微分时间有利于加快系统的响应速度,
使系统超调量减小,稳定性增加,但系统对扰
(完整)单回路PID控制系统实验报告

北京联合大学实验报告实验名称:单回路PID控制系统学院:自动化专业:自动化班级:学号:姓名:成绩:2013年 10 月24 日实验二单回路P I D控制系统组成及过程动态特性参数对控制质量的影响一、实验目的:1.熟悉Matlab仿真环境;2.理解单回路控制系统的组成;3.理解给定值扰动和负荷扰动的过渡过程曲线;4.掌握扰动通道、控制通道的静态参数和动态参数对控制质量的影响;5.掌握扰动作用位置对控制质量的影响;6.掌握对象的多个时间常数之间的关系对控制质量的影响;二、实验内容:对如下图所示的单回路控制系统进行仿真.W C(S)W V(S)W0(S)-W m(S)进入仿真环境,建立如下仿真系统:例:其中,Step input作为系统给定值;而Step1 input作为外部干扰。
注:PID模块后的比例环节可换为一阶环节。
具体步骤为:1、模块在库中,模块在库中,模块在库中,模块在库中。
模块在库的中.2、双击模块可以设定每个模块的参数,左键拖动鼠标产生连线,右键拖动鼠标可产生交接线.(一)给定值扰动:设置给定值阶跃扰动Step input为某一值,设外部干扰Step1 input为0,改变PID控制器的参数,从模块观察系统输出曲线,直到出现4:1衰减曲线。
(如图)①修改Step input模块:双击,对话框参数为:②修改PID模块:双击PID模块,出现如下对话框:在此窗口下修改P、I、D参数。
反复调整P、I、D参数,使输出成为4:1衰减曲线。
如图(二)负荷扰动:修改参数步骤与(一)相同,设Step input给定值扰动为0,负荷扰动Step1 input设置为某一值。
反复调整P、I、D参数,使输出成为4:1衰减曲线(三)观察扰动通道和控制通道参数对控制质量的影响:(调节器整定参数值不变) 1.改变扰动通道静态参数和动态参数,观察输出波形的变化;2.改变控制通道静态参数和动态参数,观察输出波形的变化;3.改变扰动作用位置,观察输出波形的变化;4.改变对象各时间常数的值,观察输出波形的变化;三、实验结果整理:1、总结单回路仿真系统的基本组成部分。
控制仿真实验报告

实验名称:基于MATLAB/Simulink的PID控制器参数优化仿真实验日期:2023年11月10日实验人员:[姓名]实验指导教师:[指导教师姓名]一、实验目的1. 理解PID控制器的原理及其在控制系统中的应用。
2. 学习如何使用MATLAB/Simulink进行控制系统仿真。
3. 掌握PID控制器参数优化方法,提高控制系统的性能。
4. 分析不同参数设置对系统性能的影响。
二、实验原理PID控制器是一种广泛应用于控制领域的线性控制器,它通过将比例(P)、积分(I)和微分(D)三种控制作用相结合,实现对系统输出的调节。
PID控制器参数优化是提高控制系统性能的关键。
三、实验内容1. 建立控制系统模型。
2. 设置PID控制器参数。
3. 进行仿真实验,分析系统性能。
4. 优化PID控制器参数,提高系统性能。
四、实验步骤1. 建立控制系统模型使用MATLAB/Simulink建立被控对象的传递函数模型,例如:```G(s) = 1 / (s^2 + 2s + 5)```2. 设置PID控制器参数在Simulink中添加PID控制器模块,并设置初始参数,例如:```Kp = 1Ki = 0Kd = 0```3. 进行仿真实验设置仿真时间、初始条件等参数,运行仿真实验,观察系统输出曲线。
4. 分析系统性能分析系统在给定参数下的响应性能,包括超调量、调节时间、稳态误差等指标。
5. 优化PID控制器参数根据分析结果,调整PID控制器参数,优化系统性能。
可以使用以下方法:- 试凑法:根据经验调整参数,观察系统性能变化。
- Ziegler-Nichols方法:根据系统阶跃响应,确定参数初始值。
- 遗传算法:使用遗传算法优化PID控制器参数。
6. 重复步骤3-5,直至系统性能满足要求五、实验结果与分析1. 初始参数设置初始参数设置如下:```Kp = 1Ki = 0Kd = 0```仿真结果如图1所示:从图1可以看出,系统存在较大的超调量和较长的调节时间,稳态误差较大。
实验七SIMULINK 仿真单回路控制系统及PID控制器参数整定
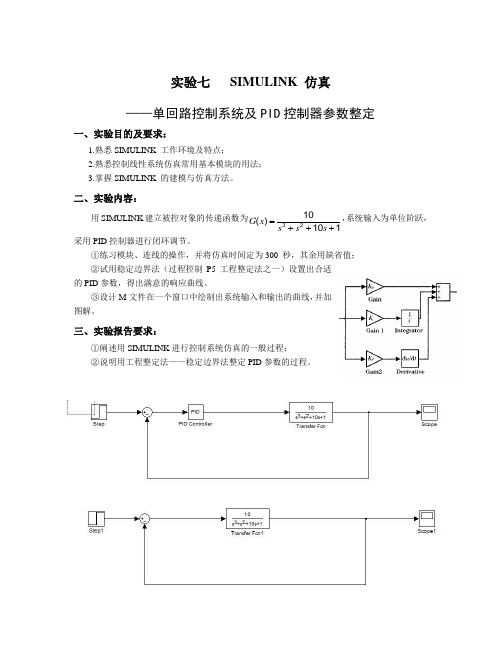
实验七 SIMULINK 仿真——单回路控制系统及PID 控制器参数整定一、实验目的及要求:1.熟悉SIMULINK 工作环境及特点;2.熟悉控制线性系统仿真常用基本模块的用法;3.掌握SIMULINK 的建模与仿真方法。
二、实验内容:用SIMULINK 建立被控对象的传递函数为11010)(23+++=s s s x G ,系统输入为单位阶跃,采用PID 控制器进行闭环调节。
①练习模块、连线的操作,并将仿真时间定为300 秒,其余用缺省值;②试用稳定边界法(过程控制P5工程整定法之一)设置出合适的PID 参数,得出满意的响应曲线。
③设计M 文件在一个窗口中绘制出系统输入和输出的曲线,并加图解。
三、实验报告要求:①阐述用SIMULINK 进行控制系统仿真的一般过程;②说明用工程整定法——稳定边界法整定PID 参数的过程。
M文件denz=[10];numz=[1 1 10 1];sysz=tf(denz,numz)%传递函数denk=[0 0.539];numk=[0 1];deni=[0 2];numi=[1 0];dend=[0.25 0];numd=[0 1];sysk=tf(denk,numk)%p调节器sysi=tf(deni,numi)%I调节器sysd=tf(dend,numd)%D调节器[denki,numki]=parallel(denk,numk,deni,numi);%P调节器与I调节器相并联[denpid,numpid]=parallel(dend,numd,denki,numki);%PI调节器与D调节器相并联组成PID调节器syspid=tf(denpid,numpid)[denkh,numkh]=series(denpid,numpid,denz,numz);%PID与传递函数串联组成开环控制系统syskh=tf(denkh,numkh)[denbh,numbh]=feedback(denkh,numkh,1,1,-1);%组成单位负反馈闭环系统sysbh=tf(denbh,numbh)t=0:0.1:300;%加入0到300的仿真时间,步进值为0.1subplot(2,1,1)plot(t,1,'b')%显示单位阶跃函数subplot(2,1,2)step(sysbh,t)%显示闭环系统对于单位阶跃函数的响应函数曲线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验七 SIMULINK 仿真
——单回路控制系统及PID 控制器参数整定
一、实验目的及要求:
1.熟悉SIMULINK 工作环境及特点;
2.熟悉控制线性系统仿真常用基本模块的用法;
3.掌握SIMULINK 的建模与仿真方法。
二、实验内容:
用SIMULINK 建立被控对象的传递函数为11010)(23+++=s s s x G ,系统输入为单位阶跃,采用PID 控制器进行闭环调节。
①练习模块、连线的操作,并将仿真时间定为300 秒,其余用缺省值;
②试用稳定边界法(过程控制P5工程整定法之一)设置出合适
的PID 参数,得出满意的响应曲线。
③设计M 文件在一个窗口中绘制出系统输入和输出的曲线,并加
图解。
三、实验报告要求:
①阐述用SIMULINK 进行控制系统仿真的一般过程;
②说明用工程整定法——稳定边界法整定PID 参数的过程。
M文件
denz=[10];
numz=[1 1 10 1];
sysz=tf(denz,numz)%传递函数
denk=[0 0.539];
numk=[0 1];
deni=[0 2];
numi=[1 0];
dend=[0.25 0];
numd=[0 1];
sysk=tf(denk,numk)%p调节器
sysi=tf(deni,numi)%I调节器
sysd=tf(dend,numd)%D调节器
[denki,numki]=parallel(denk,numk,deni,numi);%P调节器与I调节器相并联[denpid,numpid]=parallel(dend,numd,denki,numki);%PI调节器与D调节器相并联组成PID调节器
syspid=tf(denpid,numpid)
[denkh,numkh]=series(denpid,numpid,denz,numz);%PID与传递函数串联组成开环控制系统
syskh=tf(denkh,numkh)
[denbh,numbh]=feedback(denkh,numkh,1,1,-1);%组成单位负反馈闭环系统
sysbh=tf(denbh,numbh)
t=0:0.1:300;%加入0到300的仿真时间,步进值为0.1
subplot(2,1,1)
plot(t,1,'b')%显示单位阶跃函数
subplot(2,1,2)
step(sysbh,t)%显示闭环系统对于单位阶跃函数的响应函数曲线。
