2020年江苏高考招生计划中问题说明
2020年全国高考历史试题及答案-江苏卷

2020年普通高等学校招生全国统一考试(江苏卷)历史试题一、选择题:本大题共20题,每题3分,共计60分。
在每小题列出的四个选项中,只有一项最符合题目要求。
1.近年江西新干出土了一批商代青铜农具,有犁、耜、斧、铲、镰等,种类较为齐全。
某些类型的农具还是首次发现,更无使用之痕。
不少农具铸有云纹、兽面纹、蝉纹等具有神秘意义的纹饰,绝非一般农具所能铸刻。
这反映出()A.青铜农具最早出现于江西新干B.成套青铜农具有利于精耕细作C.青铜农具基本不用于农业生产D.全国经济重心已经转移到南方2.墨子提出治理天下应当像大禹那样“使劳者得息,乱者得治”,认为察“圣王之事”得“观其中国家百姓人民之利”。
由此可知,墨家学派能够兴起的主要原因在于()A.恢复前代礼乐制度B.代表下层平民利益C.强调社会等级和谐D.适应兼并战争需要3.有学者认为,如果说安史之乱以前,唐诗以豪放、浪漫色彩引人注目,那么安史之乱以后,则已代之以沉郁悲壮的情调了。
对这一评论理解正确的是()A.社会变迁影响唐诗创作B.盛唐气象推动唐诗演变C.唐诗全景再现社会真实D.安史之乱导致唐诗衰微4.孟子讲“觉”,佛教讲“悟”,程颢、程颐兄弟则将二者圆通。
北宋僧人契嵩认为儒和佛“心则一”,佛教“亦有意于天下国家矣,何尝不存其君臣父子”。
这反映出北宋()A.儒学统治地位动摇B.儒学与佛教的融合C.理学成为官方哲学D.阳明心学影响深远5.明代松江府大地主潘允端的《玉华堂日记》中,反映土地租佃关系的记事有4条。
在日记中,关于垦田挑泥、种麦等往往有发给“工本”和“工银”的记载,他的田庄产品除自用外,也有一部分投放市场。
该日记可以佐证()A.农村雇佣劳动基本普及B.地主剥削程度有所减轻C.地主收入依赖家庭副业D.农业生产经营方式多样6.自19世纪中叶洋纱大量进口后,农家不再自己纺纱,逐渐购入洋纱织布。
手工织布不但没有在机织棉布面前立即败退,反而得到一度的兴盛和繁荣,日益从农家分离出来而成为一个独立的生产行业。
自主招生、综合评价、专项计划可同时报考吗?高考加分能叠加吗?

自主招生、综合评价、专项计划可同时报考吗?高考加分能叠加吗?近年来,越来越多的考生都开始参与到自主招生、综合评价以及专项计划的考试中来,不愿再做“高考陪跑人”。
但是,仍有很多家长及考生对这三项高考捷径不是十分了解,今天小编就挑选了两个较为热门的问题进行解答,以供2020届高考生参考。
热门问题解答Q1:自主招生、综合评价、专项计划可同时报考吗?根据往年报考情况来看,绝大多数高校自主招生、综合评价和高校专项计划可以同时报考。
但也有少数高校会明确说明不能同时报考该校自主招生和高校专项计划等。
具体需以报考当年政策要求为准。
Q2:自主招生、综合评价、高校专项计划中获得的录取优惠可以叠加吗?不可以。
按照往年录取情况来看,如果一个考生同时获得自主招生、综合评价和高校专项计划的录取优惠,填报志愿时只能选择任意一种优惠。
秒懂自主招生、综合评价、专项计划对这三种招生政策都傻傻分不清楚?高考君将从概念、招生对象、报考时间、考核方式等七个方面解析自主招生、综合评价和专项计划的异同点,让你秒懂三者区别!1、区别概念(1)什么是自主招生?自主招生,是由高校拿出一定比例的招生名额,在高考的基础上通过院校的综合选拔体系(初审、笔试、面试、体质测试考核),选拔出具有学科特长和创新潜质的优秀学生,最终获得拟录取资格的考生在高考成绩达到院校标准时可在高考录取中享有一定的投档及专业录取优惠。
(2)什么是综合评价?简单来说就是进行综合评价招生的高校,综合考量考生的高考成绩、高校考核结论、高中学业水平测试成绩、综合素质评价等方面的内容,对高考成绩达到分数要求的入选考生,综合评价,择优录取。
(3)什么是专项计划?为进一步提高“重点高校”招收农村和贫困地区学生比例,我国面向农村和贫困地区学生有三大专项计划:国家专项计划、地方专项计划和高校专项计划。
招生任务由教育部直属高校和其他自主招生试点高校承担,安排招生计划不少于有关高校年度本科招生规模的2%。
2020年江苏高考政治考试说明

xx年江苏省高考政治考试说明一、命题指导思想xx年普通高等学校招生全国统一考试政治科(江苏卷)的命题将继续遵循有利于高校选拔人才,有利于中学全面实施素质教育和对学生创新精神与实践能力的培养,有利于中学思想政治课程改革的原则。
命题将充分体现普通高中新课程的理念,反映政治学科新课程标准的要求,做到紧密联系实际,贴近学生生活,富有时代气息。
坚持知识考查、能力考查与情感、态度、价值观考查的有机统一,注重考查考生对思想政治学科基础知识和基本技能的掌握,考查考生初步运用马克思主义的立场、观点和方法分析、解决实际问题的能力,考查考生对现阶段中国共产党和中国政府的基本路线和重大方针政策的内容和意义的理解。
在遵循国家统一考试要求的同时,适当体现江苏特色。
命题将充分体现高等学校招生考试的选拔性,是试卷既有较高的信度和效度,又有必要的区分度和适当的难度。
二、考试内容及要求xx年普通高等学校招生全国统一考试政治科(江苏卷)的考核目标与要求及考试范围均以教育部《普通高中思想政治课程标准(实验)》和江苏省《普通高中思想政治课程标准教学要求》为主要依据,对考试内容及要求具体说明如下:必考部分必考部分包括经济生活、政治生活、文化生活、生活与哲学、时事政治(一)经济生活1.生活与消费(1)货币了解商品的含义及基本属性理解货币的含义、货币和基本职能了解纸币的含义及其发行规律、通货膨胀、通货紧缩了解信用卡的含义、功能及优点了解外汇和汇率树立正确的金钱观(2)价格理解价格与价值的关系理解商品的价值量是由生产商品的社会必要劳动时间决定理解企业提高劳动生产率的意义理解供求关系对价格的影响理解价值规律的基本内容及表现形式,运用价值规律分析相关经济现象理解价格变动对人们生活和生产经营的影响(3)消费了解影响消费的因素了解不同的消费类型理解消费结构的含义和恩格尔系数了解消费心理和消费行为树立正确的消费观2.生产、劳动与经营(1)生产与经济制度理解生产与消费的关系理解大力发展生产力的意义了解公有制经济的含义、公有制的实现形式理解公有制经济的主体地位理解国有经济在国民经济中的主导作用了解个体经济、私营经济、外资经济的含义、地位和作用理解我国社会主义初级阶段基本经济制度的内容,实行这一制度的原因和意义(2)企业与劳动者了解企业的含义了解公司的含义、类型和组织机构理解公司经营成功的主要因素了解企业兼并与破产的原因及意义了解劳动和就业的的意义树立正确的择业观懂得应依法维护劳动者权益(3)投资的选择了解储蓄存款的含义了解利息的含义与计算方法了解我国商业银行的主要业务了解股票的含义和特点了解债券的含义、分类和特点了解商业保险的含义和种类比较储蓄、债券、股票、商业保险几种投资方式的异同,分析不同的投资行为3.收入与分配(1)个人收入的分配理解我国实行按劳分配为主体、多种分配方式并存的分配制度的客观必然性了解按劳分配的基本内容和作用了解按个体劳动者劳动成果分配和按生产要素分配了解公平与效率的含义说明公平与效率的关系(2)国家收入的分配了解财政收入的含义及其来源理解影响财政收入的因素了解财政支出的含义及其种类了解财政收支平衡和财政赤字的含义理解我国财政的作用(3)征税和纳税了解税收的含义理解税收的基本特征理解个人所得税了解税收的作用了解纳税人和负税人的含义理解依法纳税是公民的基本义务4.面向市场经济(1)走进社会主义市场经济了解市场经济的含义理解市场调节的作用及其局限性理解规范市场秩序的必要性和措施理解社会主义市场经济的基本特征理解国家宏观调控的目标和手段,说明国家宏观调控的重要性(2)小康社会的经济建设理解全面建设小康社会的奋斗目标了解全面建设小康社会经济建设的目标理解科学发展观的内涵,树立科学发展观说明促进经济持续协调发展的主要措施(3)经济全球化与对外开放了解经济全球化的含义和表现了解跨国公司的作用理解经济全球化的影响了解世界贸易组织的原则和作用理解对外开放的基本国策,全面提高对外开放的水平(二)政治生活1.公民的政治生活(1)我国的国家性质了解国家的含义和根本属性理解我国的国家性质理解人民民主专政的本质和特点理解人民民主的广泛性和真实性理解坚持人民民主专政的必要性(2)我国公民的权利和义务理解我国公民的政治权利和义务说明我国公民参与政治生活的基本原则了解我国公民政治生活的主要内容理解公民积极有序地参与政治生活的意义了解各种选举方式的特点、选择选举方式的主要依据,懂得珍惜自己的选举权利理解公民参与民主决策的方式、公民直接参与民主决策的意义了解我国的村民自治和城市居民自治,理解发展基层民主的意义了解我国公民依法行使民主监督权的渠道和方式,理解公民要负责地行使监督权利2.为人民服务的政府(1)政府的职能和责任理解我国政府的主要职能说明我国政府的宗旨和政府工作的基本原则(2)政府权力的行使和监督理解政府依法行政的意义了解提高政府依法行政水平的要求来历界对政府权力进行制约和监督的意义了解我国的行政监督体系3.建设社会主义政治文明(1)我国的人民代表大会制度理解人民代表大会及其常设机关的法律地位和职权了解人大代表的产生和职责理解人民代表大会制度的基本内容理解人民代表大会与其他国家机关之间的关系说明人民代表大会制度是适合我国国情的根本政治制度(2)我国的政党制度了解中国共产党领导地位和执政地位的确立说明中国特色社会主义事业必须坚持中国共产党的领导理解中国共产党的性质、宗旨和指导思想理解中国共产党科学执政、民主执政、依法执政的含义,懂得依法执政是中国共产党执政的基本方式理解中国特色的政党制度的基本内容和优越性理解发展社会主义政治文明最根本的就是坚持党的领导、人民当家作主和依法治国的有机统一(3)我国的民主区域自治制度及宗教政策理解我国处理民族关系的基本原则理解我国的民族区域自治制度及其优越性了解我国宗教政策的基本内容4.当代国际社会(1)国际社会的成员了解主权国家的构成要素及权利和义务了解国际组织的含义、类型和作用理解联合国的宗旨、原则和作用(2)处理国际关系的决定性因素了解国际关系的含义理解国际关系的决定因素说明我国在国家关系中必须维护自己的国家利益(3)世界政治经济发展的基本趋势了解当今时代的主题了解世界多极化在曲折中发展了解中国政府关于建立国家新秩序的主张理解当代国际竞争的实质(4)我国独立自主的和平外交政策理解我国独立自主的和平外交政策的基本内容了解中国和平发展道路的内涵(三)文化生活1.文化与生活(1)文化与社会了解文化的内涵与形式理解文化与经济、政治的关系理解文化在综合国力竞争中的地位和作用越来越突出(2)文化对人的影响理解文化对人影响的表现了解文化对人的影响的特点说明文化塑造人生的作用2.文化传承与创新(1)文化的多样性与文化传播了解世界文化多样性的表现理解世界文化与民族文化的关系理解尊重文化多样性的意义了解文化传播的多种途径了解现代文化传播手段的特点理解加强中外文化交流的意义(2)文化的继承与发展了解传统文化的特点及影响说明对待传统文化的正确态度理解文化继承与发展的关系了解影响文化发展的重要因素理解教育在文化传承中的作用(3)文化创新理解文化创新的意义理解社会实践是文化创新的源泉、动力理解创新与继承的关系理解创新与借鉴、融合的关系坚持文化创新的正确方向3.中华文化与民族精神(1)灿烂的中华文化了解中华文化源远流长、博大精深理解中国文化的包容性了解中华文化是中国各族人民共同创造的(2)弘扬和培育民族精神了解中华民族精神的基本内涵理解中华民族精神的核心和新时期爱国主义的主题了解中国共产党对民族精神的继承和弘扬说明弘扬和培育民主精神的意义和途径4.发展先进文化(1)走进文化生活了解文化市场和大众传媒的发展对人们文化生活的影响理解发展大众文化的基本要求了解落后文化与腐朽文化的含义、危害及存在原因(2)建设中国特色社会主义文化理解在当代中国发展先进文化的内涵理解发展先进文化必须坚持马克思主义为指导了解发展先进文化的根本目标理解发展先进文化,必须大力发展教育、科学和文化事业(3)文化建设的中心环节了解思想道德建设在中国特色社会主义文化建设中的地位了解社会主义思想道德建设的目标了解我国公民道德建设的基本规范说明知识文化修养与思想道德修养的关系(四)生活与哲学1.生活智慧与时代精神(1)哲学是什么了解哲学与生活的关系理解哲学是系统化理论化的世界观、哲学是世界观和方法论的统理解哲学与具体科学的关系了解真正的哲学都是自己时代的精神上的精华(2)哲学的基本问题理解哲学的基本问题及其两方面的内容(3)唯物主义和唯心主义了解划分唯物主义和唯心主义的唯一标准理解唯物主义的基本观点及其三种基本历史形态理解唯心主义的基本观点及其两种基本形态(4)马克思主义哲学的生产是哲学史上的伟大变革了解马克思主义哲学生产的阶级基础、自然科学基础和理论来源理解马克思主义哲学的基本特征理解马克思主义中国化的三大理论成果2.探索世界与追求真理(1)世界的物质性理解辩证唯物主义的物质概念、世界的真正统一性就在于它的物质性理解哲学的运动概念、物质与运动的关系、物质世界是绝对运动与相对静止的统理解规律的含义、规律的客观性和普遍性说明人可以认识和利用规律,坚持按规律办事(2)意识的起源、本质和作用了解意识是物质世界长期发展的产物了解意识是人脑的机能理解意识是客观存在的反映理解物质第一性,意识第二性,物质决定意识理解意识的能动作用坚持一切从实际出发,实事求是(3)求索真理的历程理解实践的基本含义和特点说明实践是认识的基础理解真理的含义和真理的客观性、具体性、条件性理解认识具有反复性、无限性、上升性,坚持在实践中不断追求真理3.思想方法与创新意识(1)唯物辩证法的联系观了解联系的观点是唯物辩证法的一个总特征理解联系的含义和联系的普遍性、客观性、多样性,坚持用联系的观点看问题说明整体与部分的辩证关系及其指导意义理解系统优化的方法(2)唯物辩证法的发展观了解发展是唯物辩证法的另一个总特征理解发展的实质,坚持用发展的观点看问题理解事物的发展是前进性与曲折性的统一了解量变、质变的含义说明量变与质变的辩证关系及其指导意义(3)唯物辩证法的实质和核心了解矛盾的观点是唯物辩证法的根本观点理解矛盾的含义、矛盾的同一性和斗争性的含义理解矛盾普遍性和特殊性的辩证关系及其指导意义理解主要矛盾和次要矛盾的辩证关系、矛盾的主要方面和次要方面的辩证关系,坚持两点论和重点论相统一的认识方法坚持具体问题具体分析(4)唯物辩证法与创新意识理解辩证否定的含义及实质坚持辩证的否定观,树立创新意识理解创新的社会作用4.认识社会与价值选择(1)社会发展的规律理解社会存在决定社会意识,社会意识具有相对独立性了解物质资料的生产方式是人类社会存在和发展的基础运用生产关系一定要适应生产力状况的规律分析、解决问题运用上层建筑一定要适应经济基础状况的规律分析、解决问题了解人类社会的基本矛盾理解社会主义上的基本矛盾的特点理解我国社会主义改革的性质和根本目的(2)社会历史的主体理解人民群众是历史的创造者坚持群众观点和群众路线(3)人生价值及其实现了解哲学意义上的价值理解人的价值的内涵与评价了解价值观的含义理解价值观的导向作用理解价值判断和价值选择的客观依据了解价值判断和价值选择的社会历史性与阶级性理解价值冲突与评价标准坚持在劳动和奉献中、在个人与社会的统一中、在砥砺自我中实现人生价值(五)时事政治年度见国内外重大时事(XX年4月至200年3月)中国共产党和中国政府在现阶段的基本路线和重大方针政策选考部分选考部分为经济这常识或国家和国际组织常识(一)经济学常识1、古典经济学巨匠的理论遗产(1)亚当•斯密与看不见的手了解斯密劳动价值论和收入分配理论理解斯密关于市场作用与自由放任的基本观点了解斯密的自由贸易与绝对成本学说(2)大卫・李嘉图与比较成本理论了解李嘉图的劳动价值论、收入分配理论理解李嘉图的自由贸易与比较成本学说2、马克思主义经济学的伟大贡献(1)马克思与《资本论》了解马克思主义政治经济学创立的重大意义(2)马克思的劳动价值理论了解劳动二重性学说的含义及意义理解马克思创立劳动价值论的重要意义(3)马克思的剩余价值理论理解剩余价值的含义、资本家获得剩余价值的主要方法理解剩余价值理论的意义(4)马克思的经济危机理论了解资本主义经济危机的实质和根源3、走进现代市场经济(1)罗斯福新政理解罗斯福新政的主要内容了解罗斯福新政的影响(2)凯恩斯革命理解凯恩斯革命的主要内容理解凯恩斯革命的影响和作用了解新自由主义的基本主张(3)西方现代市场经济主要模式理解三种典型市场经济模式的主要特点及成因理解西方现代市场经济模式的基本点4、社会主义经济理论的探索(1)列宁对社会主义经济理论的探索了解列宁提出的“新经济政策”的主要内容和重要意义理解列宁关于市场与社会主义关系的主要观点(2)毛泽东对社会主义商品经济的认识理解《论十大关系》关于我国经济建设的主要观点了解毛泽东对社会主义市场经济的认识5、中国特色社会主义市场经济的探索(1)邓小平对社会主义市场经济理论的创新及其意义了解我国社会主义建设初期计划经济体制建立的背景、基本特点和作用了解高度集中的计划经济体制的弊端和影响了解从计划经济到市场经济的认识过程说明邓小平关于社会主义市场经济理论的重要创新及其意义(2)建立、完善我国社会主义市场经济体制了解我国社会主义市场经济体制的基本框架理解进一步完善社会主义市场经济体制的必要性理解当前完善社会主义市场经济体制的主要任务(二)国家和国际组织常识1、各具特色的国家和国际组织(1)国家的本质了解国家的性质理解民主与专政的关系说明国体与政体的关系(2)现代国家的管理形式了解代议制的含义了解民主共和制和君主立宪制、议会制和总统制(3)现代国家的结构形式了解单一制和联邦制的区别懂得必须维护国家统一(4)国际组织了解国际组织的特征和分类理解国际组织的作用2、君主立宪制和民主共和制(1)英国的君主立宪制了解英国君主立宪制的结构和特点理解英国君主立宪制的实质(2)法国的半总统制半议会制了解法国的国家机构了解法国政体的运行及特点(3)英法政治体制的异同比较英法两国政体的异同了解英法两国政体不同的原因3、联邦制、两党制、三权分立制(1)美国的联邦制了解美国联邦制的特点和利弊(2)美国的两党制了解美国政党的特征理解美国两党制的实质(3)美国的三权分立制理解美国的三权分立与权力制衡分析美国三权分立制的利弊与实质(4)美国的利益集团了解美国利益集团的活动方式及其政治作用4、我国的人民代表大会制度(1)人民代表大会制度的形式与确立了解人民代表大会制度的确立是人民的选择、历史的必然(2)按照民主集中制建立的新型政体理解人民代表大会制度是我国的根本政治制度说明民主集中制是我国人民代表大会制度的组织和活动原则(3)人民代表大会制度的优越性说明必须坚持人民代表大会制度,绝不照搬西方的政治体制模式(4)坚持和完善人民代表大会制度理解坚持和完善人民代表大会制度必须坚持和完善中国共产党的领导理解坚持和完善人民代表大会制度必须实施依法治国的基本方略了解坚持完善人民代表大会制度必须加强人大自身建设5、日益重要的国际组织(1)联合国了解联合国的主要机构、联合国的作用理解中国在联合国中的地位和作用(2)世界贸易组织了解世界贸易组织的宗旨和主要机构理解中国加入世界贸易组织的意义(3)亚太经济合作组织了解亚太经济合作组织的宗旨和作用了解中国在亚太经济合作组织中的地位和作用(4)欧盟了解欧盟的宗旨和作用了解中国与欧盟的合作与交往三、考试形式及试卷结构(一)考试形式考试形式为闭卷,笔试。
江苏职教高考招生专刊目录

江苏职教高考招生专刊目录
江苏招生考试计划专刊目录:
关于招生计划中有关问题的说明。
考生填报志愿须知。
高考志愿填报流程。
平行院校志愿投档说明2020年招生计划简况。
2020年普通高等学校在江苏招生计划。
文科类:
一、提前录取本科院校。
二、第一批录取本科院校。
三、第二批录取本科院校。
理科类:
一、提前录取本科院校。
二、第一批录取本科院校。
三、第二批录取本科院校。
体育类:
艺术类:
2020年江苏省属普通高等学校名单。
2020年在江苏省招生的普通高等学校联系方式。
江苏省2020年军事、公安、司法院校面试、体检或体能测试安排表。
普通高等学校招生体检工作指导意见。
江苏省乡村教师定向培养计划填报问答。
院校介绍:
高等教育自学考试。
2020年江苏省成人高校招生简介。
社会证书考试。
从江苏省外调高考招生指标事件看教育公平问题

从江苏省外调高考招生指标事件看教育公平问题1. 引言1.1 事件概述江苏省外调高考招生指标事件是指近日江苏省教育厅发布通知,决定调高江苏省高考录取省外考生的指标比例,引发广泛关注和争议。
根据通知,江苏省将在今年高考中增加省外考生的招生比例,意味着江苏省内考生的竞争将进一步加剧,特别是在疫情影响下,教育资源分配已经不平衡的情况下,此举引发了社会各界的质疑和批评。
这一事件再次凸显了教育公平的重要性。
教育公平是现代社会不可或缺的基本价值,它体现了社会公正和社会进步的内在要求。
教育公平不仅仅是指每个人都有平等的接受教育的机会,更重要的是要保障每个人获取教育资源的均等权利,避免教育资源的不均衡导致社会的分化和不公平现象。
江苏省外调高考招生指标事件的发生,必将引发关于教育公平的深刻讨论和思考。
1.2 教育公平重要性教育公平是一个社会进步的基础,是实现国家繁荣富强的重要保障,也是每个国家构建公平正义社会的必经之路。
教育公平的重要性不仅在于为每个人提供平等的学习机会和发展空间,更在于激发每个人的潜能,促进社会的公平发展。
在一个教育不公平的社会,优质教育资源往往集中在少数人手中,导致社会阶层分化加剧,贫富差距拉大,最终影响整个社会的稳定和可持续发展。
保障教育公平不仅是每个国家的责任,也是每个社会成员应尽的义务。
教育公平的实现不仅仅是一项政府政策,更是全社会共同努力的结果。
只有每个人都能享有平等的教育资源和机会,才能实现个体的价值实现和社会的发展进步。
关注教育公平问题,促进教育公平的实现已成为全球共识。
在这个背景下,各国政府、教育机构、社会组织和个人都要积极参与,共同努力,为建设一个更加公平、更加和谐的社会而努力。
教育公平不仅仅关乎每个人的个人发展,更关乎整个社会的进步和未来。
2. 正文2.1 政策背景江苏省外调高考招生指标事件的政策背景可以追溯到江苏省在2018年开始实施的高校招生改革。
江苏省当时推出了新的高考政策,试图减少高考填报志愿的优势,避免出现填报志愿“死板”等现象。
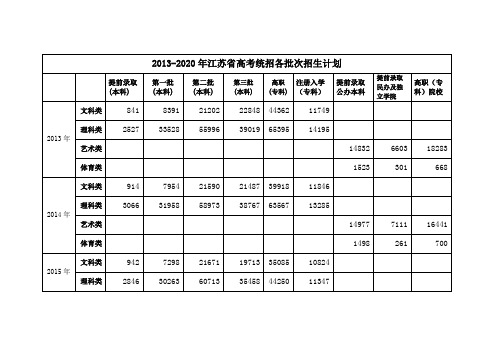
2013—2020年江苏省高考统招各批次招生计划
69171
20165
13450
艺术类
21950
9678
体育类
1970
794
2019年
文科类
2231
14405
29628
15656
10332
理科类
4998
58220
69372
23708
14059
艺术类
21945
91ቤተ መጻሕፍቲ ባይዱ2
体育类
1996
665
2020年
文科类
2282
15731
28019
15354
21671
19713
35085
10824
理科类
2846
30263
60713
35458
44250
11347
艺术类
14995
7763
12776
体育类
1482
284
578
2016年
文科类
1795
7424
21699
19742
35667
13578
理科类
3889
31772
60824
35510
38521
14147
2013-2020年江苏省高考统招各批次招生计划
提前录取
(本科)
第一批
(本科)
第二批
(本科)
第三批
(本科)
高职
(专科)
注册入学
(专科)
提前录取
公办本科
提前录取民办及独立学院
高职(专科)院校
2013年
文科类
841
8391
21202
2020年高考真题:数学(江苏卷)【含答案及解析】

2020年普通⾼等学校招⽣全国统⼀考试(江苏卷)数学Ⅰ柱体的体积V Sh =,其中S 是柱体的底面积,h 是柱体的高.一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置.......上..1.已知集合{1,0,1,2},{0,2,3}A B =-=,则A B =I _____.2.已知i 是虚数单位,则复数(1i)(2i)z =+-的实部是_____.3.已知一组数据4,2,3,5,6a a -的平均数为4,则a 的值是_____.4.将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是_____.5.如图是一个算法流程图,若输出y 的值为2-,则输入x 的值是_____.6.在平面直角坐标系xOy 中,若双曲线22x a ﹣25y =1(a >0)的一条渐近线方程为y=2x ,则该双曲线的离心率是____.7.已知y =f (x )是奇函数,当x ≥0时,()23f x x=,则f (-8)的值是____.8.已知2sin ()4p a + =23,则sin 2a 的值是____.9.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm ,高为2 cm ,内孔半轻为0.5 cm ,则此六角螺帽毛坯的体积是____cm.10.将函数y =πsin(243x ﹢的图象向右平移π6个单位长度,则平移后的图象中与y 轴最近的对称轴的方程是____.11.设{a n }是公差为d 的等差数列,{b n }是公比为q 的等比数列.已知数列{a n +b n }的前n 项和221()n n S n n n +=-+-ÎN ,则d +q 的值是_______.12.已知22451(,)x y y x y R +=Î,则22x y +的最小值是_______.13.在△ABC 中,43=90AB AC BAC ==°,,∠,D 在边BC 上,延长AD 到P ,使得AP =9,若3()2PA mPB m PC =+-u u u r u u u r u u u r (m 为常数),则CD 的长度是________.14.在平面直角坐标系xOy 中,已知0)2P ,A ,B 是圆C :221()362x y +-=上的两个动点,满足PA PB =,则△P AB 面积的最大值是__________.二、解答题:本大题共6小题,共计90分,请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.15.在三棱柱ABC -A 1B 1C 1中,AB ⊥AC ,B 1C ⊥平面ABC ,E ,F 分别是AC ,B 1C 的中点.(1)求证:EF ∥平面AB 1C 1;(2)求证:平面AB 1C ⊥平面ABB 1.16.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知3,45a c B ===°.(1)求sin C 的值;(2)在边BC 上取一点D ,使得4cos 5ADC Ð=-,求tan DAC Ð的值.17.某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底O 在水平线MN 上、桥AB 与MN 平行,OO ¢为铅垂线(O ¢在AB 上).经测量,左侧曲线AO 上任一点D 到MN 的距离1h (米)与D 到OO ¢的距离a (米)之间满足关系式21140h a =;右侧曲线BO 上任一点F 到MN 的距离2h (米)与F 到OO ¢的距离b (米)之间满足关系式3216800h b b =-+.已知点B 到OO ¢的距离为40米.(1)求桥AB 的长度;(2)计划在谷底两侧建造平行于OO ¢的桥墩CD 和EF ,且CE 为80米,其中C ,E 在AB 上(不包括端点).桥墩EF 每米造价k (万元)、桥墩CD 每米造价32k (万元)(k >0).问O E ¢为多少米时,桥墩CD 与EF 的总造价最低18.在平面直角坐标系xOy 中,已知椭圆22:143x y E +=的左、右焦点分别为F 1,F 2,点A 在椭圆E 上且在第一象限内,AF 2⊥F 1F 2,直线AF 1与椭圆E 相交于另一点B .(1)求△AF 1F 2的周长;(2)在x 轴上任取一点P ,直线AP 与椭圆E 的右准线相交于点Q ,求OP QP ×uu u r uu u r的最小值;(3)设点M 在椭圆E 上,记△OAB 与△MAB 的面积分别为S 1,S 2,若S 2=3S 1,求点M 的坐标.19.已知关于x 的函数(),()y f x y g x ==与()(,)h x kx b k b =+ÎR 在区间D 上恒有()()()f x h x g x ³³.(1)若()()222 2()f x x x g x x x D =+=-+=¥-¥+,,,,求h (x )的表达式;(2)若21ln ,()()()(0)x x g k x h kx k D f x x x =-+==-=+¥,,,,求k 的取值范围;(3)若()422242() 2()(48 () 4 3 02 f x x x g x x h x t t x t t t =-=-=--+<,,,[] , D m n =Íéë,求证:n m -£.20.已知数列{}*()În a n N 的首项a 1=1,前n 项和为S n .设λ与k 是常数,若对一切正整数n ,均有11111k k kn n n S S a l ++-=成立,则称此数列为“λ–k ”数列.(1)若等差数列{}n a 是“λ–1”数列,求λ的值;(2)若数列{}n a 是2”数列,且a n >0,求数列{}n a 的通项公式;(3)对于给定的λ,是否存在三个不同的数列{}n a 为“λ–3”数列,且a n ≥0?若存在,求λ的取值范围;若不存在,说明理由,数学Ⅱ(附加题)【选做题】本题包括A 、B 、C 三小题,请选定其中两小题,并在相应的答题区域内作答......................若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A .[选修4-2:矩阵与变换]21.平面上点(2,1)A -在矩阵11a b éù=êú-ëûM 对应的变换作用下得到点(3,4)B -.(1)求实数a ,b 的值;(2)求矩阵M 的逆矩阵1M -.B .[选修4-4:坐标系与参数方程]22.在极坐标系中,已知点1π(,)3A r 在直线:cos 2l r q =上,点2π(,6B r 在圆:4sinC r q =上(其中0r ³,02q p £<).(1)求1r ,2r 的值(2)求出直线l 与圆C 的公共点的极坐标.C .[选修4-5:不等式选讲]23.设x ÎR ,解不等式2|1|||4x x ++£.【必做题】第24题、第25题,每题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.24.在三棱锥A —BCD 中,已知CB =CD BD =2,O 为BD 的中点,AO ⊥平面BCD ,AO =2,E 为AC 的中点.(1)求直线AB 与DE 所成角的余弦值;(2)若点F 在BC 上,满足BF =14BC ,设二面角F —DE —C 的大小为θ,求sin θ的值.25.甲口袋中装有2个黑球和1个白球,乙口袋中装有3个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋,重复n 次这样的操作,记甲口袋中黑球个数为X n ,恰有2个黑球的概率为p n ,恰有1个黑球的概率为q n .(1)求p 1·q 1和p 2·q 2;(2)求2p n +q n 与2p n-1+q n-1的递推关系式和X n 的数学期望E (X n )(用n 表示).答案及解析一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置.......上..1.已知集合{1,0,1,2},{0,2,3}A B =-=,则A B =I _____.【答案】{}0,2【解析】【分析】根据集合的交集即可计算.【详解】∵{}1,0,1,2A =-,{}0,2,3B =∴{}0,2A B =I 故答案为:{}0,2.【点睛】本题考查了交集及其运算,是基础题型.2.已知i 是虚数单位,则复数(1i)(2i)z =+-的实部是_____.【答案】3【解析】【分析】根据复数的运算法则,化简即可求得实部的值.【详解】∵复数()()12z i i =+-∴2223z i i i i=-+-=+∴复数的实部为3.故答案为:3.【点睛】本题考查复数的基本概念,是基础题.3.已知一组数据4,2,3,5,6a a -的平均数为4,则a 的值是_____.【答案】2【解析】【分析】根据平均数的公式进行求解即可.【详解】∵数据4,2,3,5,6a a -的平均数为4∴4235620a a ++-++=,即2a =.故答案为:2.【点睛】本题主要考查平均数的计算和应用,比较基础.4.将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是_____.【答案】19【解析】【分析】分别求出基本事件总数,点数和为5的种数,再根据概率公式解答即可.【详解】根据题意可得基本事件数总为6636´=个.点数和为5的基本事件有()1,4,()4,1,()2,3,()3,2共4个.∴出现向上的点数和为5的概率为41369P ==.故答案为:19.【点睛】本题考查概率的求法,考查古典概型、列举法等基础知识,考查运算求解能力,是基础题.5.如图是一个算法流程图,若输出y 的值为2-,则输入x 的值是_____.【答案】3-【解析】【分析】根据指数函数的性质,判断出1y x =+,由此求得x 的值.【详解】由于20x >,所以12y x =+=-,解得3x =-.故答案为:3-【点睛】本小题主要考查根据程序框图输出结果求输入值,考查指数函数的性质,属于基础题.6.在平面直角坐标系xOy 中,若双曲线22x a ﹣25y =1(a >0)的一条渐近线方程为y=2x ,则该双曲线的离心率是____.【答案】32【解析】【分析】根据渐近线方程求得a ,由此求得c ,进而求得双曲线的离心率.【详解】双曲线22215x y a -=,故b =由于双曲线的一条渐近线方程为2y x =,即22b a a =Þ=,所以3c ===,所以双曲线的离心率为32c a =.故答案为:32【点睛】本小题主要考查双曲线的渐近线,考查双曲线离心率的求法,属于基础题.7.已知y =f (x )是奇函数,当x ≥0时,()23f x x=,则f (-8)的值是____.【答案】4-【解析】【分析】先求(8)f ,再根据奇函数求(8)f -【详解】23(8)84f ==,因为()f x 为奇函数,所以(8)(8)4f f -=-=-故答案为:4-【点睛】本题考查根据奇函数性质求函数值,考查基本分析求解能力,属基础题.8.已知2sin ()4p a + =23,则sin 2a 的值是____.【答案】13【解析】【分析】直接按照两角和正弦公式展开,再平方即得结果.【详解】221sin ()sin )(1sin 2)4222p a a a a +=+=+Q 121(1sin 2)sin 2233a a \+=\=故答案为:13【点睛】本题考查两角和正弦公式、二倍角正弦公式,考查基本分析求解能力,属基础题.9.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm ,高为2 cm ,内孔半轻为0.5 cm ,则此六角螺帽毛坯的体积是____cm.【答案】2p -【解析】【分析】先求正六棱柱体积,再求圆柱体积,相减得结果.【详解】正六棱柱体积为2624´´´圆柱体积为21()222p p ×=所求几何体体积为2p-故答案为:2p-【点睛】本题考查正六棱柱体积、圆柱体积,考查基本分析求解能力,属基础题.10.将函数y =πsin(243x ﹢的图象向右平移π6个单位长度,则平移后的图象中与y 轴最近的对称轴的方程是____.【答案】524x p =-【解析】【分析】先根据图象变换得解析式,再求对称轴方程,最后确定结果.【详解】3sin[2()]3sin(26412y x x p p p =-+=-72()()122242k x k k Z x k Z p p p p p -=+Î\=+Î当1k =-时524x p =-故答案为:524x p =-【点睛】本题考查三角函数图象变换、正弦函数对称轴,考查基本分析求解能力,属基础题.11.设{a n }是公差为d 的等差数列,{b n }是公比为q 的等比数列.已知数列{a n +b n }的前n 项和221()n n S n n n +=-+-ÎN ,则d +q 的值是_______.【答案】4【解析】【分析】结合等差数列和等比数列前n 项和公式的特点,分别求得{}{},n n a b 的公差和公比,由此求得d q +.【详解】设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q ,根据题意1q ¹.等差数列{}n a 的前n 项和公式为()2111222n n n d d P na d n a n -æö=+=+-ç÷èø,等比数列{}n b 的前n 项和公式为()1111111n n n b q b b Q q q q q-==-+---,依题意n n n S P Q =+,即22111212211n n b b d d n n n a n q q q æö-+-=+--+ç÷--èø,通过对比系数可知111212211d d a q b qì=ïïï-=-ïíï=ïï=-ï-îÞ112021d a q b =ìï=ïí=ïï=î,故4d q +=.故答案为:4【点睛】本小题主要考查等差数列和等比数列的前n 项和公式,属于中档题.12.已知22451(,)x y y x y R +=Î,则22x y +的最小值是_______.【答案】45【解析】【分析】根据题设条件可得42215y x y -=,可得4222222114+555y y x y y y y -+=+=,利用基本不等式即可求解.【详解】∵22451x y y +=∴0y ¹且42215y x y -=∴2245x y +==,当且仅当221455y y =,即2231,102x y ==时取等号.∴22xy +的最小值为45.故答案为:45.【点睛】本题考查了基本不等式在求最值中的应用.利用基本不等式求最值时,一定要正确理解和掌握“一正,二定,三相等”的内涵:一正是,首先要判断参数是否为正;二定是,其次要看和或积是否为定值(和定积最大,积定和最小);三相等是,最后一定要验证等号能否成立(主要注意两点,一是相等时参数否在定义域内,二是多次用³或£时等号能否同时成立).13.在△ABC 中,43=90AB AC BAC ==°,,∠,D 在边BC 上,延长AD 到P ,使得AP =9,若3()2PA mPB m PC =+-u u u r u u u r u u u r (m 为常数),则CD 的长度是________.【答案】185【解析】【分析】根据题设条件可设()0PA PD l l =>u u u r u u u r ,结合32PA mPB m PC æö=+-ç÷èøu u u ru u u r u u u r 与,,B D C 三点共线,可求得l ,再根据勾股定理求出BC ,然后根据余弦定理即可求解.【详解】∵,,A D P 三点共线,∴可设()0PA PD l l =>u u u r u u u r ,∵32PA mPB m PC æö=+-ç÷èøu u u r u u u r u u u r ,∴32PD mPB m PC l æö=+-ç÷èøu u u r u u u r u u u r ,即32m m PD PB PC l læö-ç÷èø=+u u u r u u u r u u u r ,若0m ¹且32m ¹,则,,B D C 三点共线,∴321m m l læö-ç÷èø+=,即32l =,∵9AP =,∴3AD =,∵4AB =,3AC =,90BAC Ð=°,∴5BC =,设CD x =,CDA q Ð=,则5BD x =-,BDA p q Ð=-.∴根据余弦定理可得222cos 26AD CD AC xAD CD q +-==×,()()()222257cos 265x AD BD AB AD BD x p q --+--==×-,∵()cos cos 0q p q +-=,∴()()2570665x x x --+=-,解得185x =,∴CD 的长度为185.当0m =时,32PA PC =u u u ru u ur ,,C D 重合,此时CD 的长度为0,当32m =时,32PA PB =u u u r u u u r ,,B D 重合,此时12PA =,不合题意,舍去.故答案为:0或185.【点睛】本题考查了平面向量知识的应用、余弦定理的应用以及求解运算能力,解答本题的关键是设出()0PA PD l l =>u u u r u u u r.14.在平面直角坐标系xOy 中,已知0)2P ,A ,B 是圆C :221()362x y +-=上的两个动点,满足PA PB =,则△P AB 面积的最大值是__________.【答案】【解析】【分析】根据条件得PC AB ^,再用圆心到直线距离表示三角形PAB 面积,最后利用导数求最大值.【详解】PA PB PC AB=\^Q设圆心C 到直线AB 距离为d ,则||1AB PC ==所以11)2PAB S d £×+=V 令222(36)(1)(06)2(1)(236)04y d d d y d d d d ¢=-+£<\=+--+=\=(负值舍去)当04d £<时,0y ¢>;当46d £<时,0y ¢£,因此当4d =时,y 取最大值,即PAB S V 取最大值为故答案为:【点睛】本题考查垂径定理、利用导数求最值,考查综合分析求解能力,属中档题.二、解答题:本大题共6小题,共计90分,请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.15.在三棱柱ABC -A 1B 1C 1中,AB ⊥AC ,B 1C ⊥平面ABC ,E ,F 分别是AC ,B 1C 的中点.(1)求证:EF ∥平面AB 1C 1;(2)求证:平面AB 1C ⊥平面ABB 1.【答案】(1)证明详见解析;(2)证明详见解析.【解析】【分析】(1)通过证明1//EF AB ,来证得//EF 平面11AB C .(2)通过证明AB ^平面1AB C ,来证得平面1AB C ^平面1ABB .【详解】(1)由于,E F 分别是1,AC B C 的中点,所以1//EF AB .由于EF Ì/平面11AB C ,1AB Ì平面11AB C ,所以//EF 平面11AB C .(2)由于1B C ^平面ABC ,AB Ì平面ABC ,所以1B C AB ^.由于1,AB AC AC B C C ^Ç=,所以AB ^平面1AB C ,由于AB Ì平面1ABB ,所以平面1AB C ^平面1ABB .【点睛】本小题主要考查线面平行的证明,考查面面垂直的证明,属于中档题.16.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知3,45a c B ===°.(1)求sin C 的值;(2)在边BC 上取一点D ,使得4cos 5ADC Ð=-,求tan DAC Ð的值.【答案】(1)sin 5C =;(2)2tan 11DAC Ð=.【解析】【分析】(1)利用余弦定理求得b ,利用正弦定理求得sin C .(2)根据cos ADC Ð的值,求得sin ADC Ð的值,由(1)求得cos C 的值,从而求得sin ,cos DAC DAC ÐÐ的值,进而求得tan DAC Ð的值.【详解】(1)由余弦定理得2222cos 922352b ac ac B =+-=+-´=,所以b =.由正弦定理得sin sin sin sin 5c b c B C C B b =Þ==.(2)由于4cos 5ADC Ð=-,,2ADC p p æöÐÎç÷èø,所以3sin 5ADC Ð==.由于,2ADC p p æöÐÎç÷èø,所以0,2C p æöÎç÷èø,所以cos 5C ==所以()sin sin DAC DAC p Ð=-Ð()sin ADC C =Ð+Ðsin cos cos sin ADC C ADC C =Ð×+Ð×34555525æö=´+-´=ç÷èø.由于0,2DAC p æöÐÎç÷èø,所以cos 25DAC Ð==.所以sin 2tan cos 11DAC DAC DAC ÐÐ==Ð.【点睛】本小题主要考查正弦定理、余弦定理解三角形,考查三角恒等变换,属于中档题.17.某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底O 在水平线MN 上、桥AB 与MN 平行,OO ¢为铅垂线(O ¢在AB 上).经测量,左侧曲线AO 上任一点D 到MN 的距离1h (米)与D 到OO ¢的距离a (米)之间满足关系式21140h a =;右侧曲线BO 上任一点F 到MN 的距离2h (米)与F 到OO ¢的距离b (米)之间满足关系式3216800h b b =-+.已知点B 到OO ¢的距离为40米.(1)求桥AB 的长度;(2)计划在谷底两侧建造平行于OO ¢的桥墩CD 和EF ,且CE 为80米,其中C ,E 在AB 上(不包括端点).桥墩EF 每米造价k (万元)、桥墩CD 每米造价32k (万元)(k >0).问O E ¢为多少米时,桥墩CD 与EF 的总造价最低?【答案】(1)120米(2)20O E ¢=米【解析】【分析】(1)根据A,B 高度一致列方程求得结果;(2)根据题意列总造价的函数关系式,利用导数求最值,即得结果.【详解】(1)由题意得2311||40640||8040800O A O A ¢¢=-´+´\=||||||8040120AB O A O B ¢¢\=+=+=米(2)设总造价为()f x 万元,21||8016040O O ¢=´=,设||O E x ¢=,32131()(1606)[160(80)],(040)800240f x k x x k x x =+-+--<<3221336()(160),()()0208008080080f x k x x f x k x x x ¢\=+-\=-=\=(0舍去)当020x <<时,()0f x ¢<;当2040x <<时,()0f x ¢>,因此当20x =时,()f x 取最小值,答:当20O E ¢=米时,桥墩CD 与EF 的总造价最低.【点睛】本题考查实际成本问题、利用导数求最值,考查基本分析求解能力,属中档题.18.在平面直角坐标系xOy 中,已知椭圆22:143x y E +=的左、右焦点分别为F 1,F 2,点A 在椭圆E 上且在第一象限内,AF 2⊥F 1F 2,直线AF 1与椭圆E 相交于另一点B .(1)求△AF 1F 2的周长;(2)在x 轴上任取一点P ,直线AP 与椭圆E 的右准线相交于点Q ,求OP QP ×uu u r uu u r的最小值;(3)设点M 在椭圆E 上,记△OAB 与△MAB 的面积分别为S 1,S 2,若S 2=3S 1,求点M 的坐标.【答案】(1)6;(2)-4;(3)()2,0M 或212,77æö--ç÷èø.【解析】【分析】(1)根据椭圆定义可得124AF AF +=,从而可求出12AF F △的周长;(2)设()0,0P x ,根据点A 在椭圆E 上,且在第一象限,212AF F F ^,求出31,2A æöç÷èø,根据准线方程得Q 点坐标,再根据向量坐标公式,结合二次函数性质即可出最小值;(3)设出设()11,M x y ,点M 到直线AB 的距离为d ,由点O 到直线AB 的距离与213S S =,可推出95d =,根据点到直线的距离公式,以及()11,M x y 满足椭圆方程,解方程组即可求得坐标.【详解】(1)∵椭圆E 的方程为22143x y +=∴()11,0F -,()21,0F 由椭圆定义可得:124AF AF +=.∴12AF F △的周长为426+=(2)设()0,0P x ,根据题意可得01x ¹.∵点A 在椭圆E 上,且在第一象限,212AF F F ^∴31,2A æöç÷èø∵准线方程为4x =∴()4,QQ y ∴()()()()200000,04,4244Q OP QP x x y x x x ×=×--=-=--³-u u u r u u u r ,当且仅当02x =时取等号.∴OP QP ×uu u r uu u r的最小值为4-.(3)设()11,M x y ,点M 到直线AB 的距离为d .∵31,2A æöç÷èø,()11,0F -∴直线1AF 的方程为()314y x =+∵点O 到直线AB 的距离为35,213S S =∴2113133252S S AB AB d ==´´´=×∴95d =∴113439x y -+=①∵2211143x y +=②∴联立①②解得1120x y =ìí=î,1127127x y ì=-ïïíï=-ïî.∴()2,0M 或212,77æö--ç÷èø.【点睛】本题考查了椭圆的定义,直线与椭圆相交问题、点到直线距离公式的运用,熟悉运用公式以及根据213S S =推出95d =是解答本题的关键.19.已知关于x 的函数(),()y f x y g x ==与()(,)h x kx b k b =+ÎR 在区间D 上恒有()()()f x h x g x ³³.(1)若()()222 2()f x x x g x x x D =+=-+=¥-¥+,,,,求h (x )的表达式;(2)若21ln ,()()()(0)x x g k x h kx k D f x x x =-+==-=+¥,,,,求k 的取值范围;(3)若()422242() 2()(48 () 4 3 02 f x x x g x x h x t t x t t t =-=-=--+<,,,[] , D m n =Íéë,求证:n m -£.【答案】(1)()2h x x =;(2)[]0,3k Î;(3)证明详见解析【解析】【分析】(1)求得()f x 与()g x 的公共点,并求得过该点的公切线方程,由此求得()h x 的表达式.(2)先由()()0h x g x -³,求得k 的一个取值范围,再由()()0f x h x -³,求得k 的另一个取值范围,从而求得k 的取值范围.(3)先由()()f x h x ³,求得t 的取值范围,由方程()()0g x h x -=的两个根,求得n m -的表达式,利用导数证得不等式成立.【详解】(1)由题设有2222x x kx b x x -+£+£+对任意的x ÎR 恒成立.令0x =,则00b ££,所以0b =.因此22kx x x £+即()220x k x +-³对任意的x ÎR 恒成立,所以()220k D =-£,因此2k =.故()2h x x =.(2)令()()()()()1ln 0F x h x g x k x x x =-=-->,()01F =.又()1x F x k x-¢=×.若k 0<,则()F x 在()0,1上递增,在()1,+?上递减,则()()10F x F £=,即()()0h x g x -£,不符合题意.当0k =时,()()()()()0,F x h x g x h x g x =-==,符合题意.当0k >时,()F x 在()0,1上递减,在()1,+?上递增,则()()10F x F ³=,即()()0h x g x -³,符合题意.综上所述,0k ³.由()()()21f x h x x x kx k -=-+--()()2110x k x k =-+++³当102k x +=<,即1k <-时,()211y x k x k =-+++在()0,+?为增函数,因为()()0010f h k -=+<,故存在()00,x Î+¥,使()()0f x h x -<,不符合题意.当102k x +==,即1k =-时,()()20f x h x x -=³,符合题意.当102k x +=>,即1k >-时,则需()()21410k k D =+-+£,解得13k -<£.综上所述,k 的取值范围是[]0,3k Î.(3)因为()423422243248x x t t x t t x -³--+³-对任意[,][x m n ÎÌ恒成立,()423422432x x t t x t t -³--+对任意[,][x m n ÎÌ恒成立,等价于()222()2320x t xtx t -++-³对任意[,][x m n ÎÌ恒成立.故222320x tx t ++-³对任意[,][x m n ÎÌ恒成立令22()232M x x tx t =++-,当201t <<,2880,11t t D =-+>-<-<,此时1n m t -£+<+<,当212t ££,2880t D =-+£,但()234248432x t t x t t -³--+对任意的[,][x m n ÎÌ恒成立.等价于()()()2322443420x t t x t t --++-£对任意的[,][x m n ÎÌ恒成立.()()()2322443420x t t x t t --++-=的两根为12,x x ,则4231212328,4t t x x t t x x --+=-×=,所以12=n m x x --==.令[]2,1,2t l l =Î,则n m -=.构造函数()[]()325381,2P l l l l l =-++Î,()()()23103331P l l l l l ¢=-+=--,所以[]1,2l Î时,()0P l ¢<,()P l 递减,()()max 17P P l ==.所以()max n m -=n m -£.【点睛】本小题主要考查利用的导数求切线方程,考查利用导数研究不等式恒成立问题,考查利用导数证明不等式,考查分类讨论的数学思想方法,属于难题.20.已知数列{}*()În a n N 的首项a 1=1,前n 项和为S n .设λ与k 是常数,若对一切正整数n ,均有11111k k kn n n S S a l ++-=成立,则称此数列为“λ–k ”数列.(1)若等差数列{}n a 是“λ–1”数列,求λ的值;(2)若数列{}n a 是2”数列,且a n >0,求数列{}n a 的通项公式;(3)对于给定的λ,是否存在三个不同的数列{}n a 为“λ–3”数列,且a n ≥0?若存在,求λ的取值范围;若不存在,说明理由,【答案】(1)1(2)21,134,2n n n a n -=ì=í׳î(3)01l <<【解析】【分析】(1)根据定义得+11n n n S S a l +-=,再根据和项与通项关系化简得11n n a a l ++=,最后根据数列不为零数列得结果;(2)根据定义得111222+1+1()3n n n n S S S S -=-,根据平方差公式化简得+1=4n n S S ,求得n S ,即得n a ;(3)根据定义得111333+11n n n SS a l +-=,利用立方差公式化简得两个方程,再根据方程解的个数确定参数满足的条件,解得结果【详解】(1)+111111101n n n n n n S S a a a a a l l l ++++-=\==\º\=/Q (2)11221100n n n n n a S S SS ++>\>\->Q111222+1+1()3n nn n S S S S -=-Q 1111112222222+1+1+11()()()3n n n n n n S S S S S S \-=-+1111111222222+1+1+1+11()=2=443n n nn n n n n n n S S S S S S S S S -\-=+\\\=111S a ==Q ,14n n S -=1224434,2n n n n a n ---\=-=׳21,134,2n n n a n -=ì\=í׳î(3)假设存在三个不同的数列{}n a 为"3"l -数列.111113333333+11+1+1()()n n n n n n n S S a S S S S l l +-=\-=-1133+1n n S S \=或11221123333333+1+1+1()()n n n n n n S S S S S S l -=+++1n n S S \=或22113333333+1+1(1)(1)(2)0n n n n SS S S l l l -+-++=∵对于给定的l ,存在三个不同的数列{}n a 为"3"l -数列,且0n a ³1,10,2n n a n =ì\=í³î或()22113333333+1+1(1)(1)(2)01n n n n S S S S l l l l -+-++=¹有两个不等的正根.()22113333333+1+1(1)(1)(2)01n n n n S S S S l l l l -+-++=¹可转化为()2133333+1+12133(1)(2)(1)01n n nnS S S S l l l l -++-+=¹,不妨设()1310n n S x x S +æö=>ç÷èø,则()3233(1)(2)(1)01x x l l l l -+++-=¹有两个不等正根,设()()3233(1)(2)(1)01f x x x l l l l =-+++-=¹.①当1l <时,32323(2)4(1)004l l l D =+-->Þ<<,即01l <<,此时()3010f l =-<,33(2)02(1)x l l +=->-对,满足题意.②当1l >时,32323(2)4(1)004l l l D =+-->Þ<<,即1l <<()3010f l =->,33(2)02(1)x l l +=-<-对,此情况有两个不等负根,不满足题意舍去.综上,01l <<【点睛】本题考查数列新定义、由和项求通项、一元二次方程实根分步,考查综合分析求解能力,属难题.数学Ⅱ(附加题)【选做题】本题包括A 、B 、C 三小题,请选定其中两小题,并在相应的答题区域内作答......................若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤.A .[选修4-2:矩阵与变换]21.平面上点(2,1)A -在矩阵11a b éù=êú-ëûM 对应的变换作用下得到点(3,4)B -.(1)求实数a ,b 的值;(2)求矩阵M 的逆矩阵1M -.【答案】(1)22a b =ìí=î;(2)121551255M -éù-êú=êúêúêúëû.【解析】【分析】(1)根据变换写出具体的矩阵关系式,然后进行矩阵的计算可得出实数,a b 的值;(2)设出逆矩阵,由定义得到方程,即可求解.【详解】(1)∵平面上点()2,1A -在矩阵 11a M b éù=êú-ëû对应的变换作用下得到点()3,4B -∴ 1 2 31 14a b éùéùéù=êúêúêú---ëûëûëû∴21324a b -=ìí--=-î,解得22a b =ìí=î(2)设1m n Mc d -éù=êúëû,则12 2 1 0=2 20 1m c n d MM m c n d -++éùéù=êúêú-+-+ëûëû∴21202021m c n d m c n d +=ìï+=ïí-+=ïï-+=î,解得25151525m n c d ì=ïïï=-ïíï=ïïï=î∴121551255M -éù-êú=êúêúêúëû【点睛】本题考查矩阵变换的应用,考查逆矩阵的求法,解题时要认真审题,属于基础题.B .[选修4-4:坐标系与参数方程]22.在极坐标系中,已知点1π(,)3A r 在直线:cos 2l r q =上,点2π(,6B r 在圆:4sinC r q =上(其中0r ³,02q p £<).(1)求1r ,2r 的值(2)求出直线l 与圆C 的公共点的极坐标.【答案】(1)1242r r ==,(2))4p【解析】【分析】(1)将A,B 点坐标代入即得结果;(2)联立直线与圆极坐标方程,解得结果.【详解】(1)以极点为原点,极轴为x 轴的正半轴,建立平面直角坐标系,11cos2,43pr r =\=Q ,因为点B 为直线6p q =上,故其直角坐标方程为3y x =,又4sin r q =对应的圆的直角坐标方程为:2240x y y +-=,由22340y x x y y ì=ïíï+-=î解得00x y ==ìíî或1x y ì=ïí=ïî对应的点为())0,0,,故对应的极径为20r =或22r =.(2)cos 2,4sin ,4sin cos 2,sin 21r q r q q q q ==\=\=Q ,5[0,2),,44p p q p q Î\=Q ,当4pq =时r =当54p q =时0r =-<,舍;即所求交点坐标为当4p 【点睛】本题考查极坐标方程及其交点,考查基本分析求解能力,属基础题.C .[选修4-5:不等式选讲]23.设x ÎR ,解不等式2|1|||4x x ++£.【答案】22,3éù-êúëû【解析】【分析】根据绝对值定义化为三个方程组,解得结果【详解】1224x x x <-ìí---£îQ 或10224x x x -££ìí+-£î或0224x x x >ìí++£î21x \-£<-或10x -≤≤或203x <£所以解集为22,3éù-êúëû【点睛】本题考查分类讨论解含绝对值不等式,考查基本分析求解能力,属基础题.【必做题】第24题、第25题,每题10分,共计20分.请在答题卡指....定区域...内作答,解答时应写出文字说明、证明过程或演算步骤.24.在三棱锥A —BCD 中,已知CB =CD BD =2,O 为BD 的中点,AO ⊥平面BCD ,AO =2,E 为AC 的中点.(1)求直线AB 与DE 所成角的余弦值;(2)若点F 在BC 上,满足BF =14BC ,设二面角F —DE —C 的大小为θ,求sin θ的值.【答案】(1)15(2)13【解析】【分析】(1)建立空间直角坐标系,利用向量数量积求直线向量夹角,即得结果;(2)先求两个平面法向量,根据向量数量积求法向量夹角,最后根据二面角与向量夹角关系得结果.【详解】(1)连,CO BC CD BO OD CO BD==\^Q 以,,OB OC OA 为,,x y z 轴建立空间直角坐标系,则(0,0,2),(1,0,0),(0,2,0),(1,0,0)(0,1,1)A B C D E -\(1,0,2),(1,1,1)cos ,15AB DE AB DE \=-=\<>==-uu u r uu u r uu u r uuu r 从而直线AB 与DE所成角的余弦值为15(2)设平面DEC 一个法向量为1(,,),n x y z =u r11200(1,2,0),00x y n DC DC x y z n DE ì+=×=ìï=\íí++=×=ïîîu v u u u vu uu v u v uu u vQ 令112,1(2,1,1)y x z n =\=-=\=-u r设平面DEF 一个法向量为2111(,,),n x y z =u u r 11221117100171(,,0),4244200x y n DF DF DB BF DB BC n DE x y z ìì+=×=ïï=+=+=\íí×=ïîï++=îu u v u u u v u uu v u u u v u u u v u u u v uu u v u uv u u u v Q 令111272,5(2,7,5)y x z n =-\==\=-u ur12cos ,n n \<>==u r u u r因此sin 13q ==【点睛】本题考查利用向量求线线角与二面角,考查基本分析求解能力,属中档题.25.甲口袋中装有2个黑球和1个白球,乙口袋中装有3个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋,重复n 次这样的操作,记甲口袋中黑球个数为X n ,恰有2个黑球的概率为p n ,恰有1个黑球的概率为q n .(1)求p 1·q 1和p 2·q 2;(2)求2p n +q n 与2p n-1+q n-1的递推关系式和X n 的数学期望E (X n )(用n 表示).【答案】(1)112212716,,332727p q p q ====;;(2)()111222+33n n n n p q p q --+=+【解析】【分析】(1)直接根据操作,根据古典概型概率公式可得结果;(2)根据操作,依次求n n p q ,,即得递推关系,构造等比数列求得2n n p q +,最后根据数学期望公式求结果.【详解】(1)11131232,333333p q ´´====´´,211131211227++3333333927p p q ´´=´´=´´=´´,211231122222516+0+3333333927q p q ´´+´=´´+=´´=´´(2)1111131212++333339n n n n n p p q p q ----´´=´´=´´,111112*********+(1)+33333393n n n n n n q p q p q q -----´´+´´=´´+--´=-´´´,因此112122+333n n n n p q p q --+=+,从而11111212(2+),21(2+1)333n n n n n n n n p q p q p q p q ----+=+\+-=-,即1111121(2+1),2133n n n n n n p q p q p q -+-=-\+=+.又n X 的分布列为nX 012P1n np q --n q np 故1()213n n n nE X p q =+=+.【点睛】本题考查古典概型概率、概率中递推关系、构造法求数列通项、数学期望公式,考查综合分析求解能力,属难题.。
江苏省2020年普通高校招生录取办法及考试违规处理办法调查问卷参考答案(艺术类44题)

20201、文科类、理科类平行院校志愿在投档过程中,如投档成绩相同,则按什么分数再次排序?(多选)正确答案为:A C DA、语文、数学两门科目的原始分(含附加分)之和从高分到低分再次排序。
B、语文、数学两门科目的原始分(不含附加分)之和从高分到低分再次排序。
C、语文、数学两门科目的原始分(含附加分)之和仍相同时,文科类考生再依次按语文(不含附加分)、数学、外语分数从高到低进行排序,理科类考生再依次按数学(不含附加分)、语文、外语分数从高到低进行排序。
D、按照排序规则排序后,如仍相同,则将这部分考生按志愿全部投档。
2、考生进入考场时需要进行身份验证,以下说法正确的有哪些?(多选)正确答案为:A B DA、使用金属探测器对考生进行检查后,再进行身份验证。
B、考生须将身份证放在考务通上的指定位置并“刷脸”进行验证身份,“刷脸”时须将面部正对身份识别设备的摄像头。
C、考生在考务通上进行身份证和“刷脸”验证时,暂时不能通过的,不能参加考试。
D、考生在考务通上进行身份证和“刷脸”验证时,暂时不能通过的,可先就座应考,待监考员进一步核验。
3、我省艺术类院校志愿投档的原则主要有以下哪些?(多选)正确答案为:A B C DA、使用音乐类专业省统考成绩录取的院校,分声乐、器乐,按专业总分及不大于招生计划数的105%,按照“满足学业水平测试成绩,专业总分优先,遵循志愿”的平行院校志愿原则投档。
B、使用美术类专业省统考成绩或广播电视编导专业省统考成绩录取的院校,按文化总分与专业总分之和及不大于招生计划数的105%,按照“满足学业水平测试成绩,文化总分与专业总分之和优先,遵循志愿”的平行院校志愿原则投档。
C、对报考部分独立设置的本科艺术院校(含部分艺术类本科专业参照执行的少数高校),文化分、专业分均达到相关招生高校自行划定的录取最低控制分数线的考生,按院校提出的调档比例投档。
D、对报考其他校考院校[部分独立设置的本科艺术院校(含部分艺术类本科专业参照执行的少数高校)],文化分达到省录取最低控制分数线且专业合格的考生,按院校提出的调档比例投档。
2020年江苏省高考数学专项训练-真题解析-专题23 数学归纳法与证明-2020年江苏省高考数学命题规律大揭秘

高考冲刺 提分必备2020年江苏省高考数学专项训练-真题解析专题23 数学归纳法与证明【真题感悟】1. 【2010江苏,23】已知△ABC 的三边长都是有理数. (1)求证cosA 是有理数;(2)求证:对任意正整数n ,cosnA 是有理数.2. 【2013江苏,23】设数列{a n }:1,-2,-2,3,3,3,-4,-4,-4,-4,…,11(1),,(1)k k k k k ----644474448L 个,…,即当1122k k k k n (-)(+)<≤(k ∈N *)时,a n =(-1)k -1k .记S n =a 1+a 2+…+a n (n ∈N *).对于l ∈N *,定义集合P l ={n |S n 是a n 的整数倍,n ∈N *,且1≤n ≤l }. (1)求集合P 11中元素的个数; (2)求集合P 2 000中元素的个数. 3. 【2014江苏,23】已知函数0sin ()(0)xf x x x=>,设()n f x 为1()n f x -的导数,*n N ∈ (1)求122()()222f f πππ+的值;(2)证明:对任意*n N ∈,等式1()()4442n n nf f πππ-+=都成立. 4.【2015江苏,23】(本小题满分10分)已知集合{}3,2,1=X ,{})(,,3,2,1*N n n Y n ∈=Λ,{,),(a b b a b a S n 整除或整除=}n Y b X a ∈∈,,令()f n 表示集合n S 所含元素的个数.(1)写出(6)f 的值;(2)当6n ≥时,写出()f n 的表达式,并用数学归纳法证明.【考纲要求】1. 数学归纳法的原理 (考查要求为了解)2. 数学归纳法的简单应用 (考查要求为理解)【考向分析】1. 江苏高考中,经常考有难度的数学归纳法,利用归纳和类比的方法进行推理是新课标倡导的精神,主要考查学生探索创新能力.2. 数学归纳法既是方法,又是思想,更是能力.不仅需要归纳能力,更需要探究能力、创新能力、构造能力.做一些有难度的数学归纳法试题,有助于培养思维品质,提高分析问题及解决问题的能力.【高考预测】近几年没有考查数学归纳法,高考对数学归纳法考查定位在能力,属难题.【迎考策略】1. 明确数学归纳法的两步证明数学归纳法是一种只适用于与正整数有关的命题的证明方法,它们的表述严格而且规范,两个步骤缺一不可.第一步是递推的基础,第二步是递推的依据,第二步中,归纳假设起着“已知条件”的作用,在n =k +1时一定要运用它,否则就不是数学归纳法.第二步的关键是“一凑假设,二凑结论”. 2. 用数学归纳法证明等式应注意的问题(1)用数学归纳法证明等式问题是常见题型,其关键点在于弄清等式两边的构成规律,等式两边各有多少项,以及初始值0n 的值.(2)由n k =到1n k =+时,除考虑等式两边变化的项外还要充分利用n k =时的式子,即充分利用假设,正确写出归纳证明的步骤,从而使问题得以证明.弄清左端应增加的项,明确等式左端变形目标,掌握恒等式变形常用的方法:乘法公式、因式分解、添拆项、配方等.简言之:两个步骤、一个结论;递推基础不可少,归纳假设要用到,结论写明莫忘掉.[来 3. 数学归纳法证明不等式的注意问题(1)当遇到与正整数n 有关的不等式证明时,应用其他办法不容易证,则可考虑应用数学归纳法. (2)用数学归纳法证明不等式的关键是由n k =成立,推证1n k =+时也成立,证明时用上归纳假设后,可采用分析法、综合法、作差(作商)比较法、放缩法等证明.4. “归纳——猜想——证明”的模式,是不完全归纳法与数学归纳法综合应用的解题模式.其一般思路是:通过观察有限个特例,猜想出一般性的结论,然后用数学归纳法证明.这种方法在解决探索性问题、存在性问题或与正整数有关的命题中有着广泛的应用.其关键是观察、分析、归纳、猜想,探索出一般规律.5. 使用数学归纳法需要注意的三个问题 在使用数学归纳法时还要明确:(1)数学归纳法是一种完全归纳法,其中前两步在推理中的作用是:第一步是递推的基础,第二步是递推的依据,二者缺一不可;(2)在运用数学归纳法时,要注意起点0n ,并非一定取1,也可能取0,2等值,要看清题目; (3)第二步证明的关键是要运用归纳假设,特别要弄清楚由n k =到1n k =+时命题变化的情况. 6. 数学归纳法常用于与正整数有关命题的证明可用数学归纳法.例如根据递推公式写出数列的前几项,通过观察项与项数的关系,猜想出数列的通项公式,再用数学归纳法进行证明,初步形成“观察—归纳—猜想—证明”的思维模式;利用数学归纳法证明不等式时,要注意放缩法的应用,放缩的方向应朝着结论的方向进行,可通过变化分子或分母,通过裂项相消等方法达到证明的目的.【强化演练】1.已知数列{}n a 满足123012323222n n n n nC C C a C +++=++++…*2n n nn C n N ++∈,. (1)求1a , 2a , 3a 的值;(2)猜想数列{}n a 的通项公式,并证明. 2.已知函数,记,当.(1)求证:在上为增函数; (2)对于任意,判断在上的单调性,并证明. 3.(1)用数学归纳法证明:当*n N ∈时,cos cos2cos3cos x x x nx +++⋅⋅⋅+=1sin 12122sin 2n xx ⎛⎫+ ⎪⎝⎭-(x R ∈,且2x k π≠, k Z ∈); (2)求234sin 2sin 3sin 4sin 6666ππππ++++ 20182018sin6π⋅⋅⋅+的值. 4.已知函数()()00,0cx df x a ac bd ax b+=≠-≠+,设()n f x 为()1n f x -的导数, *n N ∈.(1)求()()12,f x f x ;(2)猜想()n f x 的表达式,并证明你的结论.5.已知()()()()()()01111nknnnn k m n n n n n f x C x C x C x k C x n =--++--++--L L ,其中R x ∈,*N n ∈, N k ∈, k n ≤.(1)试求()1f x , ()2f x , ()3f x 的值;(2)试猜测()n f x 关于n 的表达式,并证明你的结论. 6.设,为正整数,数列的通项公式,其前项和为.(1)求证:当为偶数时,;当为奇数时,; (2)求证:对任何正整数,.7.数列{}n a 满足11a =且()1211112n nna a n n n +⎛⎫=++≥ ⎪+⎝⎭. (1)用数学归纳法证明: ()22n a n ≥≥;(2)已知不等式()ln 1x x +<对0x >成立,证明: ()3421n a e n <≥(其中无理数).8.记.(1)求的值; (2)当时,试猜想所有的最大公约数,并证明.9.设个正数满足且. (1)当时,证明:;(2)当时,不等式也成立,请你将其推广到 且个正数的情形,归纳出一般性的结论并用数学归纳法证明.10.已知数列{}n a 的各项均为正整数,对于任意n ∈N *,都有11111122111n n n na a a a n n ++++<<+-+ 成立,且24a =. (1)求1a ,3a 的值;(2)猜想数列{}n a 的通项公式,并给出证明. 11.在数列E 中,已知F ,23-,2n n a b =(2n na b =,.(1,13a =时,分别求(212(Ⅰ)求(1)f -及(2)f 的值;(Ⅱ)试探求对一切整数n ,()f n 是否一定是整数?并证明你的结论.13.各项均为正数的数列{}n x 对一切*n ∈N 均满足 (1)1n n x x +<; (2 14.设n ∈*N 且2n ≥,证明:()22221212n n a a a a a a ++⋅⋅⋅+=++⋅⋅⋅+()1232n a a a a +++⋅⋅⋅+⎡⎣()234n a a a a +++⋅⋅⋅++⋅⋅⋅]1n n a a -+.。
2022年江苏成人高考录取常见的10大问答

2022年江苏成人高考录取常见的10大问答一、今年成人高考招生政策有什么变化?近年来我省成人高校招生实行考试成绩互认改革试点,凡参加下列教育招生考试,考试成绩达到相关录取条件且未被录取的考生,可以凭原考试成绩报考相应学历层次的成人高校,由学校择优录取。
具体要求是:1.参加2022年普通高考,成绩在省第三批本科实际最低录取分数以上的考生,可报名参加成人高校的高起本录取;符合普通高考专科注册入学条件的考生,可报名参加成人高校的高起专录取。
2.参加2022年普通高校对口单招考试,成绩在省本科实际最低录取分数以上的考生,可报名参加成人高校的高起本录取;符合普通高校对口单招专科注册入学条件的考生,可报名参加成人高校的高起专录取。
3.参加2022年省教育考试院组织的普通高校“专转本”选拔考试,成绩在省实际最低录取分数以上的考生,可报名参加成人高校的专升本录取。
各类改革试点项目均不包括医学类及相关专业。
二、成人高校录取最低控制分数线如何确定?省最低录取控制分数线,是根据成人高等教育对新生的基本要求,参照考生统考科目成绩和我省的招生计划,按学历层次和科类分别划定,由省招委审核批准,向社会发布。
三、考生如何知晓自己的录取结果?考生可在各阶段录取结束时间后,登录江苏省教育考试院网站,进入查询中心,根据提示进行查询操作。
或拨打电话,查询本人成人高考的录取结果。
具体查询时间将在省内媒体上公布。
四、成人高考招生录取分为几个阶段进行?1.本科录取阶段:12月5日至12月13日。
其中:本科免试生、改革项目等考生录取时间为12月6日至7日;本科普通考生录取时间为12月7日至13日。
2.专科录取阶段:12月14日至12月24日。
其中免试生、改革项目等考生录取时间为12月14日至15日;专科普通考生录取时间为12月14日至24日进行。
五、各录取阶段的志愿在录取过程中是否相互影响?不会相互影响。
成人高考在正常录取阶段共分为本科(专升本、高起本)录取和专科录取二个阶段。
异地高考中存在的问题与解决措施

一、异地高考的本质目标1.切实解决随迁子女高考问题我国现有的高考制度仍然是以户籍为依据,采取分省命题考试和分省配额招生的制度。
随着我国社会人口结构的巨大变革,户籍制度的局限性日益突出,成为随迁子女在流入地就地高考的最大阻碍。
“根据2010年国家统计局第六次全国人口普查结果估计,我国18岁以下流动儿童数量已达3 800万,如按照农村户籍占74%的比例估计,农村户籍的随迁子女人数为2 800万左右,而城市户籍的随迁子女数量则达到近1 000万。
”[1]在进城务工人员规模不断扩大、随迁子女完成义务教育人数不断增加的背景下,开放异地高考、解决随迁子女的继续升学问题迫在眉睫。
2012年8月,国务院批准了异地高考,以期通过开放异地高考更好地解决随迁子女继续升学考试这一日益突出的问题。
《国务院办公厅转发教育部等部门关于做好进城务工人员随迁子女接受义务教育后在当地参加升学考试工作的意见的通知》(以下简称《通知》)中指出,异地高考的主要原则是“要坚持有利于保障进城务工人员随迁子女公平接受教育权利和升学机会”,也把随迁子女的教育和升学问题放在首位。
因此,异地高考从本质上讲必须抓住这一根本,一切以解决随迁子女的高考问题为出发点。
2.发挥高考选拔人才的功能“高考”即高等学校入学招生考试的简称,自产生以来,为我国的经济建设选拔了大批优秀人才,为社会发展做出了不可磨灭的贡献。
我国的高考渊源可以追溯到隋朝的科举制度,是对科举制的改良和发展,本质是通过选拔性的考试选拔社会所需的各类人才。
各种高考改革虽然在形式、内容上进行了变革,依然离不开高考的本质,即选拔人才的目的。
异地高考作为高考改革的一种具体形式,其本质仍然是选拔符合社会发展的各级各类人才。
进城务工随迁子女的基数之大,不仅产生了开放异地高考的迫切需求,更带来了产生于其中的大批优秀人才。
进城务工随迁子女中的绝大部分从小跟随父母在城市接受良好的教育,相比教育水平欠发达的农村地区,他们的综合素质得到了更为全面的发展,更加符合社会发展的需要。
2023年江苏高考志愿填报指南(附填报步骤+填报规则)

2023年江苏高考志愿填报指南(附填报步骤+填报规则)2023江苏高考志愿填报指南高考志愿填报采用“院校专业组+专业(类)”模式。
院校专业组由院校根据不同专业(或专业类)的人才培养需要和选考科目要求设置,是志愿填报的基本单位。
考生的学业水平选择性考试科目须符合报考院校专业组的选考科目要求,方可填报相关志愿。
1.平行志愿[含艺术类传统(顺序)志愿]。
考生在获知高考成绩、学业水平考试成绩、位次信息、各批次省录取控制分数线后,在省教育考试院门户网站或专设网站填报志愿。
2.征求志愿。
在各批次高考平行志愿[含艺术类传统(顺序)志愿]录取结束后,省教育考试院将及时公布未完成招生计划的院校专业组、专业(类)及计划数。
未被录取的考生在规定时间内自行上网填报征求志愿。
高考考生应认真阅读有关高校招生章程以及我省公布的招生规定、招生计划,按有关规定和要求填报院校专业组和专业(类)志愿,并对所填报志愿的真实性和准确性负责。
因考生本人疏漏或失误造成的后果,由考生本人承担。
江苏高考志愿填报步骤1、登录考生所属地的网上填报志愿系统考生登录所在省份的教育考试院,或所属地的网上填报志愿系统,在登录页面相应栏正确输入报名号、准考证号、身份证号和密码等信息后,进入网上填报志愿系统。
2、输入用户名和密码用户名是考生准考证上的14位报名号数字,第一次登录网上报名系统的初始密码是身份证号码,输入用户名和密码后即可登录网上报名系统。
3、阅读考生须知完成初始密码修改后,考生还需要仔细阅读系统公示的须知内容,了解填报志愿的相关规定和时间安排,考生一定要仔细阅读注意事项,以免误填误报。
阅读完注意事项后,考生点击“开始填报志愿”按钮进入志愿填报首页,再进行下一步操作。
4、修改初始密码考生在第一次登录网上填报志愿系统时,一定要修改初始密码,如果不修改,就会自动返回到上一步,无法继续往下操作。
点击“修改”按钮,就可以修改密码和填写录取用联系方式。
成功修改密码后,再开始填报志愿。
2020年江苏高考试卷及答案解析

绝密启用前2020 年普通高等学校招生全国统一考试(江苏卷)语文I 试题一、语言文字运用(12 分)1.在下面一段话的空缺处依次填入词语,最恰当的一组是(3 分)大禹梳理百川,班超投笔从戎,李时珍悬壶济世,林则徐虎门销烟⋯⋯每当中华民族处于艰难之际,总有一大批志士仁人挺身而出,,解民众于水火,挽狂澜于既倒。
野火沃土,,中华五千年文明史就是一部的奋斗史。
A以身许国多难兴邦不屈不挠B以身试险多难兴邦不卑不亢C .以身许国一言兴邦不卑不亢D.以身试险一言兴一言兴邦不屈不挠2.在下面的一段文字横线处填入语句,衔接最恰当的一项是(3 分)瘦西湖的景秒在巧。
,,,。
而雨丝风片,烟波画船,人影衣香,赤栏小桥,游览应以舟行最能体会到其中妙处。
①白塔与五亭桥分占圆拱门内②回视小金山③所谓面面有情,于此方得④最巧是从小金山下沿堤至“钓鱼台”⑤又在另一拱门中A.②③④①⑤B.②⑤④①③C.④①②⑤③D.④③②⑤①3.某校高三年级举行线上成人仪式后,同学们纷纷点赞、留言,相互勉励。
下列留言所引古诗文,不得体的一项是(3 分)A.惟日孜孜,无敢逸豫。
(《尚书》)B.为草当作兰,为木当作松。
(李白)C.少年辛苦终身事,莫向光阴惰寸功。
(杜荀鹤)D.谁道人生无再少?门前流水尚能西。
(苏轼)4.对下面“中国互联网发展阶段简表”的理解,不正A.自1994 年融入国际互联网大家庭以来,中国网民数量不断增加,互联网普及率现在已经超过50%。
B.中国互联网经历了电脑互联、移动互联后,当下已进入智能物联网时代,其联结主体是物与人互联。
C.伴随技术的不断进步,中国互联网的应用形式日趋丰富,目前的代表性应用有云、短视频、VR、AI 等。
D.中国互联网从模仿与追随起步,同步多年努力,如今已在一些领域实现自主创新,甚至有所超越。
二、文言文阅读(20 分)阅读下面的文言文,完成5—8 题。
外大母赵太夫人行状袁宗道天乎,天乎!何乃遽以吾外大母逝耶!悲哉!不肖宗道,稚年丧母,外大母每见不肖,辄泪涔涔下,且泣且拊曰:“儿饥否?将无寒乎?”辄取衣食衣食之。
江苏招生考试 招生计划专刊 电子版

江苏省2013年考生填报志愿须知--江苏招生考试招生计划专刊电子版温馨提示:淘宝店铺“新世纪出版社”,可办理代购业务:最新版《江苏招生考试》招生计划专刊、录取资料汇编等2013年高考填报资料。
考生填报志愿是考生对报考高校及专业意愿的书面表达形式,是高校录取新生的重要依据。
考生在填报志愿前,应认真学习有关招生政策和规定,全面了解平行院校志愿设置、投档原则,以及有关高校的录取规则,牢记每批次征求平行院校志愿(艺术类为征求院校志愿,下同)的填报及确认的时间和地点,根据自己的统考成绩、学业水平测试等级、志向和体检结论等,结合本人家庭的经济情况,慎重填报。
本须知、《2012年普通高等学校在江苏招生计划》、《关于招生.计划中有关问题的说明》等是考生填报志愿的依据,.《2012年江苏省普通高校招生百问》、高校招生章程等:是考生填报志愿的必备参考。
一、录取批次、填报志愿形式及时间安排1.高校录取分七个批次依次进行(1)提前录取本科院校,共包括六类院校(专业)计划:第一类:军事院校、军事院校(预备军官学员)、国防生计划;.第二类:公安、政法院校或专业;第三类:航海院校或专业;第四类:其他院校,包括国际关系学院(北京)、中国青年政治学院、北京电子科技学院、中国民用航空飞行学院、南京航空航天大学(飞行技术)、上海海关学院、外交学院、香港中文大学、香港城市大学、部分院校小语种计划、免费师范生计划等;第五类:体育类提前录取公办本科院校、体育类提前录取民办及独立学院本科院校;第六类:艺术类提前录取公办本科院校、艺术类提前录取民办及独立学院本科院校。
上述第一到第四类为文科类、理科类招生计划。
(2)文科类、理科类第一批本科院校。
(3)文科类、理科类第二批本科院校。
(4)文科类、理科类第三批本科院校。
(5)体育类、艺术类高职(专科)院校。
(6)文科类、理科类高职(专科)院校。
.(7)文科类、理科类高职(专科)注册入学院校。
《江苏招生考试》招生计划专刊电子版今年,我省取消了提前录取专科批次,原来公布在该批次的录取计划安排在文科类、理科类高职(专科)院校批次录取。
2024年江苏高考志愿怎么填报(速看)

2024年江苏高考志愿怎么填报(速看)2024年江苏高考志愿怎么填报(速看)各批次高考志愿填报采用“院校专业组+专业(类)”模式。
院校专业组由院校根据不同专业(或专业类)的人才培养需要和选考科目要求设置,是志愿填报的基本单位。
高考考生的学业水平选择性考试科目须符合报考院校专业组的选考科目要求,方可填报相关志愿。
考生应认真阅读有关高校招生章程以及我省公布的招生规定、招生计划,按有关规定和要求填报院校专业组和专业(类)志愿,并对所填报志愿的真实性和准确性负责。
高考考生必须在规定的时间内凭考籍号、身份证号、密码和动态口令卡网上填报平行志愿[含艺术类传统(顺序)志愿]和征求志愿,并对自己所填报信息的准确性和安全性负责,不需要现场签字确认志愿信息。
填报志愿截止时间前,考生可上网修改自己的志愿信息。
填报志愿时间截止后,任何人不得擅自更改考生志愿信息。
江苏高考志愿填报技巧是什么1.正确估分:分数出来前对一下答案,对自己有一个大概的估分;2.提前参考往年录取分数线:预估分数后,接下来要做的事情就是大面积搜索数据;3.明确各项重要的时间节点:控制分数线、各批次志愿填报及录取结果、征集志愿等;4.研读报考院校的招生章程:招生章程是高校有关招生方案、招生计划和录取规则等的政策性承诺,了解学校的招生章程对科学填报志愿有很大的指导作用。
艺考生高考志愿填报怎么报首先要确认想去的学校有哪些,然后了解各个院校的招生计划,再根据自己的分数筛选合适的学校,最后按照专业和文化做选择。
比如:文化成绩好的可以选择文化占比大的院校,专业成绩好的可以选择专业占比大的院校。
艺术类一般是在提前批提前填报。
提前批有三个志愿,第一志愿非常重要,先看合格证,看看获得了哪几个学校的合格证,找排名靠前的,再看看这个学校有没有小分的限制。
通常艺术院校很少有第二志愿录取的,因为报名人数多,第一志愿都招不完,第二志愿也不希望空着,所以建议学生填一个冷门的或外地院校的第一志愿,相反容易考上大学。
教育部发言人:期望2020年能取消统一高考

教育部发言人:期望2020年能取消统一高考2020年,我们的高考体制改革应该能有一个本质的变化。
目前这种全国统一的考试,覆盖率和影响力很大,公平性也是毋庸置疑的,但是它的弊端也越来越显现。
高考制度是在1977年中国经过十年的动乱,百废待兴,人才奇缺的情况下恢复的,但是现在我们已经不是百废待兴了,我们已经成为繁荣昌盛的教育大国,是不是还要用这个高考制度呢?很显然,高考改革势在必行。
实际上,30年来高考改革始终没有停止,3+x,3+2等,据说江苏省十年来高考改了5次。
这么多次改革应该是改到极致了,但是人们仍然不满意,而且是越来越不满意,这说明一个问题,高考改革在内部深化的同时,必须在外部寻找出路。
我做了个比喻,高考改革是个独木桥,通过这个独木桥,无数的贫穷孩子成了才,于是我们不断地改,但这些改革都是把独木桥改成了独钢桥、独铜桥,独银桥……但始终没有改变本质,要改变“独”的本性,不仅要改建桥的材质,还要另外搭建多座桥,才能解决根本的问题。
我们要赶紧搭建通往成功的多个桥,这样才达到改革的目的。
如果我们各项工作到位,我们的各项措施能够有保障,我们各个部门齐抓共管,我期望2020年的时候,能够取消全国统一高考,代之以更加多样化的、更加便于人们选择的各种类型考试。
高考不能轻易取消,在1966年我们曾经取消高考,这给民族带来了一场灾难,后果不堪设想。
取消高考也需要有前提,一定要有各项配套措施跟上。
教育不再功利2020年,全国公务员招生希望不再以学历为依据,只要达到划定的要求就可以了。
我们现在很多政策导向都是唯学历的,把这种政策导向调整过来就没有百万人参加公务员考试了。
另外,现在这么多人考公务员是因为一些非理性的要求:公务员权利过大,公务员得到的实惠过多,公务员的灰色收入太模糊,如果把这些都解决了,就不会有那么多人去考公务员了。
未来十年,通过我们的改革,教育从某种程度上讲会真正成为一件快乐的事,而不像现在是一件功利的事。
2020年高考热点难点微专题五隐圆问题

热点难点微专题五 “隐圆”问题江苏省高考考试说明中圆的方程是C 级考点,近几年在各地模考和高考的填空题和解答题中都有出现且频率较高,难度为中档题.在题设中没有明确给出圆的相关信息,而是隐含在题目中的,要通过分析、转化,发现圆(或圆的方程),从而最终利用圆的知识来求解,我们称这类问题为“隐圆”问题.例 (1)平面直角坐标系xOy 中,圆C :(x +2)2+(y -m )2=3.若圆C 存在以G 为中点的弦AB ,且AB =2GO ,则实数m 的取值范围是________.(2) 已知圆 C :(x -2)2+y 2=1,点 P 在直线 l :x +y +1=0 上,若过点 P 存在直线 m与圆 C 交于 A ,B 两点且满足 PB →=2P A → ,则点 P 横坐标x 0 的取值范围是________.(3) 若直线l :ax +y -4a =0上存在相距为2的两个动点A ,B ,圆O :x 2+y 2=1上存在点C ,使得△ABC 为等腰直角三角形(C 为直角顶点),则实数a 的取值范围为________.(4) 在平面直角坐标系xOy 中,已知圆O :x 2+y 2=1,O 1:(x -4)2+y 2=4,动点P 在直线x +3y -b =0上,过P 分别作圆O ,O 1的切线,切点分别为A ,B .若满足PB =2P A 的点P 有且只有2个,则实数b 的取值范围是________.点评:【思维变式题组训练】1. 在平面直角坐标系xOy 中,点A (-12,0),B (0,6),点P 在圆O :x 2+y 2=50上,若P A →·PB→≤20,则点P 的横坐标的取值范围是________.2. 已知圆O:x2+y2=1,圆M:(x-a)2+(y-2)2=2.若圆M上存在点P,过点P作圆O的两条切线,切点为A,B,使得P A⊥PB,则实数a的取值范围为________.。
2020年江苏省高考英语试卷解析版

2020年普通高等学校招生全国统一考试(江苏卷)英语试题第一部分听力(共两节, 满分20分)做题时, 先将答案标在试卷上。
录音内容结束后, 你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题; 每小题1分, 满分5分)听下面5段对话。
每段对话后有一个小题, 从题中所给的A、B、C三个选项中选出最佳选项, 并标在试卷的相应位置。
听完每段对话后, 你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A £19.15. B. £59.18. C. £9.15.答案是C。
1.Where does the conversation probably take place?A. In a supermarket.B. In the post officeC. In the street.【答案】C【解析】【原文】本题为听力题,解析略。
2.What did Carl do?A. He designed a medal.B. He fixed a TV set.C. He took a test. 【答案】B【解析】【原文】本题为听力题,解析略。
3.What does the man do?A. He’s a tailor.B. He’s a waiter.C. He’s a shop assistant.【答案】A【解析】【原文】本题为听力题,解析略。
4.When will the flight arrive?A. At 18:20.B. At 18:35.C. At 18:50.【答案】C【解析】【原文】本题为听力题,解析略。
5.How can the man improve his article?A. By deleting unnecessary words.B. By adding a couple of points.C. By correcting grammar mistakes.【答案】A【解析】【原文】本题为听力题,解析略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年江苏高考招生计划中问题说明一、根据国家教育部的有关规定,各院校招生计划须经其主管部门核准,未经核准的计划,不予安排招生;招生计划一经向社会公布,任何单位和个人不得随意更改。
二、计划公布的办法今年我省普通高校招收统考生计划分文科类、理科类、体育类、艺术类四个类别,按录取时间先后,分别刊登在招生计划专刊上册、下册。
上册刊登的顺序为:文科类、理科类:提前录取本科院校;第一批录取本科院校;第二批录取本科院校。
体育类、艺术类:提前录取公办本科院校;提前录取民办及独立学院本科院校。
下册刊登的顺序为:文科类、理科类:第三批录取本科院校;高职(专科)院校;高职(专科)注册入学院校。
体育类、艺术类:高职(专科)院校。
我院在公布招生计划的同时,公布了各招生院校代号及其专业代号。
院校名称前的四位数字为院校代号,专业名称前的两位字符(含数字或字母)为专业代号。
考生网上填报志愿时,应在志愿填报系统的相应位置,准确填报院校代号和专业代号。
按学院、系科或专业大类招生的院校,其学院、系科或专业大类名称后括号内所标注的为该院、系或大类所包含的专业。
按专业大类招生的专业,所包含的专业及专业方向、培养方式、专业分流方式等情况,考生须查阅招生院校的网站说明、招生简章和章程等资料。
专业名称后的括号内所标注的为该专业的专业方向或培养目标、办学地点等。
三、收费标准按院校上报的数额,我院还公布了各招生院校各专业每生每学年学费的收费标准,供考生填报志愿时参考。
按照收费管理属地化的原则,我省省内高校均执行经我省物价部门批准的收费标准,外省高校的学费应按学校所在地省级物价部门批准的标准收取。
此外,各招生院校还将收取一定数额的住宿费和公寓化管理费等费用。
除香港地区的院校收费以港币为单位计算外,其他院校收费以人民币为单位计算(特别注明的除外)。
四、关于高校对考生学业水平测试科目和等级的要求根据08高考方案规定,考生填报高考志愿须符合以下基本要求,即文科类、理科类考生必修科目测试均须达到C级及以上等级(技术科目合格);体育类、艺术类考生七门必测科目测试等级中,D级不得超过三门(技术科目不合格,视为D级);参加高职(专科)注册入学的考生须参加高考和七门科目学业水平测试,对考生学业水平测试等级要求由院校另行规定,申请注册入学考生的学业水平测试科目、等级须符合院校要求。
为方便考生填报志愿,我院将各高校招生专业计划及高校对考生学业水平测试的有关要求一并公布,供考生填报志愿时参考。
其中,在公布文科类、理科类计划时,同时公布院校对考生的必测科目和选测科目等级要求,以及除历史、物理外,院校各专业对考生另一门选测科目的建议要求;建议选测科目在录取中的作用,见院校招生章程或咨询院校。
五、关于高校招生章程招生章程是高校向社会公布招生信息的主要形式,是高校向考生的公开承诺,是其开展招生工作、录取新生的重要依据,是考生填报志愿的重要参考。
我省不单独汇编各高校招生章程,只公布各高校发布招生章程的网址和联系方式。
考生须仔细查阅所填报院校的招生章程,了解院校录取规定、录取办法,以及院校(专业)对考生的其它具体要求,如:对考生的语种、身体条件、是否应届生等。
六、军事院校招生及地方高校招收国防生今年,军事院校(含预备军官学员)及国防生招生计划数为797人。
其中,29所军事院校招收本科层次学员607人,30所地方高校招收本科层次国防生190人。
解放军理工大学另在我省定向招生6人,学员入校后不参军,毕业后面向人防系统就业。
军事院校招生和普通高校招收国防生的对象为参加今年普通高等学校招生全国统一考试的普通高中毕业生。
普通高中应届、往届毕业生均可报考。
报考基本条件:①年龄不低于17周岁、不超过20周岁(截至今年8月31日);②政治条件符合《关于军队院校招收普通高中毕业生和军队院校接收普通高等学校毕业生政治条件的规定》;③身体条件达到军队院校招收学员体格检查有关标准;④高考成绩达到省教育考试院公布的本科第二批省录取最低控制分数线及以上(艺术类除外);⑤未婚。
报考机要、潜艇、飞行、刑侦、艺术类专业的,还应符合相关专业政治条件、身体条件等方面的特殊要求,具体请查阅院校招生章程。
军事院校专业名称后括号内的“合训”是指招收的学生先在综合或有关专业院校学习训练4年,再到另一所任职院校训练1年。
2.关于“预备军官学员”:解放军艺术学院和第二、三、四军医大学招收的为预备军官学员。
学员入学不办理入伍手续,享受军队提供的相关待遇,毕业考核合格者,择优(或视军队建设需要)选拔为军队干部分配到部队工作;未被选拔为军队干部的毕业学员,面向社会自主就业,可以优先招聘录用为军队文职人员。
3.关于“国防生”:国防生是根据军队建设需要,由地方普通高校从参加国家统一招生考试中录取且毕业后到军队工作的学生。
国防生在校学习期间,享受军队提供的国防奖学金,参加军队组织的军政训练、当兵锻炼和见习代职等活动。
国防生达到相应培养目标,并按时取得学历、学位证书后,由军队办理入伍手续并任命为军队干部。
根据有关规定,军事院校(含预备军官学员)和国防生除特别注明外,均要求考生的外语语种为英语。
七、特殊院校(专业)招生1.凡招生计划中注有“口”字样的专业均要求考生外语基础及口语较好,凡报考此类专业的考生必须有外语口语等级测试成绩且成绩较好。
2.部分高校,如航海类专业、军事院校潜艇类专业等,对考生身体条件有特殊要求,考生在填报时须查阅院校招生章程。
3.在文科类或理科类招生的建筑学、城乡规划、风景园林等专业,院校一般要求考生有较好的绘画基础,新生入学后一般需加试美术,不合格者将被转入其它专业。
4.部分院校(专业)“计划数”栏中未标注数字,计划为面向全国招生的艺术类专业或招收高水平运动队、高水平艺术团等考生,其计划数不分解到省,院校计划总数未计入;部分院校(专业)后备注“只招收高水平运动队入选考生、高水平艺术团入选考生、自主招生考生”等,其学业水平测试等级要求按省有关规定和院校要求执行。
八、个别高校招生计划有关问题的说明1.经批准,今年我省继续组织省内苏州大学、扬州大学、江苏大学、南京工业大学、江苏师范大学、南京财经大学、南京工程学院、南京师范大学8所高校对口联建宿迁学院,实行联合办学。
使用其中6所联建高校独立学院计划招收本科生。
学生在宿迁学院学习,毕业后颁发联建高校独立学院的毕业证书和学位证书。
2014年5月,教育部正式批准建立宿迁学院,部分专业以宿迁学院计划招生,学生毕业后颁发宿迁学院毕业证书和学位证书。
联建招生计划和宿迁学院招生计划均公布在宿迁学院及有关高校联建宿迁学院计划代号(1598)下,按照民办院校收费标准收费。
2.经教育部批准,香港中文大学、香港城市大学招生计划安排在提前录取批次,实行计算机远程网上录取。
从2008年起,两校在内地录取新生时,不再考虑各类照顾加分等优惠政策,按高考实际成绩(含奖励分)投档。
凡被此两所院校录取的新生,凭学校的录取通知书及本人身份证、户口本、香港入境事务处签发的进入许可文件等到户口所在地公安机关办理因私赴香港的手续;学生在港期间,其内地户口不予注销;内地学生在香港学业期满,获得高等学校颁发的学历、学位证书,内地教育行政部门予以承认;内地学生毕业后,自主择业。
3.西北民族大学招收少数民族预科生4人,其招生对象为参加统考的少数民族考生。
录取时如线上生源不足可适当降分;预科班学生学习期满,经考试合格,可升入有关高等院校学习。
4.根据教育部文件精神,我省继续实施农村学生单独招生(即高校专项计划)和地方重点高校招收农村和贫困地区学生专项计划(即地方专项计划)。
实施区域为我省25个省扶持的经济薄弱县(市、区)和黄桥、茅山革命老区所涉及的14个县(市、区),只招收户籍、学籍等符合报考条件,在当地就读且经公示无异议的考生。
5.经批准,我省从2016年起继续开展农村订单定向医学生免费培养工作,为农村基层医疗机构培养适宜医学人才。
面向省内部分地区的农村订单定向医学生免费培养计划,只招收户籍等符合报考条件的应届高中毕业生(详见本刊上册第181页)。
6.经批准,我省从2016年起开展乡村教师定向培养工作,旨在为全省乡村学校培养一批扎根农村、甘于奉献、一专多能、素质全面的本土化的乡村教师。
面向省内部分地区考生的乡村教师定向培养计划,只招收户籍等符合报考条件的考生(详见本刊上册第181页)。
7.高职(专科)院校中外合作办学计划如在省控线上生源不足,降分录取后,如仍不能完成的,未完成的计划一律不得调转到其他批次和科类使用。
8.今年江苏海事职业技术学院等3所院校在我省开展定向培养士官试点工作,计划公布在高职(专科)批次。
定向培养士官学制3年,毕业后取得大专学历。
9.石家庄邮电职业技术学院为江苏省邮政公司下属有关单位定向培养计划,面向全省招生,考生录取后须签订协议,毕业后到定向培养地区就业。
10.我省部分高职(专科)院校与国外有关高校协作,举办“海外本科直通车”项目。
考生录取后,根据教学计划,分国内、国外两个阶段学习,学完国内三年专科课程,成绩合格者取得专科文凭,同时完成相关外语和国外合作院校规定的部分课程的学习,以达到进入国外高校续读的要求。
符合一定条件的学生,方可到国外协作学校就读本科课程并取得本科文凭。
该项目国外学习期间费用按国外协作高校规定的标准缴纳,国内学习期间学费标准按省物价局核定的标准收取。
11.今年我省继续在省内部分高职(专科)院校的文科类、理科类专业中试行注册入学,省内高职(专科)院校自愿申请,经批准后可参与注册入学试点。
相关工作按照省教育厅、省教育考试院有关文件规定执行。
注册入学计划与统一录取计划的性质相同,其招收的考生除录取方式不同外,在校待遇、毕业生就业政策以及毕业文凭等均与统一录取的考生相同。
12.根据《江苏省2016年普通高等学校招生工作意见》(苏招委〔2016〕1号)规定,少数民族考生,报考江苏省省属(含厅局属、市属)普通高校,录取时可加3分投档。
2016年江苏省属普通高等学校名单见本刊上册第180页。
