17材料力学习题解答(弯曲应力)
材料力学课后答案

由平衡方程,解得:
FBy 5KN; M B 13KN m
微分法画弯矩图
( M B 13KN m; M C M C 3KN m; M D 0)
2.根据强度要求确定 b
max WZ 2 bh 2 3 WZ b 6 3 M
弯矩图
M
(+)
x
3.绘制挠曲轴略图并计算wmax, A , B 令 dw 0 得 x l (0 x l ) 2 dx 所以 wmax w x l
2
挠曲轴略图
w
5ql 4 384 EI
x0
(-)
B
ql 3 24 EI
x
由式(3)知 A
max
M max ymax 176MPa IZ
max
M WZ
K
M max yK 132MPa IZ
3
5-5.图示简支梁,由 NO18 工字钢制成,在集度为q的均匀载荷作用下测得横截 4 面C底边的纵向正应变 =3.0 10 ,试计算梁内的最大弯曲正应力,已知刚的弹 FAy FBy 性模量E=200GPa,a=1m。
M yA Wy 6 M yA M zA 6M zA Wz 2b b 2 b (2b) 2
由 max 解得 b 35.6mm 故
h 2b 71.2mm
14
2.截面为圆形,确定d 由分析图及叠加原理可知: 在1,3区边缘某点分别有最大拉应力,最大压应力 其值均为:
I Z I Z 1 2 I Z 2 1.02 104 m4
2.画弯矩图 由平衡方程得 微分法画弯矩图
FCy 10KN; M C 10KN m
材料力学习题解答(弯曲变形)

Pl 2
梁的挠曲线方程和转角方程是
D1 = 0
D2
=
−
1 24
Pl 3
⎧⎪⎪⎨⎪⎪⎩ 2EEIvI2'v1'==P2P2xx2212−−PPlxlx2 1+
3 16
Pl
2
⎧⎪⎪⎨⎪⎪⎩ 2EEIvI2v1==P6P6xx2313−−P2Pl2lxx2212+
3 16
Pl 2 x2
−
1 24
Pl 3
(6) 最大挠度和最大转角发生在自由端 令x2=l:
⋅a
=
−
qa4 3EI
上海理工大学 力学教研室
7
θB
= θ B(1)
+ θB(2)
+ θ B(3)
=
−
qa3 4EI
fB
=
f B (1)
+
fB(2)
+
f B ( 3)
= − 5qa4 24EI
7.10. 桥式起重机的最大载荷为 P=20 kN。起重机大梁为 32a 工字钢,E=210 GPa,l=8.7 m。 规定[f]=l/500,试校核大梁刚度。
⎪ ⎪⎩
M
2
(
x2
)
=
−
q
(l
− x2 2
∈
[
l 2
,
l
]
(2) 挠曲线近似微分方程
⎧ ⎪⎪
EIv1"
=
M1( x1)
=
− 3ql 2 8
+
ql 2
x1
⎨
⎪ ⎪⎩
EIv2"
=
M2(x2 )
材料力学梁的弯曲应力

ab (y)dd yd
ab
dx
d
y
(a)
——横截面上距中性轴为y处的轴向变形规律。
曲率 1 ( ), 则 ( ); 曲率 1 ( ), 则 ( ); 1 C, y.
当 y0时,0;yym时 ax,ma.x
与实验结果相符。
.
9
(2)应力分布规律
在线弹性范围内,应用胡克定律
sE E y
120
B
x
180
K
FBY
y
FS 90KN
( )
() x
90KN
M ql2/867.5kNm
( )
x
.
解
30 2. C 截面最大正应力 z C 截面弯矩 MC60kNm
C 截面惯性矩
IZb1h 325.83210 5m4
s C max
M C y max IZ
60 10 3 180 10 3
2 5 . 832 10 5
92 .55 MPa
21
y
q=60KN/m
A
1m
FAY
C
l = 3m
120
B
x
180
K
FBY
y
FS 90KN
( )
() x
90KN
M ql2/867.5kNm
( )
x
.
解
30 3. 全梁最大正应力 z 最大弯矩
Mmax67.5kNm
截面惯性矩
Iz
bh 3 5.83210 5m4 12
Hale Waihona Puke s maxM max y max IZ
385.106Pa38M 5 Pa
19
材料力学弯曲变形答案

第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。
( ) 1.2 内力只作用在杆件截面的形心处。
( ) 1.3 杆件某截面上的内力是该截面上应力的代数和。
( ) 1.4 确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ) 1.5 根据各向同性假设,可认为材料的弹性常数在各方向都相同。
( ) 1.6 根据均匀性假设,可认为构件的弹性常数在各点处都相同。
( ) 1.7 同一截面上正应力ζ与切应力η必相互垂直。
( ) 1.8 同一截面上各点的正应力ζ必定大小相等,方向相同。
( ) 1.9 同一截面上各点的切应力η必相互平行。
( ) 1.10 应变分为正应变ε和切应变γ。
( ) 1.11 应变为无量纲量。
( ) 1.12 若物体各部分均无变形,则物体内各点的应变均为零。
( ) 1.13 若物体内各点的应变均为零,则物体无位移。
( ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。
( )1.15 题1.15图所示结构中,AD 杆发生的变形为弯曲与压缩的组合变形。
( )1.16 题1.16图所示结构中,AB 杆将发生弯曲与压缩的组合变形。
( )二、填空题1.1 材料力学主要研究 受力后发生的 ,以及由此产生的 。
1.2 拉伸或压缩的受力特征是 ,变形特征是 。
1.3 剪切的受力特征是 ,变形特征是 。
1.4 扭转的受力特征是 ,变形特征是 。
B题1.15图题1.16图1.5 弯曲的受力特征是 ,变形特征是 。
1.6 组合受力与变形是指 。
1.7 构件的承载能力包括 , 和 三个方面。
1.8 所谓 ,是指材料或构件抵抗破坏的能力。
所谓 ,是指构件抵抗变形的能力。
所谓 ,是指材料或构件保持其原有平衡形式的能力。
1.9 根据固体材料的性能作如下三个基本假设 , , 。
材料力学作业6(弯曲应力)

第六章 弯曲应力一、是非题1 梁在纯弯曲时,横截面上各点只有正应力。
( )2 对于等截面梁,弯矩绝对值最大的截面,就是危险截面。
( )3 抗弯截面系数是反映梁横截面抵抗弯曲变形的一个几何量,它的大小与梁的材料有关。
( )4 钢梁和木梁的截面形状和尺寸相同,在受同样大的弯矩时,木梁的应力一定大于钢梁的应力。
( )5 对于矩形截面梁,无论平放还是立放,其抗弯强度相同。
( ) 二、选择或填空1 材料弯曲变形后( )长度不变。
A .外层B .中性层C .内层 2 梁弯曲时横截面上的最大正应力在( )。
A.中性轴上B.对称轴上C.离中性轴最远处的边缘上3 若矩形截面梁的高度h 和宽度b 分别增大一倍,其抗弯截面系数将增大 ( )。
A.2倍 B.4倍 C.8倍 D.16倍4一圆截面悬臂梁,受力弯曲变形时,若其它条件不变,而直径增加一倍,则其最大正应力是原来的________倍。
A :81B :8C :2D :21 5 图示悬臂梁,在外力偶矩M 的作用下,N-N 截面应力分布图正确的是( )A B C D 6 图示横截面上的应力分布图,其中属于直梁弯曲的是图( ),属于圆轴扭转的是图( )。
7 等强度梁各横截面上 数值近似相等。
A .最大正应力B .弯矩C .面积D .抗弯截面系数8 图示,用T 形截面形状的铸铁材料作悬臂梁,从提高梁的弯曲强度考虑,图( )的方案是合理的。
A B三计算题1 图示悬臂梁,梁长L =1m ,集中载荷F =10k N ,梁截面为工字形,已知其Z W =102 cm3 试求出该悬臂梁上最大正应力。
2 长度mm 250=l 、截面宽度mm 25=b 、高度mm 8.0=h 的薄钢尺,由于两端外力偶矩的作用而弯成中心角为 60的圆弧。
已知钢的弹性模量GPa 210=E ,试求钢尺横截面上的最大正应力。
3 图示矩形截面简支梁。
试求1-1截面上a 、b 两点的正应力。
8kN4图示木梁受移动载荷kN 40=F 作用。
弯曲应力练习题

弯曲应力练习题弯曲应力是工程力学中的重要概念,涉及到物体在受到弯曲力作用时的应力分布和变化。
掌握弯曲应力的计算方法对于力学领域的学习至关重要。
在本文中,我们将介绍一些常见的弯曲应力练习题,旨在帮助读者加深对弯曲应力的理解和运用。
1. 长方形截面材料的弯曲应力考虑一块长度为L、宽度为b、高度为h的长方形截面材料,在其最大弯曲力矩为M的作用下,我们希望计算其截面处的最大弯曲应力σ。
根据工程力学的理论,我们可以使用以下公式进行计算:σ = (M * y) / (I * c)其中,y表示距离截面中性轴的距离,I是截面的惯性矩,c是截面最大应力面的最大距离。
2. 悬臂梁的最大弯曲应力考虑一个长度为L、所受力矩为M的悬臂梁,我们希望计算其截面处的最大弯曲应力σ。
对于悬臂梁而言,最大弯曲应力出现在悬臂梁固定端。
根据工程力学的理论,我们可以使用以下公式进行计算:σ = (M * L) / (I * c)其中,M是所受力矩,L是悬臂梁的长度,I是截面的惯性矩,c是截面最大应力面的最大距离。
3. 圆柱体的弯曲应力考虑一个半径为r、所受力矩为M的圆柱体,我们希望计算其截面处的最大弯曲应力σ。
根据工程力学的理论,我们可以使用以下公式进行计算:σ = (M * r) / (I * c)其中,M是所受力矩,r是圆柱体的半径,I是截面的惯性矩,c是截面最大应力面的最大距离。
以上是三个常见的弯曲应力计算问题的解决方法。
在实际的工程应用中,我们需要根据具体情况选择合适的公式并进行计算。
同时,为了准确评估材料的弯曲性能,我们还需要了解材料的力学性质,如弹性模量、截面惯性矩等。
通过练习和实践,我们可以逐渐提高对弯曲应力问题的解决能力。
总结:本文简要介绍了弯曲应力的概念和计算方法,并提供了三个常见的弯曲应力练习题。
这些题目涉及到了不同结构的材料,如长方形截面材料、悬臂梁和圆柱体。
通过解决这些练习题,读者可以深入理解弯曲应力的计算过程,进一步掌握工程力学的基础知识。
材料力学典型例题及解析 5.弯曲应力典型习题解析

9m q
4 ≤ [σ ]
A
1 πd 2
4
解得 q ≤ 1 π d 2 [σ ] = 1 × 20 ×10 −6 m 2 ×160 ×10 6 Pa = 22300 N/m = 22.3 kN/m
9m
9m
4、确定结构的许用载荷 取 AC 梁、BD 杆的许用 q 值中的小值,即为结构的许用载荷。
所以 [ q ] = 15.68 kN / m 。
切口,如图 a 所示。已知材料的许用应力 [σ ] = 100 MPa , (1) 计算切口许可的最大深度,并
画出切口处截面的应力分布图。(2) 如在杆的另一侧切出同样的切口,正应力有何变化?
F
y
(a)
38MPa
h=40mm
F
C'
M
F
CF F
F
100MPa
b=5mm (b)
(c)
(d)
题6图
解题分析:此题为偏心拉伸问题,可利用弯曲与拉伸组合变形的强度条件求出切口的允许深 度。若另一侧开同样深度切口,偏心拉伸问题变为轴向拉伸问题。 解:1、计算切口许可的最大深度
得 F B y = 12.75 kN
2、作弯矩图,确定危险截面
1
弯矩图如图 b 所示,峰值为 M C = 3.75kN ⋅ m 和 M B = − 4.5kN ⋅ m 。
B 截面的上边缘各点受拉,下边缘各点受压;C 截面的上边缘各点受压,下边缘各 点受拉。由于不能直观确定最大拉、压应力的位置,需要进一步计算。 3、计算 B、C 截面上的应力
设 A 处支反力为 F A y ,B 处支反力为 F B y ,均竖直向上。考虑梁 AD 的平衡,有
∑ M B = 0 , − F A y × 2 m − 4.5×103 N ×1m + 12×103 N ×1m = 0
材料力学习题及答案4-6

第四章弯曲应力判断图弯矩的值等于梁截面一侧所有外力的代数和。
()负弯矩说明该截面弯矩值很小,在设计时可以忽略不计。
()简支梁上向下的集中力对任意横截面均产生负弯矩。
()横截面两侧所有外力对该截面形心力矩的代数和就是该截面的弯矩值。
()梁的任一横截面上的弯矩在数值上等于该截面任一侧所有外力对该截面形心的力矩代数和。
()在计算指定截面的剪力时,左段梁向下的荷载产生负剪力。
()在计算指定截面的剪力时,右段梁向下的荷载产生正剪力。
()梁纯弯曲时中性轴一定通过截面的形心。
()简支梁上受一集中力偶作用,当集中力偶在不改变转向的条件下,在梁上任意移动时,弯矩图发生变化,剪力图不发生变化。
()图示梁弯矩图的B点是二次抛物线的顶点。
()图示梁段上集中力偶作用点两侧的弯矩直线一定平行。
()(M图)下列三种斜梁A截面的剪力均相同。
()l/2l/2l/2l/2l/2l/2下列三种斜梁B截面的剪力均相同。
()l/2l/2l/2l/2l/2l/2下列三种斜梁C截面的弯矩均相同。
()l/2l/2l/2l/2l/2l/2梁弯曲时的内力有剪力和弯矩,剪力的方向总是和横截面相切,而弯矩的作用面总是垂直于横截面。
()一端(或两端)向支座外伸出的简支梁叫做外伸梁。
()##√悬臂梁的一端固定,另一端为自由端。
()##√弯矩的作用面与梁的横截面垂直,它们的大小及正负由截面一侧的外力确定。
()##√弯曲时剪力对细长梁的强度影响很小,所以在一般工程计算中可忽略。
()##√图示,外伸梁BC段受力F作用而发生弯曲变形,AB段无外力而不产生弯曲变形()##×由于弯矩是垂直于横截面的内力的合力偶矩,所以弯矩必然在横截面上形成正应力。
()##√抗弯截面系数是反映梁横截面抵抗弯曲变形的一个几何量,它的大小与梁的材料有关。
()##×无论梁的截面形状如何,只要截面面积相等,则抗弯截面系数就相等。
()##×梁弯曲变形时,弯矩最大的截面一定是危险截面。
河海大学-材料力学第5章弯曲应力作业参考解答

IZ
=
2 × ( 1 × 60 ×1403 12
+ 60 ×140 × (70 - (76.82 - 50))2 )
+ 1 × 280 ×503 + 280 ×50 × (76.82 - 50 / 2)2 = 9.9´107 mm4 12
(3)b-b 处切应力
t b-b
=
FS
S
* z
Izb
=
27.5kN ´ (60 ´100 ´ 63.18mm3 ) 9.9 ´107 ´108 mm4 ´ 60mm
解:
A
A
z
z
A
z
y
y
y
5-23 求图所示梁的最大容许荷载 q。梁的容许正应力为 3.5MPa,容许切应力为 0.7MPa,胶 结处的容许切应力为 0.35MPa。
yc
解:(1)求内力
最大剪力为 Fs max
=
0.5ql
= 0.3q ,最大弯矩为 M z max
=
1 8
ql
2
= 0.045q 。
(2)确定形心位置及计算惯性矩
£ 0.7 ´106
解得: q £ 3.97kN / m 。
(5) 粘结处应力强度条件
t max
=
Fs
max
S
* z
Izb
=
0.3q ´ 25´ 25´ 25´10-9 3.32 ´10-6 ´ 25´10-3
£ 0.35´106
解得: q £ 6.2kN / m 。
最后容许荷载为 q £ 3.97kN / m 。
第 5 章作业参考解答
本章主要公式
梁平面纯弯曲时曲率与弯矩和弯曲刚度的关系: 1 = M r EI z
材料力学习题解答弯曲应力
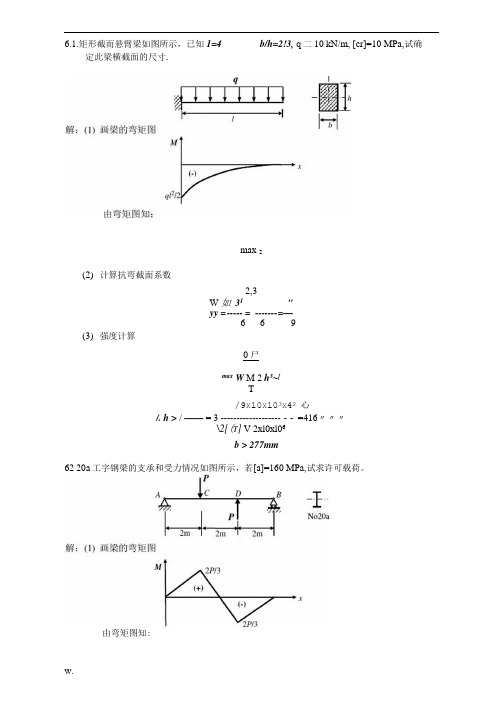
6.1.矩形截而悬臂梁如图所示,已知1=4 b/h=2!3, q二10 kN/m, [cr]=10 MPa,试确定此梁横截面的尺寸.max 2(2)计算抗弯截面系数2,3W 如31"yy = ----- = ------- =—6 6 9(3)强度计算0尸max W M 2 h3~[T/9X10X103X42心/. h > / —— = 3 ------------------- - - =416〃〃〃\2[(T] V 2xl0xl06b > 277mm62 20a工字钢梁的支承和受力情况如图所示,若[a]=160 MPa,试求许可载荷。
由弯矩图知:2P= = J_.pgEW W 3W.• A 哄=3x237xl0F60>d。
”= %.8 球2取许可载荷[P] = 57AN解:(1)画梁的弯矩图M c M c 32xl.34xl03=—=—Y = :— = 63.2MPaW c诚;. n x 0.06?"3TB截面:0.9xlO3 5z 4——;------------ -- = 62.1 MPa力以八d;、〃x0.06 〃 0.045、---- U ——r)------------ (1 —----- r-)32 矶32 0.064(3)轴内的最大正应力值(2)查表得抗弯截面系数(3)强度计算2P、=——W =237x10^7/1maxbfmax63.图示圆轴的外伸部分系空心轴.试作轴弯矩图,并求轴内最大正应力.由弯矩图知:可能危险截面是C和B截而(2)计算危险截而上的最大正应力值C截面:解:(1)画梁的弯矩图M t = 308M H(2)计算抗弯截面系数(3)强度计算 许用应力[(r] = ^- = — = 253MPa n 1.5强度校核308 inA1/rn r 】b” = —- = ------------------ I T = 1961"“ Y b maxW 1.568x1 Of压板强度足够。
第六章 弯曲应力(习题解答)

6-3、图示矩形截面梁受集中力作用,试计算1-1横截面上a 、b 、c 、d 四点的正应力。
解:(1)外力分析,判变形。
荷载在纵向对称面内,与轴线垂直,梁发生平面弯曲。
中性轴z 轴过形心C 与载荷垂直,沿水平方向。
(2)内力分析,弯矩图如图(b )所示,1-1横截面的弯矩为:1115230(M -=-⨯=-⋅kN m)(3)应力分析,梁上边有弯矩图,上侧纤维受拉。
1-1横截面上的a 点处于拉伸区,正应力为正;c 点处于中性层上,正应力为零;b 、d 两点处于压缩区,正应力为负。
3111111max2301011.1110.1800.36a a zzzM M M y y I I W σ---⨯=⋅=⋅===⨯⨯Pa MPa 。
11.11b a σσ=-=-MPa0c σ= 31133010(0.1500.050)7.4110.1800.312d d zM y I σ-⨯=-⋅=-⨯-=-⨯⨯Pa MPa37M kN V 图(kN)(a)(c)(b)(c)(e)(d)2+q l /8MkN ·m)(f)(b)180q题6-3图 题6-5图6-5、两根矩形截面简支木梁受均布荷载q 作用,如图所示。
梁的横截面有两种情况,一是如图(b)所示是整体,另一种情况如图(c)所示是由两根方木叠合而成(二方木间不加任何联系且不考虑摩擦)。
若已知第一种情况整体时梁的最大正应力为10MPa ,试计算第二种情况时梁中的最大正应力,并分别画出危险截面上正应力沿高度的分布规律图示。
解:(1)外力分析,判变形。
荷载在纵向对称面内,与轴线垂直,梁发生平面弯曲。
第一种情况中性层为过轴线的水平纵向面,中性轴z 轴过整体形心C 与载荷垂直,沿水平方向。
而第二种情况,两根木梁以各自的水平纵向面为中性层发生弯曲,两根中性轴为与荷载垂直的水平形心主轴。
如图所示。
(2)内力分析,判危险面:弯矩图如图(b )所示,跨中截面为危险面。
弯曲内力和应力基本概念练习

弯曲内力和应力基本概念练习下卷材料力学 - 1 - 弯曲内力练习一、选择题1.外伸梁受均布载荷作用,如图所示。
以下结论中()是错误的。
A.AB段剪力表达式为FQ(x)=-qx;B.AB段弯矩表达式为M(x)=-1qx2; 2C.BCqa2段剪力表达式为FQ(x)=2L2;(L-x)。
D.BC段弯矩表达式为M(x)=-qa2L题1图题2图2.外伸梁受集中力偶作用,如图所示,以下结论中()是错误的。
A.当力偶作用点C位于支座B的右侧时,梁的弯矩图为梯形;B.当C点位于支座B的右侧时,梁上各截面的弯矩M(x)≥0;C.当C点在梁上移动时,梁的剪力图不改变;D.当C点在梁上移动时,梁的中央截面上弯矩不改变。
第 1 页共 6 页题3图下卷材料力学 - 2 -3.简支梁受集中力作用,如图所示,以下结论中()是错误的。
A.AC段,剪力表达式为 FS(x)=Fb; LFbx;B.AC段,弯矩表达式为M(x)=LC.CB段,剪力表达式为 FS(x)=Fa; LFa(L-x)。
D.CB段,弯矩表达式为M(x)=L4.简支梁的四种受载情况如图,设M1、M2、M3、M4分别表示梁(a)、(b)、(c)、(d)中的最大弯矩,则下列结论中()是正确的。
A.M1 >M2 = M3 >M4;B. M1 >M2 > M3 >M4;C.M1 >M2 >M3 = M4;D. M1 >M2 >M4> M3 。
(a)(b)(c)(d)5.外伸梁受均布载荷作用,如图所示。
以下梁的剪力、弯矩图第 2 页共 6 页下卷材料力学 - 3 - 中()是正确的。
A.(a);B.(b);C.(c);D.(d)。
F sFs弯曲应力一. 选择题1.在推导弯曲正应力公式σ=My时,假设纵向线段间无挤压,IZ 这是为了()。
A.保证正应力合力FN = ∫A σdA=0;B.保证纵向线段为单向拉伸(压缩);C.保证梁发生平面弯曲;D.保证梁不发生扭转变形。
弯曲应力习题答案

弯曲应力习题答案在材料力学中,弯曲应力是结构分析中的一个重要概念,它涉及到梁或板在受到弯曲作用时内部产生的应力。
以下是一些弯曲应力习题的答案示例:习题一:简单梁的弯曲应力计算问题描述:一根长为 \( L \) 米,截面为矩形的梁,宽 \( b \) 米,高 \( h \) 米,材质为钢,弹性模量 \( E \) 为 \( 200 \) GPa。
梁的一端固定,另一端自由,中间受到一个集中力 \( P \) 的作用。
解答:1. 首先,确定梁的截面惯性矩 \( I \):\[ I = \frac{b \cdot h^3}{12} \]2. 根据梁的受力情况,计算梁的弯曲应力 \( \sigma \):\[ \sigma = \frac{M \cdot c}{I} \]其中 \( M \) 是弯矩,对于集中力 \( P \) 作用在梁的中点,弯矩 \( M \) 为 \( \frac{PL}{4} \)。
3. 将弯矩代入弯曲应力公式中:\[ \sigma = \frac{P \cdot L \cdot c}{4 \cdot I} \] 其中 \( c \) 是梁截面上距离中性轴的距离,对于矩形截面,\( c = \frac{h}{2} \)。
4. 将已知数值代入公式,计算出弯曲应力。
习题二:悬臂梁的弯曲应力分析问题描述:一根悬臂梁,长度 \( L \) 米,材料的弹性模量 \( E \) 为 \( 200 \) GPa,梁的一端固定,另一端受到一个向下的集中力 \( P \)。
解答:1. 悬臂梁在末端受到集中力作用时,最大弯矩 \( M \) 出现在梁的末端,其值为 \( P \cdot L \)。
2. 假设梁的截面为圆形,半径 \( r \),则截面惯性矩 \( I \) 为: \[ I = \frac{\pi r^4}{4} \]3. 计算弯曲应力 \( \sigma \):\[ \sigma = \frac{M}{I} = \frac{P \cdot L}{\frac{\pir^4}{4}} \]4. 将已知数值代入公式,计算出弯曲应力。
材料力学试题库精选题解精选题6_弯曲应力17页

弯曲应力1. 圆形截面简支梁A,B 套成,层间不计摩擦,材料的弹性模量E 严2E A 。
求在外力偶矩A/。
作用下,A,3中最大正应力的比值也有4个答案: (心;O(c)r 答:B2. 矩形截面纯弯梁,材料的抗 拉弹性模量耳大于材料的抗压 弹性模量瓦,则正应力在截面 上的分布图有以下4种答案:答:C3. 将厚度为2 mm 的钢板尺与一曲面密实接触,已 知测得钢尺点A 处的应变为-岛,则该曲面在点A 处的曲率半径为 ___________ mm ° 答:999 mm4. 边长为"的正方形截面梁,按图示两种不同形式放置,在相同弯矩作用下,两者最大正应力之比竺4= ________(bnux)b5•—工字截面梁,截面尺寸如图,h = b 」= 15。
的弯矩约为截面上总弯矩的88%o•工 My “ 2M 严彳 “t M/ 证: b = -j —, = —j — x J y( y^dy) = 1 820 x其中:积分限B = t + - , A = - 为翼缘弯矩2 26.直径d = 20 mm 的圆截面钢梁受力如图,已知弹性模量 E = 200 GPa , d = 200mm ,欲将其中段A3弯成 ° = 12 m 的圆弧,试求所需载荷,并计算最大弯曲北应力。
7. 钢筋横截面积为密度为° ,放在刚性平面上,一端加力提起钢筋离F2//3厂P(B)r试证明,此梁上,下翼缘承担 解:14而—第57页Ah/2h/2B开地面长度丄。
试问F应多大?3解:截面C曲率为零8.矩形截面钢条长/,总重为F,放在刚性水平面上,在钢条A端作用乂向上3 的拉力时,试求钢条内最大正应力。
解:在截面C处,有丄=^=0p EIAC段可视为受均布载荷§作用的简支梁9.图示组合梁山正方形的铝管和正方形钢杆套成,在两端用刚性平板牢固联接。
已知:钢和铝的弹性模量关系为£s=3£a;在纯弯曲时,应力在比例极限内。
材料力学习题解答(弯曲应力)

6.1. 矩形截面悬臂梁如图所示,已知l =4m , b /h =2/3,q =10kN/m ,[σ]=10MPa ,试肯定此梁横截面的尺寸. 解:(1) 画梁的弯矩图由弯矩图知:(2) 盘算抗弯截面系数32323669h bh h W ===(3) 强度盘算22maxmax 33912[]29416 277ql M ql h Wh h mm b mmσσ===⋅≤∴≥==≥6.2. 20a 工字钢梁的支承和受力情形如图所示,若[σ]=160MPa ,试求允许载荷.解:(1)画梁的弯矩图(2) 查表得抗弯截面系数6323710W m -=⨯(3) 强度盘算max max 66223[]33[]3237101601056.8822PM P W W WW P kNσσσ-===⋅≤⨯⨯⨯⨯∴≤==取允许载荷No20ax ql x[]57P kN =6.3. 图示圆轴的外伸部分系空心轴.试作轴弯矩图,并求轴内最大正应力.解:(1)(2) C 截面:3max3332 1.341063.20.0632C C C C C M M MPa d W σππ⨯⨯====⨯B 截面:3max3434440.91062.10.060.045(1)(1)32320.06B B B BB B B M M MPa D d W D σππ⨯====⨯--(3) 轴内的最大正应力值MPa C 2.63max max ==σσ6.5.把直径d =1m 的钢丝绕在直径为2m 的卷筒上,设E =200GPa,试盘算钢丝中产生的最大正应力. 解:(1) 由钢丝的曲率半径知1M E M EI I ρρ=∴=(2) 钢丝中产生的最大正应力93max200100.510100 1MR ER MPa I σρ-⨯⨯⨯====6.8. 压板的尺寸和载荷如图所示.材料为45钢,σs =380MPa ,取安全系数n=1.5.试校核压板的强度.x解:(1)(2) 232363330.030.0212(1)(1) 1.568106620bH hW m H -⨯=-=-=⨯(3) 强度盘算许用应力380[]2531.5SMPa nσσ===强度校核max 6308196[]1.56810A M MPa W σσ-===⨯压板强度足够.6.12.图示横截面为⊥形的铸铁推却纯曲折,材料的拉伸和紧缩许用应力之比为[σt ]/[σc ]=1/4.求程度翼缘的合理宽度b .解:(1) ,max 11320 c c y mm=(2) 由截面形心地位()()304006017060370320304006060510 i CiC iA y b y Ab b mm⨯-⨯+⨯⨯===⨯-+⨯=∑∑6.13. ⊥形截面铸铁梁如图所示.若铸铁的许用拉应力为[σt ]=40MPa ,许用压应力为[σc ]=4P . 解:(1)(2) A ()22max 86320.8[][]101801016010132.60.80.825096.410A C C zC zCzC C M h Ph I I I P kN h σσσ--==≤⨯⨯⨯∴≤==-⨯A 截面的最大拉应力11max 86310.8[][]1018010401052.80.80.896.410A t t zC zCzC t M h Ph I I I P kNh σσσ--==≤⨯⨯⨯∴≤==⨯⨯C 截面的最大拉应力()22max 86320.6[][]1018010401044.20.60.625096.410C t t zC zCzC t M h Ph I I I P kN h σσσ--==≤⨯⨯⨯∴≤==-⨯取许用载荷值[]44.2P kN =6.14. 铸铁梁的载荷及截面尺寸如图所示.许用拉应力[σl ]=40MPa ,许用压应力[σc ]=160MPa .解:(1) 画梁的弯矩图(2) 盘算截面几何性质42.572.522264157.542.53020021520030100157.5 30200200303020060.12510i CiC i zCAA y y mmAIy dA y dy y dy m --⨯⨯+⨯⨯===⨯+⨯==⨯⨯+⨯⨯=⨯∑∑⎰⎰⎰(3) 强度盘算B 截面的最大压应力3max620100.157552.4 []60.12510B C C C zC M y MPa I σσ-⨯⨯===⨯B 截面的最大拉应力3max6(0.23)2010(0.230.1575)24.12 []60.12510B C t t zC M y MPa I σσ--⨯-===⨯C 截面的最大拉应力3max610100.157526.2 []60.12510C C t t zC M y MPa I σσ-⨯⨯===⨯梁的强度足够.(4) 评论辩论:当梁的截面倒置时,梁内的最大拉应力产生在B 截面上.3max620100.157552.4 []60.12510B C t t ZC M y MPa I σσ-⨯⨯===⨯梁的强度不够.6.19. 试盘算图示工字形截面梁内的最大正应力和最大剪应力. xmax max 15 20 Q kN M kNm==(2) 查表得截面几何性质3*max14113.8 6z z I W cm cm b mmS ===(3) 盘算应力最大剪应力*3max max max151018.10.0060.138Z Z Q S MPabI τ⨯===⨯最大正应力3max max62010141.814110M MPa W σ-⨯===⨯6.22. 起重机下的梁由两根工字钢构成,起重机自重Q=50kN ,起重量P=10kN .许用应力[σ]=160MPa ,[τ]=100MPa .若暂不斟酌梁的自重,试按正应力强度前提选定工字钢型号,然后再按剪应力强度前提进行校核.解:(1)(2) (3) C 截面:B()(506)()501204.17C C M x x x dM x x dxx m =-=-==此时C 和D 截面的弯矩是104.25 134.05C D M kNm M kNm==D 截面:()(106)(8)()381203.17D D M x x x dM x x dxx m =+-=-==此时C 和D 截面的弯矩是98.27 140.07C D M kNm M kNm==最大弯矩值是max 140.07 M kNm=(4) 按最大正应力强度前提设计查表取25b *max1021.3z z I b mm cmS==(5) 按剪应力强度校核当起重机行进到最右边时(x =8m ),梁内剪应力最大; x剪应力强度盘算*3max maxmax581013.6[]220.010.213zzQ SMPabIττ⨯===⨯⨯剪应力强度足够.6.23. 由三根木条胶合而成的悬臂梁截面尺寸如图所示,跨度l=1 m.若胶合面上的许用切应力为0.34 MPa,木材的许用曲折正应力为[σ[τ]=1 MPa,试求允许载荷P解:(1)max maxQ P M Pl==(2) 梁曲折正应力强度前提maxmax2262[]16[]10100.10.153.75661M PlW bhbhP kNlσσσ==≤⨯⨯⨯≤==⨯(3) 梁曲折切应力强度前提maxmax633[]222[]21100.10.151033Q PA bhbhP kNτττ==≤⨯⨯⨯⨯≤==(4)胶合面上切应力强度前提2222max1336312222[]244212[]0.34100.10.153.8250.15660.02544zQ h P hy ybhIbhP kNhyτττ⎛⎫⎛⎫=-=-≤⎪ ⎪⎝⎭⎝⎭⨯⨯⨯⨯≤==⎛⎫⎛⎫--⎪ ⎪⎝⎭⎝⎭允许载荷:[P]=3.75 kN.6.27.在图中,梁的总长度为l ,受均布载荷q 感化.若支座可对称地向中点移动,试问移动距离为若干时,最为合理? 解:(1) 束缚反力2B C ql R R ==(2) 截面上的最大正弯矩和最大负弯矩22,max 2,max228822ql l ql ql qla M a qa M +-⎛⎫=--=- ⎪⎝⎭=-(3) 二者数值相等时最为合理2222822440410.20782ql qla qa a la l l a l l-=+-=-+-+===。
材料力学-弯曲应力

超静定梁
q
Hale Waihona Puke L/2L/2q
L
M
M
*
5-6 提高梁强度的主要措施
合理设计截面
合理放置截面
增大 WZ
*
5-6 提高梁强度的主要措施
合理放置截面
*
5-6 提高梁强度的主要措施
合理设计截面
*
5-6 提高梁强度的主要措施
合理设计截面
*
充分利用材料特性合理设计截面
脆性材料:
宜上下不对称截面:
T 形,不等边工字型,不等边矩形框等;
中性轴偏向受拉区的一侧
理想的中性轴的位置: 应是最大拉应力和最大压应力同时达到许用应力。
*
讨论:钢筋混凝土楼板,钢筋应该铺设在哪一边?
等强梁的概念与应用
等截面梁WZ为常数,横力弯曲时弯矩M是随截面位置变化的。只有|M|max位置的横截面上应力达到[]。 不合理!
某车间欲安装简易吊车,大梁选用工字钢。已知电葫芦自重
材料的许用应力
起重量
跨度
试选择工字钢的型号。
例题
(4)选择工字钢型号
(5)讨论
(3)根据
计算
(1)计算简图
(2)绘弯矩图
解:
36c工字钢
*
作弯矩图,寻找需要校核的截面
要同时满足
分析:
非对称截面,要寻找中性轴位置
T型截面铸铁梁,截面尺寸如图示。
强度条件
h
max
*
叠合梁问题
悬臂梁由三块木板粘接而成。跨度为1m。胶合面的许可切应力为0.34MPa,木材的〔σ〕= 10 MPa,[τ]=1MPa,求许可载荷
1.画梁的剪力图和弯矩图
弯曲应力习题

弯曲应力小结一、常用公式 (1)惯性矩公式(2)弯曲正应力公式(3)正应力强度校核(4)形心计算公式11ni cic niA yy A=∑∑(5)平行轴公式22,y yc z zc I I a A I I b A =+=+I b h Z =312,W b h Z =26I d Z =π464,W d Z =π332σ=M y I zmaxmax []ZM W σσ=≤二、补充习题1、受均布载荷作用的简支梁如图所示,试求: (1)1—1截面上1、2两点的正应力; (2)此截面上的最大正应力; (3)全梁的最大正应力;160M kNm =,545.83210z I m -=⨯,436.4810z W m -=⨯,1261.7MPa σσ==1max 92.6MPa σ=,max 104.2MPa σ=2、受纯弯曲的空心圆截面梁如图所示。
已知:弯矩M= l kN.m ,外径D=50mm ,内径d=25mm 。
试求横截面上a 、b 、c 及d 四点的应力。
74I 2.8810m z -=⨯,86.8MPa()a σ=压应力,43.4MPa()b σ=拉应力75.3MPa()c σ=压应力,0d σ=3、已知槽形截面梁弯矩如图所示,试求梁横截面上的最大拉应力。
(1)求形心mm 317mm 400250500350200400250250500350=⨯-⨯⨯⨯-⨯⨯=y过形心C 取z 轴,截面对z 轴的惯性矩为23z )250317(500350500350121{I -⨯⨯+⨯⨯=423mm ]})200317(300250400250121[-⨯⨯+⨯⨯- 46mm 101728⨯=B 截面的最大拉应力为MPa 06.1Pa )10(10172810)317500(101043633max =⨯⨯⨯-⨯⨯==--y I M σz B BtC 截面的最大拉应力为MPa 38.1Pa )10(10172810317105.743633max =⨯⨯⨯⨯⨯==--y I M σz C Ct可见,梁的最大拉应力发生在C 截面的下部边缘线上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.1. 矩形截面悬臂梁如图所示,已知l =4 m , b / h =2/3,q =10 kN/m ,[σ]=10 MPa ,试确定此梁横截面的尺寸。
解:(1) 画梁的弯矩图由弯矩图知:2max2ql M = (2) 计算抗弯截面系数32323669hbh h W === (3) 强度计算22maxmax 33912[]29416 277ql M ql h Wh h mm b mmσσ===⋅≤∴≥==≥ 6.2. 20a 工字钢梁的支承和受力情况如图所示,若[σ]=160 MPa ,试求许可载荷。
解:(1) 画梁的弯矩图由弯矩图知:No20a xql 2xmax 23P M =(2) 查表得抗弯截面系数6323710W m -=⨯(3) 强度计算max max 66223[]33[]3237101601056.8822PM P W W WW P kNσσσ-===⋅≤⨯⨯⨯⨯∴≤== 取许可载荷[]57P kN =6.3. 图示圆轴的外伸部分系空心轴。
试作轴弯矩图,并求轴内最大正应力。
解:(1) 画梁的弯矩图由弯矩图知:可能危险截面是C 和B 截面 (2) 计算危险截面上的最大正应力值C 截面:3max3332 1.341063.20.0632C C C C C M M MPa d W σππ⨯⨯====⨯ B 截面:3max3434440.91062.10.060.045(1)(1)32320.06B B B BB B B M M MPa D d W D σππ⨯====⨯-- (3) 轴内的最大正应力值MPa C 2.63max max ==σσx6.5. 把直径d =1 m 的钢丝绕在直径为2 m 的卷筒上,设E =200 GPa ,试计算钢丝中产生的最大正应力。
解:(1) 由钢丝的曲率半径知1M E MEI Iρρ=∴=(2) 钢丝中产生的最大正应力93max200100.510100 1MR ER MPa I σρ-⨯⨯⨯====6.8. 压板的尺寸和载荷如图所示。
材料为45钢,σs =380 MPa ,取安全系数n=1.5。
试校核压板的强度。
解:(1) 画梁的弯矩图由弯矩图知:危险截面是A 截面,截面弯矩是308A M Nm =(2) 计算抗弯截面系数232363330.030.0212(1)(1) 1.568106620bH h W m H -⨯=-=-=⨯(3) 强度计算许用应力380[]2531.5SMPa nσσ=== 强度校核max 6308196[]1.56810A M MPa W σσ-===⨯ 压板强度足够。
1A-Ax6.12. 图示横截面为⊥形的铸铁承受纯弯曲,材料的拉伸和压缩许用应力之比为[σt ]/[ σc ]=1/4。
求水平翼缘的合理宽度b 。
解:(1) 梁截面上的最大拉应力和最大压应力()[][]11,max ,max ,max 1,max 11400 40014320 t c zzt t c c M y My I I y y y mmσσσσσσ-==-====(2) 由截面形心位置()()304006017060370320304006060510 i CiCiA y b y Ab b mm⨯-⨯+⨯⨯===⨯-+⨯=∑∑6.13. ⊥形截面铸铁梁如图所示。
若铸铁的许用拉应力为[σt ]=40 MPa ,许用压应力为[σc ]=160 MPa ,截面对形心z c 的惯性矩I zc =10180 cm 4,h 1=96.4 mm ,试求梁的许用载荷P 。
解:(1) 画梁的弯矩图由弯矩图知:可能危险截面是A 和C 截面 (2) 强度计算A 截面的最大压应力Bz C x()22max 86320.8[][]101801016010132.60.80.825096.410A C C zC zCzC C M h Ph I I I P kN h σσσ--==≤⨯⨯⨯∴≤==-⨯A 截面的最大拉应力11max 86310.8[][]1018010401052.80.80.896.410A t t zC zCzC t M h Ph I I I P kN h σσσ--==≤⨯⨯⨯∴≤==⨯⨯C 截面的最大拉应力()22max 86320.6[][]1018010401044.20.60.625096.410C t t zC zCzC t M h Ph I I I P kN h σσσ--==≤⨯⨯⨯∴≤==-⨯取许用载荷值[]44.2P kN =6.14. 铸铁梁的载荷及截面尺寸如图所示。
许用拉应力[σl ]=40 MPa ,许用压应力[σc ]=160MPa 。
试按正应力强度条件校核梁的强度。
若载荷不变,但将T 形截面倒置成为⊥形,是否合理?何故?解:(1) 画梁的弯矩图由弯矩图知:可能危险截面是B 和C 截面 (2) 计算截面几何性质形心位置和形心惯性矩42.572.522264157.542.53020021520030100157.5 30200200303020060.12510i Ci C i zCAA y y mmAIy dA y dy y dy m --⨯⨯+⨯⨯===⨯+⨯==⨯⨯+⨯⨯=⨯∑∑⎰⎰⎰x(3) 强度计算B 截面的最大压应力3max620100.157552.4 []60.12510B C C C zC M y MPa I σσ-⨯⨯===⨯ B 截面的最大拉应力3max6(0.23)2010(0.230.1575)24.12 []60.12510B C t t zC M y MPa I σσ--⨯-===⨯C 截面的最大拉应力3max610100.157526.2 []60.12510C C t t zC M y MPa I σσ-⨯⨯===⨯ 梁的强度足够。
(4) 讨论:当梁的截面倒置时,梁内的最大拉应力发生在B 截面上。
3max620100.157552.4 []60.12510B C t t ZC M y MPa I σσ-⨯⨯===⨯梁的强度不够。
6.19. 试计算图示工字形截面梁内的最大正应力和最大剪应力。
解:(1) 画梁的剪力图和弯矩图最大剪力和最大弯矩值是max max 15 20 Q kN M kNm ==(2) 查表得截面几何性质3*max14113.8 6z z I W cm cm b mm S===(3) 计算应力最大剪应力No16 Qxx*3max max max151018.10.0060.138Z Z Q S MPa bI τ⨯===⨯最大正应力3max max62010141.814110M MPa W σ-⨯===⨯ 6.22. 起重机下的梁由两根工字钢组成,起重机自重Q=50 kN ,起重量P=10 kN 。
许用应力[σ]=160 MPa ,[τ]=100 MPa 。
若暂不考虑梁的自重,试按正应力强度条件选定工字钢型号,然后再按剪应力强度条件进行校核。
解:(1) 分析起重机的受力由平衡方程求得C 和D 的约束反力10 50C D R kN R kN ==(2) 分析梁的受力由平衡方程求得A 和B 的约束反力x R x R B A 610 650+=-=(3) 确定梁内发生最大弯矩时,起重机的位置及最大弯矩值C 截面:()(506)()501204.17C C M x x x dM x x dxx m=-=-==BR此时C 和D 截面的弯矩是104.25 134.05C D M kNm M kNm ==D 截面:()(106)(8)()381203.17D D M x x x dM x x dxx m=+-=-== 此时C 和D 截面的弯矩是98.27 140.07C D M kNm M kNm ==最大弯矩值是max 140.07 M kNm =(4) 按最大正应力强度条件设计maxmax 33max 6[]2140.0710438 2[]216010M WM W cm σσσ=≤⨯∴≥==⨯⨯查表取25b 工字钢(W=423 cm 3),并查得*max1021.3z z I b mm cm S ==(5) 按剪应力强度校核当起重机行进到最右边时(x =8 m ),梁内剪应力最大;最大剪力值是max 58 Q kN =xQ剪应力强度计算*3max max max581013.6[]220.010.213z z Q S MPa bI ττ⨯===⨯⨯剪应力强度足够。
6.23. 由三根木条胶合而成的悬臂梁截面尺寸如图所示,跨度l =1 m 。
若胶合面上的许用切应力为0.34 MPa ,木材的许用弯曲正应力为[σ]=10 MPa ,许用切应力为[τ]=1 MPa ,试求许可载荷P 。
解:(1) 截面上的最大剪力和弯矩max max Q P M Pl ==(2) 梁弯曲正应力强度条件max max 2262[]16[]10100.10.15 3.75 661M PlW bhbh P kNl σσσ==≤⨯⨯⨯≤==⨯ (3) 梁弯曲切应力强度条件max max 633[]222[]21100.10.1510 33Q PA bhbh P kNτττ==≤⨯⨯⨯⨯≤== (4)胶合面上切应力强度条件2222max 1336312222[]244212[]0.34100.10.15 3.825 0.15660.02544z Q h P h y y bh I bh P kN h y τττ⎛⎫⎛⎫=-=-≤ ⎪ ⎪⎝⎭⎝⎭⨯⨯⨯⨯≤==⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭许可载荷:[P ]=3.75 kN 。
6.27. 在图中,梁的总长度为l ,受均布载荷q 作用。
若支座可对称地向中点移动,试问移动距离为若干时,最为合理?AD解:(1) 约束反力2B C ql R R ==(2) 截面上的最大正弯矩和最大负弯矩22,max2,max 228822ql l ql ql qla M a qa M +-⎛⎫=--=- ⎪⎝⎭=-(3) 二者数值相等时最为合理222282244010.2072ql qla qa a la l a l l-=+-=-+===。
