3.2地图投影及其分类,3.3常用的地图投影解析
3.2地图投影及其分类,3.3常用的地图投影解析PPT参考幻灯片
轴投影
5
§3 常用的地图投影
❖ 1.墨卡托投影(等角正圆柱投影) 投影原理:设想地球为一透明球体,球心置一点光
源,将圆柱投影面沿赤道与地球相切,地球上的经纬网格投 影到圆柱面上
6
墨卡托投影绘制的世界地图
§3 常用的地图投影
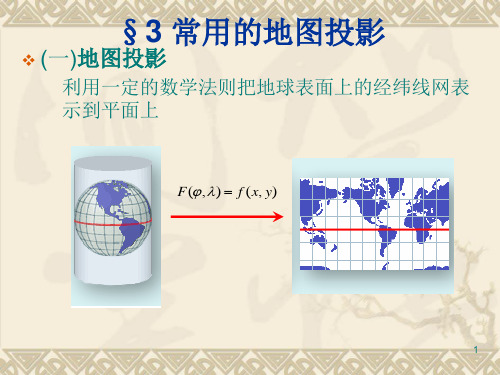
❖ (一)地图投影
利用一定的数学法则把地球表面上的经纬线网表 示到平面上
F(, ) f (x, y)
1
❖ 1. 地图投影的失真
由于地球椭球体表面是曲面,而地图通常是要绘制在平 面图纸上,因此制图时首先要把曲面展为平面,然而球 面是个不可展的曲面,即把它直接展为平面时,不可能 不发生破裂或褶皱。
为了保证地图的精度,采用分带投影方法,即将投 影范围的东西界加以限制,使其失真不超过一定的 限度,这样把许多带结合起来,可成为整个区域的 投影。
我国规定1:1 万、1:2.5 万、1:5 万、1:10万、 1:25 万、1:50 万比例尺地形图,均采用高斯克 -吕格投影。1:2.5 至1:50 万比例尺地形图采用 经差6 °分带,1:1 万比例尺地形图采用经差3° 分带。
绘制机场专用航图和涉及仪表飞行程序的基础用图; 国家大地测量和五十万分之一及更大比例尺的国家基本地形
图
13
❖ 高斯投影坐标网
经纬网(地理坐标网)
114°00 14
16
30° 202
40´
α
3396
94 -δ TH/TC
92
18 20 A( 20218 , 3394 )
90
TH/TC= α+(± δ)
几种常见地图投影各自的特点及其分带方法

几种常见地图投影各自的特点及其分带方法高斯-克吕格(Gauss-Kruger)投影,是一种“等角横切圆柱投影”。
德国数学家、物理学家、天文学家高斯(Carl Friedrich Gauss,1777一1855)于十九世纪二十年代拟定,后经德国大地测量学家克吕格(Johannes Kruger,1857~1928)于1912年对投影公式加以补充,故名。
设想用一个圆柱横切于球面上投影带的中央经线,按照投影带中央经线投影为直线且长度不变和赤道投影为直线的条件,将中央经线两侧一定经差范围内的球面正形投影于圆柱面。
然后将圆柱面沿过南北极的母线剪开展平,即获高斯一克吕格投影平面。
一、只谈比较常用的几种:“墨卡托投影”、“高斯-克吕格投影”、“UTM投影”、“兰勃特等角投影”1.墨卡托(Mercator)投影1.1 墨卡托投影简介墨卡托(Mercator)投影,是一种" 等角正切圆柱投影”,荷兰地图学家墨卡托(Gerhardus Mercator 1512-1594)在1569年拟定,假设地球被围在一中空的圆柱里,其标准纬线与圆柱相切接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。
墨卡托投影没有角度变形,由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。
墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关系的正确。
在地图上保持方向和角度的正确是墨卡托投影的优点,墨卡托投影地图常用作航海图和航空图,如果循着墨卡托投影图上两点间的直线航行,方向不变可以一直到达目的地,因此它对船舰在航行中定位、确定航向都具有有利条件,给航海者带来很大方便。
“海底地形图编绘规范”(GB/T 17834-1999,海军航保部起草)中规定1:25万及更小比例尺的海图采用墨卡托投影,其中基本比例尺海底地形图(1:5万,1:25万,1:100万)采用统一基准纬线30°,非基本比例尺图以制图区域中纬为基准纬线。
世界地图常用地图投影知识大全

世界地图常用地图投影知识大全2009-09-30 13:20在不同的场合和用途下使用不同的地图投影,地图投影方法及分类名目众多,象:墨卡托投影,空间斜轴墨卡托投影,桑逊投影,摩尔维特投影,古德投影,等差分纬线多圆锥投影,横轴等积方位投影,横轴等角方位投影,正轴等距方位投影,斜轴等积方位投影,正轴等角圆锥投影,彭纳投影,高斯-克吕格投影,等角圆锥投影等等。
一、世界地图常用投影1、等差分纬线多圆锥投影(Polyconic Projection With Meridional Interval o nSame Parallel Decrease AwayFrom Central Meridian by E qual Difference)普通多圆锥投影的经纬线网具有很强的球形感,但由于同一纬线上的经线间隔相等,在编制世界地图时,会导致图形边缘具有较大面积变形。
1963年中国地图出版社在普通多圆锥投影的基础上,设计出了等差分纬线多圆锥投影。
等差分纬线多圆锥投影的赤道和中央经线是相互垂直的直线,中央经线长度比等于1;其它纬线为凸向对称于赤道的同轴圆弧,其圆心位于中央经线的延长线上,中央经线上的纬线间隔从赤道向高纬略有放大;其它经线为凹向对称于中央经线的曲线,其经线间隔随离中央经线距离的增加而按等差级数递减;极点投影成圆弧(一般被图廓截掉),其长度等于赤道的一半(图2-30)。
通过对大陆的合理配置,该投影能完整地表现太平洋及其沿岸国家,突出显示我国与邻近国家的水陆关系。
从变形性质上看,等差分纬线多圆锥投影属于面积变形不大的任意投影。
我国绝大部分地区的面积变形在10%以内。
中央经线和±44º纬线的交点处没有角度变形,随远离该点变形愈大。
全国大部分地区的最大角度变形在10º以内。
等差分纬线多圆锥投影是我国编制各种世界政区图和其它类型世界地图的最主要的投影之一。
类似投影还有正切差分纬线多圆锥投影(Polyconic Projectionwith Me ridional Intervals on Decrease Away From Central Meridian by T angent),该投影是1976年中国地图出版社拟定的另外一种不等分纬线的多圆锥投影。
20种地图投影

20种地图投影通用横向墨卡托投影(U T M )通用横向墨卡托投影是横轴等角割圆柱投影,圆柱割地球于两条等高圈。
该投影将地球划分为60个投影带,每带经差为6度,已被许多国家作为地形图的数学基础。
一般从南纬度80到北纬度84度的范围内使用该投影,对于两极地区则采用UPS投影(通用球面极投影)。
亚尔伯斯等积圆锥投影亚尔伯斯等积圆锥投影即为双标准纬线投影,也即正轴等面积割圆锥投影。
该投影经纬网的经线为辐射直线,纬线为同心圆圆弧。
亚尔伯斯等积圆锥投影的应用在编制一些行政区划图,人口地图,地势图等方面应用较广。
如中国地势图,即是以Q1=25度,Q2=45度的亚尔伯斯等积圆锥投影。
兰伯特等角圆锥投影兰伯特等角圆锥投影也称兰勃脱正形圆锥投影,该投影的微分圆投影后仍为圆形。
经线为辐射直线,纬线为同心圆圆弧。
指定两条标准纬度线Q1,Q2,在这两条纬度线上没有长度变形,即M=N=1。
此种投影也叫等角割圆锥投影,可用来编制中,小比例尺地图。
等角圆锥投影有广泛的应用,特别适宜于作为中纬度处沿纬度线伸展的制图区域之投影,投影后经线为辐射直线,纬度线为同心圆圆弧。
我国的分省图,即为两条标准纬度线为Q1=25度,Q2=45度的兰伯特等角圆锥投影。
1962年以后,百万分一地图采用了等角圆锥投影(南纬度80度,北纬度84度),极区附近,采用等角方位投影(极球面投影)。
地图分幅为:纬度60以下,纬度差4 经差6度分幅纬度60-76,纬度差4 经差12度分幅纬度76-84,纬度差4 经差24度分幅纬度84-88,纬度差4 经差36度分幅88-90仍为一幅图每幅图内两条标准纬线的纬度:Q1=QS+40分(南纬度) Q2=QN-40分(北纬度)投影后经线是辐射直线,东西图幅可完全拼接,南北图幅有裂隙。
我国采用等角割圆锥,Q1=PHIS+35分Q2=PHIN-35分墨卡托投影(等角正圆柱投影)等角正圆柱投影也称墨卡托投影,经纬线投影为互相正交的平行直线。
测绘中常用的地图投影方法介绍

测绘中常用的地图投影方法介绍地图投影是地图制作中不可或缺的一部分,它将地球的曲面投影到一个平面上。
在测绘学中,有许多不同的地图投影方法,每一种方法都有自己的特点和适用范围。
本文将介绍一些常用的地图投影方法。
一、正轴等积圆柱投影法正轴等积圆柱投影法是最早出现的地图投影方法之一。
它以一个圆柱体为投影面,将地球的表面投影到圆柱体上,再展开成一个平面地图。
这种投影方法保持了等积性,即相等面积的地图上的面积在实际地球上也是相等的。
这使得正轴等积圆柱投影法在制作区域较大的地图时非常有用。
然而,在投影过程中,经纬度线不再是直线,而是弯曲的。
因此,这种投影方法在导航和航海等领域的应用相对较少。
二、墨卡托投影法墨卡托投影法是目前应用最广泛的地图投影方法之一。
它以一个圆柱体为投影面,将地球的表面投影到圆柱体上,再展开成一个平面地图。
与正轴等积圆柱投影法不同,墨卡托投影法保持了等角性,即相等角度的地图上的角度在实际地球上也是相等的。
这使得墨卡托投影法在导航和地图浏览等领域广受欢迎。
此外,墨卡托投影法也可以用于制作世界地图,因为它能够较为准确地展示各个地区的形状和比例关系。
三、兰勃托投影法兰勃托投影法是一种圆锥投影方法,它以一个圆锥体为投影面,将地球的表面投影到圆锥体上,再展开成一个平面地图。
兰勃托投影法保持了等距性,即相等距离的地图上的距离在实际地球上也是相等的。
这使得兰勃托投影法在制作航空地图和地理信息系统等领域得到广泛应用。
然而,由于地球是一个几乎球体状的物体,圆锥体无法完全覆盖地球的各个地区,因此在使用兰勃托投影法时需要选择合适的投影中心和标准纬度,以确保地图的准确性和正确性。
四、极射赤面投影法极射赤面投影法是一种特殊的地图投影方法,它以地球的南极或北极为投影中心,将地球的表面投影到一个平面上。
在这种投影方法中,赤道直径上的距离得以保持不变,而纬度线则以放射状的形式展开。
极射赤面投影法在制作地图时可以保持地球的真实形状,但是在极地地区附近的区域会有较大的变形。
常用的几种地图投影

常用的几种地图投影常用的几种地图投影转自#从世界范围看,各国大中比例尺地形图所使用的投影很不统一,据不完全统计有十几种之多,最常用的有横轴等角椭圆柱投影等。
中华人民共和国成立后,我国大中比例尺地形图一律规定采用以克拉索夫斯基椭球体元素计算的高斯-克吕格投影。
我国新编1:100万地形图,采用的则是边纬与中纬变形绝对值相等的正轴等角圆锥投影。
一、高斯-克吕格投影高斯-克吕格投影是一种等角横切椭圆柱投影,见图6-1所示。
我国现行的大于1:50万地形图都采用高斯-克吕格投影。
其中大于1:1万及更大比例尺地形图采用按经差3o分带,1: 2.5万~1:50万比例尺的地形图采用经差6o分带。
图6-1 高斯-克吕格投影示意图高斯-克吕格投影,欧美一些国家称之为横轴等角墨卡托投影。
美国及其它一些国家地形图使用的UTM投影(Universal Transverse Mercatol Projection,即通用横轴墨卡托投影),亦属横轴等角椭圆柱投影的系列。
UTM投影与高斯-克吕格投影的区别在于,该投影是横轴等角割椭圆柱投影。
UTM投影,在投影带内有两条长度比等于1的标准经线,而中央经线的长度比为0.9996。
因而使投影带内变形差异更小,其最大长度变形不超过0.04%。
坐标网的规定:坐标网是地图上地理坐标网(经纬网)和直角坐标网(方里网)的总称。
编绘地图时,坐标网是绘制地图图形的控制网。
使用地图时可以根据它确定地面点的位置和进行各种量算。
一般的地图只绘经纬网,在高斯-克吕格投影的地图上,为了迅速而准确地确定方向、距离、面积等,还绘有方里网,具体规定为:1.经纬网经纬网是由经线和纬线组成的坐标网。
它标示制图物体在地图上的地理位置,故又称为地理坐标网。
在1:1万~1:10万的地形图上,内图廓即是经纬线。
为了在使用时能够加密成网,在内外图廓间绘有分度带,需要时将对应点连线就构成经纬线网。
在1:20万~1:100万地形图上,图廓本身是经纬线,图面上直接绘出经纬线网,并在内图廓和图内经纬线网格上绘有按规定间隔供加密的分割线。
地图投影
变形规律
常见投影及其用途
经纬网的形状
正轴方位投影
纬线为同心圆 经线为放射直线
横轴方位投影
中央经线与赤道为互相垂直的直 线,其余经线为对称中经的曲线, 其余纬线为对称赤道的曲线
斜轴方位投影
变形规律
切点或割线无变形 等变形线以投影中心为圆心呈同心圆分布。
常见投影及其用途
正轴等积方位投影--南北两极图
§3 地 图 投 影
地图投影简介
地图投影是地图学重要组成部分之一,是构成地图的数 学基础,在地图学中的地位是相当重要的。地图投影研 究的对象就是如何将地球体表面描写到平面上,也就是 研究建立地图投影的理论和方法,地图投影的产生、发 展、直到现在,已有一千多年的历史,研究的领域也相 当广泛,实际上它已经形成了一门独立的学科。 我们学习投影的目的主要是了解和掌握最常用、最基本 的投影性质和特点以及他们的变形分布规律,从而能够 正确的辨认使用各种常用的投影。
(1)方位投影:即平面投影。以平面作为辅助投 影面,使球体与平面相切或相割,将球体表面上 的经纬网投影到平面上构成的一种投影。
根据球面与投影面之间的相对部位不同,分为正 轴方位投影、横轴方位投影、斜轴方位投影。
方位投影的特性:从投影中心向各个方向引出 的方向线投影后方位不变。
平面与球面相切或相割处无变形,故称 标准点或标准线。 等变形线是以投影中心为圆心的同心圆。
圆柱投影经纬网特征
(3)圆锥投影:以圆锥表面作为辅助投影面,使球 体与圆锥表面相切或相割,将球体表面上的经纬网 投影到圆锥表面上,然后再将圆锥表面展成平面而 构成的一种投影。 根据球面与投影面之间的相对部位不同,分为正轴圆柱 投影、横轴圆柱投影、斜轴圆柱投影。
圆锥投影经纬网的特征
地理科普25种地图投影类型

地理科普25种地图投影类型地理520公众号ID:dilizhishi520地图投影——作为GIS领域的专业词,小伙伴们一定不会陌生,甚至还时常为用什么地图投影而一度纠结。
所谓没有不变形的地图投影,根据场景选择适合自己的投影才是最好的。
小编收集了25种地图投影示例,从常见类型到新奇投影~为各位在地图制作时提供直观参考。
你最喜欢哪个?都用过哪些?欢迎留言讨论01.Aitoff埃托夫地图投影它是由俄罗斯制图员 David A. Aitoff 于 1889 年开发而成,埃托夫投影是经过改进的方位投影。
它是采用椭圆形经纬网的折衷投影。
此投影适用于绘制小比例的世界地图。
02.Azimuthal Equidistant等距方位投影等距方位投影是指使图上面积和相应的实际地面面积相等的方位投影,分为正轴,横轴、斜轴投影。
等距方位投影可以保留距中心点的距离和方向。
将地球上的所有点投影到一个平面上。
03.Behrmann贝尔曼投影贝尔曼投影是圆柱等积地图投影的一种,其标准纬线设置为南北纬30°。
由于其等积的属性,它可以高度压缩极地地区。
04.Berghaus Star AAG柏格斯星状投影也叫星状投影Hermann Berghaus 于 1879 年设计了此投影。
通常以北极为中心,可最小化大陆板块中的间断。
“美国地理学家协会”在1911 年将其中一种样式的柏哥斯星状投影用到了徽标中。
05.Bonne彭纳投影彭纳投影是一种等积伪圆锥地图投影。
其经纬网采用心形,且经常用于绘制大陆地图。
该投影是由 Claudius Ptolemy 于公元 100 年发明的,但是由于 Rigobert Bonne 在 1752 年广泛使用了这种投影,因此以他的名字命名。
06.Cassini卡西尼投影该横轴圆柱投影在沿中央子午线和所有平行于它的线的方向上,其比例保持不变,它既不是等积投影也不是等角投影。
主要适用于为北-南范围区域的大比例尺制图。
地图投影与分类

第四章海图海图(chart)是为适应航海的需要而绘制的一种地图,图上详细地标绘了航海所需要的资料,如岸形、岛屿、礁石、浅滩、水深、底质、水流资料、以及助航设施等。
海图可用于船舶航行前拟定计划航线、制定航行计划;航行中可用于航迹推算、定位与导航;航次结束后可用于总结航行经验,如发生海事可用于判断事故责任。
因此,海图是航海必备的航海资料和工具。
正确地了解海图的特点、熟悉海图上的资料、正确地使用管理海图,是船舶驾驶员的重要任务之一。
第一节地图投影与分类一、地图投影1.地图:按照一定的数学法则,将地面上的一部分或全部按照一定的比例尺绘画在平面上。
2.地图投影(map projection):将地球表面的经、纬线绘画到平面上去,成为地图的经、纬线图网的方法。
3.“地图图网”:在既定的地图投影上的经、纬线图网。
4.投影变形:用投影的方法,解决了地球曲面与地图平面之间的转化,但投影图象不能完全与地球表面相符。
5.投影变形可分为长度变形、面积变形和角度变形。
二、地图投影分类1.按投影变形的性质分类1) 等角投影(equiangle projection),又称正形投影。
定义:指投影面上任意两方向的夹角与地面上对应的角度相等。
性质:在微小的范围内,可以保持图上的图形与实地相似;不能保持其对应的面积成恒定的比例;图上任意点的各个方向上的局部比例尺都应该相等;不同地点的局部比例尺,是随着经、纬度的变动而改变的。
2) 等积投影(equalarea projection)定义:保持地球上的面积与地图上所对应的面积成恒定比例的一种投影方法。
性质:保持等积就不能同时保持等角。
3) 任意投影(orthographic projection)定义:既不是等角投影,又不是等积投影,是根据某种特殊需要或为了解决某种特定问题,而制作的一种地图投影方法。
如大圆海图。
2.按构制地图图网的方法分类1) 平面投影(plane projection),又称方位投影∶定义:将地球表面上的经、纬线投影到与球面相切或相割的平面上去的投影方法;平面投影大都是透视投影,即以某一点为视点,将球面上的图象直接投影到投影面上去。
三种常用地图投影介绍地理ppt

λ
椭球面上经线的夹角
m d Md
α
小于1的常数
n
r
sin a b
2 ab
或者:
tan 45 a
4 b
6
思考: 正轴圆锥投影的变形主要受什么因素影响?
7
2、双标准纬线等角圆锥投影
8
投影公式:
K U
,
x s cos
y sin
m
n
3
正轴:圆锥轴与地轴重合 横轴:圆锥轴与地轴垂直 斜轴:圆锥轴与地轴斜交
横轴、斜轴圆锥投影实际上很少应用。 凡在地图上注明是圆锥投影的,一般都是正轴圆锥投影。
4
对正轴圆锥投影,设区域中央经线投影作为X轴, 区域最低纬线与中央经线交点为原点。
5
1、圆锥投影(正轴)的一般公式:
f
x s cos y sin
由于每幅图的纬差仅为4°,因此投影的变形极小,长度变形 在边纬与中纬上为±0.030%,面积变形约为长度变形的两倍。
14
拼接裂隙: 投影的特点决定了:
图幅的东西方向拼接不会产 生裂隙;但南北方向拼接时, 因投影带不同,会产生裂隙。
裂隙距 裂隙角 图幅经差 L 边长 当纬度较低时,裂隙角增大, L也增大,裂隙距自然也增大。
r
K
rU
P
m2
n2
K
rU
2
0
α, K 均为投影常数:
lg r1 lg r2
lg U2 lg U1
K
r1U1
r2U
2
tan 45
U
2 ,sin e sin
tane 45
2
9
面积比等 变形线
各种地图投影

正射投影(投影的视点位于离球心无穷远处,
即D=∞);外心投影(投影的视点位于球面外有 限的距离处,即R<D<∞ );球面投影(投影的 视点位于球面上,即D=R);球心投影(投影的 视点位于球心,即D=0)。
精选完整ppt课件
55
三、方位投影变形分析及应用
1、变形特点
极点为投影中心点,投影中心点到任意点的方位 角无变形;等变形线成为圆形。
42
6、坐标规定
在高斯-克吕格投影上,规定以中央经线 为X轴,赤道为Y轴,两轴的交点为坐标原点 。X值在赤道以北为正,以南为负,Y坐标值 在中央经经以东为正,以西为负,我国的X 值均为正,但Y值在中央经线以西为负,运 用起来很不方便,故将各带的坐标纵轴西移 500km,并冠以带号,称通用坐标。
精选完整ppt课件
经纬线网是指由经线和纬线所构成的坐标网, 指示物体在地面的地理位置,又称地理坐标网。
现行图式规定,1:5000,1:1万,1:2.5万,1:5 万,1:10万地形图图幅内不绘制经纬线网;
1:25万和1:50万地形图应在图幅内绘制经纬线 网。经纬线间隔分别为15分×10分,30分×20分。
精选完整ppt课件
精选完整ppt课件
67
精选完整ppt课件
68
四、多圆锥投影:
假想多个圆锥表面与球面相切。纬线为同轴圆弧,其圆心
位于中央经线上,其余经线则投影成对称于中央经线的曲线。
精选完整ppt课件
69
精选完整ppt课件
70
精选完整ppt课件
71
五、桑逊投影
经线为正弦曲线的等积伪圆柱投影 纬线为间隔相等的平行直线,每条纬线上经线的间隔 相等。经线为对称于中央经线的正弦曲线。由法国桑逊在 1650年设计的。特点:P=1;n=1;M>1;M。=1
3.3常用地图投影

摩尔维特投影常用来编制世界,大洋图,由于离中央 经线经差±900的经线是一个圆,且圆面积恰好等于半 球面积,因此,该投影也用来编制东、西半球地图。
4、分瓣伪圆柱投影
——古德投(Goode
•
Projection)
1923年美国地理学家古德(J.Paul Goode)提出了一种对伪圆柱投影进行分 瓣的投影方法,即古德投影。 • 全图被分成几瓣,各瓣通过赤道连接在 一起,地图上仍无面积变形,核心区域的 长度、角度变形和相应的伪圆柱投影相比 明显减小,但投影的图形却出现了明显的 裂缝,这种尽量减少投影变形,而不惜图 面的连续性是古德投影的重要特征
17
3、伪圆柱投影
(1)桑逊投影(Sanson Projection)
•
桑逊投影是一种经线为正炫曲线的正轴等 积伪圆柱投影,又称桑逊-弗兰斯蒂德 (Sanson- Flamsteed)投影。该投影的纬线 为间隔相等的平行直线,经线为对称于中央经 线的正弦曲线(图2-27)。中央经线长度比为 1,即m0=1,且n=1, p=1。桑逊投影为等面 积投影,赤道和中央经线是两条没有变形的线, 离开这两条线越远,长度、角度变形越大。因 此,该投影中心部分变形较小,除用于编制世 界地图外,更适合编制赤道附近南北延伸地区 的地图,如非洲、南美洲地图等。
• 彭纳投影 4、伪圆柱投影
3.3.3 中国地图常用投影
斜轴方位投影
正轴割圆锥投影
1、斜轴方位投影
(1)斜轴等积方位投影 全中国地图,亚洲地图,半球地图 (2)斜轴等角割方位投影 中国全图 (3)斜轴等距方位投影 行政区图,交通地图
2、正轴割圆锥投影
1)正轴等角割圆锥投影 全中国及各省或大区域的地势图、气象 图与气候图,专题图。 2)正轴等积割圆锥投影 行政区划图、土地利用图、土壤图。森 林分布图。 3)正轴等距割圆锥投影 交通图及要求距离不变形的图
介绍几种常用的地图投影

介绍几种常用的,其它的投影方式请了解的朋友跟帖补充|)一、地图投影(比较常用的几种:“墨卡托投影”、“高斯-克吕格投影”、“UTM投影”)1.墨卡托(Mercator)投影1.1 墨卡托投影简介墨卡托(Mercator)投影,是一种"等角正切圆柱投影”,荷兰地图学家墨卡托(Gerhardus Mercator 1512-1594)在1569年拟定,假设地球被围在一中空的圆柱里,其标准纬线与圆柱相切接触,然后再假想地球中心有一盏灯,把球面上的图形投影到圆柱体上,再把圆柱体展开,这就是一幅选定标准纬线上的“墨卡托投影”绘制出的地图。
墨卡托投影没有角度变形,由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。
墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关系的正确。
在地图上保持方向和角度的正确是墨卡托投影的优点,墨卡托投影地图常用作航海图和航空图,如果循着墨卡托投影图上两点间的直线航行,方向不变可以一直到达目的地,因此它对船舰在航行中定位、确定航向都具有有利条件,给航海者带来很大方便。
“海底地形图编绘规范”(GB/T 17834-1999,海军航保部起草)中规定1:25万及更小比例尺的海图采用墨卡托投影,其中基本比例尺海底地形图(1:5万,1:25万,1:100万)采用统一基准纬线30°,非基本比例尺图以制图区域中纬为基准纬线。
基准纬线取至整度或整分。
1.2 墨卡托投影坐标系取零子午线或自定义原点经线(L0)与赤道交点的投影为原点,零子午线或自定义原点经线的投影为纵坐标X轴,赤道的投影为横坐标Y轴,构成墨卡托平面直角坐标系。
2.高斯-克吕格(Gauss-Kruger)投影和UTM(Universal Transverse Mercator)投影2.1 高斯-克吕格投影简介高斯-克吕格(Gauss-Kruger)投影,是一种“等角横切圆柱投影”。
地图投影的名词解释

地图投影的名词解释地图投影是将三维的地球表面投影到二维平面上的一种方法。
由于地球是一个近似于椭球体的形状,而平面是一个无限大的二维表面,所以在将地球表面转化为平面的过程中,必然会出现形状、面积、方向等的变形,这就是地图投影的本质所在。
一、地图投影的基本原理地图投影是地理学与地图制图学中的重要内容,其基本原理可以理解为建立地球和平面之间的映射关系。
在投影过程中,地球表面上的点被映射到平面上的相应点,形成了地图上的数据。
而为了准确地表示地球表面的形状、地理特征等信息,需要选择适合的投影方案。
二、地图投影的分类根据不同的目的和需求,地图投影可以分为多种类型,常见的包括等距投影、等面积投影、等角投影和混合投影等。
1. 等距投影等距投影是指投影后的地图上的任意两点之间的距离与地球上的相应两点之间的距离保持一致。
这种投影方法在测量和导航等领域非常有用,常见的等距投影有墨卡托投影和极射同圆投影等。
2. 等面积投影等面积投影是指在地球表面的任意区域上,被投影到地图上的区域与地球上相应区域的面积保持一致。
这种投影方法在研究地区的面积分布、资源分布等方面非常有用,常见的等面积投影有兰勃托投影和豪森投影等。
3. 等角投影等角投影是指投影后的地图上的任意两条曲线之间的夹角与地球上的相应两条曲线之间的夹角保持一致。
这种投影方法在表示地球表面的形状、方向等方面非常有用,常见的等角投影有兰勃托投影和伪卫星投影等。
4. 混合投影混合投影是指将两种或多种投影方法结合起来使用,通过调整参数或变换过程来达到更好的投影效果。
这种投影方法在综合考虑地球表面的形状、面积、方向等特征上非常有用,常见的混合投影有兰勃托-兰勃托投影和兰勃托-极射同圆投影等。
三、地图投影的应用领域地图投影在地理信息系统、导航、城市规划等领域具有广泛的应用。
通过合适的投影方法,可以制作出形状准确、信息完整的地图,为人们的生产、生活与研究提供参考和支持。
1. 地理信息系统地图投影在地理信息系统中是至关重要的,它将实际地球表面上的数据转化为平面上的点、线、面等要素,使得地理数据在计算机中得以处理和分析。
各种地图投影全解析

地图投影全解析科技名词定义中文名称:地图投影英文名称:map projection定义1:按照一定的数学法则,把参考椭球面上的点、线投影到可展面上的方法。
所属学科:测绘学(一级学科);测绘学总类(二级学科)定义2:根据一定的数学法则,将地球表面上的经纬线网相应地转绘成平面上经纬线网的方法。
所属学科:大气科学(一级学科);动力气象学(二级学科)定义3:运用一定的数学法则,将地球椭球面的经纬线网相应地投影到平面上的方法。
即将椭球面上各点的地球坐标变换为平面相应点的直角坐标的方法。
所属学科:地理学(一级学科);地图学(二级学科)本内容由全国科学技术名词审定委员会审定公布地图投影是利用一定数学方法则把地球表面的经、纬线转换到平面上的理论和方法。
由于地球是一个赤道略宽两极略扁的不规则的梨形球体,故其表面是一个不可展平的曲面,所以运用任何数学方法进行这种转换都会产生误差和变形,为按照不同的需求缩小误差,就产生了各种投影方法。
目录展开定义地图投影,Map Projection.把地球表面的任意点,利用一定数学法则,转换到地图平面上的理论和方法。
地图投影书面概念化定义:地图投影就是指建立地球表面(或其他星球表面或天球面)上的点与投影平面(即地图平面)上点之间的一一对应关系的方法。
即建立之间的数学转换公式。
它将作为一个不可展平的曲面即地球表面投影到一个平面的基本方法,保证了空间信息在区域上的联系与完整。
这个投影过程将产生投影变形,而且不同的投影方法具有不同性质和大小的投影变形。
由于球面上任何一点的位置是用地理坐标(λ,φ)表示的,而平面上的点的位置是用直角坐标(χ,у)或极坐标(r,)表示的,所以要想将地球表面上的点转移到平面上,必须采用一定的方法来确定地理坐标与平面直角坐标或极坐标之间的关系。
这种在球面和平面之间建立点与点之间函数关系的数学方法,就是地图投影方法。
地图投影变形是球面转化成平面的必然结果,没有变形的投影是不存在的。
地图学投影
18
我国的大地原点
建国初期,我国使用的大地测量坐标系统是从前苏联测过来 的,其坐标原点是前苏联玻尔可夫天文台 。54北京坐标系。
上个世纪70年代,中国决定建立自己独立的大地坐标系统。 通过实地考察、综合分析,最后将我国的大地原点,确定在 咸阳市泾阳县永乐镇北洪流村境内,具体坐标在:34°32′27. 00″N,108°55′25.00″E。 《中华人民共和国大地原点选点报告》:“为了使大地测量 成果数据向各方面均匀推算,原点最好在我国大陆的中部。” 而陕西泾阳县永乐镇石际寺村的确处在祖国大陆的中部。这里 距我国边界正北为880公里,距东北2500公里,距正东1000公 里,距正南1750公里,距西南2250公里,距正西2930公里,距 西北2500公里。同时,这里的地质条件比较理想。
5
6
全国水准网
7
地图投影中的地球体
大地水准面
静止海平面 地球数学表面
1.地球自然表面:地球是一个近似球体,其自然表面是一个极其复杂而 又不规则的曲面。
2. 地球物理表面:是假定海水处于 “完全” 静止状态,把海水面延伸到 (大地水准面)大陆之下形成包围整个地球的连续表面。
• 地球数学表面:假想以一个大小和形状与地球极为接近的旋转椭球面
64
65
2) 条件投影(非几何投影或解析投影)
不是借助于几何承影面,而是根据制图的 具体要求,有条件地应用数学解析的方法确定 球面与平面之间对应点的函数关系,把球面转 换为平面的投影。
66
2) 条件投影(非几何投影或解析投影) (1) 多圆锥投影
设想有更多的圆锥面与球面相切,投影后沿一 母线剪开展平。纬线投影为同轴圆弧,其圆心都在 中央经线的延长线上。中央经线为直线,其余经线 投影为对称于中央经线的曲线。
测绘技术中的地图投影类型与选择

测绘技术中的地图投影类型与选择在日常生活中,地图是我们获取空间信息的重要工具之一。
然而,地球是一个球体,而地图是平面的,这就需要使用地图投影来将球面上的地理信息转换到平面上。
地图投影类型的选择对地图的准确性和可视化效果具有重要影响。
本文将介绍测绘技术中常用的地图投影类型,并讨论选择合适的地图投影的方法。
1. 地图投影类型的分类地图投影类型可以根据其投影方式、形状变形特点等进行分类。
按照投影方式,常见的地图投影类型有圆柱投影、球面投影和锥面投影。
圆柱投影是通过将地球的经纬线投影到一个垂直于地球轴线的圆柱面上。
球面投影则是将地球表面投影到一个球面上。
锥面投影则是将地球投影到一个锥面上。
2. 常见地图投影类型的特点不同的地图投影类型各有其特点,适用于不同的地理区域和测绘需求。
接下来,我们将介绍一些常见的地图投影类型及其特点。
2.1 正射投影正射投影是一种常见的等角投影,其特点是保持方向性,即保持从地球上的任何点到地图上的连线与真实地面上的方向一致。
这使得正射投影在航空摄影和遥感影像处理中广泛应用。
然而,正射投影在大范围地图上存在面积失真的问题。
2.2 麦卡托投影麦卡托投影是一种圆柱投影,其特点是纬线等间距,经线等角度分布。
这使得麦卡托投影在海洋和大陆等大范围地图中具有较好的可视化效果。
然而,麦卡托投影在高纬度地区会出现形状失真和面积失真的问题。
2.3 兰勃托投影兰勃托投影是一种球面等面积投影,其特点是保持地球上的面积比例不变。
兰勃托投影在大范围地图绘制中常用,尤其适用于对地理统计分析进行准确度量的场景。
然而,兰勃托投影在极地地区会出现形状和方位失真的问题。
3. 地图投影的选择方法选择合适的地图投影类型需要考虑多方面因素。
以下是一些选择地图投影的方法。
3.1 地理区域根据绘制地图的地理区域的特点,选择适合该区域的地图投影类型。
例如,如果绘制的地图是涵盖极地地区的,则应选择适合极地地区的地图投影类型,以减小形状和方位的失真。
地图投影基础知识

按承影面与地轴的关系分为:正轴投影、 横轴投影、斜轴投影
按承影面与地表的关系分为:切投影、 割投影
投影分类示意图
N
N
N
S
S
S
正轴
横轴
斜轴
切园柱投影 割园柱投影 切方位投影
等积投影、等角投影、等距投影
形状不变
地图投影——地图投影的分类
圆柱投影 方位投影 圆锥投影
纬线为同心圆 经线为放射直线
• 横轴方位投影
中央经线与赤道为互相垂直的直 线,其余经线为对称中经的曲线, 其余纬线为对称赤道的曲线
• 斜轴方位投影
(2)经纬距的变化规律
• 以正轴为例
纬距
心射:急剧扩大 正射:急剧缩小 平射:逐渐扩大 等角即平射 等积:逐渐缩小 等距:相等
(3)变形规律
• 切点或割线无变形
• 等变形线以投影中心为圆心呈同心圆分 布。
(4)常见投影及其用途
• 正轴等积方位投影--南北两极图
• 横轴等积方位投影--东西半球图
• 斜轴等积方位投影--水陆半球图
• 斜轴等距方位投影--航空图 等距:指从投影中心向各个方向长度变 形为零。
2 圆锥投影
(1)经纬网的特征
• 经线为放射直线; 纬线为同心圆。
简单投影小结
• 经纬网形状简单 • 变形规律简单:等变形线分别为平行直线、同
心圆弧、同心圆 • 共性明显
高斯—克吕格投影 (Gauss-Kruger Projection)
高斯-克吕格投影是由高斯于19世纪20年代拟定,后经克吕 格补充而形成的一种地图投影方式。在英美国家称为横轴墨卡 托投影
属于横轴等角切圆柱投影。这种投影是将椭圆柱 面套在地球椭球的外面,并与某一子午线相切(此子 午线叫中央子午线或中央经线),椭圆柱的中心轴通 过地球椭球的中心,然后用等角条件将中央子午线东 西两侧各一定经差范围内的地区投影到柱面上,并将 此柱面展成平面,即获得高斯投影
常见地图投影

常见地图投影欧阳芳地图投影:按变形性质分类:等角投影,等积投影,任意投影按几何构成方法分类:方位投影,圆柱投影,圆锥投影按非几何构成方法分类:伪方位投影,伪圆柱投影,伪圆锥投影,多圆锥投影按照投影面积与地球相割或相切分类:割投影,切投影这里只介绍常见常用的地图投影。
1.常见的地图投影按变形性质分为:等角投影:定义为投影前后对应的微分面积保持图形相似,即角度变形为零,也称正形投影。
其在一点上任意方向的长度比都相等,但在不同地点长度比是不同,即不同地点上的变形椭圆大小不同。
等积投影:定义为即在投影平面上任意一块面积与椭球面上相应的面积相等,即面积变形等于零。
等距投影:在任意投影上,长度、面积和角度都有变形,它既不等角又不等积。
但是有一种比较常见的等距投影,定义为沿某一特定方向的距离,投影前后保持不变。
在这种投影图上并不是不存在长度变形,它只是在特定方向上没有长度变形。
等距投影的面积变形小于等角投影,角度变形小于等积投影。
其变形性质在微分圆上的表示列表对比为:名称特点适用范围等角投影无角度变形航海、空图、洋流图、风向图、气象图及军用地图等积投影无面积变形经济图,行政区图和人口图等距投影(属于任意投影的特殊情况)特定方向上无长度变形沿某一特定方向量测距离的地图、教学地图和交通地图2.常用的几何投影:方位投影:以平面作为投影面,使平面与球面相切或相割,将球面上的经纬线投影到平面上而成。
其中球心投影常用于航空及航海图,外心投影常用于空间透视投影。
圆柱投影:以圆柱面作为投影面,使圆柱面与球面相切或相割,将球面上的经纬线投影到圆柱面上,然后将圆柱面展为平面而成。
圆锥投影:以圆锥面作为投影面,使圆锥面与球面相切或相割,将球面上的经纬线投影到圆锥面上,然后将圆锥面展为平面而成。
圆锥投影,圆柱投影,以及方位投影的情况分别用图形表示为:方位投影,圆锥投影,圆柱投影的异同分析(此表格中不加特别说明则默认为正轴投影):名称方位投影圆柱投影圆锥投影投影面平面圆柱面圆锥面纬线投影特点同心圆平行直线同心圆圆弧经线投影特点同心圆的半径与纬线投影成的平行直线垂直的平行直线垂直于同心圆弧且相交于一点的直线束投影变形分析经线间的夹角与实地经度差相等,其等变形线为圆其变形只与纬度有关,与经差无关,同纬度上各点其变形只与纬度有关,与经差无关,同纬度上各点形的变形相同的变形相同适用范围具有圆形轮廓的区域和两极地区低纬度沿纬线伸展的区域中纬度处沿纬线伸展的区域习惯特殊投影方式及用途1.正轴等角方位投影:极球面2.等积方位投影:小比例尺地图,东西半球图3.正轴等距方位投影:南北极图4.横轴等距方位投影:东西半球图5.斜轴等距方位投影:航空中心站,地震观测中心,气象站等需满足到中心距离相等的勘测中心。
方位投影及其应用

3.3 透视方位投影
3.4 等角、等积、等距方位投影
3
3.1 球面坐标系
Q:极点 P
新轴:过Q的直径QQ1
垂直圈:过QQ1的平面与地球 所截大圆(QPQ1) 等高圈:垂直于QQ1的平面与 地球相交所截的圆 球面坐标系: Q为极点,垂直 圈与等高圈两组正交曲线构成。
Q
Q1 P1
4
( 0) 2
11
方位投影一般公式:
δ
X
ρ
Y
A点地理坐标: ( , )
Q´ A´ Q
A平面极坐标 : ( , )
A点球面坐标:
z aA
P
Z ,
f (Z ) a
12
O
Q'
一般公式:
:等高圈投影半径
:两垂直圈的夹角
Z : 极距
:方位角 1 , 2 :沿垂直圈、等高圈
20
(2)
球面透视方位投影
Q
•
视点位于地球面上
R
R
Z 2 R tan 2
•
Z
Z
S2
21
Z x cos 2 R tan cos a 2 Z y sin 2 R tan sin a 2 2 Z 1 sec 2 2 Z 2 sec 2 4 Z p sec 2 0 Z 2 R tan 2 a
p cos Z Z sin tg 2 2
2等角、等积、等距方位投影
根据不同要求按数学方法探求
方位投影。
27
(1)等角方位投影
按等角投影条件(投影后角度不变形)确定
函数 f ( Z ) 形式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
失真分类
长度失真 地表无限小线段投影到平面上,
长度的伸长或缩短 角度失真 地表无限小圆投影到平面上,其 上任意一点到圆心的直线与经线坐标轴的夹 角产生的变化 面积失真 地表无限小圆投影到平面上,其 面积发生的变化 思考:航图绘制中应当使哪种失真尽量小?
地图失真的原理X´Leabharlann Xα r α r´ ´
世界百万普通地图和百万航图的主要投影方法
5.极地方位投影
投影原理:将地球视为一透明球体,球心置一点
光源,投影面为平面,投影面通过极点与地球相 切,地球表面的经纬网格投射在平面上。
极地方位投影特点
经线是以极点为圆心的放射直线,纬线是以
极点为圆心的同心圆弧;纬差相等,纬度越 低,间隔越大 。 大圆航线为直线,等角航线为凹向极点的螺 旋曲线
§3 常用的地图投影
1.墨卡托投影(等角正圆柱投影)
投影原理:设想地球为一透明球体,球心置一点光
源,将圆柱投影面沿赤道与地球相切,地球上的经纬网格投 影到圆柱面上
墨卡托投影绘制的世界地图
墨卡托投影特点:
经线相互平行,间隔相等;纬线垂直于经线,越
向两极,间隔越大; 赤道上无任何失真; 地图等角,不等积,不等距(不能用统一的比例 尺量取航线距离) 面积失真随纬度增加明显变大。 大圆航线凸向两极;等角航线是直线(任意两点 相连的直线为等角航线)。
兰伯特投影特点:
经线是以极点为圆心的放射直线 ,纬线是以极
点为中心的同心圆。 两条标准纬线之间有一条最小比例尺纬线;两条 标准纬线之间的地区长度缩短,比例尺变小;两 条标准纬线之外的地区长度伸长,比例尺变大。 地图等角;标准纬线上无失真。 大圆航线凸向大比例尺一方;等角航线凹向极点。
用途:
用途
极地领航用图
标画大圆航线的辅助用图
N
N
N
S
N
S
N
S
N
S
S
S N
N
N
S
S
S
返回
3°E 9°E 01 02
…………
3°W 60
返回
最小比例尺
返回
返回
(一)地图投影
§3 常用的地图投影
利用一定的数学法则把地球表面上的经纬线网表 示到平面上
F ( , ) f ( x, y)
1.
地图投影的失真
面图纸上,因此制图时首先要把曲面展为平面,然而球 面是个不可展的曲面,即把它直接展为平面时,不可能 不发生破裂或褶皱。
由于地球椭球体表面是曲面,而地图通常是要绘制在平
90
TH/TC= α+(± δ)
δ= Δλ SINΦ 中央经线以东取正,以西取负
4.兰伯特投影
也叫等角切(割)正 圆锥投影,德国数学 家Lambert首创,百 万航图和世界地形图 的数学基础
投影原理:
将地球视为一透明球体, 球心置一点光源,投影 面为圆锥面,通过两条 (一条)标准纬线与地 球相割。
高斯-克吕格投影特点:
每个投影带上,中央经线和赤道为直线;其他经线关于中央
经线对称,凹向中央经线;纬线凸向赤道; 等角;中央经线上无失真,最大长度失真为0.137%; 大圆航线近似为直线;等角航线是曲率极小的螺旋曲线,领 航实施中近距离可以近似认为直线。
用途:
大比例尺航图多为此种投影,常用于研究地面目标,在通用
Y
Y´
微分圆
变形椭圆
2. 地图投影的分类
(一)按失真性质分 等角投影是指任何点上两微分线段组成的角度投影前后 保持不变,角度失真为零。 ——便于测量方位。 等距投影是指为沿某一特定方向的距离,投影前后保持 不变,即沿着该特定方向长度比为1 ——便于测量距离。 等积投影是指某一微分面积投影前后保持相等——政区、 人口密度、土地利用、森林和矿藏分布以及其他自然和 经济地图。 任意投影:存在三种失真,但三种失真都控制在较小的 范围内。 (二)按投影面的形状分圆柱投影、圆锥投影、方位投影 (三)按投影与球面的位置关系分:正轴投影、横轴投影、斜 轴投影
他经线凹向切经线; 地图等角; 切经线上无失真(切经线左右各3 ° 范围长度失真 0.137%,面积失真0.27%);同一条纬线上,离开 切经线越远,失真越大; 同一条经线上,纬度越低,变形越大。 大圆航线凹向切经线,等角航线是螺旋曲线。
用途
极地领航 国家大地测量和五十万分之一及更大比例尺的国家
高斯-克吕格分带投影:
为了保证地图的精度,采用分带投影方法,即将投
影范围的东西界加以限制,使其失真不超过一定的 限度,这样把许多带结合起来,可成为整个区域的 投影。 我国规定1:1 万、1:2.5 万、1:5 万、1:10万、 1:25 万、1:50 万比例尺地形图,均采用高斯克 -吕格投影。1:2.5 至1:50 万比例尺地形图采用 经差6 °分带,1:1 万比例尺地形图采用经差3° 分带。
用途:
赤道附近领航;海上领航; 世界时区图;卫星轨
迹图 绘制较长距离的等角航线时的辅助用图。
2.等角横圆柱投影(横墨卡托
投影) 19世纪20年代经高斯拟定 约束条件
中央经线与投影面相切,投影
后保持长度不变 投影后等角
等角横圆柱投影特点
赤道为直线,与切经线相差90°的经线是直线,其
基本地形图的数学基础。
3.高斯-克吕格投影
法国数学家高斯19世纪20年代拟定,后经克
吕格改进。 根据横墨卡托投影的特点,取可以限制投影的 经度范围,将地球表面按照经度差的分成不同 的投影带单独投影,各自建立坐标网,就可以 将失真限制在较小的范围内。 我国1:2.5万至地形图采用6º 分带法;考虑到 1:1万和更大的比例尺地形图对制图精度的要 求,采用3º 分带法。
航空飞行领域内应用广泛; 绘制机场专用航图和涉及仪表飞行程序的基础用图; 国家大地测量和五十万分之一及更大比例尺的国家基本地形 图
高斯投影坐标网
经纬网(地理坐标网)
00 14 114° 202 30° α 40´ 3396 94 92 -δ
16
18
20
TH/TC
A( 20218 , 3394 )
