韩伯棠管理运筹学(第三版)_第二章_线性规划的图解法
管理运筹学第二章 线性规划的图解法

B、约束条件不是等式的问题:
若约束条件为 ai1 x1+ai2 x2+ … +ain xn ≤ bi 可以引进一个新的变量si ,使它等于约束右 边与左边之差 si=bi–(ai1 x1 + ai2 x2 + … + ain xn ) 显然,si 也具有非负约束,即si≥0, 这时新的约束条件成为 ai1 x1+ai2 x2+ … +ain xn+si = bi
第二章 线性规划 的图解法
一、线性规划的概念 二、线性规划问题的提出 三、线性规划的数学模型 四、线性规划的图解法 五、线性规划解的情况 六、LP图解法的灵敏度分析
一、线性规划的概念
线性规划Linear Programming 简称LP,是一 种解决在线性约束条件下追求最大或最小的 线性目标函数的方法。 线性规划的目标和约束条件都可以表示成线 性的式子。
max z 3 x1 2 x2
2 x1 x2 ≤ 10 设备B台时占用 s.t. x1 x2 ≤ 8 x , x ≥ 0 产量非负 1 2
决策变量 (decision variable) 目标函数 (objective function) 约束条件 (subject to)
-ai1
x1-ai2 x2- … -ain xn = -bi 。
例1.3:将以下线性规划问题转化为标准形式 Min f = 3.6 x1 - 5.2 x2 + 1.8 x3 s. t. 2.3 x1 + 5.2 x2 - 6.1 x3 ≤15.7 4.1 x1 + 3.3 x3 ≥8.9 x1 + x2 + x3 = 38 x 1 , x 2 , x3 ≥ 0
管理运筹学_第二章_线性规划的图解法

A
1×250=250千克.
原料B 0 1 250千克
约束条件中没使用的资源或能力称之为松弛量。
用Si表示松弛量,对最优解 x1=50,x2=250来说:
约束条件
松弛变量的值
设备台时数
s1=0
原料A
s2=50
原料B
s3=0
8
线性规划标准型
加了松弛变量后例1的数学模型可写成:
目标函数:max z=50x1+100x2+0s1+0s2+0s3,
约束条件: x1+x2+s1=300,
2x1+x2+s2=400,
x2+s3=250, x1,x2,s1,s2,s3≥0
如何把模型化为 标准型?
三个特征:
一、约束条件为等式;
二、约束条件右端常数项非负;
三、所有变量非负。
称为线性规划的标准形式。
9
线性规划问题解的情况:
1.若有最优解,一定能在可行域的顶点取得。
a21x1+a22x2+…+a2nxn=b2, ………………………… am1x1+am2x2+…+am nxn=bm. x1, x2,…,xn≥0.
其中ci为第i个决策变量xi在目标函数中的系数, aij为第i个约束条件中第j个决策变量xj的系数, bj(≥0)为第j个约束条件中的常数项。
16
灵敏度分析
C 100
1设备台时获利500/10=50
元。 x1
O 100 D300 X1+X2=300
X1+X2=310
你知道对偶价格吗?
21
对偶价格的概念
管理运筹学第二章线性规划的图解法

02
图解法的基本原理
图解法的概念
图解法是一种通过图形来直观展示线性规划问题解的方法。它通过在坐标系中绘 制可行域和目标函数,帮助我们理解问题的结构和最优解的位置。
图解法适用于线性规划问题中变量和约束条件较少的情况,能够直观地展示出最 优解的几何意义。
图解法的步骤
确定决策变量和目标函数
明确问题的决策变量和目标函数,以便在图 形中表示。
目标函数是要求最小化或最大化的函数,通常表示为 $f(x) = c_1x_1 + c_2x_2 + ldots + c_nx_n$。
04
约束条件是限制决策变量取值的条件,通常表示为 $a_1x_1 + a_2x_2 + ldots + a_nx_n leq b$或 $a_1x_1 + a_2x_2 + ldots + a_nx_n = b$。
LINDO是一款开源的线性规划求解器,用 户可以免费使用。
软件工具的使用方法
Excel
用户需要先在Excel中设置好线性规划模型,然后使 用“数据”菜单中的“规划求解”功能进行求解。
Gurobi/CPLEX/LINDO
这些软件通常需要用户先在软件界面中输入线性规划 模型,然后通过点击“求解”按钮进行求解。
实例三:分配问题
总结词
分配问题是指如何根据一定的分配原则 或目标,将有限的资源分配给不同的需 求方,以最大化整体效益。
VS
详细描述
分配问题在实际生活中广泛存在,如物资 分配、任务分配等。通过图解法,可以将 分配问题转化为线性规划模型,并利用图 形直观地展示最优解的资源分配方案。在 分配问题中,通常需要考虑不同需求方的 重要性和优先级,以及资源的有限性等因 素,以实现整体效益的最大化。
管理运筹学期末复习资料【韩伯棠】

运筹学(Operational Research)复习资料第一章绪论一、名词解释1.运筹学:运筹学是应用分析、试验、量化的方法,对经济管理系统中的人力、物力、财力等资源进行统筹安排,为决策者提供有依据的最优方案,以实现最有效的管理。
二、选择题1.运筹学的主要分支包括(ABDE )A图论B线性规划C非线性规划D整数规划E目标规划2. 最早运用运筹学理论的是( A )A . 二次世界大战期间,英国军事部门将运筹学运用到军事战略部署B . 美国最早将运筹学运用到农业和人口规划问题上C . 二次世界大战期间,英国政府将运筹学运用到政府制定计划D . 50年代,运筹学运用到研究人口,能源,粮食,第三世界经济发展等问题上第二章线性规划的图解法一、选择题/填空题1.线性规划标准式的特点:(1)目标函数最大化(2)约束条件为等式(3 决策变量为非负(4 ) 右端常数项为非负2. 在一定范围内,约束条件右边常数项增加一个单位:(1)如果对偶价格大于0,则其最优目标函数值得到改进,即求最大值时,最优目标函数值变得更大,求最小值时最优目标函数值变得更小。
(2)如果对偶价格小于0,则其最优目标函数值变坏,即求最大值时,最优目标函数值变小了;求最小值时,最优目标函数值变大了。
(3)如果对偶价格等于0,则其最优目标函数值不变。
3.LP模型(线性规划模型)三要素:(1)决策变量(2)约束条件(3)目标函数4. 数学模型中,“s·t”表示约束条件。
5. 将线性规划模型化成标准形式时,“≤”的约束条件要在不等式左端加上松弛变量。
6. 将线性规划模型化成标准形式时,“≥”的约束条件要在不等式左端减去剩余变量。
7.下列图形中阴影部分构成的集合是凸集的是A【解析】:如何判断是凸集?凸集:两点之间连线在图内凹集:两点之间连线在图外8. 线性规划问题有可行解且凸多边形无界,这时CA没有无界解 B 没有可行解 C 有无界解 D 有有限最优解9. 对于线性规划问题,下列说法正确的是( D )A. 线性规划问题可能没有可行解B. 在图解法上,线性规划问题的可行解区域都是“凸”区域C. 线性规划问题如有最优解,则最优解可在可行解区域顶点上到达D. 上述说法都正确第三章线性规划问题的计算机求解一、名词解释1.相差值:相应的决策变量的目标系数需要改进的数量,使得决策变量为正值。
管理运筹学_第二章_线性规划的图解法

线性规划中超过约束最低限的部分,称为剩余量。 记s1,s2为剩余变量,s3为松弛变量,则s1=0, s2=125,
s3=0,加入松弛变量与剩余变量后例2的数学模型变为 标准型: 目标函数: min f =2x1+3x2+0s1+0s2+0s3 约束条件: x1+x2-s1=350, x1-s2=125, 2x1+x2+s3=600, x1, x2, s1,s2,s3≥0.
阴影部分的每 一点都是这个线 性规划的可行解, 而此公共部分是 可行解的集合, 称为可行域。
B
X2=250
100
100
300
x1
B点为最优解, X1+X2=300 坐标为(50, 250), Z=0=50x1+100x2 此时Z=27500。 Z=10000=50x1+100x2 问题的解: 最优生产方案是生产I产品50单位,生产Ⅱ产品250单位,可得 最大利润27500元。
Z=10000=50x1+50x2
线段BC上的所有点都代表了最优解,对应的最优值相 同: 50x1+50x2=15000。
10
3. 无界解,即无最优解的情况。对下述线性规划问题:
目标函数:max z =x1+x2 约束条件:x1 - x2≤1 -3x1+2x2≤6 x1≥0, x2≥0.
x2 -3x1+2x2=6 3
其中ci为第i个决策变量xi在目标函数中的系数, aij为第i个约束条件中第j个决策变量xj的系数, bj(≥0)为第j个约束条件中的常数项。
16
灵敏度分析
灵敏度分析:求得最优解之后,研究线性规划的
第二章 线性规划的图解法(简)

第二节 图解法
在线性规划中,对一个约束条件中没使用的资源或能力的大小称 之为松弛量。记为Si。
第二节 图解法
像这样把所有的约束条件都写成等式 ,称为线性规划模型的标准化,所得结果 称为线性规划的标准形式。
第二节 图解法
同样对于≥约束条件中,可以增加一些代表
最低限约束的超过量,称之为剩余变量,把≥约
第二章 线性规划的图解法
主要内容:
§1 问题的提出 (什么是线性规划) §2 图解法 §3 图解法的灵敏度分析
重点和难点
重点: (1)线性规划问题的主要概念 (2)线性规划问题的数学模型 (3)线性规划图解法的过程 (4)阴影价格的定义和灵敏度分析 难点: 灵敏度分析
第一节 问题的提出
约束条件对偶价格小于零时,约束条件
右边常数增加一个单位,就使得最优目
标函数值减少一个其对偶价格。
第三节 图解法的灵敏度分析
对目标函数值求最小值的情况下, 当对偶价格大于零时,约束条件右边常数增加 一个单位就使其最优目标函数值减少一个其对 偶价格; 当对偶价格等于零时,约束条件右边常数增加 一个单位,并不影响其最优目标函数值; 当对偶价格小于零时,约束条件右边常数增加 一个单位,就使得其最忧目标函数值增加一个 其对偶价格。
具有上述3个特征的问题为线性规划问题。
第一节 问题的提出
我们的仸务就是要选择一组或多组方案,使目
标函数值最大或最小。从选择方案的角度说,
这是规划问题。从使目标函数值最大或最小的
角度说,就是优化问题。
线性规划数学模型的一般表示方式
max(min) f ( x) c1 x1 c2 x2 cn xn a11 x1 a12 x2 a1n xn a x a x a x 21 1 22 2 2n n s.t. a x a x a x m2 2 mn n m1 1 x1 , x2 , , xn n : 变量个数 ; m : 约束行数 ; n m : 线性规划问题的规模 c j : 价值系数 ; b j : 右端项; aij : 技术系数 (, )b1 (, )b2 (, )bm 0
《管理运筹学》第三版(韩伯棠 )课后习题答案 高等教育出版社
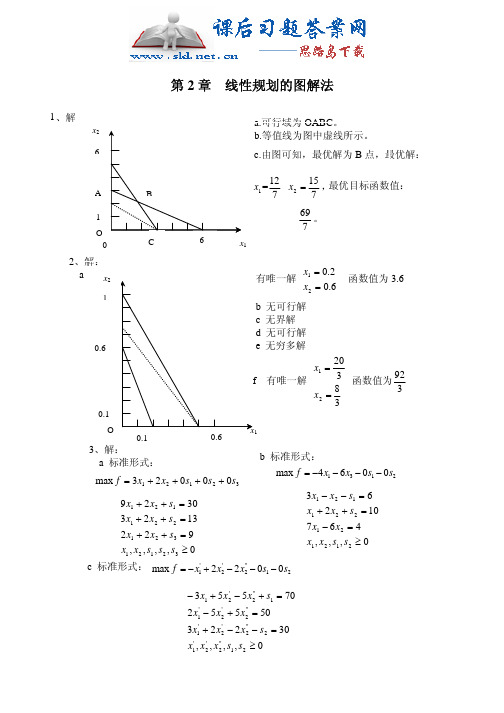
a、 在满足对职工需求的条件下,在 10 时安排 8 个临时工,12 时新安排 1 个临时工,13 时新安排 1 个临时工,15 时新安排 4 个临时工,17 时新 安排 6 个临时工可使临时工的总成本最小。
50xa + 100xb ≤ 1200000 5xa + 4xb ≥ 60000 100xb ≥ 300000 xa , xb ≥ 0 基金 a,b 分别为 4000,10000。 回报率:60000
b 模型变为: max z = 5xa + 4xb
50xa + 100xb ≤ 1200000 100xb ≥ 300000 xa , xb ≥ 0
xi ≥ 0, yi ≥ 0 i=1,2,…,11
稍微变形后,用管理运筹学软件求解可得:总成本最小为 264 元。 安排如下:y1=8( 即在此时间段安排 8 个 3 小时的班),y3=1,y5=1,y7=4,x8=6 这样能比第一问节省:320-264=56 元。
x2+x3+x4+x5+1 ≥ 3 x3+x4+x5+x6+2 ≥ 3 x4+x5+x6+x7+1 ≥ 6 x5+x6+x7+x8+2 ≥ 12 x6+x7+x8+x9+2 ≥ 12 x7+x8+x9+x10+1 ≥ 7 x8+x9+x10+x11+1 ≥ 7 x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11≥ 0 用管理运筹学软件我们可以求得此问题的解为:
b、 这时付给临时工的工资总额为 80 元,一共需要安排 20 个临时工的班 次。
约束 -------
1 2 3 4 5 6 7 8 9 10 11
管理运筹学 第三版韩伯棠 考点归纳

1.线性规划问题及其数学模型
2、约束条件不是等式的问题: 设约束条件为
ai1 x1+ai2 x2+ „ +ain xn ≤ bi 可以引进一个新的变量xs,使它等于约束右边与左边之差 xs=bi–(ai1 x1 + ai2 x2 + „ + ain xn ) 显然, xs也具有非负约束,即xs≥0,
A B B’
C’
C D x1
E
3.图解法的灵敏度分析
(二)约束条件中右边系数bi的灵敏度分析 可见,由于增加了10个台时数,使利润增加了500元,可见 每 个台时数可增加利润50元. 像这样在约束条件右边常量增加一个单位而使最优目标函数 值得到改进的数量称为这个约束条件的对偶价格。 本例中的设备对偶价格为50元/台时。 但不是每个约束条件右边常量的变化都会引起目标函数值的 变化的。 本例中,如果A原料的量增加10千克,也可以使可行域扩 大,但对最优解却没有影响,因此原料A的对偶价格为0。
3.图解法的灵敏度分析
(一)目标函数中的系数cj的灵敏度分析 由图可知,如果cj发生变化,则目标函数的等值线的斜率会 发生变化。如果要求最优解仍在B点,则会以B点为轴点而发 x 生转动。
2
z=27500=50x1+100x2
A B C
k=0
k=-c1/c2
E D x1
k=-2
k=-1
3.图解法的灵敏度分析
a11x1+a12x2+„+a1nxn≤( =, ≥ )b1 a21x1+a22x2+„+a2nxn≤( =, ≥ )b2
„„
am1x1+am2x2 +„+amnxn≤( =, ≥ )bm x1 ,x2 ,„ ,xn ≥ 0
管理运筹学_韩伯棠版答案_word版
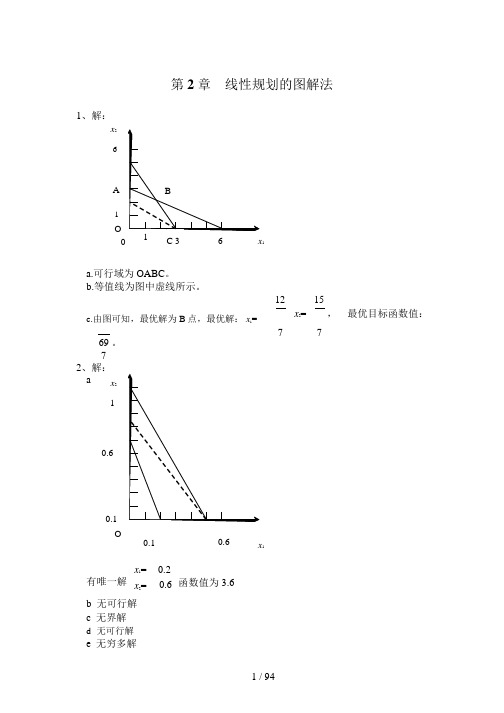
第 2 章 线性规划的图解法a.可行域为 OABC 。
b.等值线为图中虚线所示。
c.由图可知,最优解为 B 点,最优解: x 1=1215x 2=, 最优目标函数值: 69 。
77x 1=0.2有唯一解 x 2= 0.6 函数值为 3.6b 无可行解c 无界解d 无可行解e 无穷多解f 有唯一解3、解:a 标准形式:x1x2==20383函数值为923max f= 3x1+2x2+ 0s1+ 0s2+ 0s3 x+91+ =2x s30x+31x+21222 1+ s=x22+ s=139b 标准形式:x1x23s s, x2, s1, ,2 3≥ 0max f= −x x s s41− 63− 01− 023 − x− s= 6x12 1x+ + =1 2x s2 2107 x1− 6x2= 4c 标准形式:x1, x2, , ss12= − +x'x'≥ 0' −max f 2 − 2x s s0 − 021−x+2x' −2 1' + =x s3 5 5 701 2 2 12x'− 5x'+ 5x'= 501x'+312x'−222' −=2x s30x', x2',x2',, s 2 ≥ 024、解:1s 12z = x + x + + max 10 5 s s标准形式: 1 2 0 0x + 31x + 514 2 1+ s = x 21+ s = x 229 82s 1= 2, s 2= 0x 1, x 2, , s s 12≥ 05 、解:f = x + x + ++ min118s s s 标准形式:12x + 101x +2 1− s = x 21− =220331x +413x s 2 2− =9xs1836s 1= 0, s 2= 0, s 3= 13 6 、解: b 1 ≤ c 1≤ 3c 2 ≤ c 2≤ 6x 1= 6x123s s , x 2, s 1, ,23≥ 0 de x 2= 4x 1∈ [ ]8x = 16 − 2x221f 变化。
管理运筹学课后答案韩伯棠高等教育出版社第3版

管理运筹学高等教育出版社第三版韩伯棠管理运筹学作业第二章线性规划的图解法P23:Q2:(1)-(6);Q3:(2)Q2:用图解法求解下列线性规划问题,并指出哪个问题具有唯一最优解,无穷多最优解,无界解或无可行解。
(1)Min f=6X1+4X2约束条件:2X1+X2>=1,3X1+4X2>=3X1, X2>=0解题如下:如图1Min f=3.6X1=0.2, X2=0.6本题具有唯一最优解。
图1(2)Max z=4X1+8X2约束条件:2X1+2X2<=10-X1+X2>=8X1,X2>=0解题如下:如图2:Max Z 无可行解。
图2(3) Max z =X1+X2 约束条件 8X1+6X2>=24 4X1+6X2>=-12 2X2>=4 X1,X2>=0 解题如下:如图3: Max Z=有无界解。
图3(4) Max Z =3X1-2X2 约束条件:X1+X2<=1 2X1+2X2>=4 X1,X2>=0 解题如下:如图4: Max Z 无可行解。
图4(5)Max Z=3X1+9X2 约束条件:X1+3X2<=22-X1+X2<=4X2<=62X1-5X2<=0X1,X2>=0解题如下:如图5:Max Z =66;X1=4 X2=6本题有唯一最优解。
图5(6)Max Z=3X1+4X2 约束条件:-X1+2X2<=8X1+2X2<=122X1+X2<=162X1-5X2<=0X1,X2>=0解题如下:如图6Max Z =30.669X1=6.667 X2=2.667本题有唯一最优解。
图6Q3:将线性规划问题转化为标准形式(2)min f=4X1+6X2约束条件:3X1-2X2>=6X1+2X2>=107X1-6X2=4X1,X2>=0解题如下:1)目标函数求最小值化为求最大值:目标函数等式左边min改为max,等式右边各项均改变正负号。
管理运筹学 线性规划的图解法课件

线性规划的应用领域
生产计划
线性规划可以用于制定生产计划,优 化资源配置,提高生产效率。
物流优化
线性规划可以用于优化物流配送路线 、车辆调度等问题,降低运输成本。
金融投资
线性规划可以用于金融投资组合优化 ,实现风险和收益的平衡。
资源分配
线性规划可以用于资源分配问题,如 人员、资金、设备等资源的合理分配 ,提高资源利用效率。
束条件。
线性规划的目标是在满足一系列 限制条件下,使某一目标函数达
到最优值。
线性规划问题通常表示为求解一 组变量的最优值,使得这些变量 满足一系列线性等式或不等式约
束。
线性规划的数学模型
线性规划的数学模型由决策变量、目标函数和约束条 件三部分组成。
输标02入题
决策变量是问题中需要求解的未知数,通常表示为 $x_1, x_2, ldots, x_n$。
01
03
约束条件是限制决策变量取值的条件,通常表示为 $a_1x_1 + a_2x_2 + ldots + a_nx_n leq b$或 $a_1x_1 + a_2x_2 + ldots + a_nx_n = b$。
04
目标函数是问题要优化的函数,通常表示为$f(x) = c_1x_1 + c_2x_2 + ldots + c_nx_n$。
03
绿色发展与线性规 划的结合
将可持续发展理念融入线性规划 ,实现资源节约、环境友好的发 展目标。
THANKS
[ 感谢观看 ]
约束条件
生产计划问题通常受到资源限制、市场需求和生 产能力等约束条件的限制。
详细描述
生产计划问题通常涉及到如何分配有限的资源, 以最大化某种目标函数(如利润)。通过图解法 ,我们可以将约束条件和目标函数在二维平面上 表示出来,从而找到最优解。
《管理运筹学》第三版习题答案(韩伯棠教授)

0 到正无穷的范围内变化,其最优解不变,但此时最优目标函数值变化
5、解:
a 约束条件 2 的右边值增加 1 个单位,目标函数值将增加 3.622
b x2 产品的利润提高到 0.703,才有可能大于零或生产
c 根据百分之一百法则判定,最优解不变
d 因为
15 30 − 9 189
65
+
> 100 % 根据百分之一百法则二,我们不能判定
1180
设按 14 种方案下料的原材料的根数分别为 x1,x2,x3,x4,x5,x6,x7,x8,x9, x10, x11,x12,x13,x14,则可列出下面的数学模型: min f = x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11+x12+x13+x14 s.t. 2x1+x2+x3+x4 ≥ 80
基金 b 的投资额每增加 1 个单位,回报额下降 0.06
d c 不变时, c 在负无穷到 10 的范围内变化,其最优解不变
1
2
c 不变时, c 在 2 到正无穷的范围内变化,其最优解不变
2
1
e 约束条件 1 的右边值在 300000 到正无穷的范围内变化,对偶价格仍为 0.1
约束条件 2 的右边值在 0 到 1200000 的范围内变化,对偶价格仍为-0.06
111 25 − 15
其对偶价格是否有变化
第 4 章 线性规划在工商管理中的应用
1、解:为了用最少的原材料得到 10 台锅炉,需要混合使用 14 种下料方案
方案
1
2
3
4
5
第二章 线性规划的图解法

例2.某工厂在计划期内要安排Ⅰ、Ⅱ两种产 品的生产,已知生产单位产品所需的设备台 时及A、B两种原材料的消耗、资源的限制, 如下表:
设备 原料 A 原料 B 单位产品获利 Ⅰ 1 2 0 50 元 Ⅱ 1 1 1 100 元 资源限制 300 台时 400 千克 250 千克
问题:工厂应分别生产多少单位Ⅰ、Ⅱ 产品才能使工厂获利最多?
第二章 线性规划的图解法
问题1具体数据如表所示:
资源 单耗 资源 煤(t) 电(kw.h) 油(t) 单位产品价格 9 4 3 7 4 5 10 12 360 200 300 产品 甲 乙 资源限量
提出和形成问题
建立模型
求解
结果的分析和应用
第二章 线性规划的图解法
在本例中
决策变量: 甲、乙产品的计划产量,记为x1 ,x2; 目标函数: 总收入记为f,则 f=7x1 +12x2 ,为体现对其求极大化, 在f 的前面冠以极大号Max,
第二章 线性规划的图解法 例2:.某公司由于生产需要,共需要A,B两种原料至 少350吨(A,B两种材料有一定替代性),其中A原 料至少购进125吨。但由于A,B两种原料的规格不同, 各自所需的加工时间也是不同的,加工每吨A原料需 要2个小时,加工每吨B原料需要1小时,而公司总共 有600个加工小时。又知道每吨A原料的价格为2万元, 每吨B原料的价格为3万元,试问在满足生产需要的 前提下,在公司加工能力的范围内,如何购买A,B 两种原料,使得购进成本最低?
第二章 线性规划的图解法
★线性规划模型的三个基本要素:
(也是所有规划问题的三个基本要素):
(1)决策变量:甲、乙产品的产量x1 ,x2 决策变量:需要决策的量,即等待求解的未知数。 (2)目标函数:总收入最大,Max f = 7 x 1 +12 x 2 目标函数:想要达到的目标,用决策 变量的表达式表示。 (3)约束条件: 约束条件:由于资源有限,为了实现 目标有哪些资源限制,用决策变量的 等式或不等式表示。
管理运筹学第2章 线性规划的图解法

i
i
MinZ e1i e2i
i
i
s.t.eβ10i-,eβ21i无 符yi 号 β限0 制β1xi
e1i , e2i 0,i 1,2,, n
还可以加上一些特定的需求.例如,要求必须过某 一点.
16
线性规划问题的应用举例(回归分析)
新标准:最小化最大绝对误差.
–整数规划问题
• 考虑短期排班的问题
–对午休换班进行建模
• 考虑每个工人
–允许工人有不同的偏好
29
套裁下料问题
例某工厂要做100套钢架,每套用长为2.9 m,2.1 m,1.5 m的圆钢
各一根。已知原料每根长7.4 m,问:应如何下料,可使所
用原料最省?
方案 1 方案 2 方案 3 方案 4 方案 5 方案 6 方案 7 方案 8
产品名称
规格要求
单价(元/kg)
甲 原材料 1 不少于 50%,原材料 2 不超过 25%
50
乙 原材料 1 不少于 25%,原材料 2 不超过 50%
35
丙
不限
25
原材料名称
1 2 3
每天最多供应量
100 100 60
单价(元/kg) 65 25 35
9
线性规划应用举例
解:设 xij 表示第 i 种(甲、乙、丙)产品中原料 j 的含量。 这样我们建立数学模型时,要考虑:
x1 + x2 ≥ 70 x2 + x3 ≥ 60 x3 + x4 ≥ 50 x4 + x5 ≥ 20 x5 + x6 ≥ 30 x1,x2,x3,x4,x5,x6 ≥ 0
20
关于决策变量的选择的启示
韩伯棠管理运筹学(第三版)_第二章_线性规划的图解法

之为线性规划。如果目标函数是变量的非线性函数,
或约束条件中含有变量非线性的等式或不等式的数学
模型则称之为非线性规划。
把满足所有约束条件的解称为该线性规划的可行
解。把使得目标函数值最大(即利润最大)的可行解称 为该线性规划的最优解,此目标函数值称为最优目标
函数值,简称最优值。
7
对于一般线性规划问题的建模过程。应注意 如下几个问题:
x1 X1+X2=300
B点为最优解,坐标为(50,250)
12
问题的解:
最佳决策为x1=50, x2=250,此时z=27500。 这说明该厂的最优生产计划方案是生产I产品50单位,
生产Ⅱ产品250单位,可得最大利润27500元。
把x1=50, x2=250代入约束条件得: 50+250=300台时设备
分析: 可知购买的原料A与原料B的总量为
250+100=350(吨)正好达到约束条件的最低限,所需的 加工时间为2×250+1×100=600正好达到加工时间的最 高限。而原料A的购进量250吨则比原料A购进量的最 低限125吨多购进了250-125=125吨, 这个超过量在 线性规划中称为剩余量。
2×50+250=350千克原料A,
1×250=250千克原料B.
这表明了生产50单位Ⅰ产品和250单位Ⅱ产品将消
耗完所有可使用的设备台时数和原料B,但对原料A来
说只消耗了350千克,还有(400—350)=50千克没有
使用。在线性规划中,对一个≤约束条件中没使用的资
源或能力的大小称之为松弛量。
max Z=50 x1+100x2 (称为目标函数)。
其中max为最大化的符号(最小化为min);50和100分别为单位产
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2.2 图 解 法
• 对于只包含两个决策变量的线性规划问 题,可以用图解法来求解。大于两个决策 变量不能用图解法来解了。
• 图解法.首先把每个约束条件(代表一个 平面)画在300二维坐x标2 轴上。
X1+X2=3 10
400
x2
100 100
2X1+X2=400
300
目标函数在可行域内Q点处取得最小 值。Q点的
坐标下面两方程的交点:
2x1x1x2x2356000
• Q点坐标为x1=250,x2=100。也即得到此线性 规划问题的最优解,购买A原料250吨,购买B 原料100吨,可使成本最小,即 2x1+3x2=2×250+3×100=800(万元)。
• 分析: 可知购买的原料A与原料B的总量为 250+100=350(吨)正好达到约束条件的最低限, 所需的加工时间为2×250+1×100=600正好达到 加工时间的最高限。而原料A的购进量250吨则 比原料A购进量的最低限125吨多购进了250-
• 目标函数:max Z=c1x1+c2x2+…+cnxn
• 或:
min f=c1x1+c2x2+…+cnxn
•
约束条件:a11x1+a12x2+…+a1nxn=b1
•
a21x1+a22x2+…+a2nxn=b2,
•
……………………………
•
am1x1+am2x2+…+am nxn=bm.
•
x1, x2,…,xn≥0.
X2=250
100
100
300
4x1+3x2=1200
x1 X1+X2=300 20
目标函数最小化的线性规划问题
例2 某公司由于生产需要,共需要A,B两种 原料至少350吨(A,B两种材料有一定替代性) ,其中A原料至少购进125吨。但由于A,B两 种原料的规格不同,各自所需的加工时间也是 不同的,加工每吨A原料需要2个小时,加工每 吨B原料需要1小时,而公司总共有600个加工 小时。又知道每吨A原料的价格为2万元,每吨 B原料的价格为3万元,试问在满足生产需要的 前提下,在公司加工能力的范围内,如何购买 A,B两种原料,使得购进成本最低?
原料B
0
1 250千克
该工厂每生产一单位产品I可获利50元,每生产一单位产品Ⅱ可获利100 元,问工
Ⅰ 厂应分别生产多少个产品 和产品Ⅱ才能使工厂获利最多?
4
如何建立模型?
5
• 这个问题可以用以下的数学模型来加以描述。工厂目前要决 策的问题是生产多少个Ⅰ产品和生产多少个Ⅱ产品,把这个要决 策的问题用变量x1、x2来表示,则称x1和x2为决策变量,即决策 变量x1=生产I产品的数量,决策变量x2=生产Ⅱ产品的数量。
• 2×50+250=350千克原料A,
•
1×250=250千克原料B.
• 这表明了生产50单位Ⅰ产品和250单位Ⅱ产品 将消耗完所有可使用的设备台时数和原料B,但
13
松弛变量和线性规划标准化
• 为了把一个线性规划标准化,需要有代表 没使用的资源或能力的变量,称之为松弛 变量,记为Si。显然这些松弛变量对目标函 数不会产生影响,可以在目标函数中把这 些松弛变量的系数看成零,加了松弛变量 后我们得到如下的例1的数学模型:
• 用x1和x2的线性函数形式来表示工厂所要求的最大利润的目标 : max Z=50 x1+100x2 (称为目标函数)。
• 其中max为最大化的符号(最小化为min);50和100分别为单位产 品 Ⅰ、 Ⅱ的利润。同样也可以用x1和x2的线性不等式来表示问题 的约束条件。对于台时数的限制可以表示为: X1+X2≤300.
第二章 线性规划的图解法
• 线性规划是运筹学的一个重要分支。它是现 代科学管理的重要手段之一,是帮助管理者作 出最优决策的一个有效的方法。下面看看一些 在管理上经常应用的典型线性规划问题:
• 1.合理利用线材问题。现有一批长度一定的 钢管,由于生产的需要,要求截出不同规格的 钢管若干。试问应如何下料,既满足了生产的 需要,又使得使用的原材料钢管的数量最少。
• 4.用一组决策变量的等式或不等式来表示在
8
线性规划的数学模型的一般形式为:
• 目标函数: • max (min) Z=c1x1+c2x2+…+cnxn • 约束条件: • a11x1+a12x2+…+a1nxn≤( =, ≥) b1, • a21x1+a22x2+…+a2nxn≤( =, ≥) b2, • ………………………… • am1x1+am2x2+…+amnxn≤( =, ≥) bm, • x1, x2, …, xn≥0.
x1 X1+X2=300
B点为最优解,坐标为(50,250) 12
问题的解:
• 最佳决策为x1=50, x2=250,此时z=27500。 这说明该厂的最优生产计划方案是生产I产品50
单位,生产Ⅱ产品250单位,可得最大利润
27500元。
• 把x1=50, x2=250代入约束条件得: • 50+250=300台时设备
•
x1-s2=125,
•
2x1+x2+s3=600,
•
x1, x2, s1,s2,s3≥0.
• s1,s2为剩余变量,s3为松弛变量,上式中所有的 约束条件也都为等式,故这也是线性规划问题的
标准形式。对应于约束条件的剩余变量2和4 松弛变
§2.3图解法的灵敏度分析
• 由上节可知,线性规划的标准形式可写为
•
2 x1+x2≤400,
•
x2≤250,
•
x1≥0, x2≥0.
• 由于上述数学模型的目标函数为变量的线
性函数,约束条件也为变量的线性等式或不等
式,故此模型称之为线性规划。如果目标函数
是变量的非线性函数,或约束条件中含有变量
非线性的等式或不等式的数学模型则称之为非
线性规划。
• 把满足所有约束条件的解称为该线性规划 的可行解。把使得目标函数值最大(即7利润最大
• 目标函数: max z =x1+x2 • 约束条件: x1-x2≤1
•
- 3x1+2x2≤6
•
x1≥0,x2≥0.
18
-3x1+2x2=6 X1-X2=1
• 从图中可知该问
题可行域无界,
x2
注意啊
目标函数值可以 增大到无穷大,
成为无界解即无
最优解。出现这
种情况,一般说
3
明线性规划模型
有错误,该模型
中忽略了一些实
际存在的必要的
约束条件。
1
-1
12 3 4
x1
-1 Z=0=X1+X2
Z=3=X1+X2 Z=1=X1+X2
19
• 4.线性规划存在无可行解的情况。若 在例1的数学模型中再增加一个约束条件 4x1+3x2≥1200,显然可见新的线性规划的 可行域为空域,也即不存在满足所有约束 条件的x1和x2的解,当然更不存在最优解 了盾。导出致40现的0 这建种模x2情错况误是。由于约束条件自相矛
23
• 同样对于≥约束条件中,可以增加一些代表 最低限约束的超过量,称之为剩余变量,把≥约 束条件变为等式约束条件,加了松弛变量与剩余 变量后例2的数学模型变为标准型(注意松弛变 量符号为正,而剩余变量符号为负):
• 目标函数:
• min f =2x1+3x2+0s1+0s2+0s3
• 约束条件: x1+x2-s1=350,
• 目标函数:
• max Z=50x1+100x2+0s1+0s2+0s3,
• 约束条件: x1+x2+s1=300,
•
2x1+x2+s2=400,
14
• 像这样把所有的约束条件都写成等式,称 为线性规划模型的标准化,所得结果称为线性 规划的标准形式。在标准型中 bj(右边常量)都 要大于等于零, 对某个bj小于零时,只要方程 两边都乘以(-1)即可。
• 同样,两种原材料的限量可分别表示为:
• 2X1+X2≤400, X2≤250. • 除了上述约束外,显然还应该有x1≥0,x2≥0,因为Ⅰ产品, Ⅱ产
品的 产量是不能取负值的。综上所述,就得到了例1的数学模型 如下:
6
• 目标函数: max Z=50x1+100x2,
• 满足约束条件:x1+x2≤300,
• 实际上以后可看到应同时具备如下三个条件的 模型才是标准型:
• 一是约束条件必须化为等式;二是所有变量必 须化为大于或者等于零;三是约束条件中的右 端常数项必须是大于或者等于零。
• 对例1 的最优解 x1=50,x2=250来说,松弛变 量的值如下所示:
• 约束条件 松弛变量的值
15
线性规划问题解的有如下特点:
• 1.如果某一个线性规划问题有最优解,则一 定有一个可行域的顶点对应一个最优解。
• 2.线性规划存在有无穷多个最优解的情况。 若将例1中的目标函数变为求max Z =50x1+50x2, 则可见代表目标函数的直线平移到最优位置后将 和直线x1+x2=300重合。详见下图。
• 此时不仅顶点B,C都代表了最优解,而且线 段BC上的所有点都代表了最优解,这样最优解 就有无穷多个了。当然这些最优解都对应着相同 的最优值(只有一个):
