第三章LS平差的若干问题
第三章监测网平差及基准点稳定性分析

剔除动点后,其余点构成统计量
F1
ˆF 2 ˆ02
ˆF
2
=
dFT
PFF fF
dF
当F1<F分析值,分析即结束,反之,继续 剔除动点,继续检验,直到原假设不再拒绝,
最后剩下的都是稳定的点。
• 当网中存在固定点时,采用这些固定点作 基准,应用经典平差;
• 当网中某些点具有相对的稳定性,它们相 互变动是随机的情况下,则用这些点作拟 稳点,用拟稳平差对成果进行分析;
• 当监测网所有网点具有微小的随机变动时, 自由网平差是一种有效的分析方法.
因此,要合理地确定监测网的参考系,首先要 确定哪些点是稳定的或相对稳定的点,哪些点是 不稳定的点。从20世纪70年代起,人们相继提出 了多种关于监测点稳定性分析方法,其中平均间 隙法是一种比较典型的方法。
m i=1
xi =0
xm
x
1 m
m i 1
xi
0, x为水准网的高程重心.
x =0说明水准网的自由网平差参考系是网的高程重心.
以测边网为例:自由网平差
x1
1
G
T
X=
0
- y10
0 1 x10
1 0 - y20
0 1 x20
…1 …0 … ym0
0 1 xm0
y1 xm
所以:对监测网进行稳定性分析,并 根据稳定性分析结果选择平差方法,确立 一个对变形分析比较有利的参考系,是变 形观测数据处理的一项重要任务。
§3—2 监测网的参考系及其平差
起算数据称为平差问题的基准:基准给出了控制网的位 置。
尺度和方位的定义 即控制网的参考系.
• 经典平差:采用选择固定基准的办法确定参考 系. (满足待估参数的求取要求) • 监测网平差:满足有多期复测的观测值估计的 位移 是一种“绝对的”或接近绝对的位移
第三章 条件平差

AP 1 AT K W 0
此式称为联系数法方程(简称法方程)。
条件平差原理
取法方程的系数阵 AP-1AT = N,由上式易知N阵关 于主对角线对称,得法方程表达式
NK W 0
法方程数阵N的秩 即N是一个r阶的满秩方阵,且可逆。移项得
NK W
R( N ) R( AP 1 AT ) r
1 2 4
相对应的改正数条件方程式形式
v1 v 2 v 4 w1 0 v 2 v3 v5 w2 0 v 4 v6 v7 w3 0 v5 v7 v8 w4 0 v 2 v7 w5 0
其中
高程网条件方程的个数及条件方程式
ˆ LL
T
取全微分式的系数阵为
f f 1 , f 2 , , f n T
由协因数传播律得
Q FF f T Q LL f ˆˆ
f f , L ˆ ˆ ˆ 1 L L L2
f , , L ˆ ˆ L L n
上式可分别表达成矩阵形式如下
ˆ AL A0 0
AV W 0
W ( AL A0 )
条件平差原理
按求函数极值的拉格朗日乘数法,引入乘系数 K [k k k ] (联系数向量),构成函数:
T r ,1 a b r
V T PV 2 K T ( AV W )
为引入最小二乘法,将Φ 对V求一阶导数,并令其 为零 ( K T AV ) d (V T PV ) T T
QAT N E QAT 0
QAT N 1 QAT N 1 AQ Q QAT N 1 AQ E AQ 0 1 1 N N AQ 0 QAT N 1 QAT N 1 AQ 0 T 1 0 0 Q QA N AQ
测量平差所有习题
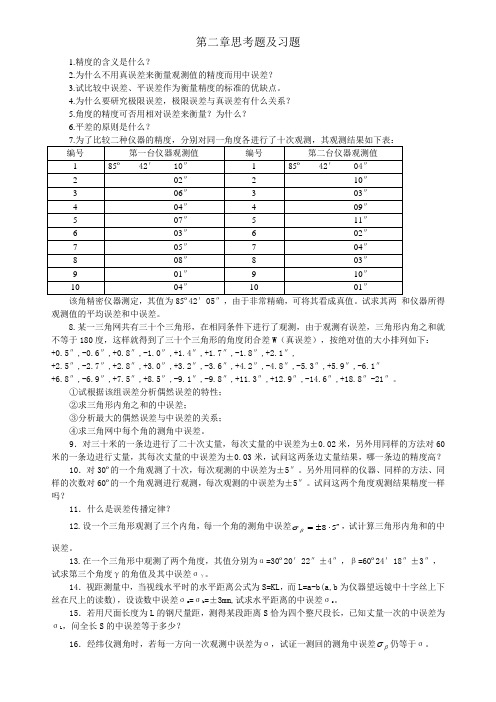
第二章思考题及习题1.精度的含义是什么?2.为什么不用真误差来衡量观测值的精度而用中误差?3.试比较中误差、平误差作为衡量精度的标准的优缺点。
4.为什么要研究极限误差,极限误差与真误差有什么关系?5.角度的精度可否用相对误差来衡量?为什么?6.平差的原则是什么?观测值的平均误差和中误差。
8.某一三角网共有三十个三角形,在相同条件下进行了观测,由于观测有误差,三角形内角之和就不等于180度,这样就得到了三十个三角形的角度闭合差W(真误差),按绝对值的大小排列如下:+0.5″,-0.6″,+0.8″,-1.0″,+1.4″,+1.7″,-1.8″,+2.1″,+2.5″,-2.7″,+2.8″,+3.0″,+3.2″,-3.6″,+4.2″,-4.8″,-5.3″,+5.9″,-6.1″+6.8″,-6.9″,+7.5″,+8.5″,-9.1″,-9.8″,+11.3″,+12.9″,-14.6″,+18.8″-21″。
①试根据该组误差分析偶然误差的特性;②求三角形内角之和的中误差;③分析最大的偶然误差与中误差的关系;④求三角网中每个角的测角中误差。
9.对三十米的一条边进行了二十次丈量,每次丈量的中误差为±0.02米,另外用同样的方法对60米的一条边进行丈量,其每次丈量的中误差为±0.03米,试问这两条边丈量结果,哪一条边的精度高?10.对30º的一个角观测了十次,每次观测的中误差为±5″。
另外用同样的仪器、同样的方法、同样的次数对60º的一个角观测进行观测,每次观测的中误差为±5″。
试问这两个角度观测结果精度一样吗?11.什么是误差传播定律?12.设一个三角形观测了三个内角,每一个角的测角中误差58''⋅±=βσ,试计算三角形内角和的中误差。
13.在一个三角形中观测了两个角度,其值分别为α=30º20′22″±4″,β=60º24′18″±3″,试求第三个角度γ的角值及其中误差σγ。
第3章:《误差理论与测量平差基础》 - 山东科技大学泰安校区

0 0 0 n n
Z [k 1 , k 2 , kn ] X k0 KX k0
n ,1
DZZ KDXX K
T
例4、根据极坐标法测设P点的坐标,设已知 点无误差,测角中误差为m,边长中误差ms, 试推导P点的点位中误差。
2 j 2 0
Qii为Li的协因数。
Q jj为L j的协因数。
Qij为Li关于L j的协因数 或相关权倒数。
1 ji Qij 2 pi 0
变换形式为:
2 i2 0 Qii 2 2 j 0 Q jj 2 ji 0 Qij
不难得出:
DXX
12 12 1n Q11 Q12 Q1n Q 2 Q22 Q2 n 21 2 2 n 2 21 0 2 Qn1 Qn 2 Qnn n1 n 2 n
山东科技大学山东科技大学资源与土木工程系资源与土木工程系误差理论与测量平差基础第六章附有参数的条件平差第二章误差分布与精度指标第三章协方差传播律及权第五章条件平差第七章间接平差第一章绪论第八章附有限制条件的间接平差第九章概括平差函数模型第十章误差椭圆第四章平差数学模型与最小二乘原理教材内容第十二章近代平差概论第一节协方差传播律第二节协方差传播律的应用第三节权与定权的常用方法第四节第五节协因数传播律第六节由真误差计算中误差及其实际应用直接观测值间接观测值函数关系具有一定精度也应该具有一定精度根据函数关系提出问题
2 (二) 选定了 0 ,即对应一组权。
(三)权是衡量精度的相对指标,为了使权起到比较 精度的作用,一个问题只选一个0。
第3章最小二乘平差

几何模型、物理模型或几何、物理综合模型。 (测量控制网如水准网、三角网、GPS网等都属于几何模型) 建立不同的函数模型,就有了不同的平差方法。测量中常 用的有: 1、条件平差法、附有参数的条件平差; 2、间接平差法、附有限制条件的间接平差;
3、附有限制条件的条件平差法。
例如:为确定一个三角形的形状,若等精度独立 观测了三角形三个内角,观测值方差为 2 。 则平差的数学模型可表达为:
L1 L1 L1 1800 0 或: E ( L1 ) E ( L1 ) E ( L1 ) 1800 0
函数模型:
随机模型:
2 0 0 Q11 0 2 DL 0 2 0 0 0 Q22 2 0 0 0 0
1、条件平差法
条件平差的函数模型 观测值的数学期望之间的函数关系式,又称为条件方程。 条件平差 以条件方程为函数模型的平差方法,称为条件平差方法。
h1 h5 h4 0 h2 h5 h6 0 h3 h4 h6 0 h1 h2 h3 0
h1 h5 h4 0 h2 h5 h6 0 h3 h4 h6 0 h1 h2 h3 0 h1 h2 h4 h6 0 .......
X1
X2
L3 X 1 X 2 180
0
t=2,选2个参数,函数模型:
选:X 1 L1 X 2 L2
1 0 0 , B0 0 B 0 1 0 1 1 180
3,1
L B XB
3,2 2,1
0
3,1
h1 h5 h4 0 h2 h5 h6 0 h3 h4 h6 0
[最新]测量平差习题
![[最新]测量平差习题](https://img.taocdn.com/s3/m/b663af6a26284b73f242336c1eb91a37f1113233.png)
第二部分 自测题第一章 自测题一、判断题(每题2分,共20分)1、 通过平差可以消除误差,从而消除观测值之间的矛盾。
( )2、 观测值i L 与其偶然真误差i ∆必定等精度。
( )3、 测量条件相同,观测值的精度相同,它们的中误差、真误差也相同。
( )4、 或然误差为最或然值与观测值之差。
( )5、 若X 、Y 向量的维数相同,则YX XY Q Q =。
( )6、 最小二乘原理要求观测值必须服从正态分布。
( )7、 若真误差向量的数学期望为0,即0=∆)(E ,则表示观测值中仅含偶然误差。
( )8、 单位权中误差变化,但权比及中误差均不变。
( )9、 权或权倒数可以有单位。
( )10、相关观测值权逆阵Q 的对角线元素ii Q 与权阵P 的对角线元素ii P 之间的关系为1=ii ii P Q 。
( )二、填空题(每空0.5分,共20分)1、测量平差就是在 基础上,依据 原则,对观测值进行合理的调整,即分别给以适当的 ,使矛盾消除,从而得到一组最可靠的结果,并进行 。
2、测量条件包括 、 、 和 ,由于测量条件的不可能绝对理想,使得一切测量结果必然含有 。
3、测量误差定义为 ,按其性质可分为 、 和 。
经典测量平差主要研究的是 误差。
4、偶然误差服从 分布,它的概率特性为 、 和 。
仅含偶然误差的观测值线性函数服从 分布。
5、最优估计量应具有的性质为 、 和 。
若模型为线性模型,则所得最优估计量称为 ,最优估计量主要针对观测值中仅含 误差而言。
要证明某估计量为最优估计量,只需证明其满足 性和 性即可。
6、限差是 的最大误差限,它的概率依据是 ,测量上常用于制定 的误差限。
7、若已知观测值向量L 或其偶然真误差向量∆的协方差阵为∑,则L 或∆的权阵定义为L P =∆P = ,由于验前精度∑难以精确求得,实用中定权公式有 、 、,特别是对独立等精度观测向量L 而言,其权阵可简单取为L P = 。
8、已知真误差向量1⨯∆n 及其权阵P ,则单位权中误差公式为 ,当权阵P 为 此公式变为中误差公式。
测量平差--条件平差原理研讨

h1=4.114 m S1=2 km
D
h3=0.758 m
S3=4 km
第三章 条件平差
最小二乘原则:
S1=2km S2=1km S3=4km
有无穷多组解
v12 v22 v32 min
V TPV
1 2
v12
v22
1 4
v32
min
2 条件平差的基本原理 第三章 条件平差
条件 方程
1 2
v12
0
v2
2v2
2ka
2kb
0
v3
1 2
v3
2kb
0
v1 2ka v2 ka kb v3 4kb
vv12
14.286 7.714
v3 2.284
kkba
7.143 0.571
fmin
1 2
v12
v22
1 4
v32
162.855
4.小结
第三章 条件平差
(1)根据问题确定实际观测数(n)、必要观测数(t)、 多余观测数(r)且有: r = n- t (条件方程数)。
第三章 条件平差
1 引例 2 条件平差的基本原理 3 解算方法 4 小结
1.引例
第三章 条件平差
测量工作中,为了确定某点(D)的高程。
(1)
HD=HA+ h1 h1
B
h2
(2)
HD=HB- h2
A
D
h3
(3)
HD=HC- h3
C
理想状态:(HD1)=
(2) (3)
HD= HD
实际中:(H1D)≠
(2)根据加权最小二乘原理,利用高等数学上的拉 格朗日乘常数法(即求条件极值的方法)进行求解。
第03讲 LS法

2 基本算法(9/14)
这就是加
即
权LS公式
ΦLΛLYL ΦLΛLΦL θ
(6)
因此,LS解即为求解上述正则方程. 当LLLL可逆时,即信号充分丰富时,则可求得的如下
加权LS估计
θ WLS
(Φ τL Λ L Φ L
)1
Φ
τ L
Λ
L
YL
(7)
上面讨论的是极小值得必要条件,其充分条件为: 即指标函数的2阶偏导矩阵为正定(偏导大于零)。
本讲主要讲授: 回归模型表述 LS法的基本原理和算法, LS估计的数值计算, LS法的应用例子,及其 LS估计值的统计特性分析.
第三讲 LS法(4/4)
1 回归模型表述(1/1)
1 回归模型表述
在讨论LS算法之前,下面先讨论在统计回归与 系统辨识中的回归模型. 静态模型(回归模型) 动态模型(自回归模型)
第三讲 最小二乘法
最小二乘(Least Square,以下 简 称 LS) 法 是 1795 年 高 斯 (Gauss)在星体运动预报研究 工作中提出来的.
第三讲 LS法(1/4)
第三讲 LS法(2/4)
LS法在数学各种分支以及其它应用科学中有广 泛应用,如: 数学 计算数学中的曲线拟合和函数逼近 概率统计中的回归分析与参数估计 非相容(矛盾)方程解理论中的LS解 系统与控制科学 实验建模(系统辨识) 测量理论中的误差分析
LS法的思想是由已知的观测数据对如下准则函 数求取最优解而获得未知参数的估计值
L
J (θ) λk[ y(k)-φτ (k-1)θ]2 k 1
[YL - ΦLθ]τ ΛL[YL - ΦLθ]
