数值分析在生活中应用举例及Matlab实现
MATLAB GUI设计在数值分析实践教学中的应用4页word文档

MATLAB GUI设计在数值分析实践教学中的应用基金项目:本文系广西教改工程2011年项目(项目编号:2011JGA055)的研究成果。
“数值分析”主要介绍科学计算的基本理论与基本方法,联系着非常广泛的背景领域,具有突出的多学科交叉特征,是所有从事与科学计算有关的科技人员都必须掌握的重要数学工具。
该课程是信息与计算科学专业、数学与应用数学专业一门主要的专业基础课,很多工科专业也把它作为一门必修课。
“数值分析”课程教学包括理论教学和实践教学两大部分。
实践教学作为课程教学体系的重要组成部分,与理论教学相辅相成、相互促进、互为补充。
必须采取切实有效的措施,使理论教学与实践教学有机融合、协调发展。
“数值分析”实践教学包括两类:课程实验和课程设计。
“数值分析”课程实验是随堂实验,主要是在“数值分析”理论课教学过程中安排适当的课时对某些重点、难点教学内容进行验证性、操作性、训练性的实验或操作,通过这些实验或操作加深学生对理论课程所涉及的知识、技能和方法的理解,为开展综合性实验打下坚实基础。
“数值分析”课程设计则在完成理论课教学后,就某些专题内容进行综合训练,着重培养学生的实践动手能力,提高学生综合分析问题、解决问题的能力,形成初步的科研意识,激发学生的科研潜能。
“数值分析”是一门理论性和实践性都很强的课程。
大力加强“数值分析”实践教学,是由“数值分析”课程性质、特点所决定的,是推进“数值分析”课程教学整体改革的必然要求。
要有效提高“数值分析”整体教学效果,既要加强理论课的教学,也重视实践课的教学。
要提高“数值分析”实践教学成效,必须借助恰当的工具和方法。
MATLAB的主要特点之一就是将高性能的数值计算和结果可视化有效融合。
利用MATLAB GUI设计非常方便实现计算结果的集成化和可视化,提高计算结果的直观性和可读性。
MATLAB GUI设计为“数值分析”实践教学提供了理想实验平台。
所谓GUI是指图形用户界面(Graphical User Interfaces),就是通过窗口、菜单、按钮、文字说明等对象(Objects)构成一个美观的界面。
一个数值分析在生活中的应用实例
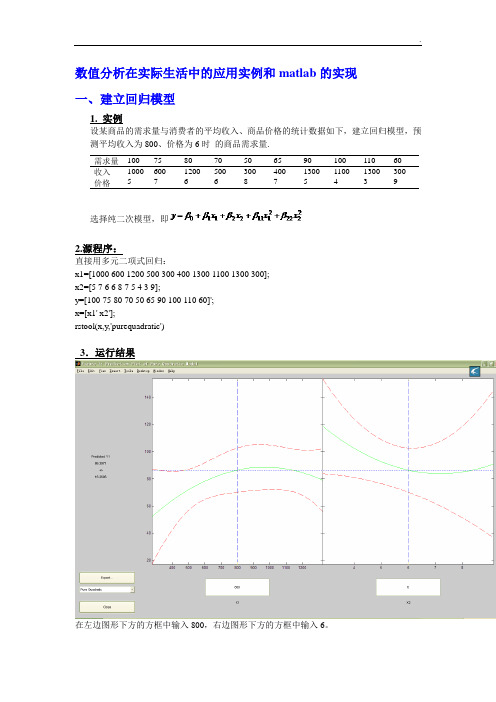
数值分析在实际生活中的应用实例和matlab的实现一、建立回归模型1. 实例设某商品的需求量与消费者的平均收入、商品价格的统计数据如下,建立回归模型,预测平均收入为800、价格为6时的商品需求量.需求量10075807050659010011060收入10006001200500300400130011001300300价格5766875439选择纯二次模型,即2.源程序:直接用多元二项式回归:x1=[1000 600 1200 500 300 400 1300 1100 1300 300];x2=[5 7 6 6 8 7 5 4 3 9];y=[100 75 80 70 50 65 90 100 110 60]';x=[x1' x2'];rstool(x,y,'purequadratic')3.运行结果在左边图形下方的方框中输入800,右边图形下方的方框中输入6。
则画面左边的“Predicted Y ”下方的数据变为86.3971,即预测出平均收入为800、价格为6时的商品需求量为86.3971.在画面左下方的下拉式菜单中选”all ”, 则beta (回归系数)、rmse (剩余标准差)和residuals (残差)都传送到Matlab 工作区中.在Matlab 工作区中输入命令: beta, rmse得结果:beta =110.5313 0.1464 -26.5709 -0.0001 1.8475 rmse =4.5362故回归模型为:2221218475.10001.05709.261464.05313.110x x x x y +--+= 剩余标准差为4.5362, 说明此回归模型的显著性较好.。
Matlab数学软件应用举例

MATLAB的发展史
70 年代中期 , 美国的穆勒教授在给学生开线 性代数课时,为了让学生能使用子程序库又不至于
在编程上花费过多的时间,便为学生编写了使用子
程序的接口程序。他将这个接口程序取名为 MATLAB,意为“矩阵实验室”。
80 年代初他们又采用 c 语言编写了 MATLAB 的
核心。目前 MATLAB 巳成为国际公认的最优秀的数
注释和标点
1. 百分号后的所有文字为注释,不参与运算。
例:syms x y
%定义符号变量x ,y
2. 多条命令可以放在同一行,用逗号或分号分隔,逗号表示要显示 该语句运行结果,分号表示不显示运行结果。 例:x=[2,3];y=[4,5];z1=x+y, z2=x’*y 结果:z1 = z2 = 6 8 12 8 10 15
(1) clc (2) clear (3) clf (4) who (5) whos (6) delete <文件名> (7) whech <文件名>
命令行的编辑与运行
( 9 ) clear all 从工作空间清除所有变量和函数 (10) help <命令名> 查询所列命令的帮助信息 (11) save name 保存工作空间变量到文件 name.mat (12) save name x y 保存工作空间变量 x y到文件 name.mat (13) load name 下载‘name’文件中的所有变量到工作空 间 (14) load name x y 下载‘name’文件中的变量x y到工作空间 (15) diary name1.m 保存工作空间一段文本到文件 name1.m … diary off (16) type name.m 在工作空间查看name.m文件内容 (17) what 列出当前目录下的m文件和mat文件
Matlab技术应用案例解析

Mat1ab技术应用案例解析引言在科学计算和数据分析领域中,Mauab是一种非常常用的软件工具。
它提供了丰富的数学函数库和强大的数据可视化功能,帮助工程师和科学家们解决了许多实际问题。
本文将通过解析几个实际的Mat1ab技术应用案例,展示MatIab在不同领域的应用。
一、电力系统优化电力系统优化是一项关键的技术,旨在通过合理地配置发电机组、输电线路和变电设备,以实现供电可靠性、经济性和环境友好性之间的平衡。
使用Mauab进行电力系统优化,可以帮助工程师们快速而准确地得出最优解。
首先,工程师需要建立电力系统的数学模型。
这可以通过Ma1Iab中的数学建模工具和仿真环境来完成。
然后,利用MaUab中的优化算法,可以对电力系统模型进行求解,以找到最优的配置方案。
例如,当工程师面临一个发电机组布置问题时,可以使用MaUab来分析各种约束条件下的不同方案,并基于经济和环境评估指标来找到最佳的解决方案。
二、图像处理图像处理是Mat1ab的另一个强大应用领域。
MaHab提供了丰富的图像处理函数库和工具箱,可以帮助工程师和科学家们对图像进行处理、分析和改进,从而满足各种不同的需求。
例如,在医学领域中,图像处理在医学影像分析和诊断中起着重要作用。
工程师和医生们可以使用Mat1ab来进行MRI、CT扫描图像的预处理、分割和特征提取,以辅助疾病的诊断和治疗。
此外,在计算机视觉领域中,图像处理也是一个热门的应用领域。
利用Mat1ab中的图像处理函数,可以实现目标检测、人脸识别和图像增强等功能。
三、机器学习随着大数据和人工智能的兴起,机器学习成为许多领域的核心技术。
Mat1ab提供了强大的机器学习工具箱,可以帮助科学家和数据分析人员开发和应用各种机器学习算法。
例如,在金融领域,使用机器学习算法可以分析市场趋势,预测股票价格,并帮助投资者做出正确的决策。
Mat1ab提供了各种机器学习算法,并具有易于使用的界面,使得科学家和分析师能够直观地分析和处理金融数据。
MATLAB在科学研究中的应用

MATLAB在科学研究中的应用MATLAB是一种广泛应用于科学研究的高级计算机语言和交互式环境。
在实际科学研究中,MATLAB被广泛应用于数据可视化、数值分析、图像处理、信号处理等方面。
本文将从这些方面介绍MATLAB在科学研究中的应用。
一、数据可视化在科学研究中,数据可视化是非常必要的一个环节。
MATLAB 提供了强大的数据可视化功能。
科学家可以使用MATLAB创建二维、三维图形,动态可视化,帮助研究者更好、更直观地了解数据分布的规律。
在实际研究中,科学家可以使用MATLAB展示图像、视频等数据,也可以使用MATLAB绘制统计图表、条形图、散点图等。
二、数值分析MATLAB的另一大优势是数值分析。
在科学研究过程中,计算相关问题必不可少。
MATLAB提供了一系列的计算函数和工具箱。
科学家可以使用MATLAB编写数值分析算法,对不同类型的数值问题进行求解。
此外,MATLAB可以处理大量数据集,包括矩阵、向量等,让科学家更加高效地处理复杂的数据问题。
三、图像处理MATLAB在图像处理方面也非常出色。
在实际研究中,科学家可以使用MATLAB对图像进行各种操作。
例如,可以使用MATLAB对图像进行透视变换,旋转,缩放等,更好的理解图像内部结构。
此外,通过使用MATLAB中的工具箱,科学家可以进行高级图像处理。
例如,使用MATLAB进行特征提取、模式识别等,可以在不同的领域发挥极大的作用。
四、信号处理MATLAB也提供了完备的处理信号的工具箱。
在实际科研中,有很多领域都需要使用信号处理技术。
例如,声音处理、图像处理、生物医学工程等。
MATLAB可以进行各种信号处理操作,如滤波、降采样、卷积、傅立叶变换等。
通过使用MATLAB,科学家可以更好地理解信号内部规律,提高研究效率。
总结综上所述,MATLAB在科学研究中的作用非常重要。
在数据可视化、图像处理、信号处理等方面,MATLAB都可以提供完整的解决方案。
科学家可以通过使用MATLAB,实现对数据的更深层次的理解。
Matlab技术实战案例分享

Matlab技术实战案例分享引言从Matlab在科学与工程领域的广泛应用,我们可以看出它的强大功能和实用性。
在本文中,我们将分享一些实际应用中的Matlab技术案例,通过这些案例,读者将更好地理解和掌握Matlab的实战应用技巧。
一、图像处理图像处理是Matlab应用最广泛的领域之一,它在医学影像分析、计算机视觉等方面具有广泛的应用。
通过Matlab的图像处理工具箱,我们可以轻松处理和分析各种类型的图像数据。
案例一:基于Matlab的肌肉图像分析在运动学研究中,肌肉图像分析是一个重要的课题。
我们可以通过Matlab将单帧肌肉图像进行分割,提取关键特征并进行测量分析,如肌肉纤维方向和长度等。
这为运动学研究提供了有力的工具和方法。
案例二:基于Matlab的图像增强和去噪在计算机视觉领域,图像增强和去噪是常见的图像处理任务。
我们可以通过Matlab中的图像滤波函数和增强算法,对图像进行降噪和增强处理,提高图像的质量和清晰度。
这对于图像识别、目标检测等任务具有重要意义。
二、信号处理信号处理是Matlab应用广泛的另一个领域,它在通信、音频处理等方面具有重要的应用。
通过Matlab的信号处理工具箱,我们可以进行各种类型的信号处理和分析。
案例三:基于Matlab的音频处理和音频特征提取在音频处理领域,Matlab提供了丰富的函数和算法可以用来进行音频处理和音频特征提取。
我们可以通过Matlab对音频信号进行降噪、滤波、频谱分析等处理,同时提取关键的音频特征,如音调、节奏等。
案例四:基于Matlab的时频分析时频分析是信号处理中重要的分析方法之一。
通过Matlab的时频分析工具箱,我们可以对信号的瞬时频率和幅度进行分析,了解信号在时域和频域上的特征。
这对于故障诊断、语音识别等任务具有重要意义。
三、数值计算与优化数值计算与优化是Matlab的另一个重要领域,它在工程计算、统计建模等方面具有广泛的应用。
通过Matlab的数值计算和优化工具箱,我们可以轻松进行各种复杂的数值计算和优化问题求解。
实验五 MATLAB在数值计算中的应用
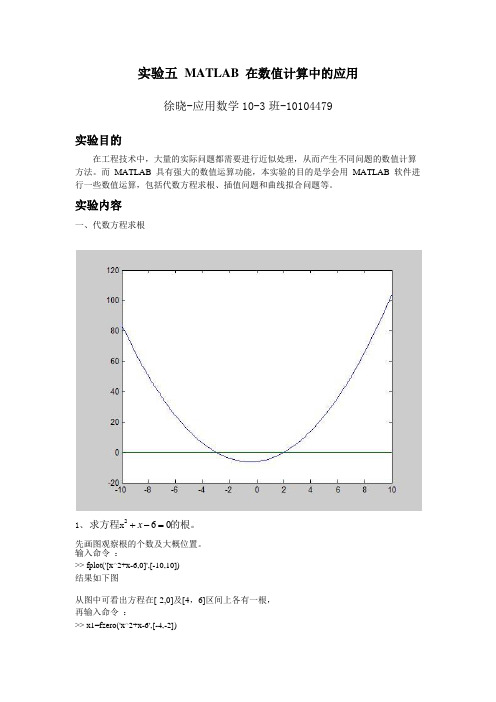
实验五 MATLAB 在数值计算中的应用徐晓-应用数学10-3班-10104479实验目的在工程技术中,大量的实际问题都需要进行近似处理,从而产生不同问题的数值计算 方法。
而 MATLAB 具有强大的数值运算功能,本实验的目的是学会用 MATLAB 软件进行一些数值运算,包括代数方程求根、插值问题和曲线拟合问题等。
实验内容一、代数方程求根1、60x +-=2求方程x 的根。
先画图观察根的个数及大概位置。
输入命令 :>> fplot('[x^2+x-6,0]',[-10,10])结果如下图从图中可看出方程在[-2,0]及[4,6]区间上各有一根, 再输入命令 :>> x1=fzero('x^2+x-6',[-4,-2])x1 = -3>> x2=fzero('x^2-4*x-5',[0,4])x2 = 22、求方程3cos ln x x 的所有的根fplot('[3*cos(x)-log(x),0]',[- 50,50])%先画图,看一下确定解得大致范围 fplot('[3*cos(x)-log(x),0]',[- 30,30])%通过图形确定解得具体范围f=inline('3*cos(x)-log(x)');fsolve(f,[-19.04,-18.62,-13,-12,-7.2 ,-5.2,-1.4,1.4,5.2,7.2,12,13,18.62,19.04])%利用单个解得最近数值进行求解。
结果为:ans =Columns 1 through 4-19.7669 + 1.0760i -19.7669 + 1.0760i -13.5544 + 1.0312i -13.5544 + 1.0312iColumns 5 through 8-7.3921 + 0.9647i -7.3921 - 0.9647i -1.4453 + 0.7984i 1.4473 - 0.0000iColumns 9 through 125.3020 + 0.0000i 7.1395 + 0.0000i 11.9702 - 0.0000i 13.1064 + 0.0000iColumns 13 through 1418.6247 - 0.0000i 19.0387 + 0.0000i3、求方程的所有的根。
MATLAB在数值分析中的应用

等,它们的原函数不能用初等函数表示成 有限形式。
11.1.3定积分问题
原因之二:有些被积函数的原函数过于复 杂,计算不便。例如
f ( x) x 的一个原函数是
F ( x) x
3 2 2
2
2x 3
2
2 x 3 3x 2 x 3 9 ln( 2 x 2 x2 3) 4 16 16 2
对一些典型的微分方程,如可分离变量方 程、一阶线性方程等,有可能找出它们的 一般解表达式,然后用初始条件确定表达 式中的任意常数,这样即能确定解 但是对于常微分方程初值问题: y ' 2x y y (0) 0 则无法求出一般解
11.2 多项式与插值
• 来源于实际、又广泛用于实际。 • 多项式插值的主要目的是用一个多项式 拟合离散点上的函数值,使得可以用该 多项式估计数据点之间的函数值。 • 可导出数值积分方法,有限差分近似 • 关注插值多项式的表达式、精度、选点 效果。
• 例 >> a=[2,-5,6,-1,9]; b=[3,-90,-18]; >> c=conv(a,b) c= 6 -195 432 -453 9 -792 -162 >> [q,r]=deconv(c,b) q= 2 -5 6 -1 9 r= 0 0 0 0 0 0 0 >> poly2sym(c) ans = 6*x^6-195*x^5+432*x^4-453*x^3+9*x^2-792*x-162
t=interp1(hours,temps,h)
plot(hours,temps,'+',h,t)
title('线性插值下的温度曲线'),
数值分析解决实际问题

数值分析解决实际问题数值分析是一门研究利用计算机对数学问题进行数值计算的学科,它通过数值方法来解决实际问题,广泛应用于工程、科学、经济等领域。
数值分析的方法包括插值法、数值积分、常微分方程数值解、线性代数方程组求解等,这些方法在解决实际问题时发挥着重要作用。
本文将介绍数值分析在实际问题中的应用,并探讨其在解决实际问题中的重要性和价值。
一、插值法插值法是数值分析中常用的方法之一,它通过已知数据点之间的插值多项式来估计未知数据点的值。
在实际问题中,插值法常用于数据的平滑处理、曲线拟合等方面。
例如,在气象学中,我们需要根据已知的气温数据点来预测未来某一时刻的气温变化,这时可以利用插值法来进行数据的预测和分析。
二、数值积分数值积分是数值分析中的另一个重要方法,它通过数值逼近来计算定积分的近似值。
在实际问题中,数值积分常用于计算曲线下面积、求解物理学中的力学问题等。
例如,在工程学中,我们需要计算某一形状的曲线或曲面的面积或体积,这时可以利用数值积分方法来进行计算。
三、常微分方程数值解常微分方程数值解是数值分析中的重要内容之一,它通过数值方法来求解常微分方程的数值解。
在实际问题中,常微分方程数值解常用于模拟物理系统、生态系统等的动态行为。
例如,在生态学中,我们需要研究种群数量随时间的变化规律,这时可以利用常微分方程数值解来模拟和预测种群数量的变化趋势。
四、线性代数方程组求解线性代数方程组求解是数值分析中的重要内容之一,它通过数值方法来求解线性代数方程组的解。
在实际问题中,线性代数方程组求解常用于工程、经济等领域的优化问题。
例如,在工程优化中,我们需要确定某一系统的最优参数配置,这时可以利用线性代数方程组求解来进行优化计算。
综上所述,数值分析在解决实际问题中发挥着重要作用,它通过插值法、数值积分、常微分方程数值解、线性代数方程组求解等方法来对实际问题进行数值计算和分析,为工程、科学、经济等领域的发展提供了重要支持。
Matlab技术的实际应用案例解析

Matlab技术的实际应用案例解析随着计算机技术的发展,Matlab作为一种高级技术语言,被广泛应用于多个领域。
无论是在科研领域还是工程实践中,Matlab都扮演着重要的角色。
本文将通过几个实际应用案例,探讨Matlab技术在不同领域的应用,以期给读者提供一些启示和参考。
一、图像处理领域图像处理是Matlab的一项重要应用领域。
利用Matlab提供的强大的图像处理工具箱,可以实现各种功能,例如图像增强、滤波、分割和识别等。
以下将介绍一个实际应用案例。
案例一:肿瘤图像分割肿瘤图像的分割对于医学诊断非常关键。
在某医院的研究中,研究人员利用Matlab进行了肿瘤图像的分割工作。
首先,他们先对肿瘤图像进行预处理,包括降噪和增强等操作。
然后,利用Matlab提供的图像分割算法,将肿瘤与周围组织分离出来。
最后,通过对分割后的图像进行计算,可以得到肿瘤的大小、形状等信息,为医生提供诊断依据。
二、信号处理领域信号处理是Matlab的另一个重要应用领域。
通过利用Matlab提供的信号处理工具箱,可以实现信号的滤波、谱分析、峰值检测等功能。
以下将介绍一个实际应用案例。
案例二:语音信号增强在通信领域,语音信号是一种常见的信号类型。
在某通信公司的项目中,研发团队利用Matlab对语音信号进行增强。
首先,他们通过Matlab提供的滤波器设计算法,设计了一种高效的降噪滤波器。
然后,他们利用该滤波器对采集到的语音信号进行滤波处理,去除噪声成分。
最后,通过对处理后的语音信号进行主观听感和客观评价,证明了该算法的有效性。
三、控制系统领域Matlab在控制系统领域的应用也非常广泛。
通过Matlab提供的控制系统工具箱,可以进行控制系统的建模、仿真和优化等操作。
以下将介绍一个实际应用案例。
案例三:智能交通信号优化在城市交通系统中,智能交通信号优化是一个重要的研究方向。
在某城市的交通管理局的项目中,研究人员利用Matlab进行了智能交通信号优化的仿真研究。
Matlab工程应用案例分析

Matlab工程应用案例分析引言:Matlab是一种广泛应用于科学计算、工程设计和数据分析的高级计算机语言和环境。
它的强大功能和使用简单性使得它成为许多工程师和科学家的首选工具。
在本文中,我们将通过几个工程应用案例来探讨Matlab在实际工程项目中的应用。
案例一:电力系统优化设计在电力系统设计中,优化是非常关键的一个环节。
通过对系统参数的优化,可以提高系统的效率和可靠性。
Matlab在电力系统优化设计中发挥了重要作用。
例如,在某城市的电力系统中,需要对输电线路进行改造以提高输电效率。
通过收集该地区的用电数据以及电线参数,可以建立一个电力系统模型。
然后,利用Matlab提供的优化算法和模拟工具,可以快速找到最优的输电线路配置,使总损耗最小化。
案例二:机器学习算法开发机器学习算法在各个领域有着广泛的应用。
然而,开发新的机器学习算法并不是一件容易的事。
Matlab提供了丰富的机器学习工具箱和函数,可以帮助工程师和科学家开发出新的机器学习算法。
例如,某个研究团队想要开发一种基于深度学习的图像分类算法。
他们可以利用Matlab提供的深度学习工具箱,通过构建神经网络模型和训练样本数据,来实现图像分类的自动化。
该算法可以广泛应用于图像识别、智能监控等领域。
案例三:控制系统设计与仿真在控制系统设计中,Matlab是一个不可或缺的工具。
控制系统的设计需要对系统进行分析和建模,然后通过调整控制器参数来实现期望的控制效果。
Matlab提供了丰富的控制系统工具箱,可以帮助工程师完成控制系统的建模和仿真。
例如,在飞机自动驾驶系统的设计中,工程师可以使用Matlab来建立飞机的数学模型,并根据不同的控制策略进行仿真。
通过与实际飞机系统进行对比和调整,可以优化控制系统的性能。
案例四:图像处理和计算机视觉Matlab在图像处理和计算机视觉领域也有很好的应用。
例如,在自动驾驶汽车的视觉系统中,需要对实时采集的图像进行处理和分析。
Matlab在数值计算方面的应用

Matlab在数值计算方面的应用摘要:Matlab的名称源自Matrix Laboratory,它的首创者是在数值线性代数领域颇有影响的Cleve MoleAr 博士。
Matlab是一种科学计算软件,专门以矩阵的形式处理数据。
目前,Matlab软件已经成为了应用最广泛的科学计算工具之一。
Matlab可以用来进行如下工作:●数值分析;●数值和符号计算;●工程与科学绘图;●控制系统的设计与仿真;●数字图像处理;●数字信号处理;●通讯系统设计与仿真;●财务与金融工程。
尤其是在电子信息领域学科和数学建模领域中,Matlab已经成为了学术研究、论文写作的有力工具。
Matlab成为许多学科的解题工具,将Matlab融入其它课程的学习中,可以大大提高运算效率和准确性。
随着计算机的普及和国民文化素质的整体提高,科学计算将会更加普及。
Matlab在矩阵及数值计算、多项式和线性代数、符号数学的基本方法等方面都有较好的应用下面我从两点阐述Matlab在数学上面的应用:一、Matlab在数值运算上的应用;二、Matlab在绘图方面的应用。
Matlab的数值运算功能Matlab是一个包含计算算法的集合。
其拥有800多个工程中要用到的数学运算函数,可以方便实现用户所需的各种计算功能。
函数中所使用的算法都是科研和工程计算中的最新研究成果,而且经过了各种优化和容错处理。
在通常情况下,可以用它来代替底层编程语言,如C和C++。
在计算相同的情况下,使用Matlab的编程工作量会大大减少。
Matlab的这些函数集包括从最简单的函数到诸如矩阵、特征向量、快速傅立叶变换的复杂函数。
函数所能解决的问题大致包括矩阵运算和现行方程组的求解,微分方程及偏微分方程的组的求解、符号运算、傅立叶变换和数据的统计分析、工程中的优化问题、复数的各种运算、三角函数和其它初等数学运算、多维数组操作以及建模动态仿真等。
1.数组运算一般的,数组是有序数据的集合,在大多数编程语言中,数组的每一个成员(元素)都属于同一种数据类型,它们使用同一个数组名称和不同的下标来惟一确定数组中的成员(元素)。
MATLAB数据分析与可视化案例展示

MATLAB数据分析与可视化案例展示概述:在如今的数据驱动时代,数据分析和可视化成为了重要的技能。
MATLAB作为一款强大的数学建模和计算软件,提供了丰富的功能来帮助研究人员、工程师和科学家进行数据分析和可视化。
本文将以实际案例为基础,展示MATLAB在数据分析和可视化方面的强大能力。
案例一:销售数据分析假设我们是一家电子产品公司,我们拥有一定数量的销售数据,包括销售额、产品种类、销售地区等信息。
现在,我们希望通过分析这些数据来了解产品的销售情况,并制定相关策略。
首先,我们可以使用MATLAB的数据导入功能导入销售数据,并进行初步的数据清洗。
接下来,我们可以使用MATLAB的数据统计和可视化工具来进行分析。
例如,我们可以通过绘制销售额的时间序列图来观察销售趋势。
MATLAB提供了丰富的绘图函数,可以根据需要选择合适的图表类型,并进行个性化设置。
通过观察时间序列图,我们可以发现销售额的季度波动和增长趋势,进而为制定销售策略提供参考。
另外,我们还可以利用MATLAB的统计分析功能对销售数据进行更深入的分析。
例如,我们可以使用MATLAB的线性回归模型拟合销售数据,预测未来销售额,并评估拟合程度。
此外,我们还可以通过绘制散点图来观察销售额与其他因素(如产品种类、销售地区)之间的关系,进一步挖掘潜在的市场机会和问题。
通过以上分析,我们可以得出一些有益的结论和建议,如推出针对不同地区和产品种类的定制化销售策略,加强对新增潜在市场的开拓,优化产品组合等。
案例二:气象数据分析与可视化气象数据是一种典型的多维数据,其中包括温度、湿度、气压等多种观测指标。
使用MATLAB可以对气象数据进行分析和可视化,进而深入了解气象变化规律,为气象预测、灾害预警等提供支持。
首先,我们可以使用MATLAB的数据导入工具导入气象观测数据,并进行数据清洗和预处理。
接下来,我们可以使用MATLAB的绘图函数来绘制各种气象图表。
例如,我们可以使用MATLAB的等值线图来展示温度分布情况。
MATLAB使用教程(5)应用举例

2019/2/16 黄建华制作 4
例5.1 雨量预报方法的评价
对于问题二,我们认为公众的感受主要体现在预测 与实际之间偏差的大小程度,然而,实际测量值未知, 因此我们考虑在分级预报中加入准确概率的方式来实 现公众满意度的提高。我们认为雨量的实测值应该在 预测值点处服从正态分布,通过合理的假设和推导, 我们得到:正态分布的均值可以取为雨量预测值,不 同雨量分级区间上的方差可以近似取为对应区间上的 总偏差平方和的平均值。运用Matlab软件编程,可以 实现对每一个预报数据的预报内容的改变,并且通过 几个不同的数据体现程序运行所得到的结果。最后, 对模型的缺点进行了讨论和改进。
2019/2/16
黄建华制作
10
例5.1 雨量预报方法的评价
将文件全部拷贝在默认的work文件加下,运行程序sjzr.m:
2019/2/16
黄建华制作
11
例5.1 雨量预报方法的评价
2019/2/16
黄建华制作
12
例5.1 雨量预报方法的评价
程序huatu.m %画一个时点预测曲面图与实测散点图比较
2019/2/16
黄建华制作
3
例5.1 雨量预报方法的评价
模型的分析: 本题的关键主要是采用Matlab软件对所提供的数 据进行分析并得到主要结论。 对于问题一,采用load命令和循环结构实现数据文 件的载入,再从实测数据文件中提出实测点位置数据, 并且依次从预测数据文件中通过曲面拟合命令 griddata得到相应日期、时段、方法下的对应位置上 的预测估计值。然后分别计算两种预报方法下的实测 值和预测值的偏差并且求对应的总偏差平方和,根据 两个总偏差平方和的大小来得出两种方法的优劣比较, 通过Matlab程序的实现得到结果为:第一种方法比第 二种方法好。
matlab简单程序运用-数值分析篇

1:三次样条插值法h0=figure('toolbar','none',...'position',[200 50 350 450],...'name','实例86');h1=axes('parent',h0,...'position',[0.10 0.45 0.8 0.5],...'visible','off');x=0:0.2:2*pi;y=sin(x);plot(x,y)b1=uicontrol('parent',h0,...'units','points',...'tag','b1',...'style','pushbutton',...'string','三次样条插值',...'backgroundcolor',[0.75 0.75 0.75],...'position',[20 60 70 20],...'callback',[...'y=0,',...'sy=0,',...'strn1=get(e2,''string'');,',...'n1=str2num(strn1);,',...'strn2=get(e3,''string'');,',...'n2=str2num(strn2);,',...'x=n1:0.2:n2;,',...'i=1;,',...'for t=n1:0.2:n2,',...'y(i)=sin(t);,',...'sy(i)=san(t,n1,n2);,',...'i=i+1;,',...'end,',...'plot(x,y,''b*'',x,sy,''r-''),',...'axis([0 7 -1.5 1.5]),',...'legend(''sin(x)'',''N-Hermite插值'')']); b2=uicontrol('parent',h0,...'units','points',...'tag','b2',...'style','pushbutton',...'string','误差比较',...'backgroundcolor',[0.75 0.75 0.75],...'position',[170 60 70 20],...'callback',[...'strdn1=get(e2,''string'');,',...'n1=str2num(strdn1);,',...'strdn2=get(e3,''string'');,',...'n2=str2num(strdn2);,',...'strdn=get(e1,''string'');,',...'dn=str2num(strdn);,',...'dd=abs(sin(dn)-san(dn,n1,n2));,',...'msgbox([''误差为:'',num2str(dd)],''计算结果'')']); e1=uicontrol('parent',h0,...'units','points',...'tag','e1',...'style','edit',...'fontsize',12,...'string','1.20',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[200 100 40 20]);t1=uicontrol('parent',h0,...'units','points',...'tag','t1',...'style','text',...'string','误差点:',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[160 100 40 20]);e2=uicontrol('parent',h0,...'units','points',...'tag','e2',...'style','edit',...'fontsize',12,...'string','1.00',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[20 85 40 20]);t2=uicontrol('parent',h0,...'units','points',...'tag','t2',...'style','text',...'string','第一节点:',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[15 105 50 20]);e3=uicontrol('parent',h0,...'units','points',...'tag','e3',...'fontsize',12,...'string','3.00',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[100 85 40 20]);t3=uicontrol('parent',h0,...'units','points',...'tag','t3',...'style','text',...'string','第二节点:',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[95 105 50 20]);b3=uicontrol('parent',h0,...'units','points',...'tag','b3',...'style','pushbutton',...'string','关闭',...'backgroundcolor',[0.75 0.75 0.75],...'position',[100 20 60 20],...'callback','close');2:NEWTON插值h0=figure('toolbar','none',...'position',[200 50 350 450],...'name','实例87');h1=axes('parent',h0,...'position',[0.10 0.45 0.8 0.5],...'visible','off');x=0:0.2:2*pi;y=sin(x);plot(x,y)b1=uicontrol('parent',h0,...'units','points',...'tag','b1',...'style','pushbutton',...'string','牛顿插值',...'backgroundcolor',[0.75 0.75 0.75],...'position',[20 60 70 20],...'callback',[...'strn=get(e1,''string'');,',...'n=str2num(strn);,',...'x=0:0.2:2*pi;,',...'for t=0:0.2:2*pi,',...'y(i)=sin(t);,',...'ynt(i)=newton(t,n);,',...'i=i+1;,',...'end,',...'plot(x,y,''b*'',x,ynt,''r-''),',...'axis([0 7 -1.5 1.5]),',...'legend(''sin(x)'',''牛顿插值'')']);b2=uicontrol('parent',h0,...'units','points',...'tag','b2',...'style','pushbutton',...'string','误差比较',...'backgroundcolor',[0.75 0.75 0.75],...'position',[170 60 70 20],...'callback',[...'strn=get(e1,''string'');,',...'n=str2num(strn);,',...'strdn=get(e2,''string'');,',...'dn=str2num(strdn);,',...'dd=abs(sin(dn)-newton(dn,n));,',...'msgbox([''误差为:'',num2str(dd)],''计算结果'')']); e1=uicontrol('parent',h0,...'units','points',...'tag','e1',...'style','edit',...'fontsize',12,...'string','5',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[50 100 40 20]);e2=uicontrol('parent',h0,...'units','points',...'tag','e2',...'style','edit',...'fontsize',12,...'string','1.20',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[200 100 40 20]);t1=uicontrol('parent',h0,...'units','points',...'tag','t1',...'string','节点数:(<6)',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[10 100 40 30]);t2=uicontrol('parent',h0,...'units','points',...'tag','t2',...'style','text',...'string','误差点:',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[160 100 40 20]);b3=uicontrol('parent',h0,...'units','points',...'tag','b3',...'style','pushbutton',...'string','关闭',...'backgroundcolor',[0.75 0.75 0.75],...'position',[100 20 60 20],...'callback','close');3mewton形式的hermite插值h0=figure('toolbar','none',...'position',[200 50 350 450],...'name','实例89');h1=axes('parent',h0,...'position',[0.10 0.45 0.8 0.5],...'visible','off');x=0:0.2:2*pi;y=sin(x);plot(x,y)b1=uicontrol('parent',h0,...'units','points',...'tag','b1',...'style','pushbutton',...'string','N-Hermite插值',...'backgroundcolor',[0.75 0.75 0.75],...'position',[20 60 70 20],...'callback',[...'strn1=get(e2,''string'');,',...'n1=str2num(strn1);,',...'strn2=get(e3,''string'');,',...'n2=str2num(strn2);,',...'x=0:0.2:2*pi;,',...'i=1;,',...'for t=0:0.2:2*pi,',...'y(i)=sin(t);,',...'ynh(i)=nhermite(t,n1,n2);,',...'i=i+1;,',...'end,',...'plot(x,y,''b*'',x,ynh,''r-''),',...'axis([0 7 -1.5 1.5]),',...'legend(''sin(x)'',''N-Hermite插值'')']);b2=uicontrol('parent',h0,...'units','points',...'tag','b2',...'style','pushbutton',...'string','误差比较',...'backgroundcolor',[0.75 0.75 0.75],...'position',[170 60 70 20],...'callback',[...'strdn1=get(e2,''string'');,',...'n1=str2num(strdn1);,',...'strdn2=get(e3,''string'');,',...'n2=str2num(strdn2);,',...'strdn=get(e1,''string'');,',...'dn=str2num(strdn);,',...'dd=abs(sin(dn)-nhermite(dn,n1,n2));,',...'msgbox([''误差为:'',num2str(dd)],''计算结果'')']); e1=uicontrol('parent',h0,...'units','points',...'tag','e1',...'style','edit',...'fontsize',12,...'string','1.20',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[200 100 40 20]);t1=uicontrol('parent',h0,...'units','points',...'tag','t1',...'style','text',...'string','误差点:',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[160 100 40 20]);e2=uicontrol('parent',h0,...'units','points',...'tag','e2',...'style','edit',...'fontsize',12,...'string','1.00',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[20 85 40 20]);t2=uicontrol('parent',h0,...'units','points',...'tag','t2',...'style','text',...'string','第一节点:',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[15 105 50 20]);e3=uicontrol('parent',h0,...'units','points',...'tag','e3',...'style','edit',...'fontsize',12,...'string','3.00',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[100 85 40 20]);t3=uicontrol('parent',h0,...'units','points',...'tag','t3',...'style','text',...'string','第二节点:',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[95 105 50 20]);b3=uicontrol('parent',h0,...'units','points',...'tag','b3',...'style','pushbutton',...'string','关闭',...'backgroundcolor',[0.75 0.75 0.75],...'position',[100 20 60 20],...'callback','close');。
MATLAB在实际生活中的应用小论文

MATLAB 在实际问题中的分析与应用自20世纪80年代以来,出现了多种科学计算语言,亦称数学软件,比较流行的有MATLAB 、Mathematical 、Maple 等。
因为他们具有功能强、效率高、简单易学等特点,在在许多领域等到广泛应用。
MATLAB 便是一种影响大、流行广的科学计算语言。
MATLAB 的语法规则简单,更加贴近人的思维方式。
MATLAB 是英文Matrix Laboratory(矩阵实验室)的缩写。
自1984年由美国Math Works 公司推向市场以来,得到了广泛的应用和发展。
在欧美各高等院校MATLAB 已经成为线性代数、自动控制理论、数字信号处理、时间序列分析、动态系统仿真、图像处理等诸多课程的基本教学工具,成为大学生、硕士生以及博士生必须掌握的基本技能。
在设计研究单位和工业部门,MATLAB 已被广泛的应用于研究和解决各种具体的工程问题。
近年来,MATLAB 在我国也开始流行,应用MATLAB 的单位和个人急剧增加。
可以预见,MATLAB 将在我国科学研究和工程应用中发挥越来越大的作用。
Mat lab 是当前数值计算方面应用地非常广泛的一种计算机软件,特别是在工程应用求解中发挥了重要作用。
其所具有的浅显易懂的编程语言、强大的绘图功能、大量的内部函数等都深深地吸引了我认真地去学习它。
同时在上《过程装备力学基础》时,其中涉及有很多的问题是超越方程、微积分的问题,难以用普通的线性方法求解,而Mat lab 在此方面有强大的功能,特别是超越方程的精确求解以及图形的绘制方面。
数学当中的绘制函数图象、绘制立体图形的交线(如绘制两个等直径圆柱体的交线)、求多项式的根等问题,这些问题如果依靠我们人工进行操作,则需要很多的时间和精力,当我们掌握了基本原理后,借助于MATLAB 进行解决则会大大提高效率和精确度。
仅举一些运用MATLAB 的例子。
常用控制命令:click :%清屏; clear :%清变量; save :%保存变量; load :%导入变量 一、利用公式直接进行赋值计算本金P 以每年n 次,每次i%的增值率(n 与i 的乘积为每年增值额的百分比)增加,当增加到r ×P 时所花费的时间T 为:(利用复利计息公式可得到下式))01.01ln(ln )01.01(i n rT i P P r nT +=⇒+=⨯(12,5.0,2===n i r )MATLAB 的表达形式及结果如下: >> r=2;i=0.5;n=12; %变量赋值 >> T=log(r)/(n*log(1+0.01*i)) 计算结果显示为:T = 11.5813即所花费的时间为T=11.5813 年。
数值分析matlab实验报告

数值分析matlab实验报告数值分析 Matlab 实验报告一、实验目的数值分析是研究各种数学问题数值解法的学科,Matlab 则是一款功能强大的科学计算软件。
本次实验旨在通过使用 Matlab 解决一系列数值分析问题,加深对数值分析方法的理解和应用能力,掌握数值计算中的误差分析、数值逼近、数值积分与数值微分等基本概念和方法,并培养运用计算机解决实际数学问题的能力。
二、实验内容(一)误差分析在数值计算中,误差是不可避免的。
通过对给定函数进行计算,分析截断误差和舍入误差的影响。
例如,计算函数$f(x) =\sin(x)$在$x = 05$ 附近的值,比较不同精度下的结果差异。
(二)数值逼近1、多项式插值使用拉格朗日插值法和牛顿插值法对给定的数据点进行插值,得到拟合多项式,并分析其误差。
2、曲线拟合采用最小二乘法对给定的数据进行线性和非线性曲线拟合,如多项式曲线拟合和指数曲线拟合。
(三)数值积分1、牛顿柯特斯公式实现梯形公式、辛普森公式和柯特斯公式,计算给定函数在特定区间上的积分值,并分析误差。
2、高斯求积公式使用高斯勒让德求积公式计算积分,比较其精度与牛顿柯特斯公式的差异。
(四)数值微分利用差商公式计算函数的数值导数,分析步长对结果的影响,探讨如何选择合适的步长以提高精度。
三、实验步骤(一)误差分析1、定义函数`compute_sin_error` 来计算不同精度下的正弦函数值和误差。
```matlabfunction value, error = compute_sin_error(x, precision)true_value = sin(x);computed_value = vpa(sin(x), precision);error = abs(true_value computed_value);end```2、在主程序中调用该函数,分别设置不同的精度进行计算和分析。
(二)数值逼近1、拉格朗日插值法```matlabfunction L = lagrange_interpolation(x, y, xi)n = length(x);L = 0;for i = 1:nli = 1;for j = 1:nif j ~= ili = li (xi x(j))/(x(i) x(j));endendL = L + y(i) li;endend```2、牛顿插值法```matlabfunction N = newton_interpolation(x, y, xi)n = length(x);%计算差商表D = zeros(n, n);D(:, 1) = y';for j = 2:nfor i = j:nD(i, j) =(D(i, j 1) D(i 1, j 1))/(x(i) x(i j + 1));endend%计算插值结果N = D(1, 1);term = 1;for i = 2:nterm = term (xi x(i 1));N = N + D(i, i) term;endend```3、曲线拟合```matlab%线性最小二乘拟合p = polyfit(x, y, 1);y_fit_linear = polyval(p, x);%多项式曲线拟合p = polyfit(x, y, n);% n 为多项式的次数y_fit_poly = polyval(p, x);%指数曲线拟合p = fit(x, y, 'exp1');y_fit_exp = p(x);```(三)数值积分1、梯形公式```matlabfunction T = trapezoidal_rule(f, a, b, n)h =(b a) / n;x = a:h:b;y = f(x);T = h ((y(1) + y(end))/ 2 + sum(y(2:end 1)));end```2、辛普森公式```matlabfunction S = simpson_rule(f, a, b, n)if mod(n, 2) ~= 0error('n 必须为偶数');endh =(b a) / n;x = a:h:b;y = f(x);S = h / 3 (y(1) + 4 sum(y(2:2:end 1))+ 2 sum(y(3:2:end 2))+ y(end));end```3、柯特斯公式```matlabfunction C = cotes_rule(f, a, b, n)h =(b a) / n;x = a:h:b;y = f(x);w = 7, 32, 12, 32, 7 / 90;C = h sum(w y);end```4、高斯勒让德求积公式```matlabfunction G = gauss_legendre_integration(f, a, b)x, w = gauss_legendre(5);%选择适当的节点数t =(b a) / 2 x +(a + b) / 2;G =(b a) / 2 sum(w f(t));end```(四)数值微分```matlabfunction dydx = numerical_derivative(f, x, h)dydx =(f(x + h) f(x h))/(2 h);end```四、实验结果与分析(一)误差分析通过不同精度的计算,发现随着精度的提高,误差逐渐减小,但计算时间也相应增加。
数值分析在生活中的应用举例及Matlab实现

一、最小二乘法,用MATLAB实现1. 数值实例下面给定的是乌鲁木齐最近1个月早晨7:00左右(新疆时间)的天气预报所得到的温度,按照数据找出任意次曲线拟合方程和它的图像。
下面用MATLAB编程对上述数据进行最小二乘拟合。
下面用MATLAB编程对上述数据进行最小二乘拟合2、程序代码x=[1:1:30];y=[9,10,11,12,13,14,13,12,11,9,10,11,12,13,14,12,11,10,9,8,7,8,9,11,9,7,6,5,3,1];a1=polyfit(x,y,3) %三次多项式拟合%a2= polyfit(x,y,9) %九次多项式拟合%a3= polyfit(x,y,15) %十五次多项式拟合%b1=polyval(a1,x)b2=polyval(a2,x)b3=polyval(a3,x)r1= sum((y-b1).^2) %三次多项式误差平方和%r2= sum((y-b2).^2) %九次次多项式误差平方和%r3= sum((y-b3).^2) %十五次多项式误差平方和%plot(x,y,'*') %用*画出x,y图像%hold onplot(x,b1, 'r') %用红色线画出x,b1图像%hold onplot(x,b2, 'g') %用绿色线画出x,b2图像%hold onplot(x,b3, 'b:o') %用蓝色o线画出x,b3图像%3、数值结果不同次数多项式拟合误差平方和为:r1=67.6659r2=20.1060r3=3.7952r1、r2、r3分别表示三次、九次、十五次多项式误差平方和。
4、拟合曲线如下图二、 线性方程组的求解( 高斯-塞德尔迭代算法 )1、实例: 求解线性方程组(见书P233页)⎪⎪⎩⎪⎪⎨⎧=++=-+=+-3612363311420238321321321x x x x x x x x x 记A x=b, 其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=363320,,12361114238321b x A x x x任取初始值()()Tx0000=,进行迭代。
Matlab软件在数值分析中的应用

《数值分析》课程设计Matlab软件在数值分析中的应用院(系)名称2013 年05 月31日数值分析课程设计评阅书课程设计任务书2012—2013学年第二学期专业班级:学号:姓名:课程设计名称:数值分析Ⅰ、Ⅱ设计题目:Matlab软件在数值分析中的应用完成期限:自2013 年05月21 日至2013年05 月31日共10天设计依据、要求及主要内容:一、设计目的实验方法与理论方法是推进科学技术发展的两大基本方法,由于这些问题不可能用实验手段来实现,因此,学习研究了数值模型.Matlab软件在解决数值模型中起到关键的作用,对于数值分析的研究也十分重要.二、设计内容(1)Matlab在数值代数、数值逼近、常微分方程中的应用(2)Matlab在数值分析中的具体应用方法(3)Matlab软件中用不同的方法解决一些数学方面难解的问题.三、设计要求1.Matlab软件利用编程解决一些复杂问题,对重点部分加以分析.2.举一些例子使用所用的方法编写Matlab程序求解.3.对于在数值分析中的应用应该总结概括完整.计划答辩时间:2013年06 月 5 日工作任务与工作量要求:查阅文献资料不少于3篇,课程设计报告1篇不少于3000字.指导教师(签字):教研室主任(签字):批准日期:2013 年05 月20 日Matlab软件在数值分析中的应用摘要Matlab已经成为国际上最流行的科学与工程计算的软件工具,是当今最优秀的科学计算软件之一,它集数值计算、图形处理、符号推演、文字处理、动态仿真等功能于一身.Matlab软件在数值分析中的应用也越来越重要,分类讨论了Matlab在数值分析中的应用如:数值代数、数值逼近、常微分方程的计算中的应用,并给出了相应的求解方法.关键词:数值分析,Matlab,数值代数,数值逼近,微分方程目录1 前言 (1)2 解题思想和方法 (1)2.1数值方法的特点: (1)2.2数制与浮点运算 (1)2.3误差分析 (2)2.4下面对于范数和极限的讨论 (2)2.5解线性方程组的直接法 (3)2.6线性代数方程组的迭代解法 (3)2.7矩阵特征值问题的求解 (4)2.8非线性方程求根 (7)2.9函数插值 (8)2.11一致逼近与平方逼近 (9)2.12数值积分 (9)3 对方程Matlab求解 (10)3.1幂法的Matlab程序 (10)3.2 用Newton法 (11)总结 (13)参考文献 (13)1 前言数值分析能提高自己的思维能力,锻炼自己的理解能力还有学习能力.通过本学期的学习,使我清楚地认识到数值分析对于我们专业的重要性.它也将运用到我们生活中的方方面面,对我们今后的工作生活也有很大的作用.而学习数值分析,我们需要树立算法意识、培养算法设计与分析的能力和应用计算的能力,掌握不同数学问题的求解理论与方法.还有更多的知识需要我们去深入研究,去获取更多的知识.还有就是数值分析在数学建模中也非常重要,他锻炼了一个人的思维能力,在建模中能够较好的去分析问题,更好的去寻找思路.数值分析也离不开Matlab,在学习中我们也常常用Matlab来编程一种计算方式的计算算法.在计算不同数学问题的求解理论方法要树立算法意识和培养算法设计与分析的能力和应用计算机的能力,通过一学期的学习深深感悟到要想把数值分析学习好,需要很深的数学功底和努力学习,在学习中我们要结合实际深刻理解定理、算法,不断有意识和无意识的发现并接受定理,算法蕴含的思想,让它为自我知能的一部分,去引领我们的生活,这样的数学学习才是完美的.2 解题思想和方法首先要有可靠的理论分析,以确保算法在理论上的收敛性和数值上的稳定性.其次要对计算的结果进行误差估计,以确定其是否满足精度,还要考虑算法的运行效率即算法的运算量和存储量.以及编写Matlab程序实现在计算机上的应用,使其能在一些问题上更快地收敛.2.1数值方法的特点:1)数值结果要能算得出来,其次结果应有一定的精度2)误差满足指定的值3)计算时间应尽可能少2.2数制与浮点运算1、数制即在计算机中一个数通常可以用十进制、二进制、八进制等表示.2、浮点数即用整数部分加小数部分来表示一个实数.对于二进制的转换举例说明: 10(291)=2(100100011) 2.3误差分析误差*x x -的具体数值无法确定,设法给出其绝对值的一个上界*x x E ε-=≤绝对误差 *x x ε-=相对误差 *x x xδ-= %x 的相对误差 对于方法的稳定:一种数值方法的传播误差应该可以控制 2.4下面对于范数和极限的讨论学习它主要目的是利用范数求特征值计算矩阵方程组 1向量范数11nj j x x ==∑{12max ,,,}n xx x x ∞=21/221()nj j x x ==∑2矩阵范数设.是n R 中的向量范数,对于任何m n R ⨯,若定义1max x A Ax ==则A 是矩阵A 的范数,得到的范数即为向量范数的从属范数.1范数的从属范数 111max mij j ni A a <≤==∑∞范数的从属范数 11max nij i mj Aa ∞<≤==∑2范数的从属范数 1(1)2nk n n k =+=∑ 另:矩阵的F 范数与谱范数均与2范数相容但F 范数不是从属范数,从属范数是所有相容范数中的最小者.2A ≤ F A对于任何,0()n n k A R A k ⨯∈→→∞的充分必要条件是()1A ρ<. 2.5解线性方程组的直接法 1.回迭过程的实现:1/()/n n nn nii ij j ii j i x b u x b u x u =+=⎧⎪⎨=-⎪⎩∑ i=n-1,….,1 整个回迭过程乘除法运算量为:1(1)2nk n n k =+=∑. 2.三对角矩阵是一类很重要的特殊矩阵,在数学和物理学中有广泛的应用.三对角矩阵的特征,用待定系数法求解三对角线性方程组的数值解,并与常用的LU 分解法从理论分析和数据实验两方面进行比较,结果表明,两者的时间复杂性前者稍差,而精度两者则相当,最后写出两者的C 程序并运行结果.接下来用一种简单和容易实现的方法求出三对角矩阵的行列式,再利用其逆矩阵可以分解成两个很特殊的矩阵的乘积,给出一种算法实现三对角矩阵的逆的简便计算.LU 分解:设A 的前n-1个顺序主子阵非奇异,则存在单位下三角矩阵L 及上三角矩阵U 使A=LU 且分解是唯一的. 2.6线性代数方程组的迭代解法迭代法发的一般形式,Ax b =改写成x Hx g =+,H 为n n R ⨯矩阵g n R ∈向量而(0)n x R ∈定义向量序列;(1)()k k x Hx g +=+, {}k x 为迭代序列解方程组的方法:Jaclbi 迭代法和Gauss-Seidel 迭代法,超松弛迭代法,对于一般的方程组Ax=b,其中n n A R ⨯∈,detA ≠0,记A=D-L-U.D 为对角部分 L 为严格下三角部分 U 严格上三角矩阵. 设方程组 i x B x f =+11()j B D L U I D A --=+=- 1J f D b -=1(1)()()111 ()i nk k k ii ij j ij j j j i ii x b a x a x a -+==+=--∑∑ 此为Jaclbi 迭代法 .11()()G B D L U I D L A --=-=-- 1()g f D L b -=-1(1)(1)()111 ()i nk k k ii ij j ij j j j i ii x b a x a x a -++==+=--∑∑ i=1,2,…..,n;k=1,2,…. 另外:编程时双保险,避免死循环给出值满足精度,知最大循环次数. 2.7矩阵特征值问题的求解它包括矩阵特征值和特征向量的计算,而矩阵特征值的计算方法本质上都是迭代法.解决问题的方法有乘幂法和反乘幂法. 乘幂法的基本公式()(1)()()()max()/k k k k k k k y Az m y z y m -⎧=⎪=⎨⎪=⎩带原点位移的反幂法的计算公式()(1)()()()()max()/k k i k k k k kA I y z m y z y m λ-⎧-=⎪=⎨⎪=⎩ 在Matlab 中的实验举例说明:function [k,lambda,vk,wc]=ydwyfmf(A,v0,jlamb,jd,max1) [n,n]=size(A);A1=A-jlamb*eye(n);jd=jd*0.1;RAl=det(A1);if RA1==0disp('A-aE的n阶行列式n1等于0,所以A-aE不能进行LU分解')returnendlambda=0;if RAl~=0for p=1:nh(p)=det(A1(1:p,1:p));endhl=h(1:n);if h(1,i)==0disp('因为A-aE的各阶主子式等于0,所以A-aE不能进行LU分解')returnendendif h(1,i)~=0disp('因为A-aE的各阶主子式都不等于0,所以A-aE不能进行LU分解')k=1;wc=1;state=1;vk=v0;while((k<=max1)&(state==1))[L U]=lu(A);Yk=L/Vk;Vk=U/Yk;[m j]=max(abs(Vk));mk=m;Vk1=Vk/mk;Yk1=L/Vk1;Vk1=U/Yk1;[m j]=max(abs(Vk1));mk1=m;Vk2=(1/mk1)*Vk1;tzw1=abs((mk-mk1)/mk1);tzw2=abs(mk1-mk);Txw1=norm(Vk)-norm(Vk1);Txw2=(norm(Vk)-norm(Vk1)) rm(Vk1);Txw=min(Txw1,Txw2);tzw=min(tzw1,tzw2);Vk=Vk2;mk=mk1;wc=max(Txw,tzw);Vk=Vk2;mk=mk1;state=0;if(wc>jd)state=1;k=k+1;%Vk=Vk2,mk=mk1endif(Wc<=jd)disp('A-aE的秩R(A-aE)和各阶顺序主子式值h1,迭代次数k,按模最小特征值的近似值lambda,特征向量的近似向量Vk,相邻两次迭代的误差Wc如下:') elsedisp('A-aE的秩R(A-aE)和各阶顺序主子式值h1,迭代次数k已经达到最大迭代次数max1,按模最小特征值的迭代值lambda,特征向量的迭代向量Vk,相邻两次迭代的误差Wc如下:')endh1,RA1endend[V,D]=eig(A,'nobalance');Vk;k=k-1;Wc;lambdan=jlamb+1/mk1;2.8非线性方程求根求()f x =0的解,设*x 为方程的根,即()*0f x =.如果存在正整数使()*()()m f x x x g x =-,且0< *()g x <∞,则称*x 为他的m 重根.当()f x 在*x 可微时,*x 为()f x 的重根的充要条件是*x 是()'f x 的根.确定根的存在性定理:若()f x 在[],a b 上连续,且()().0f a f b <,则()f x 在[],a b 上至少有一个根,steffensen 方法21()()k k k k k k k k y f x y x x f x y y +=⎧⎪⎨=-⎪+-⎩关于它还有一个重要定理,如果()f x 在*x 处二次连续可微,且'*()0f x ≠,则steffensen 方法局部平方收敛,如果'*(1)*()()0m f x f x -===,*()0m f x ≠,则steffensen方法局部线性收敛.切线法(Newton 法)在Matlab 中编程如下: function [C,D]=newploy(X,Y) n=length(X); D=zeros(n,n); D(:,1)=Y'; for j=2:nfor k=j:nD(k,j)=(D(k,j-1)-D(k-1,j-1))/(X(k)-X(k-j+1)); end end C=D(n,n); for k=(n-1):-1:1C=conv(C,poly(X(k)));m=length(C); C(m)=C(m)+D(k,k); end 2.9函数插值插值问题的提法是:假定区间[a ,b]上的实值函数f (x )在该区间上 n+1个互不相同点x 0,x 1……x n 处的值是f (x 0),……f(x n ),要求估算f (x )在[a ,b]中某点x*的值.基本思路是,找到一个函数P(x),在x 0,x 1……x n 的节点上与f(x)函数值相同(有时,甚至一阶导数值也相同),用P(x*)的值作为函数f(x*)的近似.拉格朗日插值公式对给定的n+1个节点x 0,x 1,x 2,…,x n 及对应的函数值y 0,y 1,y 2,…,y n , 构造一个n 次插值多项式:)(0x l y y k nk k ∑==简单程序示例:x=[0.0 0.1 0.195 0.3 0.401 0.5];y=[0.39849 0.39695 0.39142 0.38138 0.368120.35206 ]; T=interp1(x,y,0..25,'linear') %线性插值 (返回结果T=0.3862)T=interp1(x,y,0.25,'nearest') % 两点插值 (返回结果T=0.3814)T=interp1(x,y,0.25,'spline') % 三次样条插值 (返回结果T =0.3867)T=interp1(x,y,0.25,'cubic') %三次插值 (返回结果T =0.3867) 2.10样条函数在插值问题中,样条插值通常比多项式插值好用.用低阶的样条插值能产生和高阶的多项式插值类似的效果,并且可以避免被称为龙格现象的数值不稳定的出现.并且低阶的样条插值还具有“保凸”的重要性质.2.11一致逼近与平方逼近近似代替又称为逼近,函数 f (x ) 称为被逼近函数;P (x ) 称为逼近函数,两者之差称为逼近的误差.1、一致逼近(均匀逼近)以)()(max x p x f bx a -≤≤ 作为度量误差f (x )- P (x ) 的“大小” 标准.2、 平方逼近(均方逼近)以[]122(()())ba f x p x dx -⎰作为度量误差f (x )- P (x )的“大小” 标准.function c=pf1(f,n,a,b) %c 最佳平方逼近多项式的系数syms x; for i=1:n+1 for j=1:n+1A(i,j)=int(x^(i+j-2),x,a,b); endB(i)=int(f*x^(i-1),x,a,b); end c=inv(A)*B';2.12数值积分1.插值型的求积公式:构造出的求积0()nn k k k f x =I =A ∑,()bk k al x dx A =⎰ 公式积称为是插值型求积公式2.牛顿——柯特斯公式:设将积分区间划分为n 等分,步长 b ah n-=,选取等距节点 k x a kh =+ ,构造出的插值型求积公式:()0()()nn n k k k b a C f x =I =-∑称为牛顿—柯特斯公式,式中()001nn n kj j kt j Cdt n k j=≠-=-∏⎰例dx x x⎰+1024x=0:1/8:1; y=x./(4+x.^2); trapz(x,y) 运行结果:ans= 0.11140235452955 3 利用Matlab 求解3.1幂法的Matlab 程序用幂法计算矩阵的主特征值和对应的特征向量的Matlab 主程序 function [k,lambda,Vk,Wc]=mifa(A,V0,jd,max1) lambda=0;k=1;Wc =1; ,jd=jd*0.1;state=1; V=V0; while((k<=max1)&(state==1)) Vk=A*V; [m j]=max(abs(Vk)); mk=m; tzw=abs(lambda-mk); Vk=(1/mk)*Vk; Txw=norm(V-Vk); Wc=max(Txw,tzw); V=Vk;lambda=mk;state=0; if(Wc>jd) state=1; endk=k+1;Wc=Wc; end if(Wc<=jd)disp('请注意:迭代次数k,主特征值的近似值lambda,主特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下:')elsedisp('请注意:迭代次数k 已经达到最大迭代次数max1,主特征值的迭代值lambda,主特征向量的迭代向量Vk,相邻两次迭代的误差Wc 如下:')endVk=V;k=k-1;Wc;用幂法计算下列矩阵的主特征值和对应的特征向量的近似向量,精度. 解 (1)输入MATLAB 程序 A=[1 -1;2 4];V0=[1,1]';[k,lambda,Vk,Wc]=mifa(A,V0,0.00001,100),[V ,D] = eig (A), Dzd=max(diag(D)), wuD= abs(Dzd- lambda), wuV=V(:,2)./Vk, 运行后屏幕显示结果请注意:迭代次数k,主特征值的近似值lambda,主特征向量的近似向量Vk,相邻两次迭代的误差Wc 如下: k = lambda = Wc =33 3.00000173836804 8.691862856124999e-007Vk = V = wuV =-0.49999942054432-0.707106781186550.44721359549996-0.894428227562941.000000000000000.70710678118655-0.89442719099992-0.89442719099992Dzd = wuD =3 1.738368038406435e-006由输出结果可看出,迭代33次,相邻两次迭代的误差Wc 8.69 19e-007,矩阵的主特征值的近似值lambda3.000 00和对应的特征向量的近似向量Vk (-0.500 00,1.000 00, lambda 与例5.1.1中的最大特征值近似相等,绝对误差约为1.738 37e-006,Vk 与特征向量 的第1个分量的绝对误差约等于0,第2个分量的绝对值相同.由wuV 可以看出,的特征向量V(:,2) 与Vk 的对应分量的比值近似相等.因此,用程序mifa.m 计算的结果达到预先给定的精度. 3.2 用Newton 法例.使用Newton 法计算方程0107222=--x e x 在区间[]2,2-上的根,其初始值x.5.1解:编写主程序为:[x,time]=Newton('2*exp(2*x)-7*x^2-10',1.5,1e-5)x=0:0.01:2;y=2*exp(2*x)-7*x.^2-10;plot(x,y)grid运行并调用Newton的主程序结果为:wucha=0.2430wucha=0.0615wucha=0.0311……………wucha=2.3876e-005wucha=1.5073e-005wucha=9.5154e-006x=1.1197time=20总结通过一周的时间,数值分析课程设计终于完成了.在这期间,我收获了很多,也学习很多.以前仅仅只学习书本上的理论知识,从没有自己的动手实践.通过做这次的课程设计,使我把理论的知识与实践结合到了一起,达到了理论与实践的结合.此外,也提高了自己的动手能力.而最大难题就是程序,由于不擅长编程序,在编写程序是总是出现问题,于是,自己在网上搜了了一些资料,并通过查阅此资料.并且通过自己的修改终于能运行出来了时候,心里有一点小小的自豪感.一个学期的数值分析学习,使我有很多感悟.其中我感受最深的是数值分析是一门重视算法和原理的学科,它的内容更接近于实际,像求解线性方程组、矩阵的特征值等,是数学理论更加有实际意义,随着学习的深入,我发现要想学会数值分析必须把那些理论和定理搞得非常透彻,虽然我现在还无法真正理解那些思想,但我会不断的有意识的无意识的去熟悉那些定理和蕴含的思想.进而真正让数学帮助我们全方位的成长.通过这次课程设计,我从中学会了很多,也发现自己真的还有很多不足以及很多东西需要去学习.所以在以后的生活学习中要不断的扩大自己的视野,多学习一些与专业有关的知识,不能只满足于课本上的知识.所以在完成本专业的基础上,要不断涉猎,完善自我,希望自己在以后的课程中会得到更好的锻练.总的来说这次课程设计还是有很多的收获的,并且特别感谢我们组的成员在做课程设计的过程中对我的帮助.参考文献[1] 冯国忱黄明游.数值分析(上册)[M].北京:高等教育出版社,2007.[2] 宋叶志贾东志.MATLAB数值分析与应用[M].北京:机械工业出版社,2009.[3] 张德丰.MATLAB数值分析与应用[M].北京:国防工业出版社,2007.[4] 陈东彦李冬梅,王树忠.数学建模[M].北京:科学出版社,2007[5]李庆扬王能超易大义.数值分析[M].4版.北京清华大学出版社,2005。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、最小二乘法,用MATLAB实现1. 数值实例下面给定地是乌鲁木齐最近1个月早晨7:00左右(新疆时间)地天气预报所得到地温度,按照数据找出任意次曲线拟合方程和它地图像.下面用MATLAB编程对上述数据进行最小二乘拟合.b5E2RGbCAP2008年10月26~11月26天数 1 2 3 4 5 6 7 8 9 10 温度9 10 11 12 13 14 13 12 11 9 天数11 12 13 14 15 16 17 18 19 20 温度10 11 12 13 14 12 11 10 9 8 天数21 22 23 24 25 26 27 28 29 30 温度7 8 9 11 9 7 6 5 3 1 下面用MATLAB编程对上述数据进行最小二乘拟合2、程序代码x=[1:1:30];y=[9,10,11,12,13,14,13,12,11,9,10,11,12,13,14,12,11,10,9,8,7,8,9,11,9,7,6,5,3,1];p1EanqFDPwa1=polyfit(x,y,3) %三次多项式拟合%a2= polyfit(x,y,9) %九次多项式拟合%a3= polyfit(x,y,15) %十五次多项式拟合%b1=polyval(a1,x)b2=polyval(a2,x)b3=polyval(a3,x)r1= sum((y-b1).^2) %三次多项式误差平方和%r2= sum((y-b2).^2) %九次次多项式误差平方和%r3= sum((y-b3).^2) %十五次多项式误差平方和%plot(x,y,'*') %用*画出x,y图像%hold onplot(x,b1, 'r') %用红色线画出x,b1图像%hold onplot(x,b2, 'g') %用绿色线画出x,b2图像%hold onplot(x,b3, 'b:o') %用蓝色o线画出x,b3图像%3、数值结果不同次数多项式拟合误差平方和为:r1=67.6659r2=20.1060r3=3.7952r1、r2、r3分别表示三次、九次、十五次多项式误差平方和.4、拟合曲线如下图二、线性方程组地求解(高斯-塞德尔迭代算法)1、实例:求解线性方程组(见书P233页)3612363311420238321321321xx xxx x x x x 记A x=b, 其中363320,,12361114238321bxAxx x 任取初始值Tx00,进行迭代.2、用C 语言实现,源程序如下:#include<stdio.h> #include<stdlib.h> struct Node {double value; // 矩阵非零元素值int index;// 元素地索引(序号或列标)};struct Matrix{struct Node *data; // 记录元素数据int total_elem; // 矩阵非零元素个数int total_ln; // 矩阵地总行数int total_col; // 矩阵地总列数};// 采用MSR法实现系数矩阵地存储void Create_Matrix( struct Matrix &matrix ){int index = 0, i = 0;double value = 0.0;printf( "请输入线性方程组系数矩阵地非零元素个数及总行数、总列数: " );scanf( "%d%d%d", &matrix.total_elem, &matrix.total_ln, &matrix.total_col );DXDiTa9E3dmatrix.data = (struct Node *)malloc( sizeof(struct Node)*(matrix.total_elem+1) );RTCrpUDGiTprintf( "请依次输入矩阵地主对角线元素及每行地非零非对角线元素(行优先)\n" );for( i = 0; i <= matrix.total_elem; i++ ){if( i == matrix.total_ln )value = 0;elsescanf( "%lf", &value );matrix.data[i].value = value;}printf( "\n系数矩阵地信息相关如下(Quote为添加项,表示序列号):" );printf( "\nValue:" );for( i = 0; i < matrix.total_elem + 1; i++ )printf( "%3.0lf", matrix.data[i].value );printf( "\nQuote:" );for( i = 0; i < matrix.total_elem + 1; i++ )printf( "%3d", i );printf( "\n\n" );for( i = 0; i <= matrix.total_elem; i++ ){if( i == 0 )printf( "请参照上表输入第每行第一个非零非主对角元素地序号\n " );if( i == matrix.total_ln )matrix.data[i].index = matrix.total_elem + 1;elseif( i == matrix.total_ln + 1 )printf( "请依次输入非零非对角元素地列标\n " );if( i != matrix.total_ln )scanf( "%d", &matrix.data[i].index );}}// 显示系数矩阵地相关信息void Display_Matrix( struct Matrix matrix ){int i = 0;printf( "系数矩阵采用MSR存储法地相关信息如下(Quote为添加项,表示序列号):" ); printf( "\nQuote: " );for( i = 0; i <= matrix.total_elem; i++ )printf( "%3d", i );printf( "\nvalue: " );for( i = 0; i <= matrix.total_elem; i++ )printf( "%3.0lf", matrix.data[i].value );printf( "\nIndex: " );for( i = 0; i <= matrix.total_elem; i++ )printf( "%3d", matrix.data[i].index );printf( "\n" );}// 初始化向量,使之分量全为0void Init_X( double *X, int n ){int i = 0;for( i = 0; i < n; i++ )X[i] = 0;}// 初始化右端向量void Init_b( double *b, int n ){int i = 0;Init_X( b, n );printf( "\n请输入%d个数(方程组地右端项): ", n );for( i = 0; i < n; i++ )scanf( "%lf", &b[i] );}// 初始化未知向量,得到初始值void Init_temp_X( double *temp, int n ){int i = 0;Init_X( temp, n );printf( "请输入X 向量地初始值: " );for( i = 0; i < n; i++ )scanf( "%lf", &temp[i] );}// 采用高斯-塞德尔GS迭代法求值int Calculate_X_GS( struct Matrix A, double *X, double *b )5PCzVD7HxA{int i = 0, j = 0, sum = 0;double temp = 0.0, temp_1 = 0.0, *temp_X = 0, judge = 0.0;jLBHrnAILgtemp_X = (double *)new double[A.total_ln];Init_temp_X( temp_X, A.total_ln );for( i = 0; i < A.total_ln; i++ )X[i] = temp_X[i];sum = 0;do{judge = 0.0;for( i = 0; i < A.total_ln; i++ )temp_X[i] = X[i];for( i = 0; i < A.total_ln; i++ ){temp = 0.0;temp_1 = 0.0;for( j = A.data[i].index; A.data[j].index < i && j <= A.total_elem; j++ )xHAQX74J0X temp_1 += A.data[j].value*X[A.data[j].index];for( ; j < A.data[i+1].index && j <= A.total_elem; j++ )LDAYtRyKfEtemp += A.data[j].value * temp_X[A.data[j].index];X[i] = (b[i] - temp_1- temp)/A.data[i].value;}for( i = 0; i < A.total_ln; i++ ){if( X[i]-temp_X[i] < 0 )judge = temp_X[i]-X[i]>judge ? temp_X[i]-X[i] : judge;Zzz6ZB2Ltk elsejudge = X[i]-temp_X[i]>judge ? X[i]-temp_X[i] : judge;dvzfvkwMI1 }sum++;printf( "\n\n第%d 次迭代地结果: ", sum );for( i = 0; i < A.total_ln; i++ )printf( "\nX[%d] = %g", i, X[i] );printf( "\njudge = %g", judge );}while( judge > 0.000001 );return sum;}void main( ){struct Matrix A;// 实现系数矩阵地存储及显示Create_Matrix( A );Display_Matrix( A );double *X = 0, *b = 0;X = (double *)new double[A.total_ln];b = (double *)new double[A.total_ln];Init_X( X, A.total_ln );Init_b( b, A.total_ln );int i = 0, sum = 0;sum = Calculate_X_GS( A, X, b );printf( "\n\n线性方程组地解为: " );for( i = 0; i < A.total_ln; i++ )printf( "\nX[%d] = %g", i, X[i] );printf( "\n总共迭代了%d 次\n\n", sum );}3、运行结果如下:版权申明本文部分内容,包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some p arts, including text, pictures, and design. Copyright is personal ownership.rqyn14ZNXI 用户可将本文地内容或服务用于个人学习、研究或欣赏,以及其他非商业性或非盈利性用途,但同时应遵守著作权法及其他相关法律地规定,不得侵犯本网站及相关权利人地合法权利.除此以外,将本文任何内容或服务用于其他用途时,须征得本人及相关权利人地书面许可,并支付报酬.EmxvxOtOcoUsers may use the contents or services of this articlefor personal study, research or appreciation, and othernon-commercial or non-profit purposes, but at the same time,they shall abide by the provisions of copyright law and otherrelevant laws, and shall not infringe upon the legitimaterights of this website and its relevant obligees. In addition, when any content or service of this article is used for otherpurposes, written permission and remuneration shall beobtained from the person concerned and the relevantobligee.SixE2yXPq5转载或引用本文内容必须是以新闻性或资料性公共免费信息为使用目地地合理、善意引用,不得对本文内容原意进行曲解、修改,并自负版权等法律责任.6ewMyirQFLReproduction or quotation of the content of this articlemust be reasonable and good-faith citation for the use of news or informative public free information. It shall notmisinterpret or modify the original intention of the contentof this article, and shall bear legal liability such ascopyright.kavU42VRUs。
