数值分析在生活中的应用举例及Matlab实现

matlab曲线拟合的实际例子应用

一、问题提出在科学研究和工程实践中，曲线拟合是一种常用的数学分析方法。

而在曲线拟合的工具中，Matlab作为一种强大的数据分析工具，被广泛应用于曲线拟合的实际例子中。

本文将通过实际例子的应用，介绍Matlab曲线拟合的具体过程和方法，以及其在实际应用中的价值和意义。

二、Matlab曲线拟合的基本原理Matlab是一种专门用于计算、可视化和编程的高级技术计算语言和交互式环境。

在Matlab中，曲线拟合是一种基于最小二乘法的数学计算方法，在实际应用中具有较高的精确度和可靠性。

其基本原理是通过拟合算法，在已知数据点集的基础上，找到最能描述数据规律的曲线函数，并将其用于相关数据的预测和分析。

三、Matlab曲线拟合的具体步骤1. 数据准备：首先需要准备一组已知的数据点集，可以是实验数据、观测数据或者从其他来源获取的数据。

这些数据点集通常以数组形式输入到Matlab中。

2. 选择拟合函数：根据实际数据的特点和需要，选择合适的拟合函数类型。

常见的拟合函数包括线性函数、多项式函数、指数函数、对数函数等。

在Matlab中，可以通过内置的拟合函数库或者自定义函数进行选择和调用。

3. 参数估计：根据所选的拟合函数类型，利用最小二乘法等数学计算方法，对拟合函数的参数进行估计和优化，以使拟合曲线与实际数据最为吻合。

4. 拟合曲线绘制：根据估计的拟合函数参数，绘制拟合曲线并与实际数据点进行比较。

通过可视化方法，对拟合效果进行直观评估和分析。

5. 拟合效果评估：对拟合曲线的精确度和可靠性进行评估，包括拟合误差的计算、参数置信区间的估计等统计分析方法。

四、实际例子的应用以某企业的销售数据为例，假设已知某产品在不同时间点的月销量数据如下：时间（月份）销量（单位）1 1002 1503 2004 1805 2206 2507 3008 2809 32010 350在利用Matlab进行曲线拟合的分析过程中，可以按照上述步骤进行如下操作：1. 数据导入：将上述销售数据点集输入到Matlab中，并转化为数组形式。

Matlab技术在智能家居和智能办公中的应用

Matlab技术在智能家居和智能办公中的应用随着科技的不断发展，智能家居和智能办公的概念逐渐成为现实。

现在，我们可以通过智能设备来控制家居灯光、温度和安全系统，也可以利用智能办公设备来提高办公效率和工作质量。

而在这一系列智能设备背后，Matlab技术起着重要的作用。

本文将探讨Matlab技术在智能家居和智能办公中的应用，从而使得我们对这个领域有更深入的理解。

首先，智能家居领域是Matlab技术的一个重要应用场景。

Matlab在智能家居中的使用范围广泛，可以用来开发智能家居系统的算法和控制系统。

例如，通过使用Matlab，我们可以编写智能家居系统的自动化控制算法，从而实现家居设备的自动化控制。

利用Matlab的信号处理功能，我们可以对家居环境中的各种数据进行分析和处理，如光照强度、温度、声音等。

通过这些数据，我们可以根据用户的偏好和需求，智能地调控家居设备，从而提供更舒适和便捷的生活体验。

另外，Matlab技术在智能家居中的一个重要应用是图像处理和识别。

通过利用Matlab的图像处理工具箱，我们可以开发智能家居系统的人脸识别、物体识别等功能。

例如，通过使用Matlab的计算机视觉功能，我们可以实现智能家居系统的人脸识别和身份验证，从而提高家居安全性。

此外，利用Matlab的图像处理技术，我们还可以实现智能家居系统的物体识别功能，如识别家里的家具或者宠物等。

这些功能不仅提高了智能家居的便利性，还增加了智能家居系统的智能化程度。

除了智能家居领域，Matlab技术在智能办公中也发挥着重要作用。

智能办公的目标是通过科技手段提高工作效率和提供更好的工作环境。

Matlab技术在智能办公中的应用主要体现在数据分析和模型建立方面。

通过利用Matlab的数据处理和分析能力，我们可以对大量的办公数据进行整理和分析，从而帮助决策者进行科学决策。

例如，对于企业的销售数据，我们可以使用Matlab进行数据分析，了解产品的销售趋势和受欢迎程度。

MATLAB在实际生活中的应用小论文

MATLAB 在实际问题中的分析与应用自20世纪80年代以来，出现了多种科学计算语言，亦称数学软件，比较流行的有MATLAB 、Mathematical 、Maple 等。

因为他们具有功能强、效率高、简单易学等特点，在在许多领域等到广泛应用。

MATLAB 便是一种影响大、流行广的科学计算语言。

MATLAB 的语法规则简单，更加贴近人的思维方式。

MATLAB 是英文Matrix Laboratory(矩阵实验室)的缩写。

自1984年由美国Math Works 公司推向市场以来，得到了广泛的应用和发展。

在欧美各高等院校MATLAB 已经成为线性代数、自动控制理论、数字信号处理、时间序列分析、动态系统仿真、图像处理等诸多课程的基本教学工具，成为大学生、硕士生以及博士生必须掌握的基本技能。

在设计研究单位和工业部门，MATLAB 已被广泛的应用于研究和解决各种具体的工程问题。

近年来，MATLAB 在我国也开始流行，应用MATLAB 的单位和个人急剧增加。

可以预见，MATLAB 将在我国科学研究和工程应用中发挥越来越大的作用。

Mat lab 是当前数值计算方面应用地非常广泛的一种计算机软件，特别是在工程应用求解中发挥了重要作用。

其所具有的浅显易懂的编程语言、强大的绘图功能、大量的内部函数等都深深地吸引了我认真地去学习它。

同时在上《过程装备力学基础》时，其中涉及有很多的问题是超越方程、微积分的问题，难以用普通的线性方法求解，而Mat lab 在此方面有强大的功能，特别是超越方程的精确求解以及图形的绘制方面。

数学当中的绘制函数图象、绘制立体图形的交线（如绘制两个等直径圆柱体的交线）、求多项式的根等问题，这些问题如果依靠我们人工进行操作，则需要很多的时间和精力，当我们掌握了基本原理后，借助于MATLAB 进行解决则会大大提高效率和精确度。

仅举一些运用MATLAB 的例子。

常用控制命令：click ：%清屏； clear ：%清变量； save ：%保存变量； load ：%导入变量一、利用公式直接进行赋值计算本金P 以每年n 次，每次i%的增值率（n 与i 的乘积为每年增值额的百分比）增加，当增加到r ×P 时所花费的时间T 为：（利用复利计息公式可得到下式）)01.01ln(ln )01.01(i n rT i P P r nT +=⇒+=⨯（12,5.0,2===n i r ）MATLAB 的表达形式及结果如下： >> r=2;i=0.5;n=12; %变量赋值 >> T=log(r)/(n*log(1+0.01*i)) 计算结果显示为：T = 11.5813即所花费的时间为T=11.5813 年。

学习使用MATLAB进行数值计算和数据分析

学习使用MATLAB进行数值计算和数据分析---第一章：MATLAB的基本介绍MATLAB是一种强大的数值计算和数据分析软件，广泛应用于科学研究、工程设计等领域。

它的主要特点是简洁直观的用户界面和丰富的数学函数库。

在本章中，我们将介绍MATLAB的基本特性和使用方法。

1.1 MATLAB的历史与发展MATLAB是由MathWorks公司于1984年首次推出的。

起初，它作为一个用于矩阵计算的工具被广泛使用。

随着时间的推移，MATLAB逐渐拓展了功能，加入了许多其他数学和工程计算的功能，如符号计算、数据统计和可视化。

如今，MATLAB已经成为一种非常受欢迎的工具。

1.2 MATLAB的安装和环境设置要开始使用MATLAB，首先需要从MathWorks官网下载并安装MATLAB软件。

安装完成后，打开MATLAB并设置工作目录和默认工作文件夹。

工作目录是指存储MATLAB代码和数据文件的文件夹，而默认工作文件夹是指MATLAB打开时默认选择的文件夹。

1.3 MATLAB的基本语法和命令MATLAB的基本语法和命令非常简单易懂。

它采用类似于其他编程语言的命令行交互方式，用户可以直接在命令行输入MATLAB语句并执行。

例如，可以输入"2+2"并按回车键得到结果4。

此外，MATLAB还具有许多内置的数学函数和运算符，可以进行各种数值计算和数据分析。

1.4 MATLAB脚本和函数在MATLAB中，可以使用脚本和函数来组织和执行一系列MATLAB命令。

脚本是一系列命令的集合，可以一次性运行。

函数是一段可以重复使用的代码，可以接受输入参数并返回输出结果。

通过编写脚本和函数，可以提高MATLAB代码的可重复性和可维护性。

第二章：数值计算MATLAB作为一种数值计算工具，提供了丰富的数学函数和算法，可以用于解决各种数值计算问题。

在本章中，我们将介绍MATLAB在数值计算方面的一些常用功能和技巧。

2.1 数值计算方法MATLAB中包含了许多数值计算方法，如数值积分、数值微分、线性代数求解等。

如何使用MATLAB进行数据分析与科学计算

如何使用MATLAB进行数据分析与科学计算MATLAB（Matrix Laboratory）是一种流行的科学计算软件，广泛用于数据分析和科学计算。

本文将介绍如何使用MATLAB进行数据分析和科学计算。

文章将按照以下章节进行介绍：第一章：MATLAB简介在本章中，将介绍MATLAB的基本概念和特点。

解释MATLAB的优势，如易用性、高效性和广泛的工具箱支持等。

第二章：MATLAB环境设置和基本操作本章将介绍如何安装和设置MATLAB环境，并介绍MATLAB的基本操作，包括创建变量、执行计算、使用函数和图形界面等。

第三章：数据导入和导出在本章中，将介绍如何将外部数据导入MATLAB中进行分析。

涵盖了从Excel、CSV以及其他常见格式导入数据的方法，以及将结果导出到不同格式的文件中。

第四章：数据可视化数据可视化是数据分析的重要工具。

本章将探讨如何使用MATLAB进行数据可视化，包括绘制2D和3D图形、创建散点图、直方图和箱线图等。

第五章：数据处理与清洗在本章中，将介绍常见的数据处理和清洗技术。

包括缺失值处理、异常值检测、数据平滑和归一化等常见操作。

第六章：统计分析统计分析是数据分析的核心内容之一。

本章将介绍MATLAB 中的统计分析方法，如描述性统计、假设检验、相关性分析和线性回归等。

第七章：信号处理信号处理是MATLAB的另一个强大功能。

本章将介绍信号处理的基本概念和MATLAB中的信号处理工具箱，包括滤波、频谱分析和傅里叶变换等。

第八章：机器学习机器学习是当前热门的领域之一。

本章将介绍如何使用MATLAB进行机器学习，包括分类、聚类和回归等常见机器学习任务。

第九章：并行计算与高性能计算在本章中，将介绍如何使用MATLAB进行并行计算和高性能计算。

讨论MATLAB中的并行计算工具箱和在集群或云计算环境中进行计算的方法。

第十章：MATLAB编程MATLAB还提供了编程接口，可以编写自定义函数和脚本。

MATLAB_智能算法30个案例分析

MATLAB_智能算法30个案例分析MATLAB是一种强大的数值计算和编程工具，教育和科研领域中广泛应用于数据分析、机器学习和智能算法的研究。

在本文中，我们将介绍30个MATLAB智能算法的案例分析，并探讨其用途和优势。

分析的案例包括分类、回归、聚类、神经网络和遗传算法等不同类型的智能算法。

1. K均值聚类：利用MATLAB中的kmeans函数对一组数据进行聚类分析，得到不同的簇。

2. 随机森林：利用MATLAB中的TreeBagger函数构建一个随机森林分类器，并通过测试数据进行分类预测。

3. 人工神经网络：使用MATLAB中的feedforwardnet函数构建一个人工神经网络，并通过训练集进行预测。

4. 遗传算法：利用MATLAB中的ga函数对一个优化问题进行求解，找到最优解。

5. 支持向量机：使用MATLAB中的svmtrain和svmclassify函数构建一个支持向量机分类器，并进行分类预测。

6. 极限学习机：使用MATLAB中的elmtrain和elmpredict函数构建一个极限学习机分类器，并进行分类预测。

7. 逻辑回归：使用MATLAB中的mnrfit和mnrval函数构建一个逻辑回归模型，并进行预测。

8. 隐马尔可夫模型：使用MATLAB中的hmmtrain和hmmdecode函数构建一个隐马尔可夫模型，对一系列观测数据进行预测。

9. 神经进化算法：利用MATLAB中的ne_train函数构建一个基于神经进化算法的神经网络分类器，并进行分类预测。

10. 朴素贝叶斯分类器：使用MATLAB中的NaiveBayes对象构建一个朴素贝叶斯分类器，并进行分类预测。

11. 高斯过程回归：使用MATLAB中的fitrgp函数构建一个高斯过程回归模型，并进行回归预测。

12. 最小二乘支持向量机：使用MATLAB中的fitcsvm函数构建一个最小二乘支持向量机分类器，并进行分类预测。

13. 遗传网络：利用MATLAB中的ngenetic函数构建一个基于遗传算法和人工神经网络的分类器，并进行分类预测。

MATLAB在数值分析中的应用

MATLAB在数值分析中的应用
matlab是一种高级计算及可视化软件，在数值分析方面有着广泛的应用。

其特点是完整的数学和统计功能，强大的可视化和计算能力，易于使用的环境和脚本语言，使得matlab在数值分析领域变得非常流行。

首先，matlab具有强大的符号计算功能，可以求解复杂的多项式及微分方程，进行多项式拟合和矩阵计算等，从而支持数值分析中的基本操作。

其次，matlab还提供了一系列的工具箱，如数值分析工具箱，控制系统工具箱和数据分析工具箱等，这些工具箱可以作为matlab的拓展工具，为数值分析提供支持，有助于研究者解决复杂的问题。

此外，matlab 在多种算法的支持上也拥有全面的支持，包括线性规划、非线性规划、自动微分、数值积分、拟合优化、最优化及矩阵分解，可以用于几乎所有的数值分析任务。

最后，matlab还提供了极强的可视化功能，可以处理矩阵、标量和向量的可视化，包括3D和4D图表，可以帮助研究者快速分析结果。

因此，matlab支持的数值分析功能强大，提供了非常丰富的工具箱和算法支持，并有强大的可视化功能，使其在数值分析领域得到了广泛应用。

MATLAB数据分析方法

MATLAB数据分析方法MATLAB是一种强大的数据分析工具，它可以帮助我们对各种类型的数据进行有效的分析和处理。

在本文中，我们将介绍一些常用的MATLAB数据分析方法，希望能够帮助大家更好地利用这一工具进行数据分析。

首先，我们将介绍如何在MATLAB中进行数据可视化分析。

数据可视化是数据分析的重要环节，通过图表和图形的展示，我们可以更直观地理解数据之间的关系和规律。

在MATLAB中，我们可以利用plot函数绘制二维图表，利用surf函数绘制三维图形，还可以使用histogram函数绘制直方图等。

这些图表和图形可以帮助我们更好地理解数据的分布和趋势，从而为后续的分析提供重要参考。

其次，我们将介绍如何在MATLAB中进行数据预处理。

数据预处理是数据分析的关键步骤之一，它可以帮助我们清洗数据、填补缺失值、处理异常值等。

在MATLAB中，我们可以利用isnan函数和isinf函数来识别缺失值和异常值，利用interp1函数和fillmissing函数来填补缺失值，利用deleteoutliers函数来处理异常值等。

这些方法可以帮助我们在数据分析之前，对数据进行有效的清洗和处理，提高数据分析的准确性和可靠性。

接下来，我们将介绍如何在MATLAB中进行统计分析。

统计分析是数据分析的重要内容之一，它可以帮助我们了解数据的分布、均值、方差、相关性等。

在MATLAB中，我们可以利用mean函数和std函数计算数据的均值和标准差，利用corr函数计算数据的相关系数，利用histfit函数绘制数据的直方图和拟合曲线等。

这些方法可以帮助我们更全面地了解数据的统计特征，为后续的分析和决策提供重要依据。

最后，我们将介绍如何在MATLAB中进行数据建模分析。

数据建模分析是数据分析的高级阶段，它可以帮助我们建立数据的数学模型，预测未来的趋势和结果。

在MATLAB中，我们可以利用regress 函数进行线性回归分析，利用fit函数进行曲线拟合分析，利用forecast函数进行时间序列预测分析等。

MATLAB在实际生活中的应用小论文

MATLAB 在实际问题中的分析与应用自20世纪80年代以来，出现了多种科学计算语言，亦称数学软件，比较流行的有MATLAB 、Mathematical 、Maple 等。

因为他们具有功能强、效率高、简单易学等特点，在在许多领域等到广泛应用。

MATLAB 便是一种影响大、流行广的科学计算语言。

MATLAB 的语法规则简单，更加贴近人的思维方式。

MATLAB 是英文Matrix Laboratory(矩阵实验室)的缩写。

自1984年由美国Math Works 公司推向市场以来，得到了广泛的应用和发展。

在欧美各高等院校MATLAB 已经成为线性代数、自动控制理论、数字信号处理、时间序列分析、动态系统仿真、图像处理等诸多课程的基本教学工具，成为大学生、硕士生以及博士生必须掌握的基本技能。

在设计研究单位和工业部门，MATLAB 已被广泛的应用于研究和解决各种具体的工程问题。

近年来，MATLAB 在我国也开始流行，应用MATLAB 的单位和个人急剧增加。

可以预见，MATLAB 将在我国科学研究和工程应用中发挥越来越大的作用。

Mat lab 是当前数值计算方面应用地非常广泛的一种计算机软件，特别是在工程应用求解中发挥了重要作用。

其所具有的浅显易懂的编程语言、强大的绘图功能、大量的内部函数等都深深地吸引了我认真地去学习它。

同时在上《过程装备力学基础》时，其中涉及有很多的问题是超越方程、微积分的问题，难以用普通的线性方法求解，而Mat lab 在此方面有强大的功能，特别是超越方程的精确求解以及图形的绘制方面。

数学当中的绘制函数图象、绘制立体图形的交线（如绘制两个等直径圆柱体的交线）、求多项式的根等问题，这些问题如果依靠我们人工进行操作，则需要很多的时间和精力，当我们掌握了基本原理后，借助于MATLAB 进行解决则会大大提高效率和精确度。

仅举一些运用MATLAB 的例子。

常用控制命令：click ：%清屏； clear ：%清变量； save ：%保存变量； load ：%导入变量一、利用公式直接进行赋值计算本金P 以每年n 次，每次i%的增值率（n 与i 的乘积为每年增值额的百分比）增加，当增加到r ×P 时所花费的时间T 为：（利用复利计息公式可得到下式）)01.01ln(ln )01.01(i n rT i P P r nT +=⇒+=⨯（12,5.0,2===n i r ）MATLAB 的表达形式及结果如下： >> r=2;i=0.5;n=12; %变量赋值 >> T=log(r)/(n*log(1+0.01*i)) 计算结果显示为：T = 11.5813即所花费的时间为T=11.5813 年。

Matlab技术在数据分析中的应用

Matlab技术在数据分析中的应用引言：数据分析是当今各行各业都无法绕开的重要环节。

借助于计算机技术的快速发展，大量的数据可以通过不同的方式收集和存储。

然而，如何从这些大数据中提取有用的信息并做出明智的决策，成为了一个亟待解决的问题。

在这方面，Matlab技术具备了独特的优势，它的强大功能和丰富的工具箱为数据分析提供了一个强有力的支持。

一、数据预处理与清洗：数据分析的第一步通常是数据的预处理和清洗。

大多数数据在收集过程中不可避免地会受到各种噪声和干扰的影响，需要进行修正和整理。

Matlab提供了一系列函数和工具，例如`table`和`dataset`等，可以方便地进行数据的整理和清洗。

此外，Matlab还可以通过编程的方式对数据进行自动化处理，为后续的分析奠定基础。

二、数据可视化：数据可视化是数据分析的重要环节。

通过可视化手段，我们可以直观地观察和分析数据的分布、关系和趋势。

Matlab的`plot`函数和图形界面工具箱提供了非常便捷的绘图工具。

无论是简单的折线图、柱状图，还是更加复杂的散点图、热力图等，Matlab都能够轻松胜任。

此外，Matlab还支持交互式可视化，用户可以通过鼠标和键盘操作来实时调整图形参数和数据筛选条件，进一步提高数据分析的效果和准确性。

三、统计分析：统计分析是数据分析的核心内容之一。

Matlab提供了丰富的统计分析工具箱，包括描述统计、假设检验、方差分析等。

用户可以通过简单的函数调用，对数据进行常见的统计计算，并得到相应的分析结果。

例如，可以通过`mean`函数计算数据的均值，通过`std`函数计算数据的标准差。

此外，Matlab还提供了强大的矩阵运算功能，可以方便地进行线性回归、主成分分析等高级统计分析。

四、机器学习：机器学习是数据分析的重要分支，它通过构建数学模型和算法，实现对数据的自动化分析和预测。

Matlab提供了强大的机器学习工具箱，包括分类、回归、聚类和降维等多个领域。

MATLAB使用教程(5)应用举例

2019/2/16 黄建华制作 4
例5.1 雨量预报方法的评价
对于问题二，我们认为公众的感受主要体现在预测与实际之间偏差的大小程度，然而，实际测量值未知，因此我们考虑在分级预报中加入准确概率的方式来实现公众满意度的提高。我们认为雨量的实测值应该在预测值点处服从正态分布，通过合理的假设和推导，我们得到：正态分布的均值可以取为雨量预测值，不同雨量分级区间上的方差可以近似取为对应区间上的总偏差平方和的平均值。运用Matlab软件编程，可以实现对每一个预报数据的预报内容的改变，并且通过几个不同的数据体现程序运行所得到的结果。最后，对模型的缺点进行了讨论和改进。
2019/2/16
黄建华制作
10
例5.1 雨量预报方法的评价
将文件全部拷贝在默认的work文件加下，运行程序sjzr.m：
2019/2/16
黄建华制作
11
例5.1 雨量预报方法的评价
2019/2/16
黄建华制作
12
例5.1 雨量预报方法的评价

程序huatu.m %画一个时点预测曲面图与实测散点图比较
2019/2/16
黄建华制作
3
例5.1 雨量预报方法的评价
模型的分析：本题的关键主要是采用Matlab软件对所提供的数据进行分析并得到主要结论。对于问题一，采用load命令和循环结构实现数据文件的载入，再从实测数据文件中提出实测点位置数据，并且依次从预测数据文件中通过曲面拟合命令 griddata得到相应日期、时段、方法下的对应位置上的预测估计值。然后分别计算两种预报方法下的实测值和预测值的偏差并且求对应的总偏差平方和，根据两个总偏差平方和的大小来得出两种方法的优劣比较，通过Matlab程序的实现得到结果为：第一种方法比第二种方法好。

2-MATLAB在数值分析中的应用

分段插值
一维插值：可以分为最近插值、线性插值、三次样条插值，分段三次Hermite插值。 y=interp1(x0,y0,x) y=interp1(x0,y0,x,’method’) method= nearst: 最近插值 linear: 线性插值（默认值） spline: 分段三次样条插值 pchip:分段三次Hermite插值
-9-
Polyinterp(symbol)
symx =sym(‘x’) P = polyinterp(x0,y0,symx) pretty(P) P = simplify(P) P= x^3-2*x-5 8/3*z*(x-1)*(x-2)+1/2*x*(x-1)*(x-3)3*x*(x-2)*(x-3)-5/6*(-x+1)*(x-2)*(x-3)
0.5 0 1 2 3 4 5 6 7 8 9
-2-
插值和拟合
在平面上给定n个点(xk,yk),可以唯一确定一个最多n-1次的多项式通过这些点，这个多项式叫插值多项式
P(xk ) = yk , k = 1,2,…,n Lagrange插值多项式
x xj P( x ) k 1 j k xk x j
2 3
sk ,0 yk sk ,2 P xk 2
sk ,1 dk sk ,3
hk 2P xk P xk 1
6 P xk 1 P xk 6hk
-21-
x = 1:6; y = [16 18 21 17 15 12];
Lagrange插值多项式基函数
P( x) c1 xn1 c2 xn2 ... cn1 x cn
n 1 x1 n 1 x2 x n 1 n n2 x1 n2 x2

matlab简单程序运用-数值分析篇

1：三次样条插值法h0=figure('toolbar','none',...'position',[200 50 350 450],...'name','实例86');h1=axes('parent',h0,...'position',[0.10 0.45 0.8 0.5],...'visible','off');x=0:0.2:2*pi;y=sin(x);plot(x,y)b1=uicontrol('parent',h0,...'units','points',...'tag','b1',...'style','pushbutton',...'string','三次样条插值',...'backgroundcolor',[0.75 0.75 0.75],...'position',[20 60 70 20],...'callback',[...'y=0,',...'sy=0,',...'strn1=get(e2,''string'');,',...'n1=str2num(strn1);,',...'strn2=get(e3,''string'');,',...'n2=str2num(strn2);,',...'x=n1:0.2:n2;,',...'i=1;,',...'for t=n1:0.2:n2,',...'y(i)=sin(t);,',...'sy(i)=san(t,n1,n2);,',...'i=i+1;,',...'end,',...'plot(x,y,''b*'',x,sy,''r-''),',...'axis([0 7 -1.5 1.5]),',...'legend(''sin(x)'',''N-Hermite插值'')']); b2=uicontrol('parent',h0,...'units','points',...'tag','b2',...'style','pushbutton',...'string','误差比较',...'backgroundcolor',[0.75 0.75 0.75],...'position',[170 60 70 20],...'callback',[...'strdn1=get(e2,''string'');,',...'n1=str2num(strdn1);,',...'strdn2=get(e3,''string'');,',...'n2=str2num(strdn2);,',...'strdn=get(e1,''string'');,',...'dn=str2num(strdn);,',...'dd=abs(sin(dn)-san(dn,n1,n2));,',...'msgbox([''误差为：'',num2str(dd)],''计算结果'')']); e1=uicontrol('parent',h0,...'units','points',...'tag','e1',...'style','edit',...'fontsize',12,...'string','1.20',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[200 100 40 20]);t1=uicontrol('parent',h0,...'units','points',...'tag','t1',...'style','text',...'string','误差点：',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[160 100 40 20]);e2=uicontrol('parent',h0,...'units','points',...'tag','e2',...'style','edit',...'fontsize',12,...'string','1.00',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[20 85 40 20]);t2=uicontrol('parent',h0,...'units','points',...'tag','t2',...'style','text',...'string','第一节点：',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[15 105 50 20]);e3=uicontrol('parent',h0,...'units','points',...'tag','e3',...'fontsize',12,...'string','3.00',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[100 85 40 20]);t3=uicontrol('parent',h0,...'units','points',...'tag','t3',...'style','text',...'string','第二节点：',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[95 105 50 20]);b3=uicontrol('parent',h0,...'units','points',...'tag','b3',...'style','pushbutton',...'string','关闭',...'backgroundcolor',[0.75 0.75 0.75],...'position',[100 20 60 20],...'callback','close');2：NEWTON插值h0=figure('toolbar','none',...'position',[200 50 350 450],...'name','实例87');h1=axes('parent',h0,...'position',[0.10 0.45 0.8 0.5],...'visible','off');x=0:0.2:2*pi;y=sin(x);plot(x,y)b1=uicontrol('parent',h0,...'units','points',...'tag','b1',...'style','pushbutton',...'string','牛顿插值',...'backgroundcolor',[0.75 0.75 0.75],...'position',[20 60 70 20],...'callback',[...'strn=get(e1,''string'');,',...'n=str2num(strn);,',...'x=0:0.2:2*pi;,',...'for t=0:0.2:2*pi,',...'y(i)=sin(t);,',...'ynt(i)=newton(t,n);,',...'i=i+1;,',...'end,',...'plot(x,y,''b*'',x,ynt,''r-''),',...'axis([0 7 -1.5 1.5]),',...'legend(''sin(x)'',''牛顿插值'')']);b2=uicontrol('parent',h0,...'units','points',...'tag','b2',...'style','pushbutton',...'string','误差比较',...'backgroundcolor',[0.75 0.75 0.75],...'position',[170 60 70 20],...'callback',[...'strn=get(e1,''string'');,',...'n=str2num(strn);,',...'strdn=get(e2,''string'');,',...'dn=str2num(strdn);,',...'dd=abs(sin(dn)-newton(dn,n));,',...'msgbox([''误差为：'',num2str(dd)],''计算结果'')']); e1=uicontrol('parent',h0,...'units','points',...'tag','e1',...'style','edit',...'fontsize',12,...'string','5',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[50 100 40 20]);e2=uicontrol('parent',h0,...'units','points',...'tag','e2',...'style','edit',...'fontsize',12,...'string','1.20',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[200 100 40 20]);t1=uicontrol('parent',h0,...'units','points',...'tag','t1',...'string','节点数：（<6）',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[10 100 40 30]);t2=uicontrol('parent',h0,...'units','points',...'tag','t2',...'style','text',...'string','误差点：',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[160 100 40 20]);b3=uicontrol('parent',h0,...'units','points',...'tag','b3',...'style','pushbutton',...'string','关闭',...'backgroundcolor',[0.75 0.75 0.75],...'position',[100 20 60 20],...'callback','close');3mewton形式的hermite插值h0=figure('toolbar','none',...'position',[200 50 350 450],...'name','实例89');h1=axes('parent',h0,...'position',[0.10 0.45 0.8 0.5],...'visible','off');x=0:0.2:2*pi;y=sin(x);plot(x,y)b1=uicontrol('parent',h0,...'units','points',...'tag','b1',...'style','pushbutton',...'string','N-Hermite插值',...'backgroundcolor',[0.75 0.75 0.75],...'position',[20 60 70 20],...'callback',[...'strn1=get(e2,''string'');,',...'n1=str2num(strn1);,',...'strn2=get(e3,''string'');,',...'n2=str2num(strn2);,',...'x=0:0.2:2*pi;,',...'i=1;,',...'for t=0:0.2:2*pi,',...'y(i)=sin(t);,',...'ynh(i)=nhermite(t,n1,n2);,',...'i=i+1;,',...'end,',...'plot(x,y,''b*'',x,ynh,''r-''),',...'axis([0 7 -1.5 1.5]),',...'legend(''sin(x)'',''N-Hermite插值'')']);b2=uicontrol('parent',h0,...'units','points',...'tag','b2',...'style','pushbutton',...'string','误差比较',...'backgroundcolor',[0.75 0.75 0.75],...'position',[170 60 70 20],...'callback',[...'strdn1=get(e2,''string'');,',...'n1=str2num(strdn1);,',...'strdn2=get(e3,''string'');,',...'n2=str2num(strdn2);,',...'strdn=get(e1,''string'');,',...'dn=str2num(strdn);,',...'dd=abs(sin(dn)-nhermite(dn,n1,n2));,',...'msgbox([''误差为：'',num2str(dd)],''计算结果'')']); e1=uicontrol('parent',h0,...'units','points',...'tag','e1',...'style','edit',...'fontsize',12,...'string','1.20',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[200 100 40 20]);t1=uicontrol('parent',h0,...'units','points',...'tag','t1',...'style','text',...'string','误差点：',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[160 100 40 20]);e2=uicontrol('parent',h0,...'units','points',...'tag','e2',...'style','edit',...'fontsize',12,...'string','1.00',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[20 85 40 20]);t2=uicontrol('parent',h0,...'units','points',...'tag','t2',...'style','text',...'string','第一节点：',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[15 105 50 20]);e3=uicontrol('parent',h0,...'units','points',...'tag','e3',...'style','edit',...'fontsize',12,...'string','3.00',...'horizontalalignment','right',...'backgroundcolor',[1 1 1],...'position',[100 85 40 20]);t3=uicontrol('parent',h0,...'units','points',...'tag','t3',...'style','text',...'string','第二节点：',...'fontsize',12,...'backgroundcolor',[0.75 0.75 0.75],...'position',[95 105 50 20]);b3=uicontrol('parent',h0,...'units','points',...'tag','b3',...'style','pushbutton',...'string','关闭',...'backgroundcolor',[0.75 0.75 0.75],...'position',[100 20 60 20],...'callback','close');。

数值分析matlab实验报告

数值分析matlab实验报告数值分析 Matlab 实验报告一、实验目的数值分析是研究各种数学问题数值解法的学科，Matlab 则是一款功能强大的科学计算软件。

本次实验旨在通过使用 Matlab 解决一系列数值分析问题，加深对数值分析方法的理解和应用能力，掌握数值计算中的误差分析、数值逼近、数值积分与数值微分等基本概念和方法，并培养运用计算机解决实际数学问题的能力。

二、实验内容（一）误差分析在数值计算中，误差是不可避免的。

通过对给定函数进行计算，分析截断误差和舍入误差的影响。

例如，计算函数＄f(x) ＝＼sin(x)＄在＄x ＝ 05$ 附近的值，比较不同精度下的结果差异。

（二）数值逼近1、多项式插值使用拉格朗日插值法和牛顿插值法对给定的数据点进行插值，得到拟合多项式，并分析其误差。

2、曲线拟合采用最小二乘法对给定的数据进行线性和非线性曲线拟合，如多项式曲线拟合和指数曲线拟合。

（三）数值积分1、牛顿柯特斯公式实现梯形公式、辛普森公式和柯特斯公式，计算给定函数在特定区间上的积分值，并分析误差。

2、高斯求积公式使用高斯勒让德求积公式计算积分，比较其精度与牛顿柯特斯公式的差异。

（四）数值微分利用差商公式计算函数的数值导数，分析步长对结果的影响，探讨如何选择合适的步长以提高精度。

三、实验步骤（一）误差分析1、定义函数｀compute_sin_error` 来计算不同精度下的正弦函数值和误差。

｀｀｀matlabfunction value, error ＝ compute_sin_error(x, precision)true_value ＝ sin(x)；computed_value ＝ vpa(sin(x)， precision)；error ＝ abs(true_value computed_value)；end｀｀｀2、在主程序中调用该函数，分别设置不同的精度进行计算和分析。

（二）数值逼近1、拉格朗日插值法｀｀｀matlabfunction L ＝ lagrange_interpolation(x, y, xi)n ＝ length(x)；L ＝ 0;for i ＝ 1:nli ＝ 1;for j ＝ 1:nif j ～＝ ili ＝ li （xi x(j)）／（x(i) x(j)）；endendL ＝ L ＋ y(i) li;endend｀｀｀2、牛顿插值法｀｀｀matlabfunction N ＝ newton_interpolation(x, y, xi)n ＝ length(x)；％计算差商表D ＝ zeros(n, n)；D(：， 1) ＝ y'；for j ＝ 2:nfor i ＝ j:nD(i, j) ＝（D(i, j 1) D(i 1, j 1)）／（x(i) x(i j ＋ 1)）；endend％计算插值结果N ＝ D(1, 1)；term ＝ 1;for i ＝ 2:nterm ＝ term （xi x(i 1)）；N ＝ N ＋ D(i, i) term;endend｀｀｀3、曲线拟合｀｀｀matlab％线性最小二乘拟合p ＝ polyfit(x, y, 1)；y_fit_linear ＝ polyval(p, x)；％多项式曲线拟合p ＝ polyfit(x, y, n)；％ n 为多项式的次数y_fit_poly ＝ polyval(p, x)；％指数曲线拟合p ＝ fit(x, y, ＇exp1'）；y_fit_exp ＝ p(x)；｀｀｀（三）数值积分1、梯形公式｀｀｀matlabfunction T ＝ trapezoidal_rule(f, a, b, n)h ＝（b a) ／ n;x ＝ a:h:b;y ＝ f(x)；T ＝ h （（y(1) ＋ y(end)）／ 2 ＋ sum(y(2:end 1)））；end｀｀｀2、辛普森公式｀｀｀matlabfunction S ＝ simpson_rule(f, a, b, n)if mod(n, 2) ～＝ 0error(＇n 必须为偶数'）；endh ＝（b a) ／ n;x ＝ a:h:b;y ＝ f(x)；S ＝ h ／ 3 （y(1) ＋ 4 sum(y(2:2:end 1)）＋ 2 sum(y(3:2:end 2)）＋ y(end)）；end｀｀｀3、柯特斯公式｀｀｀matlabfunction C ＝ cotes_rule(f, a, b, n)h ＝（b a) ／ n;x ＝ a:h:b;y ＝ f(x)；w ＝ 7, 32, 12, 32, 7 ／ 90;C ＝ h sum(w y)；end｀｀｀4、高斯勒让德求积公式｀｀｀matlabfunction G ＝ gauss_legendre_integration(f, a, b)x, w ＝ gauss_legendre(5)；％选择适当的节点数t ＝（b a) ／ 2 x ＋（a ＋ b) ／ 2;G ＝（b a) ／ 2 sum(w f(t)）；end｀｀｀（四）数值微分｀｀｀matlabfunction dydx ＝ numerical_derivative(f, x, h)dydx ＝（f(x ＋ h) f(x h)）／（2 h)；end｀｀｀四、实验结果与分析（一）误差分析通过不同精度的计算，发现随着精度的提高，误差逐渐减小，但计算时间也相应增加。

数值分析在生活中的应用举例及Matlab实现

一、最小二乘法，用MATLAB实现1. 数值实例下面给定的是乌鲁木齐最近1个月早晨7：00左右（新疆时间）的天气预报所得到的温度，按照数据找出任意次曲线拟合方程和它的图像。

下面用MATLAB编程对上述数据进行最小二乘拟合。

下面用MATLAB编程对上述数据进行最小二乘拟合2、程序代码x=[1:1:30];y=[9,10,11,12,13,14,13,12,11,9,10,11,12,13,14,12,11,10,9,8,7,8,9,11,9,7,6,5,3,1];a1=polyfit(x,y,3) %三次多项式拟合%a2= polyfit(x,y,9) %九次多项式拟合%a3= polyfit(x,y,15) %十五次多项式拟合%b1=polyval(a1,x)b2=polyval(a2,x)b3=polyval(a3,x)r1= sum((y-b1).^2) %三次多项式误差平方和%r2= sum((y-b2).^2) %九次次多项式误差平方和%r3= sum((y-b3).^2) %十五次多项式误差平方和%plot(x,y,'*') %用*画出x,y图像%hold onplot(x,b1, 'r') %用红色线画出x,b1图像%hold onplot(x,b2, 'g') %用绿色线画出x,b2图像%hold onplot(x,b3, 'b:o') %用蓝色o线画出x,b3图像%3、数值结果不同次数多项式拟合误差平方和为：r1=67.6659r2=20.1060r3=3.7952r1、r2、r3分别表示三次、九次、十五次多项式误差平方和。

4、拟合曲线如下图二、线性方程组的求解（高斯-塞德尔迭代算法）1、实例：求解线性方程组（见书P233页）⎪⎪⎩⎪⎪⎨⎧=++=-+=+-3612363311420238321321321x x x x x x x x x 记A x=b, 其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=363320,,12361114238321b x A x x x任取初始值()()Tx0000=，进行迭代。

数值分析课程设计报告(MATLAB版)

（2）取右端向量 b 的三位有效数字得 b [1.83 1.08 0.783]T ，求方程组的准确解 X ，并与 X 的数据 [1 1 1]T 作比较。说明矩阵的病态性。
算法及相应结果：（1）在 MATLAB 命令窗口里输入如下命令： >> H=[1 1/2 1/3;1/2 1/3 1/4;1/3 1/4 1/5]; b=[11/6 13/12 47/60]'; >> x=H\b 回车得到结果为： x = 1.0000 1.0000 1.0000 (2)紧接着在上题基础上继续输入如下命令： >> c=[1.83 1.08 0.783]'; x1=H\c 回车得到如下结果： x1 = 1.0800 0.5400 1.4400
问题分析：考虑由直线段（2 个点）产生第一个图形（5 个点）的过程，设 P 1 和 P5 分别为原始直线段的两个端点。现在需要在直线段的中间依次插入三个点。显然， P2 位于 P P2 , P3 , P4 产生第一次迭代的图形（图 1-4） 1 点右端直线段的三分之一处， P4 点绕 P2 旋转 60 度（逆时针方向）而得到的，故可以处理为向量 P2 P4 经正交变换而得到向量 P2 P3 ，形成算法如下：（1） P2 P 1 (P 5 P 1) / 3 ；（2） P4 P 1 2( P 5 P 1) / 3 ；（3） P3 P2 ( P4 P2 ) AT ；在算法的第三步中，A 为正交矩阵。
运行结果： 0.0884 0.0580 0.0431 0.0343 0.0285 0.0243 0.0212 0.0188 0.0169 0.0154 0.0141 0.0130 0.0120 0.0112 0.0105 0.0099 0.0094 0.0087 0.0092 0.0042 （2）从 I 30 较粗略的估计值出发，我们不妨取 0.01. 源程序：

MATLAB在计算机辅助数值分析与计算中的应用

C N4321258/TP ISS N10072130X 计算机工程与科学C OMPUTER E NGI NEERI NG&SCIE NCE2002年第24卷第1期　　V ol124,N o11,2002　文章编号:10072130X(2002)0120070204MAT LAB在计算机辅助数值分析与计算中的应用ΞApplication of MAT LAB in C omputer2AidedNumerical Analysis and Calculation孙智娟,徐　杜,钟舜聪SUN Zhi2juan,XU Du,ZH ONG Shun2cong(汕头大学机电系,广东汕头　515063)(Department of Mechatronics E ngineering,Shantou U niversity,Shantou515063,China)摘　要:简要介绍了M AT LAB语言,并把M AT LAB语言应用于计算机辅助数值分析与计算中,在M AT LAB软件环境下研制了计算机辅助数值分析与计算(C ANAC)软件包,最后用一个典型实例较为深入地对其使用方法、特点和效果进行讨论。

实践表明,该软件包使用效果良好。

Abstract:This paper gives a brief introduction to M AT LAB and its application in numerical analysis and cal2 culation1It introduces how to develop a s oftware package for C AD and the analysis of numerical systems1It als o illus2 trates its usage,characteristics and effects with a typical exam ple1Practice shows that the s oftware has g ood practi2 cability and effect1关键词:M AT LAB;计算机辅助数值分析;软件包K ey w ords:M AT LAB;com puter2aided numerical analysis and calculation(C ANAC);s oftware package 中图分类号:TP391文献标识码:A1　引言M AT LAB是一种面向科学与工程计算的高级语言,同时也是适用于科学和工程计算的数学软件系统。

一个数值分析在生活中的应用实例

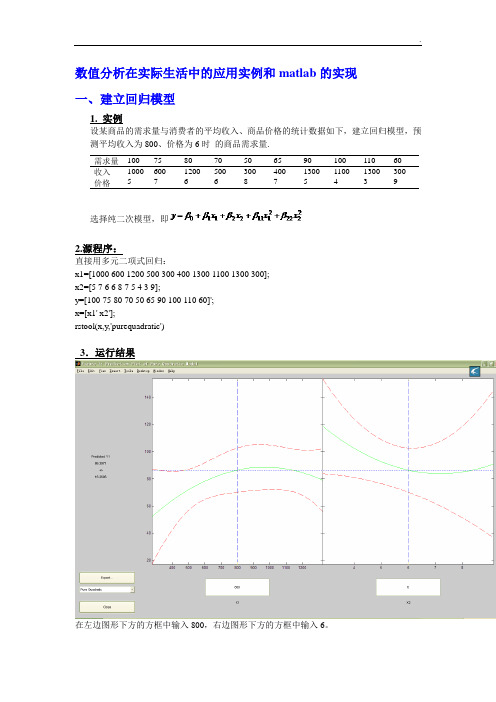
数值分析在实际生活中的应用实例和matlab的实现一、建立回归模型1. 实例设某商品的需求量与消费者的平均收入、商品价格的统计数据如下，建立回归模型，预测平均收入为800、价格为6时的商品需求量.需求量10075807050659010011060收入10006001200500300400130011001300300价格5766875439选择纯二次模型，即2.源程序：直接用多元二项式回归：x1=[1000 600 1200 500 300 400 1300 1100 1300 300];x2=[5 7 6 6 8 7 5 4 3 9];y=[100 75 80 70 50 65 90 100 110 60]';x=[x1' x2'];rstool(x,y,'purequadratic')3．运行结果在左边图形下方的方框中输入800，右边图形下方的方框中输入6。

则画面左边的“Predicted Y ”下方的数据变为86.3971，即预测出平均收入为800、价格为6时的商品需求量为86.3971.在画面左下方的下拉式菜单中选”all ”, 则beta （回归系数）、rmse （剩余标准差）和residuals （残差）都传送到Matlab 工作区中.在Matlab 工作区中输入命令： beta, rmse得结果：beta =110.5313 0.1464 -26.5709 -0.0001 1.8475 rmse =4.5362故回归模型为：2221218475.10001.05709.261464.05313.110x x x x y +--+= 剩余标准差为4.5362, 说明此回归模型的显著性较好.。

MATLAB在智能家居与智能建筑中的应用设计与数据处理技巧

MATLAB在智能家居与智能建筑中的应用设计与数据处理技巧引言：随着科技的不断发展，智能家居与智能建筑的应用已经成为现代生活的一部分。

为了实现自动化、智能化的功能，利用计算机和各种传感器技术对家居与建筑进行监控和控制已经成为一种趋势。

而Matlab作为一种强大的数学软件，被广泛应用于智能家居与智能建筑的应用设计与数据处理中。

本文将介绍Matlab在智能家居与智能建筑中的应用设计和数据处理技巧。

一、Matlab在智能家居的应用设计与数据处理技巧1. 传感器数据处理智能家居中常常使用各种传感器来感知环境和用户的状态，例如温度传感器、光照传感器、人体感应传感器等。

在获取到传感器数据后，需要对这些数据进行处理，提取有用的信息。

通过Matlab可以利用其强大的数据处理功能，实现对传感器数据的滤波、去噪等处理。

例如，可以通过使用滑动平均算法对温度传感器数据进行平滑处理，得到更加准确和稳定的温度数据。

同时，还可以利用Matlab的统计学工具箱对光照传感器数据进行分析，得到光照强度的统计特征，为智能控制提供依据。

2. 数据可视化在智能家居的设计中，数据可视化是非常重要的一环。

通过将数据以图表或图形的形式展示出来，可以直观地了解各种传感器的状态和监控设备的工作情况。

Matlab提供了丰富的可视化工具，可以轻松地生成各种类型的图表和图形。

例如，可以使用Matlab的绘图函数将温度传感器的数据绘制成折线图，以便观察温度的变化趋势；可以使用Matlab的三维绘图函数将室内光照度分布以立体图的形式展示出来，直观地了解不同区域的光照情况。

3. 控制算法设计智能家居的核心是实现对家居设备的智能控制。

在设计控制算法时，Matlab可以发挥其强大的数学建模和仿真能力。

可以利用Matlab的控制系统工具箱进行PID控制器的设计和调试。

通过将传感器数据和控制算法相结合，可以实现对家居设备的自动调节和控制。

例如，可以利用Matlab的自适应控制算法对家居照明系统进行控制，根据环境光照度的变化实时调节灯光的亮度和色温，以提供舒适的照明效果。