计算方法与实习第五版-习题答案.

合集下载

计算机05级计算方法试卷A、B及参考答案

计算机系 05 级计算方法试卷(A)（2008.1）班级_______________姓名______________学号_____________得分______________ 本卷考试时间为90分钟。

1．（10分）已知,0050.10010001≈具有七位有效数字，试从防止误差的角度给出适当的方法计算1000010001-，并说明理由。

2．（10分）简单叙述秦九韶法（或Horner 方法）计算多项式值的方法思想, 并应用该方法计算多项式322)(245+-+-=x x x x x f 在5.0=x 处的值，写出计算过程并说明计算过程中所需的乘法次数。

3．（10分）选用适当的方法求方程032=-x e x 在5.0 附近的一个根，要求所求根的误差不超过210-=ε。

4．（15分）用LU 分解法或高斯消去法解方程组5并利用插值多项式近似计算)(x f 在8.1处的值。

67．（15分）简述龙贝格（Romberg ）求积方法的思想，并选取适当的数值积分方法，求积分dx xe x ⎰102，要求误差不超过21021-⨯。

8．（15分）写出四阶龙格—库塔（Runge-Kutta ）方法，并选用适当的方法求解初值问题，取2.0=h ，计算机05级计算方法试卷(B)（2008.1）班级_______________姓名______________学号_____________得分______________ 本卷考试时间为90分钟。

3．(10分)数列{n x }满足递推公式122,n n x x -=- ,若73.130≈=x （有三位有效数字），问 ①从0x 计算到k x 时误差有多大？②上述计算是稳定的？4．(10分)给出计算多项式334)(345+-+-=x x x x x f 在0x 处的值方法，使其所需乘法次数尽可能少.6． (10分)用适当数值方法求方程310x x +-= 在区间[0,1] 上的一个根，精度310-=ε。

计算方法与实习(第五版)期末复习资料

《计算机在材料科学中的应用》习题课第一章误差等概念1. 误差来源：模型误差、观测误差、截断误差、舍入误差2. 绝对误差（限）：e=x*-x ，|e|＝|x*-x|≤ε3. 相对误差（限）：e r ＝(x*-x)/x ，|e r |＝|x*-x|/|x|≤εr4. 有效数字：|e|≤m-n 11025. 防止误差的危害：避免两相近数相减，多数作乘数或小数作除数，大数“吃”小数第二章方程求根1. 根的存在及隔离2. 二分法：误差是()k+11b-a 23. 迭代法：'1x (x)|(x)|1 ||k k x x ϕϕε+=<-<，，4. 加速法：'()L x ϕ≈取， 1111() L 1Lk k k k k k x x x x x x ϕ-+--+++⎧⎪⎨+-⎪⎩-＝＝（） 5. 牛顿迭代法：1000''1'111111'f()f()f ()0f ()f() f ()=c f()-f()f()()f ()=f()-f()f() f ()k k k k k k k k k k k k k k k k k k k k k k k x x x x x x x x x x x c x x x x x x x x x x x x x x x x λλ++--+--+->-----g ''＝, 选取时使得简化牛顿法:，＝拟牛顿法（割线法）: ，＝牛顿下山法:＝, 选取下山因子使得1|f()|<|f()|k k x x +⎧⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎩第三章方程组求解1. 消去法：高斯消去法，列主元消去法，高斯-约当法，消元因子 ()()k ikik k kka l a =消元公式 (k+1)(k)(k)ij ij ik kj (k+1)(k)(k)i i ik k a =a -l a (i,j=k+1,k+2,...,n)b =b -l b (i=k+1,k+2,...,n)⎧⎪⎨⎪⎩ 回代公式 kjn(k)(k)kjj=k+1k (k)kkb - a x x =(k=n,...,1)a∑2. 矩阵直接分解：紧凑格式3. 追赶法4. 迭代法：收敛条件1||||nii ij j j ia a =≠>∑①雅可比法迭代格式：ji n(k)i ij j=1j i(1)iib -a x x =(i=1,2,...,n) a k ≠+∑②高斯-赛德尔法迭代格式：jji i-1n(k+1)(k)i ij ij j=1j=i+1(1)iib -a x -a x x =(i=1,2,...,n)a k +∑∑第四章插值法1. 插值多项式2012j j j j (1)n+1 ()()... , (x )= f( x )= y (j=0,1,...,n) x [a,b],() ()=()-()=()(n+1)!n n n n f x P x a a x a x a x P f R x f x P x x ξω+≈=++++=插值条件，插值节点，插值区间插值余项2. 拉格朗日插值：插值基函数 n 001 () L ()()0 n nji j i i j i j j ix x i j l x x y i jx x ==≠-=⎧==⎨≠-⎩∑∏g ，3. 差商：10011002010122101k-2k 01k-2k-101k k k-1f(x )-f(x )f[x ,x ]=x -x f[x ,x ]-f[x ,x ]f[x ,x ,x ]=x -x f[x ,x ,...,x ,x ]-f[x ,x ,...,x ,x ]f[x ,x ,...,x ]=x -x 一阶差商二阶差商k 阶差商4. 牛顿插值公式f(x)=f(x 0)+f[x 0,x 1](x-x 0)+f[x 0,x 1,x 2](x-x 0)(x-x 1)+… +f[x 0,x 1,…,x n ](x-x 0)(x-x 1)…(x-x n-1) 5. 差分（等间距节点）111122111 = () , () -() -() - - k k k k k k k k k k k k k k m m m k k k x x kh x x f f x f x x h f f f f x x h f f f f x x h f f fm f f f δ+-+---+=+-∆≡∇≡≡∆=∆∆k 0k+1k 等距节点时，（k=0,1,...,n ）,h=记则在处以为步长的向前差分：在处以为步长的向后差分：在处以为步长的中心差分：同样也有各自的阶差分111111122- -m m m k k k m m m k k k f f f f f fδδδ-----+-∇=∇∇=6. 牛顿前插公式20000001012nf f f ()=()+(-)()()....()...()()h 2!h n!h n n n f x f x x x x x x x x x x x R x -∆∆∆+--++--+7. 样条插值：三次样条插值，要求光滑、连续第五章曲线拟合最小二乘原理2012n2i 01m j j j=1n (j=1,2,...,n),[]()...a (i=0,1,..., m),• (a ,...,a )= [P(x ) - y ] (x)(x,y ) m m p x a a x a x a x p n ϕ=++++∑j j 1n 有对数据(x ,y )在x ,x 上求一个m 次多项式适当选取使得,a 为最小值，则称为最小二乘拟合多项式是间的经验公式。

计算机网络第五版课后习题答案---精品管理资料

计算机网络第五版答案第一章概述1-01 计算机网络向用户可以提供那些服务？答: 连通性和共享1-02 简述分组交换的要点。

答：（1）报文分组,加首部(2）经路由器储存转发（3）在目的地合并1-03 试从多个方面比较电路交换、报文交换和分组交换的主要优缺点。

答:（1）电路交换:端对端通信质量因约定了通信资源获得可靠保障，对连续传送大量数据效率高。

（2）报文交换:无须预约传输带宽，动态逐段利用传输带宽对突发式数据通信效率高，通信迅速。

(3）分组交换：具有报文交换之高效、迅速的要点，且各分组小,路由灵活,网络生存性能好。

1—04 为什么说因特网是自印刷术以来人类通信方面最大的变革？答: 融合其他通信网络，在信息化过程中起核心作用，提供最好的连通性和信息共享，第一次提供了各种媒体形式的实时交互能力。

1-05 因特网的发展大致分为哪几个阶段？请指出这几个阶段的主要特点。

答：从单个网络APPANET向互联网发展；TCP/IP协议的初步成型建成三级结构的Internet；分为主干网、地区网和校园网；形成多层次ISP结构的Internet；ISP首次出现。

1-06 简述因特网标准制定的几个阶段？答：(1）因特网草案（Internet Draft）—-在这个阶段还不是RFC 文档。

(2）建议标准(Proposed Standard) ——从这个阶段开始就成为RFC 文档。

（3)草案标准（Draft Standard)（4）因特网标准（Internet Standard）1-07小写和大写开头的英文名字internet 和Internet在意思上有何重要区别?答：（1）internet（互联网或互连网）：通用名词,它泛指由多个计算机网络互连而成的网络。

;协议无特指（2）Internet（因特网）：专用名词,特指采用TCP/IP 协议的互联网络区别：后者实际上是前者的双向应用1-08 计算机网络都有哪些类别?各种类别的网络都有哪些特点？答：按范围：（1)广域网W AN：远程、高速、是Internet的核心网。

数值分析第五版第1章习题答案-李庆扬

第1章复习与思考题习题0，依据定义|X*X|/X*|X*-X|=X***X X：按定义求解E(lnX)=|lnX-LnX*|=ln(X/X*)=ln(1-)X|lnX ln*|/lnX*ln(1)/lnX*ln(1)/lnX*按泰勒展开求解，2(x*)=(x*)(x x*)"()(x x*)f f f1(lnX*)|lnX lnX*|lnX*(X X*)**r(lnX*)|lnX lnX*|/ln */ln *X X X X问题是解法1错了吗？很小时，ln(1-)=，求n X 的相对误差*0.02*X X ：按照定义：{(10.02)X*}*(1.02)n n X (X )(X X*)/X* 1.021(10.02)1n n n n n多项式展开，有100.02n n i i：按照泰勒展开11(X X*)*(X X*)nX*(0.02X*)0.02X*)(XX*)/X*0.02*/*0.02n n n n n nn nn nnX nX X n问题是解法1错了吗？10.02n n i i 收敛于（0.02/(1-0.02)= 0.002004008016032064128256释？应该没有错，按照泰勒展开，相当于将误差限放大了。

3、下列各数都是经过四舍五入得到的近似数，即误差限不超过最后一位的半个单位，试指出它们是几位有效数字* 1.1021x ，0.031x ，385.6，56.430，7 1.0。

解：有4位有效数字；X2有1位有效数字；X3有3位有效数字；X4有1位有效数字**24x x ，*1x x 其中***123x x x ，，，公式（2.3）：1(A*)|()*|(X )n k k kfX 解：******124124()()()()0.510x x x x x x ************1232311321234313()()()()0.031385.60.510 1.1021385.60.510 1.10210.0310.510(0.59768212.48488 1.708255)100.214790815x x x x x x x x x x x x******2*2442244323335(/)1/()/()()1/56.4300.5100.031/(56.430)0.510(10.031/56.430)/56.4300.510=(0.99945064681906787169945064681907)0.5/56.430100.885610x x x x x x x5、计算求体积要使相对误差限为1%，问度量半径R 所允许的相对误差是多少？解：球的体积公式3V R23(V)3R (R)/R 3(R)/R 0.01r有(R)0.01/3R (R)(R)/1/300r R6、设Y0=28，按递推公式11783100n nY Y ，1,2,3.....n 计算到Y100，若取27.982（解：n n n (Y )(Y Y )，所以(Y )0n 。

计算机网络第五版答案完整版

计算机网络第五版答案完整版Computers have become an integral part of our lives, and computer networking plays a crucial role in connecting various devices and enabling communication between them. In the fifth edition of the book "Computer Networks," the authors provide comprehensive answers and solutions to various exercises and questions, giving readers a complete understanding of the concepts and principles of computer networking.1. Introduction to Computer NetworksComputer networks are essential for transmitting data and enabling communication between devices. In this chapter, the authors explain the basics of networks, including the OSI model, network topology, and types of networks. They also provide answers to exercises that help readers grasp the fundamental concepts of computer networking.2. Physical LayerThe physical layer is responsible for transmitting raw bits over a communication channel. The authors cover topics such as analog and digital signals, transmission media, and modulation techniques. Through detailed explanations and examples, readers gain a solid understanding of the physical layer's functions and mechanisms.3. Data Link LayerThe data link layer ensures reliable data transfer between two connected nodes. This chapter focuses on topics like error detection and correction, flow control, and media access control. The authors provide accurateanswers to questions related to these concepts, enabling readers to comprehend the data link layer's role in establishing error-free communication.4. Network LayerThe network layer facilitates the delivery of data packets across multiple networks. Addressing, routing algorithms, and internet protocols are among the key topics discussed in this chapter. By examining the provided answers, readers can enhance their knowledge of the network layer's functionalities and protocols.5. Transport LayerThe transport layer provides end-to-end communication between applications running on different hosts. This chapter explores topics like multiplexing, demultiplexing, reliable data transfer protocols, and congestion control. The authors offer complete solutions to exercises, allowing readers to grasp the complexities and mechanisms of the transport layer.6. Application LayerThe application layer enables network applications to communicate with each other. This chapter covers topics such as domain name system (DNS), email protocols, and World Wide Web (WWW) protocols. The authors present accurate and detailed answers, enabling readers to understand the application layer's role in facilitating various network services.7. Network SecurityNetwork security is essential to protect data from unauthorized access and malicious activities. This chapter discusses topics like symmetric and asymmetric encryption, public key infrastructure (PKI), and network security protocols. The authors provide comprehensive answers, helping readers to comprehend the importance of network security and the techniques used to safeguard data.8. Multimedia NetworkingIn the modern era, multimedia applications require robust networking capabilities. This chapter delves into topics such as streaming and real-time applications, multimedia protocols, and quality of service (QoS) mechanisms. By examining the provided answers, readers can gain a deeper understanding of the challenges and solutions in multimedia networking.9. Network ManagementEfficient network management is crucial for ensuring the smooth operation of computer networks. This chapter covers topics like Simple Network Management Protocol (SNMP), network monitoring, and network troubleshooting. The authors provide accurate and comprehensive answers, allowing readers to learn about the tools and techniques used in network management.By providing complete and accurate answers to exercises, the fifth edition of "Computer Networks" equips readers with the knowledge and understanding required to master the field of computer networking. The authors' attention to detail, clear explanations, and concise yet informative solutions make this book an invaluable resource for students, professionals, and anyone interested in computer networks.。

数值分析课程第五版课后习题答案(李庆扬等)

数值分析课程第五版课后习题答案(李庆扬等)数值分析课程第五版课后习题答案(李庆扬等)第一章：数值分析导论1. 解答：数值分析是一门研究如何使用计算机来解决数学问题的学科。

它包括了从数学理论到计算实现的一系列技术。

数值分析的目标是通过近似的方式求解数学问题，其结果可能不是完全精确的，但是能够满足工程或科学应用的要求。

2. 解答：数值分析在实际应用中起着重要的作用。

它可以用于求解复杂的数学方程、计算机模拟及建模、数据的统计分析等等。

数值分析是科学计算和工程计算的基础，对许多领域都有着广泛的应用，如物理学、经济学、生物学等。

3. 解答：数值方法指的是使用数值计算的方式来求解数学问题。

与解析方法相比，数值方法一般更加灵活和高效，可以处理一些复杂的数学问题。

数值方法主要包括了数值逼近、插值、数值积分、数值微分、线性方程组的求解、非线性方程的求根等。

4. 解答：计算误差是指数值计算结果与精确解之间的差异。

在数值计算中，由于计算机的有限精度以及数值计算方法本身的近似性等因素，都会导致计算误差的产生。

计算误差可以分为截断误差和舍入误差两种。

第二章：数值误差分析1. 解答：绝对误差是指实际值与精确值之间的差异。

例如，对于一个计算出的数值近似解x和精确解x_0，其绝对误差为| x - x_0 |。

绝对误差可以衡量数值近似解的精确程度，通常被用作评估数值计算方法的好坏。

2. 解答：相对误差是指绝对误差与精确解之间的比值。

对于一个计算出的数值近似解x和精确解x_0，其相对误差为| (x - x_0) / x_0 |。

相对误差可以衡量数值近似解相对于精确解的精确度，常用于评估数值计算方法的收敛速度。

3. 解答：舍入误差是由于计算机的有限精度而引起的误差。

计算机中使用的浮点数系统只能表示有限的小数位数，因此在进行数值计算过程中，舍入误差不可避免地会产生。

舍入误差会导致计算结果与精确结果之间存在差异。

4. 解答：误差限度是指对于给定的数值计算问题，所能容忍的误差范围。

数值分析第五版课后答案2篇

数值分析第五版课后答案2篇数值分析第五版课后答案（一）第一章1.1 机器精度的数值为2^-52 ≈2.22 × 10^-16。

1.2 Example 1.2设f(x) = (1 - cosx)/sinx，则f(0)的分母为0，无法进行数值计算。

1.3 Example 1.3设f(x) = (1 - cosx)/sinx，则f(0)的分子为0，因此有f(0) = 0。

1.4 Example 1.4(a) 将x的值从1.8改为1.799，则f(x)的值由-0.000000000000159为0.000000000000313，差值为0.000000000000472。

(b) 我们有f'(x) = sinx/(1 - cosx) - 1/sin^2x。

将x的值从1.8改为1.799，利用f(x)和f'(x)的值可以得到下面的近似式：f(x + Δx) ≈ f(x) + f'(x)Δx = -0.000000000000159 + 0.449787416887455×0.001 = -0.000000000000137。

与(a)中的结果相近。

1.5 Example 1.5(a) 当x很接近于0时，函数值的符号取决于cosx的符号，其中cosx接近于1。

因此，函数值为正。

(b) 当x很接近于π时，函数值的大小趋于无穷大，因为分母趋向于0，而分子不为0。

1.6 Example 1.6(a) 因为函数在x = 0处是奇函数，所以它的导数为偶函数。

(b) 首先，我们有f''(0) = -2，因此x = 0是最大值。

其次，我们有f''(x) = -2 - 8sin^2x。

由于-f''(x)在x = 0处是正的，我们有当x越接近0时，f''(x)越小，也就意味着函数在x = 0处是严格的最大值。

1.7 Example 1.7(a) 我们有f(x) = x^3 - 2x^2 - 5x + 6，f'(x) =3x^2 - 4x - 5和f''(x) = 6x - 4。

计算方法的课后答案

《计算方法》习题答案第一章数值计算中的误差1．什么是计算方法？（狭义解释）答：计算方法就是将所求的的数学问题简化为一系列的算术运算和逻辑运算，以便在计算机上编程上机，求出问题的数值解，并对算法的收敛性、稳定性和误差进行分析、计算。

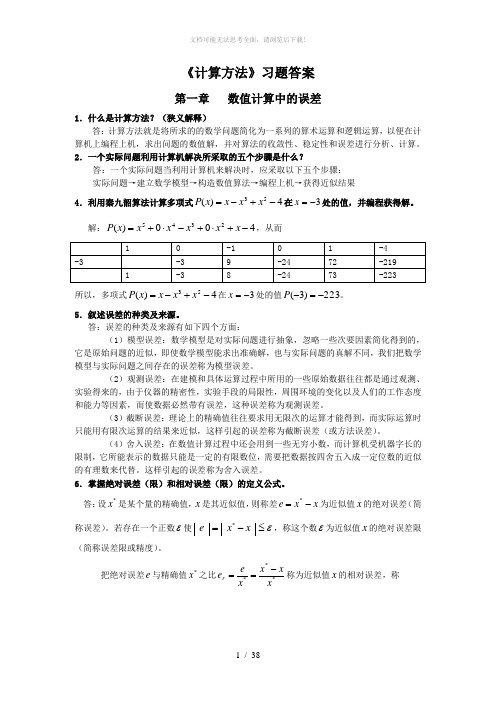
2．一个实际问题利用计算机解决所采取的五个步骤是什么？答：一个实际问题当利用计算机来解决时，应采取以下五个步骤：实际问题→建立数学模型→构造数值算法→编程上机→获得近似结果 4．利用秦九韶算法计算多项式4)(53-+-=x x x x P 在3-=x 处的值，并编程获得解。

解：400)(2345-+⋅+-⋅+=x x x x x x P ，从而所以，多项式4)(53-+-=x x x x P 在3-=x 处的值223)3(-=-P 。

5．叙述误差的种类及来源。

答：误差的种类及来源有如下四个方面：（1）模型误差：数学模型是对实际问题进行抽象，忽略一些次要因素简化得到的，它是原始问题的近似，即使数学模型能求出准确解，也与实际问题的真解不同，我们把数学模型与实际问题之间存在的误差称为模型误差。

（2）观测误差：在建模和具体运算过程中所用的一些原始数据往往都是通过观测、实验得来的，由于仪器的精密性，实验手段的局限性，周围环境的变化以及人们的工作态度和能力等因素，而使数据必然带有误差，这种误差称为观测误差。

（3）截断误差：理论上的精确值往往要求用无限次的运算才能得到，而实际运算时只能用有限次运算的结果来近似，这样引起的误差称为截断误差（或方法误差）。

（4）舍入误差：在数值计算过程中还会用到一些无穷小数，而计算机受机器字长的限制，它所能表示的数据只能是一定的有限数位，需要把数据按四舍五入成一定位数的近似的有理数来代替。

这样引起的误差称为舍入误差。

6．掌握绝对误差（限）和相对误差（限）的定义公式。

答：设*x 是某个量的精确值，x 是其近似值，则称差x x e -=*为近似值x 的绝对误差（简称误差）。

谢希仁计算机网络第五版课后习题答案(1-7)

谢希仁计算机网络第五版课后习题答案(1-7)计算机网络课后习题答案第一章概述1-01 计算机网络向用户可以提供那些服务？答：连通性和共享1-02 简述分组交换的要点。

答：（1）报文分组，加首部（2）经路由器储存转发（3）在目的地合并1-03 试从多个方面比较电路交换、报文交换和分组交换的主要优缺点。

答：（1）电路交换：端对端通信质量因约定了通信资源获得可靠保障，对连续传送大量数据效率高。

（2）报文交换：无须预约传输带宽，动态逐段利用传输带宽对突发式数据通信效率高，通信迅速。

（3）分组交换：具有报文交换之高效、迅速的要点，且各分组小，路由灵活，网络生存性能好。

1-04 为什么说因特网是自印刷术以来人类通信方面最大的变革？答：融合其他通信网络，在信息化过程中起核心作用，提供最好的连通性和信息共享，第一次提供了各种媒体形式的实时交互能力。

1-05 因特网的发展大致分为哪几个阶段？请指出这几个阶段的主要特点。

答：从单个网络APPANET向互联网发展； TCP/IP 协议的初步成型建成三级结构的Internet；分为主干网、地区网和校园网；形成多层次ISP结构的Internet； ISP首次出现。

1-06 简述因特网标准制定的几个阶段？答：（1）因特网草案(Internet Draft) ——在这个阶段还不是 RFC 文档。

（2）建议标准(Proposed Standard) ——从这个阶段开始就成为 RFC 文档。

（3）草案标准(Draft Standard)（4）因特网标准(Internet Standard)1-07小写和大写开头的英文名字 internet 和Internet在意思上有何重要区别？答：（1）internet（互联网或互连网）：通用名词，它泛指由多个计算机网络互连而成的网络。

；协议无特指（2）Internet（因特网）：专用名词，特指采用 TCP/IP 协议的互联网络区别：后者实际上是前者的双向应用1-08 计算机网络都有哪些类别？各种类别的网络都有哪些特点？答：按范围：（1）广域网WAN：远程、高速、是Internet的核心网。

数值分析第五版课后习题答案

数值分析第五版课后习题答案数值分析是一门应用数学的分支学科，主要研究如何利用数值方法解决实际问题。

在学习这门课程的过程中，课后习题是不可或缺的一部分。

本文将对《数值分析第五版》的课后习题进行一些探讨和解答。

第一章是数值分析的导论，主要介绍了误差分析和计算方法的基本概念。

在课后习题中，有一道题目是关于误差传播的。

假设有一个函数f(x, y) = x^2 + y^2，其中x和y的测量误差分别为Δx和Δy，要求计算f(x, y)的误差。

解答：根据误差传播公式，可以得到f(x, y)的误差为Δf = √[(∂f/∂x)^2 *(Δx)^2 + (∂f/∂y)^2 * (Δy)^2]。

对于本题而言，∂f/∂x = 2x，∂f/∂y = 2y。

代入公式，得到Δf = √[(2x)^2 * (Δx)^2 + (2y)^2 * (Δy)^2] = 2√(x^2 * (Δx)^2+ y^2 * (Δy)^2)。

第二章是插值与多项式逼近的内容。

其中一道习题涉及到拉格朗日插值多项式。

给定n+1个数据点(x0, y0), (x1, y1), ..., (xn, yn)，要求构造一个n次多项式p(x)，使得p(xi) = yi (i = 0, 1, ..., n)。

解答：拉格朗日插值多项式的表达式为p(x) = Σ(yi * Li(x))，其中Li(x) = Π[(x - xj) / (xi - xj)]，j ≠ i。

将数据点代入表达式中，即可得到所求的多项式。

第三章是数值微积分的内容，其中一道习题是关于数值积分的。

给定一个函数f(x)，要求使用复化梯形公式计算定积分∫[a, b]f(x)dx。

解答：复化梯形公式的表达式为∫[a, b]f(x)dx ≈ h/2 * [f(a) + 2Σf(xi) + f(b)]，其中h = (b - a)/n，xi = a + i * h (i = 1, 2, ..., n-1)。

根据给定的函数f(x)，代入公式中的各个值，即可得到近似的定积分值。

数值分析第五版第5章习题答案

第5章
）矩阵行列式的值很小。

）矩阵的范数小。

）矩阵的范数大。

（7）奇异矩阵的范数一定是零。

答：错误，
∞
•可以不为0。

（8）如果矩阵对称，则|| A||1 = || A||∞。

答：根据范数的定义，正确。

（9）如果线性方程组是良态的，则高斯消去法可以不选主元。

答：错误，不选主元时，可能除数为0。

（10）在求解非奇异性线性方程组时，即使系数矩阵病态，用列主元消去法产生的误差也很小。

答：错误。

对于病态方程组，选主元对误差的降低没有影响。

（11）|| A ||1 = || A T||∞。

答：根据范数的定义，正确。

（12）若A是n n的非奇异矩阵，则
)
(
cond
)
(
cond1-
=A
A。

答：正确。

A是n n的非奇异矩阵，则A存在逆矩阵。

根据条件数的定义有：
1
111111 cond()
cond()()
A A A
A A A A A A A
-
------
=•
=•=•=•
习题
如有侵权请联系告知删除，感谢你们的配合！。

《统计学原理(第五版)》习题计算题答案详解

《统计学原理(第五版)》习题计算题答案详解第二章统计调查与整理1．见教材P402 2．见教材P402-403 3．见教材P403-404第三章综合指标1．见教材P4322． %86.1227025232018=+++=产量计划完成相对数3．所以劳动生产率计划超额1.85%完成。

4． %22.102%90%92(%)(%)(%)===计划完成数实际完成数计划完成程度指标一季度产品单位成本，未完成计划，还差2.22%完成计划。

5．6．见教材P432 7．见教材P433理工作做得好。

但由于甲村的平原地所占比重大，山地所占比重小，乙村则相反，由于权数的作用，使得甲村的总平均单产高于乙村。

9．11．%74.94963.09222.09574.03=⨯⨯=G X 或参照课本P9912．%49.51X %49.105 08.107.105.104.102.1 X 1624632121=-=⨯⨯⨯⨯=∑⋅⋅⋅⋅⋅⋅=G ff n f f G nX X X 平均年利率：平均本利率为：(2)R=500-150=350(千克/亩) (3)“(4)根据以上计算，294.5千克/亩>283.3千克/亩>277.96千克/亩，即M 0>Me>X ，故资料分布为左偏(即下偏)。

(2) 15．见教材P435 16．见教材P40417．%86.1227025232018=+++=产量计划完成相对数18．%85.101%108%110%%(%)===计划为上年的实际为上年的计划完成程度指标劳动生产率计划超额1.85%完成19． %22.102%90%92(%)(%)(%)===计划完成数实际完成数计划完成程度指标一季度产品单位成本未完成计划，实际单位成本比计划规定数高2.22%20． %105%103% %%(%) 计划为上年的计划为上年的实际为上年的计划完成程度指标=∴=1.94% %94.101103%105%% 即计划规定比上年增长计划为上年的解得：==21．见教材P405 22．见教材P405理工作做得好。

数值分析(第五版)计算实习题第四章作业

第四章：1、（1）：复合梯形建立m文件：function t=natrapz(fname,a,b,n)h=(b-a)/n;fa=feval(fname,a);fb=feval(fname,b); f=feval(fname,a+h:h:b-h+0.001*h); t=h*(0.5*(fa+fb)+sum(f));输入：>> syms x>> f=inline('sqrt(x).*log(x);'); >> natrapz(f,eps,1,10)输出：ans =-0.417062831779470输入：>> syms x>> f=inline('sqrt(x).*log(x);'); >> natrapz(f,eps,1,100)输出：ans =-0.443117908008157输入：>> syms x>> f=inline('sqrt(x).*log(x);'); >> natrapz(f,eps,1,1000)输出：ans =-0.444387538997162复合辛普森建立m文件：function t=comsimpson(fname,a,b,n)h=(b-a)/n;fa=feval(fname,a);fb=feval(fname,b);f1=feval(fname,a+h:h:b-h+0.001*h);f2=feval(fname,a+h/2:h:b-h+0.001*h);t=h/6*(fa+fb+2*sum(f1)+4*sum(f2));输入：>> syms x>> f=inline('sqrt(x).*log(x);');>> format long；>>comsimpson(f,eps,1,10)输出：ans =-0.435297890074689输入：>>syms x>>f=inline('sqrt(x).*log(x);');>>comsimpson(f,eps,1,100)输出：ans =-0.444161178415673输入：>>syms x>>f=inline('sqrt(x).*log(x);');>>comsimpson(f,eps,1,1000)输出：ans =-0.444434117614180（2）龙贝格建立m文件：function [RT,R,wugu,h]=Romberg(fun,a,b,wucha,m) %RT是龙贝格积分表%R是数值积分值%wugu是误差估计%h是最小步长%fun是被积函数%a b是积分下、上限%m是龙贝格积分表中行最大数目%wucha是两次相邻迭代值的绝对误差限n=1;h=b-a;wugu=1;x=a;k=0;RT=zeros(4,4);RT(1,1)=h*(feval(fun,a)+feval(fun,b))/2;while((wugu>wucha)&(k<m)|(k<4))k=k+1;h=h/2;s=0;for j=1:nx=a+h*(2*j-1);s=s+feval(fun,x);endRT(k+1,1)=RT(k,1)/2+h*s;n=2*n;for i=1:kRT(k+1,i+1)=((4^i)*RT(k+1,i)-RT(k,i))/(4^i-1);endwugu=abs(RT(k+1,k)-RT(k+1,k+1));endR=RT(k+1,k+1);输入：>>fun=inline('sqrt(x).*log(x)');>> [RT,R,wugu,h]=Romberg(fun,eps,1,1e-5,13)输出：RT =1 至5 列-0.000000268546145 0 0 0-0.245064670140209 -0.326752804004897 0 0-0.358104125949240 -0.395783944552250 -0.400386020588741 0 0-0.408090073087781 -0.424752055467295 -0.426683262861631 -0.427100679405645 0-0.429474601629505 -0.436602777810080 -0.437392825966266 -0.437562819031419 -0.437603847029951-0.438389494461832 -0.441361125405941 -0.441678348578999 -0.441746372747455 -0.4417627788404596 列-0.441766844267449R =-0.441766844267449wugu =4.065426989774412e-06h =0.031250000000000（3）自适应辛普森输入：>> f=inline('sqrt(x).*log(x)');>> q=quad(f,0,1,1e-4)输出：q =-0.4439755729517282.（1）复合辛普森建立m文件function q=combinesimpson2(F,x0,a,b,n)%复合Simpson多元求积公式%F—被积函数%x0—被积函数自变量%[a,b]积分区间%n—区间份数x=linspace(a,b,n+1);q=0;for k=1:nq=q+subs(F,x0,x(k))+4*subs(F,x0,(x(k)+x(k+1))/2)+subs(F,x0,x(k+1)); endq=q*(b-a)/n/6;输入：>> clear>> syms x y;>> F=exp(-x.*y);>> s=combinesimpson2(combinesimpson2(F,'x',0,1,4),'y',0,1,4)输出：s =exp(-1)/576 + exp(-1/2)/144 + exp(-1/4)/72 + exp(-3/4)/144 + exp(-1/8)/36 +exp(-3/8)/36 + exp(-5/8)/72 + exp(-7/8)/72 + (5*exp(-1/16))/144 + exp(-3/16)/24 + exp(-5/16)/36 + exp(-7/16)/36 + exp(-9/16)/144 + exp(-1/32)/36 + exp(-3/32)/18 + exp(-5/32)/36 + exp(-7/32)/36 + exp(-9/32)/36 + exp(-15/32)/36 + exp(-21/32)/36 + exp(-1/64)/36 + exp(-3/64)/18 + exp(-5/64)/18 + exp(-7/64)/18 + exp(-9/64)/36 + exp(-15/64)/18 + exp(-21/64)/18 + exp(-25/64)/36 + exp(-35/64)/18 + exp(-49/64)/36 + 47/576>> double(s)ans =0.796599967946203高斯求积公式function q=gaussquad(F,x0,a,b,n)%Gauss求积公式%F—被积函数%x0—被积函数自变量%[a,b]积分区间%n—节点个数syms t;F=subs(F,x0,(b-a)/2*t+(a+b)/2);[x,A]=gausspoints(n);q=(b-a)/2*sum(A.*subs(F,t,x));输入：>> clear>> syms x y;F=exp(-x.*y);>> s=gaussquad(gaussquad(F,x,0,1,4),y,0,1,4)输出：s =0.7966（2）复合辛普森输入：>> syms x y;>> f=exp(-x.*y);>> s=combinesimpson2(combinesimpson2(f,y,0,sqrt(1-x^2),4),x,0,1,4)输出：s =(3^(1/2)*(exp(-3^(1/2)/4) + 2*exp(-3^(1/2)/8) + 2*exp(-3^(1/2)/16) + 2*exp(-(3*3^(1/2))/16) + 4*exp(-3^(1/2)/32) + 4*exp(-(3*3^(1/2))/32) + 4*exp(-(5*3^(1/2))/32) + 4*exp(-(7*3^(1/2))/32) + 1))/576 + (7^(1/2)*(exp(-(3*7^(1/2))/16) + 2*exp(-(3*7^(1/2))/32) + 2*exp(-(3*7^(1/2))/64) + 2*exp(-(9*7^(1/2))/64) + 4*exp(-(3*7^(1/2))/128) + 4*exp(-(9*7^(1/2))/128) + 4*exp(-(15*7^(1/2))/128) + 4*exp(-(21*7^(1/2))/128) + 1))/1152 + (15^(1/2)*(exp(-15^(1/2)/16) + 2*exp(-15^(1/2)/32) + 2*exp(-15^(1/2)/64) + 2*exp(-(3*15^(1/2))/64) + 4*exp(-15^(1/2)/128) + 4*exp(-(3*15^(1/2))/128) + 4*exp(-(5*15^(1/2))/128) + 4*exp(-(7*15^(1/2))/128) + 1))/1152 + (15^(1/2)*(exp(-(7*15^(1/2))/64) + 2*exp(-(7*15^(1/2))/128) + 2*exp(-(7*15^(1/2))/256) + 2*exp(-(21*15^(1/2))/256) + 4*exp(-(7*15^(1/2))/512) + 4*exp(-(21*15^(1/2))/512) + 4*exp(-(35*15^(1/2))/512) + 4*exp(-(49*15^(1/2))/512) + 1))/1152 + (39^(1/2)*(exp(-(5*39^(1/2))/64) + 2*exp(-(5*39^(1/2))/128) + 2*exp(-(5*39^(1/2))/256) + 2*exp(-(15*39^(1/2))/256) + 4*exp(-(5*39^(1/2))/512) + 4*exp(-(15*39^(1/2))/512) + 4*exp(-(25*39^(1/2))/512) + 4*exp(-(35*39^(1/2))/512) + 1))/1152 + (55^(1/2)*(exp(-(3*55^(1/2))/64) + 2*exp(-(3*55^(1/2))/128) + 2*exp(-(3*55^(1/2))/256) + 2*exp(-(9*55^(1/2))/256) + 4*exp(-(3*55^(1/2))/512) + 4*exp(-(9*55^(1/2))/512) + 4*exp(-(15*55^(1/2))/512) + 4*exp(-(21*55^(1/2))/512) + 1))/1152 + (63^(1/2)*(exp(-63^(1/2)/64) + 2*exp(-63^(1/2)/128) + 2*exp(-63^(1/2)/256) + 2*exp(-(3*63^(1/2))/256) + 4*exp(-63^(1/2)/512) + 4*exp(-(3*63^(1/2))/512) + 4*exp(-(5*63^(1/2))/512) + 4*exp(-(7*63^(1/2))/512) + 1))/1152 + 1/24>> double(s)ans =0.670113633359095。

《统计学原理(第五版)》习题计算题答案详解参考word

4． %22.102%90%92(%)(%)(%)===计划完成数实际完成数计划完成程度指标一季度产品单位成本，未完成计划，还差2.22%完成计划。

5．%85.011100%8%110%1=⨯++==计划完成数实际完成数计划完成程度指标计划完成数；所以计划完成数实际完成数标因为，计划完成程度指%105%103== 1.94%%94.101%103%105，比去年增长解得：计划完成数==()得出答案）将数值带入公式即可以计算公式，上的方程，给大家一个很多同学都不理解也可以得出答案，鉴于（根据第三章天）。

个月零天（也即是个月零（月）也就是大约）（上年同季（月）产量达标季（月）产量超出计划完成产量达标期完成月数计划期月数超计划提前完成时间达标期提前完成时间完成计划的时间万吨。

根据公式：提前多出万吨，比计划数万吨产量之和为：季度至第五年第二季度方法二：从第四年第三PPT PPT 6868825.8316-32070-7354-60--3707320181718=+=+=+==+++()天完成任务。

个月零年第四季度为止提前（天），所以截止第五）（根据题意可设方程：万吨完成任务。

天达到五年第二季度提前万吨。

根据题意，设第万吨达到原计划，还差万吨产量之和为：季度至第五年第一季度方法一：从第四年第二6866891-91*20)181718(1916707016918171816=++++=+++x xx6．见教材P432 7．见教材P433)/(2502500625000)/(2702500675000亩千克亩千克乙甲======∑∑∑∑f xf X x mm X在相同的耕地自然条件下，乙村的单产均高于甲村，故乙村的生产经营管理工作做得好。

计算方法习题选编及参考解答

一、选择题（每小题4分，共20分）1. 误差根据来源可以分为四类，分别是（ A ）A. 模型误差、观测误差、方法误差、舍入误差；B. 模型误差、测量误差、方法误差、截断误差；C. 模型误差、实验误差、方法误差、截断误差；D. 模型误差、建模误差、截断误差、舍入误差。

2. 若132)(356++-=x x x x f ，则其六阶差商=]3,,3,3,3[6210 f （ C ） A. 0； B. 1； C. 2； D. 3 。

3. 数值求积公式中的Simpson 公式的代数精度为（ D ）A. 0；B. 1；C. 2；D. 3 。

4. 若线性方程组Ax = b 的系数矩阵A 为严格对角占优矩阵，则解方程组的Jacobi 迭代法和Gauss-Seidel 迭代法（ B ）A. 都发散；B. 都收敛C. Jacobi 迭代法收敛，Gauss-Seidel 迭代法发散；D. Jacobi 迭代法发散，Gauss-Seidel 迭代法收敛。

5. 对于试验方程y y λ='，Euler 方法的绝对稳定区间为（ C ）A. 02≤≤-h ；B. 0785.2≤≤-h ；C. 02≤≤-h λ；D. 0785.2≤≤-h λ ；二、填空题（每空3分，共18分）1. 已知⎪⎪⎭⎫⎝⎛--='-=4321,)2,1(A x ，则 =2x 5，=1Ax 16 ，=2A22115+2. 已知3)9(,2)4(==f f ，则 f (x )的线性插值多项式为)6(2.0)(1+=x x L ,且用线性插值可得f(7)= 2.6 。

3. 要使20的近似值的相对误差界小于0.1%，应至少取 4 位有效数字。

三、利用下面数据表，10.466758.030146.042414.425693.12014f (x ) 2.6 2.4 2.2 2.0 1.8 x1. 用复化梯形公式计算积分dxx f I )(6.28.1⎰=的近似值；解：1.用复化梯形公式计算取2.048.16.2,4=-==h n 1分分分分7058337.55))6.2()2.08.1(2)8.1((22.04))()(2)((231114=+++=++=∑∑=-=f k f f b f x f a f hT k n k k2. 用复化Simpson 公式计算积分dxx f I )(6.28.1⎰=的近似值。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1．《计算方法》课程主要研究以计算机为工具的数值分析方法，并评价该算法的计算误差。 2．近似值作四则运算后的绝对误差限公式为 ( x1 x2 ) ( x1 ) ( x2 ) ，近似值 1.0341的相对误差限不大于 1 10 2 ，则它至少有三位有效数字。 4
a. 0.41003×106 c. 4.10037×105 b. 0.41004×106 d. 上溢 a．0.00235 c．0.0023 b．0.0023471 d．0.00234711

第一章绪论练习

6. 自然数e*=2.718281828459045…，取 e≈2.71828，那么e的有效数字是: ( b )
解：1）求单调区间 f’(x)=-1-cosx，可知在(3.14, 0)区间f’(x)<0，单调递减 2）在(3.14, 0)区间逐步搜索 f(0)=1-0-sin0=1>0，f(1)=1-1-sin1=-sin1<0 ∴方程1-x-sinx=0在[0,1]中有且只有1个根。 ba 1 1 3）求二分次数 k 1 k 1 *10 3
绪论
习题1——10：设 f ( x) 8x5 0.4x4 4x3 9x 1 用秦九韶法求f(3)。解：

8
0.4
24
4
0
9
1
x3
8
70.8
74.8
224.4
224.4
673.2 664.2
1992.6
1993.6
23.6
∴ f(3)=1993.6
第一章绪论练习
根的近似值
0.5000 0.7500 0.8750 0.9375 0.9063
序号
1 2 3 4 5
序号
6 7 8 9 10
根的近似值
0.9219 0.9141 0.9180 0.9200 0.9209
方程求根

习题2——3：用简单迭代法求方程ex-4x=0的根，并验证收敛性，精确到4位有效数字。解：1.找出方程的有根区间

(1)单调区间：
令f’(x)=ex-4=0, x=ln4≈1.4，所以有两个单调区间： [- ∞，1.4](递减)和[1.4， ∞](递增)

(2)有根区间：∴ 存在两个有根区间为：[0，1] 和[2，3]
[- ∞，1.4]区间：f(0)=1>0，f(1)=e-4<0，所以有根区间为：[0，1] [1.4，+ ∞]区间：f(2)=e2-8<0，f(3)=e3-12>0，所以有根区间为：[2，3]
方程求根

习题2——3：用简单迭代法求方程ex-4x=0的根，并验证收敛性，精确到4位有效数字。
第一章绪论练习

3．设数据x1，x2的绝对误差限分别为0.05和 0.005，那么两数的乘积x1x2的绝对误差限 (x1x2)= 0.05 x2 0.005x1 。 4. 0.00234711 具有 5 位有效数字的近似值是: ( b ) 5. 在β=10，t=5，－L=U=5的截断机上，与数410037对应的规格化浮点数是: ( d )
3.2589
3.2590 4.3820 0.00078925
绪论
习题1——4：已知下列近似值x1=4.8675, x2=4.08675, x3=0.08675，求x1+x2+x3 的误差限。 4 5 5 e ( x ) 0 . 5 * 10 , e ( x ) 0 . 5 * 10 , e ( x ) 0 . 5 * 10 解： 1 2 3
2）判断二分次数由(b-a)/2k+1=1/2k+1≤1/2*10-3，解得k≥3ln10/ln2≥9.965，所以需要二分10次，才能满足精度要求。
方程求根

习题2——2：用二分法求方程2e-x-sinx=0在区间[0,1]内的1个实根，要求3位有效数字。
解：3）迭代计算
∴x ≈0.921
3 ln( 10 ) k
ln( 2)
9.965
2
2
2
∴需二分10次
方程求根——二分法

习题2——2：用二分法求方程2e-x-sinx=0在区间[0,1]内的1个实根，要求3位有效数字。
解：1）判断是否在该区间有且仅有一个根
f(0)=2>0，f(1)=2/e-sin1≈-0.1<0， f’(x)=-2e-x-cosx，f’=-3,-2/e-cos1<0
计算方法(数值分析)
习题答案——第一、二章
教师：马英杰成都理工大学核自学院
绪论

习题1——1：指出下列各数有几位有效数字
4.8675 4.08675 0.08675 96.4730 96*105 5 6 4 6 2
0.00096
2Байду номын сангаас
绪论

习题1——2：对下列各数写出具有5位有效数字的近似值
3.25894 3.25896 4.382000 0.000789247

e( x1 x2 x3 ) e( x1 ) e( x2 ) e( x3 ) e( x1 x2 x3 ) e( x1 ) e( x2 ) e( x3 )
e( x1 ) e( x2 ) e( x3 )
0.5 *10 4 0.5 *105 0.5 *105 0.6 *10 4
绪论

习题1——6：一台10进制的计算机，4位字长，阶码p∈[-2,3]，可以表示的机器数有多少个？给出它的最大数、最小数及距原点最近的非零数，并求fl(x)的相对误差限。

解：β=10，t=4，L=-2，U=3

机器数个数：2*(β-1)*βt-1*(U-L+1)+1=2*9*103*6+1=108001 距原点最近的非零数：±0.1000*10-2 最大的数：0.9999*103 最小的数：-0.9999*103 相对误差限：0.5*10-3(舍入机)， 10-3(截断机)
a．5位 b．6位 c．7位 d．8位

7. 数13.013627……的有四位有效数字的近似值是: ( d )
a．13.00 c．13.014 b．13.02 d．13.013
方程求根

习题2——1：证明方程1-x-sinx=0在[0,1]中有且只有1个根，用二分法求误差不大于1/2*10-3 的根需要迭代多少次？