多项式乘以多项式学案题型
《多项式乘以多项式》教案

《多项式乘以多项式》教案一、教学目标:1. 让学生理解多项式乘以多项式的概念和意义。
2. 让学生掌握多项式乘以多项式的计算方法和步骤。
3. 培养学生运用多项式乘以多项式解决实际问题的能力。
二、教学内容:1. 多项式乘以多项式的概念和意义。
2. 多项式乘以多项式的计算方法和步骤。
3. 多项式乘以多项式在实际问题中的应用。
三、教学重点与难点:1. 教学重点:多项式乘以多项式的计算方法和步骤。
2. 教学难点:多项式乘以多项式在实际问题中的应用。
四、教学方法:1. 采用讲解法,让学生理解多项式乘以多项式的概念和意义。
2. 采用演示法,让学生掌握多项式乘以多项式的计算方法和步骤。
3. 采用案例分析法,培养学生运用多项式乘以多项式解决实际问题的能力。
五、教学过程:1. 引入新课:通过复习多项式的基本概念,引导学生进入多项式乘以多项式的新课。
2. 讲解多项式乘以多项式的概念和意义:解释多项式乘以多项式的定义,让学生理解其意义。
3. 演示多项式乘以多项式的计算方法和步骤:通过示例,让学生掌握多项式乘以多项式的计算方法。
4. 练习与巩固:布置一些练习题,让学生运用所学知识进行计算,巩固所学内容。
5. 案例分析:给出一些实际问题,让学生运用多项式乘以多项式的方法进行解决,培养学生的应用能力。
6. 小结与总结:对本节课的内容进行总结,强调多项式乘以多项式的计算方法和实际应用。
7. 作业布置:布置一些课后作业,巩固所学知识。
六、教学评价:1. 通过课堂讲解和练习,评估学生对多项式乘以多项式的概念和意义的理解程度。
2. 通过计算练习题,评估学生对多项式乘以多项式的计算方法和步骤的掌握情况。
3. 通过案例分析,评估学生运用多项式乘以多项式解决实际问题的能力。
七、教学资源:1. 多项式乘以多项式的教材和教学指导书。
2. 多媒体教学设备,如投影仪和白板。
3. 练习题和案例分析题的资料。
八、教学进度安排:1. 第1周:讲解多项式乘以多项式的概念和意义。
《多项式乘以多项式》典型例题(答案)

《多项式乘以多项式》典型例题例1 计算)2)(133(2424-++-x x x x例2 计算)3(2)2(3)1)(12()1)(13(x x x x x x x x -------++例3 利用ab x b a x b x a x +++=++)())((2,写出下列各式的结果;(1))6)(5(-+x x(2))53)(23(+-+-x x例4 计算)1)(1)(1(2++-x x x例5 已知012=-+x x ,求423+-x x 的值。
例6 计算题:(1))43)(52(y x y x -+; (2)))((22y x y x ++;(3))43)(32(y x y x -- (4))321)(421(-+x x . 例7 已知计算)35)((23+-++x x n mx x 的结果不含3x 和2x 项,求m ,n 的值。
例8 计算(1))9)(7(++x x ; (2))20)(10(+-x x ;(3))5)(2(--x x ; (3)))((b x a x ++。
参考答案例1 解:原式263363324246468-+++---+=x x x x x x x x2783248-+-=x x x说明:多项式乘法在展开后合并同类项前,要检查积的项数是否等于相乘的两项式项数的积,防止“重”、“漏”。
例2 解:原式2222663)122(133x x x x x x x x x ++-+----++=2222663122133x x x x x x x x x ++--++-+++=x x 1342+=说明:本题中)1)(12(--x x 前面有“-”号,进行多项式乘法运算时,应把结果写在括号里,再去括号,以防出错。
例3 解:(1))6)(5(-+x x)6(5)65(2-⋅+-+=x x302--=x x(2))53)(23(+-+-x x1021952)3)(52()3(22+-=⨯+--+-=x x x x说明:(2)题中的)3(x -即相当于公式中x例4 解:)1)(1)(1(2++-x x x11)1()11()()1)(1()1](1)1()11([42222222-=⋅-++-+=+-=+⋅-++-+=x x x x x x x x说明:三个多项式相乘,可先把两个多项式相乘,再把积与剩下的一个多项式相乘。
人教版八年级上册数学学案:14.1.4多项式乘以多项式

《多项式乘以多项式》导学案学习目标:1、探索的多项式乘以多项式的法则,理解多项式乘以多项式的意义。
2、理解多项式乘以多项式的运算法则,并能利用法则进行计算和解决一些实际问题。
学习重点:多项式乘以多项式的法则及应用。
学习难点:利用多项式乘以多项式法则准确运算。
导学过程:一、知识回顾1、同底数幂的乘法、幂的乘方、积的乘方法则分别是什么?2、回顾单项式乘以单项式、单项式乘以多项式法则。
3、 巩固练习(1)、3342(210)(410)-⨯⋅⨯ (2)、3214(1)6()(2)3xy x xy x x y ⎡⎤---⋅-⎢⎥⎣⎦二、多项式乘以多项式法则探究问题:一个矩形的长为(m +n )米,宽为(a +b )米,则它的面积为多少?归纳:多项式乘以多项式法则。
三、多项式乘以多项式法则应用① (2x-5y)(3x-y) ① (2x-1)(4x+2xy+y) ① (x+2)2练习:(1)(x-8y)( x-y) (2)(x-1)(2x-3) (3)(m-2n)(3m+n) (4)(x-2)(x2+4) (5)(x-y) (x2+xy+y2) (6)n(n+1)(n+2)例2、(x+2)(x+3)=;(y+4)(y+6)=.(x-2)(x+3)=;(y+4)(y-6)=.(x-2)(x-3)=;(y-4)(y-6)=.①根据上面的计算结果,同学们有什么发现?①观察右图,填空(x+m)(x+n)=( )2+( )x+( )归纳:利用发现的结论计算:(1)(m+5)(m-1)=;(x-5)(x-1) =.(2)(x-2y)(x+4y)=;(ab+7)(ab-3) =.(1)(1-3x)(1+2x)-3x(2x-1) (2)2(x-8)(x-5)-(2x-1)(x+2)例3:解方程(1)(3x-2)(2x-3)=(6x+5)(x-1)-1 (2)(x-2)(x+3) =(x+2)(x-5)三、课堂小结1、请同学们在小组内归纳本堂课的主要内容;2、你认为本堂课哪些内容不太容易掌握呢?总结一下,在小组内议一议。
《多项式乘多项式》教案导学案

《多项式乘多项式》教案导学案导学目标:1.了解多项式的定义和基本运算法则;2.理解多项式相乘的定义和方法;3.掌握多项式相乘的计算方法;4.能够应用多项式相乘解决实际问题。
导学内容:一、引入同学们在学习中学过的代数运算有哪些?请举例说明。
二、知识点导入1.多项式的定义:多项式是由一系列单项式相加(或相减)得到的表达式,即多项式是单项式的和(或差)。
2.多项式的基本运算法则:a)同类项的合并:同类项的指数相同,只有系数不同。
b)加减法的运算法则:对应项相加减,其他项保持不变。
c)乘法的运算法则:分配律。
三、多项式相乘的定义和方法1.多项式相乘的定义:将一个多项式的每一项分别与另一个多项式的每一项相乘,再将结果相加。
2.多项式相乘的方法:a)将一个多项式的每一项分别与另一个多项式的每一项相乘,得到所有可能的乘积项;b)将得到的乘积项按照指数从高到低排列,并合并同类项;c)合并同类项后,化简表达式。
四、多项式相乘的计算方法请同学们根据上述方法,计算以下多项式相乘的结果:(2x+3)(4x+5)五、实例分析1.问题:小明家有一块长方形花坛,长为3x+2,宽为4x-1、如果小明要在花坛的四周做一圈围墙,请问围墙的长度是多少?2.解析:围墙的长度就是花坛的周长,周长等于长加宽再乘以2、所以,围墙的长度可以表示为(3x+2+4x-1)×2请同学们根据以上解析,计算围墙的长度。
六、课堂练习请同学们完成以下习题:1.计算:(3x+1)(2x+5)2.计算:(4x-2)(x+3)3.计算:(x+2)(x-3)4.计算:(5x-3)(6x+4)七、课后作业1.计算:(2x-1)(3x+4)2.计算:(x+3)(x-4)3.计算:(2x+5)(3x-2)4.计算:(4x-3)(x+2)八、小结同学们,通过本节课的学习,你们掌握了多项式相乘的定义、方法和计算技巧。
在实际应用中,多项式相乘能够帮助我们解决一些问题,比如计算长度、面积等。
人教版八年级上册数学14.1.6《多项式乘以多项式》练习案

第十四章整式的乘法和因式分解14.1.6 多项式乘以多项式【知识梳理】多项式与多项式相乘,先用一个多项式的_______乘另一个多项式的_______,再把所得的相加,即____________________________.【知识点训练】多项式与多项式相乘1.计算(x+4y)(x-5y)等于( )A.x2-20y2 B.x2-9xy-20y2 C.x2-xy-20y2 D.x2+xy-20y22.下列计算正确的是( )A.(x+2)(x+1)=x2+2x+3 B.(m-3)(m-2)=m2-6m+5C.(a+5)(a-2)=a2+3a-10 D.(3x+2)(3x-1)=9x2-3x-23.下列多项式相乘的结果是a2-a-6的是( )A.(a-2)(a+3) B.(a+2)(a-3)C.(a-6)(a+1) D.(a+6)(a-1)4.计算:(2x+1)(x-1)=_____________.5.计算:(1)(3x-5)(3x+5); (2)(x-1)(x2+x+1);(3)(3x-y)(y+3x)-(4x-3y)(4x+3y).6.要使(4x-a)(x+1)的积中不含有x的一次项,则a等于( )A.-4 B.2 C.3 D.47.若a+b=3,ab=2,则代数式(a-2)(b-2)的值是_____.8.某校操场原来的长是2x米,宽比长少10米,现在把操场的长与宽都增加了5米,则整个操场的面积增了平方米.9.已知x2-5x=14,求(x-1)(2x-1)-(x+1)2+1的值.10.求出使(3x+2)(3x-4)>9(x-2)(x+3)成立的非负整数解.【综合运用】11.若a,b,k均为整数且满足等式(x+a)(x+b)=x2+kx+36,写出两个符合条件的k的值.【综合运用】9.某同学在计算一个多项式乘以-3x2时,算成了加上-3x2,得到的答案是x2-12x+1,那么正确的计算结果是多少?。
多项式乘以多形式导学案

14.1.4 整式的乘法(多项式乘以多项式)学案
学生姓名 雄县双堂乡中学
【学习目标】
1.多项式乘以多项式的运算法则及其应用
2.理解多项式乘以多项式的算理,发展有条理的思考及表达能力。
3.提倡多样化的算法,培养学生的创新精神与能力。
【自主学习】
1.复习旧知:
上节课我们学习了单项式与多项式乘法,大家还知道运算法则吗?
2.新课探究
如图,为了扩大街心花园的绿地面积,把一块原长a 米、宽m 米的长方形绿地,增长了b 米,加宽了n 米.你能用几种方法求出扩大后的绿地面积?
3. 你发现上述结果有什么规律?
4.归纳总结:多项式与多项式相乘,先用一多项式的 乘另一个多项式 ,再把所得的积 。
m n a bn
bm a m a n
5.典例练习
(1)(3x+1)(x+2) (2) (x -8y)(x -y) (3) (x+y)(x 2-xy+y 2)
通过习题练习,你觉得应该注意哪些问题?
【反馈提升】
1.计算:① ()()y x y x 73+- ②()()y x y x 2352-+
2.先化简,再求值:()()()()y x y x y x y x 4232---+-其中:1-=x ;2=y
【课堂小结】
对于本节课,你有哪些收获?或者你还有什么困惑?大胆与大家进行分享
【作业】课本102页练习1,2。
多项式乘以多项式导学案[1]
![多项式乘以多项式导学案[1]](https://img.taocdn.com/s3/m/029d93f4524de518964b7d5b.png)
14.1.4多项式乘以多项式学习目标:1、探索并理解多项式与多项式相乘的法则,并会熟练运用它们进行运算.一、知识链接1、利用法则进行计算:(1)xy x 422⋅= ; (2)322)3(x x -=(3)()()2232-⋅-a a = (4)212()2x x -= (5)(-2a) (2a ²b+3a ²-b ²)=二、新知初探1.活动:为了扩大绿地面积,要把街心花园的一块长a 米,宽m 米的长方形绿地增长b 米,加宽n 米,求扩地以后的面积是多少?思考:可以用几种方法表示扩大后绿地的面积?不同的表示方法之间有什么关系?方法1:这块花园扩地后长 米,宽 米,故这块绿地的面积为 米2.方法2:这块花园现在是由 小块组成,它们的面积分别为: 米2、 米2、 __ 米2,故这块绿地的面积为 米2.结论:由方法1和方法2可得出等式2.问题:请认真观察上述等式的特征,讨论并回答如何用文字语言叙述多项式的乘法法则?多项式与多项式相乘,用字母表示为:三、典例分析(1)(x +2)(x -3) (2)(3x -1)(2x +1) (3)(3x 1)(x 2) (x 8y)(x y ++--(4)(x -3y )(x +7y ) (5)(2x -5y )(3x -2y )四、巩固练习1、下列计算对不对?如果不对,请改正。
(1)(x -1)(x+2)=x 2-3x -2 ( ) (2)(a -3)(a+2)=a 2-a+6( )改正:(3)(x+4)(2x -5)=x 2-20x -1 ( )(4)(x -3)(x -1)=x 2-4x+3( )改正:2、计算:(1) (a+3b)(a-3b) (2)(5m+ 2)(-4m 2- 3) (3) (-4x -y )(-5x +2y )(4)22(2)(23)x y x xy y -+- (5) (a-1)(a-1) (6)(2a -3b )(2a +3b )(7) (x-y)(x 2+xy+y 2) (8)(x+1)(x 2-x+1)-(x-1) (x 2+x+1)3、解答题(1) 先化简,再求值(x-2)(x-3)+2(x+6)(x-5)-3(x 2-7x+13),其中x=2.(2)若b x x x a x +-=+⋅+5)2()(2,求a ,b 的值。
精品学案:1.4.3 多项式乘以多项式

初中数学北师大版精品学案系列
一、情境引入
查找疫情初期火神山医院的建设资料,谈谈你对中国抗击疫情的看法:
二、探究新知
抗击疫情期间,火神山医院根据需求要进行扩建.假设火神山医院原占地是一个长和宽分别为m,n的长方形,随着疫情的发展,建筑师将它的长和宽分别增加a,b,扩建后医院的面积可以怎样表示?你有几种表示方法呢?
提示:分别看成一个长方形,两个长方形,四个长方形.你发现了什么?
经历了上面的探索过程,你能总结出多项式与多项式相乘的法则吗?
多项式乘以多项式法则:
多项式与多项式相乘,先用一个多项式的_____________乘以另一个多项式的_________,再把所得的积______.
三、典型例题
例1 计算:
x x x y x y
--+-
(1)(1)(0.6)(2)(2)()
例2 计算:
+---
(1)(2)(3)(2)(2)()
x x x y x y。
8.4 多项式乘以多项式 学案
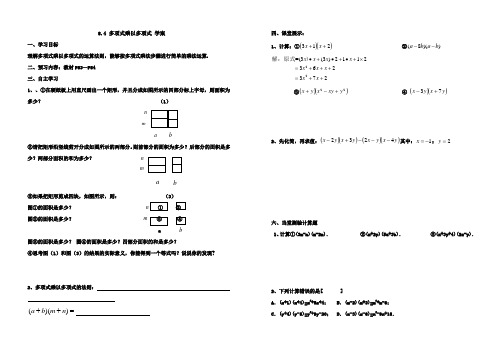
8.4 多项式乘以多项式学案一、学习目标理解多项式乘以多项式的运算法则,能够按多项式乘法步骤进行简单的乘法运算.二、预习内容:教材P83—P84三、自主学习1、、①在硬纸板上用直尺画出一个矩形,并且分成如图所示的四部分标上字母,则面积为多少?(1)nma b②请把矩形沿竖线剪开分成如图所示的两部分。
则前部分的面积为多少?后部分的面积是多少?两部分面积的和为多少?nma b③如果把矩形剪成四块,如图所示,则:(3)图①的面积是多少?图②的面积是多少?ma b图③的面积是多少?图④的面积是多少?四部分面积的和是多少?④思考图(1)和图(3)的结果的实际意义,你能得到一个等式吗?说说你的发现?2、多项式乘以多项式的法则:=++))((nmba四、课堂展示:1、计算:①()()213++xx②(8)()a b a b--22=(3(3)2112362372x x x xx x xx x∙+∙+∙+⨯=+++=++解:原式)③()()22yxyxyx+-+④()()yxyx73+-2、先化简,再求值:()()()()yxyxyxyx4232---+-其中:1-=x;2=y六、当堂测验计算题1、计算①(3m-n)(m-2n).②(x+2y)(5a+3b).③(x+3y+4)(2x-y).2、下列计算错误的是[ ]A.(x+1)(x+4)=x2+5x+4; B.(m-2)(m+3)=m2+m-6;C.(y+4)(y-5)=y2+9y-20; D.(x-3)(x-6)=x2-9x+18.。
§1.4-3《多项式乘以多项式》学案

§1.4-3《多项式乘以多项式》学案设计者:商长芹一. 准备引入、出示目标(1分钟)1、经历探索多项式乘以多项式运算法则的过程,能借助图形解释多项式乘以多项式的法则,发展几何直观。
2、了解多项式乘以多项式的运算性质,并能解决一些实际问题。
二、自学指导、自主学习(10分钟)1、复习巩固单项式与多项式相乘,就是根据______________________________________.2.计算:(1)________)3(3=-xy (2)________)23(23=-y x (3)________)102(47=⨯- (4)_________)()(2=-⋅-x x(5)______)(532=⋅-a a (6)______)()2(2532=-⋅-bc a b a3、计算:(1))132(22---x x x (2))6)(1253221(xy y x --+-4、探究活动(1)、独立思考,解决问题:如图,计算此长方形的面积有几种方法?如何计算.你从计算中发现了什么?方法一:__________________________________.方法二:__________________________________.方法三:__________________________________。
(2)、大胆尝试)2)(2(n m n m -+ )3)(52(-+n n总结:实际上,上面都进行的是多项式与多项式相乘,那么如何进行运算呢 多项式与多项式相乘,_____________________________________________ _______________________ ________________________.5、例题讲解)6.0)(1)(1(x x -- ))(2)(2(y x y x -+ 2)2)(3(y x -2)52)(4(+-x(5)(2)(3)(1)(2)x y x y ++-+- (6))2)(1(2)1(2+--+a a a a三.学情考查、合作探究(10分钟)1、计算下列各题:(1))3)(2(++x x (2))1)(4(+-a a (3))31)(21(+-y y(4))436)(42(-+x x (5))3)(3(n m n m -+ (6)2)2(+x四.交流评价、概括提升(8分钟)(统一答案、自主更正、生生互评、师生互评。
《多项式乘以多项式》教案

《多项式乘以多项式》教案一、教学目标1. 让学生理解多项式乘以多项式的概念和意义。
2. 引导学生掌握多项式乘以多项式的计算方法和步骤。
3. 培养学生的数学思维能力和解决问题的能力。
二、教学内容1. 多项式乘以多项式的概念和意义。
2. 多项式乘以多项式的计算方法和步骤。
3. 多项式乘以多项式的应用举例。
三、教学重点与难点1. 教学重点:多项式乘以多项式的计算方法和步骤。
2. 教学难点:理解多项式乘以多项式的概念和意义。
四、教学方法1. 采用直观演示法,通过示例让学生直观地理解多项式乘以多项式的概念和意义。
2. 采用讲授法,讲解多项式乘以多项式的计算方法和步骤。
3. 采用练习法,让学生通过练习巩固所学知识。
五、教学过程1. 导入:通过复习单项式乘以多项式的知识,引出多项式乘以多项式的概念。
2. 新课讲解:讲解多项式乘以多项式的计算方法和步骤,示例演示。
3. 课堂练习:布置一些简单的多项式乘以多项式的题目,让学生独立完成。
4. 解答疑问:针对学生在练习中遇到的问题,进行讲解和解答。
5. 课堂小结:总结本节课所学内容,强调多项式乘以多项式的概念和意义。
6. 作业布置:布置一些多项式乘以多项式的题目,让学生课后巩固。
六、教学反思1. 教师对自己在本节课的教学过程进行反思,分析教学方法的适用性、学生的学习效果等。
2. 思考如何改进教学方法,以提高学生的学习兴趣和参与度。
3. 对学生学习情况进行分析,找出学生的优点和不足,为下一步教学提供参考。
七、课后作业1. 布置一些多项式乘以多项式的题目,让学生课后巩固所学知识。
2. 鼓励学生进行自主学习,尝试解决遇到的困难。
3. 提醒学生在完成作业时注意计算准确性和书写规范。
八、拓展与延伸1. 引导学生思考多项式乘以多项式在实际生活中的应用。
2. 介绍一些与多项式乘以多项式相关的数学知识,如多项式除法、因式分解等。
3. 鼓励学生进行探索学习,提高学生的数学素养。
九、评价与反馈1. 对学生在课堂表现、作业完成情况进行评价,及时给予反馈。
人教版八年级数学上册学案多项式乘多项式导学案(3)

14.1.4多项式乘以多项式【学习目标】⒈让学生理解多项式乘以多项式的运算法则,能够按多项式乘法步骤进行简单的乘法运算.⒉经历探索多项式与多项式相乘的运算法则的推理过程,培养学生计算能力.⒊发展有条理的思考,逐步形成主动探索的习惯.学习重点:多项式与多项式的乘法法则的理解及应用.学习难点:多项式与多项式的乘法法则的应用.学习过程:一.预习与新知:⑴叙述单项式乘以单项式的法则?⑵计算;①()12+-x x x ②()y x xy xy 225351+⎪⎭⎫ ⎝⎛-⑶在硬纸板上用直尺画出一个矩形,并且分成如图所示的四部分标上字母,则面积为多少? n a ①m b⑷请把矩形沿竖线剪开分成如图所示的两部分。
则前部分的面积为多少?后部分的面积是多少?两部分面积的和为多少?n a ②b⑸观察图①和图②的结果你能得到一个等式吗?说说你的发现?⑹如果把矩形剪成四块,如图所示,则:图①的面积是多少? n ① ②图②的面积是多少?图③的面积是多少? a ③ ④图④的面积是多少? m b四部分面积的和是多少?观察上面的计算结果:原图形的面积;第一次分割后面积之和;第二次分割后面积之和相等吗?用式子表示?你能发现什么规律吗?试一试 (观察等式左边是什么形式?观察等式的右边有什么特点?)多项式乘以多项式的法则:二.课堂展示:⑴计算;①()()32-+x x ②()()1213+-x x注意:应用多项式的乘法法则时应注意;211x xx x ==⋅+;还应注意符号.⑵计算:① ()()y x y x 73+- ②()()y x y x 2352-+⑶先化简,再求值:()()()()y x y x y x y x 4232---+-其中:1-=x ;2=y三.随堂练习:1、课本练习第1,2题2、课本习题14.1第5题3、计算()()1225-+x x 的结果是( ) (A )2102-x (B )2102--x x (C )24102-+x x (D )25102--x x4、一下等式中正确的是( )(A )()()32232y xy x y x y x +-=-- (B )()()24412121x x x x +-=-+(C )()()22943232b a b a b a -=+- (D )()()2293232y xy x y x y x +-=-+5、先化简,再求值:()()()()22225533b a b a b a b a -++-++-其中8-=a ;6-=b ;四.小结与反思。
七年级数学下册《多项式乘以多项式》优秀教学案例

2.合作交流:组织学生进行小组讨论,分享解题思路和方法,培养学生的合作意识和团队精神。
3.翻转课堂:将课堂还给学生,让学生成为学习的主体,提高学生自主学习、探究学习的能力。
4.分层教学:针对不同层次的学生,设计不同难度的练习题,使每位学生都能在课堂上得到有效的提升。
3.各小组派代表进行成果分享,其他小组可提出疑问或补充,教师适时给予指导和评价。
(四)总结归纳
1.教师引导学生回顾本节课所学内容,总结多项式乘法的运算法则和技巧。
2.学生分享自己的学习心得和收获,教师给予肯定和鼓励。
3.强调多项式乘法在实际问题中的应用,激发学生学习数学的兴趣。
(五)作业小结
1.设计具有层次性的作业,包括基础题、提高题和拓展题,以满足不同层次学生的需求。
1.自我反思:鼓励学生在解题过程中进行自我反思,分析自己的错误原因,总结经验教训。
2.相互评价:组织学生进行相互评价,让学生从他人的解题过程中学习到新的思路和方法。
3.教师评价:教师针对学生的课堂表现和作业完成情况进行评价,肯定学生的优点,指出不足之处,并提出改进建议。
四、教学内容与过程
(一)导入新课
(三)情感态度与价值观
1.培养学生对数学的兴趣和热情,使其认识到数学在生活中的广泛应用和实用价值。
2.培养学生勇于探索、善于思考的品质,增强学生面对困难的勇气和信心。
3.培养学生良好的学习习惯,使其形成严谨、认真的学习态度。
4.培养学生的集体荣誉感,使其在合作交流中体验到团队的力量,提高团队协作能力。
二、教学目标
(一)知识与技能
1.理解多项式乘以多项式的概念,明确乘法运算的顺序和法则。
多项式与多项式相乘 精品导学案及练习附解析

第2课时 多项式与多项式相乘学习目标1.理解并经历探索多项式乘以多项式法则的过程.2.熟练应用多项式乘以多项式的法则解决问题3.培养独立思考、主动探索的习惯和初步解决问题的愿望及能力.学习重点:多项式乘以多项式的运算法则与应用.学习难点:多项式乘以多项式法则的得出与理解.学习过程:一、温故知新,导入新课:计算:⑴(-8a 2b )(-3a) ⑵2x·(2xy 2-3xy)运用的知识与方法:二、问题情境,探索发现问题一:1.如下图,某地区退耕还林,将一块长m 米、宽a 米的长方形林区的长、宽分别增加n 米和b 米.求这块林区现在的面积S.(比一比看谁的方法多,运算快)因为它们表示的都是同一块绿地的面积,按①②④可得到的结论: 按①③④可得到的结论:2.蕴含的代数、几何意义分别是:3.归纳概括, 加深理解:①多项式与多项式相乘的法则:多项式与多项式相乘, ②用字母表示为: .三、理解运用 总结方法问题二:1.计算⑴(x+2)(x-3) ⑵(3x-1)(2x+1) ⑶(x+2)(x+2y-1)a b四、反馈矫正,注重参与问题三:(下面的计算是否正确?如有错误,请改正)⑴(3x+1)(x-2) ⑵(3x-1)(2x-1) ⑶(x+2)(x-5)=3x 2-6x-2 =6x 2-3x-2x+1 =x 2+5x+2x+10 =x 2+7x+10归纳多项式与多项式相乘注意事项:① ② ③五、综合运用 拓展提高问题4:(中考链接)有一道题计算(2x +3)(3x +2)-6x (x +3)+5x +16的值,其中x =-666 ,小明把x =-666错抄成x =666,但他的结果也正确,这是为什么?问题5:(联系生活)有一个长方形的长是2x cm,宽比长少4cm,若将长方形的长和宽都增加3cm,面积增加多少? 若x =2 cm,则增加的面积是多少?六、实践运用 巩固新知1.判断下列各题是否正确,并说出理由 .(1).2(31)(2)36x x x x x +-=-+ ( ) (2).2(2)(5)710x x x x +-=++ ( )(3).22(25)(32)641510a b a b a ab ba b +-=-+- ( )2. 选择题:下列计算结果为 x 2-5x -6的是( )A.(x -2)(x -3)B. (x -6)(x +1)C. (x -2)(x +3)D. (x +2)(x -3)3.如果ax 2+bx +c =(2x +1)(x -2),则a = b = c =4.一个三角形底边长是(5m -4n),底边上的高是(2m +3n) ,则这个三角形的面积是5. 王老汉承包的长方形鱼塘,原长 2x 米,宽 x 米,现在要把四周向外扩展 y 米,问这个鱼塘的面积增加多少?七、总结反思第2课时线段的垂直平分线的有关作图一、学习目标1、会依据轴对称的性质找出两个图形成轴对称及轴对称图形的对称轴;2、掌握作出轴对称图形的对称轴的方法,即线段垂直平分线的尺规作图。
11.4多项式乘以多项式导学案(无答案)

11.4多项式乘以多项式一、导入激学为了扩大绿地面积,要把街心花园的一块长a米,宽m米的长方形绿地增长b米,加宽n米,求扩地以后的面积是多少?用几种方法表示扩大后绿地的面积?不同的表示方法之间有什么关系?二、导标引学学习目标:1、探究多项式相乘法则的过程,发展学生的逻辑思维能力和表达能力。
2、会运用多项式的乘法法则进行简单的多项式乘法法则。
3、结合所学知识,使学生掌握将复杂问题简单化的转化思想,发展数学能力。
学习重难点:多项式乘以多项式的法则的正确应用。
三、学习过程(一)导预疑学利用8分钟,自学课本,按预习要求完成下列问题,小组讨论后找出疑难问题。
1.预学核心问题:(1)多项式乘多项式的几何推导过程?(2)能用单项式乘多项式解释多项式乘多项式运算法则。
2.预学检测(1) (2)(3)(4)3.预学评价质疑通过预学,你学会了什么?还有什么疑问没有解决呢?请把它们写下来小组交流。
(二)导问互学问题一:从小组提出的问题中概括出来的核心问题是:师生设计的活动是:问题二:探究多项式乘以多项式的推导过程活动1:练一练(a+b )(m+n)==合作探究:多项式与多项式相乘的步骤:先 , 再 活动2:考一考(1) )3)(3(n m n m -+ (2))2)(1()3)(2(-+-++y x y x解决问题评价:你在解决问题时在哪里遇到了困难?此类问题今后怎么处理?(三)导根典学先化简再求值:)1)(12()2)(1()32)(1(222+----+--+a a a a a a a ,其中1-=a知识之根探索:1. 利用多项式乘多项式法则进行运算时,一定不能漏乘,为了做到不重不漏,可以在草稿纸上用箭头标注求解,如计算时根据线型指示可以得到. 2.要注意按多项式乘多项式法则展开后,要及时找到同类项并合并。
3.整式的混合运算要注意运算顺序。
(四)导标达学1、计算(1))3)(3(y x y x --+- (2))65)(52(2+-+x x x(把(a+b )看作一个整体,与多项式(m+n )相乘,用单项式乘多项式的法则展开) (再运用单项式乘多项式的法则继续运算)2、计算 2)2(+x +2)1)(2(3)2)(2(-+--+x x x x3、先化简,再求值)32)(12()1)(1(3)3)(2(-+--+++-x x x x x x ,其中x=544、已知)1)((2+++x n mx x 的结果中不含2x 项和x 项,求m ,n 的值.5、若求m ,n 的值.6、甲乙两人共同解一道题:)3)(2(b x a x ++,由于粗心,甲抄错了第一个多项式中a 前面的符号,得到的结果是101162-+x x ;乙漏抄了第二个多项式中x 的系数,得到的结果是10922+-x x .①求b a ,的值 ②计算出正确的结果7、对于任意自然数n ,代数式)2)(3()7(---+n n n n 的值都能被6整除,这个命题成立吗?请说明理由.反馈评价:请交流你出现的问题,并把它们进行更正。
34多项式乘以多项式学案.docx

3. 4多项式乘以多项式【目标导航】理解多项式乘以多项式的运算法则,并能熟练进行多项式乘法运算.【问题探究】1 •式子p(a+b)=pa+pb中的”,口J以是单项式,也口J以是多项式。
如果p=m+n,那么p(a +b)就成了(m+n)(a+b)o你会计算这个式子吗?你是怎样计算的?2.你能用图形验证你算出的式子吗?某地区在退耕述林期间,有一块原长加米、宽a米的长方形林区增长了斤米,加宽了b米。
请你表示这块林区现在的面积。
问题:(1)如何表示扩大后的林区的而积? ______________________________(2)请用两种方法表示这块绿地现在的面积。
3.你能类比单-项式与多项式相乘的法则,叙述多项式与多项式相乘的法则吗?多项式与多项式相乘的法则:____________________________________________尝试运用例1计算:(1)(x+2y)(5d+3b);(2) (2兀一3)(兀+4);⑶(x-3y)U+7y); (4) (2兀+5),)(3兀一2刃。
探究:1 •两个多项式相乘,不先计算能知道结果中(合并同类项前)有儿项吗?2.在计算屮怎样才能不重不漏?3.这个法则,对于三个或三个以上的多项式相乘,是否适用?若适用.应怎样计算?随堂练习1:计算:(1)(3x+l)(x・2) (2) (x+y)2(3)(x-8y)(x-y);(4) (x+y)(x2~xy+y2).例题2:化简也血加一刃)一(2a-b^b-4a2)f这个代数式的值与a,b的取值有关吗?随堂练习2:1.化简:3x(r2 +2x + 7)-(r2 +7)(3x-5)2>化简求值-双/+*-1),其抵=专£例题3:解方程3x(x + 2)-4(x2 +8)=(x+lXl-x)随堂练习3:解方程(1)娅+3)-&一5)(工+3)=h+i(2) (x-3)(x-2)+18 = (x+9)(x+1)例题4:.如果(x2+bx+8)(x「3x+c)的乘积中不含x?和X?的项,求b、c的值。
多项式乘以多项式-导学案可修改全文

可编辑修改精选全文完整版课题:多项式乘以多项式学习目标:⒈理解多项式乘以多项式的法则.⒉通过导图中的问题理解多项式与多项式相乘的结果.⒊能够按多项式乘法步骤进行简单的多项式乘法的运算,达到熟练地进行多项式的乘法运算的目的. 学习过程自主探究:阅读课本P100练习以下内容至P101例题6之前,解决以下问题:为了扩大绿地面积,要把街心花园的一块长a 米,宽m 米的长方形绿地增长b 米,加宽n 米,你能用几种方法表示扩大后的绿地面积吗?不同表示方法之间有什么关系?解: 方法1:这块花园现在长为 米,宽为 米,因而这块绿地的面积为: 。
方法2:这块花园现在由四小块组成,他们的面积分别是因而这块绿地的面积为: 。
结论:由方法1和方法2可得出等式 归纳多项式乘以多项式的法则多项式与多项式相乘, . 例题学习:阅读课本例题6,并仿照例题计算以下题目。
⒈计算⑴(2)(3)x x +- ⑵(31)(21)x x -+⑶(3)(7)x y x y -+ ⑷2)2(y x -自我检测1.计算:⑴)3)(12(++x x ⑵)3)(2(n m n m -+⑶2)1(-a ⑷)4)(12(2--x x⒉计算探究⑴)3)(2(++x x ⑵)1)(4(+-x x⑶)2)(4(-+y y ⑷)3)(5(--y y由上面计算的结果找规律,观察右图,填空()()()++=++x q x p x 2))((当堂作业:必做题⑴)2)(1(++n n n ⑵)168()4(2--+x x⑶)5)(1(2)13)(2(82-+-+--x x x x x ⑷2)23()3)(12(---+x x x(5))1)(12()2)(1()32)(1(222+----+--+a a a a a a a ,其中1-=a选做题⑴若))((362b x a x mx x ++=++,且m b a ,,为整数,则m 的值可能取多少个?⑵若)32)((22--++x x q px x 的展开项中不含2x 和3x 的项,求p 和q 的值.⑶对于任意自然数n ,代数式)2)(3()7(---+n n n n 的值都能被6整除,这个命题成立吗?请说明理由⑷甲乙两人共同解一道题:)3)(2(b x a x ++,由于粗心,甲抄错了第一个多项式中a 前面的符号,得到的结果是101162-+x x ;乙漏抄了第二个多项式中x 的系数,得到的结果是10922+-x x .①求b a ,的值 ②计算出正确的结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三、巩固训练
1.计算(2x-1)(5x+2)的结果是()
A.10x2-2B.10x2-5x-2
C.10x2+4x-2D.10x2-x-2
2.计算:
(1) (2x-y)(x+y)(2)(x-2y)(x2+2xy+4y2)
7.已知|2a+3b-7|+(a-9b+7)2=0,试求( a2- ab+b2)( a+b)的值.
8.解方程(3x-2)(2x-3)=(6x+5)(x-1)-1
9.求出使(3x+2)(3x-4)>9(x-2)(x+3)成立的非负整数解.
重点难点:多项式与多项式相乘的运算法则及应用。
一、自主学习
(一)新知探究
看图填空:
(1)大长方形的长是________,宽是________,面积等于_____________.
(2)图中四个小长方形的面积分别是__________、________、_______、______,则大长方形的面积等于____________________.
学习内容:14.1.4多项式乘以多项式
注意:多项式乘以多项式的结果必须是最简形式;运算中不要漏乘某项;多项式中每一项都包含它前面的符号。
活动2 观察下列各式,小组讨论回答问题:
(1)(a+2)(a+3)=a2+5a+6 (2)(a+2)(a-3)=a2-a-6
(3)(a-2)(a+3)=a2+a-6 (4)(a-2)(a-3)=a2-5a+6
(3)由此可得到等式_____________________.
总结法则:多项式与多项式相乘,先用_____________________________,再把________________.
二、小组学习
活动1 学生独立完成
(1)(x+1)(x2-x+1)(2)(a-b)(a2+ab+b2)
一、选择题
二、填空题
3.已知a-b=5,ab=3,则(a+1)(b-1)的值为________.
4.已知(4x-7y)(5x-2y)=M-43xy+14y2,则M=________.
三、计算
5.(x3-2)(x3+x2+ 3)(-5a2b3+1﹚·(-4b2c +1)
6.已知x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值。
1.计算(3x-1)(4x+2)的结果是()
A.12x2-2x-2B.12x2-10x-2
C.12x2+2x-2D.12x2+10x-2
2.若一个长方体的长、宽、高分别是3x-4,2x-1和x,则它的体积是()
A.6x3-5x2+4xB.6x3-12+x+4
四、拓展提升
3.先化简,再求值:(x-2y)(x+3y)-(2x-y)(x-4y),其中:x=-1,y=2
自学疑惑
学习目标
1.知识与能力:知道多项式乘以多项式的法则
2.过程与方法:让学生主动参与到探索过程中去,逐步形成独立思考,培养学生转化的数学思想
3.情感态度:通过分组探究,培养学生合作交流的意识,提高学生勇于探究数学的品质.
