遗传算法实验六演示文稿
遗传算法实验报告

遗传算法实验报告专业:自动化:张俊峰学号:13351067 摘要:遗传算法,是基于达尔文进化理论发展起来的一种应用广泛、高效的随机搜索与优化方法。
本实验利用遗传算法来实现求函数最大值的优化问题,其中的步骤包括初始化群体、个体评价、选择运算、交叉运算、变异运算、终止条件判断。
该算法具有覆盖面大、减少进入局部最优解的风险、自主性等特点。
此外,遗传算法不是采用确定性原则而是采用概率的变迁规则来指导搜索方向,具有动态自适应的优点。
关键词:串集最优化评估迭代变异一:实验目的熟悉和掌握遗传算法的运行机制和求解的基本方法。
遗传算法是一种基于空间搜索的算法,它通过自然选择、遗传、变异等操作以及达尔文的适者生存的理论,模拟自然进化过程来寻找所求问题的答案。
其求解过程是个最优化的过程。
一般遗传算法的主要步骤如下:(1)随机产生一个确定长度的特征字符串组成的初始种群。
〔2〕对该字符春种群迭代地执行下面的步骤a和步骤b,直到满足停止准则为止:a计算种群中每个个体字符串的适应值;b应用复制、交叉和变异等遗传算子产生下一代种群。
〔3〕把在后代中表现的最好的个体字符串指定为遗传算法的执行结果,即为问题的一个解。
二:实验要求已知函数y=f〔x1,x2,x3,x4〕=1/(x12+x22+x32+x42+1),其中-5≤x1,x2,x3,x4≤5,用遗传算法求y的最大值。
三:实验环境操作系统:Microsoft Windows 7软件:Microsoft Visual studio 2010四:实验原理与步骤1、遗传算法的思想生物的进化是以集团为主体的。
与此相对应,遗传算法的运算对象是由M个个体所组成的集合,称为群体。
与生物一代一代的自然进化过程相类似,遗传算法的运算过程也是一个反复迭代过程,第t代群体极为P〔t〕,进过一代遗传和进化后,得到第t+1代群体,他们也是由多个个体组成的集合,记做P〔t+1〕。
这个群体不断地经过遗传和进化操作,并且每次都按照有优胜劣汰的规则将适应度较高的个体更多地遗传到下一代,这样最终在群体中将会得到一个优良的个体X,它所对应的表现性X将到达或接近于问题的最优解。
实验六:遗传算法求解TSP问题实验2篇

实验六:遗传算法求解TSP问题实验2篇第一篇:遗传算法的原理与实现1. 引言旅行商问题(TSP问题)是一个典型的组合优化问题,它要求在给定一组城市和每对城市之间的距离后,找到一条路径,使得旅行商能够在所有城市中恰好访问一次并回到起点,并且总旅行距离最短。
遗传算法作为一种生物启发式算法,在解决TSP问题中具有一定的优势。
本实验将运用遗传算法求解TSP问题,以此来探讨和研究遗传算法在优化问题上的应用。
2. 遗传算法的基本原理遗传算法是模拟自然界生物进化过程的一种优化算法。
其基本原理可以概括为:选择、交叉和变异。
(1)选择:根据问题的目标函数,以适应度函数来评估个体的优劣程度,并按照适应度值进行选择,优秀的个体被保留下来用于下一代。
(2)交叉:从选出的个体中随机选择两个个体,进行基因的交换,以产生新的个体。
交叉算子的选择及实现方式会对算法效果产生很大的影响。
(3)变异:对新生成的个体进行基因的变异操作,以保证算法的搜索能够足够广泛、全面。
通过选择、交叉和变异操作,不断迭代生成新一代的个体,遗传算法能够逐步优化解,并最终找到问题的全局最优解。
3. 实验设计与实施(1)问题定义:给定一组城市和每对城市之间的距离数据,要求找到一条路径,访问所有城市一次并回到起点,使得旅行距离最短。
(2)数据集准备:选择适当规模的城市数据集,包括城市坐标和每对城市之间的距离,用于验证遗传算法的性能。
(3)遗传算法的实现:根据遗传算法的基本原理,设计相应的选择、交叉和变异操作,确定适应度函数的定义,以及选择和优化参数的设置。
(4)实验流程:a. 初始化种群:随机生成初始种群,每个个体表示一种解(路径)。
b. 计算适应度:根据适应度函数,计算每个个体的适应度值。
c. 选择操作:根据适应度值选择一定数量的个体,作为下一代的父代。
d. 交叉操作:对父代进行交叉操作,生成新的个体。
e. 变异操作:对新生成的个体进行变异操作,以增加搜索的多样性。
实验六:遗传算法求解TSP问题实验3篇

实验六:遗传算法求解TSP问题实验3篇以下是关于遗传算法求解TSP问题的实验报告,分为三个部分,总计超过3000字。
一、实验背景与原理1.1 实验背景旅行商问题(Traveling Salesman Problem,TSP)是组合优化中的经典问题。
给定一组城市和每两个城市之间的距离,求解访问每个城市一次并返回出发城市的最短路径。
TSP 问题具有很高的研究价值,广泛应用于物流、交通运输、路径规划等领域。
1.2 遗传算法原理遗传算法(Genetic Algorithm,GA)是一种模拟自然选择和遗传机制的搜索算法。
它通过选择、交叉和变异操作生成新一代解,逐步优化问题的解。
遗传算法具有全局搜索能力强、适用于多种优化问题等优点。
二、实验设计与实现2.1 实验设计本实验使用遗传算法求解TSP问题,主要包括以下步骤:(1)初始化种群:随机生成一定数量的个体(路径),每个个体代表一条访问城市的路径。
(2)计算适应度:根据路径长度计算每个个体的适应度,适应度越高,路径越短。
(3)选择操作:根据适应度选择优秀的个体进入下一代。
(4)交叉操作:随机选择两个个体进行交叉,生成新的个体。
(5)变异操作:对交叉后的个体进行变异,增加解的多样性。
(6)更新种群:将新生成的个体替换掉上一代适应度较低的个体。
(7)迭代:重复步骤(2)至(6),直至满足终止条件。
2.2 实验实现本实验使用Python语言实现遗传算法求解TSP问题。
以下为实现过程中的关键代码:(1)初始化种群```pythondef initialize_population(city_num, population_size): population = []for _ in range(population_size):individual = list(range(city_num))random.shuffle(individual)population.append(individual)return population```(2)计算适应度```pythondef calculate_fitness(population, distance_matrix): fitness = []for individual in population:path_length =sum([distance_matrix[individual[i]][individual[i+1]] for i in range(len(individual) 1)])fitness.append(1 / path_length)return fitness```(3)选择操作```pythondef selection(population, fitness, population_size): selected_population = []fitness_sum = sum(fitness)fitness_probability = [f / fitness_sum for f in fitness]for _ in range(population_size):individual = random.choices(population, fitness_probability)[0]selected_population.append(individual)return selected_population```(4)交叉操作```pythondef crossover(parent1, parent2):index1 = random.randint(0, len(parent1) 2)index2 = random.randint(index1 + 1, len(parent1) 1)child1 = parent1[:index1] +parent2[index1:index2] + parent1[index2:]child2 = parent2[:index1] +parent1[index1:index2] + parent2[index2:]return child1, child2```(5)变异操作```pythondef mutation(individual, mutation_rate):for i in range(len(individual)):if random.random() < mutation_rate:j = random.randint(0, len(individual) 1) individual[i], individual[j] = individual[j], individual[i]return individual```(6)更新种群```pythondef update_population(parent_population, child_population, fitness):fitness_sum = sum(fitness)fitness_probability = [f / fitness_sum for f in fitness]new_population =random.choices(parent_population + child_population, fitness_probability, k=len(parent_population)) return new_population```(7)迭代```pythondef genetic_algorithm(city_num, population_size, crossover_rate, mutation_rate, max_iterations): distance_matrix =create_distance_matrix(city_num)population = initialize_population(city_num, population_size)for _ in range(max_iterations):fitness = calculate_fitness(population, distance_matrix)selected_population = selection(population, fitness, population_size)parent_population = []child_population = []for i in range(0, population_size, 2):parent1, parent2 = selected_population[i], selected_population[i+1]child1, child2 = crossover(parent1, parent2)child1 = mutation(child1, mutation_rate)child2 = mutation(child2, mutation_rate)parent_population.extend([parent1, parent2]) child_population.extend([child1, child2])population =update_population(parent_population, child_population, fitness)best_individual =population[fitness.index(max(fitness))]best_path_length =sum([distance_matrix[best_individual[i]][best_individual[i +1]] for i in range(len(best_individual) 1)])return best_individual, best_path_length```三、实验结果与分析3.1 实验结果本实验选取了10个城市进行测试,遗传算法参数设置如下:种群大小:50交叉率:0.8变异率:0.1最大迭代次数:100实验得到的最佳路径长度为:1953.53.2 实验分析(1)参数设置对算法性能的影响种群大小:种群大小会影响算法的搜索能力和收敛速度。
遗传算法课件PPT ppt课件 ppt课件

2020/4/17
33
五.GA的各种变形(32)
I. 截断选择: 选择最好的前T个个体,让每一个有1/T的 选择概率,平均得到NP/T个繁殖机会。
例:NP=100,T=50 即100名学生,成绩前50名的选出。每人的选
择概率为1/50,有平均2个机会。 缺点:这种方法将花费较多的时间在适应值的
排序上。
c. k的取值: 0 M , k , k1r r0.9,0.99,9
调节 M和 r,从而来调节 k
2020/4/17
28
五.GA的各种变形(27)
d.引入 的k 目的:
调k 节选择压力,即好坏个体选择概率的
差,使广域搜索范围宽保持种群的多样性,而
局域搜索细保持收敛性。如下图表示:
k
2020/4/17
2020/4/17
34
五.GA的各种变形(33)
II. 顺序选择: a. 步骤: ⑴ 从好到坏排序所有个体 ⑵ 定义最好个体的选择概率为 q,则第 j个个
体的选择概率为:
pjq1qj1
2020/4/17
35
五.GA的各种变形(34)
⑶ 由于 N j1P q1qj1 N P q11 1q1
2020/4/17
1
遗传算法
• 五.遗传算法的各种变形 • 5.1其它编码方法 • 5.2遗传运算中的问题 • 5.3适值函数的标定(Scaling) • 5.4选择策略 • 5.5停止准则 • 六. 应用
2020/4/17
2
五.GA的各种变形(1)
5.1 其它编码方法
① 顺序编码:用1到N的自然数的不同顺序来 编码,此种编码不允许重复,即 xi 1,2,,N 且 xi x j,又称自然数编码。 该法适用范围很广:指派问题、旅行商问题和
人工智能遗传算法实验报告

人工智能实验报告学号:姓名:实验名称:遗传算法实验日期:2016.1.5【实验名称】遗传算法【实验目的】掌握遗传算法的基本原理,熟悉遗传算法的运行机制,学会用遗传算法来求解问题。
【实验原理】遗传算法( Genetic Algorithm )是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
遗传算法是从代表问题可能潜在的解集的一个种群开始的,而一个种群则由经过基因编码的一定数目的个体组成。
每个个体实际上是染色体带有特征的实体。
在一开始需要实现从表现型到基因型的映射即编码工作。
由于仿照基因编码的工作很复杂,我们往往进行简化,如二进制编码,初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度大小选择个体,并借助于自然遗传学的遗传算子进行组合交叉和变异,产生出代表新的解集的种群。
这个过程将导致种群像自然进化一样的后生代种群比前代更加适应于环境,末代种群中的最优个体经过解码,可以作为问题近似最优解。
遗传算法程度流程图为:【实验名称】遗传算法【实验目的】掌握遗传算法的基本原理,熟悉遗传算法的运行机制,学会用遗传算法来求解问题。
【实验原理】遗传算法( Genetic Algorithm )是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
遗传算法是从代表问题可能潜在的解集的一个种群开始的,而一个种群则由经过基因编码的一定数目的个体组成。
每个个体实际上是染色体带有特征的实体。
在一开始需要实现从表现型到基因型的映射即编码工作。
由于仿照基因编码的工作很复杂,我们往往进行简化,如二进制编码,初代种群产生之后,按照适者生存和优胜劣汰的原理,逐代演化产生出越来越好的近似解,在每一代,根据问题域中个体的适应度大小选择个体,并借助于自然遗传学的遗传算子进行组合交叉和变异,产生出代表新的解集的种群。
遗传算法求函数最大值实验报告

遗传算法求函数最大值实验报告遗传算法是一种模拟自然界进化过程的优化算法,它通过模拟生物进化过程中的遗传、交叉和变异等机制,逐步优化解空间中的个体,以找到问题的最优解。
在本次实验中,我们利用遗传算法来求解一个函数的最大值。
下面我们将详细介绍实验的过程和结果。
首先,我们选择了一个简单的函数作为实验对象,即f(x) = x^2,在x的范围为[-10, 10]。
我们的目标是找到使函数值最大的x。
首先,我们需要定义遗传算法中的基本元素,包括编码方式、适应度函数、选择策略、交叉和变异操作等。
在本实验中,我们选择二进制编码方式,将x的范围[-10, 10]离散化为10位的二进制编码。
适应度函数即为f(x) = x^2,它表示个体的适应度。
选择策略采用轮盘赌选择算法,交叉操作采用单点交叉,变异操作采用随机位变异。
接下来,我们需要初始化种群,并迭代进行交叉和变异操作,直到满足终止条件。
在每一代中,我们根据适应度函数对种群中的个体进行评估,并根据选择策略选择父代个体进行交叉和变异操作。
通过交叉和变异操作,产生新的子代个体,并替代原有种群中的个体。
在本次实验中,我们设置了100个个体的种群,并进行了100代的迭代。
实验结果显示,经过多次迭代,算法逐渐优化到了最优解。
最终找到了使函数值最大的x,即x=10,对应的函数值为100。
总结起来,本次实验利用遗传算法求解函数的最大值,展示了遗传算法在优化问题中的应用。
通过适当选择编码方式、适应度函数和操作策略,我们可以有效地找到问题的最优解。
在后续的研究中,我们可以进一步探索遗传算法在更复杂问题上的应用,并通过改进算法的参数和操作策略来提高算法的性能。
遗传算法的实例ppt课件.ppt

病 原 体 侵 入 机体, 消弱机 体防御 机能, 破坏机 体内环 境的相 对稳定 性,且 在一定 部位生 长繁殖 ,引起 不同程 度的病 理生理 过程
遗传算法的手工模拟计算示例
为更好地理解遗传算法的运算过程,下面用手工计算来简单地模拟遗传算法的各 个主要执行步骤。
例:求下述二元函数的最大值:
个体
A
B
C
D
病 原 体 侵 入 机体, 消弱机 体防御 机能, 破坏机 体内环 境的相 对稳定 性,且 在一定 部位生 长繁殖 ,引起 不同程 度的病 理生理 过程
步骤三:交叉
• 选中的优势个体进行交叉 ----- 由父个体生成子个体
相同的两个父个体生成相同的两个子个体
病 原 体 侵 入 机体, 消弱机 体防御 机能, 破坏机 体内环 境的相 对稳定 性,且 在一定 部位生 长繁殖 ,引起 不同程 度的病 理生理 过程
• 程序结束时,最优个体即为所求解 • 程序结束的判定
根据循环次数 根据最大适应度 根据种群中相同个体数与总个体数的比值
病 原 体 侵 入 机体, 消弱机 体防御 机能, 破坏机 体内环 境的相 对稳定 性,且 在一定 部位生 长繁殖 ,引起 不同程 度的病 理生理 过程
遗传算法各步骤的评价
• 选择 --- 优胜劣汰
011101 111001 101011 111001
配对情况 交叉点位置
1-2
1-2:2
3-4
3-4:4
交叉结果
011001 111101 101001 111011
变异点 变异结果
4 011101 5 111111 2 111001 6 111010
子代群体p(1) x1 x2
实验六:遗传算法求解TSP问题实验备课讲稿

实验六:遗传算法求解TSP问题实验一、实验目的熟悉和掌握遗传算法的原理、流程和编码策略,并利用遗传求解函数优化问题,理解求解TSP问题的流程并测试主要参数对结果的影响。
用遗传算法对TSP问题进行了求解,熟悉遗传算法地算法流程,证明遗传算法在求解TSP问题时具有可行性。
二、实验内容参考实验系统给出的遗传算法核心代码,用遗传算法求解TSP的优化问题,分析遗传算法求解不同规模TSP问题的算法性能。
对于同一个TSP问题,分析种群规模、交叉概率和变异概率对算法结果的影响。
增加1种变异策略和1种个体选择概率分配策略,比较求解同一TSP问题时不同变异策略及不同个体选择分配策略对算法结果的影响。
1. 最短路径问题所谓旅行商问题(Travelling Salesman Problem , TSP),即最短路径问题,就是在给定的起始点S到终止点T的通路集合中,寻求距离最小的通路,这样的通路成为S点到T点的最短路径。
在寻找最短路径问题上,有时不仅要知道两个指定顶点间的最短路径,还需要知道某个顶点到其他任意顶点间的最短路径。
遗传算法方法的本质是处理复杂问题的一种鲁棒性强的启发性随机搜索算法,用遗传算法解决这类问题,没有太多的约束条件和有关解的限制,因而可以很快地求出任意两点间的最短路径以及一批次短路径。
假设平面上有n个点代表n个城市的位置, 寻找一条最短的闭合路径, 使得可以遍历每一个城市恰好一次。
这就是旅行商问题。
旅行商的路线可以看作是对n个城市所设计的一个环形, 或者是对一列n个城市的排列。
由于对n个城市所有可能的遍历数目可达(n- 1)!个, 因此解决这个问题需要0(n!)的计算时间。
假设每个城市和其他任一城市之间都以欧氏距离直接相连。
也就是说, 城市间距可以满足三角不等式, 也就意味着任何两座城市之间的直接距离都小于两城市之间的间接距离。
2. 遗传算法遗传算法是由美国J.Holland教授于1975年在他的专著《自然界和人工系统的适应性》中首先提出的,它是一类借鉴生物界自然选择和自然遗传机制的随机化搜索算法。
TSP的遗传算法程序实验报告
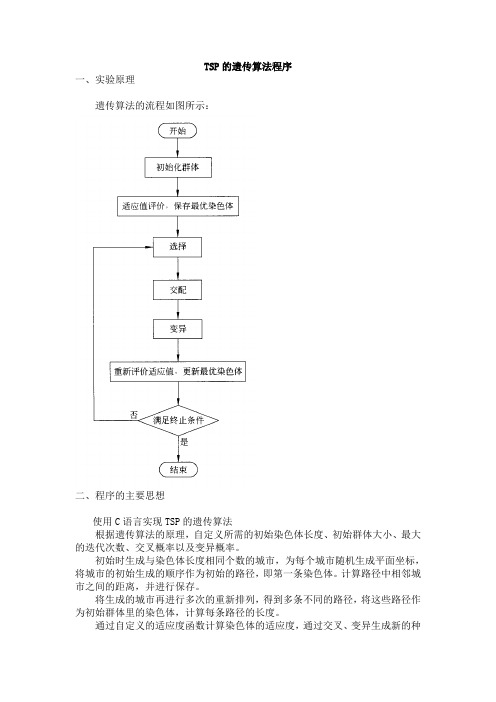
TSP的遗传算法程序一、实验原理遗传算法的流程如图所示:二、程序的主要思想使用C语言实现TSP的遗传算法根据遗传算法的原理,自定义所需的初始染色体长度、初始群体大小、最大的迭代次数、交叉概率以及变异概率。
初始时生成与染色体长度相同个数的城市,为每个城市随机生成平面坐标,将城市的初始生成的顺序作为初始的路径,即第一条染色体。
计算路径中相邻城市之间的距离,并进行保存。
将生成的城市再进行多次的重新排列,得到多条不同的路径,将这些路径作为初始群体里的染色体,计算每条路径的长度。
通过自定义的适应度函数计算染色体的适应度,通过交叉、变异生成新的种群。
对新种群继续迭代操作,直到达到初始定义的迭代次数,获得最终的路径及路径图。
三、程序的主要步骤①染色体初始化的子函数1)void initialize()2){int k,j,minx,miny,maxx,maxy;3)initdata();4)minx=0;5)miny=0;6)maxx=0;maxy=0;7)for(k=0;k<lchrom;k++)8){x[k]=rand();9)if(x[k]>maxx)maxx=x[k];10)if(x[k]<minx)minx=x[k];11)y[k]=rand();12)if(y[k]>maxy)maxy=y[k];13)if(y[k]<miny)miny=y[k];14)}15)if((maxx-minx)>(maxy-miny))16){maxxy=maxx-minx;}17)else {maxxy=maxy-miny;}18)maxdd=0.0;19)for(k=0;k<lchrom;k++)20)for(j=0;j<lchrom;j++)21){dd[k*lchrom+j]=hypot(x[k]-x[j],y[k]-y[j]);22)if(maxdd<dd[k*lchrom+j])maxdd=dd[k*lchrom+j];23)}24)refpd=dd[lchrom-1];25)for(k=0;k<lchrom;k++)26)refpd=refpd+dd[k*lchrom+k+2];27)for(j=0;j<lchrom;j++)28)dd[j*lchrom+j]=4.0*maxdd;29)ff=(0.765*maxxy*pow(lchrom,0.5));30)minpp=0;31)min=dd[lchrom-1];32)for(j=0;j<lchrom-1;j++)33){if(dd[lchrom*j+lchrom-1]<min)34){min=dd[lchrom*j+lchrom-1];35)minpp=j;36)}37)}38)initpop();39)statistics(oldpop);40)initreport();41)}7) for(k=0;k<lchrom;k++)8) {x[k]=rand();9) if(x[k]>maxx)maxx=x[k];10)if(x[k]<minx)minx=x[k];11)y[k]=rand();12)if(y[k]>maxy)maxy=y[k]13)if(y[k]<miny)miny=y[k];14)}此段程序是初始化多个城市的坐标值(x,y),其中(x[k],y[k])代表第k+1个城市的坐标值,也相当于初始染色体的第k+1个基因值。
遗传算法实验ppt课件

功能:
①创建一个以二进制编码的种群,nind指定种群规模,lind确 定染色结构,染色体的等位基因的基 本字符由基本向量basev确定。
③用于产生一个数量为nind的种群,染色体的长度为lind,染
11
色体等位基因的基本字符由基本向量basev确定。
[chrom,lind,basev]=crtbp(nind,lind);
5
单击Save按钮
6
单击Close按钮
7
§4.2 创建种群
1、创建基向量 —— crtbase
8
1、创建基向量——crtbase
调用格式 basev=crtbase(lind,base)
功能 利用基本字符集base产生由向量lind的元素确定字
符长度的串,以说明染色体中基因座的等位基因数量。 例1:在命令窗口中输入 >> basev=crtbase([4 6],[5 8]); basev =
lind = 10
basev = 5555888888
15
16
5555888888 再输入以下命令 >> [chrom,lind,basev]=crtbp(6,basev)
14
[chrom,lind,basev]=crtbp(nind, basev);
chrom = 3410713003 2241446461 2433365075 3001443372 3402254267 3140316635
§4.1 遗传算法工具箱的安装
第一步:将文件夹 gatbx拷 贝至Matlab的工具箱目录下 或硬盘任一目录中;
1
2
第二步:启动 Matlab, 并设置路径
3
单击Add Floder… 按钮或 Add With Subfloder… 按 钮弹出对话框
第6章 遗传算法及其应用PPT幻灯片

遗传算法的基本概念
选择(selection): 适应度越高的个体被选中的概率越大
轮盘赌
pi
fi
N 1
fj
j0
遗传算法的基本概念
选择(selection): 适应度越高的个体被选中的概率越大
轮盘赌 锦标赛 Elitism策略
pi
fi
N 1
fj
确定性算法: 穷举、动态规划、分支限界… 非确定性算法: 近似算法、概率算法…
A
B
C
D
E
C
D
E
D E CE C D
10
7 A
6 9
B8 9 13
C 8
12
E
5
D
问题求解策略
启发式算法
利用问题领域知识: 领域相关 利用一般性启发信息: 领域独立
元启发算法
问题求解策略
启发式算法示例: 蚁群优化算法
问题求解策略
问题求解:解空间搜索
解的表示形式 搜索的策略
问题求解策略
构造式求解: 从部分解逐步构造出完整解
确定性算法: 穷举、动态规划、分支限界…
常常面临 组合爆炸
A
B
C
D
E
C
D
E
D E CE C D
10
7 A
6 9
B8 9 13
C 8
12
E
5
D
问题求解策略
构造式求解: 从部分解逐步构造出完整解
基本思想: 模拟蚁群在寻找食物过程中发现路径的行为 信息素: 蚂蚁会优先选择信息素浓度较大的路径 信息素挥发
。。。。 。
。。。。。。。。。
遗传算法 ppt课件

到 P1 中找P2 的第一个元素赋给 C1 的相对位 置…,重复此过程,直到 P2 上得到 P1 的第 一个元素为止,称为一个循环;
P2 基因轮替原则重复 对最前的基因按 P1 、 以上过程;
⑶
⑷
重复以上过程,直到所有位都完成。
PPT课件
13
五.GA的各种变形(12)
P1
CX
245389617 P2 3 9 8 6 5 4 2 7 1
对数标定的作用:缩小目标函数值的差别
PPT课件 30
五.GA的各种变形(29)
V.
指数标定:
bf 函数表达式:f ae c
指数标定的作用:扩大差别
VI.
窗口技术: 函数表达式:f af f w
f w 为前W代中的最小目标值,它考虑了各
f min 代
fw 的波动,这样
PPT课件
PPT课件
15
五.GA的各种变形(14)
II. a.
变异的修复策略 换位变异(最常用)是随机地在染色体上选取 两个位置,交换基因的位值。
例:
b.
4312567 4312567
4512367 5431267
移位变异:任选一位移到最前
例:
PPTБайду номын сангаас件
16
五.GA的各种变形(15)
②
实数编码的合法性修复
对 min f x ,
函数表达式: f f max f x +ξ, 上述中的ξ是一个较小的数,目的是使种群中最差的个体 仍然有繁殖的机会,增加种群的多样性。
PPT课件 26
a
b= =-1,
f max +ξ ,
五.GA的各种变形(25)
《遗传算法实例参考》课件

遗传算法是一种模拟自然选择和遗传 机制的优化算法,通过模拟生物进化 过程中的基因遗传和变异过程来寻找 最优解。
特点
遗传算法具有全局搜索能力、隐含并 行性、自适应性、对初始条件要求不 高、鲁棒性强等优点。
遗传算法的基本原理
适应度函数
根据问题的目标函数来定义适 应度函数,用于评估每个个体 的适应度。
机器学习
用于支持向量机、神经网络等机器 学习模型的参数优化。
03
02
组合优化
用于求解如旅行商问题、背包问题 等组合优化问题。
调度与控制
用于生产调度、机器人路径规划等 控制系统的优化。
04
PART 02
遗传算法的实现步骤
初始化种群
初始解的产生
在遗传算法的开始阶段,需要随机生成一组初始解,这组解被称为种群。每个解 都是问题的一个潜在解决方案。
交叉操作
单点交叉(One-Point Crossover)
随机选择一个交叉点,将两个父代解在该点后的部分进行交换,形成两个子代解。
优点
能够引入新的解,增加解的多样性。
变异操作
要点一
位反转变异(Bit-Flip Mutation )
随机选择解中的一个位进行取反操作,以增加解的随机性 。
要点二
优点
能够防止算法陷入局部最优解,提高全局搜索能力。
PART 05
遗传算法实例:求解约束 优化问题
问题描述
求解约束优化问题
遗传算法可以用于求解具有约束条件的优 化问题,例如在物流、生产计划、金融等
领域中常见的优化问题。
约束条件
限制决策变量取值的条件,可以是等式或 不等式约束。
目标函数
需要最小化或最大化的目标函数,通常是 一个数学表达式,代表了问题的优化目标 。
遗传算法实验六ppt课件

NIND=40;
%定义个体数目
MAXGEN=25;
%定义最大遗传代数
PRECI=20;
%编码长度
GGAP=0.9;
%代沟
FieldD=[20;-1;2;1;0;1;1];
%区域描述器
Chrom=crtbp(NIND, PRECI);
%产生初始种群
gen=0;
%代计数器
variable=bs2rv(Chrom, FieldD);
7
;.
具有性能跟踪和图像输出功能的程序代码
%子代个体的十进制转换 variable=bs2rv(SelCh, FieldD); %计算子代的目标函数值 ObjVSel=variable.*sin(10*pi*variable)+2.0; %重插入子代的新种群 [Chrom ObjV]=reins(Chrom, SelCh, 1, 1, ObjV, ObjVSel); variable=bs2rv(Chrom, FieldD);
while gen<MAXGEN %分配适应度值 FitnV=ranking(-ObjV); %选择 SelCh=select('sus', Chrom, FitnV, GGAP); %重组 SelCh=recombin('xovsp', SelCh, 0.7); %变异 SelCh=mut(SelCh);
27
程序中的函数说明
例如: >> MatIn = [1 2 3] MatIn =
123 >> REPN = [1 2] REPN =
12 >> MatOut = rep(MatIn,REPN) MatOut =
123123
关于遗传算法的实验报告

3.014470 y=-3.814470y=-3.814470 y=-3.014470 y=-3.S14470 y—3.014170V-3.8144M V—3.81447By=-3.81447011-^3.814470 y- 3-014470
jc=4.913437
x =4,911915
3c=4.91291Sx=4.?1291& X-4.91291&x=4.913203
■M. 913283x=4.913203x-4.913203
x-4.912820>=4.912916 x=4_91291t
y- 3.014470 y=-3-814470 y=-3.814470 y=-3.814470y—3.81W0y* 3
public:
GA(){
Pc=0.25;
Pm=0.01;
Num_Population=50;
Num_Iteration=100;
}
void GA_Init();
void Crossover_Operation();
void Select_Operation();
void Mutation_Operation();
x=2.Q88621
P=2.81429?
I he
Nd.B4
鼻enEEt ion =
ei 0101 an ooei 1 eeioaai iot
x=2.Q88621
9-2-B147??
T he
4帖
jener^at ion "
fit010101aneiiRaionniiBi
«=2.08&£21
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
%定义遗传算法参数
NIND=40;
%群体中个体数目
MAXGEN=25; %最大遗传代数
PRECI=20;
%变量的二进制位数
Hale Waihona Puke 具有性能跟踪和图像输出功能的程序代码
%代沟 GGAP=0.9; %寻优结果的初始值 trace=zeros(2, MAXGEN); %建立区域描述器 FieldD=[20;-1;2;1;0;1;1]; %生成初始种群 Chrom=crtbp(NIND, PRECI);
[Chrom ObjV]=reins(Chrom,SelCh,1,1,ObjV,ObjVSel); %重插入子代到种群
Y=max(ObjV)
%当前种群最优解
gen=gen+1;
%代计数器增加
end
具有性能跟踪和图像输出功能的程序代码
figure(1);
%画出函数曲线
fplot('variable.*sin(10*pi*variable)+2.0',[-1,2]);
具有性能跟踪和图像输出功能的程序代码
%最优个体的十进制转换 variable=bs2rv(Chrom, FieldD); hold on, grid on; plot(variable,ObjV,'b*'); figure(2); plot(trace(1,:)); hold on; plot(trace(2,:),'-.');grid off legend('解的变化','种群均值的变化')
SelCh=recombin('xovsp', SelCh, 0.7);
%重组
SelCh=mut(SelCh);
%变异
variable=bs2rv(SelCh, FieldD);
%子代个体的十进制转换
ObjVSel=variable.*sin(10*pi*variable)+2.0; %计算子代的目标函数值
具有性能跟踪和图像输出功能的程序代码
%子代个体的十进制转换 variable=bs2rv(SelCh, FieldD); %计算子代的目标函数值 ObjVSel=variable.*sin(10*pi*variable)+2.0; %重插入子代的新种群 [Chrom ObjV]=reins(Chrom, SelCh, 1, 1, ObjV, ObjVSel); variable=bs2rv(Chrom, FieldD);
NIND=40;
%定义个体数目
MAXGEN=25;
%定义最大遗传代数
PRECI=20;
%编码长度
GGAP=0.9;
%代沟
FieldD=[20;-1;2;1;0;1;1];
%区域描述器
Chrom=crtbp(NIND, PRECI);
%产生初始种群
gen=0;
%代计数器
variable=bs2rv(Chrom, FieldD);
程序运行追踪结果:
代序
寻优结果
自变量
函数值
1
2.0292
2
2.2104
3
2.3577
4
2.4881
3.8423 3.7819 3.8063 3.815
5
2.6401
3.8072
程序运行追踪结果
6
2.6133
7
2.8658
8
2.9400
9
2.9120
10
2.8677
11
2.6973
12
2.7963
具有性能跟踪和图像输出功能的程序代码
%代计数器 gen=0; %计算初始种群的十进制转换 variable=bs2rv(Chrom, FieldD); %计算目标函数值 ObjV=variable.*sin(10*pi*variable)+2.0;
具有性能跟踪和图像输出功能的程序代码
while gen<MAXGEN %分配适应度值 FitnV=ranking(-ObjV); %选择 SelCh=select('sus', Chrom, FitnV, GGAP); %重组 SelCh=recombin('xovsp', SelCh, 0.7); %变异 SelCh=mut(SelCh);
具有性能跟踪和图像输出功能的程序代码
%代计数器增加 gen=gen+1; %输出最优解及其序号,并在目标函数图像 %中标出,Y为最优解,I为种群的序号 [Y, I]=max(ObjV);hold on; plot(variable(I), Y, 'bo'); %遗传算法性能跟踪 trace(1, gen)=max(ObjV); %每一代最优解 trace(2, gen)=sum(ObjV)/length(ObjV); end
遗传算法实验六演示文稿
遗传算法实验六
§5.1 简单一元函数优化实例
例 1 利用遗传算法计算下面函数的最大值
f ( x) x sin(10 * x) 2.0 x [1,2]
选择二进制编码,种群中个体数目为 40,每个 种群的长度为 20,使用代沟为 0.9,最大遗传代数 为 25
程序简化代码如下:
%初始种群的十进制转换
ObjV=variable.*sin(10*pi*variable)+2.0; %计算初始种群目标函数值
while gen<MAXGEN+1
FitnV=ranking(-ObjV);
%分配适应度值
SelCh=select('sus', Chrom, FitnV, GGAP); %选择
程序运行追踪结果
21
3.0947
22
3.1525
23
2.9147
24
2.9144
25
3.0259
3.8489 3.8496 3.8496 3.8493 3.8493
经过25次迭代后最优解及种群均值的变化如下图:
例题中用到的一些绘图函数说明
1、绘制函数图像函数—fplot 调用格式:
FPLOT(FUN,LIMS) FPLOT(FUN,LIMS,TOL) FPLOT(FUN,LIMS,N) FPLOT(FUN,LIMS,'LineSpec') 参数说明: LIMS = [XMIN XMAX]或 LIMS = [XMIN XMAX YMIN YMAX]——给出变量 范围
13
2.7317
3.7555 3.8073 3.8043 3.8321 3.8321 3.8320 3.8326 3.8318
程序运行追踪结果
14
2.7739
15
2.6521
16
2.7844
17
2.5158
18
2.7768
19
2.7907
20
2.8080
3.8318 3.8274 3.8274 3.8274 3.8285 3.8277 3.8379
