初三圆难题压轴题答案解析(终审稿)
部编数学九年级上册专题24.5圆(压轴题综合测试卷)(人教版)(解析版)含答案

专题24.5 圆(满分100)学校:___________姓名:___________班级:___________考号:___________题号一二三总分得分评卷人得分一.选择题(本大题共10小题,每小题3分,满分30分)1.(2022·重庆忠县·九年级期中)如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )A.50°B.60°C.80°D.100°【思路点拨】首先圆上取一点A,连接AB,AD,根据圆的内接四边形的性质,即可得∠BAD+∠BCD=180°,即可求得∠BAD 的度数,再根据圆周角的性质,即可求得答案.【解题过程】解:在圆上取一点A,连接AB,AD,∵点A、B,C,D在⊙O上,∠BCD=130°,∴∠BAD=50°,∴∠BOD=100°.故选D.2.(2022·江苏·九年级专题练习)如图,在平面直角坐标系中,过格点A,B,C作一圆弧,点B与下列格点的连线中,能够与该圆弧相切的是( )A.点(0,3)B.点(2,3)C.点(5,1)D.点(6,1)【思路点拨】根据垂径定理的性质得出圆心所在位置,再根据切线的性质得出,∠OBD+∠EBF=90°时F点的位置即可。
【解题过程】解:∵过格点A,B,C作一圆弧,∴三点组成的圆的圆心为:O(2,0),∵只有∠OBD+∠EBF=90°时,BF与圆相切,∴当△BOD≌△FBE时,EF=BD=2,F点的坐标为:(5,1),∴点B与下列格点的连线中,能够与该圆弧相切的是:(5,1).故选C.3.(2022·全国·九年级课时练习)如图,在⊙О中,点C在弦AB上移动,连接OC,过点C作CD⊥OC交⊙О于点D.若AB=2,则CD的最大值是()A.4B.2C D.1【思路点拨】连接OD,如图,利用勾股定理得CD,利用垂线段最短得到当OC⊥AB时,OC最小,再求出CD即可.【解题过程】4.(2022·浙江丽水·模拟预测)已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )A.B.cm C.或D.或【思路点拨】先根据题意画出图形,由于点C的位置不能确定,故应分两种情况进行讨论.【解题过程】解:连接AC,AO,∵O的直径CD=10cm,AB⊥CD,AB=8cm,5.(2022·江苏·九年级)如图,AB是⊙O的直径,点C为圆上一点,AC=3,∠ABC的平分线交AC于点D,CD=1,则⊙O的直径为()A B.C.1D.2【思路点拨】【解题过程】解:如图:过D作DE⊥AB,垂足为E∵AB是直径∴∠ACB=90°∵∠ABC的角平分线BD∴DE=DC=1在Rt△DEB和Rt△DCB中6.(2022·全国·九年级课时练习)如图,在Rt△ABC中,∠ACB=90°,以该三角形的三条边为边向形外作正方形,正方形的顶点E,F,G,H,M,N都在同一个圆上.记该圆面积为S1,△ABC面积为S2,则S1的值是()S2A.5π2B.3πC.5πD.11π2【思路点拨】【解题过程】7.(2022·全国·九年级专题练习)如图,等边△ABC中,AB=3,点D,点E分别是边BC,CA上的动点,且BD=CE,连接AD、BE交于点F,当点D从点B运动到点C时,则点F的运动路径的长度为()A B C D.【思路点拨】如图,作过A、B、F作⊙O,AFB为点F的轨迹,然后计算出AFB的长度即可.【解题过程】解:如图:作过A、B、F作⊙O,过O作OG⊥AB∵等边ΔABC∴AB=BC,∠ABC=∠C=60°∵BD=CE∴△BCE≌△ABC∴∠BAD=∠CBE∵∠ABC=∠ABE+∠EBC=60°∴∠ABE+∠BAD=60°∴∠AFB=120°∵∠AFB是弦AB同侧的圆周角∴∠AOB=120°8.(2022·全国·九年级课时练习)如图,在⊙O中,点C在优弧AB上,将弧BC沿BC折叠后刚好经过AB的中点D.若⊙O AB=4,则BC的长是( )A.B.C D【思路点拨】【解题过程】解:连接OD、AC、DC、OB、OC,作CE⊥AB于E,OF⊥CE于F,如图,∵D为AB的中点,9.(2022·全国·九年级课时练习)如图,△ABC的内切圆⊙O与AB,BC,AC相切于点D,E,F,已知AB =6,AC=5,BC=7,则DE的长是()A B C D【思路点拨】【解题过程】10.(2022·江苏无锡·九年级期中)我们定义:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形,根据定义:①等边三角形一定是奇异三角形;②在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,则a:b:c=12;③如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆ADB的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.则△ACE是奇异三角形;④在③的条件下,当△ACE是直角三角形时,∠AOC=120°,其中,说法正确的有()A.①②B.①③C.②④D.③④【答案】B【思路点拨】【解题过程】解:设等边三角形的边长为a,则a2+a2=2a2,满足奇异三角形的定义,∴等边三角形一定是奇异三角形,故①正确;在RtΔABC中,a2+b2=c2,∵c>b>a>0,∴2c2>a2+b2,2a2<b2+c2,若△ABC是奇异三角形,一定有2b2=a2+c2,∴2b2=a2+(a2+b2),∴b2=2a2,得b=.∵c2=b2+a2=3a2,∴c,∴a:b:c=1故②错误;在RtΔABC中,a2+b2=c2,∵AB是⊙O的直径,∴∠ACB=∠ADB=90°,在RtΔACB中,AC2+BC2=AB2;在RtΔADB中,AD2+BD2=AB2.∵D是半圆ADB的中点,∴AD=BD,∴AD=BD,∴AB2=AD2+BD2=2AD2,又∵CB=CE,AE=AD,∴AC2+CE2=2AE2.∴ΔACE是奇异三角形,故③正确;由③可得ΔACE是奇异三角形,∴AC2+CE2=2AE2.当ΔACE是直角三角形时,由②可得AC:AE:CE=1AC:AE:CE=1,(Ⅰ)当AC:AE:CE=1AC:CE=1AC:CB=1∵∠ACB=90∘,∴∠ABC=30°,∴∠AOC=2∠ABC=60°.(Ⅱ)当AC:AE:CE=1时,AC:CE=1,即AC:CB=1,∵∠ACB=90°,∴∠ABC=60°,∴∠AOC=2∠ABC=120°,∴∠AOC的度数为60°或120°,故④错误;故选:B.评卷人得分二.填空题(本大题共5小题,每小题3分,满分15分)11.(2022·全国·九年级课时练习)工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为____mm.【思路点拨】先根据钢珠的直径求出其半径,再构造直角三角形,求出小圆孔的宽口AB的长度的一半,最后乘以2即为所求.【解题过程】12.(2022·全国·九年级课时练习)已知⊙O的直径为10cm,AB,CD是⊙O的两条弦,AB//CD,AB=8cm,CD=6cm,则AB与CD之间的距离为________cm.【思路点拨】分两种情况考虑:当两条弦位于圆心O同一侧时,当两条弦位于圆心O两侧时;利用垂径定理和勾股定理分别求出OE和OF的长度,即可得到答案.【解题过程】解:分两种情况考虑:当两条弦位于圆心O一侧时,如图1所示,13.(2022·山东菏泽·九年级期中)如图,正方形ABCD内接于⊙O,PA,PD分别与⊙O相切于点A和点D,PD的延长线与BC的延长线交于点E.已知AB=2,则图中阴影部分的面积为___________.【思路点拨】【解题过程】14.(2022·全国·九年级课时练习)如图,⊙O是等边△ABC的外接圆,已知D是⊙O上一动点,连接AD、CD,若圆的半径r=2,则以A、B、C、D为顶点的四边形的最大面积为_____.【思路点拨】连接BO并延长交AC于E,交AC于D,根据垂径定理得到点D到AC的距离最大,根据直角三角形的性质、三角形的面积公式计算,得到答案.【解题过程】15.(2022·全国·九年级课时练习)如图,在矩形ABCD中,AB=6,BC=8,E为AD上一点,且AE=2,F为BC边上的动点,以为EF直径作⊙O,当⊙O与矩形的边相切时,BF的长为______.【思路点拨】⊙O与矩形的边相切,但没有具体说与哪个边相切,所以该题有三种情况:第一种情况是圆与边AD、BC 相切,此时BF=AE;第二种情况是圆与边AB相切,利用中位线定理以及勾股定理可求出BF的长;第三种是圆与边CD相切,同样利用中位线定理以及勾股定理求得BF.【解题过程】解:①当圆与边AD、BC相切时,如图1所示此时∠AEO=BFO=90°所以四边形AEFB为矩形即BF=AE=2;②当圆与边AB相切时,设圆的半径为R,切点为H,圆与边AD交于E、N两点,与边BC交于M、F两点,连接EM、HO,如图2所示此时OE=OF=OH=R,点O、H分别是EF、AB的中点∴2OH=AE+BF即BF=2R-2∵BM=AE=2∴MF=2R-4在Rt△EFM中,EM2+MF2=EF2∴BF=13.2评卷人得分三.解答题(本大题共9小题,满分55分)16.(2022·全国·九年级课时练习)在《阿基米德全集》中的《引理集》中记录了古希腊数学家阿基米德提出的有关圆的一个引理.如图,已知AB,C是弦AB上一点,请你根据以下步骤完成这个引理的作图过程.(1)尺规作图(保留作图痕迹,不写作法):①作线段AC的垂直平分线DE,分别交AB于点D,AC于点E,连接AD,CD;②以点D为圆心,DA长为半径作弧,交AB于点F(F,A两点不重合),连接DF,BD,BF.(2)直接写出引理的结论:线段BC,BF的数量关系.【思路点拨】【解题过程】解:(1)作出线段AC的垂直平分线DE,连接AD,CD;以D为圆心,DA长为半径作弧,交AB于点F,连接DF,BD,BF,如图示:(2)结论:BC=BF.理由如下:由作图可得:DE是AC的垂直平分线,DA=DF,∴DA=DC=DF,∴∠DAC=∠DCA,AD=FD,∴∠DBC=∠DBF,∵四边形ABFD是圆的内接四边形,∴∠DAB+∠DFB=180°,∵∠DCA+∠DCB=180°,∴∠DFB=∠DCB,∵DB=DB,∴△DCB≌△DFB,∴BC=BF.17.(2022·江西上饶·九年级期末)如图,⊙O的直径AB的长为2,点C在圆周上,∠CAB=30°.点D是圆上一动点,DE∥AB交CA的延长线于点E,连接CD,交AB于点F.(1)如图1,当DE与⊙O相切时,求∠CFB的度数;(2)如图2,当点F是CD的中点时,求△CDE的面积.【思路点拨】(1)由题意可求∠AOD=90°,即可求∠C=45°,即可求∠CFB的度数;(2)连接OC,根据垂径定理可得AB⊥CD,利用勾股定理.以及直角三角形30度性质求出CD、DE即可.【解题过程】解:(1)如图:连接OD∵DE与⊙O相切∴∠ODE=90°∵AB∥DE18.(2022·全国·九年级专题练习)如图,AB是半圆O的直径,点D是半圆O上一点,点C是AD的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC.(1)求证:GP=GD;(2)求证:P是线段AQ的中点;(3)连接CD,若CD=2,BC=4,求⊙O的半径和CE的长.【思路点拨】(1)结合切线的性质以及已知得出∠GPD=∠GDP,进而得出答案;(2)利用圆周角定理得出PA,PC,PQ的数量关系进而得出答案;(3)直接利用勾股定理结合三角形面积得出答案.【解题过程】(1)证明:连接OD,则OD⊥GD,∠OAD=∠ODA,∵∠ODA+∠GDP=90°,∠EAP+∠GPD=∠EPA+∠EAP=90°,∴∠GPD=∠GDP;∴GP=GD;(2)证明:∵AB为直径,∴∠ACB=90°,∵CE⊥AB于E,∴∠CEB=90°,∴∠ACE+∠ECB=∠ABC+∠ECB=90°,∴∠ACE=∠ABC=∠CAP,∴PC=PA,∵∠ACB=90°,∴∠CQA+∠CAP=∠ACE+∠PCQ=90°,∴∠PCQ=∠CQA,∴PC=PQ,∴PA=PQ,即P为Rt△ACQ斜边AQ的中点;(3)连接CD,∵弧AC=弧CD,∴CD=AC,∵CD=2,∴AC=2,19.(2022·全国·九年级课时练习)对于平面直角坐标系xOy中的图形P,Q,给出如下定义:M为图形P 上任意一点,N为图形Q上任意一点,如果M,N两点间的距离有最小值,那么称这个最小值为图形P,Q 间的“非常距离”,记作d(P,Q).已知点A(−2,2),B(2,2),连接AB.(1)d(点O,AB)=;(2)⊙O半径为r,若d(⊙O,AB)=0,直接写出r的取值范围;(3)⊙O半径为r,若将点A绕点B逆时针旋转α°(0°<α<180°),得到点A′.①当α=30°时d(⊙O,A′)=0,求出此时r的值;②对于取定的r值,若存在两个α使d(⊙O,A′)=0,直接写出r的范围.【思路点拨】(1)理解题意后直接利用垂线段最短即可求解.(2)先理解当⊙O与线段有交点时,d(⊙O,AB)=0,利用⊙O与线段相切和⊙O经过A点即可求解.(3)①先确定A′位于x轴上,再求出OA′的长即可求解;②先确定A′的轨迹,再利用存在两个α使d(⊙O,A')=0,确定并求出两个界点值,即可求解.【解题过程】∴∠A′NB=90°,由旋转知BA′=BA=2−(−2)=4,∵∠ABA′=30°,BA′=2,∴A′N=12∴A′位于x轴上,BN=42−22=23,∴A′M=23,∴A′O=23−2,∵对于取定的r值,若存在两个α使d(⊙O,A')=0,∴⊙O与以AH为直径的半圆有两个交点(A点和H点除外),此时有两个界点值,分别是⊙O与该半圆内切时和⊙O由B(2,2),得OB=22+22=22,当⊙O与该半圆内切时,r=4−22,当⊙O经过A点时,r=22,∴4−22<r<22.20.(2022·四川德阳·九年级阶段练习)如图1,四边形ABCD内接于⊙O,AD为直径,过点C作CE⊥AB于点E,连接AC.(1)求证:∠CAD=∠ECB;(2)若CE是⊙O的切线,∠CAD=30°,连接OC,如图2.①请判断四边形ABCO的形状,并说明理由;②当AB=2时,求AD,AC与CD围成阴影部分的面积.【思路点拨】【解题过程】解:(1)证明:∵四边形ABCD内接于⊙O,∴∠D+∠ABC=180°,∵∠EBC+∠ABC=180°,∴∠D=∠EBC,∵AD为⊙O直径,∴∠ACD=90°,∴∠D+∠CAD=90°,∵CE⊥AB,∴∠ECB+∠EBC=90°,∴∠CAD=∠ECB;(2)①四边形ABCO是菱形,理由如下:∵CE是⊙O的切线,∴OC⊥EC,∵AB⊥EC,∴∠OCE=∠E=90°,∴∠OCE+∠E=180°,∴OC∥AE,∴∠ACO=∠BAC,∴CF=3,21.(2022·全国·九年级专题练习)如图,以AB为直径的⊙O上有一动点C,⊙O的切线CD交AB的延长线于点D,过点B作BM∥OC交⊙O于点M,连接AM,OM,BC.(1)求证:AM∥CD(2)若OA=5,填空:①当AM=时,四边形OCBM为菱形;②连接MD,过点O作ON⊥MD于点N,若BD=,则ON=.【思路点拨】(1)首先根据圆周角定理可得∠MAB+∠ABM=90°,由切线的性质可得∠DOC+∠CDO=90°,再根据平行线的性质即可证得∠MAB=∠CDO,据此即可证得结论;(2)①根据菱形性质可得OM= OA=MB= 5,即可求得AB,再根据勾股定理即可求得;②首先可证得△ODC 是等腰直角三角形,再根据勾股定理及三角形的面积,即可求解.【解题过程】(1)证明:∵AB是⊙O的直径,∴∠AMB=90°,∴∠MAB+∠ABM=90°,∵CD是⊙O的切线,∴OC⊥CD,∴∠DOC+∠CDO=90°,又∵BM∥OC,∴∠ABM=∠DOC,∴∠MAB=∠CDO,∴AM∥CD;(2)解:①若四边形OCBM为菱形,则OM=OA=MB =5,∵AB是⊙O的直径,∴∠AMB=90°,∵BD=52−5,OB=5,∴OD=OB+BD=5+5∵CD是⊙O的切线,∴∠OCD=90°,22.(2022·全国·九年级课时练习)如图,AB是⊙O的直径,P为AB上一点,弦CD与弦EF交于点P,PB平分∠DPF,连DF交AB于点G.(1)求证:CD=EF;(2)若∠DPF=60°,PE∶PF=1∶3,AB=OG的长.【思路点拨】【解题过程】(1)证明:如图,过点O作OM⊥EF于点M,ON⊥CD于点N,连接OF、OD,则∠OMF=∠OND=90°,∵PB平分∠DPF,OM⊥EF,ON⊥CD,∴OM=ON,在Rt△OFM和Rt△ODN中,∵OF=OD OM=ON,∴Rt△OFM≌Rt△ODN(HL),∴FM=DN,∵OM⊥EF,ON⊥CD,23.(2022·全国·九年级课时练习)问题提出:(1)如图1,已知△ABC是边长为2的等边三角形,则△ABC 的面积为______.问题探究:(2)如图2,在△ABC中,已知∠BAC=120°,BC=△ABC的最大面积.问题解决:(3)如图3,某校学生礼堂的平面示意图为矩形ABCD,其宽AB=20米,长BC=24米,为了能够监控到礼堂内部情况,现需要在礼堂最尾端墙面CD上安装一台摄像头M进行观测,并且要求能观测到礼堂前端墙面AB区域,同时为了观测效果达到最佳,还需要从点M出发的观测角∠AMB=45°.请你通过所学的知识进行分析,在墙面CD区域上是否存在点M满足要求?若存在,求出MC的长度;若不存在,请说明理由.【思路点拨】(1)作AD⊥BC于D,由勾股定理求出AD的长,即可求出面积;(2)作△ABC的外接圆⊙O,可知点A在BC上运动,当A'O⊥BC时,△ABC的面积最大,求出A'H的长,从而得出答案;(3)以AB为边,在矩形ABCD的内部作一个等腰直角三角形AOB,且∠AOB=90°,过O作HG⊥AB于H,交CD于G,利用等腰直角三角形的性质求出OA,OG的长,则以O为圆心,OA为半径的圆与CD相交,从而⊙O上存在点M,满足∠AMB=45°,此时满足条件的有两个点M,过M1作M1F⊥AB于F,作EO⊥M1F 于E,连接OF,利用勾股定理求出OE的长,从而解决问题.【解题过程】24.(2022·江苏·苏州中学九年级阶段练习)在Rt△ABC中,∠BCA=90°,CA=CB,点D是△ABC外一动点(点B,点D位于AC两侧),连接CD,AD.(1)如图1,点O是AB的中点,连接OC,OD,当△AOD为等边三角形时,∠ADC的度数是;(2)如图2,连接BD,当∠ADC=135°时,探究线段BD,CD,DA之间的数量关系,并说明理由;(3)如图3,⊙O是△ABC的外接圆,点D在AC上,点E为AB上一点,连接CE,DE,当AE=1,BE=7时,直接写出△CDE面积的最大值及此时线段BD的长.【思路点拨】【解题过程】即△CDE面积的面积最大值为4,此时,BD。
初三+圆难题压轴题答案解析+

∵ PH=1 ,
∴tan∠POH= = = .
∴OH= .
∴点 P 的坐标为( ,﹣ 1).
同理可得: 当点 P 在第二象限时,点 P 的坐标为(﹣
,1);
当点 P 在第三象限时,点 P 的坐标为(﹣ ,﹣ 1); ②若圆 P 与直线 l 和 l1 都相切,如图 2 所示.
,
∴△ PBG≌△ PBF( SAS), ∴PG=PF.
4. 解:( 1)∵ l 1⊥ l2,⊙ O 与 l 1, l2 都相切, ∴∠ OAD=45 °, ∵AB=4 cm ,AD=4cm , ∴CD=4 cm ,AD=4cm , ∴tan∠DAC= = = , ∴∠ DAC=60 °, ∴∠ OAC 的度数为:∠ OAD+ ∠ DAC=105 °, 故答案为: 105;
综上所述:当点 P 在 y 轴上移动时,∠ APB 有最大值, 此时点 P 的坐标为( 0, )和( 0,﹣ ).
7.解答: 证明:( 1)如图,连接 PM, PN, ∵⊙ P 与 x 轴, y 轴分别相切于点 M 和点 N, ∴PM ⊥ MF ,PN ⊥ON 且 PM=PN , ∴∠ PMF =∠ PNE=90°且∠ NPM =90°,∵ PE⊥ PF, ∠NPE =∠ MPF =90°﹣∠ MPE ,
同理可得:当点 P 在第一象限时,点 P 的坐标为( , 1);
当点 P 在第二象限时,点 P 的坐标为(﹣ 当点 P 在第三象限时,点 P 的坐标为(﹣
,1); ,﹣ 1);
当点 P 在第四象限时,点 P 的坐标为( ,﹣ 1). ③若圆 P 与直线 l1 和 l 2 都相切,如图 3 所示. 同理可得:
中考数学圆_经典压轴题[带答案解析]
![中考数学圆_经典压轴题[带答案解析]](https://img.taocdn.com/s3/m/3f72e60e1fb91a37f111f18583d049649b660ec2.png)
1.如图,四边形ABCD内接于⊙O,AB是⊙O的直径,AC和BD相交于点E,且DC2=CE•CA.〔1〕求证:BC=CD;〔2〕分别延长AB,DC交于点P,过点A作AF⊥CD交CD的延长线于点F,假设PB=OB,CD =,求DF的长.2.如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F.切点为G,连接AG交CD于K.〔1〕求证:KE=GE;〔2〕假设=KD·GE,试判断AC与EF的位置关系,并说明理由;〔3〕在〔2〕的条件下,假设sinE=,AK=,求FG的长.3.如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.(1)求证:AC 平分∠DAB ;(2)求证:△PCF 是等腰三角形; (3)假设tan ∠ABC=34,BE=72,求线段PC 的长.4.5.:如图,在半径为4的⊙O 中,AB ,CD 是两条直径,M 为OB 的中点,CM 的延长线交⊙O 于点E ,且EM >M C ,连结DE ,DE=。
(1)求证:AM·MB=EM·MC;〔2〕求EM的长;〔3〕求sin∠EOB的值。
6.如图,AE切⊙O于点E,AT交⊙O于点M,N,线段OE交AT于点C,OB⊥AT于点B,∠EAT=30°,AE=3,MN=2.〔1〕求∠COB的度数;〔2〕求⊙O的半径R;〔3〕点F在⊙O上〔是劣弧〕,且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.7.如图,AB是半径O的直径,AB=2.射线AM、BN为半圆O的切线.在AM上取一点D,连接BD交半圆于点C,连接AC.过O点作BC的垂线OE,垂足为点E,与BN相交于点F.过D点作半圆O的切线DP,切点为P,与BN相交于点Q.〔1〕求证:△ABC∽△OFB;〔2〕当△ABD与△BFO的面枳相等时,求BQ的长;(3)求证:当D在AM上移动时〔A点除外〕,点Q始终是线段BF的中点8.上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.〔1〕求证:△PAC∽△PDF;〔2〕假设AB=5,,求PD的长;〔3〕在点P运动过程中,设,求与之间的函数关系式.〔不要求写出的取值范围〕1.【解答】:〔1〕证明:∵DC2=CE•CA,∴=,△CDE∽△CAD,∴∠CDB=∠DBC,∵四边形ABCD内接于⊙O,∴BC=CD;〔2〕解:如图,连接OC,∵BC=CD,∴∠DAC=∠CAB,又∵AO=CO,∴∠CAB=∠ACO,∴∠DAC=∠ACO,∴AD∥OC,∴=,∵PB=OB,CD=,∴=∴PC=4又∵PC•PD=PB•PA∴PA=4也就是半径OB=4,在RT△ACB中,AC===2,∵AB是直径,∴∠ADB=∠ACB=90°∴∠FDA+∠BDC=90°∠CBA+∠CAB=90°∵∠BDC=∠CAB∴∠FDA=∠CBA又∵∠AFD=∠ACB=90°∴△AFD∽△ACB∴在Rt△AFP中,设FD=x,那么AF =,∴在RT△APF 中有,,求得DF =.2解:〔1〕如答图1,连接OG.∵EG为切线,∴∠KGE+∠OGA=90°,∵CD⊥AB,∴∠AKH+∠OAG=90°,又OA=OG,∴∠OGA=∠OAG,∴∠KGE=∠AKH=∠GKE,∴KE=GE.〔2〕AC∥EF,理由为:连接GD,如答图2所示.∵KG2=KD GE,即=,∴=,又∠KGE=∠GKE,∴△GKD∽△EGK,∴∠E=∠AGD,又∠C=∠AGD,∴∠E=∠C,∴AC∥EF;〔3〕连接OG,OC,如答图3所示.sinE=sin∠ACH=,设AH=3t,那么AC=5t,CH=4t,∵KE=GE,AC∥EF,∴CK=AC=5t,∴HK=CK﹣CH=t.在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,即〔3t〕2+t2=〔〕2,解得t=.设⊙O半径为r,在Rt△OCH中,OC=r,OH=r﹣3t,CH=4t,由勾股定理得:OH2+CH2=OC2,即〔r﹣3t〕2+〔4t〕2=r2,解得r=t=.∵EF为切线,∴△OGF为直角三角形,在Rt△OGF中,OG=r=,tan∠OFG=tan∠CAH==,∴FG===..45.6.7.8.。
中考数学压轴题-圆的压轴题 含解析

圆的压轴题(1)1、如图,BF 为⊙O 的直径,直线AC 交⊙O 于A ,B 两点,点D 在⊙O 上,BD 平分∠OBC ,DE ⊥AC 于点E 。
(1)求证:直线DE 是⊙O 的切线;(2)若 BF=10,sin ∠BDE=,求DE 的长。
2、如图,AN 是M ⊙的直径,NB x ∥轴,AB 交M ⊙于点C .(1)若点()0,6A ,()0,2N ,30ABN =∠°,求点B 的坐标;(2)若D 为线段NB 的中点,求证:直线CD 是M ⊙的切线.x y C D M O B NA3、如图,△ABD是⊙O的内接三角形,E是弦BD的中点,点C是⊙O外一点且∠DBC=∠A,连接OE延长与圆相交于点F,与BC相交于点C.(1)求证:BC是⊙O的切线;(2)若⊙O的半径为6,BC=8,求弦BD的长.4、已知△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,若=,如图1,.(1)判断△ABC的形状,并证明你的结论;(2)设AE与DF相交于点M,如图2,AF=2FC=4,求AM的长.5、如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,过点A作切线DE的垂线,垂足为D,且与⊙O交于点F,设∠DAC,∠CEA的度数分别是α,β.(1)用含α的代数式表示β,并直接写出α的取值范围;(2)连接OF与AC交于点O′,当点O′是AC的中点时,求α,β的值.6、如图,在菱形ABCD中,点P在对角线AC上,且PA=PD,⊙O是△PAD的外接圆.(1)求证:AB是⊙O的切线;(2)若AC=8,tan∠BAC=,求⊙O的半径.7、如图,AB为⊙O的直径,CB,CD分别切⊙O于点B,D,CD交BA的延长线于点E,CO的延长线交⊙O于点G,EF⊥OG于点F.(1)求证:∠FEB=∠ECF;(2)若BC=6,DE=4,求EF的长.8、如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.(1)求证:BE与⊙O相切;(2)设OE交⊙O于点F,若DF=1,BC=2 ,求阴影部分的面积.9、如图,已知⊙O的直径CD=6,A,B为圆周上两点,且四边形OABC是平行四边形,过A点作直线EF∥BD,分别交CD,CB的延长线于点E,F,AO与BD交于G点.(1)求证:EF是⊙O的切线;(2)求AE的长.10、如图,C、D是半圆O上的三等分点,直径AB=4,连接AD、AC,DE⊥AB,垂足为E,DE交AC于点F.(1)求∠AFE的度数;(2)求阴影部分的面积(结果保留π和根号).11、如图,MN是⊙O的直径,MN=4,点A在⊙O上,∠AMN=30°,B为的中点,P是直径MN上一动点.(1)利用尺规作图,确定当PA+PB最小时P点的位置(不写作法,但要保留作图痕迹).(2)求PA+PB的最小值.12、如图,已知直线PT与⊙O相切于点T,直线PO与⊙O相交于A,B两点.(1)求证:PT2=PA•PB;(2)若PT=TB=,求图中阴影部分的面积.13、如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.(1)求证:四边形ACBP是菱形;(2)若⊙O半径为1,求菱形ACBP的面积.14、如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC边于点D,过点C作CF ∥AB,与过点B的切线交于点F,连接BD.(1)求证:BD=BF;(2)若AB=10,CD=4,求BC的长.15、如图,梯形ABCD中,AD∥BC,AE⊥BC于E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.(1)求证:CD与⊙O相切;(2)若BF=24,OE=5,求tan∠ABC的值.16、已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.求证:(1)DE是⊙O的切线;(2)ME2=MD•MN.参考答案1、【解答】解:(1)如图所示,连接OD,∵OD=OB,∴∠ODB=∠OBD,∵BD平分∠OBC,∴∠OBD=∠DBE,∴∠ODB=∠DBE,∴OD∥AC,∵DE⊥AC,∴OD⊥DE,∵OD是⊙O的半径,∴直线DE是⊙O的切线;(2)如图,连接DF,∵BF是⊙O的直径,∴∠FDB=90°,∴∠F+∠OBD=90°,∵∠OBD=∠DBE,∠BDE+∠DBE=90°,∴∠F=∠BDE,在Rt△BDF中,=sinF=sin∠BDE=,∴BD=10×=2,∴在Rt△BDE中,sin∠BDE==,∴BE=2×=2,∴在Rt△BDE中,DE===4。
2024年九年级中考数学压轴题-圆中的新定义问题(解析版)
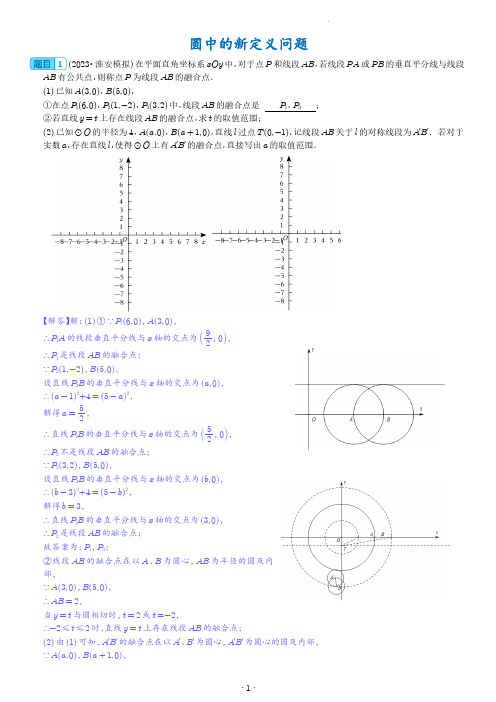
圆中的新定义问题1(2023•淮安模拟)在平面直角坐标系xOy 中,对于点P 和线段AB ,若线段PA 或PB 的垂直平分线与线段AB 有公共点,则称点P 为线段AB 的融合点.(1)已知A (3,0),B (5,0),①在点P 1(6,0),P 2(1,-2),P 3(3,2)中,线段AB 的融合点是 P 1,P 3 ;②若直线y =t 上存在线段AB 的融合点,求t 的取值范围;(2)已知⊙O 的半径为4,A (a ,0),B (a +1,0),直线l 过点T (0,-1),记线段AB 关于l 的对称线段为A B .若对于实数a ,存在直线l ,使得⊙O 上有A B 的融合点,直接写出a 的取值范围.【解答】解:(1)①∵P 1(6,0),A (3,0),∴P 1A 的线段垂直平分线与x 轴的交点为92,0,∴P 1是线段AB 的融合点;∵P 2(1,-2),B (5,0),设直线P 2B 的垂直平分线与x 轴的交点为(a ,0),∴(a -1)2+4=(5-a )2,解得a =52,∴直线P 2B 的垂直平分线与x 轴的交点为52,0,∴P 2不是线段AB 的融合点;∵P 3(3,2),B (5,0),设直线P 3B 的垂直平分线与x 轴的交点为(b ,0),∴(b -3)2+4=(5-b )2,解得b =3,∴直线P 3B 的垂直平分线与x 轴的交点为(3,0),∴P 3是线段AB 的融合点;故答案为:P 1,P 3;②线段AB 的融合点在以A 、B 为圆心,AB 为半径的圆及内部,∵A (3,0),B (5,0),∴AB =2,当y =t 与圆相切时,t =2或t =-2,∴-2≤t ≤2时,直线y =t 上存在线段AB 的融合点;(2)由(1)可知,A B 的融合点在以A 、B 为圆心,A B 为圆心的圆及内部,∵A (a ,0),B (a +1,0),∴AB =A B =1,∵⊙O 上有A B 的融合点,∴圆O 与圆A 、B 有交点,∴圆O 与圆A 、圆B 的公共区域为以O 为圆心2为半径,以O 为圆心6为半径的圆环及内部区域,当a >0时,a 的最大值为62-12=35,最小值为22-12-1=3-1,∴3-1≤a ≤35;当a <0时,a 的最大值为-22-12=-3,最小值为-62-12-1=-35-1,∴-35-1≤a ≤-3;综上所述:a 的取值范围为3-1≤a ≤35或-35-1≤a ≤-3.2(2023•西城区校级模拟)在平面内,C 为线段AB 外的一点,若以点A ,B ,C 为顶点的三角形为直角三角形,则称C 为线段AB 的直角点.特别地,当该三角形为等腰直角三角形时,称C 为线段AB 的等腰直角点.(1)如图1,在平面直角坐标系xOy 中,点M 的坐标为(-1,0),点N 的坐标为(1,0),在点P 1(2,1),P 2(-1,2),P 332,12 中,线段MN 的直角点是 P 2、P 3 ;(2)在平面直角坐标系xOy 中,点A ,B 的坐标分别为(t ,0),(0,4).①若t =4,如图2所示,若C 是线段AB 的直角点,且点C 在直线y =-x +8上,求点C 的坐标;②如图3,点D 的坐标为(m ,-2),⊙D 的半径为1,若⊙D 上存在线段AB 的等腰直角点,求出m 的取值范围.【解答】解:(1)∵P 2(-1,2),M (-1,0),∴P 2M ⊥MN ,∴P 2是线段MN 的直角点;∵M (-1,0),N (1,0),∴MN =2,∵P 332,12,∴P 3O =1,∴P 3在以O 为圆心,MN 为直径的圆上,∴∠MP 3N =90°,∴P 3是线段MN 的直角点;故答案为:P 2、P 3;(2)①∵A (4,0),B (0,4),∴OA =OB =4,∴∠OAB =∠OBA =45°.根据题意,若点C 为线段AB 的直角点,则需要分三种情况:当点B 为直角顶点,过点B 作BC 1⊥AB 于点C 1,过点C 1作C 1M ⊥y 轴于点M ,∴∠C 1BM =45°,∴C 1M =BM ,设C 1M =BM =a ,∴C 1(a ,a +4),∴-a +8=a +4,解得a =2,∴C 1(2,6);当点A 为直角顶点,过点A 作AC 2⊥AB 于点C 2,过点C 2作C 2N ⊥x 轴于点N ,∴∠C 2AN =45°,∴C 2N =AN ,设C 2N =AN =b ,∴C 2(b +4,b ),∴-(b +4)+8=b ,解得b =2,∴C 2(6,2);当点C 为直角顶点,取AB 的中点P ,则P (2,2),设C 3的横坐标为t ,则C 3(t ,-t +8),由直角三角形的性质可知,C 3P =BP =AP =22,∴(t -2)2+(-t +6)2=(22)2,解得t =4,∴C3(4,4),综上,点C的坐标为(2,6)或(6,2)或(4,4).②如图,以AB为边向下作正方形ABC1C2,连接AC1,BC2交于点C3,则C1,C2,C3是线段AB的等腰直角点.根据点A的运动可知,点C1在直线l1:x=-4上运动,C2在直线l2:y=-x-4上运动,C3在直线l3:y=-x上运动.设l2与y=-2相交于点K,l3与y=-2相交于点L,∴K(2,-2),L(2,-2).由此可得出临界情况如图:如图3(1)中,当⊙D与l1相切时,m=-5;如图3(2)中,当⊙D与l2相切时,点F为切点,连接DF,则ΔDFK为等腰直角三角形,且DF=1,∴DK=2;∴D(-2+2,-2),即m=-2+2;如图3(3)中,当⊙D与l3相切时,点G为切点,连接DG,则ΔDGL为等腰直角三角形,且DG=1,∴DL=2;∴D(2-2,-2),即m=2-2;如图3(4)中,当⊙D与l3相切时,点H为切点,连接DH,则ΔDHL为等腰直角三角形,且DH=1,∴DL=2;∴D(2+2,-2),即m=2+2;综上,符合题意的m的取值范围:-5≤m≤-2+2或2-2≤m≤2+2.3(2023•秀洲区校级二模)婆罗摩芨多是公元7世纪古印度伟大的数学家,他在三角形、四边形、零和负数的运算规则,二次方程等方面均有建树,他也研究过对角线互相垂直的圆内接四边形,我们把这类对角线互相垂直的圆内接四边形称为“婆氏四边形”;(1)若平行四边形ABCD是“婆氏四边形”,则四边形ABCD是③.(填序号)①矩形②菱形③正方形(2)如图1,RtΔABC中,∠BAC=90°,以AB为弦的⊙O交AC于D,交BC于E,连接DE、AE、BD,AB=6,sin C=35,若四边形ABED是“婆氏四边形”,求DE的长;(3)如图2,四边形ABCD为⊙O的内接四边形,连接AC,BD,OA,OB,OC,OD,已知∠BOC+∠AOD= 180°,①求证:四边形ABCD是“婆氏四边形”;②当AD+BC=4时,求⊙O半径的最小值.【解答】(1)解:∵平行四边形ABCD为⊙O的内接四边形,∴∠ABC=∠ADC,∠ABC+∠ADC=180°,∴∠ABC=∠ADC=90°,∴平行四边形ABCD是矩形,∵四边形ABCD是“婆氏四边形”,∴AC⊥BD,∴矩形ABCD是正方形,故答案为:③;(2)解:∵∠BAC=90°,AB=6,sin C=35,∴BC=10,AC=8,∴BD为直径,∴∠BED =∠DEC =90°,∵四边形ABED 是“婆氏四边形”,∴AE ⊥BD ,∴AD =DE ,AB =BE =6,设AD =DE =m ,则CD =8-m ,EC =4,在Rt ΔEDC 中,m 2+42=(8-m )2,解得m =3,∴DE =3;(3)①证明:如图2,设AC ,BD 相交于点E ,∵∠DCA =12∠AOD ,∠BDC =12∠BOC ,∠BOC +∠AOD =180°,∴∠DCA +∠BDC =12(∠AOD +∠BOC )=12×180°=90°,∴∠CED =90°,∴AC ⊥BD ,∵四边形ABCD 是⊙O 的内接四边形,∴四边形ABCD 是“婆氏四边形”;②解:过点O 作OM ⊥AD 交于M ,过O 作ON ⊥BC 交于N ,∴AM =12AD ,BN =12BC ,∠AMO =∠BNO =90°,∴∠AOM +∠OAM =90°,∵OA =BO =CO =DO ,∴∠AOM =12∠AOD ,∠BON =12∠BOC ,∵∠BOC +∠AOD =180°,∴∠AOM =∠OBN ,∴ΔOAM ≅ΔBON (AAS ),∴ON =AM =12AD ,∵AD +BC =4,设ON =AM =n ,则AD =2n ,BC =4-2n ,BN =2-n ,在Rt ΔBON 中,BO =n 2+(2-n )2=2(n -1)2+2,当n =1时,BO 有最小值2,∴⊙O 半径的最小值为2.4(2022秋•西城区期末)给定图形W 和点P ,Q ,若图形W 上存在两个不重合的点M ,N ,使得点P 关于点M 的对称点与点Q 关于点N 的对称点重合,则称点P 与点Q 关于图形W 双对合.在平面直角坐标系xOy 中,已知点A (-1,-2),B (5,-2),C (-1,4).(1)在点D (-4,0),E (2,2),F (6,0)中,与点O 关于线段AB 双对合的点是 D ,F ;(2)点K 是x 轴上一动点,⊙K 的直径为1,①若点A 与点T (0,t )关于⊙K 双对合,求t 的取值范围;②当点K 运动时,若ΔABC 上存在一点与⊙K 上任意一点关于⊙K 双对合,直接写出点K 的横坐标k 的取值范围.【解答】解:(1)当A 点是D 点的中点时,对应点为(2,-4);当B 点是D 点的中点时,对应点为(14,-4);当A 点是E 点的中点时,对应点为(-4,-6);当B 点是E 点的中点时,对应点为(8,-6);当A 点是F 点的中点时,对应点为(-8,-4);当B 点是F 点的中点时,对应点为(4,-4);当A 点是O 点的中点时,对应点为(-2,-4);当B 点是O 点的中点时,对应点为(10,-4);∴D 、F 与点O 关于线段AB 双对合,故答案为:D 、F ;(2)①设K(k,0),∵A(-1,-2),T(0,t),∴A点关于K点对称点G为(2k+1,2),T点关于K点对称点H为(2k,-t),∵点A与点T(0,t)关于⊙K双对合,∴A点关于点K的对称点在以G为圆心,∵⊙K的直径为1,∴点A关于点K的对称点在以G点为圆心,1为半径的圆上,点T关于点K的对称点在以H为圆心,1为半径的圆上,如图所示,∵点A与点T(0,t)关于⊙K双对合,∴当圆G与圆H有交点,∵GH=1+(t+2)2,∴1+(t+2)2≤2,解得-2-3≤t≤-2+3;②∵A(-1,-2),B(5,-2),C(-1,4),K(k,0),∴A点关于K点的对称点F(2k+1,2),B点关于K点的对称点E(2k-5,2),C点关于K点的对称点G(2k+1, -4),∴ΔABC上任意一点关于K点对称点在阴影区域,∵ΔABC上存在一点与⊙K上任意一点关于⊙K双对合,∴阴影区域与圆K有公共交点,∵阴影部分是由ΔEGF边上任意一点为圆心,1为半径的圆构成的区域,如图1时,k-(2k+1)=12+1,解得k=-52;如图2时,2k+1-k=12+1,解得k=12;∴-52≤k≤12时,ΔABC上存在一点与⊙K上任意一点关于⊙K双对合;过点K作KN⊥EG交于N,直线EG交x轴于点M,设直线EG的解析式为y=k x+b,∴(2k-5)k +b=2 (2k+1)k +b=-4 ,解得k =-1b=2k-3 ,∴y=-x+2k-3,∴M(2k-3,0),∵直线y=-x与y=-x+2k-3平行,∴∠KMN=45°,∴KM=2KN=322,如图3时,k-(2k-3)=322,解得k=3-322,如图4时,2k-3-k=322,解得k=3+322,∴3-322≤k≤3+322时,ΔABC上存在一点与⊙K上任意一点关于⊙K双对合;综上所述:-52≤k≤12或3-322≤k≤3+322时,ΔABC上存在一点与⊙K上任意一点关于⊙K双对合.5(2022•钟楼区模拟)概念认识:平面内,M为图形T上任意一点,N为⊙O上任意一点,将M、N两点间距离的最小值称为图形T到⊙O的“最近距离”,记作d(T-⊙O).例:如图1,在直线l上有A、C、O三点,以AC为对角线作正方形ABCD,以点O为圆心作圆,与l交于E、F两点,若将正方形ABCD记为图形T,则C、E两点间的距离称为图形T到⊙的“最近距离”.数学理解:(1)在平面内有A、B两点,以点A为圆心,5为半径作⊙A,将点B记为图形T,若d(T-⊙A)=2,则AB= 3或7.(2)如图2,在平面直角坐标系中,以O(0,0)为圆心,半径为2作圆.①将点C(4,3)记为图形T,则d(T-⊙O)=.②将一次函数y=kx+22的图记为图形T,若d(T-⊙)>0,求k的取值范围.推广运用:(3)在平面直角坐标系中,P的坐标为(t,0),⊙P的半径为2,D、E两点的坐标分别为(5,5)、(5,-5),将ΔDOE记为图形T,若d(T-⊙P)=1,则t=.【解答】解:(1)如图1中,∵d(T-⊙A)=2,∴CB=CB′=2,∵AC=5,∴AB′=5-2=3,AB=5+2=7.故答案为:3或7.(2)①如图2中,连接OC交⊙O于E.∵C(4,3),∴OC=42+32=5,∵OE=2,∴EC=3,∴d(T-⊙O)=3.故答案为:3.②如图,设直线y=kx+22与⊙O相切于E,K.连接OK,OE.∵OE⊥DE,OK⊥DK,OD=22,OE=OK=2,∴DK=OD2?OK2=(22)2-22=2,DE=OD2?OE2=(22)2-22=2,∴DE=OE=DK=OK,∴四边形DEOK是菱形,∵∠DKO=∠DEO=90°,∴四边形DEOK是正方形,∴∠ODE=∠ODK=45°,∴直线DE的解析式为y=-x+22,直线DK的解析式为y=x+22,∵d(T-⊙O)>0,∴观察图象可知满足条件的k的值为-1<k<1且k≠0.(3)如图3-1中,当点P在DE的右边时.∵D(5,5),∴∠DOP=45°,∵d(T-⊙P)=1,∴OP=5+1+2=8∴t=8.如图3-2中,当点P在∠DOE的外侧时,由题意可知OM=1,OP=1+2=3,t=-3.综上所述,满足条件的t的值为8或-3.6(2022秋•昌平区期末)已知:对于平面直角坐标系xOy中的点P和⊙O,⊙O的半径为4,交x轴于点A,B,对于点P给出如下定义:过点C的直线与⊙O交于点M,N,点P为线段MN的中点,我们把这样的点P叫做关于MN的“折弦点”.(1)若C(-2,0).①点P1(0,0),P2(-1,1),P3(2,2)中是关于MN的“折弦点”的是 P1,P2 ;②若直线y=kx+3(k≠0).上只存在一个关于MN的“折弦点”,求k的值;(2)点C在线段AB上,直线y=x+b上存在关于MN的“折弦点”,直接写出b的取值范围.【解答】解:(1)①连接OP,∵P点是弦MN的中点,∴OP⊥MN,∴∠CPO=90°,∴P点在以CO为直径的圆上,∵C(-2,0),∴P点在以(-1,0)为圆心,1为半径的圆上,∵点P1(0,0),P2(-1,1)在该圆上,∴点P1(0,0),P2(-1,1)是关于MN的“折弦点”,故答案为:P1,P2;②由①可知,P点在以(-1,0)为圆心,1为半径的圆上,设圆心D(-1,0),∵直线y=kx+3(k≠0)上只存在一个关于MN的“折弦点”,∴直线y=kx+3(k≠0)与圆D相切,过点D作DF垂直直线y=kx+3交于点F,∵直线y=kx+3与x轴交于点E-3k,0,与y轴交于点G(0,3),∴DE=-1+3k,OF=3k,OG=3,∵∠DFE=∠EOG=90°,∴ΔEGO∽ΔEFD,∴DF GO =ED EG,∴13=3k-13+3k2,解得k=3 3;(2)由(1)可知,P点在以OC为直径的圆上,∵直线y=x+b上存在关于MN的“折弦点”,∴直线y=x+b与圆D相交或相切,过D点作DF垂直直线y=x+b交于点F,∵直线y=x+b与x轴交于点(-b,0),与y轴交于点(0,b),当C点与A点重合时,b有最大值,此时D(-2,0),∴(-2+b)2=8,解得b=22+2或b=22+2(舍);当C点与B点重合时,b有最小值,此时D(2,0),∴(-b-2)2=8,解得b=22-2(舍)或b=-22-2;∴-22-2≤b≤22+2时,直线y=x+b上存在关于MN的“折弦点”.7(2022秋•东城区校级月考)如图,在平面直角坐标系xOy中,过⊙T外一点P引它的两条切线,切点分别为M,N,若60°<∠MPN<180°,则称P为⊙T的环绕点.(1)当⊙O半径为1时,①在P1(2,2),P2(2,0),P3(2,1)中,⊙O的环绕点是 P1 ;②直线y=3x+b与x轴交于点A,y轴交于点B,若线段AB上存在⊙O的环绕点,求b的取值范围;(2)⊙T的半径为2,圆心为(0,t),以-m,33m(m>0)为圆心,33m为半径的所有圆构成图形H,若在图形H上存在⊙T的环绕点,直接写出t的取值范围.【解答】解:(1)①如图,PM,PN是⊙T的两条切线,M,N为切点,连接TM,TN,当∠MPN=60°时,∵PT平分∠MPN,∴∠TPN=∠MPT=30°,∵TM⊥PM,TN⊥PN,∴∠TNP=∠PMT=90°,∴TP =2TM =2,以T 为圆心,TP 为半径作⊙T .观察图象可知:当60°<∠MPN <180°时,⊙T 的环绕点在图中的圆环内部(包括大圆上的点不包括小圆上的点),故答案为:P 1;②如图中,设小圆交y 轴的正半轴于F ,当直线y =3x +b 经过点F 时,b =1,当直线y =3x +b 与大圆相切于K (在第二象限)时,连接OK ,由题意B (0,b ),A -b 3,0,所以OB =b ,OA =b 3,AB =103b ,∵OK =2,12×AB ×OK =12×OA ×OB ,∴b =210,观察图象可知,当1<b <210时,线段AB 上存在⊙的环绕点,根据对称怀可知:当-210<b <-1时,线段AB 上存在⊙的环绕点,综上所述,满足条件的b 的值为1<b <210或-210<b <-1;(2)如图中,不妨设E -m ,33m (m >0),则点E 直线y =-33x 上,∵m >0,∴点E 在射线OE 上运动,作EM ⊥x 轴;∵E -m ,33m (m >0),∴OM =m ,EM =33m ,以E -m ,33m (m >0)为圆心,33m 为半径的⊙E 与x 轴相切,作⊙E 的切线ON ,观察图象可知:以E -m ,33m (m >0)为圆心,33m 为半径的所有圆构成图形H ,图形H 即为∠MON 的内部,包括射线OM ,ON 上,当⊙T 的圆心在y 轴的正半轴上时,假设以T 为圆心,4为半径的圆与射线ON 相切于D ,连接TD ,∵tan ∠EOM =EM OM=33,∴∠EOM =30°,∵OM ,ON 是⊙E 的切线,∴∠EON =∠EOM =30°.∴∠TOD =30°,∴OT =2DT =8,∴T (0,8),当⊙T 的圆心在y 轴的负半轴上时,且经过点O (0.0)时,T (0,-4),观察图象可知,当-4<t <8时,在图象上存在⊙T 的环绕点.8(2022秋•海淀区校级月考)对于平面直角坐标系中的线段AB 和点P (点P 不在线段AB 上),给出如下定义:当PA =PB 时,过点A (或点B )向直线PB (或PA )作垂线段,则称此垂线段为点P 关于线段AB 的“测度线段”,垂足称为点P 关于线段AB 的“测度点”.如图所示,线段AD 和BC 为点P 关于线段AB 的“测度线段”,点C 与点D为点P关于线段AB的“测度点”.(1)如图,点M(0,4)、N(2,0),①点P的坐标为(5,4),直接写出点P关于线段MN的“测度线段”的长度4;②点H为平面直角坐标系中的一点,且HM=HN,则下列四个点:Q1(0,0),Q2(3,3),Q3(1,0),Q4(0,4)中,是点H 关于线段MN的“测度点”的是;(2)直线y=-34x+6与x轴、y轴分别交于点A与点B,①点G为平面直角坐标系中一点,且GA=GB,若一次函数y=kx-14k+3上存在点G关于线段AB的“测度点”,直接写出k的取值范围为;②⊙O的半径为r,点C与点D均在⊙O上,且线段CD=65r.点K与点O位于线段CD的异侧,且KC=KD,若在线段AB上存在点K关于线段CD的“测度点”,直接写出r的取值范围为.【解答】解:(1)①∵M(0,4)、P(5,4),∴MP⎳x轴,∴点P关于线段MN的“测度线段”的长度为4,故答案为:4;②∵过点N作NF⊥MH交于F点,过点M作MG⊥NH交于点G,∵∠MFN=∠MGN=90°,∴F、G点在以MN为直径的圆上,设MN的中点为E,∵点M(0,4)、N(2,0),∴E(1,2),MN=25,∴点H关于线段MN的“测度点”在以E为圆心,5为半径的圆上,且不与M、N重合,∵Q1(0,0),Q2(3,3),Q3(1,0),Q4(0,4)中,Q1E=5,Q2E=5,Q3E=2,Q4E=5,∴Q1,Q2是点H关于线段MN的“测度点”,故答案为:Q1,Q2;(2)①当x=0时,y=6,∴B(0,6),当y=0时,x=8,∴A(8,0),∴AB的中点F(4,3),AB=10,由(1)可知,点G关于线段AB的“测度点”在以F为圆心,5为半径的圆上,且不与A、B点重合,∵一次函数y=kx-14k+3上存在点G关于线段AB的“测度点”,∴直线y=kx-14k+3与圆F相切或相交,过点F作FK垂直直线y=kx-14k+3交于点K,直线与y轴的交点为T,过点F作FL⎳KT交于交y轴于点L,过点L作SL⊥KT交于点S,∴LS =FK =5,∴LF 的直线解析式为y =kx -4k +3,∴L (0,-4k +3),T (0,-14k +3),∴TL =-10k ,∵sin ∠LTS =5-10k =11+k 2,∴k =±33,∴-33≤k ≤33时,一次函数y =kx -14k +3上存在点G 关于线段AB 的“测度点”,故答案为:-33≤k ≤33;②由(1)可知,K 点关于线段CD 的“测度点”在以CD 为直角的半圆上,且不与C 、D 重合,当CD ⎳AB ,且AB 与圆P 相切时,r 有最小值,由①可得,45=35r 6-r ,解得r =247,当CD 在AB 上时,r 有最大值,r =6,∴247≤r <6时,线段AB 上存在点K 关于线段CD 的“测度点”,故答案为:247≤r <6.9(2022•盐城一模)对于平面内的两点K 、L ,作出如下定义:若点Q 是点L 绕点K 旋转所得到的点,则称点Q 是点L 关于点K 的旋转点;若旋转角小于90°,则称点Q 是点L 关于点K 的锐角旋转点.如图1,点Q 是点L 关于点K 的锐角旋转点.(1)已知点A (4,0),在点Q 1(0,4),Q 2(2,23),Q 3(-2,23),Q 4(22,-22)中,是点A 关于点O 的锐角旋转点的是 Q 2,Q 4 .(2)已知点B (5,0),点C 在直线y =2x +b 上,若点C 是点B 关于点O 的锐角旋转点,求实数b 的取值范围.(3)点D 是x 轴上的动点,D (t ,0),E (t -3,0),点F (m ,n )是以D 为圆心,3为半径的圆上一个动点,且满足n ≥0.若直线y =2x +6上存在点F 关于点E 的锐角旋转点,请直接写出t 的取值范围.【解答】解:(1)如图,∵A (4,0),Q 1(0,4),∴OA =OQ 1=4,∠AOQ 1=90°,∴点Q 1不是点A 关于点O 的锐角旋转点;∵Q 2(2,23),作Q 2F ⊥x 轴于点F ,∴OQ 2=OF 2+Q 2F 2=22+(23)2=4=OA ,∵tan ∠Q 2OF =232=3,∴∠Q 2OF =60°,∴点Q 2是点A 关于点O 的锐角旋转点;∵Q 3(-2,23),作Q 3G ⊥x 轴于点G ,则tan ∠Q 3OG =Q 3G OG=232=3,∴∠Q3OG =60°,∴OQ 3=OG cos ∠Q 3OG =2cos60°=4=OA ,∵∠AOQ 3=180°-60°=120°,∴Q 3不是点A 关于点O 的锐角旋转点;∵Q 4(22,-22),作Q 4H ⊥x 轴于点H ,则tan ∠Q 4OH =Q 4H OH =2222=1,∴∠Q 4OH =45°,∵OQ 4=OH cos ∠Q 4OH =22cos45°=4=OA ,∴Q 4是点A 关于点O 的锐角旋转点;综上所述,在点Q 1,Q 2,Q 3,Q 4中,是点A 关于点O 的锐角旋转点的是Q 2,Q 4,故答案为:Q 2,Q 4.(2)在y 轴上取点P (0,5),当直线y =2x +b 经过点P 时,可得b =5,当直线y =2x +b 经过点B 时,则2×5+b =0,解得:b =-10,∴当-10<b <5时,OB 绕点O 逆时针旋转锐角时,点C 一定可以落在某条直线y =2x +b 上,过点O 作OG ⊥直线y =2x +b ,垂足G 在第四象限时,如图,则OT =-b ,OS =-12b ,∴ST =OS 2+OT 2=-12b 2+(-b )2=-52b ,当OG =5时,b 取得最小值,∵5×-52b =-b ×-12b ,∴b =-55,∴-55≤b <5.(3)根据题意,点F 关于点E 的锐角旋转点在半圆E 上,设点P 在半圆S 上,点Q 在半圆T 上(将半圆D 绕点E 旋转),如图3(1),半圆扫过的区域为图3(1)中阴影部分,如图3(2)中,阴影部分与直线y =2x +6相切于点G ,tan ∠EMG =2,SG =3,过点G 作GI ⊥x 轴于点I ,过点S 作SJ ⊥GI 于点J ,∴∠SGJ =∠EMG ,∴tan ∠SGJ =tan ∠EMG =2,∴GJ =355,SJ =655,∴GI =GJ +JI =3+355,∴MI =12GI =32+3510,∴OE =IE +MI -OM =352-32,即x E =t -3=352-32,解得t =352+32,如图3(3)中,阴影部分与HK 相切于点G ,tan ∠OMK =tan ∠EMH =2,EH =6,则MH =3,EM =35,∴x E =t -3=-3-35,解得t =-35,观察图象可知,-35≤t <3+352+32.10(2022秋•姜堰区期中)如图1,在平面内,过⊙T 外一点P 画它的两条切线,切点分别为M 、N ,若∠MPN ≥90°,则称点P 为⊙T 的“限角点”.(1)在平面直角坐标系xOy 中,当⊙O 半径为1时,在①P 1(1,0),②P 2-1,12,③P 3(-1,-1),④P 4(2,-1)中,⊙O 的“限角点”是②④;(填写序号)(2)如图2,⊙A 的半径为2,圆心为(0,2),直线l :y =-34x +b 交坐标轴于点B 、C ,若直线l 上有且只有一个⊙A 的“限角点”,求b 的值.(3)如图3,E (2,3)、F (1,2)、G (3,2),⊙D 的半径为2,圆心D 从原点O 出发,以2个单位/s 的速度沿直线l :y =x 向上运动,若ΔEFG 三边上存在⊙D 的“限角点”,请直接写出运动的时间t (s )的取值范围.【解答】解:(1)∵⊙O 半径为1,∴当P 为圆O 的“限角点”时,1<OP ≤2,∵OP 1=1,OP 2=52,OP 3=2,OP 4=5,∴⊙O 的“限角点”是P 2,P 3,故答案为:②③;(2)∵⊙A 的半径为2,∴当P 为圆A 的“限角点”时,2<AP ≤2,设直线l 上有且只有一个⊙O 的“限角点”P m ,-34m +b ,∴PA =2,此时AP ⊥BC ,令x =0,则y =b ,∴C (0,b ),令y =0,则x =43b ,∴B 43b ,0 ,∴tan ∠OCB =OB OC =43=AP CP ,∴CP =32,∴AC =52,∴|b -2|=52,∴b =92或b =-12;(3)∵圆心D 从原点O 出发,以2个单位/s 的速度沿直线l 移动,∴圆沿x 轴正方向移动t 个单位,沿y 轴正方向移动t 个单位,∴移动后D 点坐标为(t ,t ),设ΔEFG 边上的点P 是圆D 的“限角点”,则2<PD ≤2,在圆D 移动的过程中,当DF =2时,(t -1)2+(t -2)2=4,解得t =3-72或t =3+72,当t =3-72时,ΔEFG 边上开始出现⊙D 的“限角点”,当圆D 移动到E 点在圆上时,DE =2,(t -2)2+(t -3)2=2,解得t =5+32或t =5-32,∴3-72≤t <5-32时,ΔEFG 边上存在⊙D 的“限角点”,当圆D 再次移动到点F 在圆上时,DF =2,(t -2)2+(t -1)2=2,解得t =3+32或t 3-32,当t =3+32时,ΔEFG 三边上开始又要出现⊙D 的“限角点”;设直线EG 的解析式为y =kx +b ,直线y =x 与直线EG 的交点设为点H ,∴2k +b =33k +b=2 ,解得k =-1b =5 ,解得y =-x +5,联立方程组y =-x +5y =x,解得x =52y =52,∴H 52,52,当DH =2时,2t -52 2=4,解得t =2+52或t =-2+52,∴当t =2+52,ΔEFG 边上存在⊙D 的“限角点”,∴3+32<t ≤2+52时,ΔEFG 边上存在⊙D 的“限角点”;综上所述:3-72≤t <5-32或3+32<t ≤2+52时,ΔEFG 边上存在⊙D 的“限角点”.11(2022秋•西城区校级期中)在平面直角坐标系xOy中,已知点M(a,b),N.对于点P给出如下定义:将点P绕点M逆时针旋转90°,得到点P ,点P 关于点N的对称点为Q,称点Q为点P的“对应点”.(1)如图1,若点M在坐标原点,点N(1,1),①点P(-2,0)的“对应点”Q的坐标为 (2,0) ;②若点P的“对应点”Q的坐标为(-1,3),则点P的坐标为;(2)如图2,已知⊙O的半径为1,M是⊙O上一点,点N(0,2),若P(m,0)(m>1)为⊙O外一点,点Q为点P的“对应点”,连接PQ.①当点M(a,b)在第一象限时,求点Q的坐标(用含a,b,m的式子表示);②当点M在⊙O 上运动时,直接写出PQ长的最大值与最小值的积为.(用含m的式子表示)【解答】解:(1)①∵P(-2,0),∴P点绕点M逆时针旋转90°得到点P (0,-2),∵点P 关于点N的对称点为Q,∴Q(2,0);故答案为:(2,0);②∵Q的坐标为(-1,3),∴Q点关于N(1,1)的对称点为P (3,-1),将P 绕M点顺时针旋转90°得到点P,过P 作P F⊥x轴于点F,过点P作PE⊥x轴于点E,∵∠P OP=90°,∴∠POE+∠FOP =90°,∵∠EPO+∠EOP=90°,∴∠FOP =∠EPO,∵OP=OP ,∴ΔPOE≅△OP F(AAS),∴EO=P F=1,PE=OF=3,∴P(-1.-3),故答案为:(-1,-3);(2)①过点M作EF⊥x轴于点F,过点P 作P E⊥EF交于点E,由(1)可得ΔMPF≅△P ME(AAS),∴MF=EP ,FP=ME,∵M(a,b),P(m,0),∴EF=b+m-a,EP =b,∴P (a+b,b+m-a),∵点N(0,2),∴Q(-a-b,4-b-m+a);②P点绕O点逆时针旋转90°后得到点G,∴G(0,m),∵P (a+b,b+m-a),∴GP =2(a 2+b 2),∵M (a ,b )在圆O 上,∴a 2+b 2=1,∴GP =2,∴P 在以G 为圆心,2为半径的圆上,设G 点关于N 点的对称点为H ,则H (0,4-m ),∴QH =2(a 2+b 2)=2,∴Q 点在以H 为圆心2为半径的圆上,∴PQ 的最大值为PH +2,PQ 的最小值为PH -2,∴PQ 长的最大值与最小值的积为(PH +2)(PH -2)=2m 2-8m +14,故答案为:2m 2-8m +14.12(2022•秦淮区二模)【概念认识】与矩形一边相切(切点不是顶点)且经过矩形的两个顶点的圆叫做矩形的第Ⅰ类圆;与矩形两边相切(切点都不是顶点)且经过矩形的一个顶点的圆叫做矩形的第Ⅱ类圆.【初步理解】(1)如图①~③,四边形ABCD 是矩形,⊙O 1和⊙O 2都与边AD 相切,⊙O 2与边AB 相切,⊙O 1和⊙O 3都经过点B ,⊙O 3经过点D ,3个圆都经过点C .在这3个圆中,是矩形ABCD 的第Ⅰ类圆的是①,是矩形ABCD 的第Ⅱ类圆的是.【计算求解】(2)已知一个矩形的相邻两边的长分别为4和6,直接写出它的第Ⅰ类圆和第Ⅱ类圆的半径长.【深入研究】(3)如图④,已知矩形ABCD ,用直尺和圆规作图.(保留作图痕迹,并写出必要的文字说明)①作它的1个第Ⅰ类圆;②作它的1个第Ⅱ类圆.【解答】解:(1)由定义可得,①的矩形有一条边AD 与⊙O 1相切,点B 、C 在圆上,∴①是第Ⅰ类圆;②的矩形有两条边AD 、AB 与⊙O 2相切,点C 在圆上,∴②是第Ⅱ类圆;故答案为:①,②;(2)如图1,设AD =6,AB =4,切点为E ,过点O 作EF ⊥BC 交BC 于F ,交AD 于E ,连接BO ,设BO =r ,则OE =r ,OF =4-r ,由垂径定理可得,BF =CF =3,在Rt ΔBOF 中,r 2=(4-r )2+32,解得r =258;如图2,设AD =4,BC =6,切点为E ,过点O 作EF ⊥BC 交BC 于F ,交AD 于E ,连接BO ,设BO =r ,则OE =r ,OF =6-r ,由垂径定理可得,BF =CF =2,在Rt ΔBOF 中,r 2=(6-r )2+22,解得r =103;综上所述:第Ⅰ类圆的半径是258或103;如图3,AD =6,AB =4,过点O 作MN ⊥AD 交于点M ,交BC 于点N ,连接OC ,设AB 边与⊙O 的切点为G ,连接OG ,∴GO ⊥AB ,设OM =r ,则OC =r ,则ON =4-r ,∵OG =r ,∴BN =r ,∴NC =6-r ,在Rt ΔOCN 中,r 2=(4-r )2+(6-r )2,解得r =10-43,∴第Ⅱ类圆的半径是10-43;(3)①如图4,第一步,作线段AD 的垂直平分线交AD 于点E ,第二步,连接EC ,第三步,作EC 的垂直平分线交EF 于点O ,第四步,以O 为圆心,EO 为半径作圆,∴⊙O 即为所求第Ⅰ类圆;②如图5,第一步:作∠BAD 的平分线;第二步:在角平分线上任取点E ,过点E 作EF ⊥AD ,垂足为点F ;第三步:以点E 为圆心,EF 为半径作圆E ,交AC 于点G ,连接FG ;第四步:过点C 作CH ⎳FG ,CH 交AD 于点H ;第五步:过点H 作AD 的垂线,交∠BAD 的平分线于点O ;第六步:以点O 为圆心,OH 为半径的圆,⊙O 即为所求第Ⅱ类圆.13(2021秋•海淀区校级期末)新定义:在平面直角坐标系xOy 中,若几何图形G 与⊙A 有公共点,则称几何图形G 的叫⊙A 的关联图形,特别地,若⊙A 的关联图形G 为直线,则称该直线为⊙A 的关联直线.如图,∠M 为⊙A 的关联图形,直线l 为⊙A 的关联直线.(1)已知⊙O 是以原点为圆心,2为半径的圆,下列图形:①直线y =2x +2;②直线y =-x +3;③双曲线y =2x,是⊙O 的关联图形的是①③(请直接写出正确的序号).(2)如图1,⊙T 的圆心为T (1,0),半径为1,直线l :y =-x +b 与x 轴交于点N ,若直线l 是⊙T 的关联直线,求点N 的横坐标的取值范围.(3)如图2,已知点B (0,2),C (2,0),D (0,-2),⊙I 经过点C ,⊙I 的关联直线HB 经过点B ,与⊙I 的一个交点为P ;⊙I 的关联直线HD 经过点D ,与⊙I 的一个交点为Q ;直线HB ,HD 交于点H ,若线段PQ 在直线x =6上且恰为⊙I 的直径,请直接写出点H 横坐标h 的取值范围.【解答】解:(1)由题意①③是⊙O的关联图形,故答案为①③.(2)如图1中,∵直线l1y=-x+b是⊙T的关联直线,∴直线l的临界状态是和⊙T相切的两条直线l1和l2,当临界状态为l1时,连接TM(M为切点),∴TM=1,TM⊥MB,且∠MNO=45°,∴ΔTMN是等腰直角三角形,∴TN=2,OT=1,∴N(1+2,0),把N(1+2,0)代入y=-x+b中,得到b=1+2,同法可得当直线l2是临界状态时,b=-2+1,∴点N的横坐标的取值范围为-2+1≤N x≤2+1.(3)如图3-1中,当点Q在点P是上方时,连接BQ,PD交于点H,当圆心I在x轴上时,点H与点C重合,此时H(2,0),得到h的最大值为2,如图3-2中,当点P在点Q是上方时,直线PB,QD交于点H,当圆心I在x轴上时,点H(-6,0)得到h的最小值为-6,综上所述,-6≤h<0,0<h≤2.14(2022春•海淀区校级月考)定义:P、Q分别是两条线段a和b上任意一点,线段PQ长度的最小值叫做线段a与线段b的“冰雪距离”.已知O(0,0),A(1,1),B(m,n),C(m,n+2)是平面直角坐标系中四点.(1)根据上述定义,完成下面的问题:①当m=2,n=1时,如图1,线段BC与线段OA的“冰雪距离”是1.②当m=2时,线段BC与线段OA的“冰雪距离”是1,则n的取值范围是.(2)如图2,若点B落在圆心为A,半径为1的圆上,当n≥1时,线段BC与线段OA的“冰雪距离”记为d,结合图象,求d的最小值;(3)当m的值变化时,动线段BC与线段OA的“冰雪距离”始终为1,线段BC的中点为M.求点M随线段BC运动所走过的路径长.【解答】解:(1)①当m=2,n=1时,B(2,1),C(2,3).线段BC与线段OA的冰雪距离为AB=1.故答案为:1.②当m=2时,点A到直线BC的距离为1.若线段BC与线段OA的冰雪距离是1,则点A到BC的垂线的垂足在线段BC上,∴n≤1≤n+2,即-1≤n≤1.故答案为:-1≤n ≤1.(2)如图,B 2(0,1)为圆A 与y 轴的切点,B 11-22,1+22满足∠B 1AO =90°.当B 在B 1右侧时,冰雪距离d ≥B 1A =22.当B 在弧B 1B 2上时,冰雪距离d 为点B 到OA 的距离,结合图象可知,当且仅当B 处在点B 2时,d 取最小值22.(3)如图,当点B 位于图中弧DI 、线段IH 、弧HG 时,线段BC 与线段OA 的“冰雪距离”始终为1.当点C 位于图中弧DE 、线段EF 、弧FG 时,线段BC 与线段OA 的“冰雪距离”始终为1.当线段BC 由图中B 1D 向上平移到DC 3时,或由B 2G 向上平移到GC 4时,线段BC 与线段OA 的“冰雪距离”始终为1.对应中点M 所走过的路线长为:2π+4+22.15(2022•东城区校级开学)对于⊙C 和⊙C 上的一点A ,若平面内的点P 满足:射线AP 与⊙C 交于点Q (点Q 可以与点P 重合),且1≤PAQA ≤2,则点P 称为点A 关于⊙C 的“生长点”.已知点O 为坐标原点,⊙O 的半径为1,点A (-1,0).(1)若点P 是点A 关于⊙O 的“生长点”,且点P 在x 轴上,请写出一个符合条件的点P 的坐标 (2,0)(答案不唯一);(2)若点B 是点A 关于⊙O 的“生长点”,且满足∠BAO =30°,求点B 的纵坐标t 的取值范围;(3)直线y =3x +b 与x 轴交于点M ,且与y 轴交于点N ,若线段MN 上存在点A 关于⊙O 的“生长点”,直接写出b 的取值范围是.【解答】解:(1)根据“生长点”定义,点P 的坐标可以是(2,0),故答案为:(2,0)(答案不唯一);(2)如图,在x 轴上方作射线AM ,与⊙O 交于M ,使得∠OAM =30°,并在射线AM 上取点N ,使AM =MN ,并由对称性,将MN 关于x 轴对称,得M N ,则由题意,线段MN 和M N 上的点是满足条件的点B .作MH ⊥x 轴于H ,连接MC ,∴∠MHA =90°,即∠OAM +∠AMH =90°.∵AC 是⊙O 的直径,∴∠AMC =90°,即∠AMH +∠HMC =90°.∴∠OAM =∠HMC =30°.∴tan30°=MH AH=HC MH =33,设MH=y,则AH=3y,CH=33y,∴AC=AH+CH=433y=2,解得y=32,即点M的纵坐标为32.又由AN=2AM,A为(-1,0),可得点N的纵坐标为3,故在线段MN上,点B的纵坐标t满足:32≤t≤3,由对称性,在线段M N 上,点B的纵坐标t满足:?3≤t≤?3 2,∴点B的纵坐标t的取值范围是:32≤t≤3或?3≤t≤?32.(3)如图,Q是⊙O上异于点A的任意一点,延长AQ到P,使得PA=2AQ,∵Q的轨迹是以O为圆心,1为半径的圆,∴点P的运动轨迹是以K(1,0)为圆心,2为半径的圆,当直线MN与⊙K相切于点R时,连接KR,在RtΔKMR中,∠KRM=90°,∵直线y=3x+b与x轴夹角为60°,∴∠KMR=60°,KR=2,∴KM=2÷sin60°=433,∴OM=1+433,∴ON=3OM=4+3,∴b=-4-3,当直线MN经过G(0,-1)时,满足条件,此时b=-1,观察图象可知:当-4-3≤b≤-1时,线段MN上存在点A关于⊙O的“生长点”,根据对称性,同法可得当1≤b≤4-3时,也满足条件.故答案为:-4-3≤b≤-1或1≤b≤4-3.16(2022•东城区校级开学)在平面直角坐标系xOy中,给出如下定义:若点P在图形M上,点Q在图形N 上,称线段PQ长度的最小值为图形M,N的“近距离”,记为d(M,N).特别地,若图形M,N有公共点,规定d(M,N)=0,如图,点A(-23,0),B(0,2).(1)如果⊙O的半径为2,那么d(A,⊙O)= 23-2 ,d(B,⊙O)=;(2)如果⊙O的半径为r,且d(⊙O,AB)>0,求r的取值范围;(3)如果C(0,m)是y轴上的动点,⊙C的半径为1,使d(⊙C,AB)<1,直接写出m的取值范围为.【解答】解:(1)∵⊙O的半径为2,A(-23,0),B(0,2),∴OB=2,OA=23>2,∴点A在⊙O外,点B在⊙O上,∴d(A,⊙O)=23-2,d(B,⊙O)=0,故答案为:23-2;0;(2)如图1,过点O 作OD ⊥AB 于点D ,在Rt ΔAOB 中,∵tan ∠BAO =OB OA =223=33,∴∠BAO =30°.在Rt ΔADO 中,sin ∠BAO =DO OA =12=DO23,∴DO =3,∵d (⊙O ,AB )=0,∴r 的取值范围是0<r <3或r >23;(3)如图2,过点C 作CN ⊥AB 于点N ,由(2)知,∠BAO =30°.∵C (m ,0),当点C 在点B 的上边时,m >2,此时,d (⊙C ,AB )=BC ,∴BC ≤1,即m -2≤1,解得m ≤3;当点C 与点B 重合时,m =2,此时d (⊙C ,AB )=0,当点C 在点B 的下边时,m <2,∴BC =2-m ,∴CN =BC ⋅sin ∠OBA =32(2-m ).∵d (⊙C ,AB )<1,⊙C 的半径为1,∴0<32(2-m )<1.∴2-233<m <2.综上所述:2-233<m ≤3.故答案为:2-233<m ≤3.17(2021秋•润州区校级月考)在平面直角坐标系xOy 中,⊙C 的半径为r ,P 是与圆心C 不重合的点,点P 关于⊙C 的反称点的定义如下:若在射线CP 上存在一点P ′,满足CP +CP ′=2r ,则称P ′为点P 关于⊙C 的反称点,如图为点P 及其关于⊙C 的反称点P ′的示意图.(1)当⊙O 的半径为1时,①分别判断点M (3,1),N 32,0,T (-1,3)关于⊙O 的反称点是否存在?若存在,直接求其坐标;②将⊙O 沿x 轴水平向右平移1个单位为⊙O ′,点P 在直线y =-x +1上,若点P 关于⊙O ′的反称点P ′存在,且点P ′不在坐标轴上,则点P 的横坐标的取值范围 1-2≤x ≤1+2且x ≠2-2 ;(2)⊙C 的圆心在x 轴上,半径为1,直线y =-x +12与x 轴,y 轴分别交于点A 、B ,点E 与点D 分别在点A 与点B 的右侧2个单位,线段AE 、线段BD 都是水平的,若四边形ABDE 四边上存在点P ,使得点P 关于⊙C 的反称点P ′在⊙C 的内部,直接写出圆心C 的横坐标的取值范围.。
人教版九年级数学上册第二十四章 圆 综合压轴题练习(含详解)

人教版九年级数学上册第二十四章《圆》综合压轴题17道【答案及详解】1.如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点且AP=AC.(1)求证:P A是⊙O的切线;(2)若AB=2+,BC=4,求⊙O的半径.2.如图,△ABC是⊙O的内接三角形,BC是⊙O的直径,过点O作OF⊥BC,交AC于点E,连接AF,且AF是⊙O的切线.(1)求证:AF=EF.(2)若⊙O的半径为5,AB=,求AF的长.3.如图,AB为⊙O的直径,C,D为⊙O上的两点,∠BAC=∠DAC,过点C做直线EF ⊥AD,交AD的延长线于点E,连接BC.(1)求证:EF是⊙O的切线;(2)若∠BAC=∠DAC=30°,BC=2,求劣弧的长l.4.如图所示,AB是⊙O的直径,AD和BC分别切⊙O于A,B两点,CD与⊙O有公共点E,且AD=DE.(1)求证:CD是⊙O的切线;(2)若AB=12,BC=4,求AD的长.5.如图,直线l与⊙O相离,OA⊥l于点A,与⊙O相交于点P,OA=10.C是直线l上一点,连结CP并延长交⊙O于另一点B,且AB=AC.(1)求证:AB是⊙O的切线;(2)若⊙O的半径为6,求线段BP的长.6.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,交BC于F.(1)若∠ABC=40°,∠C=80°,求∠CBD的度数;(2)求证:DB=DE;(3)若AB=6,AC=4,BC=5,求DE的长.7.如图①,AB为⊙O的直径,点C在⊙O上,AD平分∠CAB,AD与BC交于点F,过点D作DE⊥AB于点E.(1)求证:BC=2DE;(2)如图②,连接OF,若∠AFO=45°,半径为2时,求AC的长.8.如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O 为圆心,OA为半径的圆恰好经过点D,分别交AC、AB于点E.F.(1)试判断直线BC与⊙O的位置关系,并说明理由;(2)若BD=2,BF=2,求⊙O的半径.9.如图,在四边形ABCD中,AD∥BC,AD⊥CD,AC=AB,⊙O为△ABC的外接圆.(1)如图1,求证:AD是⊙O的切线;(2)如图2,CD交⊙O于点E,过点A作AG⊥BE,垂足为F,交BC于点G.若AD =2,CD=3,求GF的长.10.如图,已知点A、C、D在⊙O上,⊙O的半径为2,CD为⊙O的直径,直线AB∥CD 且∠ADC=60°,将线段AD绕点A逆时针旋转得到线段AF,点D的对应点为点F,且点F在射线AB上,连接FC;(1)求线段AF的长;(2)若点E是上的一点,连接EF,DE,过点F作FH⊥DE于H,延长FH交⊙O 于G,若EF=2,求FG的长.11.如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.(1)求证:CD是⊙O的切线;(2)若∠CBD=30°,BC=3,求⊙O半径.12.如图,在△ABC中,AB=CB,AB是⊙O的直径,D为⊙O上一点,且弧AD=弧BD,直线l经过点C、D,连接AD,交BC于点E,若∠CAD=∠CBA.(1)求证:直线l是⊙O的切线;(2)求的值.13.如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,弦AD与BC,OC分别交于E、F.(1)求证:=;(2)若CE=1,EB=3,求⊙O的半径.14.如图,已知⊙O是等边三角形ABC的外接圆,点D在圆上,在CD的延长线上有一点F,使DF=DA,AE∥BC交CF于E.(1)求证:EA是⊙O的切线;(2)判断BD与CF的数量关系?说明理由.15.如图,CD为⊙O的直径,弦AB⊥CD,垂足为H,P是CD延长线上一点,DE⊥AP,垂足为E,∠EAD=∠HAD.(1)求证:AE为⊙O的切线;(2)已知P A=2,PD=1,求⊙O的半径和DE的长.16.如图,在△ABC中,AB=AC,AE是BC边上的高,BM平分∠ABC交AE于点M,经过B,M两点的⊙O交BC于点G,交AB于点F,FB为⊙O的直径.(1)求证:AM是⊙O的切线;(2)当BC=10,AE=12时,求AM的长度.17.如图,在△ABC中,AC=BC,以BC为直径作⊙O,交AC于点M,作CD⊥AC交AB 延长线于点D,E为CD上一点,且BE=DE.(1)证明:BE为⊙O的切线;(2)若AM=8,AB=8,求BE的长.参考答案1.如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点且AP=AC.(1)求证:P A是⊙O的切线;(2)若AB=2+,BC=4,求⊙O的半径.【解答】(1)证明:连接OA,∵∠B=60°,∴∠AOC=2∠B=120°,又∵OA=OC,∴∠OAC=∠OCA=30°,又∵AP=AC,∴∠P=∠ACP=30°,∴∠OAP=∠AOC﹣∠P=90°,∴OA⊥P A,∴P A是⊙O的切线;(2)解:过点C作CE⊥AB于点E.在Rt△BCE中,∠B=60°,BC=4,∴BE=BC=2,CE=2,∵AB=2+,∴AE=AB﹣BE=,在Rt△ACE中,AC==3,。
中考数学——圆的综合的综合压轴题专题复习附详细答案
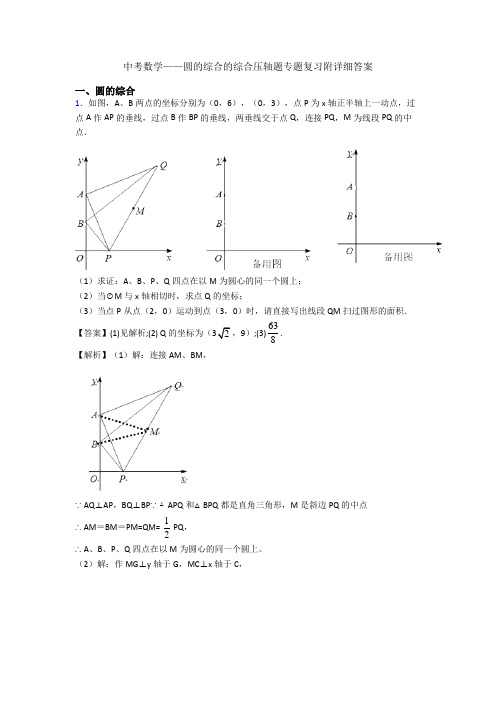
中考数学——圆的综合的综合压轴题专题复习附详细答案一、圆的综合1.如图,A、B两点的坐标分别为(0,6),(0,3),点P为x轴正半轴上一动点,过点A作AP的垂线,过点B作BP的垂线,两垂线交于点Q,连接PQ,M为线段PQ的中点.(1)求证:A、B、P、Q四点在以M为圆心的同一个圆上;(2)当⊙M与x轴相切时,求点Q的坐标;(3)当点P从点(2,0)运动到点(3,0)时,请直接写出线段QM扫过图形的面积.【答案】(1)见解析;(2) Q的坐标为(32,9);(3)63 8.【解析】(1)解:连接AM、BM,∵AQ⊥AP,BQ⊥BP∵△APQ和△BPQ都是直角三角形,M是斜边PQ的中点∴AM=BM=PM=QM= 12 PQ,∴A、B、P、Q四点在以M为圆心的同一个圆上。
(2)解:作MG⊥y轴于G,MC⊥x轴于C,∵AM=BM∴G是AB的中点,由A(0,6),B(0,3)可得MC=OG=4.5∴在点P运动的过程中,点M到x轴的距离始终为4.5则点Q到x轴的距离始终为9,即点Q的纵坐标始终为9,当⊙M与x轴相切时则PQ⊥x轴,作QH⊥y轴于H,HB=9-3=6,设OP=HQ=x由△BOP∽△QHB,得x2=3×6=8,x=2∴点Q的坐标为(2,9)(3)解:由相似可得:当点P在P1(2,0)时,Q1(4,9)则M1(3,4.5)当点P在P2(3,0)时,Q2(6,9),则M2(4.5,4.5)∴M1M2=92-3=32, Q1Q2=6-4=2线段QM扫过的图形为梯形M1M2Q2Q1其面积为:12×(32+2)×4.5=638.【解析】【分析】根据已知可得出三角形APQ和三角形BPQ都是直角三角形,再根据这个条件结合题意直接解答此题.【详解】(1)解:连接AM、BM,∵AQ⊥AP,BQ⊥BP∵△APQ和△BPQ都是直角三角形,M是斜边PQ的中点∴AM=BM=PM=QM= PQ,∴A、B、P、Q四点在以M为圆心的同一个圆上。
中考数学与圆的综合有关的压轴题及详细答案

中考数学与圆的综合有关的压轴题及详细答案一、圆的综合1.如图,点P在⊙O的直径AB的延长线上,PC为⊙O的切线,点C为切点,连接AC,过点A作PC的垂线,点D为垂足,AD交⊙O于点E.(1)如图1,求证:∠DAC=∠PAC;(2)如图2,点F(与点C位于直径AB两侧)在⊙O上,»»BF FA=,连接EF,过点F作AD 的平行线交PC于点G,求证:FG=DE+DG;(3)在(2)的条件下,如图3,若AE=23DG,PO=5,求EF的长.【答案】(1)证明见解析;(2)证明见解析;(3)EF=32.【解析】【分析】(1)连接OC,求出OC∥AD,求出OC⊥PC,根据切线的判定推出即可;(2)连接BE交GF于H,连接OH,求出四边形HGDE是矩形,求出DE=HG,FH=EH,即可得出答案;(3)设OC交HE于M,连接OE、OF,求出∠FHO=∠EHO=45°,根据矩形的性质得出EH∥DG,求出OM=12AE,设OM=a,则HM=a,AE=2a,AE=23DG,DG=3a,求出ME=CD=2a,BM=2a,解直角三角形得出tan∠MBO=12MOBM=,tanP=12COPO=,设OC=k,则PC=2k,根据OP=5k=5求出k=5,根据勾股定理求出a,即可求出答案.【详解】(1)证明:连接OC,∵PC为⊙O的切线,∴OC⊥PC,∵AD⊥PC,∴OC∥AD,∴∠OCA=∠DAC,∵OC=OA,∴∠PAC=∠OCA,∴∠DAC=∠PAC;(2)证明:连接BE交GF于H,连接OH,∵FG∥AD,∴∠FGD+∠D=180°,∵∠D=90°,∴∠FGD=90°,∵AB为⊙O的直径,∴∠BEA=90°,∴∠BED=90°,∴∠D=∠HGD=∠BED=90°,∴四边形HGDE是矩形,∴DE=GH,DG=HE,∠GHE=90°,∵»»BF AF=,∴∠HEF=∠FEA=12∠BEA=1902o⨯=45°,∴∠HFE=90°﹣∠HEF=45°,∴∠HEF=∠HFE,∴FH=EH,∴FG=FH+GH=DE+DG;(3)解:设OC交HE于M,连接OE、OF,∵EH=HF,OE=OF,HO=HO,∴△FHO≌△EHO,∴∠FHO=∠EHO=45°,∵四边形GHED是矩形,∴EH∥DG,∴∠OMH=∠OCP=90°,∴∠HOM=90°﹣∠OHM=90°﹣45°=45°,∴∠HOM=∠OHM,∴HM=MO,∵OM⊥BE,∴BM=ME,∴OM=12 AE,设OM=a,则HM=a,AE=2a,AE=23DG,DG=3a,∵∠HGC=∠GCM=∠GHE=90°,∴四边形GHMC是矩形,∴GC=HM=a,DC=DG﹣GC=2a,∵DG=HE,GC=HM,∴ME=CD=2a,BM=2a,在Rt△BOM中,tan∠MBO=122 MO aBM a==,∵EH∥DP,∴∠P=∠MBO,tanP=12 COPO=,设OC=k,则PC=2k,在Rt△POC中,,解得:在Rt△OME中,OM2+ME2=OE2,5a2=5,a=1,∴HE=3a=3,在Rt△HFE中,∠HEF=45°,∴.【点睛】考查了切线的性质,矩形的性质和判定,解直角三角形,勾股定理等知识点,能综合运用性质进行推理是解此题的关键.2.如图,⊙O是△ABC的外接圆,点E为△ABC内切圆的圆心,连接AE的延长线交BC于点F,交⊙O于点D;连接BD,过点D作直线DM,使∠BDM=∠DAC.(1)求证:直线DM是⊙O的切线;(2)若DF=2,且AF=4,求BD和DE的长.【答案】(1)证明见解析(2)23【解析】【分析】(1)根据垂径定理的推论即可得到OD⊥BC,再根据∠BDM=∠DBC,即可判定BC∥DM,进而得到OD⊥DM,据此可得直线DM是⊙O的切线;(2)根据三角形内心的定义以及圆周角定理,得到∠BED=∠EBD,即可得出DB=DE,再判定△DBF∽△DAB,即可得到DB2=DF•DA,据此解答即可.【详解】(1)如图所示,连接OD.∵点E是△ABC的内心,∴∠BAD=∠CAD,∴¶¶BD CD=,∴OD⊥BC.又∵∠BDM=∠DAC,∠DAC=∠DBC,∴∠BDM=∠DBC,∴BC∥DM,∴OD⊥DM.又∵OD为⊙O半径,∴直线DM是⊙O的切线.(2)连接BE.∵E为内心,∴∠ABE=∠CBE.∵∠BAD=∠CAD,∠DBC=∠CAD,∴∠BAD=∠DBC,∴∠BAE+∠ABE=∠CBE+∠DBC,即∠BED=∠DBE,∴BD=DE.又∵∠BDF=∠ADB(公共角),∴△DBF∽△DAB,∴DF DBDB DA=,即DB2=DF•DA.∵DF=2,AF=4,∴DA=DF+AF=6,∴DB2=DF•DA=12,∴DB=DE=23.【点睛】本题主要考查了三角形的内心与外心,圆周角定理以及垂径定理的综合应用,解题时注意:平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧;三角形的内心到三角形三边的距离相等;三角形的内心与三角形顶点的连线平分这个内角.3.图 1 和图 2 中,优弧»AB纸片所在⊙O 的半径为 2,AB=3,点P为优弧»AB上一点(点P 不与A,B 重合),将图形沿BP 折叠,得到点A 的对称点A′.发现:(1)点O 到弦AB 的距离是,当BP 经过点O 时,∠ABA′=;(2)当BA′与⊙O 相切时,如图 2,求折痕的长.拓展:把上图中的优弧纸片沿直径MN 剪裁,得到半圆形纸片,点P(不与点M, N 重合)为半圆上一点,将圆形沿NP 折叠,分别得到点M,O 的对称点A′, O′,设∠MNP=α.(1)当α=15°时,过点A′作A′C∥MN,如图 3,判断A′C 与半圆O 的位置关系,并说明理由;(2)如图 4,当α= °时,NA′与半圆O 相切,当α= °时,点O′落在»NP上.(3)当线段NO′与半圆O 只有一个公共点N 时,直接写出β的取值范围.【答案】发现:(1)1,60°;(2)3;拓展:(1)相切,理由详见解析;(2)45°;30°;(3)0°<α<30°或45°≤α<90°.【解析】【分析】发现:(1)利用垂径定理和勾股定理即可求出点O到AB的距离;利用锐角三角函数的定义及轴对称性就可求出∠ABA′.(2)根据切线的性质得到∠OBA′=90°,从而得到∠ABA′=120°,就可求出∠ABP,进而求出∠OBP=30°.过点O作OG⊥BP,垂足为G,容易求出OG、BG的长,根据垂径定理就可求出折痕的长.拓展:(1)过A'、O作A'H⊥MN于点H,OD⊥A'C于点D.用含30°角的直角三角形的性质可得OD=A'H=12A'N=12MN=2可判定A′C与半圆相切;(2)当NA′与半圆相切时,可知ON⊥A′N,则可知α=45°,当O′在»PB时,连接MO′,则可知NO′=12MN,可求得∠MNO′=60°,可求得α=30°;(3)根据点A′的位置不同得到线段NO′与半圆O只有一个公共点N时α的取值范围是0°<α<30°或45°≤α<90°.【详解】发现:(1)过点O作OH⊥AB,垂足为H,如图1所示,∵⊙O的半径为2,AB=23,∴OH=22OB HB-=222(3)1-=在△BOH中,OH=1,BO=2∴∠ABO=30°∵图形沿BP折叠,得到点A的对称点A′.∴∠OBA′=∠ABO=30°∴∠ABA′=60°(2)过点O作OG⊥BP,垂足为G,如图2所示.∵BA′与⊙O相切,∴OB⊥A′B.∴∠OBA′=90°.∵∠OBH=30°,∴∠ABA′=120°.∴∠A′BP=∠ABP=60°.∴∠OBP=30°.∴OG=12OB=1.∴3.∵OG⊥BP,∴3.∴3.∴折痕的长为3拓展:(1)相切.分别过A'、O作A'H⊥MN于点H,OD⊥A'C于点D.如图3所示,∵A'C∥MN∴四边形A'HOD是矩形∴A'H=O∵α=15°∴∠A'NH=30∴OD=A'H=12A'N=12MN=2∴A'C与半圆(2)当NA′与半圆O相切时,则ON⊥NA′,∴∠ONA′=2α=90°,∴α=45当O′在»PB上时,连接MO′,则可知NO′=12 MN,∴∠O′MN=0°∴∠MNO′=60°,∴α=30°,故答案为:45°;30°.(3)∵点P,M不重合,∴α>0,由(2)可知当α增大到30°时,点O′在半圆上,∴当0°<α<30°时点O′在半圆内,线段NO′与半圆只有一个公共点B;当α增大到45°时NA′与半圆相切,即线段NO′与半圆只有一个公共点B.当α继续增大时,点P逐渐靠近点N,但是点P,N不重合,∴α<90°,∴当45°≤α<90°线段BO′与半圆只有一个公共点B.综上所述0°<α<30°或45°≤α<90°.【点睛】本题考查了切线的性质、垂径定理、勾股定理、三角函数的定义、30°角所对的直角边等于斜边的一半、翻折问题等知识,正确的作出辅助线是解题的关键.4.如图,AB为⊙O的直径,点E在⊙O上,过点E的切线与AB的延长线交于点D,连接BE,过点O作BE的平行线,交⊙O于点F,交切线于点C,连接AC(1)求证:AC是⊙O的切线;(2)连接EF,当∠D=°时,四边形FOBE是菱形.【答案】(1)见解析;(2)30.【解析】【分析】(1)由等角的转换证明出OCA OCE ∆∆≌,根据圆的位置关系证得AC 是⊙O 的切线. (2)根据四边形FOBE 是菱形,得到OF=OB=BF=EF ,得证OBE ∆为等边三角形,而得出60BOE ∠=︒,根据三角形内角和即可求出答案.【详解】(1)证明:∵CD 与⊙O 相切于点E ,∴OE CD ⊥,∴90CEO ∠=︒,又∵OC BE P ,∴COE OEB ∠=∠,∠OBE=∠COA∵OE=OB ,∴OEB OBE ∠=∠,∴COE COA ∠=∠,又∵OC=OC ,OA=OE ,∴OCA OCE SAS ∆∆≌(), ∴90CAO CEO ∠=∠=︒,又∵AB 为⊙O 的直径,∴AC 为⊙O 的切线;(2)解:∵四边形FOBE 是菱形,∴OF=OB=BF=EF ,∴OE=OB=BE ,∴OBE ∆为等边三角形,∴60BOE ∠=︒,而OE CD ⊥,∴30D ∠=︒.故答案为30.【点睛】本题主要考查与圆有关的位置关系和圆中的计算问题,熟练掌握圆的性质是本题的解题关键.5.如图,在锐角△ABC 中,AC 是最短边.以AC 为直径的⊙O ,交BC 于D ,过O 作OE ∥BC ,交OD 于E ,连接AD 、AE 、CE .(1)求证:∠ACE=∠DCE ;(2)若∠B=45°,∠BAE=15°,求∠EAO 的度数;(3)若AC=4,23CDF COE S S ∆∆=,求CF 的长.【答案】(1)证明见解析,(2)60°;(3)43 【解析】 【分析】 (1)易证∠OEC =∠OCE ,∠OEC =∠ECD ,从而可知∠OCE =∠ECD ,即∠ACE =∠DCE ; (2)延长AE 交BC 于点G ,易证∠AGC =∠B +∠BAG =60°,由于OE ∥BC ,所以∠AEO =∠AGC =60°,所以∠EAO =∠AEO =60°;(3)易证12COE CAE S S =V V ,由于23CDF COE S S =V V ,所以CDF CAE S S V V =13,由圆周角定理可知∠AEC =∠FDC =90°,从而可证明△CDF ∽△CEA ,利用三角形相似的性质即可求出答案.【详解】(1)∵OC =OE ,∴∠OEC =∠OCE .∵OE ∥BC ,∴∠OEC =∠ECD ,∴∠OCE =∠ECD ,即∠ACE =∠DCE ;(2)延长AE 交BC 于点G .∵∠AGC 是△ABG 的外角,∴∠AGC =∠B +∠BAG =60°.∵OE ∥BC ,∴∠AEO =∠AGC =60°.∵OA =OE ,∴∠EAO =∠AEO =60°.(3)∵O 是AC 中点,∴12COE CAE S S =V V . 23CDF COE S S =V V Q ,∴CDF CAE S S V V =13. ∵AC 是直径,∴∠AEC =∠FDC =90°.∵∠ACE =∠FCD ,∴△CDF ∽△CEA ,∴CF CA =3,∴CF =3CA =43.【点睛】本题考查了圆的综合问题,涉及平行线的性质,三角形的外角的性质,三角形中线的性质,圆周角定理,相似三角形的判定与性质等知识,需要学生灵活运用所学知识.6.如图,在ABC V 中,90ACB ∠=o ,BAC ∠的平分线AD 交BC 于点D ,过点D 作DE AD ⊥交AB 于点E ,以AE 为直径作O e .()1求证:BC 是O e 的切线;()2若3AC =,4BC =,求tan EDB ∠的值.【答案】(1)见解析;(2)1tan 2EDB ∠=. 【解析】【分析】 ()1连接OD ,如图,先证明OD//AC ,再利用AC BC ⊥得到OD BC ⊥,然后根据切线的判定定理得到结论;()2先利用勾股定理计算出AB 5=,设O e 的半径为r ,则OA OD r ==,OB 5r =-,再证明BDO V ∽BCA V ,利用相似比得到r :()35r =-:5,解得15r 8=,接着利用勾股定理计算5BD 2=,则3CD 2=,利用正切定理得1tan 12∠=,然后证明1EDB ∠∠=,从而得到tan EDB ∠的值.【详解】()1证明:连接OD ,如图,AD Q 平分BAC ∠,12∴∠=∠,OA OD =Q ,23∴∠=∠,13∴∠=∠,//OD AC ∴,AC BC ⊥Q ,OD BC ∴⊥,BC ∴是O e 的切线;()2解:在Rt ACB V 中,5AB ==, 设O e 的半径为r ,则OA OD r ==,5OB r =-, //OD AC Q ,BDO V ∴∽BCA V ,OD ∴:AC BO =:BA ,即r :()35r =-:5,解得158r =, 158OD ∴=,258OB =,在Rt ODB V 中,52BD ==, 32CD BC BD ∴=-=, 在Rt ACD V 中,312tan 132CD AC ∠===, AE Q 为直径,90ADE ∴∠=o ,90EDB ADC ∴∠+∠=o ,190ADC ∠+∠=o Q ,1EDB ∴∠=∠,1tan 2EDB ∴∠=. 【点睛】本题考查了切线的判定与性质:经过半径的外端且垂直于这条半径的直线是圆的切线;圆的切线垂直于经过切点的半径.判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”;也考查了圆周角定理和解直角三角形.7.如图,已知⊙O 的半径为1,PQ 是⊙O 的直径,n 个相同的正三角形沿PQ 排成一列,所有正三角形都关于PQ 对称,其中第一个△A 1B 1C 1的顶点A 1与点P 重合,第二个△A 2B 2C 2的顶点A 2是B 1C 1与PQ 的交点,…,最后一个△A n B n C n 的顶点B n 、C n 在圆上.如图1,当n=1时,正三角形的边长a 1=_____;如图2,当n=2时,正三角形的边长a 2=_____;如图3,正三角形的边长a n =_____(用含n 的代数式表示).3831343n 【解析】 分析:(1)设PQ 与11B C 交于点D ,连接1B O ,得出OD=1A D -O 1A ,用含1a 的代数式表示OD ,在△O 1B D 中,根据勾股定理求出正三角形的边长1a ;(2)设PQ 与2B 2C 交于点E ,连接2B O ,得出OE=1A E-O 1A ,用含2a 的代数式表示OE ,在△O 2B E 中,根据勾股定理求出正三角形的边长2a ;(3)设PQ 与n B n C 交于点F ,连接n B O ,得出OF=1A F-O 1A ,用含an 的代数式表示OF ,在△O n B F 中,根据勾股定理求出正三角形的边长an . 本题解析:(1)易知△A 1B 1C 1的高为323 ∴a 13.(2)设△A 1B 1C 1的高为h ,则A 2O =1-h ,连结B 2O ,设B 2C 2与PQ 交于点F ,则有OF =2h -1. ∵B 2O 2=OF 2+B 2F 2,∴1=(2h -1)2+2212a ⎛⎫ ⎪⎝⎭ . ∵h 32,∴1=32-1)2+14a 22, 解得a 2=8313. (3)同(2),连结B n O ,设B n C n 与PQ 交于点F ,则有B n O 2=OF 2+B n F 2, 即1=(nh -1)2+212n a ⎛⎫ ⎪⎝⎭. ∵h 3a n ,∴1=14a n 2+2312n na ⎛⎫- ⎪ ⎪⎝⎭, 解得a n 43n8.如图1O e ,的直径12AB P =,是弦BC 上一动点(与点B C ,不重合)30ABC o ,∠=,过点P 作PD OP ⊥交O e 于点D .()1如图2,当//PD AB 时,求PD 的长;()2如图3,当»»DC AC =时,延长AB 至点E ,使12BE AB =,连接DE . ①求证:DE 是O e 的切线;②求PC 的长.【答案】(1)26;(2)333-①见解析,②.【解析】分析:()1根据题意首先得出半径长,再利用锐角三角函数关系得出OP PD ,的长; ()2①首先得出OBD V 是等边三角形,进而得出ODE OFB 90∠∠==o ,求出答案即可;②首先求出CF 的长,进而利用直角三角形的性质得出PF 的长,进而得出答案. 详解:()1如图2,连接OD ,//OP PD PD AB ⊥Q ,,90POB ∴∠=o ,O Q e 的直径12AB =,6OB OD ∴==,在Rt POB V 中,30ABC o ∠=,3tan30623OP OB ∴=⋅==o 在Rt POD V 中, 22226(23)26PD OD OP =-=-=;()2①证明:如图3,连接OD ,交CB 于点F ,连接BD ,»»DC AC =Q ,30DBC ABC ∴∠=∠=o ,60ABD o ∴∠=,OB OD =Q ,OBD ∴V 是等边三角形,OD FB ∴⊥,12BE AB =Q , OB BE ∴=,//BF ED ∴,90ODE OFB o ∴∠=∠=,DE ∴是O e 的切线;②由①知,OD BC ⊥,3cos306332CF FB OB ∴==⋅=⨯=o 在Rt POD V 中,OF DF =, 13(2PF DO ∴==直角三角形斜边上的中线,等于斜边的一半), 333CP CF PF ∴=-=.点睛:此题主要考查了圆的综合以及直角三角形的性质和锐角三角函数关系,正确得出OBD V 是等边三角形是解题关键.9.如图,A 是以BC 为直径的⊙O 上一点,AD ⊥BC 于点D ,过点B 作⊙O 的切线,与CA 的延长线相交于点E ,G 是AD 的中点,连结CG 并延长与BE 相交于点F ,延长AF 与CB 的延长线相交于点P .(1)求证:BF =EF :(2)求证:PA 是⊙O 的切线;(3)若FG =BF ,且⊙O 的半径长为2,求BD 的长度.【答案】(1)证明见解析;(2) 证明见解析;(3)22【解析】分析:(1)利用平行线截三角形得相似三角形,得△BFC∽△DGC且△FEC∽△GAC,得到对应线段成比例,再结合已知条件可得BF=EF;(2)利用直角三角形斜边上的中线的性质和等边对等角,得到∠FAO=∠EBO,结合BE是圆的切线,得到PA⊥OA,从而得到PA是圆O的切线;(3)点F作FH⊥AD于点H,根据前两问的结论,利用三角形的相似性质即可以求出BD 的长度.详解:证明:(1)∵BC是圆O的直径,BE是圆O的切线,∴EB⊥BC.又∵AD⊥BC,∴AD∥BE.∴△BFC∽△DGC,△FEC∽△GAC,∴BFDG=CFCG,EFAG=CFCG,∴BFDG=EFAG,∵G是AD的中点,∴DG=AG,∴BF=EF;(2)连接AO,AB.∵BC是圆O的直径,∴∠BAC=90°,由(1)得:在Rt△BAE中,F是斜边BE的中点,∴AF=FB=EF,可得∠FBA=∠FAB,又∵OA=OB,∴∠ABO=∠BAO,∵BE 是圆O 的切线,∴∠EBO =90°,∴∠FBA +∠ABO =90°,∴∠FAB +∠BAO =90°,即∠FAO =90°,∴PA ⊥OA ,∴PA 是圆O 的切线;(3)过点F 作FH ⊥AD 于点H ,∵BD ⊥AD ,FH ⊥AD ,∴FH ∥BC ,由(2),知∠FBA =∠BAF ,∴BF =AF .∵BF =FG ,∴AF =FG ,∴△AFG 是等腰三角形.∵FH ⊥AD ,∴AH =GH ,∵DG =AG ,∴DG =2HG . 即12HG DG =, ∵FH ∥BD ,BF ∥AD ,∠FBD =90°,∴四边形BDHF 是矩形,∴BD =FH ,∵FH ∥BC∴△HFG ∽△DCG , ∴12FH HG CD DG ==, 即12BD CD =, ∴23 2.153≈,∵O 的半径长为32, ∴BC =62, ∴BD =13BC =22. 点睛:本题考查了切线的判定、勾股定理、圆周角定理、相似三角形的判定与性质.结合已知条件准确对图形进行分析并应用相应的图形性质是解题的关键.10.如图,△ABC 内接于⊙O ,弦AD ⊥BC,垂足为H ,连接OB .(1)如图1,求证:∠DAC=∠ABO;(2)如图2,在弧AC 上取点F,使∠CAF=∠BAD,在弧AB 取点G ,使AG ∥OB ,若∠BAC=600, 求证:GF=GD;(3)如图3,在(2)的条件下,AF 、BC 的延长线相交于点E,若AF :FE=1:9,求sin ∠ADG 的值。
备战中考数学圆的综合-经典压轴题附答案解析

一、圆的综合真题与模拟题分类汇编(难题易错题)1.如图,⊙M交x轴于B、C两点,交y轴于A,点M的纵坐标为2.B(﹣33,O),C(3,O).(1)求⊙M的半径;(2)若CE⊥AB于H,交y轴于F,求证:EH=FH.(3)在(2)的条件下求AF的长.【答案】(1)4;(2)见解析;(3)4.【解析】【分析】(1)过M作MT⊥BC于T连BM,由垂径定理可求出BT的长,再由勾股定理即可求出BM的长;(2)连接AE,由圆周角定理可得出∠AEC=∠ABC,再由AAS定理得出△AEH≌△AFH,进而可得出结论;(3)先由(1)中△BMT的边长确定出∠BMT的度数,再由直角三角形的性质可求出CG 的长,由平行四边形的判定定理判断出四边形AFCG为平行四边形,进而可求出答案.【详解】(1)如图(一),过M作MT⊥BC于T连BM,∵BC是⊙O的一条弦,MT是垂直于BC的直径,∴BT=TC=123∴124;(2)如图(二),连接AE,则∠AEC=∠ABC,∵CE⊥AB,∴∠HBC+∠BCH=90°在△COF中,∵∠OFC+∠OCF=90°,∴∠HBC=∠OFC=∠AFH,在△AEH和△AFH中,∵AFH AEHAHF AHE AH AH∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AEH≌△AFH(AAS),∴EH=FH;(3)由(1)易知,∠BMT=∠BAC=60°,作直径BG,连CG,则∠BGC=∠BAC=60°,∵⊙O的半径为4,∴CG=4,连AG,∵∠BCG=90°,∴CG⊥x轴,∴CG∥AF,∵∠BAG=90°,∴AG⊥AB,∵CE⊥AB,∴AG∥CE,∴四边形AFCG为平行四边形,∴AF=CG=4.【点睛】本题考查的是垂径定理、圆周角定理、直角三角形的性质及平行四边形的判定与性质,根据题意作出辅助线是解答此题的关键.2.如图,以O为圆心,4为半径的圆与x轴交于点A,C在⊙O上,∠OAC=60°.(1)求∠AOC的度数;(2)P为x轴正半轴上一点,且PA=OA,连接PC,试判断PC与⊙O的位置关系,并说明理由;(3)有一动点M从A点出发,在⊙O上按顺时针方向运动一周,当S△MAO=S△CAO时,求动点M所经过的弧长,并写出此时M点的坐标.【答案】(1)60°;(2)见解析;(3)对应的M点坐标分别为:M1(2,﹣23)、M2(﹣2,﹣23)、M3(﹣2,23)、M4(2,23).【解析】【分析】(1)由于∠OAC=60°,易证得△OAC是等边三角形,即可得∠AOC=60°.(2)由(1)的结论知:OA=AC,因此OA=AC=AP,即OP边上的中线等于OP的一半,由此可证得△OCP是直角三角形,且∠OCP=90°,由此可判断出PC与⊙O的位置关系.(3)此题应考虑多种情况,若△MAO、△OAC的面积相等,那么它们的高必相等,因此有四个符合条件的M点,即:C点以及C点关于x轴、y轴、原点的对称点,可据此进行求解.【详解】(1)∵OA=OC,∠OAC=60°,∴△OAC是等边三角形,故∠AOC=60°.(2)由(1)知:AC=OA,已知PA=OA,即OA=PA=AC;∴AC=12OP,因此△OCP是直角三角形,且∠OCP=90°,而OC是⊙O的半径,故PC与⊙O的位置关系是相切.(3)如图;有三种情况:①取C点关于x轴的对称点,则此点符合M点的要求,此时M点的坐标为:M1(2,﹣3劣弧MA的长为:6044 1803ππ⨯=;②取C点关于原点的对称点,此点也符合M点的要求,此时M点的坐标为:M2(﹣2,﹣23);劣弧MA的长为:12048 1803ππ⨯=;③取C点关于y轴的对称点,此点也符合M点的要求,此时M点的坐标为:M3(﹣2,23);优弧MA的长为:240416 1803ππ⨯=;④当C、M重合时,C点符合M点的要求,此时M4(2,23);优弧MA的长为:300420 1803ππ⨯=;综上可知:当S△MAO=S△CAO时,动点M所经过的弧长为481620,,,3333ππππ对应的M点坐标分别为:M1(2,﹣23)、M2(﹣2,﹣23)、M3(﹣2,23)、M4(2,23).【点睛】本题考查了切线的判定以及弧长的计算方法,注意分类讨论思想的运用,不要漏解.3.如图,⊙O的半径为6cm,经过⊙O上一点C作⊙O的切线交半径OA的延长于点B,作∠ACO的平分线交⊙O于点D,交OA于点F,延长DA交BC于点E.(1)求证:AC∥OD;(2)如果DE⊥BC,求AC的长度.【答案】(1)证明见解析;(2)2π.【解析】试题分析:(1)由OC=OD,CD平分∠ACO,易证得∠ACD=∠ODC,即可证得AC∥OD;(2)BC切⊙O于点C,DE⊥BC,易证得平行四边形ADOC是菱形,继而可证得△AOC是等边三角形,则可得:∠AOC=60°,继而求得弧AC的长度.试题解析:(1)证明:∵OC=OD,∴∠OCD=∠ODC.∵CD平分∠ACO,∴∠OCD=∠ACD,∴∠ACD=∠ODC,∴AC∥OD;(2)∵BC切⊙O于点C,∴BC⊥OC.∵DE⊥BC,∴OC∥DE.∵AC∥OD,∴四边形ADOC 是平行四边形.∵OC=OD,∴平行四边形ADOC是菱形,∴OC=AC=OA,∴△AOC是等边三角形,∴∠AOC=60°,∴弧AC的长度=606 180π⨯=2π.点睛:本题考查了切线的性质、等腰三角形的判定与性质、菱形的判定与性质以及弧长公式.此题难度适中,注意掌握数形结合思想的应用.4.如图,在ABC∆中,90,BAC∠=︒2,AB AC==AD BC⊥,垂足为D,过,A D 的⊙O分别与,AB AC交于点,E F,连接,,EF DE DF.(1)求证:ADE∆≌CDF∆;(2)当BC与⊙O相切时,求⊙O的面积.【答案】(1)见解析;(2)24π.【解析】分析:(1)由等腰直角三角形的性质知AD=CD、∠1=∠C=45°,由∠EAF=90°知EF是⊙O 的直径,据此知∠2+∠4=∠3+∠4=90°,得∠2=∠3,利用“ASA”证明即可得;(2)当BC与⊙O相切时,AD是直径,根据∠C=45°、AC=2可得AD=1,利用圆的面积公式可得答案.详解:(1)如图,∵AB=AC,∠BAC=90°,∴∠C=45°.又∵AD⊥BC,AB=AC,∴∠1=12∠BAC=45°,BD=CD,∠ADC=90°.又∵∠BAC=90°,BD=CD,∴AD=CD.又∵∠EAF=90°,∴EF是⊙O的直径,∴∠EDF=90°,∴∠2+∠4=90°.又∵∠3+∠4=90°,∴∠2=∠3.在△ADE和△CDF中.∵123CAD CD∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△ADE≌△CDF(ASA).(2)当BC与⊙O相切时,AD是直径.在Rt△ADC中,∠C=45°,AC2,∴sin∠C=ADAC,∴AD=AC sin∠C=1,∴⊙O的半径为12,∴⊙O的面积为24π.点睛:本题主要考查圆的综合问题,解题的关键是熟练掌握等腰直角三角形的性质、全等三角形的判定与性质、与圆有关的位置关系等知识点.5.如图,在⊙O中,直径AB⊥弦CD于点E,连接AC,BC,点F是BA延长线上的一点,且∠FCA=∠B.(1)求证:CF是⊙O的切线;(2)若AE=4,tan∠ACD=3,求FC的长.【答案】(1)见解析【解析】分析:(1)利用圆周角定理以及等腰三角形的性质得出∠OCF=90°,进而得出答案;(2)根据正切的性质求出EC的长,然后利用垂径定理求出圆的半径,再根据等边三角形的性质,利用勾股定理求出即可.详解:(1)证明:连接OC.∵AB是⊙O的直径,∴∠ACB=90°,∴∠OCB+∠ACO=90°.∵OB=OC,∴∠B=∠OCB.又∵∠FCA=∠B,∴∠FCA=∠OCB,∴∠FCA+∠ACO=90°,即∠FCO=90°,∴FC⊥OC,∴FC是⊙O切线.(2)解:∵AB⊥CD,∴∠AEC=90°,∴EC=AE43 tan ACE3∠==设OA=OC=r,则OE=OA-AE=r-4.在Rt△OEC中,OC2=OE2+CE2,即r2=(r-4)2+32,解得r=8.∴OE=r-4=4=AE.∵CE⊥OA,∴CA=CO=8,∴△AOC是等边三角形,∴∠FOC=60°,∴∠F=30°.在Rt△FOC中,∵∠OCF=90°,OC=8,∠F=30°,∴OF=2OC=16,∴FC22OF OC83-=.点睛:此题主要考查了切线的判定、垂径定理的推论以及勾股定理等知识,得出BC的长是解题关键.6.如图,△ABC中,∠A=45°,D是AC边上一点,⊙O经过D、A、B三点,OD∥BC.(1)求证:BC与⊙O相切;(2)若OD=15,AE=7,求BE的长.【答案】(1)见解析;(2)18.【解析】分析:(1)连接OB,求出∠DOB度数,根据平行线性质求出∠CBO=90°,根据切线判定得出即可;(2)延长BO交⊙O于点F,连接AF,求出∠ABF,解直角三角形求出BE.详解:(1)证明:连接OB.∵∠A=45°,∴∠DOB=90°.∵OD∥BC,∴∠DOB+∠CBO=180°.∴∠CBO=90°.∴直线BC是⊙O的切线.(2)解:连接BD.则△ODB是等腰直角三角形,∴∠ODB=45°,BD=OD=15,∵∠ODB=∠A,∠DBE=∠DBA,∴△DBE∽△ABD,∴BD2=BE•BA,∴(15)2=(7+BE)BE,∴BE=18或﹣25(舍弃),∴BE=18.点睛:本题考查了切线的判定,圆周角定理,解直角三角形等知识点,能综合运用定理进行推理和计算是解此题的关键,题目综合性比较强,难度偏大.7.如图,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA 的延长线相交于点E,G是AD的中点,连结CG并延长与BE相交于点F,延长AF与CB的延长线相交于点P.(1)求证:BF=EF:(2)求证:PA是⊙O的切线;(3)若FG=BF,且⊙O的半径长为32,求BD的长度.【答案】(1)证明见解析;(2) 证明见解析;(3)22【解析】分析:(1)利用平行线截三角形得相似三角形,得△BFC∽△DGC且△FEC∽△GAC,得到对应线段成比例,再结合已知条件可得BF=EF;(2)利用直角三角形斜边上的中线的性质和等边对等角,得到∠FAO=∠EBO,结合BE是圆的切线,得到PA⊥OA,从而得到PA是圆O的切线;(3)点F作FH⊥AD于点H,根据前两问的结论,利用三角形的相似性质即可以求出BD 的长度.详解:证明:(1)∵BC是圆O的直径,BE是圆O的切线,∴EB⊥BC.又∵AD⊥BC,∴AD∥BE.∴△BFC∽△DGC,△FEC∽△GAC,∴BFDG=CFCG,EFAG=CFCG,∴BFDG=EFAG,∵G是AD的中点,∴DG=AG,∴BF=EF;(2)连接AO,AB.∵BC是圆O的直径,∴∠BAC=90°,由(1)得:在Rt△BAE中,F是斜边BE的中点,∴AF =FB =EF ,可得∠FBA =∠FAB ,又∵OA =OB ,∴∠ABO =∠BAO ,∵BE 是圆O 的切线,∴∠EBO =90°,∴∠FBA +∠ABO =90°,∴∠FAB +∠BAO =90°,即∠FAO =90°,∴PA ⊥OA ,∴PA 是圆O 的切线;(3)过点F 作FH ⊥AD 于点H ,∵BD ⊥AD ,FH ⊥AD ,∴FH ∥BC ,由(2),知∠FBA =∠BAF ,∴BF =AF .∵BF =FG ,∴AF =FG ,∴△AFG 是等腰三角形.∵FH ⊥AD ,∴AH =GH ,∵DG =AG ,∴DG =2HG . 即12HG DG =, ∵FH ∥BD ,BF ∥AD ,∠FBD =90°,∴四边形BDHF 是矩形,∴BD =FH ,∵FH ∥BC∴△HFG ∽△DCG , ∴12FH HG CD DG ==,即12 BDCD=,∴23 2.15≈,∵O的半径长为32,∴BC=62,∴BD=13BC=22.点睛:本题考查了切线的判定、勾股定理、圆周角定理、相似三角形的判定与性质.结合已知条件准确对图形进行分析并应用相应的图形性质是解题的关键.8.如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M 为⊙O上一点,并且∠BMC=60°.(1)求证:AB是⊙O的切线;(2)若E,F分别是边AB,AC上的两个动点,且∠EDF=120°,⊙O的半径为2,试问BE+CF的值是否为定值?若是,求出这个定值;若不是,请说明理由.【答案】(1)证明见试题解析;(2)BE+CF的值是定值,为等边△ABC边长的一半.【解析】试题分析:(1)连结OB、OD,如图1,由于D为BC的中点,由垂径定理的推理得OD⊥BC,∠BOD=∠COD,即可得到∠BOD=∠M=60°,则∠OBD=30°,所以∠ABO=90°,于是得到AB是⊙O的切线;(2)作DM⊥AB于M,DN⊥AC于N,连结AD,如图2,由△ABC为正三角形,D为BC 的中点,得到AD平分∠BAC,∠BAC=60°,利用角平分线性质得DM=DN,得∠MDN=120°,由∠EDF=120°,得到∠MDE=∠NDF,于是有△DME≌△DNF,得到ME=NF,得到BE+CF=BM+CN,由BM=12BD,CN=12OC,得到BE+CF=12BC,即可判断BE+CF的值是定值,为等边△ABC边长的一半.试题解析:(1)连结OB、OD,如图1,∵D为BC的中点,∴OD⊥BC,∠BOD=∠COD,∴∠ODB=90°,∵∠BMC=12∠BOC,∴∠BOD=∠M=60°,∴∠OBD=30°,∵△ABC为正三角形,∴∠ABC=60°,∴∠ABO=60°+30°=90°,∴AB⊥OB,∴AB是⊙O的切线;(2)BE+CF的值是为定值.作DM⊥AB于M,DN⊥AC于N,连结AD,如图2,∵△ABC为正三角形,D为BC的中点,∴AD平分∠BAC,∠BAC=60°,∴DM=DN,∠MDN=120°,∵∠EDF=120°,∴∠MDE=∠NDF,在△DME和△DNF中,∵∠DME=∠DNF.DM=DN,∠MDE=∠NDF,∴△DME≌△DNF,∴ME=NF,∴BE+CF=BM﹣EM+CN+NF=BM+CN,在Rt△DMB中,∵∠DBM=60°,∴BM=12BD,同理可得CN=12OC,∴BE+CF=12OB+12OC=12BC,∴BE+CF的值是定值,为等边△ABC边长的一半.考点:1.切线的判定;2.等边三角形的性质;3.定值问题;4.探究型;5.综合题;6.压轴题.9.如图1,已知⊙O是ΔADB的外接圆,∠ADB的平分线DC交AB于点M,交⊙O于点C,连接AC,BC.(1)求证:AC=BC;(2)如图2,在图1 的基础上做⊙O的直径CF交AB于点E,连接AF,过点A作⊙O的切线AH,若AH//BC,求∠ACF的度数;(3)在(2)的条件下,若ΔABD的面积为63,ΔABD与ΔABC的面积比为2:9,求CD 的长.【答案】(1)证明见解析;(2)30°;(3)33【解析】分析:(1)运用“在同圆或等圆中,弧相等,所对的弦相等”可求解;(2)连接AO并延长交BC于I交⊙O于J,由AH是⊙O的切线且AH∥BC得AI⊥BC,易证∠IAC=30°,故可得∠ABC=60°=∠F=∠ACB,由CF是直径可得∠ACF的度数;(3)过点D作DG⊥AB ,连接AO,知ABC为等边三角形,求出AB、AE的长,在RtΔAEO 中,求出AO的长,得CF的长,再求DG 的长,运用勾股定理易求CD的长.详解:(1)∵DC平分∠ADB,∴∠ADC=∠BDC,∴AC=BC.(2)如图,连接AO并延长交BC于I交⊙O于J∵AH是⊙O的切线且AH∥BC,∴AI⊥BC,∴BI=IC,∵AC=BC,∴IC=1AC,2∴∠IAC=30°,∴∠ABC=60°=∠F=∠ACB.∵FC是直径,∴∠FAC=90°,∴∠ACF=180°-90°-60°=30°.⊥,连接AO(3)过点D作DG AB由(1)(2)知ABC为等边三角形∵∠ACF=30°,⊥,∴AB CF∴AE=BE , ∴2ΔABC 3273S AB ==, ∴AB=63,∴33AE =.在RtΔAEO 中,设EO=x ,则AO=2x ,∴222AO AE OE =+,∴()()222233x x =+,∴x =6,⊙O 的半径为6,∴CF=12.∵ΔABD 11636322S AB DG DG =⨯⨯=⨯⨯=, ∴DG=2.如图,过点D 作DG CF '⊥,连接OD .∵AB CF ⊥,DG AB ⊥,∴CF//DG ,∴四边形G ′DGE 为矩形,∴2G E '=, 63211CG G E CE +=++'==',在RtΔOG D '中,5,6OG OD ='=,∴11DG '=,∴2221111233CD DG CG =+=+=''点睛:本题是一道圆的综合题.考查了圆的基本概念,垂径定理,勾股定理,圆周角定理等相关知识.比较复杂,熟记相关概念是解题关键.10.如图,已知△ABC ,AB=2,3BC =,∠B=45°,点D 在边BC 上,联结AD , 以点A 为圆心,AD 为半径画圆,与边AC 交于点E ,点F 在圆A 上,且AF ⊥AD .(1)设BD 为x ,点D 、F 之间的距离为y ,求y 关于x 的函数解析式,并写出定义域; (2)如果E 是DF 的中点,求:BD CD 的值;(3)联结CF ,如果四边形ADCF 是梯形,求BD 的长 .【答案】(1) 2442y x x (0≤x≤3); (2) 45; (3) BD 的长是1或1+5. 【解析】【分析】 (1)过点A 作AH ⊥BC ,垂足为点H .构造直角三角形,利用解直角三角形和勾股定理求得AD 的长度.联结DF ,点D 、F 之间的距离y 即为DF 的长度,在Rt △ADF 中,利用锐角三角形函数的定义求得DF 的长度,易得函数关系式.(2)由勾股定理求得:AC=22AH DH +.设DF 与AE 相交于点Q ,通过解Rt △DCQ 和Rt △AHC 推知12DQ CQ =.故设DQ=k ,CQ=2k ,AQ=DQ=k ,所以再次利用勾股定理推知DC 的长度,结合图形求得线段BD 的长度,易得答案.(3)如果四边形ADCF 是梯形,则需要分类讨论:①当AF ∥DC 、②当AD ∥FC .根据相似三角形的判定与性质,结合图形解答.【详解】(1)过点A 作AH ⊥BC ,垂足为点H .∵∠B =45°,AB 2∴·cos 1BH AH AB B ===.∵BD 为x ,∴1DH x =-.在Rt △ADH 中,90AHD ∠=︒,∴22222AD AH DH x x =+=-+. 联结DF ,点D 、F 之间的距离y 即为DF 的长度.∵点F 在圆A 上,且AF ⊥AD ,∴AD AF =,45ADF ∠=︒.在Rt △ADF 中,90DAF ∠=︒,∴2442cos AD DF x x ADF ==-+∠ ∴2442y x x =-+.()03x ≤≤ ;(2)∵E 是DF 的中点,∴AE DF ⊥,AE 平分DF .∵BC=3,∴312HC =-=.∴225AC AH HC +=.设DF 与AE 相交于点Q ,在Rt △DCQ 中,90DQC ∠=︒,tan DQ DCQ CQ ∠=. 在Rt △AHC 中,90AHC ∠=︒,1tan 2AH ACH HC ∠==.∵DCQ ACH ∠=∠,∴12DQ CQ =. 设,2DQ k CQ k ==,AQ DQ k ==,∵3k =k =,∴53DC ==. ∵43BD BC DC =-=,∴4:5BD CD =. (3)如果四边形ADCF 是梯形 则①当AF ∥DC 时,45AFD FDC ∠=∠=︒.∵45ADF ∠=︒,∴AD BC ⊥,即点D 与点H 重合. ∴1BD =.②当AD ∥FC 时,45ADF CFD ∠=∠=︒.∵45B ∠=︒,∴B CFD ∠=∠.∵B BAD ADF FDC ∠+∠=∠+∠,∴BAD FDC ∠=∠.∴ABD ∆∽DFC ∆.∴AB AD DF DC =. ∵DF =,DC BC BD =-.∴2AD BC BD =-.即23x =-,整理得 210x x --=,解得 12x ±=(负数舍去).综上所述,如果四边形ADCF 是梯形,BD 的长是1 【点睛】此题属于圆的综合题,涉及了平行四边形的性质、相似三角形的判定与性质、三角函数值以及勾股定理等知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.。
中考压轴题--圆含答案

中考压轴题--圆含答案(总49页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--中考压轴题(一)--------与圆有关压轴题1.如图,在M 中,AB 所对的圆心角为120,已知圆的半径为2cm ,并建立如图所示的直角坐标系. (1)求圆心M 的坐标;(2)求经过A B C ,,三点的抛物线的解析式;(3)点D 是弦AB 所对的优弧上一动点,求四边形ACBD 的最大面积; (4)在(2)中的抛物线上是否存在一点P ,相似若存在,求出点P 的坐标;若不存在,请说明[解] (1)如图(1),连结MA MB ,.则120AMB ∠=60CMB ∴∠=,30OBM ∠=.112OM MB ∴==,(01)M ∴,. (2)由A B C ,,三点的特殊性与对称性,知经过A B C ,,三点的抛物线的解析式为2y ax c =+.1OC MC MO =-=,223OB MB OM =-=,(01)(30)C B ∴-,,,.113c a ∴=-=,2113y x ∴=-.(3)ABC ABD ACBD S S S =+△△四边形,又ABC S △与AB 均为定值,∴当ABD △边AB 上的高最大时,ABD S △最大,此时点D 为M 与y 轴的交点,如图1.211143cm 222ABC ABD ACBD S S S AB OC AB OD AB CD ∴=+=+==△△四边形···. (4)方法1:如图2,ABC △为等腰三角形,303ABABC BC∠==,,yA MO BCyxBCAM POy xAM OBCDABC PAB ∴△∽△等价于302336PAB PB AB PA PB ∠=====,,.设()P x y ,且0x >,则cos3033323x PA AO =-=-=·,sin303y PA==·. 又(233)P ,的坐标满足2113y x =-,∴在抛物线2113y x =-上,存在点(233)P ,,使ABC PAB △∽△. 由抛物线的对称性,知点(233)-,也符合题意.∴存在点P ,它的坐标为(233),或(233)-,. 方法2:如图(3),当ABC PAB △∽△时,30PAB BAC ∠=∠=,又由(1)知30MAB ∠=,∴点P 在直线AM 上.设直线AM 的解析式为y kx b =+,将(30)(01)A M -,,,代入,解得31.k b ⎧=⎪⎨⎪=⎩,∴直线AM 的解析式为31y x =+. 解方程组231113y x y x ⎧=+⎪⎪⎨⎪=-⎪⎩,得(233)P ,. 又tan 3233PBx ∠==-,60PBx ∴∠=.30P ∴∠=,ABC PAB ∴△∽△.∴在抛物线2113y x =-上,存在点(233)P ,,使ABC PAB △∽△. 由抛物线的对称性,知点(233)-,也符合题意.∴存在点P ,它的坐标为(233),或(233)-,. 方法3:如图3,ABC △为等腰三角形,且3ABBC=,设()P x y ,则 图3 ABC PAB △∽△等价于23PB AB ==,36PA AB ==.当0x >时,得2222(3)23(3) 6.x y x y ⎧-+=⎪⎨⎪++=⎩,解得(233)P ,.又P 的坐标满足2113y x =-,∴在抛物线2113y x =-上,存在点P ,使ABC PAB △∽△.由抛物线的对称性,知点(-也符合题意.∴存在点P,它的坐标为或(-. [点评]本题是一道综合性很强也是传统型的压轴题,涉及了函数、方程、相似、圆等大量初中数学的重点知识,解这类问题要求学生必须稳固的掌握各个领域的数学知识,须注意的是在第4小问中涉及了相似三角形的问题,很有可能会有多解的情况出现,此时就要求学生拥有较强的数形结合思想去探索结论的存在性。
最新《圆》中考压轴题精选含答案全面.pptx
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
THANK YOU 中小学上门、在线教学领导品牌
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
Thanks for watching
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
中小学上门、在线教学领导品牌 精选
九年级圆 几何综合(篇)(Word版 含解析)

九年级圆 几何综合(篇)(Word 版 含解析)一、初三数学 圆易错题压轴题(难)1.如图,以A (0,3)为圆心的圆与x 轴相切于坐标原点O ,与y 轴相交于点B ,弦BD 的延长线交x 轴的负半轴于点E ,且∠BEO =60°,AD 的延长线交x 轴于点C .(1)分别求点E 、C 的坐标;(2)求经过A 、C 两点,且以过E 而平行于y 轴的直线为对称轴的抛物线的函数解析式;(3)设抛物线的对称轴与AC 的交点为M ,试判断以M 点为圆心,ME 为半径的圆与⊙A 的位置关系,并说明理由.【答案】(1)点C 的坐标为(-3,0)(2)2343333y x x =++3)⊙M 与⊙A 外切【解析】试题分析:(1)已知了A 点的坐标,即可得出圆的半径和直径,可在直角三角形BOE 中,根据∠BEO 和OB 的长求出OE 的长进而可求出E 点的坐标,同理可在直角三角形OAC 中求出C 点的坐标; (2)已知了对称轴的解析式,可据此求出C 点关于对称轴对称的点的坐标,然后根据此点坐标以及C ,A 的坐标用待定系数法即可求出抛物线的解析式;(3)两圆应该外切,由于直线DE ∥OB ,因此∠MED=∠ABD ,由于AB=AD ,那么∠ADB=∠ABD ,将相等的角进行置换后可得出∠MED=∠MDE ,即ME=MD ,因此两圆的圆心距AM=ME+AD ,即两圆的半径和,因此两圆外切.试题解析:(1)在Rt△EOB 中,3cot60232EO OB =⋅︒==, ∴点E 的坐标为(-2,0).在Rt△COA 中,tan tan60333OC OA CAO OA =⋅∠=⋅︒==,∴点C 的坐标为(-3,0).(2)∵点C 关于对称轴2x =-对称的点的坐标为F (-1,0),点C 与点F (-1,0)都在抛物线上.设()()13y a x x =++,用(03A ,代入得 ()()30103a =++,∴33a =. ∴()()313y x x =++,即 2343333y x x =++. (3)⊙M 与⊙A 外切,证明如下:∵ME ∥y 轴,∴MED B ∠=∠.∵B BDA MDE ∠=∠=∠,∴MED MDE ∠=∠.∴ME MD =.∵MA MD AD ME AD =+=+,∴⊙M 与⊙A 外切.2.如图①,一个Rt △DEF 直角边DE 落在AB 上,点D 与点B 重合,过A 点作二射线AC 与斜边EF 平行,己知AB=12,DE=4,DF=3,点P 从A 点出发,沿射线AC 方向以每秒2个单位的速度运动,Q 为AP 中点,设运动时间为t 秒(t >0)•(1)当t=5时,连接QE ,PF ,判断四边形PQEF 的形状;(2)如图②,若在点P 运动时,Rt △DEF 同时沿着BA 方向以每秒1个单位的速度运动,当D 点到A 点时,两个运动都停止,M 为EF 中点,解答下列问题:①当D 、M 、Q 三点在同一直线上时,求运动时间t ;②运动中,是否存在以点Q 为圆心的圆与Rt △DEF 两个直角边所在直线都相切?若存在,求出此时的运动时间t ;若不存在,说明理由.【答案】(1)平行四边形EFPQ 是菱形;(2)t=;当t 为5秒或10秒时,以点Q 为圆心的圆与Rt △DEF 两个直角边所在直线都相切.【解析】 试题分析:(1)过点Q 作QH ⊥AB 于H ,如图①,易得PQ=EF=5,由AC ∥EF 可得四边形EFPQ 是平行四边形,易证△AHQ ∽△EDF ,从而可得AH=ED=4,进而可得AH=HE=4,根据垂直平分线的性质可得AQ=EQ ,即可得到PQ=EQ ,即可得到平行四边形EFPQ 是菱形;(2)①当D 、M 、Q 三点在同一直线上时,如图②,则有AQ=t ,EM=EF=,AD=12-t ,DE=4.由EF ∥AC 可得△DEM ∽△DAQ ,然后运用相似三角形的性质就可求出t 的值;②若以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切,则点Q在∠ADF的角平分线上(如图③)或在∠FDB的角平分线(如图④)上,故需分两种情况讨论,然后运用相似三角形的性质求出AH、DH(用t表示),再结合AB=12,DB=t建立关于t的方程,然后解这个方程就可解决问题.试题解析:(1)四边形EFPQ是菱形.理由:过点Q作QH⊥AB于H,如图①,∵t=5,∴AP=2×5=10.∵点Q是AP的中点,∴AQ=PQ=5.∵∠EDF=90°,DE=4,DF=3,∴EF==5,∴PQ=EF=5.∵AC∥EF,∴四边形EFPQ是平行四边形,且∠A=∠FEB.又∵∠QHA=∠FDE=90°,∴△AHQ∽△EDF,∴.∵AQ=EF=5,∴AH=ED=4.∵AE=12-4=8,∴HE=8-4=4,∴AH=EH,∴AQ=EQ,∴PQ=EQ,∴平行四边形EFPQ是菱形;(2)①当D、M、Q三点在同一直线上时,如图②,此时AQ=t,EM=EF=,AD=12-t,DE=4.∵EF∥AC,∴△DEM∽△DAQ,∴,∴,解得t=;②存在以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切,此时点Q在∠ADF的角平分线上或在∠FDB的角平分线上.Ⅰ.当点Q在∠ADF的角平分线上时,过点Q作QH⊥AB于H,如图③,则有∠HQD=∠HDQ=45°,∴QH=DH.∵△AHQ∽△EDF(已证),∴,∴,∴QH=,AH=,∴DH=QH=.∵AB=AH+HD+BD=12,DB=t,∴++t=12,∴t=5;Ⅱ.当点Q在∠FDB的角平分线上时,过点Q作QH⊥AB于H,如图④,同理可得DH=QH=,AH=.∵AB=AD+DB=AH-DH+DB=12,DB=t,∴-+t=12,∴t=10.综上所述:当t为5秒或10秒时,以点Q为圆心的圆与Rt△DEF两个直角边所在直线都相切.考点:1.圆的综合题;2.线段垂直平分线的性质;3.勾股定理;4.菱形的判定;5.相似三角形的判定与性质.3.如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE//BD,交BC于点F,交AB于点E.(1)求证:∠E=∠C;(2)若⊙O的半径为3,AD=2,试求AE的长;(3)在(2)的条件下,求△ABC的面积.【答案】(1)证明见解析;(2)10;(3)48 5.【解析】试题分析:(1)连接OB,利用已知条件和切线的性质证明:OE∥BD,即可证明:∠E=∠C;(2)根据题意求出AB的长,然后根据平行线分线段定理,可求解;(3)根据相似三角形的面积比等于相似比的平方可求解.试题解析:(1)如解图,连接OB,∵CD为⊙O的直径,∴∠CBD=∠CBO+∠OBD=90°,∵AB是⊙O的切线,∴∠ABO=∠ABD+∠OBD=90°,∴∠ABD=∠CBO.∵OB、OC是⊙O的半径,∴OB=OC,∴∠C=∠CBO.∵OE∥BD,∴∠E=∠ABD,∴∠E=∠C;(2)∵⊙O的半径为3,AD=2,∴AO=5,∴AB=4.∵BD∥OE,∴=,∴=,∴BE=6,AE=6+4=10(3)S △AOE==15,然后根据相似三角形面积比等于相似比的平方可得S△ABC= S△AOE==4.如图①,已知Rt△ABC中,∠ACB=90°,AC=8,AB=10,点D是AC边上一点(不与C 重合),以AD为直径作⊙O,过C作CE切⊙O于E,交AB于F.(1)若⊙O半径为2,求线段CE的长;(2)若AF=BF,求⊙O的半径;(3)如图②,若CE=CB,点B关于AC的对称点为点G,试求G、E两点之间的距离.【答案】(1)CE=2;(2)⊙O的半径为3;(3)G、E两点之间的距离为9.6【解析】【分析】(1)根据切线的性质得出∠OEC=90°,然后根据勾股定理即可求得;(2)由勾股定理求得BC,然后通过证得△OEC∽△BCA,得到OE OCBC BA=,即8610r r-=解得即可; (3)证得D 和M 重合,E 和F 重合后,通过证得△GBE ∽△ABC ,GB GE AB AC=,即12108GE =,解得即可. 【详解】解:(1)如图①,连接OE ,∵CE 切⊙O 于E ,∴∠OEC =90°,∵AC =8,⊙O 的半径为2, ∴OC =6,OE =2,∴CE =2242OC OE -= ;(2)设⊙O 的半径为r ,在Rt △ABC 中,∠ACB =90°,AB =10,AC =8,∴BC 22AB A C -=6,∵AF =BF ,∴AF =CF =BF ,∴∠ACF =∠CAF ,∵CE 切⊙O 于E ,∴∠OEC =90°,∴∠OEC =∠ACB ,∴△OEC ∽△BCA ,∴OE OC BC BA =,即8610r r -= 解得r =3,∴⊙O 的半径为3;(3)如图②,连接BG ,OE ,设EG 交AC 于点M ,由对称性可知,CB=CG,∵CE=CG,∴∠EGC=∠GEC,∵CE切⊙O于E,∴∠GEC+∠OEG=90°,∵∠EGC+∠GMC=90°,∴∠OEG=∠GMC,∵∠GMC=∠OME,∴∠OEG=∠OME,∴OM=OE,∴点M和点D重合,∴G、D、E三点在同一直线上,连接AE、BE,∵AD是直径,∴∠AED=90°,即∠AEG=90°,又CE=CB=CG,∴∠BEG=90°,∴∠AEB=∠AEG+∠BEG=180°,∴A、E、B三点在同一条直线上,∴E、F两点重合,∵∠GEB=∠ACB=90°,∠B=∠B,∴△GBE∽△ABC,∴GB GEAB AC=,即12108GE=∴GE=9.6,故G、E两点之间的距离为9.6.【点睛】本题考查了切线的判定,轴的性质,勾股定理的应用以及三角形相似的判定和性质,证得G、D、E三点共线以及A、E、B三点在同一条直线上是解题的关5.已知:图1 图2 图3(1)初步思考:如图1, 在PCB ∆中,已知2PB =,BC=4,N 为BC 上一点且1BN =,试说明:12PN PC = (2)问题提出:如图2,已知正方形ABCD 的边长为4,圆B 的半径为2,点P 是圆B 上的一个动点,求12PD PC +的最小值. (3)推广运用:如图3,已知菱形ABCD 的边长为4,∠B ﹦60°,圆B 的半径为2,点P 是圆B 上的一个动点,求12PD PC -的最大值. 【答案】(1)详见解析;(2)5;(3)最大值37DG =【解析】【分析】(1)利用两边成比例,夹角相等,证明BPN ∆∽BCP ∆,得到PN BN PC BP =,即可得到结论成立;(2)在BC 上取一点G ,使得BG=1,由△PBG ∽△CBP ,得到12PG PC =,当D 、P 、G 共线时,12PD PC +的值最小,即可得到答案; (3)在BC 上取一点G ,使得BG=1,作DF ⊥BC 于F ,与(2)同理得到12PG PC =,当点P 在DG 的延长线上时,12PD PC -的值最大,即可得到答案. 【详解】(1)证明:∵2,1,4PB BN BC ===,∴24,4PB BN BC =⋅=,∴2PB BN BC =⋅, ∴BN BP BP BC=,∵B B ∠=∠, ∴BPN BCP ∆∆∽, ∴12PN BN PC BP ==, ∴12PN PC =; (2)解:如图,在BC 上取一点G ,使得BG=1,∵242,212PB BC BG PB ====, ∴,PB BC PBG PBC BG PB=∠=∠, ∴PBG CBP ∆∆∽,∴12PG BG PC PB ==, ∴12PG PC =, ∴12PD PC DP PG +=+; ∵DP PG DG +≥, ∴当D 、P 、G 共线时,12PD PC +的值最小, ∴最小值为:22435DG =+=;(3)如图,在BC 上取一点G ,使得BG=1,作DF ⊥BC 于F ,与(2)同理,可证12PG PC =, 在Rt △CDF 中,∠DCF=60°,CD=4,∴DF=CD •sin60°=23CF=2,在Rt△GDF中,DG=22(23)537+=,∴12PD PC PD PG DG -=-≤,当点P在DG的延长线上时,12PD PC-的值最大,∴最大值为:37DG=.【点睛】本题考查圆综合题、正方形的性质、菱形的性质、相似三角形的判定和性质、两点之间线段最短等知识,解题的关键是学会构建相似三角形解决问题,学会用转化的思想思考问题,把问题转化为两点之间线段最短解决,题目比较难,属于中考压轴题.6.如图,△ABC内接于⊙O,AB是直径,过点A作直线MN,且∠MAC=∠ABC.(1)求证:MN是⊙O的切线.(2)设D是弧AC的中点,连结BD交AC于点G,过点D作DE⊥AB于点E,交AC于点F.①求证:FD=FG.②若BC=3,AB=5,试求AE的长.【答案】(1)见解析;(2)①见解析;②AE=1【解析】【分析】(1)由AB为直径知∠ACB=90°,∠ABC+∠CAB=90°.由∠MAC=∠ABC可证得∠MAC+∠CAB=90°,则结论得证;(2)①证明∠BDE=∠DGF即可.∠BDE=90°﹣∠ABD;∠DGF=∠CGB=90°﹣∠CBD.因为D是弧AC的中点,所以∠ABD=∠CBD.则问题得证;②连接AD、CD,作DH⊥BC,交BC的延长线于H点.证明Rt△ADE≌Rt△CDH,可得AE=CH.根据AB=BH可求出答案.【详解】(1)证明:∵AB是直径,∴∠ACB=90°,∴∠CAB+∠ABC=90°;∵∠MAC=∠ABC,∴∠MAC+∠CAB =90°,即MA ⊥AB ,∴MN 是⊙O 的切线;(2)①证明:∵D 是弧AC 的中点,∴∠DBC =∠ABD ,∵AB 是直径,∴∠CBG+∠CGB =90°,∵DE ⊥AB ,∴∠FDG+∠ABD =90°,∵∠DBC =∠ABD ,∴∠FDG =∠CGB =∠FGD ,∴FD =FG ;②解:连接AD 、CD ,作DH ⊥BC ,交BC 的延长线于H 点.∵∠DBC =∠ABD ,DH ⊥BC ,DE ⊥AB ,∴DE =DH ,在Rt △BDE 与Rt △BDH 中,DH DE BD BD=⎧⎨=⎩, ∴Rt △BDE ≌Rt △BDH (HL ),∴BE =BH ,∵D 是弧AC 的中点,∴AD =DC ,在Rt △ADE 与Rt △CDH 中,DE DH AD CD =⎧⎨=⎩, ∴Rt △ADE ≌Rt △CDH (HL ).∴AE =CH .∴BE =AB ﹣AE =BC+CH =BH ,即5﹣AE =3+AE ,∴AE =1.【点睛】本题是圆的综合题,考查了切线的判定,圆周角定理,全等三角形的判定与性质,等腰三角形的判定,正确作出辅助线来构造全等三角形是解题的关键.7.我们把“有两条边和其中一边的对角对应相等的两个三角形”叫做“同族三角形”,如图1,在△ABC和△ABD中,AB=AB,AC=AD,∠B=∠B,则△ABC和△ABD是“同族三角形”.(1)如图2,四边形ABCD内接于圆,点C是弧BD的中点,求证:△ABC和△ACD是同族三角形;(2)如图3,△ABC内接于⊙O,⊙O的半径为32,AB=6,∠BAC=30°,求AC的长;(3)如图3,在(2)的条件下,若点D在⊙O上,△ADC与△ABC是非全等的同族三角形,AD>CD,求ADCD的值.【答案】(1)详见解析;(2)33+3;(3)ADCD=622+或62.【解析】【分析】(1)由点C是弧BD的中点,根据弧与弦的关系,易得BC=CD,∠BAC=∠DAC,又由公共边AC,可证得:△ABC和△ACD是同族三角形;(2)首先连接0A,OB,作点B作BE⊥AC于点E,易得△AOB是等腰直角三角形,继而求得答案;(3)分别从当CD=CB时与当CD=AB时进行分析求解即可求得答案.【详解】(1)证明:∵点C是弧BD的中点,即BC CD=,∴BC=CD,∠BAC=∠DAC,∵AC=AC,∴△ABC和△ACD是同族三角形.(2)解:如图1,连接OA,OB,作点B作BE⊥AC于点E,∵2,AB=6,∴OA2+OB2=AB2,∴△AOB是等腰直角三角形,且∠AOB=90°,∴∠C=∠AOB=45°, ∵∠BAC=30°,∴BE=AB=3,∴AE=22AB BE -=33,∵CE=BE=3,∴AC=AE+CE=33+3.(3)解:∵∠B=180°﹣∠BAC ﹣∠ACB=180°﹣30°﹣45°=105°,∴∠ADC=180°﹣∠B=75°,如图2,当CD=CB 时,∠DAC=∠BAC=30°,∴∠ACD=75°, ∴AD=AC=33+3,CD=BC=2BE=32,∴AD 333CD 32+==62+; 如图3,当CD=AB 时,过点D 作DF ⊥AC ,交AC 于点F ,则∠DAC=∠ACB=45°,∴∠ACD=180°﹣∠DAC ﹣∠ADC=60°,∴33 ∴2DF=36∴AD 36CD 6==62综上所述:AD CD =622或62 【点睛】本题考查圆的综合应用问题,综合运用弧与弦的关系,等腰三角形的性质结合图形作辅助线进行分析证明以及求解,难度较大.8.如图,在ABC ∆中,90ACB ∠=︒,45ABC ∠=︒,12BC cm =,半圆O 的直径12DE cm =.点E 与点C 重合,半圆O 以2/cm s 的速度从左向右移动,在运动过程中,点D 、E 始终在BC 所在的直线上.设运动时间为()x s ,半圆O 与ABC ∆的重叠部分的面积为()2S cm .(1)当0x =时,设点M 是半圆O 上一点,点N 是线段AB 上一点,则MN 的最大值为_________;MN 的最小值为________.(2)在平移过程中,当点O 与BC 的中点重合时,求半圆O 与ABC ∆重叠部分的面积S ;(3)当x 为何值时,半圆O 与ABC ∆的边所在的直线相切?【答案】(1)24cm ,()926cm ;(2)2(189)cm π+;(3)0x =或6x =或932x =-【解析】【分析】(1)当N 与点B 重合,点M 与点D 重合时,MN 最大,此时121224()MN DB DE BC cm ==+=+=如图①,过点O 作ON AB ⊥于N ,与半圆交于点M ,此时MN 最小,MN ON OM =-,261218()92()2OB OC CB cm ON BN cm =+=+====,所以926()MN ON OM cm =-=; (2)当点O 与BC 的中点重合时,如图②,点O 移动了12cm ,设半圆与AB 交于点H ,连接OH 、CH ,6OH OC OB ===,29016669183602BOH HOC S S S ππ∆=+=⋅+⨯⨯=+阴影扇形; (3)当半圆O 与直线AC 相切时,运动的距离为0或12,所以0x =(秒)或6(秒);当半圆O 与直线AB 相切时,如图③,连接OH ,则OH AB ⊥,6OH =,262OB OH ==1262OC BC OB =-=-61262182()cm +--,运动时间为1862932x -==-). 【详解】解:解(1)当N 与点B 重合,点M 与点D 重合时,MN 最大,此时121224()MN DB DE BC cm ==+=+=如图①,过点O 作ON AB ⊥于N ,与半圆交于点M ,此时MN 最小,MN ON OM =-,45ABC ∠=︒,45NOB ∴∠=︒,在Rt ONB ∆中,61218()OB OC CB cm =+=+=292()2ON BN OB cm ∴===, 926()MN ON OM cm ∴=-=-,故答案为24cm ,(926)cm -;(2)当点O 与BC 的中点重合时,如图②,点O 移动了12cm ,设半圆与AB 交于点H ,连接OH 、CH .BC 为直径,90CHB ∴∠=︒,45ABC ∠=︒45HCB ∴∠=︒,HC HB ∴=,OH BC ∴⊥,6OH OC OB ===,29016669183602BOH HOC S S S ππ∆=+=⋅+⨯⨯=+阴影扇形; (3)当半圆O 与直线AC 相切时,运动的距离为0或12,0x ∴=(秒)或6(秒);当半圆O 与直线AB 相切时,如图③,连接OH ,则OH AB ⊥,6OH =45B ∠=︒,90OHB ∠=︒,262OB OH ∴==,1262OC BC OB =-=-, 移动的距离为612621862()cm +-=-, 运动时间为1862932x -==-(秒), 综上所述,当x 为0或6或932-时,半圆O 与ABC ∆的边所在的直线相切.【点睛】本题考查了圆综合知识,熟练掌握勾股定理以及圆切线定理是解题的关键.要注意分类讨论.9.如图①②,在平面直角坐标系中,边长为2的等边CDE ∆恰好与坐标系中的OAB ∆重合,现将CDE ∆绕边AB 的中点(G G 点也是DE 的中点),按顺时针方向旋转180︒到△1C DE 的位置.(1)求1C 点的坐标;(2)求经过三点O 、A 、1C 的抛物线的解析式;(3)如图③,G 是以AB 为直径的圆,过B 点作G 的切线与x 轴相交于点F ,求切线BF 的解析式;(4)抛物线上是否存在一点M ,使得:16:3AMF OAB S S ∆∆=.若存在,请求出点M 的坐标;若不存在,请说明理由.【答案】(1)13)C ;(2)2323y x x =;(3)323y x =;(4)128383,M M ⎛⎛- ⎝⎭⎝⎭.【解析】【分析】(1)利用中心对称图形的性质和等边三角形的性质,可以求出.(2)运用待定系数法,代入二次函数解析式,即可求出.(3)借助切线的性质定理,直角三角形的性质,求出F ,B 的坐标即可求出解析式. (4)当M 在x 轴上方或下方,分两种情况讨论.【详解】解:(1)将等边CDE ∆绕边AB 的中点G 按顺时针方向旋转180︒到△1C DE , 则有,四边形'OAC B 是菱形,所以1C 的横坐标为3,根据等边CDE ∆的边长是2,利用等边三角形的性质可得1C ;(2)抛物线过原点(0,0)O ,设抛物线解析式为2y ax bx =+,把(2,0)A,C '代入,得42093a b a b +=⎧⎪⎨+=⎪⎩解得3a =,b = ∴抛物线解析式为233y x x =-;(3)90ABF ∠=︒,60BAF ∠=︒,30AFB ∴∠=︒,又2AB =,4AF ∴=,2OF ∴=, (2,0)F ∴-,设直线BF 的解析式为y kx b =+,把B ,(2,0)F -代入,得20k b k b ⎧+=⎪⎨-+=⎪⎩,解得3k =b = ∴直线BF的解析式为y x =+; (4)①当M 在x轴上方时,存在2()M x ,211:[4)]:[216:322AMF OAB S S ∆∆=⨯⨯⨯=, 得2280x x --=,解得14x =,22x =-,当14x =时,244y , 当12x =-时,2(2)(2)y =--=183(4,)M ∴,283(2,)M -; ②当M 在x 轴下方时,不存在,设点2323(,)M x x x -, 213231:[4()]:[23]16:322AMF OAB S S x x ∆∆=-⨯⨯-⨯⨯=, 得2280x x -+=,240b ac -<无解,综上所述,存在点的坐标为183(4,)M ,283(2,)M -. 【点睛】此题主要考查了旋转,等边三角形的性质,菱形的判定和性质,以及待定系数法求解二次函数解析式和切线的性质定理等,能熟练应用相关性质,是解题的关键.10.如图,在O 中,AB 为直径,过点A 的直线l 与O 相交于点C ,D 是弦CA 延长线上一点,BAC ∠,BAD ∠的平分线与O 分别相交于点E ,F ,G 是BF 的中点,过点G 作MNAE ,与AF ,EB 的延长线分别交于点M ,N .(1)求证:MN 是O 的切线; (2)若24AE =,18AM =. ①求O 的半径;②连接MC ,求tan MCD ∠的值. 【答案】(1)见解析;(2)①13;②2741 【解析】【分析】(1)如图1,连接 GO 、GA ,先根据角平分线的定义证明∠MAE=12(∠BAC+∠BAD )=90°,由圆周角定理和同圆的半径相等得∠OGA=∠FAG ,则OG ∥AM ,所以∠MGO=180-∠M=90,从而得结论;(2)①延长GO 交AE 于点P ,证明四边形 MGPA 为矩形,得GP=MA=18,∠GPA=90°,设OA=OG=r ,则OP=18-r ,根据勾股定理列方程解出即可;②如图3,过M 作MH ⊥l ,连接BC ,延长NE 交l 于I ,连接GO 交延长交AE 于P ,tan ∠MAH=tan ∠ABE=tan ∠BIA=125,BI=2BE=20,根据三角函数计算MH ,AH ,CI 的长,最后计算MH 和HC 的长,代入tan ∠MCD=MH HC,可得结论. 【详解】(1)证明:如图1,连接GO ,GA ,∵BAC ∠,BAD ∠的平分线与O 分别相交于点E ,F , ∴1()902MAE BAC BAD ∠=∠+∠=︒. ∵MN AE ,∴18090M MAE ∠=︒-∠=︒.∵G 是BF 的中点,∴FG BG =,∴FAG BAG ∠=∠.∵OA OG =,∴OGA BAG ∠=∠,∴OGA FAG ∠=∠,∴OG AM ∥,∴18090MGO M ∠=︒-∠=︒.∵OG 为O 半径, ∴MN 是O 的切线.(2)解:①如图2,连接GO 并延长交AE 于点P ,∵90MGO M MAE ∠=∠=∠=︒,∴四边形MGPA 为矩形,∴18GP MA ==,90GPA ∠=︒,即OP AE ⊥,∴1122AP AE ==. 设OA OG r ==,则18OP r =-,在Rt OAP △中,∵222OA OP AP =+,∴222(18)12r r =-+,解得:13r =,故O 的半径是13.②如图3,过M 作MH l ⊥,连接BC ,延长NE 交l 于I ,连接GO 并延长交AE 于P ,由①知:13OG =,18PG =,∴5OP =.∵AB 是O 的直径,∴90AEB AEI ∠=∠=︒.∵BAE EAC ∠=∠,∴ABE AIB ∠=∠,∵AM NI ∥,∴MAH BIA ABE ∠=∠=∠,∴12tan tan tan 5MAH ABE BIA ∠=∠=∠=,220BI BE ==. ∵12cos 13HM AMH AM ∠==,5sin 13AH AMH AM ∠==,5sin 13CI CBI BI ∠==, ∴181********MH ⨯==,185901313AH ⨯==,5100201313CI =⨯=, ∴100238261313AC AI CI =-=-=, ∴23890328131313HC AH AC =+=+=, ∴21627tan 32841MH MCD HC ∠===. 【点睛】 本题考查了切线的判定,圆周角定理,解直角三角形,勾股定理,矩形的性质和判定,正确作出辅助线是解题的关键.。
中考压轴题--圆含答案

.中考压轴题(一)--------与压轴题 1.如图,在M 中,A B 所对角为120,已知圆为2c m ,并建立如图所示的直角. (1)M 的坐标;(2过A ,B ,C 三点的抛物线的解析式; (3)点D 是弦AB 所对的优弧上一动点,求四边形ACBD 的最大面积; (4)在(2)中的抛物线上是否存在一点P ,使△P A B 和△A B C相似?若存在,求出点P 的坐标;若不存y 理由.[解](1)如图(1结MA ,MB . 则AMB120CMB60,OBM30. 1 OMMB1,M(0,1). 2 (2)由A ,B ,C 三点的特殊性与对称性, M y x 过A ,B ,C 三点的抛物线的解析式为 2 yaxc .A OBC DOCMCMO1, 223 OBMBOM , MC(0,1),B(3,0). xOB Ac1,a1 3 12 yx1.3 C(3)S 四边形ACBD S △ABCS △ABD ,又S △ABC 与AB 均为定值,图1 当△ABD 边AB 上的高最大时,S △ABD最大,此时点D 为M 与y 轴的交点,如图1.111 2 S 四边形S △S △AB ·OCAB ·ODAB ·CD43cm . ACBDABCABD 222 (4)方法1:如图2,△ABC 为等腰三角形,ABC30AB3,, BC y P M O xA BC 图2△ABC ∽△PAB 等价于PAB30,PBAB23,PA3PB6.设P (x ,y)且x0,则x PA ·cos30AO33323,yPA ·sin303.12又P (2yx1,在抛物线 312yx 上,存在点P(23,3),使△ABC ∽△PAB .1 3..由抛物线的对称性,知点(23,3)也符合题意.存在点P ,它的坐标为(23,3)或(23,3). 方法2:如图(3),当△ABC ∽△PAB 时,PABBAC30,又由(1)知MAB30, 点P 在直线AM 上.设直线AM 的解析式为ykxb ,将A(3,0),M(0,1)代入,解得k b 3 , 3 2.直线AM 的解析式为3 yx1.3 3yx 3解方程组1 2yx 31,得P(23,3). 1又3 tanPBx3,PBx60.P30,233△ABC ∽△PAB .在抛物线 12yx 上,存在点P(23,3),使△ABC ∽△PAB .1 3由抛物线的对称性,知点(23,3)也符合题意.存在点P ,它的坐标为(23,3)或(23,3). 方法3:AB如图3BC,设P(x ,y)则图3 △ABC ∽△PAB 等价于PBAB23,PA3AB6.当x0时,得22(x 3)y23 ,解得P(23,3).22 (x 3)y6.1 2又P (2yx1,在抛物线 312yx 上,存在点P(23,3),使△ABC ∽△PAB .1 3由抛物线的对称性,知点(23,3)也符合题意.存在点P ,它的坐标为(23,3)或(23,3).]本题是一道综合性很强也是传统型的压轴题,涉及了函数、方程、相似、圆等大量初中数学的重点知识,解这 类问题要求学生必须稳固的掌握各会有多解的情况出现,此时就要求3.(06湖南湘潭卷)已知:如图,抛物线 323 2 yxx3的图象与x 轴分别交于A ,B 两点,与y 轴交于C 33 点,M 点O 及点A ,C ,点D 是劣弧OA 上一动点(D 点与A ,O 不重合). (1)求抛(2)求M 的面积; (C D 说明理由..[解](1)抛物线3232yxx333yECM33 2 x2x1333FAOBx343 2x1E 3343 1,3D G(AC ;M 过A ,O ,C ,∠AOC90AC 为O 的直径.AC 而OA3,OC3r3 2Sr M23yEC (3)当点DOA 的中点时,直线GA 与M 相切M理由:在Rt △ACO 中,OA3,OC33tan3∠ACO .3AF D GOBx∠ACO60,∠CAO30点D 是OA 的中点ADDO ∠ACG ∠DCO30OFOCtan301,∠CFO60在△G A F 中,A F 2,F G 2∠A F G ∠C F O 60△A G F ∠CAG ∠GAF ∠CAO90又AC 为直径,当D 为OA 的中点时,GA 为M 的切线 ]本题将抛物线与圆放在同一坐标系中研究,因此数形结合的解题思想是作图D 点的位置。
中考数学—圆的综合的综合压轴题专题复习附详细答案

中考数学—圆的综合的综合压轴题专题复习附详细答案一、圆的综合1.如图,已知Rt△ABC中,C=90°,O在AC上,以OC为半径作⊙O,切AB于D点,且BC=BD.(1)求证:AB为⊙O的切线;(2)若BC=6,sinA=35,求⊙O的半径;(3)在(2)的条件下,P点在⊙O上为一动点,求BP的最大值与最小值.【答案】(1)连OD,证明略;(2)半径为3;(3)最大值35+3 ,35-3.【解析】分析:(1)连接OD,OB,证明△ODB≌△OCB即可.(2)由sinA=35且BC=6可知,AB=10且cosA=45,然后求出OD的长度即可.(3)由三角形的三边关系,可知当连接OB交⊙O于点E、F,当点P分别于点E、F重合时,BP分别取最小值和最大值.详解:(1)如图:连接OD、OB.在△ODB和△OCB中:OD=OC,OB=OB,BC=BD;∴△ODB≌△OCB(SSS).∴∠ODB=∠C=90°.∴AB为⊙O的切线.(2)如图:∵sinA=35,∴CB3AB5=,∵BC=6,∴AB=10,∵BD=BC=6,∴AD=AB-BD=4,∵sinA=35,∴cosA=45,∴OA=5,∴OD=3,即⊙O的半径为:3.(3)如图:连接OB,交⊙O为点E、F,由三角形的三边关系可知:当P点与E点重合时,PB取最小值.由(2)可知:OD=3,DB=6,∴223635+=∴PB=OB-OE=353.当P点与F点重合时,PB去最大值,PB=OP+OB=3+35点睛:本题属于综合类型题,主要考查了圆的综合知识.关键是对三角函数值、勾股定理、全等三角形判定与性质的理解.2.已知:如图,在矩形ABCD中,点O在对角线BD上,以OD的长为半径的⊙O与AD,BD分别交于点E、点F,且∠ABE=∠DBC.(1)判断直线BE与⊙O的位置关系,并证明你的结论;(2)若sin ∠ABE=33,CD=2,求⊙O 的半径.【答案】(1)直线BE 与⊙O 相切,证明见解析;(2)⊙O 的半径为32. 【解析】分析:(1)连接OE ,根据矩形的性质,可证∠BEO =90°,即可得出直线BE 与⊙O 相切; (2)连接EF ,先根据已知条件得出BD 的值,再在△BEO 中,利用勾股定理推知BE 的长,设出⊙O 的半径为r ,利用切线的性质,用勾股定理列出等式解之即可得出r 的值. 详解:(1)直线BE 与⊙O 相切.理由如下:连接OE ,在矩形ABCD 中,AD ∥BC ,∴∠ADB =∠DBC . ∵OD =OE ,∴∠OED =∠ODE . 又∵∠ABE =∠DBC ,∴∠ABE =∠OED , ∵矩形ABDC ,∠A =90°,∴∠ABE +∠AEB =90°,∴∠OED +∠AEB =90°,∴∠BEO =90°,∴直线BE 与⊙O 相切;(2)连接EF ,方法1:∵四边形ABCD 是矩形,CD =2,∴∠A =∠C =90°,AB =CD =2. ∵∠ABE =∠DBC ,∴sin ∠CBD =33sin ABE ∠= ∴23DCBD sin CBD∠==在Rt △AEB 中,∵CD =2,∴22BC =. ∵tan ∠CBD =tan ∠ABE ,∴2222DC AE AEAE BC AB ,,==∴=, 由勾股定理求得6BE =在Rt △BEO 中,∠BEO =90°,EO 2+EB 2=OB 2.设⊙O 的半径为r ,则222623r r +=()(),∴r 3, 方法2:∵DF 是⊙O 的直径,∴∠DEF =90°.∵四边形ABCD 是矩形,∴∠A =∠C =90°,AB =CD =2. ∵∠ABE =∠DBC ,∴sin ∠CBD =33sin ABE ∠=. 设3DC x BD x ==,,则2BC x =.∵CD =2,∴22BC =. ∵tan ∠CBD =tan ∠ABE ,∴22222DC AE AEAE BC AB ,,=∴=∴=, ∴E 为AD 中点.∵DF 为直径,∠FED =90°,∴EF ∥AB ,∴132DF BD ==,∴⊙O 的半径为32.点睛:本题综合考查了切线的性质、勾股定理以及三角函数的应用等知识点,具有较强的综合性,有一定的难度.3.如图,⊙M 与菱形ABCD 在平面直角坐标系中,点M 的坐标为(3,﹣1),点A 的坐标为(﹣2,3),点B 的坐标为(﹣3,0),点C 在x 轴上,且点D 在点A 的左侧. (1)求菱形ABCD 的周长;(2)若⊙M 沿x 轴向右以每秒2个单位长度的速度平移,同时菱形ABCD 沿x 轴向右以每秒3个单位长度的速度平移,设菱形移动的时间为t (秒),当⊙M 与BC 相切,且切点为BC 的中点时,连接BD ,求: ①t 的值; ②∠MBD 的度数;(3)在(2)的条件下,当点M 与BD 所在的直线的距离为1时,求t 的值.【答案】(1)8;(2)①7;②105°;(3)t=636+33. 【解析】分析:(1)根据勾股定理求菱形的边长为2,所以可得周长为8;(2)①如图2,先根据坐标求EF 的长,由EE '﹣FE '=EF =7,列式得:3t ﹣2t =7,可得t 的值;②先求∠EBA =60°,则∠FBA =120°,再得∠MBF =45°,相加可得:∠MBD =∠MBF +∠FBD =45°+60°=105°;(3)分两种情况讨论:作出距离MN 和ME ,第一种情况:如图5由距离为1可知:BD为⊙M 的切线,由BC 是⊙M 的切线,得∠MBE =30°,列式为3t =2t +6,解出即可; 第二种情况:如图6,同理可得t 的值. 详解:(1)如图1,过A 作AE ⊥BC 于E .∵点A 的坐标为(﹣2),点B 的坐标为(﹣3,0),∴AE ,BE =3﹣2=1,∴AB=2. ∵四边形ABCD 是菱形,∴AB =BC =CD =AD =2,∴菱形ABCD 的周长=2×4=8; (2)①如图2,⊙M 与x 轴的切点为F ,BC 的中点为E . ∵M (3,﹣1),∴F (3,0).∵BC =2,且E 为BC 的中点,∴E (﹣4,0),∴EF =7,即EE '﹣FE '=EF ,∴3t ﹣2t =7,t =7;②由(1)可知:BE =1,AE∴tan ∠EBA =AEBE =,∴∠EBA =60°,如图4,∴∠FBA =120°. ∵四边形ABCD 是菱形,∴∠FBD =12∠FBA =11202⨯︒=60°. ∵BC 是⊙M 的切线,∴MF ⊥BC .∵F 是BC 的中点,∴BF =MF =1,∴△BFM 是等腰直角三角形, ∴∠MBF =45°,∴∠MBD =∠MBF +∠FBD =45°+60°=105°;(3)连接BM ,过M 作MN ⊥BD ,垂足为N ,作ME ⊥BC 于E ,分两种情况: 第一种情况:如图5.∵四边形ABCD 是菱形,∠ABC =120°,∴∠CBD =60°,∴∠NBE =60°. ∵点M 与BD 所在的直线的距离为1,∴MN =1,∴BD 为⊙M 的切线. ∵BC 是⊙M 的切线,∴∠MBE =30°.∵ME =1,∴EB ∴3t =2t +6,t =6 第二种情况:如图6.∵四边形ABCD 是菱形,∠ABC =120°,∴∠DBC =60°,∴∠NBE =120°. ∵点M 与BD 所在的直线的距离为1,∴MN =1,∴BD 为⊙M 的切线. ∵BC 是⊙M 的切线,∴∠MBE =60°.∵ME =MN =1,∴Rt △BEM 中,tan60°=ME BE ,EB =160tan ︒∴3t =2t t综上所述:当点M 与BD 所在的直线的距离为1时,t =6或6+3.点睛:本题是四边形和圆的综合题,考查了菱形的性质、圆的切线的性质和判定、特殊的三角函数值、等腰直角三角形的性质、动点运动问题,此类问题比较复杂,弄清动点运动方向、速度、时间和路程的关系,并与方程相结合,找等量关系,求出时间t的值.4.等腰Rt△ABC和⊙O如图放置,已知AB=BC=1,∠ABC=90°,⊙O的半径为1,圆心O 与直线AB的距离为5.(1)若△ABC以每秒2个单位的速度向右移动,⊙O不动,则经过多少时间△ABC的边与圆第一次相切?(2)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,则经过多少时间△ABC的边与圆第一次相切?(3)若两个图形同时向右移动,△ABC的速度为每秒2个单位,⊙O的速度为每秒1个单位,同时△ABC的边长AB、BC都以每秒0.5个单位沿BA、BC方向增大.△ABC的边与圆第一次相切时,点B运动了多少距离?【答案】(1)522-;(2)52-;(3)20423-【解析】分析:(1)分析易得,第一次相切时,与斜边相切,假设此时,△ABC移至△A′B′C′处,A′C′与⊙O切于点E,连OE并延长,交B′C′于F.由切线长定理易得CC′的长,进而由三角形运动的速度可得答案;(2)设运动的时间为t秒,根据题意得:CC′=2t,DD′=t,则C′D′=CD+DD′-CC′=4+t-2t=4-t,由第(1)的结论列式得出结果;(3)求出相切的时间,进而得出B点移动的距离.详解:(1)假设第一次相切时,△ABC移至△A′B′C′处,如图1,A′C′与⊙O切于点E,连接OE并延长,交B′C′于F,设⊙O与直线l切于点D,连接OD,则OE⊥A′C′,OD⊥直线l,由切线长定理可知C′E=C′D,设C′D=x,则C′E=x,∵△ABC是等腰直角三角形,∴∠A=∠ACB=45°,∴∠A′C′B′=∠ACB=45°,∴△EFC′是等腰直角三角形,∴2x,∠OFD=45°,∴△OFD也是等腰直角三角形,∴OD=DF,∴2x+x=1,则2-1,∴CC′=BD-BC-C′D=5-1-2-1)2,∴点C运动的时间为522;则经过522秒,△ABC的边与圆第一次相切;(2)如图2,设经过t秒△ABC的边与圆第一次相切,△ABC移至△A′B′C′处,⊙O与BC 所在直线的切点D移至D′处,A′C′与⊙O 切于点E ,连OE 并延长,交B′C′于F , ∵CC′=2t ,DD′=t ,∴C′D′=CD+DD′-CC′=4+t -2t=4-t , 由切线长定理得C′E=C′D′=4-t , 由(1)得:4-t=2-1, 解得:t=5-2,答:经过5-2秒△ABC 的边与圆第一次相切; (3)由(2)得CC′=(2+0.5)t=2.5t ,DD′=t , 则C′D′=CD+DD′-CC′=4+t-2.5t=4-1.5t , 由切线长定理得C′E=C′D′=4-1.5t , 由(1)得:4-1.5t=2-1, 解得:t=10223-, ∴点B 运动的距离为2×10223-=20423-.点睛:本题要求学生熟练掌握圆与直线的位置关系,并结合动点问题进行综合分析,比较复杂,难度较大,考查了学生数形结合的分析能力.5.问题发现.(1)如图①,Rt △ABC 中,∠C =90°,AC =3,BC =4,点D 是AB 边上任意一点,则CD 的最小值为______.(2)如图②,矩形ABCD 中,AB =3,BC =4,点M 、点N 分别在BD 、BC 上,求CM+MN 的最小值.(3)如图③,矩形ABCD 中,AB =3,BC =4,点E 是AB 边上一点,且AE =2,点F 是BC 边上的任意一点,把△BEF 沿EF 翻折,点B 的对应点为G ,连接AG 、CG ,四边形AGCD 的面积是否存在最小值,若存在,求这个最小值及此时BF 的长度.若不存在,请说明理由.【答案】(1) 125CD =;(2) CM MN +的最小值为9625.(3) 152【解析】试题分析:(1)根据两种不同方法求面积公式求解;(2)作C 关于BD 的对称点C ',过C '作BC 的垂线,垂足为N ,求C N '的长即可;(3) 连接AC ,则ADC ACG AGCD S S S =+V V 四,321GB EB AB AE ==-=-=,则点G 的轨迹为以E 为圆心,1为半径的一段弧.过E 作AC 的垂线,与⊙E 交于点G ,垂足为M ,由AEM ACB V V ∽求得GM 的值,再由ACD ACG AGCD S S S =+V V 四边形 求解即可.试题解析:(1)从C 到AB 距离最小即为过C 作AB 的垂线,垂足为D ,22ABC CD AB AC BCS ⋅⋅==V , ∴341255AC BC CD AB ⋅⨯===, (2)作C 关于BD 的对称点C ',过C '作BC 的垂线,垂足为N ,且与BD 交于M ,则CM MN +的最小值为C N '的长, 设CC '与BD 交于H ,则CH BD ⊥, ∴BMC BCD V V ∽,且125CH =,∴C CB BDC ∠=∠',245CC '=,∴C NC BCD 'V V ∽,∴244965525CC BC C N BD ⨯⋅==='', 即CM MN +的最小值为9625.(3)连接AC ,则ADC ACG AGCD S S S =+V V 四,321GB EB AB AE ==-=-=,∴点G 的轨迹为以E 为圆心,1为半径的一段弧. 过E 作AC 的垂线,与⊙E 交于点G ,垂足为M , ∵AEM ACB V V ∽, ∴EM AEBC AC=, ∴24855AE BC EM AC ⋅⨯===, ∴83155GM EM EG =-=-=,∴ACD ACG AGCD S S S =+V V 四边形,113345225=⨯⨯+⨯⨯, 152=. 【点睛】本题考查圆的综合题、最短问题、勾股定理、面积法、两点之间线段最短等知识,解题的关键是利用轴对称解决最值问题,灵活运用两点之间线段最短解决问题.6.已知:BD 为⊙O 的直径,O 为圆心,点A 为圆上一点,过点B 作⊙O 的切线交DA 的延长线于点F ,点C 为⊙O 上一点,且AB =AC ,连接BC 交AD 于点E ,连接AC . (1)如图1,求证:∠ABF =∠ABC ;(2)如图2,点H 为⊙O 内部一点,连接OH ,CH 若∠OHC =∠HCA =90°时,求证:CH =12DA ; (3)在(2)的条件下,若OH =6,⊙O 的半径为10,求CE 的长.【答案】(1)见解析;(2)见解析;(3)215. 【解析】【分析】 ()1由BD 为O e 的直径,得到D ABD 90∠∠+=o ,根据切线的性质得到FBA ABD 90∠∠+=o ,根据等腰三角形的性质得到C ABC ∠∠=,等量代换即可得到结论;()2如图2,连接OC ,根据平行线的判定和性质得到ACO COH ∠∠=,根据等腰三角形的性质得到OBC OCB ∠∠=,ABC CBO ACB OCB ∠∠∠∠+=+,根据相似三角形的性质即可得到结论;()3根据相似三角形的性质得到AB BD 2OH OC==,根据勾股定理得到22AD BD AB 16=-=,根据全等三角形的性质得到BF BE =,AF AE =,根据射影定理得到212AF 916==,根据相交弦定理即可得到结论. 【详解】()1BD Q 为O e 的直径,90BAD ∴∠=o ,90D ABD ∴∠+∠=o ,FB Q 是O e 的切线,90FBD ∴∠=o ,90FBA ABD ∴∠+∠=o ,FBA D ∴∠=∠,AB AC =Q ,C ABC ∴∠=∠,C D ∠=∠Q ,ABF ABC ∴∠=∠;()2如图2,连接OC ,90OHC HCA ∠=∠=o Q ,//AC OH ∴,ACO COH ∴∠=∠,OB OC =Q ,OBC OCB ∴∠=∠,ABC CBO ACB OCB ∴∠+∠=∠+∠,即ABD ACO ∠=∠,ABC COH ∴∠=∠,90H BAD ∠=∠=o Q ,ABD ∴V ∽HOC V ,2AD BD CH OC∴==, 12CH DA ∴=; ()3由()2知,ABC V ∽HOC V ,2AB BD OH OC∴==, 6OH =Q ,O e 的半径为10, 212AB OH ∴==,20BD =,2216AD BD AB ∴=-=,在ABF V 与ABE V 中,90ABF ABE AB AB BAF BAE ∠=∠⎧⎪=⎨⎪∠=∠=⎩o , ABF ∴V ≌ABE V ,BF BE ∴=,AF AE =,90FBD BAD ∠=∠=o Q ,2AB AF AD ∴=⋅,212916AF ∴==, 9AE AF ∴==,7DE ∴=,2215BE AB AE =+=,AD Q ,BC 交于E ,AE DE BE CE ∴⋅=⋅,9721155AE DE CE BE ⋅⨯∴===. 【点睛】本题考查了切线的性质,圆周角定理,全等三角形的判定和性质,相似三角形的判定和性质,平行线的性质,勾股定理,射影定理,相交弦定理,正确的识别图形是解题的关键.7.如图1,等边△ABC 的边长为3,分别以顶点B 、A 、C 为圆心,BA 长为半径作¶AC 、¶CB、¶BA ,我们把这三条弧所组成的图形称作莱洛三角形,显然莱洛三角形仍然是轴对称图形,设点l 为对称轴的交点.(1)如图2,将这个图形的顶点A 与线段MN 作无滑动的滚动,当它滚动一周后点A 与端点N 重合,则线段MN 的长为 ;(2)如图3,将这个图形的顶点A 与等边△DEF 的顶点D 重合,且AB ⊥DE ,DE =2π,将它沿等边△DEF 的边作无滑动的滚动当它第一次回到起始位置时,求这个图形在运动过程中所扫过的区域的面积;(3)如图4,将这个图形的顶点B 与⊙O 的圆心O 重合,⊙O 的半径为3,将它沿⊙O 的圆周作无滑动的滚动,当它第n 次回到起始位置时,点I 所经过的路径长为 (请用含n 的式子表示)【答案】(1)3π;(2)27π;(3)3.【解析】试题分析:(1)先求出¶AC 的弧长,继而得出莱洛三角形的周长为3π,即可得出结论; (2)先判断出莱洛三角形等边△DEF 绕一周扫过的面积如图所示,利用矩形的面积和扇形的面积之和即可;(3)先判断出莱洛三角形的一个顶点和O 重合旋转一周点I 的路径,再用圆的周长公式即可得出.试题解析:解:(1)∵等边△ABC 的边长为3,∴∠ABC =∠ACB =∠BAC =60°,¶¶¶AC BC AB ==,∴¶¶AC BC l l ==¶AB l =603180π⨯=π,∴线段MN 的长为¶¶¶AC BC ABl l l ++=3π.故答案为3π; (2)如图1.∵等边△DEF 的边长为2π,等边△ABC 的边长为3,∴S 矩形AGHF =2π×3=6π,由题意知,AB ⊥DE ,AG ⊥AF ,∴∠BAG =120°,∴S 扇形BAG =21203360π⨯=3π,∴图形在运动过程中所扫过的区域的面积为3(S 矩形AGHF +S 扇形BAG )=3(6π+3π)=27π;(3)如图2,连接BI 并延长交AC 于D .∵I 是△ABC 的重心也是内心,∴∠DAI =30°,AD =12AC =32,∴OI =AI =3230AD cos DAI cos ∠=︒=3,∴当它第1次回到起始位置时,点I 所经过的路径是以O 为圆心,OI 为半径的圆周,∴当它第n 次回到起始位置时,点I 所经过的路径长为n •2π•3=23n π.故答案为23n π.点睛:本题是圆的综合题,主要考查了弧长公式,莱洛三角形的周长,矩形,扇形面积公式,解(1)的关键是求出¶AC 的弧长,解(2)的关键是判断出莱洛三角形绕等边△DEF 扫过的图形,解(3)的关键是得出点I 第一次回到起点时,I 的路径,是一道中等难度的题目.8.已知,ABC ∆内接于O e ,点P 是弧AB 的中点,连接PA 、PB ;(1)如图1,若AC BC =,求证:AB PC ⊥;(2)如图2,若PA 平分CPM ∠,求证:AB AC =;(3)在(2)的条件下,若24sin 25BPC ∠=,8AC =,求AP 的值.【答案】(1)见解析;(2)见解析5【解析】【分析】(1)由点P 是弧AB 的中点,可得出AP=BP , 通过证明APC BPC ∆≅∆ ,ACE BCE ∆≅∆可得出AEC BEC ∠=∠进而证明AB ⊥ PC.(2)由PA 是∠CPM 的角平分线,得到∠MPA=∠APC, 等量代换得到∠ABC=∠ACB, 根据等腰三角形的判定定理即可证得AB=AC.(3)过A 点作AD ⊥BC,有三线合一可知AD 平分BC,点O 在AD 上,连结OB ,则∠BOD =∠BAC ,根据圆周角定理可知∠BOD=∠BAC, ∠BPC=∠BAC ,由∠BOD=∠BPC 可得sin sin BD BOD BPC OB∠=∠=,设OB=25x ,根据勾股定理可算出OB 、BD 、OD 、AD 的长,再次利用勾股定理即可求得AP 的值.【详解】解:(1)∵点P 是弧AB 的中点,如图1,∴AP =BP ,在△APC 和△BPC 中 AP BP AC BC PC PC =⎧⎪=⎨⎪=⎩,∴△APC ≌△BPC (SSS ),∴∠ACP =∠BCP ,在△ACE 和△BCE 中AC BC ACP BCP CE CE =⎧⎪∠=∠⎨⎪=⎩,∴△ACE ≌△BCE (SAS ),∴∠AEC =∠BEC ,∵∠AEC +∠BEC =180°,∴∠AEC =90°,∴AB ⊥PC ;(2)∵PA 平分∠CPM ,∴∠MPA =∠APC ,∵∠APC +∠BPC +∠ACB =180°,∠MPA +∠APC +∠BPC =180°,∴∠ACB =∠MPA =∠APC ,∵∠APC =∠ABC ,∴∠ABC =∠ACB ,∴AB =AC ;(3)过A 点作AD ⊥BC 交BC 于D ,连结OP 交AB 于E ,如图2,由(2)得出AB =AC ,∴AD 平分BC ,∴点O 在AD 上,连结OB ,则∠BOD =∠BAC ,∵∠BPC =∠BAC ,∴sin sin BOD BPC ∠=∠=2425BD OB =, 设OB =25x ,则BD =24x ,∴OD 22OB BD -7x ,在Rt ABD V 中,AD =25x +7x =32x ,BD =24x ,∴AB 22AD BD +40x ,∵AC =8,∴AB =40x =8,解得:x =0.2,∴OB =5,BD =4.8,OD =1.4,AD =6.4,∵点P 是¶AB 的中点,∴OP 垂直平分AB ,∴AE =12AB =4,∠AEP =∠AEO =90°, 在Rt AEO ∆中,OE 223AO AE -=,∴PE =OP ﹣OE =5﹣3=2,在Rt APE ∆中,AP =22222425PE AE +=+=.【点睛】本题是一道有关圆的综合题,考查了圆周角定理、勾股定理、等腰三角形的判定定理和三线合一,是初中数学的重点和难点,一般以压轴题形出现,难度较大.9.如图,□ABCD 的边AD 是△ABC 外接圆⊙O 的切线,切点为A ,连接AO 并延长交BC 于点E ,交⊙O 于点F ,过点C 作直线CP 交AO 的延长线于点P ,且∠BCP =∠ACD . (1)求证:PC 是⊙O 的切线;(2)若∠B =67.5°,BC =2,求线段PC ,PF 与弧CF 所围成的阴影部分的面积S .【答案】(1)见解析;(2)14π-【解析】 【分析】(1) 过C 点作直径CM ,连接MB ,根据CM 为直径,可得∠M+∠BCM =90°,再根据AB ∥DC 可得∠ACD =∠BAC ,由圆周角定理可得∠BAC =∠M ,∠BCP =∠ACD ,从而可推导得出∠PCM =90°,根据切线的判定即可得;(2)连接OB ,由AD 是⊙O 的切线,可得∠PAD =90°,再由BC ∥AD ,可得AP ⊥BC ,从而得BE =CE = 12BC =1,继而可得到∠ABC =∠ACB =67.5°,从而得到∠BAC =45°,由圆周角定理可得∠BOC=90°,从而可得∠BOE =∠COE =∠OCE = 45°,根据已知条件可推导得出OE =CE =1,PC =OC 22OE CE 2+部分的面积.【详解】(1) 过C 点作直径CM ,连接MB ,∵CM 为直径,∴∠MBC =90°,即∠M+∠BCM =90°,∵四边形ABCD 是平行四边形,∴AB ∥DC ,AD ∥BC ,∴∠ACD =∠BAC ,∵∠BAC =∠M ,∠BCP =∠ACD ,∴∠M =∠BCP ,∴∠BCP+∠BCM =90°,即∠PCM =90°,∴CM ⊥PC ,∴PC 与⊙O 相切;(2)连接OB ,∵AD是⊙O的切线,切点为A,∴OA⊥AD,即∠PAD=90°,∵BC∥AD,∠AEB=∠PAD=90°,∴AP⊥BC.∴BE=CE=12BC=1,∴AB=AC,∴∠ABC=∠ACB=67.5°,∴∠BAC=180°-∠ABC-∠ACB=45°,∴∠BOC=2∠BAC=90°,∵OB=OC,AP⊥BC,∴∠BOE=∠COE=∠OCE= 45°,∵∠PCM=90°,∴∠CPO=∠COE=∠OCE= 45°,∴OE=CE=1,PC=OC=22OE CE2+=,∴S=S△POC-S扇形OFC=()245π21π22123604⨯⨯⨯-=-.【点睛】本题考查了切线的判定与性质、圆周角定理、垂径定理、扇形面积等,综合性较强,准确添加辅助线是解题的关键.10.如图1,是用量角器一个角的操作示意图,量角器的读数从M点开始(即M点的读数为0),如图2,把这个量角器与一块30°(∠CAB=30°)角的三角板拼在一起,三角板的斜边AB与量角器所在圆的直径MN重合,现有射线C绕点C从CA开始沿顺时针方向以每秒2°的速度旋转到与CB,在旋转过程中,射线CP与量角器的半圆弧交于E.连接BE.(1)当射线CP经过AB的中点时,点E处的读数是,此时△BCE的形状是;(2)设旋转x秒后,点E处的读数为y,求y与x的函数关系式;(3)当CP旋转多少秒时,△BCE是等腰三角形?【答案】(1)60°,直角三角形;(2)y=4x(0≤x≤45);(3)7.5秒或30秒【解析】【分析】(1)根据圆周角定理即可解决问题;(2)如图2﹣2中,由题意∠ACE=2x,∠AOE=y,根据圆周角定理可知∠AOE=2∠ACE,可得y=2x(0≤x≤45);(3)分两种情形分别讨论求解即可;【详解】解:(1)如图2﹣1中,∵∠ACB=90°,OA=OB,∴OA=OB=OC,∴∠OCA=∠OAC=30°,∴∠AOE=60°,∴点E处的读数是60°,∵∠E=∠BAC=30°,OE=OB,∴∠OBE=∠E=30°,∴∠EBC=∠OBE+∠ABC=90°,∴△EBC是直角三角形;故答案为60°,直角三角形;(2)如图2﹣2中,∵∠ACE=2x,∠AOE=y,∵∠AOE=2∠ACE,∴y=4x(0≤x≤45).(3)①如图2﹣3中,当EB=EC时,EO垂直平分线段BC,∵AC⊥BC,∵EO∥AC,∴∠AOE=∠BAC=30°,∴∠ECA=1∠AOE=15°,2∴x=7.5.②若2﹣4中,当BE=BC时,易知∠BEC=∠BAC=∠BCE=30°,∴∠OBE=∠OBC=60°,∵OE=OB,∴△OBE是等边三角形,∴∠BOE=60°,∴∠AOB=120°,∴∠ACE=1∠ACB=60°,2∴x=30,综上所述,当CP旋转7.5秒或30秒时,△BCE是等腰三角形;【点睛】本题考查几何变换综合题、创新题目、圆周角定理、等腰三角形的判定和性质等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,属于中考压轴题.11.如图,已知AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC、AC,且∠BOC<90°,直线BC和直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE(1)求证:直线CG为⊙O的切线;(2)若点H为线段OB上一点,连接CH,满足CB=CH,①△CBH∽△OBC②求OH+HC的最大值【答案】(1)证明见解析;(2)①证明见解析;②5.【解析】分析:(1)由题意可知:∠CAB=∠GAF,由圆的性质可知:∠CAB=∠OCA,所以∠OCA=∠GCE,从而可证明直线CG是⊙O的切线;(2)①由于CB=CH,所以∠CBH=∠CHB,易证∠CBH=∠OCB,从而可证明△CBH∽△OBC;②由△CBH∽△OBC可知:BC HBOC BC=,所以HB=24BC,由于BC=HC,所以OH+HC=4−24BC+BC,利用二次函数的性质即可求出OH+HC的最大值.详解:(1)由题意可知:∠CAB=∠GAF,∵AB是⊙O的直径,∴∠ACB=90°∵OA=OC,∴∠CAB=∠OCA,∴∠OCA+∠OCB=90°,∵∠GAF=∠GCE,∴∠GCE+∠OCB=∠OCA+∠OCB=90°,∵OC是⊙O的半径,∴直线CG是⊙O的切线;(2)①∵CB=CH,∴∠CBH=∠CHB ,∵OB=OC ,∴∠CBH=∠OCB ,∴△CBH ∽△OBC②由△CBH ∽△OBC 可知:BC HB OC BC = ∵AB=8,∴BC 2=HB•OC=4HB , ∴HB=24BC , ∴OH=OB-HB=4-24BC ∵CB=CH ,∴OH+HC=4−24BC +BC , 当∠BOC=90°,此时BC=42∵∠BOC <90°,∴0<BC <42,令BC=x 则CH=x ,BH=24x ()221142544OH HC x x x ∴+=-++=--+ 当x=2时,∴OH+HC 可取得最大值,最大值为5点睛:本题考查圆的综合问题,涉及二次函数的性质,相似三角形的性质与判定,切线的判定等知识,综合程度较高,需要学生灵活运用所知识.12.如图,在中,,以为直径作,交边于点,交边于点,过点作的切线,交的延长线于点,交于点.(1)求证:;(2)若,,求的半径.【答案】(1)证明见解析;(2)4.【解析】试题分析:(1)连接AD,根据等腰三角形三线合一即可证明.(2)设⊙O的半径为R,则FO=4+R,FA=4+2R,OD=R,连接OD,由△FOD∽△FAE,得列出方程即可解决问题.试题解析:(1)连接AD,∵AB是直径,∴∠ADB=90°,∵AB=AC,AD⊥BC,∴BD=DC.(2)设⊙O的半径为R,则FO=4+R,FA=4+2R,OD=R,连接OD、∵AB=AC,∴∠ABC=∠C,∵OB=OD,∴∠ABC=∠ODB,∴∠ODB=∠C,∴OD∥AC,∴△FOD∽△FAE,∴,∴,整理得R2﹣R﹣12=0,∴R=4或(﹣3舍弃).∴⊙O的半径为4.考点:切线的性质、等腰三角形的性质等知识.13.已知Rt△ABC,∠BAC=90°,点D是BC中点,AD=AC,BC=3A,D两点作⊙O,交AB于点E,(1)求弦AD的长;(2)如图1,当圆心O在AB上且点M是⊙O上一动点,连接DM交AB于点N,求当ON 等于多少时,三点D、E、M组成的三角形是等腰三角形?(3)如图2,当圆心O不在AB上且动圆⊙O与DB相交于点Q时,过D作DH⊥AB(垂足为H)并交⊙O于点P,问:当⊙O变动时DP﹣DQ的值变不变?若不变,请求出其值;若变化,请说明理由.【答案】(1)23(2)当ON等于13﹣1时,三点D、E、M组成的三角形是等腰三角形(3)不变,理由见解析【解析】【分析】(1)根据直角三角形斜边上的中线等于斜边的一半即可得到AD的长;(2)连DE、ME,易得当ED和EM为等腰三角形EDM的两腰,根据垂径定理得推论得OE⊥DM,易得到△ADC为等边三角形,得∠CAD=60°,则∠DAO=30°,∠DON=60°,然后根据含30°的直角三角形三边的关系得DN=1233;当MD=ME,DE为底边,作DH⊥AE,由于3∠DAE=30°,得到3,∠DEA=60°,DE=2,于是OE=DE=2,OH=1,又∠M=∠DAE=30°,MD=ME,得到∠MDE=75°,则∠ADM=90°-75°=15°,可得到∠DNO=45°,根据等腰直角三角形的性质得到33;(3)连AP、AQ,DP⊥AB,得AC∥DP,则∠PDB=∠C=60°,再根据圆周角定理得∠PAQ=∠PDB,∠AQC=∠P,则∠PAQ=60°,∠CAQ=∠PAD,易证得△AQC≌△APD,得到DP=CQ,则DP-DQ=CQ-DQ=CD,而△ADC为等边三角形,3DP-DQ的值.【详解】解:(1)∵∠BAC=90°,点D是BC中点,BC=3∴AD=12BC=3(2)连DE、ME,如图,∵DM>DE,当ED和EM为等腰三角形EDM的两腰,∴OE⊥DM,又∵AD=AC,∴△ADC为等边三角形,∴∠CAD=60°,∴∠DAO=30°,∴∠DON =60°,在Rt △ADN 中,DN =12AD ,在Rt △ODN 中,ON DN =1, ∴当ON 等于1时,三点D 、E 、M 组成的三角形是等腰三角形;当MD =ME ,DE 为底边,如图3,作DH ⊥AE ,∵AD=∠DAE =30°,∴DH ∠DEA =60°,DE =2,∴△ODE 为等边三角形,∴OE =DE =2,OH =1,∵∠M =∠DAE =30°,而MD =ME ,∴∠MDE =75°,∴∠ADM =90°﹣75°=15°,∴∠DNO =45°,∴△NDH 为等腰直角三角形,∴NH =DH∴ON ﹣1;综上所述,当ON 等于11时,三点D 、E 、M 组成的三角形是等腰三角形;(3)当⊙O 变动时DP ﹣DQ 的值不变,DP ﹣DQ =.理由如下:连AP 、AQ ,如图2,∵∠C =∠CAD =60°,而DP ⊥AB ,∴AC ∥DP ,∴∠PDB =∠C =60°,又∵∠PAQ =∠PDB ,∴∠PAQ =60°,∴∠CAQ =∠PAD ,∵AC =AD ,∠AQC =∠P ,∴△AQC ≌△APD ,∴DP =CQ ,∴DP ﹣DQ =CQ ﹣DQ =CD =【点睛】本题考查了垂径定理和圆周角定理:平分弧的直径垂直弧所对的弦;在同圆和等圆中,相等的弧所对的圆周角相等.也考查了等腰三角形的性质以及含30°的直角三角形三边的关系.14.结果如此巧合!下面是小颖对一道题目的解答.题目:如图,Rt△ABC的内切圆与斜边AB相切于点D,AD=3,BD=4,求△ABC的面积.解:设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x.根据切线长定理,得AE=AD=3,BF=BD=4,CF=CE=x.根据勾股定理,得(x+3)2+(x+4)2=(3+4)2.整理,得x2+7x=12.所以S△ABC=12 AC•BC=12(x+3)(x+4)=12(x2+7x+12)=12×(12+12)=12.小颖发现12恰好就是3×4,即△ABC的面积等于AD与BD的积.这仅仅是巧合吗?请你帮她完成下面的探索.已知:△ABC的内切圆与AB相切于点D,AD=m,BD=n.可以一般化吗?(1)若∠C=90°,求证:△ABC的面积等于mn.倒过来思考呢?(2)若AC•BC=2mn,求证∠C=90°.改变一下条件……(3)若∠C=60°,用m、n表示△ABC的面积.【答案】(1)证明见解析;(2)证明见解析;(3)S△ABC=3mn;【解析】【分析】(1)设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x,仿照例题利用勾股定理得(x+m)2+(x+n)2=(m+n)2,再根据S△ABC=AC×BC,即可证明S△ABC=mn.(2)由AC•BC=2mn,得x2+(m+n)x=mn,因此AC2+BC2=(x+m)2+(x+n)2=AB2,利用勾股定理逆定理可得∠C=90°.(3)过点A作AG⊥BC于点G,在Rt△ACG中,根据条件求出AG、CG,又根据BG=BC-CG得到BG .在Rt△ABG中,根据勾股定理可得x2+(m+n)x=3mn,由此S△ABC=BC•AG=mn.【详解】设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x,根据切线长定理,得:AE=AD=m、BF=BD=n、CF=CE=x,(1)如图1,在Rt△ABC中,根据勾股定理,得:(x+m)2+(x+n)2=(m+n)2,整理,得:x2+(m+n)x=mn,所以S△ABC=AC•BC=(x+m)(x+n)=[x2+(m+n)x+mn]=(mn+mn)=mn;(2)由AC•BC=2mn,得:(x+m)(x+n)=2mn,整理,得:x2+(m+n)x=mn,∴AC2+BC2=(x+m)2+(x+n)2=2[x2+(m+n)x]+m2+n2=2mn+m2+n2=(m+n)2=AB2,根据勾股定理逆定理可得∠C=90°;(3)如图2,过点A作AG⊥BC于点G,在Rt△ACG中,AG=AC•sin60°=(x+m),CG=AC•cos60°=(x+m),∴BG=BC﹣CG=(x+n)﹣(x+m),在Rt△ABG中,根据勾股定理可得:[(x+m)]2+[(x+n)﹣(x+m)]2=(m+n)2,整理,得:x2+(m+n)x=3mn,∴S△ABC=BC•AG=×(x+n)•(x+m)=3x2+(m+n)x+mn]=3(3mn+mn)3.【点睛】本题考查了圆中的计算问题、与圆有关的位置关系以及直角三角形,注意掌握方程思想与数形结合思想的应用.15.已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.(1)求证:DF为⊙O的切线;(2)若等边三角形ABC 的边长为4,求图中阴影部分的面积.【答案】(1)见解析(2)332 23π-【解析】试题分析:(1)连接DO,要证明DF为⊙O的切线只要证明∠FDP=90°即可;(2)首先由已知可得到CD,CF的长,从而利用勾股定理可求得DF的长;再连接OE,求得CF,EF的长,从而利用S直角梯形FDOE﹣S扇形OED求得阴影部分的面积.试题解析:(1)证明:连接DO.∵△ABC是等边三角形,∴∠A=∠C=60°.∵OA=OD,∴△OAD是等边三角形.∴∠ADO=60°,∵DF⊥BC,∴∠CDF=90°﹣∠C=30°,∴∠FDO=180°﹣∠ADO﹣∠CDF=90°,∴DF为⊙O的切线;(2)∵△OAD是等边三角形,∴AD=AO=AB=2.∴CD=AC﹣AD=2.Rt△CDF中,∵∠CDF=30°,∴CF=CD=1.∴DF=,连接OE,则CE=2.∴CF=1,∴EF=1.∴S直角梯形FDOE=(EF+OD)•DF=,∴S扇形OED==,∴S阴影=S直角梯形FDOE﹣S扇形OED=﹣.【点睛】此题考查学生对切线的判定及扇形的面积等知识点的掌握情况,当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.也考查了等边三角形的性质和利用割补法计算补规则图形的面积.。
中考数学——圆的综合的综合压轴题专题复习及答案解析

中考数学——圆的综合的综合压轴题专题复习及答案解析一、圆的综合1.(1)如图1,在矩形ABCD 中,点O 在边AB 上,∠AOC =∠BOD ,求证:AO =OB ; (2)如图2,AB 是⊙O 的直径,PA 与⊙O 相切于点A ,OP 与⊙O 相交于点C ,连接CB ,∠OPA =40°,求∠ABC 的度数.【答案】(1)证明见解析;(2)25°.【解析】试题分析: (1)根据等量代换可求得∠AOD=∠BOC ,根据矩形的对边相等,每个角都是直角,可知∠A=∠B=90°,AD=BC ,根据三角形全等的判定AAS 证得△AOD ≌△BOC ,从而得证结论.(2)利用切线的性质和直角三角形的两个锐角互余的性质得到圆心角∠POA 的度数,然后利用圆周角定理来求∠ABC 的度数.试题解析:(1)∵∠AOC=∠BOD∴∠AOC -∠COD=∠BOD-∠COD即∠AOD=∠BOC∵四边形ABCD 是矩形∴∠A=∠B=90°,AD=BC∴AOD BOC ∆≅∆∴AO=OB(2)解:∵AB 是O e 的直径,PA 与O e 相切于点A ,∴PA ⊥AB ,∴∠A=90°.又∵∠OPA=40°,∴∠AOP=50°,∵OB=OC ,∴∠B=∠OCB.又∵∠AOP=∠B+∠OCB , ∴1252B OCB AOP ∠=∠=∠=︒.2.已知O e 的半径为5,弦AB 的长度为m ,点C 是弦AB 所对优弧上的一动点. ()1如图①,若m 5=,则C ∠的度数为______o ;()2如图②,若m 6=.①求C ∠的正切值;②若ABC V 为等腰三角形,求ABC V 面积.【答案】()130;()2C ∠①的正切值为34;ABC S 27=V ②或43225. 【解析】【分析】 ()1连接OA ,OB ,判断出AOB V 是等边三角形,即可得出结论;()2①先求出10AD =,再用勾股定理求出8BD =,进而求出tan ADB ∠,即可得出结论;②分三种情况,利用等腰三角形的性质和垂径定理以及勾股定理即可得出结论.【详解】()1如图1,连接OB ,OA ,OB OC 5∴==,AB m 5==Q ,OB OC AB ∴==,AOB ∴V 是等边三角形,AOB 60∠∴=o ,1ACB AOB 302∠∠∴==o , 故答案为30;()2①如图2,连接AO 并延长交O e 于D ,连接BD ,AD Q 为O e 的直径,AD 10∴=,ABD 90∠=o ,在Rt ABD V 中,AB m 6==,根据勾股定理得,BD 8=, AB 3tan ADB BD 4∠∴==, C ADB ∠∠=Q ,C ∠∴的正切值为34; ②Ⅰ、当AC BC =时,如图3,连接CO 并延长交AB 于E ,AC BC =Q ,AO BO =,CE ∴为AB 的垂直平分线,AE BE 3∴==,在Rt AEO V 中,OA 5=,根据勾股定理得,OE 4=,CE OE OC 9∴=+=,ABC 11S AB CE 692722∴=⨯=⨯⨯=V ; Ⅱ、当AC AB 6==时,如图4,连接OA 交BC 于F ,AC AB =Q ,OC OB =,AO ∴是BC 的垂直平分线,过点O 作OG AB ⊥于G , 1AOG AOB 2∠∠∴=,1AG AB 32==, AOB 2ACB ∠∠=Q ,ACF AOG ∠∠∴=,在Rt AOG V 中,AG 3sin AOG AC 5∠==, 3sin ACF 5∠∴=, 在Rt ACF V 中,3sin ACF 5∠=, 318AF AC 55∴==, 24CF 5∴=, ABC 111824432S AF BC 225525∴=⨯=⨯⨯=V ; Ⅲ、当BA BC 6==时,如图5,由对称性知,ABC 432S 25=V .【点睛】圆的综合题,主要圆的性质,圆周角定理,垂径定理,等腰三角形的性质,三角形的面积公式,用分类讨论的思想解决问题是解本题的关键.3.如图,AB 为O e 的直径,弦//CD AB ,E 是AB 延长线上一点,CDB ADE ∠=∠. ()1DE 是O e 的切线吗?请说明理由;()2求证:2AC CD BE =⋅.【答案】(1)结论:DE 是O e 的切线,理由见解析;(2)证明见解析.【解析】【分析】(1)连接OD ,只要证明OD DE ⊥即可;(2)只要证明:AC BD =,CDB DBE V V ∽即可解决问题.【详解】()1解:结论:DE 是O e 的切线.理由:连接OD .CDB ADE ∠=∠Q ,ADC EDB ∴∠=∠,//CD AB Q ,CDA DAB ∴∠=∠,OA OD =Q ,OAD ODA ∴∠=∠,ADO EDB ∴∠=∠,AB Q 是直径,90ADB ∴∠=o ,90ADB ODE ∴∠=∠=o ,DE OD ∴⊥,DE ∴是O e 的切线.()2//CD AB Q ,ADC DAB ∴∠=∠,CDB DBE ∠=∠,AC BD ∴=n n, AC BD ∴=,DCB DAB ∠=∠Q ,EDB DAB ∠=∠,∴∠=∠,EDB DCB∴V∽DBECDBV,CD DB∴=,BD BE2BD CD BE∴=⋅,2∴=⋅.AC CD BE【点睛】本题考查相似三角形的判定和性质、圆周角定理、切线的判定等知识,解题的关键是学会添加常用辅助线,准确寻找相似三角形解决问题,属于中考常考题型.4.如图,在△ABP中,C是BP边上一点,∠PAC=∠PBA,⊙O是△ABC的外接圆,AD是⊙O的直径,且交BP于点E.(1)求证:PA是⊙O的切线;(2)过点C作CF⊥AD,垂足为点F,延长CF交AB于点G,若AG•AB=12,求AC的长.【答案】(1)证明见解析(2)3【解析】试题分析:(1)根据圆周角定理得出∠ACD=90°以及利用∠PAC=∠PBA得出∠CAD+∠PAC=90°进而得出答案;(2)首先得出△CAG∽△BAC,进而得出AC2=AG·AB,求出AC即可.试题解析:(1)连接CD,如图,∵AD是⊙O的直径,∴∠ACD=90°,∴∠CAD+∠D=90°,∵∠PAC=∠PBA,∠D=∠PBA,∴∠CAD+∠PAC=90°,即∠PAD=90°,∴PA⊥AD,∴PA是⊙O的切线;(2)∵CF⊥AD,∴∠ACF+∠CAF=90°,∠CAD+∠D=90°,∴∠ACF=∠D,∴∠ACF=∠B,而∠CAG=∠BAC,∴△ACG∽△ABC,∴AC:AB=AG:AC,∴AC2=AG•AB=12,∴AC=23.5.如图,AB是半圆O的直径,C是的中点,D是的中点,AC与BD相交于点E.(1)求证:BD平分∠ABC;(2)求证:BE=2AD;(3)求DEBE的值.【答案】(1)答案见解析(2)BE=AF=2AD(3)21 2 -【解析】试题分析:(1)根据中点弧的性质,可得弦AD=CD,然后根据弦、弧、圆周角、圆心角的性质求解即可;(2)延长BC与AD相交于点F, 证明△BCE≌△ACF, 根据全等三角形的性质可得BE=AF=2AD;(3)连接OD,交AC于H.简要思路如下:设OH为1,则BC为2,OB=OD=2,DH=21-, 然后根据相似三角形的性质可求解.试题解析:(1)∵D是的中点∴AD=DC∴∠CBD=∠ABD∴BD 平分∠ABC(2)提示:延长BC 与AD 相交于点F,证明△BCE ≌△ACF,BE=AF=2AD(3)连接OD,交AC 于H.简要思路如下:设OH 为1,则BC 为2,OB=OD=2 , DH=21-, DE BE =DH BCDE BE =212-6.在⊙O 中,点C 是AB u u u r上的一个动点(不与点A ,B 重合),∠ACB=120°,点I 是∠ABC 的内心,CI 的延长线交⊙O 于点D ,连结AD,BD .(1)求证:AD=BD .(2)猜想线段AB 与DI 的数量关系,并说明理由.(3)若⊙O 的半径为2,点E ,F 是»AB 的三等分点,当点C 从点E 运动到点F 时,求点I 随之运动形成的路径长.【答案】(1)证明见解析;(2)AB=DI ,理由见解析(323 【解析】分析:(1)根据内心的定义可得CI 平分∠ACB ,可得出角相等,再根据圆周角定理,可证得结论;(2)根据∠ACB=120°,∠ACD=∠BCD ,可求出∠BAD 的度数,再根据AD=BD ,可证得△ABD 是等边三角形,再根据内心的定义及三角形的外角性质,证明∠BID=∠IBD ,得出ID=BD ,再根据AB=BD ,即可证得结论;(3)连接DO ,延长DO 根据题意可知点I 随之运动形成的图形式以D 为圆心,DI 1为半径的弧,根据已知及圆周角定理、解直角三角形,可求出AD的长,再根据点E,F是弧AB ⌢的三等分点,△ABD是等边三角形,可证得∠DAI1=∠AI1D,然后利用弧长的公式可求出点I 随之运动形成的路径长.详解:(1)证明:∵点I是∠ABC的内心∴CI平分∠ACB∴∠ACD=∠BCD∴弧AD=弧BD∴AD=BD(2)AB=DI理由:∵∠ACB=120°,∠ACD=∠BCD∴∠BCD=×120°=60°∵弧BD=弧BD∴∠DAB=∠BCD=60°∵AD=BD∴△ABD是等边三角形,∴AB=BD,∠ABD=∠C∵I是△ABC的内心∴BI平分∠ABC∴∠CBI=∠ABI∵∠BID=∠C+∠CBI,∠IBD=∠ABI+∠ABD∴∠BID=∠IBD∴ID=BD∵AB=BD∴AB=DI(3)解:如图,连接DO,延长DO根据题意可知点I随之运动形成的图形式以D为圆心,DI1为半径的弧∵∠ACB=120°,弧AD=弧BD∴∠AED=∠ACB=×120°=60°∵圆的半径为2,DE是直径∴DE=4,∠EAD=90°∴AD=sin∠AED×DE=×4=2∵点E,F是弧AB ⌢的三等分点,△ABD是等边三角形,∴∠ADB=60°∴弧AB的度数为120°,∴弧AM、弧BF的度数都为为40°∴∠ADM=20°=∠FAB∴∠DAI1=∠FAB+∠DAB=80°∴∠AI1D=180°-∠ADM-∠DAI1=180°-20°-80°=80°∴∠DAI1=∠AI1D∴AD=I1D=2∴弧I1I2的长为:点睛:此题是一道圆的综合题,有一定的难度,熟记圆的相关性质与定理,并对圆中的弦、弧、圆心角、圆周角等进行灵活转化是解题关键,注意数形结合思想的渗透.7.四边形ABCD 的对角线交于点E,且AE=EC,BE=ED,以AD 为直径的半圆过点E,圆心为O.(1)如图①,求证:四边形ABCD 为菱形;(2)如图②,若BC 的延长线与半圆相切于点F,且直径AD=6,求弧AE 的长.【答案】(1)见解析;(2)π2【解析】试题分析:(1)先判断出四边形ABCD 是平行四边形,再判断出AC ⊥BD 即可得出结论; (2)先判断出AD =DC 且DE ⊥AC ,∠ADE =∠CDE ,进而得出∠CDA =30°,最后用弧长公式即可得出结论.试题解析:证明:(1)∵四边形ABCD 的对角线交于点E ,且AE =EC ,BE =ED ,∴四边形ABCD 是平行四边形.∵以AD 为直径的半圆过点E ,∴∠AED =90°,即有AC ⊥BD ,∴四边形ABCD 是菱形;(2)由(1)知,四边形ABCD 是菱形,∴△ADC 为等腰三角形,∴AD =DC 且DE ⊥AC ,∠ADE =∠CDE .如图2,过点C 作CG ⊥AD ,垂足为G ,连接FO .∵BF 切圆O 于点F ,∴OF ⊥AD ,且132OF AD ==,易知,四边形CGOF 为矩形,∴CG =OF =3. 在Rt △CDG 中,CD =AD =6,sin ∠ADC =CG CD =12,∴∠CDA =30°,∴∠ADE =15°. 连接OE ,则∠AOE =2×∠ADE =30°,∴¶3031802AE ππ⋅⨯==.点睛:本题主要考查菱形的判定即矩形的判定与性质、切线的性质,熟练掌握其判定与性质并结合题意加以灵活运用是解题的关键.8.如图AB 是△ABC 的外接圆⊙O 的直径,过点C 作⊙O 的切线CM ,延长BC 到点D ,使CD=BC ,连接AD 交CM 于点E ,若⊙OD 半径为3,AE=5, (1)求证:CM ⊥AD ; (2)求线段CE 的长.【答案】(1)见解析;(2)5【解析】分析:(1)连接OC,根据切线的性质和圆周角定理证得AC垂直平分BD,然后根据平行线的判定与性质证得结论;(2)根据相似三角形的判定与性质证明求解即可.详解:证明:(1)连接OC∵CM切⊙O于点C,∴∠OCE=90°,∵AB是⊙O的直径,∴∠ACB=90°,∵CD=BC,∴AC垂直平分BD,∴AB=AD,∴∠B=∠D∵∠B=∠OCB∴∠D=∠OCB∴OC∥AD∴∠CED=∠OCE=90°∴CM⊥AD.(2)∵OA=OB,BC=CD∴OC=1AD2∴AD=6∴DE=AD-AE=1易证△CDE~△ACE∴CE DEAE CE∴CE 2=AE×DE ∴CE=5点睛:此题主要考查了切线的性质和相似三角形的判定与性质的应用,灵活判断边角之间的关系是解题关键,是中档题.9.已知:如图,在矩形ABCD 中,点O 在对角线BD 上,以OD 的长为半径的⊙O 与AD ,BD 分别交于点E 、点F ,且∠ABE=∠DBC .(1)判断直线BE 与⊙O 的位置关系,并证明你的结论; (2)若sin ∠ABE=33,CD=2,求⊙O 的半径.【答案】(1)直线BE 与⊙O 相切,证明见解析;(2)⊙O 的半径为3. 【解析】分析:(1)连接OE ,根据矩形的性质,可证∠BEO =90°,即可得出直线BE 与⊙O 相切; (2)连接EF ,先根据已知条件得出BD 的值,再在△BEO 中,利用勾股定理推知BE 的长,设出⊙O 的半径为r ,利用切线的性质,用勾股定理列出等式解之即可得出r 的值. 详解:(1)直线BE 与⊙O 相切.理由如下:连接OE ,在矩形ABCD 中,AD ∥BC ,∴∠ADB =∠DBC . ∵OD =OE ,∴∠OED =∠ODE . 又∵∠ABE =∠DBC ,∴∠ABE =∠OED , ∵矩形ABDC ,∠A =90°,∴∠ABE +∠AEB =90°,∴∠OED +∠AEB =90°,∴∠BEO =90°,∴直线BE 与⊙O 相切;(2)连接EF ,方法1:∵四边形ABCD 是矩形,CD =2,∴∠A =∠C =90°,AB =CD =2. ∵∠ABE =∠DBC ,∴sin ∠CBD =3sin ABE ∠= ∴23DCBD sin CBD∠==在Rt △AEB 中,∵CD =2,∴22BC =.∵tan ∠CBD =tan ∠ABE ,∴22222DC AE AEAE BC AB ,,=∴=∴=, 由勾股定理求得6BE =.在Rt △BEO 中,∠BEO =90°,EO 2+EB 2=OB 2.设⊙O 的半径为r ,则222623r r +=-()(),∴r =32, 方法2:∵DF 是⊙O 的直径,∴∠DEF =90°. ∵四边形ABCD 是矩形,∴∠A =∠C =90°,AB =CD =2. ∵∠ABE =∠DBC ,∴sin ∠CBD =33sin ABE ∠=. 设3DC x BD x ==,,则2BC x =.∵CD =2,∴22BC =. ∵tan ∠CBD =tan ∠ABE ,∴22222DC AE AEAE BC AB ,,=∴=∴=, ∴E 为AD 中点.∵DF 为直径,∠FED =90°,∴EF ∥AB ,∴132DF BD ==,∴⊙O 的半径为32.点睛:本题综合考查了切线的性质、勾股定理以及三角函数的应用等知识点,具有较强的综合性,有一定的难度.10.如图,AB 是半圆O 的直径,半径OC ⊥AB ,OB =4,D 是OB 的中点,点E 是弧BC 上的动点,连接AE ,DE .(1)当点E 是弧BC 的中点时,求△ADE 的面积; (2)若3tan 2AED ∠=,求AE 的长; (3)点F 是半径OC 上一动点,设点E 到直线OC 的距离为m ,当△DEF 是等腰直角三角形时,求m 的值.【答案】(1)62ADE S =;(2)1655AE =;(3)23m = ,22m =,71m =-.【解析】 【分析】(1)作EH ⊥AB ,连接OE ,EB ,设DH =a ,则HB =2﹣a ,OH =2+a ,则EH =OH =2+a ,根据Rt △AEB 中,EH 2=AH•BH ,即可求出a 的值,即可求出S △ADE 的值;(2)作DF ⊥AE ,垂足为F ,连接BE ,设EF =2x ,DF =3x ,根据DF ∥BE 故AF ADEF BD=,得出AF =6x ,再利用Rt △AFD 中,AF 2+DF 2=AD 2,即可求出x ,进而求出AE 的长; (3)根据等腰直角三角形的不同顶点进行分类讨论,分别求出m 的值. 【详解】解:(1)如图,作EH ⊥AB ,连接OE ,EB , 设DH =a ,则HB =2﹣a ,OH =2+a , ∵点E 是弧BC 中点, ∴∠COE =∠EOH =45°, ∴EH =OH =2+a ,在Rt △AEB 中,EH 2=AH•BH , (2+a )2=(6+a )(2﹣a ),解得a =222±-, ∴a =222-, EH=22,S △ADE =1622AD EH =n n ;(2)如图,作DF ⊥AE ,垂足为F ,连接BE设EF =2x ,DF =3x ∵DF ∥BE ∴AF ADEF BD=∴622AF x ==3 ∴AF =6x在Rt △AFD 中,AF 2+DF 2=AD 2 (6x )2+(3x )2=(6)2 解得x =255 AE =8x =1655(3)当点D 为等腰直角三角形直角顶点时,如图设DH =a由DF=DE,∠DOF=∠EHD=90°,∠FDO+∠DFO=∠FDO+∠EDH , ∴∠DFO=∠EDH ∴△ODF ≌△HED ∴OD =EH =2在Rt △ABE 中,EH 2=AH•BH (2)2=(6+a )•(2﹣a ) 解得a =±232- m =23当点E 为等腰直角三角形直角顶点时,如图同理得△EFG ≌△DEH设DH =a ,则GE =a ,EH =FG =2+a 在Rt △ABE 中,EH 2=AH•BH (2+a )2=(6+a )(2﹣a ) 解得a =222± ∴m =2当点F 为等腰直角三角形直角顶点时,如图同理得△EFM≌△FDO设OF=a,则ME=a,MF=OD=2∴EH=a+2在Rt△ABE中,EH2=AH•BH(a+2)2=(4+a)•(4﹣a)-解得a=±71m=71-【点睛】此题主要考查圆内综合问题,解题的关键是熟知全等三角形、等腰三角形、相似三角形的判定与性质.11.如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D,E是AB延长线上一点,CE交⊙O于点F,连接OC、AC.(1)求证:AC平分∠DAO.(2)若∠DAO=105°,∠E=30°①求∠OCE的度数;②若⊙O的半径为22,求线段EF的长.【答案】(1)证明见解析;(2)①∠OCE=45°;②EF =23【解析】【试题分析】(1)根据直线与⊙O相切的性质,得OC⊥CD.又因为AD⊥CD,根据同一平面内,垂直于同一条直线的两条直线也平行,得:AD//OC. ∠DAC=∠OCA.又因为OC=OA,根据等边对等角,得∠OAC=∠OCA.等量代换得:∠DAC=∠OAC.根据角平分线的定义得:AC平分∠DAO.(2)①因为 AD//OC,∠DAO=105°,根据两直线平行,同位角相等得,∆中,∠E=30°,利用内角和定理,得:∠OCE=45°.∠EOC=∠DAO=105°,在OCE②作OG⊥CE于点G,根据垂径定理可得FG=CG,因为OC=2,∠OCE=45°.等腰直角三2倍,得CG=OG=2. FG=2.在Rt△OGE中,∠E=30°,得GE=23则EF=GE-FG=23【试题解析】(1)∵直线与⊙O相切,∴OC⊥CD.又∵AD⊥CD,∴AD//OC.∴∠DAC=∠OCA.又∵OC=OA,∴∠OAC=∠OCA.∴∠DAC=∠OAC.∴AC平分∠DAO.(2)解:①∵AD//OC,∠DAO=105°,∴∠EOC=∠DAO=105°∵∠E=30°,∴∠OCE=45°.②作OG⊥CE于点G,可得FG=CG∵OC=22,∠OCE=45°.∴CG=OG=2.∴FG=2.∵在Rt△OGE中,∠E=30°,∴GE=23.∴EF=GE-FG=23-2.【方法点睛】本题目是一道圆的综合题目,涉及到圆的切线的性质,平行线的性质及判定,三角形内角和,垂径定理,难度为中等.12.如图,在△ABC中,AB=AC,以AB为直径的⊙O与边BC交于点D,DE⊥AC,垂足为E,交AB的延长线于点F.(1)求证:EF是⊙O的切线;(2)若∠C=60°,AC=12,求»BD的长.(3)若tan C=2,AE=8,求BF的长.【答案】(1)见解析;(2) 2π;(3)10 3.【解析】分析:(1)连接OD,根据等腰三角形的性质:等边对等角,得∠ABC=∠C,∠ABC=∠ODB ,从而得到∠C=∠ODB ,根据同位角相等,两直线平行,得到OD ∥AC ,从而得证OD ⊥EF ,即 EF 是⊙O 的切线;(2) 根据中点的性质,由AB=AC=12 ,求得OB=OD=12AB =6,进而根据等边三角形的判定得到△OBD 是等边三角形,即∠BOD=600,从而根据弧长公式七届即可;(3)连接AD ,根据直角三角形的性质,由在Rt △DEC 中, tan 2DEC CE== 设CE=x,则DE=2x ,然后由Rt △ADE 中, tan 2AEADE DE∠== ,求得DE 、CE 的长,然后根据相似三角形的判定与性质求解即可.详解:(1)连接OD ∵AB=AC ∴∠ABC=∠C ∵OD=OB ∴∠ABC=∠ODB ∴∠C=∠ODB ∴OD ∥AC又∵DE ⊥AC ∴OD ⊥DE ,即OD ⊥EF ∴EF 是⊙O 的切线 (2) ∵AB=AC=12 ∴OB=OD=12AB =6 由(1)得:∠C=∠ODB=600 ∴△OBD 是等边三角形 ∴∠BOD=600∴»BD=6062180ππ⨯= 即»BD的长2π (3)连接AD ∵DE ⊥AC ∠DEC=∠DEA=900在Rt △DEC 中, tan 2DEC CE== 设CE=x,则DE=2x ∵AB 是直径 ∴∠ADB=∠ADC=900∴∠ADE+∠CDE=900 在Rt △DEC 中,∠C+∠CDE=900 ∴∠C=∠ADE 在Rt △ADE 中, tan 2AEADE DE∠== ∵ AE=8,∴DE=4 则CE=2∴AC=AE+CE=10 即直径AB=AC=10 则OD=OB=5 ∵OD//AE ∴△ODF ∽△AEF ∴OF OD AF AE = 即:55108BF BF +=+解得:BF=103即BF的长为103.点睛:此题考查了切线的性质与判定、圆周角定理、等腰三角形的性质、直角三角形以及相似三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.13.如图1,D是⊙O的直径BC上的一点,过D作DE⊥BC交⊙O于E、N,F是⊙O上的一点,过F的直线分别与CB、DE的延长线相交于A、P,连结CF交PD于M,∠C=12∠P.(1)求证:PA是⊙O的切线;(2)若∠A=30°,⊙O的半径为4,DM=1,求PM的长;(3)如图2,在(2)的条件下,连结BF、BM;在线段DN上有一点H,并且以H、D、C 为顶点的三角形与△BFM相似,求DH的长度.【答案】(1)证明见解析;(2)PM=32;(3)满足条件的DH的值为632-或1223+【解析】【分析】(1)如图1中,作PH⊥FM于H.想办法证明∠PFH=∠PMH,∠C=∠OFC,再根据等角的余角相等即可解决问题;(2)解直角三角形求出AD,PD即可解决问题;(3)分两种情形①当△CDH∽△BFM时,DH CD FM BF=.②当△CDH∽△MFB时,DH CDFB MF=,分别构建方程即可解决问题;【详解】(1)证明:如图1中,作PH⊥FM于H.∵PD⊥AC,∴∠PHM=∠CDM=90°,∵∠PMH=∠DMC,∴∠C=∠MPH,∵∠C=12∠FPM,∴∠HPF=∠HPM,∵∠HFP+∠HPF=90°,∠HMP+∠HPM=90°,∴∠PFH=∠PMH,∵OF=OC,∴∠C=∠OFC,∵∠C+∠CMD=∠C+∠PMF=∠C+∠PFH=90°,∴∠OFC+∠PFC=90°,∴∠OFP=90°,∴直线PA是⊙O的切线.(2)解:如图1中,∵∠A=30°,∠AFO=90°,∴∠AOF=60°,∵∠AOF=∠OFC+∠OCF,∠OFC=∠OCF,∴∠C=30°,∵⊙O的半径为4,DM=1,∴OA=2OF=8,CD=3DM=3,∴OD=OC﹣CD=4﹣3,∴AD=OA+OD=8+4﹣3=12﹣3,在Rt△ADP中,DP=AD•tan30°=(12﹣3)×33=43﹣1,∴PM=PD﹣DM=4 3﹣2.(3)如图2中,由(2)可知:BF =12BC =4,FM =3BF =43 ,CM =2DM =2,CD =3 , ∴FM =FC ﹣CM =43﹣2, ①当△CDH ∽△BFM 时,DH CD FM BF = , ∴ 3432=- ,∴DH =63- ②当△CDH ∽△MFB 时,DH CD FB MF =, ∴34432DH =- ,∴DH =1223+ , ∵DN =()22443833--=- ,∴DH <DN ,符合题意,综上所述,满足条件的DH 的值为63- 或1223+. 【点睛】本题考查圆综合题、切线的判定、解直角三角形、相似三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,学会用分类讨论的思想思考问题.14.如图,已知AB 是⊙O 的直径,点C 、D 在⊙O 上,∠D =60°且AB =6,过O 点作OE ⊥AC ,垂足为E .(1)求OE 的长;(2)若OE 的延长线交⊙O 于点F ,求弦AF 、AC 和弧CF 围成的图形(阴影部分)的面积.(结果保留π)【答案】(1)OE 的长为32; (2)阴影部分的面积为32π 【解析】(1)OE=32 (2)S=32π15.结果如此巧合!下面是小颖对一道题目的解答.题目:如图,Rt△ABC的内切圆与斜边AB相切于点D,AD=3,BD=4,求△ABC的面积.解:设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x.根据切线长定理,得AE=AD=3,BF=BD=4,CF=CE=x.根据勾股定理,得(x+3)2+(x+4)2=(3+4)2.整理,得x2+7x=12.所以S△ABC=12 AC•BC=12(x+3)(x+4)=12(x2+7x+12)=12×(12+12)=12.小颖发现12恰好就是3×4,即△ABC的面积等于AD与BD的积.这仅仅是巧合吗?请你帮她完成下面的探索.已知:△ABC的内切圆与AB相切于点D,AD=m,BD=n.可以一般化吗?(1)若∠C=90°,求证:△ABC的面积等于mn.倒过来思考呢?(2)若AC•BC=2mn,求证∠C=90°.改变一下条件……(3)若∠C=60°,用m、n表示△ABC的面积.【答案】(1)证明见解析;(2)证明见解析;(3)S△ABC=3mn;【解析】【分析】(1)设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x,仿照例题利用勾股定理得(x+m)2+(x+n)2=(m+n)2,再根据S△ABC=AC×BC,即可证明S△ABC=mn.(2)由AC•BC=2mn,得x2+(m+n)x=mn,因此AC2+BC2=(x+m)2+(x+n)2=AB2,利用勾股定理逆定理可得∠C=90°.(3)过点A作AG⊥BC于点G,在Rt△ACG中,根据条件求出AG、CG,又根据BG=BC-CG得到BG .在Rt△ABG中,根据勾股定理可得x2+(m+n)x=3mn,由此S△ABC=BC•AG=mn.【详解】设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x,根据切线长定理,得:AE=AD=m、BF=BD=n、CF=CE=x,(1)如图1,在Rt△ABC中,根据勾股定理,得:(x+m)2+(x+n)2=(m+n)2,整理,得:x2+(m+n)x=mn,所以S△ABC=AC•BC=(x+m)(x+n)=[x2+(m+n)x+mn]=(mn+mn)=mn;(2)由AC•BC=2mn,得:(x+m)(x+n)=2mn,整理,得:x2+(m+n)x=mn,∴AC2+BC2=(x+m)2+(x+n)2=2[x2+(m+n)x]+m2+n2=2mn+m2+n2=(m+n)2=AB2,根据勾股定理逆定理可得∠C=90°;(3)如图2,过点A作AG⊥BC于点G,在Rt△ACG中,AG=AC•sin60°=(x+m),CG=AC•cos60°=(x+m),∴BG=BC﹣CG=(x+n)﹣(x+m),在Rt△ABG中,根据勾股定理可得:[(x+m)]2+[(x+n)﹣(x+m)]2=(m+n)2,整理,得:x2+(m+n)x=3mn,∴S△ABC=BC•AG=×(x+n)•(x+m)=34[x2+(m+n)x+mn]=34×(3mn+mn)3.【点睛】本题考查了圆中的计算问题、与圆有关的位置关系以及直角三角形,注意掌握方程思想与数形结合思想的应用.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三圆难题压轴题答案解析公司内部档案编码:[OPPTR-OPPT28-OPPTL98-OPPNN08]圆难题压轴题答案解析1. 解:(1)如图1,设⊙O的半径为r,当点A在⊙C上时,点E和点A重合,过点A作AH⊥BC于H,∴BH=AB?cosB=4,∴AH=3,CH=4,∴AC==5,∴此时CP=r=5;(2)如图2,若AP∥CE,APCE为平行四边形,∵CE=CP,∴四边形APCE是菱形,连接AC、EP,则AC⊥EP,∴AM=CM=,由(1)知,AB=AC,则∠ACB=∠B,∴CP=CE==,∴EF=2=;(3)如图3:过点C作CN⊥AD于点N,∵cosB=45,∴∠B<45°,∵∠BCG<90°,∴∠BGC>45°,∵∠AEG=∠BCG≥∠ACB=∠B,∴当∠AEG=∠B时,A、E 、G 重合,∴只能∠AGE=∠AEG,∵AD∥BC,∴△GAE∽△GBC,∴=,即=,解得:AE=3,EN=AN﹣AE=1,∴CE===.2.解:(1)①若圆P与直线l和l2都相切,当点P在第四象限时,过点P作PH⊥x轴,垂足为H,连接OP,如图1所示.设y=x的图象与x轴的夹角为α.当x=1时,y=.∴tanα=.∴α=60°.∴由切线长定理得:∠POH=(180°﹣60°)=60°.∵PH=1,∴tan∠POH===.∴OH=.∴点P的坐标为(,﹣1).同理可得:当点P在第二象限时,点P的坐标为(﹣,1);当点P在第三象限时,点P的坐标为(﹣,﹣1);②若圆P与直线l和l1都相切,如图2所示.同理可得:当点P在第一象限时,点P的坐标为(,1);当点P在第二象限时,点P的坐标为(﹣,1);当点P在第三象限时,点P的坐标为(﹣,﹣1);当点P在第四象限时,点P的坐标为(,﹣1).③若圆P与直线l1和l2都相切,如图3所示.同理可得:当点P在x轴的正半轴上时,点P的坐标为(,0);当点P在x轴的负半轴上时,点P的坐标为(﹣,0);当点P在y轴的正半轴上时,点P的坐标为(0,2);当点P在y轴的负半轴上时,点P的坐标为(0,﹣2).综上所述:其余满足条件的圆P的圆心坐标有:(,﹣1)、(﹣,1)、(﹣,﹣1)、(,1)、(﹣,1)、(﹣,﹣1)、(,﹣1)、(,0)、(﹣,0)、(0,2)、(0,﹣2).(2)用线段依次连接各圆心,所得几何图形,如图4所示.由图可知:该几何图形既轴对称图形,又是中心对称图形,由对称性可得:该几何图形的所有的边都相等.∴该图形的周长=12×(﹣)=8.3.(1)解:连接OB,OD,∵∠DAB=120°,∴所对圆心角的度数为240°,∴∠BOD=120°,∵⊙O的半径为3,∴劣弧的长为:×π×3=2π;(2)证明:连接AC,∵AB=BE,∴点B为AE的中点,∵F是EC的中点,∴BF为△EAC的中位线,∴BF=AC,∵=,∴+=+,∴=,∴BD=AC,∴BF=BD;(3)解:过点B作AE的垂线,与⊙O的交点即为所求的点P,∵BF为△EAC的中位线,∴BF∥AC,∴∠FBE=∠CAE , ∵=,∴∠CAB=∠DBA ,∵由作法可知BP ⊥AE , ∴∠GBP=∠FBP , ∵G 为BD 的中点, ∴BG=BD ,∴BG=BF ,在△PBG 和△PBF 中,,∴△PBG ≌△PBF (SAS ), ∴PG=PF .4.解:(1)∵l 1⊥l 2,⊙O 与l 1,l 2都相切, ∴∠OAD=45°,∵AB=4cm ,AD=4cm , ∴CD=4cm ,AD=4cm , ∴tan ∠DAC===,∴∠DAC=60°,∴∠OAC 的度数为:∠OAD+∠DAC=105°, 故答案为:105;(2)如图位置二,当O 1,A 1,C 1恰好在同一直线上时,设⊙O 1与l 1的切点为E ,连接O 1E ,可得O 1E=2,O 1E ⊥l 1,在Rt △A 1D 1C 1中,∵A 1D 1=4,C 1D 1=4, ∴tan ∠C 1A 1D 1=,∴∠C 1A 1D 1=60°, 在Rt △A 1O 1E 中,∠O 1A 1E=∠C 1A 1D 1=60°, ∴A 1E==,∵A 1E=AA 1﹣OO 1﹣2=t ﹣2,∴t ﹣2=, ∴t=+2,∴OO 1=3t=2+6;(3)①当直线AC 与⊙O 第一次相切时,设移动时间为t 1,如图,此时⊙O 移动到⊙O 2的位置,矩形ABCD 移动到A 2B 2C 2D 2的位置,设⊙O 2与直线l 1,A 2C 2分别相切于点F ,G ,连接O 2F ,O 2G ,O 2A 2, ∴O 2F ⊥l 1,O 2G ⊥A 2G 2,由(2)得,∠C 2A 2D 2=60°,∴∠GA 2F=120°, ∴∠O 2A 2F=60°,在Rt △A 2O 2F 中,O 2F=2,∴A 2F=,∵OO 2=3t ,AF=AA 2+A 2F=4t 1+,∴4t 1+﹣3t 1=2, ∴t 1=2﹣,②当直线AC 与⊙O 第二次相切时,设移动时间为t 2,记第一次相切时为位置一,点O 1,A 1,C 1共线时位置二,第二次相切时为位置三,由题意知,从位置一到位置二所用时间与位置二到位置三所用时间相等, ∴+2﹣(2﹣)=t 2﹣(+2),解得:t 2=2+2,综上所述,当d <2时,t 的取值范围是:2﹣<t <2+2.5.解:(1)证明:如图1, ∵CE 为⊙O 的直径, ∴∠CFE=∠CGE=90∵EG⊥EF, ∴∠FEG=90°.∴∠CFE=∠CGE=∠FEG=90°. ∴四边形EFCG 是矩形. (2)①存在. 连接OD ,如图2①, ∵四边形ABCD 是矩形, ∴∠A=∠ADC=90°. ∵点O 是CE 的中点, ∴OD=OC.∴点D 在⊙O 上.∵∠FCE=∠FDE,∠A=∠CFE=90°, ∴△CFE∽△DAB. ∴=()2.∵AD=4,AB=3, ∴BD=5, S △CFE =()2S △DAB=××3×4 =.∴S 矩形ABCD =2S △CFE =.∵四边形EFCG 是矩形,∴FC∥EG.∴∠FCE=∠CEG.∵∠GDC=∠CEG,∠FCE=∠FDE,∴∠GDC=∠FDE.∵∠FDE+∠CDB=90°,∴∠GDC+∠CDB=90°.∴∠GDB=90°Ⅰ.当点E在点A(E′)处时,点F在点B(F′)处,点G在点D(G′处,如图2①所示.此时,CF=CB=4.Ⅱ.当点F在点D(F″)处时,直径F″G″⊥BD,如图2②所示,此时⊙O与射线BD相切,CF=CD=3.Ⅲ.当CF⊥BD时,CF最小,此时点F到达F″′,如图2③所示.S=BC?CD=BD?CF″′.△BCD∴4×3=5×CF″′∴CF″′=.∴≤CF≤4.=,∵S矩形ABCD∴×()2≤S≤×42.矩形ABCD≤12.∴≤S矩形ABCD∴矩形EFCG的面积最大值为12,最小值为.②∵∠GDC=∠FDE=定值,点G的起点为D,终点为G″,∴点G的移动路线是线段DG″.∵∠GDC=∠FDE,∠DCG″=∠A=90°,∴△DCG″∽△DAB.∴=.∴=.∴DG″=.∴点G移动路线的长为.[来6.解:(1)以AB为边,在第一象限内作等边三角形ABC,以点C为圆心,AC为半径作⊙C,交y轴于点P1、P2.在优弧AP1B上任取一点P,如图1,则∠APB=∠ACB=×60°=30°.∴使∠APB=30°的点P有无数个.故答案为:无数.(2)①当点P在y轴的正半轴上时,过点C作CG⊥AB,垂足为G,如图1.∵点A(1,0),点B(5,0),∴OA=1,OB=5.∴AB=4.∵点C为圆心,CG⊥AB,∴AG=BG=AB=2.∴OG=OA+AG=3.∵△ABC是等边三角形,∴AC=BC=AB=4.∴CG===2.∴点C的坐标为(3,2).过点C作CD⊥y轴,垂足为D,连接CP2,如图1,∵点C的坐标为(3,2),∴CD=3,OD=2.∵P 1、P 2是⊙C 与y 轴的交点,∴∠AP 1B=∠AP 2B=30°.∵CP 2=CA=4,CD=3,∴DP 2==.∵点C 为圆心,CD⊥P 1P 2,∴P 1D=P 2D=.∴P 2(0,2﹣).P 1(0,2+).②当点P 在y 轴的负半轴上时,同理可得:P 3(0,﹣2﹣).P 4(0,﹣2+).综上所述:满足条件的点P 的坐标有:(0,2﹣)、(0,2+)、(0,﹣2﹣)、(0,﹣2+).(3)当过点A 、B 的⊙E 与y 轴相切于点P 时,∠APB 最大. ①当点P 在y 轴的正半轴上时,连接EA ,作EH⊥x 轴,垂足为H ,如图2.∵⊙E 与y 轴相切于点P ,∴PE⊥OP∵EH⊥AB,OP⊥OH,∴∠EPO=∠POH=∠EHO=90°.∴四边形OPEH 是矩形.∴OP=EH,PE=OH=3∴EA=3.∵∠EHA=90°,AH=2,EA=3,∴EH===∴OP=∴P(0,).②当点P在y轴的负半轴上时,同理可得:P(0,﹣).理由:①若点P在y轴的正半轴上,在y轴的正半轴上任取一点M(不与点P重合),连接MA,MB,交⊙E于点N,连接NA,如图2所示.∵∠ANB是△AMN的外角,∴∠ANB>∠AMB.∵∠APB=∠ANB,∴∠APB>∠AMB.②若点P在y轴的负半轴上,同理可证得:∠APB>∠AMB.综上所述:当点P在y轴上移动时,∠APB有最大值,此时点P的坐标为(0,)和(0,﹣).7.解答:证明:(1)如图,连接PM,PN,∵⊙P与x轴,y轴分别相切于点M和点N,∴PM⊥MF,PN⊥ON且PM=PN,∴∠PMF=∠PNE=90°且∠NPM=90°,∵PE⊥PF,∠NPE=∠MPF=90°﹣∠MPE,在△PMF和△PNE中,,∴△PMF≌△PNE (ASA),∴PE=PF,(2)解:①当t>1时,点E在y轴的负半轴上,如图,由(1)得△PMF≌△PNE,∴NE=MF=t,PM=PN=1,∴b=OF=OM+MF=1+t,a=NE﹣ON=t﹣1,∴b﹣a=1+t﹣(t﹣1)=2,∴b=2+a,②0<t≤1时,如图2,点E在y轴的正半轴或原点上,同理可证△PMF≌△PNE,∴b=OF=OM+MF=1+t,a=ON﹣NE=1﹣t,∴b+a=1+t+1﹣t=2,∴b=2﹣a,(3)如图3,(Ⅰ)当1<t<2时,∵F(1+t,0),F和F′关于点M对称,∴F′(1﹣t,0)∵经过M、E和F′三点的抛物线的对称轴交x轴于点Q,∴Q(1﹣t,0)∴OQ=1﹣t,由(1)得△PMF≌△PNE∴NE=MF=t,∴OE=t﹣1当△OEQ∽△MPF∴=∴=,解得,t=,当△OEQ∽△MFP时,∴=,=,解得,t=,(Ⅱ)如图4,当t>2时,∵F(1+t,0),F和F′关于点M对称,∴F′(1﹣t,0)∵经过M、E和F′三点的抛物线的对称轴交x轴于点Q,∴Q(1﹣t,0)∴OQ =t﹣1,由(1)得△PMF≌△PNE∴NE=MF=t,∴OE=t﹣1当△OEQ∽△MPF ∴=∴=,无解,当△OEQ∽△MFP 时,∴=,=,解得,t =2±,所以当t =,t =,t =2±时,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似.8.答::(1)∵DF⊥AB,EF⊥AC,∴∠BDF=∠CEF=90°.∵△ABC为等边三角形,∴∠B=∠C=60°.∵∠BDF=∠CEF,∠B=∠C,∴△BDF∽△CEF.(2)∵∠BDF=90°,∠B=60°,∴sin60°==,cos60°==.∵BF=m,∴DF=m,BD=.∵AB=4,∴AD=4﹣.∴S△ADF=ADDF=×(4﹣)×m=﹣m2+m.同理:S△AEF=AEEF=×(4﹣)×(4﹣m)=﹣m2+2.∴S=S△ADF+S△AEF=﹣m2+m+2=﹣(m2﹣4m﹣8)=﹣(m﹣2)2+3.其中0<m<4.∵﹣<0,0<2<4,∴当m=2时,S取最大值,最大值为3.∴S与m之间的函数关系为:S═﹣(m﹣2)2+3(其中0<m<4).当m=2时,S取到最大值,最大值为3.(3)如图2,∵A、D、F、E四点共圆,∴∠EDF=∠EAF.∵∠ADF=∠AEF=90°,∴AF是此圆的直径.∵tan∠EDF=,∴tan∠EAF=.∴=.∵∠C=60°,∴=tan60°=.设EC=x,则EF=x,EA=2x.∵AC=a,∴2x+x=A.∴x=.∴EF=,AE=.∵∠AEF=90°,∴AF==.∴此圆直径长为.9.解答:解:(1)连接OA,过点B作BH⊥AC,垂足为H,如图1所示.∵AB与⊙O相切于点A,∴OA⊥AB.∴∠OAB=90°.∵OQ=QB=1,∴OA=1.∴AB===.∵△ABC是等边三角形,∴AC=AB=,∠CAB=60°.∵sin∠HAB=,∴HB=AB?sin∠HAB=×=.∴S△ABC=AC?BH=××=.∴△ABC的面积为.(2)①当点A与点Q重合时,线段AB与圆O只有一个公共点,此时α=0°;②当线段A1B所在的直线与圆O相切时,如图2所示,线段A1B与圆O只有一个公共点,此时OA1⊥BA1,OA1=1,OB=2,∴cos∠A1OB==.∴∠A1OB=60°.∴当线段AB与圆O只有一个公共点(即A点)时,α的范围为:0°≤α≤60°.(3)连接MQ,如图3所示.∵PQ是⊙O的直径,∴∠PMQ=90°.∵OA⊥PM,∴∠PDO=90°.∴∠PDO=∠PMQ.∴△PDO∽△PMQ.∴==∵PO=OQ=PQ.∴PD=PM,OD=MQ.同理:MQ=AO,BM=AB.∵AO=1,∴MQ=.∴OD=.∵∠PDO=90°,PO=1,OD=,∴PD=.∴PM=.∴DM=.∵∠ADM=90°,AD=A0﹣OD=,∴AM===.∵△ABC是等边三角形,∴AC=AB=BC,∠CAB=60°.∵BM=AB,∴AM=BM.∴CM⊥AB.∵AM=,∴BM=,AB=.∴AC=.∴CM===.∴CM的长度为.10.解答:(1)证明:∵CD是⊙O的直径,∴∠DFC=90°,∵四边形ABCD是平行四边形,∴∠A=∠C,AD∥BC,∴∠ADF=∠DFC=90°,∵DE为⊙O的切线,∴DE⊥DC,∴∠EDC=90°,∴∠ADF=∠EDC=90°,∴∠ADE=∠CDF,∵∠A=∠C,∴△ADE∽△CDE;(2)解:∵CF:FB=1:2,∴设CF=x,FB=2x,则BC=3x,∵AE=3EB,∴设EB=y,则AE=3y,AB=4y,∵四边形ABCD是平行四边形,∴AD=BC=3x,AB=DC=4y,∵△ADE∽△CDF,∴=,∴=,∵x、y均为正数,∴x=2y,∴BC=6y,CF=2y,在Rt△DFC中,∠DFC=90°,由勾股定理得:DF===2y,∴⊙O的面积为π(DC)2=πDC2=π(4y)2=4πy2,四边形ABCD的面积为BCDF=6y2y=12y2,∴⊙O与四边形ABCD的面积之比为4πy2:12y2=π:3.11.(1)证明:∵,∴∠DPF=180°﹣∠APD=180°﹣所对的圆周角=180°﹣所对的圆周角=所对的圆周角=∠APC.在△PAC和△PDF中,,∴△PAC∽△PDF.(2)解:如图1,连接PO,则由,有PO⊥AB,且∠PAB=45°,△APO、△AEF都为等腰直角三角形.在Rt△ABC中,∵AC=2BC,∴AB2=BC2+AC2=5BC2,∵AB=5,∴BC=,∴AC=2,∴CE=ACsin∠BAC=AC=2=2,AE=ACcos∠BAC=AC=2=4,∵△AEF为等腰直角三角形,∴EF=AE=4,∴FD=FC+CD=(EF﹣CE)+2CE=EF+CE=4+2=6.∵△APO为等腰直角三角形,AO=?AB=,∴AP=.∵△PDF∽△PAC,∴,∴,∴PD=.(3)解:如图2,过点G作GH⊥AB,交AC于H,连接HB,以HB为直径作圆,连接CG并延长交⊙O于Q,∵HC⊥CB,GH⊥GB,∴C、G都在以HB为直径的圆上,∴∠HBG=∠ACQ,∵C、D关于AB对称,G在AB上,∴Q、P关于AB对称,∴,∴∠PCA=∠ACQ,∴∠HBG=∠PCA.∵△PAC∽△PDF,∴∠PCA=∠PFD=∠AFD,∴y=tan∠AFD=tan∠PCA=tan∠HBG=.∵HG=tan∠HAGAG=tan∠BACAG==,∴y==x.12. 解答:解:(1)证明:连接OH,如图①所示.∵四边形ABCD是矩形,∴∠ADC=∠BAD=90°,BC=AD,AB=CD.∵HP∥AB,∴∠ANH+∠BAD=180°.∴∠ANH=90°.∴HN=PN=HP=.∵OH=OA=,∴sin∠HON==.∴∠HON=60°∵BD与⊙O相切于点H,∴OH⊥BD.∴∠HDO=30°.∴OD=2.∴AD=3.∴BC=3.∵∠BAD=90°,∠BDA=30°.∴tan∠BDA===.∴AB=3.∵HP=3,∴AB=HP.∵AB∥HP,∴四边形ABHP是平行四边形.∵∠BAD=90°,AM是⊙O的直径,∴BA与⊙O相切于点A.∵BD与⊙O相切于点H,∴BA=BH.∴平行四边形ABHP是菱形.(2)△EFG的直角顶点G能落在⊙O上.如图②所示,点G落到AD上.∵EF∥BD,∴∠FEC=∠CDB.∵∠CDB=90°﹣30°=60°,∴∠CEF=60°.由折叠可得:∠GEF=∠CEF=60°.∴∠GED=60°.∵CE=x,∴GE=CE=x.ED=DC﹣CE=3﹣x.∴cos∠GED===.∴x=2.∴GE=2,ED=1.∴GD=.∴OG=AD﹣AO﹣GD=3﹣﹣=.∴OG=OM.∴点G与点M重合.此时△EFG的直角顶点G落在⊙O上,对应的x的值为2.∴当△EFG的直角顶点G落在⊙O上时,对应的x的值为2.(3)①如图①,在Rt△EGF中,tan∠FEG===.∴FG=x.∴S=GEFG=x x=x2.②如图③,ED=3﹣x,RE=2ED=6﹣2x,GR=GE﹣ER=x﹣(6﹣2x)=3x﹣6.∵tan∠SRG===,∴SG=(x﹣2).∴S△SGR=SGRG=(x﹣2)(3x﹣6).=(x﹣2)2.∵S△GEF=x2,∴S=S△GEF ﹣S△SGR=x2﹣(x﹣2)2.=﹣x2+6x﹣6.综上所述:当0≤x≤2时,S=x2;当2<x≤3时,S=﹣x2+6x﹣6.当FG与⊙O相切于点T时,延长FG交AD于点Q,过点F作FK⊥AD,垂足为K,如图④所示.∵四边形ABCD是矩形,∴BC∥AD,∠ABC=∠BAD=90°∴∠AQF=∠CFG=60°.∵OT=,∴OQ=2.∴AQ=+2.∵∠FKA=∠ABC=∠BAD=90°,∴四边形ABFK是矩形.∴FK=AB=3,AK=BF=3﹣x.∴KQ=AQ﹣AK=(+2)﹣(3﹣x)=2﹣2+x.在Rt△FKQ中,tan∠FQK==.∴FK=QK.∴3=(2﹣2+x).解得:x=3﹣.∵0≤3﹣≤2,∴S=x2=×(3﹣)2=﹣6.∴FG与⊙O相切时,S的值为﹣6.13解答:(1)证明:连结OC、OE,OE交AB于H,如图1,∵E是弧AB的中点,∴OE⊥AB,∴∠EHF=90°,∴∠HEF+∠HFE=90°,而∠HFE=∠CFD,∴∠HEF+∠CFD=90°,∵DC=DF,∴∠CFD=∠DCF,而OC=OE,∴∠OCE=∠OEC,∴∠OCE+∠DCE=∠HEF+∠CFD=90°,∴OC⊥CD,∴直线DC与⊙O相切;(2)解:连结BC,∵E是弧AB的中点,∴弧AE=弧BE,∴∠ABE=∠BCE,而∠FEB=∠BEC,∴△EBF∽△ECB,∴EF:BE=BE:EC,∴EF?EC=BE2=(r)2=r2;(3)解:如图2,连结OA,∵弧AE=弧BE,∴AE=BE=r,设OH=x,则HE=r﹣x,在Rt△OAH中,AH2+OH2=OA2,即AH2+x2=r2,在Rt△EAH中,AH2+EH2=EA2,即AH2+(r﹣x)2=(r)2,∴x2﹣(r﹣x)2=r2﹣(r)2,即得x=r,∴HE=r﹣r=r,在Rt△OAH中,AH===,∵OE⊥AB,∴AH=BH,而F是AB的四等分点,∴HF=AH=,在Rt△EFH中,EF===r,∵EF?EC=r2,∴r?EC=r2,∴EC=r.14. 解:(1)连结O1A、O2B,如图,设⊙O1的半径为r,⊙O2的半径为R,∵⊙O1与⊙O2外切与点D,∴直线O1O2过点D,∴MO2=MD+O2D=4+R,∵直线l与两圆分别相切于点A、B,∴O1A⊥AB,O2B⊥AB,∵tan∠AM01=,∴∠AM01=30°,在Rt△MBO2中,MO2=O2B=2R,∴4+R=2R,解得R=4,即⊙O2的半径为4;(2)∵∠AM02=30°,∴∠MO2B=60°,而O2B=O2D,∴△O2BD为等边三角形,∴BD=O2B=4,∠DBO2=60°,∴∠ABD=30°,∵∠AM01=30°,∴∠MO1A=60°,而O1A=O1D,∴∠O1AD=∠O1DA,∴∠O1AD=∠MO1A=30°,∴∠DAB=60°,∴∠ADB=180°﹣30°﹣60°=90°,在Rt△ABD中,AD=BD=4,AB=2AD=8,∴△ADB内切圆的半径===2﹣2,∴△ADB内切圆的面积=π(2﹣2)2=(16﹣8)π;(3)存在.在Rt△MBO2中,MB=O2B=×4=12,当△MO2P∽△MDB时,=,即=,解得O2P=8;当△MO2P∽△MBD时,=,即=,解得O2P=8,综上所述,满足条件的O2P的长为8或8.15.解:(1)连接PA,如图1所示.∵PO⊥AD,∴AO=DO.∵AD=2,∴OA=.∵点P坐标为(﹣1,0),∴OP=1.∴PA==2.∴BP=CP=2.∴B(﹣3,0),C(1,0).(2)连接AP,延长AP交⊙P于点M,连接MB、MC.如图2所示,线段MB、MC即为所求作.四边形ACMB是矩形.理由如下:∵△MCB由△ABC绕点P旋转180°所得,∴四边形ACMB是平行四边形.∵BC是⊙P的直径,∴∠CAB=90°.∴平行四边形ACMB是矩形.过点M作MH⊥BC,垂足为H,如图2所示.在△MHP和△AOP中,∵∠MHP=∠AOP,∠HPM=∠OPA,MP=AP,∴△MHP≌△AOP.∴MH=OA=,PH=PO=1.∴OH=2.∴点M的坐标为(﹣2,).(3)在旋转过程中∠MQG的大小不变.∵四边形ACMB是矩形,∴∠BMC=90°.∵EG⊥BO,∴∠BGE=90°.∴∠BMC=∠BGE=90°.∵点Q是BE的中点,∴QM=QE=QB=QG.∴点E、M、B、G在以点Q为圆心,QB为半径的圆上,如图3所示.∴∠MQG=2∠MBG.∵∠COA=90°,OC=1,OA=,∴tan∠OCA==.∴∠OCA=60°.∴∠MBC=∠BCA=60°.∴∠MQG=120°.∴在旋转过程中∠MQG的大小不变,始终等于120°.16.解:(1)如图1,∵AB是⊙O的直径,∴∠AEB=90°.∴AE⊥BC.(2)如图1,∵BF与⊙O相切,∴∠ABF=90°.∴∠CBF=90°﹣∠ABE=∠BAE.∵∠BAF=2∠CBF.∴∠BAF=2∠BAE.∴∠BAE=∠CAE.∴∠CBF=∠CAE.∵CG⊥BF,AE⊥BC,∴∠CGB=∠AEC=90°.∵∠CBF=∠CAE,∠CGB=∠AEC,∴△BCG∽△ACE.(3)连接BD,如图2所示.∵∠DAE=∠DBE,∠DAE=∠CBF,∴∠DBE=∠CBF.∵AB是⊙O的直径,∴∠ADB=90°.∴BD⊥AF.∵∠DBC=∠CBF,BD⊥AF,CG⊥BF,∴CD=CG.∵∠F=60°,GF=1,∠CGF=90°,∴tan∠F==CG=tan60°=∵CG=,∴CD=.∵∠AFB=60°,∠ABF=90°,∴∠BAF=30°.∵∠ADB=90°,∠BAF=30°,∴AB=2BD.∵∠BAE=∠CAE,∠AEB=∠AEC,∴∠ABE=∠ACE.∴AB=AC.设⊙O的半径为r,则AC=AB=2r,BD=r.∵∠ADB=90°,∴AD=r.∴DC=AC﹣AD=2r﹣r=(2﹣)r=.∴r=2+3.∴⊙O的半径长为2+3.17.解答:解:(1)当k=1时,抛物线解析式为y=x 2﹣1,直线解析式为y=x+1.联立两个解析式,得:x 2﹣1=x+1,解得:x=﹣1或x=2,当x=﹣1时,y=x+1=0;当x=2时,y=x+1=3,∴A(﹣1,0),B (2,3).(2)设P (x ,x 2﹣1).如答图2所示,过点P 作PF∥y 轴,交直线AB 于点F ,则F (x ,x+1).∴PF=y F ﹣y P =(x+1)﹣(x 2﹣1)=﹣x 2+x+2.S △ABP =S △PFA +S △PFB =PF (xF ﹣xA )+PF (xB ﹣xF )=PF (xB ﹣xA )=PF ∴S△ABP=(﹣x 2+x+2)=﹣(x ﹣)2+当x=时,yP=x2﹣1=﹣.∴△ABP面积最大值为,此时点P坐标为(,﹣).(3)设直线AB:y=kx+1与x轴、y轴分别交于点E、F,则E(﹣,0),F(0,1),OE=,OF=1.在Rt△EOF中,由勾股定理得:EF==.令y=x2+(k﹣1)x﹣k=0,即(x+k)(x﹣1)=0,解得:x=﹣k或x=1.∴C(﹣k,0),OC=k.假设存在唯一一点Q,使得∠OQC=90°,如答图3所示,则以OC为直径的圆与直线AB相切于点Q,根据圆周角定理,此时∠OQC=90°.设点N为OC中点,连接NQ,则NQ⊥EF,NQ=CN=ON=.∴EN=OE﹣ON=﹣.∵∠NEQ=∠FEO,∠EQN=∠EOF=90°,∴△EQN∽△EOF,∴,即:,解得:k=±, ∵k>0, ∴k=.∴存在唯一一点Q ,使得∠OQC=90°,此时k=.18. 解:(1)设抛物线为y=a (x ﹣4)2﹣1,∵抛物线经过点A (0,3),∴3=a(0﹣4)2﹣1,; ∴抛物线为;(3分)(2)相交.证明:连接CE ,则CE⊥BD, 当时,x 1=2,x 2=6.A (0,3),B (2,0),C (6,0),对称轴x=4,∴OB=2,AB==,BC=4,∵AB⊥BD,∴∠OAB+∠OBA=90°,∠OBA+∠EBC=90°,∴△AOB∽△BEC, ∴=,即=,解得CE=, ∵>2, ∴抛物线的对称轴l 与⊙C 相交.(7分)(3)如图,过点P 作平行于y 轴的直线交AC 于点Q ;可求出AC 的解析式为;(8分)设P 点的坐标为(m ,), 则Q 点的坐标为(m ,);∴PQ=﹣m+3﹣(m 2﹣2m+3)=﹣m 2+m .∵S △PAC =S △PAQ +S △PCQ =×(﹣m 2+m )×6=﹣(m ﹣3)2+;∴当m=3时,△PAC 的面积最大为;此时,P点的坐标为(3,).(10分)19、【解】:(1)如图1,设⊙O与AB、BC、CA的切点分别为D、E、F,连接OD、OE、OF,则AD=AF,BD=BE,CE=CF.∵⊙O为△ABC的内切圆,∴OF⊥AC,OE⊥BC,即∠OFC=∠OEC=90°.∵∠C=90°,∴四边形CEOF是矩形,∵OE=OF,∴四边形CEOF是正方形.设⊙O的半径为rcm,则FC=EC=OE=rcm,在Rt△ABC中,∠ACB=90°,AC=4cm,BC=3cm,∴AB==5cm.∵AD=AF=AC﹣FC=4﹣r,BD=BE=BC﹣EC=3﹣r,∴4﹣r+3﹣r=5,解得r=1,即⊙O的半径为1cm.(2)如图2,过点P作PG⊥BC,垂直为G.∵∠PGB=∠C=90°,∴PG∥AC.∴△PBG∽△ABC,∴.∵BP=t,∴PG=,BG=.若⊙P与⊙O相切,则可分为两种情况,⊙P与⊙O外切,⊙P与⊙O内切.①当⊙P与⊙O外切时,如图3,连接OP,则OP=1+t,过点P作PH⊥OE,垂足为H.∵∠PHE=∠HEG=∠PGE=90°,∴四边形PHEG是矩形,∴HE=PG,PH=CE,∴OH=OE﹣HE=1﹣,PH=GE=BC﹣EC﹣BG=3﹣1﹣=2﹣.在Rt△OPH中,由勾股定理,,解得t=.②当⊙P与⊙O内切时,如图4,连接OP,则OP=t﹣1,过点O作OM⊥PG,垂足为M.∵∠MGE=∠OEG=∠OMG=90°,∴四边形OEGM是矩形,∴MG=OE,OM=EG,∴PM=PG﹣MG=,OM=EG=BC﹣EC﹣BG=3﹣1﹣=2﹣,在Rt△OPM中,由勾股定理,,解得t=2.综上所述,⊙P与⊙O相切时,t=s或t=2s.20.:(1)如图2,连接OA、OB、OC、OD.∵S=S△AOB+S△BOC+S△COD+S△AOD=+++=,∴r=.(2)如图3,过点D作DE⊥AB于E,∵梯形ABCD为等腰梯形,∴AE===5,∴EB=AB﹣AE=21﹣5=16.在Rt△AED中,∵AD=13,AE=5,∴DE=12,∴DB==20.∵S△ABD===126,S△CDB===66,∴===.。
