哈工大结构动力学作业-威尔逊-θ法
哈工大机械原理大作业——连杆机构运动分析16___2014

Harbin Institute of Technology机械原理大作业——连杆机构运动分析课程名称:机械原理院系:能源科学与工程学院班级:完成者:学号:题号: 16任课教师:丁刚完成内容:在完成题目计算要求的同时,扩展了内容,程序为该结构的通用程序,可解决机构在不同条件下的运动情况,文本最末为几种情况的分析哈尔滨工业大学16、如图所示机构,已知机构各构件的尺寸为,试求构件5的角位移、角速度和角加速度,并对计算结构进行分析。
(1)、结构分析从侧面看原机构为此机构分为级杆组(原动件1),级杆组RRP(2号套筒、3号杆),级杆组RRP(4号套筒、5号杆)(2)、建立坐标系(3)、各个杆组的运动分析采用逆推法,从RRP杆组(4号套筒、5号杆)开始分析已知,,,,现在假定已知,,其中,,,即消去,可得可求得,也可以通过书上3-23式求得通过正弦定理可求得再来看看角速度关系对于加速度,有如下关系其中到此4、5杆就分析完毕了,别忘记之前的假设,我假设了已知,,为求,,,现在来分析RRP杆组(2号套筒、3号杆)已知,,,已知,,,,其中,,,即消去,可得反解,即可求得,也可以通过书上3-23式求得通过正弦定理可求得继续,我们来看看角速度关系对于加速度,有如下关系其中现在,只需将所求得的,,和,,关联起来这是同一根杆,,,现在来看,,,由题目得,,和是未知的,但不影响整体,不然给一个初值,,当然,这是可以随意更改的。
基于以上的基本原理,matlab R2012b程序如下syms theta theta1 theta2 lamuda lamuda1 lamuda2 sigma sigma1 sigma2 beta beta1 beta2 l1 l11 l2 l21 t output itheta1=10;theta2=0;i=0;for theta3=60:420theta=theta3/180*pi;beta=asin((100/200)*sin(theta))+theta;l1=0.2*sin(beta)/sin(theta);beta1=(-theta1*(l1*sin(theta))*sin(theta)+theta1*(l1*cos(theta))*cos(theta))/(0.2*(sin(theta)*sin(b eta)+cos(theta)*cos(beta)));l11=-(theta1*(l1*sin(theta))*l1*cos(beta)+theta1*(l1*cos(theta))*l1*sin(beta))/(0.2*(sin(theta)*si n(beta)+cos(theta)*cos(beta)));C=(theta1^2)*0.2*cos(beta)-theta2*l1*sin(theta)-(theta1^2)*l1*cos(theta)-2*l11*theta1*sin(theta) ;D=(theta1^2)*0.2*cos(beta)+theta2*l1*sin(theta)-(theta1^2)*l1*cos(theta)+2*l11*theta1*sin(thet a);beta2=(-C*sin(theta)+D*cos(theta))/(0.2*(sin(theta)*sin(beta)+cos(theta)*cos(beta)));lamuda=beta-pi/2;lamuda1=beta1;lamuda2=beta2;sigma=asin((100/200)*sin(lamuda))+lamuda;l2=0.2*sin(sigma)/sin(lamuda);sigma1=(-lamuda1*(l2*sin(lamuda))*sin(lamuda)+lamuda1*(l2*cos(lamuda))*cos(lamuda))/(0.2 *(sin(lamuda)*sin(sigma)+cos(lamuda)*cos(sigma)));l21=-(lamuda1*(l2*sin(lamuda))*l2*cos(sigma)+lamuda1*(l2*cos(lamuda))*l2*sin(sigma))/(0.2* (sin(lamuda)*sin(sigma)+cos(lamuda)*cos(sigma)));A=(lamuda1^2)*0.2*cos(sigma)-lamuda2*l2*sin(lamuda)-(lamuda1^2)*l2*cos(lamuda)-2*l21*la muda1*sin(lamuda);B=(lamuda1^2)*0.2*cos(sigma)+lamuda2*l2*sin(lamuda)-(lamuda1^2)*l2*cos(lamuda)+2*l21*l amuda1*sin(lamuda);sigma2=(-A*sin(lamuda)+B*cos(lamuda))/(0.2*(sin(lamuda)*sin(sigma)+cos(lamuda)*cos(sigma )));i=i+1;output(i,1)=fix(theta/pi*180);output(i,2)=fix(sigma/pi*180);output(i,3)=fix(sigma1);output(i,4)=fix(sigma2);endoutputa=output(:,1);b=output(:,2);c=output(:,3);d=output(:,4);h1=plot(a,b);hold on;h2=plot(a,c);hold on;h3=plot(a,d);hold on;set(h1,'color',[1 0 0],'linewidth',2);set(h2,'color',[0 1 1],'linewidth',1);set(h3,'color',[0 0 1],'linewidth',2);m=legend('角位移','角速度','角加速度');x label('θ');title('平面连杆机构运动分析');figure;h1=plot(a,b);hold on;x label('θ');ylabel('角位移');title('平面连杆机构运动角度——角位移图');figure;h2=plot(a,c);hold on;x label('θ');ylabel('角速度');title('平面连杆机构运动角度——角速度图'); figure;h3=plot(a,d);hold on;x label('θ');ylabel('角加速度');title('平面连杆机构运动角度——角加速度图');汇总图各自的图像结果分析,上面的图形只是在一个初值,的条件下得出的,为了能解决所有问题,修改程序如下syms theta theta1 theta2 lamuda lamuda1 lamuda2 sigma sigma1 sigma2 beta beta1 beta2 l1 l11 l2 l21 t output iprompt={'输入:', '输入' ,'输入' };%设置提示字符串name='输入初值';%设置标题 numlines=1;%指定输入数据的行数 defAns={'60','10','0'};%设定默认值 Resize='on';%设定对话框尺寸可调节answer=inputdlg(prompt,name,numlines,defAns,'on');%创建输入对话框 h= str2num(answer{1}); theta1= str2num(answer{2}); theta2= str2num(answer{3}); i=0;for theta3=h:(360+h) theta=theta3/180*pi;beta=asin((100/200)*sin(theta))+theta; l1=0.2*sin(beta)/sin(theta);beta1=(-theta1*(l1*sin(theta))*sin(theta)+theta1*(l1*cos(theta))*cos(theta))/(0.2*(sin(theta)*sin(b eta)+cos(theta)*cos(beta)));l11=-(theta1*(l1*sin(theta))*l1*cos(beta)+theta1*(l1*cos(theta))*l1*sin(beta))/(0.2*(sin(theta)*si n(beta)+cos(theta)*cos(beta)));C=(theta1^2)*0.2*cos(beta)-theta2*l1*sin(theta)-(theta1^2)*l1*cos(theta)-2*l11*theta1*sin(theta) ;D=(theta1^2)*0.2*cos(beta)+theta2*l1*sin(theta)-(theta1^2)*l1*cos(theta)+2*l11*theta1*sin(thet a);beta2=(-C*sin(theta)+D*cos(theta))/(0.2*(sin(theta)*sin(beta)+cos(theta)*cos(beta)));lamuda=beta-pi/2;lamuda1=beta1;lamuda2=beta2;sigma=asin((100/200)*sin(lamuda))+lamuda;l2=0.2*sin(sigma)/sin(lamuda);sigma1=(-lamuda1*(l2*sin(lamuda))*sin(lamuda)+lamuda1*(l2*cos(lamuda))*cos(lamuda))/(0.2 *(sin(lamuda)*sin(sigma)+cos(lamuda)*cos(sigma)));l21=-(lamuda1*(l2*sin(lamuda))*l2*cos(sigma)+lamuda1*(l2*cos(lamuda))*l2*sin(sigma))/(0.2* (sin(lamuda)*sin(sigma)+cos(lamuda)*cos(sigma)));A=(lamuda1^2)*0.2*cos(sigma)-lamuda2*l2*sin(lamuda)-(lamuda1^2)*l2*cos(lamuda)-2*l21*la muda1*sin(lamuda);B=(lamuda1^2)*0.2*cos(sigma)+lamuda2*l2*sin(lamuda)-(lamuda1^2)*l2*cos(lamuda)+2*l21*l amuda1*sin(lamuda);sigma2=(-A*sin(lamuda)+B*cos(lamuda))/(0.2*(sin(lamuda)*sin(sigma)+cos(lamuda)*cos(sigma )));i=i+1;output(i,1)=fix(theta/pi*180);output(i,2)=fix(sigma/pi*180);output(i,3)=fix(sigma1);output(i,4)=fix(sigma2);endoutputa=output(:,1);b=output(:,2);c=output(:,3);d=output(:,4);h1=plot(a,b);hold on;h2=plot(a,c);hold on;h3=plot(a,d);hold on;set(h1,'color',[1 0 0],'linewidth',2);set(h2,'color',[0 1 1],'linewidth',1);set(h3,'color',[0 0 1],'linewidth',2);m=legend('角位移','角速度','角加速度');x label('θ');title('平面连杆机构运动分析');figure;h1=plot(a,b);hold on;xlabel('θ');y label('角位移');title('平面连杆机构运动角度——角位移图');figure;h2=plot(a,c);hold on;xlabel('θ');y label('角速度');title('平面连杆机构运动角度——角速度图');figure;h3=plot(a,d);hol d on;xlabel('θ');y label('角加速度');title('平面连杆机构运动角度——角加速度图');这样,在运行程序时就会弹出一个如下图所示的对话框,可以任意给定初值,解决不同问题。
哈尔滨工业大学 结构力学II 第二套张金生 结构动力学-9

1 T 2 最大动能为 Ti max X i m X i i 2 1 T 最大势能为 U i max X i k X i 2 Ti max U i max 由能量守恒,有
mN
y N (t )
X T k X i i i2 X T mX i i
2
5.04 1 m 4 9.08 归一化 X 1.8 k 2.24 11.22
1
4.667 m 8.334 归一化 k 10.334 4.99 m 8.98 归一化 k 11.19
k
k
1.取自重引起的位移 y1 3mg / k y2 y1 2mg / k 5mg / k
mg
mg
y1
y3 y1 mg / k 6mg / k
3 X 1 5 精确解: 2 6 1 0.198k / m T X 1 k X 1 2 1 0.445 k / m 1 T X 1 mX 1 14k 0.2k / m 1 0.447 k / m 70m
X n D n 1 n 一直算到 X 与 X 成比例为止. X n 为基本振型. 这时下式成立 1 n 1 n n X DX X 2
1
X
基本频率由下式计算
令பைடு நூலகம்
X 2 mX D m ---动力矩阵 1 X DX ---标准特征值问题 2
j
1 2 j
( a b 2 ) j
例.求图示体系的正交阻尼矩阵 c 和阻尼比 3 . 已知: 1 2 0.05
m m
k k
3 2 1
哈工大结构动力学作业-威尔逊-θ法

结构动力学大作业(威尔逊- 法)姓名:学号:班级:专业:威尔逊—θ法原理及应用【摘要】在求解单自由度体系振动方程时我们用了常加速度法及线加速度法等数值分析方法。
在多自由度体系中,也有类似求解方法,即中心差分法及威尔逊—θ法。
实际上后两种方法也能求解单自由度体系振动方程。
对于数值方法,有三个重要要求:收敛性、稳定性及精度。
本文推导了威尔逊-θ法的公式,并利用MATLAB 编程来研究单自由度体系的动力特性。
【关键词】威尔逊—θ法 冲击荷载 阻尼比【正文】威尔逊-θ法可以很方便的求解任意荷载作用下单自由度体系振动问题。
实际上,当 1.37θ>时,威尔逊—θ法是无条件收敛的. 一、威尔逊—θ法的原理威尔逊-θ法是线性加速度法的一种拓展(当1θ=时,两者相同),其基本思路和实现方法是求出在时间段[],t t t θ+∆时刻的运动,其中1θ≥,然后通过内插得到i t t +∆时刻的运动(见图 1。
1)。
图 1。
11、公式推导推导由t 时刻的状态求t t θ+∆时刻的状态的递推公式:{}{}{}{})(t t t t t yy t y y -∆+=∆++θτθτ对τ积分{}{}{}{}{})(22t t t t t t yy t y y y-∆++=∆++θτθττ{}{}{}{}{}{})(6232t t t t t t t yy t y y y y -∆+++=∆++θτθτττt ∆=θτ{}{}{}{}{})(21t t t t t t t yy t y t y y -∆+∆+=∆+∆+θθθθ{}{}{}{}{})2(6)(2t t t t t tt yy t y t y y +∆+∆+=∆+∆+θθθθ {}{}{}{}{}t t t t t t t y y t y y t y26)()(62-∆--∆=∆+∆+θθθθ{}{}{}{}{}t t t t t t t yty y y t y22)(3∆---∆=∆+∆+θθθθ[]{}[]{}[]{}{}P y k y C ym =++ []{}[]{}[]{}{}t t t t t t t t P y k y C y m ∆+∆+∆+∆+=++θθθθ[]{}{}t t tt R y k ∆+∆+=θθ[][][][]c tm t k k ∆+∆+=θθ3)(62[]{}{}{}[]{}{}{}[]{}{}{})223()26)(6()(2t tt t t t t tt ty ty y t c y y t y t m P P P R ∆++∆++∆+∆+-+=∆+θθθθθ2、MA TLAB 源程序: clc;clear;K=input (’请输入结构刚度k (N/m )'); M=input ('请输入质量(kg )');C=input (’请输入阻尼(N *s/m )'); t=sym (’t ’);%产生符号对象t Pt=input(’请输入荷载);Tp=input (’请输入荷载加载时长(s)'); Tu=input ('请输入需要计算的时间长度(s ) ’); dt=input ('请输入积分步长(s)'); Sita=input('请输入θ’);uds=0:dt:Tu;%确定各积分步时刻pds=0:dt:Tp;Lu=length(uds);Lp=length(pds);if isa(Pt,'sym')%荷载为函数P=subs(Pt,t,uds); %将荷载在各时间步离散if Lu〉LpP(Lp+1:Lu)=0;endelseif isnumeric(Pt)%荷载为散点if Lu〈=LpP=Pt(1:Lu);elseP(1:Lp)=Pt;P(Lp+1:Lu)=0;endendy=zeros(1,Lu);%给位移矩阵分配空间y1=zeros(1,Lu);%给速度矩阵分配空间y2=zeros(1,Lu);%给加速度矩阵分配空间pp=zeros(1,Lu-1);%给广义力矩阵分配空间yy=zeros(1,Lu-1);%给y(t+theta*t)矩阵分配FF=zeros(1,Lu);%给内力矩阵分配空间y(1)=input('请输入初位移(m)’);y1(1)=input(’请输入初速度(m/s)');%——-—-——-———--———--初始计算-—-—------———————--——--——y2(1)=(P(1)—C*y1(1)-K*y(1))/M;%初始加速度FF(1)=P(1)-M*y2(1);l=6/(Sita*dt)^2;q=3/(Sita*dt);r=6/(Sita*dt);s=Sita*dt/2;for z=1:Lu—1kk=K+l*M+q*C;pp(z)=P(z)+Sita*(P(z+1)—P(z))+(l*y(z)+r*y1(z)+2*y2(z))*M+(q*y(z)+2*y1(z)+s*y2(z))*C;yy(z)=pp(z)/kk;y2(z+1)=l/Sita*(yy(z)—y(z))-l*dt*y1(z)+(1-3/Sita)*y2(z);y1(z+1)=y1(z)+dt/2*(y2(z+1)+y2(zp));y(z+1)=y(z)+y1(z)*dt+dt*dt/6*(y2(z+1)+2*y2(z));FF(z+1)=P(z+1)—M*y2(z+1);endplot (uds ,y ,’r ’),xlabel('时间 t ’),ylabel('位移 y ’),title ('位移图形’) 二、利用威尔逊-θ法求冲击荷载下的结构反应1、矩形脉冲研究不同时长脉冲作用下,体系振动位移。
中心差分法、纽马克法和威尔逊-θ法与精确解的误差分析

中心差分法、纽马克法和威尔逊-θ法与精确解的误差分析作者:于津津贾慧敏宋敏来源:《教育周报·教育论坛》2018年第05期摘要:在动荷载作用下的物体位移、速度和加速度的计算中,中心差分法、纽马克法和威尔逊-θ法三类方法都是可取的,为结构动力学的理论研究提供了参考。
但三类方法与精确值之间均存在一定的误差,本文基于这一问题进行研究和计算,通过图表展示这三类方法与精确值之间的关系。
关键词:结构动力学;中心差分法;纽马克法;威尔逊-θ法一、引言:结构动响应的数值计算问题,主要针对多自由或者连续体经过空间散离后建立的二阶常微分方程组形式的运动控制方程:[M] {¨x}+[ C] {﹒x}+[ K ]{x}=Q ;;(1)为了探究三种方法相较于精确解的误差,用如下具体问题进行具体分析。
如图1所示,该体系在冲击荷载 p(t)=[0 10]T 作用下,求该体系的位移反应表达式,质量单位Kg,弹簧k单位N/cm。
另:自由振动的周期T1=4.45,T2=2.8,使用中心差分法计算,取时间步长Δt=0.1,T2=0.28,并假定X0=0;V0=0试计算这个系统在前12个时间步长的反应。
取δ=0.25,γ=0.5,用纽马克法计算该系统的动力反应。
取θ=1.4,用威尔逊-θ法计算该系统的反应。
二、计算方法简介1、精确解计算根据精确解的计算公式可得:X1(t)=1-5/3×cos(2^0.5×t)+2/3×cos(5^0.5×t)X2(t);=3-5/3×cos(2^0.5×t)-4/3×cos(5^0.5×t)速度的计算公式为位移的导数,加速度的公式为速度的导数。
(下同)2、中心差分法用位移向前一步的差分表示的速度后一步的差分表示的速度的平均来确定当前时刻的速度,得到以当前时刻t为中心的前后时刻位移的差分表示的速度,即:若:x=x0-1/(2×a1)×d x0+1/(2×a0)×d2x0; ;x1(t)=x0(1);x2(t)=x0(2);3、纽马克法当在t时刻的响应{x}t,{﹒x}t,{¨x}t,已知时,要求下一时刻t+Δt的响应值{x} t+Δt,{﹒x} t+Δt,{¨x} t+Δt,令在待求时刻动力学方程成立,即:{﹒x} t+Δt={﹒x}t+Δt(1-γ){¨x} t +γΔt{¨x} t+Δt ;;(2){x} t+Δt={x}t+{﹒x}tΔt+(0.5-δ){¨x} tΔt^2+δ{¨x} t+ΔtΔt^2 ;(3)β,γ为按积分精度和稳定性要求而确定的参数,由式3可解得:1/{¨X}t+Δt;=βΔt 2({X}t+Δt -{x}t)-βΔt ×1/{﹒x}t-(2β-1) ×1/{¨x}t ;;(4)将(4)带入(2)得:{﹒x}t+Δt =γ/βΔt 2×({x}t+Δt -{x}t)+(1 –γ/β){﹒x}t +(1 -1/2β)t{¨x}t ;;(5){x}t +Δt 可由t +Δt 时刻的运动方程求得,即:[M]{¨X}t+Δt +[C]{¨X}t +Δt +[K]{X}t +Δt =[F] t +Δt ;;(6)將式(4)、式(5)代入式(6),可求得求得{X}t+Δt,后求{﹒X}t +Δt 和{¨X}t +Δt。
哈工大结构动力学张金生老师讲稿-4
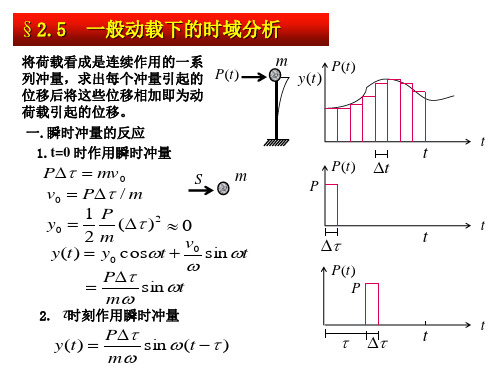
& v 0 = y ( t1 ) = 0
y ( t ) = y 0 cos ω t =
π
2
y st cos ω t
最大位移反应
T t 1 > ( β < 1) 2
最大位移反应发生于第一阶段; 最大位移反应发生于第一阶段;
T t 1 < ( β > 1) 2
最大位移反应发生于第二阶段; 最大位移反应发生于第二阶段;
一. 矩形脉冲 1. 位移反应
P(t )
m
y (t )
P(t )
荷载离开前 ( 0 ≤ t ≤ t1 ) t P y (t ) = ∫ sin ω ( t − τ ) d τ 0 mω = y st (1 − cos ω t )
= y st µ 1 ( t )
k
P
t
t1
2
µ 1 ( t ) = 1 − cos ω t = 2 sin
y(t) = Ae
−ξωt
P(τ ) −ξω (t −τ ) sin( ωDt +ϕ) + ∫ e sinωD (t −τ )dτ 0m ωD
t
§2.6 冲击荷载的动力反应
冲击荷载的特点---作用时间短。 冲击荷载的特点---作用时间短。 ---作用时间短 结构动力反应的特点---最大反应出现快、荷载消失前 结构动力反应的特点---最大反应出现快、 ---最大反应出现快 后反应不同。 后反应不同。 计算特点: 计算特点: 不计阻尼; 1. 不计阻尼; 要考虑瞬态振动; 2. 要考虑瞬态振动; 3. 要分析荷载消失前后两种状态
f = 1/ k
---柔度系数 ---柔度系数
PE = Pt 1ω
---冲量等效荷载 ---冲量等效荷载
【哈工大 结构动力学】SD 第10章 多自由度体系2020

11
以上分析方法就是代数方程中的特征值分析,自振频率相应 于特征值,而振型即是特征向量。
得到体系的N 个自振频率和振型后,可以把振型和自振频率
分别写成矩阵的形式,
1 2 N
1 0 0
0
2
0
或
1,2,3
T
n
jqj(t)
j
2.0jjqj(t )
j
2 j
qj(t
)
T j
M
Mj
I
ug(t )
振型分解法仅需知道各振型阻尼比 ξ,不需要知道阻尼矩阵[C]
定义振型参与系数γj
j
jT M I
Mj
jT M I jT M j
基本性质
[] 1
两边同时除以振型参与系数γj ,得到:(j=1,2,…N)
得到三个根 :
B1 0.3515, B2 1.6066, B3 3.5420
利用关系式
Bn n2 600
可得结构的三个自振频率:
12 210.88
1 14.522
22 963.96 2 31.048 (rad / s)
32 2125.20
3 46.100
19
算例10-1
求振型 : (K n 2 M ) n 0
7
将位移向量{u}和加速度向量{ü}代入无阻尼自由振动方程:
u 2 sin( t ) u s in ( t )
M u K u 0
( 2 M K ) sin( t ) 0
因为sin(ωt+θ)为任意的,可以消去,因此,
(K 2 M ) 0
上式是关于{φ}的N阶齐次线性方程组,表征了振型和自振
结构动力学哈工大版课后习题解答

第一章 单自由度系统1.1 总结求单自由度系统固有频率的方法和步骤。
单自由度系统固有频率求法有: 牛顿第二定律法、动量距定理法、拉格朗日方程法和能量守恒定理法。
1. 牛顿第二定律法适用范围: 所有的单自由度系统的振动。
解题步骤: (1) 对系统进行受力分析,得到系统所受的合力;(2) 利用牛顿第二定律∑=F x m,得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根, 得到该系统的固有频率。
2. 动量距定理法适用范围: 绕定轴转动的单自由度系统的振动。
解题步骤: (1) 对系统进行受力分析和动量距分析;(2) 利用动量距定理J ∑=M θ,得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根, 得到该系统的固有频率。
3. 拉格朗日方程法:适用范围: 所有的单自由度系统的振动。
解题步骤: (1)设系统的广义坐标为 , 写出系统对于坐标 的动能T 和势能U 的表达式;进一步写求出拉格朗日函数的表达式: L=T-U ;(2)由格朗日方程 =0, 得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根, 得到该系统的固有频率。
4. 能量守恒定理法适用范围: 所有无阻尼的单自由度保守系统的振动。
解题步骤: (1)对系统进行运动分析、选广义坐标、写出在该坐标下系统的动能T 和势能U 的表达式;进一步写出机械能守恒定理的表达式 T+U=Const (2)将能量守恒定理T+U=Const 对时间求导得零,即 , 进一步得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根, 得到该系统的固有频率。
1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。
用衰减法求单自由度系统阻尼比的方法有两个: 衰减曲线法和共振法。
方法一: 衰减曲线法。
求解步骤:(1)利用试验测得单自由度系统的衰减振动曲线, 并测得周期和相邻波峰和波谷的幅值 、 。
(2)由对数衰减率定义 , 进一步推导有,因为 较小, 所以有πδζ2=。
哈尔滨工业大学结构动力学PPT课件

x0 x0 , x0 x0 xt c1n cosnt c2n sinnt
c1 x0 n , c2 x0
第36页/共42页
x
t
x0
n
sin nt
x0
cos nt
令
x0 cos n
, x0 sin
则可化为
其中:
xt sinnt
2
x02
x0
n
tg x0n arctg x0n
T1
1 2
l 0
d
l
2
x2
1 2
(1 3
l)x2
1 m1 23
x2TΒιβλιοθήκη T1Tm1 2
m1 3
m
x2
1 2
meq x2
又因为: 弹簧的势能与弹簧质量无关, 则
V 1 kx2 2
由能量法,可得
meq x kx 0 弹性元件质量不能忽略时,利用等
效质量,将质量折算到质量块上, 弹性元件仍看作无质量的。
• 18世纪线性振动理论成熟期。
第11页/共42页
• 19世纪非线性振动理论,各种工程实际结构振动的近似 求解方法。
• 20世纪50年代初由于航空航天工程的发展,原本确定性 理论无法解释包含随机变化的工程问题,发展了随机振 动理论。
• 20世纪后期计算机技术的飞速发展,数值计算方法和理 论成为主要研究方法之一。
第7页/共42页
三、结构动力学研究的内容
结构动力学就是研究结构系统在激励力作用下产生的响 应规律的科学,研究激励力、结构和响应三者关系的科 学。
现代结构动力学主要研究以下三个方面的内容 第一类问题:响应分析(结构动力计算)
输入 (动力荷载)
哈工大研究生课程-高等结构动力学-第三章2

解:选用广义坐标 x 和
T
V
1 2
1 2
Mx
2
2
1 2
2 2 2 2 m [( x l co s ) l sin ]
K x m g l (1 co s )
对于线性系统运动,运动是微幅的 代入动能和势能:
1 x M m T 2 m l
x1 x2
2
A1
(i)
i 1
2
1 ( i ) sin ( it i ) u2
A1 sin ( it i )
(i) i
x u
i 1
u1 u2
(1)
(1)
u1
(2)
u i
振型,主振型也称为主模态。
u1 1 (i) (i ) u2 u2
3
2
2 10
3
A1 0 3 2 2 1 0 1 0 .2 2 A 2 2 10
11 16 11
17 11 9
设 q
l
3
768EI
则有
0 1 0 0 0 1
K
1
1 M m 0 0
23 1 22
9 22 23
V V0
( q
i 1
n
V
i
) qi
0
1
( q q 2
i 1 j 1 i
n
n
V
2
)0 qi q j
j
为势能在平衡位置处的大小,(0)0表示(0) 在平衡位置处的值。
基于Wilson-θ和Newmark-β法的非线性动力学方程改进算法

基于Wilson-θ和Newmark-β法的非线性动力学方程改进算法刘广;刘济科;陈衍茂【摘要】When using Wilson-θ or Newmark-β method to solve nonlinear dynamic equations,usually,we rewrite the equations in the form of incremental equilibrium equations.The coefficient matrix has to be updated in each integral step according to the state variables.In essence,this procedure is to linearize the considered nonlinear system in a single time step.It is usually difficult,however,to handle some strongly nonlinear problems with multiple-degrees-of-freedom.By using an incremental process,in the paper a new fast algorithm was proposed based on Wilson-θ method or Newmark-β method.According to the obtained solution at one time point,we present an initial guessed solution at the next time instant.Then the guessed solution can converge to the true solution via iterative corrections.Numerical examples show that,using the presented fast algorithm together with Wilson-θ method or Newmark-β method,one can get highly accurate solutions.Moreover,the presented algorithm can provide us with a simple way to adjust the convergence as necessary.As the presented methods avoid linearization of the considered nonlinear dynamic systems,they are not only more applicable but also more computationally efficient.%Wilson-θ法和Newmark-β法是非线性动力学方程求解的常用方法.它们的一个基本步骤是,将方程改写为增量平衡的形式,在每一个积分步长内用状态参量修正平衡方程的系数矩阵,其本质是在单个步长内对系统的非线性环节进行了线性化处理.本文基于增量思想分别改进了Wilson-θ法和Newmark-β法,根据即时解给出下一步的猜测解,然后对猜测解进行迭代校正,最终得到收敛的近似解.算例表明,改进算法的精度更高,且收敛准则简单.更为重要的是,本文方法无须对非线性项进行线性化处理,因而计算效率更高,适应范围更广.【期刊名称】《计算力学学报》【年(卷),期】2017(034)004【总页数】7页(P433-439)【关键词】Wilson-θ法;Newmark-β法;非线性动力学方程;猜测解;迭代校正【作者】刘广;刘济科;陈衍茂【作者单位】中山大学力学系,广州 510275;中山大学力学系,广州 510275;中山大学力学系,广州 510275【正文语种】中文【中图分类】O322Wilson-θ 法和 Newmark-β 法都是动力学方程数值计算常用的经典方法[1-5]。
多自由度体系wilson-θ法程序编写

多自由度体系wilson-θ法程序编写多自由度体系Wilson-θ法是一种广泛应用于多体动力学和结构动力学领域的数值计算方法。
本文将介绍如何使用Python编程语言编写多自由度体系Wilson-θ法的程序。
一、引言多自由度体系Wilson-θ法是一种基于有限元法的数值计算方法,适用于求解多体动力学和结构动力学中的问题。
该方法通过将体系分解为一系列有限元子系统,并采用θ矩阵方法进行求解,能够有效地处理大规模的多自由度体系。
二、程序编写1. 导入必要的库和模块在编写程序之前,需要导入必要的库和模块,包括numpy、scipy 和matplotlib等。
这些库提供了必要的数学运算、数值分析和图形绘制等功能。
2. 定义体系结构和有限元节点首先需要定义多自由度体系的结构和有限元节点的位置。
可以使用网格划分工具将体系划分为有限元网格,并定义每个节点的位置和编号。
3. 构建有限元矩阵和求解器使用Wilson-θ法进行数值计算,需要构建有限元矩阵和求解器。
该矩阵可以采用三角矩阵的形式进行表示,并使用θ矩阵方法进行求解。
在程序中,需要实现矩阵的构建、求解器的初始化等操作。
4. 迭代求解体系响应使用构建好的矩阵和求解器,可以进行迭代求解多自由度体系的响应。
在每次迭代中,需要输入当前时刻的体系响应作为初值,并输出下一时刻的响应结果。
5. 结果可视化最后,可以使用matplotlib等库将求解得到的响应结果进行可视化。
可以将时间历程、振型、频率响应等结果进行绘制,以便更好地分析体系的动态特性。
三、示例代码以下是一个简单的示例代码,用于演示如何使用Python编程语言编写多自由度体系Wilson-θ法的程序。
代码中假设体系由3个自由度的弹簧-质量系统组成,采用三角形矩阵进行求解。
```pythonimport numpy as npfrom scipy.sparse import csc_matrix, dia_matriximport matplotlib.pyplot as plt# 定义体系结构和有限元节点nodes = np.array([[0], [0.5], [1]]) # 节点位置数组degrees_of_freedom = 3 # 自由度数量system_size = len(nodes) # 体系大小node_indices = np.arange(system_size) # 节点编号数组# 构建有限元矩阵和求解器theta_matrix = csc_matrix(dia_matrix(system_size - degrees_of_freedom, 0)) # θ矩阵mass_matrix = csc_matrix(np.diag([0.5, 0.5, 1])) # 质量矩阵solution = np.zeros((system_size, degrees_of_freedom)) # 初始响应数组forces = np.zeros((system_size, degrees_of_freedom)) # 输出力数组forces[:degrees_of_freedom] = np.zeros((system_size, degrees_of_freedom)) # 初始输出力数组为零向量solver = theta_matrix.dot(solution) +theta_matrix.dot(forces) + mass_matrix # 初始化求解器theta_vector = np.zeros(system_size) # θ向量用于控制有限元矩阵的构造和更新# 进行迭代求解体系响应for iteration in range(100): # 迭代次数限制为100次response = solver.dot(theta_vector) # 输入当前时刻的响应作为初值进行迭代求解下一时刻的响应结果输出为力向量output_forces在每个节点上作用在体系的上结果可与theta向量用于控制有限元矩阵的构造和更新为了演示程序的基本结构和流程以上给出了一个简单的示例代码其中包含的主要内容有定义体系结构和有限元节点构建有限元矩阵和求解器以及进行迭代求解体系响应结果可视化等当然在实际应用中可能还需要考虑更多的因素例如如何处理边界条件如何处理体系的非线性特性等等因此在实际应用中需要根据具体问题对程序进行适当的修改和优化以下是一些可能需要的注意事项和技巧:1. 选择合适的有限元网格划分工具和算法,以确保计算的精度和效率。
结构力学(I)-04-3 结构静力分析篇(力矩分配法)@@

C C1
பைடு நூலகம்
2ql
ql2/4 ql2/64 B 1 ql2/16 A C A 3ql2/64
µ
MF
分配 传递
0 0 0
1/4 -1/4 -1/8
3 32
11 32
0
3 64
3 64
0
−
−
3 16
− 1 16
9 64
1 64
3 64
3 64
M
11ql2/32
M
所得结果是 近似解吗? 近似解吗
哈工大 土木工程学院
可避免解联立方程 不需要求出角位移 计算程式简单机械
哈工大 土木工程学院
2 / 31
第四章 超静定结构受力分析
一. 基本概念
远端支撑 固定 铰支 滑动 转动刚度S 转动刚度 4i 3i i 传递系数C 传递系数 1/2 0 -1
θ =1
θ =1
θ =1
4i
2i
3i
哈工大 土木工程学院
i
3 / 31
哈工大 土木工程学院
9 / 31
第四章 超静定结构受力分析
例题:用力矩分配法求图示结构弯矩图。 例题:用力矩分配法求图示结构弯矩图。 固定状态: 固定状态:
M
F AB
q = 12kN/m
1 2 = ql = 100 kN ⋅ m 12
A
ql 2/12
EI
B
EI
C
M
F BA
= −100 kN ⋅ m
A EI=1 3m A 3m 160kN B EI=1 6m B 3m E C 3m 160kN EI=1 3m D
3m 160kN
3m
结构动力学数值积分方法-wilson

(10)
求解(10)式,得到位移 u t t 。然后采用(6)式计算得到加速度 a t t 。
a t t
6
t
2
6 u t t u t t v t 2a t
(11)
将加速度 a t t 代入到(1)式中,并令 t ,可以计算出加速度 a t t 。
其中,激振力可以用下式表达。
p t t p t p t t p t
(8)
(9)
由振动控制方程得到关于 u t t 表达式如下:
6m 3c k u t t 2 t t p t p t t p t 6 6 t 3 m u t v t 2 a t u t 2v t a t c 2 t 2 t t
2.5 2 1.5 1 0.5 0 -0.5 -1 -1.5 -2 -2.5
0
1
2
3
4
5
6
7
8
9
3/3
西安交大 航天学院 仲继泽(hnskzjz@)
结构动力学数值积分方法(Wilson-θ) 及其 Matlab 实现
Xjtu-Zjz
Wilson-θ 方法是线性加速度方法的一种拓展。 假设加速度在时间段 t , t t 内线性变化,首先计算时刻 t t 的位移,然后通过内插得到 t t 时刻的位移 (u)、速度(v)及加速度(a)。其中 1 ,相关研究证明, 1.37 时,Wilson-θ 方法 是无条件稳定的。一般情况下,取 1.4 (至于为什么,本人没有做深入的研究)。 Wilson-θ 方法理论推导如下: 记 t 为时间段 t , t t 内的任一时刻,对于一个单自由度振动系统来说, 其初始时刻 t 的位移 u t 、速度 v t 及加速度 a t 为已知量,其 t 时刻的加速 度可以用 t 时刻和 t t 时刻的加速度线性表达,见下式。
哈工大威海理论力学学习课件配哈工大第七版动力学引言

刚体的平面运动微分方程
动能ቤተ መጻሕፍቲ ባይዱ理,机械能守恒定律
动静法——达朗贝尔原理
虚位移原理
动
力
学
动力学:研究物体的机械运动与作用力之间的关系。
空气动力学
结构动力学
动力学
超高速碰撞动力学
动力学的抽象模型
质点:具有一定质量而几何形状和尺寸大小可 忽略不计的物体。
质点动力学
质点系:由几个或无限个相互有联系的质点组 成的系统。
质点系动力学
刚体:特殊质点系,其中任意两点之间的距离 保持不变。
本篇的基本内容
哈工大研究生课程-高等结构动力学-第四章2

§4.4 梁的弯曲振动
常见的约束状况与边界条件
(1)固定端
y ( x, t ) 0
挠度和截面转角为零
y ( x, t ) x 0
x0 或 l
( x) 0
( x ) 0
(2)简支端
y ( x, t ) 0
挠度和弯矩为零
M EI y ( x, t)
2
x
2
0
dx
x
[G J p
( x, t ) x
]d x
得:
Jp
( x, t )
2
t
2
GJ p
2
( x, t )
2
x
2
2
设c
G
则有:
n
c
( x, t) t
c
2
( x, t)
2
x
2
它的解为
c :表示剪切波在杆内的传播速度
x B co s
i
i (x)
无穷多个
第 i 阶主振动: y ( i ) ( x , t ) a i i ( x ) sin( i t i )
a i 和 i 由系统的初始条件确定
系统的自由振动是无穷多个主振动的叠加:
y ( x, t )
a
i i 1
i
( x ) sin( i t i )
2 2
x
[ EI
y ( x, t)
2
x
2
] S
y ( x, t)
2
t
2
f ( x, t )
x
m ( x, t)
哈工大结构动力学第六讲

k ( y)
m( y) y(t ) c( y) y(t ) k ( y)y(t ) Fp (t )
或
m( y) u g (t )
----非线性体系的增量方程 观察增量方程与上图, 给出与线性体系比较的结论 当Δt足够小时, 上面割线的斜率可用切线斜率来代替, 既有:
例2. 用线加速度法计算此题.
§5.3 多自由度体系的逐步积分法-线加速度法 既可以用于线性体系, 又可以用于非线性体系. 它也是处理 耦合的线性振型方程的有效方法.
(T 5c)
(6) 按 y(t ) (K * )1 Fp* (t ) 计算第一步增量位移 y (t )
(7) 将增量位移代入式 (T 4), 计算增量速度 y (t )
3 1 y (t ) ( y (t ) y (t ) t y (t ) t 2 ) t 6
要求: 1. 手算两步; 2. CAI作业; 3. 通过CAI中例题,体现精度、收敛性、稳定性问题。
5.2.5 算例
例1. 用线加速度法计算体系的反应. 手算前两步. 对照电算结果检查对错.
Fp (t )
m 0.2k s 2 /m
c=0.4kN· s/m
K=8kN/m
Fs ( y)
Fs ( y) [8 y 4(2 y / 3)3 ] kN
或
m(t ) u g (t )
5.2.2 单自由度体系非线性运动的线加速度法
基本假设: 设体系加速度在[t+Δt]间隔内线性变化, 既有:
y (t ) y (t )
线加速度逐步积分基本公式推导: (1)对(T-1)式积分, 得: (2)由(T-2)第二式, 得:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
